Finding the spatial co-variation of brain deformation with principal component analysis

Abstract

Objective:

Strain and strain rate are effective traumatic brain injury metrics. In finite element (FE) head model, thousands of elements were used to represent the spatial distribution of these metrics. Owing that these metrics are resulted from brain inertia, their spatial distribution can be represented in more concise pattern. Since head kinematic features and brain deformation vary largely across head impact types [1], we applied principal component analysis (PCA) to find the spatial co-variation of injury metrics (maximum principal strain (MPS), MPS rate (MPSR) and MPS×MPSR) in four impact types: simulation, football, mixed martial arts and car crashes, and used the PCA to find patterns in these metrics and improve the machine learning head model (MLHM).

Methods:

We applied PCA to decompose the injury metrics for all impacts in each impact type, and investigate the spatial co-variation using the first principal component (PC1). Furthermore, we developed a MLHM to predict PC1 and then inverse-transform to predict for all brain elements. The accuracy, the model complexity and the size of training dataset of PCA-MLHM are compared with previous MLHM [2].

Results:

PC1 explained > 80% variance on the datasets. Based on PC1 coefficients, the corpus callosum and midbrain exhibit high variance on all datasets. Finally, the PCA-MLHM reduced model parameters by 74% with a similar MPS estimation accuracy.

Conclusion:

The brain injury metric in a dataset can be decomposed into mean components and PC1 with high explained variance.

Significance:

The spatial co-variation analysis enables better interpretation of the patterns in brain injury metrics. It also improves the efficiency of MLHM.

I. Introduction

Traumatic brain injury (TBI) is a major public health concern globally. Approximately, there are more than 55 million prevalent TBI cases, and over 20 million new cases of TBI are estimated to occur in developed countries annually [3]. Each year, more than 1 million people suffer TBI in the United States alone [4]. The onsets of TBI can be attributed to head impacts from multiple sources, including but not limited to accidental falls, traffic accidents, blasts, various contact sports, and domestic abuse [5]–[9]. While single-incidence TBI can immediately cause loss of consciousness and disabilities, repetitive incidence of milder TBI can also lead to long-term cognitive deficits, and even neurodegenerative diseases and chronic traumatic encephalopathy in some cases [10], [11].

Recently, with the development of finite element head models (FEHMs), deformation-based injury metrics such as maximal principal strain (MPS), MPS rate (MPSR) and MPS×MPSR have been proposed to detect TBI for better protection and prevention [2], [12]–[15]. Physiologically, in head impact, the acceleration and deceleration of the head result in brain deformation because of brain inertia. Based on the measured head kinematics, FEHMs calculate injury metrics at every elements. High magnitudes of injury metrics are correlated with multiple TBI pathologies, such as traumatic axonal injury (TAI) and blood-brain-barrier disruption [13]–[20], and the 95th percentile of metrics across all elements were used to represent the risk of TBI [21], [22]. Because the whole-brain deformation are caused by the inertia associated with the head kinematics and the kinematics features in a certain type of head impacts share similar characteristics [1], we hypothesize that spatial co-variations of the injury metrics exist among brain elements for a type of head impact. To investigate the co-variations of injury metrics, we applied Principal Component Analysis (PCA) to MPS, MPSR and MPS×MPSR and studied how many principal components, which are spatial pattern in this study, are needed to represent the these injury metrics at thousands of elements.

PCA is a tool to reduce dimensions and identify the dominating component of dataset. It applies linear projection to find the axes with the highest co-variation among coordinates. Besides decomposition on brain injury metrics, PCA was used to boost the size of head impact dataset by simulating kinematics with the principal components [23]. Outside the TBI field, PCA has been used in risk management of portfolios, sensor-based pattern recognition and visualization of high-dimensional data [24], [25].

Based on the PCA results for four types of head impacts (head model simulations, college football, mixed martial arts and racing car crashes), we found that the first principal component (PC1) can explain more than 80% variance of injury metrics in every head impact dataset. As results, the spatial distribution of injury metrics for a type of head impact can be represented by the mean component (PC0) and PC1: brain regions with high PC0 values have high injury metrics in average, while brain regions with high PC1 have high variability across head impacts and may bear high deformation. In the previous studies, the brain deformation at specific brain regions have been investigated because of the different susceptibilities to injury. For example, high strain and strain rate at corpus callosum, a large bundle of axonal fibers connecting two brain hemispheres, were found in mTBI [8], [26], [27], and were correlated with the neuro-structure changes [28], [29]. Therefore, the corpus callosum has been considered as a sub-region of brain where strain and strain rate were used as the predictor of TBI [21], [30]. Because of the relatively high stiffness, falx cerebri displacement in lateral and horizontal impacts was found to result in high strain at corpus callosum and brain-stem [27], [31]. Similarly, higher cumulative stain damage measure (CSDM) of corpus callosum and thalamus were observed in lateral and horizontal head impacts, while this was not found for the whole brain and basal ganglia [32]. Besides corpus callosum, the strain, strain rate and stress at brain regions such as brain-stem, mid-brain were investigated and correlated with TBI [31], [33]. MPS and maximum axonal strain (MAS) at white matter, corpus callosum, brain-stem, hippocampus and thalamus calculated by a customized detail head model were compared in coronal head rotation [34].

As more than 80% of variance in MPS, MPSR and MPS×MPSR can be explained by PC1, the injury metrics can be decomposed into PC0 and PC1. This simplification can benefit the development of the machine learning head model (MLHM) [2], [35], [36], which rapidly predicts the injury metrics, by allowing using simpler network structure and fewer training data. MLHM was firstly presented to predict 95% MPS and MAS at corpus callosum and white matter [35], then the models to predict the MPS over the whole brain were developed [2], [36]. To achieve higher accuracy, complex network structure is needed to learn the brain physics and therefore more training data are required. By applying PCA and developing MLHM to predict one variable (the value on PC1) for each impact, the model complexity can be reduced significantly and fewer training data are needed. In TBI studies, besides MLHM, machine learning was used to detect the false triggering events [37], [38], and a feature matrix based on fiber strain was proposed as a brain injury criterion [39]. Furthermore, an approach to find the kinematics that yield similar level of brain strain was proposed by combing MLHM and pre-computed atlas brain model [40].

In this paper, we firstly present PCA on three brain injury metrics (MPS, MPSR and MPS×MPSR) in four head impact datasets (HM, CF, MMA, NASCAR) and show that PC1 can explain more than 80% of co-variance. Secondly, we analyze the patterns of PC0 and PC1 of different injury metrics at different brain regions. Then, because PCA is able to decompose the injury metrics and reduce the variables that MLHM need to predict, we develop PCA-MLHM which can achieve similar accuracy with simpler network structure and smaller training dataset compared with previous MLHMs [2].

II. Methods

A. Datasets: head kinematics and brain finite element model

Noticing the distinctive characteristics of head kinematics and injury metrics in different types of head impacts [1], [21], we included 3,161 impacts in four datasets of head impacts: 1) 2,130 impacts simulated by FE models of a Hybrid III headform and neck [41] impacted by a pneumatic linear impactor (labeled as HM for head model); 2) 302 college football impacts measured by the Stanford Instrumented Mouthguard (CF) [42], [43]; 3) 457 mixed martial arts impacts measured by the Stanford Instrumented Mouthguard (MMA) [9], [44]; 4) 272 reconstructed impacts using a FE model of a Hybrid III dummy body and measured car dynamics from the National Association for Stock Car Auto Racing (NASCAR) [45].

A finite element model of the human head was used to calculate the brain strain and strain rate. Since the brain is deformed by its own inertia, the skull of FE models was assumed to be rigid and moved according to the collected head kinematics. In this study, we used the KTH FE model (Stockholm, Sweden) [12]. With 4,124 brain elements, the KTH FE model models the brain, skull, scalp, meninges, falx, tentorium, subarachnoid cerebrospinal fluid (CSF), ventricles, and 11 pairs of the largest bridging veins. The model has been validated by the experimental data of brain-skull relative motion [46], intracranial pressure [46], and brain strain [47]. In this study, the MPS and MPSR for each of the 4,124 brain elements were calculated by the KTH model. As a result, the entire datasets can be represented by three 3,161 × 4,124 matrices for MPS, MPSR and MPS×MPSR respectively. The distribution of the MPS and MPSR modeled by KTH FE model for these datasets is shown in Fig. 1.

Fig. 1.

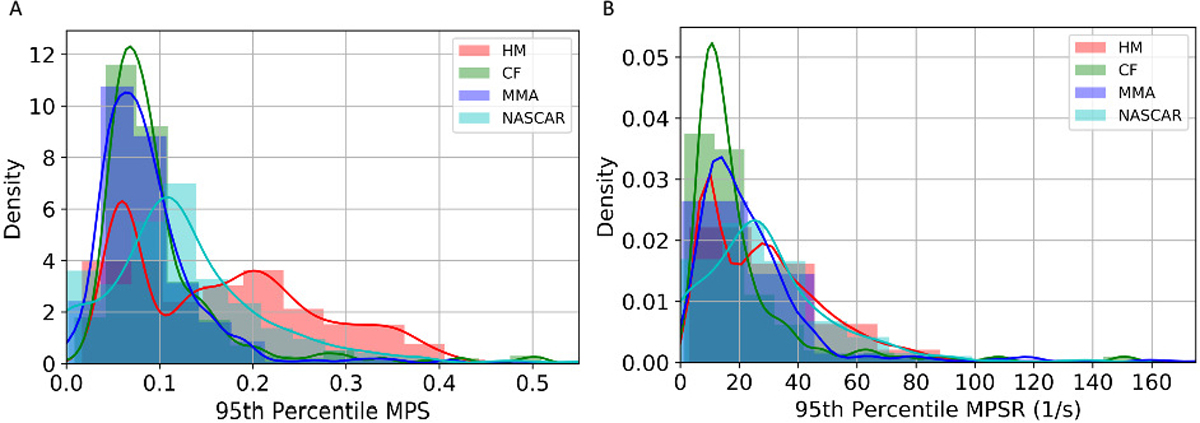
The distribution of 95th percentile MPS (A) and 95th percentile MPSR (B) across different head impact datasets.

B. Finding spatial co-variation with principal component analysis

To find the spatial co-variation and the potential reduced-order representation of the whole-brain injury metrics for a specific dataset, we leveraged the principal component analysis (PCA), an unsupervised dimensionality reduction method with co-variation analysis. PCA finds the reduced-order representation of data by finding the directions where the variance is maximized. In this study, each impact of the four datasets can be denoted as $x^{\overrightarrow{(i)}}$; i = 1, 2, ..., n, $x^{\overrightarrow{(i)}}\in {\mathrm{IR}}^{4124}$ where n is the number of impacts for a specific dataset (e.g., n = 302 for dataset CF). To begin with, the data were centered by removing the mean vector: ${\tilde{x}}^{(i)}=x^{\overrightarrow{(i)}}-\overrightarrow{\mu }$, where $\overrightarrow{\mu }\in {\mathrm{IR}}^{4124}$ is the mean vector across different samples in a specific dataset. The mean vector represents the center of the distribution of a particular impact dataset and injury metric, which was regarded as principal component zero (PC0) in this study. In order to find the set of basis vectors $\overrightarrow{v_1},\overrightarrow{v_2},\dots ,\overrightarrow{v_k}\in {\mathrm{IR}}^{4124}$, k < 4124, where the data resolved onto the directions represented by the basis vectors are with the highest variance, singular value decomposition (SVD) is performed on the data matrix $\text{X}$:

$$\tilde{\text{X}}=\text{U}\times \mathrm{\Sigma }\times {\text{V}}^T$$ (1)

Upon ranking the singular values from large to small, the associated vectors $\overrightarrow{v_1},\overrightarrow{v_2},\dots ,\overrightarrow{v_k}\in {\mathrm{IR}}^{4124}$, k < 4124 in V represent the projection directions with the widest data spread (i.e., highest variance). These vectors are also referred to as the principal components (PCs) or the PC coefficients. The transformed low-dimensional data along each direction: $\overrightarrow{{\alpha }_1},\overrightarrow{{\alpha }_2},\dots ,\overrightarrow{{\alpha }_k}\in {\mathrm{IR}}^{\text{n}}$ can be computed by solving the following optimization problem:

$${\mathrm{argmin}}_{\overrightarrow{{\alpha }_1},\overrightarrow{{\alpha }_2},\dots ,\overrightarrow{{\alpha }_k}}{\Vert \tilde{\text{X}}-{\mathrm{\Sigma }}_j^k\overrightarrow{{\alpha }_j}\times {\overrightarrow{v_j}}^T\Vert }^2$$ (2)

This results in the projection of the high-dimensional data onto these basis vectors: $\overrightarrow{{\alpha }_j}=<\overrightarrow{v_j},\tilde{X}>$. With PCA, we can reduce the dimensionality of the data from 4124-D to k-D. To determine how many orders suffice, we calculated the explained variance (R²) with varying values of k. Upon determining k, the brain injury metric matrices can be compressed from n × 4124 matrices to n × k matrices. With the PCA, the reduced-order approximation of the original data matrix X can be represented as:

$$\text{X}=\overrightarrow{1}\times {\overrightarrow{\mu }}^T+{\mathrm{\Sigma }}_j^k\overrightarrow{{\alpha }_j}\times {\overrightarrow{v_j}}^T$$ (3)

where the $\overrightarrow{1}\in {\mathrm{IR}}^{\mathrm{n}}$ denotes a vector with ones as its elements. The first term in this approximation equation denotes the PC0 contributions to the injury metrics. For each dataset, we found that PC1 can explain more than 80% variations among impacts, which means that the distribution of metrics can be represented by PC0 and PC1 (See Results Section). Therefore, the injury metrics can be decomposed into PC0 and PC1. In a specific brain region, if more of the injury metrics are contributed by PC0, which is the mean across the dataset, the injury metrics in this region are more consistent across impacts. Vice versa, if more injury metrics are contributed by PC1, larger differences of injury metrics in this region can be found across the impacts. To compare the contribution of the components to different injury metrics at specific brain regions, we define the contribution ratio as:

$${\text{c}}_i={\mathrm{mean}}_j\left(\frac{P(i,j)}{T(i,j)}\right),i=1,2,\dots ,n$$ (4)

where P(i, j) denotes the injury metric of the i-th impact and j-th brain element that is contributed by a principal component (PC0, PC1, PC2, etc.) and T(i, j) denotes the reference injury metric of the i-th impact and j-th brain element given by the KTH FE model (MPS, MPSR, MPS×MPSR). The contribution ratios are averaged over the elements in the brain regions including brainstem (BS), corpus callosum (CC), cerebellum (CL), gray matter (GM), midbrain (MB), thalamus (TH) and white matter (WM). According to (3), the P(i, j) from all PCs adds up to T(i, j). Furthermore, subgroups of interest were selected to compare the contribution ratios of components in the impacts with high injury metrics in the dataset. Considering the subgroup should represent the high injury metric impacts of the dataset while not be influenced by extremely high impacts, we selected the top 5% when all the impacts in the dataset were ranked by the 95th percentile of injury metrics. It should be noted that this subgroup has the highest injury metric in the dataset, which did not necessarily suggested that these head impact led to injury. Additionally, since the contribution of components are normalized by the reference, the contribution ratio can be compared across different injury metrics.

C. Application in machine learning head models

State-of-the-art FE simulations cannot provide real-time monitoring of injury metrics, while MLHMs can approximate FEHMs to compute injury metrics such as MPS, MPSR and MPS×MPSR [2]. However, the MLHMs, with thousands of output units for the brain elements, require large quantities of training data. The decomposition of injury metrics with PCA can reduce the dimensionality of the output and therefore simplify the training objective in the development of MLHMs. To verify this, we leveraged the PCA models to get the low-dimensional injury metrics representations, developed PCA-MLHMs to predict the value on the k PCs based on 510 kinematics features [48] (with k determined in the first results section), and reconstructed whole-brain MPS, MPSR and MPS×MPSR with the accuracy evaluated.

The 510 kinematics features were extracted from the four types of kinematics describing head movement: linear acceleration at the head center of gravity a(t), angular velocity ω(t), angular acceleration α(t) and angular jerk j(t). Among them, a(t) and ω(t) were measured by the sensors while α(t) and j(t) were calculated from ω(t) with a five-point stencil numerical derivative equation. The features include both the temporal features such as the maximum values, and the spectral densities within 19 frequency windows, because these features were found to show high predictability of brain strain and strain rate in our previous work [2].

The PCA-MLHM was developed on two datasets: 1) dataset HM: the 2,130 head model simulated impacts, and 2) dataset MIX: the mixture of all four datasets with 3,161 impacts. To develop the models, we firstly partitioned the datasets into a training set (70%), a validation set (15%) and a test set (15%), according to the same protocol mentioned in our previous studies [2]. The training set was used to train the model parameters, the validation set was used to tune the hyperparameters (such as the number of neurons in each layer, the number of epochs to train the models), and the test set was used to evaluate the model accuracy. In order to get robust results, we randomly partitioned the datasets 20 times and did 20 parallel experiments.

Then, we trained the PCA dimensionality reduction model on the training set and recorded PC0 and the principal components (PC1, PC2, ..., PCk). A five-layer deep neural network (besides the input and output layers) was developed to learn the mapping from the kinematics features to the values on the k principal components. The second and the fourth layers were the dropout layers with a dropout rate of 0.5. L2 regularization was used to further regularize the models and avoid overfitting. To further optimize the accuracy, we adopted the data augmentation strategy: adding slight Gaussian noises to generate shadow samples [2], [49], [50].

Upon training the model, in the prediction stage, we reconstructed the 4124-D MPS, MPSR and MPS×MPSR by taking the inverse-transform on the predicted values on the k PCs. To evaluate the model accuracy, we calculated the mean absolute errors (MAE) and coefficient of determination (R²) between the predicted MPS/MPSR/MPS×MPSR and the reference values given by the KTH FE model.

To show the effectiveness of PCA in improving MLHM accuracy and efficiency by reducing model complexity and allowing fewer training data, we compared the prediction of MPS by PCA-MLHMs with conventional MLHMs [2] (MLHMs [2] only predict MPS). Two more studies were performed: firstly, on dataset HM and CF, we compared the accuracy, the model complexity (i.e., number of parameters in the deep neural network) and number of training impacts. Secondly, to compare the performance of PCA-MLHM and MLHM with similar model structure, we followed the same strategy of developing MLHMs and developed the MLHMs with the same input and hidden layers as the PCA-MLHMs (referred to as ”restricted MLHM”, as we kept the layers other than the output layer same as the PCA-MLHM models), and compare the model accuracy. The restriction on the layer structure aimed to keep the PCA-MLHM and MLHM with similar model complexity. It should be mentioned that even when we kept the input and hidden layers the same, the PCA-MLHM still had fewer model parameters because the number of output units was 1 while the number of output units was 4,124 for the restricted MLHM.

III. Results

A. Determination of the orders of principal components for injury metrics

In determining the orders for the three injury metrics, we firstly computed the explained variance based on the PCA. According to the results shown in Fig. 2, PC0 and PC1 are able to explain more than 80% variance in each dataset. Therefore, we chose PC0 and PC1 as the reduced-order representations of the three injury metrics. To visualize the contributions, we plotted the reference values of the injury metrics, the contribution of PC0, and the contribution of both PC0 and PC1 in Fig. 3 on dataset HM as an example (results on other datasets shown in Supplementary S1–3). The results indicate that PC0 and PC1 can represent the majority of the variation of the entire dataset. Visually, although PC0 cannot explain the details in the reference value heatmaps, the addition of PC1 enables the explanation of much of the details in the heatmaps. The Bland Altman plots for the reconstruction error distribution on four datasets and three injury metrics are shown in Fig. S6, showing that the PC0 and PC1 can lead to the accurate injury metrics values for the majority of data.

Fig. 2.

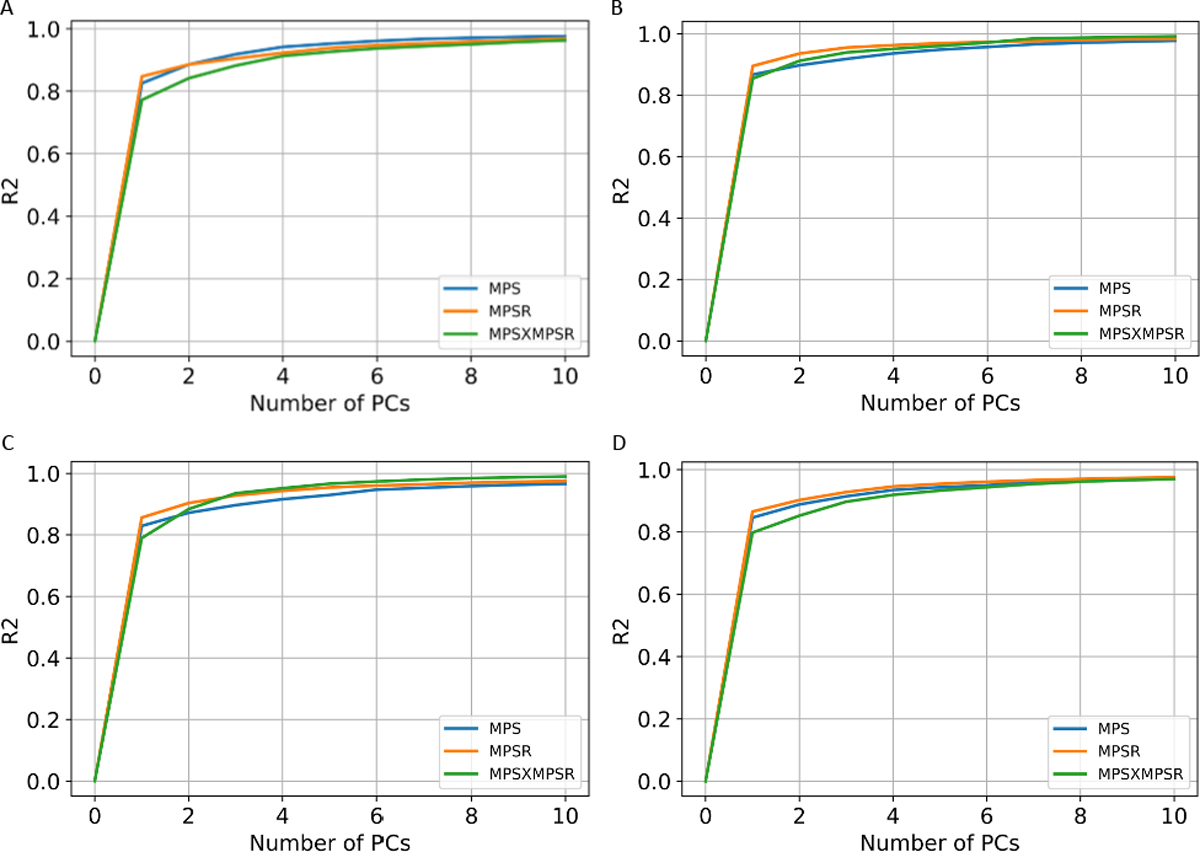
The cumulative explained variance with different orders of principal components. The explained variance for the three injury metrics on dataset HM (A), CF (B), MMA (C) and NASCAR (D).

Fig. 3.

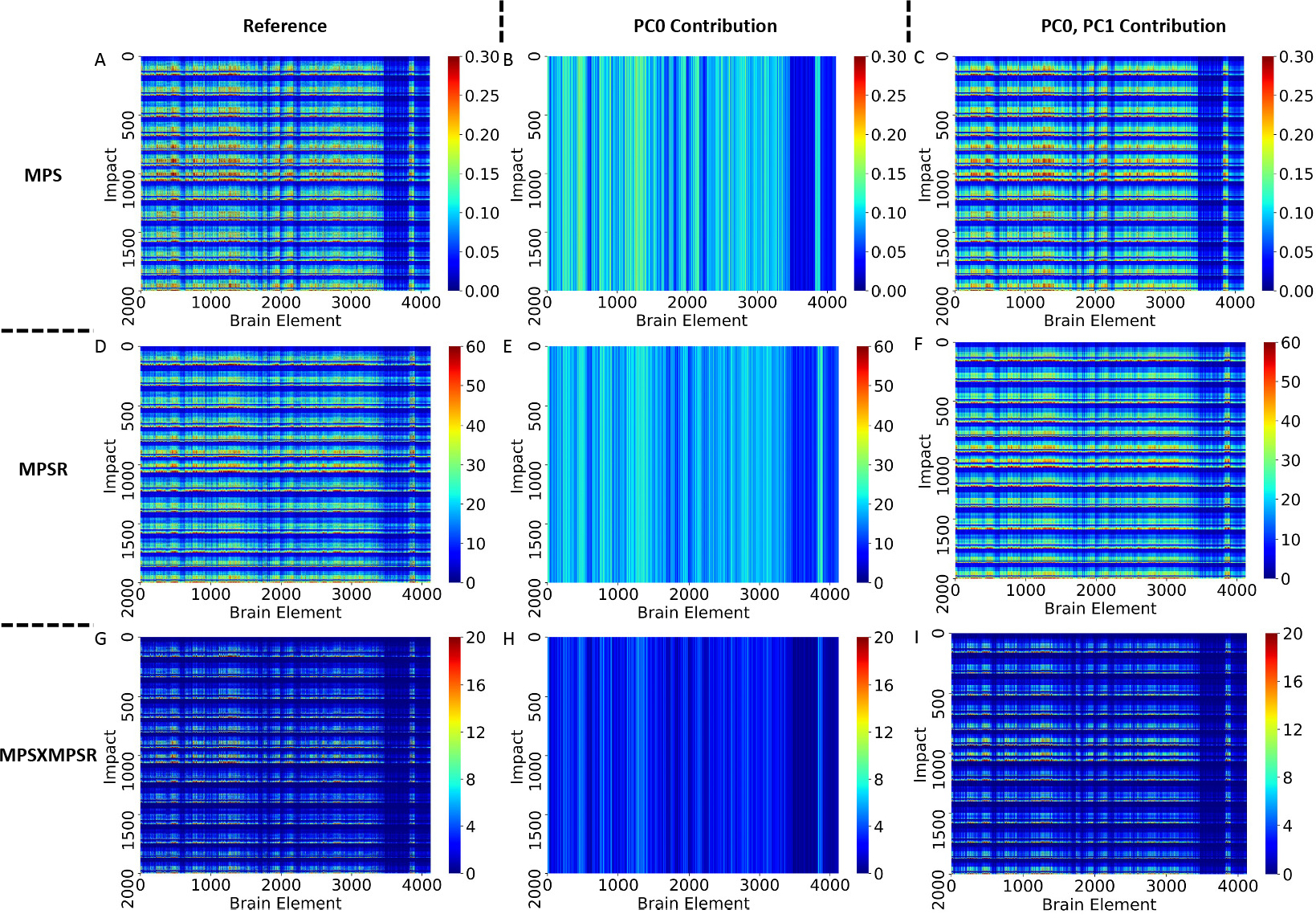
The heatmap visualization of the reduced-order brain injury metric representation on dataset HM. The reference values of the injury metrics, the contribution from PC0 only and the contribution from PC0 and PC1.

B. Spatial distribution of injury metrics

As the injury metrics can be decomposed to PC0 and PC1, we show the spatial distribution of PC1 $(\overrightarrow{v_1})$, which implies the variance on specific brain elements. After normalizing $\overrightarrow{v_1}$, we extracted and averaged the values of different brain regions and visualized them in Fig. 4 (dataset HM and CF as examples). The results show the corpus callosum, gray matter, midbrain and white matter show higher contribution to $\overrightarrow{v_1}$, which indicates the MPS/MPSR/MPS×MPSR variance on these brain regions may be larger than that on brainstem, cerebellum and thalamus. To visualize the contribution to PC1, we plotted the high contribution regions with the low contribution regions masked (with MPS and MPSR as examples) in Fig. 5. The results show different impact types can lead to varying patterns in brain injury metrics variation. For example, on dataset HM, CF and MMA, the cerebral cortex, corpus callosum and midbrain show higher variance in MPS and MPSR. On dataset NASCAR, the high variance occurs in midbrain and corpus callosum regions, while the cerebral cortex may not show higher variation in MPS and MPSR.

Fig. 4.

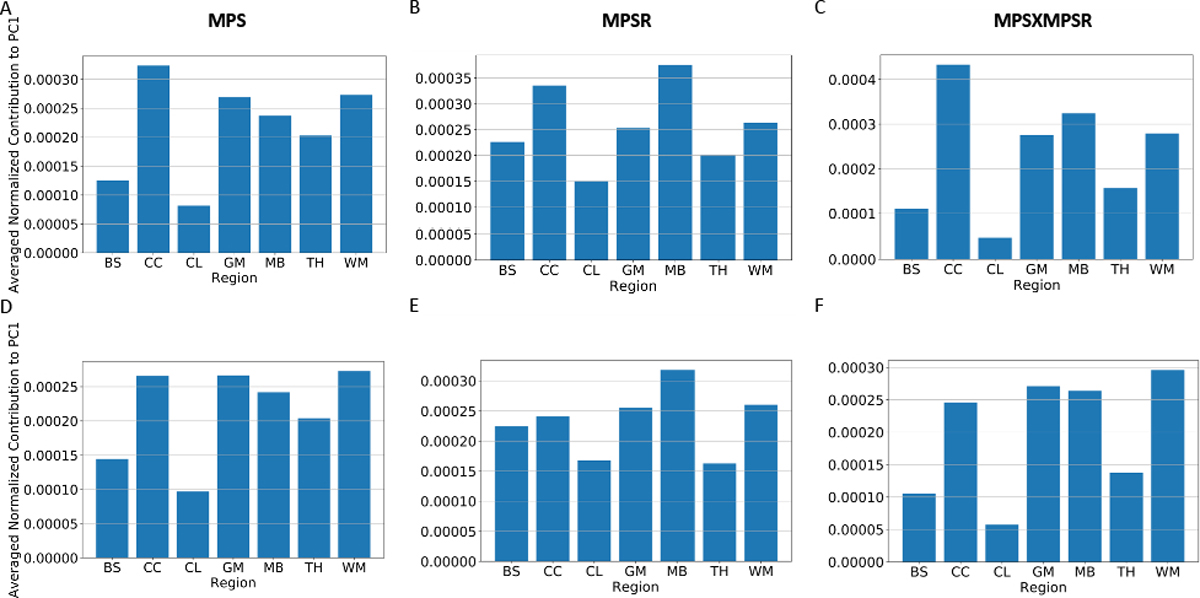
The averaged PC1 coefficients of different brain regions. The results come from dataset HM (A-C) and CF (D-F). The contribution was normalized by the sum over 4124 brain elements and averaged over the brain elements in the same region. The different brain regions include: brainstem (BS), corpus callosum (CC), cerebellum (CL), gray matter (GM), midbrain (MB), thalamus (TH) and white matter (WM).

Fig. 5.

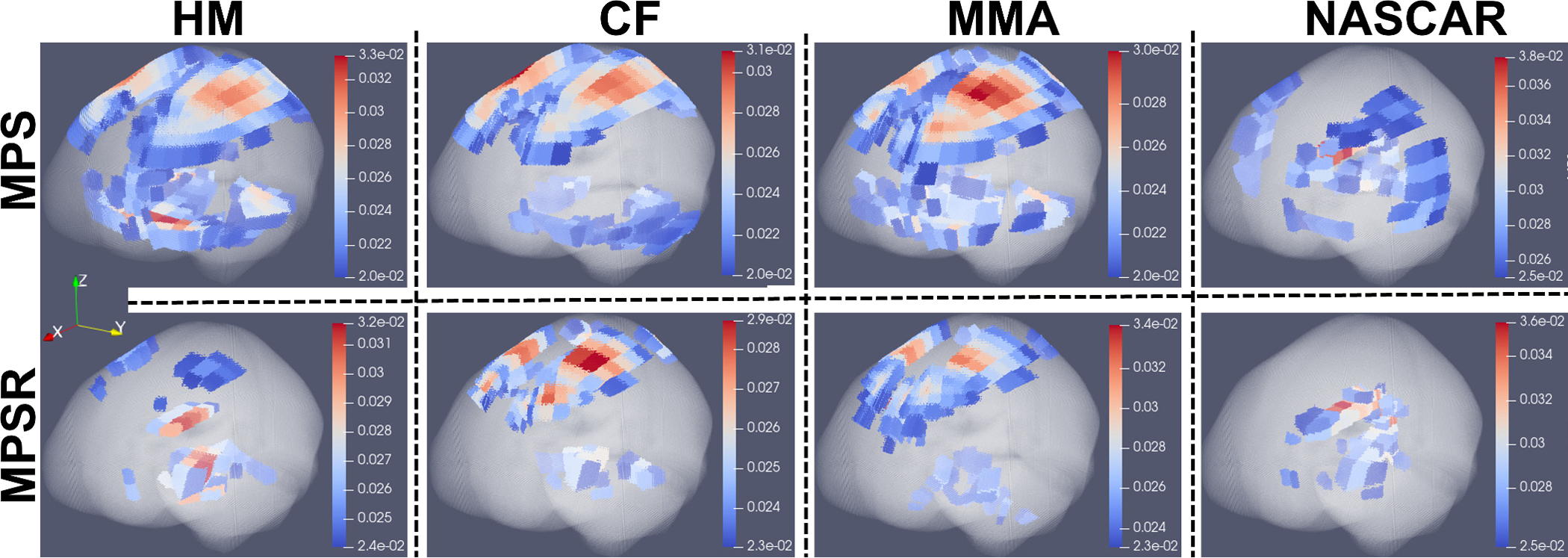
The 3-D visualization of PC1 coefficients for MPS and MPSR across different impact datasets. The high PC1 coefficients $\left(\overrightarrow{v_1}\right)$ for MPS and MPSR are based on the entire dataset HM, CF, MMA, NASCAR, respectively. In each plot, the whole brain elements were plotted in the anatomical coordinates (X: posterior to anterior; Y:right to left; Z: inferior to superior). The brain elements where the PC1 coefficient is smaller than the lower limit of the colorbar were rendered as transparent so that the brain elements with large coefficients inside the brain can be easily seen.(The 3-D without rendering elements as transparent are given in Supplementary Fig. S4–5)

The contribution ratios of PC0 and PC1 of impacts in the high-injury metric subgroup (top 5% injury metrics) were shown in Fig. 6. It can be found that the contribution ratios of PC1 are significantly higher than those of PC0 in the high injury-metric subgroup (p ≤ 0.05), which shows that PC1 exerts more influence in the high-injury metric subgroup. Furthermore, the corpus callosum, midbrain and cerebellum regions have higher PC1 contribution ratios, which indicate that the injury metrics at these regions in the high-injury metric subgroup are more different from the average (PC0). Besides brain regions, contribution ratios can also be compared among the injury metrics: MPS×MPSR has the highest PC1 contribution ratios and the lowest PC0 contribution ratios, which indicates that MPS×MPSR in the high-injury metric subgroup have larger deviations from the average (PC0) than MPS and MPSR. Additionally, the PC1 contribution ratios of MPS×MPSR have larger variance than MPS and MPSR, which suggests that MPS×MPSR also has better distinction in the high-injury metric subgroup.

Fig. 6.

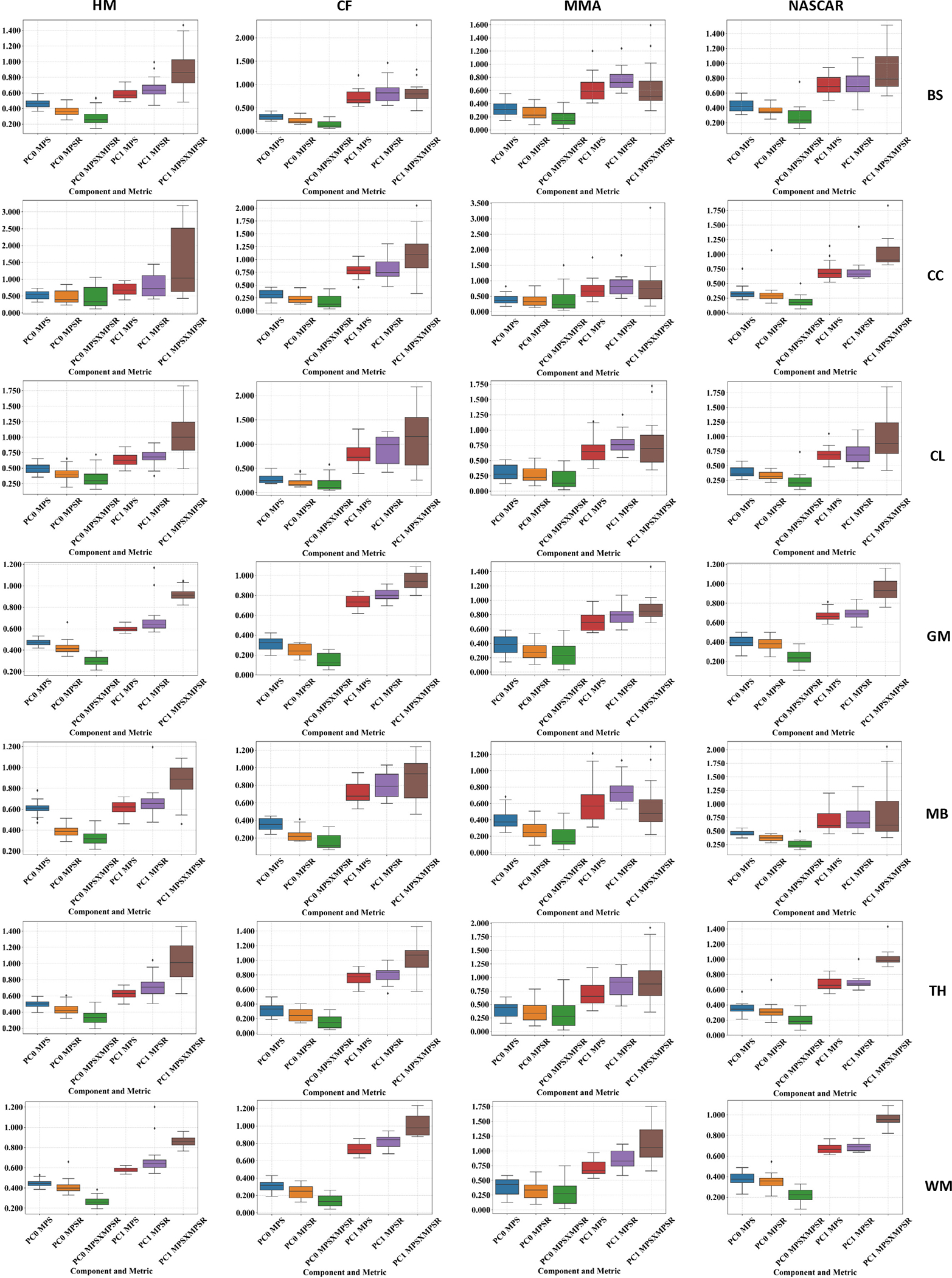
The contribution ratio to the brain injury metrics from PC0 and PC1 in high-injury metrics subgroups (top 5%) in the different brain regions across four different impact datasets. The different brain regions include: brainstem (BS), corpus callosum (CC), cerebellum (CL), gray matter (GM), midbrain (MB), thalamus (TH) and white matter (WM).

C. Assessment of machine learning head model with PCA

Based on the reduced-order brain injury metrics representations with PCA, we further validated its effectiveness by developing PCA-MLHMs to predict the values on PC1 (i.e., $\overrightarrow{{\alpha }_1}$) from kinematics features and then reconstructed the whole-brain MPS/MPSR/MPS×MPSR. The R² between the predicted values of the injury metrics and the reference values are shown in Fig. 7. The accuracy in terms of R² values was comparable with the MLHMs previously developed [2], [36], which indicates that predicting the values on PC1 is enough to accurately predict the whole-brain strain and strain rate. Additionally, as we visualize the distributions of the predicted values given by the PCA-MLHMs and the reference KTH model in Fig. 8 (A)–(C), it is shown that the PCA-MLHMs can generally reproduce the similar overall distributions of the MPS, MPSR, and MPS×MPSR when compared with the reference values. However, the prediction distributions are still slightly different from those given by the reference KTH model, which may be caused by the omission of the higher-order principal components. Furthermore, according to the error box plots in Fig. 8 (D)–(F), the median MAE (over 20 parallel experiments with random dataset partitions) was smaller than 0.018 for MPS prediction, smaller than 3.7s⁻¹ for MPSR prediction and smaller than 1.1s⁻¹ for MPS×MPSR prediction on both dataset HM and dataset MIX. The MAE for MPS and MPSR predictions was much smaller than the presumed human concussion thresholds ( 0.3 for MPS and 25s⁻¹ for MPSR [12], [51], [52]) and the thresholds for accurate brain contusion volume prediction in rat model (0.3 for MPS and 2500s⁻¹ for MPSR reported by [18]).

Fig. 7.

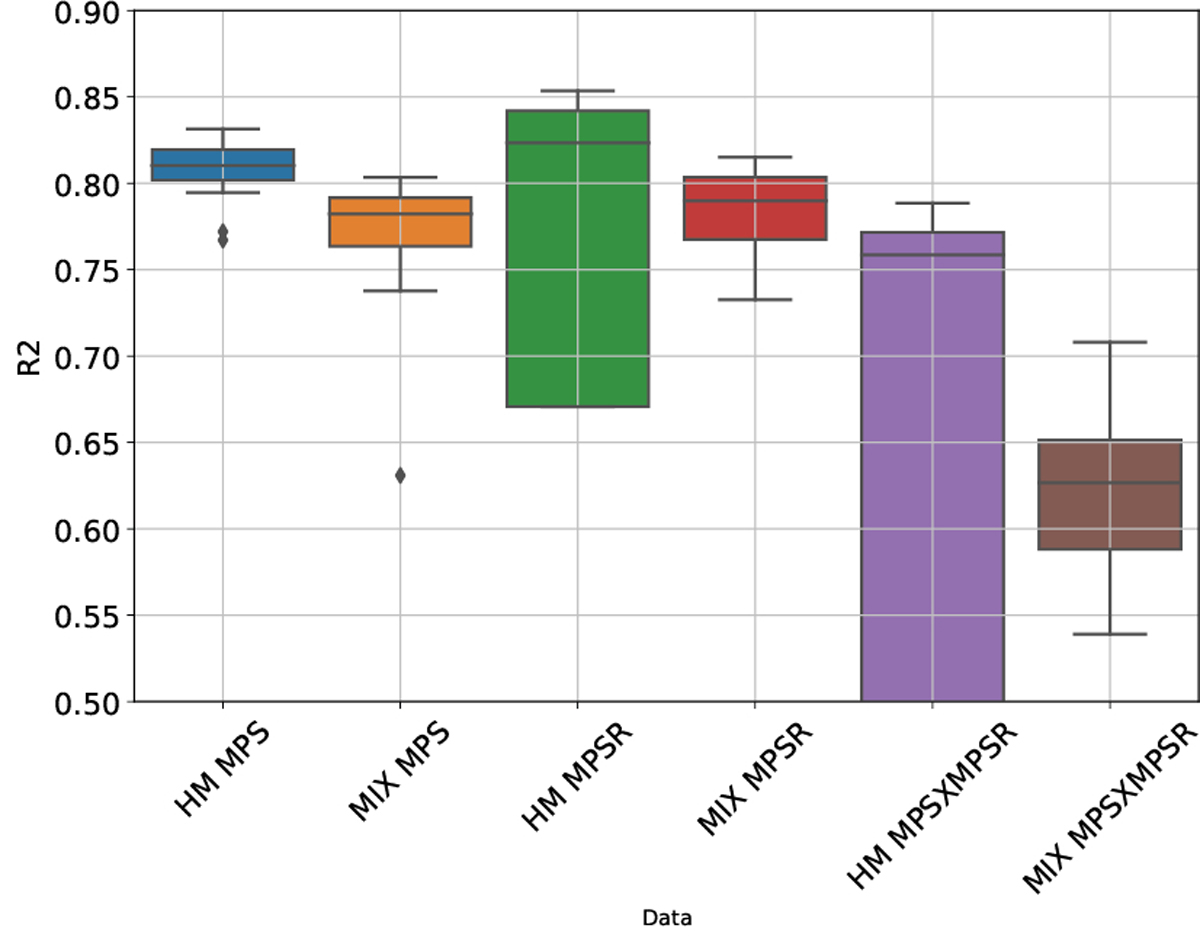
The accuracy of predicting the whole-brain injury metrics in terms of R². The prediction was done on dataset HM and dataset MIX, respectively. The box plots show the results over 20 parallel experiments with random dataset partitions.

Fig. 8.

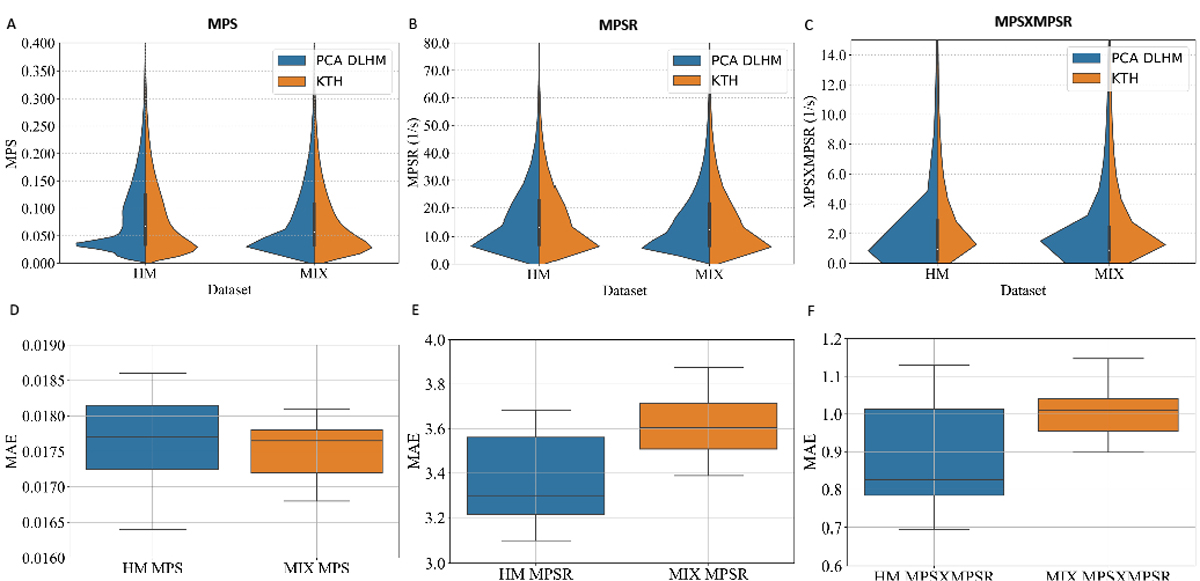
The violin plots of the predictions and reference values and the boxplots of mean absolute error (MAE) in the predictions. The violin plots of the overall distribution of predicted and reference values on the dataset HM or the mixture of all datasets. The MAE between the predicted values and the reference values given by the KTH model on the dataset HM or the mixture of all datasets.

To compare the PCA-MLHM with conventional MLHM, firstly, we evaluated the model accuracy, number of model parameters and the training set size on dataset HM and CF and compared with the results of the previous published study [2]. We showed the mean, median and standard deviation (STD) of the MAE of MPS predictions on three datasets and compared the results in Table 1. According to the results, on dataset HM and CF, the PCA-MLHM reached similar accuracy when compared with the MLHM, with MAE ranging from 0.013 to 0.018, smaller than 10% the concussion threshold [12], [51], [52]. However, the PCA-MLHM significantly reduces the model complexity by reducing the neural network parameters from over 150k to below 50k. Additionally, once we restricted the model complexity of MLHMs by keeping the input layer and the hidden layers the same as those of PCA-MLHM, the accuracy of the PCA-MLHM significantly outperformed the restricted MLHMs (p ≤ 0.05, Wilcoxon signed-rank test). These results indicated that with similar model complexity, adopting PCA can effectively improve the accuracy. Furthermore, in the previous study, to improve model accuracy, the data fusion strategy (combine dataset HM with dataset CF for training) was used. This study shows that with PCA, the model accuracy can reach that of the data fusion strategy without the large training dataset created by data fusion.

TABLE I.

The statistics of the prediction accuracy, number of model parameters and training set size of the MLHMs with/without PCA.

Dataset	Model	Number of Model Parameters	Number of Training Data	MAE Mean	MAE Median	MAE STD
HM	PCA-MLHM	42,721	1,490	0.018	0.018	0.001
HM	MLHM [2]	167,024	1,490	0.013	0.013	0.001
HM	Restricted MLHM	88,074	1,490	0.020	0.021	0.001
CF	PCA-MLHM	42,721	210	0.013	0.013	0.001
CF*	MLHM [2]	167,024	2,247*	0.013	0.012	0.002
CF	Restricted MLHM	88,074	210	0.017	0.017	0.003

^*HM was included to augment the training data [2]

IV. Discussion

In this study, we use PCA to analyze the co-variance of three injury metrics (MPS, MPSR and MPS×MPSR), which represent the severity of brain tissue deformation during head impact, in four datasets including simulated headform impacts (HM), college football (CF), mixed martial arts (MMA) and National Association for Stock Car Auto Racing (NASCAR). We found the first order of principal component (PC1) is able to explain more than 80% variance in every dataset in terms of coefficient of determination (R²). The concentration of the explained variance in PC1 indicates characteristics of the injury metrics distribution can be investigated via PC1 and the mean component (PC0). For all four datasets, we found the corpus callosum and midbrain exhibit high variance, and high variance in the cerebral cortex was only found in HM, CF and MMA. Then, high-injury metrics subgroups were selected from datasets, and the contribution ratio was defined to quantify the contribution of PC0 and PC1. Higher contribution ratios of PC1 were found at corpus callosum, midbrain and cerebellum. We also found the contribution ratio of PC1 for MPS×MPSR was higher than that for MPS and MPSR in the high-injury metric subgroup. Furthermore, because PCA is able to reduce the order to represent injury metrics, it was used to simplify MLHMs, which were developed to predict the MPS, MPSR and MPS×MPSR [2], [36]. PCA takes advantage of the spatial relationship among brain elements and reduces the dimension of prediction output. Therefore, we developed a PCA-MLHM and compared it with our previously published MLHM [2] and showed that the PCA-MLHM can accurately predict the MPS, MPSR and MPS×MPSR with less training data and simpler neural network.

Due to different impact conditions (e.g., helmeted or unhelmeted, head-to-head or punch), the relationship between head kinematics and injury metrics varies largely across impact datasets [1], [21]. Consequently, brain regions that often experience severe deformation vary across impact types. Performing PCA on the data matrices, whose two dimensions are elements and impacts, provides a tool to simplify the analysis of the spatial distribution of the injury metrics. As PC1 is able to explain more than 80% of the variance of the brain (Fig. 2), PC0 and PC1 can represent the whole dataset (Fig. 3). As PC0 is the mean component same for every impact, the spatial distribution in the high-injury subgroup is mainly decided by PC1. Therefore, the PC1 vector is an indicator to show the vulnerable (i.e., with high injury metric value) brain regions for specific impact types. For the HM, CF, MMA and NASCAR impacts, the PC1 is visualized as a 3-D plot (5), and high values were found at the corpus callosum, cerebral cortex and midbrain, which indicate that these regions have a higher risk of high MPS or MPSR. This finding agrees with previous studies comparing the mechanical loading on different brain regions [27], [53], [54], and these regions were found to change after TBI [55], [56].

The pattern of PC0 and PC1 in data-driven decomposition of brain injury metrics suggests the discrepant loadings on different brain regions. As the injury metrics (MPS, MPSR and MPS×MPSR) can be decomposed into PC0 and PC1, we can further analyze the patterns of brain regions with high values of injury metrics: if brain regions are with high PC0 contribution ratios and low PC1 contribution ratios, the regions may suffer from high strain/strain rate more constantly because the high strain/strain rate come from the mean part from the PC0 contribution; if brain regions are with low PC0 contribution ratios and high PC1 contribution ratios, the brain regions may suffer from high strain/strain rate occasionally rather than constantly because the high strain/strain rate contribution come from the variance part from the PC1 contribution. By analyzing the patterns across impact types, we observed the patterns related to different impact types. Furthermore, since the whole-brain injury metrics can be resolved onto the PC1, PC1 scores (i.e., the elements of $\overrightarrow{{\alpha }_1}$) have potential to be used as an injury metric. The PC1 scores, which are different across impacts, are the reduced-order summary of the whole-brain injury metrics, may represent the overall risk better than the 95th percentile values [13].

Different mechanical metrics (MPS, MPSR, MPS×MPSR) were proposed to indicate the risk of the pathology. In high injury-metric subgroups, we found that MPS×MPSR exhibited higher contribution ratio of PC1 and lower contribution ratio of PC0 than MPS and MPSR. We also found that the variance of PC1 contribution ratio for MPS×MPSR was larger than that of MPS and MPSR. Both of these findings showed that MPS×MPSR have larger distinction among impacts, which suggest the potential explanation of high sensitivity of MPS×MPSR and the potentially better discrimination ability of using MPS×MPSR to classify injury or non-injury, as found in the animal models studies [13], [15], [57].

The different variation patterns of different types of head impacts can be shown by PC1 coefficients $\overrightarrow{v_1}$ (shown in Fig. 5). The patterns shown by the football-like impacts (without helmet) in dataset HM and the patterns shown by the college football impacts (with helmet) in dataset CF are very different. The patterns shown in the MMA impacts (without helmets) are also quite distinct from those shown in the NASCAR impacts (with helmets). Based on the PC1 coefficients, besides the analysis of the PC1 coefficients across the different types of head impacts, we can further leverage the PC1 coefficients to study the effects of different types of protective gears. For example, the patterns of PC1 coefficients for the impacts with or without helmets can be investigated the PC1 coefficients, because it is possible that different types of protective helmets for American football players may exert different effects on the changing patterns of the PC1 coefficients and therefore, they may redistribute the MPS/MPSR/MPS×MPSR. The analysis of the PC1 coefficients enables the visualization of the protective effect of helmets in the metrics other than the simple reduction of kinematics-based metrics (e.g., peak resultant angular velocity) and strain-based metrics.

The pattern of PC1 coefficients indicates the occurrence of high MPS and MPSR in specific brain regions when severe head impacts happen. Therefore, these patterns have the potential to suggest the vulnerability of neuropathology following TBI, which can be detected by medical magnetic resonance imaging (MRI) scans. In Fig. 4, high PC1 coefficients were found in the midbrain, corpus callosum and white matter in dataset HM and CF, which indicate that these brain regions have a higher chance of experiencing severe mechanical loading. In a recent study about collegiate football, significant reductions of the integrity of the midbrain white matter were found in players after a single season [58]. In another study about female concussion, the micro-structure at the corpus callosum was found to vary significantly from the control subjects [59]. Although the cortex is not included as a category of brain regions in this study, we observed high coefficients in the cortex (Fig. 5), and abnormalities of the neuro-physiology were found in the primary motor cortex [60].

The application of PCA in the development of MLHMs to estimate whole-brain MPS, MPSR and MPS×MPSR also worths further discussion. MLHMs have shown their effectiveness in reducing the computational cost associated with state-of-the-art FEM in previous studies [2], [36], [48]. They are developed for different FEM as function approximators of FEM when the mapping between the head impact kinematics and the brain injury metrics is learned through impact data. However, although the KTH model we used in this study contains 4,124 brain elements, the recently developed FE models have larger numbers of brain elements [61], [62].

Due to the high dimensionality of the output to be modeled by the MLHMs, more parameters are generally needed in the models. Therefore, large quantities of impact data are needed to train these parameters in the MLHMs. For example, in the previously published MLHMs [2] to estimate MPS, data fusion strategy was used to augment the training data to get a more accurate MPS estimation results. In this study, to address the model complexity and the reliance on the large quantities of training data, we propose to apply the PCA to firstly decompose the brain injury metrics and reduce the dimension of output for the MLHMs to model, where the value on PC1 is the only target to be predicted. The PCA incorporates the spatial co-variation into the learned PC1 coefficients and the MLHMs can benefit from the spatial co-variation. After we inverse-transform the PCA process, high accuracy in the predictions of MPS, MPSR and MPS×MPSR have been achieved by the PCA-MLHMs developed in this study. We have shown in the comparison with the MLHMs without PCA, for one thing, the PCA-MLHM can reach similar accuracy with significantly less complicated model (over 70% reduction in neural network parameters) and with significantly fewer training data. For another, if the structures of PCA-MLHMs and MLHMs are kept similar, which means the model complexity of the MLHMs are regularized, the PCA-MLHMs outperformed the MLHMs in MPS estimation accuracy with statistical significance. These results indicate that the PCA can enable more efficient training of MLHMs with simpler model structures and fewer training data. This feature may be more helpful when developing MLHMs for more complicated FE model with more output brain elements (e.g., Global Human Body Models Consortium (GHBMC) [62]).

Although this study provides readers with a novel data-driven brain injury metrics decomposition based on PCA, there are several limitations that worth notice. Firstly, in this study, we applied the KTH FE model to compute MPS and MPSR. Although the KTH FE model has been validated with experimental data of brain-skull relative motion [46], intracranial pressure [46], and brain strain [47], it is relatively limited when compared with the FE models recently developed [61], [63]. For example, the KTH model does not consider the gyri and sulci which may significantly affect the behavior of the FE models. Additionally, it does not involve the cerebral vasculature in the modeling, which limits the modeling to be within the parenchyma. However, it has been shown by previous studies that the cerebral vasculature could significantly affect the shear stress modeled by FE models [64]. Therefore, for higher fidelity in brain dynamics modeling, more advanced FE models can be adopted in the future with a similar analytical pipeline introduced by this study.

Furthermore, we applied PCA considering: 1) it applies linear projection, which has high simplicity and interpretability; 2) it enables relative importance ranking among different latent variables (PCs); 3) once the data matrices are given, the PCs are definite, irrespective of the number of PCs we finally select to reconstruct the brain injury metrics; 4) it ensures invertibility for whole-brain MPS, MPSR and MPS×MPSR reconstruction. Therefore, we did not apply more complex unsupervised dimensionality reduction approaches such as variational autoencoders (VAEs) [65], which may bear higher representation capability with deep neural network encoders and decoders, though at the sacrifice of interpretability and clear latent variable importance weighting. In the future, the powerful deep-learning-based dimensionality reduction approaches can be applied to disentangle the latent variables in brain injury metrics decomposition. Additionally, we did not investigate the spatio-temporal characteristics of MPS/MPSR/MPS×MPSR. In the future, such novel approaches as the eigenvalue decomposition of Hankel matrix can be applied to the time traces of the MPS/MPSR/MPS×MPSR [66], which may be able to further manifest the potential time-frequency representations of the brain dynamics.

In the development of MLHMs to predict the values on PC1, there are several limitations. Firstly, while we focus on the modeling of PC1, the influences of the mean components (PC0) and other components should not be ignored. It is possible that the part of the variance explained by the other PCs include more detailed information closely related to the injury outcome, which warrants further validation. For the development of MLHMs, in the current model, the mean components are extracted based on the mean over the training impacts, and this practice may lead to a significant decrease in prediction accuracy if the test impacts are sampled from a significantly different data distribution. Additionally, as we did not consider the higher-order PCs besides PC1, the MLHM accuracy may be capped by the predictability of PC1 (i.e., the R² has an upper bound of around 0.8–0.9). The limitation can also be visualized in Fig. 8, where even though the overall distributions of the predictions resemble the reference distributions, the prediction distributions are still different from the reference distributions. The incorporation of more higher-order principal components may enable more accurate predictions. In the future, to enable even more accurate MLHMs based on the brain injury metrics decomposition approach, higher-order principal components may be included as the targets of modeling as well, with the loss function weighing the PC1 more during the training of the MLHM.

Secondly, we extracted features from the temporal signals of head impact kinematics to be the input of the MLHMs, considering the potential temporal mismatch of peaks based on different measurement devices. With more data collected from various types of measurement devices, completely data-driven modeling based on convolutional neural networks [36] and recurrent neural networks may be leveraged to extract features from the signals in a data-driven manner, which may even lead to higher accuracy in predicting the PC1 values and enable better whole-brain MPS and MPSR predictions.

V. Conclusion

In this study, we applied PCA to decompose the patterns in three brain injury metrics (MPS, MPSR, MPS×MPSR) based on the spatial co-variation in four types of head impacts. The reduced-order representation of the injury metrics enables better interpretation of the patterns in brain injury metrics across different impact types and reduces the dimensionality for the development of machine learning head models (MLHMs). According to the results, we found the mean component (PC0) and the first principal component (PC1) are able to explain more than 80% variance in most datasets. Then, we investigated the distributions among different brain regions and different injury metrics with the PC1. We showed that the corpus callosum and midbrain manifest high variance on all datasets and the MPS×MPSR had the largest distinction in the dataset. Finally, we leveraged the PCA to develop PCA-MLHMs to predict the three injury metrics with fewer training data and simpler neural network structure and reached comparable predicting accuracy with the original MLHMs.