Abstract
Following a pandemic disease outbreak, people travel to areas with low infection risk, but at the same time the epidemiological situation worsens as mobility flows to those areas increase. These feedback effects from epidemiological conditions to inflows and from inflows to subsequent infections are underexplored to date. This study investigates the two-way relationship between mobility flows and COVID-19 cases in a context of unrestricted mobility without COVID-19 vaccines. To this end, we merge data on COVID-19 cases in Spain during the summer of 2020 at the province level with mobility records based on mobile position tracking. Using a control function approach, we find that a 1% increase in arrivals translates into a 3.5% increase in cases in the following week and 5.6% ten days later. A simulation exercise shows the cases would have dropped by around 64% if the Second State of Alarm had been implemented earlier.
Keywords: COVID-19, Mobility flows, Infectious cases, Smartphone location
1. Introduction
Coronavirus disease 2019 (COVID-19) has completely disrupted the world economy and people's lives. It was declared a pandemic by the World Health Organization (WHO) on March 11, 2020, and by April 2022 the WHO had counted more than 380 million confirmed cases and more than 5.6 million deaths globally. COVID-19 has substantially increased people's economic anxieties and worries (Fetzer et al., 2021; Brodeur et al., 2021) and reduced people's quality of life by around 10–20% through comorbidity (Briggs et al., 2021). In the short run, the pandemic has been associated with increases in unemployment (Forsythe et al., 2020), drops in household consumption (Chen et al., 2021) and has dramatically hit the restaurant, hospitality and travel sectors (Alexander and Karger, 2021).
Epidemics tend to follow a cycle dynamic: following a fast exponential growth process, once the infection curve peaks at a maximum, it is followed by a period of decreasing incidence until it starts growing again. During the so-called first wave of the COVID-19 pandemic (March–May 2020), many governments around the world implemented stay-at-home orders, mobility restrictions, and enforced lockdowns to contain the spread of the virus. After the worst phase of the curve, and due to the important social and economic effects of confinements, governments relaxed restrictions and allowed their populations to move freely while the number of cases remained under control. However, the premature relaxation of social distancing policies has been shown to contribute to rapid surges in COVID-19 cases (Pellegrini, 2021). In this context, accurate tracking of population flows and how they correlate with the number of cases might be highly informative from both an epidemiological (Jia et al., 2020) and an economic perspective (Qiu et al., 2020).1
Recent evidence has shown that the number of cases depends on mobility flows (Carteni et al., 2020; Fang et al., 2020; Mangrum and Niekamp, 2022). Human mobility and interaction propagate the disease, either by personal contagion through travelling itself, at the destination by those who move, or though indirect dispersal. However, mobility does not translate into higher cases immediately but with some lag. In this regard, the medical literature indicates that COVID-19 has an incubation period that usually takes around 5 days (Lauer et al., 2020). At the same time, individuals make mobility decisions based on the threat of infection (Engle et al., 2020; Hu et al., 2021). A growing stream of literature documents substantial voluntary drops in consumption and nonessential mobility as the pandemic situation worsens (Chen et al., 2021; Alexander and Karger, 2021). As documented in Brinkman and Mangum (2022), a high level of infection in a region i might reduce the willingness of both recreational travellers and daily commuters to travel there. An important question is how much voluntary drops in mobility due to exposure risk can help to mitigate the subsequent virus spread in a setting with no mobility restrictions.
The aim of this paper is to analyse (i) the influence of arrivals on the evolution of the disease during the reopening of the economy after a lockdown period and (ii) how flows react to the epidemiological situation at the destination. In this way, we assess the two-way relationship between flows and COVID-19 cases. While there is an emerging body of research concerned with how mobility propagates disease (Carteni et al., 2020; Fang et al., 2020; Mangrum and Niekamp, 2022; Wan and Wan, 2022) and how people avoid travelling to areas with high infection rates (Brinkman and Mangum, 2022; Goolsbee and Syverson, 2021; Hu et al., 2021), the feedback effects from epidemiological conditions to inflows and from inflows to subsequent infections are underexplored to date. We aim to fill this gap.
Spain is taken as the case study for the analysis. This country was among the most affected in the first wave of the pandemic and by the beginning of 2022 it has counted more than 10 million cases and almost 94,000 deaths (World Health Organization, 2021). We use mobility data based on mobile phone tracking, which has started to be used to analyse the linkages between mobility flows and the spread of COVID-19 disease (Brinkman and Mangum, 2022; Mangrum and Niekamp, 2022; Jia et al., 2020). We consider the period from the end of the first State of Alarm (24 June) to the end of September (30 September) 2020. After a strict lockdown that started on March 15, 2020, the Spanish economy was ‘reopened’ and the country returned to the so-called ‘new normal’. During the summer period, people were free to move within the country without restrictions. Therefore, this time span is suitable to assess the bivariate relationship between mobility and cases because no lockdowns or government-mandated movement restrictions were in force. In this way, the paper studies whether unrestricted flows in the middle of the pandemic contribute to the appearance of small epidemic outbreaks that subsequently generated the second wave in October–November 2020. The time lag in the response of cases to inflows is exploited for identification. Furthermore, we also examine state dependence in cases by which the number of cases in period t depends on the accumulated incidence in both 7 and 14 days. To properly identify the causal relationship, we use exogenous variation in the moving average of weather conditions as instruments. Based on our model estimates, we conduct a counterfactual analysis to estimate the associated drop in COVID-19 cases if the second State of Alarm that reintroduced mobility restrictions had been passed earlier. From this perspective, the paper complements that by Orea and Alvarez (2022), who also study the potential reduction in cases if the Spanish lockdown during the first wave had been implemented earlier.
Our research connects other works that investigate the relationship between mobility and cases. Among this literature, the closely related studies are those by Glaeser et al. (2020) and Brinkman and Mangum (2022). On the one hand, Glaeser et al. (2020) study the relationship between the total cases per capita and mobility, finding that the elasticity of cases with respect to mobility is around 3. They focus on how drops in mobility due to restrictions during the first wave reduce the disease spread. In contrast, we pay attention to the reversal: how increases in mobility between the first and the second wave are associated with new outbreaks. From this viewpoint, the paper offers new insights into how the premature relaxation of social distancing policies contributes to new pandemic spikes (Pellegrini, 2021). On the other hand, Brinkman and Mangum (2022) show consistent evidence that people avoid travelling to areas with larger outbreaks to reduce exposure. They also document that greater exposure to outside cases through mobility translates into higher local case numbers. However, they do not consider how the inflow of people to a region is determined by its epidemiological situation and how these arrivals contribute to the spread of COVID-19 within the region later on. Our paper thus differs from previous studies primarily in that we model the bidirectional relationship between accumulated incidence, contemporaneous arrivals in a province and subsequent local case numbers.
The remainder of the paper is structured as follows. Section 2 reviews the related literature, providing some background for the analysis. Section 3 presents the datasets and some descriptive statistics. Section 4 outlines the econometric modelling. Section 5 discusses the main findings and some robustness checks. Finally, Section 6 summarizes the main results and concludes.
2. Background
Viruses spread through social interactions represent an important threat to human health and a costly externality. The economic literature on rational epidemics has put forward that behavioural responses are highly dependent on the degree of prevalence of the disease in the population and transmission rates (Oster, 2005; Auld, 2006) and personal beliefs about the true risks (Kremer, 1996). Usually, individuals’ microeconomic incentives are not aligned and require public intervention to contain the spread of viruses (Fenichel, 2013). This body of research agrees that public health authorities need to find a balance between protecting vulnerable and high-risk people while avoiding social panic. Typical non-pharmaceutical interventions range from travel-related controls or mobility restrictions that reduce social interactions to strict quarantines and lockdowns. In situations in which the epidemic becomes a pandemic, travel restrictions have less capacity to contain the virus spread and generally require more severe interventions.
Although there is some evidence of public acceptance of voluntary home confinement during an epidemic (Orset, 2018), the enforcement of movement restrictions and lockdowns is generally difficult for the population to accept and leads to important macroeconomic costs. For instance, Mesnard and Seabright (2009) show that quarantine measures can induce people to escape from centres of disease, thereby imposing important negative externalities on other communities. Brodeur et al. (2021) document a substantial increase in the Internet search intensity for the keywords ‘loneliness’, ‘worry’ and ‘sadness’ in Europe and the US caused by the pandemic and its associated lockdowns. Similarly, Fetzer et al. (2021) report that COVID-19 has produced a large increase in economic anxieties and worries.
To date, the work by Adda (2016) is possibly one of the most important contributions to the understanding of the economic determinants of the spread of viruses across time and space. Using high-frequency data for 25 years in France, this author documents that although the closure of schools or public transportation networks as a response to epidemic outbreaks reduces disease prevalence, it involves important trade-offs that are not cost-effective.
2.1. Mobility patterns and the spread of diseases
A growing body of literature has started to investigate the linkages between mobility flows, travel restrictions, and the spread of COVID-19 cases. We focus our attention on those works that study the first and second waves during 2020, when vaccines were still not developed. From a theoretical viewpoint, Cuñat and Zymek (2022) develop a structural-gravity model in which mobility flows are governed by a gravity equation and contribute to the spread of the disease. Their model combines an epidemiological framework with a dynamic model of individual location choice, which is calibrated using data for Great Britain. They provide some evidence about the welfare trade-offs between mobility restrictions and disease control.
At the empirical level, most existing research has focused on the Chinese context. Wan and Wan (2022) document that intercity high speed rail connections with Wuhan during the first wave of the pandemic accounted for around 45% of infections by facilitating human mobility and disease transmission. Chinazzi et al. (2020) examine the impact of travel restrictions on both national and international spread of COVID-19 in Wuhan. They show that travel limitations have modest effects on containing the spread of the disease unless paired with additional public health interventions and behavioural changes. In contrast, Fang et al. (2020) quantify the causal impact of the lockdown of Wuhan on the containment and delay of the spread of COVID-19. Using a difference-in-differences research design, they report that the lockdown was effective at reducing total cases outside the city. Drawing on different counterfactual analyses, Qiu et al. (2020) show that the different health policy measures implemented in China (mainly related to a massive and strict lockdown) were effective in achieving the goal of reducing the number of infections and deaths. These authors also present evidence that population outflows from Wuhan represented the most important determinant of the number of new cases.
An emerging body of research has started to make use of mobile-phone traffic data to analyse how real-time trends in movement patterns translate into cases. Jia et al. (2020) study the impact of population flows from Wuhan to mainland China in January 2020 on the spread of COVID-19. They document that flows from Wuhan accurately predict the relative frequency and geographical distribution of cases. Using data for 25 counties in the USA between January and April 2020, Badr et al. (2020) show that the drop in mobility is strongly correlated with lower COVID-19 case growth rates, especially for the most affected areas. Mangrum and Niekamp (2022) look at the role of university students’ mobility in the spread of COVID-19 cases and mortality, exploiting variation in spring breaks across US states. They find causal evidence that counties with earlier spring breaks had 20% higher cases per capita. Students who travelled to airports had a greater than average impact on COVID-19 cases. Carteni et al. (2020) study the effect of mobility habits in the spread of COVID-19 in Italy. These authors report that trips made three weeks before are the main determinants of daily new cases.
Glaeser et al. (2020) examine the relationship between mobility and the number of cases using mobile tracking data for five cities in the US. Using different model specifications, they show that a 10% decrease in mobility leads to a 30% fall in cases per capita. Nevertheless, they document important heterogeneity across cities. In their analysis, they consider the possible reverse causality between cases and mobility. Additionally, they show that mobility decreased in those areas in which COVID-19 cases were increasing, which suggests that the initial infection rate also affects mobility decisions.
Focusing on the Spanish case, Orea and Alvarez (2022) report that the onset of COVID-19 is significantly correlated with province characteristics. They show that the most-populated provinces and those areas that are more strongly connected to foreign countries have more intensive coronavirus epidemics. Saez et al. (2020) study the ex-ante effectiveness of the mitigation strategies launched by the Spanish government to battle the spread of COVID-19 in mid-March 2020. They find that the lockdown was effective at flattening the curve. More recently, Gutiérrez et al. (2021) evaluate the regional inequalities in cases and deaths across Spanish regions. They show that part of the heterogeneity in the disease incidence across territories is due to differences in mobility flows.
2.2. Infection risk and mobility flows
As introduced before, mobility flows not only contribute to the spread of a viral disease but also react to it. Consistent with utility maximization, people engage in public avoidance behaviour to minimize the likelihood of getting infected (Chen et al., 2011); as the epidemic becomes more prevalent and salient in the population, people increase their willingness to protect themselves against the disease (Geoffard and Philipson, 1996). In this respect, previous health crises have shown that the disclosure of information by both public authorities and peers is a useful channel through which people learn to reduce their exposure gradually over time (Bennett et al., 2015), especially against novel risks. Recent evidence by Mendolia et al. (2021) supports this for the case of COVID-19. Although some people consciously avoid information (Golman et al., 2017), the media can exert a non-negligible role on the social awareness of COVID-19 (Allcott et al., 2020).
The theoretical rationale for why infection risks deter mobility flows can be found in the work by Engle et al. (2020). These authors show that the cost of travelling each unit of distance comprises one component that is independent of the epidemic and one component that directly depends on a risk index of contracting the disease. They show that mobility decreases as a response to rises in local infection rates and also due to increases in the number of cases in the neighbouring regions. Hu et al. (2021) examine the variation in the number of trips per person following the pandemic outbreak in the USA. They find that trips are negatively associated with the number of new cases in the county and the new cases in adjacent countries. Similarly, by examining the interconnections among coronavirus cases across 41 countries, Milani (2021) reports that social behaviour and risk perceptions are highly dependent on health shocks in neighbouring countries. Exploiting cellular phone records, Goolsbee and Syverson (2021) show that legal mobility restrictions only explain a small share of the decline in customer visits to individual businesses: the observed drop is more dependent on individual choices to avoid infection. These authors also document that traffic started dropping before the legal orders were in place and people switched their visits from “nonessential” towards “essential” businesses only. More recently, Brinkman and Mangum (2022) find that people in the USA travelled less and avoided areas with relatively larger outbreaks during the early phase of COVID-19. These authors show that mobility voluntarily decreased more in counties with more cases, and the activity that did occur avoided areas with higher local cases.
Stay-at-home orders and recommendations and the development of new technologies have increased remote working (Brynjolfsson et al., 2020) and therefore reduced commuting mobility (Beck et al., 2020). Interestingly, evidence presented by Cronin and Evans (2020) shows that a large share of the drop in mobility is due to self-imposed precautionary behaviour. Borkowski et al. (2021) document that the decline in job-related mobility is strongly associated with the fear of getting infected with COVID-19. Relatedly, people have also reduced their leisure-related trips during the pandemic (Landry et al., 2021,). In this vein, there is wide evidence in the tourism literature that people become reluctant to travel for recreation to risky areas if they perceive their health to be threatened (e.g., Chien et al., 2017). Using annual data on tourist flows for 188 countries during 2000–2018, Mertzanis and Papastathopoulos (2021) show that the number of inbound tourists is negatively affected by an index of epidemiological susceptibility conditional on a wide set of economic controls.
Some other studies have found a significant drop in spending in sectors associated with mobility because of COVID-19 and stay-at-home orders. By exploiting billions of daily and hourly individual transaction data for goods and services purchased at the local level in France, Bounie et al. (2020) document a shift from offline to online purchases. Chen et al. (2021) show that dining & entertainment and travel in China experienced expenditure declines of 72% and 64%, respectively, and that consumption responded negatively to day-to-day changes in epidemic severity. Similarly, Alexander and Karger (2021) report large reductions in spending in restaurants and retail stores in the USA. Menezes et al. (2022) show substantial drops in electricity consumption during the lockdown in Brazil. For the case of Mexico, Campos-Vazquez and Esquivel (2021) find a decline in points of interest expenditures. The authors suggest that this could be due to the fear of contagion among wealthy individuals.
3. Data
3.1. Context and study period
Due to the fast propagation of COVID-19 disease, on 15 March 2020 the Spanish government passed a State of Alarm that dictated a strict national lockdown. This policy intervention forbade the population to go on the streets except for well-justified reasons and forced all shops (except pharmacies and stores selling basic necessities) to close. This was similar to other European countries like France or Italy. Furthermore, during mid-April and because the number of cases continued growing, the government tightened the lockdown by instructing all non-essential workers to stay at home (telework if possible).
The State of Alarm was in force until June 21, 2020. Prior to that date, the provinces started to go back to normal life gradually and asymmetrically according to their respective epidemiological situations. From 21 June onwards, mobility restrictions were fully eliminated, and people were free to move within the whole country. Since at that time the epidemic was under control (national mean of 14-day accumulated incidence per 100,000 inhabitants = 7.9) and given the great contribution of tourism to the Spanish GDP (around 11%), there was a great interest at that moment in recovering mobility during the summer period to foster the recovery of the tourism industry.
Our study covers the period from the end of the State of Alarm (24 June) to the end of September (30 September) 2020, a time span during which people could move across the Spanish territory without any movement restriction. We do not consider the month of October because at that time some local governments imposed some lockdowns and mobility limitations due to the surge in the number of cases. On 25 October, the central government declared a second State of Alarm to battle the uncontrolled propagation of the virus.
3.2. Dataset on mobility flows
Data on mobility flows (e.g., workplace, retail, and recreational activities, etc.) is obtained from the Spanish National Statistics Institute (INE). In 2019, INE initiated an ambitious project aimed at measuring daily mobility based on tracking spatio-temporal mobile position data. Smartphone movement data has been shown to be a useful and reliable tool for analysing both job-related and recreational flows within the country (Couture et al., 2022). To this end, INE signed a contract with the big three mobile phone operators by which anonymized, population-aggregated, real-time, mobile device GPS location data would be exploited for statistical purposes.2 Following a preliminary experiment in November 2019, INE started to provide public-access files about aggregate mobility flows from mid-March 2020 to December 2020.3
The area of residence of the owner of each mobile phone (mobility area, see below) is determined as the one in which the phone is observed most of the time between 0:00 and 6:00 h considering a 60-day period.4 This is provided by the corresponding mobile phone operator. To determine the destination mobility area, the operator provides daily information on the area(s) in which the phone is observed between 10:00 and 16:00 h. Based on this, the area in which most time is spent is taken as the destination area. If the area of most frequent stay is the one of residence, the individual is assumed to have not moved that day. In this way, short trips to non-residence areas are not counted as a flow if they represent a shorter period than that at the place of residence, even though the individual has indeed moved.5
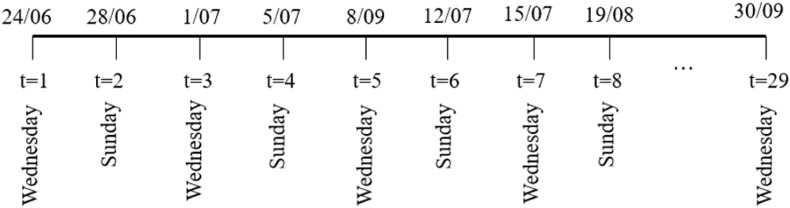
The data is disaggregated at three different regional levels: (i) autonomous communities (), (ii) provinces (), and (iii) mobility areas ().6 The data is collected at the mobility area level and then aggregated up to the province and the autonomous community level. Since the number of cases is not provided at the mobility area level, we take the province (NUTS 3) as the unit of analysis (for ).7 Mobility data is provided on a bi-weekly basis for both a selected weekday (always Wednesday) and a weekend day (always Sunday). As discussed before, we consider the period between 24 June and September 30, 2020. Accordingly, we have information for 29 time periods (two data points per week), resulting in a panel dataset of arrivals that includes a total of 1508 observations (). Fig. 1 illustrates the time dimension of the dataset.
Fig. 1.
Time dimension of the dataset on arrivals.
The number of arrivals in each province and their contribution to the spread of COVID-19 disease are likely to relate to the population size of the host province. On the one hand, highly populated provinces are more likely to receive more inflows for both work-related (commuting flows) and recreational reasons (visiting friends or relatives, shopping, tourism activities), ceteris paribus. On the other hand, the same number of arrivals might have a different effect on the spread of COVID-19 cases depending on the population size of the province. Therefore, we normalize the inflow of people that province i receives and express it in arrivals per 100,000 inhabitants (denoted by ), as is customary in the literature.
3.3. Dataset on cases
Information about the daily number of confirmed cases (through a positive PCR test) per province is collected from the National Epidemiological Surveillance Network (RENAVE).8 Since this data has daily frequency, we collect longitudinal data on a daily basis from 10 June to September 30, 2020.9 To make the number of cases comparable across provinces, they are also expressed in cases per 100,000 inhabitants (). Next, the accumulated incidence in the past 7 and 14 days (per 100,000 inhabitants) for each province is calculated as the corresponding rolling sum of daily cases up to each day ( and , respectively).
3.4. Dataset on weather conditions
The inflow of people to a region associated with recreational demand is likely to be affected by weather conditions (Dundas and von Haefen, 2020). Similarly, the accumulated COVID-19 incidence has been shown to correlate with atmospheric conditions (Méndez-Arriaga, 2020; Iqbal et al., 2020; Li et al., 2020; Notari, 2021). To consider meteorological conditions in the analysis, we gathered information on average temperature of each province on a daily basis from the Spanish Meteorological Agency (AEMET in Spanish), which provides detailed information on weather conditions based on data retrieved from more than 800 stations. That is, the original data consists of daily average temperature at several stations for each province (denoted by ). With this information, we subsequently calculated (i) the 7-day (14-day) moving average of daily temperatures before period t ( and ) and (ii) the 7-day (14-day) moving average of the daily standard deviation of mean temperature of each province. The latter aims to capture the large heterogeneity in temperature across stations within provinces ( and ).
3.5. Descriptive statistics
Since we have bi-weekly observations of mobility flows (Fig. 1), we only consider the values of , , , , , and that correspond to the Wednesdays and Sundays of each week. Table 1 presents descriptive statistics of the merged dataset. The mean number of confirmed cases per 100,000 inhabitants is 10.2, ranging from 0 to 72.59. Nevertheless, compared to the figures by the end of March 2020 (161.2) or the end of November 2020 (275.5), the summer of 2020 was a ‘valley’ period between the first and the second wave in which the epidemic was quite controlled. The mean number of arrivals per 100,000 inhabitants is around 17,000. The 7-day and 14-day accumulated incidences are about 71 and 133 cases per 100,000 inhabitants, on average. Finally, the average temperature is 22.6 °C, ranging from a minimum of 11.9 °C to a maximum of 31.7 °C.
Table 1.
Descriptive statistics of the dataset (N = 1508).
| Mean | SD | Min | Max | |
|---|---|---|---|---|
| cases | 10.212 | 11.249 | 0 | 72.590 |
| arrivals | 16,959.310 | 4046.828 | 6763.138 | 29,776.900 |
| AI7days | 71.286 | 77.653 | 0 | 429.796 |
| AI14days | 133.260 | 149.870 | 0 | 844.389 |
| Temp | 22.664 | 4.046 | 9.707 | 34.600 |
| Temp7days | 22.737 | 3.526 | 11.941 | 31.737 |
| SDTemp7days | 1.728 | 0.672 | 0 | 3.975 |
| Temp14days | 22.745 | 3.289 | 14.216 | 31.041 |
| SDTemp14days | 1.727 | 0.658 | 0 | 3.971 |
| Wednesday | 0.517 | 0.499 | 0 | 1 |
| Sunday | 0.482 | 0.499 | 0 | 1 |
| June | 0.069 | 0.253 | 0 | 1 |
| July | 0.310 | 0.462 | 0 | 1 |
| August | 0.310 | 0.462 | 0 | 1 |
| September | 0.310 | 0.462 | 0 | 1 |
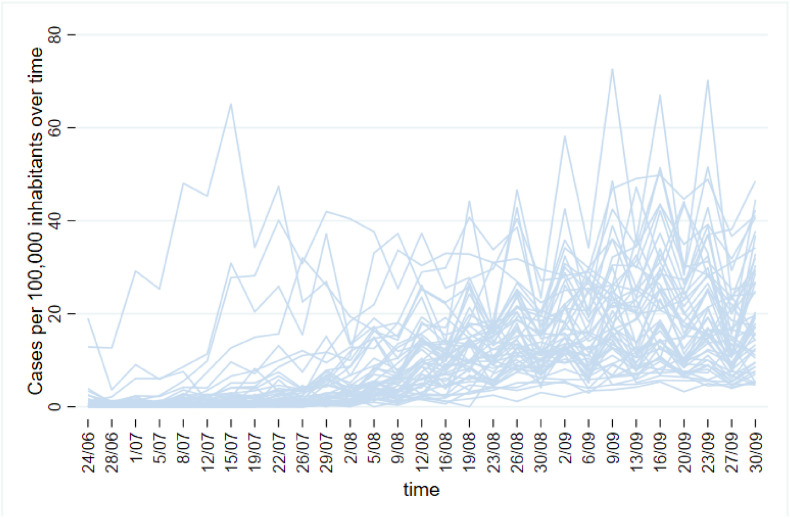
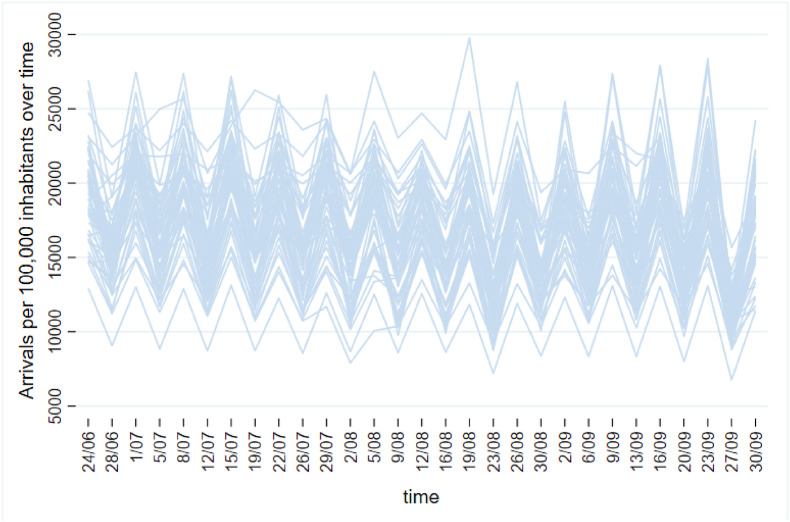
Fig. 2 illustrates the time evolution of cases during the study period.10 COVID-19 cases increased over time but with notable heterogeneity across provinces. Similarly, Fig. 3 plots the time evolution of arrivals. We see that the inflow of people to the provinces is always higher during weekdays (Wednesdays) than during weekends (Sundays). Fig. 3, Fig. 4 in the Supplementary Material plot the inter-weekly percentage change in cases and arrivals over time, calculated as the rate of change with respect to the same day the week before. As can be seen there, despite the large level differences in both variables between provinces, there is also strong temporal variability. As illustrated in Figure A4, arrivals vary considerably for both Wednesdays and Sundays relative to their figures the week before.
Fig. 2.
Time evolution of (normalized) cases per province during the study period.
Fig. 3.
Time evolution of (normalized) arrivals per province during the study period.
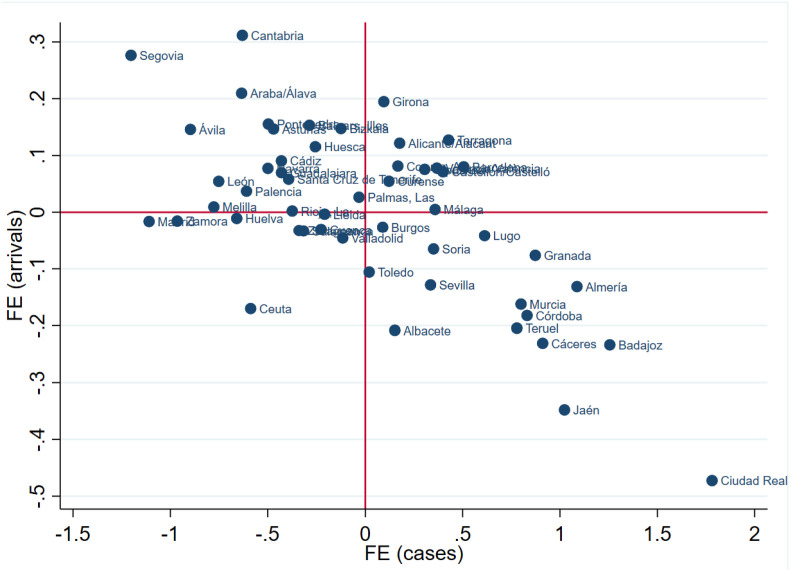
Fig. 4.
Scatterplot of the FEs estimates of the arrivals equation on the cases equation.
4. Empirical strategy
In this section, we describe our empirical strategy. First, we characterize how arrivals translate into a greater number of cases some days later. Second, we model how arrivals depend at the same time on the epidemiological circumstances of the destination province, which act as a deterrence factor. Finally, we discuss some endogeneity aspects and the exclusion restrictions used for the model identification.
4.1. First way: the effect of arrivals on cases
One of the most important aspects when studying the relationship between COVID-19 cases and mobility flows is to define the time lag that elapses between potential contagiousness and detection. Although there is no clear consensus in the medical literature, Lauer et al. (2020) report that the average incubation time is 5.1 days and that 97.5% of the symptoms mainly occur within 11.5 days of infection.11 In the main analysis, we consider a 7-day time lag. Nonetheless, in robustness checks we expand the time span to 10 and 14 days.
We initially propose the following regression model to explain the role of inflows in the number of cases:
| (1) |
where is a constant term, refers to the number of people per 100,000 inhabitants who arrived in province i the same day the week before (t-2), is the 7-day accumulated incidence per 100,000 inhabitants in province i in period t, is a vector of time controls including a time trend (in levels and in a squared form to capture non-linearities in the evolution of cases) and day (Sunday) and month (August and September) fixed effects, , and are parameters to be estimated, are province individual effects, and is the idiosyncratic error term. Both and are specified in logs to facilitate interpretation so that is understood as an elasticity (i.e. the percentage increase in new cases if there is a 1% increase in arrivals the week before).12 As done in Glaeser et al. (2020), we use the approximation ln (x+0.01) when the number of cases equals 0 (7.4% of the sample).
4.2. Second-way: how arrivals depend on epidemiological circumstances
Equation (1) models the role of the inflow of people to the province on COVID-19 cases a week later. However, as discussed before, it is highly likely that reacts to the epidemiological conditions in the province at that time. When threatened by the risk of infection, people engage in self-protective actions like avoiding unnecessary trips, changing the choice of destination, or staying at home. This pattern has been empirically documented in several works (Engle et al., 2020; Goolsbee and Syverson, 2021; Hu et al., 2021; Brinkman and Mangum, 2022), implying that part of the surge in cases associated with mobility could be subsequently compensated by the drop in arrivals in highly affected areas.
From an econometric viewpoint, is a potentially endogenous variable in (1) since both recreational and job-related flows might share unobservables with the cases 7 days before. For instance, unmeasured events that decrease the inflow of people to region i are likely to also affect the contemporaneous contagion rate, which translates into cases some days later. In this regard, Glaeser et al. (2020) documents potential reverse causality. Similar to their two-stage approach, we specify a second reduced-form equation for modelling as follows:
| (2) |
where is a constant term, is the accumulated incidence per 100,000 inhabitants in region i in t-2 (one week before), is the 7-day mean accumulated incidence in period t-2 in all the other regions except region i, denotes the mean temperature in province i in period t-2, is the same time controls defined for (1) but lagged two periods, , and are parameters to be estimated, are province individual effects, and is the error term.
Consistent with the theoretical framework developed by Engle et al. (2020), we assume that the decision to travel to region i in period t-2 is affected by the risk of contagion based on the accumulated incidence there at that time (. Weather conditions on that day () are also assumed to affect province inflows, particularly unscheduled trips. Time controls and province fixed effects capturing the heterogeneity in arrivals across provinces and over time are also considered here. The 7-day mean accumulated incidence in all the regions except region i ( captures epidemiological circumstances in all other provinces at that time that might deter province inflows through increased perceived risk (Engle et al., 2020; Matsuura and Saito, 2022) and is computed as follows:
| (3) |
Note this variable varies over time and across regions. This variable together with province's mean temperature are used as the exclusion restrictions for identification. It is assumed that the number of cases detected in region i in period t (equation (1)) is not affected by the mean national incidence excluding province i nor by the mean temperature in province i the week before conditional on the rest of controls including the instrumentalized (see below).13 Formal tests of these assumptions are presented in the Supplementary Material, Table 1, Table 2 .
Table 2.
Coefficient estimates.
| (1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
|---|---|---|---|---|---|---|
| Main equation |
Reduced form equation |
Reduced form equation |
Main equation |
Reduced form equation |
Reduced form equation |
|
| Dependent variable | ||||||
| 3.483*** (1.235) | 4.080*** (1.246) | |||||
| 0.022*** (0.003) | ||||||
| 0.011*** (0.001) | ||||||
| 0.506*** (0.152) | 10.410** (5.183) | 0.686*** (0.151) | 11.014 (9.570) | |||
| 0.185 (0.204) | 23.306*** (8.506) | 0.472** (0.193) | 29.862* (15.712) | |||
| 0.726* (0.397) | 2.020 (2.329) | 0.917** (0.405) | 4.434 (4.299) | |||
| 0.334*** (0.038) | 5.695*** (0.892) | 0.347*** (0.039) | 14.072*** (1.888) | |||
| −0.009*** (0.001) | −0.039 (0.030) | −0.010*** (0.001) | −0.144** (0.062) | |||
| −3.819*** (1.269) | −4.593*** (1.305) | |||||
| −0.014*** (0.003) | −0.008*** (0.001) | |||||
| −0.001*** (4.7e-04) | ||||||
| −2.9e-04*** (6.0e-05) | ||||||
| −0.001*** (2.9e-04) | ||||||
| −1.5e-04*** (3.3e-05) | ||||||
| −0.052*** (0.016) | −0.049*** (0.015) | |||||
| −0.014 (0.012) | −0.019 (0.012) | |||||
| 0.041** (0.020) | 0.038* (0.020) | |||||
| −0.317*** (0.005) | −0.316*** (0.005) | |||||
| −0.008*** (0.003) | −0.009*** (0.003) | |||||
| 4.2e-04*** (1.0e-04) | 0.001*** (1.2e-04) | |||||
| 0.002* (0.001) | 0.002* (0.001) | |||||
| −3.750*** (0.740) | ||||||
| −26.318*** (4.966) | ||||||
| −13.308*** (1.752) | ||||||
| −55.739*** (11.655) | ||||||
| constant | −37.208*** (12.375) | 9.979*** (0.021) | 116.771*** (18.371) | −43.103*** (12.467) | 9.941*** (0.031) | 348.805*** (40.394) |
| Province fixed effects |
YES |
YES |
YES |
YES |
YES |
YES |
| Number of provinces | 52 | 52 | 52 | 52 | 52 | 52 |
| Number of time periods | 27 | 27 | 29 | 27 | 27 | 29 |
| R-squared | 0.692 | 0.758 | 0.580 | 0.684 | 0.758 | 0.618 |
| Observations | 1404 | 1404 | 1508 | 1404 | 1404 | 1508 |
Note: Standard errors in parentheses; ***p < 0.01, **p < 0.05, *p < 0.1. Standard errors for the main equation have been bootstrapped after 1000 replications. The reference categories are June/July and Wednesday.
4.3. Endogeneity issues
The inclusion of in (1) aims to capture the existence of state dependence in the evolution of cases by which the current state depends on the accumulated state in the last period (Adda, 2016), even after controlling for and . Since is constructed as the 7-day moving average of the number of cases, the strict exogeneity assumption is ruled out unless = 0 because shocks affecting in period t affect future values of . In this case, the within-group (FE) estimator is inconsistent (Nickell, 1981). Similar to the empirical strategy implemented by Qiu et al. (2020), we specify a reduced-form equation using the 7-day moving average of provincial temperatures as instruments in the following manner:
| (4) |
where is a constant term, refers to the 7-day moving average of temperatures in province i in period t, is the standard deviation of , is the vector of time controls introduced before, , , and are parameters to be estimated, are time-invariant province individual effects, and is the idiosyncratic error term.
The mean levels of temperature during a week are expected to determine the accumulated incidence but to be uncorrelated with the number of cases detected in period t conditional on , and . The rationale is that temperature and its variability across space have been shown to be negatively correlated with transmission rates (e.g., reproduction number) through different causal mechanisms, including less resistance of the virus in aerosols or better functioning of the immune system when temperatures are high (Notari, 2021; Ratnesar-Shumate and Williams, 2020). However, the moving average of temperature is unlikely to determine the specific cases detected in period t except through its effect on and on . In other words, it is assumed that the rolling average of weather conditions affects the daily cases only through its effect on accumulated incidence/transmission rates but not through its effect on the specific cases detected in t. Table A3 in the Supplementary Material provides IV fixed-effects regression results showing that and are valid instruments: (i) they are sufficiently correlated with according to the first-stage F statistic, and (ii) they comply with the exogeneity requirements according to the Sargan test. Moreover, the Durbin-Wu-Hausman test confirms that is endogenous. Figures A5 and A6 in the Supplementary Material offer additional evidence on their uncorrelation with cases based on binned scattered regressions.
The model in (1), (2), (3), (4) is estimated using the control function approach (Wooldridge, 2015) by which the predicted residuals from equations (2), (4) conditional on the province effects ( and ) are added to equation (1) together with and . In this way, the effects of the accumulated incidence and (the lag of) the flow of arrivals on cases can be consistently estimated.14 Because we use fitted values in a two-stage procedure, standard errors are bootstrapped after 1000 replications following common practice.
Before moving on, as discussed in Mangrum and Niekamp (2022), we acknowledge that the data on the number of cases might not truly represent the real incidence of the epidemic due to undetected cases, unknown asymptomatic individuals, or differences in diagnostic tests.15 Unfortunately, there is no available data on PCR diagnostic tests for all the provinces during the study period. Nevertheless, this is partially alleviated by the inclusion of province fixed effects in the analysis, as discussed in Glaeser et al. (2020). Although there might be time variation in this, the time trend polynomial also partially controls for increases in the number of tests over time.
5. Results
5.1. Main findings
Columns 1–3 in Table 2 present the estimation results of the model in equations (4), (5), (6). A Hausman test (chi2(6) = 26.61, p-value<0.001) favours the treatment of province effects as parameters to be estimated (as opposed to random effects). The dummies Wednesday, June, and July are taken as the reference categories.
The residuals of the auxiliary first-stage regressions in (5), (6) are statistically significant for explaining the (log of) cases. This means there is evidence of endogeneity in both the number of arrivals and the accumulated incidence that needs to be accounted for. Specifically, unobservable factors affecting the arrivals a week before (t-2) and the cases detected in period t are negatively correlated. A naive model that treats and as if they were exogenous (Supplementary Material, Table A4) renders a non-significant but negative coefficient estimate for (t = −0.73).
Once these residuals have been conditioned out, we find that a 1% increase in the number of arrivals in period t-2 translates into a 3.5% increase in the number of confirmed cases the following week (t). This finding falls in line with the results by Carteni et al. (2020) and Mangrum and Niekamp (2022). Compared to the IV and panel estimates by Glaeser et al. (2020) for the USA, the elasticity of cases to arrivals is higher (3.5% vs 2.5–3.0%). Similarly, unobservable factors explaining the 7-day accumulated incidence negatively impact daily cases. Conditional on that, there is evidence of state dependence in the epidemiological evolution, consistent with previous findings for other epidemic diseases (Oster, 2005; Auld, 2006). A ten-case increase in the 7-day accumulated incidence translates into a 2.2% increase in daily cases. Furthermore, the number of cases has significantly increased over the study period according to the positive and significant estimated time trend (although at a decreasing rate). Note that these terms also capture any factor that impacts cases in all the provinces and varies over time. We also document that the average number of cases is significantly higher in August (relative to June/July) but does not differ significantly between Wednesdays and Sundays at a 95% confidence level.
Moving to the reduced form equation for , the inflow of people to the province in period t is negatively associated with both the 7-days accumulated incidence of the province and the 7-days accumulated incidence of the rest of the country at that moment. This result is consistent with Engle et al. (2020), Brinkman and Mangum (2022), Hu et al. (2021), and Matsuura and Saito (2022). Specifically, an increase of ten cases in translates into a 0.3% decrease in the number of arrivals. This implies that as the epidemiological situation of the province worsens, some people become reluctant to travel there. Nonetheless, the effect size is quite reduced. In the same fashion, an increase of ten cases in the mean accumulated incidence of all the other provinces is associated with a 1% decrease in the number of arrivals. Since this effect is conditional on , this indicates that a greater relative worsening of the epidemiological situation in the provinces of origin reduces total arrivals, in line with Matsuura and Saito (2022). Interestingly, contemporaneous temperature is only weakly correlated with the inflow of people to the province.
As for the reduced form equation for , we find that the accumulated incidence is negatively related to both the mean and the standard deviation of temperatures within the province, with both variables being statistically significant. This is consistent with previous evidence on the spread of COVID-19 showing that temperatures negatively affect COVID-19 transmission rates (Méndez-Arriaga, 2020; Iqbal et al., 2020; Li et al., 2020; Notari, 2021).
Columns 4–6 in Table 2 report the coefficient estimates for a model that replaces and by and , respectively. The time span for the mean and standard deviation of temperatures is also increased to 14 days. In this way, a longer period for the accumulated incidence is considered. The sign of the coefficients remains unchanged, and the magnitude of the estimates is very similar.
Fig. 4 presents a scatterplot of the province fixed effects (FEs) estimates from equations (1), (2). For the arrivals equation, these FEs capture factors that determine mobility flows like connectivity between provinces and their geographical position (Brinkman and Mangum, 2022), the sociodemographic structure of the population (Engle et al., 2020), the degree of economic activity and structure of labour markets for business trips, and regional attractiveness for leisure trips, among others. For the cases equation, the FEs control for aspects like the population density (Orea and Alvarez, 2022), the ability of regional health authorities to deal with the pandemic (Gutiérrez et al., 2021), potential differences in cultural traits (Chen et al., 2021), air pollution (Carteni et al., 2020), or the sociodemographic composition of the population (Glaeser et al., 2020), all which have been shown to affect infection rates. There seems to be a negative association between the two, implying that provinces with greater normalized inflows have fewer normalized cases, ceteris paribus. Although the FEs capture a plethora of time-invariant factors explaining both variables, this negative association could suggest that areas that receive a small number of arrivals (either due to reduced business activity or low tourism attractiveness) are the most vulnerable to the pandemic. As discussed in Gutiérrez et al. (2021), the large disparities in mean age, share of people in social exclusion and public expenditure on health services across Spanish regions partially explain the observed inequality in COVID-19 spread.
5.2. Robustness checks
Some robustness checks were performed. First, we consider both a 10-day and a 14-day lag period rather than a week to study the relationship between mobility flows and confirmed cases. That is, given the structure of the data, is replaced by and . The regression outputs are presented in Tables A5 and A6 of the Supplementary Material, respectively. The results are similar, although the impact of the number of arrivals on the number of cases is greater as the time span increases. Specifically, a 1% increase in the number of inflows is significantly associated with a 5.6% (5.2%) increase in the number of confirmed COVID19 cases 10 days (14 days) later. Second, since people typically schedule their trips some time in advance, we used further lags of the accumulated incidence for explaining arrivals in equation (2). The results are consistent with the output in Table 2 (Table A7 in Supplementary Material).
Third, Fig. 2 shows notable level differences between Wednesdays and Sundays. Although this is controlled for though the dummy indicator for Sundays, we conducted separate regressions by day of the week to inspect potential intra-week heterogeneity in the bivariate relationship between mobility flows and cases. The estimation results can be found in Tables A8 and A9 of the Supplementary Material. We find that the elasticity of cases to arrivals is notably higher on Sundays than on Wednesdays. This tentatively suggests that the propagation of COVID-19 cases is more sensitive to leisure than to labour mobility.
Fourth, authors like Glaeser et al. (2020) document substantial geographical heterogeneity in the relationship between mobility flows and cases. To explore this, we split the sample into two groups: northern and inland provinces on the one hand and southern and Mediterranean coastal provinces on the other. We find some heterogeneity in the influence of lagged arrivals on cases, with the elasticity being higher in southern-Mediterranean areas (Supplementary Material, Table A10).
Fifth, we have re-estimated the model including rainfall as an additional weather instrument. Specifically, we used the registered precipitation (, measured in millimetres) in equation (2) and the 7-day (14-day) moving average mean and standard deviation of precipitation ( and ) in equation (4). The data also comes from the Spanish Meteorological Agency. The estimation results are presented in Table A11. Contrary to temperature, rainfall is never significant for explaining either the inflow of people or the accumulated incidence. This is the reason why we only use temperature as the exclusion restriction.
Finally, although PCR tests are the official and most common way to detect cases, other methods like antigen or antibody tests are accepted. We repeated the estimation using the total (normalized) number of confirmed positive cases from any source instead of only from PCR tests. The estimates remain very similar, although the sensitivity of cases to flows is somewhat larger (Table A12 in the Supplementary Material).
5.3. Simulation analysis: what if the second State of Alarm had been implemented earlier?
As mentioned before, the central government declared a second State of Alarm on 25 October that set the following limitations: (i) a curfew between 11:00 and 6:00 h, and (ii) restrictions on entering and exiting the autonomous communities’ borders. Suppose that this second State of Alarm had been passed earlier. What would have been the reduction in cases if mobility flows had started to be restricted by, for instance, the beginning of September? In what follows, we perform a simulation analysis to answer this question based on our model estimates.
Assume that this hypothetical policy that restricts mobility reduces the inflow of people to each province by a fixed proportion . Suppose this policy is applied when some epidemiological criteria are met and that is why varies across provinces and over time (i.e., a subset of provinces are ‘treated’ by the policy and the rest are not). Let us adopt a potential outcomes framework where and denote the counterfactual (1) and actually observed (0) log of cases for province i in each period t, respectively. Let measure the log variation (rate change) in cases associated with the policy scenario (counterfactual minus observed) for each province and period:
| (5) |
with by construction for all non-treated provinces. For the subset of treated provinces, the log change in cases in t + 2 caused by the prior decrease in arrivals in t (one week before) will be given by:
| (6) |
However, the expected drop in cases in t + 2 will also decrease the number of cases in subsequent periods through the decline in accumulated incidence (. Therefore, the mobility limitation policy will produce two effects on the log variation in cases: (i) a direct drop caused by the decrease in the (log of) arrivals that would reduce the propagation of the virus through social interactions and (ii) an indirect effect associated with the decrease in the overall accumulated incidence among residents due to the prior drop in arrivals. For example, assuming , for t + 4 we would have16 :
| (7) |
Since and according to our model estimates in Table 2, equation (7) becomes:
| (8) |
where . The log variation in cases for subsequent periods t + s () is derived in a similar fashion. By rearranging equation (5), the predicted counterfactual number of cases under the policy scenario for each period t + s is obtained as:
| (9) |
Note that by substituting (9) and (6) in (8), the indirect effect in equation (8) explicitly depends on (see Supplementary Material for further details).
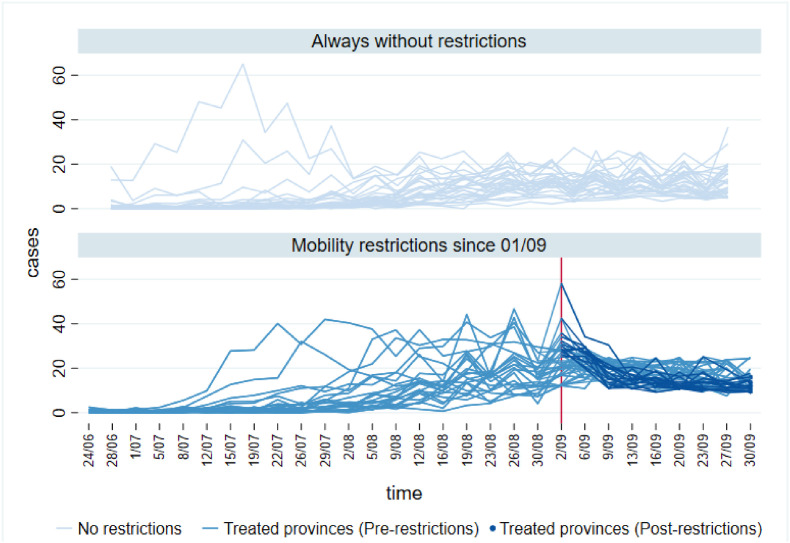
To perform this counterfactual exercise, let us first define a threshold over which the pandemic situation starts to become uncontrolled. According to the Harvard Global Health Institute (2020), more than 25 daily cases per 100,000 inhabitants was considered to represent a very high risk of COVID-19 transmission at that time (summer of 2020). Suppose that on 1 September the central government had set movement restrictions in those provinces with daily cases over such a threshold that translate into a drop in (normalized) arrivals by 25% on average. Importantly, the restrictions take effect only when the province surpasses 25 cases per 100,000 inhabitants, so that provinces enter and exit mobility restrictions in any period depending on their epidemiological circumstances.
Fig. 5 plots the time evolution of normalized COVID-19 cases from this simulation analysis, separately for those with and without mobility restrictions since 1 September. Table A13 in the Supplementary Material presents actual and simulated cases for each calendar date in our sample. We document that even a relatively small reduction in mobility by the end of the summer could have produced large drops in daily cases. Had arrivals in caseload areas decreased by 25%, provinces would have had 58% fewer cases by the beginning of September and 64% fewer at the end of September. This falls in line with studies documenting that mobility restrictions are especially effective in the beginning stages of growth (Orea and Alvarez, 2022; Saez et al., 2020; Fang et al., 2020; Brinkman and Mangum, 2022). This implies that cutting down mobility flows before the pandemic runs out of control proves to be an effective mechanism to avoid stricter measures later.17
Fig. 5.
Time evolution of normalized COVID-19 cases from the simulation analysis.
6. Conclusions
At the start of disease epidemics and while pharmaceutical interventions like vaccines are under development, public authorities typically resort to mobility restrictions, perimetric enclosures, stay-at-home orders, and, in some cases, enforced lockdowns to contain the propagation of the virus in the phases of exponential growth. This imposes important economic and social effects. During those periods in which the disease spread is kept under control and the incidence ratio lies within acceptable levels, governments start to relax the social distancing enforcement and the economy recovers certain dynamism (re-opening). However, the lifting of movement restrictions and resumption of normal activities make the risk of a flare-up in cases again a serious threat. The social benefits of mobility limitations therefore depend on the magnitude of the link between mobility and disease. The potential recurrence of distinct epidemic diseases in the near future calls for a deeper understanding of their driving sources.
Taking Spain as the case study, this paper has examined the bivariate (two-way) relationship between mobility flows and the spread of COVID-19 cases considering the time span between the first and second waves of the pandemic (summer of 2020). The high reliance of the Spanish economy on the tourism sector was one of the reasons why there was a need to incentivize domestic leisure trips. By combining longitudinal data on arrivals from mobile phone position tracking and official records of cases at the province level, the paper sheds light on how unrestricted flows contribute to disease recurrence.
Once having controlled for potential reverse causality and endogeneity using a control function approach, the estimates show that 1% increase in the number of arrivals in a province in period t translates into an increase of around 3.5% in the number of cases seven days later and about 5.6% ten days later. This clearly suggests that inflows positively impact new cases. Given that the incubation period of COVID-19 is around a week, arrivals translate into disease spread though social interactions with some delay. Therefore, it seems that summer flows are partially responsible for the Spanish second wave that started in September 2020 and peaked in November 2020. The results from a simulation analysis suggest that early mobility restrictions in those provinces with more severe outbreaks could have been highly effective at containing the virus spread. According to our estimates, cutting down mobility by 25% by the beginning of September 2020 would have contained the subsequent COVID-19 spread that led to the second State of Alarm (−64% fewer cases by the end of September).
The results also show there is state dependence in the propagation of COVID-19. Consistent with epidemiological models, we document that a greater accumulated incidence in the province translates into more cases. This is robust to the time window considered. Interestingly, we show that arrivals in the province are negatively affected by its epidemiological situation. As the moving average of accumulated incidence rises, the province becomes less attractive to potential commuters and tourists. This is consistent with people engaging in avoidance behaviour to minimize risks when the risk becomes highly prevalent. As such, in the absence of further public intervention, a bad epidemiological situation in a province partially helps to contain the number of arrivals and the associated propagation to other areas. Put another way, the outbreak would have spread faster had mobility not partially dropped. However, since cases are detected with some delay, by the time a province starts to decrease its number of arrivals, the virus might have already spread to other areas. The main takeaway is therefore that unrestricted mobility contributes to the spread of COVID-19, but as the infection rate rises, voluntary reductions in arrivals through increased exposure help to partially control the virus outbreak.
The findings have some important implications that contribute to the existing debate about public interventions to battle COVID-19 and future epidemics. Public information about the spread of the virus appears to be highly relevant, since people voluntarily avoid caseload areas, which partially helps to naturally control case growth. Nonetheless, this is not enough. The analysis also suggests that a widespread relaxation of social distancing during periods in which the disease is apparently under control can quickly accelerate the resurgence of disease spread. Accurate tracking of mobility flows through anonymized mobile phone geolocation can help public authorities to identify those areas that are receiving greater inflows and to possibly reinforce controls and awareness messages, and even impose some restrictions if needed before the epidemiological situation becomes out of control again. Moderate mobility restrictions at early stages can help to quickly ‘flatten the curve’ through drops in social interactions between neighbouring regions and lead to a subsequent decline in local infections through decreased incidence.
The study has some limitations. First, we lack data on the number of diagnostic tests performed in each province. Similarly, official records on the number of cases might underestimate the true prevalence of the disease due to asymptomatic individuals and undetected cases. Nevertheless, we assume that they are an accurate approximation of the true cases. Second, we cannot determine whether the disease spread associated with province arrivals emerges from travelling itself or through interactions at the destination. Finally, the analysis is performed for the summer of 2020 after a strict lockdown period. This means that the value of the elasticity of cases to mobility flows could be different if computed in other countries or even considering a different time span for Spain. This calls for further studies on the two-way linkages between mobility flows and disease spread in different areas and periods.
Funding
The author acknowledges financial support from the grant PID2020-115183RB-C21 funded by MCIN/AEI//10.13039/501100011033.
Declaration of competing interest
The author(s) have no conflict of interest to state.
Acknowledgements
The author gratefully thanks helpful comments and suggestions made by the Editor, the Associate Editor and two anonymous referees.
Footnotes
In this sense, some recent works have highlighted the need to use high-frequency data to track economic activity, particularly during crises (Menezes et al., 2022; Lourenço and Rua, 2021).
The three operators (Movistar, Orange, and Vodafone) represent 78.7% of the mobile phone market (more than 42 million users) in Spain (National Commission for Markets and Competence, 2019). Since all three have a significant market share in each province, this data is representative.
The dataset is freely available at: https://www.ine.es/experimental/movilidad/experimental_em.htm.
Mobile phones that are not registered in Spain (roaming by tourists) are excluded from the analysis so that the data only refers to Spanish residents.
We therefore work with data about mobility between areas but not within areas. As discussed in Brinkman and Mangum (2022) this form of mobility is the most likely to spread COVID-19 over the territory. Additionally, due to the impossibility of geolocating a mobile phone with full precision, there is some potential measurement error at the borders. Nevertheless, the impact of this is expected to be minimal.
Each mobility area corresponds to municipalities with between 5000 and 50,000 inhabitants or the aggregation of several municipalities having up to 5000 inhabitants. Mobility areas are thus more homogeneous than municipalities. The average size of each mobility area is 15,000 people (12,000 mobile phones). Cities with more than 50,000 inhabitants are disaggregated into several mobility areas (districts or neighbourhoods).
In Spain, the province is the geographical unit most commonly used by health authorities to track cases and impose mobility restrictions and lockdowns (Orea and Alvarez, 2022).
Counts of daily new cases come from the department of public health of each autonomous community, disaggregated into the different provinces that belong to each autonomous community. The data is available at https://cnecovid.isciii.es/covid19/.
As introduced before, the analysis starts on 24 June 2020. However, we collected data on cases starting in 10 June to compute the one-week and two-week accumulated incidence for each province for the first observation period.
To illustrate the geographical variability, Fig. 1, Fig. 2 in the Supplementary Material map the normalized number of cases and arrivals in each province at four selected periods (24 June, 2 August, 2 September and 30 September).
Recall the analysis uses data for the summer of 2020. At that time, incubation rates were different from those of subsequent coronavirus variants.
Importantly, the calculation of does not include detected in period t but the ones 7 days before.
For being a valid instrument, we must also rule out potential indirect effects on through second-order autocorrelation in the residuals in (1). Inoue and Solon (2006) LM test does not reject the null hypothesis of no autocorrelation of order two (IS-stat = 51.6, p-value = 0.451). We thank an anonymous reviewer for spotting this issue.
The CF method produces coefficient estimates that are equivalent to the 2SLS procedure (Hausman, 1978). However, it has the advantage that it provides a heteroskedasticity-robust Hausman test of endogeneity by simply testing whether the coefficient estimates for and are statistically significant in the structural equation (Wooldridge, 2015).
Some recent works have started to focus on the estimation of unreported cases by combining SIR (Susceptible-Infected-Recovered) models with stochastic frontier analysis (Orea et al., 2021; Millimet and Parmeter, 2022).
Because of the bi-weakly time structure of our data, we make the assumption that the new 7-day accumulated incidence under the policy is approximately seven times the new cases the same day the week before.
Further descriptive statistics and details on the actual and simulated cases can be found in the Supplementary Material.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.econmod.2022.106083.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
Data availability
Data will be made available on request.
References
- Adda J. Economic activity and the spread of viral diseases: evidence from high frequency data. Q. J. Econ. 2016;131(2):891–941. [Google Scholar]
- Alexander D., Karger E. 2021. Do Stay-At-Home Orders Cause People to Stay at Home? Effects of Stay-At-Home Orders on Consumer Behavior. The Review of Economics and Statistics, forthcoming. [DOI] [Google Scholar]
- Allcott H., Boxell L., Conway J., Gentzkow M., Thaler M., Yang D. Polarization and public health: partisan differences in social distancing during the coronavirus pandemic. J. Publ. Econ. 2020;191 doi: 10.1016/j.jpubeco.2020.104254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auld M.C. Estimating behavioral response to the AIDS epidemic. B E J. Econ. Anal. Pol. 2006;5(1) doi: 10.2202/1538-0645.1235. [DOI] [Google Scholar]
- Badr H.S., Du H., Marshall M., Dong E., Squire M.M., Gardner L.M. Association between mobility patterns and COVID-19 transmission in the USA: a mathematical modelling study. Lancet Infect. Dis. 2020;20:1247–1254. doi: 10.1016/S1473-3099(20)30553-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck M.J., Hensher D.A., Wei E. Slowly coming out of COVID-19 restrictions in Australia: implications for working from home and commuting trips by car and public transport. J. Transport Geogr. 2020;88 doi: 10.1016/j.jtrangeo.2020.102846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett D., Chiang C.F., Malani A. Learning during a crisis: the SARS epidemic in Taiwan. J. Dev. Econ. 2015;112:1–18. doi: 10.1016/j.jdeveco.2014.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borkowski P., Jazdzewska-Gutta M., Szmelter-Jarosz A. Lockdowned: everyday mobility changes in response to COVID-19. J. Transport Geogr. 2021;90 doi: 10.1016/j.jtrangeo.2020.102906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bounie D., Camara Y., Galbraith J. 2020. Consumers' Mobility, Expenditure and Online-Offline Substitution Response to COVID-19: Evidence from French Transaction Data. Available at: SSRN 3588373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggs A.H., Goldstein D.A., Kirwin E., Meacock R., Pandya A., Vanness D.J., Wisloff T. Estimating (quality-adjusted) life-year losses associated with deaths: with application to COVID-19. Health Econ. 2021;30(3):699–707. doi: 10.1002/hec.4208. [DOI] [PubMed] [Google Scholar]
- Brinkman J., Mangum K. The geography of travel behavior in the early phase of the COVID-19 pandemic. J. Urban Econ. 2022;127 doi: 10.1016/j.jue.2021.103384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodeur A., Clark A.E., Fleche S., Pwdthavee N. COVID-19, lockdowns and well-being: evidence from google trends. J. Publ. Econ. 2021;193 doi: 10.1016/j.jpubeco.2020.104346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brynjolfsson E., Horton J.J., Ozimek A., Rock D., Sharma G., TuYe H. 2020. COVID-19 and Remote Work: an Early Look at US Data. NBER Working Paper 27344. [Google Scholar]
- Campos-Vazquez R.M., Esquivel G. Consumption and geographic mobility in pandemic times. Evidence from Mexico. Rev. Econ. Househ. 2021;19:353–371. doi: 10.1007/s11150-020-09539-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carteni A., Di Francesco L., Martino M. How mobility habits influenced the spread of the COVID-19 pandemic: results from the Italian case study. Sci. Total Environ. 2020;741(1) doi: 10.1016/j.scitotenv.2020.140489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C., Frey C.B., Presidente G. Culture and contagion: individualism and compliance with COVID-19 policy. J. Econ. Behav. Organ. 2021;190:191–200. doi: 10.1016/j.jebo.2021.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F., Jiang M., Rabidoux S., Robinson S. Public avoidance and epidemics: insights from an economic model. J. Theor. Biol. 2011;278:107–119. doi: 10.1016/j.jtbi.2011.03.007. [DOI] [PubMed] [Google Scholar]
- Chen H., Qian W., Wen Q. The impact of the COVID-19 pandemic on consumption: learning from high-frequency transaction data. Am. Econ. Rev.: P&P. 2021;111:307–311. [Google Scholar]
- Chien P.M., Sharifpour M., Ritchie B.W., Watson B. Travelers' health risk perceptions and protective behavior: a psychological approach. J. Trav. Res. 2017;56(6):744–759. [Google Scholar]
- Chinazzi M., Davis J.T., Ajelli M., Gioannini C., et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science. 2020;368:395–400. doi: 10.1126/science.aba9757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couture V., Dingel J.I., Green A., Handbury J., Williams K.R. Measuring movement and social contact with smartphone data: a real-time application to COVID-19. J. Urban Econ. 2022;127 doi: 10.1016/j.jue.2021.103328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cronin C.J., Evans W.N. 2020. Private Precaution and Public Restrictions: what Drives Social Distancing and Industry Foot Traffic in the COVID-19 Era? NBER Working Paper 27531. [Google Scholar]
- Cuñat A., Zymek R. The (structural) gravity of epidemics. Eur. Econ. Rev. 2022;144 [Google Scholar]
- Dundas S.J., von Haefen R.H. The effects of weather on recreational fishing demand and adaptation: implications for a changing climate. Journal of the Association of Environmental and Resource Economists. 2020;7(2):209–242. [Google Scholar]
- Engle S., Stromme J., Zhou A. 2020. Staying at Home: Mobility Effects of COVID-19. Available at: SSRN. [DOI] [Google Scholar]
- Fang H., Wang L., Yang Y. Human mobility restrictions and the spread of the Novel Coronavirus (2019-nCoV) in China. J. Publ. Econ. 2020;191 doi: 10.1016/j.jpubeco.2020.104272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fenichel E.P. Economic considerations for social distancing and behavioral based policies during an epidemic. J. Health Econ. 2013;32:440–451. doi: 10.1016/j.jhealeco.2013.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetzer T., Hensel L., Hermle J., Roth C. Coronavirus perceptions and economic anxiety. Rev. Econ. Stat. 2021;103(5):968–978. [Google Scholar]
- Forsythe E., Kahn L.B., Lange F., Wiczer D. Labor demand in the time of COVID-19: evidence from vacancy postings and UI claims. J. Publ. Econ. 2020;189 doi: 10.1016/j.jpubeco.2020.104238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geoffard P.Y., Philipson T. Rational epidemics and their public control. Int. Econ. Rev. 1996;37(3):603–624. [Google Scholar]
- Glaeser E.L., Gorback C., Redding S.J. How much does COVID-19 increase with mobility? Evidence from New York and four other U.S. cities. J. Urban Econ. 2020;127 doi: 10.1016/j.jue.2020.103292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golman R., Hagmann D., Loewenstein G. Information avoidance. J. Econ. Lit. 2017;55(1):96–135. [Google Scholar]
- Goolsbee A., Syverson C. Fear, lockdown and diversion: comparing drivers of pandemic economic decline 2020. J. Publ. Econ. 2021;193 doi: 10.1016/j.jpubeco.2020.104311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutiérrez M.J., Inguanzo B., Orbe S. Distributional impact of COVID-19: regional inequalities in cases and deaths in Spain during the first wave. Appl. Econ. 2021;53(31):3636–3657. [Google Scholar]
- Harvard Global Health Institute . 2020. Key Metrics for COVID Suppression.https://globalepidemics.org/key-metrics-for-covid-suppression/ July 1, 2020. Available at: [Google Scholar]
- Hausman J. Specification tests in econometrics. Econometrica. 1978;46(6):1251–1271. [Google Scholar]
- Hu S., Xiong C., Yang M., Younes H., Luo W., Zhang L. A big-data driven approach to analyzing and modeling human mobility trend under non-pharmaceutical interventions during COVID-19 pandemic. Transport. Res. Part C. 2021;124 doi: 10.1016/j.trc.2020.102955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoue A., Solon G. A portmanteau test for serially correlated errors in fixed effects models. Econom. Theor. 2006;22:835–851. [Google Scholar]
- Iqbal M.M., Abid I., Hussain S., Shahzad N., Waqas M.S., Iqbal M.J. The effects of regional climatic condition on the spread of COVID-19 at global scale. Sci. Total Environ. 2020;739 doi: 10.1016/j.scitotenv.2020.140101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia J.S., Lu X., Yuan Y., Xu G., Jia J., Christakis N.A. Population flow drives spatio-temporal distribution of COVID-19 in China. Nature. 2020;582:389–394. doi: 10.1038/s41586-020-2284-y. [DOI] [PubMed] [Google Scholar]
- Kremer M. Integrating behavioral choice into epidemiological models of AIDS. Q. J. Econ. 1996;111(2):549–573. [Google Scholar]
- Landry C.E., Bergstrom J., Salazar J., Turner D. How has the COVID-19 pandemic affected outdoor recreation in the U.S.? A revealed preference approach. Appl. Econ. Perspect. Pol. 2021;43(1):443–457. [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of Coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;179(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Xu X., Dai D., Huang Z., Ma Z., Guan Y. Air pollution and temperature are associated with increased COVID-19 incidence: a time series study. Int. J. Infect. Dis. 2020;97:278–282. doi: 10.1016/j.ijid.2020.05.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço N., Rua A. The Daily Economic Indicator: tracking economic activity daily during the lockdown. Econ. Modell. 2021;100 doi: 10.1016/j.econmod.2021.105500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mangrum D., Niekamp P. College student travel contributed to local COVID-19 spread. J. Urban Econ. 2022;127 doi: 10.1016/j.jue.2020.103311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuura T., Saito H. The COVID-19 pandemic and domestic travel subsidies. Ann. Tourism Res. 2022;92 doi: 10.1016/j.annals.2021.103326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Méndez-Arriaga F. The temperature and regional climate effects on communitarian COVID-19 contagion in Mexico throughout phase 1. Sci. Total Environ. 2020;735 doi: 10.1016/j.scitotenv.2020.139560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendolia S., Stavrunova O., Yerokhin O. Determinants of the community mobility during the COVID-19 pandemic: the role of government regulations and information. J. Econ. Behav. Organ. 2021;184:199–231. doi: 10.1016/j.jebo.2021.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menezes F., Figer V., Jardim F., Medeiros P. A near real-time economic activity tracker for the Brazilian economy during the COVID-19 pandemic. Econ. Modell. 2022;112 doi: 10.1016/j.econmod.2022.105851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mertzanis C., Papastathopoulos A. Epidemiological susceptibility and tourist flows around the world. Ann. Tourism Res. 2021;86 [Google Scholar]
- Mesnard A., Seabright P. Escaping epidemics through migration? Quarantine measures under incomplete information about infection risk. J. Publ. Econ. 2009;93:931–938. [Google Scholar]
- Milani F. COVID-19 outbreak, social response, and early economic effects: a global VAR analysis of cross-country interdependencies. J. Popul. Econ. 2021;34:223–252. doi: 10.1007/s00148-020-00792-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millimet D.L., Parmeter C.F. COVID-19 severity: a new approach to quantifying global cases and deaths. J. Roy. Stat. Soc. 2022;185:1178–1215. doi: 10.1111/rssa.12826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickell S. Biases in dynamic models with fixed effects. Econometrica. 1981;49(6):1417–1426. [Google Scholar]
- Notari A. Temperature dependence of COVID-19 transmission. Sci. Total Environ. 2021;763 doi: 10.1016/j.scitotenv.2020.144390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orea L., Alvarez I.C. How effective has the Spanish lockdown been to battle COVID-19? A spatial analysis of the coronavirus propagation across provinces. Health Econ. 2022;31:154–173. doi: 10.1002/hec.4437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orea L., Alvarez I.C., Wall A. 2021. Estimating the Propagation of the COVID-19 Virus with a Stochastic Frontier Approximation of Epidemiological Models: a Panel Data Econometric Model with an Application to Spain. Efficiency Series Paper 1/2021. [Google Scholar]
- Orset C. People's perception and cost-effectiveness of home confinement during an influenza pandemic: evidence from the French case. Eur. J. Health Econ. 2018;19:1335–1350. doi: 10.1007/s10198-018-0978-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oster E. Sexually transmitted infections, sexual behavior, and the HIV/AIDS epidemic. Q. J. Econ. 2005;120(2):467–515. [Google Scholar]
- Pellegrini I.S. Oxford Bulletin of Economics and Statistics; 2021. Untimely Reopening? Increase in the Number of New COVID-19 Cases after Reopening in One Brazilian State. [DOI] [Google Scholar]
- Qiu Y., Chen X., Shi W. Impacts of social and economic factors on the transmission of coronavirus disease 2019 (COVID-19) in China. J. Popul. Econ. 2020;33:1127–1172. doi: 10.1007/s00148-020-00778-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratnesar-Shumate S., Williams G., et al. Simulated sunlight rapidly inactivates SARS-CoV-2 on surfaces. J. Infect. Dis. 2020;222(2):214–222. doi: 10.1093/infdis/jiaa274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saez M., Tobias A., Varga D., Barceló M.A. Effectiveness of the measures to flatten the epidemic curve of COVID-19. The case of Spain. Sci. Total Environ. 2020;727 doi: 10.1016/j.scitotenv.2020.138761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan L., Wan Q. High-speed railway and the intercity transmission of epidemics: evidence from COVID-19 in China. Econ. Modell. 2022;114 doi: 10.1016/j.econmod.2022.105934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wooldridge J.M. Control function methods in applied econometrics. J. Hum. Resour. 2015;50(2):420–445. [Google Scholar]
- World Health Organization . 2021. World Health Organization Coronavirus Disease (COVID-19) Dashboard.https://covid19.who.int/ Available at: [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.