Abstract
Neuroimaging‐driven brain age estimation has become popular in measuring brain aging and identifying neurodegenerations. However, the single estimated brain age (gap) compromises regional variations of brain aging, losing spatial specificity across diseases which is valuable for early screening. In this study, we combined brain age modeling with Shapley Additive Explanations to measure brain aging as a feature contribution vector underlying spatial pathological aging mechanism. Specifically, we regressed age with volumetric brain features using machine learning to construct the brain age model, and model‐agnostic Shapley values were calculated to attribute regional brain aging for each subject's age estimation, forming the brain age vector. Spatial specificity of the brain age vector was evaluated among groups of normal aging, prodromal Parkinson disease (PD), stable mild cognitive impairment (sMCI), and progressive mild cognitive impairment (pMCI). Machine learning methods were adopted to examine the discriminability of the brain age vector in early disease screening, compared with the other two brain aging metrics (single brain age gap, regional brain age gaps) and brain volumes. Results showed that the proposed brain age vector accurately reflected disorder‐specific abnormal aging patterns related to the medial temporal and the striatum for prodromal AD (sMCI vs. pMCI) and PD (healthy controls [HC] vs. prodromal PD), respectively, and demonstrated outstanding performance in early disease screening, with area under the curves of 83.39% and 72.28% in detecting pMCI and prodromal PD, respectively. In conclusion, the proposed brain age vector effectively improves spatial specificity of brain aging measurement and enables individual screening of neurodegenerative diseases.
Keywords: brain aging, individual early screening, neurodegenerative diseases, Shapley values, spatial specificity
We combined brain age modeling with SHAP feature attribution to measure brain aging as a feature contribution vector underlying spatial pathological aging mechanism. The proposed brain age vector accurately revealed disorder‐specific spatial abnormal aging patterns, and enhanced individual early screening of neurodegenerative diseases.
1. INTRODUCTION
Brain aging is accompanied by complex and specific morphological change patterns across the lifespan (Good et al., 2001; Kennedy et al., 2009; Lemaitre et al., 2012; Long et al., 2012). These age‐related brain changes can also be aggravated by neurodegenerative diseases. For instance, regional accelerated atrophies demonstrate strong aging effects in many neurodegenerative disorders, such as Alzheimer disease (AD) and Parkinson disease (PD; Fioravanti et al., 2015; McDonald et al., 2009). To measure brain aging, one of the most popular approaches is to regress age based on neuroimaging data, using machine learning (Cole et al., 2017; Franke & Gaser, 2019; Franke et al., 2010), and the deviation between the estimated age and chronological age, termed “brain age gap”, can simply assess the degree of abnormal aging (acceleration or deceleration). Previous studies have demonstrated a positive brain age gap existing in several neurological diseases, such as AD (Franke et al., 2010; Gaser et al., 2013), PD (Beheshti et al., 2020), mild cognitive impairment (MCI; Franke & Gaser, 2012), dementia (Wang et al., 2019), schizophrenia (Kuo et al., 2020), and further suggested that the degree of accelerated brain aging could considerably determine the likelihood of diseases (Koutsouleris et al., 2014).
However, the single estimated brain age (gap) losses spatial specificity across diseases, and shows poor discriminability in identifying early neurodegenerations with subtle brain changes. Brain aging is not a linear trajectory, but a complex process that differs among regions. While the thalamus volumes gradually decrease since adulthood, the hippocampal volumes are found to slightly increase until age of 40, and decrease rapidly after 60 years (Jernigan et al., 2001; Long et al., 2012). Likewise, although apparently accelerated atrophies in the striatum have been reported in early PD, cortical changes are relatively subtle (Lewis et al., 2016). Nevertheless, early AD patients show extensive cortical changes with the most severe atrophy in the medial temporal (Johnson et al., 2012). Therefore, it is obvious that a single metric (estimated brain age) cannot fully characterize these complex regional variations across diseases. To solve this issue, Kaufmann et al. (2019) have trained brain age models for each of the brain regions and demonstrated specific neuroanatomical distribution of brain age gaps for several brain disorders . However, the fineness of the neuroanatomical distribution is limited by the number of regional models. Besides, brain regions with low age correlation may affect the accuracy of regional models. Therefore, precise approaches to characterizing regional variations of brain aging are needed to improve the disorder specificity of brain aging measurement.
Model interpretation methods provide a new perspective for investigating disease mechanism. Generally, these methods establish dependencies between multiple features and the machine learning target by quantifying feature contributions to the model (estimations). Then, neuroimaging features (regions, voxels, etc.) with greater contributions are considered with more disorder specificity for disease discrimination (Bloch & Friedrich, 2021; Li et al., 2020; Oh et al., 2019). A popular recent addition, Shapley Additive Explanations (SHAP), provides individual feature attribution based on game theory (Lundberg & Lee, 2017b; Lundberg et al., 2019). Bloch and Friedrich (2021) have applied SHAP analysis in AD classification, and indicated the volume of the left hippocampus as one of the most disorder‐specific features in predicting AD conversion. Besides, consistent results of feature variations in healthy people have also shown across different types of brain age models, using SHAP (Ball et al., 2021). In age estimation of patients, SHAP can be used to attribute the estimated brain age gap to each brain feature, thus brain aging can be specifically refined to regional feature contributions underlying spatial pathological aging mechanism.
In this study, we proposed a brain age vector to measure disorder‐specific brain aging for individual early screening of AD and PD based on model‐agnostic SHAP. Specifically, the brain age estimation model was first trained on a multicenter brain MRI (magnetic resonance imaging) data set consisting of a large number of healthy people (N = 4174). Then, SHAP feature attribution was implemented on age estimations of the external clinical data sets (consisting of normal aging [N = 171], prodromal PD [N = 174], stable MCI [sMCI; N = 69], and progressive MCI [pMCI; N = 64] subjects) to construct the brain age vector for each subject. Furthermore, we compared the spatial specificity and individual discriminability of the brain age vector with the other two brain aging metrics (single brain age gap and regional brain age gaps) and brain volumes. We hypothesized that the proposed brain age vector could reveal disorder‐specific abnormal aging patterns and enhance individual screening of neurodegenerative diseases.
2. MATERIALS AND METHODS
2.1. Data preparation
Data used in this study were obtained from six independent public data sets including the IXI database (https://brain-development.org/ixi-dataset/), Open Access Series of Imaging Studies (OASIS; https://www.oasis-brains.org/), Southwest University Longitudinal Imaging Multimodal Brain Data Repository (SLIM; Liu et al., 2017), International Neuroimaging Data sharing (INDI; https://fcon_1000.projects.nitrc.org/indi/IndiPro.html/), Alzheimer Disease Neuroimaging Initiative (ADNI; www.loni.ucla.edu/ADNI/), and Parkinson Progression Markers Initiative (PPMI; www.ppmi-info.org). Each site received approval from an ethical committee on human experimentation before study's initiation.
A total of 4652 T1‐weighted MRI scans acquired at either 1.5 or 3 T were obtained in this study. Subjects with unclear demographic information were removed. We included 4174 T1‐weighted MRI scans of healthy subjects (aged 9–96 years) from the IXI, OASIS, SLIM, INDI, and ADNI in the brain age modeling (training and evaluation) data set to ensure the generalizability of the brain age estimator. Clinical data sets consisted of AD and PD groups. Subjects in AD groups included 69 sMCI patients and 64 pMCI (prodromal AD) patients from ADNI. Specifically, sMCI subjects were diagnosed as MCI at all available points at least for 3 years, and the baseline T1w MRI scans were selected. pMCI subjects were diagnosed as MCI, but converted to AD in subsequent follow‐ups without any reversion, and the T1 images scanned within 2 years (more than 1 year) before diagnosis of AD were selected. Complete follow‐up records for at least 3 successive years are available for each subject in AD groups, and participants that did not pass quality control in the 3 years were excluded. Subjects in PD groups included 174 prodromal PD patients, and 171 HC from PPMI, for which only the baseline scans were obtained. The diagnostic criteria of prodromal PD followed the inclusion criteria for prodromal patients of the PPMI study (https://www.ppmi-info.org/study-design/research-documents-and-sops). Both AD and PD groups were matched for age.
For AD groups, the Mini‐Mental State Examination (MMSE) and Clinical Dementia Rating (CDR) were obtained as clinical parameters. For PD groups, the Movement Disorder Society‐Sponsored Revision of the Unified Parkinson Disease Rating Scale (MDS‐UPDRS), part III (UPDRS III), the REM (Rapid Eye Movement) Sleep Behavior Disorder Screening Questionnaire (RBDSQ), and the Epworth Sleepiness Score (ESS) were considered. The demographic details are summarized in Table 1.
TABLE 1.
Characteristics of multicenter subjects
| Brain age modeling data set | Clinical data sets | p Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data set | ADNI | OASIS | IXI | SLIM | INDI | ADNI | ADNI | PPMI | PPMI | ADNI | PPMI |
| Category | HC | HC | HC | HC | HC | sMCI | pMCI | HC | Prodromal PD | sMCI vs. pMCI | HC vs. prodromal PD |
| No of subject | 1444 | 1136 | 461 | 453 | 680 | 69 | 64 | 171 | 174 | ‐ | ‐ |
| Female/Male | 751/693 | 696/440 | 256/205 | 287/166 | 371/309 | 28/41 | 26/38 | 65/106 | 97/77 | ‐ | ‐ |
| Age (years) | 76.43 ± 6.37 | 67.71 ± 8.81 | 51.18 ± 15.99 | 44.91 ± 17.57 | 25.82 ± 10.71 | 76.10 ± 6.77 | 76.95 ± 6.89 | 60.45 ± 11.68 | 61.06 ± 7.53 | .477 | .574 |
| MMSE | ‐ | ‐ | ‐ | ‐ | ‐ | 27.88 ± 1.84 | 25.50 ± 2.38 | ‐ | ‐ | <.001*** | ‐ |
| CDR | ‐ | ‐ | ‐ | ‐ | ‐ | 0.5 ± 0.0 | 0.5 ± 0.06 | ‐ | ‐ | .301 | ‐ |
| UPDRS III | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | 0.92 ± 1.94 | 2.64 ± 3.95 | ‐ | <.001*** |
| ESS | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | 5.42 ± 3.41 | 5.37 ± 3.37 | ‐ | .891 |
| RBDSQ | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ | 2.89 ± 2.29 | 4.14 ± 2.98 | ‐ | <.001*** |
Note: All data are presented in mean ± SD mode, and p values are significant of p < .05 (uncorrected for Tukey HSD test). *, p < .05; **, p < .01; ***, p < .001.
Abbreviations: CDR, Clinical Dementia Rating; ESS, Epworth Sleepiness Score; HSD, honestly significant difference; MMSE, Mini‐Mental State Examination; RBDSQ, REM (Rapid Eye Movement) Sleep Behavior Disorder Screening Questionnaire; UPDRS III, Movement Disorder Society‐Sponsored Revision of the Unified Parkinson Disease Rating Scale (MDS‐UPDRS), part III.
2.2. Image processing and feature extraction
In this study, all T1 images were processed using the exact same pipeline, and a total of 98 volumetric features were extracted. Specifically, 95 volumetric features based on the “Desikan‐Killiany‐Tourville” (DKT) atlas were obtained using FastSurfer (Henschel et al., 2020). To eliminate the between‐subject variability in brain tissue volumes caused by the variation in head size (Mathalon et al., 1993), all parcel volumes were normalized by the intracranial volume (ICV) calculated by SPM12, which shows outstanding performance in ICV estimation (Malone et al., 2015). The volume fraction of gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) obtained in the process of calculating ICV (by SPM12) were also added to features to better fit the brain age model.
2.3. Model training and brain age estimation
The brain age estimation model is built upon 98 volumetric features together with sex info based on the XGBoost algorithm (Chen & Guestrin, 2016), which has shown outstanding performance in machine learning competitions as well as brain age modeling (Kaufmann et al., 2019). First, we split the brain age modeling data set into a training set comprising 3344 samples of HC, and an independent test set comprising 830 samples of HC. Ten‐fold cross‐validation was carried out on the training set to tune the model parameters. Finally, the learning rate was set to 0.01, the number of estimators was set to 6000, the max depth was set to 7, the subsample was set to 0.8, and other parameters were set to default. After determining the optimal parameters, the whole training set was used to train the final model with the optimal parameters. Model accuracy was evaluated on the test set using the MAE (mean absolute error), R 2 (coefficient of determination score), and the r (Pearson correlation coefficient). The model training process was performed using the XGBoost (1.2.1) package (Chen et al., 2019) in Python 3.8.3, and the model evaluation process was performed using scikit‐learn (0.23.1) package (Pedregosa et al., 2011).
The trained brain age model was then applied to estimate brain age in clinical groups, and the brain age gap (deviation between estimated age and chronological age) was calculated for each subject. Furthermore, we used a general linear model approach, controlling the covariates of age, sex, and ICV (calculated by SPM12), to compare the brain age gap between groups (sMCI vs. pMCI and HC vs. prodromal PD). The threshold for statistical significance was set at p < .05.
Site effects on the estimated brain age gap were also evaluated both on the test set (830 healthy subjects from 5 public data sets) and the clinical sets (171 HC, 174 prodromal PD from PPMI, and 69 sMCI, 64 pMCI from ADNI) using a linear mixed model approach. For the test set, age and sex were controlled as covariates, and for the clinical sets, the grouping of diseases was also controlled as well. The threshold for statistical significance was set at p < .05.
2.4. Construction of the brain age vector
We used model‐agnostic SHAP (Shapley values) to attribute regional brain aging for each subject‘s age estimation to construct the brain age vector.
Model‐agnostic Shapley values originated from coalition game theory to quantify the contribution of each variable to the final result (Shapley, 2016). When compared with other model interpretation techniques, SHAP provides both global and local interpretations, which permits feature attribution for each subject's estimation. Specifically, we employed SHAP on the age estimation of clinical groups to attribute abnormal aging to each brain feature for each subject as:
where represents the estimated brain age of a single sample ; represents a fixed baseline, which in this case is the average chronological age of the training set ; is the number of input features; and is the Shapley value which represents the contribution of feature to the estimated brain age of . The technical overview refers to Lundberg and Lee (2017a) and (2017b). To accelerate the calculation of Shapley values based on tree model, we used Tree SHAP (Lundberg et al., 2019) in this study. Therefore, Shapley values of 99 input features (98 brain volumes and sex) composed a feature contribution vector. Hypothesizing that the feature contributions measured the degree of brain aging in the corresponding brain regions, the brain age vector could characterize regional variations of brain aging. This process was performed using the shap (0.39.0) package implemented in Python (3.8.3).
To measure the reliability of the brain age vector, we also collected repeated scans (scanned on the same date but of different descriptions) of sMCI (N = 68) and pMCI (N = 63) subjects in ADNI. Again, using SHAP feature attribution based on the brain age estimation model, brain age vectors were constructed for each subject's repeated scans, and the intraclass correlation coefficient (ICC[2,1]; Shrout & Fleiss, 1979) was calculated comparing the brain age vector between repeated scans within each group (sMCI and pMCI).
In addition, we also compared the feature contribution calculated by SHAP with the feature importance of XGBoost, which calculates feature contributions as the information gain in the model optimization process, to confirm the feature attribution results of the brain age model.
2.5. Detection of disorder‐specific regional abnormal aging
Group comparisons involved Tukey HSD (honestly significant difference) test (Abdi & Williams, 2010) were implemented on the features in the brain age vector between prodromal patients and controls for AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD) groups, respectively. The threshold for statistical significance was set at a p value of false discovery rate (FDR) corrected p < .05. Features with FDR‐corrected p < .05 indicated significant abnormal aging in the corresponding brain regions. In contrast, we also implemented the same group comparisons on the brain volumes used for brain age modeling to compare the disorder‐specific patterns derived from aging metrics (brain age vector) and structural metrics (brain volumes). This disorder‐specific pattern detecting process only included features based on the DKT atlas.
To examine the reproducibility of the disorder‐specific patterns revealed by the brain age vector, we also sampled 70% (120 HC, 122 prodromal PD, 48 sMCI, and 45 pMCI) and 50% (86 HC, 87 prodromal PD, 34 sMCI, and 32 pMCI) of the subjects in the clinical sets to repeat our experiment.
2.6. Classification experiments of early disease screening
Aiming to further examine the discriminability of the brain age vector in early disease screening, we conducted supervised learning experiments to classify prodromal patients and controls (sMCI vs. pMCI and HC vs. prodromal PD). Two classification models (i.e., XGBoost, logistic regression) were selected to detect pMCI or prodromal PD patients based on the brain age vector. We first split each clinical group into a training set (75%) and a test set (25%), and 5‐fold cross‐validation was carried out on the training sets to evaluate the classification performance. Furthermore, we also evaluate the generalizability of the classification models (trained on the whole traing sets) on the external test sets. The performance of each classification task was quantified in terms of classification accuracy (ACC), sensitivity (SEN), specificity (SPE), as well as the area under the curve (AUC) of receiver operating characteristic. Shapley value of sex was removed from the brain age vector, and the true age and sex of each subject were added to features for classification.
In contrast, we also tested the discriminability of the other two brain aging metrics: the single estimated brain age gap, and the regional brain age gaps (Kaufmann et al., 2019). Regional brain age (gaps) was first proposed to improve spatial specificity of brain age, and has been proved useful to reveal specific spatial patterns among brain disorders. By training brain age estimators on volumetric features of occipital, frontal, temporal, parietal, cingulate, insula, and cerebellar‐subcortical areas, respectively, brain age gaps of each of these regions were calculated to measure regional abnormal aging for each subject. In addition, we also compared the classification performance of the brain age vector with structural brain metrics (98 brain volumes used for brain age modeling). The age and sex of each subject were also added to features in each task to match the classification task of the brain age vector.
In addition, 10‐fold cross‐validation was also carried out on the clinical sets and their subsets of 70% and 50% subjects to verify the classification performance of the four brain metrics (i.e., single brain age gap, regional brain age gaps, brain volumes, and brain age vector).
All model training and evaluation were performed using the scikit‐learn package (0.23.1) in Python (3.8.3; Pedregosa et al., 2011). To fit the XGBoost classifier, we used the xgboost (1.2.1) package in Python (3.8.3; Chen et al., 2019), and all parameters of XGBoost classifiers were set to default.
An overview of the brain age vector framework is given in Figure 1.
FIGURE 1.
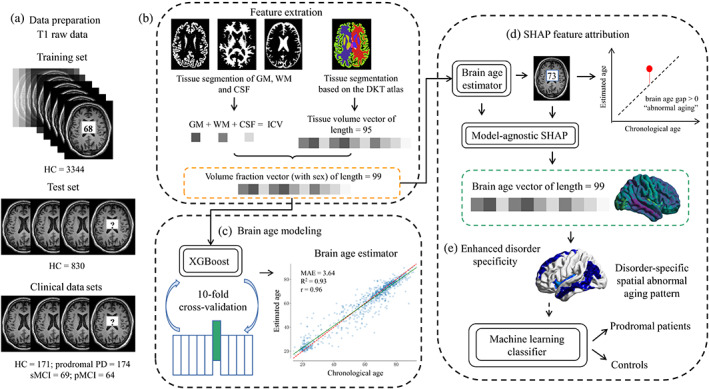
The brain age vector framework, including (a) data preparation. (b) Feature extraction: 95 volumetric features based on DKT atlas were extracted using FastSurfer, and the other three volumetric features of GM, WM, and CSF were extracted by SPM12. All brain volumes were normalized by ICV. (c) Brain age modeling: A total of 98 volume fractions and sex info were used to construct the brain age model based on XGBoost algorithm. Ten‐fold cross‐validation was carried out to tune the model parameters, and the whole training set was used to train the final brain age estimator with the optimal parameters. (d) SHAP feature attribution: We used SHAP to attribute brain aging to each brain region by calculating feature contributions (Shapley values) for each age estimation in the clinical data sets, and the 99 calculated Shapley values formed the brain age vector. (e) Enhanced disorder specificity: The brain age vector reflected disorder‐specific spatial abnormal aging patterns and was further used to classify prodromal patients and controls based on machine learning methods. CSF, cerebrospinal fluid; DKT, Desikan‐Killiany‐Tourville; GM, gray matter; HC, healthy control; ICV, intracranial volume; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; SHAP, Shapley Additive Explanations; sMCI, stable mild cognitive impairment; WM, white matter
3. RESULTS
3.1. Demographic information
The demographic characteristics of the multicenter subjects in this study was shown in Table 1. There were no significant age differences between prodromal patients and controls in both AD (sMCI vs. pMCI, p = .477) and PD (HC vs. prodromal PD, p = .574) groups. For other clinical parameters, a significantly lower cognitive level (MMSE) was observed in pMCI, compared with sMCI (p < .001), but there was no significant difference in CDR (p = .301). For HC versus prodromal PD, significant differences were observed in UPDRS III and RBDSQ (p< .001), but not in ESS (p = .891). All group comparisons of demographic characteristics were based on Tukey HSD test, and p values are significant at p < .05.
3.2. Performance and estimation of the brain age model
The constructed brain age model yielded satisfactory performance on the test set, with an MAE = 3.64 years, R 2 = 0.93, and r = 0.96, which is comparable with previous brain age studies in these and other cohorts (see Table 2; Cole et al., 2017, 2018; Jónsson et al., 2019; Wang et al., 2019).
TABLE 2.
Performance comparison between our brain age model and published brain age modeling
| Method | MAE (years) | R 2 | r |
|---|---|---|---|
| Cole et al. (2017) | 4.16 | ‐ | 0.96 |
| Cole et al. (2018) | 5.02 | 0.88 | 0.94 |
| Jónsson et al. (2019) | 3.39 | 0.87 | ‐ |
| Wang et al. (2019) | 4.45 | ‐ | 0.85 |
| Ours | 3.64 | 0.93 | 0.96 |
Abbreviations: MAE, mean absolute error; R 2, coefficient of determination score; r, Pearson correlation coefficient.
Regarding the age estimation of clinical groups, the brain age gap significantly differed between sMCI and pMCI (p = .016), with the following means of sMCI = −0.45 years and pMCI = 1.48 years. In addition, there was also a weak significant difference between HC and prodromal PD (p = .046), with the following means of HC = −0.87 years and prodromal PD = 0.56 years (see Figure 2). Such a result indicated significant abnormal aging in prodromal patients of both AD and PD at the whole brain level, but the specific areas for each disorder cannot be determined.
FIGURE 2.
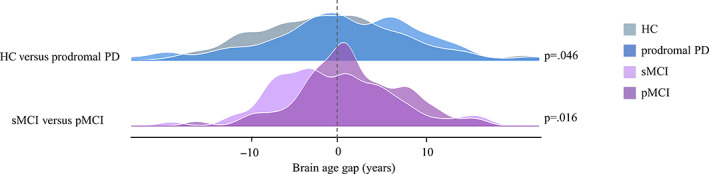
Estimated brain age gap for each clinical group. Significant differences in the estimated brain age gap were observed between prodromal patients and controls, with p = .016 for sMCI versus pMCI, and p = .046 for HC versus prodromal PD. HC, healthy control; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; sMCI, stable mild cognitive impairment
Both the test set (p = .139) and clinical sets (p = .384) showed no significant site effects on the estimated brain age gap, indicating stable prediction of the brain age model across different sites, laying the foundation for reliable feature attribution that formed the brain age vector.
3.3. Feature attribution and the brain age vector
At the global level, the feature contribution calculated by SHAP and the feature importance of XGBoost showed consistent feature attribution results (Figure S1). Both SHAP and XGBoost regarded the GM, WM‐hypointensities, and CSF as the three most important features of the brain age model. For the top 10 important features, 7 features overlapped in the results of the 2 feature attribution methods; for the top 20 important features, 14 features overlapped.
However, since the feature importance of XGBoost is based on model optimization process, it can only get the impact of features on the model, but cannot estimate the relationship between features and individual estimations. One of the most prominent advantages of SHAP is that it provides local interpretation for each sample. Figure 3 shows a feature attribution result of a prodromal PD patient using SHAP, which formed a brain age vector attributing regional brain aging.
FIGURE 3.

A brain age vector of a prodromal PD patient (aged 62) derived from SHAP feature attribution. The base value (59.52 years) shows the mean chronological age in the training set. Each value (Shapley value) in the brain age vector represents the feature contribution to the estimated brain age (68.03 years). The red features with positive Shapley values contribute to the increase of the brain age estimation from the base value, whereas the blue features with negative Shapley values contribute to the decrease. The arrow lengths indicate the absolute Shapley values, and the corresponding input feature values are explained below the arrows. The sum of the base value and all Shapley values in the brain age vector equals the estimated brain age (68.03 years)
Another advantage of SHAP is the consistency of feature attribution (Lundberg & Lee, 2017a, 2017b). Not surprisingly, the brain age vector demonstrated high test–retest reliability between repeated scans with ICCs of 0.990 (±0.024) and 0.993 (±0.012) for sMCI and pMCI groups, respectively (Figure S2).
3.4. Disorder‐specific brain aging patterns
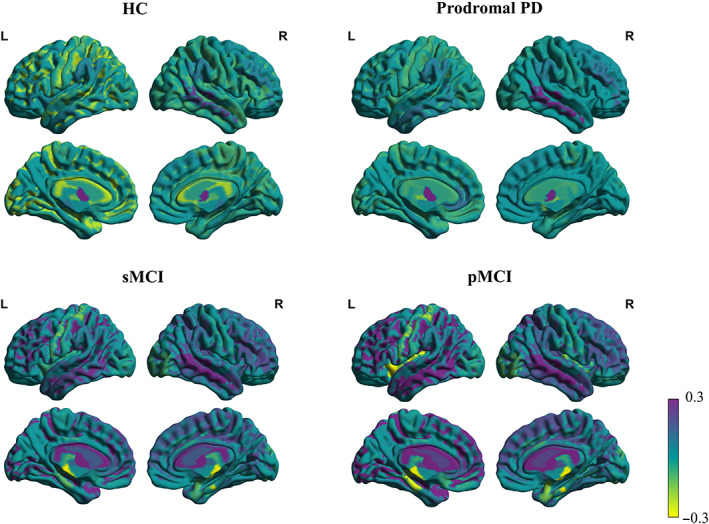
The brain age vector showed specific regional variations of brain aging for each clinical group, which cannot be characterized by a single metric (estimated brain age; Figure 4), and significant regional abnormal aging was located for prodromal AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD), respectively (see Figure 5). For sMCI versus pMCI, 15 feature regions of significant abnormal aging (FDR‐corrected p < .05) were detected, consisting of 7 cortical structures in the temporal lobe, especially most of the structures in the medial temporal (bilateral entorhinal and parahippocampal), 1 cortical structure in the frontal lobe, 1 cortical structure in the parietal lobe, 2 structures in the insula, and 4 subcortical structures including the hippocampus and amygdala. Similar pattern was also detected by brain volumes, with the temporal lobe suffering the most. However, pMCI patients also showed more extensive structural changes in the frontal and parietal lobes compared with sMCI (Table S1). For HC versus prodromal PD, five feature regions of significant abnormal aging (FDR‐corrected p < .05) were detected, including the bilateral pallidum and right caudate in the striatum, the left rostral anterior cingulate, and CSF; while no brain regions with significant atrophy were found based on brain volumes. All feature regions for prodromal AD and PD detected by the brain age vector are listed in Table 3, respectively. Consistent spatial patterns related to the medial temporal for sMCI versus pMCI, and the striatum for HC versus prodromal PD through the brain age vector were also reproduced on the subsets (see Tables S2 and S3).
FIGURE 4.
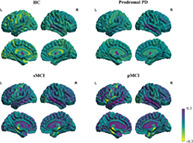
Visualizations of the brain age vector based on the DKT atlas for HC, prodromal PD, sMCI, and pMCI. The color bar indicates the feature value (Shapley value) in the brain age vector for each brain region, measuring the degree of regional brain aging. Region values in the visualization map have been set at −0.3 minimum threshold and capped at 0.3 maximum to better show regional variations. HC, healthy control; L, left hemisphere; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; R, right hemisphere; sMCI, stable mild cognitive impairment
FIGURE 5.
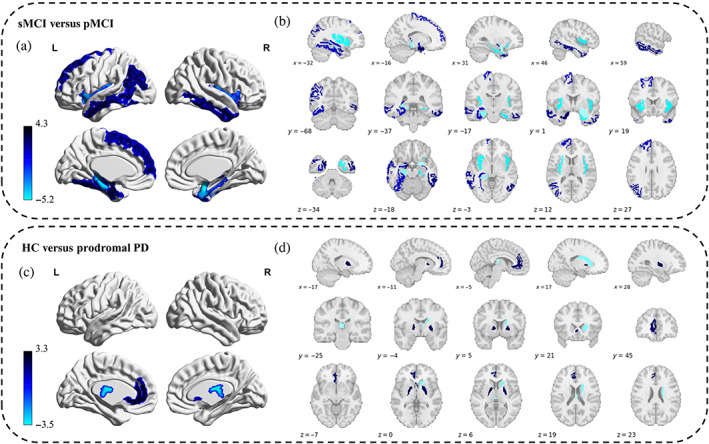
Disorder‐specific abnormal aging patterns for prodromal AD and PD derived from the brain age vector. Upper part: sMCI versus pMCI. (a) Abnormal aging distribution (FDR‐corrected p < .05) for prodromal AD. (b) Feature regions with significant abnormal aging (FDR‐corrected p < .05) for prodromal AD. The color bar indicates the statistic value (of Tukey HSD test) of each region in the brain age vector between sMCI and pMCI. Lower part: HC versus prodromal PD. (c) Abnormal aging distribution (FDR‐corrected p < .05) for prodromal PD. (d) Feature regions with significant abnormal aging (FDR‐corrected p < .05) for prodromal PD. The color bar indicates the statistic value (of Tukey HSD test) of each region in the brain age vector between HC and prodromal PD. FDR, false discovery rate; HC, healthy control; HSD, honestly significant difference; L, left hemisphere; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; R, right hemisphere; sMCI, stable mild cognitive impairment
TABLE 3.
Feature regions with significant abnormal aging for prodromal AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD) detected by the brain age vector
| 69 sMCI vs. 64 pMCI | 171 HC vs. 174 prodromal PD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Feature regions | p value | Effect size (d) | 95% CI | Power | Feature regions | p Value | Effect size (d) | 95% CI | Power | |
| Temporal lobe | Parahippocampal (lh) | .012* | −0.807‐ | (−1.161, −0.454) | 0.996 | |||||
| Inferior temporal (rh) | .012* | 0.671 | (0.321, 1.020) | 0.970 | ||||||
| Entorhinal (rh) | .012* | −0.620 | (−0.968, −0.272) | 0.944 | ||||||
| Middle temporal (lh) | .012* | 0.607 | (0.259, 0.953) | 0.935 | ||||||
| Entorhinal (lh) | .012* | 0.760 | (0.408, 1.112) | 0.992 | ||||||
| Fusiform (lh) | .037* | 0.494 | (0.149, 0.840) | 0.807 | ||||||
| Parahippocampal (rh) | .048* | −0.475 | (−0.819, −0.130) | 0.775 | ||||||
| Frontal lobe | Superior frontal (lh) | .037* | 0.502 | (0.156, 0.847) | 0.819 | |||||
| Parietal lobe | Inferior parietal (lh) | .012* | 0.599 | (0.252, 0.947) | 0.929 | |||||
| Insula | Insula (lh) | .032* | −0.529 | (−0.875, −0.183) | 0.857 | |||||
| Insula (rh) | .037* | −0.493 | (−0.839, −0.148) | 0.805 | ||||||
| Cingulate gyrus | Rostral anterior cingulate (lh) | .049* | 0.328 | (0.115, 0.540) | 0.859 | |||||
| Subcortical | Amygdala (rh) | .012* | −0.904 | (−1.261, −0.547) | 0.999 | Caudate (rh) | .045* | −0.338 | (−0.551, −0.126) | 0.879 |
| Inferior lateral ventricle (rh) | .012* | 0.649 | (0.300, 0.998) | 0.960 | Pallidum (lh) | .045* | 0.360 | (0.147, 0.573) | 0.915 | |
| Hippocampus (lh) | .037* | 0.494 | (0.149, 0.839) | 0.807 | Pallidum (rh) | .045* | 0.347 | (0.134, 0.560) | 0.895 | |
| Inferior lateral ventricle (lh) | .037* | 0.506 | (0.161, 0.852) | 0.825 | CSF | .045* | −0.374 | (−0.587, −0.161) | 0.934 | |
| Occipital lobe | ||||||||||
Note: The p values are significant of p < .05 (FDR corrected for Tukey HSD test). The effect size refers to the Cohen's d effect size, and the significant level for statistical power was set to 0.05. *, p < .05; **, p < .01; ***, p < .001.
Abbreviations: CI, confidence interval; CSF, cerebrospinal fluid; FDR, false discovery rate; lh, left hemisphere; rh, right hemisphere.
3.5. Early screening performance
To evaluate the discriminability of the brain age vector in detecting prodromal patients, classification performance based on machine learning was compared among three different brain aging metrics (i.e., single brain age gap, regional brain age gaps, and brain age vector) and brain volumes.
As demonstrated in Figures 6, 7, and Table 4, the brain age vector showed the best classification performance in both AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD) groups, compared with the other two brain aging metrics. In 5‐fold cross‐validation, the brain age vector achieved AUCs of 83.39% (LR) and 72.28% (XGB) in detecting pMCI and prodromal PD, respectively, while the best AUCs of other aging metrics were only 71.27% (regional brain age gaps, XGB) and 66.44% (single brain age gap, XGB), respectively. In addition, the brain age vector also outperformed the other metrics in accuracy and sensitivity, suggesting that our approach of brain age vector effectively improved individual screening performance of brain aging measurement. Moreover, the brain age vector demonstrated at least comparable discriminability with brain volumes (AUC = 80.81% for sMCI vs. pMCI; AUC = 66.66% for HC vs. prodromal PD), showing competitiveness with structural brain metrics. On the external test set, the brain age vector also yielded excellent generalizability compared with other brain metrics, with AUCs of 83.33% (XGB) and 68.02% (XGB) in early screening of AD and PD, respectively. Similar classification results were also verified on the subsets (see Tables S4 and S5), showing good reproducibility.
FIGURE 6.
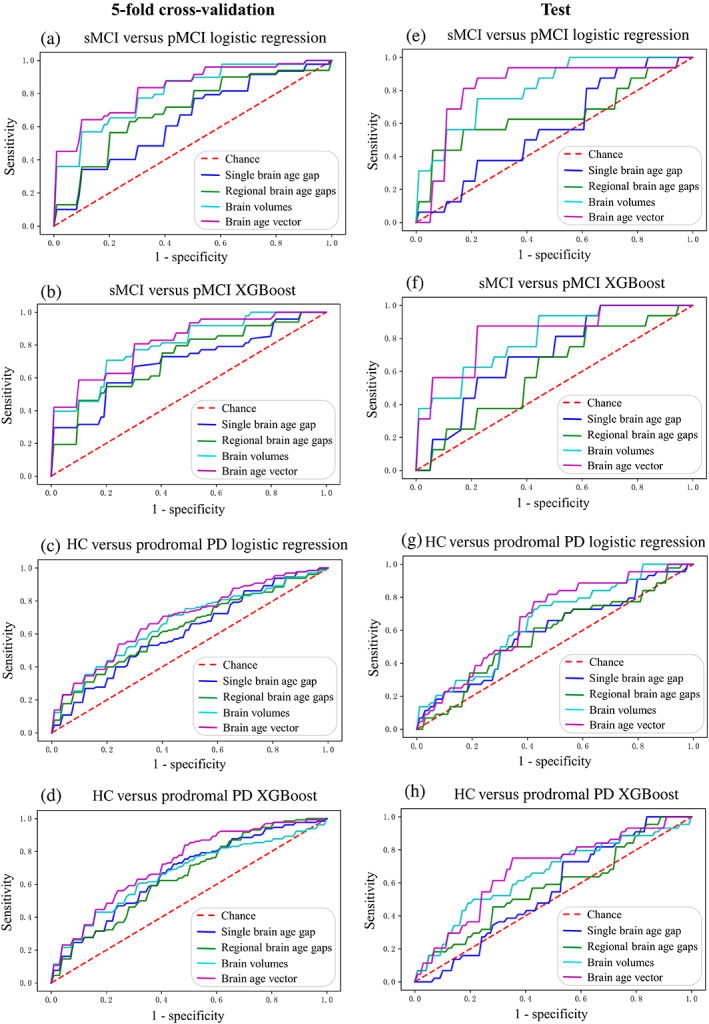
ROC curves of individual classification in early disease screening based on three different brain aging metrics and brain volumes. (a) sMCI versus pMCI using logistic regression classifier under 5‐fold cross‐validation. (b) sMCI versus pMCI using XGBoost classifier under 5‐fold cross‐validation. (c) HC versus prodromal PD using logistic regression classifier under 5‐fold cross‐validation. (d) HC versus prodromal PD using XGBoost classifier under 5‐fold cross‐validation. (e) sMCI versus pMCI using logistic regression classifier on the test set. (f) sMCI versus pMCI using XGBoost classifier on the test set. (g) HC versus prodromal PD using logistic regression classifier on the test set. (h) HC versus prodromal PD using XGBoost classifier on the test set. HC, healthy control; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; ROC, receiver operating characteristic; sMCI, stable mild cognitive impairment
FIGURE 7.
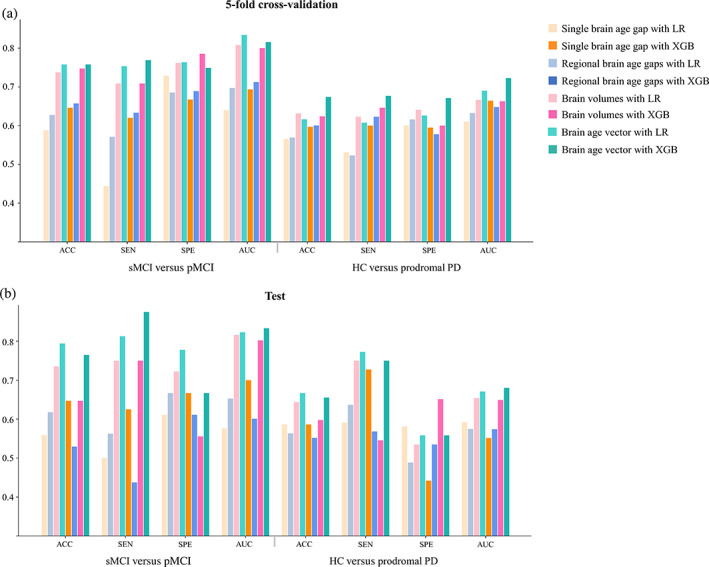
Classification performance of early disease screening measured by accuracy, sensitivity, specificity, and area under ROC curve: (a) under 5‐fold cross‐validation, and (b) on the test set. ACC, accuracy; HC, healthy control; LR, logistic regression; AUC, area under receiver operating characteristic (ROC) curve; PD, Parkinson disease; pMCI, progressive mild cognitive impairment; SEN, sensitivity; sMCI, stable mild cognitive impairment; SPE, specificity; XGB, XGBoost
TABLE 4.
Classification performance of early disease screening
| HC vs. prodromal PD | sMCI vs. pMCI | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Brain metrics | Single brain age gap | Regional brain age gaps | Brain volumes | Brain age vector | Single brain age gap | Regional brain age gaps | Brain volumes | Brain age vector | |
| Logistic regression (5‐fold cross‐validation) | ACC | 0.5654 | 0.5693 | 0.6315 | 0.6164 | 0.5879 | 0.6274 | 0.7374 | 0.7579 |
| SEN | 0.5308 | 0.5231 | 0.6231 | 0.6077 | 0.4444 | 0.5711 | 0.7089 | 0.7533 | |
| SPE | 0.6006 | 0.6160 | 0.6409 | 0.6262 | 0.7291 | 0.6855 | 0.7618 | 0.7636 | |
| AUC | 0.6104 | 0.6326 | 0.6666 | 0.6902 | 0.6397 | 0.6974 | 0.8081 | 0.8339 | |
| XGBoost (5‐fold cross‐validation) | ACC | 0.5968 | 0.6005 | 0.6240 | 0.6740 | 0.6463 | 0.6574 | 0.7474 | 0.7579 |
| SEN | 0.6000 | 0.6231 | 0.6462 | 0.6769 | 0.6200 | 0.6333 | 0.7089 | 0.7689 | |
| SPE | 0.5948 | 0.5778 | 0.6000 | 0.6711 | 0.6673 | 0.6891 | 0.7855 | 0.7491 | |
| AUC | 0.6644 | 0.6479 | 0.6629 | 0.7228 | 0.6937 | 0.7127 | 0.8002 | 0.8156 | |
| Logistic regression (test) | ACC | 0.5862 | 0.5632 | 0.6437 | 0.6667 | 0.5588 | 0.6176 | 0.7353 | 0.7941 |
| SEN | 0.5909 | 0.6364 | 0.7500 | 0.7727 | 0.5000 | 0.5625 | 0.7500 | 0.8125 | |
| SPE | 0.5814 | 0.4884 | 0.5349 | 0.5581 | 0.6111 | 0.6667 | 0.7222 | 0.7778 | |
| AUC | 0.5920 | 0.5745 | 0.6538 | 0.6707 | 0.5764 | 0.6528 | 0.8160 | 0.8229 | |
| XGBoost (test) | ACC | 0.5862 | 0.5517 | 0.5977 | 0.6552 | 0.6471 | 0.5294 | 0.6471 | 0.7647 |
| SEN | 0.7273 | 0.5682 | 0.5455 | 0.7500 | 0.6250 | 0.4375 | 0.7500 | 0.8750 | |
| SPE | 0.4419 | 0.5349 | 0.6512 | 0.5581 | 0.6667 | 0.6111 | 0.5556 | 0.6667 | |
| AUC | 0.5515 | 0.5740 | 0.6490 | 0.6802 | 0.6997 | 0.6007 | 0.8021 | 0.8333 | |
Note: The best results for each classification task are shown in bold. Abbreviations: ACC, accuracy; SEN, sensitivity; SPE, specificity; AUC, area under the curve (AUC) of receiver operating characteristic.
4. DISCUSSION
Brain age modeling has recently become a popular approach to identifying individual differences in brain aging and investigating neurological disorders (Cole & Franke, 2017; Cole et al., 2017, 2018; Franke & Gaser, 2012; Jónsson et al., 2019; Kaufmann et al., 2019). In this study, we introduced model‐agnostic SHAP to construct a brain age vector measuring disorder‐specific brain aging. While the single estimated brain age gap only showed significant differences between prodromal patients and controls at the whole brain level, specific regional abnormal aging was located for prodromal AD and PD, respectively (e.g., hippocampus [lh] for sMCI vs. pMCI; caudate [rh] for HC vs. prodromal PD) through the brain age vector. In addition, the brain age vector reflected disorder‐specific abnormal aging patterns related to the medial temporal and the striatum for prodromal AD and PD, respectively. Furthermore, compared with other brain aging metrics (single brain age gap and regional brain age gaps), the brain age vector demonstrated enhanced discriminability in early screening of AD (AUC = 83.39%) and PD (AUC = 72.28%), which was also competitive with structural brain metrics (brain volumes).
We observed that the single brain age gap lacked spatial specificity across diseases and showed poor discriminability in classifying prodromal patients and controls (AUC: 63.97% [LR], 69.37% [XGB] for sMCI vs. pMCI; AUC: 61.04% [LR], 66.44% [XGB] for HC vs. prodromal PD), in line with previous brain age studies (Kaufmann et al., 2019; Koutsouleris et al., 2014). Based on machine learning, brain age is a “black‐box” indicator with unclear mechanism for its variation (increase or decrease), which is crucial for understanding of the complex brain aging process. Using model‐agnostic SHAP, we built up dependencies between multiple brain features (regions) and the estimated brain age. As most brain age studies using model interpretation methods focus on the important features that drive age estimation based on model training of healthy people (Ball et al., 2021; Koutsouleris et al., 2014; Wang et al., 2019), they failed to establish the relationship between brain aging and neurodegeneration mechanism. We performed feature attribution of brain age estimation on the patients with neurodegenerative diseases, taking advantage of the local interpretation of SHAP. Assigning the estimated brain age gap to each brain regions, structures resulting in abnormal aging were specifically attributed. This enhanced characterization of spatial pathological mechanism of brain aging promotes disorder specificity for individual screening.
For prodromal AD (sMCI vs. pMCI), we found the temporal lobe, especially the medial temporal (the hippocampus, the entorhinal, and the parahippocampal) related to memory and cognitive functions, was the most disorder‐specific area with the most serious abnormal aging being detected through the brain age vector. This is consistent with postmortem and imaging studies where pathological changes in the medial temporal have been widely reported in the disease progression, and has been recognized as a critical diagnostic marker of AD (Barkhof et al., 2007; Duara et al., 2008; Jack et al., 1998; Rusinek et al., 2004; Teipel et al., 2006). Moreover, studies have demonstrated that the brain atrophy caused by AD starts from the medial temporal and then extends to the neocortex of the temporal lobe (Johnson et al., 2012). Significant abnormal aging was also found in subcortical structures including the hippocampus and the amygdala, where atrophy is more prevalent, even years before clinical symptoms appear (Aylward et al., 1999; Wachinger et al., 2016). Additionally, the insula was also detected with severe abnormal aging. As an integrating hub, insula interacts with multiple brain networks involved in executive and cognitive processes, and has been reported as a gatekeeper of executive control (Kurth et al., 2010; Molnar‐Szakacs & Uddin, 2022). It indicates that abnormal aging in the insula could be associated with the decline of cognition and execution in AD patients.
Prodromal PD (HC vs. prodromal PD) showed slighter abnormal aging (5 feature regions) compared with prodromal AD (15 feature regions), and the spatial pattern is significantly different. The striatum was found to be the most serious abnormal aging area for prodromal PD, which contributes to dopaminergic hypofunction, causing motor deficits in PD patients (Hornykiewicz, 1998, 2006; Hustad & Aasly, 2020; Kaasinen & Vahlberg, 2017), and has been widely suggested to be a biomarker of the progression of PD (Brooks et al., 2003; Hopes et al., 2016; Khan et al., 2019; Wang et al., 2013). In addition, significant abnormal aging was also observed in the anterior cingulate cortex, in line with previous studies that have indicated it to be involved with cognitive impairment, even in the earliest prodromal form of PD (Hong et al., 2012; Vogt, 2019).
Regarding structural brain metrics (brain volumes), similar disorder‐specific pattern related to the temporal lobe in sMCI versus pMCI were confirmed, but more feature regions detected in the frontal and parietal lobes indicates that structural brain changes are more extensive than abnormal aging in AD. However, consistent with other imaging studies, structural brain changes are insignificant in PD in terms of brain volumes, but accelerated brain aging has developed in the striatum in the prodromal stage according to the brain age vector. These findings suggest that the brain age vector is not fully dictated by brain structures (volumes), but reasoning with aging. Abnormal brain aging is a key factor in neurodegenerations. When compared with other traditional T1w MRI metrics, our method of brain age vector transfers the knowledge of brain aging evaluation to neurodegenerative disease screening, which not only shows competitiveness with traditional structural metrics (brain age vector: AUC = 83.39% for sMCI vs. pMCI, AUC = 72.28% for HC vs. prodromal PD; brain volumes: AUC = 80.81% for sMCI vs. pMCI, AUC = 66.66% for HC vs. prodromal PD), but also emphasizes the important role of brain aging in the process of neurodegenerations.
Furthermore, the brain age vector also outperformed the other two aging metrics in detecting prodromal patients from controls (single brain age gap: AUC = 69.37% for sMCI vs. pMCI, AUC = 66.44% for HC vs. prodromal PD; regional brain age gaps: AUC = 71.27% for sMCI vs. pMCI, AUC = 64.79% for HC vs. prodromal PD), and demonstrated excellent generalizability on the test set (AUC = 83.33% for sMCI vs. pMCI, AUC = 68.02% for HC vs. prodromal PD). Overall, attributing abnormal aging to each brain region from age estimation, the brain age vector demonstrated consistent findings of disorder‐specific spatial patterns with previous studies, and finally improved the discriminability in early screening of neurodegenerative diseases.
This study was not without limitations. First, the brain age model seemed to be less sensitive in detecting brain age changes between sMCI and pMCI compared with previous study (Gaser et al., 2013). This may be due to the use of simple volumetric features for brain age modeling, which compromised complex age‐related brain changes. More comprehensive brain features (e.g., brain surface, thickness, and areas) underlying brain aging evolution are needed to improve the sensitivity of the brain age model to neurodegenerative brain changes. Second, the feature attribution of SHAP is based on a fixed baseline of the mean age of training data, making the calculated Shapley values depend on the chronological age of subjects. We matched age across groups to make it comparable between prodromal patients and controls, but individual variation caused by age still remained. Future studies may consider adaptive age‐matched baseline for SHAP algorithm, thus allowing more accurate individual feature attribution for age estimation.
In conclusion, we proposed a new brain aging measure which refined regional variations of brain aging underlying neurodegeneration mechanism. The proposed brain age vector accurately revealed disorder‐specific spatial abnormal aging patterns for prodromal AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD), respectively, and demonstrated excellent performance in detecting prodromal patients. Through feature attribution of patients' age estimation, our method of brain age vector represents both the temporal (aging) and the spatial characteristics of the diseased brain, which not only enhances disorder specificity of brain aging measurement in terms of spatial specificity and individual early screening, but also highlights the significance of aging in neurodegenerations.
AUTHOR CONTRIBUTIONS
Chen Ran did data cleaning, processing, and statistical analyses. Chen Ran and Yanwu Yang drafted the article and figures. Chenfei Ye collected data and supervised data processing and figure preparation. Haiyan Lv pre‐processed the neuroimages, and provides the GPU platforms. Ting Ma conceived and supervised the whole study and revised the article.
CONFLICT OF INTEREST
The author declares that there is no conflict of interest that could be perceived as prejudicing the impartiality of the research reported.
Supporting information
FIGURE S1 Global feature attribution comparison of the brain age model. (A) Top 20 important features derived from SHAP. The abscissa represents the mean absolute value of Shapley values, and the ordinate represents the importance ranking of features. (B) Top 20 important features derived from feature importance of XGBoost. The abscissa represents the feature importance score (gain), and the ordinate represents the importance ranking of features. lh, left hemisphere; rh, right hemisphere
FIGURE S2 Test–retest reliability of the brain age vector. The scatter plot represents the ICC[2,1] between repeated scans of each subject in sMCI (N = 68) and pMCI (N = 63) group. ICC, intraclass correlation coefficient; pMCI, progressive mild cognitive impairment; sMCI, stable mild cognitive impairment
TABLE S1 Feature regions with significant structural changes for prodromal AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD) derived from brain volumes
TABLE S2 Feature regions detected by the brain age vector for sMCI versus pMCI on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S3 Feature regions detected by the brain age vector for HC versus. prodromal PD on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S4 Classification performance of 10‐fold cross‐validation for sMCI versus pMCI on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S5 Classification performance of 10‐fold cross‐validation for HC versus prodromal PD on the subsets of 50%, 70%, and 100% subjects of the clinical sets.
Ran, C. , Yang, Y. , Ye, C. , Lv, H. , & Ma, T. (2022). Brain age vector: A measure of brain aging with enhanced neurodegenerative disorder specificity. Human Brain Mapping, 43(16), 5017–5031. 10.1002/hbm.26066
Chen Ran and Yanwu Yang contributed equally to this study.
Funding information Basic Research Foundation of Shenzhen Science and Technology Stable Support Program, Grant/Award Number: GXWD20201230155427003‐20200822115709001; Innovation Team and Talents Cultivation Program of National Administration of Traditional Chinese Medicine, Grant/Award Number: ZYYCXTD‐C‐202004; National Natural Science Foundation of China, Grant/Award Number: 62106113
Contributor Information
Yanwu Yang, Email: yanwu.yang1111@gmail.com.
Ting Ma, Email: tma@hit.edu.cn.
DATA AVAILABILITY STATEMENT
Data from the IXI, OASIS, SLIM, INDI, ADNI, and PPMI database are made available via: http://brain-development.org/ixi-dataset/, https://www.oasis-brains.org/, http://fcon_1000.projects.nitrc.org/indi/IndiPro.html/, www.loni.ucla.edu/ADNI/, and www.ppmi-info.org. The code for the computational pipeline is publicly available at https://github.com/Kecici/Brain-age-vector-construction.git.
REFERENCES
- Abdi, H. , & Williams, L. J. (2010). Tukey's honestly significant difference (HSD) test. Encyclopedia of Research Design, 3(1), 1–5. [Google Scholar]
- Aylward, E. H. , Li, Q. , Honeycutt, N. A. , Warren, A. C. , Pulsifer, M. B. , Barta, P. E. , Chan, M. D. , Smith, P. D. , Jerram, M. , & Pearlson, G. D. (1999). MRI volumes of the hippocampus and amygdala in adults with Down's syndrome with and without dementia. American Journal of Psychiatry, 156(4), 564–568. [DOI] [PubMed] [Google Scholar]
- Ball, G. , Kelly, C. E. , Beare, R. , & Seal, M. L. (2021). Individual variation underlying brain age estimates in typical development. NeuroImage, 235, 118036. [DOI] [PubMed] [Google Scholar]
- Barkhof, F. , Polvikoski, T. M. , van Straaten, E. , Kalaria, R. N. , Sulkava, R. , Aronen, H. J. , Niinistö, L. , Rastas, S. , Oinas, M. , Scheltens, P. , & Erkinjuntti, T. (2007). The significance of medial temporal lobe atrophy: A postmortem MRI study in the very old. Neurology, 69(15), 1521–1527. [DOI] [PubMed] [Google Scholar]
- Beheshti, I. , Mishra, S. , Sone, D. , Khanna, P. , & Matsuda, H. (2020). T1‐weighted MRI‐driven brain age estimation in Alzheimer's disease and Parkinson's disease. Aging and Disease, 11(3), 618–628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloch, L. , & Friedrich, C. M. (2021). Developing a machine learning workflow to explain black‐box models for Alzheimer's disease classification. In HEALTHINF (pp. 87‐99).
- Brooks, D. , Frey, K. , Marek, K. , Oakes, D. , Paty, D. , Prentice, R. , Shults, C. W. , & Stoessl, A. (2003). Assessment of neuroimaging techniques as biomarkers of the progression of Parkinson's disease. Experimental Neurology, 184, 68–79. [DOI] [PubMed] [Google Scholar]
- Chen, T. , & Guestrin, C. (2016). XGBoost: A scalable tree boosting system.In Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785‐794).
- Chen, T. , He, T. , Benesty, M. , & Khotilovich, V. (2019). Package XGBoost. R version, 90, 1–66. [Google Scholar]
- Cole, J. H. , & Franke, K. (2017). Predicting age using neuroimaging: Innovative brain ageing biomarkers. Trends in Neurosciences, 40(12), 681–690. [DOI] [PubMed] [Google Scholar]
- Cole, J. H. , Poudel, R. P. , Tsagkrasoulis, D. , Caan, M. W. , Steves, C. , Spector, T. D. , & Montana, G. (2017). Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage, 163, 115–124. [DOI] [PubMed] [Google Scholar]
- Cole, J. H. , Ritchie, S. J. , Bastin, M. E. , Hernández, M. V. , Maniega, S. M. , Royle, N. , Corley, J. , Pattie, A. , Harris, S. E. , Zhang, Q. , Wray, N. R. , Redmond, P. , Marioni, R. E. , Starr, J. M. , Cox, S. R. , Wardlaw, J. M. , Sharp, D. J. , & Deary, I. J. (2018). Brain age predicts mortality. Molecular Psychiatry, 23(5), 1385–1392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duara, R. , Loewenstein, D. , Potter, E. , Appel, J. , Greig, M. , Urs, R. , Shen, Q. , Raj, A. , Small, B. , Barker, W. , Schofield, E. , Wu, Y. , & Potter, H. (2008). Medial temporal lobe atrophy on MRI scans and the diagnosis of Alzheimer disease. Neurology, 71(24), 1986–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fioravanti, V. , Benuzzi, F. , Codeluppi, L. , Contardi, S. , Cavallieri, F. , Nichelli, P. , & Valzania, F. (2015). MRI correlates of Parkinson's disease progression: A voxel based morphometry study. Parkinson's Disease, 2015, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke, K. , & Gaser, C. (2012). Longitudinal changes in individual BrainAGE in healthy aging, mild cognitive impairment, and Alzheimer's disease. GeroPsych, 25, 235–245. [Google Scholar]
- Franke, K. , & Gaser, C. (2019). Ten years of brainage as a neuroimaging biomarker of brain aging: What insights have we gained? Frontiers in Neurology, 10, 789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franke, K. , Ziegler, G. , Klöppel, S. , Gaser, C. , & Alzheimer's Disease Neuroimaging Initiative . (2010). Estimating the age of healthy subjects from T1‐weighted MRI scans using kernel methods: Exploring the influence of various parameters. NeuroImage, 50(3), 883–892. [DOI] [PubMed] [Google Scholar]
- Gaser, C. , Franke, K. , Klöppel, S. , Koutsouleris, N. , Sauer, H. , & Alzheimer's Disease Neuroimaging Initiative . (2013). BrainAGE in mild cognitive impaired patients: Predicting the conversion to Alzheimer's disease. PLoS One, 8(6), e67346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good, C. D. , Johnsrude, I. S. , Ashburner, J. , Henson, R. N. , Friston, K. J. , & Frackowiak, R. S. (2001). A voxel‐based morphometric study of ageing in 465 normal adult human brains. NeuroImage, 14(1), 21–36. [DOI] [PubMed] [Google Scholar]
- Henschel, L. , Conjeti, S. , Estrada, S. , Diers, K. , Fischl, B. , & Reuter, M. (2020). Fastsurfer‐a fast and accurate deep learning based neuroimaging pipeline. NeuroImage, 219, 117012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong, J. Y. , Lee, J. E. , Sohn, Y. H. , & Lee, P. H. (2012). Neurocognitive and atrophic patterns in Parkinson's disease based on subjective memory complaints. Journal of Neurology, 259(8), 1706–1712. [DOI] [PubMed] [Google Scholar]
- Hopes, L. , Grolez, G. , Moreau, C. , Lopes, R. , Ryckewaert, G. , Carrière, N. , Auger, F. , Laloux, C. , Petrault, M. , Devedjian, J.‐C. , Bordet, R. , Defebvre, L. , Jissendi, P. , Delmaire, C. , & Devos, D. (2016). Magnetic resonance imaging features of the nigrostriatal system: Biomarkers of Parkinson's disease stages? PLoS One, 11(4), e0147947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hornykiewicz, O. (1998). Biochemical aspects of Parkinson's disease. Neurology, 51(2 Suppl 2), S2–S9. [DOI] [PubMed] [Google Scholar]
- Hornykiewicz, O. (2006). The discovery of dopamine deficiency in the parkinsonian brain. In Riederer P., Reichmann H., Youdim M. B. H., & Gerlach M. (Eds.), Parkinson's disease and related disorders (pp. 9–15). Springer Vienna. [DOI] [PubMed] [Google Scholar]
- Hustad, E. , & Aasly, J. O. (2020). Clinical and imaging markers of prodromal Parkinson's disease. Frontiers in Neurology, 11, 395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack, C. R. , Petersen, R. C. , Xu, Y. , O'Brien, P. C. , Smith, G. E. , Ivnik, R. J. , Tangalos, E. G. , & Kokmen, E. (1998). Rate of medial temporal lobe atrophy in typical aging and Alzheimer's disease. Neurology, 51(4), 993–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jernigan, T. L. , Archibald, S. L. , Fennema‐Notestine, C. , Gamst, A. C. , Stout, J. C. , Bonner, J. , & Hesselink, J. R. (2001). Effects of age on tissues and regions of the cerebrum and cerebellum. Neurobiology of Aging, 22(4), 581–594. [DOI] [PubMed] [Google Scholar]
- Johnson, K. A. , Fox, N. C. , Sperling, R. A. , & Klunk, W. E. (2012). Brain imaging in Alzheimer disease. Cold Spring Harbor Perspectives in Medicine, 2(4), a006213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jónsson, B. A. , Bjornsdottir, G. , Thorgeirsson, T. , Ellingsen, L. M. , Walters, G. B. , Gudbjartsson, D. F. , Stefansson, H. , Stefansson, K. , & Ulfarsson, M. O. (2019). Brain age prediction using deep learning uncovers associated sequence variants. Nature Communications, 10(1), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaasinen, V. , & Vahlberg, T. (2017). Striatal dopamine in Parkinson disease: A meta‐analysis of imaging studies. Annals of Neurology, 82(6), 873–882. [DOI] [PubMed] [Google Scholar]
- Kaufmann, T. , van der Meer, D. , Doan, N. T. , Schwarz, E. , Lund, M. J. , Agartz, I. , Alnæs, D. , Barch, D. M. , Baur‐Streubel, R. , Bertolino, A. , Bettella, F. , Beyer, M. K. , Bøen, E. , Borgwardt, S. , Brandt, C. L. , Buitelaar, J. , Celius, E. G. , Cervenka, S. , Conzelmann, A. , & Córdova‐Palomera, A. (2019). Common brain disorders are associated with heritable patterns of apparent aging of the brain. Nature Neuroscience, 22(10), 1617–1623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy, K. M. , Erickson, K. I. , Rodrigue, K. M. , Voss, M. W. , Colcombe, S. J. , Kramer, A. F. , Acker, J. D. , & Raz, N. (2009). Age‐related differences in regional brain volumes: A comparison of optimized voxel‐based morphometry to manual volumetry. Neurobiology of Aging, 30(10), 1657–1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan, A. R. , Hiebert, N. M. , Vo, A. , Wang, B. T. , Owen, A. M. , Seergobin, K. N. , & MacDonald, P. A. (2019). Biomarkers of Parkinson's disease: Striatal sub‐regional structural morphometry and diffusion MRI. NeuroImage: Clinical, 21, 101597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutsouleris, N. , Davatzikos, C. , Borgwardt, S. , Gaser, C. , Bottlender, R. , Frodl, T. , Falkai, P. , Riecher‐Rössler, A. , Möller, H.‐J. , Reiser, M. , Pantelis, C. , & Meisenzahl, E. (2014). Accelerated brain aging in schizophrenia and beyond: A neuroanatomical marker of psychiatric disorders. Schizophrenia Bulletin, 40(5), 1140–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo, C.‐Y. , Lee, P.‐L. , Hung, S.‐C. , Liu, L.‐K. , Lee, W.‐J. , Chung, C.‐P. , Yang, A. C. , Tsai, S.‐J. , Wang, P.‐N. , Chen, L.‐K. , Chou, K.‐H. , & Lin, C.‐P. (2020). Large‐scale structural covariance networks predict age in middle‐to‐late adulthood: A novel brain aging biomarker. Cerebral Cortex, 30(11), 5844–5862. [DOI] [PubMed] [Google Scholar]
- Kurth, F. , Zilles, K. , Fox, P. T. , Laird, A. R. , & Eickhoff, S. B. (2010). A link between the systems: Functional differentiation and integration within the human insula revealed by meta‐analysis. Brain Structure and Function, 214(5), 519–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemaitre, H. , Goldman, A. L. , Sambataro, F. , Verchinski, B. A. , Meyer‐Lindenberg, A. , Weinberger, D. R. , & Mattay, V. S. (2012). Normal age‐related brain morphometric changes: Nonuniformity across cortical thickness, surface area and gray matter volume? Neurobiology of Aging, 33(3), 617.e611–617.e619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis, M. M. , Du, G. , Lee, E.‐Y. , Nasralah, Z. , Sterling, N. W. , Zhang, L. , Wagner, D. , Kong, L. , Tröster, A. I. , Styner, M. , Eslinger, P. J. , Mailman, R. B. , & Huang, X. (2016). The pattern of gray matter atrophy in Parkinson's disease differs in cortical and subcortical regions. Journal of Neurology, 263(1), 68–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, X. , Zhou, Y. , Dvornek, N. C. , Gu, Y. , Ventola, P. , & Duncan, J. S. (2020). Efficient Shapley explanation for features importance estimation under uncertainty.In International Conference on Medical Image Computing and Computer‐Assisted Intervention (pp. 792‐801). Springer, Cham. [DOI] [PMC free article] [PubMed]
- Liu, W. , Wei, D. , Chen, Q. , Yang, W. , Meng, J. , Wu, G. , Bi, T. , Zhang, Q. , Zuo, X.‐N. , & Qiu, J. (2017). Longitudinal test‐retest neuroimaging data from healthy young adults in Southwest China. Scientific Data, 4(1), 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, X. , Liao, W. , Jiang, C. , Liang, D. , Qiu, B. , & Zhang, L. (2012). Healthy aging: An automatic analysis of global and regional morphological alterations of human brain. Academic Radiology, 19(7), 785–793. [DOI] [PubMed] [Google Scholar]
- Lundberg, S. M. , Erion, G. , Chen, H. , DeGrave, A. , Prutkin, J. M. , Nair, B. , Katz, R. , Himmelfarb, J. , Bansal, N. , & Lee, S.‐I. (2019). Explainable AI for trees: From local explanations to global understanding. arXiv preprint arXiv:1905.04610 . doi: 10.48550/arXiv.1905.04610 [DOI] [PMC free article] [PubMed]
- Lundberg, S. M. , & Lee, S.‐I. (2017a). Consistent feature attribution for tree ensembles. arXiv preprint arXiv:1706.06060 . doi: 10.48550/arXiv.1706.06060 [DOI]
- Lundberg, S. M. , & Lee, S.‐I. (2017b). A unified approach to interpreting model predictions. Advances in neural information processing systems, 30.
- Malone, I. B. , Leung, K. K. , Clegg, S. , Barnes, J. , Whitwell, J. L. , Ashburner, J. , Fox, N. C. , & Ridgway, G. R. (2015). Accurate automatic estimation of total intracranial volume: A nuisance variable with less nuisance. NeuroImage, 104, 366–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathalon, D. H. , Sullivan, E. V. , Rawles, J. M. , & Pfefferbaum, A. (1993). Correction for head size in brain‐imaging measurements. Psychiatry Research: Neuroimaging, 50(2), 121–139. [DOI] [PubMed] [Google Scholar]
- McDonald, C. , McEvoy, L. , Gharapetian, L. , Fennema‐Notestine, C. , Hagler, D. , Holland, D. , Koyama, J. , Brewer, J. B. , Dale, A. , & Alzheimer's Disease Neuroimaging Initiative . (2009). Regional rates of neocortical atrophy from normal aging to early Alzheimer disease. Neurology, 73(6), 457–465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Molnar‐Szakacs, I. , & Uddin, L. Q. (2022). Anterior insula as a gatekeeper of executive control. Neuroscience & Biobehavioral Reviews, 139, 104736. [DOI] [PubMed] [Google Scholar]
- Oh, K. , Chung, Y.‐C. , Kim, K. W. , Kim, W.‐S. , & Oh, I.‐S. (2019). Classification and visualization of Alzheimer's disease using volumetric convolutional neural network and transfer learning. Scientific Reports, 9(1), 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa, F. , Varoquaux, G. , Gramfort, A. , Michel, V. , Thirion, B. , Grisel, O. , Blondel, M. , Müller, A. , Nothman, J. , Louppe, G. , Prettenhofer, P. , Weiss, R. , Dubourg, V. , Vanderplas, J. , Passos, A. , Cournapeau, D. , Brucher, M. , Perrot, M. , & Duchesnay, E. (2011). Scikit‐learn: Machine learning in python. The Journal of Machine Learning Research, 12, 2825–2830. [Google Scholar]
- Rusinek, H. , Endo, Y. , De Santi, S. , Frid, D. , Tsui, W.‐H. , Segal, S. , Convit, A. , & de Leon, M. (2004). Atrophy rate in medial temporal lobe during progression of Alzheimer disease. Neurology, 63(12), 2354–2359. [DOI] [PubMed] [Google Scholar]
- Shapley, L. S. (2016). A value for n‐person games (Vol. 17). Princeton University Press. [Google Scholar]
- Shrout, P. E. , & Fleiss, J. L. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86(2), 420–428. [DOI] [PubMed] [Google Scholar]
- Teipel, J. S. , Pruessner, J. C. , Faltraco, F. , Born, C. , Rocha‐Unold, M. , Evans, A. , Möller, H.‐J. , & Hampel, H. (2006). Comprehensive dissection of the medial temporal lobe in AD: Measurement of hippocampus, amygdala, entorhinal, perirhinal and parahippocampal cortices using MRI. Journal of Neurology, 253(6), 794–800. [DOI] [PubMed] [Google Scholar]
- Vogt, B. A. (2019). Cingulate cortex in Parkinson's disease. Handbook of Clinical Neurology, 166, 253–266. [DOI] [PubMed] [Google Scholar]
- Wachinger, C. , Salat, D. H. , Weiner, M. , Reuter, M. , & Alzheimer's Disease Neuroimaging Intiative . (2016). Whole‐brain analysis reveals increased neuroanatomical asymmetries in dementia for hippocampus and amygdala. Brain, 139(12), 3253–3266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J. , Hoekstra, J. G. , Zuo, C. , Cook, T. J. , & Zhang, J. (2013). Biomarkers of Parkinson's disease: Current status and future perspectives. Drug Discovery Today, 18(3–4), 155–162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, J. , Knol, M. J. , Tiulpin, A. , Dubost, F. , de Bruijne, M. , Vernooij, M. W. , Adams, H. H. H. , Ikram, M. A. , Niessen, W. J. , & Roshchupkin, G. V. (2019). Gray matter age prediction as a biomarker for risk of dementia. Proceedings of the National Academy of Sciences of the United States of America, 116(42), 21213–21218. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 Global feature attribution comparison of the brain age model. (A) Top 20 important features derived from SHAP. The abscissa represents the mean absolute value of Shapley values, and the ordinate represents the importance ranking of features. (B) Top 20 important features derived from feature importance of XGBoost. The abscissa represents the feature importance score (gain), and the ordinate represents the importance ranking of features. lh, left hemisphere; rh, right hemisphere
FIGURE S2 Test–retest reliability of the brain age vector. The scatter plot represents the ICC[2,1] between repeated scans of each subject in sMCI (N = 68) and pMCI (N = 63) group. ICC, intraclass correlation coefficient; pMCI, progressive mild cognitive impairment; sMCI, stable mild cognitive impairment
TABLE S1 Feature regions with significant structural changes for prodromal AD (sMCI vs. pMCI) and PD (HC vs. prodromal PD) derived from brain volumes
TABLE S2 Feature regions detected by the brain age vector for sMCI versus pMCI on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S3 Feature regions detected by the brain age vector for HC versus. prodromal PD on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S4 Classification performance of 10‐fold cross‐validation for sMCI versus pMCI on the subsets of 50%, 70%, and 100% subjects of the clinical sets
TABLE S5 Classification performance of 10‐fold cross‐validation for HC versus prodromal PD on the subsets of 50%, 70%, and 100% subjects of the clinical sets.
Data Availability Statement
Data from the IXI, OASIS, SLIM, INDI, ADNI, and PPMI database are made available via: http://brain-development.org/ixi-dataset/, https://www.oasis-brains.org/, http://fcon_1000.projects.nitrc.org/indi/IndiPro.html/, www.loni.ucla.edu/ADNI/, and www.ppmi-info.org. The code for the computational pipeline is publicly available at https://github.com/Kecici/Brain-age-vector-construction.git.


