Intracellular connections between basal bodies promote the coordinated behavior of motile cilia

Abstract

Hydrodynamic flow produced by multiciliated cells is critical for fluid circulation and cell motility. Hundreds of cilia beat with metachronal synchrony for fluid flow. Cilia-driven fluid flow produces extracellular hydrodynamic forces that cause neighboring cilia to beat in a synchronized manner. However, hydrodynamic coupling between neighboring cilia is not the sole mechanism that drives cilia synchrony. Cilia are nucleated by basal bodies (BBs) that link to each other and to the cell’s cortex via BB-associated appendages. The intracellular BB and cortical network is hypothesized to synchronize ciliary beating by transmitting cilia coordination cues. The extent of intracellular ciliary connections and the nature of these stimuli remain unclear. Moreover, how BB connections influence the dynamics of individual cilia has not been established. We show by focused ion beam scanning electron microscopy imaging that cilia are coupled both longitudinally and laterally in the ciliate Tetrahymena thermophila by the underlying BB and cortical cytoskeletal network. To visualize the behavior of individual cilia in live, immobilized Tetrahymena cells, we developed Delivered Iron Particle Ubiety Live Light (DIPULL) microscopy. Quantitative and computer analyses of ciliary dynamics reveal that BB connections control ciliary waveform and coordinate ciliary beating. Loss of BB connections reduces cilia-dependent fluid flow forces.

INTRODUCTION

Hydrodynamic flow supports a myriad of biological functions, including the circulation of cerebrospinal fluid in the brain ventricles, mucosal clearance in the airway, transport of eggs in the oviduct, and cell motility in aquatic environments. In these specialized cell types, fields of motile cilia or multiciliary arrays decorate the cell surface. Motile cilia beat in a rhythmic and directed manner for unidirectional fluid flow.

Ciliary beating exerts motive forces on both the fluid environment and the cell body of multiciliary arrays. The direction and magnitude of cilia-driven forces are defined by several factors that include the ciliary waveform and the ciliary beat frequency. The ciliary waveform refers to the propagation of bends along the cilium length during ciliary beating. According to the “sliding filament model,” ciliary bends are promoted by sliding between radially arranged and coupled doublet microtubules within the ciliary axoneme (Satir, 1968; Summers and Gibbons, 1971; Brokaw, 1972a,b). Tight spatiotemporal regulation over this process is fundamental to the formation of unique ciliary waveforms (Warner and Satir, 1974; Naitoh and Sugino, 1984). During the power stroke, the cilium, which is akin to an oar of a boat, pushes fluid along the cell’s anterior–posterior (AP) axis while maintaining a relatively straight profile. This ensures that the magnitude of drag forces is maximized for effective propulsion of fluid along the cell body (Naitoh and Sugino, 1984). Concurrently, ciliary forces are also transmitted into the cell body. In motile multiciliated organisms, the opposing forces from fluid propulsion are utilized for cell motility. Once complete, the power stroke transitions into the recovery stroke whereby the cilium moves in the opposite direction. Notably, the cilium adopts a prominent bend while maintaining a low trajectory across the cell surface. This reduces drag forces on the cilium as it travels in the opposite direction. Then, the cycle repeats. The ciliary beat frequency, which reflects the speed of ciliary movement, also defines the magnitude of ciliary forces (Naitoh and Sugino, 1984; Teff et al., 2008; Bottier et al., 2019). Together, the direction and magnitude of cilia-driven forces depend on the ciliary waveform and the ciliary beat frequency.

The coordination of ciliary beating is achieved by dynamic interactions between neighboring, oriented cilia (Lighthill, 1976; Elgeti and Gompper, 2013; Maestro et al., 2018). Hydrodynamic coupling synchronizes ciliary beating by interactions between cilia through their fluid environment (Tamm, 1984; Elgeti and Gompper, 2013; Maestro et al., 2018). Neighboring and oriented cilia undulate sequentially such that when one cilium beats, the fluid forces exerted upon its neighbor serve to coordinate their beating. Adjacent cilia beat with a temporal delay, or phase difference, but remain in synchrony. The coordinated undulation of cilia appears as metachronal waves that propagate across the multiciliary array. Computer modeling suggests that hydrodynamic coupling is sufficient to promote coordinated ciliary behavior if cilia are near one another (Riedel et al., 2005; Elgeti and Gompper, 2013). Experimental and modeling data demonstrate that when separated by greater than 50% of a cilium length, fluid-driven cilia coordination becomes less effective (Brumley et al., 2014). Consequently, this leads to inconsistent ciliary waveforms and inefficient fluid flow (Elgeti and Gompper, 2013; Brumley et al., 2014). While hydrodynamic coupling is integral to coordinated ciliary beating, it may not be the only mechanism for promoting ciliary synchrony. For example, metachronal waves traveling along the cell cortex continue to propagate across multiciliary arrays even when hydrodynamic flow is physically blocked (Narematsu et al., 2015). In addition, Chlamydomonas cells with cilia positioning defects fail to beat in coordination even when the cilia are positioned within hydrodynamic range (Hoops et al., 1984; Quaranta et al., 2015; Wan and Goldstein, 2016). This suggests that alternate mechanisms can coordinate ciliary movement along the cell cortex.

The cell cortex is thought to synchronize ciliary beating by transmitting cilia coordination cues through the cellular cortical cytoskeleton (Hyams and Borisy, 1975; Tamm, 1999; Narematsu et al., 2015; Quaranta et al., 2015). However, the nature of this cue has not been established. In the multiflagellate Koruga, cortical contractions were proposed to promote “body waves,” which lead to the formation of metachronal waves across the cell cortex (Cleveland and Cleveland, 1966). However, subsequent studies suggested that “body waves” did not arise from intracellular cortical contraction (Machemer, 1974) and inhibition of ciliary beating in Koruga abolishes “body waves” (Tamm, 1999). This suggests that cilia-driven forces are transmitted into the cell cortex, and this in turn induces “body waves,” opening the possibility that ciliary forces themselves provide intracellular coordination cues (Tamm, 1999). At the cell cortex, basal bodies (BBs) nucleate and anchor cilia. BB-associated appendages mediate BB–BB and BB–cell cortex connections (Allen, 1967; Jerka-Dziadosz et al., 1995; Iftode et al., 1996; Werner et al., 2011; Vladar et al., 2012; Galati et al., 2014; Junker et al., 2019; Soh et al., 2020). In addition, BBs are embedded in the underlying cortical cytoskeleton that comprises microtubules, actin, and intermediate filaments (Gordon, 1982; Hard and Rieder, 1983; Lemullois et al., 1987; Williams, 2006; Werner et al., 2011; Mahuzier et al., 2018; Yasunaga et al., 2022). Hence, BBs, at the base of cilia, are physically interconnected by an underlying cytoskeletal matrix. Ciliary beating and linkages between BBs deform BBs and their associated accessory structures (Warner and Satir, 1974; Vernon and Woolley, 2004; Khanal et al., 2021; Junker et al., unpublished data). It is proposed that the extent of the connections between BBs and the cell cortex determines the magnitude of transmitted ciliary forces between BBs, which then shape the ciliary waveform (Junker et al., unpublished data). Whether the transmission of ciliary forces through neighboring BBs serves as a mechanical cue for controlling ciliary waveforms and coordinating ciliary beating remains to be investigated directly.

Connections between BBs are required for coordinated ciliary dynamics in biflagellate and multiciliated organisms. However, the underlying mechanisms remain unclear. In the case of the biflagellated Chlamydomonas, the beat patterns of the two cilia or flagella are coordinated by striated fibers (SFs) that connect the BBs at the base of the flagella (Ringo, 1967; Quaranta et al., 2015; Wan and Goldstein, 2016). The Chlamydomonas mutant vfl3 disrupts SFs and displays abnormal beating patterns of the two flagella (Hoops et al., 1984; Quaranta et al., 2015; Wan and Goldstein, 2016). This would suggest that the coupling between BBs coordinates ciliary behavior. Notably, the loss of connections between the two BBs in vfl3 mutants is also associated with BB disorientation, whereby BBs no longer dock at the cell cortex in a polarized manner (Hoops et al., 1984). Proper BB orientation in biflagellates and in multiciliary arrays is fundamental for polarized ciliary beating to drive fluid flow and cell motility (Soh and Pearson, 2021). It is plausible that disoriented BBs lead to ciliary beating defects, which consequently cause the loss of cilia coordination (Quaranta et al., 2015; Wan and Goldstein, 2016; Gilpin et al., 2017b). However, this has not yet been tested. In the case of vertebrate multiciliary arrays, the cortical actin network organizes BBs (Werner et al., 2011; Mahuzier et al., 2018). Loss of cortical actin causes cilia mispositioning and undocking from the cell cortex (Werner et al., 2011; Mahuzier et al., 2018). Moreover, synchronized ciliary beating is disrupted. Therefore, the cortical actin and BB network not only is required for cilia organization but is also necessary for normal ciliary dynamics. Finally, the metachronal behavior of multiciliary arrays in the ciliate Paramecium responds to physical manipulations to the cell cortex. Experimentally induced cyclical stretching along the Paramecium cell cortex changes their metachronal wave frequency (Narematsu et al., 2015). Together, these data suggest that the cell cortex of multiciliary arrays also regulates ciliary coordination. However, the nature of the cortical elements, how forces are propagated between cilia, and the direct impact on ciliary beating are not understood.

RESULTS AND DISCUSSION

Tetrahymena cilia are intracellularly coupled

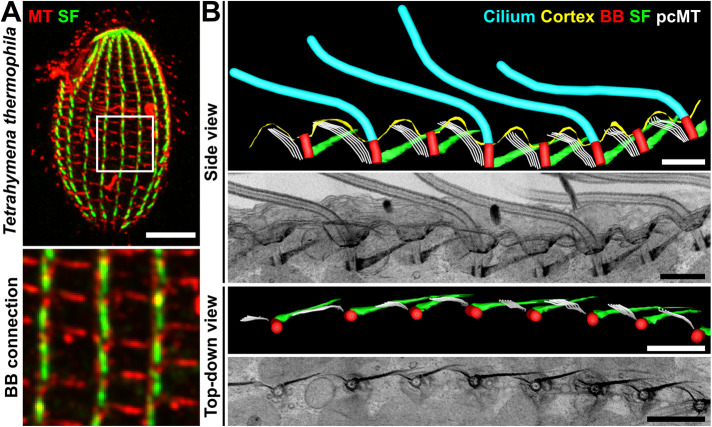
To understand how the BB and cytoskeletal network synchronizes ciliary dynamics in multiciliary arrays, the interconnectedness of the underlying cortical architecture in Tetrahymena ciliary arrays was visualized. Individual Tetrahymena BBs establish connections with their BB neighbors and the cell cortex (Pitelka, 1961; Allen, 1967; Galati et al., 2014; Soh et al., 2020). However, the extent of these interactions across the entire cell surface has not been characterized. Using fluorescence microscopy and focused ion beam scanning electron microscopy (FIB-SEM) in Tetrahymena cells, we observed that each ciliary row is longitudinally connected along the entire cell length (Figure 1). Consistent with prior work, each BB connection consists of an anteriorly oriented BB-associated SF that is connected to the postciliary microtubule (pcMTs) bundle of the anterior BB (Figure 1, Supplemental Figure S1A, and Supplemental Movie 1; Allen, 1967; Galati et al., 2014; Junker et al., 2019; Soh et al., 2020). SF-pcMT linkages are short (16.0 ± 4.6 nm in length; Soh et al., 2020), and the resolution of FIB-SEM was not sufficient to resolve these structures. Therefore, we defined BB connections through SFs and pcMTs as those positioned within 1 SD of the average SF-pcMT linkage length (16.0 ± 4.6 nm). BB connections also occur between ciliated and unciliated BBs, whereby the SFs of ciliated BBs interact with the pcMTs of anteriorly positioned unciliated BBs (Figure 1B and Supplemental Figure S1B). In addition, ciliated BBs with long SFs can interact with the pcMTs of the anterior BB that are positioned two BBs away (Figure 1B and Supplemental Figure S1B). Thus, BBs within a ciliary row are longitudinally connected (Figure 1B). Between adjacent BB rows, the BB-associated transverse microtubules (tMTs) connect to the cell cortex in alignment with the adjacent ciliary row (Supplemental Figure S1A and Supplemental Movie 1; Junker et al., 2019). The distal ends of tMTs point toward the right adjacent ciliary row (when viewed from above the cell) and either associate with or are near to (within 20 nm) the SFs and pcMTs of the adjacent ciliary row (Supplemental Figure S1A and Supplemental Movie 1; Allen, 1967; Junker et al., 2019; Soh et al., 2020). Whether the tMT distal ends directly connect with these structures was not resolved in our images but suggests that such interactions exist. In summary, Tetrahymena cilia are longitudinally and laterally connected across the cell surface by an underlying BB and cortical cytoskeletal network (Figure 1, Supplemental Figure S1A, and Supplemental Movie 1).

FIGURE 1:

Cilia are intracellularly coupled by BBs. (A) Immunofluorescent image depicting a Tetrahymena cell. Bottom panel: Inset (white box) illustrating top-down views of the BB network. Microtubule (MT), red; SF, green. Scale bar, 10 µm. Inset width, 11.0 µm. (B) FIB-SEM (two-dimensional projection) and model images showing the intracellularly coupled ciliary array of a Tetrahymena cell. Cilia, cyan; cortex, yellow; BB, red; SF, green; Postciliary microtubule (pcMT), white. Scale bars, 1 µm.

Movie S1.

Download video file ^{(20.5MB, mov)}

FIB-SEM image volume illustrating WT Tetrahymena cortical architecture. Cilia, cyan. BB, red. SF, green. MT appendages, white. Scale bar, 2 μm.

The FIB-SEM analyses also showed that the long, proximal-distal axis of BBs is not uniformly perpendicular to the cell cortex (Supplemental Figure S1, C and D). This suggests that BBs rock or rotate back and forth during ciliary beating in response to the mechanical forces from beating cilia. However, the limited sample size precluded our ability to determine whether BB angles directly correlate with cilia positions during their beat cycles (Supplemental Figure S1E). It is possible that BB rotations are caused by ciliary forces. At least two types of ciliary forces could cause BB movement. First, compressive and tensile forces from doublet microtubule sliding within the ciliary axoneme could impose forces directly on the BB (Vernon and Woolley, 2004; Riedel-Kruse et al., 2007; Khanal et al., 2021; Junker et al., unpublished data). Second, and not exclusive of the first model, forces from neighboring ciliated BBs may be transmitted by intracellular BB connections. This is supported by the occurrence of unciliated BBs that are rotated relative to the cell cortex (Supplemental Figure S1, C and D) and by our studies suggesting that ciliary forces are transmitted to BBs by SFs (Junker et al., unpublished data). Further studies are required to uncover the source and magnitude of forces that promote BB rotation.

Visualizing live Tetrahymena ciliary dynamics using DIPULL microscopy

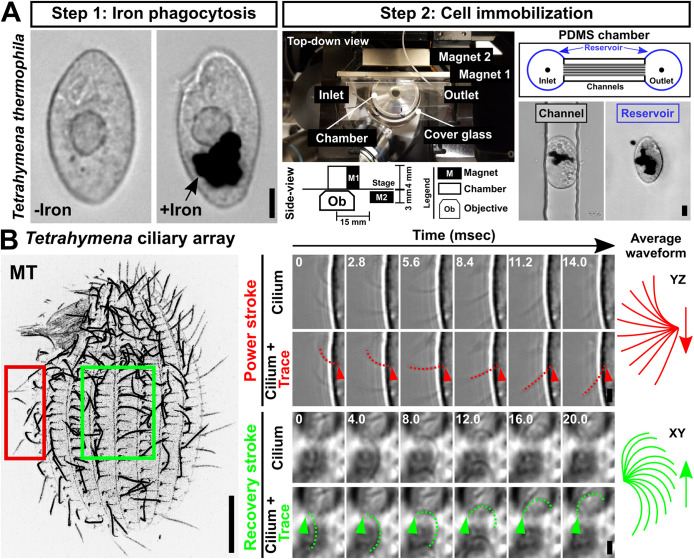
To test whether connections between BBs are required for normal ciliary beating, we developed a strategy to visualize ciliary beating in live Tetrahymena cells. Rapid Tetrahymena movements during swimming obstructs the visualization and quantification of ciliary beating. We developed a method to immobilize live cells to visualize both extracellular fluid flow and ciliary dynamics. Prior live Tetrahymena cell immobilization strategies cause cytotoxicity or disrupt ciliary dynamics (Spoon et al., 1977; Aufderheide, 1986; Larsen and Satir, 1991; Kumano et al., 2012). To circumvent these issues, we developed Delivered Iron Particle Ubiety Live Light (DIPULL) microscopy to trap live Tetrahymena cells (Figure 2A). Tetrahymena cells were fed 1–2 μm iron particles that are engulfed by phagocytosis (Figure 2A [Step 1] and Supplemental Figure S2A; Rifkin and Ballentine, 1976; Kim et al., 2010). Cells were then trapped and immobilized within polydimethylsiloxane (PDMS) microfluidic chambers using magnetism and then visualized using an inverted microscope (Figure 2A [Step 2] and Supplemental Figure S2J). As far as we can detect, DIPULL does not compromise ciliary dynamics, cell morphology, or cell division (Supplemental Figure S2, A–F, H). This immobilization strategy traps live Tetrahymena cells, allowing for quantitative visualization of ciliary dynamics.

FIGURE 2:

Tetrahymena live cell immobilization technique. (A) DIPULL microscopy setup. Step 1: Tetrahymena cells are fed iron particles. Cell images pre- and post–iron engulfment. Step 2: Cells are introduced into a microfluidic chamber and immobilized via a constant external magnetic field. To track intracellular dynamics, imaging was performed on cells that were trapped within channels (black outline). The visualization of extracellular dynamics was performed on cells that are trapped within the chamber reservoir (blue outline). Scale bars, 10 µm. (B) Visualization of ciliary dynamics via DIPULL-immobilized live Tetrahymena cells. Left panel: Tetrahymena ciliary array. Bar, 10 µm. Right panel: Time-lapse images of power and recovery strokes. Time intervals (ms) are indicated. Dotted lines mark manual cilia traces. Average power stroke, red; average recovery stroke, green. Scale bars, 2 µm.

BB connections and orientation are required for efficient fluid flow

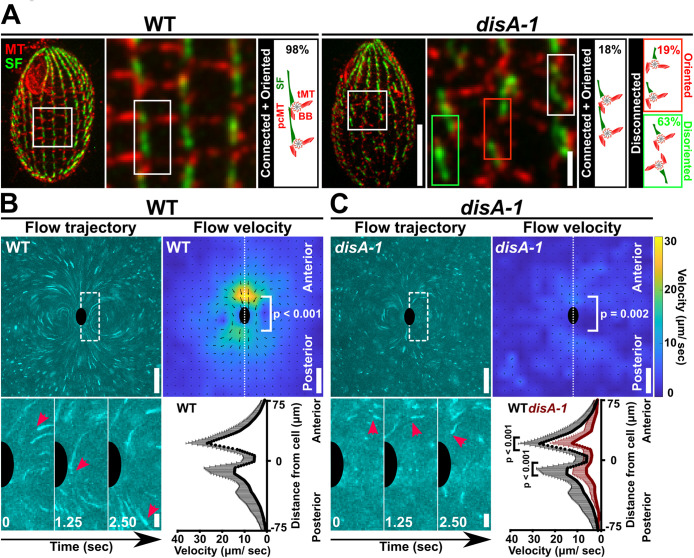
Using DIPULL, we tested whether BB disconnection and disorientation affects cilia-dependent fluid flow. To investigate whether cilia-driven fluid flow is disrupted when BB connections and orientation are lost, fluid flow was quantified in wild-type (WT) and disA-1 cells at 25°C (Figure 3A). disA-1 mutants swim more slowly and possess short SFs, where 82% of BBs are disconnected from their neighbors (Figure 3A; Galati et al., 2014; Nabi et al., 2019; Soh et al., 2020). Cells were immobilized in the DIPULL chamber reservoir to avoid boundary effects from the chamber walls (Figure 2A). Fluid flow was visualized by tracking the movement of 0.5 μm fluorescent beads that were added to the media (Figure 3, B and C). The movements of beads were visualized by projecting images from a time lapse of 2.5 s (100 frames; Supplemental Movie 2). Sustained fluid flow traveling from the cell’s anterior (A) pole to the posterior (P) pole was observed in WT cells at 25°C (Figure 3B [left] and Supplemental Movie 2 [left]). Flow was faster at the cell anterior pole compared with that at the posterior pole (Figure 3B [right]; WT mean fluid flow velocity: anterior pole: 26.0 ± 8.6 µm/s; posterior pole: 14.0 ± 9.9 µm/s; Mann–Whitney test; P value < 0.001). disA-1 cells with disconnected and disoriented BBs exhibit shorter fluorescent bead movements, indicating that fluid flow is slower (Figure 3C [left] and Supplemental Movie 2 [right]). Like WT cells, disA-1 cells have faster fluid flow at the cell anterior compared with that at the posterior (Figure 3C [right]; disA-1 mean fluid flow velocity: anterior pole: 11.0 ± 9.0 µm/s; posterior pole: 5.6 ± 5.9 µm/s; P value = 0.002). Consistent with the reduced swimming speed of disA-1 mutants, the fluid flow velocities are approximately 50% of those of WT cells (Figure 3, B and C; Mann–Whitney test; P value < 0.001; Galati et al., 2014). This suggests that BB connections may be important for sustained fluid flow (Figure 3, B and C). However, in addition to being disconnected, 63% of BBs in disA-1 cells are disoriented, making it impossible to distinguish whether the observed fluid flow reduction results from BB disconnections and/or BB disorientation. Consistent with the model that both disconnection and disorientation negatively impact fluid flow, cell motility is reduced as disA-1 cells experience increased temperature, a condition where BB disorientation and disconnection is exacerbated (Jerka-Dziadosz et al., 1995; Galati et al., 2014; Soh et al., 2020). Here, we focus on the role of BB connection in promoting ciliary forces.

FIGURE 3:

BB connections and orientation are required for cilia-dependent fluid flow. (A) Fluorescent images depicting the cortical organization of WT and disA-1 cells at 25°C. Most disA-1 cells display BB disconnection (82%). Disconnected disA-1 bodies are either oriented (19% of total) or disoriented (63% of total). Microtubule (MT), red; SF, green. Scale bars, 10 and 2 µm. (B) BB connections are required for normal fluid flow movements and velocity at 25°C. Fluid flow is assessed by tracking fluorescent beads in media. Fluid flow trajectories are depicted as time-projected images over 2.5 s (100 frames). Inset (white box with dashed line) illustrates the movement of a fluorescent bead (red arrowheads) relative to the cell (black half oval). Fluid flow velocity is represented as heatmaps. Cooler colors indicate slower fluid flow, while warmer colors indicate faster fluid flow. The predicted cell position is marked by a black oval. (C) disA-1 disrupts fluid flow velocity at 25°C. Inset (white box with dashed line) illustrates the movement of a fluorescent bead (red arrowheads) relative to the cell (black half oval). WT (black line): n = 9 cells. disA-1 (brown line): n = 13 cells. Mann–Whitney test. Mean ± SD. Scale bars, 50 µm (full field of view) and 10 µm (inset).

Movie S2.

Download video file ^{(11.8MB, mov)}

WT and disA-1 fluid flow dynamics. Imaging frame interval, 40 fps. Movie frame rate, 20 fps. Scale bar, 50 μm.

Loss of BB connections reduces ciliary forces

To test whether BB connections specifically impact ciliary forces, we focused on individual cilia with BBs that are disconnected but still oriented. Oriented cilia were identified as those in which the power stroke occurs along the cell’s AP axis and remain in focus during the entire power stroke before transiting into the recovery stroke, where they exit the imaging focal plane (Figure 2B [right] and Supplemental Movie 3; WT: left; disA-1 oriented cilia: middle; disA-1 disoriented cilia: right). We also imposed the requirement that the anterior and posterior neighboring cilia are similarly oriented (Supplemental Movie 3). Of the BBs acceptable for analysis, we predict that 51% will be disconnected from neighboring BBs (Figure 3A [right]; 51% of oriented cilia are disconnected). Ciliary parameters that affect fluid flow are defined at minimum by ciliary length, ciliary beat frequency or speed, ciliary sweep trajectory, and ciliary curvature. Ciliary length is not changed in disA-1 mutants (Supplemental Figure S2I; WT: 5.0 ± 0.7 µm; disA-1: 5.2 ± 0.6 µm; Student’s t test; P = 0.35), and we therefore focused on the remaining three parameters to determine whether they were impacted when BBs are disconnected.

Movie S3.

Download video file ^{(16.3MB, mov)}

WT and disA-1 ciliary power stroke. Cell anterior pole is oriented to the top of the movie. Disoriented cilia do not beat in a uniform direction, and they beat out of the imaging plane. Imaging frame interval, 793 fps. Movie frame rate, 20 fps. Scale bar, 5 μm.

Loss of BB connections slows the power stroke but does not impact the overall ciliary beat frequency.

To test whether the disruption of BB connections specifically reduces ciliary beat frequency and ciliary speed, the ciliary beat frequency was quantified using kymograph analysis of oriented cilia viewed from the side (Figure 4A). The average ciliary beat frequency of WT cells at 25°C is 24.0 ± 5.7 Hz (Figure 4, B and C). Faster ciliary beat frequencies were previously reported for Tetrahymena cells (Stoddard et al., 2018), and we suggest that this is attributed to differences in strain background, the position of the cilia along the cell cortex, and reduced temperature. The average ciliary beat frequencies of both oriented and disoriented disA-1 cilia are comparable to those of WT cilia (Figure 4C and Supplemental Figure S3C; ciliary beat frequency; WT: 24.0 ± 5.7 Hz; oriented disA-1: 24.0 ± 7.4 Hz; disoriented disA-1: 23.0 ± 7.8 Hz; Mann–Whitney test; P = 0.55 and 0.94, respectively). The distribution of ciliary beat frequency in the disoriented cilia appears bimodal, whereby a subpopulation of cilia has reduced ciliary beat frequencies, but the overall mean ciliary beat frequency is like that of oriented cilia (Supplemental Figure S3C). The ciliary beat frequency was next imaged from above the cell to track the ciliary power stroke trajectory (Supplemental Figure S3A). Consistent with results using side views, top views of oriented disA-1 cilia had ciliary beat frequencies comparable to those of WT cilia (Supplemental Figure S3B; WT: 24.0 ± 4.8 Hz; disA-1: 25.0 ± 7.6 Hz; Mann–Whitney test; P = 0.51). These results suggest that BB connections and orientation are not required for the overall ciliary beat frequency (Figure 4C and Supplemental Figure S3C). While Chlamydomonas vlf3 mutants with disconnected BBs exhibit variable and reduced ciliary beat frequency (Wan and Goldstein, 2016), Tetrahymena disA-1 mutants appear to have relatively normal ciliary beat frequencies (Figure 4C and Supplemental Figure S3, B and C).

FIGURE 4:

Loss of BB connections does not inhibit ciliary beat frequency. (A) Schematic image depicting ciliary beat frequency quantification using kymograph analysis. The X-axis represents time (total duration: 105 ms). The Y-axis represents distance. Scale bar, 2 µm. (B) Kymographs of WT and disA-1 cilia. disA-1 cilia display variable ciliary trajectories between ciliary beat cycles (red arrowheads). Scale bar, 2 µm. (C) Quantification of WT and disA-1 ciliary beat frequency of individual cilia. Three cilia per cell were sampled. disA-1 cilia exhibit ciliary beat frequencies comparable to those of WT cilia. WT: n = 28 cells (84 cilia). disA-1: n = 38 cells (72 oriented cilia; 41 disoriented cilia). Mann–Whitney test. Mean ± SD. (D) Duration of power and recovery strokes of WT and disA-1 cilia. WT: n = 11 cells (25 cilia). disA-1: n = 13 cells (32 cilia). Mann–Whitney test. F test for variance comparison. Mean ± SD. (E) Schematic illustrating comparable average durations of ciliary beat cycle for WT and disA-1 cilia. disA-1 cilia beat at a ciliary beat frequency comparable to that of WT cilia with a longer power stroke duration and a shorter recovery stroke duration.

WT and disA-1 cilia tips were imaged from above the cell to quantify the relative durations of the power and recovery strokes. The power stroke duration of WT and disA-1 cilia is 17.0 ± 4.4 and 23.0 ± 11.0 ms, respectively (Figure 4D; Mann–Whitney test; P value = 0.09). The disA-1 power stroke duration was more variable, with a subpopulation of cilia exhibiting a longer-duration power stroke (Figure 4D; F test for variance comparison; P < 0.001). This variability may reflect the mixture of connected and disconnected BBs present in the analysis (Figure 3A), as we are not able to determine whether BBs are connected in our live imaging approach. In summary, the average disA-1 power stroke duration is longer than that in WT. The recovery stroke of disA-1 cilia is 4.0 ms shorter than that in WT (Figure 4D; WT: 26.0 ± 6.9 ms; disA-1: 22.0 ± 7.6 ms; P value = 0.02). Thus, the average total duration of each ciliary beat cycle is comparable between WT and disA-1 cilia (Figure 4E; average total duration per ciliary beat cycle; WT: 43.0 ± 8.2 ms [23.2 Hz]; disA-1: 45.0 ± 16.0 ms [22.2 Hz]; Mann–Whitney test; P value = 0.51) and is consistent with the ciliary beat frequency.

The above measurements are based on tracking the ciliary tip, thereby making quantification of the ciliary waveform through the ciliary beat cycle impossible. To quantify the ciliary generated forces, both ciliary sweep trajectory and cilia curvature must be quantified (see below), which requires the entire cilium to be within the imaging focal plane. The relative start and end positions of the power stroke were defined as when cilia first appear and exit the side view imaging focal plane, respectively (Figure 2B, red box). The same method was applied to define the average start and stop positions of the recovery stroke when cilia were imaged from the top of the cell (Figure 2B, green box). Importantly, this method captures only a portion of the complete power and recovery strokes when cilia are in focus. The WT power stroke duration was 18.0 ± 9.3 ms, while that of disA-1 cilia was 11.0 ± 1.8 ms (Mann–Whitney test; P value = 0.018). While the WT power stroke duration is similar to that in the above analyses, the disA-1 power stroke is much shorter and likely represents a shorter duration in the imaging plane. The WT and disA-1 recovery stroke durations were similar to each other but significantly reduced compared with the above analyses (WT = 10.0 ± 4.3 ms and disA-1 = 10.0 ± 3.1 ms; Mann–Whitney test; P value = 0.73). Like the power stroke, this shorter measured duration likely results from the recovery stroke moving out of the imaging focal plane. These limited segments of the ciliary beat cycle were next used to quantify the ciliary waveforms and predicted force outputs.

BB connections support normal ciliary waveforms.

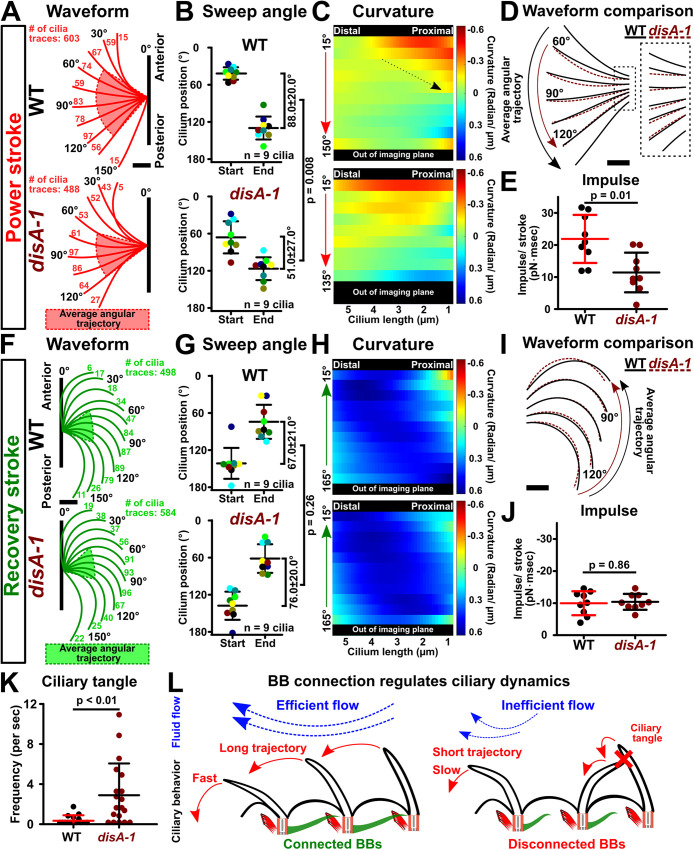
The sweep trajectory of disA-1 cilia is not always consistent between beat strokes (Figure 4B, red arrowheads), suggesting that the ciliary waveform is disrupted when BBs are disconnected. Both the power and recovery strokes were imaged and quantified using a semiautomated image analysis regime (Figures 2B and 5A and Supplemental Movies 3 and 4; Bottier et al., 2019). The proximal approximately 1.5 µm of the cilium was not observed using this analysis regime. Thus, the cilium base is defined as the point where the proximal end of the cilium could be visualized by differential interference contrast (DIC) imaging. Generally, the ciliary trajectories for WT power and recovery strokes are comparable to those in prior qualitative studies (Figure 5, A and F; Wood et al., 2007; Urbanska et al., 2018; Fabritius et al., 2021; Joachimiak et al., 2021). Quantitative comparisons between the ciliary waveforms of oriented cilia suggest that disA-1 cilia display a shorter sweep angle along the power stroke compared with that of WT cilia (Figure 5, A and B, and Supplemental Figure S3I; WT cilia: 88.0 ± 20.0°; disA-1 cilia: 51.0 ± 27.0°; Mann–Whitney test; P = 0.008). These average representative waveforms are generated from many individual ciliary traces that are standardized by using the average start and stop positions of all analyzed cilia (Figure 5, A [red highlights] and B; n = 9 cilia, six ciliary beat cycles each, nine cells ). disA-1 cilia initiate the power stroke at 66.0 ± 26.0° compared with WT cilia at 42.0 ± 10° and then transition into the recovery stroke at 120.0 ± 18.0° compared with 130.0 ± 19.0° for WT cilia (Figure 5, B and G). Subtle increases in variance were observed in disA-1 cilia and may be explained by the subpopulation (49%) of oriented cilia with connected BBs that we expect to behave like WT cilia. The disA-1 power stoke is shorter, suggesting that BB connections promote a long ciliary power stroke trajectory (Figures 4B and 5, A and B, and Supplemental Figure S3I).

FIGURE 5:

BB connections support ciliary waveform and coordination. (A) Tetrahymena power stroke waveform. Top panel: Average WT power stroke waveform. Bottom panel: Average disA-1 power stroke waveform. Red highlight indicates the average angular trajectory (n = 9 cilia). Cilium position is defined by the angle from the cilium distal end (4.5 µm up from the cilium base) relative to the cell’s AP axis. Angles are categorized into 15° bins. Each angular bin contains at least 1% of all ciliary traces per condition. The number of cilia traces for each bin is indicated. (B) Angular trajectories of WT and disA-1 cilia during the power stroke. disA-1 cilia undergo shorter trajectories than WT cilia. Each cilium in the analysis is color coded. (C) Curvature heatmaps of WT and disA-1 cilia through the power stroke (blue: the cilium bends toward the cell anterior pole; red: the cilium bends away from the cell anterior pole; green: straight cilium). The Y-axis marks the cilium position through the power stroke. Dotted arrow indicates the change in WT cilium curvature at the start to middle of the power stroke. WT power stroke: n = 603 cilia traces (nine cilia, six ciliary beat cycles each, nine cells). disA-1 power stroke: n = 488 cilia traces (nine cilia, six ciliary beat cycles each, nine cells). (D) Superimposed WT (black lines) and disA-1 (brown dashed lines) average power stroke waveform. Curvature differences are depicted only for stages of the power stroke that fall within the average angular trajectories of WT and disA-1 cilia. (E) Ciliary power stroke impulses were estimated using RFT. WT cilia exert greater impulse (area under the force-time curve) than disA-1 cilia along the AP axis per power stroke (n = 9 cilia). (F) Tetrahymena recovery stroke waveform. Top panel: Average WT recovery stroke waveform. Bottom panel: Average disA-1 recovery stroke waveform. Green highlight indicates the average angular trajectory (n = 9 cilia). Cilium position is defined by the angle from the cilium distal end (4.5 µm up from the cilium base) relative to the cilium’s power stroke axis. Angles are categorized into 15° bins. Each angular bin is at least 1% of all ciliary traces per condition. The number of cilia traces for each bin is indicated. (G) Angular trajectories of WT and disA-1 cilia. Each cilium in the analysis is color coded. disA-1 cilia undergo trajectories comparable to those of WT cilia during the recovery stroke. (H) Curvature heatmaps of WT and disA-1 cilia through the recovery stroke (blue: the cilium bends toward the cell anterior pole; red: the cilium bends away from the cell anterior pole; green: straight cilium). The Y-axis marks the cilium position through the recovery stroke. WT recovery stroke: n = 498 cilia traces (nine cilia, six ciliary beat cycles each, nine cells). disA-1 recovery stroke: n = 584 cilia traces (nine cilia, six ciliary beat cycles each, nine cells). (I) Superimposed WT (black lines) and disA-1 (brown dashed lines) average recovery stroke waveform. Curvature differences are depicted only for stages of the recovery stroke that fall within the average angular trajectories of WT and disA-1 cilia. (J) Ciliary recovery stroke impulses were estimated using RFT. WT and disA-1 cilia exert comparable impulses (area under the force-time curve) along the AP axis per recovery stroke (n = 9 cilia). (K) Frequency of ciliary tangles. WT: n = 11 cells (14 cilia pairs); disA-1: n = 13 cells (19 cilia pairs). (L) Schematic illustrates the model that BB connections promote fast and long power stroke trajectories for coordinated ciliary beating and effective fluid flow propulsion. Scale bars, 1 µm.

Movie S4.

Download video file ^{(3.7MB, mov)}

WT and disA-1 ciliary recovery stroke. Cell anterior pole is oriented to the top of the movie. Ciliary tangles within and between ciliary rows occur when disA-1 cilia (black arrow) undergo inconsistent power stroke. Examples of ciliary tangles in two disA-1 cells are provided. Imaging frame interval, 793 fps. Movie frame rate, 20 fps. Scale bar, 5 μm.

Changes to ciliary curvature alter the efficiency of fluid flow as straight cilia promote greater fluid propulsion than bent cilia (Gray and Hancock, 1955; Brokaw, 1972a; Naitoh and Sugino, 1984). We assessed the impact of BB connections on cilia curvature. A curvature value of zero indicates a straight cilium, a negative curvature value indicates a concave cilium profile that bends away from the cell anterior, and a positive curvature value indicates a convex cilium profile that bends toward the cell anterior. The greatest differences between WT and disA-1 ciliary curvature occur primarily at the start to the middle of the power stroke (Figure 5D and Supplemental Figure S3D). WT cilia are approximately 12-fold more bent than disA-1 cilia at the proximal end of the cilium (Figure 5D [inset]; WT: –0.17 ± 0.05 rad/µm; disA-1: 0.01 ± 0.11 rad/µm; Mann–Whitney test; P < 0.0001). Importantly, the most proximal region of cilia (1.5 μm) could not be detected in our imaging. There may be unobservable differences between WT and disA-1 in this proximal region. At the medial region of the cilium, disA-1 cilia are twofold more bent than WT cilia (Figure 5D; WT: –0.08 ± 0.02 rad/µm; disA-1: –0.14 ± 0.04 rad/µm; Mann–Whitney test; P < 0.0001). Together, these results suggest that BB connections influence ciliary curvature during the power stroke (Figure 5, A–D, and Supplemental Figure S3D).

The recovery stroke returns cilia back to the start of the power stroke. Unlike the power stroke, BB connections do not appear to impact the angular trajectory of the recovery stroke (Figure 5G and Supplemental Figure S3J; WT cilia: 67.0 ± 21.0°; disA-1 cilia: 76.0 ± 20.0°; Mann–Whitney test; P = 0.26). We were unable to visualize the transition from the power to the recovery stroke and vice versa because cilia move out of the focal plane during the three-dimensional ciliary beat stroke. Seemingly contradictory, the recovery stroke trajectory of WT and disA-1 cilia appear to be similar despite the shorter average sweep trajectory of the disA-1 power stroke (Figure 5, B and G). One explanation is that the recovery stroke imaging planes of WT and disA-1 cilia are different, whereby WT cilia move closer to the cell cortex. This would result in comparable recovery stroke trajectory angles between WT and disA-1 cilia, but the total distance traveled would be reduced for disA-1 cilia. Alternatively, disA-1 cilia may change their trajectory during transitions between power and recovery strokes outside the imaging focal plane. We next measured the difference in curvature in disA-1 cilia and found that they are slightly more bent during the recovery stroke than in WT (Figure 5I; WT: 0.46 ± 0.11 rad/µm; disA-1: 0.51 ± 0.10 rad/µm; Mann–Whitney test; P < 0.0001). Thus, our results suggest that BB connections are not required for normal recovery stroke angular sweep trajectories but do reduce ciliary curvature (Figure 5I and Supplemental Figure S3, E and J).

Ciliary changes resulting from BB disconnections reduce ciliary-driven force.

To test whether the shorter sweep angle and abnormal curvature exhibited by disA-1 cilia during the power stroke reduce ciliary effectiveness, the magnitude of force along the AP axis was estimated using resistive force theory (RFT). RFT uses resistive force coefficients to determine the distributed viscous drag applied to the cilium by the surrounding fluid based on the orientation and velocity of the cilium as a function of arc length and time (Gray and Hancock, 1955). Overall force produced by a cilium during its beat stroke will be affected by the cilium length, angular sweep rate, beat shape, and viscosity of the medium. WT cilia exerted an average force of 1.41 ± 0.60 pN during the observed power stroke (Supplemental Figure S3F and Table 1; maximum power stroke force by WT cilia: 2.70 ± 0.88 pN). The average force exerted during the observed power stroke by disA-1 cilia is reduced by 18% (Supplemental Figure S3F and Table 1; disA-1; average power stroke force: 1.16 ± 0.79 pN; maximum power stroke force: 2.11 ± 1.19 pN). As shown in Figure 5D, differences in curvature of WT and disA-1 cilia are concentrated at the beginning of the power stroke, whereas differences in force output are greater toward the middle and end of the power stroke. This suggests that the reduced force of disA-1 cilia is due not to the change in curvature but rather to the reduced angular sweep rate (Table 1; WT: 6.62 ± 2.72°/ms; disA-1: 5.20 ± 2.88°/ms). The magnitude of force production in the opposite direction during the recovery stroke was similar between WT and disA-1 cilia (Supplemental Figure S3G and Table 1; average recovery stroke force; WT: –1.05 ± 0.34 pN; disA-1: –1.13 ± 0.40 pN; Mann–Whitney test; P value = 0.68).

TABLE 1:

Tabulation of results of ciliary force estimation.

Parameter	WT	disA-1	P value
Average power stroke force, pN	1.41 ± 0.60	1.16 ± 0.79	0.07
Maximum power stroke force, pN	2.70 ± 0.88	2.11 ± 1.19	0.001
Average recovery stroke force, pN	–1.05 ± 0.34	–1.13 ± 0.40	0.73
Maximum recovery stroke force, pN	–1.51 ± 0.51	–1.68 ± 0.56	0.15
Average power stroke sweep rate, °/ms	6.62 ± 2.72	5.20 ± 2.88	0.04
Maximum power stroke sweep rate, °/ms	10.69 ± 4.18	7.74 ± 4.00	0.002
Average recovery stroke sweep rate, °/ms	5.83 ± 1.94	6.37 ± 2.28	0.31
Maximum recovery stroke sweep rate, °/ms	7.60 ± 2.02	9.13 ± 3.11	0.008
Average power stroke basal moment, pN·μm	2.86 ± 0.87	1.93 ± 1.44	0.00003
Maximum power stroke basal moment, pN·μm	10.58 ± 3.16	8.37 ± 5.05	0.0005
Average recovery stroke basal moment, pN·μm	1.13 ± 0.59	1.36 ± 0.72	0.16
Maximum recovery stroke basal moment, pN·μm	4.90 ± 1.98	5.10 ± 1.93	0.44
Average power stroke power, aW	870 ± 600	690 ± 640	0.02
Average recovery stroke power, aW	420 ± 220	500 ± 310	0.27
Swimming speed, μm/s	272	123	—
Body force/cilium, pN	–0.26	–0.12	—

Ciliary forces were estimated from manual traces using previously described resistive force coefficients (C_N = 1.53μ, C_T = 0.64μ; Bayly et al., 2011). The viscosity of water, μ, applied in analysis was 0.889 cP at 25°C. All average values for ciliary quantities were calculated by averaging values within the mean sweep angle range for each traced ciliary beat stroke (54 total beat strokes each in four data sets) and then calculating the average and SD of the average quantities. Maximum values were calculated by taking the maximum value for each stroke within the mean sweep angle range and then calculating the average and SD for the maximum quantities. All force values integrate forces in the AP axis direction over the length of the cilium trace. Sweep rates are calculated by numerically differentiating the angle from the base of the cilium trace to 4.5 μm up from the cilium with respect to time. Calculation of basal moments and power is described in Materials and Methods, Ciliary force estimation. WT and disA-1 swim speeds (Galati et al., 2014) were used to estimate viscous drag forces on the Tetrahymena cell body using previously described methods (Chwang and Wu, 1975; Bayly et al., 2011).

Not only do disA-1 cilia produce lower power stroke forces on average, but they also appear to spend a shorter duration of time producing that force due to the shorter sweep angle in our segmented analysis using only cilia in focus (Figure 5, A and B). This leads to a lower impulse, the measure of the area under the force-time curve. The mean axial impulse of WT cilia was 21.9 ± 7.5 pN·ms, and that of disA-1 cilia was 11.4 ± 6.2 pN·ms (Figure 5E; Mann–Whitney test; P = 0.01). During the recovery stroke, WT cilia produce an impulse of –10.0 ± 3.7 pN·ms and disA-1 cilia produce an impulse of –10.4 ± 2.5 pN·ms (Figure 5J; Mann–Whitney test; P = 0.86). Though the power stroke of disA-1 cilia is significantly less productive, the recovery stroke produces a similar amount of drag impulse. The average measured impulses sum to 11.9 ± 8.4 pN·ms per beat for WT cilia and 1.0 ± 6.7 pN·ms per beat for disA-1 cilia, providing an estimate of the overall effectiveness of each beat. It should be noted that it was not possible to measure power and recovery strokes on the same cilia and that the SDs on the power and recovery stroke impulses for disA-1 cilia are larger than the difference in their magnitudes. For WT cilia, multiplying the net average impulse of 11.9 pN·ms per beat by the average frequency of 24 Hz gives an average total force per cilium of 0.29 pN, which compares well to the body drag force per cilium of –0.26 pN (Table 1). In summary, disA-1 cilia are less effective, in part due to their lower average force output during their beat stroke, but more significantly due to the shorter time duration spent sweeping a shorter trajectory.

A possible explanation for both the reduced propulsive force and shorter angular trajectory of disA-1 cilia is greater rotational compliance of the BB within the power stroke plane due to the lack of SF support (Junker et al., unpublished data). The estimated average bending moment at disA-1 BBs during the ciliary power stroke is reduced by 33% compared with that of WT (Table 1; WT: 2.86 ± 0.87 pN·μm; disA-1: 1.93 ± 1.44 pN·μm; P < 0.0001). If the BB has rotational compliance, the moment due to viscous forces on the cilium will tend to rotate it in the opposite direction of the cilium during the power stroke. We expect that the BB rotation predicted for WT cells in Figure 1 would increase in disA-1 cells where BBs are no longer connected. BB rotation will have the effect of reducing the sweep angle for a given ciliary deformation cycle. Reducing the sweep angle alone would reduce the sweep rate for a given ciliary deformation, thereby reducing the applied forces. This complex interaction requires further experimental and modeling work. Recovery stroke parameters are largely unaffected in disA-1 cells, perhaps because the recovery stroke occurs in a plane orthogonal to the BB axis and structural connections other than the SF are sufficient to stabilize it against moments about its axis.

BB connections promote coordinated ciliary beating

For cilia to beat in coordination, each cilium undulates with a constant temporal delay or phase difference relative to its neighbors. BB disconnections in disA-1 cells lead to slower, inconsistent power strokes and altered ciliary power stroke waveforms (Figure 5, A–C, and Supplemental Figure S3, D and I). We hypothesized that inconsistent power stroke speed and altered ciliary power stroke waveforms would disrupt the synchronization of a cilium undulating with its neighbors. To test this hypothesis, the phase difference between adjacent and oriented cilia was quantified when cilia were imaged from above the cell. The axis of the power stroke served as a proxy for BB orientation (Supplemental Figure S3A). The phase difference between cilia is influenced by the strength of their hydrodynamic coupling (Elgeti and Gompper, 2013). When cilia are positioned far apart, they are poorly hydrodynamically coupled and this leads to variable phase differences (Brumley et al., 2014). To rule out this possibility, only WT and disA-1 cilia that were spaced apart by comparable distances were analyzed (intercilia spacing; WT: 2.3 ± 1.3 µm; disA-1: 2.0 ± 0.7 µm; Mann–Whitney test; P = 0.40). disA-1 cilia exhibit more variable phase differences compared with WT cilia (Supplemental Figure S3H; phase difference; WT: –4.9 ± 5.4 ms; disA-1: –0.8 ± 14.0 ms; F test for variance comparison; P < 0.001). Thus, BB disconnections in disA-1 cells appear to disrupt consistent phase difference.

We next hypothesized that the inconsistent phase differences in disA-1 mutants would increase the probability of ciliary tangles in which neighboring cilia physically interact. Consistent with this, an eightfold increase in ciliary tangles was observed in oriented cilia of disA-1 cells compared with WT cells (Figure 5K; WT: ∼20 events/min; disA-1: ∼170 events/min; Mann–Whitney test; P = 0.004). Ciliary tangles occur when a disA-1 cilium beats slower than its anterior and posterior neighbors during the power stroke (Supplemental Movie 4 [middle and right]; black arrows mark examples of this event in two disA-1 cells). This uncoordinated behavior caused neighboring cilia within the same ciliary row to physically interfere with one another. Subsequently, these uncoordinated cilia also clash with cilia from adjacent ciliary rows that are undergoing the recovery stroke, leading to ciliary tangles between neighboring ciliary rows (Supplemental Movie 4). Therefore, consistent with the biflagellate Chlamydomonas, BB connections are required for coordinated ciliary beating in the multiciliated Tetrahymena thermophila (Quaranta et al., 2015; Wan and Goldstein, 2016). Notably, our study suggests that BB connections promote consistent power stroke speed and waveform to minimize ciliary tangles during coordinated ciliary beating (Figure 5L).

Summary

Together with hydrodynamic coupling between cilia, the underlying cortical architecture of multciliary arrays promotes ciliary coordination. Here we show that intracellular connections between BBs span the cell cortex (Figure 1). We propose that the interconnected nature of the cortical architecture transmits ciliary forces that serve as coordination cues for metachronal ciliary beating. A Tetrahymena cell immobilization technique (Figure 2) was developed to show that BB connections influence ciliary dynamics, independent of disoriented ciliary beating. BB connections promote long ciliary trajectories during the power stroke for effective fluid propulsion (Figures 3 and 5). BB connections also promote consistent ciliary speed and waveform to maintain productive phase differences between neighboring cilia (Figures 4 and 5). This minimizes ciliary tangles, ensuring that cilia beat in a coordinated manner to promote efficient fluid flow and cell motility (Figure 5L).

MATERIALS AND METHODS

Tetrahymena culture

Tetrahymena thermophila cells were grown in 2% SPP media (2% proteose peptone, 0.2% glucose, 0.1% yeast extract, and 0.003% Fe-EDTA). All studies were performed under cycling conditions. Cells were grown to mid–log phase (2.5–4 × 10⁵ cells/ml) before immobilization. The cell concentration was determined using a Coulter Counter Z1 (Beckman Coulter). All analyses were restricted to nondividing cells as judged by the absence of a developing oral structure.

Tetrahymena immobilization (DIPULL microscopy)

Tetrahymena cells are fed iron particles (Sigma-Aldrich; 267953-5G [particle size: <10 μm]; Figure 2A and Supplemental Figure S2A; Rifkin and Ballentine, 1976). To determine the ideal iron concentration for DIPULL, a growth assay was performed on cells that were fed with a range of iron concentrations (1–5 mg/ml). Tetrahymena cells readily phagocytose iron particles, and the amount of engulfed iron is concentration dependent (Supplemental Figure S2, B and C). The tested iron concentrations applied in DIPULL do not disrupt Tetrahymena cell growth or morphology (Supplemental Figure S2, A and D). For consistency, cells were supplemented with an iron concentration of 2.5 mg/ml (suspended in 10 mM Tris-HCl, pH 7.4) for all live cell imaging experiments performed in this study. Final media concentration was 1.3% SPP and 3.3 mM Tris-HCl (pH 7.4).

Next, Tetrahymena cells containing phagocytosed iron were introduced into microfluidic chambers of the specified dimensions (Figure 2A and Supplemental Figure S2J). For extended live cell imaging, microfluidic chambers with channels that constrain Tetrahymena cells were used (Supplemental Figure S2, G and J; minimum chamber width and depth: 27.0 and 27.0 µm). To study ciliary dynamics, two different microfluidic chambers were used. To image the power stroke plane, iron particle–fed Tetrahymena cells were introduced into wide chambers with narrow depth (Supplemental Figure S2J; chamber dimensions: 50.0 µm × 27.0 µm; cell width: 26.0 ± 2.7 µm; cilia length: 5.0 ± 0.7 µm; mean ± SD). The wider axis of the chamber allows for unimpeded ciliary beating along the side of the cell. The shallow depth restricts cellular motion in the axial axis and maintains the cell within the same imaging plane. To image the recovery stroke plane, a deeper chamber was utilized to image cilia positioned at the top of the cell to avoid boundary effects (away from the cover glass) (Supplemental Figure S2J; chamber dimensions: 27.0 µm × 50 µm; cell width: 26.0 ± 2.7 µm; cilia length: 5.0 ± 0.7 µm; mean ± SD).

To immobilize Tetrahymena cells, a constant external magnetic field using two bar magnets was applied (X-bet MAGNET N52 grade; Supplemental Figure S2J). Bar magnets are oriented to face opposing poles. Magnetic fields were previously shown to disrupt Paramecium motility (Nakaoka et al., 2002). To establish optimal magnetic field strength for DIPULL, we investigated the Tetrahymena swim path in the presence of a constant magnetic field exerted by the two bar magnets. Tetrahymena cells display normal swim paths and a slightly elevated swim speed in the presence of the applied magnetic field (Supplemental Figure S2, E and F). When cells were not stably immobilized via two magnets, an additional magnet was placed below the microscope stage insert to further stabilize Tetrahymena immobilization without impacting ciliary beat frequency (Supplemental Figure S2H). By coupling magnetism and microfluidic chambers to achieve cell immobilizations, DIPULL microscopy is applicable for short- or long-term live cell imaging.

Microfluidic chamber fabrication

Microfluidic immobilization chambers were fabricated in PDMS, which has been shown to be salubrious for hosting long-term cell culture and imaging (Bascom et al., 2016). Standard soft lithography protocols (Xia and Whitesides, 1998) were used to produce PDMS chambers, which were bonded to cover glass to enable imaging by light microscopy. Briefly, negative photoresist (SU 8; Kayaku Advanced Materials, Westborough, MA) was spun upon a silicon wafer to the desired depth, baked, and exposed to channel patterns by illumination with collimated UV light through a shadow mask. Rinsing and washing in developer solution revealed a positive mold of the channel network, which was then covered with uncured, degassed PDMS and baked for 70°C for 4 h to cure. Devices were completed and bonded by trimming the bas relief replica, punching holes for fluid and cell introduction and removal, exposure to an oxygen plasma (Herrick), and placement in contact with a clean coverslip.

Light microscopy

Imaging experiments were performed with an inverted wide-field microscope (Ti Eclipse; Nikon). Depending on the experiment, a 20× objective lens (Ti Eclipse; Nikon) or 60×A DIC Plan-Apo (NA 1.40) objective lens (Nikon) was used. Images were captured with a scientific complementary metal-oxide semiconductor (CMOS) camera (Zyla; Andor Technology).

Visualizing Tetrahymena ciliary mobility.

Owing to the three-dimensional waveform of Tetrahymena cilia, two differential interference contrast (DIC) imaging regimes were used to track the power and recovery strokes along the XY-axes of the imaging plane. To visualize the power stroke, cilia mobility along the side of the cell opposite the bar magnets was imaged (Figure 2B and Supplemental Movie 3). To track the recovery stroke, cilia positioned on the top of the cell opposite the cover glass were imaged (Figure 2B and Supplemental Movie 4). Imaging frame rates were between 1.3 and 2.0 ms.

Imaging fluid flow dynamics.

To track fluid flow, the displacement of 0.5 μm fluorescent beads in the SPP growth media (Polysciences; 18339) was imaged using a 20× objective lens (Ti Eclipse; Nikon). To improve signal:noise, movies were acquired with 3 × 3 binning. Each movie duration was 12.5 s (imaging frame rate: 40 frames per second).

FIB-SEM

High-pressure freezing and freeze substitution (HPF-FS) and sample preparation were done as previously described (Meehl et al., 2009; Giddings et al., 2010; Soh et al., 2020). Heavy metal–stained, resin-embedded samples were sectioned, and consecutive sections were screened by transmission electron microscopy (TEM) imaging to identify cells appropriate for FIB-SEM (embedded cells with intact morphology and that were not sectioned). The specimen was trimmed, mounted on a stub, and introduced into a Zeiss Crossbeam 550 FIB-SEM instrument. Image acquisition and processing followed a general schema outlined in our prior study (Baena et al., 2021). Briefly, SEM imaging of the sectioned face allowed the relocalization of these cells, which were protected with a patterned platinum and carbon pad and exposed orthogonally by controlled FIB milling up until the appearance of the tips of cilia. Automated FIB-SEM acquisition cycles of milling and imaging were executed over a period of several days, with SEM image pixel sampling of 5 nm in the imaging plane and 15 nm FIB mill “z step” size. The resulting stack of hundreds of images was aligned, contrast inverted, and binned by a factor of 3 to yield 8 bit, isotropic 15 nm voxel image volume reconstructions. Subvolumes of interest from these were then segmented and analyzed.

Tetrahymena cell image analysis

Quantification of BB angle at the cell cortex.

Undulation at the cell cortex may cause erroneous interpretations of BB docking orientation (Figure 1B and Supplemental Figure S1C). To rule out nonuniformity along the cell cortex, two reference axes were utilized for BB angle measurements. In method 1, a reference axis that spans the distal ends of two flanking BBs and the BB of interest was utilized (Supplemental Figure S1D; the straight line was fitted through the midpoint on the distal end of three consecutive BBs). In method 2, the highest points of the cell cortex that span three consecutive BBs were used as an alternate reference axis (Supplemental Figure S1D; the straight line was fitted through the highest points along the cell cortex). The BB angle relative to the cell cortex was determined from the angle between the BB longitudinal axis and the two reference axes (methods 1 and 2). To establish whether the BB angle depends on the cilium’s position, the position of the cilium along the power stroke was quantified by measuring the angle from 1.5 to 2.0 µm up the cilium relative to the reference axes.

Quantification of Tetrahymena iron phagocytosis.

Fluorescence quantification of iron uptake was performed by a semiautomated strategy that utilizes the FIJI macro scripting language and plug-ins (Schindelin et al., 2012). Images (two-dimensional) were preprocessed by a local background subtraction. To obtain the area of the engulfed iron particles, a uniform intensity threshold was applied to generate a binary mask over iron particles. The area of the binary mask served as a proxy for the area of ingested iron particles.

Tetrahymena motility analysis.

Tetrahymena cell motility was imaged on an inverted wide-field microscope using a 20× objective lens (Ti Eclipse; Nikon). Each movie is 2.5 s in duration (frame rate: 20 frames per second). To quantify swim rates, the relative displacement of the anterior or posterior pole of cells was tracked for 500 ms via the FIJI MTrackJ plug-in (Meijering et al., 2012). Analyses were restricted to cells that swim along the same XY plane.

Cilia length measurement.

To measure cilium length, the FIJI freehand tool was used to trace from the ciliary base to tip. Live cilia movies acquired by DIC microscopy were used in this analysis. Analysis was restricted to cilia positioned at the cell’s medial region. Six cells (three cilia per cell) were analyzed.

Ciliary kinetics measurements.

To quantify cilia beat frequency, kymograph analysis on movies of Tetrahymena ciliary beating acquired by DIC microscopy was performed. Kymograph analysis was performed on cilia that were positioned along the cell’s medial region (Figure 2B, red box). The number of in-focused cilia at the cell’s medial region is usually three. To ensure equal weightage, three cilia per cell were analyzed. For each cilium, three consecutive beat cycles were followed. To assess BB orientation along the side of the cell, three criteria were imposed on the cilia that were selected for this analysis. First, cilia must transverse the cell’s AP axis. Second, cilia must remain in-focus during the entire power stroke before transitioning into the recovery stroke where they exit the imaging focal place (Figure 2B, right). Third, the anteriorly and posteriorly positioned neighboring cilia must also remain in-focus (Supplemental Movie 3). Kymographs were generated from an 11-pixel-wide (pixel size: 108 nm) line that was positioned approximately 1.5 µm from the ciliary base. Using FIJI, three kymographs (one per cilium) were generated for each cell (FIJI Multi Kymograph plug-in). Each ciliary beat cycle is represented as a peak on the kymograph, whereby the upward slope marks the power stroke while the downward slope marks the recovery stroke (Figure 4A). Based on the duration of three consecutive beat cycles, the average cilia beat frequency (per second) was quantified.

To provide better assessment of BB orientation, kymograph analysis was also performed on cilia that were imaged from the top of the cell (Figure 2B, green box). To quantify BB orientation, the difference in angle along the power stroke axis between two adjacent cilia, or power stroke angular difference, was measured (Supplemental Figure S3A). An average power stroke angular difference was quantified from each cilia pair across three consecutive ciliary beat cycles. WT cilia pairs exhibit a power stroke with an average angular difference of 3.7 ± 16.0°. disA-1 cilia pairs were considered oriented if their power stroke angular differences fall within 1 SD of the average WT power stroke angular difference. To avoid boundary effects from the imaging chamber, cilia that were positioned away from the chamber ceiling were quantified. Ciliary beat frequencies are comparable between cilia that were imaged from the side view and top-down view.

To quantify the duration of the power and recovery strokes, kymograph analyses were performed on cilia that were imaged from the top of the cell. The average power and recovery stroke duration was calculated from three consecutive ciliary beat cycles. The phase difference between adjacently positioned cilia was also quantified using kymograph analyses. To measure the temporal delay between when a cilium undergoes its ciliary beat cycle relative to its neighbor, kymographs were generated from an 11-pixel-wide (pixel size: 108 nm) line that bisected two adjacent and in-focused cilia. In addition, the line was positioned at approximately 1.5 µm from the ciliary base of both cilia. An average phase difference between two adjacent cilia was calculated from three consecutive ciliary beat cycles.

Ciliary force estimation.

Calculation of forces based on ciliary waveform analysis using RFT.

Forces on Tetrahymena cilia were calculated using RFT (Gray and Hancock, 1955). Estimates for the value of the resistive force coefficient vary from approximately 1 to 3.5-fold the viscosity of the fluid (Lighthill, 1976; Riedel-Kruse et al., 2007; Bayly et al., 2011). We used the values obtained for WT Chlamydomonas reinhardtii cilia as previously described (Bayly et al., 2011; C_N = 1.53 × 10^–3 pN·s/μm², C_T = 0.64 ×10^–3 pN·s/μm²). These values were corrected to account for changes in the viscosity of the surrounding fluid due to temperature differences.

The average ciliary waveform was generated using a previously published protocol (Bottier et al., 2019). To ensure equal weightage, each cilium was followed for six consecutive beat cycles. Nine cilia (each from a different cell) were analyzed. Briefly, consecutive frames of Tetrahymena cilia undergoing a power stroke (XY) and a recovery stroke (YZ) were manually traced (Figure 2B). Owing to poor image contrast at the cilium proximal end (∼1.5 µm), this study was unable to accurately determine the position of the cilium base. Images were processed to improve cilia contrast using FIJI Unsharp mask (radius: 1 pixel; mask weight: 0.9). For the power stroke, each cilium was aligned along the cell’s AP axis using the base of the anterior cilium as a reference point. For the recovery stroke, each cilium was aligned relative to the power stroke axis of the same cilium and the cell’s AP axis. Next, each trace was fitted with a polynomial function. Two-dimensional average ciliary waveforms of the power stroke and recovery stroke were generated by averaging across a large number of individual ciliary traces (nine cilia, six ciliary beat cycles each, nine cells). The cilium position is defined by its orientation from the cilium’s distal end (4.5 µm up from the cilium base) relative to the cilium’s base and cell’s anterior pole. Because the differential interference contrast microscopy (DIC) does not detect the proximal region of the cilium, the base is defined as the proximal most position where the cilia can be detected. The power stroke was divided into three stages based on the orientation of the cilium relative to the cell’s AP axis (start: 0–60°; middle: 61–120°; end: 121–180°). The recovery stroke was divided into three stages based on the orientation of the cilium relative to the cell’s posterior pole (start: 180–121°; middle: 120–61°; end: 60–0°). Cilium positions are categorized into 15° bins for both the power and recovery strokes. The start and end positions of each cilium along the power stroke and recovery stroke were defined by the orientation of the first and last ciliary traces that appear along the imaging focal plane. The reference point for angle measurement is 4.5 µm up from the cilium base relative to the cell’s AP axis. The average start and stop positions for each cilium were calculated by averaging the start and end positions across six ciliary beat cycles. The angular trajectories for both the power and recovery strokes were quantified by measuring the angle between the average start and end positions of each cilium. Analyses were focused on ciliary traces that fell within the average angular trajectories (Figure 5, B and G). The net difference in ciliary curvature between WT and disA-1 cilia was computed by subtracting the average curvature of disA-1 from that of WT. Absolute values of the net difference in ciliary curvature is presented (Supplemental Figure S3, D and E).

Cilium velocity, v_c (s, t), as a function of the arclength coordinate, s, and time, t, was calculated by numerically differentiating the coordinates of the cilium traces with respect to t. Velocities are projected onto the tangent and normal vectors along the cilium for calculation of the distributed resistive forces (Bayly et al., 2011). Power per unit length (fW/μm) along the cilium is calculated as the dot product of the distributed force and velocity, P(s, t) = F(s, t)·v(s, t).

The total power produced by the cilium at a given time is obtained by numerically integrating the power over the length of the cilium. The moment at the cilium basal attachment (pN μm) is calculated as the integral along the length of the cilium of the cross-product of the position relative to the basal attachment and the distributed force.

Calculation of forces on the cell body.

Forces on the cell body were calculated for comparison against ciliary forces estimated from RFT. Average swimming velocities for WT and disA-1 cells used in calculations were based on the results of a previously reported study (Galati et al., 2014). The cell body was modeled as an ellipsoid moving along its major axis (Chwang and Wu, 1975; Bayly et al., 2011). To estimate the average force for each cilium, the body drag force along the cell’s AP axis was divided by the estimated number of cilia, 400 (assuming that all BBs are ciliated; Galati et al., 2015).

Fluid flow analysis

To quantify fluid flow dynamics, we measured the displacement of fluorescent beads by immobilized Tetrahymena cells using PIVlab (Thielicke, 2021). Fifty consecutive image frames were first processed using the wiener2 denoise filter (3 pixel; imaging frame rate: 40 frames per second). Depending on the signal:noise of the movies, two interrogation windows (64 pixel only or both 64 and 32 pixels) were utilized to track fluorescent bead motility. An averaged vector map that depicts fluid flow velocity was generated for each cell. To measure fluid flow along the length of the cell, the polyline tool was used to measure fluid velocity along the AP axis of the cell. The fluid flow was visualized using the FIJI Flowtrace plug-in (Gilpin et al., 2017a).

Statistical analysis

All data sets were assessed for normal distribution using the Shapiro–Wilk or Kolmogorov–Smirnov test. A Student’s t test was performed on normally distributed data sets. A Mann–Whitney test was performed on data sets that do not conform to a normal distribution. An F test was performed to compare variance between conditions. Tests for significance were unpaired and two tailed. All error bars indicate SD. The P value is indicated for all statistical analyses. All analyses were performed on samples obtained from three independent experiments.

Abbreviations used:

BB

basal body

FIB-SEM

focused ion beam scanning electron microscopy

MCA

multiciliary array

PDMS

polydimethylsiloxane

RFT

resistive force theory

SF

striated fiber.