Abstract
Artificial neural network (ANN) which is an information processing technique developed by modeling the nervous system of the human brain is one of the most powerful learning methods today. One of the factors that make ANN successful is its training algorithm. In this paper, an improved butterfly optimization algorithm (IBOA) based on the butterfly optimization algorithm was proposed for training the feed-forward artificial neural networks. The IBOA algorithm has the chaotic property which helps optimization algorithms to explore the search space more dynamically and globally. In the experiments, ten chaotic maps were used. The success of the IBOA algorithm was tested on 13 benchmark functions which are well known to those working on global optimization and are frequently used for testing and analysis of optimization algorithms. The Tent-mapped IBOA algorithm outperformed the other algorithms in most of the benchmark functions. Moreover, the success of the IBOA-MLP algorithm also has been tested on five classification datasets (xor, balloon, iris, breast cancer, and heart) and the IBOA-MLP algorithm was compared with four algorithms in the literature. According to the statistical performance metrics (sensitivity, specificity, precision, F1-score, and Friedman test), the IBOA-MLP outperformed the other algorithms and proved to be successful in training the feed-forward artificial neural networks.
Keywords: Artificial neural networks, Butterfly optimization algorithm, Chaos, Multilayer perceptron, Training artificial neural networks
Introduction
Today, computers and computer systems have been intertwined with our lives and have become an inseparable part. Computers are used in almost every aspect of our lives. While computers were only performing calculations or data transfers in the past, over time they have turned into more effective machines that can analyze large amounts of data and make comments about events using this data. Today, this development continues, and computers have gained the ability to both make decisions about events and learn the relationship between events. Thus, problems that could not be formulated mathematically and could not be solved have begun to be solved by computers. One of the most important factors of this advancement in computing is the field of artificial intelligence and artificial neural networks (ANNs) are one of the subjects with the most research in the field of artificial intelligence.
The first artificial neural network modeling work was put forward by Warren McCulloch and Walter Pitts in 1943. ANN is one of the most important inventions in its field, developed by taking the movement of the human brain as a role model. ANN is used in many areas such as classification, recognition, prediction (Tümer et al. 2020), and optimization (Madenci and Gülcü 2020). ANN which was developed by imitating the human brain has proven its success in the field of optimization as in many other fields.
ANN, which is one of the most powerful learning methods today, is used to predict and classify unknown functions. The most commonly used ANN method while performing these operations is the multilayer perceptron (MLP). The ability of ANN to give more accurate results and to make more successful classifications is ensured by updating the bias and weight values in the most appropriate way. ANN which is trained with optimum values can reach more accurate results in finding classification values. Many researchers have proposed algorithms in the literature to train multilayer perceptron. However, gradient techniques from these proposed algorithms often encounter problems in solving optimization problems in the real world. They get stuck in the local optimum and produce poor-quality solutions (Gülcü 2022b; Mirjalili 2015; Tang et al. 2018). To overcome these difficulties, meta-heuristic algorithms have been used to train ANNs (Gülcü 2022a; Jaddi and Abdullah 2018). Meta-heuristic algorithms, designed by taking the biological movements of living things as role models such as hunting, reproduction, and feeding, aim to find the optimum result to problems in a reasonable time. One of these meta-heuristic algorithms is the butterfly optimization algorithm (BOA) which is based on swarm intelligence. The BOA algorithm was developed by Arora and Singh (2019) inspired by nature. The BOA is a meta-heuristic algorithm designed by modeling the mating and foraging behaviors of butterflies that communicate with each other through the scent they emit. The BOA is an algorithm designed by modeling butterflies to find food and mating mates using their senses of smell, sight, taste, touch, and hearing. These senses are also useful for migrating from place to place, escaping from a predator, and laying eggs in suitable places. Among all these senses, smell is the most important one that helps the butterfly find food, such as nectar, even from long distances. The BOA has shown excellent performance for several continuous, discrete, single-objective, and multi-objective optimization problems compared to several state-of-the-art meta-heuristics and evolutionary algorithms. Due to the success of the BOA, it has been applied to many different optimization problems including engineering design problems (Arora and Anand 2018; Sharma et al. 2021), feature selection (Long et al. 2021), power plant management (Dey et al. 2020), reliability optimization problems (Sharma 2021), and healthcare systems (Dubey 2021). Therefore, these motivated our attempts to improve the butterfly optimization algorithm and to employ it for training the feed-forward artificial neural networks.
In this study, the IBOA algorithm was developed for the solution of single-objective optimization problems, which is a sub-branch of continuous optimization problems. The IBOA algorithm is an improved algorithm by adding parameter analysis and chaotic maps to the BOA algorithm. While developing the IBOA, 10 chaotic maps (Chebyshev, Circle, Gauss, Iterative, Logistic, Piecewise, Sine, Singer, Sinusoidal, and Tent) were used to update and optimize the p (key probability) value, which is one of the most important parameters of the BOA algorithm. The developed IBOA algorithm was tested on 13 benchmark functions. These functions are well known to those working on global optimization and are frequently used for testing optimization algorithms. The results of the BOA algorithm and the results of the IBOA algorithm with 10 different maps were compared. According to the results, the Tent-mapped IBOA algorithm is more successful. In the second part of this study, the training of the ANN was carried out using the IBOA algorithm and this proposed new algorithm is named IBOA-MLP. The IBOA algorithm tries to find the optimum bias and weight values of the MLP. In the experimental study, five datasets (xor, iris, heart, balloon, breast cancer) taken from the UCI machine learning repository were used. The results obtained were compared with the results of four different MLP algorithms in the literature. According to the comparison result, it was seen that the IBOA-MLP algorithm achieved a good performance.
The main contributions of this article are: (1) A new improved butterfly optimization algorithm (IBOA) is proposed. (2) The IBOA algorithm is applied for training ANN and optimizes the weights and biases of ANN. (3) The IBOA-MLP algorithm has the ability to escape from local optima. (4) The initial parameters and positions don’t affect the performance of the IBOA-MLP algorithm. (5) The features of the IBOA-MLP algorithm are simplicity, requiring only a few parameters, solving a wide array of problems, and easy implementation.
This study is organized as follows: In the first section, the history of ANN is briefly explained, the problem is explained, and the main contributions in this article are emphasized. In the second section, the current studies in the literature on the training of ANN are examined. In the third section, detailed information about the ANN and BOA algorithms is given. Then, the developed IBOA algorithm and the training of ANN by the IBOA algorithm (IBOA-MLP) are explained in detail. In the fourth section, the experimental results of the developed algorithms are presented. First of all, the benchmark functions used in experimental studies are introduced and the experimental results of the IBOA algorithm with 10 different maps on these benchmark functions are given. The results of the IBOA and BOA algorithms are compared in terms of the success and computational time of the algorithms, and it is shown that the IBOA algorithm is more successful. In the second part of this section, five classification datasets are introduced and the experimental results of the IBOA-MLP algorithm are presented. The experiments are carried out on the classification problems and the results of the IBOA-MLP algorithm are compared with the results of algorithms in the literature. It is seen that the IBOA-MLP algorithm is more successful than other algorithms on most of the classification problems according to the statistical performance metrics. Finally, in the fifth section, the general results obtained in the study are given as a summary. In addition, suggestions for future work are given.
Related works
After reviewing the literature in detail, it is seen that many meta-heuristic algorithms have been used for the training of ANN. For the scope of the literature research of this article, some of the important studies were examined and evaluated. Moreover, the summary of studies about the training of ANN is presented in Table 1.
Table 1.
Summary of studies about the training of ANN
| Method | References | Dataset(s) |
|---|---|---|
| Particle swarm optimization + Back-propagation algorithm | Zhang et al. (2007) | Three bits parity problem, function approximate problem, and classification problem |
| Ant colony optimization | Özbakir et al. (2009) | Classification problem |
| Particle swarm optimization | Zamani and Sadeghian (2010) | Classification problem |
| Genetic algorithm + Tabu search + simulated annealing | Zanchettin et al. (2011) | Classification problem |
| Harmony search algorithm | Kulluk et al. (2012) | Classification problem, and a real-world problem (quality defects common in textiles) |
| Social spider algorithm | Pereira et al. (2014) | Classification problem |
| Particle swarm optimization + Cuckoo search algorithm | Chen et al. (2015) | Function estimation, and classification problem |
| Gray wolf optimization | Mirjalili (2015) | Classification problem, and function approximate problem |
| Particle swarm optimization + artificial bee colony algorithm | Al Nuaimi and Abdullah (2017) | Classification problem |
| Shuffled frog leaping algorithm | Dash (2018) | Forecast of the US dollar |
| Kidney-inspired algorithm | Jaddi and Abdullah (2018) | Classification problem, and a real-world problem (rainfall forecasting) |
| Whale optimization algorithm | Aljarah et al. (2018) | Classification problem |
| Artificial bee colony algorithm | Ghaleini et al. (2019) | A real-world problem (safety factor of retaining walls) |
| Cuckoo search algorithm | Gullipalli (2021) | Classification problem |
| Crow search algorithm | Erdogan and Gulcu (2021) | Classification problem |
| Animal migration optimization | Gülcü (2022a) | Classification problem, and a real-world problem (civil engineering) |
| Dragonfly algorithm | Gülcü (2022b) | Classification problem, and a real-world problem (civil engineering) |
Zhang et al. (2007) proposed a hybrid algorithm based on the particle swarm optimization (PSO) algorithm and the traditional back-propagation algorithm. The proposed algorithm was applied for the training of ANN on three bits parity problem, function approximate problem, and classification problem. According to the experimental, the performance of the proposed algorithm was better than the performance of the other two algorithms used for comparison, and the proposed algorithm obtained satisfactory results in terms of the convergence speed.
Özbakir et al. (2009) developed a new meta-heuristic algorithm based on ant colony optimization (ACO) to detect the relations among the classification data and extract the rules. The proposed algorithm trained ANN, and its performance was measured on the benchmark classification data such as ECG, iris, Ljubljana breast cancer, nursey, pima, and Wisconsin breast cancer. The algorithm is compared with the NBTree, DecisionTable, Part, and C4.5 approaches. The experimental results were quite successful.
Zamani and Sadeghian (2010) used the PSO algorithm for training artificial neural networks. The proposed approach for classification was tested on the iris, wine, heart, and ionosphere datasets. The effects and successes of different parameters for PSO and ANN were investigated. According to the experimental results, the PSO algorithm obtained satisfactory results in training ANN.
Zanchettin et al. (2011) developed a hybrid approach (GaTSa) consisting of the combination of the genetic algorithm (GA), Tabu search (TS), and simulated annealing (SA) algorithms for ANN training. The performance of the approach was compared with the performance of five algorithms. To measure the performance of the algorithms, an artificially obtained dataset and ten different datasets (iris, diabetes, thyroid, card, cancer, glass, heart, horse, soybean, and mglass) are frequently handled in the literature were used. The author stated that their proposed approach produced more successful and satisfactory results than other algorithms.
Kulluk et al. (2012) discussed the application of harmony search (HS) algorithms for the supervised training of feed-forward type ANNs, which are frequently used for classification problems. In the study, special attention was paid to the self-adaptive global best-fit search (SGHS) algorithm and five different variants of the fit search algorithm were examined. The proposed approach was tested on six different benchmark classification datasets (glass, ionosphere, iris, thyroid, wine, Wisconsin breast cancer) and a real-world dataset based on the classification of quality defects common in textiles. According to the experimental results, the proposed algorithm showed a very successful and competitive performance for the training of ANN.
Pereira et al. (2014) trained the ANN using the social spider algorithm. The proposed approach was used to classify different datasets (ionosphere, satimage, diadol, mea, and spiral) in the field of medicine. The performance of the approach was compared with the performance of five different algorithms (ABC, CSS, FFA, PSO, and SGHS) and although it was not achieved high success, it showed competitive results with most algorithms and achieved an average level of success.
Chen et al. (2015) successfully combined PSO and Cuckoo search (CS) algorithms to create a hybrid model (PSOCS) and used it for ANN training. In the proposed approach, the successful aspects of both algorithms were combined and developed. The algorithm was applied to a mathematical function estimation and iris classification data. The performance of the algorithm was compared with the performance of its components, PSO and CS algorithms. According to the experimental results, the performance success of the model surpassed the other two algorithms.
Mirjalili (2015) used the gray wolf optimization (GWO) algorithm for multilayer perceptron (MLP) training. The experiments were performed on five classification datasets (xor, balloon, iris, breast cancer, and heart) and three standard functions (sigmoid, cosine, and sine) to measure the performance of the proposed method. The proposed algorithm was compared with five meta-heuristic algorithms (PSO, GA, ACO, ES, and PBIL) that are frequently used in the literature. According to the results, the algorithm obtained competitive results. In addition, it achieved a high level of success in classification.
Al Nuaimi and Abdullah (2017) proposed a new hybrid algorithm combining PSO and ABC algorithms and applied the proposed algorithm for the training of ANN. Four benchmark classification datasets (iris, cancer, diabetes, and glass) were used to evaluate the algorithms. The approach was compared with the PSO and ABC algorithms. The proposed approach achieved more successful results than the other two algorithms.
Dash (2018) used the improved Shuffled frog leaping algorithm (SFLA) for ANN training. The proposed algorithm was applied to the datasets on the forecast of the US dollar according to 3 different exchange rates. The performance of the proposed algorithm is compared with the performance of SFLA, PSO, and DE algorithms. According to the results, the success of the algorithm was better than the other algorithms.
Jaddi and Abdullah (2018) used the kidney-inspired algorithm modeled based on the behaviors of the kidneys in the human body to optimize the ANN parameters. With the α value changed between the minimum and maximum values in the developed algorithm, exploration and exploitation capabilities were strengthened, and this had a significant impact on ANN training. The proposed method was applied to the different benchmark classification datasets (iris, diabetes, thyroid, cancer, card, glass, mglass, and gas furnace) and a real-world problem (rainfall forecasting). The algorithm was compared with four algorithms and the proposed algorithm was promising according to the results.
Aljarah et al. (2018) trained a feed-forward neural network by using the whale optimization algorithm (WOA). The proposed model was tested on twenty different benchmark classification datasets with different difficulty levels. The performance of the algorithm was compared with the performance of seven different algorithms (BP, GA, PSO, ACO, DE, ES, and PBIL) that are frequently used in the literature. The qualitative and quantitative results proved that the proposed trainer was able to outperform seven algorithms on the majority of datasets in terms of both local optima avoidance and convergence speed.
Ghaleini et al. (2019) proposed a model in which the ANN was trained by the ABC algorithm to predict the safety factors of retaining walls. The weight and bias values of the ANN were optimized by the ABC algorithm to get higher accuracy and performance estimation in safety factors. The proposed approach was analyzed by different ANN models with a different number of hidden layers. According to the results, the network performance was strengthened with the model proposed.
Gülcü (2022a) developed a new meta-heuristic approach, animal migration optimization with Levy flight feature, and used it for training the ANN. The proposed hybrid algorithm is named IAMO-MLP. Thirteen benchmark functions, five classification datasets, and one real-world problem in civil engineering were used in the experiments. It was observed that the initial positions of the individuals did not affect the performance of the developed algorithm and the IAMO-MLP algorithm successfully escaped from the local optima.
Gullipalli (2021) performed ANN training using the CS algorithm. It was aimed to increase the convergence capability of the algorithm by applying different modifications to the CS algorithm. The proposed approach was tested on eight classification data (car, german-credit, hypothyroid, mfeat, nursey, page-blocks, segment, sick) from the UCI machine learning repository. The performance of the proposed algorithm was compared with the performance of the Hoeffding tree and CS forest approaches. According to the experimental results, the algorithm was sufficient and competitive in terms of performance.
Erdogan and Gulcu (2021) proposed a new hybrid algorithm CSA-MLP for training the ANN. The algorithm CSA-MLP was based on the crow search algorithm which is a population-based meta-heuristic optimization inspired by the behavior of crows to store their excess food and retrieve it from the landfill when needed. The experimental results showed that the crow search algorithm was a reliable approach in training the ANN.
Many researchers have proposed algorithms in the literature to train multilayer perceptron. However, gradient techniques from these proposed algorithms often encounter problems in solving optimization problems in the real world. They get stuck in the local optimum and produce poor-quality solutions (Gülcü 2022b; Mirjalili 2015; Tang et al. 2018). To overcome these difficulties, meta-heuristic algorithms have been used to train ANNs (Gülcü 2022a; Jaddi and Abdullah 2018). Due to the success of the BOA, it has been applied to many different optimization problems. Therefore, these motivated our attempts to improve the butterfly optimization algorithm and to employ it for training the feed-forward artificial neural networks.
Materials and methods
In this section, artificial neural networks, multilayer perceptron, butterfly optimization algorithm, improved butterfly optimization algorithm, and training of artificial neural networks using improved butterfly optimization algorithm are explained in detail.
Artificial neural network
The artificial neural network is an information processing technique developed by modeling the nervous system of the human brain. In other words, it is the transfer of synaptic connections between neurons in the human brain to a digital platform. Biological nervous system elements and their task equivalents in artificial neural networks are shown in Table 2 (Koç et al. 2004).
Table 2.
Elements in the biological nervous system and their equivalents in ANN
| Nervous system | Artificial neural networks |
|---|---|
| Neuron | Process element |
| Dendrite | Addition function |
| Cell body | Activation function |
| Axon | Element output |
| Synapse | Weights |
An artificial nerve cell was developed by imitating the human nerve cell. An artificial neuron is shown in Fig. 1. To obtain the net input of the neuron, the inputs coming to the neuron are multiplied by their connection weights and then combined with the aggregate function. The result is processed with the activation function and thus the net output of the neuron is calculated.
Fig. 1.
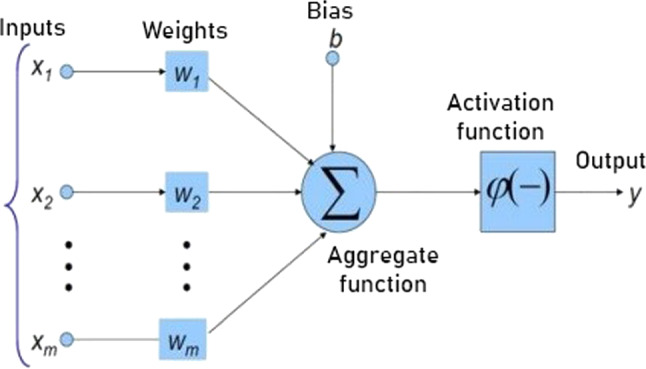
Artificial nerve cell
ANNs are formed by the combination and grouping of artificial nerve cells. This integration consists of layers, and as a result, ANN consists of more than one interconnected layer. ANN consists of three layers: input layer, hidden layer, and output layer. However, in some cases, the number of hidden layers may be more than one. In many ANN models, processes run sequentially. In short, the hidden layer receives the data from the previous input layer, processes it, and forwards it to the next output layer. The features of the three layers that make up the ANN can be summarized as follows:
Input layer: It is the layer where information input is made. There is no operation in this layer, the information coming to the layer is transmitted directly to the hidden layers. Each node has only one input and one output.
Hidden layers: These are the layers where outputs will be produced by mathematical operations according to the inputs. They provide communication between the input layer and the output layer and transfer information. An ANN can have more than one hidden layer.
Output layer: It is the layer that takes the result produced in the hidden layers, processes it, and creates the output by transferring it to the outside of the system.
As mentioned above, activation functions are used to obtain the net output of the neuron. The function that maps inputs and outputs and establishes a connection with each other is the activation function. If the activation function is not used, ANNs would be polynomials of one degree. Since non-activated ANNs would be linear, their learning capabilities would be very low. If the neural network is desired to learn nonlinear states, it is important to use an activation function. There are many activation functions in the literature. Which activation function to choose is crucial for learning ability. The mathematical representation of the sigmoid activation function which is one of the most frequently used activation functions in the literature is presented in Eq. (1).
| 1 |
The most preferred type of ANN is the multilayer perceptron (MLP). A multilayer perceptron is a feed-forward network structure with one or more hidden layers between the input layer and the output layer. The backpropagation algorithm is generally used as the learning algorithm in MLP (Turkoglu and Kaya 2020). Figure 2 shows the fundamental structure of MLPs. Turkoglu and Kaya (2020) stated that an MLP consists of the following components: artificial neuron, layers, aggregate function, activation function, error function, and learning algorithm.
Fig. 2.
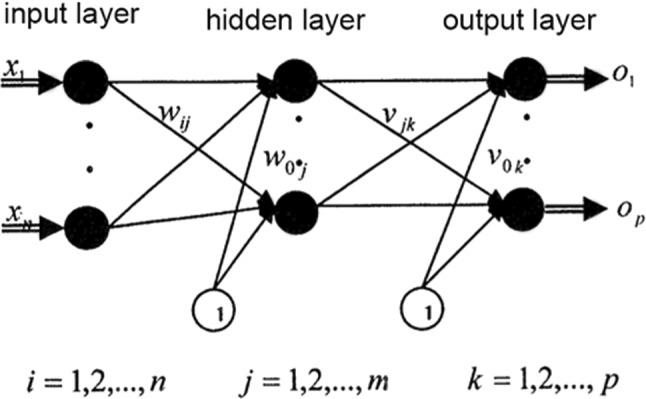
Structure of the multilayer perceptron (Irmak and Gülcü 2021)
The artificial nerve cell, which consists of inputs, aggregate, and activation function, has been developed by imitating the human nervous system. In the artificial neuron, the input values are multiplied by the node weights and sent to the aggregate function. The result returned from the aggregate function is sent to the activation function and thus the net output of the artificial neuron is obtained. The function that takes the net input by combining the weights of the incoming inputs is called the aggregate function. The results from the aggregate function are sent to the activation function and converted to output. It is also called compression or threshold function in the literature. This is because the output signals are limited to the range [0, 1] or [−1, 1]. In this study, the sigmoid function was chosen as the activation function. The reason for this is that its derivative can be taken and its success has been proven by its frequent use in the literature.
It is known that ANN is a learning-based system and an objective function is defined to find the error in this system. In statistics, the mean squared error (MSE) of an estimator gives the mean of the squares of the errors. That is, it measures the mean squared difference between the estimated values and the actual value. The MSE formula is shown in Eq. (2). Since there may be more than one neuron in the output layer of the MLP, the MSE formula used in this study is shown in Eq. (3). MSE measures the performance of a machine learning model. It is always positive and it can be said that the model with an MSE value close to zero performs better.
| 2 |
where N stands for the number of samples. and represent the actual value and the predicted value for the sample i, respectively.
| 3 |
where N stands for the number of samples, and K stands for the number of neurons in the output layer in the MLP. and represent the actual value and predicted value of the neuron j in the output layer for the sample i, respectively.
Finally, to talk about the learning algorithm which is the component of MLP, MLPs are mostly trained using the backpropagation algorithm. Training the MLP by the backpropagation algorithm takes place in three stages: (1) The progression of the network input from the input layer to the output layer, (2) the calculation of the error in the output neurons, (3) the backpropagation, and updating the weights according to the backward propagated error (Turkoglu and Kaya 2020). After the training of the network is complete, the MLP works forward.
Butterfly optimization algorithm
In the Linnaean Animal Kingdom system, butterflies are in the class Lepidoptera. There are more than 18,000 species of butterflies in the world. The reason for their survival for millions of years lies in their senses (Saccheri et al. 1998). Butterflies use their senses of smell, sight, taste, touch, and hearing to find food and mating partners. These senses also help in migrating from one place to another, escaping from the predator, and laying eggs in suitable places. Among all these senses, smell is the most important sense that helps the butterfly find food even from long distances (Blair and Launer 1997). Butterflies use sensory receptors used for smelling to find the source of nectar, and these receptors are distributed over body parts such as the antennae, legs, and fingers of the butterfly. These receptors are nerve cells on the body surface of the butterfly and are called chemoreceptors. These chemoreceptors guide the butterfly to find the best mating partner to maintain a strong genetic line. A male butterfly can identify a female by means of pheromones which are scent secretions that the female butterfly emits to cause certain reactions (Arora and Singh 2019). Based on scientific observations, it has been found that butterflies have a very accurate perception of the source of the odor (Raguso 2008). They can also distinguish different odors and sense their intensity (Wyatt 2003).
The butterfly optimization algorithm (BOA) which is based on swarm intelligence was developed by Arora and Singh (2019) inspired by nature to solve global optimization problems. BOA is mainly based on the moving strategy of butterflies which uses their sense of smell to locate nectar or mating mates. Butterflies detect and analyze odor with their sense sensor as noted above to determine the potential direction of a nectar/mating mate. The BOA mimics this behavior to find the optimum in the search space. The BOA is an algorithm designed by modeling butterflies to find food and mating mates using their senses of smell, sight, taste, touch, and hearing. Among all these senses, smell is the most important which helps the butterfly find food, usually nectar, even from long distances. Butterflies are search agents for optimization in the BOA algorithm. A butterfly will produce scent with an intensity associated with its fitness. Namely, as a butterfly moves from one location to another its fitness will change. The scent spreads over the distance, other butterflies can sense it, and butterflies can share their personal information with other butterflies and create a collective social information network. When a butterfly can detect the scent of another butterfly, the butterfly will move toward it, and this step is called global search in the proposed algorithm (Arora and Singh 2019).
The BOA was developed by taking the following three features as role models. (i) All butterflies are expected to emit a scent that makes the butterflies attract each other. (ii) Each butterfly will move randomly or toward the best butterfly that emits more scents. (iii) The stimulus intensity of a butterfly is affected or determined by the value of its objective function.
In the BOA which is based on the behavior of butterflies, the three stages can be explained as follows: (1) Initialization Phase: Parameters are determined, and an initial population is generated for the algorithm. When creating the initial population, the position of the butterflies is randomly assigned by calculating the odor values. (2) Iteration Phase: This is the part where the main processes are carried out and each butterfly tries to reach the best result with parameters specific to the BOA. At each iteration, all butterflies in the search space are moved to new positions, and then their fitness values are evaluated. (3) The last stage: It is the part where the stopping criterion is met and the optimum or closest to the optimum result is reported.
Understanding the BOA modality relies on three key concepts. These concepts are sensory method (c), stimulus intensity (I), and power exponent (α). The sensory method refers to the raw input used by the sensors to measure the sensory energy form and process it in similar ways. The stimulus intensity parameter I is limited to an exponential value. According to previous studies by scientists, this is because as the stimulus gets stronger, the insects go intensely to the stimulus and eventually become less sensitive to it. The parameter α is used to correct this situation. The parameter α is the power base that is dependent on modality (smell in BOA). If α = 1, it means that there is no odor absorption. Namely, the amount of scent emitted by a particular butterfly is perceived by other butterflies with the same capacity. This brings us closer to a single solution, usually the optimum. If α = 0, it means that the scent emitted by any butterfly cannot be perceived by other butterflies. This provides the local search. α and c represent a random number between [0, 1], f represents the perceived magnitude of the odor, and I represents the stimulus intensity. There are two important stages in the algorithm: local search and global search. The global search is shown in Eq. (5) and the local search is shown in Eq. (6). In the local search, the butterfly xit does not move toward the global best (), but instead exhibits a random walk in the search space.
| 4 |
| 5 |
where represents the best available solution among all the solutions in the current iteration, Xit and Xkt represent the butterflies in the search spaces, r represents the parameter that provides randomness in the range [0, 1], and fi represents the perceived scent of the butterfly.
| 6 |
where, unlike the global search, the butterfly xit does not move toward the global best (), but instead exhibits a random walk in the search space.
Searching for food and mating partners with butterflies can occur on both the local and global scales. Thus, a switching probability p is used in the BOA to switch between the global search and the local search. The switching probability decides whether a butterfly will move to the best butterfly or randomly. The flowchart of the BOA algorithm is shown in Fig. 3.
Fig. 3.
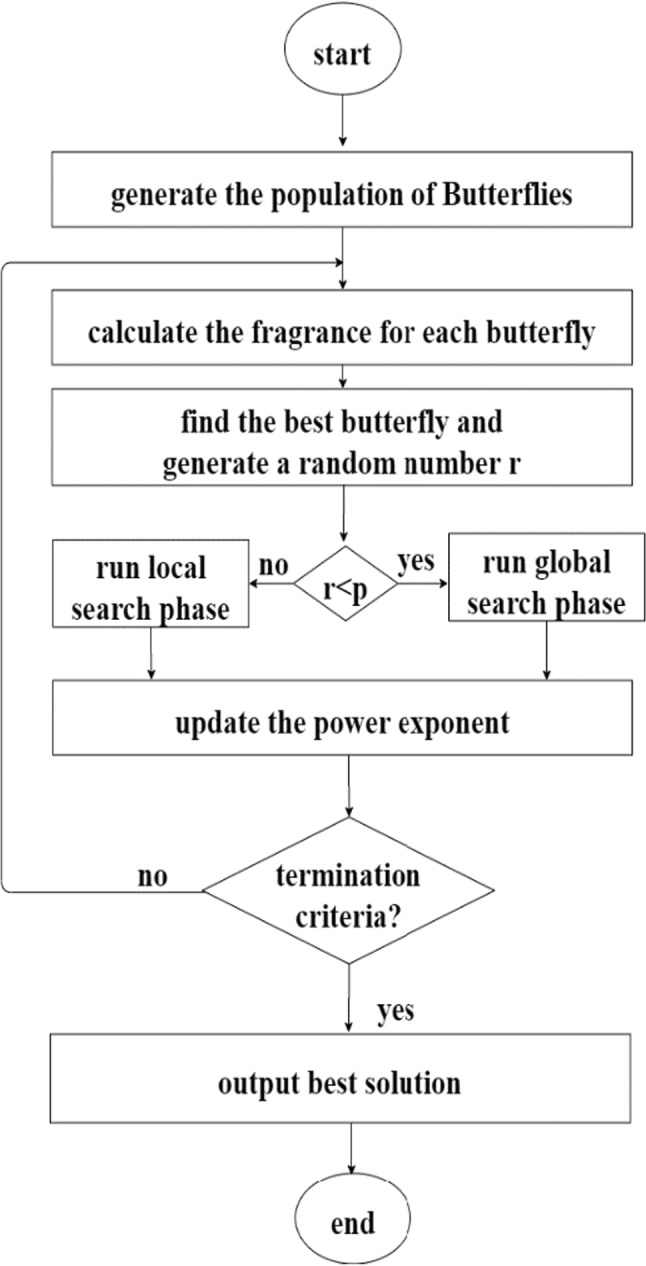
Flowchart of the BOA algorithm
Improved butterfly optimization algorithm
We propose an improved butterfly optimization algorithm using chaotic maps to solve getting stuck in local optima and early convergence problems of the butterfly optimization algorithm. There is a wide variety of chaotic maps used in the optimization field. However, in this study, the ten most frequently used chaotic maps in the literature were selected and used. The origin of the word chaotic in chaotic maps comes from the word chaos, in which the universe was formless and disorganized, discordant and chaotic before it came into order. The word maps here means matching or associating with some parameters using behavior that can be described as chaos in the algorithms used. Therefore, chaotic maps are maps that show the complex and dynamic behavior in nonlinear systems (Pecora and Carroll 1990). In recent years, chaotic maps have been widely appreciated in the optimization field for their dynamic behavior that helps optimization algorithms to explore the search space more dynamically and globally. Its behavior is predictable only under initial conditions, but then it behaves randomly.
Chebyshev map: the formula for the Chebyshev map is shown in Eq. (7).
| 7 |
Circle map: the formula for the Circle map is shown in Eq. (8).
| 8 |
Gauss map: the formula for the Gauss map is shown in Eq. (9).
| 9 |
Iterative map: the formula for the Iterative map is shown in Eq. (10).
| 10 |
Logistic map: the formula for the Logistic map is shown in Eq. (11).
| 11 |
Piecewise map: the formula for the Piecewise map is shown in Eq. (12).
| 12 |
where 0 < P ≤ 0.5.
Sine map: The formula for the Sine map is shown in Eq. (13).
| 13 |
Singer map: The formula for the Singer map is shown in Eq. (14).
| 14 |
where the P is the control parameter and its values are between 0.9 and 1.08.
Sinusoidal map: The formula for the Sinusoidal map is shown in Eq. (15).
| 15 |
Tent map: The formula for the Tent map is shown in Eq. (16).
| 16 |
The key element of the BOA establishes the balance between the equations shown in Eqs. (5)-(6) is the parameter p. It was seen that this parameter p was set to 0.8 in the BOA algorithm. However, the parameter p in IBOA is dynamically adjusted using chaotic maps. In the experimental studies, the IBOA algorithm with 10 chaotic maps was tested on 13 different benchmark functions and it was seen that the IBOA was successful.
At the beginning of the IBOA algorithm, the butterfly population is randomly generated. Each member of the population can be represented as xi. First, butterflies need their sense of smell to understand modality. Here, the odor value is calculated using Eq. (4). Then, the value of the key probability p controlling the global and the local search capabilities is then calculated by the chaotic map. Thus, the value of the p is changed from the fixed value of 0.8, and it is updated by taking advantage of the chaos in each iteration so that diversity is created. The flowchart and the pseudo-code of the IBOA algorithm are shown in Figs. 4 and 5.
Fig. 4.
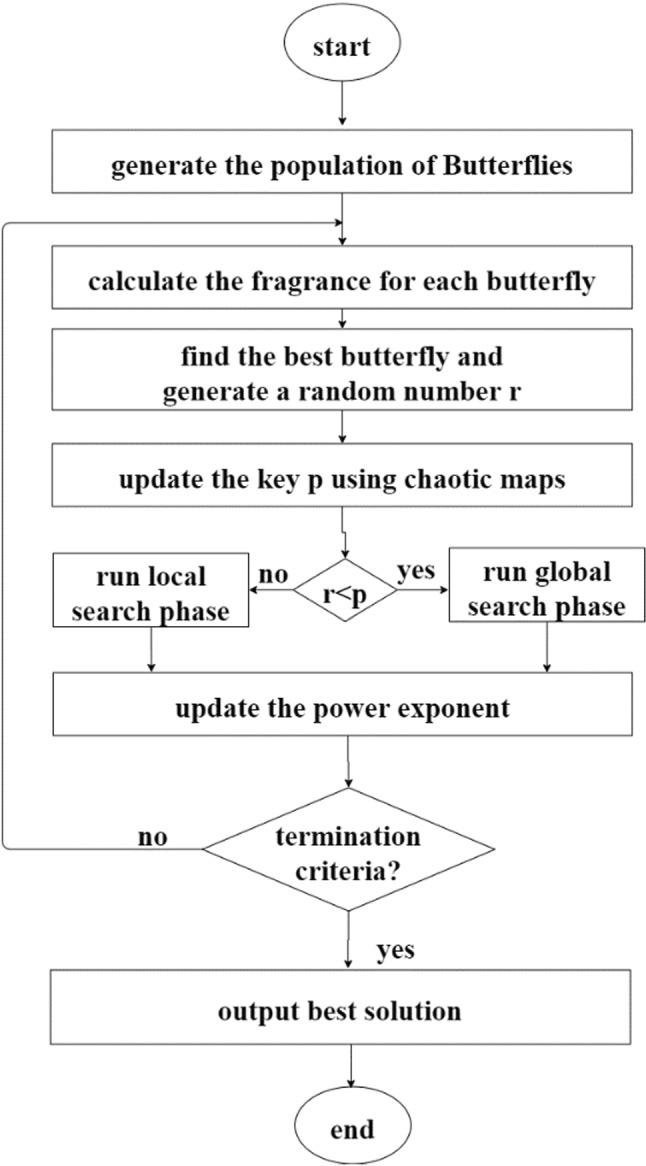
Flowchart of the IBOA algorithm
Fig. 5.

Pseudo-code of the IBOA algorithm
Training multilayer perceptron using IBOA
ANN learns from inputs and outputs. Therefore, the values of the weights and biases in the ANN are updated according to the inputs and outputs (Kiranyaz et al. 2009). The ability of ANN to give accurate results and to make successful classifications is ensured by updating the values of the weights and biases in the most appropriate way. In the literature, researchers have proposed various algorithms to train the Multilayer Perceptron (MLP). Two popular methods of them are gradient techniques and meta-heuristic algorithms. Gradient techniques often encounter problems in solving this optimization problem (training the MLP). The most important ones of these problems are the getting stuck in the local optima and the producing poor-quality solutions. To overcome these difficulties, meta-heuristic algorithms are used to train the MLP (Gulcu 2020). In this study, a hybrid IBOA-MLP algorithm was developed to optimize the values of the weights and biases. The IBOA algorithm which is a meta-heuristic algorithm was used for the first time in MLP training. Meanwhile, the optimization process of the weights and biases is shown in Fig. 6. To optimize the weights and biases in MLP, the weights and biases must first be represented by the butterflies in the IBOA-MLP algorithm. For this purpose, a representation vector consisting of weights and biases is used. This vector is shown in Eq. (17) according to the MLP structure in Fig. 6.
| 17 |
where represents the values of the weights between the input layer and the hidden layer, and represents the values of the weights between the hidden layer and the output layer. represents the bias values between the input layer and the hidden layer, and represents the bias values between the hidden layer and the output layer. The notation represents the union of two sets.
Fig. 6.
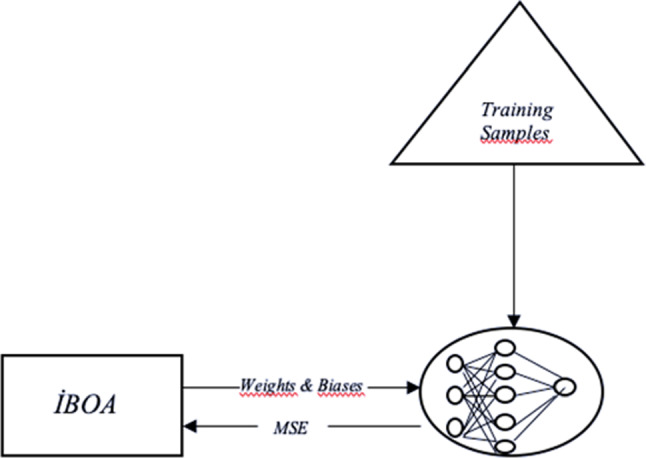
The optimization process of weights and bias in IBOA-MLP
At the beginning of the IBOA-MLP algorithm, the butterfly population is randomly generated. Each butterfly represents a different MLP, namely the representation vector in Eq. (17). Then, using the training dataset, the odor of each butterfly is calculated and the best butterfly in the population is found. Then the position of each butterfly, namely the values of the weights and biases in the MLP, is updated using Eqs. (5)–(6) according to the parameter p. The smaller the value of the parameter p, the more likely Eq. (5) will be selected, and the larger the value of the parameter p, the more Eq. (6) will be selected. The important point here is to optimize the value of the parameter p to ensure the balance between these two equations. The chaotic maps were used for optimization and the training process was started. This process continues until the termination criteria are met.
Experimental results
In this section, the experimental results of the IBOA and IBOA-MLP algorithms developed in this study are presented. The success of the IBOA algorithm was tested on both benchmark functions and classification datasets. Therefore, this section was divided into two parts (the benchmark functions, and classification datasets). The features of the hardware and software used in the experiments are as follows: Microsoft Windows 10, Intel i5-3470 3.20 GHz, 6 GB memory. The algorithms were coded and run in MATLAB R2018a. All statistical analyzes in this study were performed with the software Microsoft Excel 2013.
Benchmark functions
In this section, the experimental results of the IBOA algorithm on 13 benchmark functions are presented. Table 3 shows the formulas, dimensions, global minimums, and search range of these 13 benchmark functions. These functions are well known to those working on global optimization and are frequently used for testing and analysis of optimization algorithms. The f1–f5 functions are the single-mode functions. f6 is a discontinuous step function with a minimum. The f7 function is a noisy quadratic function. f8–f13 are multi-mode test functions. The number of local minimums for these functions increases exponentially with the size of the problem. These functions belong to the most difficult problem class for most optimization problems. The names of f1–f13 functions in the literature are as follows, respectively: sphere, schwefel 2.22, schwefel 1.2, schwefel 2.21, rosenbrock, step, quartic with noise, schwefel, rastrigin, ackley, griewank, penalized1, penalized2. These 13 benchmark functions with different difficulty levels were used in experiments to test the performance of the IBOA algorithm and to compare the IBOA with other algorithms. The dimension of these benchmark functions was taken as 30. All functions except f8 have a global minimum value of zero. Because the functions have different difficulty levels the search intervals are different as shown in Table 3.
Table 3.
Test functions, dimensions, global minimum, and search range
| Function | D | fmin | Search range |
|---|---|---|---|
| 30 | 0 | [−100, 100] | |
| 30 | 0 | [−10, 10] | |
| 30 | 0 | [−100, 100] | |
| 30 | 0 | [−100, 100] | |
| 30 | 0 | [−30, 30] | |
| 30 | 0 | [−100, 100] | |
| 30 | 0 | [−1.28, 1.28] | |
| 30 | −418.9829*D | [−500, 500] | |
| 30 | 0 | [−5.12, 5.12] | |
| 30 | 0 | [−32, 32] | |
| 30 | 0 | [−600, 600] | |
|
|
30 | 0 | [−50, 50] |
| 30 | 0 | [−50, 50] |
In the experiments, the BOA algorithm and the IBOA algorithm with 10 different maps were compared. To fairly compare the algorithms, each algorithm performed the same number of fitness function evaluations (FEs) on each run: 75,000 FEs for f1, f6, f12, and f13; 100,000 FEs for f2 and f11; 150,000 FEs for f7, f8, and f9; 250,000 FEs for f3, f4, and f5. The population size was set to 50 in the algorithms. Algorithms were run independently 30 times on each function.
Table 4 shows the average results of the BOA algorithm and the IBOA algorithm with 10 different maps. The best results in the table are shown in bold. When the results are examined, it is seen that the IBOA algorithm with the Tent map achieves better results than other methods. Also, in Table 5, the average computational times of the algorithms are shown in seconds.
Table 4.
Average of 30 run results of functions
| Chebyshev | Circle | Gauss | İterative | Logistic | Piecewise | Sine | Singer | Sinusoidal | Tent | BOA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | 2.32E−12 | 1.39E−12 | 6.56E−05 | 3.43E−12 | 3.37E−12 | 9.03E−05 | 3.58E−12 | 2.81E−12 | 1.61E−07 | 7.11E−28 | 3.61E−12 |
| f2 | 8.86E+13 | 3.68E−10 | 4.04E+03 | 5.24E−10 | 3.74E−10 | 3.31E+00 | 3.87E−10 | 4.67E−10 | 2.53E−08 | 2.20E−15 | 5.31E−10 |
| f3 | 3.52E−17 | 3.50E−17 | 4.34E−10 | 5.88E−17 | 5.81E−17 | 4.38E−10 | 7.09E−17 | 6.45E−17 | 3.70E−17 | 4.26E−28 | 5.13E−17 |
| f4 | 2.77E−13 | 2.14E−13 | 1.17E−04 | 2.83E−13 | 2.84E−13 | 1.22E−04 | 2.76E−13 | 2.64E−13 | 1.08E−10 | 3.33E−15 | 2.78E−13 |
| f5 | 2.87E+01 | 2.87E+01 | 2.69E+01 | 2.87E+01 | 2.86E+01 | 2.70E+01 | 2.86E+01 | 2.86E+01 | 2.82E+01 | 2.90E+01 | 2.86E+01 |
| f6 | 1.89E+00 | 3.27E+00 | 3.48E−01 | 1.80E+00 | 2.07E+00 | 3.41E−01 | 2.10E+00 | 2.38E+00 | 1.11E−01 | 7.41E+00 | 1.94E+00 |
| f7 | 1.01E−03 | 8.26E−04 | 1.15E−02 | 9.84E−04 | 1.08E−03 | 1.25E−02 | 1.05E−03 | 9.53E−04 | 6.57E−04 | 1.92E−04 | 9.69E−04 |
| f8 | −6.03E+03 | −6.54E+03 | −5.21E+03 | −5.41E+03 | −5.50E+03 | −5.30E+03 | −5.40E+03 | −5.80E+03 | −8.66E+03 | −5.33E+02 | −5.32E+03 |
| f9 | 7.74E+01 | 4.60E+00 | 1.57E+02 | 6.67E+01 | 6.91E+01 | 1.69E+02 | 7.61E+01 | 3.96E+01 | 2.51E+00 | 0.00E+00 | 5.89E+01 |
| f10 | 4.60E−14 | 1.61E−10 | 7.56E−02 | 4.74E−13 | 3.14E−15 | 8.30E−02 | 1.95E−15 | 1.32E−13 | 2.70E−04 | 7.64E−15 | 1.31E−11 |
| f11 | 4.42E−15 | 0.00E+00 | 9.53E−04 | 0.00E+00 | 0.00E+00 | 1.17E−03 | 2.96E−17 | 0.00E+00 | 6.37E−08 | 0.00E+00 | 0.00E+00 |
| f12 | 1.23E−01 | 3.24E−01 | 4.11E−01 | 1.04E−01 | 1.70E−01 | 3.34E−01 | 1.67E−01 | 6.17E−02 | 6.33E−03 | 1.61E+00 | 1.72E−01 |
| f13 | 1.50E+00 | 1.43E+00 | 8.73E−01 | 1.51E+00 | 1.69E+00 | 6.85E−01 | 1.69E+00 | 6.66E−01 | 1.44E−01 | 3.00E+00 | 1.82E+00 |
Table 5.
The average computational time of algorithms (in seconds)
| Chebyshev | Circle | Gauss | Iterative | Logistic | Piecewise | Sine | Singer | Sinusoidal | Tent | BOA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | 7.3 | 7.4 | 8.8 | 8.9 | 6.9 | 8.1 | 8.5 | 8.7 | 10.9 | 8.1 | 7.8 |
| f2 | 9.8 | 10.3 | 12.2 | 12.0 | 9.6 | 11.3 | 12.1 | 12.5 | 11.0 | 11.5 | 10.8 |
| f3 | 64.9 | 65.4 | 70.1 | 69.8 | 61.4 | 67.8 | 66.4 | 67.5 | 70.2 | 69.6 | 65.6 |
| f4 | 25.2 | 24.8 | 29.3 | 28.3 | 23.0 | 26.9 | 28.9 | 29.8 | 29.1 | 29.5 | 25.2 |
| f5 | 30.0 | 30.2 | 35.1 | 33.9 | 27.5 | 32.0 | 34.4 | 35.1 | 33.6 | 35.2 | 30.3 |
| f6 | 7.6 | 7.7 | 9.1 | 8.5 | 7.0 | 8.8 | 8.9 | 9.1 | 10.8 | 10.4 | 8.0 |
| f7 | 16.5 | 17.3 | 20.0 | 19.4 | 16.0 | 19.1 | 19.7 | 20.3 | 18.4 | 19.0 | 18.2 |
| f8 | 17.1 | 17.2 | 20.0 | 19.7 | 16.2 | 18.7 | 20.2 | 20.2 | 19.2 | 19.4 | 18.0 |
| f9 | 16.3 | 16.6 | 19.8 | 18.9 | 16.0 | 18.4 | 19.3 | 19.6 | 18.8 | 19.7 | 16.9 |
| f10 | 8.3 | 8.4 | 10.0 | 9.5 | 8.4 | 9.4 | 9.6 | 9.9 | 10.0 | 12.5 | 8.8 |
| f11 | 11.7 | 12.3 | 14.1 | 13.1 | 11.8 | 13.3 | 14.1 | 14.5 | 13.3 | 13.7 | 12.8 |
| f12 | 13.3 | 13.4 | 14.4 | 14.1 | 12.6 | 14.0 | 14.8 | 14.9 | 14.4 | 19.3 | 13.9 |
| f13 | 13.1 | 13.3 | 14.4 | 14.0 | 12.5 | 14.2 | 14.8 | 14.9 | 14.3 | 14.8 | 13.8 |
According to the results of the algorithms in Table 4, it is clear that the Tent-mapped IBOA algorithm outperforms the other algorithms in most of the benchmark functions. Tent-mapped IBOA algorithm achieved the best results in seven benchmark functions. It also has the third-best result in the benchmark function f10. According to Table 4, it is clear that the proposed IBOA algorithm with the Tent map has better performance than the classical BOA algorithm.
Classification datasets
To test the performance of the IBOA-MLP algorithm and compare it with other studies, five classification datasets with different training/test samples and different difficulty levels were used in the experiments. These five datasets are xor, balloon, heart, breast cancer, and iris. Balloon, heart, breast cancer, and iris datasets were taken from the well-known UCI repository and are widely used for testing machine learning algorithms.
In the literature, there are some studies about dimensionality reduction, and extracting the most important features of datasets (Gundluru et al. 2022; Lakshmanna et al. 2022). But, dimensionality reduction and feature extraction was not applied to datasets in this study. To fairly compare the algorithms, the algorithms used the same training and test subsets taken from www.seyedalimirjalili.com. All datasets were normalized by using the min–max normalization function given in Eq. (18) to eliminate the effect of attributes that may have different effective rates on the classification.
| 18 |
where x′ is the normalized value of x which is in the range [xmin, xmax]. The normalized value x′ will be in the range [0, 1].
Table 6 shows the characteristics of the datasets. It is seen that the xor dataset is the easiest problem with 8 training and 8 test examples, 3 attributes, and 2 classes. The balloon dataset has 4 features, 20 training examples, 20 test examples, and 2 classes. The iris dataset has 4 features, 150 training samples, 150 test samples, and 3 classes. The breast cancer dataset includes 9 features, 599 training samples, 100 test samples, and 2 classes. In the heart dataset, there are 22 features, 80 training samples, 187 test samples, and 2 classes. These training and testing datasets were taken from www.seyedalimirjalili.com and were also used in the (Mirjalili 2015) study. As can be seen, the different training/test samples and the datasets with different difficulty levels were selected to verify the success of the IBOA-MLP algorithm.
Table 6.
Characteristics of the classification dataset
| Dataset | # Of features | # Of training instances | # Of test instances | # Of classes | Structure of MLP | Vector size |
|---|---|---|---|---|---|---|
| Xor | 3 | 8 | 8 | 2 | 3–7–1 | 36 |
| Balloon | 4 | 20 | 20 | 2 | 4–9–1 | 55 |
| Iris | 4 | 150 | 150 | 3 | 4–9–3 | 75 |
| Breast cancer | 9 | 599 | 100 | 2 | 9–19–1 | 210 |
| Heart | 22 | 80 | 187 | 2 | 22–45–1 | 1081 |
To verify the success of IBOA-MLP, the IBOA-MLP algorithm was compared with the BOA-MLP (Irmak and Gülcü 2021) based on the butterfly optimization algorithm (Arora and Singh 2019), BAT-MLP based on the bat optimization algorithm (Yang 2010), SMS-MLP (Gulcu 2020) based on the states of matter optimization algorithm (Cuevas et al. 2014), and BP (Hecht-Nielsen 1992) algorithms in the literature. For all datasets, the initial values of biases and weights were randomly generated in the range of [−10, 10]. The parameters (number of training/tests, number of classes, MLP structure, and vector size) of the algorithms used for comparison are shown in Table 6. In this study, we did not focus on finding the optimal number of neurons in the hidden layer. In the literature, the number of neurons in the hidden layer is usually calculated with the formula (. Therefore, in this study, we obtained the number of neurons in the hidden layer by this formula. In the formula, n is the number of neurons in the input layer. Table 6 shows the MLP structure used in the datasets. As the activation function, the sigmoid function which is mostly used in the literature was chosen.
In Table 7, the MSE results of the IBOA-MLP algorithm were compared with the MSE results of four algorithms (BOA-MLP, BAT-MLP, SMS-MLP, and BP) in the literature. The results of the BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms were taken from the study (Irmak and Gülcü 2021). While making the comparison, the Sine map which produced the most successful results among the ten maps was selected. When Table 7 is examined, it is observed that the IBOA-MLP algorithm surpasses the BAT-MLP, SMS-MLP, and BP algorithms. The IBOA-MLP algorithm surpasses the BOA-MLP algorithm on the xor and iris datasets and exhibits competitive results on other datasets. The best results in the table are shown in bold.
Table 7.
Mean and standard deviation of MSE results on training data
| Dataset | IBOA-MLP | BOA-MLP | BAT-MLP | SMS-MLP | BP |
|---|---|---|---|---|---|
| Xor | 5.24E−03 ± 7.95E−03 | 7.83E−03 ± 9.62E−03 | 1.27E−01 ± 6.22E−02 | 1.33E−01 ± 3.39E−02 | 1.41E−01 ± 1.65E−01 |
| Balloon | 2.89E−09 ± 8.54E−09 | 2.79E−09 ± 6.90E−09 | 1.07E−02 ± 2.83E−02 | 1.11E−02 ± 1.31E−02 | 1.00E−01 ± 1.51E−01 |
| Iris | 4.71E−02 ± 7.91E−03 | 4.74E−02 ± 8.15E−03 | 2.10E−01 ± 1.38E−01 | 2.58E−01 ± 5.12E−02 | 5.38E−02 ± 1.30E−01 |
| Breast cancer | 1.82E−03 ± 8.02E−05 | 1.78E−03 ± 8.25E−05 | 6.83E−03 ± 7.92E−03 | 2.27E−02 ± 4.33E−03 | 2.88E−02 ± 1.21E−01 |
| Heart | 1.19E−01 ± 6.37E−03 | 1.15E−01 ± 4.75E−03 | 1.51E−01 ± 3.21E−02 | 1.18E−01 ± 3.13E−02 | 2.98E−01 ± 1.32E−01 |
Table 8 shows the average classification accuracy of the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on the test data. When the results in Table 8 are examined, it is seen that the IBOA-MLP is successful. Table 9 shows the average calculation times of the algorithms. According to Table 9, the fastest algorithm is the BP algorithm.
Table 8.
Average classification accuracy on test data
| Dataset | IBOA-MLP | BOA-MLP | BAT-MLP | SMS-MLP | BP |
|---|---|---|---|---|---|
| Xor | 100.00 | 100.00 | 85.00 | 83.75 | 84.17 |
| Balloon | 100.00 | 100.00 | 98.83 | 99.17 | 90.00 |
| Iris | 97.18 | 97.18 | 82.91 | 86.78 | 90.82 |
| Breast cancer | 99.43 | 99.37 | 96.13 | 85.67 | 93.03 |
| Heart | 74.83 | 74.46 | 71.35 | 68.57 | 61.66 |
Table 9.
Average calculation times of algorithms (in seconds)
| Dataset | IBOA-MLP | BOA-MLP | BAT-MLP | SMS-MLP | BP |
|---|---|---|---|---|---|
| Xor | 8.9 | 9.2 | 4.7 | 5.5 | 1.6 |
| Balloon | 37.9 | 37.0 | 19.4 | 20.2 | 1.7 |
| Iris | 1338.7 | 1408.6 | 775.2 | 881.6 | 9.6 |
| Breast cancer | 5035.1 | 5101.9 | 2607.3 | 2830.3 | 29.5 |
| Heart | 1686.6 | 1479.0 | 937.0 | 892.4 | 16.5 |
The statistical performance metrics used to measure the success of the algorithms in the experiments are the sensitivity, specificity, precision, and F1-Score metrics. The sensitivity mathematically defines the accuracy of a test that reports the presence of a condition and its formula is shown in Eq. (19). Specificity mathematically defines the accuracy of a test that reports the absence of a condition and its formula is shown in Eq. (20). Precision shows how many of the values we predicted as positive are positive and its formula is shown in Eq. (21). F1-Score value shows the harmonic mean of the values of the precision and the sensitivity. Its formula is shown in Eq. (22).
| 19 |
| 20 |
| 21 |
| 22 |
where TP, FN, TN, and FP represent the true positive, the false negative, the true negative, and the false positive, respectively.
Table 10 shows the results of the sensitivity, specificity, precision, and F1-score values obtained statistically by the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on the xor dataset. According to Table 10, the IBOA-MLP algorithm surpasses the BAT-MLP, SMS-MLP, and BP algorithms and exhibits the same success rate as the BOA-MLP algorithm.
Table 10.
Sensitivity, specificity, precision, and F1-score for the xor dataset
| Algorithm | Sensitivity (%) | Specificity (%) | Precision (%) | F1-Score |
|---|---|---|---|---|
| IBOA-MLP | 100.00 | 100.00 | 100.00 | 1.0000 |
| BOA-MLP | 100.00 | 100.00 | 100.00 | 1.0000 |
| BAT-MLP | 82.50 | 87.50 | 89.44 | 0.8435 |
| SMS-MLP | 81.70 | 86.70 | 88.90 | 0.8349 |
| BP | 84.17 | 84.17 | 85.94 | 0.8221 |
Table 11 shows the values of the sensitivity, specificity, precision, and F1-score obtained by the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on the balloon dataset. When Table 11 is examined, it is observed that the IBOA-MLP algorithm surpasses the BAT-MLP, SMS-MLP, and BP algorithms, and exhibits the same success rate as the BOA-MLP algorithm. Another point to note here is that the values of the sensitivity, precision, and F1-score of the BP algorithm are low.
Table 11.
Sensitivity, specificity, precision, and F1-score for the balloon dataset
| Algorithm | Sensitivity (%) | Specificity (%) | Precision (%) | F1-Score |
|---|---|---|---|---|
| IBOA-MLP | 100.00 | 100.00 | 100.00 | 1.0000 |
| BOA-MLP | 100.00 | 100.00 | 100.00 | 1.0000 |
| BAT-MLP | 99.17 | 98.61 | 98.30 | 0.9859 |
| SMS-MLP | 99.20 | 99.20 | 98.80 | 0.9894 |
| BP | 75.00 | 100.00 | 86.67 | 0.7838 |
For the iris dataset, there are 4 neurons in the input layer, 9 neurons in the hidden layer and 3 neurons in the output layer in the MLP structure and the MLP structure has 75 dimensions. The sensitivity, specificity, precision, and F1-score values of the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on the iris dataset are shown in Table 12. According to Table 12, the IBOA-MLP surpasses the BAT-MLP, SMS-MLP, and BP algorithms, and shows competitive results to the BOA-MLP algorithm.
Table 12.
Sensitivity, specificity, precision, and F1-score for the iris dataset
| Algorithm | Sensitivity (%) | Specificity (%) | Precision (%) | F1-Score |
|---|---|---|---|---|
| IBOA-MLP | 97.18 | 98.59 | 97.22 | 0.9718 |
| BOA-MLP | 97.38 | 98.69 | 97.42 | 0.9738 |
| BAT-MLP | 82.91 | 91.46 | 78.07 | 0.7883 |
| SMS-MLP | 82.10 | 91.10 | 81.00 | 0.8002 |
| BP | 90.82 | 95.41 | 88.43 | 0.8899 |
Another challenging dataset that has an important place in the literature is the breast cancer dataset. For the breast cancer dataset, the MLP consists of 9 input neurons, 19 hidden layer neurons, and 1 output neuron. The vector length has 210 dimensions. The sensitivity, specificity, precision, and F1-score values of the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on this dataset are shown in Table 13. According to Table 13, the IBOA-MLP surpasses all the algorithms and is successful.
Table 13.
Sensitivity, specificity, precision, and F1-score for the breast cancer dataset
| Algorithm | Sensitivity (%) | Specificity (%) | Precision (%) | F1-score (%) |
|---|---|---|---|---|
| IBOA-MLP | 99.05 | 99.54 | 98.33 | 0.9866 |
| BOA-MLP | 99.05 | 99.45 | 98.02 | 0.9850 |
| BAT-MLP | 87.46 | 98.44 | 93.29 | 0.8922 |
| SMS-MLP | 50.20 | 95.10 | 83.70 | 0.5828 |
| BP | 85.87 | 94.94 | 81.16 | 0.8255 |
For the heart dataset, the MLP consists of 22 input neurons, 45 hidden layer neurons, and one output neuron. The vector length has 1081 dimensions. The sensitivity, specificity, precision, and F1-score values of the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on this dataset are shown in Table 14. When Table 14 is examined, it is observed that IBOA-MLP surpasses all algorithms and is successful. In addition, the low success of the BP algorithm on this dataset is remarkable.
Table 14.
Sensitivity, specificity, precision, and F1-score for the heart dataset
| Algorithm | Sensitivity (%) | Specificity (%) | Precision (%) | F1-Score |
|---|---|---|---|---|
| IBOA-MLP | 74.90 | 74.00 | 97.09 | 0.8446 |
| BOA-MLP | 74.71 | 71.56 | 96.79 | 0.8422 |
| BAT-MLP | 71.32 | 71.78 | 96.73 | 0.8180 |
| SMS-MLP | 68.39 | 70.67 | 96.41 | 0.7980 |
| BP | 62.00 | 57.78 | 88.48 | 0.6965 |
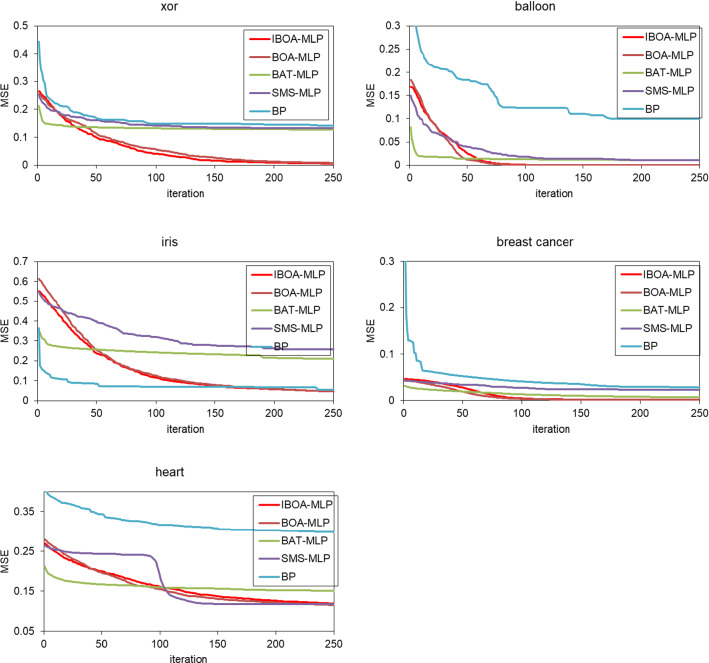
Figure 7 shows the convergence graphs of the algorithms. When the convergence graphs are examined, it is seen that the IBOA-MLP and BOA-MLP algorithms give better results on the xor and balloon datasets. It is seen that the IBOA-MLP, BOA-MLP, and BP algorithms give better results on the iris dataset. On the breast cancer dataset, all algorithms show competitive results, but the IBOA-MLP, BOA-MLP, and BAT-MLP algorithms seem to be more insistent on seeking the global optimum. On the heart dataset, it is seen that the IBOA-MLP and BOA-MLP algorithms give better results. In general, it can be said that the IBOA-MLP algorithm does not get stuck at the local optima and insists on searching for the global optimum.
Fig. 7.
Convergence graphs of algorithms
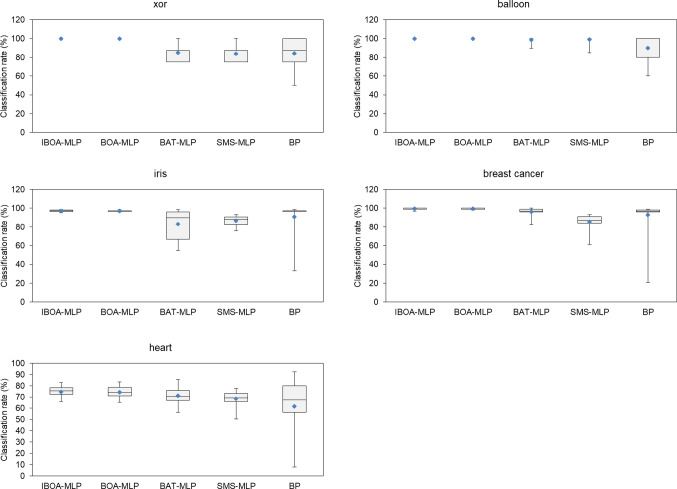
Figure 8 shows the boxplots of the classification accuracy results of the algorithms. According to the boxplots, the IBOA-MLP appears to have been successful. In Table 15, the Friedman test results of the IBOA-MLP, BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms are presented. The Friedman test is a statistical analysis technique used to make meaningful comparisons between dependent groups in cases where the assumption of normality is not provided. According to Table 15, the best result belongs to the IBOA-MLP algorithm. Another remarkable point is the low performance of SMS-MLP and BP algorithms. According to the Friedman test result, the IBOA-MLP algorithm ranks higher than other algorithms with a ranking score of 4.7. The BOA-MLP algorithm has the second ranking with a ranking score of 4.3. The BAT-MLP algorithm ranks third with a ranking score of 2.4. The SMS-MLP algorithm and the BP algorithm rank fourth with a ranking score of 1.8.
Fig. 8.
Boxplots of algorithms
Table 15.
Average ranking of algorithms according to the classification rate (Friedman test)
| Algorithm | Ranking |
|---|---|
| IBOA-MLP | 4.7 |
| BOA-MLP | 4.3 |
| BAT-MLP | 2.4 |
| SMS-MLP | 1.8 |
| BP | 1.8 |
Conclusions
In this study, the IBOA algorithm is proposed to train the ANN and optimize the weights and biases. The IBOA algorithm is the improved version of the BOA algorithm by utilizing chaotic maps. The key parameter p of the IBOA algorithm, which establishes the balance between the local search and the global search, is updated using chaotic maps.
The main contributions of this article are: A new improved butterfly optimization algorithm (IBOA) is proposed. The IBOA algorithm is applied for training ANN and optimizes the weights and biases of ANN. The IBOA-MLP algorithm has the ability to escape from local optima. The initial parameters and positions don’t affect the performance of the IBOA-MLP algorithm. The features of the IBOA-MLP algorithm are simplicity, requiring only a few parameters, solving a wide array of problems, and easy implementation.
In the experiments, the success of the IBOA algorithm was verified on 13 benchmark functions. The IBOA algorithm with the Tent map outperformed the other algorithms on the benchmark functions. Afterward, the proposed IBOA-MLP algorithm was used to optimize the values of the biases and weights in the ANN, and it was aimed to increase the learning ability of the ANN. In the experiments, the IBOA-MLP algorithm was tested on the classification datasets (xor, iris, balloon, heart, and breast cancer) in the literature. The IBOA-MLP algorithm was compared with four algorithms (BOA-MLP, BAT-MLP, SMS-MLP, and BP). According to the results, it was observed that the IBOA-MLP algorithm outperformed the BOA-MLP, BAT-MLP, SMS-MLP, and BP algorithms on most of the datasets. In addition, the IBOA-MLP algorithm had the first ranking according to the Friedman test results. It was concluded that the IBOA algorithm was successful in optimizing the biases and weights. Therefore, it was proven suitable for training the MLP. In conclusion, the IBOA and IBOA-MLP algorithms can escape from local optima thanks to the chaotic map.
This study has some limitations. On smaller datasets, the IBOA-MLP algorithm tends to overfit. It memorizes the training data and does not generalize well to new examples. The IBOA-MLP algorithm needs more extensive datasets for training. Therefore, the IBOA-MLP algorithm requires high computation power and computational resources.
In future work, the IBOA-MLP algorithm can be applied to different datasets such as COVID-19. The IBOA-MLP algorithm can be hybridized with a meta-heuristic algorithm such as the particle swarm optimization or the crow search algorithm to increase the performance of the IBOA-MLP algorithm. Further research regarding the role of the activation function and the parameters of the butterfly optimization algorithm would be worthwhile.
Funding
The authors declare that no funds, grants, or other support were received during the preparation of this manuscript.
Data availability
Enquiries about data availability should be directed to the authors.
Declaration
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Conflict of interest
The authors declare that they have no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Al Nuaimi ZNAM, Abdullah R. Neural network training using hybrid particlemove artificial bee colony algorithm for pattern classification. J Inf Commun Technol. 2017;16(2):314–334. [Google Scholar]
- Aljarah I, Faris H, Mirjalili S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018;22(1):1–15. doi: 10.1007/s00500-016-2442-1. [DOI] [Google Scholar]
- Arora S, Anand P. Learning automata-based butterfly optimization algorithm for engineering design problems. Int J Comput Mater Sci Eng. 2018;7(04):1850021. [Google Scholar]
- Arora S, Singh S. Butterfly optimization algorithm: a novel approach for global optimization. Soft Comput. 2019;23(3):715–734. doi: 10.1007/s00500-018-3102-4. [DOI] [Google Scholar]
- Blair RB, Launer AE. Butterfly diversity and human land use: species assemblages along an urban grandient. Biol Cons. 1997;80(1):113–125. doi: 10.1016/S0006-3207(96)00056-0. [DOI] [Google Scholar]
- Chen J-F, Do QH, Hsieh H-N. Training artificial neural networks by a hybrid PSO-CS algorithm. Algorithms. 2015;8(2):292–308. doi: 10.3390/a8020292. [DOI] [Google Scholar]
- Cuevas E, Echavarría A, Ramírez-Ortegón MA. An optimization algorithm inspired by the States of Matter that improves the balance between exploration and exploitation. Appl Intell. 2014;40(2):256–272. doi: 10.1007/s10489-013-0458-0. [DOI] [Google Scholar]
- Dash R. Performance analysis of a higher order neural network with an improved shuffled frog leaping algorithm for currency exchange rate prediction. Appl Soft Comput. 2018;67:215–231. doi: 10.1016/j.asoc.2018.02.043. [DOI] [Google Scholar]
- Dey PP, Das DC, Latif A, Hussain SS, Ustun TS. Active power management of virtual power plant under penetration of central receiver solar thermal-wind using butterfly optimization technique. Sustainability. 2020;12(17):6979. doi: 10.3390/su12176979. [DOI] [Google Scholar]
- Dubey AK. Optimized hybrid learning for multi disease prediction enabled by lion with butterfly optimization algorithm. Sādhanā. 2021;46(2):1–27. doi: 10.1007/s12046-021-01574-8. [DOI] [Google Scholar]
- Erdogan F, Gulcu S. Training of the artificial neural networks using crow search algorithm. Int J Intell Syst Appl Eng. 2021;9(3):101–108. doi: 10.18201/ijisae.2021.237. [DOI] [Google Scholar]
- Ghaleini EN, Koopialipoor M, Momenzadeh M, Sarafraz ME, Mohamad ET, Gordan B. A combination of artificial bee colony and neural network for approximating the safety factor of retaining walls. Eng Comput. 2019;35(2):647–658. doi: 10.1007/s00366-018-0625-3. [DOI] [Google Scholar]
- Gulcu Ş. Training of the artificial neural networks using states of matter search algorithm. Int J Intell Syst Appl Eng. 2020;8(3):131–136. doi: 10.18201/ijisae.2020363532. [DOI] [Google Scholar]
- Gullipalli TR. An improved under sampling approaches for concept drift and class imbalance data streams using improved cuckoo search algorithm. Turk J Comput Math Educ (turcomat) 2021;12(2):2267–2275. doi: 10.17762/turcomat.v12i2.1945. [DOI] [Google Scholar]
- Gundluru N, Rajput DS, Lakshmanna K, Kaluri R, Shorfuzzaman M, Uddin M, Rahman Khan MA (2022) Enhancement of detection of diabetic retinopathy using Harris Hawks optimization with deep learning model. Comput Intell Neurosci [DOI] [PMC free article] [PubMed]
- Gülcü Ş. An improved animal migration optimization algorithm to train the feed-forward artificial neural networks. Arab J Sci Eng. 2022;47(8):9557–9581. doi: 10.1007/s13369-021-06286-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gülcü Ş. Training of the feed forward artificial neural networks using dragonfly algorithm. Appl Soft Comput. 2022;1:1. doi: 10.1016/j.asoc.2022.109023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht-Nielsen R (1992) Theory of the backpropagation neural network. In: Neural networks for perception. Academic Press, pp 65–93. 10.1016/B978-0-12-741252-8.50010-8
- Irmak B, Gülcü Ş. Training of the feed-forward artificial neural networks using butterfly optimization algorithm. Manas J Eng. 2021;9(2):160–168. doi: 10.51354/mjen.917837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaddi NS, Abdullah S. Optimization of neural network using kidney-inspired algorithm with control of filtration rate and chaotic map for real-world rainfall forecasting. Eng Appl Artif Intell. 2018;67:246–259. doi: 10.1016/j.engappai.2017.09.012. [DOI] [Google Scholar]
- Kiranyaz S, Ince T, Yildirim A, Gabbouj M. Evolutionary artificial neural networks by multi-dimensional particle swarm optimization. Neural Netw. 2009;22(10):1448–1462. doi: 10.1016/j.neunet.2009.05.013. [DOI] [PubMed] [Google Scholar]
- Koç ML, Balas CE, Arslan A. Preliminary design of ruble mound breakwaters by using artificial neural networks. Tech J Turk Chamber Civ Eng. 2004;15(74):3351–3375. [Google Scholar]
- Kulluk S, Ozbakir L, Baykasoglu A. Training neural networks with harmony search algorithms for classification problems. Eng Appl Artif Intell. 2012;25(1):11–19. doi: 10.1016/j.engappai.2011.07.006. [DOI] [Google Scholar]
- Lakshmanna K, et al. A Review on Deep Learning Techniques for IoT Data. Electronics. 2022;11(10):1604. doi: 10.3390/electronics11101604. [DOI] [Google Scholar]
- Long W, Jiao J, Liang X, Wu T, Xu M, Cai S. Pinhole-imaging-based learning butterfly optimization algorithm for global optimization and feature selection. Appl Soft Comput. 2021;103:107146. doi: 10.1016/j.asoc.2021.107146. [DOI] [Google Scholar]
- Madenci E, Gülcü Ş. Optimization of flexure stiffness of FGM beams via artificial neural networks by mixed FEM. Struct Eng Mech. 2020;75(5):633–642. doi: 10.12989/sem.2020.75.5.633. [DOI] [Google Scholar]
- Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl Intell. 2015;43(1):150–161. doi: 10.1007/s10489-014-0645-7. [DOI] [Google Scholar]
- Özbakir L, Baykasoğlu A, Kulluk S, Yapıcı H. TACO-miner: an ant colony based algorithm for rule extraction from trained neural networks. Expert Syst Appl. 2009;36(10):12295–12305. doi: 10.1016/j.eswa.2009.04.058. [DOI] [Google Scholar]
- Pecora LM, Carroll TL. Synchronization in chaotic systems. Phys Rev Lett. 1990;64(8):821. doi: 10.1103/PhysRevLett.64.821. [DOI] [PubMed] [Google Scholar]
- Pereira LA, Rodrigues D, Ribeiro PB, Papa JP, Weber SA (2014) Social-spider optimization-based artificial neural networks training and its applications for Parkinson's disease identification. In: 2014 IEEE 27th international symposium on computer-based medical systems, 2014, pp 14–17. 10.1109/CBMS.2014.25
- Raguso RA. Wake up and smell the roses: the ecology and evolution of floral scent. Annu Rev Ecol Evol Syst. 2008;39:549–569. doi: 10.1146/annurev.ecolsys.38.091206.095601. [DOI] [Google Scholar]
- Saccheri I, Kuussaari M, Kankare M, Vikman P, Fortelius W, Hanski I. Inbreeding and extinction in a butterfly metapopulation. Nature. 1998;392(6675):491–494. doi: 10.1038/33136. [DOI] [Google Scholar]
- Sharma TK. Enhanced butterfly optimization algorithm for reliability optimization problems. J Ambient Intell Humaniz Comput. 2021;12(7):7595–7619. doi: 10.1007/s12652-020-02481-2. [DOI] [Google Scholar]
- Sharma TK, Sahoo AK, Goyal P. Bidirectional butterfly optimization algorithm and engineering applications. Mater Today: Proc. 2021;34:736–741. [Google Scholar]
- Tang R, Fong S, Deb S, Vasilakos AV, Millham RC. Dynamic group optimisation algorithm for training feed-forward neural networks. Neurocomputing. 2018;314:1–19. doi: 10.1016/j.neucom.2018.03.043. [DOI] [Google Scholar]
- Turkoglu B, Kaya E. Training multi-layer perceptron with artificial algae algorithm. Eng Sci Technol Int J. 2020;23(6):1342–1350. doi: 10.1016/j.jestch.2020.07.001. [DOI] [Google Scholar]
- Tümer A, Edebali S, Gülcü Ş. Modeling of removal of chromium (VI) from aqueous solutions using artificial neural network. Iran J Chem Chem Eng (IJCCE) 2020;39(1):163–175. doi: 10.30492/ijcce.2020.33257. [DOI] [Google Scholar]
- Wyatt TD. Pheromones and animal behaviour: communication by smell and taste. Cambridge University Press; 2003. [Google Scholar]
- Yang X-S (2010) A new metaheuristic bat-inspired algorithm. In: Nature inspired cooperative strategies for optimization (NICSO 2010). Springer, pp 65–74
- Zamani M, Sadeghian A (2010) A variation of particle swarm optimization for training of artificial neural networks. In: Computational ıntelligence and modern heuristics. IntechOpen. 10.5772/7819
- Zanchettin C, Ludermir TB, Almeida LM. Hybrid training method for MLP: optimization of architecture and training. IEEE Trans Syst Man Cybern Part B (cybernetics) 2011;41(4):1097–1109. doi: 10.1109/TSMCB.2011.2107035. [DOI] [PubMed] [Google Scholar]
- Zhang J-R, Zhang J, Lok T-M, Lyu MR. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl Math Comput. 2007;185(2):1026–1037. doi: 10.1016/j.amc.2006.07.025. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data availability
Enquiries about data availability should be directed to the authors.
Enquiries about data availability should be directed to the authors.