Estimation of Occupational Noise–Induced Hearing Loss Using Kurtosis-Adjusted Noise Exposure Levels

Objectives:

Studies have shown that in addition to energy, kurtosis plays an important role in the assessment of hearing loss caused by complex noise. The objective of this study was to investigate how to use noise recordings and audiometry collected from workers in industrial environments to find an optimal kurtosis-adjusted algorithm to better evaluate hearing loss caused by both continuous noise and complex noise.

Design:

In this study, the combined effects of energy and kurtosis on noise-induced hearing loss (NIHL) were investigated using data collected from 2601 Chinese workers exposed to various industrial noises. The cohort was divided into three subgroups based on three kurtosis (β) levels (K₁: 3 ≤ β ≤ 10, K₂: 10 <β ≤ 50, and K₃: β > 50). Noise-induced permanent threshold shift at test frequencies 3, 4, and 6 kHz (NIPTS₃₄₆) was used as the indicator of NIHL. Predicted NIPTS₃₄₆ was calculated using the ISO 1999 model for each participant, and the actual NIPTS was obtained by correcting for age and sex using non-noise-exposed Chinese workers (n = 1297). A kurtosis-adjusted A-weighted sound pressure level normalized to a nominal 8-hour working day (L_Aeq,8h) was developed based on the kurtosis categorized group data sets using multiple linear regression. Using the NIPTS₃₄₆ and the L_Aeq.8h metric, a dose-response relationship for three kurtosis groups was constructed, and the combined effect of noise level and kurtosis on NIHL was investigated.

Results:

An optimal kurtosis-adjusted L_Aeq,8h formula with a kurtosis adjustment coefficient of 6.5 was established by using the worker data. The kurtosis-adjusted L_Aeq,8h better estimated hearing loss caused by various complex noises. The analysis of the dose-response relationships among the three kurtosis groups showed that the NIPTS of K₂ and K₃ groups was significantly higher than that of K₁ group in the range of 70 dBA ≤ L_Aeq,8h < 85 dBA. For 85 dBA ≤ L_Aeq,8h ≤ 95 dBA, the NIPTS₃₄₆ of the three groups showed an obvious K₃ > K₂ > K₁. For L_Aeq,8h >95 dBA, the NIPTS₃₄₆ of the K₂ group tended to be consistent with that of the K₁ group, while the NIPTS₃₄₆ of the K₃ group was significantly larger than that of the K₁ and K₂ groups. When L_Aeq,8h is below 70 dBA, neither continuous noise nor complex noise produced significant NIPTS₃₄₆.

Conclusions:

Because non-Gaussian complex noise is ubiquitous in many industries, the temporal characteristics of noise (i.e., kurtosis) must be taken into account in evaluating occupational NIHL. A kurtosis-adjusted L_Aeq,8h with an adjustment coefficient of 6.5 allows a more accurate prediction of high-frequency NIHL. Relying on a single value (i.e., 85 dBA) as a recommended exposure limit does not appear to be sufficient to protect the hearing of workers exposed to complex noise.

Researchers have long found that impulsive noise or complex noise with impulse/impact components is more hazardous to hearing than continuous steady state (Gaussian) noise at similar noise exposure levels (e.g., Nilsson et al. 1977; Evans and Ming 1982; Taylor et al. 1984; Theiry and Meyer-Bisch 1988; Lataye and Campo 1996). Current noise standards (such as ISO 1999) are based on hearing loss due to continuous steady-state noise. As a result, they underestimate the damage to hearing caused by non-Gaussian complex noise with equivalent sound pressure levels (Zhao et al. 2010; Zhang et al. 2021). Two earlier versions of the ISO 1999 document have mentioned corrections to the estimated noise exposure level to account for the increased hazard of noise with complex temporal characteristics, specifically noise containing impulsive components. The ISO 1999:1971 specified a correction of 10-dB, and the ISO 1999:1990 proposed a correction of 5-dB for impulsive/impact noise to compensate for the greater hazard of complex noise. However, the ISO 1999:2013 contained no mention of possible corrections. This may be due to the lack of a precise quantitative definition of impulse noise in previous versions, making such adjustments less feasible. Moreover, it has been found that for the same exposure level, complex noise can produce up to 30 to 40 dB more noise-induced hearing loss (NIHL) than Gaussian noise in animal models (Hamernik et al. 2003; Qiu et al. 2006, 2007). Thus, a 5- or 10-dB correction may not adequately address the greater hazard associated with non-Gaussian complex noise.

Complex noise consists of regular or irregular impulsive/impact components embedded in continuous Gaussian background noise and is very common in certain industrial (such as manufacturing and construction) and military settings. How to properly measure or characterize the great diversity of non-Gaussian noise found in industry is a challenging task. Erdreich (1986) proposed to use kurtosis to distinguish noise with impulsive components from steady-state noise. Inspired by Erdreich’s work, Hamernik and his colleagues designed a series of animal (chinchilla) experiments in which different groups of animals were exposed to noise with the same energy but different kurtosis values (Lei et al. 1994; Hamernik et al. 2003, 2007; Qiu et al. 2006, 2007, 2013). The results show that for a fixed noise level, there is a monotonic relation between noise-induced hearing loss and kurtosis, and the hearing loss (defined as a permanent hearing threshold shift or loss of outer/inner hair cells) increases with the increase of kurtosis value. In other words, the kurtosis can differentiate the degree of hearing damage caused by noise with different temporal structures at the same noise exposure level in animals. These findings were also validated by human data in subsequent epidemiological studies (Zhao et al. 2010; Davis et al. 2012; Xie et al. 2016; Zhang et al. 2021). Although it is impossible to directly count hair cell loss in humans, noise-induced permanent hearing threshold shifts were verified in noise-exposed subjects.

Kurtosis is a statistical measure that defines how heavily the tails of distribution differ from the tails of a Gaussian distribution. For noise, kurtosis can be used to describe whether there is the presence of a high-amplitude sound (impact/impulse) that is different from the underlying continuous steady-state (Gaussian) noise and the degree of the impulsiveness of the noise (Qiu et al. 2020). A Gaussian noise has a kurtosis of 3. Noise with impulsive components embedded in Gaussian background noise will have kurtosis greater than 3. In general, the higher the kurtosis value, the stronger the noise impulsivity. It should be emphasized that kurtosis can only be used as an adjunct metric to energy in the assessment of NIHL. In other words, the application of kurtosis must be based on the energy of noise. If the equivalent sound pressure level of noise exposure is very low, then kurtosis has no effect on hearing loss (Qiu et al. 2006).

Goley et al. (2011) proposed a scheme to apply kurtosis to adjust the measured equivalent A-weighted, 8-hour, noise exposure level (L_Aeq,8h) with the equation as follows:

$$L{\text{'}}_{Aeq,8h}=L_{Aeq,8h}+\lambda lo{g}_{10}\frac{{\beta }_N}{{\beta }_G}$$ (1)

where β_N is the kurtosis of noise and β_G is the kurtosis of Gaussian noise, which is equal to 3. One of the most attractive features of the Goley et al. model is that it directly corrects the measured noise energy using the kurtosis of noise. It can be seen that using the kurtosis adjustment method is equivalent to adding a penalty, determined by the second term in the formula, to the overall sound pressure level (L_Aeq,8h). Because the kurtosis of complex noise (β_N) is higher than that of β_G, it has a positive correction term indicating that the risk of complex noise is higher. In the formula, λ is a key adjustment coefficient. Although the coefficient is not scaled in dB, the correction can be expressed that way. In the case of fixed noise kurtosis, it determines the degree of kurtosis adjustment for L_Aeq.8h. Goley et al. (2011) determined this coefficient to be 4.02 based on the results of animal (chinchilla) experiments. Due to the differences in the auditory system between animals and humans (such as the different frequency sensitivity range to sound) and the complexity of industrial noises in the real world, this coefficient may not be appropriate for humans. The validity of the adjustment factor for humans in the Goley model can only be validated by data from workers exposed to a variety of industrial noises.

In this study, we collected a large database of 3898 participants, including shift-long noise recordings and hearing levels of 2601 workers from various Chinese industries, and a control group of 1297 participants with no history of occupational noise exposure. The noise environments in these industries had a wide range of noise levels and kurtosis values that allowed for a comprehensive evaluation of the role of kurtosis in assessing NIHL. The objective of this study was to investigate how workers’ and control data could be used to find an optimal adjustment coefficient (λ) for humans by studying the combined effects of noise level and kurtosis on high-frequency hearing loss, and to determine whether a kurtosis-adjusted L_Aeq,8h using the Goley model improves the accuracy of prediction of hearing loss due to complex noise.

MATERIALS AND METHODS

This cross-sectional study was conducted in Zhejiang and Jiangsu provinces, eastern China. The study protocol was approved by the Ethics Committee of Zhejiang and Jiangsu Provincial Centers for Disease Control and Prevention (approval reference number: ZJCDC-T-043-R and JSCDCLL-2017-025).

Recruitment of Participants

A total of 4916 subjects were initially introduced to the purpose of the study and invited to participate between 2008 and 2018. This cohort included 3244 noise-exposed and 1672 non-noise-exposed workers. All participants signed an informed consent form. For inclusion in the study, all participants had to satisfy the following three criteria: (1) no history of genetic or drug-related hearing loss, head wounds, or ear diseases; (2) no history of military service or shooting activities; and (3) good conditions of the external auditory canal, tympanic membrane, and the middle ear on otoscopic examination. Noise-exposed participants needed to satisfy additional criteria: (1) consistently worked in the same job category and at the same worksite (noise exposure area) for the period from the beginning of a worker’s career to the date of the investigation; (2) a minimum of at least one year of employment in their current position; (3) having an A-weighted noise exposure level (L_Aeq) at their jobs between 70 and 95 dBA. As a result, a total of 2601 noise-exposed participants and 1297 non-noise-exposed participants (control) were included from the original pool of 3244 and 1672, respectively.

The reason for choosing workers exposed to L_Aeq.8h between 70 and 95 dBA is that a previous study (Zhang et al. 2021) indicated that the recommended exposure limit of 85 dBA, as an 8-hour time-weighted average (NIOSH 1998), may not be a safe noise exposure limit, especially for complex noise with impulsive components and, therefore, it may be necessary to observe the biological effects of lower noise exposure levels on hearing. It was observed that when the L_Aeq,8h was less than 95 dBA, workers rarely used hearing protection devices; when the noise L_Aeq,8h was equal to or greater than 95 dBA, the proportion of hearing protection devices used increased significantly. Because an accurate unprotected dose-response relationship is the basis of this study, we needed to exclude data of workers exposed to higher than 95 dBA.

Most participants still did not use a hearing protection device (HPD) despite the implementation of hearing conservation programs on a wide scale in China starting in 2012. The use of HPDs, usually earplugs, both on and off the job, was assessed through field observations by the researchers and in the questionnaire and reported to be low and infrequent. At high noise exposure levels, that is, ~95 dBA and above, the use of HPDs was observed to be sporadic. The inclusion of these participants would, to some extent, have an effect on the relationship between noise level and noise-induced permanent threshold shift (NIPTS). We expected this effect to occur primarily in the participants exposed to noise above 95 dBA. For those participants who have never used HPDs, the members of the research team recommended the use of appropriate HPDs after data collection. During this study, workers in the investigated factories received training on how to properly use HPDs.

Questionnaire Survey

All participants were required to complete a noise exposure and health questionnaire, which was followed by a face-to-face interview by an occupational hygienist for quality control. The questionnaire included the following information: general demographic information (age, sex, etc.); occupational history (factory, worksite, job description, length of employment, duration of daily noise exposure, and history of using hearing protection); and overall health status (including any history of ear disease and/or ototoxic drug exposure).

Audiometric Evaluation

Each participant underwent an otologic and audiometric examination. Otoscopy was carried out initially to ensure participants had no external ear abnormalities. Air conduction pure-tone hearing threshold levels were tested at 0.5, 1, 2, 3, 4, 6, and 8 kHz in each ear by an experienced audiologist. Testing was conducted in a double-walled audiometric booth using an audiometer (Madsen OB40, Denmark) with an air conduction headphone (Sennheiser HDA 300). The tests were conducted manually, and the measurement was based on the threshold determination methods of the American Speech-hearing-Language Association (ASHA 2005). Before the implementation of the project, the audiometer and headphone were calibrated by the Zhejiang Institute of Metrology of China, according to the Chinese national standard (GB4854-84). During the duration of the project, a bioacoustic check and a listening check of the headphone were performed daily. The noise floor of the booth was compliant with ANSI S3.1-1999 specifications from 125 to 8000 Hz (ANSI 2008). Audiograms were measured at least 16 hours after the participants’ last occupational noise exposure.

Noise Data Collection

A digital noise recorder (ASV5910-R, Hangzhou Aihua Instruments Co., Ltd., China) was used to record a shift-long personal noise exposure for each participant. The instrument uses a ¼-inch pre-polarized condenser microphone with a broad response frequency (20 to 20 kHz) and high-sensitivity level (2.24 mV/Pa). The measurement ranges from 40 dB(A) to 141 dB(A). The recorder can work continuously for 23 hours under full charge. One full-shift recording of each participant’s noise exposure was captured by the ASV5910-R at 32-bit resolution with a 48-kHz sampling rate and saved in a raw audio format (WAV file). The noise record was saved on a 32 GB micro SD card and transferred to a portable hard disk for subsequent analysis. It was performed one time for each participant. Before recording, a hygienist confirmed with each participant that this was the noise they were typically exposed to on an average working day. The members of the research team monitored the noise collection of individual participants in the workplace. The microphone was placed on the shoulder of each participant at the start of the work shift and collected at the end of the shift. The participants were trained to wear the recorder properly.

Calculation of Noise Metrics

Two noise metrics were used in this study: (1) the A-weighted equivalent sound pressure level normalized to a nominal 8-hour working day (L_Aeq,8h); (2) the kurtosis of noise exposure (β_Ν). A program using MATLAB (The MathWorks, R2017) software was developed for analyzing the full-shift noise waveforms that were collected on each participant. The program was designed to extract the L_Aeq,8h, and kurtosis, i.e.,

• 1) L_Aeq,8h level, in A-weighted decibels, is given by the formula (ISO 1999, 2013):

$$L_{Aeq,8h}=L_{Aeq,T_e}+10\text{log}(T_e/T_0)$$

where L_Aeq,Te is the A-weighted equivalent continuous sound pressure level for T_e; T_e is the effective duration of the working day in hours, and T₀ is the reference duration (T₀ = 8-hour).

• 2) Calculation of the kurtosis of noise exposure in a typical work day (β_N)

The kurtosis of the recorded noise signal was computed over consecutive 60-second time windows without overlap over the shift-long noise record using a sampling rate of 48 kHz for noise recording (Tian et al. 2021). For a sample of N values, the kurtosis is calculated as:

$$\beta =\frac{1}{N}{\displaystyle {\sum }_{i=1}^n{(x_i-\overline{x})}^4/{\left(\frac{1}{N}{\displaystyle {\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}\right)}^2}$$ (3)

where $x_i$ is the i^th value of noise amplitude and $\overline{x}$ is the sample mean. The average of the measured kurtosis values (β_j) at every 60 seconds is used as the kurtosis of noise exposure (β_N), which is calculated as

$${\beta }_{\text{N}}=\frac{1}{N}{\displaystyle {\sum }_{j=1}^N{\beta }_j}$$ (4)

where N is the number of kurtosis values of the full-shift noise exposure.

Noise-Induced Permanent Threshold Shift Estimation

The analysis focused on the noise-sensitive frequency range of 3 to 6 kHz because the noise-induced hearing loss from continuous noise occurs predominantly in this range initially (Lie et al. 2016). The actual NIPTS for each noise-exposed participant at test frequencies 3, 4, and 6 kHz were obtained by subtracting normal median hearing threshold levels by age- and sex-matched populations of the control group collected in this study. The thresholds of the better ear were determined for all participants across the test frequencies. The better ear was used because this was the criteria for establishing median hearing threshold levels of the control group in ISO 1999:2013 (Hoffman et al. 2010). Because the participants were typically exposed to only one type of high-level occupational noise throughout their working life, and since their working environments were consistent over the course of their employment, the observed hearing-loss estimates were likely attributable to the measured industrial noise exposures.

The actual value of NIPTS of each individual participant was compared with the median NIPTS predicted by ISO 1999 (2013), and the accuracy of ISO 1999 predictions for NIPTS was evaluated statistically. The ISO 1999 median NIPTS prediction for each participant was determined using the equations described in the ISO 1999 document as follows:

$$NIPTS=\left\{\begin{array}{c}\left[u+v\log \left(\frac{t}{t_0}\right)\right]{\left(L_{Aeq,8h}-L_0\right)}^2,10\le t\le 40\\ \frac{\text{log}(t+1)}{\text{log}(11)}\left[u+v\log \left(\frac{10}{t_0}\right)\right]{\left(L_{Aeq,8h}-L_0\right)}^2,t<10\end{array}\right.$$ (5)

where L_Aeq,8h is the noise exposure level normalized to a nominal 8-hour working day; t is noise exposure duration in years, $t_0=1$ year; $L_0$ is the reference sound pressure level in Table 1 of ISO 1999 (2013); u and v are coefficients given as a function of audiometric test frequency in Table 1 of ISO 1999 (2013).

TABLE 1.

Selected values of the statistical distribution of hearing threshold levels in decibels of the control group according to frequency classified by age and sex

Frequency (Hz)	Hearing Threshold Level (dB)
	Age* (yrs)
	20			30			40			50			60
							Percentages
	10	50	90	10	50	90	10	50	90	10	50	90	10	50	90
Male
500	3	6	10	−1	6	12	0	6	13	1	8	15	3	11	17
1000	1	6	12	−2	4	11	−2	6	15	1	7	15	2	9	17
2000	−2	4	11	−2	4	12	−2	6	15	0	8	18	2	13	24
3000	1	5	12	−2	6	12	−2	8	19	1	11	12	5	15	32
4000	−3	6	12	−3	5	12	−3	8	18	4	13	26	−2	15	41
6000	3	12	25	4	13	25	4	17	28	10	23	44	14	28	57
Female
500	2	6	12	−1	5	11	0	6	13	2	8	15	4	12	25
1000	0	6	12	−2	4	11	−2	5	13	0	7	17	4	12	27
2000	−1	5	12	−2	5	12	−2	5	13	2	9	18	5	14	27
3000	−2	5	12	−2	5	13	−2	6	16	1	10	18	5	19	34
4000	−3	4	12	−4	3	12	−4	5	15	−1	8	17	3	19	34
6000	7	13	22	3	13	21	3	15	27	8	19	33	11	31	52

^*Age is grouped in 10-yr intervals; that is, “30” represents ages 25 to 34 yrs, etc.

published online ahead of print April 21, 2022.

Kurtosis Categories

To analyze the effect of kurtosis on NIPTS, we grouped the data according to the noise kurtosis value (β_N) that each worker was exposed to. The kurtosis group should be divided so that the mean NIPTS of workers within this group is significantly different from that of other groups. The participants were partitioned into one of three groups based on the kurtosis value of their noise exposure:

1. K₁: 3 ≤ β_N ≤ 10;

2. K₂: 10 < β_N ≤ 50;

3. K₃: β_N > 50

Based on our analysis of individual noise data collected from more than 3000 workers, the kurtosis of industrial noise can be as high as about 1000. More details on the kurtosis grouping described above are available in the Discussion section.

Kurtosis-Adjusted L_Aeq,8h

The kurtosis adjustment was calculated according to Eq. 1 (Goley et al. 2011). Taking actual NIPTS as the dependent variable and L_Aeq,8h and log₁₀(β_N/3) as independent variables, the coefficient λ was calculated by multiple linear regression model:

$$\text{NIPTS}=b_0+b_1{L}_{Aeq,8h}+b_{2}lo{g}_{10}\left({\beta }_N/3\right)+\epsilon$$ (6)

where b₀ is the NIPTS-intercept; b₁ and b₂ are the regression coefficients representing the change in NIPTS relative to a one-unit change in L_Aeq.8h and log₁₀(β_N/3), respectively; ɛ is the model’s random error (residual) term. The regression analysis obtains the optimal values for b₀, b_1, and b₂ that minimizes ε, and λ = b₂/b₁. The dependent variable is actual NIPTS₃₄₆, that is, the average of actual NIPTS at 3, 4, and 6 kHz. The model was validated by comparing the difference between actual NIPTS₃₄₆ and estimated NIPTS₃₄₆ (with or without kurtosis adjustment) using the ISO 1999:2013 formula.

Statistical Analysis

Noise exposure level (L_Aeq,8h), duration of exposure, kurtosis, age, and sex were summarized in Table 2 as count, mean, and standard deviation or range (minimum to maximum). The actual measured NIPTS₃₄₆ and the difference between the actual NIPTS₃₄₆ and the ISO 1999 predicted NIPTS₃₄₆ were analyzed using a mixed model where the NIPTS₃₄₆ or the NIPTS₃₄₆ difference served as the dependent variable, and noise level (L_Aeq,8h), kurtosis, and their interaction served as independent variables. The group means for noise level and kurtosis, and their 95% confidence interval (CI) were calculated. A significance level of p < 0.05 was applied to the overall test for all factors and their interaction. Pairwise comparisons were processed among NIPTS₃₄₆ and kurtosis groups. For all pairwise comparisons, Bonferroni adjustment was applied in evaluating significance. The analyses were performed using IBM® SPSS Statistics (version 22).

TABLE 2.

A breakdown of typical noise sources, sex, average age, noise exposure level, and exposure duration corresponding to workers in three noise kurtosis categories

Kurtosis Category	Typical Noise Sources	Participants			Noise Exposure
		Male (n)	Female (n)	Age (yrs)	Duration (yrs)	LAeq (dBA)
3 ≤ βN ≤ 10	Spinning, weaving, pulping	377	140	36.4 ± 9.4	9.9 ± 7.6	88.6 ± 4.6
10 < βN ≤ 50	Punching, stamping, metalworking, heat treating, assembly, drilling	1125	412	36.3 ± 9.0	9.7 ± 7.8	87.2 ± 5.1
βN > 50	Woodworking, nail gunning, assembly	463	84	34.6 ± 9.9	6.5 ± 6.5	87.9 ± 4.8

Note: age, duration, and L_Aeq: mean±1 SD.

RESULTS

Demographics of Experimental Groups

The 1297 participants in the control group had no history of exposure to high-level workplace noise. They are factory office workers, technology company programmers, and health care workers working in environments with noise levels below 70 dBA. Table 1 shows selected values of the statistical distribution of hearing threshold levels in decibels of the control group according to frequency classified by age and sex. The median hearing thresholds were used to estimate the actual NIPTS of noise-exposed workers.

Data were collected on 2601 workers exposed to various industrial noises. The workers were classified into three groups according to the kurtosis value of noise they were exposed to. Table 2 presents a breakdown of typical noise sources, sex, average age, noise exposure level, and exposure duration corresponding to workers in three noise kurtosis categories.

Scatter Plots of NIPTS₃₄₆ Raw Data

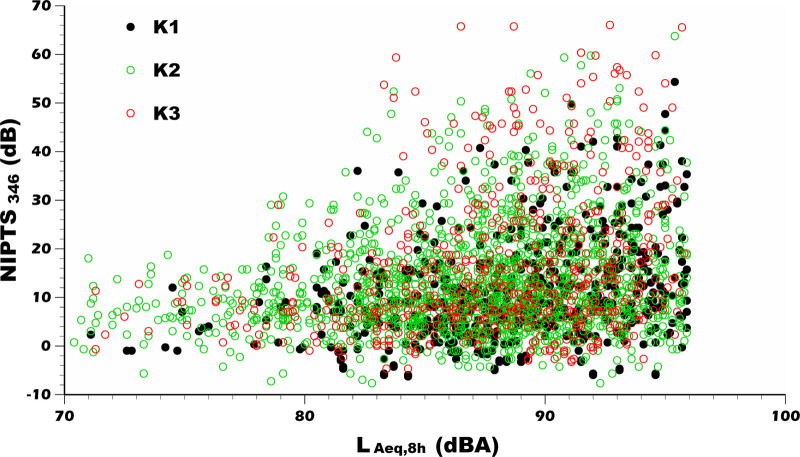
Some perspective on the relationship between NIPTS₃₄₆ and L_Aeq,8h can be obtained by plotting actual NIPTS₃₄₆ for each noise exposure level (from 70 to 95 dBA). Figure 1 shows the resulting scatter plot for the entire data pool of noise-exposed workers (n = 2601). Large variations were observed for each kurtosis category across the L_Aeq,8h range.

Fig. 1.

Scatter plot showing noise-induced hearing loss (NIPTS₃₄₆) as a function of noise exposure level L_Aeq,8h. The kurtosis value ranges are K₁:3 ≤ β_N ≤ 10; K₂: 10 < β_N ≤ 50; K₃: β_N > 50.

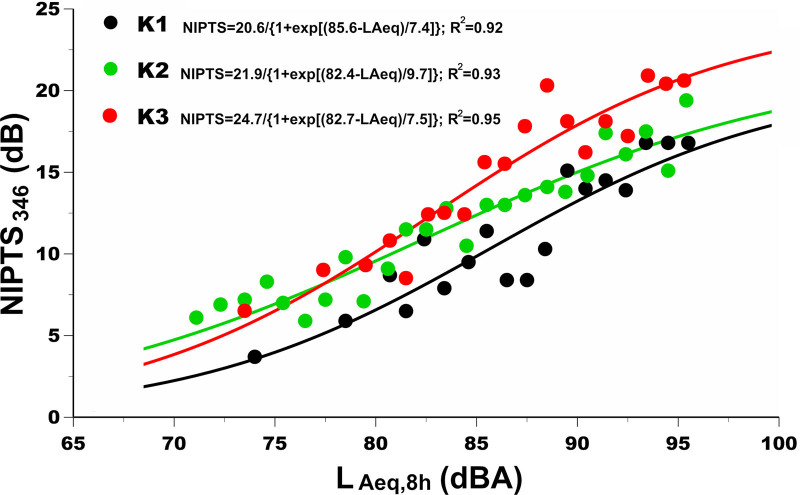
The effects of different kurtosis categories are evident when the noise exposure level (L_Aeq.8h) measurements are collapsed into 1-dB bins, and the mean noise level within each bin is plotted against the mean actual NIPTS₃₄₆ for that bin. These effects are shown in Figure 2. In this figure, the abscissa represents the mean L_Aeq.8h, and the ordinate is the mean NIPTS₃₄₆ for the data points belonging to a specific kurtosis category within the 1-dB bin. The figure clearly shows a positive relationship between the L_Aeq.8h and NIPTS₃₄₆ for each kurtosis category. Because the data shown in Fig. 2 suggest both linear and nonlinear relations among the L_Aeq,8h and NIPTS₃₄₆, a logistic function that would allow nonlinear and nearly linear descriptions of the data of the form NIPTS = a/[1+e^(b-LAeq)/c] was chosen to describe the results of the three kurtosis categories. For the appropriately set parameters a, b, and c, this relation allows NIPTS to approach a positive number close to zero as L_Aeq,8h approaches 0 dBA, and NIPTS to a ceiling value as L_Aeq,8h approaches a high level (e.g., greater than 95 dBA). Note: As can be seen in Figure 1, for the K₁ group (solid black circles), due to the small sample size of L_Aeq.8h when it is less than 80 dBA, there are not enough samples in the 1-dB interval, so the samples of L_Aeq.8h in the 70 to 79 dBA region are divided into two groups to ensure a certain number of samples in each group. The samples of L_Aeq,8h in the range of 70 to 75 dBA were averaged to get an average point, and the data samples in the range of 76 to 79 dBA were averaged to get another data point, as shown in Figure 2. Similarly, for the K₃ group (hollow red circles in Fig. 1), sample averages within the range of 70 to 75 dBA and 76 to 78 dBA were taken to obtain two data points with L_Aeq,8h less than 79 dBA in the K₃ group. For the K₂ group (hollow green circles in Fig. 1), since there are enough sample points at each 1-dB interval, all the average points in Figure 2 can be obtained by averaging the sample points at each 1-dB interval.

Fig. 2.

Scatterplot showing noise-induced hearing loss (NIPTS₃₄₆) as a logistic function of noise exposure level L_Aeq,8h, and kurtosis category using 1-dB noise-level bins. The kurtosis value ranges are K₁:3 ≤ β_N ≤ 10; K₂: 10 < β_N ≤ 50; K₃: β_N > 50.

Multiple Linear Regression

Initially, the regression analyses used the average NIPTS at 3, 4, and 6 kHz as the dependent variable, with age, sex, duration, L_Aeq,8h, and log₁₀(β_N/3) as the independent variables. As mentioned above, actual NIPTS of each noise-exposed worker were obtained by subtracting normal median hearing threshold levels by age- and sex-matched populations of the control group. As a result, the correlation between NIPTS and age or sex was reduced. The inclusion of age and sex as independent variables did not significantly improve the model fitting using the multiple linear regression analysis. The data points in Figure 2 were used for multiple regression. As shown in Figure 2, the 1-dB bin analysis method highlighted the relationship between L_Aeq.8h and NIPTS₃₄₆ functions under each kurtosis category but smoothened out the influence of exposure duration on exposure duration multiple linear regression. Consequently, the inclusion of the duration as an independent variable did not significantly improve the model’s performance. Eventually, L_Aeq.8h and log₁₀(β_N/3) were used as independent variables of the multiple linear regression equation, controlling for the effects of age, sex, and exposure duration. Table 3 shows the results of two regression models, one using L_Aeq,8h as the exposure variable and the other using the kurtosis-adjusted L_Aeq,8h. It is clear from Table 3 that the L_Aeq,8h alone (Model 1 in Table 3) is a fairly strong predictor of hearing loss with a coefficient of determination R² = 0.75, whereas the kurtosis-adjusted model (Model 2 in Table 3) has an R² = 0.88 (an increase of 0.13 over the R² value in Model 1). The difference in R² between the two models is significant (p < 0.001). This significant change in the overall model fit indicates that the model attribution of hearing loss has an important change from L_Aeq,8h to kurtosis-adjusted L_Aeq,8h (i.e.,$\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$). In other words, the kurtosis-adjusted L_Aeq,8h can significantly improve the accuracy of noise-induced hearing loss assessment. Using the human data collected in China, the coefficients b₁ and b₂ in Model 2 were obtained as 0.56 and 3.64, respectively. Consequently, the adjustment coefficient can be calculated as λ = b₂/b₁ = 6.50.

TABLE 3.

Results of regression models using L_Aeq,8h and kurtosis-adjusted L_Aeq,8h to estimate NIPTS₃₄₆

	Coefficients B	λ (b2/b1)	t Stat	p value	B Lower 95%	B Upper 95%
Model 1: NIPTS346 = b0+b1LAeq,8h		N/A			R2 = 0.75	F = 182.20
Intercept	−36.25		−10.02	<0.0001	−43.30	−29.02
LAeq	0.57		13.50	<0.0001	0.49	0.66
Model 2: NIPTS346 = b0+b1LAeq,8h+b2log10(βN/3)		6.50			R2 = 0.88	F = 225.81
Intercept	−38.64		−15.41	<0.0001	−43.66	−33.62
LAeq	0.56		19.31	<0.0001	0.50	0.62
log10(βN/3)	3.64		8.22	<0.0001	2.79	4.40

Note: the effects of age, sex, and duration were controlled in the models.

Application of Kurtosis-Adjusted L_Aeq,8h to the Estimation of NIPTS

The kurtosis-adjusted L_Aeq,8h (i.e.,$\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$) was used to estimate NIPTS₃₄₆, and the results were compared with those from unadjusted L_Aeq,8h. According to the above multiple linear regression results, the following equation was used for $\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$:

$$\text{L}{\text{'}}_{Aeq,8\text{h}}=L_{Aeq,8h}+6.5*lo{g}_{10}({\beta }_N/3)$$ (7)

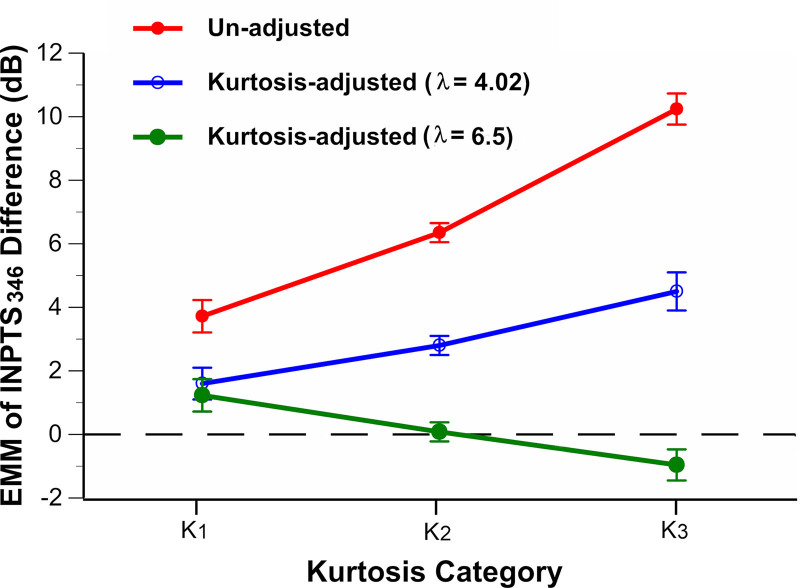
The NIPTS₃₄₆ of each individual noise-exposed worker was estimated by ISO prediction formula [Eq. (5)] using either L_Aeq,8h (un-adjusted) or $\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$ (kurtosis-adjusted). The values of estimated NIPTS₃₄₆ using L_Aeq,8h or $\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$ were compared with corresponding actual NIPTS₃₄₆, respectively. The mixed model analysis showed that there was a significant adjustment effect (df = 1, F = 346.6, p < 0.001), and kurtosis by adjustment interaction effect (df = 2, F = 40.3, p < 0.001) on the NIPTS₃₄₆ difference. The estimated marginal mean (EMM) for each group is summarized in Table 4.

TABLE 4.

The estimated marginal means and standard errors of NIPTS₃₄₆ difference between the actual measured NIPTS₃₄₆ and the ISO 1999 predicted NIPTS₃₄₆ for BAA and kurtosis by BAA groups

Effect	Group	Estimated Mean	Standard Error	95% Confidence Interval
				Lower Bound	Upper Bound
BAA*	Unadjusted (UA)	6.77	0.26	6.27	7.27
	KA	0.03	0.26	−0.47	0.53
Kurtosis×BAA†	K1×KA	1.23	0.51	0.23	2.23
	K1×UA	3.72	0.51	2.73	4.72
	K2×KA	0.08	0.29	−0.50	0.66
	K2×UA	6.35	0.29	5.77	6.92
	K3×KA	−0.96	0.49	−1.93	0
	K3×UA	10.24	0.49	9.27	11.21

BAA, before-and-after-adjustment; KA, Kurtosis-adjusted.

^*p value for NIPTS₃₄₆ difference between KA and UA is <0.001.

^†p values for NIPTS₃₄₆ difference between (K_i×KA) and (K_i×UA) pairs (i = 1, 2, and 3) are <0.001.

Figure 3 displays the EMM of underestimated NIPTS₃₄₆ for each kurtosis level before and after kurtosis adjustment. The results show that, for unadjusted L_Aeq.8h, the ISO 1999 formula underestimates NIPTS₃₄₆ by an average of 3.72 dB for kurtosis group K₁; by 6.35 dB for group K₂; 10.24 dB for group K₃. After the noise levels (L_Aeq,8h) were adjusted for kurtosis using Equation 7, the ISO 1999 predictions underestimated NIPTS by an average within 1.23 dB for kurtosis group K₁; within 0.08 dB for group K₂; and within -0.96 dB for group K₃. Figure 3 demonstrates that a kurtosis-adjusted noise exposure level (i.e.,$\text{L}{\text{'}}_{\text{Aeq},8\text{h}}$) using adjustment coefficient of λ = 6.5 can effectively correct the ISO formula’s underestimates due to complex noise with high kurtosis values. As a comparison, another adjustment coefficient λ = 4.02, derived from chinchilla data by Goley et al. (2011), was used to calculate kurtosis-adjusted L_Aeq.8h. The EMM of underestimated NIPTS₃₄₆ for each kurtosis level after kurtosis adjustment using λ = 4.02 was also shown in Figure 3. The results showed that after the noise levels were adjusted for kurtosis using λ = 4.02, the ISO 1999 predictions underestimated NIPTS by an average of 1.6 dB for kurtosis group K₁; by 2.8 dB for group K₂; and by 4.5 dB for group K₃. While kurtosis-adjusted L_Aeq.8h using λ = 4.02 could correct underestimations of NIHL due to complex noise exposure to a certain extent, its correction degree is insufficient for human data.

Fig. 3.

The estimated marginal mean of underestimated NIPTS₃₄₆ by ISO 1999:2013 model for three kurtosis levels under un-adjusted and kurtosis-adjusted noise levels. Error bars: standard error. The kurtosis value ranges are K₁:3 ≤ β_N ≤10; K₂: 10 < β_N ≤ 50; K₃: β_N > 50.

DISCUSSION

The Classification of Noise Kurtosis

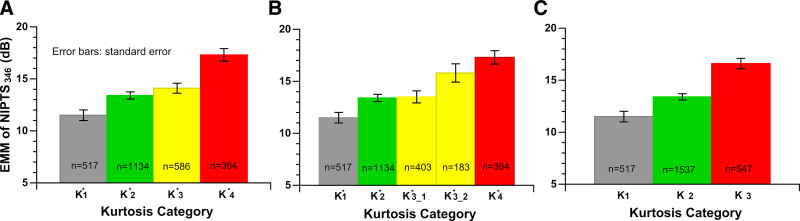
One method to analyze the effect of kurtosis on NIHL is to make a reasonable clustering of data according to the kurtosis values of noise exposed by individual workers and then compare the differences of NIPTS₃₄₆ in each data class under a similar noise level. The data used in this study between 85 and 95 dBA are the same as those used in the previous study (Zhang et al, 2021). The kurtosis (β) was classified into four categories in Zhang’s study (2021), that is, 3 ≤ β ≤ 10 (${\text{K}}_1^{*}$), 10 < β ≤ 30 (${\text{K}}_2^{*}$), 30 < β ≤ 75 (${\text{K}}_3^{*}$), and β > 75 (${\text{K}}_4^{*}$). In this study, we initially divided data into the same four categories as above. Figure 4A shows the EMM of NIPTS₃₄₆ obtained from these four groups. For group${\text{K}}_1^{*}$, the EMM of NIPTS₃₄₆ was 11.5 dB, which was significantly lower than the 13.4 dB in group ${\text{K}}_2^{*}$ (p = 0.01), the 14.1dB in group ${\text{K}}_3^{*}$ (p = 0.001), and the 17.3 dB in group ${\text{K}}_4^{*}$ (p < 0.001). There was no significant difference in NIPTS₃₄₆ between group ${\text{K}}_2^{*}$ and group ${\text{K}}_3^{*}$ (p = 0.24), but their EMMs of NIPTS₃₄₆ were significantly smaller than that of group ${\text{K}}_4^{*}$ (p < 0.001 for both ${\text{K}}_2^{*}$-${\text{K}}_4^{*}$ and ${\text{K}}_3^{*}$-${\text{K}}_4^{*}$ group pairs). Thus, the groups ${\text{K}}_2^{*}$ and ${\text{K}}_3^{*}$ can be considered to be merged as one group. Due to the high kurtosis values that were included in group ${\text{K}}_3^{*}$ and the large span of this group, group ${\text{K}}_3^{*}$ was further divided into two subgroups:30 < β ≤ 50 (${\text{K}}_{3\_1}^{*}$) and 50 < β ≤ 75 (${\text{K}}_{3\_2}^{*}$), as shown in Fig. 4B. The EMM of NIPTS₃₄₆ in group ${\text{K}}_{3\_1}^{*}$ was 13.5 dB, which was very close to that of group ${\text{K}}_2^{*}$ (p = 0.9), while EMM of NIPTS₃₄₆ in group ${\text{K}}_{3\_2}^{*}$ was 15.8 dB, which was significantly higher than that of group ${\text{K}}_{3\_1}^{*}$ (p = 0.03), but there was no significant difference between group ${\text{K}}_4^{*}$ and group ${\text{K}}_{3\_1}^{*}$ (p = 0.06). Thus, it is reasonable to merge ${\text{K}}_2^{*}$ and ${\text{K}}_{3\_1}^{*}$ into one group and merge ${\text{K}}_{3\_2}^{*}$ and ${\text{K}}_4^{*}$ into another group. Eventually, the three groups of kurtosis were classified as shown in Figure 4C, that is, 3 ≤ β ≤ 10 (K₁);10 < β ≤ 50 (K₂), and β≥50 (K₃). The EMMs of NIPTS₃₄₆ in these three groups were 11.5, 13.4 dB, and 16.6 dB, respectively. The NIPTS₃₄₆ differences among these three groups were statistically significant, with p values as follows: p = 0.007 for K₁- K₂ group pair, p < 0.001 for K₁ to K₃ and K₂ to K₃ group pairs. Based on the above kurtosis classification, the combined effects of noise level and kurtosis on high-frequency NIPTS were analyzed, and the Goley model was studied.

Fig. 4.

The estimated marginal mean of NIPTS₃₄₆ at each kurtosis category. A, Four kurtosis categories (${\text{K}}_1^{*},{\text{K}}_2^{*},{\text{K}}_3^{*},\text{and}{\text{K}}_4^{*}$) in Zhang et al. (2021); (B) five kurtosis categories; and (C) three kurtosis categories (K₁, K₂, and K₃) used in the current study. Error bars: standard error. n: number of workers in the kurtosis category.

Types of Work and Their Kurtosis Distributions

Table 5 displays the kurtosis distribution information of some work tasks in the manufacturing industry and corresponding correction values for measured L_Aeq,8h. The kurtosis value of a work type in Table 5 was calculated by averaging the kurtosis of individuals of the same work type. The correction value was calculated by 6.5*log₁₀(β/3). Table 5 lists the mean, standard deviation, and maximum and minimum values of each work type’s kurtosis values. As shown in Table 5, the primary sources of steady-state noise are textile mills and paper mills. However, non-Gaussian complex noise is more common than steady-state noise in the manufacturing industry. Among these noises, the complex noise with a kurtosis of 10 < β_N ≤ 50 accounts for the majority, such as stamping, drilling, casting, metal processing, etc. In this study, the highly impulsive complex noises (β_N > 50) mainly existed in the workplaces of wood processing, nail gunning, and assembly in various manufacturing plants (including automobile, furniture, and electronic machinery manufacturers). It is worth noting that many work types have a wide range of kurtosis values, some spanning two kurtosis categories, some even three kurtosis categories. Examples include stamping, drilling, casting, metalworking, etc., with kurtosis values ranging from 7 to 86. The kurtosis and level of noise received by individual workers can largely depend on such factors as the position of work, the frequency of tool use, and the intensity of background noise. Therefore, the kurtosis of the noise exposure of individual workers should be calculated according to the actual noise exposed for each worker.

TABLE 5.

The kurtosis distribution information of some work types in the manufacturing industry [n: the number of workers investigated in the kurtosis analysis in the corresponding work type; correction value = 6.5*log₁₀(β/3), where the β is the mean of the kurtosis values of all the workers in that work type]

Industry	Work Type	Kurtosis (β)	Correction (dB)	Unadjusted LAeq.8h (dBA)
		Mean±SD (Min–Max)		Mean±SD (Min–Max)	n
K1 (3 ≤ βN ≤ 10)
Textile mill	Spinning	3.3 ± 2.1 (3.0–9.4)	0.3	98.7 ± 2.3 (93.8–102.0)	109
	Weaving	4.1 ± 3.0 (3.1–11.7)	0.9	92.4 ± 2.4 (85.9–95.6)	49
	Knitter	5.2 ± 2.2 (3.3–17.5)	1.6	97.5 ± 1.8 (93.3–104.9)	84
	Mechanist	8.6 ± 4.6 (4.0–17.8)	3.0	93.5 ± 5.0 (84.9–98.4)	14
Spandex	Winding	9.7 ± 4.4 (3.2–23.7)	3.3	95.8 ± 4.7 (82.3–104)	52
Papermill	Defibrinating	6.6 ± 2.8 (4.3–8.4)	2.2	87.1 ± 2.2 (84.5–90.4)	7
	Pulping	9.0 ± 3.8 (3.0–15.4)	3.1	89.0 ± 4.1 (82.2–96.9)	28
	Rewinder	8.6 ± 2.3 (3.5–12)	3.0	88.3 ± 2.5 (84.9–92.5)	11
K2 (10 < βN ≤50)
Auto brake pad manufactory	Assemblyman	36.3 ± 16.1 (9.6–72.8)	7.0	85.6 ± 5.2 (71.7–96.7)	57
	Machining	32.6 ± 28.1 (8.6–141.9)	6.7	89.0 ± 5.2 (77.4–103.8)	100
Auto parts manufactory	Thread rolling	11.2 ± 4.9 (3.9–25.3)	3.7	89.5 ± 2.8 (82.5–94.6)	41
	Depositing	13.7 ± 7.1 (5.0–32.1)	4.3	88.8 ± 3.0 (83.0–97.7)	19
	Tapping	15.2 ± 7.0 (6.8–27.9)	4.6	90.1 ± 1.7 (86.5–92.9)	14
	Numerical control machine	15.5 ± 9.4 (7.8–32.0)	4.6	87.0 ± 5.5 (79.3–93.1)	6
	Spot welding	16.1 ± 5.0 (6.6–22.5)	4.7	90.2 ± 2.0 (87–93.5)	11
	Lathe worker	16.6 ± 13.7 (4.1–63.3)	4.8	85.9 ± 4.3 (72.8–92.4)	21
	Drawing wire	17.4 ± 8.4 (7.0–32.5)	5.0	88.9 ± 4.1 (82.9–98.0)	16
	Packing	21.2 ± 10.5 (6.4–43.2)	5.5	85.2 ± 4.7 (73.6–91.0)	33
	Sorting	22.2 ± 14.8 (4.2–81.3)	5.6	87.0 ± 3.7 (78.7–93.6)	38
Automotive fasteners	Electroplating	17.3 ± 12.7 (4.1–63.4)	4.9	89.9 ± 6.4 (76–103.8)	31
	Cold heading	25.2 ± 16.9 (4.7–79.7)	6.0	90.4 ± 5.2 (80.9–104.7)	60
	Polishing	25.7 ± 16 (4.8–54.8)	6.1	92.1 ± 6.4 (80.7–100.3)	10
	Heat treatment	27.3 ± 18.7 (6.5–78)	6.2	89.9 ± 4.1 (82.5–99.9)	31
	Automatic lathe work	29.6 ± 17 (6.3–67.6)	6.5	89.2 ± 4.8 (81.5–96.7)	16
Baby carriage manufactory	Punch	15.6 ± 5.4 (7.5–29.0)	4.6	93.9 ± 3.2 (87.6–98.6)	42
	Stamping	28.4 ± 18.4 (7.8–85.9)	6.3	91.7 ± 8.2 (73.5–105.4)	85
Commercial vehicle body factory	Craneman	24.0 ± 20.2 (3.5–88.7)	5.9	90.6 ± 6.0 (78.6–104.3)	25
	Spot welding	26.6 ± 21.6 (5–104.4)	6.2	89.8 ± 3.3 (83.7–97.8)	23
	Electric welder	40.0 ± 29.4 (3.4–187.1)	7.3	91.5 ± 7.4 (77.3–104.1)	79
Electrical appliance factory	Stretching	26.3 ± 9.7 (15.8–47.7)	6.1	87.6 ± 3.1 (82.9–95.6)	12
	Sanding	26.9 ± 20.1 (6.1–76.8)	6.2	87.1 ± 5.0 (75.8–94.6)	9
Electrical appliance factory	Forming	27.8 ± 12.6 (12.9–50.4)	6.3	79.8 ± 3.8 (75.3–88.0)	8
	Assemblyman	50.0 ± 27.7 (19.7–91.8)	7.9	76.4 ± 2.5 (73.0–80.1)	18
Final assembly plant for automobiles	Machining	19.7 ± 8.9 (8.1–34.6)	5.3	88.8 ± 4.7 (82.7–98.6)	9
	Assemblyman	28.0 ± 25.2 (3.4–196.2)	6.3	90.9 ± 5.0 (79.8–105.6)	221
Hardware factory	Sand blast	11.4 ± 2.9 (8.1–15.8)	3.8	90.1 ± 2.1 (87.5–93.5)	8
	Stamping	20.2 ± 11.0 (7.1–48.5)	5.4	87.5 ± 4.2 (76–93.5)	20
	Benchwork	33.2 ± 24.3 (10.0–92.4)	6.8	83.2 ± 5.3 (75–92.7)	11
Heavy truck engine factory	Casting	21.2 ± 16.1 (8–55.7)	5.5	89.7 ± 9.0 (81.9–113)	10
Hydroelectric	Drilling	21.3 ± 10.6 (7.2–39.1)	5.5	90.2 ± 5.5 (81.5–99.7)	15
	Cold operating	42.4 ± 18.9 (13.4–78.4)	7.5	95.6 ± 3.6 (90.3–100.3)	8
	Modeling	42.8 ± 18.1 (12.0–75.3)	7.5	88.9 ± 6.2 (73.5–94.6)	10
Iron and steel plant	Steel rolling	14.4 ± 9.1 (4.6–58.9)	4.4	90.5 ± 5.3 (76.9–96.7)	41
	Finishing	16.8 ± 8.2 (6.1–42.4)	4.9	88.4 ± 4.3 (74.2–99.8)	21
	Loading	22.4 ± 4.1 (13.3–25.1)	5.7	86.7 ± 2.9 (83.3–90.6)	8
Machinery	Grinding	26.2 ± 10.4 (16.1–58.7)	6.1	84.6 ± 6.4 (72.6–93.8)	13
	Metal processing	47.6 ± 19.6 (26.2–80.5)	7.8	82.2 ± 2.3 (79.0–85.4)	7
Machinery and electric	Assemblyman	37.8 ± 28.6 (7.8–240.7)	7.1	86.2 ± 3.2 (77.7–98.0)	147
K3 (βN > 50)
Electrical appliance	Wiring	53.7 ± 41.7 (16.2–156.6)	8.1	75.6 ± 2.3 (71.2–79.2)	10
Furniture manufactory	Frame nailing	81.7 ± 44.3 (24.9–158.5)	9.3	89.5 ± 5.4 (76.3–100.5)	51
	Woodworking	119.2 ± 71.6 (21.3–306.8)	10.4	88.5 ± 3.6 (81.9–95.4)	23
	Assemblyman	102.4 ± 69.6 (42.2–250)	10.0	89.2 ± 4.3 (83.9–96.9)	12
	Nail gunning	246.5 ± 172.2 (31.5–925.5)	12.4	89.0 ± 4.4 (76.7–98.8)	213
Grid structure	Assemblyman	103.0 ± 69.7 (34.3–315.6)	10.0	93.8 ± 3.5 (87.3–101)	26
Kitchen and bath manufacturing	Assemblyman	69.7 ± 62.9 (17.4–177.2)	8.9	81.6 ± 2.3 (77.9–85.0)	13

In this study, most workers did not wear hearing protection devices, and a small population of workers with high noise exposure (L_Aeq~95 dBA) may wear devices. A recent study of 385 workers at an automobile manufacturing plant in China (Gong et al. 2021) found that earplug use had no significant effect on the prevalence of high-frequency hearing loss among study participants, despite the requirement to wear earplugs at all times during work. There are many reasons for this, such as poor training, poor fit, and workers not wearing earplugs all the time. Workers in this study had the same problem even when they used earplugs. Therefore, the overall reliability of the dose-response relationship was not affected by the fact that very few people in this data had worn earplugs.

Based on the data analysis of 2601 workers in this study, 19.9% of workers were exposed to steady-state noise (3 ≤ β_N ≤ 10), 59.1% of workers to complex noise with low or moderate impulsive components (10 < β_N ≤ 50), and 21% of workers to complex noise with high kurtosis (β_N > 50). Because non-Gaussian complex noise is common in the manufacturing industry, and the current noise standards (e.g., ISO 1999:2013) are based solely on steady-state noise data, kurtosis adjustment is a promising method to correct the noise level so as to accurately identify the risk of NIHL.

The Combined Effect of Noise Level and Kurtosis on NIHL

A logistic function was used to fit the dose-response data shown in Figure 2 for three kurtosis categories. The general expression of the logistic function is as follows:

$$NIPT{S}_{346}=\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$(1+e^{(b-L_{Aeq,8h})/c})$}\right.$$ (8)

Figure 2 shows that there was a good relationship between L_Aeq,8h and NIPTS₃₄₆ using logistic function fitting in each kurtosis category (coefficient of determination R² > 0.9 for all three curves). For the sake of discussion, the three equations reflecting L_Aeq,8h and NIPTS₃₄₆ were named after the kurtosis category, which is the K₁ curve, K₂ curve, and K₃ curve, respectively.

The K₁ curve (the black line) in Figure 2 reflects the relationship between continuous steady-state noise and high-frequency hearing loss (NIPTS₃₄₆), and its fitting curve equation is$NIPT{S}_{346}=20.6/[1+e^{(85.6-L_{Aeq,8h})/7.4}]$. Based on this equation, the NIPTS₃₄₆ can be calculated when L_Aeq,8h is at a specific level. Considering the situation when L_Aeq,8h = 75 dBA, where the calculated value of NIPTS₃₄₆ is 3.9 dB, this is very close to the actual value (i.e., 3.7 dB at L_Aeq.8h = 74 dBA) in Fig. 2. When L_Aeq,8h = 78 dBA, the calculated NIPTS₃₄₆ is 5.4 dB, showing an increased hearing shift (hearing loss) at the high frequencies, which is consistent with ISO 1999:2013. The ISO 1999:2013 specifies a damage risk threshold L_Aeq,8h equal to 75 dBA (at 4 kHz); however, NIPTS is not predicted until the exposure level reaches 78 dBA. When L_Aeq,8h = 80 dBA, the calculated value of NIPTS₃₄₆ will be 6.6 dBA according to the K₁ curve. The exposure level of 80 dBA was set as the action level (need to wear hearing protection devices) by the European Union (Directive 2003/10/EC). When the L_Aeq,8h equals 85 dBA, the calculated NIPTS₃₄₆ is 9.9 dB. High-frequency hearing loss is apparent at this level. This level was set as recommended exposure level (REL) by the US National Institute for Occupational Safety and Health (NIOSH 1998) and Action Level by the U.S. Occupational Safety and Health Administration (OSHA 1983).

The K₂ curve (the green line) in Figure 2 presents the relationship between non-Gaussian noise with low or moderate impulsive components (10 < β ≤ 50) and high-frequency hearing loss (NIPTS₃₄₆). The equation of this curve is: $NIPT{S}_{346}=21.9/[1+e^{(82.4-L_{Aeq,8h})/9.7}]$. As shown in Figure 2, when L_Aeq,8h = 70 dBA, the calculated value of NIPTS₃₄₆ is 4.7 dB. When the L_Aeq,8h is 75 dBA, the calculated value of NIPTS₃₄₆ is 7 dB. From Figure 2, it can be seen that the actual NIPTS₃₄₆ values of group K₂ were all about 7 dB within the range of 72 to 77 dBA, which is near twice the magnitude of the shifts at this level in group K₁. When the L_Aeq,8h equals 80 dB, the calculated value of NIPTS₃₄₆ is 9.6 dB, indicating that the non-Gaussian complex noise had begun to produce significant NIPTS₃₄₆ at this exposure level. It is worth noting that when the exposure level of complex noise is 80 dBA, and the kurtosis value was greater than ten and less than 50, the high-frequency hearing loss caused by complex noise is comparable to that induced by continuous steady state noise at 85 dBA (NIPTS₃₄₆ = 9.6 versus 9.9 dB). Therefore, for complex noise (β > 10), the NIOSH noise exposure REL and OSHA Action Level may need to be lowered from 85 dBA to 80 dBA in the United States and elsewhere. It is worth noting that Smoorenburg (2003) suggested an exposure limit of 80 dBA for impulse sounds. An interesting trend in the K₁ and K₂ curves is that they converge L_Aeq,8h increases. When L_Aeq,8h ≥100 dB, the difference of NIPTS₃₄₆ between the curves is only 0.3 dB. This convergence suggests that hearing loss from complex noise with moderate kurtosis values (10 < β ≤ 50) tends to produce a comparable level of hearing loss when the noise level reaches a fairly high level (100 dBA). However, when L_Aeq,8h was less than 100 dBA, especially in the range of 70 to 90 dBA, for a fixed exposure level, the NIPTS₃₄₆ in group K₂ was significantly higher than that in group K₁.

The K₃ curve (the red line) in Figure 2 demonstrates the relationship between NIPTS₃₄₆ and complex noise with high kurtosis values (β > 50). The fitting curve equation is as follows: $NIPT{S}_{346}=24.7/[1+e^{(82.7-L_{Aeq,8h})/7.5}]$. When L_Aeq,8h is equal to 70 dBA, the calculated value of NIPTS₃₄₆ is 3.8 dB. When L_Aeq,8h = 75 dBA, the calculated NIPTS₃₄₆ is 6.5 dB. It is worth noting that the K₃ curve and K₂ curve intersect around L_Aeq,8h = 78 dBA. When the noise level is greater than 78 dBA, the NIPTS₃₄₆ difference between groups K₃ and K₂ becomes larger and larger. Especially when L_Aeq,8h ≥ 85 dBA, the NIPTS₃₄₆ in group K₃ was significantly higher than that in groups K₂ and K₁. At the range between 85 and 95 dBA, the higher the noise level, the greater the difference in NIPTS₃₄₆. According to the equations of the three fitting curves, it can be found that when L_Aeq.8h is greater than 100 dBA, the NIPTS₃₄₆ difference between K₃ group and K₁/K₂ group tends to be stable (about 4 dB).

It is worth mentioning that, as we pointed out in our previous study, kurtosis is an adjunct metric to energy in the evaluation of NIHL (Qiu et al. 2006); that is to say, energy is the primary metric. If the noise energy does not reach a certain “threshold,” then kurtosis will not have much effect on NIHL. As can be seen from the previous discussion, if L_Aeq,8h is below 70 dBA, neither continuous noise nor complex noise can produce significant NIPTS₃₄₆. Therefore, we can infer that the noise level of L_Aeq,8h = 70 dBA is the “threshold” for the effect of kurtosis. When L_Aeq,8h < 70 dBA, the value of kurtosis does not have an impact on NIHL evaluation.

Animal Versus Human Adjustment for Kurtosis

Animal and epidemiological studies have shown that the temporal structure of noise (kurtosis) plays a vital role in NIHL evaluation (Lei et al. 1994; Qiu et al. 2006; Hamernik et al. 2007; Zhao et al. 2010). Based on these animal and epidemiological studies’ findings, Goley (2011) proposed a scheme to correct the measured noise level (L_Aeq,8h) using kurtosis and derived the adjustment coefficient of λ = 4.02 from an analysis of chinchilla noise-exposure data. However, it is essential to note that the NIHL results observed in chinchillas are different from those observed in humans, where chinchillas are more susceptible to developing hearing loss following noise exposures. Therefore, the adjustment coefficient (λ) obtained from the chinchilla noise data does not necessarily apply to humans. As a comparison, we directly applied λ = 4.02 to workers’ data, and the results are shown in Figure 3. It can be seen that, although using this coefficient can reduce the underestimation of NIHL caused by complex noise to some extent, for example, the K₂ group’s underestimation was reduced from the original average of 6.35 dB to 2.8 dB, the underestimation degree of K₃ group was reduced from the original average of 10.24 dB to 4.5 dB, but the degree of hearing damage caused by noise with high kurtosis value was still vastly underestimated.

Since human hearing is not as sensitive as that of chinchilla, it can be seen from adjustment formula (7) that to suffer a fixed NIHL, the adjustment coefficient of the human model should be larger than that of chinchilla. In other words, humans need to receive more noise energy than chinchillas do to suffer a comparable NIHL. Using data collected from the industrial and non-noise population in China and the ISO 1999 prediction formula for NIPTS, we derived an optimum adjustment coefficient (λ = 6.5) that could be applied practically to protect the hearing of workers by using Goley’s correction formula. As can be seen from Figure 3, after the adjustment of L_Aeq,8h by kurtosis, (1) for workers exposed to steady state noise (β ≤ 10, group K₁), the underestimation of NIPTS₃₄₆ by ISO 1999 decreased significantly from 3.72 dB to 1.23 dB; (2) for workers exposed to complex noise with medium kurtosis (10 < β_N ≤ 50, group K₂), the underestimation of NIPTS₃₄₆ by ISO 1999 decreased significantly from 6.35 dB to 0.08 dB. It is clear that after kurtosis adjustment, ISO 1999 was able to accurately predict high-frequency hearing loss of workers in the K₂ group. Considering that most occupational noises belong to this type of non-Gaussian complex noise (59.1% of the total number of workers exposed to this type of noise in our collected data), the adjustment of kurtosis to L_Aeq is of great significance for the correction of the ISO 1999 prediction formula. (3) For workers exposed to complex noise with high kurtosis (β_N > 50, group K₃), the underestimation of NIPTS₃₄₆ by ISO 1999 decreased significantly from 10.24 dB to −0.96 dB. This result shows that kurtosis has a significant adjustment on L_Aeq with greater impulsive content (β > 50), although the overall adjustment effect is slightly over-adjusted (about 1 dB overestimation for NIPTS₃₄₆). It is worth pointing out that in the Introduction of the ISO 1999:2013 document, it is particularly emphasized that: “Throughout this International Standard, the term NIPTS is applied to changes in the noise-induced permanent threshold shift of statistical distributions of groups of people; it is not to be applied to individuals.” Similarly, the evaluation of the kurtosis adjustment effect on NIPTS in this study is also based on groups of people rather than individuals.

The reason for choosing 3 to 6 kHz for investigating NIPTS in this study is that hearing loss initially occurs mainly in this frequency range under stable noise exposure conditions. Therefore, from the perspective of hearing protection, we should study the dose-response relationship in the frequency band where it is the most sensitive to NIHL and find the optimal kurtosis adjustment algorithm to evaluate NIHL better to prevent hearing loss to the greatest extent. However, the NIPTS produced by complex noise may have different trajectories in frequency from continuous noise. In addition, NIPTS of other test frequencies (e.g., 1, 2, and 8 kHz) should also be studied, as these bands are important for speech recognition and understanding. The above topics are beyond the scope of this study and will be of great significance as future research work.

ISO 1999 Implications and Kurtosis Application

In the formulation and revision of ISO1999 over the years, researchers have taken into account the different effects of impulsive noise and steady-state noise on hearing. Therefore, in the ISO1999:1971, it was pointed out that a correction of 10-dB should be added on the basis of the measured L_Aeq for impulsive noise. In ISO 1999:1990, the correction value was changed to 5 dB. Since no specific method is given to distinguish steady-state noise from impulsive noise, such correction is arbitrary. Using the kurtosis correction formula of Equation 7 with the adjustment coefficient λ = 6.5, one may find that a correction of 5 dB corresponds to a moderately impulsive complex noise with a moderate kurtosis value (e.g., β = ~20), and a correction of 10-dB corresponds to a highly impulsive complex noise with a high kurtosis value (β > 75). Therefore, the kurtosis correction formula can be explicitly used to evaluate the hearing loss of complex noise with different impulsive components, which can help government agencies develop better noise standards and hearing protection programs. Once there is an international standard to address what should be measured, how it is measured, and how it can be applied, adding a kurtosis metric is a straightforward modification to the software included in a sound level meter or dosimeter.

Meanwhile, we should pay attention to the application scope of kurtosis. Since the kurtosis metric is an adjunct to energy in the evaluation of trauma from complex noise exposure, the validity of kurtosis depends on the noise exposure level. If the equivalent energy level of the noise exposure is low (e.g., less than 70 dB), it will not contribute to hearing loss no matter how high the value of kurtosis is. On the other hand, if the peak level of an impulse noise exceeds 140 dB SPL, the mechanisms of hearing damage include both mechanical and strains. The use of kurtosis would be questionable because there are no data about its effectiveness in this area. In order to greatly reduce the dose-response bias due to the wearing of hearing protection devices, the noise exposure range of this study was 70 to 95 dBA. In addition, due to the insufficient sample size at 70 to 78 dBA (especially for K₁ and K₃ groups), more data are needed to explore the relationship between kurtosis and energy interaction in this region.

Consideration of Race/Ethnicity Influences on the Outcomes

The database in this study was collected from a population of Chinese workers. There can be concern about the extent to which the results are applicable to populations of other non-Chinese ethnicities. Evans and Ming (1982) investigated 300 subjects exposed to industrial noise and 200 non-exposed (control) subjects in Hong Kong. Their results indicated that there was no evidence for ethnic differences between Western groups and Cantonese Chinese either for general hearing levels or for response to prolonged exposure to industrial noise. Furthermore, in the Chinese national standard document GZB 49-2014 (2014), the table showing the statistical distribution of median hearing thresholds as a function of age for an otologically screened population is the same as Annex A in ISO 1999 (1990). Also, Korea recently conducted the Korean National Health and Nutrition Examination Survey (KNHANES) 2010 to 2012 (Park et al. 2016). Median hearing thresholds between the KNHANES 2010 to 2012 and the USA National Health and Nutrition Examination Survey 1999 to 2004 were compared across age groups and gender. No difference in hearing thresholds between the USA population and the Korean population was found. From these studies, it was found that the hearing threshold of Chinese people was not significantly different from that of Americans or Westerners. It follows that the outcomes of this study can be applied to different ethnic groups.

CONCLUSIONS

In this study, the combined effects of noise exposure level and kurtosis on NIHL were analyzed by using data collected from 2601 Chinese workers exposed to various industrial noises in comparison to non-noise exposed workers (n = 1297). The Goley model was re-investigated, and the adjustment coefficient, that is, λ, was recalculated. The following conclusions can be addressed:

1. Because non-Gaussian complex noise is present in a wide range of industries, the temporal characteristics of noise (i.e., kurtosis) must be considered when evaluating occupational NIHL.

2. For non-Gaussian complex noise (β > 10), NIHL may occur when L_Aeq is greater than 70 dBA, and NIHL is pronounced when L_Aeq is larger than 80 dBA. Therefore, any singular occupational REL will be insufficient to protect the hearing of workers unless kurtosis adjustment is applied.

3. A kurtosis-adjusted L_Aeq,8h with an adjustment coefficient of 6.5 allows a more accurate prediction of high-frequency NIHL in the region of 70 dBA ≤ L_Aeq ≤ 95 dBA, which is very important for the hearing protection of workers exposed to various complex noises.

ACKNOWLEDGMENTS

The authors wish to thank those who agreed to participate in the study for their time, interest, and cooperation. Drs. David Byrne, Thais Morata, and Christa Themann from the US National Institute for Occupational Safety and Health, Dr. Alice Suter, and Mr. Barry Lempert provided helpful critiques of the manuscript. This work was sponsored by Grant 200-2015-M-63857, 200-2016-M-91922 from the National Institute for Occupational Safety and Health, USA; Grant N00014-17-1-2198 from Office of Naval Research, USA; Zhejiang province key research and development project (2015C03039), China; Zhejiang Provincial Program for the Cultivation of High-level Innovative Health Talents, China; Health Commission of Zhejiang Province (2019KY057), China. Grant No. 81771936 from National Natural Science Foundation, China; The Program of Occupational Health Risk Assessment of China NIOHP (Grant No. 13103109000160004); Preliminary Program on Occupational Health Standards of China NIOHP (No. 2021 10102); and Jiangsu Provincial Outstanding Medical Academic Leader and Innovation Team (CXTDA2017029) from the Province Health Commission of Jiangsu Province, China.