Abstract
Background
Each training program has its own internal policies and restrictions, which must be considered while developing trainee schedules. Designing these schedules is complex and time consuming, and the final schedules often contain undesirable aspects for trainees.
Objective
We developed a decision-support system (DSS) to optimally schedule daily assignments and monthly rotations for trainees. The proposed DSS aims to 1) reduce the schedule development time, 2) maximize trainee preferences for desired rotations and vacation times, and 3) ensure adaptability of the DSS across multiple graduate medical programs through a flexible design and intuitive graphical user interface.
Methods
Using mixed-integer linear programming, we developed a scheduling model that 1) maximized trainees’ preferences on specific rotations and vacation times and 2) ensured fairness by assigning equal numbers of vacation days and a balanced schedule of difficult versus easy rotations among trainees. The model was successfully implemented in the Mayo Clinic Division of Pulmonary and Critical Care for the academic year 2018–2019.
Results
Using the DSS, it took only a few minutes to produce a schedule versus several days of preparation time required by the manual process. Compared with the manually developed schedule, the DSS schedule satisfied 11% more rotation preferences and improved fairness by 19%. All trainees met duty hours in the DSS schedule compared with 83% in the manually developed schedule.
Conclusion
The proposed DSS can dramatically reduce the schedule preparation time, accommodate more of trainees’ preferences, and improve fairness in assigning rotations.
Keywords: decision-support system, rotation scheduling, mixed-integer linear programming model
Training programs have education program coordinators (EPCs), who are supervised by the program directors and develop a year-long monthly schedule to manage the rotation schedule of each trainee to ensure that the education requirements of the trainees, programs, and the Accredited College of Graduate Medical Education (ACGME) are met and to make sure that the staffing requirements of different rotations are met to ensure patient care.
The scheduling process is challenging, because training programs have internal policies and restrictions that need to be considered along with the trainees’ preferences such as requests for vacation and time off without compromising patient care. This is also time consuming and expensive, considering that an EPC spends a substantial amount of time constructing these schedules, which are also susceptible to errors. To address these challenges, we developed a decision support system (DSS), at the core of which lies a mixed-integer linear optimization model to generate optimal rotation schedules. The DSS has an intuitive Excel-based graphical user interface (GUI) that can be adopted by any graduate training program. A user can enter the raw data; in other words, individuals’ program requirements and the staffing needs of different medical units in formatted Excel tables, followed by running the optimization algorithm to obtain the optimal schedule. The model provides a comprehensive structure to assign trainees to different service rotations in a way that meets staffing needs of various rotations and satisfies the educational requirements.
Personnel scheduling problems have been studied in various industries (e.g., airlines, hotels, and hospitals). Different solution methods are proposed to solve the personnel scheduling problems, such as integer programming, goal programming, decomposition, and metaheuristics (1). Various mathematical formulations are developed to deal with these problems (2–9). Trainee scheduling is one of the application areas of personnel scheduling in health care that has not been well studied thus far.
Several studies have focused on developing mathematical models to address trainee scheduling problems; however, there is limited work to develop a DSS for the scheduling problem (10). The existing models in the literature are usually customized for a specific application; therefore, scalability and adoptability have been an issue. In addition, there are limited studies to design the DSS in a way that can be used by people who are not familiar with advanced optimization software. In this study, we developed a DSS with an Excel-based GUI to interact with the optimization model. Using mixed-integer linear programming (MILP), we formulated a novel optimization model. Our main contribution to the literature is twofold: 1) The DSS can be easily adopted by any training program because of its accessible Excel-based GUI. 2) The DSS is very flexible where the EPCs and program directors can easily change the inputs and examine the effect of changes in the output.
Methods
In this section, we formulate the fellow scheduling problem as a MILP model. We also describe how to design a DSS using the MILP model as the core engine to generate an optimal schedule.
The proposed model was implemented for the Division of Pulmonary and Critical Care Medicine (PCCM) at the Mayo Clinic in the academic year 2018–2019. The PCCM division has multiple fellowship programs. The largest is the 3-year accredited PCCM fellowship program that recruits nine to 10 fellows a year. The yearly schedule for the fellows, particularly for the intensive care unit (ICU) rotations, has to be closely scheduled with the critical care internal medicine (CCIM) fellows, critical care anesthesia (CCA) fellows, and the anesthesia residents. The participation of multiple training programs in various ICU rotations adds complexity in scheduling for the PCCM fellowship program and its fellows.
Formulation of the Fellow Scheduling Problem
Two types of schedules are considered here: monthly and daily. The monthly schedule specifies where each fellow should rotate in each month, whereas the daily schedule shows a more detailed schedule in terms of the assignment of individuals to night and day shifts and specifies which days the fellow (or fellows) will be off, on vacation, and so forth. We formulate two MILP models: The first one assigns fellows to monthly rotations, and the second model takes the output of the first model as input and optimizes the daily schedules.
The main decision of which fellow should be assigned to which rotation (shift) in a particular month (day) are formulated as binary variables. We considered two types of constraints: 1) hard constraints, which need to be always met, and 2) soft constraints, which may not be entertained at a cost or penalty.
There are a few fundamental needs that we considered in our formulation as hard constraints. First, we enforced that a sufficient number of fellows were assigned to the core rotations to meet the patients’ needs. Second, we ensured that each fellow meets the minimum number of core and elective rotations in each academic year. Third, we included a constraint to guarantee that the number of rotations assigned to each fellow in a given month would satisfy the program and ACGME requirements. Finally, we formulated a set of hard constraints to limit the number of times a fellow rotated in a specific unit in the academic year between predetermined lower and upper bounds on the basis of established policies and data from the PCCM fellowship program.
We formulated a set of soft constraints as penalties associated with different weightage in a weighted-sum objective function, with a higher weight indicating higher importance for that soft constraint. The soft constraints included 1) matching the assigned rotations with the preferences of fellows for specific rotations, 2) allowing time off for the requested dates, and 3) avoiding assignment of two consecutive ICU rotations to prevent workload fatigue. The model parameters included the minimum and maximum staffing levels that needed to be covered in each unit; the minimum and maximum number of times that a fellow can rotate in a specific unit; the preferences of fellows in terms of rotating in specific ICUs and time off on desired dates; and, finally, the number of day and night shifts that are required to be covered in each week.
DSS Design
We adapted the model for the PCCM fellowship program at the Mayo Clinic through the implementation of an Excel-based GUI. The input from the GUI is passed to the optimization model, which is coded in Python using Gurobi optimization libraries (11).
The DSS is designed so that the program coordinator (PC) can enter the inputs into easily extendible Excel tables, as shown in Figures 1 and 2. Figure 1 shows the input tables designed for entering the required data to construct monthly rotation schedules. Figure 1A shows the input tables used to enter the minimum and maximum available capacities of the rotations for accommodating fellows. As can be seen, the tabular format can be easily extended to accommodate different numbers of rotations for different residency and fellowship programs. The list of core and elective rotations are entered using the input table shown in Figure 1B. The names of the fellows were separated according to year in the program and were entered in tabular format, as shown in Figure 1C. The input table format shown in Figure 1D was used to enter the minimum- and maximum-rotation assignment for each fellow depending on their current progress in the fellowship program. Figure 1E shows the input table for vacation requests, where each row indicates whether a fellow has requested vacation in a specific month or not (1 or 0). Figure 1F shows the input table used to enter the preferences of fellows for a specific rotation in a specific month.
Figure 1.
Input tables for constructing monthly rotation schedules, including (A) minimum and maximum capacity available in different rotations for accommodating fellows, (B) the list of core and elective rotations, (C) names of fellow separated by year-in-the-program, (D) the minimum and maximum rotation assignment for each fellow depending on their current progress in the fellowship program, (E) vacation requests in specific months, and (F) the preferences of fellows for a specific rotation in a specific month.
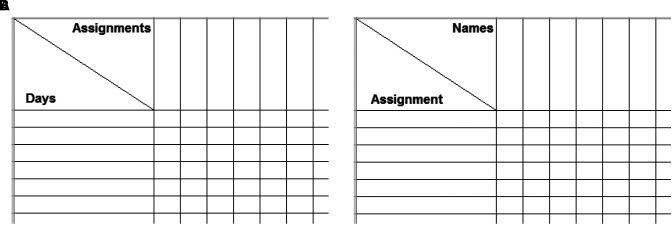
Figure 2.
Input tables for constructing daily rotation schedules, including (A) the minimum number and maximum number of times that each assignment needs to be covered in each day and (B) the maximum number of assignments for each fellow in each week.
Figure 2 shows the input tables designed for entering the required data to construct daily schedules. The user enters the minimum number and maximum number of assignments that need to be covered in each day, as shown in the table in Figure 2A. The maximum number of times that each fellow can be assigned to each assignment per week can be entered as shown in the table in Figure 2B.
The weights associated with violating the model’s soft constraints are set as follows. The weight for matching assigned rotations with fellows’ preferences is set at 10. Allowing time off for requested dates is weighted at 55 for third-year fellows, 25 for second-year fellows, and 5 for first-year fellows. The weight to avoid the assignment of two consecutive ICU rotations to minimize workload fatigue is set at 60. The weights are ordered on the basis of their importance, with higher weighted values given more importance in the model. For example, when it comes to time off, the model gives third-year fellows more weight than first- and second-year fellows. It means that the model prioritizes accommodating more time-off requests for third-year fellows than for first- and second-year fellows.
Once the inputs are entered, the PC can optimize the rotation schedules by pushing the “Optimize” button shown in Figure 3. The optimal rotation schedule shows the assignment of fellows to different units in each month.
Figure 3.
The output of the optimization model. Each row shows the optimal rotation schedules for a specific fellow.
Results
The proposed model was successfully implemented for the PCCM fellowship program at the Mayo Clinic to optimize the rotation schedule of the academic year 2018–2019. We compared the monthly and daily schedules, manually prepared by an experienced PC who was supervised by the program director, with those generated by the DSS. The results of comparison of the monthly schedules and daily schedules are summarized in Tables 1 and 2, respectively.
Table 1.
Comparison of monthly rotation schedules generated by the DSS versus those manually prepared by an experienced PC supervised by the program director
| Schedule Generator | % Covering the Preferences for Rotations | No. Having a Same Core Rotation in Two Consecutive Months | % Covering the Preferences for Vacation Times |
|---|---|---|---|
| DSS | 78 | 1 | 85 |
| Manual | 70 | 8 | 85 |
Definition of abbreviations: DSS = decision-support system; PC = program coordinator.
Table 2.
Comparison of daily schedules generated by the DSS versus those manually prepared by an experienced PC supervised by the program director
| Schedule Generator | % Fairness In Distributing the Rotations among Fellows | % Having at Least One Day Off per Week per Fellow |
|---|---|---|
| DSS | 83 | 100 |
| Manual | 70 | 82 |
Definition of abbreviations: DSS = decision-support system; PC = program coordinator.
As shown in Table 1, the monthly rotation schedule automatically generated by the DSS fulfills 78% of the fellow preferences for getting assigned to specific rotations in a desired period, whereas it is only 70% for the manually prepared schedule. For a given fellow, it is not desirable to rotate in the same core unit in two consecutive months. The number of rotations in a same core unit in two consecutive months is reduced from eight in the manually prepared schedule to one in the automatically generated schedule. Both schedules satisfy 85% of the vacation requests.
Table 2 compares the performance of the daily schedules prepared manually versus those generated automatically by the DSS. As can be seen from the table, the fairness metric improved from 70% in the manually prepared schedule to 83% in the automatically generated schedule. Fairness is defined as the degree of equality in assigning off days and difficult versus easy assignments among fellows. In addition, the automatically generated schedule was able to assign at least one day off per week per fellow 100% of the time to prevent fatigue (and to meet the duty hours), whereas it was possible 82% of the time in the manually prepared schedule. Fatigue and burnout are widespread in fellowship and residency programs. The model’s results can persuade decision makers to use such a DSS model to help address workload intensity and burnout.
The DSS takes about 120 seconds to generate both the monthly rotation and daily schedules, and it takes, on average, 5 hours to fill out the forms, whereas it took substantially more time and more resources (i.e., a full-time PC and program director) when the schedules were prepared manually.
Discussion
The results demonstrate that the proposed DSS is capable of generating high-quality schedules in a short time period. Not only can the DSS help with the tactical (i.e., monthly rotation scheduling) and operational (i.e., daily scheduling) planning, but it can also be used to answer important strategic questions for residency and fellowship programs, including the optimal number of residents and fellows to recruit in each academic year. To answer this question, we can optimize schedules under different scenarios having different numbers of first-year residents and fellows and evaluate the impact of first-year class size on the coverage of different units by residents and fellows and whether each individual resident and fellow can feasibly satisfy the program requirements.
Our study is limited to implement the DSS tool on the basis of the specific rules of the PCCM fellowship program at the Mayo Clinic. Although the methodology is flexible and can be easily generalized for other programs, such an adoption requires the incorporation of rules specific to each program.
Future work will focus on increasing the flexibility of the DSS by designing the system so that the user can systematically configure the DSS to incorporate different rules and constraints unique to each program. When we finish building a generic model, we intend to release the DSS as a commercial product.
Conclusion
We developed a DSS to schedule monthly rotation and daily schedules of fellows within the PCCM fellowship program for the academic year 2018–2019. The proposed DSS reduced time to prepare the schedules with an increased percentage of meeting fellows’ requests for specific rotations and vacation times. The designed DSS has an Excel-based GUI, making the implementation straightforward. In addition, because of intuitive formats for the input tables, the users can quickly test different scenarios by changing the inputs and check the effect of changes on the schedule.
Footnotes
Author disclosures are available with the text of this article at www.atsjournals.org.
References
- 1. Alfares HK. Survey, categorization, and comparison of recent tour scheduling literature. Ann Oper Res . 2004;127:145–175. [Google Scholar]
- 2. Proano RA, Agarwal A. Scheduling internal medicine resident rotations to ensure fairness and facilitate continuity of care. Health Care Manage Sci . 2017;21:1–14. doi: 10.1007/s10729-017-9403-9. [DOI] [PubMed] [Google Scholar]
- 3. Franz LS, Miller JL. Scheduling medical residents to rotations: solving the large-scale multiperiod staff assignment problem. Oper Res . 1993;41:269–279. [Google Scholar]
- 4. Beliën J, Demeulemeester E. Building cyclic master surgery schedules with leveled resulting bed occupancy. Eur J Oper Res . 2007;176:1185–1204. [Google Scholar]
- 5. Smalley HK, Keskinocak P. Automated medical resident rotation and shift scheduling to ensure quality resident education and patient care. Health Care Manage Sci . 2016;19:66–88. doi: 10.1007/s10729-014-9289-8. [DOI] [PubMed] [Google Scholar]
- 6. Bard JF, Shu Z, Leykum L. A network-based approach for monthly scheduling of residents in primary care clinics. Oper Res Health Care . 2014;3:200–214. [Google Scholar]
- 7. Bard JF, Shu Z, Morrice DJ, Leykum LK. Annual block scheduling for internal medicine residents with 4 + 1 templates. J Oper Res Soc . 2016;67:911–927. [Google Scholar]
- 8. Topaloglu S. A multi-objective programming model for scheduling emergency medicine residents. Comput Ind Eng . 2006;51:375–388. [Google Scholar]
- 9. Guo J, Morrison DR, Jacobson SH, Jokela JA. Complexity results for the basic residency scheduling problem. J Sched . 2014;17:211–223. [Google Scholar]
- 10. Perelstein E, Rose A, Hong Y-C, Cohn A, Long MT. Automation improves schedule quality and increases scheduling efficiency for residents. J Grad Med Educ . 2016;8:45–49. doi: 10.4300/JGME-D-15-00154.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gurobi Optimization [Website] https://www.gurobi.com/