A Multidimensional Matrix Model for Predicting the Effects of Male-Biased Sex Ratios on Fish Populations

Abstract

Laboratory experiments have established that exposure to certain endocrine-active substances prior to and/or during the period of sexual differentiation can lead to skewed sex ratios in fish. However, the potential long-term population impact of biased sex ratio depends on multiple factors including the life history of the species and whether the ratio is male or female-biased. In the present study, we describe a novel multidimensional, density-dependent matrix model that analyzes age class-structure of both males and females over time, allowing for the quantitative evaluation of the effects of biased sex ratio on population status. This approach can be used in conjunction with field monitoring efforts and/or laboratory testing to link effects on sex ratio due to chemical and/or nonchemical stressors to adverse outcomes in whole organisms and populations. For demonstration purposes, we applied the model to evaluate population trajectories for fathead minnow (Pimephales promelas) exposed to prochloraz, an aromatase inhibitor, during sexual differentiation. The model also was used to explore the population impact in a more realistic exposure scenario in which both adult and early life stages of fish are exposed concurrently to prochloraz, which, in addition to altering sex ratio during development, can decrease vitellogenin and egg production in adult females. For each exposure scenario, the model was used to analyze total population size, numbers of females and of males, and sex specific recruitment of the F1 generation. The present study illustrates the utility of multidimensional matrix population models for ecological risk assessment in terms of integrating effects across a population of an organism even when chemical effects on individuals are manifested via different pathways depending on life stage.

INTRODUCTION

Potential ecological effects of chemicals that interact with the vertebrate hypothalamic pituitary gonadal and/or thyroidal (HPG/T) axes continue to be of scientific and regulatory concern throughout the world (Matthiessen et al., 2017). A variety of in vitro and in vivo assays have been developed to help identify endocrine-active chemicals (EACs) with the potential to affect different aspects of estrogen, androgen and thyroid hormone signaling in vertebrate wildlife (Coady et al., 2017). Many of these assays involve evaluation of molecular, biochemical, cellular and tissue-level changes that reflect perturbation of HPG/T function. While changes at these biological levels of organization can be highly diagnostic of perturbation of specific pathways, there remains the challenge of translating them into potential adverse effects meaningful to risk assessors/managers. The adverse outcome pathway (AOP) framework (Ankley et al., 2010) seeks to establish transparent, causal linkages between responses at different levels of organization and, hence, has been proposed as a basis for utilizing data from pathway-based EAC assays for higher-level risk assessments (Browne et al., 2017; Coady et al., 2017; Knapen et al., 2020; McCardle et al., 2020). One of the challenges in developing AOPs relevant to assessment of EAC risk(s) has been establishing linkages between changes in apical responses in individuals and potential impacts on populations. In making causal linkages between changes in individuals and populations, it is necessary both to identify assay endpoints relevant to population status and develop flexible modeling constructs that employ these endpoints (Kramer et al., 2011; Marty et al., 2017).

The relative number of functional males and females in a reproducing cohort is an important parameter potentially influencing population status which can be affected both by chemical and nonchemical stressors (Dang & Kienzler, 2019; Norris & Carr, 2020; Yamamoto, 1969). Studies in fish have established that changes in normal sex ratios can be caused by different types of EACs that alter signaling controlled by endogenous estrogens and androgens (ECHA 2008; OECD 2018). These changes can occur in conjunction with EAC exposure both during early development (organizational effects) and in reproductively mature adults (activational events; Ankley & Johnson, 2004; Guillette et al., 1995). Effects of EACs on sex ratios can either be direct, caused by chemicals that mimic or block the actions of endogenous steroids with estrogen and/or androgen receptors, or indirect through alteration of the synthesis of endogenous steroids (Ankley & Johnson, 2004; Guillette et al., 1995).

Reports of masculinized or male-biased fish populations in the field are less common than female-skewed populations (Matthiessen & Weltje, 2015) but have been reported in conjunction with runoff from animal feedlots or pulp and paper mill discharges, some of which contain androgen receptor agonists (Bortone & Cody, 1999; Durhan et al., 2006; Hanson et al., 2005; Howell et al., 1980; Larsson et al., 2000; Orlando et al., 2004; Parks et al., 2001; Soto et al., 2004). In fact, natural and synthetic androgens have been used for many years in aquaculture to intentionally produce male-biased populations in a variety of fish species (e.g., Arslan & Phelps, 2004; Galvez et al., 1996; Kitano et al., 2000; Singh, 2013). Bogers et al. (2006) showed that exposure of fathead minnows (Pimephales promelas) to the synthetic androgen receptor agonist methyl dihydrotestosterone during early development produced populations skewed toward males as determined through inspection of gonad morphology/histology. Male-biased fish populations also can be produced by chemicals, such as the model EAC fadrozole, that inhibit the activity of aromatase (cytochrome P450191a1; CYP19), which catalyzes the conversion of endogenous androgens such as testosterone to 17β-estradiol (Kitano et al., 2000; Kwon et al., 2000; Le Page et al., 2010; Piferrer et al., 1994). Other chemicals that can inhibit CYP19 activity such as some conazole fungicides also can produce male-biased populations when fish are exposed during the period of sexual differentiation (Matthiessen & Weltje, 2015). For example, exposures of non-sexually differentiated early life stages of both zebrafish (Danio rerio) and fathead minnow to the conazole prochloraz has been shown to produce male-biased sex ratios based on gonad differentiation (Holbech et al., 2012; Kinnberg et al., 2007; Thorpe et al., 2011). The ability of aromatase inhibitors to affect sex differentiation in fish has been well enough characterized that a putative AOP capturing the process has been developed (Society for the Advancement of Adverse Outcome Pathways [SAAOP], 2016; AOP346).

Alterations in phenotypic sex ratios in fish have been used in a variety of screening and testing assays designed to detect EACs in a regulatory setting (Ankley & Johnson, 2004; Dang & Kienzler, 2019). A relevant example of this is the Fish Sexual Development Test (FSDT) developed and validated through activities coordinated by the Organisation for Economic Co-operation and Development (Holbech et al., 2012; OECD 2018). The FSDT (OECD TG 234) is a multi-endpoint assay initiated with newly fertilized embryos and proceeding through early adulthood. The design can accommodate testing with several model small fish species, including zebrafish and fathead minnow (Holbech et al., 2012). Endpoints evaluated include those that can be used as a basis to estimate sex ratios, such as gonad differentiation and secondary sex characteristics, and responses indicative of other aspects of HPG axis function (e.g., gonadal abnormalities, vitellogenin [VTG]; egg yolk protein precursor protein] expression or production). Consequently, the assay is capable of detecting changes associated with multiple molecular initiating events (MIEs) relevant to AOPs (e.g., SAAOP, 2016; AOPs 346, 25, 23).

To employ data from assays such as the FSDT to estimate ecological risks to fish populations, a flexible population modeling approach that can incorporate multi-generational responses is ideal. Since their introduction over 50 years ago, structured population models have become a central modeling formalism, and are commonly used in ecology (Caswell, 2001; Ellner, 2009). The use of matrix population models within ecological risk assessments is advantageous because such models can integrate effects across the life cycle, link endpoints observed in the individual to ecological risk for the population as a whole, and project outcomes over future timespans allowing for management planning scenarios.

A matrix model includes analysis of the dynamics of the total population, whereby changes are predicted from the collective of the individuals comprising the population. Matrix population models originally were designed to classify individuals by a single characteristic (Leslie, 1945; Lewis, 1942). Using this approach, population dynamics are described in terms of a single dimension (for example, age) of individuals making up the population (Caswell, 2001; Metz & Dickmann, 1986). The model projects the distribution of the population as a set of possible outcomes assigned to the dimension over time (i.e., age classes), where individuals move among these possible outcomes (age classes) according to vital rates presented in a Leslie matrix. However, as data collection methods have advanced and more sophisticated data sets are produced in the laboratory and field settings (a relevant example being the FDST assay), utilizing multiple dimensions (i.e. age, size, sex) within demographic models will become increasingly important. A multidimensional, density dependent matrix population model for assessing risk of stressors to fish populations was recently described by Miller et al. (2020). Such an approach allows for the inclusion of density dependent effects, the ability to incorporate higher dimensions into matrix models, and the extension of demographic state spaces, as well as directly impacting data usage to guide conservation and population management practices.

Traditional matrix modeling approaches use a single dimension to describe population dynamics. An assumed sex ratio is implicitly built into the model. Most often, the model is female based (Caswell, 2001; Ellner, 2009; Gotelli, 1998). In this way the model predicts recruitment of females, by females, and all age classes refer to surviving females over time. If the sex ratio is assumed to be constant at 50% female and 50% male, then the total population size can be determined by scaling the output of the projection accordingly. Alternatively, if a form of the logistic equation is used along with the assumption of an equal sex ratio, then the total population size can be expressed as a fraction of carrying capacity (Miller et al.,, 2013, 2015; Thursby, 2009, 2016; Thursby et al., 2018).

In the present study, we describe and apply a multidimensional density dependent matrix model to examine the impact of a chemical stressor that results in a male-biased sex ratio over time. The model allows for the sex ratio of the population to be explicitly defined, such that population dynamics of both females and males are explicitly quantified under scenarios using varying sex ratios. Furthermore, we demonstrate how the model can be applied to examine the impact of simultaneous effects on both sexual differentiation (sex ratio; i.e., AOP 346) and adult female fecundity (i.e., AOP 25; Conolly et al., 2017; Miller et al., 2007) on exposure of an entire cohort of fish to an EAC. Overall, the model provides support for a causal link between a male-biased sex ratio and reduced population trajectory (i.e., https://aopwiki.org/relationships/2147, accessed January 31, 2021) for species with a life history analogous to that of fathead minnows.

METHODS

Theory and conceptual demonstration

The present multidimensional model builds on the population modeling approach originally described by Miller and Ankley (2004), which is a density-dependent logistic matrix model constructed using a Leslie projection matrix (Leslie, 1945) in combination with the logistic equations and had been used for a variety of species and applications (Miller & Ankley, 2004, Miller et al., 2007, Ankley et al., 2008, Miller et al., 2013, Miller et al., 2015):

$${\mathbf{\text{n}}}_{t+1}=\exp \left(-r{P}_t/K\right){\mathbf{\text{M}}}_1{\mathbf{\text{n}}}_t$$ (1)

$${\mathbf{\text{M}}}_1=\mathbf{\text{M}}-{\text{C}}_t$$ (2)

In the context of the present model, n_t+1 is the vector of population age and sex structure at time t + 1, n_t is the vector of population age and sex structure at time t, r is the intrinsic rate of increase, P_t is the population size at time t, K is carrying capacity, and M₁ is the Leslie matrix containing vital rates (survivorship and fertility) that have been adjusted to include an age-specific and/or sex-specific percentage reductions in fertility and/or survival over the time step t resulting from an exposure to chemical and/or nonchemical stressors. Thus, within Equation 2, C_t is a matrix representing the discount to vital rates resulting from exposure to the stressor(s) at time t (Miller et al., 2013). In addition, the density dependence accounted for by the model acts cumulatively on the population over life stages and generations resulting in stabilization of the population. The formulation of the model of Equation 1 and Equation 2 provides a link between life-history parameters that can be directly measured in the laboratory or at the field site, the logistic equation, and Leslie's original projection matrix.

Using birth pulse survival probabilities, birth pulse fertilities, and a prebreeding census (Caswell, 2001; Gotelli, 1998), the Leslie matrix, as used in the present study (Equation 3), can be written as a multidimensional projection matrix with two binary sexes within three age classes (with two non-overlapping sex classes per age class):

$$\mathbf{\text{M}}=\left|\begin{array}{llllll}{F}_{1,F,F}\hfill & F_{1,F,M}\hfill & F_{2,F,F}\hfill & F_{2,F,M}\hfill & F_{3,F,F}\hfill & F_{3,F,M}\hfill \\ F_{1,M,F}\hfill & F_{1,M,M}\hfill & F_{2,M,F}\hfill & F_{2,M,M}\hfill & F_{3,M,F}\hfill & F_{3,M,M}\hfill \\ S_{1,F}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & S_{1,M}\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & S_{2,F}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & S_{2,M}\hfill & 0\hfill & 0\hfill \end{array}\right|$$ (3)

In examining the vital rates within the matrix M, fertility rates are indexed first by the age class producing offspring, second by the sex of the fish being produced, and third by the sex of the fish producing offspring. For example, F_3,F,F corresponds to recruitment of female offspring of by Age 3 fish that are female. Survival rates are indexed first by current age class, second by sex of the fish that will move into the sequential age class over the time step t. Thus, S_2,F would represent the survival rate of Age 2 females moving from age Class 2 into age Class 3 over the time step t. Within the matrix M, fertility rates are calculated by adjusting fecundity by the percentage of maturity and age class 0 survival (Gotelli, 1998, Caswell, 2001). The dominant eigenvalue of the Leslie matrix represents the finite rate of increase. Taking the natural log of the dominant eigenvalue of the Leslie matrix results in the intrinsic rate of increase, an estimate of the per capita rate of population increase associated with a population represented by the rates in the matrix.

In simple qualitative terms, application of the density-dependent logistic matrix model of Equations 1 and 2 requires no additional parameters beyond what is found in a combined life and fecundity table that contains sex ratio estimates by age, which is converted to the projection matrix (Equation 3). The model also requires an estimate of carrying capacity and an estimate of the effect of the chemical stressor on the vital rates of fertility and survivorship as found in the projection matrix.

A multi-dimensional projection matrix (Equation 3) was developed for fathead minnow. Life history characteristics for the fathead minnow were collected and analyzed from multiple studies (Duda, 1989; Gleason & Nacci, 2001; Westman, 1938; Zischke et al., 1983), and are summarized in Table 1. Fathead minnows breed annually within a breeding period that lasts 2–3 months. Female fathead minnows mature at age 1 year and reproduce annually with reproductive output that varies with age (Duda, 1989; Gleason & Nacci, 2001; Westman, 1938; Zischke et al., 1983). A corresponding multidimensional projection matrix that utilized a formulation containing birth pulse fertilities and a pre-breeding census based on Equation 3 was constructed (Figure 1).

TABLE 1:

Life table for the fathead minnow vital rates derived from populations^a

Age (years)	Survival (per year)	Fecundity (eggs/year)
0	1	0
1	0.001	750
2	0.00039	1500
3	0.0001521	3000
4	0	N/A

^aWestman (1938); Zischke et al. (1983); Duda (1989); Gleason and Nacci (2001).

FIGURE 1:

Multi-dimensional projection matrix for fathead minnow using birth-pulse fertilities and a pre-breeding census.

We conducted simulations investigating how an environmental stressor that causes multigenerational effects including male-biased sex ratio and altered reproductive capacity would theoretically impact total population size, age structure and sex structure for a fathead minnow population initially at carrying capacity. For all simulations, the population was initiated with the population having an equal sex ratio. At time Step 1 in each simulation, the population projection was altered in favor of male over female production. We investigated a range of potential male-biased sex ratios including 60% male and 40% female, 70% male and 30% female, 80% male and 20% female, and 90% male and 10% female. In addition, for each simulation, trends in total males and total females were analyzed over time to allow for an understanding of differences in the increase of males versus females as a component of total population size. Each simulation was initiated at stable age distribution as calculated from the projection matrix. Stable age distribution was determined from the matrix by finding an eigenvector (right eigenvector) associated with the dominant eigenvalue of the matrix and rescaling the eigenvector (Caswell, 2001; Gotelli, 1998). To provide an indication of relative impact, output of the model can be expressed invariant of actual carrying capacity by plotting population size proportional to carrying capacity at each time step in the model. In demonstrating model output in this manner; a value of 1.0 represents a population at carrying capacity and values between 0 and 1.0 represent a population below the carrying capacity threshold (Miller et al., 2013, 2015, 2020). The population model was executed over a 10-year simulation period, and results were recorded using an annual time step. All model projections utilized the intrinsic rate of increase as calculated from the Leslie matrix.

Case study: Modeling exposure to prochloraz

We evaluated performance of the model construct using data from a FSDT study with prochloraz, a model inhibitor of CYP19 (Holbech et al., 2012; Table 2). Sex ratio data were used as input to the multidimensional density dependent population model in Equations 1 and 2. We calculated several measures including total population size over time, and number of male and female fish in the population over time, as a function of the sex ratio changes caused by prochloraz.

TABLE 2:

Concentration response data consisting of changes to the proportion of female fish resulting from exposure to prochloraz (Holbech et al., 2012)^a

	Control	31 µg/L		106 µg/L		301 µg/L
Sex	Percentage In population	Percentage In population	Relative change From control	Percentage In population	Relative change From control	Percentage In population	Relative change From control
Female %	47	44	−6.4	40	−14.9	7	−85.1
Male %	47	44	−6.4	54	+14.9	79	+68
Undifferentiated %	6	12	+100	6	0	14	+133

^aUndifferentiated fish at 120 days post hatch are considered to be uncapable of breeding.

Next, we expanded the application of the multidimensional density dependent population model to predict multigenerational effects caused by inhibition of CYP19 in both early development and adult life stages. Again, data used to evaluate model performance came from the fathead minnow FSDT reported by Holbech et al. (2012). In addition to the sex ratio data (Table 2), Holbech et al. (2012) also reported the effects of prochloraz on VTG concentrations in adult females from the exposure (Table 3). The approach of Miller et al. (2007) was used to predict egg production based on VTG concentrations in females using a linear model (Equation 4; Conolly et al., 2017; Miller et al., 2007):

$$\left(\text{fecundity}=-0.042+0.95\text{VTG},p<0.01,r^2=0.88\right)$$ (4)

TABLE 3:

Concentration response data consisting of changes to vitellogenin (VTG) in adult female fish resulting from the exposure to prochloraz (Holbech et al., 2012)

Exposure	VTG ng/g homogenate	Relative VTGa	Relative Fecundityb
Control	300 000	N/A	N/A
31 µg/L	100 000	33.33%	31.6215
106 µg/L	30 000	10%	9.458
301 µg/L	50	0.0001%	0c

^aRelative change is calculated in relation to VTG of control fish.

^bRelative fecunidity is predicted in relation to the fecundity of control fish using the equation: (Relative Fecundity) = −0.042 + 0.95 × (Relative VTG) taken from Miller et al. (2007).

^cEstimated relative fecundity canť be negative.

This relationship was integrated into the multidimensional density dependent population model to translate changes in VTG concentrations of female fathead minnows to alterations in reproductive capacity that would thus impact population trajectory.

Simulation results were structured into a progressive format. First, we calculated total population size over time, number of male fish in the population over time, and number of female fish in the population over time as a consequence of prochloraz-induced decreases in VTG. Second, we calculated the same population-level measures (i.e., total population size, number of male and female fish in the population) quantifying the combined effects resulting from both altered sex ratio and decreased VTG in prochloraz-exposed fish. For all simulations in the case study, the population of fathead minnow initially existed at carrying capacity and was subsequently exposed to prochloraz.

All calculations were performed using a combination of software packages including Microsoft Excel for Microsoft 365, SPSS, and Mathcad. Example calculations demonstrating the application of the model can be found in Supporting Information.

RESULTS

Conceptual demonstration: Consequences of a male-biased sex ratio

The multidimensional matrix yielded an intrinsic rate of increase of 0.337 in a control fathead minnow population (Figure 1). The annual vital rates of fertility across the age classes within the projection matrix were subsequently adjusted to account for different degrees of a male-biased population, ranging from 60% to 90% male, and projected trends in total population size over time were calculated as a function of baseline carrying capacity with Equations 1 and 2 (Figure 2). A fathead minnow population at carrying capacity exposed to a stressor that resulted in a male-biased sex ratio of 60:40 exhibited an approximate 7.9% decrease in population size after 2 years, a 26.8% reduction in population size after 5 years, and a 36.1% reduction in population size after 10 years (Figure 2). At the other end of the spectrum, a male-biased sex ratio of 90:10 had a 31.6% reduction in population size after years, an 87.6% reduction in population size after 5 years, and a 99.1% reduction in population size after 10 years (Figure 2).

FIGURE 2:

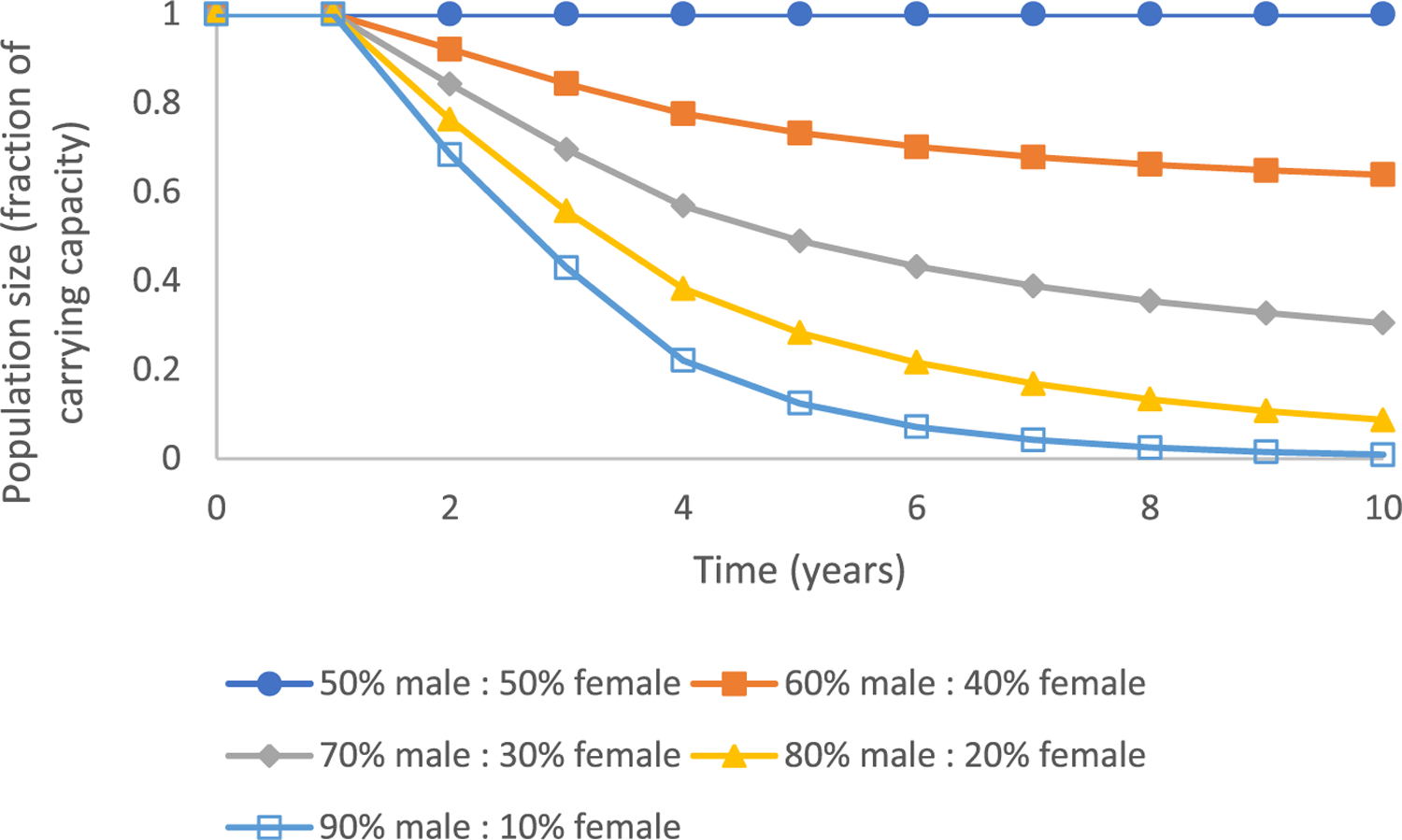
Projected trends in total population size over time for a fathead minnow population existing at carrying capacity and subsequently exposed to varying levels of chemical stress that resulted in egg production that yielded a male-biased sex ratio of 60% male: 40% female, 70% male: 30% female, 80% male: 20% female, and 90% male: 10% female.

Output consisting of time series trends in population status over time were also generated specific to a given dimension of the matrix to examine patterns in abundance of total males versus total females. For example, trajectories for males and females over time for a fathead minnow population initially at carrying capacity and subsequently exposed to a stressor that resulted in a male-biased sex ratio of 70:30 is shown in Figure 3. In contrast to a total population size that remains unchanged at the carrying capacity after one time step, the male-biased sex ratio resulted in an immediate increase in males from 50% to approximately 64.8% and a corresponding decrease in females. This is the highest point for both sexes, after which population decline results from the male-bias (as these fish reach breeding capability).

FIGURE 3:

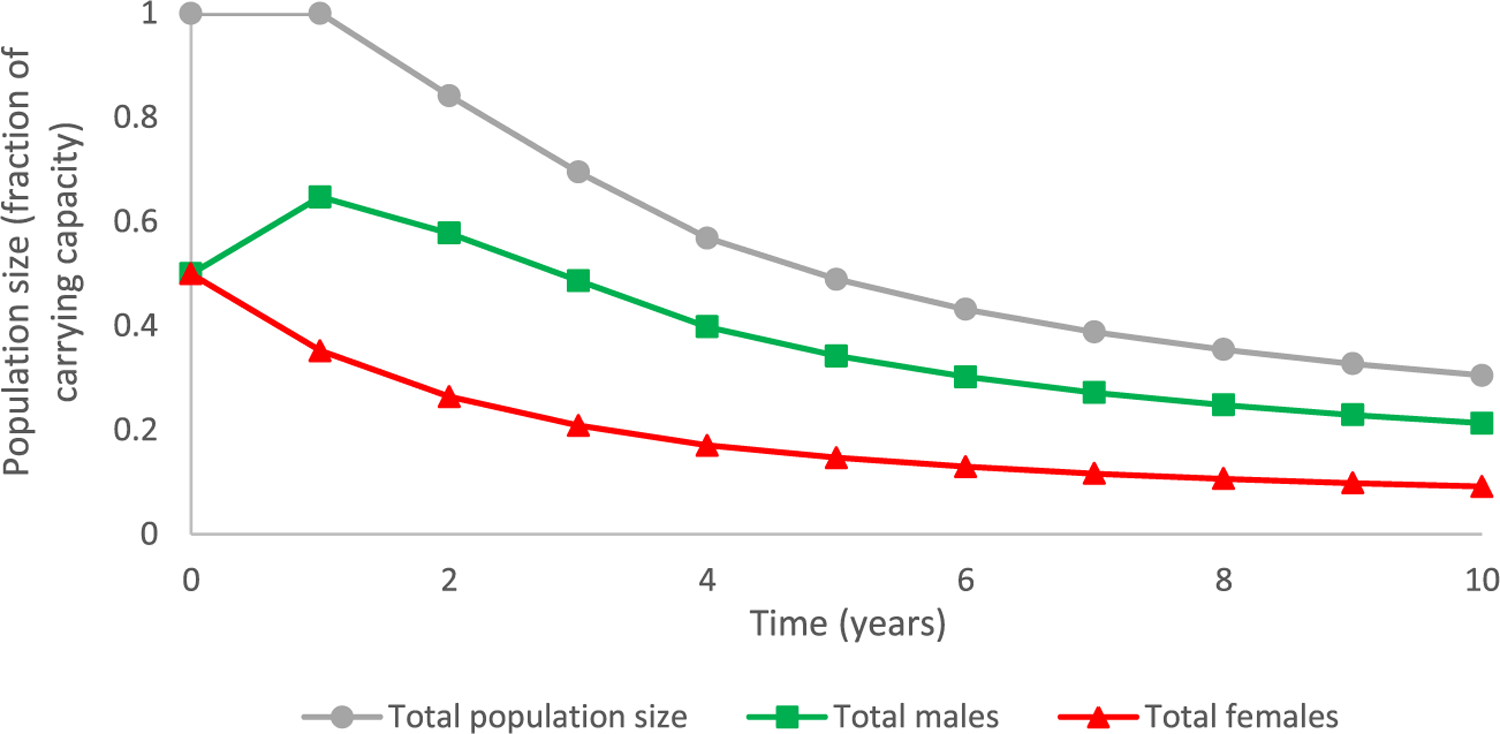
Trajectories for males and females over time for a fathead minnow population initially at carrying capacity and subsequently exposed to chemical stress that resulted in altered fecundity exhibiting a male-biased sex ratio yielding 70% male egg: 30% female egg production.

Practical demonstration: Effects of an EAC

We subsequently evaluated performance of the model using data from controlled studies with a known EAC, prochloraz (Holbech et al., 2012; Table 2). Fertility rates within the projection matrix corresponding to the recruitment of males and females were based on sex ratio data for the 31, 106 and 301 μg/L treatment groups. All the prochloraz treatments resulted in a predicted decline in total population size over time (Figure 4). For example, observed changes in sex ratio at 31 μg prochloraz /L would cause a 2.5% decrease in average population size after 2 years, an 8.8% reduction in population size after 5 years, and a 11.4% reduction in population size after 10 years. Considering effects on sex ratio alone, exposure to 301 μg prochloraz/L was projected to cause an approximate 33.6% decrease in predicted population size after 2 years, a 91.8% reduction after 5 years and, basically, complete extinction (99.7% reduction) after 10 years. The model predicted declining trends in both total male fish and total female fish in the population that were more prevalent with increased exposure concentration (Figure 5).

FIGURE 4:

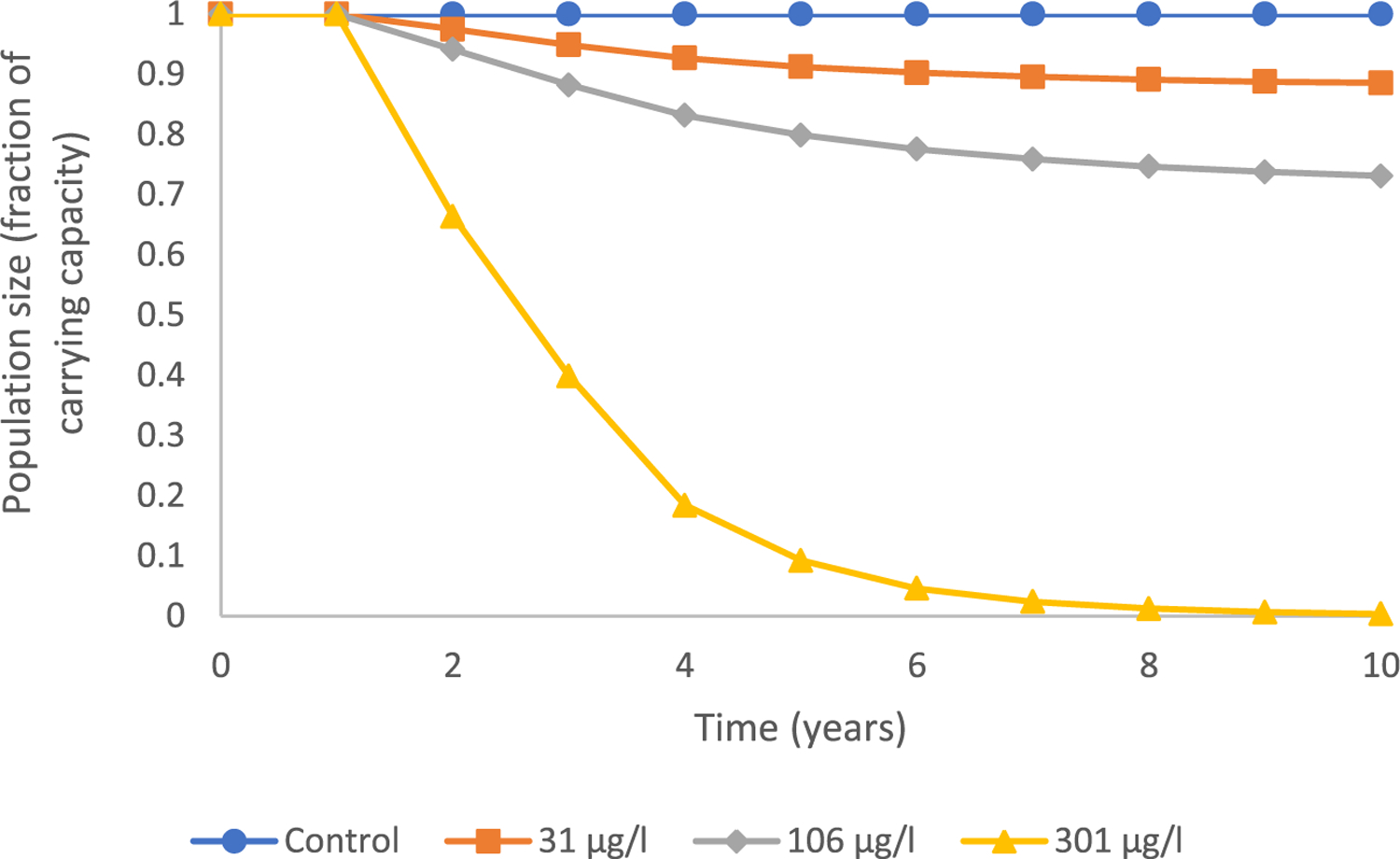
Projected trends in total population size over time for a fathead minnow population existing at carrying capacity and subsequently exposed to varying levels of prochloraz including 31, 106, and 301 μg/L taking into account developmental effects on young of year that resulted in male-biased sex ratio only.

FIGURE 5:

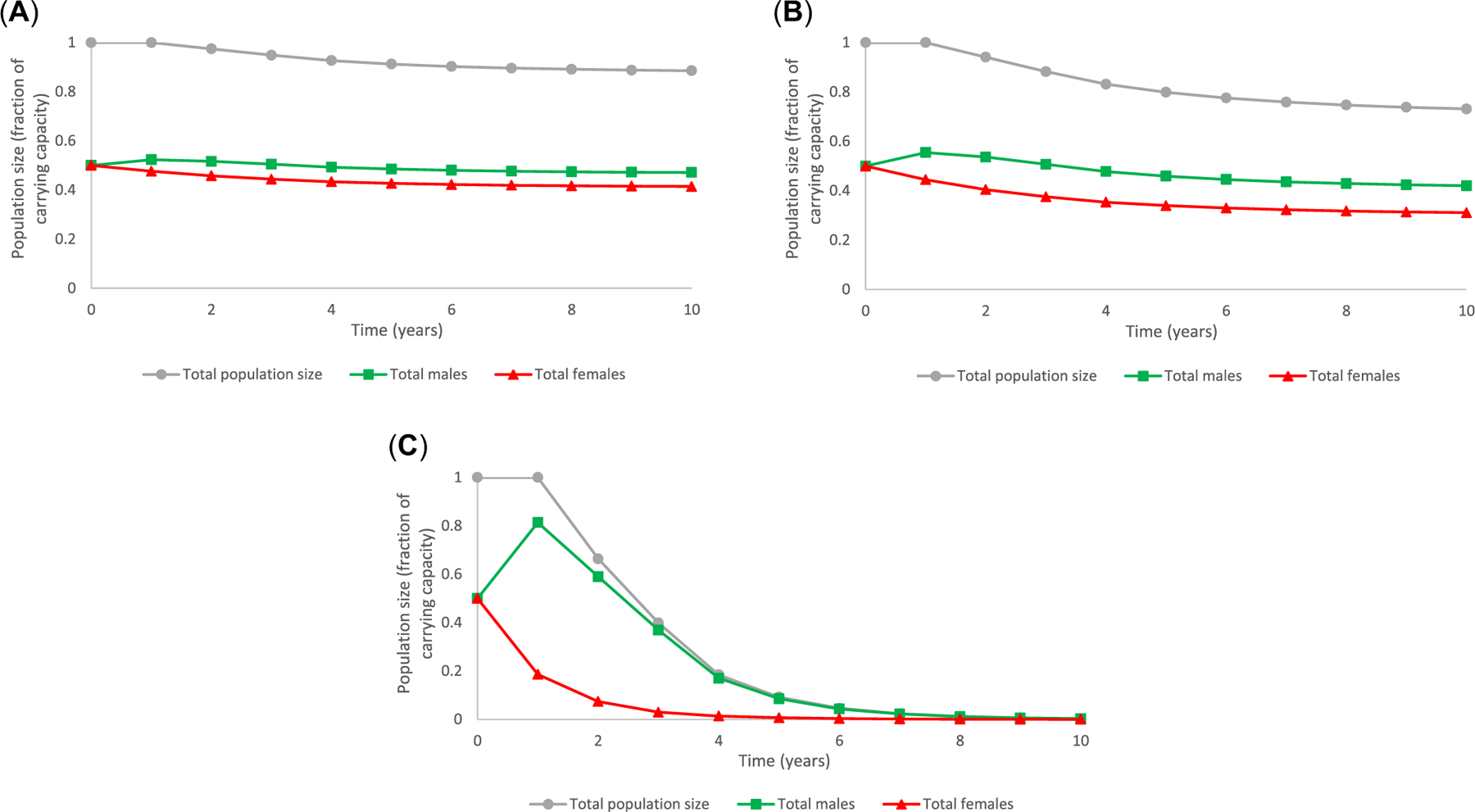
The population model of Equations 1 and 2 was used to investigate trends in population status over time generated specific to a given dimension of the matrix to examine patterns in abundance of total males versus total females within the population associated with each exposure concentration in considering developmental effects on young of year fish that resulted in male-biased sex ratio only. Panel A: Exposure to 31 μg/L prochloraz. Panel B: Exposure to 106 μg/L prochloraz Panel C: Exposure to 301 μg/L prochloraz.

In applying the multidimensional model to evaluate only reduced VTG production by adult females on population size, exposure to all concentrations of prochloraz resulted in reduced reproductive capacity of adult female fish that translated into a decline in total population size over time (Figure 6). For example, a fathead minnow population at carrying capacity and subsequently exposed to prochloraz at 31 μg/L resulted in an approximate 68.0% decrease after 2 years, a 89.5% reduction after 5 years, and a 97.8% reduction after 10 years. Consequences of decreased VTG in adult females on predicted population size in the 106 and 301 μg prochloraz/L treatments exhibited similar concentration-dependent temporal trends (Figure 6). Model-predicted decreases in population size due to prochloraz-induced reductions of VTG were expressed to the same degree in both males and females (data not shown).

FIGURE 6:

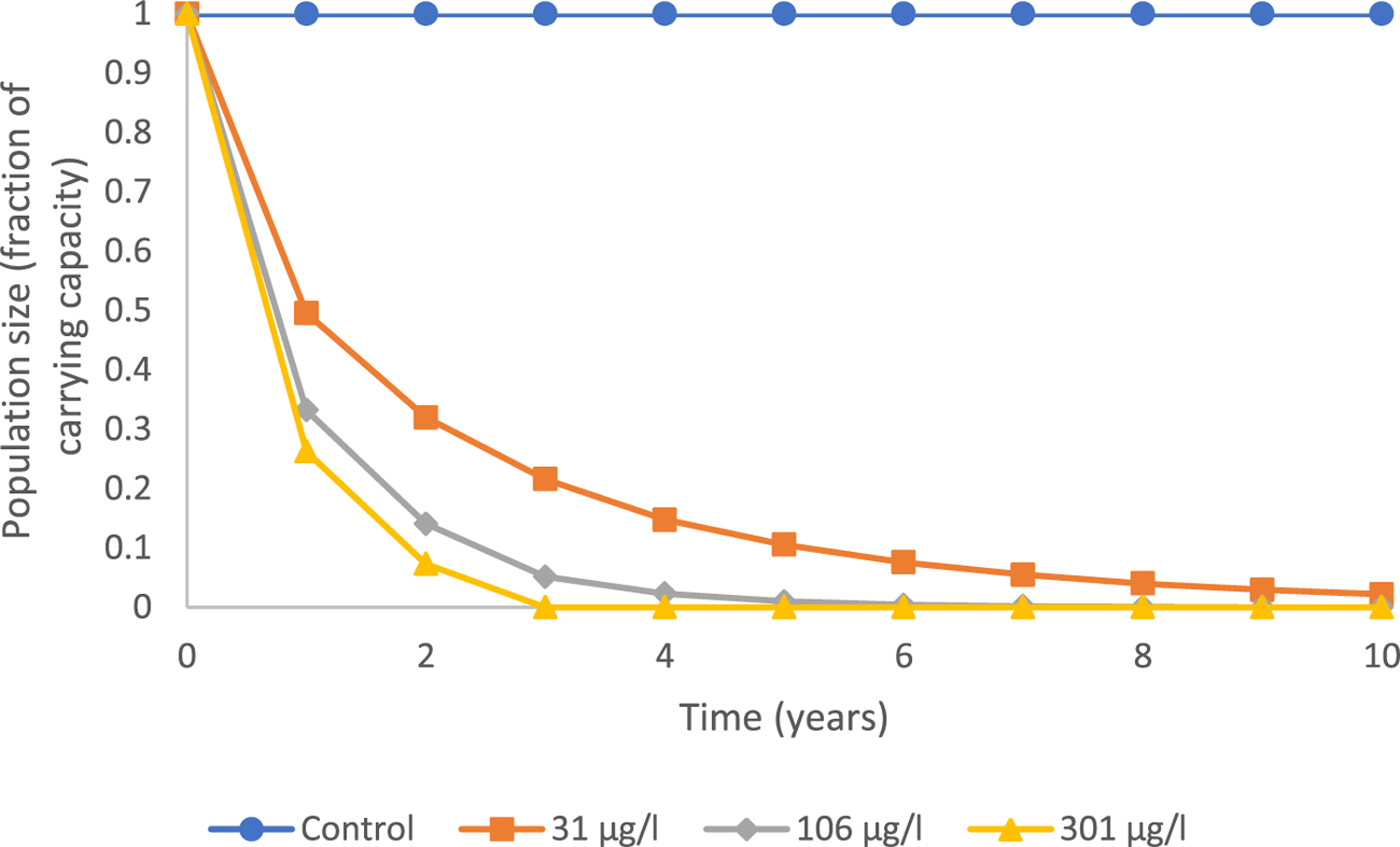
Population trajectories for a fathead minnow population existing at carrying capacity and subsequently exposed to varying levels of prochloraz of 31, 106, and 301 μg/L were calculated using the population model of Equations 1 and 2 in combination with the predictive relationship between vitellogenin (VTG) and fecundity of adult females, Equation 4. These projections are considering only the effects on reduced reproductive capacity of adult female fish resulting from decreased VTG.

Finally, the model was applied to consider the combined effects of both the altered sex ratio and impacts on adult female VTG concentrations (Figure 7). All three concentrations of prochloraz affected sex ratio and reduced reproductive capacity of adult female fish, which together translated into a decline in total population size over time. The effects of prochloraz on VTG in adult females elicited a more immediate and greater impact on total population size than observed changes in sex ratio in a given treatment group (Figure 7). For example, the combined effects of a male-skewed sex ratio and decreased VTG in females in fish exposed to 31 μg prochloraz/L, resulted in an approximate 68.3% decrease in average population size after 2 years, a 91.3% reduction after 5 years, and a 98.3% reduction after 10 years. These values were virtually the same as predictions based only on reduced VTG (Figure 6). Trends in overall population size were concentration-dependent, with population extinction occurring within 10 and years in the 106 and 301 μg prochloraz/L treatments, respectively (Figure 7). Again, these predictions were the same as those generated using reductions in VTG only (Figure 6). However, in the forecasts considering both the effect on sex ratio and VTG concentrations in adult females, there was a greater relative decrease in females than in males compared to predicted population impacts due to reductions in VTG alone (Figure 8).

FIGURE 7:

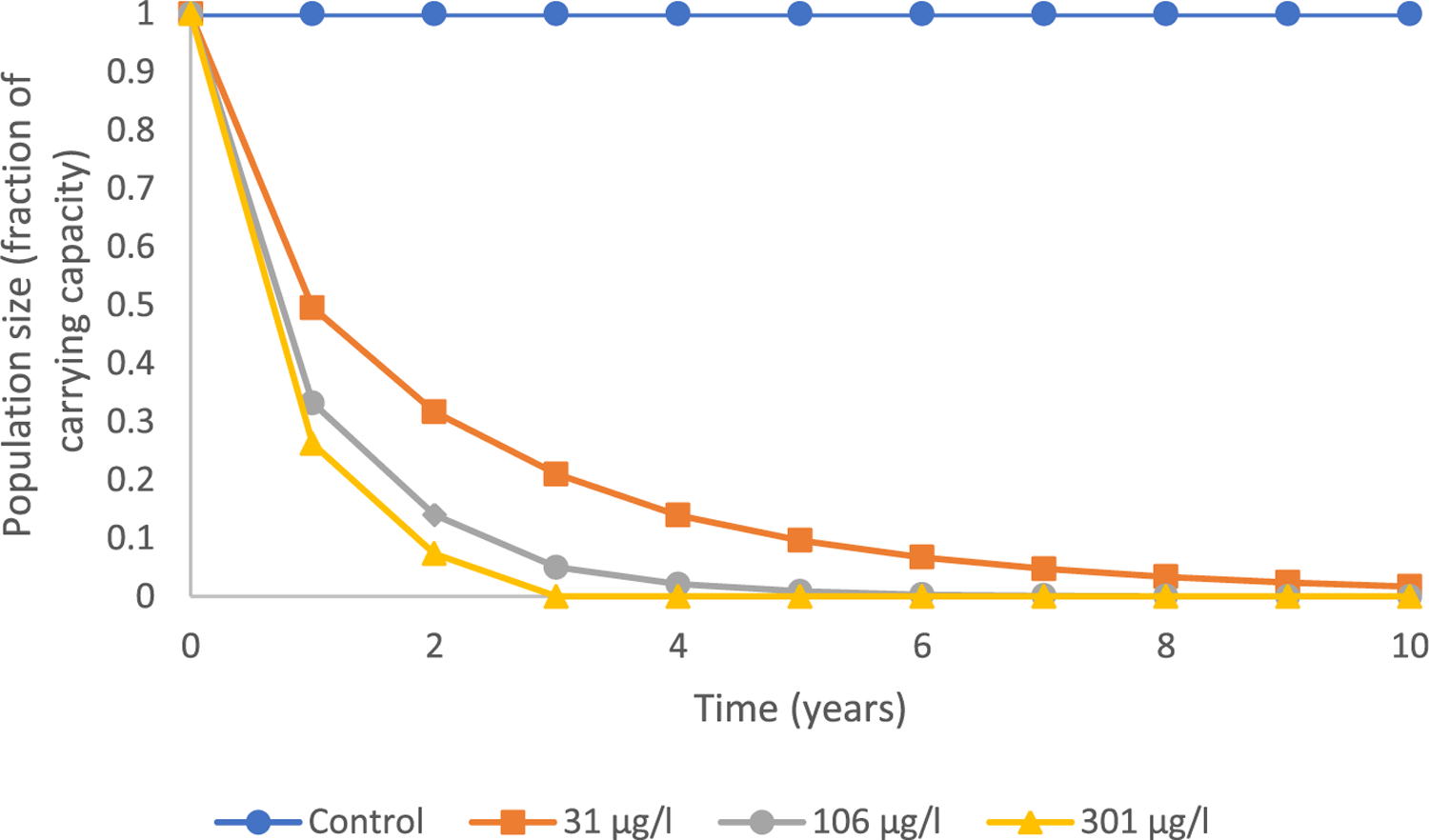
Exposure to prochloraz at concentrations of 31, 106, and 301 μg/L resulted in effects on population sex ratio and reduced reproductive capacity of adult female fish that translated to a decline in total population size over time.

FIGURE 8:

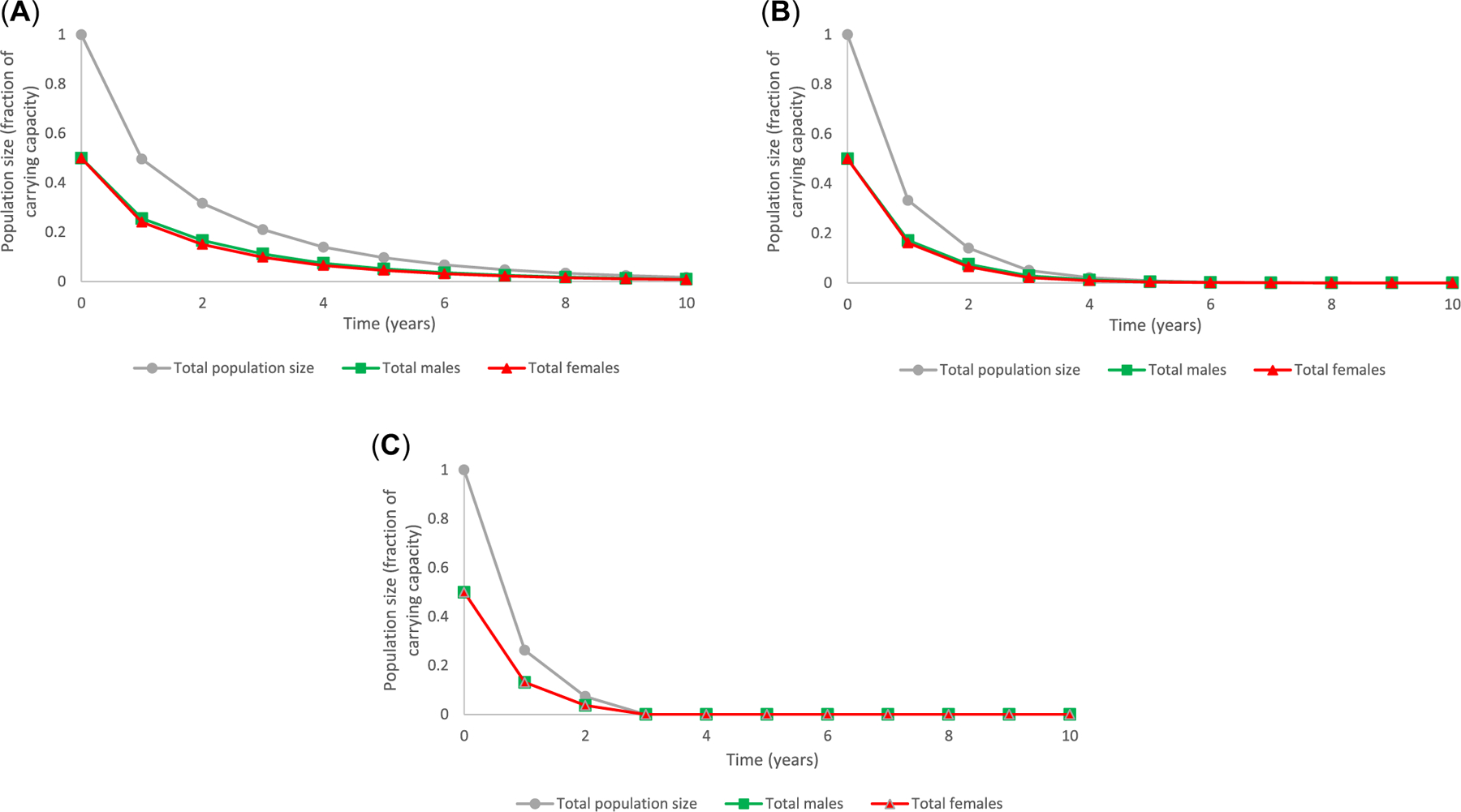
A fathead minnow population initially at carrying capacity and subsequently exposed to prochloraz at an exposure concentration of 31 μg/L (Panel A), 106 μg/L (Panel B), and 301 μg/L (Panel C) exhibited effects including a male-biased sex ratio and alterations to vitellogenin (VTG) in adult female fish that resulted in declining trends in both total male fish and total female fish in the population that increased with increased exposure concentration of prochloraz.

DISCUSSION

Occurrence and potential impacts of EACs in fish and wildlife species are an ongoing concern worldwide. Screening/testing and monitoring programs for EACs entering or already present in the environment typically involve two considerations: (a) evaluation of whether a chemical (or chemical mixture) actually alters HPG/T function, and (b) whether this alteration has the potential to produce adverse effects in individuals and populations (Matthiessen et al., 2017). A variety of novel in vitro and in vivo assays employing molecular, biochemical and cellular endpoints have been developed to address the potential for chemicals to interact with endocrine pathways in nonmammalian vertebrates (Coady et al., 2017). However, bridging the gap from results of these mechanistic assays to determination of whether changes in basic endocrine function in fact cause adverse effects in individuals and populations has been challenging (Matthiessen et al., 2017). The focus of the AOP concept on assessing and depicting causal linkages in responses across biological levels of organization provides a logical basis for making the key connection between changes in HPG/T axis function and impacts meaningful to risk assessment (e.g., Browne et al., 2017; Coady et al., 2017; Knapen et al., 2020; McCardle et al., 2020). But, even within the context of the AOP framework, linking changes in individuals to population status remains a vexing problem and one that, apart from a few notable efforts (e.g., Kidd et al., 2007), has not been addressed for EACs based on experimental data. Consequently, there is a need for robust modeling approaches to predict the consequences of endocrine-relevant changes in individuals on population status (Kramer et al., 2011; Marty et al., 2017). We believe that the model described in the present study meets these needs in the context of providing a flexible, easily implemented approach to enhance prediction of population level impacts of EACs with the potential to affect multiple endpoints at different lifestages. The present model is easily adaptable to any species for which a life table containing vital rates of survivorship and fecundity, sex and age measurements of the population, and the effect of stressors on vital rates is available.

Various population level analysis (i.e., individual based models, Beverton-Holt models, matrix projection models) have been considered as relevant tools to examine changes in population viability resulting from impacts on fish due to endocrine disruption (Brown et al., 2015; Hanson et al., 2005; Hazlerigg et al., 2014; Meng et al., 2006; Miller & Ankley, 2004). In the present study, we evince the ability to effectively employ sex ratio data relative to predicting population effects, and demonstrate that skewed sex ratio has the potential to impact population sustainability over time. Sex ratio is an endpoint known to be altered by EACs that affect estrogen/androgen signaling (and one used in extant EAC testing assays, e.g., Ankley & Johnson, 2004; Holbech et al., 2012). Female-biased populations are a concern with respect to exposures to environmental estrogens (e.g., Purdom et al., 1994; World Health Organization, 2002). However, experimental data show that perturbation of some HPG pathways of concern (e.g., androgen receptor activation, aromatase inhibition) can produce male-biased populations (Ankley & Johnson, 2004; Guillette et al., 1995) potentially producing effects in the field (Bortone & Cody, 1999; Durhan et al., 2006; Hanson et al., 2005; Howell et al., 1980; Larsson et al., 2000; Orlando et al., 2004; Parks et al., 2001; Soto et al., 2004). The present model circumvents the limitation of previous models that employ Leslie projection matrices that consider only females, by allowing for explicit quantification and consideration of how dynamics of both sexes induce changes in population status. Formulation of the model in this way allows for effects from a stressor to be quantified for fish in the population specific to any given combination of sex and age.

The modeling approach demonstrated in the present study enables simultaneous consideration of impacts of EACs on multiple life-stages. Many types of EACs are capable of affecting multiple HPG pathways, potentially dependent on the life stage exposed. Exposures to EACs in field settings are complex often involving multiple chemicals that could impact different HPG pathways. Such exposures also will often be relevant to multiple generations within a population, particularly if inputs of an EAC(s) are constant, as would be the case for persistent or pseudo-persistent chemicals (Ankley et al., 2007). Consequently, population models that can consider the combined effects of an EAC(s) on different pathways relevant to different life-stages can provide a more realistic prediction of EAC impacts on a population than previous models. Practical applicability of the model of Equations 1 and 2 to consider multigenerational EAC effects was demonstrated using a dataset from a FSDT design that enables collection of HPG-responsive endpoints at different life-stages (Holbech et al., 2012; OECD 2018). The modeling demonstrated that although either the effect on sex ratio (AOP 346) or the impact on VTG production in adult females (AOP 25) could be expected to have a population-level effect, in combination it was the effect on female fecundity (via the reduced VTG) that was the more significant of the two impacts. A multidimensional modeling construct as presented herein could be used in this manner for other types of EACs/exposure scenarios to discern most susceptible endpoints/lifestages.

While the modeling and case study employed in the present study focused on potential impacts of EACs, other environmental stressors also have potential to bias sex ratios in fish and some other vertebrates. For example, many reptiles and some fish are known to have temperature dependent sex determination (Ospina-Álvarez & Piferrer, 2008; Shen & Wang, 2014; Yamaguchi & Iwasa, 2018) and warmer waters associated with global climate change have potential to masculinize some wild populations (Geffroy & Wedekind, 2020; Honeycutt et al., 2019). Alterations in habitat color or exposure to stress hormones like cortisol have also been shown to potentially create male bias in some species (Mankiewicz et al., 2013). Consequently, the multidimensional model illustrated in the present study can be expected to have applications beyond EACs and the specific AOPs examined.

Conceptually, the model can also be applied to a diversity of species. However, life history in relation to exposure dynamics and the mechanism(s) of sex determination employed in different fish species are an important consideration. The subject of the present modeling effort, the fathead minnow, is viewed as a r-selected species that produces a large number of offspring, each with a fairly low probability of survival. However, certain fish species are K-selected and produce comparatively few offspring, have longer times to sexual maturity, and an overall greater chance of reaching reproductive maturity. Adjustment of the vital rates within the life table (that result in the corresponding survivorship curves and maternity schedules) to the species of interest is critical in successful application of the model. For example, Thursby (2009) describes a methodology for formulating the survivorship curve for R versus K-selected species using a Weibull function. In addition, although aromatase activity and the ratios of estrogen to androgen concentration during differentiation appears critical to sex ratio determination in many species (see AOP 346; https://aopwiki.org/relationships/2167; accessed January 31, 2021), the same mechanism(s) may not hold in all species. Thus, reproductive strategy, mechanisms of differentiation, and even habitat with regard to potential for immigration and emigration all come into play when considering application to other species.

The model of Equations 1 and 2 utilized the assumption of a closed system. However, a metapopulation modeling approach (Galic et al., 2010) that integrates multi-patch spatial dynamics within Equation 1 can accommodate both immigration and emigration scenarios using the addition of population vectors to represent individuals of each age class entering or exiting the population at each time step. For example, expanding Equation 1 yields:

$${\mathbf{\text{n}}}_{\mathbf{t}+1}=\exp \left(-r{P}_t/K\right){\mathbf{\text{M}}}_1{\mathbf{\text{n}}}_t+{\text{i}}_t-{\text{e}}_t$$ (5)

where i_t is a vector of age structure at time t entering the population through immigration, and e_t is a vector of age structure at time t exiting the population through emigration. Application of a model construct whereby immigration and emigration fluxes are included will affect the resulting population trajectories because of the influence of the age structure, sex, and exposure history of fish moving into and out of the population at each time step. Such an approach would be appropriate for examining habitats that are spatially complex or for fish stocking programs whereby the immigration vector acts to include fish stocked, potentially of a specific age and/or sex.

In summary, the multidimensional matrix modeling approach employed in the present study can project population age structure for both females and males under conditions for which the sex ratio of the population varies over any given length of exposure time series. The model provides support for an inferred causal connection between male-biased sex ratio and potential adverse population-level consequences (AOP 346; https://aopwiki.org/relationships/2147). Further, this model allows for analysis that integrates multiple dimensions, such as evaluation of a given age class of a given sex. The modeling construct was successfully demonstrated to investigate complex multigenerational responses anchored to separate AOPs acting in concert on an exposed population of fish. The population model derived and applied in the present study facilitates inclusion of more than one attribute of the individual, as determined in field monitoring efforts (e.g., through effects-based monitoring programs) and/or laboratory experiments to link effects resulting from exposure to stressors to adverse outcomes in individuals and populations.

Data Availability Statement—

Data, associated metadata, and calculation tools are available from the corresponding author (miller.davidh@epa.gov).