Nonplanar 3D Printing of Bifurcating Forms

Abstract

The introduction of robotic arms in additive manufacturing enables the scaling up of three-dimensional (3D) printing processes and the realization of nonplanar path geometries. As a result, novel design potential is unlocked by having control over the layered configuration of paths in the object, and 3D printing becomes viable for architectural applications. However, the various challenges associated with creating feasible nonplanar layered paths for the realization of large-scale objects are hindering their integration in the design process and broad use. This work presents methods that contribute to the flexible and intuitive design of nonplanar layered paths for robotic printing. We focus on the challenges related to the realization of single-shell bifurcating structures, with emphasis on the paths' behavior on the bifurcating moments of the shapes. Our methods are based on the use of design techniques that originate from implicit shape representation and on the detection of critical points on the surface through the lens of distance functions. We present fabricated prototypes printed with nonplanar paths that showcase the possibilities of our methods.

Introduction

Recent advances in additive manufacturing (AM) technologies have revolutionized the way physical objects can be produced. AM opens a new world of possibilities, promising to enable the realization of nonstandard forms with unprecedented geometric complexity, at no extra cost, and with minimal waste. Fused deposition modeling (FDM), one of the most widely used three-dimensional (3D) printing technologies, is a process during which the filament of thermoplastic material is extruded continuously from a hot nozzle in linear segments that are accumulated to create a shape. FDM is not only a hobbyist technology but it also has noteworthy applications in the industry. In the realm of architecture and construction, FDM can be used to create multifunctional architectural components such as façade panels,^1,2 bespoke floors,³ molds for concrete casting,^4–6 full-scale pavilions,^7–9 or it can be integrated into multimaterial prints with enhanced properties.^10,11

While three-axis gantry system printers commonly enable FDM, lately, a lot of research explores the potential of using machines with five or more degrees of freedom by attaching the extruder or print base to a robotic arm. This facilitates the creation of bigger parts and the realization of nonplanar paths, that is, paths that are not sliced along a fixed direction and can vary in orientation and layer height. The resulting flexibility in the geometry of paths can help tackle various disadvantages inherent to planar 3D printing, such as the discretization artifacts,¹² the need for additional support on overhanging parts,^13,14 and the anisotropy of printed objects.^15,16 This body of research demonstrates the significant impact that the configuration of paths can have on the feasibility, cost, machining time, aesthetics, and structural properties of a 3D-printed object.

However, various challenges come along with the novel possibilities for the realization of nonplanar paths. In the motion planning and fabrication process, collision, reachability, and smoothness constraints complicate the translation of a path geometry into fabrication commands. In addition, the design of paths increases in complexity, as the slicing problem is no longer well defined and requires additional constraints or requirements to narrow down the vast space of possible solutions. These can take the form of optimization objectives, user input, or a combination thereof. While various approaches have been proposed for optimizing the paths' geometry,^14,16 not a lot of research has been devoted to methodologies for enabling the user's control over the print paths.

We focus on enabling the user-controlled design of print paths that have the potential of scaling up and can thus be viable for architectural applications. Large-scale paths are qualitatively different from smaller scale paths. They spread more, forming oriented surfaces, and their interruption becomes more challenging as the material deposition rates increase. These characteristics require a print process with as few interruptions as possible and with smooth changes in path orientations. Also, scaling up dictates that the fabricated object must remain static during the print process instead of being attached to a mobile platform,^13,14,16 so that its mass can increase without influencing the process. To address these requirements, we investigate the 3D printing of single-shell surfaces that consist of one layer per level without infill, offsets, or support. These are printed with continuous spiral paths, using an extruder attached to a robotic arm while the object remains static.

In this article, we extend existing work¹⁷ and focus on enabling the user-controlled design of nonplanar paths for shapes that contain bifurcations, as there are various challenges and opportunities associated with the nonplanar printing of these geometries. We also propose a method for partitioning higher genus geometries into simpler bifurcating shapes, which makes our approach relevant for a great variety of geometries. The overall aim of the proposed methods is to facilitate the flexible and intuitive design of nonplanar layered print paths for FDM printing, driven by user input.

Background

Nonplanar 3D printing

Curved base

One of the first attempts to create truly 3D layers by printing offsets of constant layer height on a curved base was proposed in Curved Layer Deposition Modeling,¹⁸ where nonplanar paths are aligned with the surface of shell-like geometries. This method results in better surface quality compared with planar layered 3D printing, as well as improved strength due to fiber continuity.¹⁹ The printing of variable thickness layers on a curved base,²⁰ the smoothing of the printing path, and the adjustment of the material feed rate to account for the overlap between adjacent paths²¹ can further improve the surface quality of FDM thin shells. A disadvantage of such methods is that they require a custom base that can constrain the geometry, raise the cost, and the material waste for the parts' production.

Planar base

Height variation within individual layers enables the realization of curved layers on planar generic support and can help to improve the quality and strength of the prints. In Anti-aliasing for FDM,¹² layers are printed by altering both the material feed rate and the height of the nozzle achieving height variations that compensate for the discretization artifacts. In Support-Free Volume Printing,¹⁴ curved print paths with smooth changes in orientation are used to achieve support-free printing. With a similar objective of reducing the need for support, Xu et al.²² propose a slicing process based on tracing the isocontours of the shape's geodesic distance from a planar base. In Reinforced FDM,¹⁶ curved layers are designed to align with the principal stress directions, leading to improved mechanical properties of the printed object. These methods are based on optimizing predefined objectives, using computational processes that do not enable direct design control over the paths' configuration.

On the contrary, methods have been proposed to incorporate user input, given in the form of boundary conditions. Zhong et al.²³ propose an interactive modeling and fabrication framework that relies on sweeping surfaces as a design tool to create clay single-shell surfaces. Another recent work, Print Paths Key-framing,¹⁷ which is the precursor to our work, proposes the design of print paths by interpolating user-defined boundaries. This method relies on calculating an interpolating distance field, leading to paths described as isolines that morph between the boundaries. However, the types of shapes that can be realized with that method are limited to simple geometries. Our work builds upon this method, proposing extensions that address existing limitations, facilitate the user input, and enable the generation of feasible paths for a broader type of geometries.

Shape partitioning

The decomposition of models for 3D printing is a well-investigated topic that can facilitate various aspects of the printing process. We can distinguish two segmentation workflows: the segmentation into pieces that are printed separately and assembled in a later step, and the segmentation into pieces that are printed on top of each other in the same printing process, resulting in one object. The first workflow can be used to address the challenge of objects exceeding the machine's printing volume,²⁴ reduce the print time,²⁵ save printing space, or preserve surface details.²⁶ The second workflow aims to facilitate or simplify the design and fabrication process by meaningfully decomposing the object into simpler parts that constitute smaller domains, which are easier to design and plan for than when considering the entire shape at once. In FDM research, this partitioning workflow has been used in combination with multiaxis printing to reduce the need for additional support. The object is decomposed into parts printed on a mobile platform with different orientations, having one discrete rotation for the print of every part.^13,27,28 In our work, we present a partitioning method that adheres to this second workflow, that is, the different parts are printed on top of each other in one printing process, producing a single final piece.

Morphology of a scalar function

A discrete function defined on the mesh vertices can be linearly interpolated in each face so that a piecewise constant gradient can be associated with each face.²⁹ The gradient of a function is a vector field representing the magnitude and direction of its greatest increase rate.

Given a scalar function defined over a manifold, Morse Theory³⁰ investigates the structure and topology of the surface through the lens of the function's values by looking at critical points (i.e., minima, maxima, saddles) where the gradient vanishes. The critical points correspond to changes in the topology of the level sets of the function, where they split, merge, change genus, appear, and disappear. The contour tree is a graph that describes the relationship between the critical points in a simply connected domain.^31,32 The Reeb graph, which we use in this work, is a generalization of the contour tree for more complex domains.³³ Although initially devised for smooth functions on continuous manifolds, Morse Theory has been extended to the discrete setting, with piecewise linear functions on triangle meshes.^34,35 In this setting, critical points occur at the vertices of the mesh.

A plethora of applications in geometry processing is based on Morse Theory and Reeb graphs. The most relevant to our work are the analysis and decomposition of a model based on critical points that has been used to extract salient features of a shape^36,37 and has been applied to various processes, such as analysis of terrains³⁸ or segmentation of molecular structures.³⁹ Inspired by these approaches, we use the critical points of the geodesic distance function on the mesh to partition complex shapes and help with the task of selecting targets for the design of the nonplanar paths.

Method

We present extensions to the approach proposed in Mitropoulou et al.¹⁷ to design nonplanar paths for single-shell layered robotic 3D printing, driven by user-defined targets that are interpolated. Our methods address several challenges identified in that work related to the design and fabrication of bifurcating shapes. These challenges concern the following points: first, the selection of targets for complex shapes; second, the interpolation of more than two curves on the same shape; and third, the handling of nonuniform path spacing in the proximity of saddle points of the distance function that occur at the bifurcating points.

Our contributions that address the issues described above can be summarized in the following points. Based on the detection of critical points, we propose heuristics that facilitate the target selection and enable a scheme for surface segmentation, leading to a more uniform distribution of paths, avoiding holes in the saddle points near bifurcations. In addition, we present combination operations that enable the interpolation of multiple target curves on the same shape. We also propose a method to handle interpolation of asymmetric target curves with respect to the base using offsetting of their distance functions. Finally, we present fabricated prototypes that demonstrate the forms that can be fabricated using the proposed methods.

Workflow

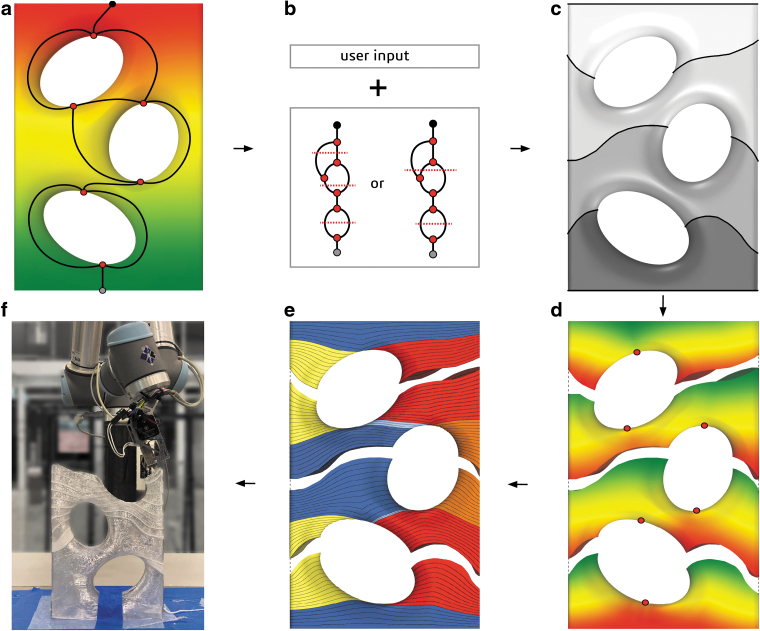
Our workflow begins with the input of a triangular mesh placed on the build platform. The heuristics, described in the section “Target selection heuristics,” that are based on the Reeb graph of the shape (Fig. 1a) guide the user in the process of providing the targets that control the orientation of paths (Fig. 1b). Once the targets have been set (Fig. 1c), cuts are created on their position, splitting the mesh into components (Fig. 1d), which reduces the challenge to interpolating the targets on each component. We propose various methods to interpolate groups of targets based on alternative combinations of their geodesic distances, described in the section “Target interpolation.” If a target consists of multiple curves that have uneven geodesic distances from the other target of the component, offsets are calculated to equalize their average distance from the other target, leading to smoother interpolation results, described in the section “Offsetting.” Once the interpolation method and offsets have been specified, the hidden partitioning of the surface modifies the paths in the vicinity of saddle points to avoid the appearance of holes, while keeping the orientation of the paths intact in the rest of the shape (Fig. 1e), as described in the section “Hidden partitioning.” Finally, the interpolating paths are generated for each part, and the production data are sent to the robot for fabrication (Fig. 1f).

FIG. 1.

Overview of the workflow. (a) Creation of the Reeb graph using the geodesic distance from the base as a scalar function. (b) Heuristics and user input in the form of curves creating targets that control the orientation of the paths. (c) Creation of cuts in the position of the targets splitting the mesh into components. (d) Identification of the saddle points of the interpolating distance function of each component. (e) Hidden partitioning of the components into parts using cuts that intersect the saddle points and generation of paths on each part. (f) Fabrication process of each part, resulting in one piece where the hidden cuts are no longer visible.

Target selection heuristics

The creation of targets to be interpolated is the main way the user can interact with the process to control the orientation of paths. At the same time, their shape and location play a critical role in the feasibility of the generated paths. A challenge in the creation of targets is that not all inputs can lead to feasible results. In fact, finding suitable targets that lead to printable paths requires a lot of experience and trial-and-error attempts. The following method aims to facilitate the users' task of providing targets by guiding them regarding where to position the targets.

The critical points and Reeb graph of a scalar function over a mesh convey important information about its topological structure. We use the geodesic distance from the vertices that lie on the base as a scalar function. Considering this function, we find the critical points and evaluate the level-set evolution to create the Reeb graph (Fig. 2). Based on that, we propose simple heuristics that can guide the user while selecting targets.

FIG. 2.

Local minima (gray markers), local maxima (black markers), saddle points (red markers), and Reeb graphs in a collection of two-dimensional shapes (a, b) and three-dimensional shapes (c–e) considering the geodesic distance from the base of each shape, shown with a color gradient. In the areas where many neighboring local minima or maxima vertices are positioned, they are displayed with a single marker.

The distance function attributes at each vertex i a distance value v_i. To find the vertices that are critical points, we walk around the neighborhood (i.e., the link) of every vertex $i,$ and for each neighbor j we count the number of sign changes of $v_j-v_i$. If the number of sign changes equals two, then the point is regular; otherwise, it is critical, as described in Zhou and Huang.³⁷ To avoid unwanted critical points, we preprocess the function space with an iterative Laplacian smoothing, which cancels critical points that appear due to small local variations or noise.⁴⁰

Our empirical experimentations lead us to propose the following two heuristics for the targets' location. First, targets should be situated in the vicinity of the local maxima, so that their interpolating function does not have great variations in evolution speed. When the local maxima are situated on naked edges, then the entire edge can be used as a target to create a smooth finishing. Second, when closed loops are formed in the Reeb graph, which correspond to high genus meshes, targets should be positioned to split the loops into simpler parts. This can be achieved by placing targets across the cycles of the graph, so that the subsequent step of cutting the shape along the targets results in parts that do not contain cycles (Figs. 1b, 2b, e). In complex shapes, there is often more than one option for how to cut through the cycles (Fig. 1b); in that case, any of the ways can lead to the desired results.

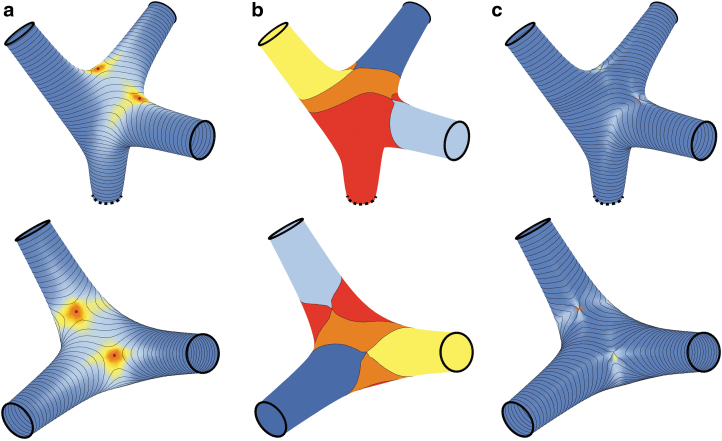
In Figure 3, the advantages of the presented heuristics are demonstrated with examples. The use of targets in the vicinity of the local maxima leads to paths with smaller variation in layer height (Fig. 3a). The splitting of the cycles is useful when the branches have different sizes, and thus, the distance traversed on one is different than the distance traversed on another. When the cycles are not split, the same number of paths is fit in all branches leading to large layer height variations (Fig. 3b, left). Splitting the cycles allows fitting the suitable number of paths on each branch, maintaining a layer height with fewer variations (Fig. 3b, right).

FIG. 3.

(a) Generation of print paths using a target away from (left) and in the vicinity of (right) the local maximum. (b) Generation of print paths on a mesh that contains a handle without splitting the loop (left) and after splitting the loop (right). An indication of the properties of the interpolating distance fields is given by the visualization of the magnitude of their gradient in color scale, which is calculated per face for t = 0.5, showing the speed with which the underlying distance field is evolving; as this decreases, two neighboring isocontours become further apart.

The output of the application of the heuristics is a schematic representation, annotated with the proposed locations of targets in a way similar to Figure 2, provided as guidance to the user. While this facilitates finding a suitable number and location of targets, their exact position and form are left for the user to define, allowing to maintain the design freedom in the process.

Target interpolation

Once the targets have been defined, the surface is split along them into components whose Reeb graphs do not contain cycles, and which might or might not have bifurcations. On each component, the target curves are grouped into two targets labeled as “base” or “upper” targets considering the relationship of the component with the entire shape, which describes their role as start or end in the subsequent interpolation step. In the figures, the base targets are marked with dotted black lines, and the upper targets are displayed with continuous black lines. For the remainder of this section, we describe the subsequent process for a single component that has one or more bifurcations.

Union operations

The interpolation of two targets on shapes without bifurcations has been described in Mitropoulou et al.¹⁷ There the interpolating distance field is given by

where d₁, $d_2$ are the geodesic distances from the two targets, and t is the interpolation parameter in the domain (0,1].

In bifurcating shapes, however, Equation (1) is not directly applicable as there are more than two curves that need to be interpolated. For example, the shape illustrated in Figure 4 has three curves; the distance fields of the two upper curves need to be combined into one for the interpolation step. Combining distance fields offers broad possibilities for design variation while also impacting the fabrication process parameters.

FIG. 4.

Union operations for the combination of the curves of the upper target (in continuous black lines) that are interpolated with the base target (in black dotted lines). (a) Standard union. (b) Smooth union. (c) Chamfer union. (d) Stairs' union.

Assuming that the lower and upper targets consist of N and M curves, respectively, then the geodesic distances are calculated from each curve, leading to two sets of distances $D_1=\left\{d_1,\dots ,d_N\right\}$ and $D_2=\left\{d_1,\dots ,d_M\right\}$. Multiple geodesic distance calculations can be computed efficiently on the same mesh using the heat geodesic method by solving a sparse linear system that can be prefactored and efficiently resolved many times.⁴¹

The geodesic distances are combined using union operations. The simplest union $\cup$ of distance fields consists of taking the minimum of the distances that originate from each source.⁴² Then the interpolating distance function (1) for the generation of K isolines becomes

where $\cup \left(D\right)$ is the union, in this case, minimum of all the values in D (Fig. 4a). A disadvantage of this union is that it creates visible nonsmooth kinks in the proximity of the saddle points. These cause abrupt changes in orientation and layer height, which pose fabrication challenges and can lead to inferior surface quality.

A blending union operation can smoothen these discontinuities. From the various blend unions, such as quadratic, cubic, or exponential smooth minimum,⁴³ we use the quadratic smooth minimum (Fig. 4b) ${\cup }^{blend}\left(D,r\right)$ that for N distance fields is defined by the recurrence relationship

where r is the blend radius that determines the scale of the influence of the smoothing operation, and

The initial condition ${\cup }_0$ is a number significantly higher than the geodesic distances appearing on the shapes. As opposed to smoothing the entire distance function, this blend only affects the areas close to the transition from one distance field to the other, leading to a smoother variation of orientations and layer heights in that area.

Further design articulation of the paths can be achieved by using other union operations that morph the isocontours in the areas around the saddle points, such as the operations described in hg_sdf,⁴⁴ developed within the context of implicit modeling and ray-marching rendering. For example, the chamfer union (Fig. 4c) ${\cup }^{chamfer}\left(D,r\right)$, defined by the recurrence relationship

creates a chamfered edge (the diagonal of a square of size r). Also, the stairs' union (Fig. 4d) ${\cup }^{stairs}\left(D,r,p\right)$ produces a stair effect with p peaks, defined by the recurrence relationship

This nonexhaustive description of union operations shows that the different combinations of targets offer additional design flexibility to create aesthetic path configurations that would not be possible with traditional slicing methods.

Offsetting

In a union operation of a target's distance fields that originate from different sources (either curves or isolated points) $C_1,\dots ,C_N$, differences in the average geodesic distance of these sources from the base can create paths with inconsistent spacing (Fig. 5a–e left). To tackle this, we use the following scheme to offset the distance fields according to their average geodesic distance from the base (Fig. 5a–e right).

FIG. 5.

Interpolation between targets that consist of sources with uneven average geodesic distances. Red letters show the source values k_i that define at which point during the interpolation each curve is “reached” by the isocurve of the interpolating distance field. The color scale indicates the norm of the gradient of the distance field. (a–e). Left: Naive interpolation, corresponding to all source values being t = 1.0. Right: Offsetted interpolation where each source value k_i is defined by its average geodesic distance from the base. (f) Controlling the position of the saddle point using the source values.

From every source C_i we calculate the average geodesic distance d_i to the base, and subsequently, assign it a source value $k_i=\frac{d_i}{d_{max}}$, where $d_{max}=max\left(d_1,\dots ,d_N\right)$. We then compute one interpolating distance field per source with interpolation parameter ${\overline{t}}_i=\frac{t_i}{k_i}$, $t_i\in \left[0,1\right]$, and finally, apply the selected union operation to achieve a single interpolating field for each of the K desired isolines. Then Equation (2) becomes

The source values k_i (shown in Fig. 5 in red letters) define at which point during the interpolation the source C_i is “reached” by the isocurve of the interpolating field. By changing k_i the saddle points situated between the sources change location. Manually assigning k_i enables the user to control the position of the saddle points within a certain range (Fig. 5f).

Hidden partitioning

The gaps that appear in the area of the saddle points are a central challenge in the fabrication of bifurcating shapes (Fig. 6a). These gaps increase when smooth or other morphing union operations are applied, leading to artifacts, holes, or failure in the fabrication process. To tackle this, we propose a hidden partitioning method that aims to remove these artifacts while maintaining the orientation of the paths intact wherever possible. This is achieved by creating cuts that intersect the saddle points while following the contours of the interpolating distance field, which separate the mesh into a set of simpler parts without saddle points (Fig. 6b). The interpolation on each produced part separately results in better spaced paths (Fig. 6c). In addition to this benefit, the segmentation is meaningful for the fabrication process, as each resulting part can be printed with a continuous, uninterrupted spiral path. The hidden partitioning does not change the overall behavior of the paths, except in the areas of the saddle points, where artifacts would otherwise be produced. As a result, these cuts are not visible on the final printed object.

FIG. 6.

Surface partitioning intersecting the saddle points of the distance function into parts that can be printed with one uninterrupted path. (a) Gaps between neighboring paths created on saddle points. (b) Segmented surface. (c) Paths on the segmented surface.

The partitioning process consists of two steps. First, we find the interpolation distance fields that intersect each of the P saddle points, represented by their interpolation weights $t_c=\left\{t_{c1},\dots ,t_{cP}\right\}$. Since there are small variations in the location of the saddle points as t varies, t_c is found with iterative refinement. Initially, the location of saddle points is coarsely specified using $t=\frac{1}{2}$. After that, one or more steps of refinement are performed, searching near the identified saddle points for parameters $t_{ci}$, which produce interpolation fields that intersect the saddle points, that is, produce a value near 0 on the vertex where the saddle point is situated.

Subsequently, one cut is created at the isoline that corresponds to each $t_{ci}$. Due to the finite precision, the resulting isoline deviates from exactly intersecting the vertex where the saddle point is located. To remedy this, we modify the isoline by merging the parts that intersect edges with the saddle point (Fig. 7a). The cut is created by splitting each edge crossed by the modified isoline in two. The segments of the cutting isoline that are not in the proximity of the saddle point are not used to create cuts, as illustrated in Figure 7a, where the red dotted line is ignored. Figure 7b–d shows the result of the segmentation on various meshes.

FIG. 7.

(a) Details in the creation of the cut. (b–d) Results of surface segmentation on various shapes.

Fabrication setup

Our fabrication setup consists of a UR5 robot and a custom FDM extruder with nozzle diameter mm ø_n $=2.5$, which extrudes the polyethylene terephthalate glycol filament with a diameter of ø_f $=2.75$ mm (Fig. 8b). The print process is carried out with a constant linear print speed of 20 mm/s, which is scaled down to 10 mm/s in the areas of large changes in path orientations or layer heights. The end-effector orientation varies and it is selected so that the tool points toward the direction of closest solidified support within an angle threshold, while taking into account collisions and smoothness considerations.¹⁷ The material feed rate at each position is calculated to match the required volume of material for the desired layer height at each path segment.

FIG. 8.

Overview of the process for the fabrication of a bifurcating shape. (a) Surface segmentation. (b) Print process. (c) Final prototype.

Results

Using the techniques described above, we successfully fabricated the following prototypes that showcase the type of geometries and print path geometries that can be achieved. The implementation of our work is available in the open-source python package compas_slicer,⁴⁵ based on the libraries compas⁴⁶ and libigl.⁴⁷ The geometries of the shapes were generated using the Grasshopper⁴⁸ library Axolotl.⁴⁹

The single-shell print method with continuous paths that we are using makes sense for printing at a larger scale of furniture or architectural components. The prototypes that we present in this section are scaled studies that address only the geometric aspects of the design of paths. The scale of the prototypes ranges from a height of 10 to 40 cm. The scale indication in the photos of prototypes represents centimeters. The models were sliced with an average layer height of ∼1.4 mm, considering a constant layer width of 2.5 mm.

The different combination operations were tested on a simple bifurcating shape (Fig. 9). The paths generated using the standard union (Fig. 9a) have an abrupt change in orientation and layer height around the saddle point, which can be realized with significantly slower print speed around that area. The paths generated using the smooth union (Fig. 9b) are a lot easier to fabricate as their orientation and layer height vary smoothly; therefore, constant speed can be kept in the print process. The chamfer union (Fig. 9c) poses challenges due to the risk for collisions, as the almost-straight paths created from the chamfering meet in an extended area around the saddle point, where the tool can collide with paths from the other side. To avoid these collisions, the area around the saddle point was printed with an almost vertical tool orientation. Finally, the stairs' union (Fig. 9d) also poses fabrication challenges due to the nonsmooth changes in orientation and layer height around the peaks of the stair pattern. Another challenge in this union comes from the two additional maxima that appear, which create disconnected islands that need to be printed separately with lower print speed. However, with the correct tuning of print speed and print orientation, all combination operations are feasible, creating an aesthetic result that would not be possible with traditional slicing methods.

FIG. 9.

Fabrication of paths generated with different union operations. (a) Standard union. (b) Smooth union. (c) Chamfer union. (d) Stairs' union. The change in filament color was done without interrupting the print process with the purpose of visually accentuating the geometry of the paths.

As the smooth union was found to be the most favorable for both path design and fabrication, it was applied to the demonstrators presented in this work. The prototypes illustrated in Figures 8c and 10a are shapes that are branching out and have an upper target that consists of multiple curves with uneven average geodesic distances from the base. For the generation of their paths, we used the offsetting of each curve's distance field that we described in the previous section. The prototype in Figure 10c, on the contrary, demonstrates a shape that is branching in from a base target that consists of multiple curves to an upper target with a single curve. Here the same offsetting technique was used, applied instead on the base target's distance functions with respect to the upper target. The prototype in Figure 10b is an example of how a shape with handles can be realized with our method. This shape was partitioned into simpler components (Fig. 1) that were printed on top of the other to form a single object. White stripes of filament were added in the model to accentuate the paths' varying orientations. Finally, the prototype in Figure 10d demonstrates how closed shapes can be fabricated using targets that consist of single points situated on the local maxima of the distance function from the base, resulting in spiral paths that create a closed surface with peaks.

FIG. 10.

Fabricated prototypes. (a) Shape that is branching out. (b) Shape with handles. (c) Shape that is branching in. (d) Closed surface.

Contributions

In this work, we extend the method presented in Mitropoulou et al.¹⁷ for the user-controlled design of nonplanar paths, using the same fabrication process and material. In the previous work, the range of geometries that could be fabricated was very limited, and the results were picked to conform to the limitations; the targets had to be equidistant from the base (making unfeasible, e.g., all the shapes illustrated in Figs. 5 and 10, allowing only for shapes similar to the one in Fig. 7c). Also, closed loops could only consist of branches of the same size (making unfeasible shapes such as the one in Figs. 3b or 10b), and there was no control over the behavior of the paths around the saddle points of the distance function (such as in Figs. 5f and 9). As a result, the printed prototypes presented in this article (Figs. 8–10) were not possible with the previous method. With these, our work contributes to increasing the range of geometries and the flexibility in the inputs that can be used for nonplanar slicing of single-shell shapes that contain bifurcations.

Discussion

The realization of bifurcating shapes using nonplanar paths with the described methods exhibits various aesthetic and practical advantages; it decreases the need for external support of overhanging parts and leads to paths that follow the morphology of the geometries. The main strength of our approach in comparison with the existing state of the art is that it enables intuitive design control over the print paths so that their generation can become part of the design process.

However, a series of limitations must be discussed. Our methods do not provide a formal guarantee for the feasibility of the resulting paths, which remains dependent on the user-provided inputs. The most common issue causing a print to be unfeasible is when the distance between the neighboring paths exceeds the maximum layer height that can be achieved with the fabrication setup. The software spots these occurrences, and a warning is issued that notifies the user that further processing of the inputs is needed. In addition, while our prototypes have remarkably good surface quality, they can still exhibit artifacts occurring in areas where the smoothness of the end-effector motion has to be compromised with abrupt changes in orientation to avoid collisions with the environment or the object being printed. Finally, other fabrication constraints have not been considered, such as the object's stability during the print, which can be precarious when it has a base with a small footprint and receives lateral forces from the extruder. This needs to be considered for the further scaling up of the prototypes, where such instabilities can cause the failure of the fabrication process.

Conclusion

We presented methods that enable designing nonplanar print paths in a flexible and intuitive way for robotic 3D printing in this work. We focused on the challenges posed by bifurcating shapes printed with a single shell that have targets consisting of multiple sources. We also presented a segmentation method that helps avoid artifacts and holes around the saddle points of the distance function while partitioning the objects into simpler parts that can be printed with one continuous path.

Bifurcating shapes appear in the architecture in different forms, making our work relevant for a variety of future applications. Vertical supports such as freeform columns often form tree structures with bifurcations that can transfer distributed loads efficiently to the ground and have a strong aesthetic character. In addition, bifurcations appear in joints of nonstandard assemblies that have branches in the directions of the elements that they connect. Finally, the application of topology optimization on surface elements results in high genus structures with a number of handles. These shapes can be partitioned into simpler bifurcating shapes using the described methods. The design of paths for these shapes can also be a future application of our method.

While the presented prototypes demonstrate the usefulness of nonplanar paths for filament extrusion, our methods could be applied to other fabrication systems and materials. For scaling up, pellet plastic extrusion could be a promising method as it enables significantly higher material deposition rates in comparison with filament extrusion. Architectural materials such as clay or concrete are also promising candidates for printing with our methods since they are commonly used for single-shell shapes realized with continuous paths. For the application of the presented methods in materials other than plastic, the ratio of minimum to maximum layer height that can be realized with a given fabrication setup, as well as the maximum overhangs that can be achieved, needs to be defined. We speculate that our methods can be feasible for concrete or clay printing, however, they might require smoother changes in the path orientation and more conservative thresholds in the allowable overhangs and variations of layer height.

The results of this work are encouraging, as they show various aesthetic and practical advantages of using continuous nonplanar paths. We are confident that the further scaling up of the prototypes is feasible, which will be the next step of our work. With this, our work contributes to the development of methodologies that facilitate the design of nonplanar paths that can be viable for large-scale 3D printing.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

This work is supported by the Architecture & Technology (A&T) Ph.D. scholarship of the Institute of Technology in Architecture, ETH Zurich.