Virtual Particle Monte Carlo (VPMC), a new concept to avoid simulating secondary particles in proton therapy dose calculation

Abstract

Background:

In proton therapy dose calculation, Monte Carlo (MC) simulations are superior in accuracy but more time consuming, compared to analytical calculations. Graphic Processing Units (GPUs) are effective in accelerating MC simulations but may suffer thread divergence and racing condition in GPU threads that degrades the computing performance, due to the generation of secondary particles during nuclear reactions.

Purpose:

A novel concept of virtual particle (VP) MC (VPMC) is proposed to avoid simulating secondary particles in GPU-accelerated proton MC dose calculation and take full advantage of the computing power of GPU.

Methods:

Neutrons and gamma rays were ignored as escaping from the human body; doses of electrons, heavy ions, and nuclear fragments were locally deposited; the tracks of deuterons were converted into tracks of protons. These particles, together with primary and secondary protons, are considered to be the realistic particles. Histories of primary and secondary protons were replaced by histories of multiple VPs. Each VP corresponded to one proton (either primary or secondary). A continuous-slowing-down-approximation (CSDA) model, an ionization model, and a large angle scattering event (LAE) model corresponding to nuclear interactions were developed for VPs by generating probability distribution functions (PDFs) based on simulation results of realistic particles using MCsquare. For efficient calculations, these PDFs were stored in the Compute Unified Device Architecture (CUDA) textures. VPMC was benchmarked with TOPAS and MCsquare in phantoms and with MCsquare in thirteen representative patient geometries. Comparisons between the VPMC calculated dose and dose measured in water during patient-specific quality assurance (PSQA) of the selected 13 patients were also carried out. Gamma analysis was used to compare the doses derived from different methods and calculation efficiencies were also compared.

Results:

Integrated-depth dose and lateral-dose profiles in both homogeneous and inhomogeneous phantoms all matched well among VPMC, TOPAS, and MCsquare calculations. The 3D-3D Gamma passing rates with a criterion of 2%/2mm and a threshold of 10% was 98.49% between MCsquare and TOPAS, and 98.31% between VPMC and TOPAS in homogeneous phantoms, and 99.18% between MCsquare and TOPAS and 98.49% between VPMC and TOPAS in inhomogeneous phantoms, respectively. In patient geometries, the 3D-3D Gamma passing rates with 2%/2mm/10% between dose distributions from VPMC and MCsquare were 98.56±1.09% in patient geometries. The 2D-3D Gamma analysis with 3%/2mm/10% between the VPMC calculated dose distributions and the 2D measured planar dose distributions during PSQA was 98.91±0.88%. VPMC calculation was highly efficient and took 2.84±2.44 seconds to finish for the selected 13 patients running on four NVIDIA Ampere GPUs in patient geometries.

Conclusion:

VPMC was found to achieve high accuracy and efficiency in proton therapy dose calculation.

Introduction

Pencil beam scanning proton therapy (PBS) is the most advanced form of proton therapy. It has distinct advantages of high conformality of target coverage and superior protection of nearby organs-at-risk (OARs) when compared with the photon-based therapy and passive scattering proton therapy, which was brought by its exceedingly high flexibility at the beamlet level in treatment planning and dose delivery^1–4. A sufficiently accurate dose calculation engine is the foundation for plan optimization and evaluation in PBS to achieve “what you see is what you get”. Meanwhile, a large amount of calculation is required due to the large number of voxels and the large number of beamlets with multiple perturbed scenarios considered in robust optimization^5–32. Thus, the dose calculation engine should be fast enough and meet the efficiency requirement in clinical practices of robust PBS treatment planning.

Analytical dose engines^33–35 are widely used in the commercial and in-house treatment planning systems (TPSs), which are fast, but with less accuracy. On the other hand, Monte Carlo (MC) simulations are considered to be the gold standard for dose calculation in proton therapy. Clinically significant differences between the dose distributions from analytical and MC dose calculation engines have been reported, especially in heterogeneous geometries such as the lung and head and neck (H&N) sites^36,37 with bones, air cavities, and dental implants, etc. The resulting inaccurate dose distributions might mislead healthcare practitioners and cause unexpected adverse events (AEs) and local failure in cancer patients treated with PBS.

General-purpose MC codes (e.g. Geant4³⁸, MCNPX³⁹, FLUKA^40,41, and TOPAS⁴²) have been proven accurate, but are time-consuming (several hours or days for a single plan dose calculation), and are therefore considered inefficient for clinical use. Whilst fast MC codes (e.g. track-repeating⁴³, macro Monte Carlo⁴⁴, gMC⁴⁵, gPMC⁴⁶, FRED⁴⁷, and MCsquare⁴⁸), dedicated to proton dose calculations with simplified physics models and/or graphic processing unit (GPU) acceleration, have significantly reduced the time for one plan dose calculation to several minutes. Recently, some fast MC software have been released for clinical use in mainstream commercial treatment planning systems (TPSs), such as Eclipse™ (Varian Medical Systems, Palo Alto, CA)^49,50 and RayStation™ (RaySearch, Stockholm, Sweden)^50,51.

Nonetheless, the aforementioned fast MC codes are not yet fast enough for advanced optimizations in PBS treatment planning, such as 4D robust optimization^22,52,53 and linear-energy-transfer (LET)-guided robust optimization^13,15,54,55. In a 4D robust optimization, tens or even hundreds of perturbed scenarios need to be considered due to the additional respiratory phases, while in the LET-guided robust optimization many independent influence matrices related to LET are required. Therefore, it is crucial to reduce the MC-based proton dose calculation time to seconds or even sub-seconds for real-time and adaptive treatment planning and advanced optimizations. Recently, RaySearch reported that its latest fast MC-based proton dose engine could finish plan dose calculation with a median time of 5.2 seconds and a median calculation speed of 8.4 million particles per second.⁵⁶ Although still far from ideal, this may be the first MC-based proton dose calculation engine that enables real time and adaptive PBS treatment planning.

All the current fast MC codes use physics models to handle the interactions between particles and mediums. The generated secondary particles are stored in the shared memory buffers. MC simulation must decide the probability, type, and momentum of the generation of various kinds of secondary particles and then access the shared memory buffer accordingly at each MC step. Therefore, sophisticated logic controls and large shared memory buffers are required. Fortunately, this can be effectively handled by central processing units (CPUs), such as in MCsquare⁴⁸.

However, unlike CPUs, GPUs have very simple control logic and very limited shared memory buffer for a single thread. Within a block of threads, the threads executed in a group of 32 is called a warp. Thread divergence occurs when different threads in a warp need to execute different tasks. In the worst-case scenario, if one thread in a warp diverges, the 32 threads in this warp might need to stop and revert to the end of the previous step to redo the dose calculation. Therefore, GPU’s computing performance will be degraded and could be 32 times slower in the worst case. Thread divergence is a significant problem in GPU-based proton dose calculation engines if the “one particle per thread” technique (a GPU thread tracks a particle until the end conditions are satisfied) is adopted in the design of parallelization⁴⁵.

Racing condition is another significant problem in large scale shared memory parallel computation, where multiple threads happen to access and manipulate the same shared memory address simultaneously, resulting in possible memory conflicts among different threads. The generation of secondary particles is random and leads to sophisticated computation logic and unexpected computation burdens to the corresponding thread, and the randomly increased number of particles per thread due to the generation of secondary particles greatly increases the chance of racing condition. These two problems are inherent to the hardware architecture of GPUs and prevent taking full advantage of the GPU computing power and achieving MC-based sub-second plan dose calculation based on GPUs. All GPU-accelerated fast MC-based proton dose calculation engines (GPU version of track-repeating⁵⁷, gMC, gPMC, and FRED) had tried to mitigate the aforementioned thread divergence and racing condition problems.

In this paper, we propose a fast MC-based proton dose calculation engine based on a novel concept of virtual particles (VPs). VPs inherit essential physical properties from realistic particles but are conceptually designed for parallel computing in GPUs by avoiding the simulation of secondary particles. Therefore, simulation of VPs instead of realistic particles (primary protons and secondary particles) can take full advantage of the unique hardware architectures of GPUs (many simultaneous threads but simple control logics and limited shared memory buffers for a single thread), leading to greatly enhanced usage efficiency of the computing power of GPUs.

Methods and Materials

A. Implementation of VP

A.1. Converting realistic particles to VPs

Figure 1 shows the process of converting the histories of realistic particles into equivalent histories of VPs. Three simplifications were made to further speed up the calculations and still meet the clinical accuracy requirements: (1) the doses of electrons, heavy ions, and nuclear fragments were locally deposited (from Fig. 1(a) to Fig. 1(b)), (2) neutrons and gamma rays were considered to escape from the human body and thus ignored as energy loss, (from Fig. 1(b) to Fig. 1(c)) (3) the tracks of deuterons were converted into tracks of protons since deuterons have a low generating possibility in proton dose calculation of clinical proton therapy energies (0~230 MeV) and contribute less than 1% to the final dose⁵⁸ while having a range less than but close to protons. After these simplifications, one primary proton could be represented by multiple VPs that started at the same starting position of the primary proton (from Fig. 1(c) to Fig. 1(d)). Assuming the number of secondary protons and deuterons generated from one primary proton in the MC simulation is M, the number of VPs starting at the same starting position of the primary proton would be M+1 for this primary proton.

Figure 1.

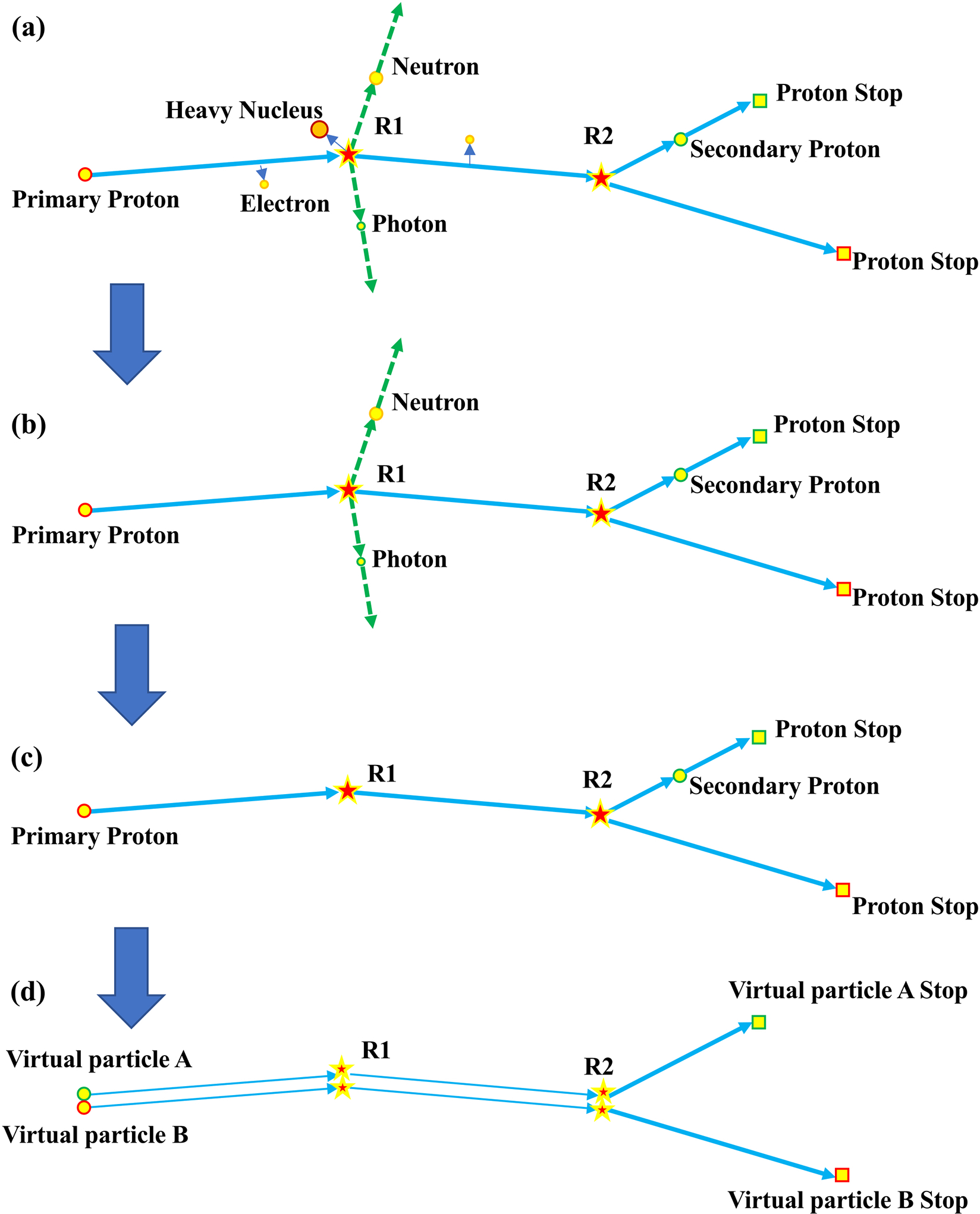
Diagram of converting the track histories of a realistic proton and its secondaries in a conventional Monte Carlo simulation into two virtual particles (a) Track history of a realistic proton. (b) the doses of electrons, heavy ions, and nuclear fragments were locally deposited. (c) neutrons and gamma rays were considered to escape from human bodies and thus ignored. (d) Track history of two virtual particles to have the same path from the starting point to R2. These two VPs are independent from each other. This figure is only used to demonstrate the concept of VP.

Please note that VP is a statistical concept. Every VP evolves independently based on the pre-generated corresponding possibility distribution functions (PDFs) of the multiple Coulomb scattering, ionization, and nuclear physics models (please see the following subsections for details). Given a large number of VPs, the simulation results following the pre-generated PDFs will converge to the simulation results of a large number of realistic particles (including secondary particles and the final dose), since the PDFs are generated based on the simulation results of realistic particles. Two VPs were used in Figure 1 only for the demonstration purpose. In Figure 1, we showed in a very simplified and unrealistic way how we could use two VPs to get the equivalent dose distribution from one primary proton and one secondary proton. The path before two VPs to diverge at R2 shown in Figure 1(d) is random and is determined by the calculated possibility of the nuclear reaction model discussed in the following subsection.

After converting the histories of realistic particles into histories of VPs that generate the same dose as realistic particles, statistic models consisting of probability distribution functions (PDFs) of the corresponding parameters were obtained to describe the behaviors of VPs. The models were derived by performing a statistics study of the track histories of realistic protons and their corresponding secondary particles from a conventional MC simulation (please see the rest of Sec. A for details). The open-source fast MC code, MCsquare^35,59–62 has been thoroughly validated against other MC codes and measurements in both phantoms and patient geometries^{59,60,62–68}. In addition, MCsquare has been fully commissioned and has been incorporated into our in-house treatment planning system, Shiva^52,69–73, and has been clinically used as the second monitor unit (MU) check system at our proton center for years^60,62 and other proton centers⁷⁴. Therefore, we chose MCsquare to generate all the PDFs used in the VPMC dose engine. To generate the PDFs of physics parameters, 20 million primary monoenergetic protons with infinitesimal spot sizes were used to irradiate normally into a water phantom of 20.1×20.1×40cm, so that all the generated PDFs could reach a statistical uncertainty (please see subsection D. Statistical uncertainty and efficiency for details) as low as 0.093% to guarantee that VPMC calculated dose based on those PDFs could reach a sufficiently low statistical uncertainty as well.

As for how the PDF databases of the physics parameters were generated and how HU-to-materials and HU-to-density conversions were done, please refer to Sec. A and B in Supplementary Materials for details.

A.2. Multiple Coulomb scattering

A continuing-slowing-down-approximation (CSDA) model (condensed class-II) was used to describe the Multiple coulomb scattering (MCS, i.e., soft electromagnetic interactions) for VPs. Rather than an on-the-fly calculation of the related physics parameters (the deposited energy, energy straggling, the deflection angle, and the ionization probability) based on physics models in MCsquare (and other MC codes), VPMC directly calculated such physics parameters using the 2D Compute Unified Device Architecture (CUDA) textures, i.e., look up tables (LUTs), with 2 dimension self-variables as the energy of VPs (E) and the Hounsfield Units (HU) value (HU) of the VP location for each MC step, which greatly sped up the calculation⁷⁵.

To generate such CUDA textures, the energy and HU value were scaled (0 to 230 MeV for energy and −1050 to 29000 for HU values, respectively) in MCsquare, and the calculated physics parameters were recorded and used to obtain PDFs describing the relationship between physics parameters and the energy and HU value, i.e., X(E, HU), where X indicates either of the deposited energy, energy straggling, the deflection angle, or the ionization probability. Since X(E, HU) was not linear, further tuning (please refer to Sec. A in Supplementary Materials for details) work was done to render VPMC achieve the same dose accuracy as MCsquare.

A.3. Ionization

Based on the ionization cross section interpolated from the CUDA texture generated in the CSDA step, the ionization for VPs was modelled in VPMC. If ionization happened, the status of VPs was updated based on the same analytical formula used in MCsquare.

A.4. Nuclear reaction

A large angle event (LAE) model was used to handle the nuclear reaction. During the nuclear reactions, possible secondary particles were generated, and resulted in an increased number of realistic particles. In conventional MC simulations, such secondary particles would randomly appear in the middle of the calculation (Fig. 1(a)) and need to be tracked thereafter as primary particles, which caused the possible thread divergence and higher chance of racing condition in GPU threads. However, in VPMC, these realistic particles (including both primary and secondary particles) were replaced by VPs, which appeared from the very beginning of the MC simulation (Fig. 1(d)).

Therefore, the total number of VPs was pre-determined (please refer to Sec. C in Supplementary Materials for details) before the MC simulation and did not change during the MC simulation. Thus, besides the conventional physics parameters of the nuclear reaction probability, the deposited energy, the energy loss (energies from neutrons and gamma rays escaped from human bodies), and the deflection angle, we introduced another parameter called “weight gain”. Weight gain is the fraction of the dose contributed by one certain VP at a certain step. This parameter is unique to VPs and does not exist in the MC simulation of realistic particles. During the dose scoring stage of the MC simulation, the weight gain would be multiplied to the dose contribution of the corresponding VP within the corresponding step to get the correct dose distribution as generated by realistic particles. Taking Figure 1(d) as an example, the first two steps of the MC simulation before the bifurcation at R2 were shared by two VPs, thus these two VPs in these two steps would be assigned a weight gain of 0.5 for the dose scoring. While after the bifurcation at R2, both VPs (A and B) exclusively possessed their own third step, therefore, the weight gain would be changed to 1.0 for both VPs for the corresponding third step during the dose scoring stage.

Similar to the CSDA model, the LAE model was not calculated on-the-fly either but was derived using all the related parameters (i.e., the nuclear reaction probability, the deposited energy, the energy loss, the deflected angle, and the weight gain) obtained based on the pre-generated database using MCsquare^48,60 with 20 million monoenergetic primary protons with infinitesimal spot sizes irradiating normally into phantoms stored in the CUDA textures for efficient calculation.

A.5. Range shifter

Two institution-specific range shifters, range shifter positioned at the exit of nozzle (labeled as RS) and extended range shifter positioned at an extended position (labelled as ERS), were also included in the VPMC dose engine. The range shifters were made of ABS Resin composed of hydrogen, carbon, nitrogen, and oxygen. The water equivalent thickness was 4.5 cm for both range shifters. RS was positioned at 42.5 cm from isocenter, while ERS was positioned 30 cm from isocenter. Similar to the track histories of VPs in patient geometries, the track histories of VPs in the range shifter were also modeled by various PDFs. However, unlike the highly heterogenous patient geometries, the range shifter was a homogenous medium with a fixed HU value. Therefore, the 2D CUDA textures for the CSDA model in patient geometries was reduced to a 1D CUDA textures with the fixed HU value corresponding to the range shifter material.

B. Workflow of VPMC

Figure 2 shows the workflow of VPMC. At the very beginning, all the pre-calculated databases of the CSDA model in range shifter (energy deposit, energy straggling, deflection angle, and ionization probability), the CSDA model in patient geometry (energy deposit, energy straggling, deflection angle, and ionization probability), and the LAE model (energy deposit, energy loss, deflection angle, weight gain, and nuclear reaction probability) were loaded. Once loaded, such databases were stored in shared memories as CUDA textures for repeated and efficient access from the subsequent VP simulations. For the VP simulations, a number of VPs were sampled at first with parameters of energy, position, and momentum and each VP was assigned to a certain GPU thread.

Figure 2.

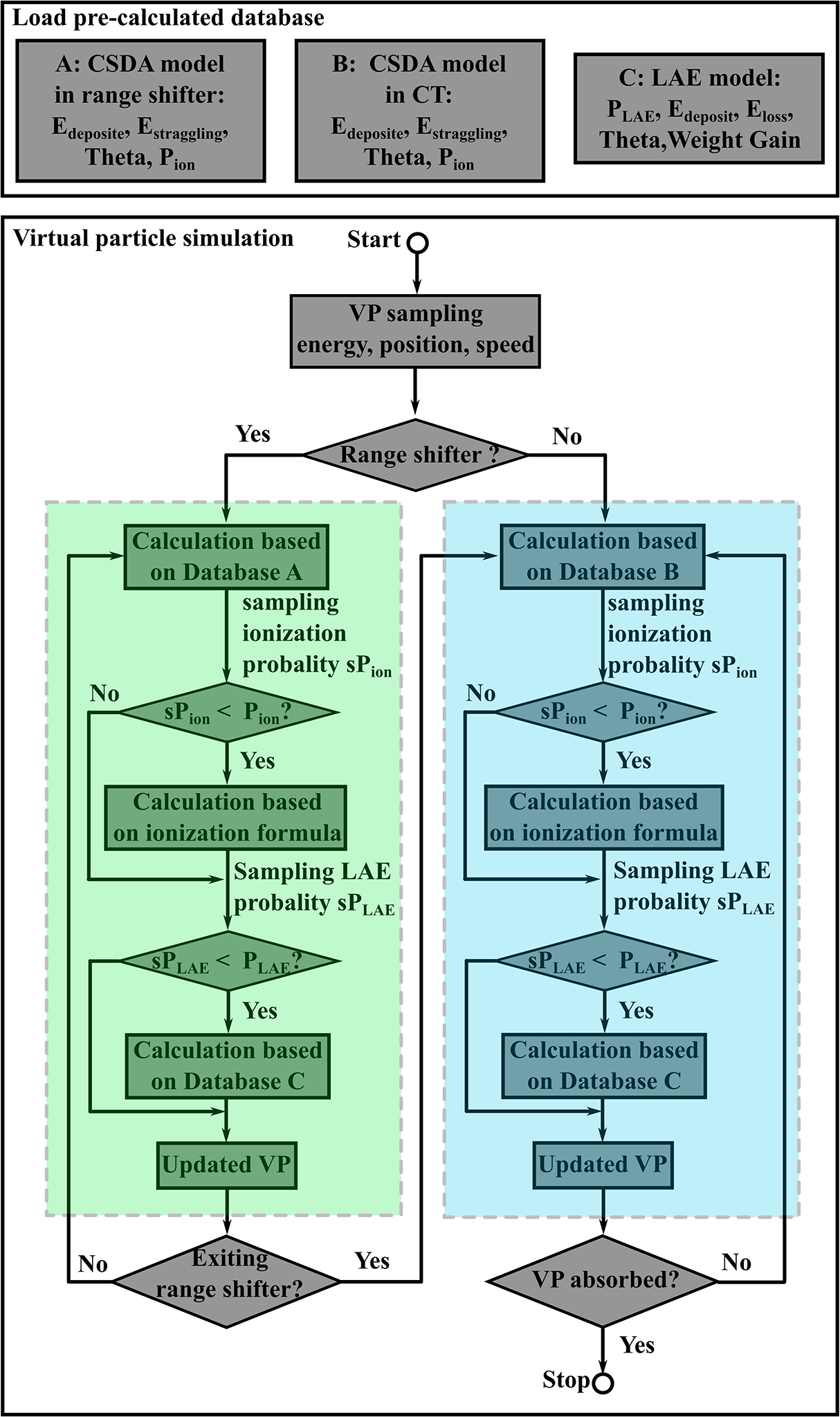
Workflow of VPMC. The upper box shows the loading process of the pre-calculated databases of the CSDA model in range shifter, the CSDA model in patient geometry, and the LAE model. The lower box shows the simulation process of VPs. The steps in the green box indicates the simulations in range shifter, while the steps in the blue box indicates the simulations in patient geometry.

As for the model used for particle sampling, we commissioned VPMC to get a single set of phase space parameters suitable for all three machines (one without range shifter, one with RS, and the other with ERS). In order to speed up the calculation we did not simulate the particle transport in the nozzle.^76,77 Instead, we derived the phase space at the exit of the nozzle (but before any beam modifiers such as range shifters) using integrated depth dose (IDD) curves and in-air lateral profiles at five positions of proton beams. Hence, the phase space has a large emittance due to the scattering of the beamline components in the nozzle and we chose to use double Gaussian lateral profile to model the beam source more accurately^48,60. For our synchrotron-based system we commissioned 97 discrete energies, rather than a selected number of energies as are typical for a cyclotron-based system.⁴⁶ The MU calibration curve and the corresponding CT calibration curve were also commissioned accordingly as in MCsquare^48,60.

If a range shifter (either RS or ERS) was used, VPs were first simulated in the range shifter (green box in Fig. 2), and then simulated in the patient geometry (blue box in Fig. 2). In the range shifter, by comparing the ionization probability (P_ion) calculated based on the VP parameters and the sampled ionization probability (sP_ion), the ionization process was considered based on the same analytical formula as used in MCsquare if needed (sP_ion < P_ion). Then the nuclear reaction probability (P_LAE) calculated based on the LAE model was compared to the sampled nuclear reaction probability (sP_LAE). If a nuclear reaction happened (sP_LAE < P_LAE), the status of VPs would be updated based on the LAE model. This stage ended when VPs exited the range shifter.

The calculation in the patient geometry was similar to the calculation in the range shifter with some minor differences: (1) the CSDA model in patient geometry was used instead of the CSDA model in range shifter, (2) the CT DICOM coordinate was used instead of the beam eye view coordinate, (3) dose scoring was done to each voxel, which was globally shared among all threads in memory buffers, in the patient geometry, while no dose scoring was done in the calculation in the range shifter. The calculation in the patient geometry ended when VPs were absorbed in the patient geometry or exited the patient geometry. The whole simulation ended when the calculation in the patient geometry ended.

The dose scoring to each voxel from each VP simulated by a certain thread took place once the VP status was updated. Atomic addition function⁴⁶ was used to guarantee “thread-safe”, i.e., operations of the per-voxel dose, which was globally shared among all threads in memory buffers, by one thread was not interfered by other threads. This would avoid possible racing conditions with some compromise of the computing performance. The avoidance of the simulation of the secondary particles would further greatly minimize the chance of the possible racing conditions in VPMC.

C. Validation

The validation was first done in homogeneous/inhomogeneous phantoms and then in patient geometries. For phantoms, a proton beam with a nominal energy of 228.8 MeV and a weight of 1 MU was normally irradiated to the phantom surface. Two phantoms were used: (1) a homogeneous water phantom and (2) an inhomogeneous phantom with a cube of HU=1000 in the middle of water blocking part of the beamlet path (Fig. 3). Dose distributions for each phantom were generated from three different dose engines, respectively: (1) VPMC, (2) MCsquare, and (3) TOPAS (ver. 3.7)^78,79, which is a standard MC code. TOPAS simulation results were considered as golden standard. 3D-3D Gamma analysis^80,81 between MCsquare and TOPAS, and between VPMC and TOPAS was used to assess the agreement between the dose distributions in these phantoms, respectively. The size and resolution of the phantoms used for benchmark were 400×201×201, and 1.0 mm×1.0 mm×1.0 mm, respectively. 1×10⁷ primary protons were simulated in MCsquare, while 2×10⁷ VPs were simulated in VPMC to guarantee low statistical uncertainty (<0.2%, Table S-1). More VPs in VPMC than primary protons in MCsquare were used because primary protons would generate secondary particles, thus resulting in more realistic particles than the number of the initial primary protons in a MCsquare simulation.

Figure 3.

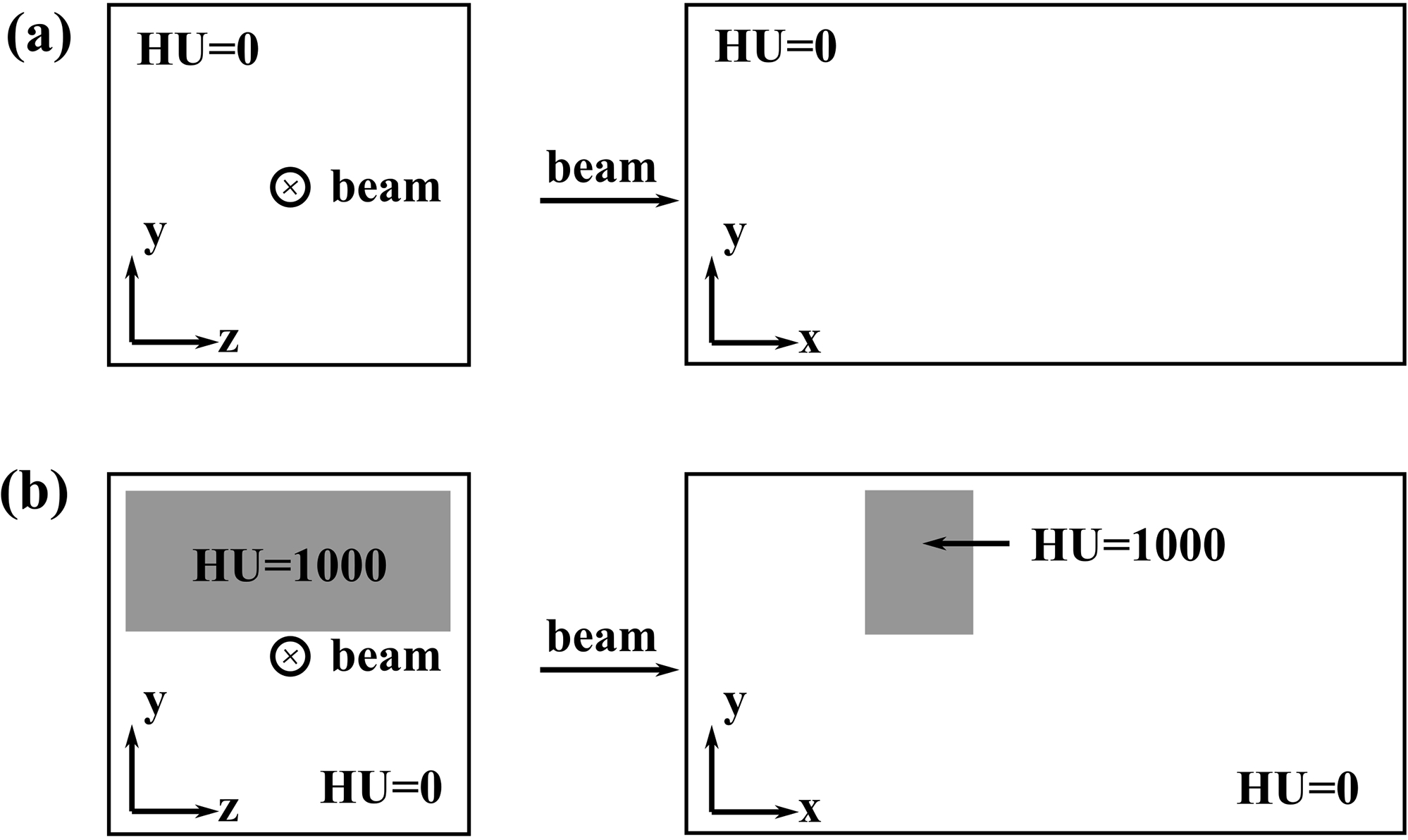
Illustration of the homogenous phantom (a) and inhomogeneous phantom. The beam enters the phantoms at the center of the y-z plane. The larger white boxes are composed of the water (HU = 0), the smaller grey boxes are composed of the blocking material (HU = 1000).

For patient geometries, clinically approved PBS plans for thirteen patients with different disease sites and a wide range of total spot number were selected to representatively cover most clinical scenarios. Range shifter was used in 6 plans. Detailed characteristics of the selected plans were included in Table 1. Three dose distributions were generated for each plan from three different dose engines, respectively: (1) VPMC, (2) MCsquare, and (3) the analytical dose engine in our commercial treatment planning system, Eclipse™ ver. 15.6 (Varian Medical Systems, Palo Alto, CA). 3D-3D Gamma analysis between VPMC and MCsquare and between Eclipse™ and MCsquare were performed, respectively. The same dose grid resolution of 2.5 mm in all three directions was used for all dose calculations included in the study.

Table. 1.

Characteristics of selected plans.

Patient #	Disease site	Range shifter	Total spot	Dose grid size
1	Prostate	No	2,235	168*115*216
2	Prostate	No	1,786	149*109*171
3	Head & Neck	ERS	6,501	123*89*105
4	Head & Neck	ERS	17,224	226*119*154
5	Brain	No	5,035	223*164*161
6	Orbit	No	1,644	213*162*171
7	Pelvis	No	26,850	200*125*189
8	Thorax	No	3,802	256*104*125
9	Chest wall	ERS	60,690	260*129*188
10	Lung	ERS	20,403	229*184*174
11	Liver	No	9,758	217*151*144
12	Chest wall	RS	67,875	257*164*204
13	Chest wall	RS	51,965	251*136*161

abbreviations: RS for range shifter located at a regular position, ERS for range shifter located at an extended position.

Comparisons between the VPMC-calculated in-water dose and the measured in-water dose during patient-specific quality assurance (PSQA) and comparisons between the Eclipse™-calculated in-water dose and the measured in-water dose during PSQA for the 13 selected plans were also carried out. The PSQA procedure at our institution⁸¹ was done by delivering treatment plans to a water tank measured with a 2D MatrixxPT ionization chamber array (IBA Dosimetry GmbH, Schwarzenbruck, Germany). For each field of the delivered plan, 2D plane doses at two or three representative axial depths were measured. For each measured plane, 1,020 detection points were included. The measured plane doses were then compared to the calculated 3D dose distribution in water from different dose engines. 2D (measurements)-3D (calculated dose) Gamma analysis^81,82 was used for the comparison. The detector, MatriXX PT, is used with a resolution of 7.6 mm * 7.6 mm⁸¹.

American Association of Physicists in Medicine (AAPM) Task Group 218 recommended a criterion of 3%/2mm and a threshold of 10% for the Gamma analysis done in PSQA for intensity-modulated radiation therapy (IMRT)⁸³. Thus, in the 2D-3D Gamma analysis between the 3D VPMC calculation and the in-water 2D planar measurements in PSQA, the recommended criterion of 3%/2mm with 10% threshold was used, with the in-water measured 2D planar dose as references. However, one may have possible concerns of the inflated Gamma passing rates derived from comparing the two MC-calculated dose distributions due to the statistical noises inherent in MC-calculated dose distributions. Therefore, in the 3D-3D Gamma analysis in both phantoms and patient geometries, a more stringent criterion of 2%/2mm with a threshold of 10% was used. For the 3D-3D Gamma analysis in both homogeneous and inhomogeneous phantoms, the TOPAS simulation results were chosen as the reference doses, while for the 3D-3D Gamma analysis in patient geometries where there were no TOPAS simulations, simulation results from the comprehensively-benchmarked MCsquare were chosen as the reference doses. For all Gamma analysis, trilinear interpolation was performed through CUDA textures on the evaluation grid. A global criterion was applied.

D. Statistical uncertainty and efficiency

The statistical uncertainty of a certain MC simulation in terms of a chosen number of simulated particles, was calculated using the equation⁸⁴:

$$\sigma =\frac{1}{N_{d_i>20\mathrm{\%}{D}_{max}}}\sum _{d_i>20\mathrm{\%}{D}_{max}}\frac{{\sigma }_i}{D_{max}^i}$$

where $N_{d_i>20\%D_{max}}$ is the number of voxels, whose dose is larger than the 20% of the maximum dose D_max of the whole dose distribution, σ_i is the statistical uncertainty for voxel i and calculated by the equation:

$${\sigma }_i=\sqrt{\frac{\stackrel{-}{d_{ɩ}^2}-{\stackrel{-}{d_{ɩ}}}^2}{N_{run}-1}}$$

in which $\stackrel{-}{d_{ɩ}^2}$ is the average square dose for voxel i among a number of repeated simulations, and ${\stackrel{-}{d_{ɩ}}}^2$ is the square of average dose for voxel i among a number of repeated simulations. N_run is the number of repeated simulations. $D_{max}^i$ is the maximum dose among the N_run simulations for voxel i. In this study, N_run was set to 10 for each simulation scenario, and the number of particles to be simulated in both phantoms and patient geometries was chosen carefully to guarantee that a low statistical uncertainty (< 1%) was achieved in all simulations.

Due to the fundamental difference between the realistic particles tracked in MCsquare and VPs tracked in VPMC, to fairly compare the efficiency between MCsquare and VPMC, the index $e=1/{(\sigma }^{2}t)$ was used to compare efficiency between MCsquare and VPMC⁸⁴. σ is the statistical uncertainty as defined above, while t is the calculation time for one simulation.

Results

A. Validations in phantoms

Figure 4 shows comparison among dose distributions calculated by TOPAS (magenta), MCsquare (blue), and VPMC (orange). Subpanels in the top row are results calculated in the homogeneous phantom, while subpanels in the bottom row are results calculated in the inhomogeneous phantom. From left to right, the four columns are IDD curves, MCsquare and VPMC IDD differences to TOPAS, log-scale lateral dose profile at the Bragg Peak, and MCsquare and VPMC lateral dose profile differences to TOPAS at the Bragg Peak, respectively. For both homogeneous and inhomogeneous phantoms, excellent agreement was observed among the dose distributions generated by TOPAS, MCsquare, and VPMC. The 3D-3D Gamma passing rates between MCsquare and TOPAS and between VPMC and TOPAS were 98.49% and 98.31% in the homogeneous phantom and 99.18% and 98.49% in the inhomogeneous phantom, respectively.

Figure 4.

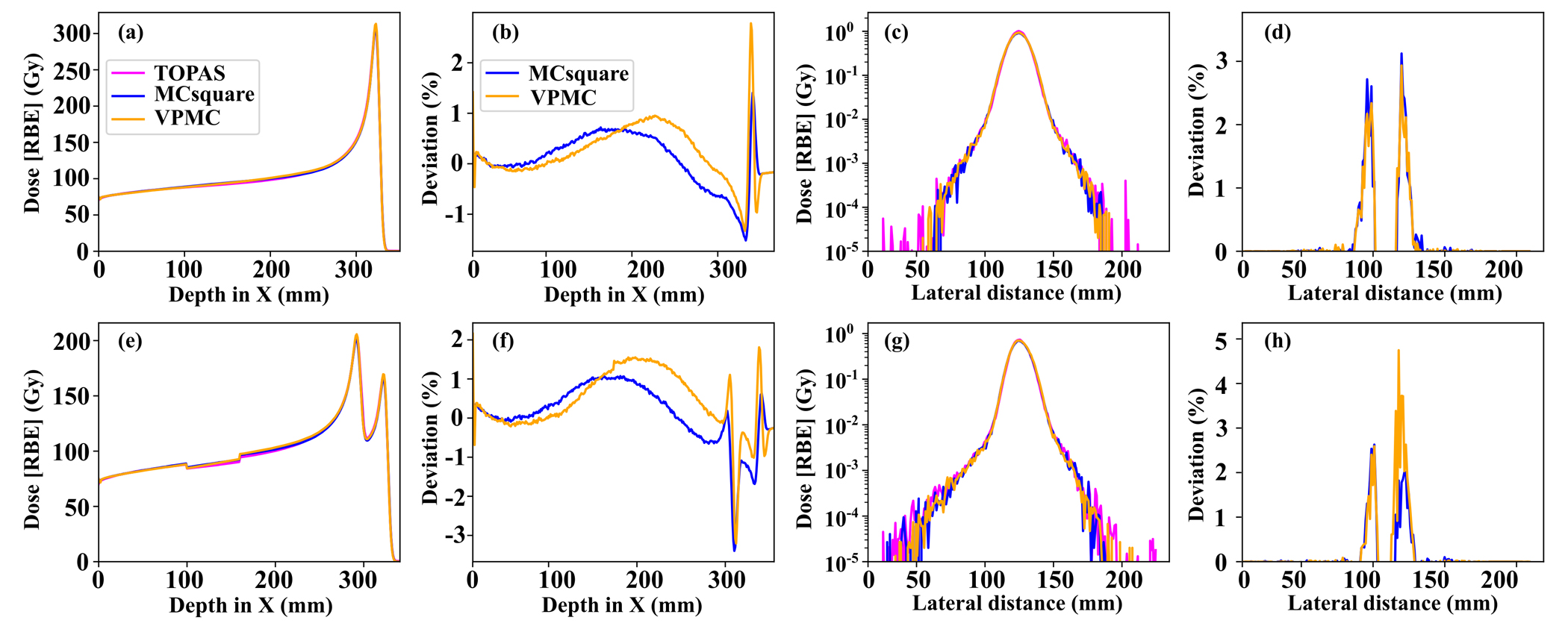
The IDD curves (a)(e), log-scale lateral profiles at the Bragg peak (c)(g) of the dose distribution generated by TOPAS (magenta), MCsquare (blue), and VPMC (orange), and the corresponding IDD (b)(f) and lateral profile (d)(h) differences between MCsquare and TOPAS (blue) and the differences between VPMC and TOPAS (orange), in a homogeneous phantom (top row) and in an inhomogeneous phantom (bottom row). RBE = 1.1.

B. Validations in patient geometries

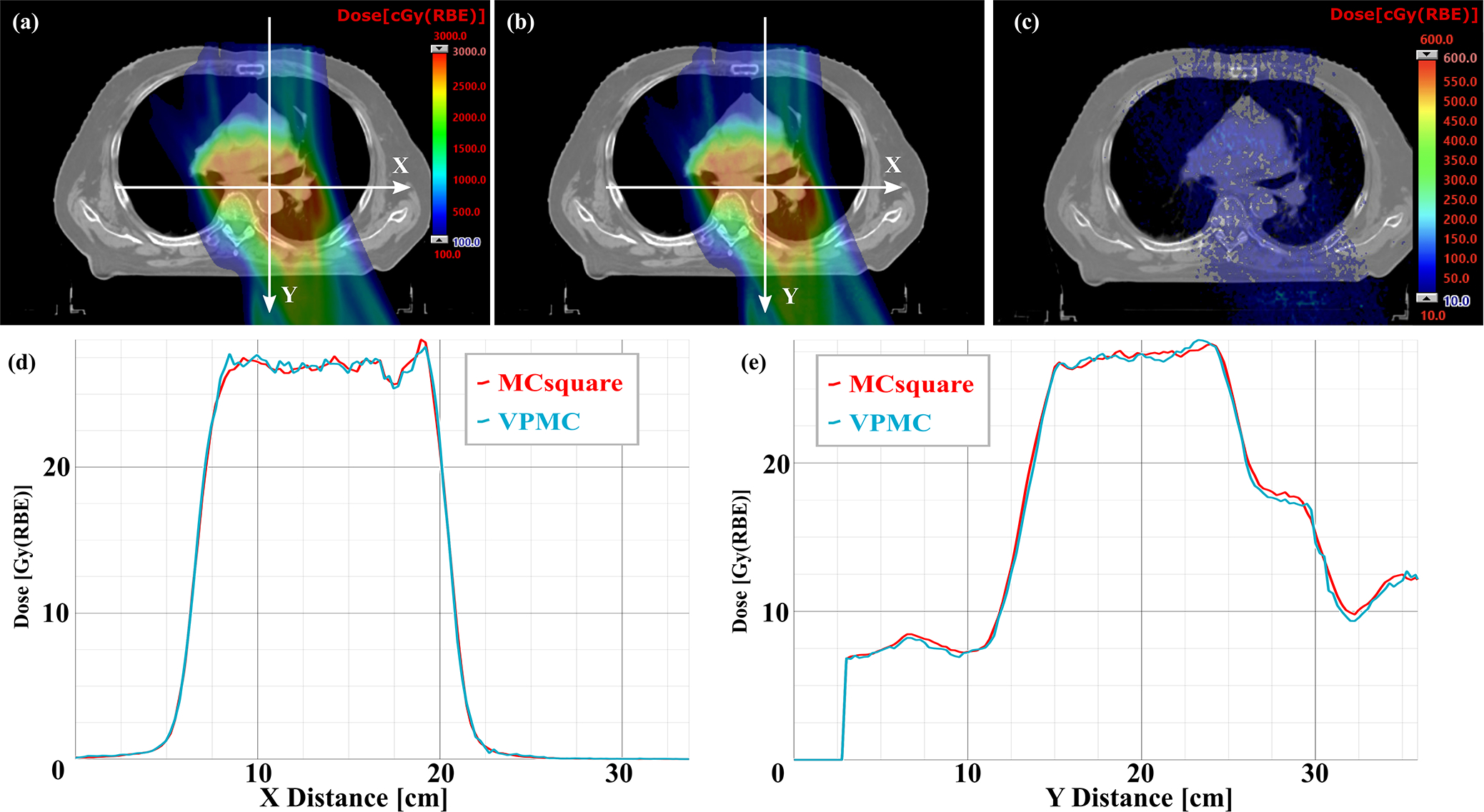
The validation results in patient geometries were shown in Table 2. The mean 3D-3D Gamma passing rate between VMPC and MCsquare was 98.58±1.09%, while the 3D-3D Gamma passing rate between Eclipse™ and MCsquare was 89.60±7.24% with 2%/2mm/10%. VPMC drastically reduced the dose calculation time for a plan to 2.84±2.33 seconds, compared to 112.56±114.38 seconds for MCsquare, running on AMD EPYC™ 7543 equipped with 4 NVIDIA Ampere A100 GPUs. Patient 12 took the longest dose calculation time of 8.9 seconds for VMPC. This patient had the largest number of spots (67,875) and the largest number of voxels (5,495,896). The average statistical uncertainty of MCsquare was 0.27±0.08%, while the average statistical uncertainty of VPMC was 0.57±0.23%. The average efficiency was 0.62±1.05 × 10⁴ s⁻¹ for MCsquare, and 5.37±9.96 × 10⁴ s⁻¹ for VPMC. VPMC is 8.66 times more efficient than MCsquare. VPMC calculations with more VPs achieved a statistical uncertainty (0.36±0.13%) closer to MCsquare and an enhanced efficiency (7.86±15.85×10⁴ s⁻¹, which is now 12.5 times better than the average efficiency of MCsquare), at a cost of prolonged calculation time (5.41±4.94 seconds) (Table S-5). Three representative patients (one prostate patient without range shifter, one H&N patient with ERS, and one chest wall patient with RS) were selected to compare the dose profile on typical transverse planes between VPMC and MCsquare (Fig. 5–7). We found that VPMC agreed well with MCsquare in patient geometry. Please note that the MCsquare used in this comparison was the modified version, which had been successfully enhanced to be about 10 times as fast as the original MCsquare⁶⁰.

Table. 2.

Comparison between VPMC and MCsquare in the 13 selected patients. 3D-3D Gamma analysis was done with 2%/2mm/10%.

Patient #	3D-3D Gamma referenced to MC2 (%)		Time (s)		Statistical Uncertainty (%)		Efficiency (10e4*1/s)
	ECL	VPMC	MC2	VPMC	MC2	VPMC	MC2	VPMC
1	75.80	98.97	9.84	0.91	0.34	0.40	0.88	6.86
2	72.40	99.19	8.63	0.82	0.31	0.34	1.23	10.84
3	96.43	98.93	70.22	1.23	0.20	0.68	0.36	1.74
4	94.05	97.35	92.25	2.46	0.38	0.91	0.08	0.49
5	91.23	99.58	100.19	1.65	0.22	0.45	0.20	3.05
6	90.00	99.63	23.71	1.25	0.24	0.46	0.72	3.82
7	96.27	99.84	171.01	3.28	0.19	0.35	0.17	2.55
8	95.22	98.12	19.13	0.84	0.38	0.76	0.37	2.06
9	91.19	97.62	188.12	6.02	0.26	0.72	0.08	0.32
10	93.73	99.25	133.01	3.98	0.34	0.59	0.07	0.73
11	92.99	99.44	23.13	1.17	0.11	0.15	3.88	36.91
12	90.19	96.74	410.89	7.89	0.33	0.84	0.02	0.18
13	85.25	96.64	213.10	5.46	0.29	0.80	0.06	0.29
Mean	89.60	98.56	112.56	2.84	0.27	0.57	0.62	5.37
SD	7.24	1.09	114.38	2.33	0.08	0.23	1.05	9.96

abbreviations: MC2 stands for MCsquare, ECL stands for the analytical dose engine of Eclipse™ver. 15.6, SD stands for standard Deviation.

Figure 5.

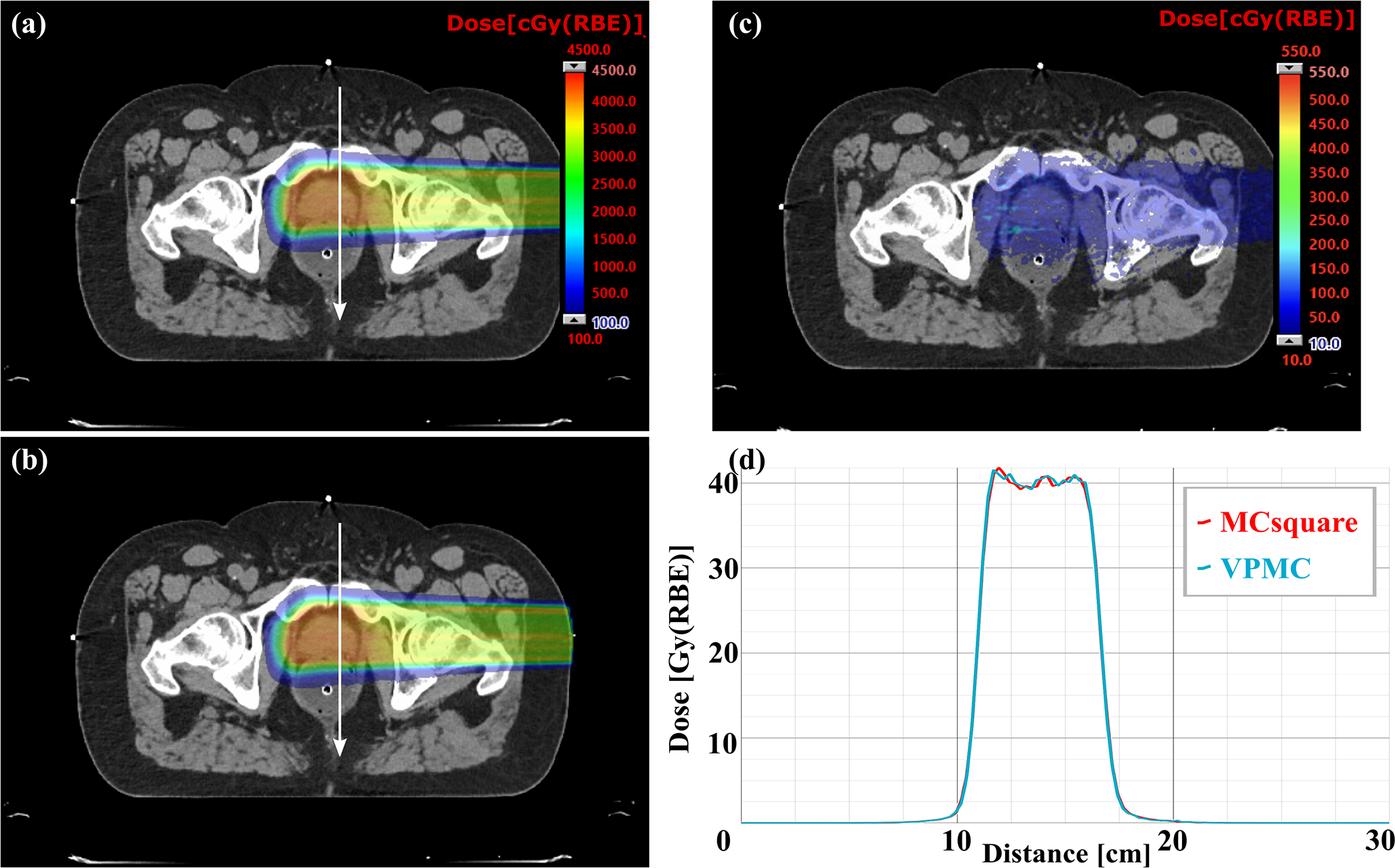
Comparison of dose profiles on typical transverse planes of a prostate patient without range shifter between VPMC and MCsquare. (a) Dose map from MCsquare, (b) Dose map from VPMC, (c) Absolute dose difference map between the MCsquare calculated dose and the VPMC calculated dose. The white arrow indicates the position and direction of the dose profiles in (c). The red curve in (d) is the dose profile from MCsquare, while the blue curve is the one from VPMC. RBE = 1.1.

Figure 7.

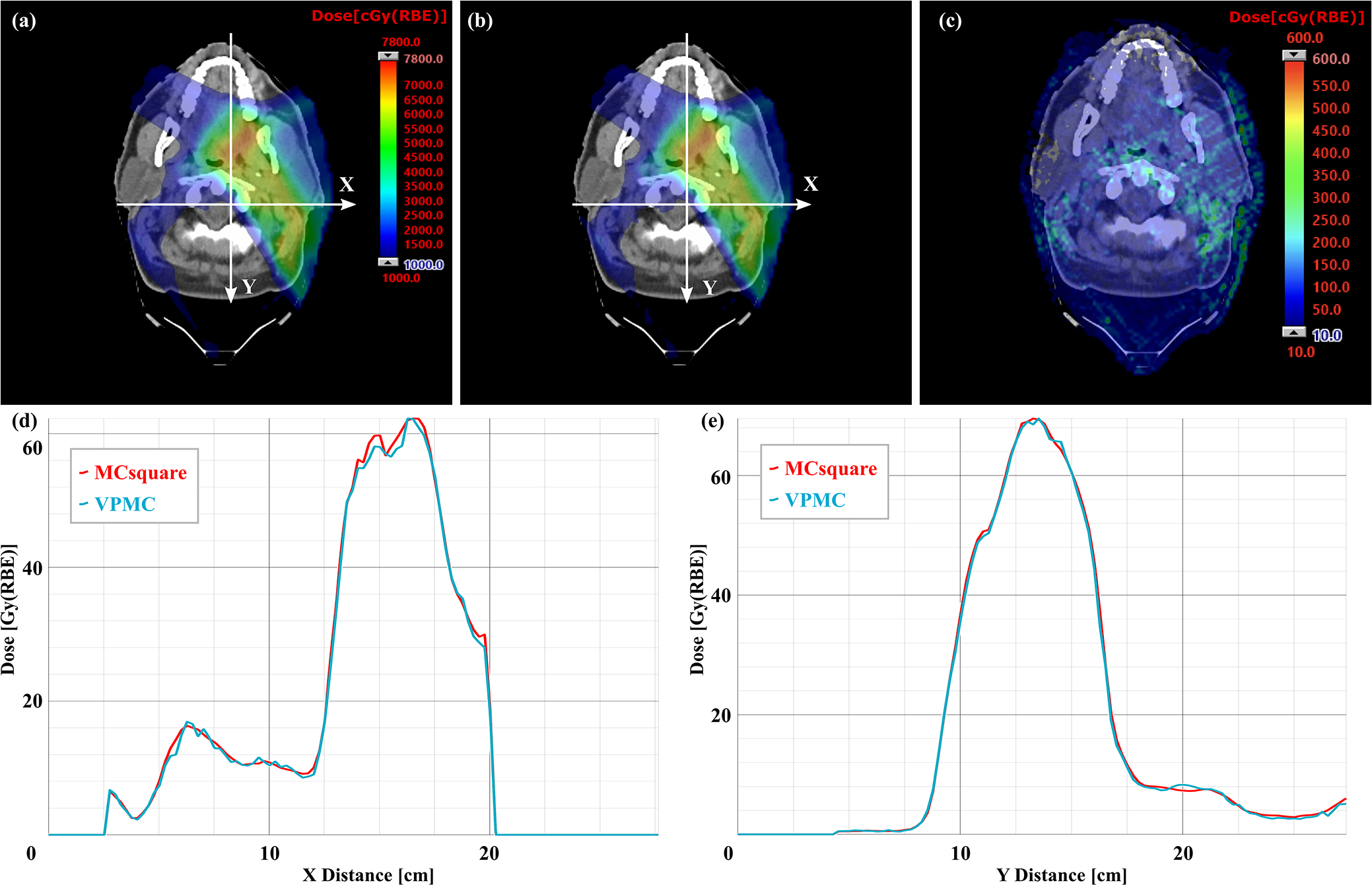
Comparison of dose profiles on typical transverse planes of a H&N patient with RS between VPMC and MCsquare. (a) Dose map from MCsquare, (b) Dose map from VPMC, (c) Absolute dose difference map between the MCsquare calculated dose and the VPMC calculated dose. The white arrows indicate the position and directions of the dose profile in (d) dose profile in X direction and (e) dose profile in Y direction. The red curves in (d) and (e) are the dose profile from MCsquare, while the blue curves are the ones from VPMC. RBE = 1.1.

C. Comparisons with PSQA measurements

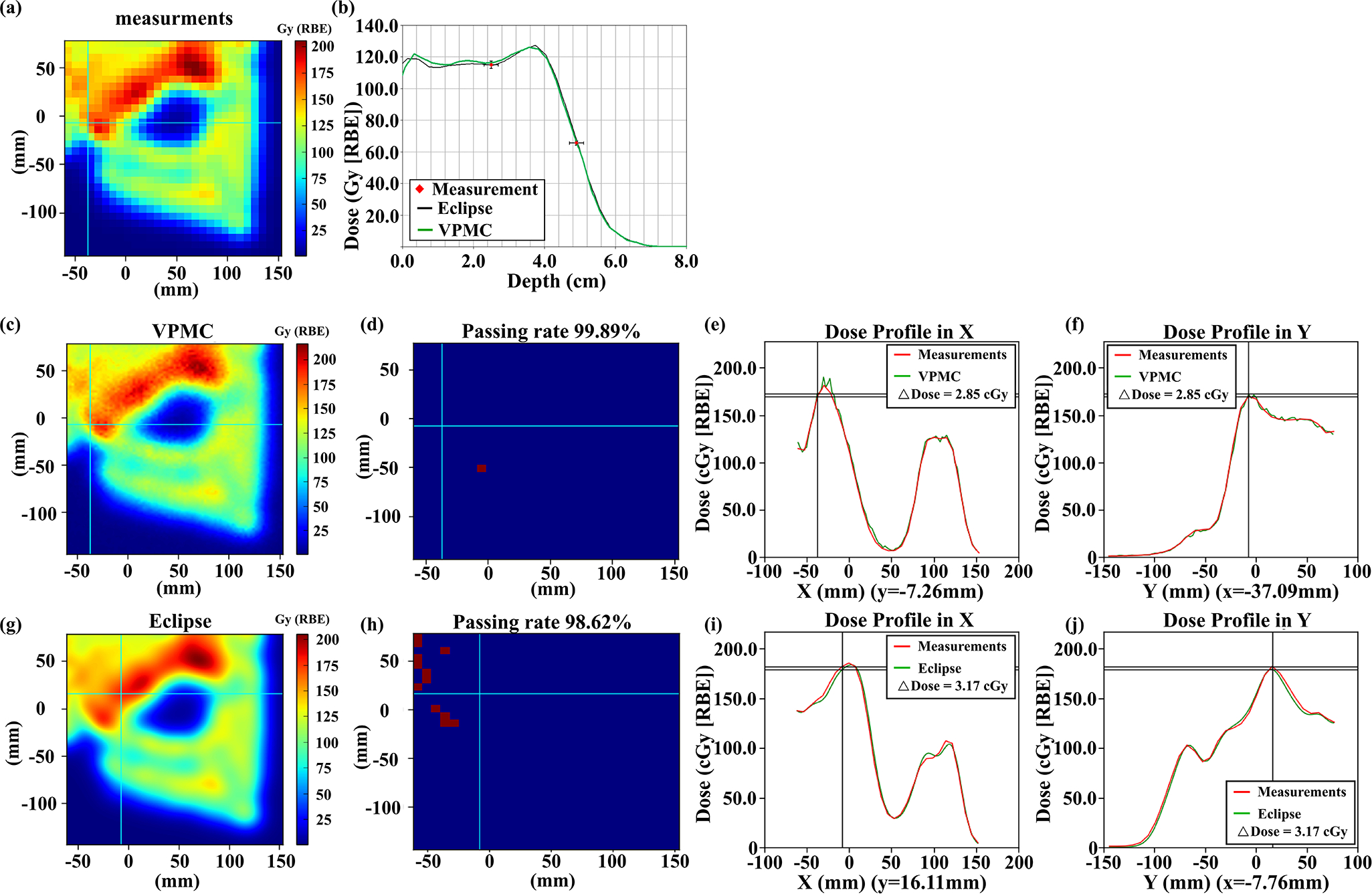
Table 3 shows the comparison of the 2D-3D gamma analysis passing rates, with a criterion of 3%/2mm and a threshold of 10%, between Eclipse™ and VPMC calculation results with the measured 2D plane dose during PSQA, respectively. The average passing rate for Eclipse™ was 98.87% ± 1.12%, while the average passing rate for VPMC was 98.91% ± 0.88%. 2D-3D Gamma passing rates at different measurement locations of each field for all patients included in this study comparing the Eclipse™ and VPMC calculation results with the 2D measured plane doses are reported in Table S-4. Figure 8–10 shows the comparisons of dose maps between Eclipse and VPMC calculation results with the measured 2D plane dose during PSQA in three selected typical patients (without range shifter, with RS, and with ERS). We found that the VPMC calculation results agreed well with the measured results and the Eclipse calculation results in PSQA.

Table 3.

2D-3D Gamma passing rates comparing Ecplise™ and VPMC calculation results with the 2D measured plane doses during PSQA with a criterion of 3%/2mm and a threshold of 10%.

Patient #	2D-3D Gamma analysis (%)
	ECL vs Measurements	VPMC vs Measurements
1	98.93	98.50
2	96.94	97.83
3	99.97	100.00
4	99.93	100.00
5	98.42	97.47
6	99.48	98.44
7	99.60	99.47
8	99.57	99.67
9	97.60	97.83
10	100.00	99.37
11	98.91	98.56
12	99.22	99.89
13	96.80	98.79
Mean	98.87	98.91
SD	1.12	0.88

abbreviations: ECL for the analytical dose engine of Eclipse™, SD stands for standard deviation.

Figure 8.

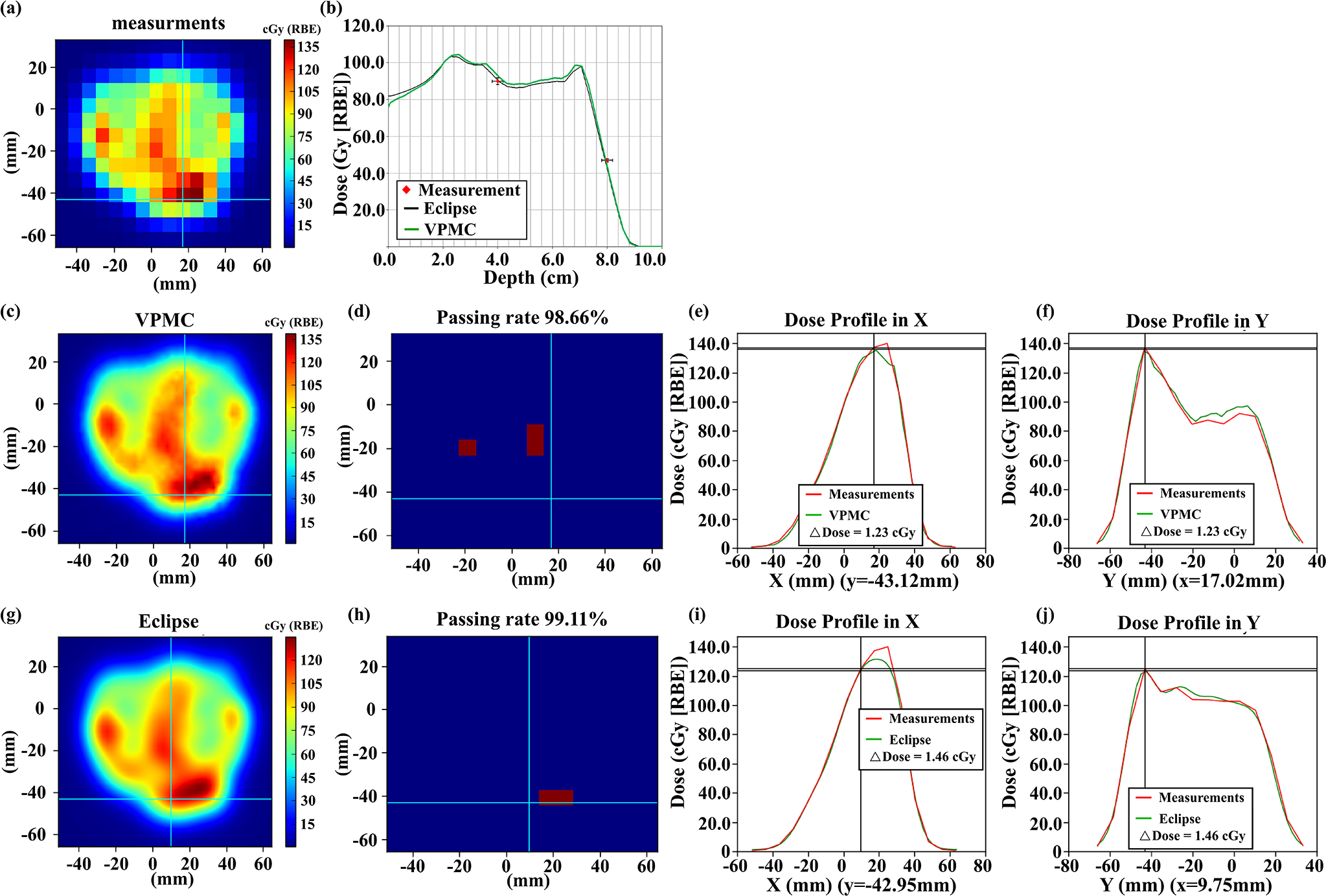
Comparisons of the measured 2D plane dose during PSQA (a) with VPMC calculation result (c), and Eclipse™ calculation result (g) at a depth of 4.0 cm for a lung cancer patient without range shifter. The corresponding 2D-3D Gamma analysis pass/fail maps are shown in (d) and (h) with 3%/2mm/10%. Subpanel (b) displays the dose profiles from VPMC and Eclipse™ in the beam direction. The black line is from the Eclipse™ calculation result, while the green line is from the VPMC calculation result. Red points are the measured results with an error bar of 2%/2mm. Subpanel (e) (f) displays the dose profile comparison between the VPMC calculated dose and the measured dose in the X direction at the Y position indicated by the horizonal line in (c) and in the Y direction at the X position indicated by the vertical line in (c), respectively. Subpanel (i) (j) displays the dose profile comparison between the Eclipse™ calculated dose and measured dose in the X direction at the Y position indicated by the horizonal line in (g) and in the Y direction at the X position indicated by the vertical line in (g), respectively. RBE = 1.1.

Figure 10.

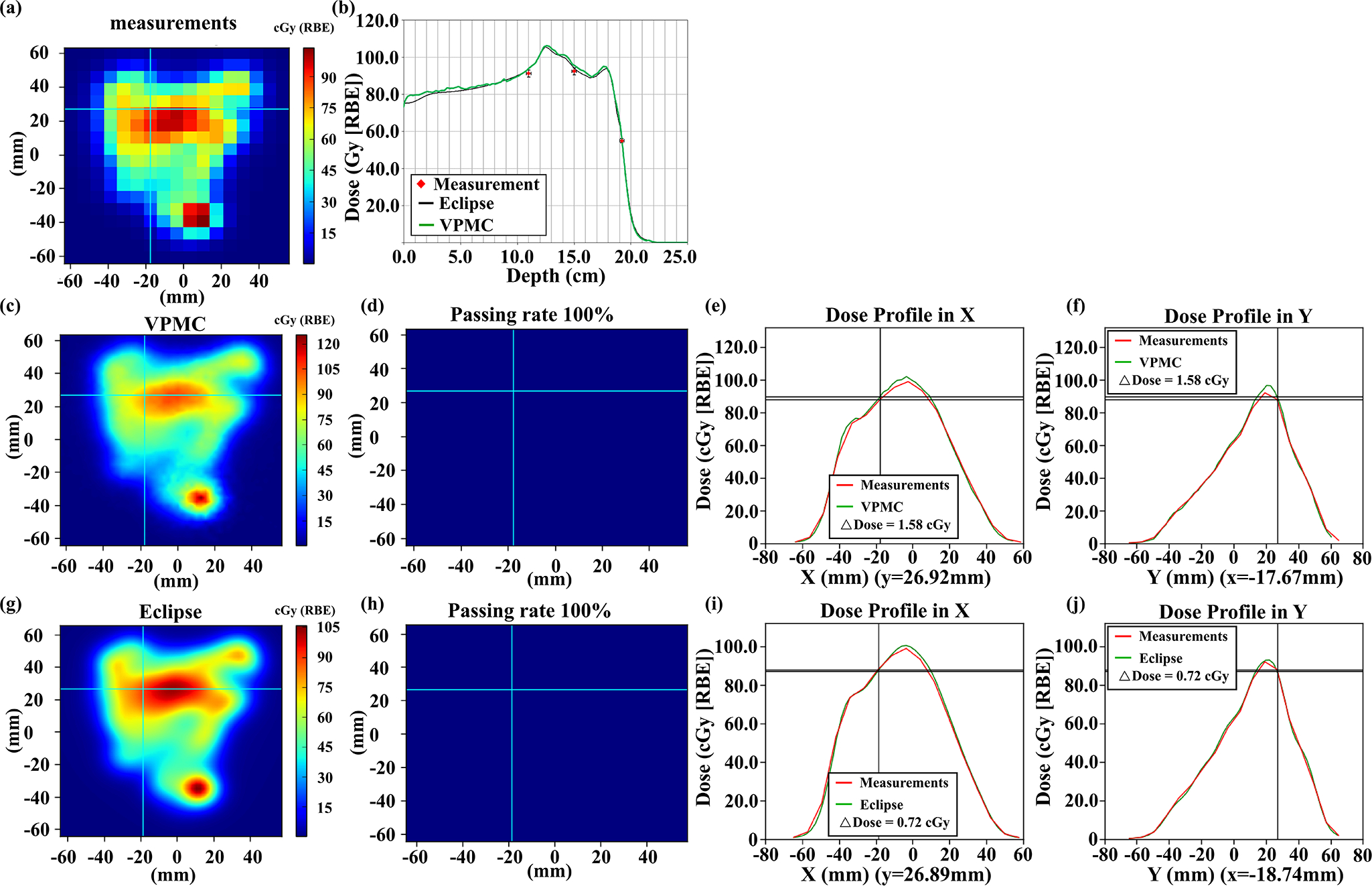
Comparisons of the measured 2D plane dose during PSQA (a) with VPMC calculation results (c) and Eclipse™ calculation results (g) at a depth of 15.0 cm for a H&N patient with ERS. The corresponding 2D-3D Gamma analysis results were shown in (d) and (h) with 3%/2mm/10%. Subpanel (b) displays the dose profiles from VPMC and Eclipse™ in the beam direction. The black line is from the Eclipse™ calculation result, while the green line is from the VPMC calculation result. Red points are the measured results with an error bar of 2%/2mm. Subpanel (e) (f) displays the dose profile comparison between the VPMC calculated dose and the measured dose in the X direction at the Y position indicated by the horizonal line in (c) and in the Y direction at the X position indicated by the vertical line in (c), respectively. Subpanel (i) (j) displays the dose profile comparison between the Eclipse™ calculated dose and measured dose in the X direction at the Y position indicated by the horizonal line in (g) and in the Y direction at the X position indicated by the vertical line in (g), respectively. RBE = 1.1.

Discussion

In this study, we report the successful development of a GPU-accelerated fast MC dose engine, based on the novel concept of VP to avoid the simulation of the secondary particles generated during nuclear reactions. Pre-calculated PDF databases of the needed parameters were generated using the well-established open-source fast MC dose engine, MCsquare^48,60. The PDFs were stored as CUDA texture LUTs for efficient calculation in VMPC. After fine-tuning of parameters needed in VPMC, VPMC agreed well with MCsquare. Moreover, VPMC significantly reduced the dose calculation time of a plan to 2.84±2.33 seconds, which was about 40 times faster and 9 times more efficient than the enhanced version of MCsquare, which is about 10 times faster than the original MCsquare⁶⁰.

Pre-calculated parameter database is a commonly used technique to increase the calculation efficiency in MC simulation^43,85–87, by using database querying instead of on-the-fly calculation. Such technique can perform even better on GPUs than CPUs, since the possible interpolation can be done efficiently using the unique characteristics of the GPU textures. However, there is an inherent drawback for using pre-calculated parameter databases. Once the system is updated, for example with a new CT calibration curve⁸⁸, the pre-calculated parameter database must be updated accordingly. Fortunately, the corresponding pre-calculated parameter databases only need to be generated once and can then be stored as the CUDA texture LUTs for future calculation.

Compared to other CPU-based fast MC codes using the pre-calculated databases, the proposed VPMC had some unique features. In Macro MC (MMC)^85,86, the pre-calculated databases were generated based on macro blocks (such as slab, cylinder, or sphere). And realistic particles, including both primary and secondary particles, were simulated in the conventional way. In the track-repeating^43,87 algorithm, a database of proton trajectories, including secondary protons, was generated in water with discrete steps, where the step length, angles relative to the previous step, energy loss, and energy deposit were stored. Then the extrapolation from water to other materials was achieved by scaling the path length of each step and the angle between steps. When a tracked history was selected for a proton, the proton was then transported as if it followed this assigned track. By re-tracing the proton track from the database of the pre-calculated-histories, dose distribution could be calculated in heterogeneous mediums.

VPMC’s pre-calculated database was similar to how MMC used the pre-calculated database, where the parameter PDFs of each step were stored. It is thus different from how the track-repeating algorithm used the pre-calculated database, where proton histories were stored. At each step, VPMC and MMC required sampling based on the parameter PDFs, while track-repeating needed scaling the corresponding step length and the corresponding angle. However, despite the similar use of the pre-calculated parameter databases, VPMC used realistic small steps between two events in MC instead of macro blocks (such as slab, cylinder, or sphere) in MMC. In addition, VPMC was specifically developed for GPU-acceleration and introduced a GPU-friendly concept of VP to avoid the simulation of the secondary particles generated during the nuclear reaction, while MMC was originally developed for CPU-based computing platforms with conventional methods to handle secondary particles. Therefore, if one attempts to adapt the MMC in the GPU-based computing platforms, the aforementioned thread divergence problem needs to be considered properly.

GPU has been widely used to accelerate calculations in MC-based proton dose calculation. To help mitigate the thread divergence problem in GPU threads, various efforts have been made. In gMC⁴⁵, two loops of particle simulation were used. In the first loop of primary particles simulation, the secondary particles generated in nonelastic nuclear interactions were grouped and stored for further processing. After the first loop of primary particles simulation was completed, the second loop of the stored secondary particles simulation would take place. The daughter secondary particles generated in the second loop would be handled accordingly as well. Such loops would repeat until all secondary particles were simulated. In gPMC⁴⁶, protons were simulated in batches. In each batch, a number (M) of protons that could be transported by GPU simultaneously would be generated and simulated. At the same time, a special stack was created to store secondary particles, which would be continuously monitored. When the number of stored secondary particles reached or surpassed the number of M, the stack would pop up M secondary particles to GPU to be simulated in the following batch. FRED⁴⁷ employed a similar idea to address the thread divergence as gMC and gPMC, in which secondary particles were queued for later simulation. In the GPU version of track-repeating⁵⁷, the same proton history was used within a block, but with different starting positions in the normal direction of the beam. Such technique was very GPU-friendly since each GPU thread essentially performed the same operations all the time.

VPMC used a novel concept of VPs to avoid the simulation of secondary particles generated in nuclear reactions to take full advantage of the computing capacity of GPUs. The concept of VPs theoretically avoided the possible thread divergence in GPU threads. Every VP is simulated equivalently with the same control logic and the same memory buffer, which is very friendly to the GPU hardware architecture. Therefore, by assigning the simulation of a VP to a GPU thread, every thread within a warp is equally executing the same computation task. Therefore, the thread divergence can be effectively avoided.

The concept of VP was originally developed from the perspective of statistics, rather than the perspective of physics models. Therefore, a descriptive LAE model was used to describe the nuclear reaction, where secondary particles could be generated, with five parameters of VP: nuclear reaction probability, reflected angle, energy loss, energy deposit, and weight gain. Weight gain was an arbitrary parameter specifically introduced to get the correct final dose during the scoring stage. And the PDF databases of those parameters were pre-calculated and stored using the CUDA texture LUTs for efficient calculation. The fast CPU-based MC code, MCsquare, was used for generating these databases by the statistical analysis of the pre-calculated 20 million primary particles in all materials defined during the commissioning of MCsquare based on our proton machine and CT simulator⁶⁰. Theoretically, any fully-blown MC codes can be used for this purpose accordingly.

In the future, other auxiliary methods will be exploited to further accelerate the calculation speed and improve the calculation accuracy of VPMC. We will try to enhance the current CT resampling of a fixed resolution by introducing the more advanced adaptive resolution resampling method to reduce the number of the voxels, thus accelerating the calculation speed. We will also integrate the bias sampling method⁸⁹ in particle generation, in which the central high dose region of a beamlet will be down-sampled, while the lateral low dose region of a beamlet will be up-sampled to reduce the total number of particles for simulation to accelerate the calculation speed without compromising the calculation accuracy. Particle splitting⁹⁰ is another well recognized method in MC simulations to speed up calculations in which fewer numbers of particles are initially generated, but more particles are dynamically generated in the regions with high statistical noise. Essentially the total number of particles can be reduced without compromising the calculation efficiency, thus leading to faster calculation. We will also try the dynamic step size method, such as random-hinge^91,92 to enhance the calculation efficiency.

Conclusion

We have developed a GPU-friendly MC dose engine based on the novel concept of VP to avoid the simulation of secondary particles generated during the nuclear reactions. The concept of VP avoided the thread divergence problem caused by secondary particles in GPU threads to take full advantage of the computing power of GPUs. We found that the proposed VPMC can calculate proton dose distributions efficiently and accurately in PBS.

Figure 6.

Comparison of dose profiles on typical transverse planes of a chest wall patient with ERS between VPMC and MCsquare. (a) Dose map from MCsquare, (b) Dose map from VPMC, (c) Absolute dose difference map between the MCsquare calculated dose and the VPMC calculated dose. The white arrows indicate the position and directions of the dose profiles in (d) dose profile in X direction and (e) dose profile in Y direction. The red curves in (d) and (e) are the dose profile from MCsquare, while the blue curves are the ones from VPMC. RBE = 1.1.

Figure 9.

Comparisons of the measured 2D plane dose during PSQA (a) with VPMC calculation results (c) and Eclipse™ calculation results (g) at a depth of 2.0 cm for a chest wall patient with RS. The corresponding 2D-3D Gamma analysis pass/fail maps are shown in (d) and (h) with 3%/2mm/10%. Subpanel (b) displays the dose profiles from VPMC and Eclipse™ in the beam direction. The black line is from the Eclipse™ calculation result, while the green line is from the VPMC calculation result. Red points are the measured results with an error bar of 2%/2mm. Subpanel (e) (f) displays the dose profile comparison between the VPMC calculated dose and the measured dose in the X direction at the Y position indicated by the horizonal line in (c) and in the Y direction at the X position indicated by the vertical line in (c), respectively. Subpanel (i) (j) displays the dose profile comparison between the Eclipse™ calculated dose and measured dose in the X direction at the Y position indicated by the horizonal line in (g) and in the Y direction at the X position indicated by the vertical line in (g), respectively. RBE = 1.1.

Data availability statement

Data available on request from the authors.