Effect of non-normality on the monitoring of simple linear profiles in two-stage processes: a remedial measure for gamma-distributed responses

Abstract

The relationship between the response variable and one or more independent variables refers to the quality characteristic in some statistical quality control applications, which is called profile. Most research dealt with the monitoring of profiles in single-stage processes considering a basic assumption of normality. However, some processes are made up of several sub-processes; thus, the effect of cascade property in multistage processes should be considered. Moreover, sometimes in practice, the assumption of normally distributed data does not hold. This paper first examines the effect of non-normal data to monitor simple linear profiles in two-stage processes in Phase II. We study non-normal distributions such as the skewed gamma distribution and the heavy-tailed symmetric t-distribution to measure the non-normality effect using the average run length criterion. Next, generalized linear models have been used and a monitoring approach based on generalized likelihood ratio (GLR) has been developed for gamma-distributed responses as a remedial measure to reduce the detrimental effects of non-normality. The results of simulation studies reveal that the performance of the GLR procedure is satisfactory for the multistage non-normal linear profiles. Finally, the simulated and real case studies with gamma-distributed data have been provided to show the application of the competing monitoring approaches.

1. Introduction

Nowadays, technology development has been done due to the more complicated products. Besides, the need for monitoring quality characteristics and process conditions is much more pronounced. When the products are the output of multistage processes, the stages are usually dependent. Disrespect to the relationship between the stages (the cascade effect of such processes) results in incorrect interpretation and weak performance of the control charts with misleading outcomes [4]. Hauck et al. [12] showed one of the basic researches to monitor multistage processes. They expanded the work by Hawkins [13] in the multivariate quality control concept. Loredo et al. [23] provided a method to monitor autocorrelated observations based on the regression adjustment in multistage processes. Niaki and Davoodi [28] examined the monitoring of the multivariate-multistage process using the MAR (1) model in line with artificial neural networks. Ding and Zeng [5] investigated the effect of measurement errors in the monitoring of regression-adjusted processes by comparing the ordinary least squares and the total least squares estimators. Pan et al. [32] developed a new approach for detecting the process changes in multistage systems. They provided residual control charts to monitor autocorrelated processes which can improve the detect-ability in Phase II monitoring. Apparently, most studies on multistage processes are conducted based on the normal assumption. However, in real practice, this assumption may be violated. Applying the common methods without considering the mentioned assumption leads to the failure in the proper results. Hence, if the quality characteristic is not distributed normally, the existing procedures require some adjustments. Jearkpaporn et al. [15] examined the situation in which the quality characteristic in a multistage process follows a gamma distribution. They used generalized linear model (GLM) and constructed new control charts based on that. Skinner et al. [33] studied the monitoring of multiple discrete counts and applied GLM-based control charts for Poisson data. Jearkpaporn et al. [14,16] considered the monitoring of response variables in a multistage manufacturing process where the variables followed a mixture of normal and non-normal distributions. Amiri et al. [2] studied two-stage processes with binomial data and proposed GLM-based control charts to monitor such processes effectively. Kim et al. [22] proposed a GLM for beta-distributed data in multistage processes. They developed two approaches for process monitoring called model-based SPC charts and a beta regression model. Suman and Das [34] underlined the issue of monitoring multiple product portfolios via a single process model. They proposed a new fault diagnostic approach for the early detection of developing faults. Asadzadeh and Baghaei [3] devised some monitoring procedures in multistage processes for Weibull-distributed data in the presence of outliers using accelerated failure time regression models.

Moreover, in some cases, there is a relationship between the response variable and one or more independent variables, called profile, which should be thoroughly monitored. Kang and Albin [19] conducted one of the most well-known works on simple linear profile monitoring and proposed T² and EWMA/R control charts in Phase I and Phase II respectively. Kim et al. [21] provided an EWMA-3 scheme to monitor simple linear profiles in Phase II. Zou et al. [36] presented a monitoring approach for general linear profiles and compared its performance with Kim et al. [21] method. Mahmoud [25] illustrated a new method for monitoring multiple linear regression profiles in Phase I to find changes in the intercept, slope, and variance parameters. Noorossana et al. [29] examined the issue of autocorrelated observations in simple linear profiles and provided three approaches based on time series models to eliminate the autocorrelation effect. Noorossana et al. [31] investigated the effect of non-normal observations in the monitoring of simple linear profiles. Mahmoud [26] measured the statistical performance of simple linear profile monitoring methods when the profile parameters are estimated in terms of in-control data set in Phase I. Noorossana and Ayoubi [30] proposed a nonparametric bootstrap control chart based on T² statistic for monitoring simple linear profiles. Hadidoust et al. [10] considered the problem of monitoring spline-modeled nonlinear profiles in Phase II in line with the estimation of change-point. Ershadi et al. [7] studied the economic-statistical design of a control chart with variable sampling intervals for monitoring linear profiles. Hadizadeh and Soleimani [11] examined simple linear profile monitoring with generalized autoregressive conditional heterogeneity (GARCH) models. Amiri et al. [1] considered the simultaneous monitoring of correlated multivariate linear and GLM regression profiles in Phase II.

Although a lot of attention has been given to control profile quality characteristics in recent years, a few papers have been dedicated to profile monitoring in multistage processes with cascade property. Eghbali Ghahyazi et al. [6] provided a method to monitor simple linear profiles in two-stage processes. They used the method proposed by Hauk et al. [12] based on the U statistic. Khedmati and Niaki [20] addressed the general linear profile monitoring problem in multistage processes and applied T²chart and LRT-based scheme for Phase I monitoring. Esmaeeli et al. [8] considered a two-stage process monitoring with a normal profile quality characteristic. They proposed two methods to monitor the quality characteristic in both stages. Kalaei et al. [17, 18] examined the performance of the U method in detecting various shifts in slope, intercept, and standard deviation parameters in Phase I monitoring of multistage profiles.

The common point in the papers dealing with multistage profile monitoring is that normally distributed quality variables are addressed; thus, simple linear regression can be effectively applied for modeling purposes. However, this assumption may not exist in some processes such as the ones in the semiconductor industry where a planarization scheme consists of two stages called plasma oxide deposition and oxide etch. In this two-stage process, the range of thickness is automatically measured at the end of each process as the main quality characteristic which follows a gamma distribution. Besides, the range of thickness is a function of gas flow; so, a relationship called profile should be monitored. Consequently, in this paper, we first examine the effect of non-normal data on the monitoring of simple linear profiles for two-stage processes in Phase II. Then, we introduce a remedial measure based on GLM and generalized likelihood ratio (GLR) methods to reduce the destructive effects of non-normal data. This modification makes the model-based control chart more flexible with the distribution of the quality characteristics. It should be noted that the main focus of this paper is on the use of GLM-based control charts for gamma-distributed responses for two-stage profiles.

The rest of this paper is structured as follows. In Section 2, we introduce some existing methods to monitor multistage profiles in Phase II. Non-normal distributions in linear profiles have been described in Section 3. Numerical results to measure the effect of non-normal data on monitoring two-stage linear profiles are presented in Section 4. In Section 5, a procedure based on GLM and GLR methods has been developed as a remedial measure. Section 6 investigates the performance of the GLR-based control chart. Simulated and real case studies have been provided in Sections 7 and 8 respectively. The concluding remarks are presented in the final section.

2. Monitoring two-stage linear profiles

The importance of monitoring simple linear profiles in multistage processes with cascade property is prominent and critical. For example, in semiconductor industries, plasma oxide deposition and oxide etch are the two stages of the planarization scheme. As mentioned in the previous section, the range of thickness should be monitored at the end of each stage. Due to the fact that this quality characteristic has different behavior based on the value of gas flow, the relationship is advisable to be considered for the sake of optimal process monitoring. Moreover, the response quality characteristic in the second stage is affected by the one related to the first stage. Thus, a two-stage profile monitoring is under consideration:

$$\begin{array}{rl}{y}_{ij1}& =A_0+A_1{x}_i+{ϵ}_{ij1}\end{array}$$ (1)

$$\begin{array}{rl}{y}_{ij2}& =\varphi y_{ij1}+B_1+B_2{x}_i+{ϵ}_{ij2}\end{array}$$ (2)

where $A_0$ and $A_1$ are the intercept and slope parameters corresponding to the first profile. Similarly, $B_1$ and $B_2$ are the intercept and slope parameters of the second profile and $\varphi$ is the correlation (cascade) parameter. Finally, in general, ${ϵ}_{ij1}$ and ${ϵ}_{ij2}$ are the normal random error terms with mean zero and variance ${\sigma }^2$. Thus, the second-stage profile in Equation (2) can be represented as follows:

$$y_{ij2}=\left(A_0\varphi +B_1\right)+\left(A_1\varphi +B_2\right)x_i+\varphi {ϵ}_{ij1}+{ϵ}_{ij2}$$ (3)

We suppose for the j^th (j=1, 2, … , m) sample collected over the time, $\left(x_i,y_{ij1}\right)$ and $\left(x_i,y_{ij2}\right)$ are the i^th (i=1, 2, … , n) observations of Stages 1 and 2 respectively. The next subsections elaborate on the existing monitoring approaches for normal responses.

2.1.  T² method

The U statistic for two-stage simple linear profiles can be expressed by the following equations:

$$\begin{array}{rl}{\mathbf{U}}_{j1}& ={\mathbf{A}}_1\end{array}$$ (4)

$$\begin{array}{rl}{\mathbf{U}}_{j2}& ={\mathbf{A}}_2-\sum _{21}\sum _{11}^{-1}{\mathbf{A}}_1\end{array}$$ (5)

where ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ are the vectors of intercept and slope estimators in Stage 1 and Stage 2. ${\sum }_{11}$ is the variance-covariance matrix of the intercept and slope estimators at Stage 1 and ${\sum }_{21}$ is the covariance matrix of intercept and slope estimators between Stages 1 and 2:

$$\sum _{21}=\left[\begin{array}{cc}\varphi {\sigma }^2\left(\frac{1}{n}+\frac{{\overline{X}}^2}{S_{xx}}\right)& -\varphi \frac{\overline{X}{\sigma }^2}{S_{xx}}\\ -\varphi \frac{\overline{X}{\sigma }^2}{S_{xx}}& \varphi \frac{{\sigma }^2}{S_{xx}}\end{array}\right]$$ (6)

It should be noted that ${\mathbf{U}}_{j1}$ and ${\mathbf{U}}_{j2}$ have a normal distribution with mean vector and covariance matrix as follows (Eghbali Ghahyazi et al. [6]):

$$\begin{array}{rl}{\mu }_{{\mathbf{U}}_{j1}}& ={\mu }_{{\mathbf{A}}_1}\end{array}$$ (7)

$$\begin{array}{rl}\sum _{{\mathbf{U}}_{j1}}& =\sum _{{\mathbf{A}}_1}=\sum _{11},\end{array}$$ (8)

$$\begin{array}{rl}{\mu }_{{\mathbf{U}}_{j2}}& ={\mu }_{{\mathbf{A}}_2}-\sum _{21}\sum _{11}^{-1}{\mu }_{{\mathbf{A}}_1}\end{array}$$ (9)

$$\begin{array}{rl}\sum _{{\mathbf{U}}_{j2}}& =\sum _{22}-\sum _{21}\sum _{11}^{-1}\sum _{12}\end{array}$$ (10)

Subsequently, the $T^2$ approach, proposed by Kang and Albin [19], could be applied. Hence, for the j^th collected sample in each stage, the $T^2$ statistic for s^th stage is calculated as follows:

$$T_{{\mathbf{U}}_{js}}^2=\left({\mathbf{U}}_{js}-{\mu }_{{\mathbf{U}}_{js}}\right)\sum _{{\mathbf{U}}_{js}}^{-1}({\mathbf{U}}_{js}-{\mu }_{{\mathbf{U}}_{js}}{)}^{T}s=1,2$$ (11)

The upper control limit for each stage is equal to ${\chi }_{\alpha ,2}^2$, where $\alpha$ is the significance level for each stage. It is notable that the significance level for each stage is derived from the significance level for the entire stages according to the Bonferroni method.

2.2. MEWMA method

The MEWMA statistic is calculated based on the U statistic, defined in the previous subsection, for each stage in the following manner [24]:

$${\mathbf{Z}}_{{\mathbf{U}}_{js}}^2=\theta \left({\mathbf{U}}_{js}-{\mu }_{{\mathbf{U}}_{js}}\right)+\left(1-\theta \right){\mathbf{Z}}_{{\mathbf{U}}_{\left(j-1\right)s}}s=1,2$$ (12)

where $\theta \left(0<\theta \le 1\right)$ is smoothing constant. The $j^{th}$ statistic of the modified MEWMA control chart is

$$T_{{\mathbf{z}}_{{\mathbf{U}}_{\text{js}}}}^2={\mathbf{Z}}_{{\mathbf{U}}_{js}}\sum _{{\mathbf{z}}_{{\mathbf{U}}_{\text{js}}}}^{-1}{\mathbf{Z}}_{{\mathbf{U}}_{js}}^T$$ (13)

in which, the covariance matrix is

$$\sum _{{\mathbf{z}}_{{\mathbf{U}}_{\text{js}}}}=\left[\frac{\theta }{\left(2-\theta \right)}\right]\sum _{{\mathbf{U}}_{js}}$$ (14)

As soon as the updated statistic goes beyond the upper control limit, denoted by H, the control chart shows an out-of-control signal. It is noteworthy that H is selected by simulation in a way to obtain a pre-determined in-control average run length (ARL).

3. Non-normal data

Non-normal condition is often examined in terms of individual observations. Non-normality is not an important problem with large size groups because due to the central limit theorem, sample means are almost normally distributed. However, for a small size group, that is a common situation, monitoring statistics may follow other distributions. Many studies have been conducted to examine the effect of non-normal data, most of which considered ‘t-distribution’ and ‘gamma distribution’ as symmetric and skewed distributions respectively [31]. As the kurtosis of t-distribution depends on the degrees of freedom, it is a proper symmetric distribution to measure the effect of non-normal data. We also examine the effect of a skewed distribution such as gamma distribution on the monitoring of two-stage linear profiles. Although the mean and variance of gamma and normal distributions could be equal in some situations, these distributions may have different forms which is actually due to the differences in other parameters such as third and fourth moments. Herein, the generalized gamma distribution, denoted by GAM $\left(\alpha ,\mathrm{\text{β}},\gamma \right)$, has been used with the following probability density function:

$$f\left(x\right)=\frac{{\left(x-\gamma \right)}^{\alpha -1}}{{\mathrm{\text{β}}}^{\alpha }\mathrm{\Gamma }\left(\alpha \right)}\exp \left\{-\left(x-\gamma \right)/\mathrm{\text{β}}\right\}x>\gamma (\gamma >0,\alpha >0,\mathrm{\text{β}}>0)$$ (15)

where $\alpha$ is the shape parameter, $\mathrm{\text{β}}$ is the scale parameter, and $\gamma$ is the location parameter. Moreover, the mean and variance are calculated via the following Equations (16) and (17) respectively:

$$\mu =\gamma +\alpha \mathrm{\text{β}}$$ (16)

$${\sigma }^2=\alpha {\mathrm{\text{β}}}^2$$ (17)

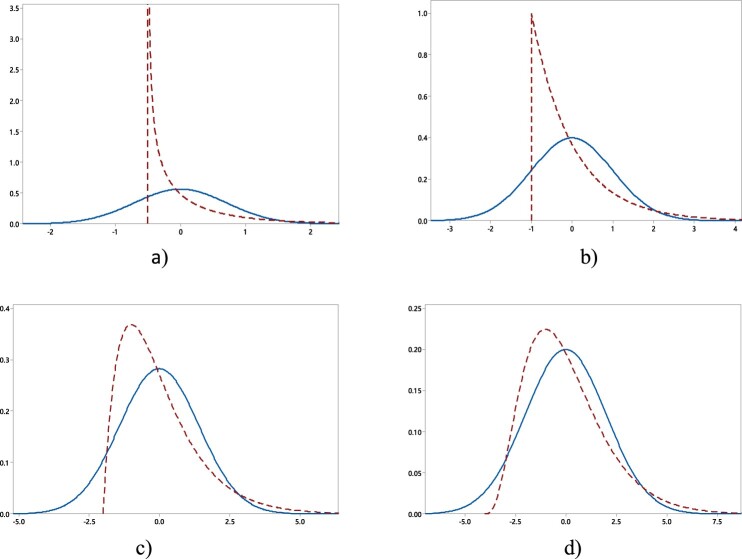
Figure 1 shows gamma and normal distributions. The shape parameter $\alpha$ is equal to 0.5, 1, 2, and 4. The scale parameter $\mathrm{\text{β}}$ has the fixed value of one and the location parameter is determined as $\gamma =-\alpha \mathrm{\text{β}}$.

Figure 1.

Some normal and gamma distributions: (a) PDF's for Gam(0.5, 1,−0.5) and N(0, 0.707); (b) PDF's for Gam(1, 1, −1) and N(0, 1); (c) PDF's for Gam(2, 1, −2) and N(0, 1.414); and (d) PDF's for Gam(4, 1, −4) and N(0, 2), [31].

According to Figure 1, when the α parameter increases, gamma distribution moves toward normal distribution.

4. Effect of non-normal data on the monitoring of two-stage linear profiles

In this section, the ARL values are examined taking into account normal and non-normal distributions in the described two-stage process with simple linear profiles. The first and second-stage profiles were elaborated in Section 2. Without loss of generality, the example discussed in Eghbali Ghahyazi et al. [6] has been used throughout the paper. To this end, the first and second profiles are $y_{ij1}=3+2x_i+{ϵ}_{ij1}$ and $y_{ij2}=\left(3\varphi +B_1\right)+\left(2\varphi +B_2\right)x_i+\varphi {ϵ}_{ij1}+{ϵ}_{ij2}$, respectively such that $\left(3\varphi +B_1\right)=2$ and $\left(2\varphi +B_2\right)=1$. The values of x are determined to be fixed as 2, 4, 6, and 8. In addition, we considered different values for $\varphi$ as the correlation parameter (cascade property) in our study. The total in-control ARL is equal to 200 and the in-control ARL for each stage is 400. Thus, the upper control limit (UCL) is ${\chi }_{0.0025,2}^2$ for the T²method at each stage. Subsequently, for the MEWMA method, the smoothing constant $\theta$ is selected to be 0.2 and the UCL is chosen by simulation study as 11.185 to yield the total in-control ARL of 200.

4.1. In-control ARL

This subsection deals with investigating the effect of t and gamma distributions on the performance of $T^2$ and MEWMA control charts for the in-control condition. It is apparent that t-distribution kurtosis is significantly different from normal distribution for small degrees of freedom. Moreover, concentrating on gamma distribution, it is remarkable that for a fixed scale parameter, increasing the shape parameter makes the skewness and kurtosis criteria closer to normal distribution. Besides, the kurtosis of gamma distribution with the small shape parameter is significantly larger than the kurtosis of normal distribution. Table 1 provides the non-normal data effect on the in-control ARL (ARL₀) of the $T^2$ and MEWMA control charts considering t-distribution. It should be noted that the ARLs are calculated with 10,000 simulation runs.

Table 1.

ARL₀ values for the T² and MEWMA control charts (t-distribution with different degrees of freedom).

	ν
ARL0 T2	5	8	10	15	20	30	40	50	100	1000
$\varphi$ = 0
$T_{total}^2$	40.57	63.34	78.61	104.34	119.92	141.59	157.11	162.77	178.58	198.37
$T_{\text{stage2}}^{\text{2}}$	79.59	126.70	155.50	206.17	240.81	285.63	305.92	325.68	358.68	389.368
$T_{\text{stage1}}^{\text{2}}$	81.55	126.60	154.54	208.82	238.72	283.11	308.74	329.11	357.77	389.18
$\varphi$ = 0.1
$T_{\text{total}}^{\text{2}}$	40.71	64.13	79.07	104.96	120.96	142.16	154.78	163.02	178.90	198.94
$T_{\text{stage2}}^{\text{2}}$	81.43	126.31	155.81	208.57	242.53	287.05	312.87	335.89	361.68	394.95
$T_{\text{stage1}}^{\text{2}}$	81.55	126.60	154.54	209.82	240.72	285.11	310.74	332.11	359.77	395.18
$\varphi$ = 0.5
$T_{\text{total}}^{\text{2}}$	40.61	64.02	76.79	104.30	120.41	144.69	151.69	164.59	180.89	196.54
$T_{\text{stage2}}^{\text{2}}$	80.12	130.19	154.39	204.63	242.15	283.31	303.11	330.70	351.18	391.36
$T_{\text{stage1}}^{\text{2}}$	79.68	128.82	153.30	208.46	242.45	284.01	306.85	332.89	355.11	393.93
$\varphi$ = 0.9
$T_{\text{total}}^{\text{2}}$	27.34	40.22	64.33	76.30	102.75	121.43	143.74	157.29	162.79	179.59
$T_{\text{stage2}}^{\text{2}}$	54.22	80.04	125.83	155.69	204.39	239.42	284.57	311.89	332.92	371.61
$T_{\text{stage1}}^{\text{2}}$	54.75	79.94	127.54	154.73	204.97	239.86	284.35	310.56	330.89	368.56
	ν
ARL0 MEWMA	5	8	10	15	20	30	40	50	100	1000
$\varphi$ = 0
$\text{MEWM}{\text{A}}_{\text{total}}$	107.01	144.84	161.17	175.98	179.35	189.61	190.94	195.99	199.22	202.87
$\text{MEWM}{\text{A}}_{\text{stage2}}$	213.71	290.70	314.42	345.08	360.99	380.71	381.98	381.12	389.28	397.89
$\text{MEWM}{\text{A}}_{\text{stage1}}$	213.71	290.70	314.41	345.08	360.99	380.71	381.97	381.12	389.27	397.89
$\varphi$ = 0.1
$\text{MEWM}{\text{A}}_{\text{total}}$	107.01	144.84	161.17	175.98	179.35	189.61	191.93	195.993	199.22	204.87
$\text{MEWM}{\text{A}}_{\text{stage2}}$	214.17	287.50	315.59	344.63	363.02	378.29	382.79	378.68	392.49	400.05
$\text{MEWM}{\text{A}}_{\text{stage1}}$	213.71	290.70	314.41	345.08	360.99	380.71	381.97	381.12	389.27	397.89
$\varphi$ = 0.5
$\text{MEWM}{\text{A}}_{\text{total}}$	108.49	145.85	157.54	174.88	181.29	192.16	192.63	197.13	198.86	201.48
$\text{MEWM}{\text{A}}_{\text{stage2}}$	216.33	288.82	312.00	342.65	357.86	380.20	381.85	385.88	392.52	396.11
$\text{MEWM}{\text{A}}_{\text{stage1}}$	217.44	285.84	314.92	340.87	355.97	378.40	383.69	386.72	398.99	399.98
$\varphi$ = 0.9
$\text{MEWM}{\text{A}}_{\text{total}}$	108.43	144.43	157.47	173.54	179.31	188.33	193.94	194.59	198.09	201.59
$\text{MEWM}{\text{A}}_{\text{stage2}}$	215.53	285.84	316.11	346.10	363.97	372.64	384.71	390.23	393.07	401.82
$\text{MEWM}{\text{A}}_{\text{stage1}}$	214.17	281.50	315.58	344.62	363.02	373.29	382.79	388.67	392.48	398.82

Table 1 reveals that the effect of non-normality on ARL₀ values of $T^2$ and MEWMA schemes is significant, particularly for the degree of freedom less than about 15. In these conditions, t-distribution has a heavier tail compared to normal distribution and the number of outlier data and the false alarm rates increase. Obviously, as the degree of freedom of t-distribution increases, the shape of the t-distribution gets closer to normal distribution. As a result, the ARL₀, obtained for the case with 1000 degrees of freedom, is near to the ARL₀ of normal distribution.

Next, the effect of gamma-distributed data on the performance of existing control charts has been investigated (Table 2).

Table 2.

ARL₀ values for the $T^2$ and MEWMA control charts (gamma distribution with different shape parameter and $\mathrm{\text{β}}=1$).

	α
ARL0 $T^2$	0.5	1	2	3	4	8	16	64	256	1024
$\varphi$ = 0
$T_{\text{total}}^{\text{2}}$	19.12	25.21	36.29	45.12	52.64	76.99	105.966	162.86	187.58	198.50
$T_{\text{stage2}}^{\text{2}}$	37.38	50.45	71.62	90.16	104.42	154.60	209.03	326.85	374.62	395.45
$T_{\text{stage1}}^{\text{2}}$	37.17	49.83	70.24	89.12	104.32	152.61	214.97	321.56	377.11	388.78
$\varphi$ = 0.1
$T_{\text{total}}^{\text{2}}$	18.76	25.89	35.25	44.98	52.23	77.03	106.43	161.83	188.61	197.65
$T_{\text{stage2}}^{\text{2}}$	37.19	50.57	70.91	90.25	106.11	156.22	214.58	327.33	377.65	389.17
$T_{\text{stage1}}^{\text{2}}$	37.17	49.73	71.74	90.28	106.46	153.97	215.25	323.97	378.60	395.03
$\varphi$ = 0.5
$T_{\text{total}}^{\text{2}}$	18.96	25.19	35.64	45.03	52.88	78.06	107.12	162.38	188.39	197.95
$T_{\text{stage2}}^{\text{2}}$	37.55	49.89	71.47	88.48	104.91	155.30	211.32	324.49	371.37	391.19
$T_{\text{stage1}}^{\text{2}}$	38.01	50.06	72.96	90.53	105.48	152.23	213.18	326.98	382.84	391.93
$\varphi$ = 0.9
$T_{\text{total}}^{\text{2}}$	18.71	25.09	35.960	45.45	53.34	76.63	107.87	161.11	190.23	200.23
$T_{\text{stage2}}^{\text{2}}$	36.59	49.68	70.24	88.36	106.83	154.32	215.42	321.60	384.99	397.39
$T_{\text{stage1}}^{\text{2}}$	37.55	50.26	71.74	90.81	105.95	153.67	211.11	326.80	372.92	391.53
	α
ARL0 MEWMA	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5	0.5
$\varphi$ = 0
$\text{MEWM}{\text{A}}_{\text{total}}$	61.09	82.43	108.86	125.95	136.59	162.21	182.07	193.86	200.86	201.35
$\text{MEWM}{\text{A}}_{\text{stage2}}$	120.94	164.06	219.33	252.82	273.67	320.81	355.48	388.38	392.37	402.21
$\text{MEWM}{\text{A}}_{\text{stage1}}$	118.77	160.45	216.21	251.24	274.82	324.34	354.44	382.30	397.93	398.51
$\varphi$ = 0.1
$\text{MEWM}{\text{A}}_{\text{total}}$	61.21	80.35	108.9798	127.53	139.09	162.76	178.55	202.66	201.48	202.28
$\text{MEWM}{\text{A}}_{\text{stage2}}$	122.09	161.81	213.05	249.11	271.53	324.39	358.51	385.49	399.16	402.04
$\text{MEWM}{\text{A}}_{\text{stage1}}$	122.79	163.09	217.62	251.60	275.54	322.13	354.92	386.23	398.21	399.37
$\varphi$ = 0.5
$\text{MEWM}{\text{A}}_{\text{total}}$	60.89	80.52	109.83	125.22	135.47	160.92	183.06	199.99	203.14	200.98
$\text{MEWM}{\text{A}}_{\text{stage2}}$	119.44	161.83	212.66	247.26	274.49	328.05	355.83	386.66	398.29	400.51
$\text{MEWM}{\text{A}}_{\text{stage1}}$	118.77	160.45	216.21	251.24	274.82	324.34	354.44	382.30	397.93	398.51
$\varphi$ = 0.9
$\text{MEWM}{\text{A}}_{\text{total}}$	60.79	82.43	109.82	125.59	137.46	164.08	183.10	195.99	204.29	201.49
$\text{MEWM}{\text{A}}_{\text{stage2}}$	122.03	164.38	216.24	247.53	274.83	326.17	355.53	391.86	399.78	402.52
$\text{MEWM}{\text{A}}_{\text{stage1}}$	119.70	160.57	213.38	249.06	272.14	323.72	355.88	390.71	398.27	401.63

The careful consideration of Table 2 reveals that for the shape parameters of less than about 16, the performance of $T^{\text{2}}$ and MEWMA control charts reduces, and the ARLs will be significantly different from the ones obtained for normal distribution. As the shape parameter increases, the ARL values corresponding to each stage are approximately 400 and the total ARL reaches its expected value for normally distributed data which is 200.

4.2. Out-of-control ARLs

This subsection intends to assess the impact of non-normal data on the performance of competing control charts in the out-of-control condition considering various shifts in intercept and slope parameters. The following tables show the out-of-control ARLs, denoted by ARL₁, when a shift occurs in the profile parameters. It should be noted that t-distribution with 5 degrees of freedom has been considered; thus, the variance of the distribution is equal to $5/\phantom{53}3$. For gamma distribution, we considered the value of $5/\phantom{53}3$ for the shape parameter ( $\alpha$), 1 for the scale parameter ( $\mathrm{\text{β}}$), and $-5/\phantom{-53}3$ for the location parameter ( $\gamma$) so that the error terms have gamma distribution with zero mean and $5/\phantom{53}3$ variance [31]. Tables 3 and 4 show the ARL values for the existing control procedures when there is a shift, denoted by ${\lambda }_1$ and ${\lambda }_2$, in the intercept and the slope of the first-stage profile.

Table 3.

ARL values of Stage 2 under the shifts in intercept of Stage 1 from $A_0$ to $A_0+{\lambda }_1\sigma$ in $T^2$ and MEWMA control charts.

	${\lambda }_1$
ARL $T^2$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi$ = 0
Normal	403.41	401.72	398.81	397.69	405.88	404.98	403.89	405.20	397.45	404.14	408.79
Gamma	63.88	65.84	64.02	64.94	64.16	65.36	63.33	64.92	65.09	65.10	65.06
t	79.59	81.43	80.18	80.12	80.86	80.04	80.88	80.30	80.00	79.99	80.34
$\varphi$ = 0.1
Normal	400.94	403.00	397.49	404.14	405.58	400.66	401.67	404.17	399.68	399.85	401.57
Gamma	63.88	65.83	64.02	64.95	64.16	65.35	63.32	64.92	65.09	65.09	65.06
t	79.58	81.42	80.17	80.12	80.86	80.04	80.88	80.30	80.00	79.99	80.34
$\varphi$ = 0.9
Normal	400.94	403.00	397.49	404.14	403.58	400.66	401.67	404.17	399.68	399.85	401.56
Gamma	63.88	65.83	64.03	64.95	64.16	65.35	63.32	64.93	65.09	65.09	65.06
t	79.19	80.68	80.32	79.52	81.03	80.61	81.57	81.62	80.59	80.30	80.64
	${\lambda }_1$
ARL MEWMA	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi$ = 0
Normal	403.12	398.29	404.72	402.59	400.29	406.53	404.42	402.85	396.48	393.93	403.37
Gamma	198.18	195.81	200.64	205.68	198.68	201.55	198.86	197.97	199.51	201.11	201.36
t	212.92	216.67	214.03	214.93	215.93	216.87	214.59	213.48	211.56	215.21	214.28
$\varphi$ = 0.1
Normal	401.58	404.88	401.34	407.24	400.27	400.17	399.03	407.34	406.89	398.28	404.24
Gamma	202.73	203.84	201.46	201.69	200.01	200.67	201.64	204.06	200.66	200.34	201.02
t	213.19	214.76	215.98	215.61	215.66	212.90	213.85	212.34	214.42	215.99	212.82
$\varphi$ = 0.9
Normal	401.59	404.88	401.34	404.24	400.27	400.17	399.03	403.34	401.59	404.88	401.34
Gamma	201.54	193.42	197.05	199.28	201.79	201.62	202.69	201.98	201.98	202.43	201.58
t	213.75	216.09	215.41	213.84	214.47	214.92	214.39	214.43	214.42	216.72	215.48

Table 4.

ARL values of Stage 2 under the shifts in slope of Stage 1 from $A_1$ to $A_1+{\lambda }_2\sigma$ in $T^2$ and MEWMA control charts.

	λ2
ARL $T^2$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi$ = 0
Normal	400.95	403.01	397.49	405.14	405.59	400.66	401.67	405.17	399.68	399.85	401.57
Gamma	63.88	65.83	64.03	64.95	64.16	65.36	63.32	64.93	65.09	65.09	65.06
t	79.59	81.43	80.18	80.12	80.86	80.04	80.88	80.30	80.00	79.99	80.34
$\varphi$ = 0.1
Normal	404.60	401.25	400.07	405.76	403.17	405.69	399.68	397.57	399.29	404.99	405.84
Gamma	65.84	64.54	65.40	64.74	65.33	64.74	64.79	65.70	65.55	64.75	64.66
t	79.19	80.68	80.33	79.52	81.03	80.61	81.58	81.62	80.59	80.30	80.64
$\varphi$ = 0.9
Normal	403.07	402.99	402.17	402.96	393.51	401.13	404.41	398.95	402.45	400.75	405.19
Gamma	63.88	65.83	64.03	64.95	64.16	65.36	63.32	64.93	65.09	65.09	65.06
t	80.42	81.14	80.54	80.83	81.28	80.56	79.81	81.16	80.61	80.77	81.13
	λ2
ARL MEWMA	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi$ = 0
Normal	401.59	404.88	401.34	405.24	400.27	400.17	399.03	405.34	404.89	398.28	403.25
Gamma	200.67	197.87	198.74	202.60	200.93	199.27	200.10	197.31	200.03	199.22	199.29
t	211.49	212.49	213.76	215.21	214.56	214.32	214.27	213.35	215.49	212.30	213.95
$\varphi$ = 0.1
Normal	400.39	402.65	404.32	403.22	401.57	400.84	399.66	402.92	399.13	404.84	394.99
Gamma	203.58	202.51	202.38	202.95	197.98	198.53	203.31	200.75	199.92	199.57	200.52
t	215.40	210.67	216.45	212.83	214.29	213.06	215.76	212.13	213.26	212.51	215.59
$\varphi$ = 0.9
Normal	401.59	404.88	401.34	405.24	400.27	400.17	399.031	404.34	402.89	398.28	405.24
Gamma	197.38	198.41	201.45	200.16	199.52	199.64	200.41	202.06	199.17	201.19	202.04
t	214.64	215.49	213.06	212.80	212.76	214.69	216.12	214.78	215.29	215.21	212.97

Concentrating on the performance for monitoring the second-stage profile, the existing control charts do not signal this change. In other words, it is desirable that the control chart for monitoring the second stage does not generate a signal when there is a shift in the intercept or slope of Stage 1. This implies that the U statistic can effectively remove the effect of cascade property, and the two stages have become independent from each other. Non-normal distributions influence the ARL₁ values seriously in a similar fashion occurred for the ARL₀; however, the cascade property does not affect the second stage, and the monitoring methods are roughly robust for the shifts in the slope and intercept of the first-stage profile. In general, it is concluded that the effect of non-normality is almost similar for $T^2$ and MEWMA charts since the ARL values for a specified control chart are approximately close together especially for the large shifts. Moreover, it indicates that gamma distribution has more deleterious effects on the ARL values; hence, in the following section, we examine the performance of GLR-based control scheme in the presence of gamma distribution.

5. A remedial measure for monitoring simple linear profiles in two-stage processes with non-normal responses

In this section, a remedial measure is proposed for monitoring simple linear profiles in multistage processes with non-normal data. The monitoring procedure is based on GLR to guard against the detrimental effect of non-normality.

The GLM is a flexible generalization of the ordinary linear regression that enables the response variable to have an error distribution model other than normal distribution. The use of GLM allows to consider non-normal data and to relax the assumption of constant variance. Consider the following response variable for a multistage process to illustrate this method as discussed in [14]:

$$y_{cs}\sim F\left(0\right)\text{ with mean}{\mu }_{y_{cs}}$$ (18)

where the response variable $y_{cs}$ has the cumulative distribution $F\left(0\right)$ and ${\mu }_{y_{cs}}$ is the mean of the c^th output at stage s. The mean ${\mu }_{y_{cs}}$ is a function of the quality characteristic of prior stages $\left(y_t\right)$ and the input variable at the present stage ( $X_s$). It can be calculated as follows:

$${\mu }_{y_{cs}}=g^{-1}\left(f_{cs}\left(X_s\right)+\sum _{t=1}^{s-1}{f}_{c,s.t}\left(y_t\right)\right)$$ (19)

where $g^{-1}$ denotes the inverse function and $f_{cs}\left(X_s\right)$ represents a function of $X_s$ that affects the output $y_{cs}$ at the $s^{th}$ stage of the process. $f_{c,s.t}\left(y_t\right)$ explains a function of $y_t$ which has an effect on the $c^{th}$ output at stage s of the process.

Subsequently, the GLR approach for monitoring linear profiles with non-normal response in two-stage processes is applied. Without loss of generality, the number of response output is considered to be one at each stage and the index c has been eliminated. Hence, the null hypothesis of $H_0:{\mu }_{y_s}={\mu }_{y_{s{0}_{}}}$ can be considered against $H_1:{\mu }_{y_s}\ne {\mu }_{y_{s{0}_{}}}$ where ${\mu }_{y_{s{0}_{}}}$ is the in-control value of the mean, irrespective of the data distribution. This hypothesis can be tested with GLR statistics. First, consider the modified GLR for testing the mentioned hypothesis for the i^th observation of the j^th sample of two-stage profiles:

$$\text{GL}{\text{R}}_{ijs}=-2\text{ln}\left(\frac{l_1}{l_0}\right)=-2\left(\text{ln}{l}_1-\text{ln}{l}_0\right)s=1,2$$ (20)

where $l_0$ and $l_1$ represent the in-control and out-of-control likelihood functions respectively. Concentrating on the gamma-distributed data, the likelihood function is the gamma probability density function introduced via Equation (15). Without loss of generality, the location parameter of the gamma distribution is considered to be zero; thus, $\mu =\alpha \mathrm{\text{β}}$. Subsequently, the likelihood function can be rewritten in terms of $\mu$ as follows:

$$l=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)y}{\left(\frac{y\alpha }{\mu }\right)}^{\alpha }\exp \left\{-y\alpha /\mu \right\}$$ (21)

Under the null hypothesis $H_0:{\mu }_y={\mu }_{y_0}$, the maximum likelihood function for the i^th observation of the $j^{th}$ sample of two-stage profiles is given by

$$l_0\left(y_{ijs}\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)y_{ijs}}{\left(\frac{y_{ijs}\alpha }{{\mu }_{y_{is0}}}\right)}^{\alpha }\exp \left\{-y_{ijs}\alpha /{\mu }_{y_{is0}}\right\}s=1,2$$ (22)

where ${\mu }_{y_{is0}}$ is the maximum likelihood estimator of ${\mu }_{y_{is}}$ under the null hypothesis (herein, the in-control parameter). Similarly, the maximum likelihood function is expressed as follows under the alternative hypothesis:

$$l_1\left(y_{ijs}\right)=\frac{1}{\mathrm{\Gamma }\left(\alpha \right)y_{ijs}}{\left(\frac{y_{ijs}\alpha }{{\mu }_{y_{is1}}}\right)}^{\alpha }\exp \left\{-y_{ijs}\alpha /{\mu }_{y_{is1}}\right\}s=1,2$$ (23)

in which ${\hat{\mu }}_{y_{is1}}$ is the maximum likelihood estimator of ${\mu }_{y_{is}}$ under the alternative hypothesis. Thus, the GLR is derived by the following formula:

$$\begin{array}{rl}\text{GL}{\text{R}}_{ijs}& =-2\left(\text{ln}{l}_1-\text{ln}{l}_0\right)=-2\left(\ln \left(\frac{1}{\mathrm{\Gamma }\left(\alpha \right)y_{ijs}}{\left(\frac{y_{ijs}\alpha }{{\hat{\mu }}_{y_{is1}}}\right)}^{\alpha }\exp \left\{-\frac{y_{ijs}\alpha }{{\hat{\mu }}_{y_{is1}}}\right\}\right)\right.\\ & -\left.\text{ ln}\left(\frac{1}{\mathrm{\Gamma }\left(\alpha \right)y_{ijs}}{\left(\frac{y_{ijs}\alpha }{{\mu }_{y_{is0}}}\right)}^{\alpha }\exp \left\{-\frac{y_{ijs}\alpha }{{\mu }_{y_{is0}}}\right\}\right)\right)\\ & =-2\left(\ln {\left(\frac{{\mu }_{y_{is0}}}{{\hat{\mu }}_{y_{is1}}}\right)}^{\alpha }\text{--}\frac{y_{ijs}\alpha }{{\hat{\mu }}_{y_{is1}}}+\frac{y_{ijs}\alpha }{{\mu }_{y_{is0}}}\right)\\ & =-2\alpha \left(-\ln \left(\frac{{\hat{\mu }}_{y_{is1}}}{{\mu }_{y_{is0}}}\right)-\frac{y_{ijs}}{{\hat{\mu }}_{y_{is1}}}+\frac{y_{ijs}}{{\mu }_{y_{is0}}}\right)s=1,2\end{array}$$ (24)

It should be noted that under the alternative hypothesis, ${\hat{\mu }}_{y_{is1}}$ is simply the observation $y_{ijs}$. Therefore,

$$\text{GL}{\text{R}}_{ijs}=-2\alpha \left(-\ln \left(\frac{y_{ijs}}{{\mu }_{y_{is0}}}\right)\text{--}1+\frac{y_{ijs}}{{\mu }_{y_{is0}}}\right)s=1,2$$ (25)

In general, the GLR statistic can be defined for the $j^{th}$ sample (with n observations) of two-stage profiles with a gamma distribution as follows:

$$\text{GL}{\text{R}}_{js}=-2\alpha \sum _{i=1}^n\left(-\ln \left(\frac{y_{ijs}}{{\mu }_{y_{is0}}}\right)-1+\frac{y_{ijs}}{{\mu }_{y_{is0}}}\right)s=1,2$$ (26)

For a normal distribution, the GLR is calculated in a similar fashion discussed for gamma distribution taking into account the normal probability density function:

$$\text{GL}{\text{R}}_{js}=\left(\frac{{\mathbf{y}}_{js-}{\mathit{\mu }}_{y_{s0}}}{\sigma }\right)\ast {\left(\frac{{\mathbf{y}}_{js-}{\mathit{\mu }}_{y_{s0}}}{\sigma }\right)}^{T}s=1,2$$ (27)

where $T$ shows the transpose of a matrix or vector.

Subsequently, the upper control limits (H) of the corresponding statistics have been calculated for gamma and normal distributions to reach the in-control ARL of total stages nearly 200, and for each stage about 400 using the simulation method.

6. The performance of the GLR-based monitoring scheme

This section evaluates the performance of the proposed GRL-based monitoring approach while the data follow a gamma distribution. First, the total ARL of the GLR-based control chart is investigated when there is a shift in the intercept ( ${\lambda }_1$) and slope ( ${\lambda }_2$) of the profile corresponding to the first stage (see Table 5).

Table 5.

ARL values of the GRL-based control chart for total stages under the shifts in intercept ( ${\lambda }_1$) and slope ( ${\lambda }_2$) of Stage 1.

	${\lambda }_1$
$\text{AR}{\text{L}}_{\text{Total}}$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\phi =0.0$	200.35	154.34	113.80	81.51	55.07	37.99	25.75	17.33	12.03	8.22	5.77
$\phi =0.1$	200.53	154.39	112.71	80.12	56.47	38.04	26.12	17.36	12.01	8.23	5.71
$\phi =0.3$	200.54	157.36	115.31	81.13	56.21	38.63	26.18	17.44	11.94	8.37	5.72
$\phi =0.5$	200.60	157.95	114.44	82.44	55.40	37.52	26.07	17.20	11.83	8.11	5.75
$\phi =0.7$	200.28	157.05	113.29	80.77	54.75	36.72	24.54	16.68	11.26	7.63	5.33
$\phi =0.9$	200.26	160.58	117.71	83.89	57.29	39.27	25.55	17.42	11.99	7.98	5.61
${\lambda }_2$
$\text{AR}{\text{L}}_{\text{Total}}$	0	0.025	0.05	0.075	0.1	0.125	0.15	0.175	0.2	0.225	0.25
$\phi =0.0$	200.19	177.14	155.62	131.13	114.83	94.76	79.69	66.10	54.36	45.88	36.51
$\phi =0.1$	200.39	176.12	155.23	133.92	113.95	95.87	79.89	66.70	54.72	44.24	36.68
$\phi =0.3$	200.20	178.01	156.81	131.89	116.47	95.18	80.47	66.09	54.60	46.04	36.35
$\phi =0.5$	200.11	179.69	154.75	136.17	116.77	96.83	80.97	66.03	55.05	45.38	37.73
$\phi =0.7$	200.11	178.67	153.15	131.77	114.13	95.43	78.01	64.73	53.40	43.37	35.58
$\phi =0.9$	200.55	183.67	160.19	139.74	119.75	101.36	83.01	68.61	56.23	46.24	36.91

According to Table 5, if there is a constant shift in the intercept or slope of the first stage profile, the total ARL is roughly the same for different correlation parameters. In other words, the total ARL obtained for a specific shift does not depend on the correlation or cascade parameter. This is in fact due to the optimal removal of the cascade property from the monitoring statistic, specifically for small and moderate cascade parameters. It is apparent that for a large cascade parameter, namely 0.9, the total ARL values differ from the others slightly. Next, the ARL values of Stage 2 under the shift in intercept and slope of the first-stage profile are reported.

Form Table 6, it is remarkable that the GLR statistic could reduce the dependency of the stages for gamma distribution to a large extent. The GLR-based control chart is quite robust against the shifts that occurred in the upcoming quality characteristic. However, when the correlation between the stages is very strong $(\varphi =0.9)$, the ARL values are moderately affected.

Table 6.

ARL values of the GRL-based control chart for Stage 2 under the shifts in intercept ( ${\lambda }_1$) and slope ( ${\lambda }_2$) of Stage 1.

	${\lambda }_1$
$\text{AR}{\text{L}}_{\text{stage2}}$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\phi =0.0$	400.1	400.96	401.46	394.16	405.99	404.72	403.08	403.31	402.68	397.18	395.98
$\phi =0.1$	400.04	392.1	395.14	390.46	392.59	396.03	394.25	392.45	387.42	396.13	402.7
$\phi =0.3$	400.21	401	403.1	402.7	405.8	402.2	405.3	400.1	399	404.1	393
$\phi =0.5$	399.5	396	395.3	398	394.8	393.5	395	394	392.3	390	396.5
$\phi =0.7$	399.78	394	403.1	397.3	403.3	401	397.1	396.5	389	395	398
$\phi =0.9$	399.83	390.5	393.86	390	391.1	390	393.8	393.2	391.2	390	390.9
	${\lambda }_2$
$\text{AR}{\text{L}}_{\text{stage2}}$	0	0.025	0.05	0.075	0.1	0.125	0.15	0.175	0.2	0.225	0.25
$\phi =0.0$	400.13	400.01	401	395.1	403	404.5	403.08	405.3	402.69	397.18	396
$\phi =0.1$	399.78	403.4	395	397.12	400	400	398.15	400	400	392.8	390.5
$\phi =0.3$	399.71	403	404.5	393.61	403.51	400	404.15	405.1	404.3	396	393.8
$\phi =0.5$	399.45	397	385.2	393.8	393.06	394.5	394.5	394	390	399	395
$\phi =0.7$	399.65	397	396.4	390.2	389	400.1	395	403.5	400	393	390.1
$\phi =0.9$	398.99	392	393.1	392	392	393.5	391	390	389.1	388	390

Finally, the ARL values of total stages for the existing and the proposed monitoring schemes are computed and recorded under the shift in the intercept of Stage 1. Table 7 reports the results for gamma and normal distributions respectively.

Table 7.

ARL values of total stages for the competing monitoring schemes under the shifts in intercept ( ${\lambda }_1$) of Stage 1 considering gamma and normally distributed data.

	${\lambda }_1$
$\text{AR}{\text{L}}_{\text{Total}}$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi =0.0$	gamma-distributed data
GLR	200.35	154.34	113.8	81.51	55.07	37.99	25.75	17.33	12.03	8.22	5.77
$T^2$	200.4	187.34	142.65	127.54	96.34	65.98	42.76	30.92	21.87	12.73	8.54
MEWMA	200.12	172.87	134.76	118.5	81.45	50.65	34.15	23.63	19.35	10.38	6.48
$\varphi =0.1$	gamma-distributed data
GLR	200.53	154.39	112.71	80.12	56.47	38.04	26.12	17.36	12.01	8.23	5.71
$T^2$	200.35	186.04	141.61	126.75	95.24	64.91	42.65	31.56	22.65	12.82	8.27
MEWMA	200.31	172.45	133.89	119.34	80.35	51.85	34.87	22.93	18.54	10.22	5.56
$\varphi =0.9$	gamma-distributed data
GLR	200.26	160.58	117.71	83.89	57.29	39.27	25.55	17.42	11.99	7.98	5.61
$T^2$	200.12	187.12	142.64	125.56	95.81	65.82	42.17	30.91	22.01	11.59	7.77
MEWMA	200.43	171.65	133.49	118.36	80.39	50.61	34.62	22.73	19.62	10.03	5.99
	${\lambda }_1$
$AR{L}_{Total}$	0	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
$\varphi =0.0$	normally distributed data
GLR	200.35	56.34	15.65	7.45	4.23	3.76	2.45	2.12	1.76	1.56	1.23
$T^2$	202.57	162.01	89.82	41.56	19.57	9.62	5.28	3.21	2.18	1.64	1.33
MEWMA	201.12	67.37	18.45	8.74	5.62	4.17	3.32	2.8	2.44	2.19	2.02
$\varphi =0.1$	normally distributed data
GLR	200.53	55.65	14.87	7.47	4.76	3.23	2.18	2.01	1.37	1.29	1.01
$T^2$	200.71	160.94	87.76	41.54	19.35	9.53	5.29	3.18	2.20	1.61	1.33
MEWMA	202.17	67.22	18.53	8.78	5.59	4.16	3.34	2.80	2.44	2.18	2.02
$\varphi =0.9$	normally distributed data
GLR	200.26	55.35	13.58	7.83	4.13	3.36	2.12	2.02	1.21	1.09	1.06
$T^2$	199.61	161.26	88.05	41.24	19.14	9.73	5.19	3.22	2.19	1.63	1.33
MEWMA	200.29	67.40	18.64	8.75	5.64	4.15	3.31	2.81	2.45	2.19	2.01

Table 7 indicates that the GRL-based control chart outweighs the existing counterparts in that the ARL values are less than those obtained for the $T^2$ and MEWMA. The reason is actually due to the normality assumption which is the fundamental concept in constructing the existing control procedures. Moreover, one can observe that the ARL values are roughly constant for a specific shift regardless of the values corresponding to the correlation parameter. Besides, the GLR-based control chart developed for normal distribution is superior in comparison with its competing monitoring methods, and it can detect out-of-control situations much more quickly. Thus, it can be concluded that the remedial measure based on the GRL-based scheme can be effectively applied to monitor the described two-stage process. The similar results, obtained for the shift in the slope parameter, are not reported here to save space.

7. Simulated case study

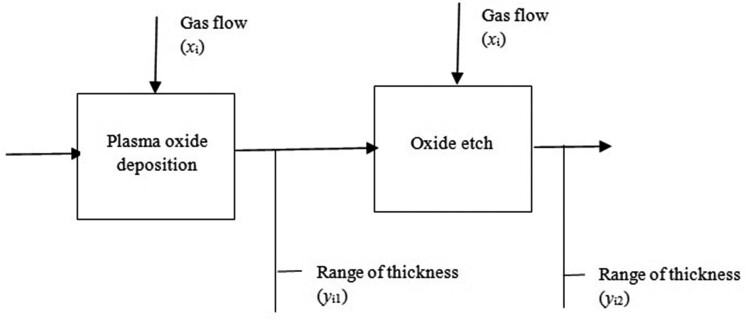
In this section, a simulated case study, based on what has been discussed in [14], is presented to evaluate the performance of the GLR-based monitoring scheme in the semiconductor industry. As mentioned before, the planarization process in this industry consists of two sub-processes called plasma oxide deposition and oxide etch. The main quality characteristic for each stage is actually the range of thickness which should be measured at four pre-determined values of gas flow. Thus, a two-stage process with a profile at each stage can be considered. Figure 2 illustrates this process.

Figure 2.

The data model for a simple two-stage semiconductor manufacturing process.

Suppose the data set is a total of 50 profiles with 4 replicates at each stage, out of which the first 25 samples are usually used in Phase I to estimate the profile parameters, and the remaining 25 samples are implemented in Phase II to evaluate the performance of the chart and to quickly detect the shift. Once the distributions of the response, the link function, and a set of input variables are determined, an iterative procedure is used to obtain the maximum likelihood estimates of the regression coefficients. Myers et al. [27] provide detailed discussions of parameter estimation, diagnostics, and model establishment in the GLM. In addition, the parameter estimation for nonparametric regression is described by Takezawa [35].

Without loss of generality, consider that the maximum likelihood estimation (MLE) method has been used for parameter estimation and the in-control profiles with regard to each stage are:

$$\begin{array}{rl}{y}_{ij1}& =11.3+0.88x_i+{ϵ}_{ij1}i=1,2,3,4\end{array}$$ (28)

$$\begin{array}{rl}{y}_{ij2}& =0.29y_{ij1}+12.67+0.75x_i+{ϵ}_{ij2}i=1,2,3,4\end{array}$$ (29)

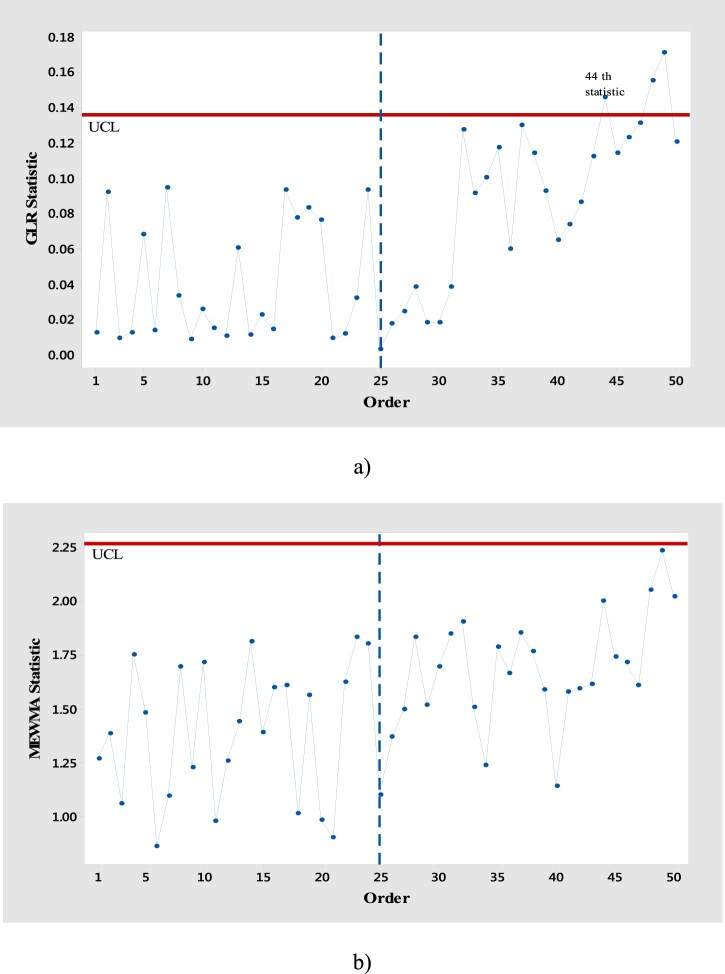
where ${ϵ}_{ij1}\sim \text{GAM}\left(1.7,0.9\right)$ and ${ϵ}_{ij2}\sim \text{GAM}\left(1.85,0.77\right)$. Hence, the monitoring of two-stage gamma profiles is under investigation. The upper control limits for the GLR-based control chart and the MEWMA chart have been selected in a way to reach the approximate value of 400 for each stage and 200 for total stages. For calculating the control limits and the ARLs, simulation studies were conducted with 10,000 replications in a similar fashion discussed in the previous sections. In Phase II, the next generated 25 statistics corresponding to the competing control charts were plotted to detect out-of-control parameters (see Figure 3). It should be noted that a shift of size 2 in the intercept of the second profile has been considered for generating out-of-control data in phase II. The results of plotting the data reveal that the GLR-based control procedure signals the shifts on Stage 2 (on the 44th statistic) more quickly than the MEWMA chart. This indicates the better performance of the GLR-based control chart compared with MEWMA chart. Note that both control charts declare the in-control states in Stage 1; thus, for reasons of space their figures have not been provided.

Figure 3.

The performance of the proposed and existing control charts for detecting shifts in Stage 2, (a) the GLR-based control chart and (b) the MEWMA control chart.

8. Real case study of piston manufacturing process

In this section, a real case study of the piston manufacturing process, firstly studied by Fong and Lawless [9], is used to show the application of the proposed control scheme. In this practical case, a piston, which is used in engines to impart motion by means of piston-rod, is produced in a four-stage machining process, wherein each stage, the diameters of a piston are inspected in a micron precision at heights 4, 10, 36.7, and 58.7 mm from the bottom of the part [9]. In this case study, the relationship between the height and diameter of each piston provides a situation to consider a profile model to monitor each stage of this process. Without loss of generality and for the sake of studying a two-stage process, we only investigate the first two stages of this piston manufacturing process. There are a total of 96 pistons and the first 30 profiles with 4 replicates in each of the four heights are considered to estimate the in-control parameter using the MLE method. It should be noted that the focus of this paper is on phase II monitoring and not phase I. However, based on what has been discussed in Myers et al. [27], the in-control parameters of the two profiles in phase I are derived taking into account gamma-distributed error terms (Table 8).

Table 8.

Estimated parameters of the profiles for the two-stage piston manufacturing process.

					The first gamma-distributed random error		The second gamma-distributed random error
$A_0$	$A_1$	ϕ	$B_1$	$B_2$	$\alpha$	$\mathrm{\text{β}}$	$\alpha$	$\mathrm{\text{β}}$
74.11	−0.013	0.21	55.12	−0.034	4.22	3.75	4.22	3.83

Next, the remaining 66 profiles are used in phase II to investigate the application of the proposed method. It should be noted that Equation (26) has been used to generate the statistic which should be plotted on the GLR-based control chart. Herein, the values of ${\mu }_{y_{is0}}$ are calculated respectively (under the in-control condition) based on what has been obtained in phase I:

$$\begin{array}{rl}fors=1,{\mu }_{y_{i10}}& =E\left(y_{i1}\right)=E(A_0+A_1{x}_i+{ϵ}_{i1})=74.11-0.013x_i+\left(4.22\ast 3.75\right)\\ & =74.11-0.013x_i+15.825=89.935-0.013x_i\end{array}$$

$$\begin{array}{rl}fors=2,{\mu }_{y_{i20}}& =E\left(y_{i2}\right)=E\left(\varphi y_{i1}+B_1+B_2{x}_i+{ϵ}_{i2}\right)\\ & =0.21E\left(y_{i1}\right)+55.12-0.034x_i+\left(4.22\ast 3.83\right)\\ & =0.21E\left(y_{i1}\right)+55.12-0.034x_i+16.162\\ & =0.21\left(89.935-0.013x_i\right)+71.282-0.034x_i\\ & =90.1683-0.03673x_i\end{array}$$

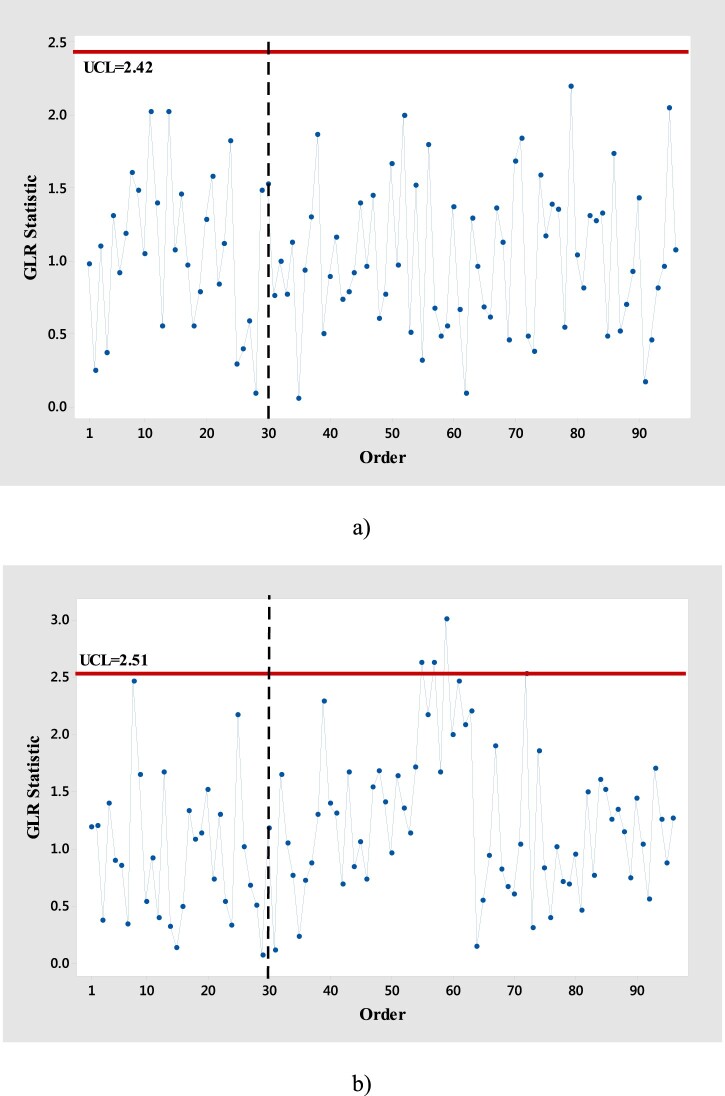
Moreover, the upper control limits for the proposed control chart were selected as before to reach the value of 400 for each stage respectively. Consequently, plotting the GLR statistics with regard to each stage (using Equation (26)) yields Figure 4.

Figure 4.

The application of the proposed GLR-based control chart to the piston manufacturing process (a) the first stage and (b) the second stage.

From Figure 4, it is apparent that the first stage is in-control while the second stage is out of control and remedial action is needed to make the process in control. In other words, the first stage of the piston manufacturing process is statistically in control, whereas an assignable cause is observed in the second stage. Hence, it can be concluded that the remedial measure based on the proposed GRL-based method can be properly used to monitor the described two-stage process.

9. Conclusion

This paper investigated the effect of non-normal data following symmetric distributions with high kurtosis such as t-distribution, and skewed distributions such as gamma distribution on the monitoring performance of simple linear profiles in cascade processes. Two-stage processes and the well-known approaches such as $T^2$ and MEWMA for linear profiles monitoring in Phase II were considered. The results revealed that non-normal data decreases the performance of $T^2$ and MEWMA control charts when the process is in-control. Also, in the case of out-of-control conditions, the performance of the existing monitoring approaches erodes; however, the MEWMA method is more robust than $T^2$ method for non-normal data while taking into account the shift in the intercept and slope parameters. To alleviate the non-normality effect in line with removing the dependency structure of the stages, the GLR-based scheme has been developed and used as a remedial measure for gamma-distributed responses. The simulation outputs revealed that the GLR-based control chart does not signal a change in Stage 2 due to the shifts in the slope and intercept of Stage 1. Moreover, it has been shown that the GLR-based monitoring method outperforms the existing control charts in both scenarios including gamma and normally distributed data while eliminating the cascade property effectively. Next, the application of the GLR-based control charts to the semiconductor industry in line with the piston manufacturing industry have been fully studied which proved its ability for detecting out-of-control situations compared to its competing counterpart. Finally, an interesting area worthy of continued research efforts is to compare the results obtained here with other methods used for the construction of control charts such as non-parametric approaches. The second area includes multistage profile monitoring of reliability data where the presence of censoring mechanism is also pronounced.

Disclosure statement

No potential conflict of interest was reported by the author(s).