Applying antagonistic activation pattern to the single-trial classification of mental arithmetic

Abstract

Background

At present, the application of fNIRS in the field of brain-computer interface (BCI) is being a hot topic. By fNIRS-BCI, the brain realizes the control of external devices. A state-of-the-art BCI system has five steps which are cerebral cortex signal acquisition, data pre-processing, feature selection and extraction, feature classification and application interface. Proper feature selection and extraction are crucial to the final fNIRS-BCI effect. This paper proposes a feature selection and extraction method for the mental arithmetic task. Specifically, we modified the antagonistic activation pattern approach and used the combination of antagonistic activation patterns to extract features for enhancement of the classification accuracy with low calculation costs.

Methods

Experiments are conducted on an open-acquisition dataset including fNIRS signals of eight healthy subjects of mental arithmetic (MA) tasks and rest tasks. First, the signals are filtered using band-pass filters to remove noise. Second, channels are selected by prior knowledge about antagonistic activation patterns. We used cerebral blood volume (CBV) and cerebral oxygen exchange (COE) of selected each channel to build novel attributes. Finally, we proposed three groups of attributes which are CBV, COE and CBV + COE. Based on attributes generated by the proposed method, we calculated temporal statistical measures (average, variance, maximum, minimum and slope). Any two of five statistical measures were combined as feature sets.

Main results

With the LDA, QDA, and SVM classifiers, the proposed method obtained higher classification accuracies the basic control method. The maximum classification accuracies achieved by the proposed method are 67.45 ± 14.56% with LDA classifier, 89.73 ± 5.71% with QDA classifier, and 87.04 ± 6.88% with SVM classifier. The novel method reduced the running time by 3.75 times compared with the method incorporating all channels into the feature set. Therefore, the novel method reduces the computational costs while maintaining high classification accuracy. The results are validated by another open-access dataset including MA and rest tasks of 29 healthy subjects.

Functional near-infrared spectroscopy; BCI; Mental arithmetic; Antagonistic activation pattern; Vector-based phase analysis

1. Introduction

The current brain-computer interface (BCI) systems are divided into two categories according to different ways of detecting and measuring brain activity. One is invasive technology, and the other is non-invasive technology. Invasive BCIs place electrodes in the cerebral cortex where they interact directly with neurons. This method requires invasive surgery on the subject and requires a well-established medical condition. Subjects are also at risk for possible post-surgical infection [1]. Electrocorticography (ECoG) has gained more use due to its partially invasive nature, which requires only the electrode array to be placed within the skull and directly above the cortex. The advantages are low demanding conditions for the surgery and a reduced risk of infection [2, 3, 4, 5]. However, invasive BCIs techniques still face significant challenges for subjects compared to non-invasive techniques [6, 7, 8]. Non-invasive BCIs are free of surgical risks, medical limitations. Therefore, it gained wider adoption. Non-invasive BCIs record electrophysiological signals or hemodynamic response signals. The technique that uses electrophysiological signals is electroencephalography (EEG), which records the electrical signals generated by the neuronal activity of the brain [9, 10]. Non-invasive BCI for recording hemodynamic responses uses functional neuroimaging techniques, for example, functional magnetic resonance imaging (fMRI) and functional near-infrared spectroscopy (fNIRS) [11, 12, 13, 14]. fMRI and fNIRS capture the changes in oxygen concentration in the blood consumed by neuronal activity in the brain and indirectly record neuronal activity. Besides the two above, Non-invasive BCI techniques include magnetoencephalography (MEG) and positron emission tomography (PET). MEG directly measures the weak bio-magnetic signals emitted by neural currents in the brain [15, 16, 17, 18, 19]. PET uses an isotope-labeled drug called the imaging agent that is injected into the body to study the pharmacokinetics of the tracer molecule. The aggregation of imaging agents in the brain can be obtained by detectors set around the brain. There are brightly displayed areas of high metabolic rate and darkly displayed areas of low metabolic rate on PET [20, 21]. Hybrid BCIs have also been used in recent studies, where hybrid BCI means a combination of two or more technologies (i.e. fNIRS, fMRI, EEG, MEG, PET or other techniques). Hybrid BCI can take different combinations of techniques depending on the characteristics of the brain activity elicited by a particular task [22, 23, 24, 25]. Among the non-invasive techniques, EEG and fNIRS are widely used in BCI systems because they have lower costs and better temporal and spatial resolution [26]. fNIRS and EEG are safer, more reliable, less costly and more portable compared to fMRI. fNIRS indirectly detects brain activity by measuring changes in the concentration of hemoglobin oxygenated (HbO) and deoxygenated hemoglobin (HbR). Since fNIRS measures directly on the scalp via a near-infrared light emitter and optical sensor, it is more robust to noise and electromagnetic interference [27, 28, 29, 30].

The BCI system requires subjects to perform a designed experimental task and decodes the subject’s brain responses. The experimental tasks most frequently used to complete BCI decoding include mental arithmetic (MA), motor execution and motor imagery. The decoding researches of mental arithmetic and resting-state two-classification tasks started earlier and a lot of decoding methods have been proposed. The decoding of mental arithmetic tasks and resting tasks provides inputs for the BCI system to control rehabilitation robots and drone equipment to meet the use needs of human. A state-of-the-art BCI system has five steps which are cerebral cortex signal acquisition, data pre-processing, feature selection and extraction, feature classification and application interface.

One of the challenges faced by fNIRS-based BCI systems is the selection of a suitable brain region for feature extraction. There is no consensus on choosing which regions to aim for a specific task. Recent studies have shown that proper filtering signal channels that have little relevance to trial tasks about MA can improve classification accuracies. Arcara et al compared the brain activity of the participants and divided their responses into fast and slow [31]. Analysis of the entire brain indicated that the rapid response has a higher degree of activation in the right dorsolateral prefrontal cortex. The results showed that although the left and right parietal cortex differ in the time of participation, these two areas have contributed to solving MA problems. Pfurtscheller et al investigated antagonistic activation patterns, which showed HbO has a focal bilateral increase in the dorsolateral prefrontal cortex (DLPFC) and simultaneously an HbO decrease in the medial area of the anterior prefrontal cortex (APFC) [32]. Bauernfeind et al used the antagonistic HbO features recorded by two channels over the prefrontal cortex to detect the focal antagonistic hemodynamic response pattern during MA tasks and increased the classification accuracies [33]. Those works inspired us that a prior knowledge can help us find channels that are highly relevant to the type of trial tasks, allowing us to achieve high accuracies with a few feature dimensions.

The antagonistic activation pattern approach proposed by Pfurtscheller et al found an antagonistic relationship between DLPFC and APFC. Bauernfeind et al applied antagonistic activation patterns in the field of BCI decoding, but the obtained classification accuracy was not high (79.69%). Based on the research of Bauernfeind et al, this paper proposes a novel feature extraction method aiming for improving classification accuracies of two-classification BCIs that decode MA tasks and rest periods. We tested the proposed method with an open-access fNIRS data set [33]. In the proposed method, we gathered channels that may be sensitive to mental arithmetic tasks and are involved in the antagonistic activation pattern approach, instead of screening for channels with the best classification accuracy per subject as in the method of Bauernfeind et al. The benefit of this approach is that it does not require a separate optimization strategy for each subject, which makes the antagonistic activation pattern approach more robust. Furthermore, our method reduces the number of channels compared with the method to incorporate all channel information into the feature set. The decoding accuracy of our method may be lower. To maintain high decoding accuracy while reducing the number of channels, we introduce a vector-based phase analysis (VPA) method (more explanation in next section). VPA was proposed by Yoshino et al [34]. Nazeer et al applied it to improve BCI decoding accuracy [35]. We used VPA to compute features of channels selected by antagonistic activation patterns. The integrated procedure of the basic method and the proposed method includes four steps shown in Figure 1 (a) and (b). The novelty of our work is the combination of vector-based phase analysis and antagonistic activation patterns. We wish the novel method to realize high classification accuracies with low calculation costs.

Figure 1.

Innovation points of the proposed method (b) compared with the basic method (a) are highlighted in red font. Both the proposed method and the basic method use the same preprocessing method to filter clutter. The proposed method uses vector phase analysis to enhance the classification performance of the features extracted based on the antagonistic activation pattern. The features in the basic method are statistical measures calculated from the traditional signals (HbO and HbR) obtained by averaging all channels.

In the second section of our paper, we describe the details of the data used for this study, which include subject information, experimental paradigm, channel configuration, and signal acquisition. In section three, the method is described, which includes signal pre-processing, the novel/basic feature extraction method, normalization, classification, and statistical analysis. Section four describes the classification accuracy results and running time results obtained by the novel method and the control method groups, and the results of the statistical analysis. The fifth section interprets the results and compares the results with the findings obtained from similar studies. We also point out the limitations of this paper. The last section concludes the whole paper.

2. Materials

2.1. Subjects and experimental paradigm

For the present investigations, we used an open-access dataset of eight participants (three males, five females, mean age 26 years, standard deviation 2 years) during the performance of MA tasks. This experience used block design. In periods of the initial state, the screen kept blank and subjects remained relaxed. Two seconds before the task started, a green bar appeared. After the cue (e.g., 97–4), Subjects were asked to subtract a single digit from a two-digit number within 12 s as soon as possible, and then had a 28-second rest period (Figure 2). Subjects repeated the above experiment 18 or 24 times (subjects S01, S02 and S03 are 18 trials, and subjects S04, S05, S06, S07 and S08 are 24 trials).

Figure 2.

Each subject included 3 or 4 sessions. Each session consisted of a 10-sec initial state and followed trials with 6 repetitions. Each trial included a 12-sec mental arithmetic task and a 28-sec of rest task. X denotes signal recorded by fNIRS equipment, i the number of trials.

2.2. Channel configuration and signal acquisition

The dataset was collected through a continuous-wave fNIRS system (ETG-4000, Hitachi Medical Co., Japan). This equipment consists of 52 channels that are produced by 16 photo-detectors and 17 light emitters (3 × 11 grid). The placement of channels is shown in Figure 3 [33]. An emissions detector split from cortical areas of approximately 3 cm is proposed to measure hemodynamic reaction signals. The fNIRS system collects prefrontal cortex signals at a fixed sampling frequency of 10 Hz. The wavelengths used for the instrument are 695 nm and 830 nm, respectively.

Figure 3.

Channels positions are overlaid on a Montreal Neurological Institute (MNI) -152 system compatible canonical brain which is optimized for NIRS analysis. The lowest line of channels is arranged along FP1–FP2 line of the international EEG 10–20 system, with channel 48 exactly at FP1 position. Red circles are near-infrared light sources, blue circles are the detector and green blocks constitute measurement channels. Bilateral dorsolateral prefrontal cortex (DLPFC) and the anterior prefrontal cortex (APFC) are defined by Brodmann area and are circled in red rectangles in the figure. (Note: this figure is drawn with reference to the literature [32].)

3. Methods

3.1. Signal preprocessing

For the fNIRS raw signal processing, evaluations were carried out using modified Beer-Lambert law (MBLL) to measure the concentration changes in HbO and HbR.

$$\left[\frac{\Delta HbO\left(t\right)}{\Delta HbR\left(t\right)}\right]=\frac{{\left[\begin{array}{cc}\Delta {\alpha }_{HbO}\left({\lambda }_1\right)& \Delta {\alpha }_{HbR}\left({\lambda }_1\right)\\ \Delta {\alpha }_{HbO}\left({\lambda }_2\right)& \Delta {\alpha }_{HbR}\left({\lambda }_2\right)\end{array}\right]}^{-1}\begin{array}{c}\Delta A\left(t,{\lambda }_1\right)\\ \Delta A\left(t,{\lambda }_2\right)\end{array}}{l\times d}$$ (1)

In Eq. (1), l is the source and detector distance. d is the curved path length factor. A(t, λ₁) and A(t, λ₂) are the absorptions at two different light source wavelengths of λ_i (where i = 1, 2). Δα_HbO (λ) and Δα_HbR (λ) are HbO’s and HbR’s extinction coefficients. ΔHbO (t) and ΔHbR (t) are the changes in concentration of HbO and HbR respectively.

HbO and HbR data include instrumental noises and physiological noises, which consist of blood pressure (Mayer waves), respiration (0.3–0.5 Hz), heartbeat (1–1.5 Hz), and artifacts. Therefore, signals were filtered using the fourth-order 0.01–0.1 Hz band-pass Butterworth filter to remove low and high frequency noises.

3.2. Proposed method

3.2.1. Channel selection

We referred to the study of Pfurtscheller et al [32]. According to Brodmann area, they found that simple MA caused a relative focal bilateral increase of HbO in DLPFC in parallel with a decrease in the medial area of APFC. We used an arithmetic expression to devise our filter.

$$C_s\left(x,y,z\right)=\{\begin{array}{cc}\in C_R,& if\left(x,y,z\right)\in S_{ROI}\\ \notin C_R,& if\left(x,y,z\right)\notin S_{ROI}\end{array}$$ (2)

In formula (2), C_S denotes a set of signal values of HbO and HbR before filtering. C_R is a set of processed signal values of HbO and HbR. x, y and z are channel’s Montreal Neurological Institute (MNI) space coordinates. S_ROI is a scope presented by MNI-space coordinates of regions of interest (ROI). In the open-access dataset that we adopted, MNI-coordinates of channel that our paper included are given in Table 1. We chose 9 channels to extract features using VPA. Channel average was not performed in these 9 channels.

Table 1.

According to the Channel number and corresponding MNI coordinates, we estimated the location of cortical surface of each ROI (Note: this table is drawn referring to the paper [39].)

ROI	Channel	Cortical areas
		x	y	z
1.Anterior prefrontal cortex (APFC)	46	23	72	8
	47	-8	73	6
	48	-31	66	3
2.Left dorsolateral prefrontal cortex (Left DLPFC)	18	-51	23	41
	28	-47	39	28
	29	-61	11	28
3.Right dorsolateral prefrontal cortex (Right DLPFC)	13	48	31	42
	23	57	26	29
	24	45	62	29

3.2.2. Vector-based phase analysis

In order to solve the question that fNIRS-BCIs have an inherent delay in the current fNIRS-BCI research, VPA is proposed for detecting initial dips produced by brain activity [36, 37, 38, 39, 40, 41]. As shown in Figure 4, HbO and HbR signals defined an orthogonal vector coordinate plane. And then, we defined another orthogonal plane composed of CBV and COE. There was an inclination angle of 45° counter-clockwise between this plane and the previous plane. CBV and COE are calculated according to (3), (4).

$$CBV=\frac{HbO+HbR}{\sqrt{2}}$$ (3)

$$COE=\frac{HbR-HbO}{\sqrt{2}}$$ (4)

Figure 4.

HbO and HbR form a set of orthogonal planes, and this plane is rotated 45° counterclockwise to obtain another set of orthogonal planes composed of CBV and COE. The plane generated by VPA shows eight phases. The dotted circle shows the maximum value of the baseline signal from the resting state.

In addition, there were two attributes in VPA, which are the magnitude (|L|) and the phase angle (k). |L| and k are calculated according to (5), (6).

$$\left|L\right|=\sqrt{\frac{Hb{O}^2+Hb{R}^2}{2}}$$ (5)

$$k={\tan }^{-1}\left(\frac{COE}{CBV}\right)$$ (6)

The dashed circles in Figure 4 represent thresholds that distinguish between rest tasks and MA tasks, with the threshold value taken as the maximum value of the signal in the resting state. Channel values higher than the threshold are in the active state, while channel values below the threshold are in the resting phase. The whole vector plane was divided into eight phase angles, where phases one to five are the phases that produce the initial inclination, and in those phases, HbR or COE shows an increase. Phases six to eight are the hemodynamic response region, where HbR and COE show a decrease. We used two attributes (i.e. CBV and COE) to execute statistical calculations in each trial. The reason for which CBV and COE were chosen is that in the study of Nazeer et al, the CBV + COE achieved maximum accuracies with minimum feature dimensions [35].

3.2.3. Statistical measures

In this paper, we chose five widely used statistical measures which are average, variance, maximum, minimum and slope calculated in temporal dimension [42, 43, 44, 45, 46].

Average is the signal average, which is the sum of all data values divided by the number of all data. Average is calculated according to formula (7).

$$\overline{X}=\frac{1}{n}\sum X$$ (7)

where X denotes the signal value, n the number of data, $\overline{X}$ the average of the samples.

Variance is a measure that reflects the degree of dispersion of a set of data. Variance formula is shown in formula (8).

$$S^2=\frac{\sum {\left(X-\overline{X}\right)}^2}{n-1}$$ (8)

where X denotes the signal value, $\overline{X}$ the average of the signal value, n the number of data, S² the variance of the sample data.

Maximum (or minimum) is the maximum (or minimum) signal amplitude within the MA (/rest period) trial time window.

Slope reflects the coefficient of the first-order term of the first-order function fitting to the temporal fluctuation of signals. We used all data points of MA and rest periods to fit.

We used MATLAB® (version: R2019a) to achieve the above five statistical measures. The functions involved in this paper are shown in Table 2. We used two statistical measures of nine channels, therefore total feature dimensions are 9 × 2 = 18 for CBV and COE and the total feature dimensions of CBV + COE are 9 × 2 × 2 = 36.

Table 2.

In this paper, five statistical measures were used, and we completed the calculations using the corresponding functions in MATLAB®.

Statistical measures	Functions
Average	mean
Variance	var
Maximum	max
Minimum	min
Slope	polyfit

3.3. Basic method

As a comparison group, we calculated another set of features by the basic method. First, we averaged HbO and HbR of all channels. Second, signals were calculated on the time level using statistical measures. Third, any two of the five statistical measures that were used in the proposed method formed a set of feature groups. We proposed three groups of features for HbO, HbR as well as HbO + HbR, separately. Therefore, total features are 2, 2 and 4 for HbO, HbR and HbO + HbR. The method of extracting the basic features is popular in current studies, considering the influence of every channel on classification and avoiding an increase in computational complexity.

3.4. Other methods

We used a combination of the VPA features and the method averaging all channels as Hybrid Method 1 and a combination of the traditional features and antagonistic activation pattern approach as Hybrid Method 2. In addition, to further verify how effective the proposed method is in reducing the number of channels while improving the classification accuracies, we also designed an additional experiment with the VPA method to extract the features of all channels, called Hybrid Method 3. We used 4 control groups to compare with the novel method.

3.5. Normalization

For eliminating the effect of dimensions on the convergence rate, the feature values obtained by five methods were scaled by a normalization process. We applied formula (9) to achieve normalized scaling to the features within each subject:

$$X^{\prime }=\frac{X-X_{\min }}{X_{\max }-X_{\min }}$$ (9)

where X′ is the scaled feature, X the unscaled feature, X_max the maximum of the column feature, X_min the minimum of the column feature.

3.6. Classification

Linear Discriminant Analysis (LDA), quadratic discriminant analysis (QDA) and support vector machine (SVM) have been verified in the data sets we used. We used 5 times 10-fold cross-validation to estimate of performance classification of five methods. The entire dataset was first divided into 10 roughly equal parts. Nine out of ten parts were used in turn as the training set and the remaining one as the prediction set for testing.

3.6.1. Linear Discriminant Analysis (LDA)

Due to low computational costs and high speed, LDA is often used as a classifier in fNIRS-BCI [47, 48, 49, 50, 51]. The basic idea of LDA is to project the data in low dimensions with the goal that the distance within a class is as close as possible and the distance between the classes is maximized to realize the classification. The specific method is to maximize the ratio of the variance between classes and minimize the ratio of variance within classes.

3.6.2. Quadratic discriminant analysis (QDA)

QDA is a generalization of LDA. QDA presupposes that the classification labels are two classes and that the measurements obey a normal distribution. The difference with LDA is that QDA estimates a covariance matrix for each class. In addition, the surface used to separate the subspaces is a conic section. Thereby QDA enables the classifier to perform more effectively and enhances classification accuracies [52].

3.6.3. Support vector machine (SVM)

SVM is a binary classification model. It is widely used in fNIRS-BCI because SVM performs well in classifying high-dimensional features and SVM is able to handle nonlinear problems by applying kernel tricks. In this paper, we used radial basis function (RBF) kernel function. The reason is that we found that using RBF kernel achieves higher classification accuracy compared to other kernel functions (e.g., linear kernel function) for both the benchmark methods and the proposed method. We used a penalty parameter C = 100 and parameter gamma was 1. The MATLAB® tool libsvm was used for achieving SVM with RBF kernel.

3.7. Statistical analysis

We used paired sample t-tests to assess statistical differences. Given the VPA features, we perform statistical significance analysis on the novel method and Hybrid Method 2. Similarly, given the traditional features, we perform statistical significance analysis on Hybrid Method 1 and the basic method. On each classifier, we chose the maximum classification accuracies.

4. Results

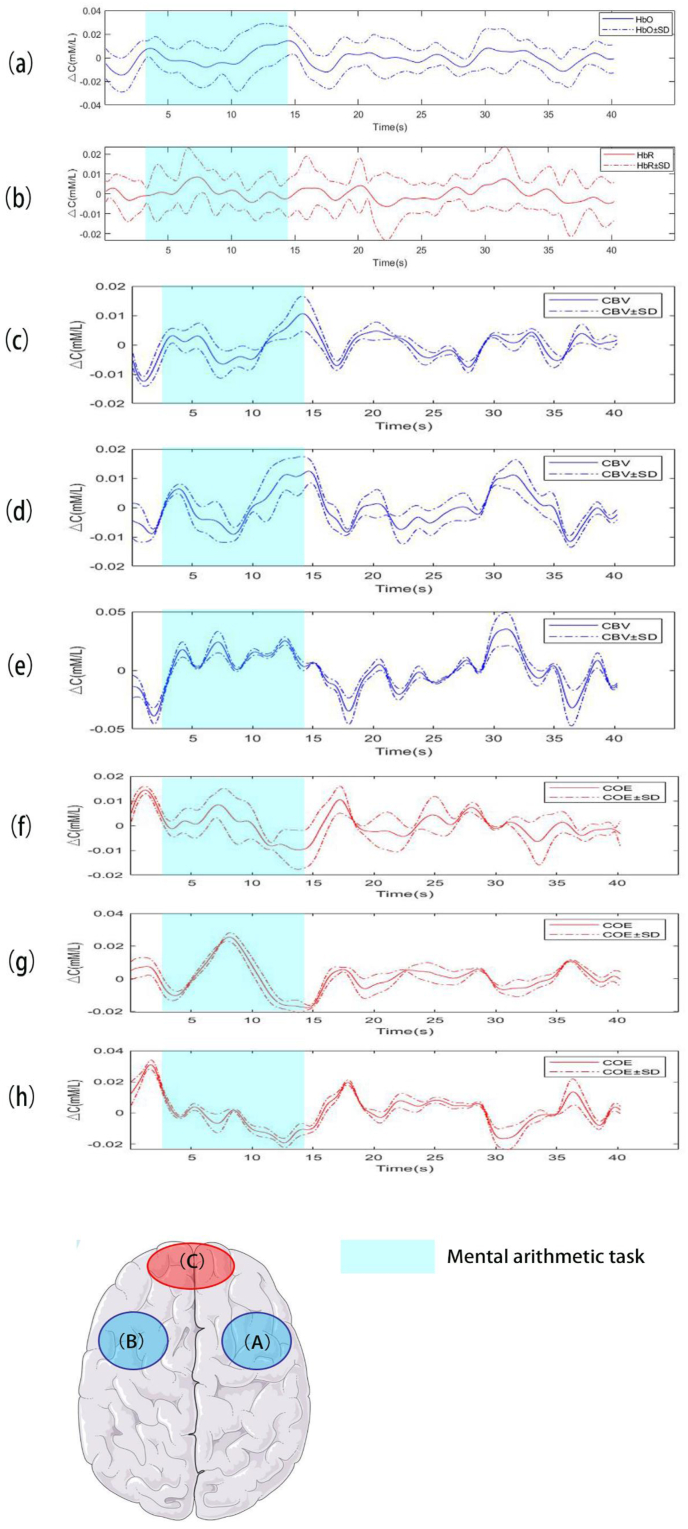
The averages of all channels of HbO and HbR are shown in Figure 5 (a and b) and the averages of CBV and COE in 3 ROIs in the time domain are shown in Figure 5 (c–h). The signals originated from the first trial of subject 5. The basic method and proposed method extracted features from the above signals. We measured average, variance, maximum, minimum and slope in the temporal dimension of those signals.

Figure 5.

Averaged HbO (a) and HbR (b) with standard deviation means all channels in the time domain. Averaged CBV and COE with standard deviation come from three regions of interest (ROIs) (A, B and C). According to Brodmann area, ROI1 (A) is located approximately in the right dorsolateral prefrontal cortex (DLPFC). ROI2 (B) is located approximately in the left DLPFC. ROI3 (C) is located approximately in the medial area of anterior prefrontal cortex (APFC) (c, d, e) are averaged CBV with standard deviation and (f, g, h) are averaged COE with standard deviation. Above signals extract from trial 1 of subject S05.

We classified the features generated by the novel method and the control method using diagLDA, diagQDA and SVM classifiers. The average classification accuracies with diagLDA, diagQDA and SVM are shown in Table 3 respectively. The maximum classification accuracies of the proposed method using diagLDA, diagQDA and SVM classifiers are 67.45 ± 14.56%, 89.73 ± 5.71% and 87.04 ± 6.88%, respectively. While the maximum classification accuracies of the basic method using the above three classifiers are 61.19 ± 10.7%, 76.68 ± 6.96% and 61.95 ± 16.65%, respectively. The maximum average accuracies obtained by Hybrid Method 3 are 67.11 ± 12.58% (diagLDA), 90.23 ± 4.78% (diagQDA) and 53.01 ± 19.12% (SVM). The classification accuracies using the novel method exceed the classification accuracies of the basic method in all three classifiers and have classification accuracies close to those of Hybrid Method 3.

Table 3.

We used diagLDA, diagQDA and SVM to classify novel features and basic features. The bold stands for the average and standard deviation of maximum accuracies achieved by each feature group.

		CBV + COE	CBV	COE	HbO + HbR	HbO	HbR
diagLDA
average variance		63.45 ± 16.49	62.43 ± 15.87	61.92 ± 18.0	57.88 ± 12.01	59.56 ± 7.53	55.96 ± 14.21
average minimum		62.3 ± 15.82	58.92 ± 15.39	63.55 ± 13.64	53.89 ± 12.63	56.05 ± 11.74	52.51 ± 10.5
average maximum		62.13 ± 19.57	64.23 ± 14.48	56.96 ± 19.38	59.13 ± 12.4	59.38 ± 7.82	56.4 ± 14.73
average slope		60.97 ± 10.58	60.22 ± 10.77	60.4 ± 10.29	53.55 ± 11.56	53.83 ± 10.07	49.7 ± 13.97
variance minimum		62.67 ± 15.08	61.45 ± 14.74	63.01 ± 14.11	55.13 ± 16.02	55.55 ± 12.13	53.96 ± 13.24
variance maximum		63.2 ± 17.13	67.45 ± 14.56	57.93 ± 17.2	58.79 ± 12.48	59.66 ± 9.63	55.2 ± 15.27
variance slope		64.61 ± 14.17	64.18 ± 13.58	63.03 ± 11.45	59.29 ± 10.83	58.21 ± 9.42	57.18 ± 14.33
minimum maximum		63.99 ± 16.32	65.71 ± 14.01	60.29 ± 15.73	56.55 ± 14.47	57.7 ± 12.03	54.33 ± 15.32
minimum slope		63.31 ± 11.64	62.11 ± 14.54	63.3 ± 10.19	55.26 ± 13.15	56.39 ± 11.39	53.79 ± 11.59
maximum slope		63.35 ± 14.21	64.36 ± 14.41	59.72 ± 13.02	61.19 ± 10.7	59.54 ± 8.24	58.83 ± 14.98
diagQDA
average variance	88.83 ± 5.9		83.12 ± 12.34	89.19 ± 5.54	76.68 ± 6.96	68.91 ± 6.31	69.5 ± 9.1
average minimum	89.73 ± 5.71		85.97 ± 7.86	89.37 ± 6.32	75.01 ± 5.7	68.45 ± 4.6	67.71 ± 8.66
average maximum	89.35 ± 4.12		81.84 ± 12.63	88.24 ± 5.36	76.03 ± 7.6	69.65 ± 7.66	71.34 ± 8.63
average slope	87.64 ± 5.99		83.74 ± 6.32	87.03 ± 5.8	72.77 ± 7.93	69.0 ± 7.08	67.29 ± 9.96
variance minimum	62.27 ± 14.64		60.8 ± 14.2	62.86 ± 11.39	55.11 ± 12.01	55.46 ± 8.31	53.35 ± 11.3
variance maximum	63.23 ± 15.71		65.52 ± 13.59	61.14 ± 12.81	59.15 ± 10.54	59.2 ± 8.2	55.6 ± 12.58
variance slope	66.98 ± 14.11		67.22 ± 12.71	64.77 ± 10.17	62.43 ± 11.63	61.04 ± 8.82	58.65 ± 14.09
minimum maximum	64.12 ± 13.91		63.5 ± 14.34	63.93 ± 12.19	56.11 ± 11.04	57.16 ± 9.58	54.44 ± 10.51
minimum slope	66.78 ± 12.43		63.68 ± 13.24	65.35 ± 11.52	58.29 ± 10.57	59.87 ± 8.11	55.29 ± 11.14
maximum slope	67.43 ± 13.53		65.53 ± 12.1	66.15 ± 10.77	65.18 ± 12.12	62.79 ± 7.62	60.05 ± 16.07
SVM
average variance	75.44 ± 11.34		79.2 ± 11.92	81.74 ± 9.66	58.58 ± 16.52	51.6 ± 12.61	48.63 ± 15.73
average minimum	73.08 ± 9.35		81.89 ± 9.12	79.55 ± 8.81	52.01 ± 14.52	45.56 ± 13.73	39.91 ± 11.47
average maximum	74.66 ± 10.74		81.68 ± 10.08	87.04 ± 6.88	61.95 ± 16.65	51.74 ± 13.29	49.68 ± 16.24
average slope	71.11 ± 9.49		77.98 ± 6.33	79.73 ± 6.0	53.36 ± 11.96	46.82 ± 12.2	37.64 ± 9.94
variance minimum	61.53 ± 20.25		62.65 ± 15.73	65.31 ± 15.59	49.61 ± 17.63	46.29 ± 16.71	45.8 ± 13.65
variance maximum	65.19 ± 15.83		61.99 ± 14.04	65.44 ± 14.94	53.51 ± 19.68	48.41 ± 18.13	50.87 ± 17.41
variance slope	63.53 ± 19.53		64.44 ± 13.96	63.9 ± 14.12	53.97 ± 15.44	49.65 ± 16.04	48.39 ± 17.29
minimum maximum	63.88 ± 16.75		64.79 ± 12.47	66.8 ± 14.19	51.45 ± 19.0	48.5 ± 19.01	48.74 ± 17.42
minimum slope	58.1 ± 19.27		63.8 ± 10.76	63.68 ± 12.79	47.25 ± 14.89	41.34 ± 14.65	40.75 ± 11.92
maximum slope	63.47 ± 16.63		67.29 ± 11.88	68.9 ± 11.24	56.69 ± 16.74	51.32 ± 13.95	50.74 ± 19.11

We evaluated the algorithmic complexity of the novel method and control methods. Due to the low time delay requirement of the BCI decoding task, we focused on the time complexity of the algorithm. In terms of file reading, feature calculation and extraction, the time spent by the novel method and control methods is basically the same level, so the main difference in time cost is focused on the training and prediction of the classifier. We analyzed the three classifiers used separately. For an LDA classifier, the time is usually O(ndt + t³), where n is the number of samples, d is the feature dimension and t = min(n, d) [53]. For the QDA classifier, the time complexity is O(vdn² ​+ vn³(1/k + 1/v)), where k is the number of sample classes and v is the number of copies of the data to be equally divided during cross-validation [54]. The time complexity of the SVM classifier is not stable. For SVM whose kernel function is radial basis, the algorithm complexity may be O(N_s³ + N_s²n + N_sdn + N_sd), O(N_s³ + N_sn + N_sdn + N_sd), O(N_s² + N_sdn + N_sd) or O(dn² + N_sd) [55]. N_s is the number of support vectors. The algorithm complexity of SVM mainly depends on the relative value of the number of support vectors and the number of training sample points and whether the majority of support vectors are on the upper boundary. From the above analysis, it can be seen that the time complexity of classifier training and prediction largely depends on the number of samples and feature dimension. When tested on the same dataset, the novel method and control methods have the same number of samples, so the time complexity is mainly related to the feature dimension. The feature dimension of the novel method is the same as that of the hybrid method 1, lower than that of the hybrid method 3 and higher than that of the hybrid method 2 and the basic method. Therefore, the time complexity of the novel method is at the same level as Hybrid Method 1, lower than Hybrid Method 3 and higher than Hybrid Method 2 and the base method. In addition, we also calculated the time cost of all methods using post-hoc statistical methods. We timed the processing of all trials (reading the data, training, prediction, and exporting classification accuracies) for all 8 subjects. Under Windows 10 operating system, MATLAB R2019a and Intel(R) Core (TM) i7-6700HQ CPU environment, the program running times are shown in Table 4. The basic method and Hybrid Method 2 are at the level of the shortest computation time. The proposed method and Hybrid Method 1 are at the level of moderate computation time. Hybrid method 3 is at the level of the highest computational time.

Table 4.

We completed the classification of all subject data on the diagLDA, diagQDA and SVM classifiers to obtain the running time of the program.

Methods	Running time (s)
The novel method	24.712152
The basic method	14.445573
Hybrid Method 1	26.750237
Hybrid Method 2	14.261240
Hybrid Method 3	92.756068

Figure 6 is a display of the experimental data and shows the two-dimensional feature spaces of features generated by basic method (a) and proposed method (b). All feature dimensions of the novel method and the basic method are compressed on a two-dimensional feature space consisting of maximum and average values. Compared with the basic method, the novel method adds some feature dimensions. Figure 7 illustrates statistical distributions of accuracies for each method using diagLDA, diagQDA and SVM classifiers. By t-tests, we get the results that the classification accuracies of the novel method are significantly higher than that of Hybrid Method 2 (a–c) and the classification accuracies of Hybrid Method 1 are significantly higher than that of the basic method (d–f). Figure 8 shows maximum accuracies the novel method (a–c) and the basic method (d–f) represented by confusion matrix with diagLDA, diagQDA and SVM classifiers. The validation sets have samples from 18 to 24 trials of each subject. Each subject performed a 10-fold cross-validation with 5 repetitions. Each trial was used as a test sample and was reused 5 times, so the number of test samples in the validation sets per subject is 90 or 120. The total number of validation sets is 90 × 3 + 120 × 5 = 870. The three classifiers (diagLDA, diagQDA and SVM) use the proposed method to obtain less misjudgment of labels than the basic method, which presents that the proposed method achieves better classification in each category than the basic method.

Figure 6.

We extracted the feature distribution of trial 1 of subject S01 from the base method and the proposed method. The feature distribution is shown in the 2D feature space.

Figure 7.

The statistical difference between the novel method and Hybrid Method 2 (a, b and c) and between Hybrid Method 1 and the basic method (d, e and f) with diagLDA, diagQDA and SVM classifiers are shown as boxplots (∗∗: p < 0.01, ∗: p < 0.05).

Figure 8.

Confusion matrixes are shown using the best accuracies of total test sets for all subjects achieved by novel features (a) and basic features (d) with diagLDA, achieved by novel features (b) and basic features (e) with diagQDA and achieved by novel features (c) and basic features (f) with SVM. The label “1” denotes rest periods and the label “2” denotes MA.

4.1. Verification

We validate the proposed method on a publicly available dataset [56]. This dataset contains the ΔHbO and ΔHbR signals for the mental arithmetic task and the baseline task for 29 subjects. Each task consisted of 30 trials. We used 10 repetitions of 5-fold cross-validation on the samples on the LDA classifier. Applying the proposed method, we obtained the maximum average accuracy of 72.26 ± 4.64%. Using the base method, we got the maximum average accuracy of 65.72 ± 8.90%. We used the VPA method to calculate all channel features and got the 80.40 ± 7.42% maximum average accuracy. The program running time of the proposed method, the base method and the method calculating all channels VPA features under Windows 10 operating system, MATLAB 2019a and Intel(R) Core(TM) i7-6700HQ CPU environment is 121 s, 63 s and 1754 s. Compared with the basic method, the proposed method improves the accuracy by 6.54% (p-value < 0.05), and the computational costs are 1.92 times that of the basic method. The novel method has no enhancement than the VPA method calculating all channel features, but its computational costs reduce 14.50 times than that of the VPA method calculating all channel features. The proposed method improves the accuracy without significantly increasing the computational costs.

5. Discussion

In this study, we successfully extracted features using VPA from 3 ROIs which have a close association with MA to improve the performance of classification. The proposed method is different from most other studies that used the average of all channels or a specific channel value and also does not employ the traditional HbO and HbR features [57, 58, 59, 60, 61, 62, 63]. This study shows classification accuracies are enhanced by using the novel method compared to the basic method. As Figure 7 shows, both VPA features and the antagonistic activation pattern approach play a role in improving the classification accuracy. The results are improved from 61.19 ± 10.7% to 67.45 ± 14.56% with diagLDA classifier, and 76.68 ± 6.96% to 89.73 ± 5.71% with diagQDA classifier, and 61.95 ± 16.65% to 87.04 ± 6.88% with SVM classifier. It can be seen from Table 4 that our proposed method effectively reduces the computational time complexity compared with the hybrid method 3. The novel method reduces the running time by 3.75 times compared with the hybrid method 3 while maintaining high classification accuracy. These results are also confirmed using another publicly available dataset.

In order to evaluate the findings of this work, the results of the proposed method are compared to a reported by Bauernfeind et al using the same dataset [64]. They employed SVM to achieve 86.6 ± 7.3% maximum accuracies with 52 feature dimensions. In the recent literature, such type of report achieved 93.26% maximum classification accuracies using the same dataset with SVM classifier, but they used 832 feature dimensions of 104 channels [65]. When the number of channels is 72, the accuracy that they achieved is 86.99%. The results are lower than the accuracies achieved by the feature group of CBV + COE using SVM (87.04 ± 6.88%) and the feature dimensions (36 dimensions) that we used is less than theirs. Because the research using the same dataset is not enough, we glean some papers using other datasets. In another study of distinguishing MA and REST with a different dataset, they extracted Hilbert transform and summed derivative features [66]. Finally, they achieved 84.94% classification accuracy. The paper of Aydin et al acquired 88.67% accuracies for a MA dataset [67]. In their study, they used stepwise regression analysis based on sequential feature selection and ReliefF methods to optimize subject-specific feature subsets. The average number of subjects’ channels is 18.9. Therefore, our proposed method achieved good accuracies with less feature dimension. The low feature dimension is able to achieve a decrease of calculation costs when the algorithmic complexity of classifiers is related to the feature dimension.

This finding suggests two possible reasons. One of reason is that channel selection based on antagonistic activation patterns probable reduces the number of irrespective features. The other reason is when we used the features extracted by VPA, the classification performance of features based on antagonistic active patterns may be enhanced, which be explained as CBV and COE possibly include more information about changes in oxygen metabolism. The above two factors bring on classification accuracy improvement and exclusion of the features that have few effects on the classification accuracy.

The limitations of this study are as follows. we utilized prior knowledge about antagonistic active patterns to experiment with two classifications between MA tasks and rest periods, while the current trend about BCI systems is towards multi-level classification. The next step is to aim at other specific tasks, such as motor imagination or motor execution, to establish a feature extraction strategy including ROIs involving motor imagination and motor execution.

6. Conclusion

This paper aims to assess the performance of a novel method for enhancing classification accuracies with low calculation costs. We used the antagonistic activation patterns to select features and calculated two new features using VPA, which are considered potentially to contain more information about blood oxygen changes. Compared with methods as control groups in this paper, the proposed method obtained high classification accuracies with low calculation costs. In comparison with other similar studies, the accuracy achieved by our proposed method is also at a high level. The feature dimensions of our proposed method are lower than the results of the papers used as comparisons.

Declaration

Author contribution statement

Shixian liu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of interest’s statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.