Acid–base quantification: a review of developing technology

Learning objectives.

By reading this article, you should be able to:

• •Recall the key historical developments of acid–base quantification.
• •Explain the similarities and differences between the classical (bicarbonate) and Stewart (physicochemical) models of acid–base quantification.
• •Describe the principles of measuring devices for acid–base quantification.

Key points.

• •Historically, methods of acid–base quantification depended on the technology available at the time.
• •Traditional models of acid–base quantification are designed to estimate the concentrations of unmeasured or unmeasurable substances.
• •The bicarbonate model describes the flux of the carbonic acid/bicarbonate system, as this model is the predominant buffer in humans.
• •Stewart's physicochemical approach focuses on the concentrations of strong ions as the primary determinant of acid–base status, with the concentrations of carbonic acid and bicarbonate responding to the concentrations of stronger acids or bases.
• •Point-of-care testing allows several previously unmeasurable substances to be quantified at the bedside, which has made the debate on the pros and cons of the classical and Stewart approaches less relevant.

In a previous article in this journal, we discussed normal acid–base homeostatasis.¹ In this review, we describe the advances in acid–base quantification that have taken place over the past 70 yrs. We discuss the development of the pH and Pco₂ electrodes and their role in describing the classical (bicarbonate) model of acid–base quantification. We then compare the classical model with the physicochemical model of Peter Stewart.

The relative merits of the classical and physicochemical models have been a matter of great debate over the years. Both approaches rely on clinical measurement techniques that were available at the time the methodologies were developed. Recently, the development of point-of-care (POC) tests for lactate and ketones has rendered the classical vs physiochemical debate less relevant.

The use of blood gas analysis for pH and Pco₂ in clinical practice began during the poliomyelitis epidemic of the 1950s. In 1952, development centred in the Blegdamhospital in the Danish city of Copenhagen. The chief physician, Henry Lassen, faced with a number of cases of severe bulbar poliomyelitis, sought the assistance of anaesthetist Bjørn Ibsen. Lassen and Ibsen hypothesised that patients with polio were dying not of hypoxia but from lack of ventilation, with an associated high Pco₂. Lassen and Ibsen were supported in their theory by the director of the clinical laboratory, Poul Astrup.

In the 1950s, clinicians had a limited diagnostic window through which to view their patients' pathophysiology, as the only directly measurable acid–base variable was pH, with Pco₂ being derived. Taking the newly available pH electrode from the laboratory into the clinical environment, Astrup was able to estimate the Pco₂ of patients suffering from polio and show that Ibsen and Lassen's theory was correct.

The pH electrode

When a thin glass membrane divides two solutions of differing pH, an electrical potential difference develops across the membrane. The glass within the electrode is selectively permeable to hydrogen ions (H⁺), and the development of a potential difference is thought to be caused by the migration of hydrogen ions into the glass matrix.

If one solution consists of a standard concentration of hydrogen ions, the pH of the other solution can be estimated by measurement of the potential difference between the two solutions. No current flows in this device, which does not wear out, in contrast to the Clark oxygen electrode (fuel cell).

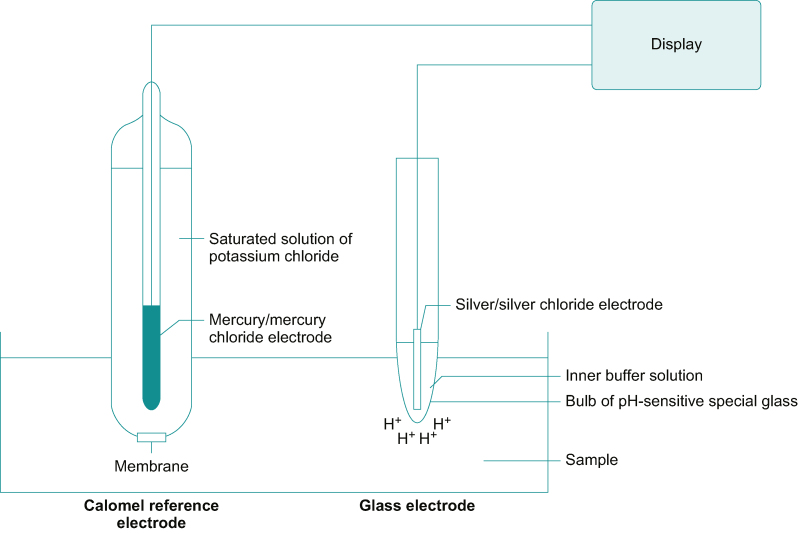
The pH electrode, shown in Figure 1, consists of two electrochemical half-cells: one a silver/silver chloride (Ag/AgCl) electrode and the other a mercury/mercury chloride (Hg/HgCl₂, calomel) electrode.² Each electrode maintains a fixed electrical potential. The Ag/AgCl electrode is surrounded by a buffer solution of known pH, enclosed in hydrogen ion sensitive glass. Outside the glass membrane is the test solution, usually blood. The calomel electrode is separated from the sampled solution by a porous plug and a potassium chloride salt bridge. The sensitivity of the system is about 60 mV per unit of pH change at 37°C.

Fig 1.

The pH electrode. See text for description. Figure redrawn with permission from Al-Shaikh and Stacey, figure 13.7.²

The pH electrode actually responds to hydrogen ion activity rather than concentration. Besides concentration, hydrogen ion activity is also determined by ionic concentration and temperature. Ideally, pH should be measured in a solution containing only hydrogen ions. When other ionic species are present, molecular interactions occur that partially inhibit the free movement of hydrogen ions, affecting its activity. To accommodate for the difference between activity and concentration, the electrode is calibrated at 37°C against standard buffer solutions of pH 6.841 and 7.383, giving a two-point calibration.

Measuring Pco₂ and the bicarbonate concentration

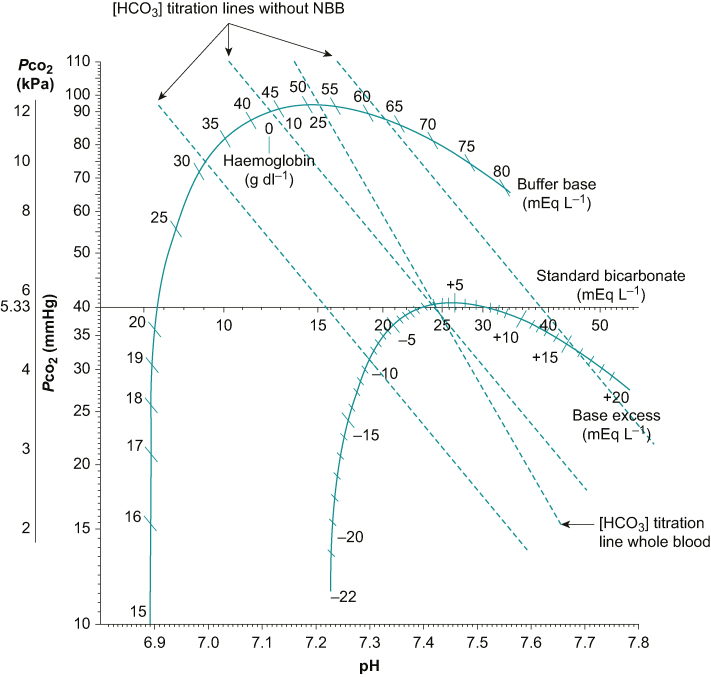
Astrup showed that in the clinically relevant range, there is a linear relationship between pH (i.e. –log₁₀[H⁺]) and the logarithm of the carbon dioxide concentration (log₁₀[CO₂]) (Fig. 2). In its simplest form, the Pco₂/pH nomogram shows how changes in Pco₂ influence pH without affecting the bicarbonate (HCO₃^–) concentration. In laboratory testing, fixing the bicarbonate concentration alters the Pco₂/pH relationship in a predictable way, in essence adding a series of bicarbonate titration lines (marked as bicarbonate titration lines without non-bicarbonate buffer [NBB] in Fig. 2) to the Pco₂/pH nomogram. This process allowed calculation of the patient's Pco₂ and bicarbonate concentration from their pH. Estimating Pco₂ and bicarbonate concentration involved a three-stage process:

• (i)First, the pH of the patient's sample was measured.
• (ii)Second, the sample was equilibrated against two solutions containing a known Pco₂. The pH at each value of Pco₂ was then measured.
• (iii)Third, a graph of pH against Pco₂ was plotted and a straight line drawn between the two calibration points. By marking the pH of the patient's sample on this line, their actual Pco₂ and HCO₃^– concentration could then be read.

Fig 2.

Siggaard-Andersen Pco₂/pH nomogram. Graph showing bicarbonate titration lines for whole blood, with and without NBBs.

Incorporating NBBs

The model described previously assumes that the only buffer is the carbonic acid/bicarbonate system. In vivo, NBB systems also have an action, in particular haemoglobin. NBB systems reduce the change in pH for any given change in Pco₂, increasing the gradient of the titration line. To accommodate for the effect of NBB systems, Professor Ole Siggaard-Andersen constructed a more detailed Pco₂/pH nomogram completing the classical diagram shown in Figure 2.³

Buffer base and base excess

The Siggaard-Andersen nomogram incorporated a curve on which are marked the haemoglobin concentration and the buffer base. The buffer base is a measure of the total buffering capacity of the blood, which is made up mainly from the concentrations of bicarbonate, haemoglobin, plasma proteins and phosphate. The buffer base is normally approximately 48 mEq L⁻¹.

A second curve was also included, indicating the base excess (BE), defined as the concentration of hydrogen ions required to return the pH to 7.4 with a Pco₂ fixed at 5.33 kPa in vitro at 37°C. The BE is a substitute for unmeasurable acids and is influenced by the haemoglobin concentration attributable to its function as the main buffer in blood. The standard BE adjusts for the average haemoglobin in the total extracellular fluid (estimated as 50 g L⁻¹).

Pco₂ electrode

Using the three-stage process described previously, the patient's actual Pco₂ could be estimated and also the buffer base concentration and the BE. The technique, although valid, is laborious. In 1956, Professor John Severinghaus from the University of California, San Francisco, took the next step in developing a clinically reliable electrode for measuring Pco₂.^4,5

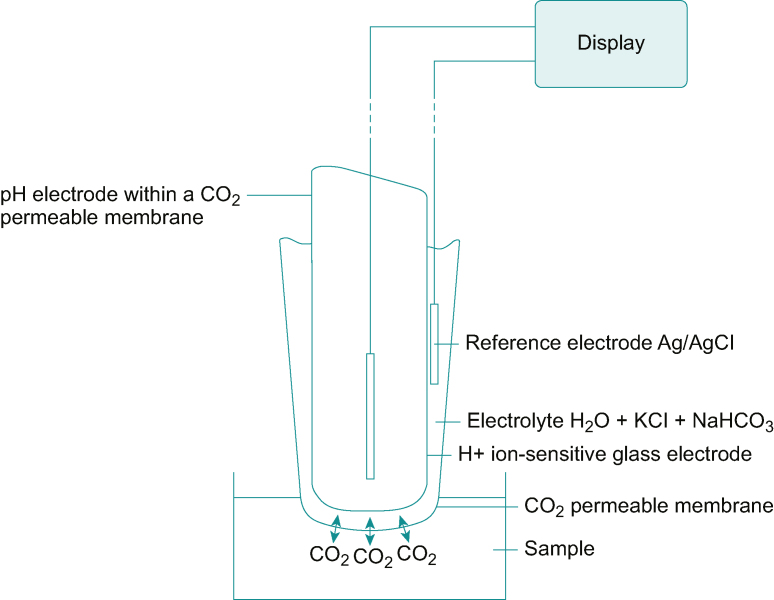
The Pco₂ electrode (Fig. 3) is essentially a pH electrode covered by a membrane selectively permeable to carbon dioxide. The equilibrium relationship between hydrogen ions and dissolved carbon dioxide concentration is shown as follows:

$$\mathrm{C}{\mathrm{O}}_2+{\mathrm{H}}_2\mathrm{O}\leftrightharpoons {\mathrm{H}}_2\mathrm{C}{\mathrm{O}}_3\leftrightharpoons {\mathrm{H}}^{+}+\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}$$ (1)

Fig 3.

Pco₂ electrode. See text for description. Figure redrawn with permission from Al-Shaikh and Stacey, figure 13.8.²

Thus, a change in the dissolved carbon dioxide concentration is reflected by a changing hydrogen ion concentration, and hence, a potential difference develops, which can be measured.

As originally described by Richard Stow from Ohio State University, the pH-sensitive glass was surrounded by distilled water. John Severinghaus replaced distilled water with a bicarbonate buffer solution, increasing the probe's sensitivity and stability.^3,4 Blood gas samples are typically cooled to reduce the effects of ongoing cellular metabolism, with the consumption of oxygen and the production of carbon dioxide. However, a fall in temperature makes carbon dioxide more soluble in blood, reducing the effective Pco₂. Therefore, the temperatures of the sample must be corrected to 37°C before analysis. Errors may also occur because of air bubbles in the sample, excess heparin, gas absorption into the container's plastic walls, protein deposition on the electrode, and signal processing errors.

Severinghaus would later incorporate the pH and Pco₂ electrodes, along with an oxygen fuel cell, into one machine, resulting in the first blood gas analyser, which became available in 1959.

Classification of acid–base disturbances

The classical bicarbonate model of acid–base disturbances centres on the equilibrium between bicarbonate and its reciprocal acid (carbonic acid) and on the Henderson–Hasselbalch equation, shown as follows:

$$\mathrm{p}\mathrm{H}={\mathrm{p}\mathrm{K}}_a+{\log }_{10}\frac{\left[{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{–}\right]}{\left[H_2{\mathrm{C}\mathrm{O}}_3\right]},$$ (2)

where pK_a is the negative logarithm (base 10) of the carbonic acid dissociation constant. The equation applies to the carbonic acid-bicarbonate equilibrium:

$$C{O}_2+H_{2}O\iff H_{2}C{O}_3\iff H^{+}+HC{O}_3^{-}$$

Alternatively, the Henderson-Hasselbalch equation may be written as:

$$\mathrm{p}\mathrm{H}={\mathrm{p}\mathrm{K}}_a+{\log }_{10}\frac{\left[{\mathrm{H}\mathrm{C}\mathrm{O}}_3^{–}\right]}{\alpha \left[{\mathrm{C}\mathrm{O}}_2\right]},$$ (3)

where α is the carbon dioxide solubility constant. The value for pK_a is 6.1 and the value for α (in mmHg) is approximately 0.03.

Bicarbonate is a weak base whose pKa (the negative of the logarithm of the dissociation constant) is 6.1, which is well below physiological pH, and therefore displaced from the point at which it has greatest buffer power. The importance of the bicarbonate buffer system comes from the high concentration present in the body.

The Davenport diagram (Fig. 4), developed by Professor Horace W. Davenport, demonstrates the relationship between pH, bicarbonate concentration, and Pco₂, and can be used to classify acid–base disturbances. To produce the diagram, samples of blood were held at a fixed Pco₂ using a similar process to that used in producing the Siggaard-Andersen plot, described earlier. Aliquots of strong acids or bases were added and the bicarbonate concentration measured. The process was repeated at different concentrations of Pco₂ to produce a family of isopleths (contour lines), each representing the changes in bicarbonate with a change in pH at a fixed Pco₂. Each time the Pco₂ in the chamber is changed, the pH of the sample will move to a new equilibration point with bicarbonate. If joined together, these points form a buffer line. The gradient of the buffer line depends on the buffering capacity of blood. The buffering capacity of blood is predominately determined by the bicarbonate/carbonic acid system. However, the presence of NBBs increases the gradient of the line. The position of the buffer line depends on the metabolic composition of the blood, moving down when there is a relative excess of organic acids (as seen with diabetic ketoacidosis) and upwards in a relative deficit (as seen with persistent vomiting).

Fig 4.

Davenport diagram. See text for details. Diagram includes quadrants indicating the respiratory or metabolic acidosis or alkalosis.

With the Davenport diagram, we have a simple way of classifying a patient's acid–base disturbance. By plotting the patient's pH and bicarbonate concentration, the primary acid–base disturbance can be determined (Fig. 4). For instance, a patient with a pH of 7.2 and a bicarbonate concentration of 16 mmol L⁻¹ has a metabolic acidosis. Without physiological compensation, the patient's sample would show a Pco₂ remaining on the Pco₂=5.3 kPa isopleth, indicated as position ‘a’ in Figure 4. With respiratory compensation (i.e. hyperventilation), the effect is to move along the buffer line to a lower Pco₂ isopleth—to point ‘b’. Because the physiological response would not normally correct beyond a normal pH of 7.4, the patient remains in the metabolic acidosis quadrant.

In the ideal scenario, Pco₂ and bicarbonate concentration should represent independent variables, unaffected by other systems. Simple analysis shows that they are not. Siggaard-Andersen suggested using the anion gap, a factor independent of Pco₂, to quantify a metabolic disturbance. The anion gap may be defined as:

$$\mathrm{A}\mathrm{n}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{a}\mathrm{p}=\left(\left[\mathrm{N}{\mathrm{a}}^{+}\right]+\left[{\mathrm{K}}^{+}\right]\right)-\left(\left[\mathrm{C}{\mathrm{l}}^{–}\right]+\left[\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}\right]\right)$$ (4)

Using the above definition, the normal range for the anion gap is 8–16 mmol L⁻¹.

The law of electrical neutrality states that the sum of anions and cations in the body must be balanced. The anion gap represents the unmeasured anions. In health, unmeasured anions are mostly attributable to albumin. In disease, unmeasured anions may be attributable to accumulation of lactate, ketoacids and other substances. Clearly, there are limitations in the system, so researchers looked for alternative approaches.

Stewart's physicochemical approach

Peter Stewart proposed an alternative model to the classical bicarbonate system.^6,7 The fundamental difference of his physicochemical approach to the classical model is that the bicarbonate concentration is not an independent determinant of acid–base status but is a result of changes in other systems. In this context, bicarbonate is often described as a ‘follower rather than a leader’.

Strong acids are highly dissociated at physiological pH. Carbonic acid/bicarbonate being a weak acid/base, the equilibrium moves towards carbonic acid in the presence of a strong acid; see Equation (1). Stewart described a series of equations (Table 1) that predict the total body hydrogen ion concentration, based on three independent variables⁸:

• (i)Pco₂
• (ii)The total weak acid concentration (plasma proteins—mainly albumin—and phosphate)
• (iii)The strong ion difference (SID); the total dissociated cations (Na⁺, K⁺, Ca²⁺, and Mg²⁺) minus the dissociated anions (Cl^–, lactate, and sulphate)

Table 1.

Stewart's equations for acid–base quantification. The three primary determinants of pH (SID, total concentration of non-volatile weak acids, and Pco₂) are shown in red. [A^–], concentration of ionised, non-volatile weak acids; A_TOT, total concentration of weak, non-volatile acids (proteins and inorganic phosphate); [HA], concentration of non-ionised, non-volatile weak acids; K_A, dissociation constant for non-volatile, weak acids; K_c, combined equilibrium and solubility constants between K_d, dissociation constant for carbonate; K_W, ion-product constant of liquid water; Pco₂ and the bicarbonate concentration.

Name	Equations
Water dissociation equilibrium	$\left[{\mathrm{H}}^{+}\right]\times \left[\mathrm{O}{\mathrm{H}}^{–}\right]={\mathrm{K}}_{\mathrm{W}}^{\prime }$
Weak acid dissociation equilibrium	$\left[{\text{H}}^{+}\right]\times \left[{\text{A}}^{-}\right]={\mathrm{K}}_{\mathrm{A}}\times \left[\text{HA}\right]$
Conservation of mass for weak acids	$\left[{\mathrm{A}}_{\mathrm{T}\mathrm{O}\mathrm{T}}\right]=\left[{\mathrm{H}}^{+}\right]\times \left[{\mathrm{A}}^{–}\right]$
Bicarbonate ion formation equilibrium	$\left[{\mathrm{H}}^{+}\right]\times \left[\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}\right]={\mathrm{K}}_{\mathrm{c}}\times \mathrm{p}\mathrm{C}{\mathrm{O}}_2$
Carbonate ion formation equilibrium	$\left[{\mathrm{H}}^{+}\right]\times \left[\mathrm{C}{\mathrm{O}}_3^{–}\right]={\mathrm{K}}_{\mathrm{d}}\times \left[\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}\right]$
Law of electrical neutrality	$\mathrm{S}\mathrm{I}\mathrm{D}+\left[{\mathrm{H}}^{+}\right]-\left[\mathrm{H}\mathrm{C}{\mathrm{O}}_3^{–}\right]-\left[{\mathrm{A}}^{–}\right]-\left[\mathrm{C}{\mathrm{O}}_3^{–}\right]-\left[\mathrm{O}{\mathrm{H}}^{–}\right]=0$

The effect of the SID is attributable to the dissociation of water that occurs, with a relative imbalance between cations and anions, to maintain electrical neutrality. The dissociation of water increases the free hydrogen ion concentration, resulting in a fall in pH. Because of the relatively low concentrations of Ca²⁺, Mg²⁺, lactate, and sulphate, the SID is often simplified to:⁹

$$\mathrm{S}\mathrm{I}\mathrm{D}=\left[\mathrm{N}{\mathrm{a}}^{+}\right]+\left[{\mathrm{K}}^{+}\right]-\left[\mathrm{C}{\mathrm{l}}^{–}\right]$$ (5)

With this simplification, the SID is normally approximately 40 mEq L⁻¹, being mainly composed of bicarbonate with a smaller contribution from albumin and the weak acids (Fig. 5). A low SID describes reduced amounts of free bicarbonate as a result of an increase in strong acids and indicates an acidosis. An increased SID implies an alkalosis.⁷

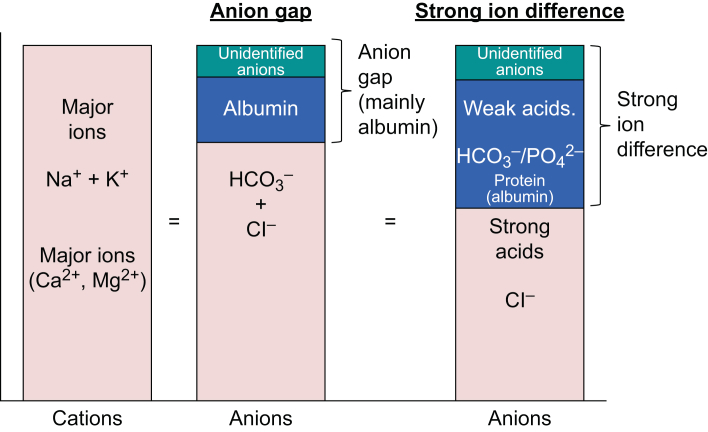
Fig 5.

Comparison of anion gap and SID. The graphic on the left shows the main cations in extracellular fluid. The two right-hand graphics compare the anions responsible for the anion gap and the SID.

If we compare the anion gap with the SID diagrammatically, we see striking similarities (Fig. 5). Whilst Stewart's approach does not fundamentally alter our classification of acid–base disturbances, it does improve our understanding of the underlying processes. For example, infusing normal (0.9%) saline causes a hyperchloraemic metabolic acidosis. Normal saline contains equal parts Na⁺ and Cl^– (150 mmol L⁻¹) and has a SID of zero. In contrast, in plasma the concentrations of sodium and chloride are approximately 140 and 105 mmol L⁻¹, respectively. Thus, normal saline causes a relatively larger increase in the chloride concentration than sodium concentration, reducing the SID, and so causing acidosis.⁷

Hypoalbuminaemia (such as occurs with liver, gastrointestinal, and renal disease) is associated with a metabolic alkalosis. Albumin is the principal weak acid in plasma. Low serum albumin concentration reduces the total non-volatile weak acid concentration, thereby causing an alkalosis.

The effect of hypoalbuminaemia on the BE can be quantified as:⁸

$$\mathrm{A}\mathrm{l}\mathrm{b}\mathrm{u}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{B}\mathrm{E}=0.25\times \left(42-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{l}\mathrm{b}\mathrm{u}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\right)$$ (6)

where albumin concentration is measured in g L⁻¹.

There has been much debate as to the relative advantages and disadvantages of the bicarbonate and Stewart's models. Both are based on the technology that was available at the time to measure factors integral to acid–base disturbance in an attempt to quantify other factors that cannot (or could not) be directly measured. The main disadvantage of Stewart's approach is the complexity involved in solving the equations. Today, solving these equations is easily done with a smartphone. Whilst smartphone applications based on the physiochemical approach are available, they are not widely used.

POC testing

Today, POC devices are readily available at the bedside to measure lactate and ketones in blood, two important causes of metabolic acidosis. Point-of-care devices are also available for measuring salicylates, paracetamol, and myoglobin from blood; benzodiazepines and opioids from urine; and ethanol from breath, all of which can directly cause or contribute to acidosis.¹⁰ Many of the previously unmeasurable substances are now quantifiable, which has led to improved diagnostic accuracy with the potential for more appropriate and timely intervention. For instance, in patients with septic shock, serum lactate is predictive of mortality and is used to identify which patients need early aggressive resuscitation.^11,12

Most POC devices function as electrochemical biosensors, containing an enzyme that triggers a chemical reaction in the substance of interest in the sample.^13,14 The chemical reaction produces a substance that can donate electrons at an electrode (e.g. NADH or H₂O₂). The concentration of the substance measured is then quantified using an electrochemical detector. The enzymes, enzymatic reactions and electrochemical reactions found in POC devices for lactate and beta-hydroxybutyrate, the predominant ketone in patients with diabetic ketoacidosis, are shown in Table 2.

Table 2.

Enzymatic and electrochemical reactions in POC testing devices for ketones and lactate. ∗Predominant ketone present in patients with diabetic ketoacidosis. β-HB, beta-hydroxybutyrate.

Substance	Enzyme	Enzymatic reaction	Electrochemical reaction
Lactate	Lactate oxidase	$\mathrm{L}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}+{\mathrm{O}}_2\rightleftharpoons \mathrm{p}\mathrm{y}\mathrm{r}\mathrm{u}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}+{\mathrm{H}}_2{\mathrm{O}}_2$	${\mathrm{H}}_2{\mathrm{O}}_2\rightleftharpoons {\mathrm{O}}_2+2{\mathrm{H}}^{+}+2{\mathrm{e}}^{–}$
Lactate	Lactate dehydrogenase	$\mathrm{L}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}+\mathrm{N}\mathrm{A}{\mathrm{D}}^{+}\rightleftharpoons \mathrm{p}\mathrm{y}\mathrm{r}\mathrm{u}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}+\mathrm{N}\mathrm{A}\mathrm{D}\mathrm{H}+{\mathrm{H}}^{+}$	$\mathrm{N}\mathrm{A}\mathrm{D}\mathrm{H}\rightleftharpoons \mathrm{N}\mathrm{A}{\mathrm{D}}^{+}+{\mathrm{H}}^{+}+2{\mathrm{e}}^{–}$
β-HB∗	β-HB dehydrogenase	$\mathrm{\beta }-\mathrm{H}\mathrm{B}+\mathrm{N}\mathrm{A}{\mathrm{D}}^{+}\rightleftharpoons \mathrm{a}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}+\mathrm{N}\mathrm{A}\mathrm{D}\mathrm{H}+{\mathrm{H}}^{+}$	$\mathrm{N}\mathrm{A}\mathrm{D}\mathrm{H}\rightleftharpoons \mathrm{N}\mathrm{A}{\mathrm{D}}^{+}+{\mathrm{H}}^{+}+2{\mathrm{e}}^{–}$

Conclusions

In the 70 yrs since the polio epidemic, there have been major advances in the quantification of acid–base disturbances. Initially, clinicians only had the pH electrode with which to assess their patients' metabolic states. Equilibrating samples at known Pco₂ allowed the patients' Pco₂ and bicarbonate concentrations to be estimated from their pH. However, the process was laborious. Advances in technology allowed the direct measurement of Pco₂, which simplified the process. The physiochemical approach of Peter Stewart improved our understanding of the determinants of pH. However, the physiochemical approach does not fundamentally alter the classification of acid–base disturbances and has not been widely adopted into clinical practice. Recently, the advent of POC testing devices, notably for lactate and ketones, has allowed direct measurement of previously unmeasurable acids to be performed at the bedside, rendering the debate between the bicarbonate and physiochemical models less relevant.

Declaration of interests

PM is an editor and editorial board member of BJA Education. IS declares no conflicts of interests

Biographies

Ian Shaw FRCA is a consultant anaesthetist at Sheffield Teaching Hospitals NHS Trust. He was an examiner for the Primary FRCA for 13 yrs and has authored a number of the Royal College of Anaesthetists e-learning modules in physiology and the FRCA physiology revision guide.

Patrick Magee PhD FRCA is a retired consultant anaesthetist who was an examiner for the Primary FRCA. His expertise is in the field of physics and clinical measurement, and he has contributed to a number of major texts on this subject. He is an editor and editorial board member of BJA Education.

Matrix codes: 1A03, 2A04, 3C00

MCQs

The associated MCQs (to support CME/CPD activity) are accessible at www.bjaed.org/cme/home for subscribers to BJA Education.