Data-driven scalable pipeline using national agent-based models for real-time pandemic response and decision support

Abstract

This paper describes an integrated, data-driven operational pipeline based on national agent-based models to support federal and state-level pandemic planning and response. The pipeline consists of (i) an automatic semantic-aware scheduling method that coordinates jobs across two separate high performance computing systems; (ii) a data pipeline to collect, integrate and organize national and county-level disaggregated data for initialization and post-simulation analysis; (iii) a digital twin of national social contact networks made up of 288 Million individuals and 12.6 Billion time-varying interactions covering the US states and DC; (iv) an extension of a parallel agent-based simulation model to study epidemic dynamics and associated interventions. This pipeline can run 400 replicates of national runs in less than 33 h, and reduces the need for human intervention, resulting in faster turnaround times and higher reliability and accuracy of the results. Scientifically, the work has led to significant advances in real-time epidemic sciences.

Justification for ACM Gordon Bell Special Prize for HPC-based COVID-19 research

We describe a novel data-driven integrated pipeline for analyzing various scenario projections using an individualized agent model for COVID-19 response planning. The pipeline can execute an experiment with over 400 replicates (4–8 cells, 50–100 replicates per cell) for the US (288 Million nodes, 12.6 Billion edges) in under 33 h.

Performance attributes

Table 1

Table 1.

Performance attributes.

Category of achievement	Scalability, Time-to-solution
Type of method	Not applicable
Results reported (basis)	Whole application including I/O
Precision reported	Mixed precision
System scale	Results measured on full-scale system
Measurement mechanism	Timers

Overview of the problem

We study the scenario projection problem: Given the current conditions on the ground, and a set of possible future scenarios, the goal is to assess the likelihood of epidemiological outcomes for each of these scenarios by analyzing the simulated variability dictated by the starting conditions. The scenario projection problem is different from the forecasting problem, where the goal is to forecast the future course of the pandemic over a given time period. Scenario projection is closely related to counter-factual analysis, but differs in that counter-factual analysis studies the impact of various interventions in a what-if setting. Our group has been doing scenario projections from the start of the COVID-19 pandemic for various state and federal agencies, including the Commonwealth of Virginia, Department of Defense (DoD), and the Centers for Disease Control and Prevention (CDC).

Our state-level scenario projections are briefed to Virginia Department of Health (VDH) and senior State officials each week (VDH, 2021). These projections use both meta-population models and, for specific cases, agent-based models.

In this paper, we describe the national agent-based models that we use for the COVID-19 Scenario Modeling Hub—a collaborative effort to support CDC decision-making by creating an ensemble of several distinct models that project requested epidemiological scenarios. These models were developed to support DoD and CDC (SHUB, 2021). Our agent-based models have been used for Rounds 6 through 9.¹

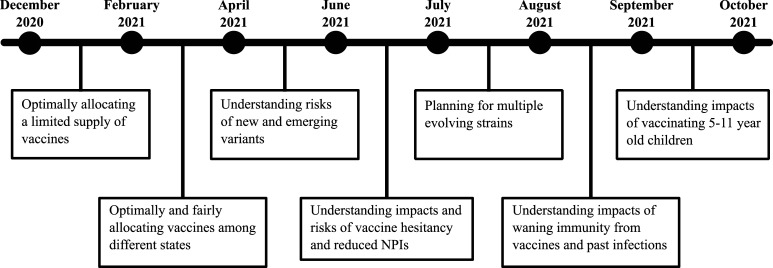
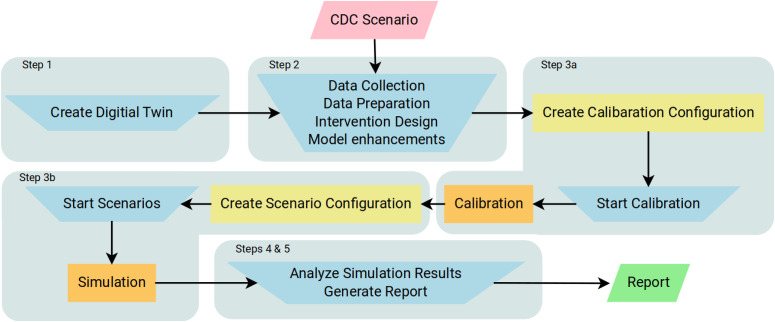
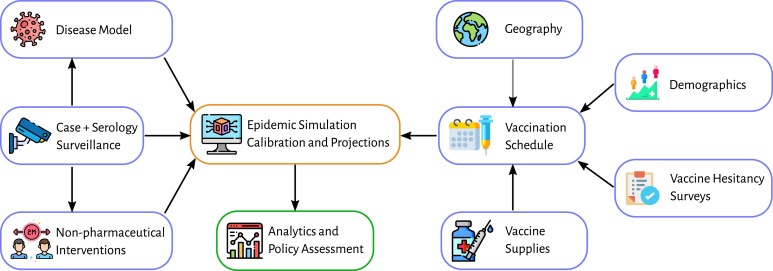
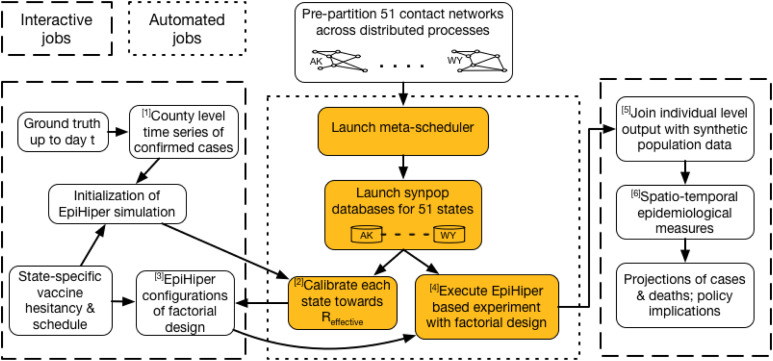
Additional scenarios were considered for the DoD. Each scenario comprises of a possible set of futures, and modeling teams use their models to try to project the epidemiological outcomes. Figure 1 illustrates the timeline of policy questions driving the computational pipelines, and Figure 2 shows the process used to respond to a single scenario. For brevity, we describe here only scenarios that involve vaccine allocation and distribution during an ongoing pandemic. Figure 3 shows the data fusion problem that is necessary to answer these questions.

Figure 1.

Timeline of the different preparations and response-related policy questions arising during the COVID-19 pandemic.

Figure 2.

Process for responding to a CDC scenario (input, human activity, automated processes, Wormulon-enabled simulations, and output). Our pipeline development is focused on minimizing the human supervision of the automated processes. Details of the steps are provided in the “Overall Methodology” section.

Figure 3.

An overview of the different data sources that were used to generate the realistic epidemiological models.

Supporting policies

The scenario projections carried out using national agent-based models have been used to support policymaking. Our national model is one of the 7–9 models used in the ensemble. The projections have been summarized in the Morbidity and Mortality Weekly Report (MMWR) (Borchering et al., 2021), on the live website, and also briefed to the White House by the COVID-19 Response Team (Walensky and Fauci 2021). This work has been discussed in the national media and by the head of the CDC on one of their video briefings in the Summer 2021. Details about how such models are assessed and presented can be found in companion papers that consist of all participating teams of Scenario HUB (Truelove et al., 2022). This paper focuses on the national agent-based models developed by our team.

Need for the pipeline

Running national-level scenario projections can be a lengthy and compute-intensive process. The clock starts when the question or scenario is posed to us, and runs through data collection, model calibration, and validation, only ending when the output is analyzed to aid in the production of needed plots and briefings. The datasets involved are quite large—our agent-based model simulations depend on a synthetic population contact network (a “digital twin” of the actual US population consisting of 288 Million individuals and 12.6 Billion time-varying interactions). Furthermore, given the stochastic nature of our work, multiple simulations must be run per scenario, amounting to over 400 national-level replicates (4–8 cells with 50–100 replicates for each cell). Although we were fortunate to have access to two high performance computing systems for running these simulations, coordinating runs across systems while minimizing reservations—particularly important on these widely shared resources—was an additional challenge. Finally, given the time-sensitive nature of our work in the face of the rapidly evolving pandemic, we needed to reduce processing time in order to be reactive.

To overcome these limitations, we developed an integrated, data-driven operational pipeline to streamline our national scenario projection process. Our pipeline can run over 400 replicates of national runs in less than 33 h; this time does not include the initial time for scenario specification, organizing data products, and preparing briefings. A number of computational advances were required to obtain the end-to-end operational pipeline, including (i) the development of novel methods for scheduling replicates across multiple supercomputers; (ii) the development of a strategy to represent the rich set of complex interventions required to capture the ground-truth reality; and (iii) the implementation of methods to automatically process large amounts of input and output data, reducing human intervention, resulting in faster turnaround times and higher reliability and accuracy of the results. The implementation details of this pipeline are described in more detail in later sections. The pipeline has been validated over the course of many studies, including the ones covered in this paper.

This process pipeline provides time-sensitive, large scale data processing and analytical modeling coordination. It is configurable for timely and direct operational support of complex epidemic-related decision making. The decision cycles it supports are defined by the demanding timely response requirements for particular decisions and actions related to crisis event management as defined by the daily activities and processes of engaged, responsible operational agencies.

Current state of the art

Our group was the first to publish a data-driven, agent-based model to support epidemic analysis (Eubank et al., 2004). Since then, the field has been steadily developed by both our group (Bisset et al. 2009, 2012, 2014; Barrett et al., 2008; Bhatele et al., 2017; Yeom et al., 2014) and others (Perumalla and Seal 2012; Skvortsov et al., 2007; Grefenstette et al., 2013).

Recently, there has been a flurry of papers on developing agent-based and equation-based models for planning and response for the COVID-19 pandemic; see (Google 2021; Kerr et al., 2021; Fitzpatrick and Galvani 2021; Agrawal et al., 2020; Ferguson et al., 2020; Verity et al., 2020; Chinazzi et al., 2020; Kraemer et al., 2020; Peng et al., 2020; Roosa et al., 2020; Gandon and Lion 2022). Smaller regions have been studied with detailed models, and larger areas with aggregate models, but excepting the work of Ferguson et al. (2020), we are not aware of a national scale epidemic planning and forecasting exercise for COVID-19 that uses such detailed models. Ferguson et al. (2020) largely focused on the United Kingdom (UK), although basic results were provided for the US as well.

We implemented a new agent-based model (EpiHiper) and developed digital twin populations to support the COVID-19 pandemic response. Case studies done in the context of COVID-19 response, using earlier versions of the modeling environment include: (i) network-based vaccine allocation (Chen et al., 2021, 2022); (ii) contact tracing (Hoops et al., 2021); (iii) economic impact analysis (Chen et al., 2020a,b); and (iv) the role of basic non-pharmaceutical interventions (Machi et al., 2021).

The present work differs from the earlier work in several ways: (i) the digital twin of the social contact network used here is perhaps the most detailed national model ever built; (ii) the EpiHiper framework can represent rich sets of interventions and is designed specifically to run on large parallel machines; (iii) the modeling pipeline presented here comprises not only the agent-based model and the synthetic social contact network, but also an end-to-end pipeline to ingest data, initialize the models, collect simulation output, carry out analyses, and produce meaningful insights; (iv) it demonstrates the operational use of the integrated distributed HPC pipeline to support real-time epidemic science. A key novel feature of the present work is to harness multiple supercomputers using new scheduling methods and data intensive processing pipelines. We are not aware of any other group that has achieved the required level of scalability, speed, reliability, and automation.

The idea of providing a unified interface to multiple HPC resources is not a novel one. With the popularity of “Grid Computing”, many such systems, such as Argo and Balsam (Childers et al., 2017; Salim et al., 2019), Radical Pilot (Merzky et al., 2021), and Leiden Grid Infrastructure (Somers 2019), were developed to provide a unified interface to multiple HPC resources. However, the huge diversity in HPC setups—their compute node configurations, file system layouts, compilers and supported software, clusters management software and their configuration, security requirements, etc.—makes it difficult to maintain and efficiently use such systems. Thus, for our system pipeline system Wormulon, we took the inverse approach. The onus of abstracting out the differences in HPC clusters is on the user and not on the system. When using Wormulon, the user has to provide a concretizer module that lets Wormulon run abstract tasks on the different HPC clusters. We feel that this approach is better suited for HPC tasks where users are strongly encouraged (XSEDE 2021) to carefully optimize setup to the specific HPC resources on which they will be running their code.

There has also been work in forecasting, and pipelines have been created to support forecasting influenza-like illness (ILI) dynamics; CDC runs an annual challenge in this area. Several important advances have been made to improve the overall forecasts. Most of the work in this space is either statistical time series models or simple compartmental mass action models; see (Shaman and Karspeck 2012; Reich et al., 2019; Pei et al., 2018; Wang et al., 2019).

Developing scalable pipelines and workflows for HPC tasks involving large datasets has also been well-studied in the literature (Farnes et al., 2018; Hendrix et al., 2016; Paraskevakos et al., 2019; Lyons et al., 2019). For example, the authors of (Farnes et al., 2018) presented a technique for building scalable workflows for analyzing large volumes of satellite imagery data, while Lyons et al. (2019) presented a system for analyzing workflows related to weather-sensing data. Other studies have presented generalized methodologies for building scalable workflows for tasks requiring HPC platforms (Hendrix et al., 2016; Castellana et al., 2019).

The present paper is not about our modeling work; that work is covered in a companion paper (Truelove et al., 2022). Here the primary focus is on the creation of a scalable workflow that allows projections to be run on a weekly basis through the integration of approximately 3100 county-level surveillance datasets. The resulting challenges are unique and form the basis for an important data-driven simulation and artificial intelligence platform.

Overall Methodology

The overall methodology comprises five broad steps as outlined below and depicted in Figure 2. The details of the digital twin (synthetic population and network) and simulator are published as companion papers. However, the modeling extensions and innovations pertaining to this report are described here.

Step 1: Create a digital twin. Instantiate a digital twin of a time-varying social contact network of the US. We use national-scale data to develop realistic populations and contact networks for the 50 US states and the District of Columbia (DC) (Mortveit et al., 2020).

To construct a population for a geographic region R (e.g., Virginia), we first choose a collection of person attributes from a set $\mathcal{D}$ (e.g., age, gender, and employment status) and a set ${\mathcal{T}}_A$ of activity types (e.g., Home, Work, Shopping, Other, and School). The precise choices of $\mathcal{D}$ and ${\mathcal{T}}_A$ are guided by the particular scenarios or analyses the population will serve. Described at a high level, we (i) construct people and places, (ii) assign activity sequences to people, (iii) map each activity for each person to a location (including the time of the visit), and, from this, (iv) derive a contact network using co-occupancy and a contact model to infer edges.

Step 2: Initialize. Extend the digital twin to initialize the multi-agent simulation system. This includes dis-aggregating observed data to the individual level, for example, assigning individuals attributes such as infection, vaccination, and immunity levels.

This step brings the reported case data into alignment with the data that is needed to initialize the simulation. This data integration process has become progressively more complicated and important as more data has become available. Even when it is available, the data is often misaligned in time, aggregated, delayed, partial, and noisy. This includes: (i) confirmed cases, for which only aggregate county-level counts are available; (ii) age distribution of confirmed cases, for which only limited information is available; (iii) vaccine uptake at the state level and coarsely stratified by age group; (iv) vaccine acceptance rates at the state level; (v) various information on non-pharmaceutical interventions (NPIs), including social distancing mandates, school closure/openings, and survey results on compliance to these interventions. The individual-level initializations based on aggregate-level data involve the following.

• 1. Assign a health state. An individual can be either never infected (susceptible), currently infected, or previously infected but now recovered. Everyone is susceptible by default. We consider the cumulative confirmed cases up to 15 days prior to the simulation start date as prior infections who have recovered. We consider the confirmed cases reported in the 15 days before the simulation start date as current infections. We use the case ascertainment rate (the ratio between confirmed cases and all actual infections, reported or not, symptomatic and asymptomatic) to scale the confirmed cases to calculate the actual number of infections by county and age group. For prior infections, we randomly select individuals and set each of them to recovered state or partially susceptible state if waning immunity is modeled; the latter is determined by the waning distribution and node infection time. For current infections, we randomly select individuals and set each of them to exposed state on the exposed date which is projected by a statistical model based on their confirmation date.

• 2. Assign vaccination status. Each individual is set to unvaccinated by default. Based on vaccine uptake and hesitancy data, we generate a weekly vaccination schedule of the number of people receiving vaccines by vaccine type (Johnson and Johnson, Pfizer/Moderna first dose or second dose) and age group. For prior vaccinations on the schedule, we randomly select individuals and set them to a vaccinated state or partially susceptible state if waning immunity is modeled; again, the latter is determined by the waning distribution and node vaccination time. For future vaccinations on the schedule, we randomly select individuals and set them to a vaccinated state at the scheduled time.

• 3. Assign behavior changes. For NPIs, we schedule changes with dates or triggering conditions for the affected individuals who may be randomly selected if the NPI has a compliance rate. The changes usually affect edges of the contact network.

Step 3: Calibrate and simulate. This step is fully automated under the Wormulon system and runs across two separate HPC clusters.

• • Step 3a: Calibrate. Calibrate the disease model to fit the observed data. After initialization, we calibrate the transmissibility of the disease τ to currently observed region-specific values of effective reproductive number R_effective. We use k = 5 replicates to obtain a robust estimate for R_effective.

• • Step 3b: Execute simulation jobs. Execute the multi-agent simulation for each replicate in each cell of the experimental design that represents the scenarios.

Step 4: Create probabilistic projections of scenario-specific reportable epidemic measures. In a sense, this is the reverse of Step 2. Construct epidemiologically relevant aggregate data from the raw simulated outcomes. In this step, we aggregate individual-level state transition data from simulation outputs to desirable spatial, temporal, and social resolutions, for example, state-level weekly new infections, new hospital admissions, and new deaths in children and adults, respectively. We need to map these numbers to confirmed numbers by applying the same ascertainment rate used in Step 2 and a statistical model to account for uncertainties. The projections will be distributions of these measures, which are often represented by quantiles.

Step 5: Analyze results for interpretation and policy implications. Analyze aggregated data and detailed epidemic evolution data in the simulation. Run network structure analytics to understand changes to the contact network during the simulation due to nodes being infected and vaccinated, and NPIs affecting person-person interactions.

Several basic modules, including construction of digital twins, EpiHiper, and the basic disease models, have been described in our earlier publications (Barrett et al., 2009; Chen et al., 2020a,b; Machi et al., 2021; Chen et al., 2021).

Extensive effort has been made to ensure the validity of our underlying models and the quality of the synthetic data. The published papers discuss this. Extensive effort has also been made to ensure the correctness of our code (verification).

Innovations realized

Policy support poses significant challenges

Challenge 1: HPC

Executing a well-powered experimental design involving large-scale stochastic simulations requires high performance computing (HPC) resources, and the availability of such resources is limited.

Challenge 2: Flexible model specification

Representing layered intervention scenarios—including vaccine allocation, waning immunity, and multiple strains, as well as a host of non-pharmaceutical interventions—requires an easily adaptable model.

Challenge 3: Big data

Integrating detailed county-level information about vaccine production schedules, vaccine acceptance, disease progression parameters, and non-pharmaceutical interventions for the US is a massive data fusion problem.

In this paper, building on our earlier work, we report on the following advances: first, orchestrating a workflow distributed across two separate HPC clusters simultaneously to reduce overall execution time, increase fault tolerance, and improve human productivity; second, extensions to our HPC agent-based simulator to represent vaccinated individuals, waning immunity, multiple strains, and production schedules; third, a data integration pipeline that can execute US-scale models and associated workflows; and, finally, a detailed analysis of the vaccine allocation problem. We are interested in understanding the spatial and temporal heterogeneity across the US. We describe these innovations in detail below.

Reliable end-to-end HPC cloud pipeline

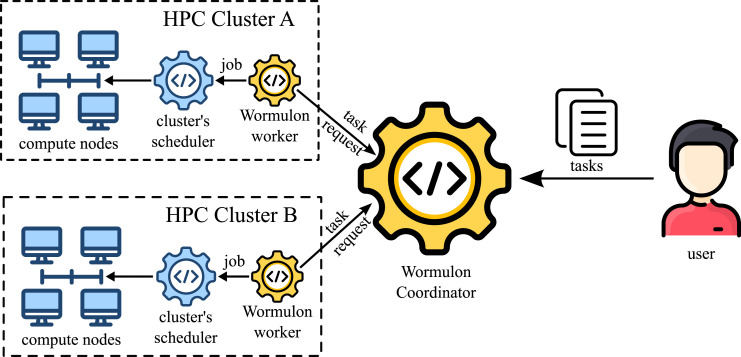
Wormulon is an HPC meta-scheduler that can be used to distribute HPC tasks across multiple HPC clusters to minimize the time to completion of all tasks. The design philosophy of Wormulon is pragmatic. Wormulon utilizes the cluster’s local HPC schedulers to run HPC jobs, and depends on user-provided logic—via the concretizer module—to convert abstract task definitions into actual jobs that run on the HPC clusters. Wormulon also uses a master coordination server, through which cluster-local agents can coordinate the distribution of tasks. The cluster-local agents communicate with the Wormulon master server using JSON RPC over HTTP(S) which is hosted on the public internet outside of the clusters. This architecture allows us to deploy Wormulon easily, avoiding security concerns arising from opening clusters to new inbound connections.

Tasks in Wormulon can depend on each other, and results from earlier tasks can be utilized by subsequent tasks. Wormulon uses this semantic knowledge about tasks to do semantic-aware scheduling. Wormulon also supports semantic-aware fault tolerance. Using the user-provided concretizer module, it can check for the successful completion of tasks and retry them in the case of failures due to, for example, node, network, file system, or scheduler communication failures.

Modeling innovations

EpiHiper is a general agent-based HPC tool for computational analysis of epidemics, and supports a broad range of interventions. The disease models comprise parameterized disease states, disease transmissions (through contacts), and disease progressions, and are specified independently of the people and their contact network over which the disease spreads. All individuals have the same model, but parameter values can be functions of individual traits, attributes, and history that may have resulted from, for example, vaccinations, mask-wearing, and interventions more broadly.

All input files to EpiHiper are provided in JSON format, with the exception of the contact network, which, due to its large size, may be either in comma-separated value (CSV) or binary format.

To address questions involving vaccination and waning immunity, we enhanced the default model. Vaccination is supported by adding states, transmissions, and progressions describing the protection provided through vaccination. We are considering three levels of vaccination: (i) single dose (Johnson and Johnson), (ii) first dose, and (iii) second dose (Pfizer or Moderna).

Waning immunity is modeled by adding states, transmissions, and progressions which encode the reduction in infection and probability of severe illness for previously vaccinated or recovered susceptible individuals. Individuals who are vaccinated or recovered progress through the new susceptible state with a dwell time sampled from an exponential distribution calibrated to the scenario’s specified waning period, for example, 1 or 3 years.

We have implemented customizable interventions, which are described in JSON format. Interventions work on subsets of nodes or contact edges, and can modify their attributes. Subsets can be selected based on node or edge attributes. Customizable read-only attributes of edges and nodes are defined in an external database, facilitating the selection of arbitrary subsets. We provide two ways to resolve conflicts when an edge or node attribute is changed multiple times during a single simulation step: (i) ordering of changes, and (ii) definition of conditions for changing the attribute.

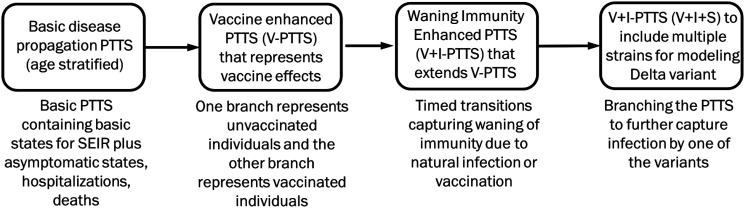
Figure 4 illustrates how our models have progressed over the course of the pandemic. Our models are multi-scale, multi-theory agent-based models. They include social contact networks at various spatial and temporal scales, and multi-theory behavior expressed at various levels (policies vs individual).

Figure 4.

This workflow shows how models were enhanced progressively to capture complex vaccine scenarios.

Calibration improvements

Before the development of the current system, this was a manual process using human intuition to select the next trial transmission value, but this was not sustainable. We developed a semi-automatic bisection method with limited human intervention to start the next iteration for regions which had not yet achieved calibration. For Scenario Modeling Hub rounds 8 and 9, we had completely automated this process by incorporating an optimizer directly into the pipeline. For this study, we use Brent’s method (Brent 1973) to minimize the required number of iterations.

Innovations in digital twins and model initialization

The state of the individuals and edges at the beginning of the simulation must represent the ground truth. To correctly represent previously diagnosed cases, we utilize New York Times county-level data (NYT-DATA, 2020) accumulated 15 days prior to the simulation start date. To represent the current state of the epidemic, that is, the current numbers of exposed or infectious people, we use a burn-in period where we expose for 15 days individuals based on daily changes in the New York Times data. We turn off transmission during the burn-in period to avoid additional cases. This is achieved by using the extensive intervention framework supported in EpiHiper. Transmission is turned on at the beginning of the simulation. The age distribution of previous and current cases is based on the nationally observed age distribution of cases.

Previous vaccination is handled similarly; however, we only have state-wide age distributions of vaccinated people. Current and future vaccination is implemented through a scenario-defined vaccination schedule which considers the expected percentage of vaccination and/or the start date for vaccination of children under 12.

We also use information for current mask wearing, social distancing, and school or work closure to disable the appropriate contacts during the initialization. Individual adherence to these interventions is achieved by the customizable sampling framework.

To account for waning immunity in the current state, we calculate the mean exposure and vaccination date of previous cases. We sample among the previous cases using the probability 1 − exp ((mean date − start date)/waning period) to select people who have become partially susceptible.

Role of data-driven AI models

The present work uses data-driven AI methods to support scenario projections. To the best of our knowledge, this is the first time US-scale data-driven AI models with realistic social contact networks have been used to study the impact of vaccines and vaccine acceptance. In (Foster et al., 2020; Hager et al., 2019), the authors describe the use of AI-driven multi-agent models and digital twins for studying complex questions. In (Foster et al., 2020; Hager et al., 2019; Perrault et al., 2019), Perrault et al. highlight the need for developing operational AI systems, calling it a data-to-deployment pipeline. The authors highlight the need for operational AI. The integrated pipeline outlined here is a step in this direction. Our work takes a step toward making computations seamless across multiple HPC systems, and demonstrates how HPC clouds can be used for real-world problems in public health. We also address emerging AI challenges that deal with epistemic and aleatoric uncertainty by building causal models with statistical experimental designs, and paucity of data by developing models using synthetic individualized data that is privacy preserving.

Wormulon: an intelligent job submission system for HPC schedulers

Wormulon is the system that we use to run tens of thousands of EpiHiper simulations (tasks) with real-time deadlines using two geographically distributed clusters concurrently. Tasks in Wormulon can be generated statically (scenario projection mode), or dynamically by using information from tasks that have completed execution (calibration mode). When using Wormulon, users need to provide a concretizer module that makes Wormulon aware of the task and cluster semantics—how to convert tasks to schedulable jobs on clusters, how to check for failures, etc. The overall objective of the Wormulon system is to minimize the time to completion for all tasks by maximally utilizing available resources.

Requirements for our job submission system

For our specific tasks, we needed a job submission system that met the following requirements:

• 1. Ability to leverage existing HPC schedulers present on the HPC clusters to quickly schedule HPC jobs, preferably using the Process Management Interface (PMI) for quick startup.

• 2. Ability to run on modern secure clusters where login and services like ssh are secured with single sign-on with central authentication, two-factor authentication, networks isolated with VPNs, etc.

• 3. Ability to support task-dependency networks and dynamic on-the-fly task generation.

• 4. Ability to retry tasks based on task semantic-aware fault detection and recovery.

• 5. Ability to support disparate HPC site-specific configurations with minimal reconfiguration.

• 6. Ability to submit tasks to multiple HPC clusters.

Many systems exist—such as: HPC cluster schedulers like Slurm (Yoo et al., 2003) and PBS (Feng et al., 2007), pilot-based systems such as Radical Pilot (Merzky et al., 2021), multi-cluster schedulers like Argo and Balsam (Childers et al., 2017; Salim et al., 2019) and Leiden Grid Infrastructure (Somers 2019), and modern big data and machine learning-oriented schedulers like Mesos (Hindman et al., 2011), Yarn (Vavilapalli et al., 2013), Dask (Rocklin 2015) and Ray (Moritz et al., 2018)—but none of these systems satisfied all of the requirements as stated above. Thus, we developed Wormulon to satisfy our task-specific needs.

Design and architecture of Wormulon

Architecture overview

Figure 5 shows the overall architecture of the Wormulon system. A Wormulon setup consists of a single coordinator and one or more workers. The Wormulon coordinator is hosted on a network that is accessible from all HPC clusters. Each participating HPC cluster runs its own Wormulon worker, and the workers communicate with the coordinator, implementing a star topology. Users of Wormulon interact with the Wormulon setup only via the coordinator.

Figure 5.

Overall architecture of the Wormulon meta scheduler.

Task: A unit of work

In Wormulon, a task is an abstract unit of work. To execute a task on a specific cluster, it must be converted to a concrete schedulable job. The responsibility of converting an abstract task to a concrete job lies with the user-provided concretizer module, which is described later in this section. A task can be executed on any cluster that has the required resources available.

A task must specify a size and a runtime. Since the actual amount of resources needed to run a task and the runtime of the task may vary depending on which HPC cluster the task is executed on, in Wormulon the size and runtime of tasks are provided as abstract metrics. These are used to load balance the tasks on different clusters. At a high level, the size of a task is expected to be proportional to the amount of resources that it needs from a cluster. Similarly, the runtime estimate provided is expected to be proportional to the actual runtime of the task. The compute load of a task is the product of its size and runtime, and is used for prioritizing tasks.

Batch: a set of tasks

A batch is a set of related tasks

Tasks in a given batch can depend on other tasks in the same batch. Let G_b = {V_b, E_b} be the task dependency network for task batch b. Then, each vertex t ∈ V_b corresponds to a task in batch b, and each directed edge (t_i, t_j) in E_b represents a dependency relation corresponding to task t_j depending on task t_i. The task dependency network for every batch G_b must be a directed acyclic graph. In the above case, the task t_j can start execution only after task t_i has completed execution, and may use results generated by t_i.

Users of Wormulon can submit multiple batches of jobs to the system. Tasks can be created and added to a batch dynamically during runtime. Each batch is also assigned a numeric priority by the user. A task from a lower priority batch will be scheduled to run only when no other ready jobs from higher priority batches are available.

Lifecycle of a task

The Wormulon coordinator tracks the lifecycle of tasks via finite state machines with the following states: waiting, ready, assigned, completed, and failed. Tasks with dependencies start off in the waiting state, and are moved to ready state when all of their dependencies are in the completed state. Tasks without dependencies start off in the ready state.

Wormulon workers on different HPC clusters periodically request the Wormulon coordinators for ready tasks. The coordinator maintains a priority queue with the ready tasks. The tasks are prioritized first by their respective parent batch’s priority, and second by the compute load of the task. By default, Wormulon uses the largest-job-first heuristic for scheduling. The Wormulon coordinator ensures that, at any point in time, the sum of the sizes of the tasks assigned to a given worker is less than or equal to the size capacity of the worker.

Once a ready task is assigned to a specific worker, it is moved to the assigned state. Once the worker informs the coordinator that the task has been executed successfully, it is moved to the completed state. In case the worker is unable to execute the task to completion, it is moved to the failed state.

Once a task is marked completed, all its dependent tasks are checked to see if they are ready for execution, and, if so, they are moved to the ready state.

Concretizer: Specifying semantic knowledge of tasks and clusters

HPC clusters vary widely in terms of their compute node configurations, cluster schedulers (both implementation and configuration), the software implementations available on them, and their file system structures. Many HPC meta-schedulers (Merzky et al. (2021); Salim et al. (2019)) try to abstract out these differences. We find, however, that HPC software authors will often optimize their software setup—compilers and libraries used, MPI implementation used, OpenMPI CPU affinity setups, filesystem usage, etc.—to maximize performance of their software on the individual clusters. To allow for this flexibility when using Wormulon, users provide a concretizer module that encodes the logic of how to run a specific task on a specific cluster. For example, on a cluster running the Slurm scheduler, the concretizer module, given an abstract task definition, must be able to generate the sbatch command to be used to schedule the corresponding job on the cluster.

Jobs on HPC schedulers can fail in numerous ways. A particularly difficult-to-handle set of failures are the ones that happen when the job executes successfully (finishing with exit code zero), but, due to intermittent issues of the network and the underlying networked file system, the results are not committed to the filesystem/data store correctly. Thus, the concretizer module in Wormulon has an additional role in semantic fault tolerance, where it encapsulates the semantic knowledge to check if the job finished successfully. The concretizer is also used to provide Wormulon with the logic on how to restore a failed job’s runtime environment to a runnable state.

Life cycle of a job

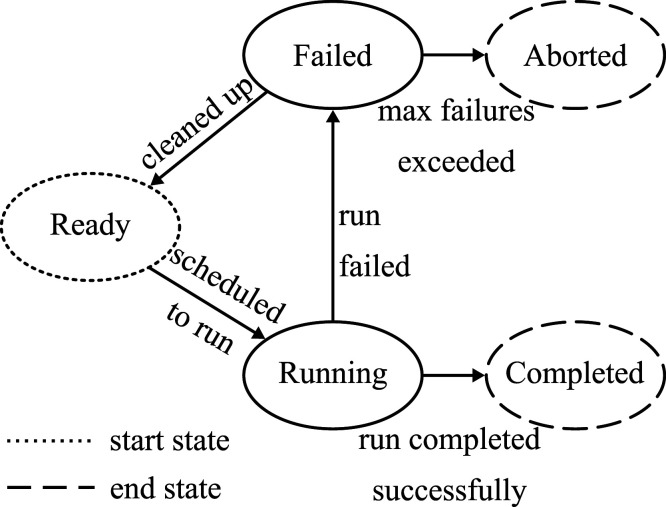
Once a Wormulon worker is assigned a task by the coordinator, it converts the task into a concrete job using the user-provided concretizer module. Similar to how the Wormulon coordinator tracks the lifecycle of tasks, Wormulon workers track the lifecycle of jobs via finite state machines with the following states: ready, running, failed, completed, and aborted (Figure 6). All jobs start off in the ready state. During the processing of the ready jobs, each job is scheduled to run using the local cluster’s scheduler, and is moved to the running state.

Figure 6.

Life cycle of job.

Wormulon workers periodically check to see if the running jobs have finished execution. Jobs that have completed successfully—as determined by the concretizer module—are moved to the completed state; otherwise, they are moved to the failed state.

During handling of failed jobs, they are cleaned up—using the concretizer module—and moved to ready state. If a job fails more than a preconfigured number of times, it is moved to the aborted state.

When the job corresponding to a task moves to the aborted or completed state, the Wormulon worker informs the coordinator of this status.

The Wormulon data store

The Wormulon coordinator and workers together implement a distributed key-value data store. This data store is used to provide shared configuration parameters and configuration files to the tasks. Additionally, the data store is also used to share results of tasks such that any dependent tasks may use those results.

Note that this data store is not intended to distribute large datasets. For that purpose, we recommend using alternate methods—such as Globus—to distribute the data among the HPC clusters.

The key-value store implemented by Wormulon is immutable, and the addition operation is idempotent with “first writer wins” semantics. Keys once added to a running Wormulon setup may not be removed during the runtime of the setup.

The primary copy of the data store is kept at the coordinator. The worker processes maintain read-only copies of the data store. All write operations go directly to the coordinator. The worker processes periodically query the coordinator for changes and update their local copy.

The workers always update the local copy of the data store before requesting new tasks to execute. This ensures that the configuration parameters needed for executing the tasks are always available locally at the HPC cluster.

System implementation

The Wormulon coordinator and workers are written in the Python programming language.

Both the Wormulon coordinator and workers expose remote procedure call (RPC) endpoints for interaction. Wormulon uses JSON RPC over HTTP(S) for implementing remote procedure calls.

The Wormulon coordinator and workers use SQLite3 files to maintain state and store the local copy of the distributed configuration data store.

When configuring a Wormulon setup, a concretizer module must be provided to each Wormulon worker at each HPC cluster. The concretizer module is implemented as a Python module and defines a class which inherits from an abstract concretizer class. The abstract concretizer class defines the set of methods that the provided concretizer class must implement.

How performance was measured

Performance of EpiHiper

EpiHiper is used to efficiently simulate an epidemic spreading over a contact network. It supports configurable disease models and complex interventions changing individual (node) and contact (edge) attributes. We measured the total runtime of each simulation, as well as the time used in different sections. The internal time was measured in nanoseconds and recorded for each simulation step and for each MPI process. The time for each section was accumulated during the whole simulation for all processes. The internal statistics were collected on Rivanna (see Table 2) for individual replicate runs.

Table 2.

Compute node configuration of Bridges2 and Rivanna.

	Bridges2	Rivanna
# Total nodes	488	115
# Allocated nodes	50	30
# CPUs/node	2	2
# Cores/CPU	64	20
RAM per node	256 GB (DDR4)	384 GB (DDR4)
CPU	AMD EPYC 7742	Intel Xeon Gold 6148
Network	Mellanox ConnectX-6	Mellanox ConnectX-5
OS	CentOS Linux 8	CentOS Linux 7
Filesystem	Lustre	Lustre

Performance of Wormulon

The primary goal of the Wormulon system is to minimize the time to completion of all tasks. Here, all tasks can be created statically, as in the case of the scenario projection pipeline, or dynamically, as in the case of the calibration pipeline.

In the following sections, the primary metric presented when evaluating the Wormulon system is the time to completion of a given set of tasks. The time to completion is computed as the difference between the start time—when the (initial) tasks are submitted to the master Wormulon server—to the end time—when the result of the last task reaches the master Wormulon server. Additionally, we also use the number of simulated days (for the whole US population) per unit wall clock time as a metric for measuring system performance.

For the strong scaling experiments, 40 replicates of the national simulation (scenario projection pipeline) were used corresponding to four different configurations/cells. The four configurations (or cells) correspond to the four scenarios from round 8 of the Scenario Modeling hub.

We also report the time to completion for a typical scenario consisting of 400 national-level replicates, which is the typical number of replicates used for actual submissions to Scenario Modeling Hub.

Additionally, we also present the time to completion for the calibration pipeline, which tunes the effective transmissibility, τ, for each of the 50 US states and DC, so that the resulting reproductive number R measured from simulated outcomes matches the state’s reported value for COVID-19. In this case, the tasks are generated dynamically by the optimization algorithm (Brent’s method) given a range for the effective transmissibility.

All experiments were run using the Bridges2 and Rivanna clusters. The Wormulon master server was hosted at University of Virginia on a server with a similar configuration to the Rivanna compute nodes. The Wormulon cluster agents were run on one of the compute nodes on Rivanna and Bridges2. Table 2 describes the configuration of the Rivanna and Bridges2 clusters. Note that we only use 30 compute nodes on Rivanna and 50 compute nodes on Bridges2. Additionally, the configurations of the compute nodes on the two clusters are very different in terms of the number of CPU cores per compute node, the memory available per CPU core, and the clock frequency of the CPUs.

Performance results

Performance of a single EpiHiper replicate

In order to respond to the request, we must be able to run the maximum number of simulations within the given resource and time limits. Therefore, we did not strive to get the shortest time per simulation; instead, we opted for the minimal resources which supported any given problem.

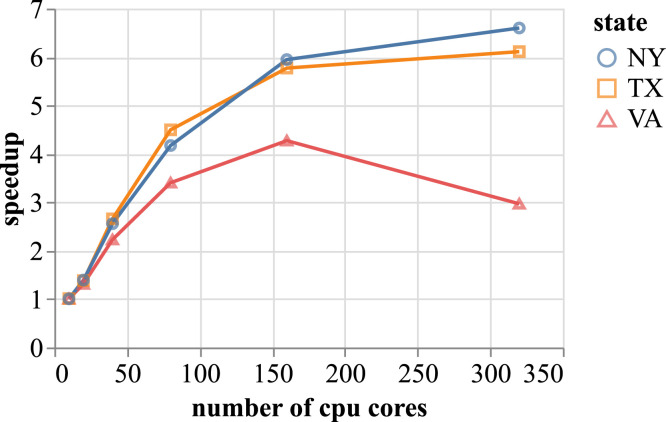
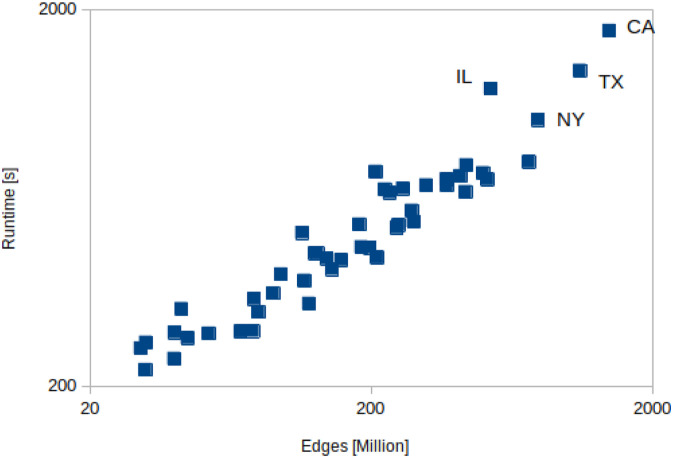
All EpiHiper single replicate performance evaluations have been performed on Rivanna, but results on Bridges2 are comparable. The strong-scaling experiment (Figure 7) shows good scaling behavior for large problems (NY, TX) up to 120 CPU cores, and for medium-sized problems (VA) up to 80 CPU cores. Since the scaling curves are concave, the smallest number of CPU cores would lead to the highest throughput. On Rivanna, we chose 80 cores for NY and TX, and 24 cores for VA, with 9.6 GB of memory per core. For Bridges2, which has only 2 GB per core, we experimentally determined that limiting the number of utilized cores per node to half of the available, that is, effectively doubling the amount of available memory to 4 GB per core, leads to reduced runtime. The reason for this is that the memory bus is the limiting performance factor. By reducing the number of cores, we avoided this problem. Furthermore, we benefited from the processor’s capability to increase the clock speed if not all the cores are utilized (Klonower 2021). This led to the following number of cores: (i) NY: 64, (ii) TX: 128, and (iii) VA: 26.

Figure 7.

Speedup of EpiHiper simulations for the states of New York (NY), Texas (TX) and Virginia (VA) with increasing numbers of CPU cores on Rivanna.

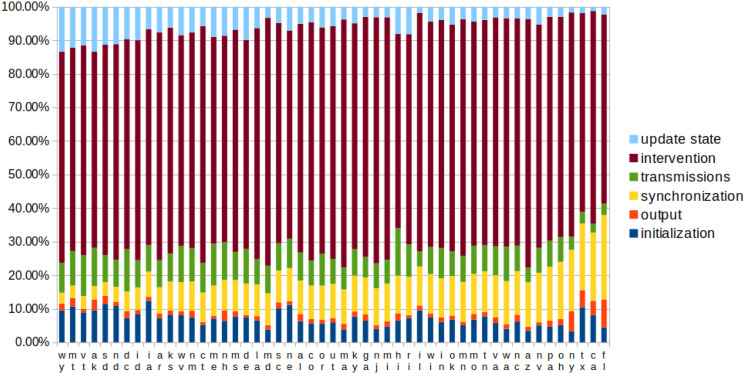
Figure 8 indicates that increasing the number of cores by a factor of 60 (from two for small states—AK, DC, MT, ND, SD, VT, WY—to 120 for CA) only increases the synchronization by a factor of 8 (3.23%–25.2%), indicating that inter-processes communication scales approximately $\sqrt{N}$ where N is the number of cores.

Figure 8.

Distribution of simulation tasks for scenario A (other scenarios lead to similar results). A large amount of time is spent in interventions, whereas the disease transmission uses less than 1/4 of the time. The states are sorted by the time spent in synchronization.

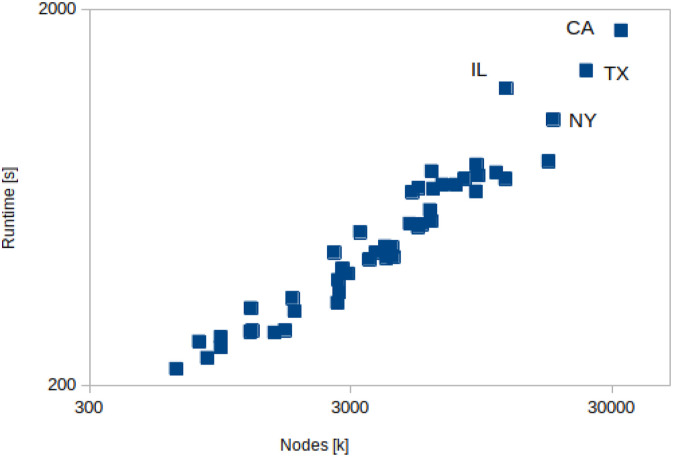
Figures 9 and 10 show that the scaling of the EpiHiper runtime for our resource configuration, which targets throughput, is linear relative to the size of the problem measured, either in nodes or edges.

Figure 9.

EpiHiper runtime depending on contact edges of states.

Figure 10.

EpiHiper runtime depending on contact nodes of states.

Performance for Wormulon, the cluster meta-scheduler

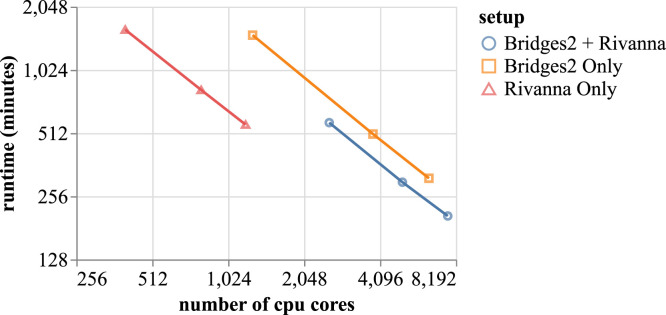
Figure 11 shows strong scaling results when running a US-scale scenario projection pipeline with four configurations—corresponding to configurations from CDC Scenario Modeling Hub round eight setting—and 10 replicates per configuration with three different setups: (A) using Bridges2 and Rivanna together, (B) using Bridges2 only, and (C) using Rivanna only. In (A), we use three different compute node pairings: 50 nodes on Bridges2 + 30 nodes on Rivanna, 33 nodes on Bridges2 + 20 nodes on Rivanna, and 17 nodes on Bridges2 + 10 nodes on Rivanna. For (B) we use 50, 30, and 10 nodes on Bridges2. Finally, for (C) we use 30, 20, and 10 nodes on Rivanna. Figure 11 shows that for each of the setups, the runtime drops almost linearly on a log-log scale with increasing numbers of CPU cores. Table 3 shows the number of simulated days per minute (realtime) and corresponding speedup when using the different setup configurations.

Figure 11.

Strong scaling results of the scenario projection pipeline for the entire US with four cells and 10 replicates.

Table 3.

Number of simulated dates per minute (realtime) and speedup when using different configuration setups. Here R(X) and B(Y) means when using X compute nodes on Rivanna and Y compute nodes on Bridges2, respectively.

Setup	# CPU cores	Sim days/min	Speedup
R (10)	400	51.93	1.00
R (20)	800	107.06	1.93
R (30)	1200	156.55	2.83
B (10)	1280	58.69	1.06
B (30)	3840	173.62	2.95
B (50)	6400	282.05	4.80
B (17)+R (10)	2576	153.27	2.77
B (33)+R (20)	5024	294.46	5.32
B (50)+R (30)	7600	426.54	7.72

Finally, we also ran a US-scale scenario projection pipeline with the four configurations and 100 replicates. This is the typical number of replicates necessary to compute the confidence interval ranges that we report to Scenario Modeling Hub. We ran the pipeline using 50 compute nodes on Bridges2 and 30 compute nodes on Rivanna, which is the typical setup that we actually use to run the pipelines. This run, with 400 national-level replicates, completed in 32 h and 42 min.

Table 4 shows the runtime of the US-scale calibration pipeline using three different setups: (A) using Bridges2 and Rivanna together, (B) using Bridges2 only, and (C) using Rivanna only. As can be observed from the table, while there is some gain in using the two systems together, the improvement is not as significant as in the case of the scenario projection pipeline. This is because the calibration process currently used for each state is largely sequential. At each round, the optimizer used in the calibration pipeline uses Brent’s method for optimization (Brent 1973) to select an effective transmissibility value τ, and runs k = 5 replicates to get a robust estimate of basic reproduction ratio R for COVID-19. The optimizer continues to generate and test new effective transmissibility values τ until a termination condition is met—the obtained R is within 0.02 absolute distance of the publicly reported value R. Thus, the time-to-completion/runtime of the pipeline is dominated by the state which is slowest to converge.

Table 4.

Runtime of calibration pipeline for entire USA.

Setup	# Compute nodes	Runtime (minutes)
Bridges2 and Rivanna	30 + 50	153
Bridges2 Only	50	175
Rivanna Only	30	324

This limitation, however, is entirely due to the current optimizer used, and due to running the scenario projection pipeline only after the whole calibration pipeline completes. Recently, a number of innovations in the area of black box optimization have been made, motivated by hyperparameter tuning issues in machine learning (Wu et al., 2019). A number of new Bayesian optimization frameworks have been developed (Nogueira 2014; Louppe 2017) that allow testing of multiple candidates in parallel to alleviate the issue of sequential testing. Additionally, in the future we intend to combine the calibration and scenario projection pipelines to minimize the time-to-completion of the joint pipeline.

Case study: role of waning immunity

In this section, we study the role of waning immunity, both natural immunity obtained from infections and vaccine immunity in the COVID-19 epidemic evolution.

Scenarios. In summer 2021, we started to see more and more cases of COVID-19 in people who were vaccinated. Some of these cases were breakthrough infections, but many were due to waning of immunity from their initial vaccinations (Naaber et al., 2021; Juthani et al., 2021). There were also many cases of reinfection in previously infected people whose naturally-obtained immunity had waned. To study the impact of waning immunity and its co-dynamics with infections and vaccination, we considered four scenarios: (A) no waning at all; (B) waning of natural and vaccine-induced immunity with 1-year average time, and high protection against infection and severe disease after waning; (C) waning with 3-year average time and low protection; (D) waning with 1-year average time and low protection.

Implementation. In addition to the settings on waning, we considered the same parameterizations of simulation initializations, vaccine efficacy and age-stratified vaccine uptake with hesitancy in different states, and non-pharmaceutical interventions (NPIs), including reduced generic social distancing and mask wearing, voluntary home isolation of symptomatic cases, and school reopening with in-person learning from the end of August 2021. For the disease model, we assumed that in August 2021 the more infectious Delta variant was responsible for almost 100% of US cases and would remain so for the next 6 months. Therefore, we used a single-variant COVID-19 disease model for our simulations, and made the following extensions to model waning immunity.

We added a partially susceptible state immS which has a smaller susceptibility than a naively susceptible state S; and added state transitions from the recovered and vaccinated states to immS with probability 1.0 and dwell time t following an exponential distribution p(t) = λe^−λt, 1/λ = 1-year (fast waning) or 3-year (slow waning). Note that, in this implementation, there are nodes entering and leaving the immS state continuously at the population level instead of reducing the immunity of individual nodes continuously. This assumption substantially reduces the model’s computational complexity model while computing the same aggregate dynamics. To implement protection against infections and severe disease for nodes in the immS state, we assign a reduced susceptibility and smaller transition probability from exposed to symptomatic states for those nodes in immS state compared to those in S state, and the exact parameterizations are age specific: people ≤65 years old have more protection than those $>rbin\mathit{65}$.

In simulation initializations, we implemented the following for waning in prior infections and vaccinations. In this case study, our simulations start in July 2021. For infections prior to the beginning of the simulation period, we chose nodes based on age distribution of cases, and set them to either recovered state or immS state, depending on when they were infected. For nodes vaccinated prior to the beginning of the simulation period, we move them into the immS state depending on when they were vaccinated, and following the exponential distribution defined for the particular scenario.

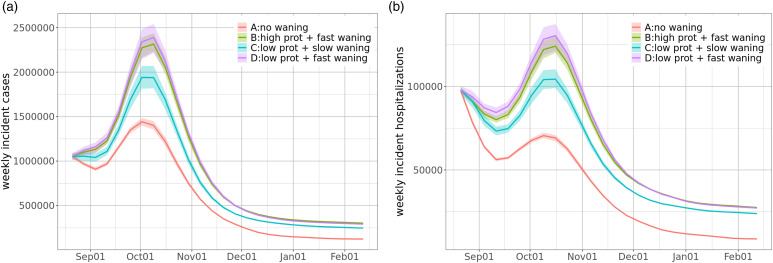
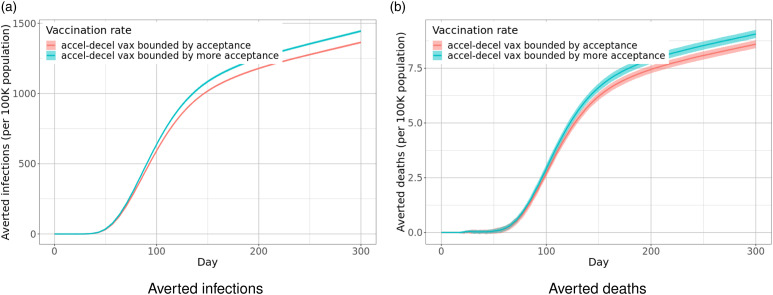
Results.Figure 13 shows the projections of weekly incident cases and hospitalizations in the US for 6 months from August 2021 under different scenarios of waning immunity. As expected, there will be more cases with fast waning, and the assumption of no waning substantially underestimates the cases. The reason is that more people become susceptible to SAR-CoV-2 again with fast waning, even if they are partially protected against infection. Without waning, the population reaches herd immunity at a lower peak and a smaller total number of cases. In all scenarios, we can expect that cases peak in early October. We have similar observations regarding hospitalizations, except that the effect of protection on hospitalizations seems more significant than its effect on infections.

Figure 13.

Projections of (a) weekly incident cases and (b) weekly incident hospitalizations in the US from Aug. 2021 to Feb. 2022 under four different scenarios. Note that the ribbons show interquartile ranges of the probabilistic projections. (a) As expected, there will be more cases with fast waning and the effect of protection is relatively small; and the assumption of no waning substantially underestimates the cases. In all scenarios, we will see cases peak in early October, then start decreasing. (b) We have similar observations regarding hospitalizations, except that the effect of protection on hospitalizations seems more significant.

Implications

As mentioned earlier, the integrated end-to-end pipeline has been used for a number of case studies, including scenario projections. The pipeline has continually improved during this time, taking into account the challenges we identified along the way. Here, we briefly describe a set of case studies addressing the complex question of vaccine allocation as COVID-19 was evolving. Our studies for this series of tasks started around October 2020, and have continued as the pandemic continues to evolve. We describe these five studies briefly here, and two of the case studies in more detail in Appendix B. Figure 12 and 13 shows the workflow of a typical case study, which includes steps 2 to 5 described in the “Overall Methodology” section, and the sizes of the input and output datasets fed into and generated by the simulations.

Figure 12.

COVID-19 Scenario Modeling Hub study workflow. This figure illustrates a workflow for case studies of the COVID-19 Scenario Modeling Hub where various scenarios are modeled and simulated to generate projections of cases, hospitalization, and deaths in the US at national and state levels. [1] Confirmed case count data includes over 3100 US counties × over 500 days [2] The calibration involves a base configuration and about 5 iterations, 10 replicates per iteration, and generates about 1 TB individual-level output data from 51 states × 50 replicates = 2550 simulation instances. [3] The factorial design in this case study has 4 scenarios × 51 states × 50 replicates = 10,200 simulation instances. [4] The size of individual-level output data: 4 cells × 51 states × 50 replicates × multi-million state transitions = multi-billion entries, about 4 TB. [5] Synthetic population data includes person, household, location, and activities data. Our analysis mainly uses person data, which is over 20 GB. [6] The size of the aggregate epidemiological data: 4 cells × 51 states × 50 replicates × 250 days × 200 health states × 3 counts (number of nodes entering a state, number of nodes currently in a state, and cumulative number of nodes entering a state) = 1.5 billion entries, or 4 GB.

Implications for understanding the spread of COVID-19 and the role of vaccines

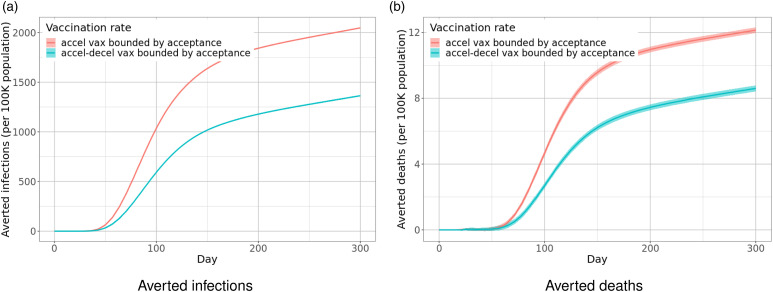
Case Study 1. Oct 2020–January 2021: Optimal allocation of limited vaccine supplies. During this period, authorities were interested in understanding how to allocate the limited supply of vaccines. Vaccine allocation is a complex problem that has been studied extensively; the novelty of this study was in studying the problem when we have a schedule for vaccine production and delivery. We investigated the use of social networks to design and analyze network-based prioritization schemes. Our results show that the strategy is extremely effective.

Case Study 2. January 2021–March 2021: Optimal spatial and age-based allocation. Interest turned to allocation strategies on two levels: (i) between-state allocation based on population and prevalence, and (ii) within-state allocation using age-based prioritization.

Case Study 3. April 2021–June 2021: Evaluating the role of vaccine hesitancy. As vaccines became available, the question turned to hesitancy. Initially the problem with vaccine allocation was largely a supply-side problem, but starting around May it became a demand-side problem. We saw that hesitancy varied across states, and weekly uptake of vaccines started slowing down significantly. This study focused on the impact of hesitancy.

Case Study 4. June 2021–July 2021: Layered interventions to control the new outbreak caused by the new Delta variant (Round 6 and 7 of the Scenario Modeling Hub). Summer 2021 saw the quick spread of the Delta variant which led to significant outbreaks across many parts of the country. This study built on case study three to assess the role of vaccine uptake and hesitancy in light of the Delta variant.

Case Study 5. August 2021–September 2021: Understanding the impact of waning immunity (Round 8 of the Scenario Modeling Hub). The most recent question pertained to waning immunity. As the outbreak slowed and vaccine mandates began to be put in place, there was concern that waning immunity might cause a new outbreak in the fall. Our results show that, depending on assumptions about the rate of waning, residual immunity, and protection against infection and severe disease, cases and hospitalizations may peak in early October before they drop.

We have continued our effort to support Scenario Modeling Hub using our simulations. At the time of this writing, Round 12 of Scenario Modeling Hub was concluded, focusing on understanding the impact of the Omicron variant of COVID-19 in the United States.

Implications for future HPC systems

We have been using HPC models for about 20 years to support pandemic planning and response. Based on this experience and the ongoing effort, we are able to identify a few key considerations for the designers of next generation HPC systems to support such large-scale socio-technical simulations.

First, our application is interaction-intensive. Running the simulation without any interventions already poses challenges on the effective use of GPUs. We had done earlier tests where we saw modest improvements for an older version of our simulator. Second, from the perspective of system support, scaling our systems to exascale platforms will require us to explore program models such as Charm++. We have already begun collaboration within the team to explore this. Finally, use of parallel machines for long periods of time poses challenges in terms of dedicated accessibility. The HPC consortium and Pittsburgh Supercomputing Center (PSC) have generously given us cycles over these 18 months, but those are still not adequate. It is unwise to rely on large portions of any machine being dedicated to a single application over extended periods of time, especially during a crisis. Establishing strategic computing reserves will help. The multi-system scheduling system we have built is a step towards harnessing such HPC systems in a reliable, efficient, and fair way. We believe the proposed solution can be generalized for other applications as well. Recently, Stoica and Shenker (2021) have also discussed the need to harness multiple cloud resources to support complex workflows; the general idea of hybrid clouds is closely related to the work described here and needs to be developed in the context of high performance computing systems. Our work takes a step in that direction.

Author biographies

Parantapa Bhattacharya is a Research Scientist at the Biocomplexity Institute at University of Virginia. His research areas include High Performance Computing, Agent-Based Modeling, and Explainable AI methods for Natural Language Processing (NLP) models.

Jiangzhuo Chen is a Research Associate Professor at the Biocomplexity Institute at University of Virginia. His research areas include big data analytics, model-based forecasting modeling, simulation, and analysis of large-scale social networks, computational epidemiology, and computational economics.

Stefan Hoops is a Research Associate Professor at the Biocomplexity Institute at University of Virginia. His research areas include modeling and simulation of biochemical systems, management and analysis of systems biology data sets, and reverse-engineering of biochemical networks.

Dustin Machi is a Senior Software Architect at the Biocomplexity Institute at University of Virginia. His research areas include cyberinfrastructure, high-performance computing (HPC), and software engineering.

Bryan Lewis is a computational epidemiologist with two decades of experience crafting infectious disease models for public policy and decision support. He has provided real-time epidemic support to federal and state partners for the 2009 influenza pandemic, 2014-15 West African Ebola pandemic, and the COVID-19 pandemic.

Srinivasan (Srini) Venkatramanan is a Research Assistant Professor at the Biocomplexity Institute at University of Virginia. His areas of expertise include computational epidemiology, mathematical modeling, data science, and network science.

Mandy Wilson is a Research Scientist at the Biocomplexity Institute at University of Virginia. Her primary areas of interest are database architectures and data mining, but she also has expertise in graphical user interface design and data-driven web applications.

Brian Klahn is a Research Scientist at the Biocomplexity Institute at University of Virginia. Brian has years of experience with production-grade software and data systems. Brian often draws on connections and parallels from his diverse experiences. This includes an M.S. in [neuro]physiology, molecular biology, genetics, multiple programming languages and paradigms, and even nuclear engineering (U.S. Navy).

Aniruddha Adiga is a Research Scientist at the Biocomplexity Institute at University of Virginia. His research areas include signal processing, machine learning, data mining, forecasting, big data analysis etc.

Benjamin Hurt is a Data Scientist at the Biocomplexity Institute at University of Virginia. His focus has been the development of epidemiological forecasting, analysis, and visualization, along with financial contagion modeling.

Joseph Outten is a Software Engineer at the Biocomplexity Institute at University of Virginia. His research interests and projects revolve around synthetic biology and bioinformatics, as well as some machine learning and algorithm design.

Abhijin Adiga is a Research Assistant Professor at the Biocomplexity Institute at University of Virginia. His interests include network science, modeling, algorithms, combinatorics, and game theory, with current focus on dynamical processes over networks and design and implementation of complex simulation systems.

Andrew Warren is a Research Assistant Professor at the Biocomplexity Institute at University of Virginia. His interests lie in developing and applying algorithms for processing biological data for insight and hypothesis testing using comparative genomics, experimental analysis, machine learning, data mining, and graph modeling with a focus on promoting human health and security.

Young Yun Baek is a Senior Scientist at the Biocomplexity Institute at University of Virginia. Her interests include statistical methodologies for data analyses, data imputation, agent-based modeling, and synthetic information.

Przemyslaw Porebski is a Software Engineer and Data Scientist at the Biocomplexity Institute at University of Virginia. Currently he supports the computational epidemiology efforts at the institute.

Achla Marathe is a Professor at the Biocomplexity Institute and at the Department of Public Health Sciences at University of Virginia.

Dawen Xie is a Research Scientist at the Biocomplexity Institute at University of Virginia. His primary work focuses on Geographic Information Systems (GIS), visual analytics, information management systems, and databases.

Samarth Swarup is a Research Associate Professor at the Biocomplexity Institute at University of Virginia.

Anil Vullikanti is a Professor at the Biocomplexity Institute and the Dept. of Computer Science at University of Virginia. His research interests are in the broad areas of network science, dynamical systems, foundations of machine learning, combinatorial optimization, and distributed computing, and their applications to computational epidemiology and social networks.

Henning S. Mortveit is an Associate Professor at the Biocomplexity Institute and at the Department of Engineering Systems and Environment at University of Virginia. His interests include massively interacting systems (MMS), mathematical frameworks and modeling for MMS, software architectures and designs for MMS, and the construction of digital twins in support of their simulation models.

Stephen Eubank is a Professor at the Biocomplexity Institute and in the Dept. of Public Health Sciences at University of Virginia. He was PI on one of three original research groups in the NIH-sponsored Models of Infectious Disease Agent Study (MIDAS). He currently serves as a Jefferson Science Fellow at the US Dept. of State.

Christopher L. Barrett is an endowed Distinguished Professor in Biocomplexity, the Executive Director of the Biocomplexity Institute, and Professor of the Department of Computer Science at the University of Virginia. Over the past 35 years, Barrett has conceived, founded, and led large interdisciplinary complex systems research projects and organizations, established national and international technology programs, and co-founded organizations for federal agencies such as the Department of Defense, the Department of Energy and the Department of Homeland Security. He has served in various advisory and collaborative scientific roles internationally.

Madhav Marathe is a Distinguished Professor at the Biocomplexity Institute and division director of the Network Systems Science and Advanced Computing Division at the Institute. He is also a Professor in the Department of Computer Science at University of Virginia. Over the last 20 years, his division has supported federal and state authorities in their effort to combat epidemics in real-time, including the H1N1 pandemic in 2009, the Ebola outbreak in 2014 and, most recently, the COVID-19 pandemic. He is a Fellow of the IEEE, ACM, SIAM, and AAAS.

Appendix.

The Appendix is organized as follows: in Appendix A, we describe the disease model, and in Appendix B we provide additional details on two of the case studies. The disease model, EpiHiper, and the construction of the digital twin are described in our earlier published works; see (Chen et al., 2020a,b; Machi et al., 2021; Barrett et al., 2009; Chen et al., 2021).

A. The disease model parameters

Figure 14.

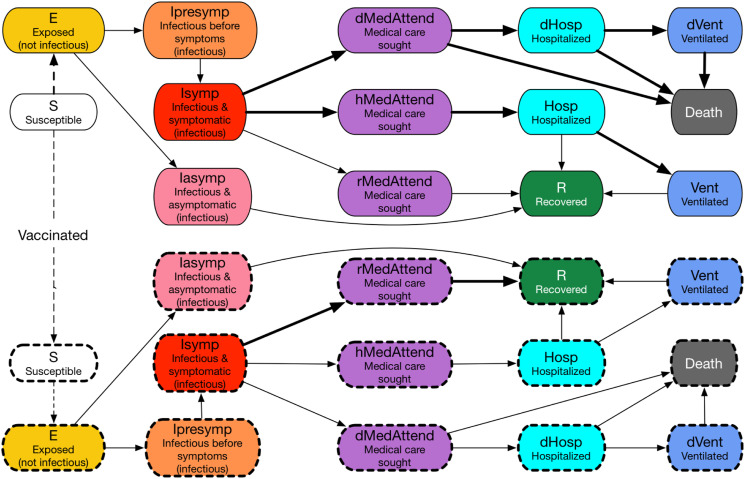
The COVID-19 disease model with both unvaccinated and vaccinated states. This disease progression model is represented as a probabilistic timed transition system (PTTS): the state transitions are probabilistic, and, in many cases, are timed, that is, transitions after a given time period. An individual starts from the upper state S (Susceptible). If an individual receives a vaccine, the individual enters a new susceptible state represented by a dotted box. The dashed lines represent state transitions triggered by either interactions with infectious individuals or vaccination. The solid lines represent probabilistic timed state transitions. The shapes with a solid border represent states of an unvaccinated individual; those with a dashed border represent states of a vaccinated individual. The thicker lines represent larger probabilities. Therefore, a vaccinated individual has a smaller probability of getting infected (protection against infection), and, even if infected, the individual has a smaller probability of being hospitalized, needing ventilation, or dying (protection against severe illness).

The within-host disease transmission model is shown in Figure 14. Transmission may occur when an individual in one of the states Susceptible or RX Failure comes in contact with one or more individuals in the states Presymptomatic, Symptomatic, or Asymptomatic. The individual transmissions are governed by the parameters in Table 5. Progression from one disease state to the next is governed by the parameters in Table 6.

Table 5.

Disease transmission parameters.

State	Attribute	Value
	Transmissibility	0.18
Presymptomatic	Infectivity	0.8
Symptomatic	Infectivity	1.0
Asymptomatic	Infectivity	1.0
Susceptible	Susceptibility	1.0
RX Failure	Susceptibility	1.0

Table 6.

Disease progression parameters as given by the CDC document (CDC-Planning-Parameters). One value per line applies to all age groups. Abbreviations: prob: probability, dt: dwell time, Attd: attended, Hosp: hospitalized, Vent: ventilated, (D): resulting in death, and (H): resulting in hospitalization.

		Age
Progression	Attribute	0–4	5–17	18–49	50–64	65+
Exposed - Asympt	prob	0.35
Exposed - Asympt	dt-mean	5
Exposed - Asympt	dt-std dev	1
Asympt - Recovered	prob	1
Asympt - Recovered	dt-mean	5
Asympt - Recovered	dt-std dev	1
Exposed - Presympt	prob	0.65
Exposed - Presympt	dt-fixed	3
Presympt - Sympt	prob	1
Presympt - Sympt	dt-fixed	2
Sympt - Attd	prob	0.9594	0.9894	0.9594	0.912	0.788
Sympt - Attd	dt-discrete	1:0.175, 2:0.175, 3:0.1, 4:0.1, 5:0.1, 6:0.1, 7:0.1, 8:0.05, 9:0.05, 10:0.05
Attd - Recovered	prob	1
Attd - Recovered	dt-mean	5
Attd - Recovered	dt-std dev	1
Sympt - Attd(D)	prob	0.0006	0.0006	0.0006	0.003	0.017
Sympt - Attd(D)	dt-fixed	2
Attd(D) - Hosp(D)	prob	0.95
Attd(D) - Hosp(D)	dt-fixed	2
Hosp(D) - Vent(D)	prob	0.06	0.06	0.06	0.15	0.225
Hosp(D) - Vent(D)	dt-fixed	2
Vent(D) - Death	prob	1
Vent(D) - Death	dt-fixed	4
Hosp(D) - Death	prob	0.94	0.94	0.94	0.85	0.775
Hosp(D) - Death	dt-fixed	6
Attd(D) - Death	prob	0.05
Attd(D) - Death	dt-fixed	8
Sympt - Attd(H)	prob	0.04	0.01	0.04	0.085	0.195
Sympt - Attd(H)	dt-fixed	1
Attd(H) - Hosp	prob	1
Attd(H) - Hosp	dt-mean	5	5	5	5.3	4.2
Attd(H) - Hosp	dt-std dev	4.6	4.6	4.6	5.2	5.2
Hosp - Recovered	prob	0.2
Hosp - Recovered	dt-mean	3.1	3.1	3.1	7.8	6.5
Hosp - Recovered	dt-std dev	3.7	3.7	3.7	6.3	4.9
Hosp - Vent	prob	0.06	0.06	0.06	0.15	0.225
Hosp - Vent	dt-mean	1
Hosp - Vent	dt-std dev	0.2
Vent - Recovered	prob	1
Vent - Recovered	dt-mean	2.1	2.1	2.1	6.8	5.5
Vent - Recovered	dt-std dev	3.7	3.7	3.7	6.3	4.9

B. Selected case studies and scenario projections

As discussed earlier in the paper, the integrated pipeline has been used for a number of case studies over the past year. The pipeline as presented here has been improved iteratively during this time period. Here we describe two case studies in some detail.

Case study 2: the role of vaccine allocation strategies

In this section, we study the role of vaccine distribution strategies in controlling the spread and negative effects of COVID-19 in the US.

In early 2021, the Pfizer and Moderna vaccines started becoming available for larger portions of the US population. However, due to production and logistical issues, not enough vaccines were available for everyone eligible. Thus, because of high demand and low supply, a key question at the time was: how should we fairly distribute vaccines across the US states?

During that time, we studied this issue and tried to find answers for the following questions: (i) What are the different “fair” allocation strategies for distributing vaccines to the different states? (ii) By how much do these vaccine distribution strategies reduce the impact of COVID-19 on the US population as a whole? (iii) What effect do these global vaccine distribution strategies have on the reduction of COVID-19 in the Commonwealth of Virginia (our institution’s home state)?

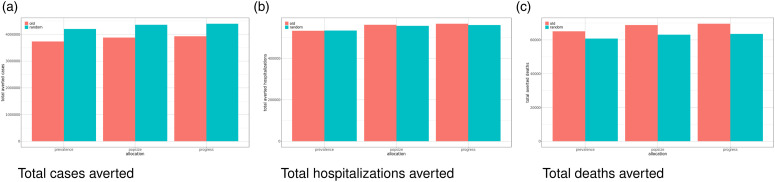
Scenarios. To answer these questions, we studied the following scenarios for different vaccine distribution strategies by using an agent-based simulation model. The experimental design consisted of two factors: (i) three interstate vaccine distribution strategies, and (ii) two intrastate vaccine distribution strategies. The interstate vaccine distribution strategies were: (a) vaccines are distributed to the US states in proportion to their population size (popsize) (b) vaccines are distributed to the US states in proportion to the prevalence of COVID-19 in the state (prevalence) and (c) vaccines are distributed to the US states in proportion to the progress of vaccination in the state (progress). The two intrastate vaccine distribution strategies were: (a) preference given to older individuals (old) and (b) available vaccines were distributed to eligible individuals uniformly at random. In addition, a baseline strategy was considered which involved letting the epidemic progress without any vaccination. Combining the above cases, we have seven scenarios (a 7-cell experiment).

Implementation. Our simulations used synthetic populations, with accompanying synthetic contact networks, for the 50 US states and Washington DC. The initial conditions of the simulation were calibrated such that they matched the COVID-19 conditions of each state as of early Feburary 2021. Each simulation was run for 300 days. Due to the stochastic nature of the simulations, we ran each simulation configuration 15 times to get a robust estimate of the metrics of interest.

The disease model used for the simulation was the best guess version of the “COVID-19 Pandemic Planning Scenarios” as prepared by the US Centers for Disease Control and Prevention (CDC) SARS-CoV-2 modeling team (CDC-MODEL). The above disease model is a Susceptible-Exposed-Infectious-Recovered (SEIR) model, where state transitions follow the parameters as defined in (CDC-MODEL). The model provides different transition probabilities for five different age groups: preschool (0–4 years), students (5–17), adults (18–49), older adults (50–64) and seniors (65+). The transition probabilities also change depending on whether a person is vaccinated or not.

Results. Figure 15(a) shows that the progress-based vaccine allocation strategy paired with random distribution (without preference), maximizes the total number of averted cases. However, in terms of the number of averted deaths, Figure 15(c) shows that the progress-based vaccine allocation strategy paired with the age-prioritized intrastate distribution strategy works the best. Finally, Figure 15(b) shows that, in terms of averted hospitalizations, both population-based allocation (popsize) and vaccination progress-based allocation (progress), when taken together with the age-based intrastate prioritization strategy, work the best among the choices.

Figure 15.

Total number of cases, hospitalizations, and deaths averted due to vaccinations over the entire US. Case study 3: the role of vaccine acceptance in controlling COVID-19 spread.

In this section, we study the role of vaccine hesitancy in controlling the spread of COVID-19 in the US using AI-driven agent-based models.

With the introduction of COVID-19 vaccines, the US has seen a significant decline in cases as an increasingly larger fraction of the population is vaccinated. When vaccine rollout initially began, the availability of vaccines was the biggest bottleneck. However, since mid-2021, the problem of vaccine allocation in the US has shifted from a supply-side problem to a demand-side problem due to vaccine hesitancy.

We are interested in the following questions: (i) Do differences in vaccine hesitancy across different states change the effectiveness of vaccinations in those states? (ii) By how much does vaccine hesitancy reduce the effectiveness of vaccinations? (iii) By how much would infections and deaths due to COVID-19 be reduced if the hesitancy levels could be reduced?

Scenarios. The experimental design consists of three factors: (i) two vaccine acceptance levels: survey-based acceptance rate and improved acceptance rate (improved by 10%); (ii) two vaccination demand schedules: accelerated (accel) and accelerated-decelerated (accel-decel); (iii) two prioritization schemes: no priority and age-based prioritization. Combining these three factors, we have eight cells, plus a cell (no-vax) where the NPIs are in place, but the vaccinations are not applied.

Implementation. To run this study, we used the same agent-based simulation model, with the same simulation initializations and NPIs, as in case study 2. But instead of a constant vaccination rate proportional to either state population size, disease prevalence, or vaccination progress, we took state-specific vaccine acceptance rates and implemented both an accelerated vaccination schedule where each week vaccinations increase and an accelerated-decelerated schedule where vaccinations first increase each week, then start to decrease, both schedules having cumulative vaccine uptake upper-bounded by vaccine acceptance level.

Figure 16.

Due to vaccine saturation, vaccination rate decreases after the initial acceleration. This leads to less averted infections (a) and less averted deaths (b), comparing with a constant acceleration of vaccination rate.

Figure 17.

If we can increase vaccine acceptance by 10%, we can reduce cases further in terms of (a) infection and (b) deaths.

Results. At the national level, the accelerated-decelerated vaccination demand due to vaccine hesitancy leads to more infections/deaths (fewer averted infections/deaths), compared to the accelerated vaccination schedule. This is shown in Figure 16. With an accelerated vaccination schedule, 2042 infections and 12 deaths can be averted per 100K people. At the national level, this results in a total reduction of 6.7 m infections and 39.4 K deaths. With an accelerated-decelerated vaccination demand schedule, the averted infections and deaths decrease to 1364 and 8.6, respectively, per 100K. At the national level, it reduces 4.5 m infections and 28.2 K deaths in total.

These numbers highlight the health and human costs of a slower vaccination schedule due to saturation in demand for vaccination and vaccine hesitancy. Although the same number of people are vaccinated at the end of both vaccination schedules, because vaccines are administered faster in one schedule than the other, the vaccines protect more people in the accelerated scenario through indirect protections, that is, more people avoid getting infected before getting vaccinated.

Suppose we can increase the vaccine acceptance rate by 10% in each state. Figure 17 shows that this can improve aversion of infections and deaths over the effect of vaccination at the current acceptance level. With an accelerated-decelerated vaccination schedule, 10% more vaccine acceptance can increase infection aversion from 1364 to 1445 and death aversion from 8.6 to 9.1 per 100K of the national population, corresponding to a total aversion of 4.7 m infections and 29.9 K deaths. Although a smaller effect compared to what an accelerated vaccination schedule can achieve, the improvement is still significant.

Additional References

CDC-MODEL (2020) Covid-19 pandemic planning scenarios. https://www.cdc.gov/coronavirus/2019-ncov/hcp/planning-scenarios.html. [Online, accessed 10 May 2021].

CDC-Planning-Parameters (2020) Planning parameters for COVID-19 outbreak scenarios. In: Circulated in COVID-19 Modeling working groups.

ORCID iDs

Parantapa Bhattacharya https://orcid.org/0000-0002-3626-9939

Srinivasan Venkatramanan https://orcid.org/0000-0002-0874-8692

Benjamin Hurt https://orcid.org/0000-0002-3803-2900

Andrew Warren https://orcid.org/0000-0003-2660-0103

Przemyslaw Porebski https://orcid.org/0000-0001-8012-5791

Madhav Marathe https://orcid.org/0000-0003-1653-0658