Abstract
We model the post-hexaploidy evolution of four genomes from the Solanaceae, a group of flowering plants comprising tomatoes, potatoes and their relatives. The hexaploidy that these genomes descend from occurred through two sequential allopolyploidy events and was marked by the unequal losses of duplicated genes from the different progenitor subgenomes. In contrast with the hexaploid Brassiceae (broccoli and its relatives), where the subgenome with the most surviving genes arrived last in the hexaploidy, among the Solanaceae the most preserved subgenome descends from one of the original two tetraploid progenitors. In fact, the last-arriving subgenome in these plants actually has the fewest surviving genes in the modern genomes. We explore whether the distribution of repetitive elements (REs) in these genomes can explain the biases in gene losses, but while the signals we find are broadly consistent with a role for high RE density in driving gene losses, the REs turn over so quickly that little signal of the RE condition at the time of paleopolyploidy is extant in the modern genomes.
Keywords: Solanaceae, polyploidy, biased fractionation, hexaploidy, repetitive elements
1. Introduction
(a) . Polyploidy and genome evolution
The existence of eukaryotes with more than two copies of the genome in their nuclei has long been known [1–4], and prescient suggestions as to the evolutionary importance of such polyploidy events were made throughout the twentieth century [4–6]. However, in an era before the availability of complete genomic sequences, our understanding of how genomes evolved after polyploidy was necessarily limited. For instance, population genetic arguments strongly suggested that the ‘fully duplicated’ state, where every ancestral gene was present in two copies, should be evolutionarily unstable [6–8]. But it was only with the cataloguing of the complete gene complement of a polyploid organism that this loss process could be directly measured [9]. Complete genome sequences have also dramatically expanded the timescale at which polyploidies can be detected, leading to the discovery or confirmation of numerous ancient polyploidy events among flowering plants, vertebrates and other animals [10].
Dense genome sampling from species of yeast with and without their ancient polyploidy allowed for the first careful studies of the timing and distribution of gene losses after polyploidy [11–14]. These analyses demonstrated that the two ‘subgenomes’ created by the yeast whole-genome duplication (WGD) had lost genes in roughly equal fractions. However, as other ancient polyploidy events were studied [15–18], it became evident that the yeast event was unusual in this respect. In fact, of the paleopolyploidies we have so far analysed with our tool the Polyploid Orthology Inference Tool (POInT) [19], only the yeast WGD shows such a balance: in every other case, one of the subgenomes is favoured and has lost many fewer genes than have the others. This imbalance in losses is termed biased fractionation [20].
A polyploid genome can form either through the merging of two genomes of the same species (autopolyploidy) or the merger through hybridization of genomes from distinct species (allopolyploidy) [2,3,21]. A pattern of biased fractionation between the resulting subgenomes is more explicable in the case of an allopolyploidy [18], since it is difficult to understand how an autopolyploidy, where the two subgenomes are identical, would generate such biases. However, allopolyploidy need not generate biases either, with the yeast WGD being an allopolyploidy without biased fractionation [22,23].
(b) . Hexaploidy, biased fractionation and the Solanaceae
One of the more interesting paleopolyploidy events in the flowering plants is that shared by tomatoes and their relatives in the family Solanaceae. Even prior to the publication of the first genomes from this family, authors studying genetic maps and expressed sequence tags had proposed the presence of a paleopolyploidy shared by tomatoes and potatoes [24–27]. The completion of the tomato genome made it clear that this event was in fact a hexaploidy [28]. Hexaploid genomes are interesting because there is no known mechanism for generating them in a single mutational step. As a result, they are presumed to form when a tetraploid intermediate undergoes a further polyploidy by hybridization with another diploid [15,29] to yield a triplicated state relative to the ancestor. There is hence, an order to the arrival of the subgenomes for hexaploids that is potentially inferable.
Hexaploid genomes also show biases in their gene losses. Our analysis of the Brassiceae hexaploidy confirmed that one of the three subgenomes retained many more homoeologous genes than did the other two, and we determined that this ‘least fractionated’ (LF) subgenome was the last arriving of the three present [30]. The ‘order of arrival’ effect, therefore, is a potential source of the biased fractionation in hexaploids and makes them a useful system for testing hypotheses about its origins. There are, in essence, three currently proposed drivers of biased fractionation, with the order of subgenome arrival being the first. The second is that a ‘bloom’ of transposable elements (TEs) from one of the subgenomes spread to the other subgenome(s) after the polyploidy, overwriting genes in those subgenomes [31]. The third hypothesis, which is very much the consensus at the moment [32], is that the ancestral subgenomes with high TE density prior to hybridization experienced a global repression of their gene expression after polyploidy and hence suffered more gene losses [32–34]. This idea is mechanistically plausible and consistent with other data. For instance, recent polyploidies show reduced expression from their less-favoured subgenomes, and genes of lower expression should be more prone to homoeologue loss over evolutionary time [34–38]. Since it is also known that the mechanisms by which the host genome silences TEs can reduce the expression of genes in the immediate neighbourhood of those TEs [39], a quite convincing model can be made whereby a higher TE load in a subgenome will drive its average expression level down and, as a longer term consequence, reduce the chances that its encoded genes survive. Interestingly, in many cases, the subgenome with fewest losses in extant polyploid genomes is indeed the one with the lowest TE density [34,35,37,38,40].
However, the current data are incomplete in a few respects. Both a recent transposon bloom and a high ancestral TE load could give rise to a high TE density in fractionated subgenomes. Moreover, TE element turnover is rapid in evolutionary terms [41], raising the question of how reflective of the ancestral condition the modern genomes are. In theory, a phylogenetically informed analysis of multiple genomes sharing a hexaploidy could disentangle these various possibilities.
Here, we use POInT to show that the Solanaceae hexaploidy differs from that in the Brassiceae in that the last-arriving subgenome is in fact the most fractionated; the subgenome with the most surviving genes was instead one of the two arriving in the initial tetraploidy event. We find that the data do not speak clearly as to the role of TE load in driving fractionation because little signal of the ancestral TE distribution survives into the modern genomes. However, to the extent that a pattern is discernible, it is consistent with ancient repetitive element (RE) density being inversely associated with the number of surviving genes from a subgenome.
2. Results
(a) . Reconstruction of triple-conserved synteny regions from the Solanaceae hexaploidy
Using our previously described approach [22,30], we inferred a set of triple-conserved synteny (TCS) blocks shared by Solanum lycopersicum (tomato), Solanum melongena (eggplant), Capsicum annuum (pepper) and Petunia axillaris. These blocks consist of 6919 ancestral ‘pillars’ triplicated through hexaploidy; they include 34 148 gene models from across the four genomes. This computation can be thought of as roughly analogous to the multiple alignment step of a phylogenetic analysis. The resulting data are then used as the basis for the POInT analyses that infer orthology between the chromosomal segments of the four extant genomes and make the assignments of genes into subgenomes (see below). Notably, only six of these pillars show the retention of all three gene copies in each of the four genomes, whereas our previous analysis of the Brassiceae hexaploidy found that 418 of 14 050 pillars were fully retained.
(b) . Modelling homoeologous gene loss after hexaploidy
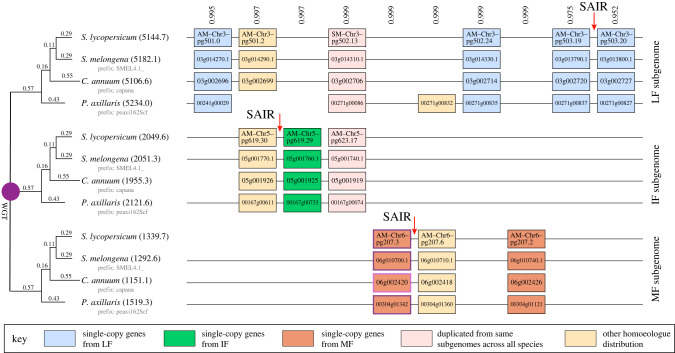
POInT models the loss of homoeologous genes after polyploidy along a phylogeny with a discrete-character maximum-likelihood model similar to that described by Lewis [42]. Because the orthology between the syntenic regions in each genome is not known a priori, POInT computes the likelihood of every possible orthology relationship (and thus subgenome assignment) at each pillar and then uses a hidden Markov model (HMM) to condition the orthology inferences at each pillar on those to the left and right [19]. Because for each genome there are 3!=6 possible subgenome arrangements, there are 6n = 1296 possible orthology relationships at each pillar for these n = 4 genomes. Figure 1 shows POInT's regional orthology inferences, including the estimated confidence in those orthology relationships and subgenome assignments relative to the other 1296-1 relationships. All of these inferences are also available through POInTbrowse (wgd.statgen.ncsu.edu).
Figure 1.
Subgenome assignment and inference of gene loss after the shared hexaploid in four Solanaceae species, showing our inferences of an LF subgenome and two more fractionated ones (IF and MF). The tree at the left illustrates POInT's estimates of the homoeologue loss rates at each stage of the evolution of these four hexaploid genomes. POInT's estimated branch length (αt) for each branch is shown above it. This length is used by the model to compute the probability of a gene that is triplicated at the start of the branch experiencing one or more gene losses along that branch. In parentheses, after each taxa are the extant number of genes that POInT estimates survive from that subgenome in that particular modern genome. Shown at the right is an example window of 16 loci produced by whole genome triplication (WGT). Each column (or pillar) corresponds to an ancestral locus triplicated through the hexaploidy, with the boxes representing extant genes. Pairs of genes are connected by lines if they are genomic neighbours in the modern genome. The numbers above each pillar are the posterior probabilities assigned to these combinations of orthology relationships related to the other 64-1 possible orthology states. Three subgenome-assigned intergenic regions (SAIRs) are illustrated (see Methods). (Online version in colour.)
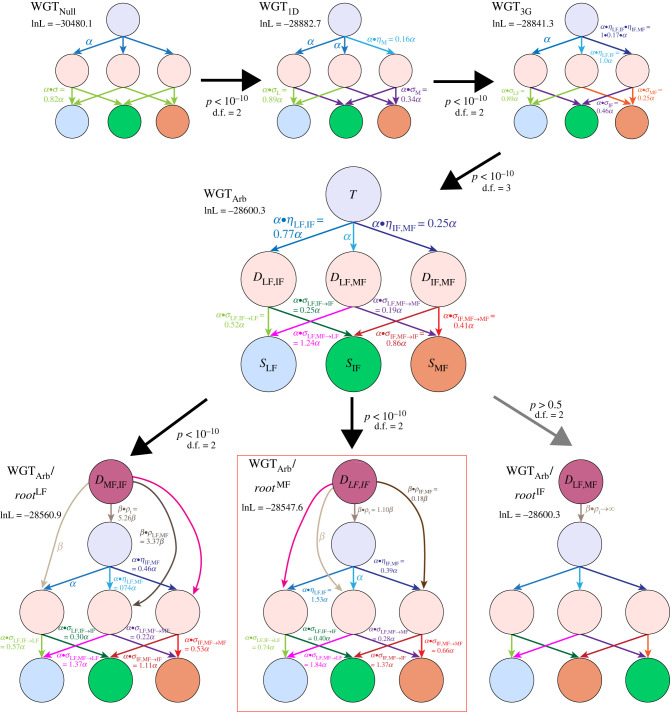
The gene loss models can vary in their complexity, with the simplest one having the rate of loss from the triplicated state be the same for all three subgenomes, meaning transitions from the triplicated state T to the three duplicated states (DX,Y) occur at the same rate (figure 2). Losses from the duplicated states to the single-copy ones (Sx in figure 2) are similarly balanced. We refer to this model as WGTNull. Notice that with this model, we cannot assign genes to subgenomes, as all three subgenomes are equivalent in their gene loss rates and statistically indistinguishable.
Figure 2.
Nested models of hexaploid evolution, showing the loss of duplicated material from the triplicated state (T) first to duplicated states (DX,Y, where X and Y are the subgenomes where the ancestral gene survives) and then to single-copy states (SX, where X is the subgenome preserving the ancestral gene). Arrows depict possible loss events, with the parameters giving the relative rate of loss from that state. All rates are relative to the base loss rate α. Using the pillars of TCS (figure 1), we model the losses in those pillars with a series of increasingly complex models of gene loss. WGTNull treats all three of the subgenomes as equivalent: allowing one of the three subgenomes to experience fewer losses (WGT1D) significantly improves the fit to the data (p < 10−10; likelihood ratio test with two d.f.). Similarly, using the WGT3G model to distinguish the other two subgenomes, those of intermediate and most fractionation also improves the fit (p < 10−10; likelihood ratio test with two d.f.). Because the parameters of this WGT3G model are slightly odd (see Results), we also fit the WGTArb model, which allows every possible transition between states to occur at an independent rate. This model is an improvement over WGT3G (p < 10−10; likelihood ratio test with three d.f.). Finally, we tested different models of hexaploid formation, positing models with each subgenome being the ‘last arriving’. In such models, the other two subgenomes formed the initial tetraploid and are shown as duplicated states at the top of each diagram. Hence, if LF is last arriving, all pillars start in state DIF,MF, corresponding to IF and MF having formed in the initial tetraploid. Of these three models, that with IF arriving last collapses into the WGTArb model. Both the LF and MF model improve the fit (p < 10−10; likelihood ratio test with two d.f. in both cases). However, it is the MF late arrival model that has the highest ln-likelihood and that is consistent with a model where the WGTArb model is allowed to have differing parameters on the root branch compared to the others (Results, electronic supplementary material, figure S2). (Online version in colour.)
We can add complexity to the model by allowing one of the three subgenomes (LF) to experience fewer losses than do the other two, creating a model we refer to as WGT1D. We find that the WGT1D model fits our pillar data significantly better than does WGTNull (p < 10−10; figure 2), showing that at least one of the three subgenomes is marked by a lower rate of losses after polyploidy. (Recall that POInT infers the identity of the subgenomes from the pillar data via maximum likelihood.) We next proposed a model allowing the two remaining subgenomes to have differing loss rates as well, namely the WGT3G model (figure 2). Again, this model fits our data significantly better than does WGT1D (p < 10−10; figure 2), showing that all three subgenomes have differing loss rates. In contrast with our prior nomenclature of MF1 and MF2 for the two more fractionated subgenomes, here we will use the abbreviation ‘IF’ for the subgenome of intermediate fractionation and ‘MF’ for the most fractionated subgenome (figure 1).
The parameter values we infer when fitting the WGT3G model to our data are somewhat difficult to interpret, with the formation of duplicates from LF and either IF or MF (DLF,IF and DLF,MF, respectively) apparently occurring at equal rates. By contrast, in the Brassiceae hexaploidy, IF was favoured over MF both in the formation of duplicated and single-copy genes (electronic supplementary material, figure S1). We sought to resolve this confusion with a new ‘arbitrary’ model of hexaploid evolution where each of the nine possible transitions in the model could occur at an independent rate (WGTArb, figure 2). This model fits our data better than did WGT3G (p < 10−10; figure 2) and more clearly distinguishes the IF and MF subgenomes.
Using this WGTArb model, we can therefore infer the number of genes from each subgenome surviving in the modern genomes and probabilistically assign individual genes to those subgenomes based on the model's confidence in the regional subgenome assignments (figure 1). Across the four genomes, we infer the number of surviving genes from the MF subgenome to be less than a third of the number surviving from LF, with IF falling in between, with slightly fewer than twice as many surviving genes as MF (figure 1).
(c) . Order of subgenome arrival
The models employed so far do not directly address the question of the order of arrival of the subgenomes. To explore that question, we used our prior approach [30] of comparing three ‘arrival’ models, each proposing a different last-arriving subgenome. The model proposing that IF arrived last collapses back into the WGTArb model and can be dismissed (p > 0.5). However, both the model that proposes that MF was last arriving and the one proposing that LF was last arriving fit the data better than does WGTArb (p < 10−10 in both cases; figure 2). Between these two models, which are of equivalent complexity, the model having MF arrive last has the higher likelihood (figure 2) and can therefore be preferred over the model with LF arriving last. For completeness, we applied these same models to our pillar data from the Brassiceae hexaploidy to see if our conclusion that LF was the last-arriving subgenome for that triplication changed with the more complex models used here. However, using the WGTArb model coupled to the three arrival models still supports LF being the last-arriving subgenome for the Brassiceae hexaploidy (electronic supplementary material, figure S1).
Given that both the models with LF and MF being the last-arriving subgenome fit the pillar data significantly better than does WGTArb, one might be concerned that our data are not sufficient to distinguish between these two arrival models. However, we can also fit a version of the WGTArb model that allows the root branch to have different values of the model parameters than do the remaining branches. The results of using this model are shown in electronic supplementary material, figure S2. Were the MF subgenome the last arriving, we would expect that transitions from the triplicated state to states preserving this subgenome would be more favoured on the root branch than on the later ones, because MF was present for less of the time represented by that root branch and hence, would have had less time to experience a gene loss than would LF or IF. This pattern is indeed what we observe, with the model favouring transitions from T to DLF,MF over those to DLF,IF on the root branch, but with this preference reversing on the later branches (electronic supplementary material, figure S2). To explain this pattern in a scenario where LF is last arriving, we would be forced to posit that MF was favoured over IF during the tetraploid phase but that this preference switched after the arrival of LF. While not impossible, this explanation is less parsimonious than MF being generally least favoured in fractionation terms over the entire history of these subgenomes.
(d) . Conserved intergenic regions show higher densities of ancestral repetitive elements in the subgenomes of intermediate and most fractionation
To explore the distribution of REs in the different subgenomes, we used POInT's orthology inferences to identify subgenome-assigned intergenic regions (SAIRs). These regions are identified by first finding a pair of neighbouring pillars in the POInT data where one of the three subgenomes has genes present in all four species for both pillars and where each of those pairs of genes from each of four extant genomes are syntenic neighbours (illustrated in figure 1). We then filter these pillar pairs on orthology confidence, retaining only those with confidence greater than or equal to 95%. The intergenic regions between these pairs of high-confidence pillars are then the SAIRs: in other words, orthologous intergenic regions where we know their subgenome of origin with high confidence in all four species.
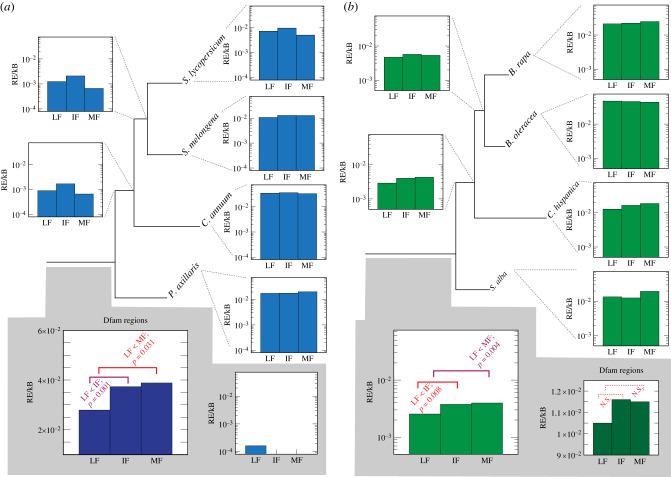
We first used BLASTN [43] to search these regions against the set of green plant REs from RepBase v. 27 [44]. As figure 3 shows, there is a good deal of variability in the RE distribution between the individual genomes, with no clear pattern as to which subgenome has the highest RE density. However, it is also clear that nearly all of the REs in question are recent: there is often an order of magnitude difference in the density of REs found in an individual genome compared to the density of RE insertions that are shared in orthologous positions across the genomes studied and hence assumed to be ancestral (Methods).
Figure 3.
Independent and shared RE density in SAIRs. For each extant genome at the phylogeny tips (right of the trees), we show the repeat density (RE/kB) for each subgenome, inferred with BLASTN and RepBase (Methods). At the phylogeny roots (grey shaded regions) and internal branches (left of the tree), we show the density of repeats that are found in orthologous SAIRs for the species in that clade (e.g. for the root branch, all four species in the tree). Note the log-scale on the y-axis of all diagrams except that for Dfam, reporting RE hits per kilobase (kB) of SAIR sequence. For the Brassiceae, there are significantly fewer such insertions shared between all species in the LF genome (see Methods), but this difference is not seen for the Solanaceae genomes. For the Solanaceae, LF is significantly deficient in shared REs when the larger Dfam set of elements is used as a query, but the differences, while in the same direction for the Brassiceae, are non-significant (Methods). (Online version in colour.)
In fact, for the SAIRs shared by the four Solanaceae genomes, only nine RE hits are found to be phylogenetically conserved in orthologous positions across the four genomes, and all nine of these are found in the LF subgenome. This observation is not in itself surprising, because LF has 1733 SAIRs, compared to 329 and 110 for IF and MF, respectively. For the four Brassiceae genomes, 147 conserved RE hits are found, and the LF subgenome has significantly lower RE density than either IF or MF (figure 3; p = 0.008 and 0.004, respectively; see Methods). However, closer analysis showed that all but two of the conserved elements identified were actually tRNA genes. When we repeated our search of the Brassiceae genomes with a tRNA database [45], we found that indeed LF had lower tRNA density in conserved positions than did IF or MF (p = 0.002 and p < 0.001, respectively). LF was also the subgenome with the lowest tRNA density in the individual Brassiceae genomes. However, the Solanaceae genomes again only had seven tRNA genes, all from LF, conserved across the SAIRs from the four genomes, and tRNAs were not universally less frequent in LF across these genomes (data not shown).
Because we identified so few RE positions in the Solanaceae genomes using the RepBase dataset, we broadened our search by scanning against all known REs in the Dfam database using nhmmer (see Methods; [46]). When considering the RE regions identified with nhmmer in the tomato genome that showed strongly conserved local alignments to the other three genomes (Methods), we did find that the LF subgenome showed lower RE density than did IF or MF (figure 3; p = 0.001 and 0.0318, respectively). When we conducted the corresponding Dfam search in the Brassiceae, identifying Dfam hits in Brassica rapa and aligning those regions to the other three genomes, LF showed the numerically lowest RE density, but there was no statistical difference between the subgenomes in RE density (figure 3; p > 0.05).
3. Discussion
Having two groups of taxa that have independently acquired a hexaploid state illustrates both commonalities and some surprising differences in the patterns of evolution after those events. Most strikingly, unlike in the Brassiceae [15], the order of subgenome arrival does not appear to have greatly influenced which subgenome was favoured for homoeologue retention among the polyploid Solanaceae. Instead, the current LF subgenome was one of the two founding subgenomes, with the MF subgenome arriving later and experiencing a very rapid loss of its genes, such that today it has the fewest surviving genes in each of the extant genomes (figure 1). Of course, the existence of (single formation step) tetraploidies possessing biased fractionation [17] adequately refutes order-of-arrival as the sole source of biased fractionation. But it is still striking that, even with its later arrival, MF was so disfavoured as to be the subgenome with fewest survivors today.
If arrival order is not driving fractionation biases in the Solanaceae, what is? TEs or repetitive sequences more generally are still strong candidates [31–34]. However, it may be worth taking a slightly wider perspective. The gene expression biases in new allopolyploids [34–38] provide a selective environment favouring the loss of the more lowly expressed homoeologous copies. Any process producing such expression biases might, therefore, in the longer term, give rise to subgenomes with fractionation biases. While the repression of repetitive sequences could certainly drive expression biases [39], other differences in the genomic expression landscape between the progenitor species could as well. Bottani et al. [38] have pointed out that genomes of differing sizes will experience differing levels of off-target transcription factor binding. As a result, in a larger genome, either the local affinity of a transcription factor for its regulatory motif or the expression of that transcription factor would need to be higher than what is seen in the smaller genome in order to achieve equivalent expression of the target gene between the two genomes.
Hence, we should probably view the RE repression hypothesis as one of a number of potential differences between progenitor genomes that drive biases first in expression and eventually in losses. From that perspective, the major conclusion of our analysis of REs is in fact a negative one: we cannot easily infer the ancestral RE content of the subgenomes from the REs seen in the modern genomes. This conclusion is in accord with our prior finding of little phylogenetic signal in the RE distributions across many species in the Brassiceae [41]. On this basis, we would argue that the RE density of modern subgenomes is probably irrelevant to the question of whether RE density drove biased fractionation in paleopolyploidies.
We nonetheless do find some evidence of increased ancestral RE density in the IF and MF subgenomes for both the Solanaceae and Brassiceae hexaploidies (figure 3), supporting the RE hypothesis for bias formation. Unfortunately, it is difficult to know how much faith to place in these results. The results in the Brassiceae are entirely driven by the density of tRNA genes and, while this is not true of the Solanaceae results, the Dfam database used to find the conserved RE regions is strongly biased to animals [44], so it is somewhat surprising that more hits were found using it that with the green plant REs from Repbase [47].
The bias in tRNA distribution between subgenomes may also support the need for a broader study of factors affecting expression bias in hybrids. In this view, TEs, base composition, epigenetics and gene density will all alter chromatin state and hence, gene expression [31,38,48]. Understanding these effects should illuminate the behaviour of hybrids more generally, including phenomena such as hybrid vigour and heterosis [49,50]. As a result, studying the repressive effects of RE density in recent polyploids remains a very worthwhile endeavour, especially if such studies are coupled to a broader survey of chromatin dynamics both in the allopolyploid and in its progenitors.
4. Methods
(a) . Genomes, homology search and synteny block inference
We analysed four genomes sharing the Solanaceae hexaploidy: Solanum lycopersicum (tomato; [28]), Solanum melongena (eggplant; [51]), Capsicum annuum (hot pepper; [52]) and Petunia axillaris [53]. The genome of Coffea canephora [54] was used as a nonhexaploid reference. The genomes of S. lycopersicum, P. axillaris and C. canephora were obtained from CoGe [55] with accession IDs 57947, 54659 and 54651, respectively. Genome data for S. melongena and C. annuum were obtained from the Sol Genomes Network [56].
For each of the four hexaploidy genomes, we followed a three-step process for identifying the TCS blocks produced by the hexaploidy. First, we conducted a homology search against C. canephora using GenomeHistory v 2.0 [57]. GenomeHistory uses BLASTP [43] to search for pairs of homologous protein sequences and then aligns them [58] and computes the synonymous and non-synonymous divergence of their encoding genes using the likelihood approach of Muse and Gaut/Goldman and Yang [59,60]. We required homologous pairs of proteins between each hexaploid genome and C. canephora to show a maximum BLAST E-value of 10−10 and 70% sequence identity over 80% or more of their length. Any genes whose proteins showed no homologue in the other genome at these stringencies were searched again using GenomeHistory with an increased E-value cutoff of 10−7 and 50% identity.
Second, using the pairs of homologous genes identified as just described, we sought to identify the TCS blocks in each of the hexaploid genomes. We have previously described this inference process [22,30]: briefly, for a single gene in C. canephora, up to three of the homologous genes in a hexaploid genome are allowed to be the homoeologues of that gene triplicated in the hexaploidy. Using simulated annealing [61], we then seek a combination of a gene order and homoeologous gene assignments that maximizes the number of genes that are each other's genomic neighbours.
Third and finally, we merged these TCS blocks from each genome into a global set of ‘pillars’ consisting of between 1 and 3 genes from each hexaploid genome using the C. canephora genes as a reference, resulting in 6919 pillars where every gene in that set had at least one synteny relationship with another gene in the set. We then further optimized the pillar order by performing rearrangements on these inferred blocks. This approach approximates the ancestral order that existed before the whole-genome triplication (WGT) and maximizes the number of genes that are neighbours, yielding a total of 5605 synteny breaks across the four genomes.
(b) . Assessing alternative phylogenetic relationships with POInT
Assuming that S. lycopersicum and S. melongena are sister taxa, we tested the remaining three possible rooted phylogenetic relationships between these four taxa with the WGTArb model of homoeologue loss: the topology shown in figure 1 has higher log-likelihood than either one placing P. axillaris as sister to the Solanum species or the one making C. annuum and P. axillaris sister to each other (−28 600.3 versus −28 793.9 and −28 814.6, respectively).
(c) . Testing models of post-polyploidy homoeologue losses with POInT
We next fit a series of nested models of homoeolog loss to the pillar data using POInT (figure 2, [62]). Under the simplest of these models (WGTNull), we allowed a uniform rate of homoeologue loss from the triplicated state T for each of the three subgenomes, with a potentially different rate of loss σ from the three resulting duplicated states (DX,Y; figure 2). This model corresponds to the case where the three genomes that formed the hexaploid merged instantaneously and without bias. We then sequentially fit models that further differentiated among the subgenomes, first allowing one to have more surviving homoeologues than the other two (WGT1D), then allowing all three subgenomes to differ in their loss propensities (WGT3G) and finally, allowing the loss rates from each of the three duplicated states to differ (WGTArb). For comparison, we also fit each of these models to the Brassiceae hexaploidy we had previously analysed [30].
(d) . Fitting models of subgenome arrival order
Because hexaploidies are not unitary events, it would be desirable to understand which two of the three extant subgenomes merged first. We have previously described how POInT can model hexaploid formation by allowing each of the three subgenomes to be the ‘last arriving’ [30], as depicted in figure 2. To assess the quality of these models, we also fit a separate version of the WGTArb model that allowed the root branch of the polyploidy to show different loss parameters than the other branches (electronic supplementary material, figure S2) [22].
(e) . Identifying orthologous intergenic regions from different subgenomes
We identified pairs of nearby pillars in our ancestral order for which we had both high (greater than or equal to 95%) confidence in the subgenome assignments and for which all four genomes had genes present for a given subgenome in each pillar that were each other's syntenic neighbours. Such conserved SAIRs are those for which we have very high confidence in both the orthology of the regions and in their subgenome of origin (figure 1).
(f) . Identifying transposable elements in the conserved intergenic regions
We used two datasets to identify REs in these SAIR intergenic regions: (i) the green plant repeat set from RepBase v. 27 [44] and (ii) Dfam v 3.5 [47]. We identified matches between the Repbase repeats and the SAIRs of all Solanaceae and Brassiceae genomes using BLASTN [43] with an E-value cutoff of E ≤ 10−5. We used a parsimony approach to identify REs putatively conserved since the common ancestor of the four Solanaceae genomes studied and similarly for the four Brassiceae genomes. Specifically, we considered an RE as ancestral if a hit to that RE was present in all four orthologous intergenic regions at the specified stringency.
To assess whether the differences in RE abundance between the subgenomes were statistically significant, we used a randomization approach. Taking the set of RE hits to SAIRs in an extant genome, we randomized the order of those hits and then placed them at random in the SAIRs. To make such random placements, we determined the total number of positions t in the SAIRs available for insertion by subtracting from each region the length of the RE hit and omitting any SAIRs shorter than the RE hit. We then drew a uniform random number between 0 and t to assign placement. For the next RE hit, we omitted all previously randomly assigned regions from the computation of t, meaning that two randomly assigned hits could never overlap. We computed the density of REs in each subgenome as the number of hits in that subgenome over the total length of all SAIRs from that subgenome. The difference in the RE densities for the randomized hits was compared to that seen for the real genomes. In the case of the ancestral REs, we used a similar approach, using one of the four genomes (S. lycopersicum or B. rapa) as a base genome for performing the randomizations.
Because almost all of the conserved REs found among the Brassiceae genomes were actually tRNA genes, we similarly searched the SAIRs against a tRNA database [45] using the same approach to search and randomization.
The Dfam database is much larger than RepBase and allows for more precise RE identification using hidden Markov models. Hence, we took a different approach for identifying REs from Dfam. First, we used nhmmer from the hmmer 3.3.2 package [46] to search the intergenic regions of S. lycopersicum and B. rapa against the full Dfam HMM collection with an E-value cutoff of less than or equal to 10−5. This search is computationally costly and will yield regions where multiple RE HMM models may intersect or overlap. Thus, instead of repeating this search in other genomes, we first assembled RE ‘regions’ by merging any HMM hits to SAIRs that overlapped by at least one DNA base. We next used these RE regions from S. lycopersicum or B. rapa as queries for local alignment [63] against the orthologous SAIRs from the other three genomes. Our alignment scoring function was matches: +4, mismatches: −5, gap opening penalty: −8, gap extension penalty: −4. Any RE region with a local alignment of at least 80 bases and an alignment score of 200 or more in each of the other three genomes was considered to be an ancestral RE region. Then, we again used the S. lycopersicum and B. rapa SAIRs as references and applied the same randomization approach as above to assess the significance of any differences in the RE density between the subgenomes.
Acknowledgements
We would like to thank M. Mabry and J.C. Pires for helpful comments and C. Smith for computational assistance.
Data accessibility
All of the data used in this manuscript were previously published and are freely accessible via the accession numbers provided in the text. The POInT software package is available from GitHub: https://github.com/gconant0/POInT/releases/tag/v1.55. All of the underlying inferences, models, phylogenetic trees and gene order sets are freely available from the POInTbrowse web portal: wgd.statgen.ncsu.edu.
Data are also provided in the electronic supplementary material [64].
Authors' contributions
L.M.: investigation, visualization, writing—original draft and writing—review and editing; A.B.: methodology, resources and writing—review and editing; G.C.: conceptualization, investigation, methodology, software, supervision, visualization, writing—original draft and writing—review and editing.
All authors gave final approval for publication and agreed to be held accountable for the work performed therein.
Conflict of interest declaration
We declare we have no competing interests.
Funding
We received no funding for this study.
References
- 1.Simunek M, Hoßfeld U, Wissemann V. 2011. ‘Rediscovery' revised–the cooperation of Erich and Armin von Tschermak-Seysenegg in the context of the ‘rediscovery' of Mendel's laws in 1899–1901. Plant Biol. 13, 835-841. ( 10.1111/j.1438-8677.2011.00491.x) [DOI] [PubMed] [Google Scholar]
- 2.Clausen R, Goodspeed T. 1925. Interspecific hybridization in Nicotiana. II. A tetraploid glutinosa-tabacum hybrid, an experimental verification of Winge's hypothesis. Genetics 10, 278. ( 10.1093/genetics/10.3.278) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kuwada Y. 1911. Maiosis in the pollen mother cells of Zea Mays L.(With Plate V.). 植物学雑誌 (The Botanical Magazine) 25, 163-181. [Google Scholar]
- 4.Taylor JS, Raes J. 2004. Duplication and divergence: the evolution of new genes and old ideas. Annu. Rev. Genet. 38, 615-643. ( 10.1146/annurev.genet.38.072902.092831) [DOI] [PubMed] [Google Scholar]
- 5.Ohno S. 1970. Evolution by gene duplication. 160. New York, NY: Springer. [Google Scholar]
- 6.Haldane JBS. 1933. The part played by recurrent mutation in evolution. Am. Nat. 67, 5-9. ( 10.1086/280465) [DOI] [Google Scholar]
- 7.Li WH. 1980. Rate of gene silencing at duplicate loci: a theoretical study and interpretation of data from tetraploid fish. Genetics 95, 237-258. ( 10.1093/genetics/95.1.237) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nei M, Roychoudhury AK. 1973. Probability of fixation of nonfunctional genes at duplicate loci. Am. Nat. 107, 362-372. ( 10.1086/282840) [DOI] [Google Scholar]
- 9.Wolfe KH, Shields DC. 1997. Molecular evidence for an ancient duplication of the entire yeast genome. Nature 387, 708-713. ( 10.1038/42711) [DOI] [PubMed] [Google Scholar]
- 10.Van de Peer Y, Mizrachi E, Marchal K. 2017. The evolutionary significance of polyploidy. Nat. Rev. Genet. 18, 411-424. ( 10.1038/nrg.2017.26) [DOI] [PubMed] [Google Scholar]
- 11.Kellis M, Birren BW, Lander ES. 2004. Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisiae. Nature 428, 617-624. ( 10.1038/nature02424) [DOI] [PubMed] [Google Scholar]
- 12.Dietrich FS, et al. 2004. The Ashbya gossypii genome as a tool for mapping the ancient Saccharomyces cerevisiae genome. Science 304, 304-307. ( 10.1126/science.1095781) [DOI] [PubMed] [Google Scholar]
- 13.Scannell DR, Byrne KP, Gordon JL, Wong S, Wolfe KH. 2006. Multiple rounds of speciation associated with reciprocal gene loss in polyploid yeasts. Nature 440, 341-345. ( 10.1038/nature04562) [DOI] [PubMed] [Google Scholar]
- 14.Byrne KP, Wolfe KH. 2005. The Yeast Gene Order Browser: combining curated homology and syntenic context reveals gene fate in polyploid species. Genome Res. 15, 1456-1461. ( 10.1101/gr.3672305) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tang H, Woodhouse MR, Cheng F, Schnable JC, Pedersen BS, Conant G, Wang X, Freeling M, Pires JC. 2012. Altered patterns of fractionation and exon deletions in Brassica rapa support a two-step model of paleohexaploidy. Genetics 190, 1563-1574. ( 10.1534/genetics.111.137349) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Woodhouse MR, Schnable JC, Pedersen BS, Lyons E, Lisch D, Subramaniam S, Freeling M. 2010. Following tetraploidy in maize, a short deletion mechanism removed genes preferentially from one of the two homeologs. PLoS Biol. 8, e1000409. ( 10.1371/journal.pbio.1000409) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Thomas BC, Pedersen B, Freeling M. 2006. Following tetraploidy in an Arabidopsis ancestor, genes were removed preferentially from one homeolog leaving clusters enriched in dose-sensitive genes. Genome Res. 16, 934-946. ( 10.1101/gr.4708406) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Garsmeur O, Schnable JC, Almeida A, Jourda C, D'Hont A, Freeling M. 2014. Two evolutionarily distinct classes of paleopolyploidy. Mol. Biol. Evol. 31, 448-454. ( 10.1093/molbev/mst230) [DOI] [PubMed] [Google Scholar]
- 19.Hao Y, Fleming J, Petterson J, Lyons E, Edger PP, Pires JC, Thorne JL, Conant GC. 2022. Convergent evolution of polyploid genomes from across the eukaryotic tree of life. G3 (Bethesda) 12, jkac094. ( 10.1093/g3journal/jkac094) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Freeling M. 2009. Bias in plant gene content following different sorts of duplication: tandem, whole-genome, segmental, or by transposition. Annu. Rev. Plant Biol. 60, 433-453. ( 10.1146/annurev.arplant.043008.092122) [DOI] [PubMed] [Google Scholar]
- 21.Stebbins GL Jr. 1947. Types of polyploids: their classification and significance. In Advances in Genetics (ed. M Demerec), pp. 403-429, Amsterdam, The Netherlands: Elsevier. [DOI] [PubMed] [Google Scholar]
- 22.Emery M, et al. 2018. Preferential retention of genes from one parental genome after polyploidy illustrates the nature and scope of the genomic conflicts induced by hybridization. PLoS Genet. 14, e1007267em. ( 10.1371/journal.pgen.1007267) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marcet-Houben M, Gabaldon T. 2015. Beyond the whole-genome duplication: phylogenetic evidence for an ancient interspecies hybridization in the baker's yeast lineage. PLoS Biol. 13, e1002220. ( 10.1371/journal.pbio.1002220) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gebhardt C, Walkemeier B, Henselewski H, Barakat A, Delseny M, Stüber K. 2003. Comparative mapping between potato (Solanum tuberosum) and Arabidopsis thaliana reveals structurally conserved domains and ancient duplications in the potato genome. Plant J. 34, 529-541. ( 10.1046/j.1365-313X.2003.01747.x) [DOI] [PubMed] [Google Scholar]
- 25.Schlueter JA, Dixon P, Granger C, Grant D, Clark L, Doyle JJ, Shoemaker RC. 2004. Mining EST databases to resolve evolutionary events in major crop species. Genome 47, 868-876. ( 10.1139/g04-047) [DOI] [PubMed] [Google Scholar]
- 26.Blanc G, Wolfe KH. 2004. Widespread paleopolyploidy in model plant species inferred from age distributions of duplicate genes. Plant Cell 16, 1679-1691. ( 10.1105/tpc.021410) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cui L, et al. 2006. Widespread genome duplications throughout the history of flowering plants. Genome Res. 16, 738-749. ( 10.1101/gr.4825606) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Consortium TG. 2012. The tomato genome sequence provides insights into fleshy fruit evolution. Nature 485, 635. ( 10.1038/nature11119) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Cheng F, Wu J, Fang L, Sun S, Liu B, Lin K, Bonnema G, Wang X. 2012. Biased gene fractionation and dominant gene expression among the subgenomes of Brassica rapa. PLoS ONE 7, e36442. ( 10.1371/journal.pone.0036442) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hao Y, et al. 2021. The contributions of the allopolyploid parents of the mesopolyploid Brassiceae are evolutionarily distinct but functionally compatible. Genome Res. 31, 799-810. ( 10.1101/gr.270033.120) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wendel JF, Lisch D, Hu G, Mason AS. 2018. The long and short of doubling down: polyploidy, epigenetics, and the temporal dynamics of genome fractionation. Curr. Opin. Genet. Dev. 49, 1-7. ( 10.1016/j.gde.2018.01.004) [DOI] [PubMed] [Google Scholar]
- 32.Alger EI, Edger PP. 2020. One subgenome to rule them all: underlying mechanisms of subgenome dominance. Curr. Opin. Plant Biol. 54, 108-113. ( 10.1016/j.pbi.2020.03.004) [DOI] [PubMed] [Google Scholar]
- 33.Woodhouse MR, Cheng F, Pires JC, Lisch D, Freeling M, Wang X. 2014. Origin, inheritance, and gene regulatory consequences of genome dominance in polyploids. Proc. Natl Acad. Sci. USA 111, 5283-5288. ( 10.1073/pnas.1402475111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Freeling M, Woodhouse MR, Subramaniam S, Turco G, Lisch D, Schnable JC. 2012. Fractionation mutagenesis and similar consequences of mechanisms removing dispensable or less-expressed DNA in plants. Curr. Opin. Plant Biol. 15, 131-139. ( 10.1016/j.pbi.2012.01.015) [DOI] [PubMed] [Google Scholar]
- 35.Edger PP, et al. 2017. Subgenome dominance in an interspecific hybrid, synthetic allopolyploid, and a 140-year-old naturally established neo-allopolyploid monkeyflower. Plant Cell 29, 2150-2167. ( 10.1105/tpc.17.00010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Adams KL, Cronn R, Percifield R, Wendel JF. 2003. Genes duplicated by polyploidy show unequal contributions to the transcriptome and organ-specific reciprocal silencing. Proc. Natl Acad. Sci. USA 100, 4649-4654. ( 10.1073/pnas.0630618100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cheng F, Sun C, Wu J, Schnable J, Woodhouse MR, Liang J, Cai C, Freeling M, Wang X. 2016. Epigenetic regulation of subgenome dominance following whole genome triplication in Brassica rapa. New Phytol. 211, 288-299. ( 10.1111/nph.13884) [DOI] [PubMed] [Google Scholar]
- 38.Bottani S, Zabet NR, Wendel JF, Veitia RA. 2018. Gene expression dominance in allopolyploids: hypotheses and models. Trends Plant Sci. 23, 393-402. ( 10.1016/j.tplants.2018.01.002) [DOI] [PubMed] [Google Scholar]
- 39.Hollister JD, Gaut BS. 2009. Epigenetic silencing of transposable elements: a trade-off between reduced transposition and deleterious effects on neighboring gene expression. Genome Res. 19, 1419-1428. ( 10.1101/gr.091678.109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Edger PP, et al. 2019. Origin and evolution of the octoploid strawberry genome. Nat. Genet. 51, 541-547. ( 10.1038/s41588-019-0356-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Beric A, Mabry ME, Harkess AE, Brose J, Schranz ME, Conant GC, Edger PP, Meyers BC, Pires JC. 2021. Comparative phylogenetics of repetitive elements in a diverse order of flowering plants (Brassicales). G3 11, jkab140. ( 10.1093/g3journal/jkab140) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lewis PO. 2001. A likelihood approach to estimating phylogeny from discrete morphological character data. Syst. Biol. 50, 913-925. ( 10.1080/106351501753462876) [DOI] [PubMed] [Google Scholar]
- 43.Altschul SF, Madden TL, Schaffer AA, Zhang JH, Zhang Z, Miller W, Lipman DJ. 1997. Gapped blast and psi-blast: a new-generation of protein database search programs. Nucleic Acids Res. 25, 3389-3402. ( 10.1093/nar/25.17.3389) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bao W, Kojima KK, Kohany O. 2015. Repbase Update, a database of repetitive elements in eukaryotic genomes. Mob. DNA 6, 11. ( 10.1186/s13100-015-0041-9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Juhling F, Morl M, Hartmann RK, Sprinzl M, Stadler PF, Putz J. 2009. tRNAdb 2009: compilation of tRNA sequences and tRNA genes. Nucleic Acids Res. 37, D159-D162. ( 10.1093/nar/gkn772) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Eddy SR. 2020. Hmmer v. 3.3.2. http://hmmer.org.
- 47.Storer J, Hubley R, Rosen J, Wheeler TJ, Smit AF. 2021. The Dfam community resource of transposable element families, sequence models, and genome annotations. Mobile DNA 12, 1-14. ( 10.1186/s13100-020-00230-y) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Renny-Byfield S, Rodgers-Melnick E, Ross-Ibarra J. 2017. Gene fractionation and function in the ancient subgenomes of maize. Mol. Biol. Evol. 34, 1825-1832. ( 10.1093/molbev/msx121) [DOI] [PubMed] [Google Scholar]
- 49.Birchler JA, Auger DL, Riddle NC. 2003. In search of the molecular basis of heterosis. Plant Cell 15, 2236-2239. ( 10.1105/tpc.151030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Birchler JA, Yao H, Chudalayandi S. 2006. Unraveling the genetic basis of hybrid vigor. Proc. Natl Acad. Sci. USA 103, 12 957-12 958. ( 10.1073/pnas.0605627103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Barchi L, et al. 2019. A chromosome-anchored eggplant genome sequence reveals key events in Solanaceae evolution. Sci. Rep. 9, 1-13. ( 10.1038/s41598-019-47985-w) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kim S, et al. 2014. Genome sequence of the hot pepper provides insights into the evolution of pungency in Capsicum species. Nat. Genet. 46, 270-278. ( 10.1038/ng.2877) [DOI] [PubMed] [Google Scholar]
- 53.Bombarely A, et al. 2016. Insight into the evolution of the Solanaceae from the parental genomes of Petunia hybrida. Nat. Plants 2, 1-9. ( 10.1038/nplants.2016.74) [DOI] [PubMed] [Google Scholar]
- 54.Denoeud F, et al. 2014. The coffee genome provides insight into the convergent evolution of caffeine biosynthesis. Science 345, 1181-1184. ( 10.1126/science.1255274) [DOI] [PubMed] [Google Scholar]
- 55.Lyons E, Freeling M. 2008. How to usefully compare homologous plant genes and chromosomes as DNA sequences. Plant J. 53, 661-673. ( 10.1111/j.1365-313X.2007.03326.x) [DOI] [PubMed] [Google Scholar]
- 56.Fernandez-Pozo N, et al. 2015. The Sol Genomics Network (SGN)–from genotype to phenotype to breeding. Nucleic Acids Res. 43, D1036-D1041. ( 10.1093/nar/gku1195) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Conant GC, Wagner A. 2002. GenomeHistory: a software tool and its application to fully sequenced genomes. Nucleic Acids Res. 30, 3378-3386. ( 10.1093/nar/gkf449) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Needleman SB, Wunsch CD. 1970. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48, 443-453. ( 10.1016/0022-2836(70)90057-4) [DOI] [PubMed] [Google Scholar]
- 59.Goldman N, Yang Z. 1994. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol. Biol. Evol. 11, 725-736. ( 10.1093/oxfordjournals.molbev.a040153) [DOI] [PubMed] [Google Scholar]
- 60.Muse SV, Gaut BS. 1994. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol. Biol. Evol. 11, 715-724. ( 10.1093/oxfordjournals.molbev.a040152) [DOI] [PubMed] [Google Scholar]
- 61.Kirkpatrick S, Gelatt CDJ, Vecchi MP. 1983. Optimization by simulated annealing. Science 220, 671-680. ( 10.1126/science.220.4598.671) [DOI] [PubMed] [Google Scholar]
- 62.Conant GC, Wolfe KH. 2008. Probabilistic cross-species inference of orthologous genomic regions created by whole-genome duplication in yeast. Genetics 179, 1681-1692. ( 10.1534/genetics.107.074450) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Smith TF, Waterman MS. 1981. Identification of common molecular subsequences. J. Mol. Biol. 147, 195-197. ( 10.1016/0022-2836(81)90087-5) [DOI] [PubMed] [Google Scholar]
- 64.McRae L, Beric A, Conant GC. 2022. Hybridization order is not the driving factor behind biases in duplicate gene losses among the hexaploid Solanaceae. Figshare. ( 10.6084/m9.figshare.c.6251452) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- McRae L, Beric A, Conant GC. 2022. Hybridization order is not the driving factor behind biases in duplicate gene losses among the hexaploid Solanaceae. Figshare. ( 10.6084/m9.figshare.c.6251452) [DOI] [PMC free article] [PubMed]
Data Availability Statement
All of the data used in this manuscript were previously published and are freely accessible via the accession numbers provided in the text. The POInT software package is available from GitHub: https://github.com/gconant0/POInT/releases/tag/v1.55. All of the underlying inferences, models, phylogenetic trees and gene order sets are freely available from the POInTbrowse web portal: wgd.statgen.ncsu.edu.
Data are also provided in the electronic supplementary material [64].