Designing an optimization model for the vaccine supply chain during the COVID-19 pandemic

Abstract

The COVID-19 pandemic has affected people's lives worldwide. Among various strategies being applied to addressing such a global crisis, public vaccination has been arguably the most appropriate approach to control a pandemic. However, vaccine supply chain and management have become a new challenge for governments. In this study, a solution for the vaccine supply chain is presented to address the hurdles in the public vaccination program according to the concerns of the government and the organizations involved. For this purpose, a robust bi-level optimization model is proposed. At the upper level, the risk of mortality due to the untimely supply of the vaccine and the risk of inequality in the distribution of the vaccine is considered. All costs related to the vaccine supply chain are considered at the lower level, including the vaccine supply, allocation of candidate centers for vaccine injection, cost of maintenance and injection, transportation cost, and penalty cost due to the vaccine shortage. In addition, the uncertainty of demand for vaccines is considered with multiple scenarios of different demand levels. Numerical experiments are conducted based on the vaccine supply chain in Kermanshah, Iran, and the results show that the proposed model significantly reduces the risk of mortality and inequality in the distribution of vaccines as well as the total cost, which leads to managerial insights for better coordination of the vaccination network during the COVID-19 pandemic.

1. Introduction

Over the last four decades, at least 30 new infectious diseases have emerged (Mukherjee, 2017). Researchers and medical professionals believe this trend could increase due to increasing human-animal contact, climate change, land change, global population growth, and global cohesion (Buchy et al., 2021). The latest global health crisis is the COVID-19 pandemic since late 2019, which has caused a significant impact worldwide and become one of the critical public health concerns in the 21st century due to its severity of prevalence and mortality rate (Valizadeh and Mozafari, 2021, Govindan et al., 2020, Melo et al., 2021). In most countries, significant preventive actions were taken to control the spread of the virus, such as border closures, traffic restrictions, social distance, and home quarantine (Mofijur et al., 2021). Meanwhile, many countries have made significant efforts to develop COVID-19 vaccines since general vaccination is considered the most appropriate way to deal with such a global crisis (Coccia, 2021). Accordingly, researchers have received much more attention from the vaccine supply chain (VSC). The VSC during an epidemic differs from a traditional VSC in many ways because, often, governments directly supply and distribute vaccines (Abbasi et al., 2020). Hence, practical solutions and strategies are needed to provide and distribute COVID-19 in a timely and appropriate manner.

A shortage of vaccines due to the failure of the VSC will make circumstances more confounded (Alam et al., 2021). In addition, due to various limitations, such as storage at specific temperatures and high sensitivity, the VSC is considered a complex problem that requires proper planning. In general, the success of a vaccination plan depends on a diversity of factors, including the population's beliefs, attitudes, knowledge, and behavior, which may vary from region to region. The biggest challenge is bridging the gaps and reducing vaccine access inequalities (Xie et al., 2021). An efficient vaccine planning (VP) should meet the demand while ensuring adequate scheduling and achieving specific cost-effectiveness. However, VP usually faces complex challenges because of the uncertain nature of the demand, the clustering of candidates, and the preference of some population groups, which will impose severe restrictions that significantly increase the risk of distribution inequality.

To control the COVID-19 pandemic, it is essential to implement a rapid vaccination program and immunization campaign worldwide (Antal et al., 2021). Pharmaceutical companies have made great efforts to produce and deliver vaccines on time (Haque and Pant, 2020, Vuong et al., 2022). While the vaccine supply chain is fraught with many challenges in different countries, several aspects are likely to influence the success of the COVID-19 immunization program. Vaccination rates have not been very favorable in some countries for various reasons, including vaccine shortages, resistance by some population groups, inappropriate financial and timing policies, or ignorance of vaccination's potential benefits. Therefore, a central authority (either government) should regulate the vaccine distribution so that the vaccination rates can reach the desired level. Herein, the central government's primary goal is ensuring fair distribution with an intervention plan that stimulates vaccine supply chain stakeholders to make the right decisions that benefit the community.

This research aims to address the two levels of concerns among the VSC stakeholders, including the government as a leader and medical centers as followers in the vaccination network. For this purpose, a bi-level programming (BLP) model for the vaccine supply chain network (VSCN) under uncertain demand is proposed. The upper level reduces the risk of mortality due to untimely vaccine supply and distribution inequality of vaccines. At the same time, the lower-level considers the operational cost and penalty cost due to vaccine shortage. This research addresses the following questions: (1) How can the interaction between the government and vaccination centers be formulated considering the mortal risk and risk of distribution inequality of vaccines? (2) Given the uncertainty in demand for vaccines, what is the best strategy for the appropriate assignment of the capacity of vaccination centers and vehicles? (3) How to design a robust solution for VSC during the COVID-19 pandemic against uncertainty?

The remainder of this paper is structured as follows. Section 2 briefly reviews the literature related to this study, followed by developing a new mathematical model and algorithms solution introduced in Section 3 and Section 4, respectively. Section 5 provides the numerical experiments. In Section 6, the model is tested and validated using data from real life, and the numerical results are evaluated and discussed. Section 7 provides a set of managerial insights obtained from this study. Finally, in Section 8, conclusions and future research directions are presented.

2. Literature review and related work

Due to the importance of the subject, much research has been carried out in the field of the VSC. This section reviews the VSC and vaccination network planning literature during the COVID-19 pandemic. The VSC for the epidemic is a complex and multi-layered decision-making process in which the primary focus of vaccine allocation depends on many factors (Abbasi et al., 2020). In the conventional VSC, some drug and medical equipment companies and other related organizations, such as vaccine suppliers (i.e., health care providers), purchase vaccines from manufacturers and distribute them among medical centers and pharmacies. However, most governments directly supervise the supply and distribution system (Golan et al., 2021). Therefore, all healthcare providers work with the government along this supply chain. Asgary et al. (2020) introduced a drive-through simulation tool during the COVID-19 pandemic, which was a hybrid model that integrated event-based and factor-based modeling techniques. This study examined the average processing and waiting time, number of vehicles and medical staff, service lines, screening, registration, immunization, and recovery time in a simulated manner. Georgiadis and Georgiadis (2021) proposed a mathematical model for the VSCN. They considered a two-step decomposition strategy based on a divide and conquer approach, and an aggregation approach was proposed for solving large-scale problems. Alam et al. (2021) examined critical challenges in the VSC during the COVID-19 pandemic. They identified 15 challenges, including “limited number of vaccine companies, ”inadequate coordination with local organizations,“ lack of vaccine monitoring institutions, ”difficulties in monitoring and controlling vaccine temperature,“ and ”vaccination costs and shortages.“ Financial support for vaccine purchases is the most critical challenge. Goodarzian et al. (2021) proposed a sustainable integrated network for the medical supply chain during the pandemic of COVID-19. This model considered production, distribution, inventory, and location network. They have considered the perishability of some drugs related to the proposed model. One of their research objectives was to reduce the medical supply chain network costs, which is consistent with part of the paper. Ferranna et al. (2021) evaluated COVID-19 vaccine prioritization strategies. They examined the main epidemiological, economic, logistical, and political issues that arise when determining a prioritization strategy.

Several studies have been conducted to investigate various government interventions in the production and distribution of vaccines, taking into account multiple uncertainties. Arifoğlu et al. (2012) studied the impact of uncertainty (supply-side) and self-interested consumers (demand side) on the efficiency of influenza VSC. They also considered the relative effectiveness of government interventions on supply and demand. They created two semi-centralized scenarios where the government intervenes on the demand or supply side, but not both. Adida et al. (2013) examined operational issues and uncertainties in the vaccine markets. The effects of central policymakers using incentives for consumers and vaccine manufacturers were investigated. They also found that a fixed two-part subsidy could not harmonize the market. Chick et al. (2017) discussed a planning issue for the government to purchase the flu vaccine considering production uncertainty. They have examined the provision of influenza vaccines by the government when a profitable supplier of the vaccine has uncertainty in production. Their purpose was to minimize expected social costs (including vaccine costs, vaccine prescriptions, and flu treatment costs), which is entirely consistent with the economics of the present study. Demirci & Erkip (2020) have proposed a mechanism that considers two intervention tools to resolve the inefficiencies in the system for the vaccine market and allow the actors to make socially desirable decisions. The results have shown that the proposed strategy is very effective regarding vaccination percentages achieved and budget savings realized beyond the current practices. The improvement in vaccination percentages is even more significant when uncertainty in the system is higher. Williams et al. (2021) discussed ethical thinking about how to vaccinate during a pandemic and examined VP when demand exceeded supply. Martonosi et al. (2021) priced the COVID-19 vaccine using mathematical modeling. They used optimization techniques and game theory to model the COVID-19 vaccine market. The results show that even when production and distribution costs are very high, the government can negotiate prices with producers to keep public sector prices as low as possible while meeting demand and ensuring that every producer makes a profit.

Lin et al. (2021) studied the production and procurement decisions concerning the influenza VSC. They developed a novel model framework considering the risks resulting from uncertainties on both supply and demand sides. Finally, they proposed a procurement strategy that provided the social planner with two ordering opportunities. They explored the conditions under which the two members would be willing to accept the strategy. Chandra et al. (2021) investigated the critical factors for improving the performance of the existing VSC system by implementing the next-generation vaccine supply chain (NGVSC) in India. The outcome of the analysis contends that demand forecasting is the topmost supply chain barrier and sustainable financing is the most critical enabler to facilitating the implementation of the NGVSC. Table 1 illustrates the detailed specification of bi-level programming approaches adopted in VSC problems.

Table 1.

Overview of relevant models in the literature.

Authors	Objective type		Model feature		Model type			Virus type		Uncertain
	Single Objective	Multi Objective	single-level	Bi-Level	Cost	Risk	Time	COVID-19	Influenza	Stochastic optimization	Fuzzy optimization	Robust optimization
Hovav & Tsadikovich (2015)	√		√		√				√
Carvalho et al. (2019)		√	√		√					√
Sadjadi et al. (2019)	√		√		√					√
Lin et al. (2020)			√						√
Dai et al. (2020)	√		√		√	√		√
Enayati & Özaltın (2020)	√		√						√	√
Karmaker et al. (2021)	√		√					√			√
Rastegar et al. (2021)	√		√						√
De Boeck et al. (2021)			√			√
Dai et al. (2021)			√		√		√	√
Lin et al. (2021)	√		√			√			√	√
Alam et al. (2021)			√			√		√			√
Sazvar et al. (2021)	√		√		√				√		√	√
Bamakan et al. (2021)		√						√
Thul & Powell (2021)		√	√					√		√
This paper		√		√	√	√	√	√		√		√

2.1. Research gap and contributions

To the best of the authors' knowledge, no research has so far addressed government concerns about the vaccination network during the COVID-19 pandemic. In addition, there is no article in the field of the VSC that considers fair distribution in vaccine supply. Previous researchers have also proposed various models for the VSC problem, but studies have shown that there are no studies that consider the risks associated with mortality due to the untimely vaccine supply. By reviewing the research literature and Table 1, we state the following as research contributions:

• Given the prevalence of the COVID-19 virus and the global effort to combat this dangerous virus, this research provides a decision support system based on a mathematical model for the VSC network during the COVID-19 pandemic. In this research, we have tried to propose a Bi-Level Programming (BLP) model that considers the vaccination program's concerns at two levels as a leader–follower.

• At the upper level of the proposed model, the network risks included mortality risks of untimely vaccine supply and risks of unfair distribution. In addition, due to the significant costs imposed on all countries to control the virus, at the lower level of the proposed model, the total cost of the VSC during the COVID-19 pandemic, including vaccine supply, allocation of candidate centers for vaccine injection, cost of maintaining and injecting, transportation costs and penalties related to the vaccine shortage.

• Due to the high demand for the COVID-19 vaccine during the pandemic, uncertainty in the demand for vaccines is an issue that has been considered in this study. For this purpose, four various scenarios have been considered for the number of demands. For this purpose, Mulvey's method has been used to provide a robust model and deal with demand uncertainty.

• Finally, it has considered two types of vaccine injection centers; the first type includes fixed injection centers where people refer to and receive the vaccine. The second type is mobile vaccine injection centers (vehicles), which are considered for the disabled (elderly or people with diseases and disabilities) who are not able to go to fixed centers. In addition, the bi-level model presented by the Karush Kuhn Tucker (KKT) condition has become a single-level problem. Finally, the proposed model with the data of Kermanshah city has been evaluated as a case study.

3. Model development

This section proposes a bi-level programming (BLP) model to optimize the VSC during COVID-19. Governments' concern is formulated at the upper level to include the mortal risk of untimely vaccine supply and the risk of distribution inequality of the vaccine. At the lower level, various costs related to vaccine supply are considered. Fig. 1 presents the schematic structure of the BLP model.

Fig. 1.

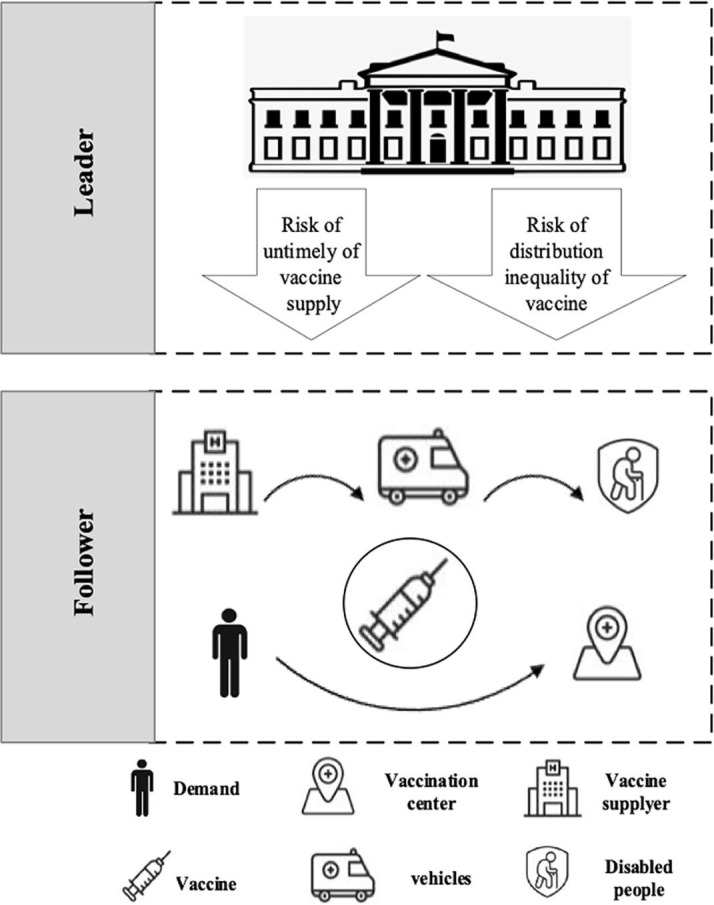
The schematic structure of the proposed BLP model.

As shown in Fig. 1, the proposed model focuses on two levels of concern. The leader's decision (Upper Level) significantly affects followers' reactions (Lower Level). To consider the uncertainty of demand, we consider multiple scenarios of different demand levels for vaccines. Mulvey's approach is adopted to limit the model to a stochastic state. To solve the BLP model, Karush–Kuhn–Tucker (KKT) conditions are used to turn it into a single-level model. Moreover, the following assumptions have been considered in model development.

A1. Considering the possibility of the COVID-19 outbreak in crowded places, the number of people assigned to vaccination centers has been determined in advance. In other words, to prevent congestion and virus spread, limited capacities of vaccination centers are considered.

A2. In the proposed model, the routing plans of vehicle movement have been determined. Each vehicle is allowed to move only along specified routes. The vehicle routing problem is excluded from this study.

A3. Demand transfer is not allowed in the proposed model. Therefore, if a person visits a vaccination center or mobile station, they must be accepted.

3.1. The VSC model

During the COVID-19 pandemic, governments are concerned about rising mortality rates (Valizadeh et al., 2021). To control this pandemic, vaccine companies have provided different types of vaccines. The main problem is the limited capacity of vaccination centers against many vaccine applications. On the other hand, properly implementing the vaccination program will involve many costs in addition to relevant risks that must be managed appropriately. By providing a decision support system based on a bi-level programming model, we address the concerns of the government and the organizations involved in the VSC.

Due to the contents of the previous sections, the upper-level objective function reflects the concern of the government (mortality risk), which includes two parts and should be minimized. The lower-level objective function also reflects the lower-level concerns (costs) of the organizations involved in the vaccination program, which have six parts and should be minimized. Constraints of the model also show the budget, capacity, and some limitations related to vaccine supply flow. The ultimate goal of the proposed model is to consider both upper and lower-level concerns and, simultaneously reduce mortality risk and network costs in the vaccination network during the COVID-19 pandemic. To solve this problem and according to the stated assumptions and requirements, we have presented a Mixed-Integer Programming (MIP) model.

3.1.1. Notations

The relevant variables and parameters used throughout this paper are summarized below.

Index and set
$i,j\in N$	Index of city areas
$p\in P$	Index of people
$f\in F$	Index of vaccine suppliers (Hospitals and Related Organizations)
$r\in R$	Index of candidate locations for allocating fixed vaccination centers
$k\in K$	Index of vehicles (Mobile Vaccination Bases)
$h\in H$	Index of vaccine
$t\in T$	Index related to periods
$s\in S$	Index of scenario
$A$	A large constant
Parameter
${\mathit{fc}}_{\mathit{rt}}$	Fixed cost related to the allocation of candidate centers$r$ during period $t$
${\mathit{ck}}_{\mathit{kijt}}$	Cost of supplying each vehicle $k$ for vaccination of people of points $i$ and $j$ during period $t$
${\mathit{ch}}_{\mathit{ht}}$	The cost of supplying each unit of vaccine $h$ during the period $t$
${\mathit{ce}}_{\mathit{ht}}$	The cost of storage of each unit of vaccine $h$ over a period of $t$
${\mathit{ct}}_k$	The cost of transporting each vehicle $k$ to travel per kilometer
${\mathit{cs}}_{\mathit{ht}}$	The penalty related to the shortage of each vaccine unit $h$ during period $t$
${\mathit{dis}}_{\mathit{fij}}$	The distance between points $i,j$ and $f$ based on kilometers
${\mathit{np}}_{\mathit{pht}}$	Number of people $p$ affected by the mortality risk due to not receiving the vaccine $h$ during the period $t$
${\sigma }_{\mathit{ht}}$	Relative coefficient of the risk due to untimely of vaccine supply during period $t$
${\xi }_{\mathit{ht}}$	Relative coefficient of the risk of distribution inequality of vaccine $h$ during period $t$
$d_{\mathit{ht}}$	Demand for vaccine $h$ during period $t$
${\mathit{nr}}_{\mathit{rt}}$	Number of candidate centers $r$ to provide services during the period $t$
${\mathit{nk}}_{\mathit{kijt}}$	Number of vehicles $k$ required to cover points $i$ and $j$ during period $t$
$g_k$	Vehicle capacity $k$
${\mathit{nh}}_{\mathit{ft}}$	Number of vaccines $h$ supplied by supplier $f$ during period $t$
$B$	Total budget
${\mathit{Vcap}}_h$	Number of the available vaccines $h$
Variable
${\alpha }_{\mathit{rt}}$	If the vaccination center $r$ is set up during time $t$, its value is 1; otherwise, it is 0.
${\beta }_{\mathit{tkij}}$	If the vehicle $k$ visits the points of $i$ and $j$ during period $t$, its value is 1, and otherwise, it is 0.
${\mathrm{{\rm Y}}}_{\mathit{ktf}}$	If vehicle $k$ visits point $f$ during period $t$, its value is 1; otherwise, it is 0.
${\partial }_{\mathit{ht}}$	Number of shortages of vaccine $h$ during period $t$
$U_{\mathit{hft}}$	Vaccine supply capacity by suppliers $f$ during period $t$
$V_{\mathit{ht}}$	Vaccine distribution capacity during period $t$
${U1}_{\mathit{stik}}$	Auxiliary variable for sub-tour elimination
${V1}_{\mathit{stik}}$	Auxiliary variable for sub-tour elimination

The equations for the upper and lower objective functions are as follows:

$A={\sum }_h{\sum }_r{\sum }_t{\xi }_{\mathit{ht}}n{h}_{\mathit{ft}}{V}_{\mathit{ht}}$	The risk of distribution inequality of the vaccine during the vaccination program under scenario $s$
$B={\sum }_h{\sum }_p{\sum }_t{\sigma }_{\mathit{ht}}n{p}_{\mathit{pht}}{\partial }_{\mathit{ht}}$	The risk of mortality due to the untimely supply of the vaccine
$H={\sum }_h{\sum }_f{\sum }_{t}c{h}_{\mathit{ht}}n{h}_{\mathit{ft}}{U}_{\mathit{hft}}$	The cost of supplying the vaccine
$J={\sum }_h{\sum }_f{\sum }_{t}c{e}_{\mathit{ht}}n{h}_{\mathit{ft}}{V}_{\mathit{ht}}$	The costs of storage the vaccine
$K={\sum }_r{\sum }_{t}f{c}_{\mathit{rt}}n{r}_{\mathit{rt}}{\alpha }_{\mathit{rt}}$	The fixed costs of allocation of vaccination centers
$L={\sum }_i{\sum }_j{\sum }_k{\sum }_{t}c{k}_{\mathit{kijt}}n{k}_{\mathit{kijt}}{\beta }_{\mathit{tkij}}$	The fixed costs of allocation of supplying vehicles
$Q={\sum }_i{\sum }_j{\sum }_f{\sum }_k{\sum }_{t}c{t}_{k}n{k}_{\mathit{kijt}}di{s}_{\mathit{fij}}{\beta }_{\mathit{tkij}}$	The transportation costs
$R={\sum }_h{\sum }_{t}c{s}_{\mathit{ht}}{d}_{\mathit{ht}}{\partial }_{\mathit{ht}}$	The penalty for vaccine shortage

The equations for the upper and lower objective functions are as follows:

$$\mathit{Min}{Z}_1=A+B$$ (1)

$$\mathit{Min}{Z}_2=H+J+K+L+Q+R$$ (2)

S.t

$$\left(\sum _r\sum _{t}f{c}_{\mathit{rt}}{\alpha }_{\mathit{rt}}^s+\sum _i\sum _j\sum _k\sum _{t}c{k}_{\mathit{kijt}}{\beta }_{\mathit{tkij}}^s\right)\le B\forall s\in S$$ (3)

$$\sum _t{V}_{\mathit{ht}}\le Vca{p}_h\forall h\in H$$ (4)

$$\sum _h{V}_{\mathit{ht}}\le BigM\left(\sum _r{\alpha }_{\mathit{rt}}^s+\sum _{i,j/(i\ne j)}\sum _k{\beta }_{\mathit{tkij}}^s\le B\right)\forall t\in T,s\in S$$ (5)

$$\sum _r{\alpha }_{\mathit{rt}}^s=1\forall t\in T,s\in S$$ (6)

$$\sum _f{U}_{\mathit{hft}}n{h}_{\mathit{ft}}\ge d_{\mathit{ht}}^s+{\partial }_{\mathit{ht}}^s\forall h\in H,t\in T,s\in S$$ (7)

$$\sum _h{\partial }_{\mathit{ht}}^s=1\forall t\in T,s\in S$$ (8)

$$\sum _h\sum _f{U}_{\mathit{hft}}\ge 1\forall t\in T$$ (9)

$$\sum _i\sum _k{\beta }_{\mathit{tkij}}^s+\sum _f\sum _k{\gamma }_{\mathit{ktf}}^s=1\forall t\in T,s\in S$$ (10)

$$\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkij}}^s+\sum _f{\gamma }_{\mathit{ktf}}^s=\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkji}}^s+\sum _f{\gamma }_{\mathit{ktf}}^s\forall k\in K,t\in T,s\in S$$ (11)

$$\sum _f{\gamma }_{\mathit{ktf}}^s=1\forall k\in K,t\in T,s\in S$$ (12)

$$\mathit{BigM}\sum _f{\gamma }_{\mathit{ktf}}^s\ge \sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkij}}^s\forall k\in K,t\in T,s\in S$$ (13)

$$\sum _h\sum _f{U}_{\mathit{hft}}\ge \sum _h{V}_{\mathit{ht}}\forall t\in T$$ (14)

$$\sum _{i,j/(i\ne j)}\sum _k{\beta }_{\mathit{tkij}}^s{g}_k\le \sum _h\sum _f{U}_{\mathit{hft}}\forall t\in T,s\in S$$ (15)

$$\sum _h\sum _{i,j/(i\ne j)}\sum _t{d}_{\mathit{ht}}^s{\beta }_{\mathit{tkij}}^s\le g_k\forall k\in K,s\in S$$ (16)

$$U_{\mathit{stik}}^1-V_{\mathit{stjk}}^1+N{\beta }_{\mathit{tkij}}^s\le N-1\forall i\in N,j\in N,k\in K,t\in T,s\in S$$ (17)

$${\alpha }_{\mathit{rt}}^s,{\beta }_{\mathit{tkij}}^s,{\gamma }_{\mathit{ktf}}^s\in \left\{0,1\right\}\forall i,j/(i\ne j)\in N,r\in R,k\in K,f\in F,t\in T,s\in S$$ (18)

$$U_{\mathit{hft}},V_{\mathit{ht}},U_{\mathit{stik}}^1,V_{\mathit{stjk}}^1,{\partial }_{\mathit{ht}}^s\ge 0\forall i\in N,r\in R,h\in H,f\in F,t\in T,s\in S$$

Eq. (1) shows the upper-level objective function, reflecting the government's concern. The first part of this objective function indicates the risk of distribution inequality of the vaccine during the vaccination program, and the second part indicates the risk of mortality due to the untimely supply of the vaccine. Eq. (2) is the lower level objective function to reflect the concerns of all organizations involved in the vaccination program, which has six parts. The first and second parts show the costs of supplying and storing vaccines. The third and fourth parts show the fixed costs of vaccination centers and vehicle supply allocation, respectively. The fifth part shows the transportation cost related to vehicles (mobile vaccination centers), and finally, the sixth part shows the penalty for vaccine shortage.

Constraint (3) indicates the budget limitation for allocating fixed vaccination centers and supplying vehicles. Constraint (4) indicates the capacity of vaccination centers. Constraint (5) represents the limitation of the vaccine distribution capacity. Constraint (6) ensures at least one vaccination center in the network. Constraint (7) indicates the balance of vaccine supply flow. Constraint (8) represents the possible shortage of at least one dose of vaccine in the network. Constraint (9) indicates the capacity of vaccine suppliers. Constraint (10) ensures that the vehicle allocated visits the determined points. Constraint (11) indicates that the number of vehicles entering point $i$ will leave the point after vaccination (in other words, stopping is not allowed, and each vehicle must go from point $i$ to point $j$ after visiting or returning to the vaccination center $r$). Constraint (12) ensures that at least one vehicle goes to the location of the vaccine suppliers to receive the vaccines. Constraint (13) ensures that the vaccine supply capacity is more than the capacity of vaccination centers (this constraint ensures that the vaccine supply flow is positive). Constraints (14), (15) indicate the capacity limitation of vehicles. Constraints (16) are related to sub-tour elimination. Finally, Constraints (17), (18) show the variables.

3.2. Robust VSC model

A popular type of stochastic programming for supply chain design problems under uncertainty is scenario-based, which considers discrete scenarios and their corresponding probability of occurrence for random variables (Valizadeh et al., 2020). Scenario-based stochastic programming typically optimizes the expected value of the objective functions without directly applying the decision makers' preferences (Azaron et al. 2008). Because of the significance of uncertainty, many researchers have addressed stochastic parameters when designing the supply chain (Valizadeh et al. 2021). Research that considers uncertainty can be categorized according to two primary approaches: probabilistic and scenario approaches. Some parameters are regarded as random variables with known probability distributions for the probabilistic method. The scenario approach represents uncertainty by setting up different scenarios representing uncertain parameter realizations (Valizadeh et al., 2021, Valizadeh et al., 2021). The scenario approach aims to find a robust solution that ensures the solution is “close” to the optimum in response to changing input data, considering all specified scenarios. Robust optimization is a scenario-based method used to deal with uncertainty in programming problems. Mulvey et al. (1995) first proposed this method. Robust optimization includes two types of robustness: “solution robustness” and “model robustness” (Edalatpour et al., 2018). Considering the uncertain demand for the COVID-19 vaccines for various reasons, uncertainty is incorporated in this section's VSC model proposed by Mulvey et al. (1995). This study proposes a robust optimization model in which the solution is approximate to the optimum and feasible in all likely scenarios.

Parameter
${\rho }_s$	Probability of occurrence of scenario ‌$s$
$\omega$	Variability significance coefficient
$\lambda$	The coefficient of the significance of the model
	Variable
${\theta }_s$	Deviation variables of objective functions (continuous and negative)
${\theta }_{s\prime }$	Deviation variables of objective functions (For the variability of parameter $s\prime$)
${\delta }_{\mathit{ks}}$	Variable of control constraint
${\delta }_{\mathit{ks}\prime }$	Variable of control constraint (For the variability of parameter $s\prime$)

The general form of a robust optimization model is as follows:

$$\mathit{MinZ}=\sigma \left(x,y_1,y_1,...,y_n\right)+\omega \rho \left({\delta }_1,{\delta }_1,...,{\delta }_s\right),$$ (19)

s.t:

$$\mathit{Ax}=b;$$ (20)

$$B_{s}x+C_s{y}_s+{\delta }_s=e_s;\forall s\in \mathrm{\Omega }$$ (21)

$$x\ge 0,y_s\ge 0;\forall s\in \mathrm{\Omega }$$ (22)

The first part of the objective function represents the robustness of the solution and evaluates the solution closest to the optimization for all scenarios. The second part is a robustness criterion of the model, which checks the feasibility of the model for all possible scenarios. In other words, it will find control constraints in some scenarios if they violate the feasibility zone of the model. Eq. (21) checks the condition between the optimality and feasibility of the model. For example, if$B_{s}x+C_s{y}_s+{\delta }_s=0$, the solution may be outside the feasible space (i.e., infeasible solution). If the value is large enough, the model not only preserves its feasibility in different scenarios but also causes an increase in cost (Tavanayi et al., 2020). The definition $\left(x,y_1,y_1,...,y_n\right)$ is given as follows:

$$\sigma \left(x,y_1,y_1,...,y_n\right)=\sum _{s\in \mathrm{\Omega }}{\rho }_s{\xi }_s+\lambda \sum _{s\in \mathrm{\Omega }}{\rho }_s\left({\xi }_s-\sum _{s^{\prime }\in \mathrm{\Omega }}{\rho }_{s^{\prime }}{\xi }_{s^{\prime }}\right)$$ (23)

The variability weight $\mathrm{\lambda }$ denotes the sensitivity rate of the objective function to variations in the input data under different scenarios. The variability (variance) decreases when objective function increases (Akbari et al., 2021). The latter is also defined as follows:

$$\rho \left({\delta }_1,{\delta }_1,...,{\delta }_s\right)=\sum _{s\in S}{\rho }_s{\delta }_s$$ (24)

Therefore, the objective function of the model can be reformulated as follows:

$$\mathit{MinZ}=\sum _{s\in S}{\rho }_s{\zeta }_s+\lambda \sum _{s\in S}{\rho }_s\left({\zeta }_s-\sum _{s^{\prime }\in S}{\rho }_{s^{\prime }}{\zeta }_{s^{\prime }}\right)+\omega \sum _{s\in S}{\rho }_s{\delta }_s$$ (25)

Following the approach Mulvey et al. (1995) proposed, the VSC model is transformed to a robust counterpart, named R-VSC, with consideration of multiple scenarios. During the COVID-19 pandemic, the governments are concerned about rising mortality rates (Valizadeh et al., 2021). To control this pandemic, vaccine companies have provided different types of vaccines. The main problem is the limited capacity of vaccination centers against a large number of demands for vaccines. Moreover, proper implementation of the vaccination program requires a lot of cost in addition to relevant risks that must be properly managed. A Mixed-Integer Programming (MIP) model is developed to solve this problem.

The relevant variables and parameters used throughout this paper are summarized below.

Parameter
$d_{\mathit{ht}}^s$	Demand for vaccine $h$ during period $t$ in scenario‌$s$
	Variable
${\alpha }_{\mathit{rt}}^s$	If the vaccination center $r$ is set up during time $t$ under scenario‌ $s$, its value is 1; otherwise, it is 0.
${\beta }_{\mathit{tkij}}^s$	If the vehicle $k$ visits the points of $i$ and $j$ during period $t$ under scenario‌ $s$, its value is 1, and otherwise, it is 0.
${\mathrm{{\rm Y}}}_{\mathit{ktf}}^s$	If vehicle $k$ visits point $f$ during period $t$ under scenario‌ $s$, its value is 1; otherwise, it is 0.
${\partial }_{\mathit{ht}}^s$	Number of shortages of vaccine $h$ during period $t$ under scenario‌$s$
$U_{\mathit{hft}}$	Vaccine supply capacity by suppliers $f$ during period $t$
$V_{\mathit{ht}}$	Vaccine distribution capacity during period $t$
${U1}_{\mathit{stik}}$	Auxiliary variable for sub-tour elimination
${V1}_{\mathit{stik}}$	Auxiliary variable for sub-tour elimination

The equations for the upper and lower objective functions are as follows:

$A={\sum }_h{\sum }_r{\sum }_t{\xi }_{\mathit{ht}}n{h}_{\mathit{ft}}{V}_{\mathit{ht}}$	The risk of distribution inequality of the vaccine during the vaccination program under scenario $s$
$B_s={\sum }_h{\sum }_p{\sum }_t{\sigma }_{\mathit{ht}}n{p}_{\mathit{pht}}{\partial }_{\mathit{ht}}^s$	The risk of mortality due to the untimely supply of the vaccine under scenario $s$
$H={\sum }_h{\sum }_f{\sum }_{t}c{h}_{\mathit{ht}}n{h}_{\mathit{ft}}{U}_{\mathit{hft}}$	The cost of supplying the vaccine under scenario $s$
$J={\sum }_h{\sum }_f{\sum }_{t}c{e}_{\mathit{ht}}n{h}_{\mathit{ft}}{V}_{\mathit{ht}}$	The costs of storage the vaccine under scenario $s$
$K_s={\sum }_r{\sum }_{t}f{c}_{\mathit{rt}}n{r}_{\mathit{rt}}{\alpha }_{\mathit{rt}}^s$	The fixed costs of allocation of vaccination centers under scenario $s$
$L_s={\sum }_i{\sum }_j{\sum }_k{\sum }_{t}c{k}_{\mathit{kijt}}n{k}_{\mathit{kijt}}{\beta }_{\mathit{tkij}}^s$	The fixed costs of allocation of supplying vehicles under scenario $s$
$Q_s={\sum }_i{\sum }_j{\sum }_f{\sum }_k{\sum }_{t}c{t}_{k}n{k}_{\mathit{kijt}}di{s}_{\mathit{fij}}{\beta }_{\mathit{tkij}}^s$	The transportation costs under scenario $s$
$R_s={\sum }_h{\sum }_{t}c{s}_{\mathit{ht}}{d}_{\mathit{ht}}^s{\partial }_{\mathit{ht}}^s$	The penalty for vaccine shortage under scenario $s$

The complete VSC model is presented as follows:

$$\mathit{Min}{Z}_1=A+\sum _{s\in S}{B}_s+\lambda \sum _{s\in S}{\rho }_s\left(B_s-\sum _{s^{\prime }\in S}{\rho }_{s^{\prime }}{B}_{s^{\prime }}+2{\theta }_s\right)+\omega \sum _{s\in S}\sum _{k\in K}{\rho }_s{\delta }_{\mathit{ks}}$$ (26)

$$\begin{array}{c}\mathit{Min}{Z}_2=H+J+\sum _{s\in S}{K}_s+\sum _{s\in S}{L}_s+\sum _{s\in S}{Q}_s+\sum _{s\in S}{R}_s+\\ \lambda \sum _{s\in S}{\rho }_s\left[\left(K_s+L_s+Q_s+R_s\right)-\left(\sum _{s^{\prime }\in S}{\rho }_{s^{\prime }}\left(K_{s^{\prime }}+L_{s^{\prime }}+Q_{s^{\prime }}+R_{s^{\prime }}\right)+2{\theta }_s^{\prime }\right)\right]+\\ \omega \sum _{s\in S}\sum _{k\in K}{\rho }_s{\delta }_{\mathit{ks}}^{\prime }\end{array}$$ (27)

s.t:

$$B_s-B_{s^{\prime }}+{\theta }_s\ge 0\forall s\in S$$ (28)

$$\left(K_s+L_s+Q_s+R_s\right)-\left(K_{s^{\prime }}+L_{s^{\prime }}+Q_{s^{\prime }}+R_{s^{\prime }}\right)+{\theta }_{s^{\prime }}\ge 0\forall s\in S$$ (29)

Eqs (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18).

3.3. Robust Bi-Level VSC (R-B-VSC) model

As mentioned earlier, this study intends to address two levels of concern among stakeholders, and to this end, a bi-level programming model (BLP) for VSCN has been proposed. Nevertheless, different approaches have been used in the literature to robustify the model against changes and risks of the scenarios. One method is to consider various scenarios that might be faced in the implementation process. Robust optimization and bi-level programming (RBL) are applicable in research and practice on a wide range of subjects. For instance, they can be used for communication between decision-makers in a competitive environment so that the decision results of each factor affect those of other factors. This approach aims to strike a logical balance between robust optimization and bi-level modeling. Unlike other traditional optimization approaches, the proposed model seeks a robust solution based on the bi-level preferences of decision-makers. We state that the solution obtained by this method is reliable and almost optimal for all possible states of the parameters with uncertainty.

It is well recognized that bi-level optimization problems are difficult to be solved optimally. It has particularly been proven that the simplest linear bi-level programming model is strongly NP-hard (Amirtaheri et al., 2017). We convert the problem into a simpler form to better understand the complexities of the proposed model. It is assumed that the number of demands is the same in different areas. To cover each demand, we need a vaccine supplier, a vehicle, two doses of vaccine, and a vaccination center. The demands must be covered within a specified time period. In addition, some demands are covered by vehicles. It is clear that the above problem is a VRP problem with high complexity and is typically NP-hard; hence, it can be concluded that the complexity of the problem is also at least typically NP-hard. But, since also bi-level programming is presented for this problem, so the complexity of the problem is increased, and we conclude that the problem is explicitly NP-hard (Valizadeh et al., 2021, Valizadeh et al., 2021). As a result, a large body of research on bi-level programming is dominated by heuristic and metaheuristic solution approaches to achieve local optimality (Pouriani et al., 2019). However, not any algorithm has polynomial-time guarantee, even for the simplest bi-level optimization problem, e.g., convex bi-level optimization problems (Dempe et al., 2015). Specifically, in addition to the difficulties brought by the framework of the bi-level model, there is also a complicating term ${\sum }_{s\in S}{\rho }_s{\delta }_s^{\prime }$ which consists of the product of two continuous decision variables in the objective function of R-B-VSC. In addition to these approaches, the KKT conditions necessary and sufficient for the optimality in the bi-level problem can be used to reduce the original problem to its single-level regular version, which is solvable with the help of available commercial software (Saeidi-Mobarakeh et al., 2020). In this study, since the vaccine supply chain problem is continuous, linear, and convex, its KKT conditions can be easily rewritten. In a BLP model, KKT conditions, which are necessary and sufficient conditions for optimizing a lower-level problem, can convert the main problem to its single-level equivalent, allowing the solution to be solved by existing optimization software. The following four KKT conditions can be substituted in this subsection to convert the BLP model to a single-level problem.

3.3.1. Static constraints

These constraints are derived directly from the Lagrange function corresponding to the objective function of the lower level problem. To form the Lagrange function, first, the constraints of the quadratic model in the robust optimization formula, i.e. Eqs (6), (8), (10), and (12), are written in the form ($\ge 0$) or ($=0$), and then, the Lagrange coefficients or the double variables to the left of the rewritten constraints are multiplied. Finally, the sum of these multiplications as well as the lower level objective function is calculated, which is equivalent to the Lagrange function of the lower level problem.

Appendix A provides the complete R-B-VSC model. Under static constraints, the gradient of the Lagrange function relative to the lower-level decision-making variables is zero. Constraints (30), (31), (32), (33), (34), (35), (36), (37), (38), (39), (40) indicate the first-order KKT conditions.

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{ts}}^7{\beta }_{\mathit{tkij}}^s{g}_k=0;\forall i,j/(i\ne j)\in N,k\in K,t\in T,s\in S$$ (30)

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{kts}}^4+{\pi }_{\mathit{kts}}^5=0;\forall k\in K,t\in T,s\in S$$ (31)

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{kts}}^4+{\pi }_{\mathit{kts}}^5-{\pi }_{\mathit{ts}}^7{\beta }_{\mathit{tkij}}^s{g}_k=0;\forall i,j/(i\ne j)\in N,k\in K,t\in T,s\in S$$ (32)

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{ts}}^1=0;\forall t\in T,s\in S$$ (33)

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{kts}}^6=0;\forall k\in K,t\in T,s\in S$$ (34)

$${\psi }_{\mathit{ts}}-{\pi }_{\mathit{hts}}^2+{\pi }_{\mathit{ts}}^3=0;\forall h\in H,t\in T,s\in S$$ (35)

$${\psi }_{\mathit{ts}}=\left({\sigma }_{\mathit{ht}}n{p}_{\mathit{pht}}\right)\left({\rho }_s\left(1+\lambda \left(1-{\rho }_s\right)\right)\right)+\left(1-{\rho }_s\right){\pi }_s^8;\forall h\in H,p\in P,t\in T,s\in S$$ (36)

$$2\lambda {\rho }_s-{\pi }_s^8-{\pi }_s^{10}=0;\forall s\in S$$ (37)

$$\begin{array}{c}{\psi }_{\mathit{ts}}=\left(f{c}_{\mathit{rt}}n{r}_{\mathit{rt}}+c{k}_{\mathit{kijt}}n{k}_{\mathit{kijt}}+c{t}_{k}n{k}_{\mathit{kijt}}di{s}_{\mathit{fij}}+c{s}_{\mathit{ht}}+{\sigma }_{\mathit{ht}}n{p}_{\mathit{pht}}\right)\\ \left({\rho }_s\left(1+\lambda \left(1-{\rho }_s\right)\right)\right)+\left(1-{\rho }_s\right){\pi }_s^9;\end{array}\begin{array}{c}\forall i,j/(i\ne j)\in N,k\in K,t\in T,\\ f\in F,h\in H,r\in R,s\in S\end{array}$$ (38)

$$2\lambda {\rho }_s-{\pi }_s^9-{\pi }_s^{11}=0;\forall s\in S$$ (39)

$$\omega {\rho }_s-{\pi }_s^{10}-{\pi }_{\mathit{ks}}^{12}=0;\forall k\in K,t\in T,s\in S$$ (40)

3.3.2. The feasible constraints of the initial problem

Constraints on the feasibility of the initial problem under KKT conditions indicate that the constraints of the upper-level problem must be established in the presence of the optimal amount of decision variables and not violated. These constraints include Eqs. (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15).

3.3.3. The feasible constraints of the dual problem

Constraints of the feasibility of the dual problem in the KKT context state that the duality problem must remain feasible in return for the optimal solution. Accordingly, Lagrange coefficients corresponding to constraints greater than or equal to zero should be defined in the same way, and other constraints in the form of equations and their coefficients should be considered unconditionally in the model. Note that these coefficients are the same as the two problem variables.

3.3.4. Supplementary deficiencies

Supplementary deficiency conditions express the general relationship between the initial constraints and their corresponding Lagrange coefficients, in which the product of the deficit variables in the initial constraints with their corresponding Lagrange coefficients is zero. Additional deficiency constraints concerning upper-level constraints are formulated as Constraints (41), (42), (43), (44), (45), (46), (47), (48), (49), (50), (51), (52).

$${\pi }_{\mathit{ts}}^1\left(\sum _r{\alpha }_{\mathit{rt}}^s-1\right)=0\forall t\in T,s\in S$$ (41)

$${\pi }_{\mathit{hts}}^2\left(\left[d_{\mathit{ht}}^s+{\partial }_{\mathit{ht}}^s\right]-\sum _h\sum _f{U}_{\mathit{hft}}n{h}_{\mathit{ft}}\right)=0\forall h\in H,t\in T,s\in S$$ (42)

$${\pi }_{\mathit{ts}}^3\left(\sum _h{\partial }_{\mathit{ht}}^s-1\right)=0\forall t\in T,s\in S$$ (43)

$${\pi }_{\mathit{kts}}^4\left(\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkji}}^s-1\right)=0\forall k\in K,t\in T,s\in S$$ (44)

$${\pi }_{\mathit{kts}}^5\left(-\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkji}}^s\right)=0\forall k\in K,t\in T,s\in S$$ (45)

$${\pi }_{\mathit{kts}}^6\left(\sum _f{\gamma }_{\mathit{ktf}}^s-1\right)=0\forall k\in K,t\in T,s\in S$$ (46)

$${\pi }_{\mathit{ts}}^7\left(\sum _h\sum _f{U}_{\mathit{hft}}-\sum _{i,j/(i\ne j)}\sum _k{\beta }_{\mathit{tkij}}^s{g}_k\right)=0\forall t\in T,s\in S$$ (47)

$$\forall s\in S-\sum _{s\in S}{\pi }_s^8\left(\left(B_s\right)-\left(B_{s^{\prime }}\right)+{\theta }_s\right)=0$$ (48)

$$\forall s\in S{\pi }_s^9\left(\left(K_s+L_s+Q_s+R_s\right)-\left(K_{s^{\prime }}+L_{s^{\prime }}+Q_{s^{\prime }}+R_{s^{\prime }}\right)+{\theta }_{s^{\prime }}\right)=0$$ (49)

$$\forall s\in S{\pi }_s^{10}\left({\theta }_s\right)=0$$ (50)

$$\forall s\in S{\pi }_s^{11}\left({\theta }_s^{\prime }\right)=0$$ (51)

$$\forall k\in K,s\in S{\pi }_{\mathit{ks}}^{12}\left({\delta }_{\mathit{ks}}\right)=0$$ (52)

Therefore, the single-level formula for R-VSC, which is a nonlinear mixed-integer programming model, is obtained as follows:

• The upper-level objective function (1)

• The lower level objective function (2)

• Model constraints include (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), and (28), (29)

• Static constraints include (30), (31), (32), (33), (34), (35), (36), (37), (38), (39), (40)

• The feasible constraints of the initial problem include Eqs. (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15).

• The feasible constraints of the dual problem include (${\pi }_{\mathit{kts}}^4,{\pi }_{\mathit{kts}}^5,{\pi }_{\mathit{ts}}^7,{\pi }_s^9$ , ${\pi }_s^{10},{\pi }_s^{11}$ , ${\pi }_{\mathit{ks}}^{12}$)

• Supplementary deficiencies constraints include (41), (42), (43), (44), (45), (46), (47), (48), (49), (50), (51), (52)

The obtained single-level formula is named R-B-VSC, which results from a nonlinear relationship between the initial constraints and their corresponding Lagrange coefficients in Eqs. (41), (42), (43), (44), (45), (46), (47), (48), (49), (50), (51), (52). A simple method to eliminate this type of nonlinearity is to replace each nonlinear constraint with a new set of linear constraints (Azadeh et al., 2017). For example, the nonlinear Eq. (41) in the R-B-VSC model is replaced by the linear Eqs. (53), (54), (55). In these equations, $M$ is a large constant.

$$\forall k\in K,t\in T,s\in S{\pi }_{\mathit{kts}}^4\le M{A}_{\mathit{ts}}$$ (53)

$$\forall t\in T,s\in S\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkij}}^s-1=M\left(1-A_{\mathit{ts}}\right)$$ (54)

$$\forall t\in T,s\in S{A}_{\mathit{ts}}\in \left\{0,1\right\}$$ (55)

4. Solution approach

According to (Mori et al., 2017), there is a conflict between risk reduction and cost, so they cannot reach the optimal solution at the same time. Therefore, improving one objective of the multi-objective optimization model may lead to the loss of another objective. This study employs the Epsilon restriction method to solve small-scale problems and three meta-heuristic algorithms to solve medium- and large-scale problems.

4.1. Genetic algorithm (GA) algorithm

The genetic algorithm (GA) is a stochastic optimization method that simulates the process of natural evolution to solve problems (Cao et al., 2020), which is among the methods of evolutionary computation (Valizadeh et al., 2021). We consider the chromosomes corresponding to the binary variables of the robust model (${\alpha }_{\mathit{rt}}^s$, ${\beta }_{\mathit{tkij}}^s$, ${\mathrm{{\rm Y}}}_{\mathit{ktf}}^s$). Hence, the value of each variable is a two-dimensional matrix called $X$. The number of rows equals the number of scenarios, while the number of matrix columns equals the number of vaccination centers. Note that in a matrix $Y$, the number of columns is equal to the number of vehicles. The data of the matrix represents vaccines in the VSC network under different scenarios. Matrix $X$ and matrix $Y$ are illustrated in Fig. 2 :

Fig. 2.

The detail of Matrix $X$ and..$Y$

Next, the chromosomes must be encoded to determine the variables (${\alpha }_{\mathit{rt}}^s$, ${\beta }_{\mathit{tkij}}^s$, ${\mathrm{{\rm Y}}}_{\mathit{ktf}}^s$). The chromosomes are encoded according to the following pseudocode:

Algorithm 1

The procedure of computing the binary variables.

Step 1: Input matrix ($X$)

Step 2:  For (r$=1$ to R)

Step 3:  For (k$=1$ to K)

Step 4   For ($s=1$ to S)

Step 5:    If$X\left(r,k\right)=i$then;

Step 6:     ${\alpha }_{\mathit{rt}}^s=1$;

${\beta }_{\mathit{tkij}}^s=1$;

${\mathrm{{\rm Y}}}_{\mathit{ktf}}^s=1$;

Step 7    End If

Step 8:   End For

Step 9:   End For

Step 10:  End For

Step 11: Return${\alpha }_{\mathit{rt}}^s$, ${\beta }_{\mathit{tkij}}^s$, ${\mathrm{{\rm Y}}}_{\mathit{ktf}}^s$

In the next step, the process of crossover is performed, which includes the process of combining chromosomes. At this step, two chromosomes are selected from the initial population, called parents, and then a crossover is performed using one (or more) combination methods. There are various methods for operating on intersections, including one-point intersections, two-point intersections, $k$-point intersections, and uniform intersections (Valizadeh et al., 2021). The chromosomes produced are called offspring chromosomes. Then, by keeping the second part of the offspring chromosomes constant, we remove the duplicate genes (numbers) in the first part and put the numbers that have not been used in the chromosome in the empty genes (See Fig. 3 ).

Fig. 3.

Position updating in GWO (Gu et al., 2019).

In the next step, the mutation operator, as another operator, is placed next to the intersection operator. In other words, this operator makes unplanned, random changes on different chromosomes and inserts genes that were not present in the original population. In this research, the mutation operator in the form of exchange or displacement has been used. After selecting a chromosome from the original population, two genes are randomly selected from among the genes on that chromosome. Then a new chromosome will be produced by moving the two selected genes (See Fig. 4a, Fig. 4b ).

Fig. 4a.

PBO global search (Połap and Wozniak, 2017).

Fig. 4b.

PBO global search (Połap and Wozniak, 2017).

The pseudocode of the proposed GA is as below:

Algorithm 2

Pseudocode of the proposed GA.

Step 1: Generate initial population for leader’s Pop (Create random population (nPop));

Step 2: Evaluate population (nPop)) to create fitness values

Step 3: Sort ' 'leader's population and save the best solution;

Step 4:  While (Not termination condition) do:

Select P1 and P2 by roulette wheel selection;

Apply crossover to P1 and P2 and obtain two offspring's P′1 and P′2

Evaluate P′1 and P′2

Generate P (n+1) from P1 and P2, P′1 and P′2

Set n:=n+1

End.

Step 5: Stop.

4.2. Grey Wolf Optimizer (GWO) algorithm

The Grey Wolf Optimizer algorithm was proposed in 2014 based on the life of gray wolves (Mirjalili et al., 2014). These animals live in groups and the group leader, Alpha, is responsible for making decisions such as attack and timing. The hunting method for these animals, inspired by this optimization algorithm, includes the following three steps:

• Catching, stalking, and approaching the game

• Stalking and surrounding prey until prey stops moving

• Attack on the hunting side

To model, the social behavior of wolves, a random population of solutions is generated, and the best solution called alpha ($\alpha$), the second and third-best solutions, are also called beta ($\beta$) and delta ($\delta$), respectively. Other solutions are also considered omega ($\omega$) lobes. The gray lobe algorithm uses three solutions $\beta$, $\alpha$, and δ to guide hunting (optimization) and the $\omega$ solutions follow these three. For three-dimensional modeling, the points around the prey are determined, then the prey is moved, and finally, the prey is attacked (Mirjalili et al., 2014).

4.3. Polar bear optimization (PBO) algorithm

Polar bear optimization is a population-based meta-heuristic optimization algorithm that was first introduced by Połap and Woźniak (2017). PBO algorithm simulates the hunting abilities of polar bear in severe arctic territories. This algorithm has three distinctive phases of search in search space namely local search by encircling and catching prey, global search by gliding ice floats and dynamic population. Each of these stages represents some vital characteristic of Polar Bear's hunting method in arctic zones and is described below.

PBO algorithm begins its search by arbitrarily adjusting each polar bear having $n$ coordinates as characterized by $\overline{X}=\left(x_1,x_1,...,x_{n-1}\right)$ and then propels itself to find optimum solution in search space using global and local search strategies. The polar bear search methods for food shows in Fig. 5a, Fig. 5b (Połap & Woźniak, 2017). (1) PBO global search: Possible positions of polar bear while global movement on the ice floe in the search of seal habitats for hunting. (2) PBO local search: polar bear hunting movement in search for the best position to attack the seal.

Fig. 5c.

Hard besiege with progressive rapid dives.

Fig. 5a.

Soft besiege with one hawk.

Fig. 5b.

Soft besiege with progressive rapid dives.

4.4. Harris hawks Optimization (HHO) algorithm

The HHO algorithm is a new swarm intelligence optimization algorithm that was proposed by Heidari et al. (2019). The algorithm has been shown to perform efficiently in the optimization domain relative to other metaheuristic algorithms. Moreover, the algorithm can be extended to successfully solve multiple types of optimization problems, exhibiting a good level of performance (Chen et al., 2020).

HHO algorithm is presented based on the hunting of the hawk. This bird has a unique mechanism to find prey and hunt it. The hunting mechanism is such that some hawks make short tours or searches one after the other and then land on relatively high places. As such, hawks sometimes perform a “leapfrog” movement across the target area, rejoining and separating several times to actively search for the target animal Harris's hawks' main tactic for catching prey is the “surprise pounce,” also known as the “seven kills” strategy. In this clever strategy, several hawks attempt to jointly attack the prey from different directions, simultaneously converging on a fleeing rabbit detected outside cover.

The attack may be completed quickly by capturing the prey by surprise in seconds. But sometimes, depending on the prey's escape capabilities and behavior, seven kills may involve multiple, short, rapid dives near the prey over several minutes. Harris's hawks can display various pursuit styles that depend on the dynamic nature of the conditions and patterns of escape from prey. The switching tactic occurs when the best hawk (leader) lands on the prey and is lost, and a group member continues the chase. Harris's hawk hunting mechanism with four types of hunting attacks is shown in Fig. 6 . (Heidari et al., 2019).

Fig. 6.

Comparison of the GA, GWO, PBO, and HHO algorithms for medium and large-scale problems.

5. Numerical experiments

To validate the proposed model, we conduct comprehensive numerical experiments using Kermanshah city as a case study, which is the fifth metropolis in Iran with a population of about 1.3 million. Like other cities in Iran, this city has suffered many casualties during the COVID-19 epidemic. In this study, we consider two types of vaccination centers for vaccination programs in Kermanshah, including fixed vaccination centers and vehicles serving as mobile stations for the vaccination of citizens who cannot travel to the vaccination centers (e.g., the disabled and the elderly). Hospitals are considered vaccine suppliers for vaccine centers, which are also vaccine banks for vehicles. In other words, hospitals have no vaccination operation, and they are only responsible for providing vaccines to other centers. All problem instances are solved by CPLEX 12.9 on a Core i7 CPU 3.40 GHz computer equipped with 8:00 GB RAM under Windows 10.

5.1. Experimental design

In Kermanshah, eight hospitals provide the necessary vaccines for 12 fixed vaccination centers and 15 vehicles (mobile stations). Relevant data used in the numerical experiments are collected from multiple sources, like the Statistics Center of Iran and the Health Center of Kermanshah, shown in Table 2 .

Table 2.

Relevant parameter values.

Parameter	Surface	Parameter	Surface
${\mathit{fc}}_{\mathit{rt}}$	∼ U (11000, 85000)	${\sigma }_{\mathit{ht}}$	∼ U (0.2, 1)
${\mathit{ck}}_{\mathit{kijt}}$	∼ U (25000, 65,000)	${\xi }_{\mathit{ht}}$	∼ U (0.2, 1)
${\mathit{ch}}_{\mathit{ht}}$	∼ U (2, 6)	$d_{\mathit{ht}}$	∼ U (200000, 800000)
${\mathit{ce}}_{\mathit{ht}}$	∼ U (5, 12)	${\mathit{nr}}_{\mathit{rt}}$	∼ U (10, 30)
${\mathit{ct}}_k$	∼ U (20, 55)	${\mathit{nk}}_{\mathit{kijt}}$	∼ U (4, 15)
${\mathit{cs}}_{\mathit{ht}}$	∼ U (5000, 60000)	$g_k$	∼ U (5000, 12000)
${\mathit{np}}_{\mathit{pht}}$	∼ U (10000, 400000)	${\mathit{nh}}_{\mathit{ft}}$	∼ U (600000, 1800000)

To calculate the distribution inequality rate of the vaccine, we assume two coordinate axes with a length of 100 units. Suppose we ideally connect the intersection of each point of the curve related to the population with the time of receiving the vaccine. In that case, the even vaccine distribution index curve is obtained as a straight line with a square diameter. If people in the community do not receive the vaccine or receive the vaccine later than others, the curve will deviate from the ideal state. This deviation is calculated by the following equation and shows a value between zero and one:

$$r{l}_{\mathit{vltcp}}=\frac{1}{E\left({\mu }^n\right)}{\int }_0^n{x}^{n}df\left(n\right),\forall x\ge 0,n\in N$$ (56)

Four categories of multiple demand levels scenarios are considered: low demand, medium demand, high demand, and very high demand, and each comes with its corresponding probability. Table 3 shows the demand for 18 different areas in Kermanshah.

Table 3.

The amount of demand in different scenarios.

Possibility	Number of demands									Scenarios
	1	2	3	4	5	6	7	8	9
0.25	467	359	325	409	379	379	305	488	392	Very High demand
0.35	342	315	294	305	335	311	300	297	355	High demand
0.25	314	279	242	237	259	241	235	211	330	Medium demand
0.15	112	125	151	97	154	103	100	165	246	Low demand
	10	11	12	13	14	15	16	17	18
0.25	392	503	459	372	547	467	457	399	413	High demand
0.35	383	374	355	335	388	305	330	365	369	Medium demand
0.25	207	207	294	236	285	262	251	228	263	Low demand
0.15	154	182	190	135	149	114	162	126	105	Very Low demand

The distances between the identified areas for dispatching vehicles serving for vaccination are shown in Table 4 .

Table 4.

Transportation distance by a vehicle between areas (km).

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
1	–	–	–	–	–	–	–	–	6	–	–	–	–	–	–	–	–	–
2	–	–	–	–	–	–	–	–	–	7	–	–	–	–	–	–	–	–
3	–	–	–	–	–	–	–	–	–	–	3.4	–	–	–	–	–	–	5.36
4	–	–	–	–	–	3.85	–	–	–	–	–	–	–	–	–	–	–	–
5	–	–	–	–	–	–	–	–	–	–	–	–	5.15	–	–	–	–	–
6	–	–	–	–	2.61	–	4.19	–	–	–	–	–	–	–	–	2.18	–	–
7	–	–	–	–	–	–	–	2.56	–	–	–	5.03	–	–	–	–	–	–
8	2.17	–	–	–	–	–	–	–	4.1	–	–	–	2.43	–	–	–	–	–
9	–	–	–	3.02	–	–	–	–	–	–	4	–	–	–	–	–	–	–
10	–	1.55	–	–	–	–	–	–	–	–	–	–	–	4.22	3.96	–	–	–
11	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
12	–	–	3.84	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
13	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	3.7	–
14	–	–	–	–	–	–	–	3.89	–	–	–	–	–	–	–	–	–	–
15	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–	–
16	–	–	–	–	–	–	–	–	–	3.8	–	–	–	–	–	–	–	–
17	–	–	–	–	–	–	–	–	–	–	4.21	–	–	–	–	–	–	–
18	–	–	–	–	4.18	–	–	–	–	–	–	–	–	–	–	4.18	–	–

In order to adjust the parameters of the meta-heuristic algorithms, several statistical methods exist for designing experiments. Taguchi (1986) improved a family of partial factorial experiment matrices so that he could, after much experimentation, execute a test design in such a way as to reduce the number of experiments for a problem. In general, Taguchi (1986) recommended analyzing changes using a properly selected signal-to-noise ($S/N$). The term signal refers to the optimal value (solution variable), and the noise refers to the unfeasible value (standard deviation). Three ratios are usually considered as below:

Best nominal: Used if it is intended to reduce variability around a specific target value.

$$\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$N_T$}\right.=10\log \left(\frac{\overline{y^2}}{s^2}\right)$$ (57)

Larger is better: Used if system optimization is achieved when the solution is as large as possible.

$$\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$N_L$}\right.=-10\log \left(\frac{1}{n}\sum _i^n\frac{1}{y_i^2}\right)$$ (58)

Smaller is better: Used if system optimization is achieved when the solution is as small as possible.

$$\raisebox{1ex}{$S$}\!\left/ \!\raisebox{-1ex}{$N_S$}\right.=-10\log \left(\frac{1}{n}\sum _i^n{y}_i^2\right)$$ (59)

wherein $N$ is the number of runs of each experiment and $y_i$ is the process solutions. Two meta-heuristic algorithms are used in the numerical experiments to obtain and compare solutions under different problem settings, as shown in Table 5 .

Table 5.

Parameter settings of the two meta-heuristic algorithms for different problem sizes.

Problem size	Algorithm	Number of repetitions	Population	Mutation rate	Intersection probability
Small-scale	GA	100	50	0.7	0.2
	GWO	80	30	0.7	0.1
	PBO	100	60	0.8	0.1
	HHO	100	60	0.8	0.1
Medium-scale	GA	100	50	0.7	0.2
	GWO	100	60	0.8	0.2
	PBO	100	60	0.8	0.2
	HHO	100	60	0.8	0.2
Large-scale	GA	120	100	0.7	0.3
	GWO	120	100	0.8	0.3
	PBO	120	100	0.8	0.3
	HHO	120	100	0.8	0.3

5.2. Results and discussion

Table 6 shows the comparison results (based on ten problem instances) between the exact solution method (Epsilon restriction method in the GAMS software) and the proposed GA, GWO, PBO, and HHO algorithms. It can be observed that the Epsilon restriction method fails to solve the problem on a large scale, and the computation time increases exponentially with increasing problem size, which is due to the NP-hardness of the problem.

Table 6.

Comparison of the results for different problem sizes.

Problem	Exact		GA			GWO			PBO			HHO
	Time	result	Time	Ave.	Best	Time	Ave.	Best	Time	Ave.	Best	Time	Ave.	Best
S01	44	903,687	93	800,327	790,287	83	835,365	815,305	98	771,618	713,822	89	787,200	765,038
S02	45	1,208,304	94	901,033	890,993	84	959,698	939,638	99	868,711	803,631	90	891,557	879,429
S03	53	1,507,789	104	1,517,660	1,517,660	93	1,754,154	1,553,554	110	1,463,220	1,353,435	100	1,515,926	1,413,681
M04	55	1,560,602	108	1,867,934	1,841,248	98	1,975,366	1,867,276	114	1,800,928	1,666,067	104	1,848,391	1,746,076
M05	72	3,698,894	110	4,951,038	4,872,923	99	5,239,371	4,949,626	116	4,773,437	4,416,054	106	4,810,293	4,806,066
M06	89	6,293,699	116	8,902,063	8,670,748	104	9,507,349	8,903,618	122	8,582,733	7,941,041	112	8,724,873	8,420,541
L07	NA	NA	120	10,717,159	10,288,680	108	15,633,464	10,766,502	126	10,332,719	9,570,510	116	10,422,285	10,017,928
L08	NA	NA	130	16,139,720	15,616,984	117	19,951,159	16,282,902	137	15,560,764	14,427,878	125	15,915,250	15,510,993
L09	NA	NA	133	23,525,212	22,742,367	120	26,320,433	23,763,227	141	22,681,328	21,036,410	129	22,935,963	22,331,644
L10	NA	NA	144	26,480,396	24,421,138	130	29,693,021	26,772,977	152	25,530,505	23,684,319	139	26,043,348	24,039,035
Average	NA	NA	115	9,580,254	9,165,303	103	11,129,478	9,632,565	122	9,236,596	8,561,317	111	9,389,509	8,993,043

In Table 6, the input data for solving the model are classified into ten rows. We have three rows for the small-scale problem, denoted by S01-S03. In addition, three rows for the medium-scale problem with M04-M06 and finally-four rows for the large-scale problem with L07-L10. Based on the data in Table 6, it can be seen that the GWO algorithm needs less time to solve the problem and performs better than the GA, PBO, and HHO algorithms and the Epsilon method. However, due to the nature of the minimization of objective functions, it can be seen that the exact solution method in solving small and medium scales with a significant difference has a suitable performance compared to the proposed algorithms. Finally, the solutions obtained from the GA, PBO, and HHO algorithms are relatively close to each other, but the PBO algorithm performs better than the other algorithms in finding the optimal solution.

After coding, to evaluate the efficiency and performance of the GA, GWO, PBO, and HHO algorithms, the problem was evaluated in 10 sample problems, as Table 6. Ten sample problems are generated to compare GA, GWO, PBO, and HHO algorithms using the criteria: Percentage of Improvement Best Solution (PIBS), Percentage of Improvement Average Solution (PIAS) and computational time. PIBS and PIAS can be calculated by Eqs (60), (61), respectively. The comparison results are shown in Table 7 .

$$\%PIBS=\frac{\mathit{Bes}{t}_{A\lg 1}-Bes{t}_{A\lg 2}}{\mathit{Bes}{t}_{A\lg 1}}$$ (60)

$$\%PIAS=\frac{\mathit{Av}{e}_{A\lg 1}-Av{e}_{A\lg 2}}{\mathit{Av}{e}_{A\lg 1}}$$ (61)

Table 7.

Comparison of GA, GWO, PBO, and HHO based on sample problems.

Problem	GA & GWO		GA & PBO		GA & HHO		GWO & PBO		GWO & HHO		PBO & HHO
	%PIAS	%PIBS	%PIAS	%PIBS	%PIAS	%PIBS	%PIAS	%PIBS	%PIAS	%PIBS	%PIAS	%PIBS
1	0.032	0.043	0.093	0.032	0.028	0.040	0.122	0.051	0.059	0.032	0.067	0.020
2	0.053	0.062	0.094	0.032	0.009	0.020	0.142	0.073	0.061	0.048	0.086	0.026
3	0.024	0.136	0.105	0.032	0.065	0.065	0.126	0.055	0.087	0.021	0.043	0.035
4	0.015	0.055	0.092	0.032	0.048	0.061	0.105	0.086	0.062	0.061	0.046	0.026
5	0.016	0.056	0.090	0.032	0.010	0.025	0.105	0.086	0.026	0.079	0.081	0.008
6	0.027	0.065	0.080	0.032	0.025	0.050	0.105	0.095	0.051	0.080	0.057	0.016
7	0.045	0.315	0.066	0.032	0.022	0.062	0.108	0.337	0.067	0.331	0.045	0.009
8	0.042	0.192	0.072	0.032	0.003	0.035	0.111	0.218	0.045	0.200	0.070	0.022
9	0.044	0.107	0.071	0.032	0.014	0.047	0.112	0.136	0.057	0.126	0.058	0.011
10	0.089	0.109	0.026	0.032	0.012	0.089	0.113	0.138	0.099	0.120	0.015	0.020
Average	0.039	0.114	0.079	0.032	0.024	0.049	0.115	0.127	0.062	0.110	0.057	0.019

As it can be seen from the average of reports obtained in Table 7, the lowest averages obtained are between the values of GA and HHO algorithms. In contrast, the highest average value is related to GWO and PBO algorithms.

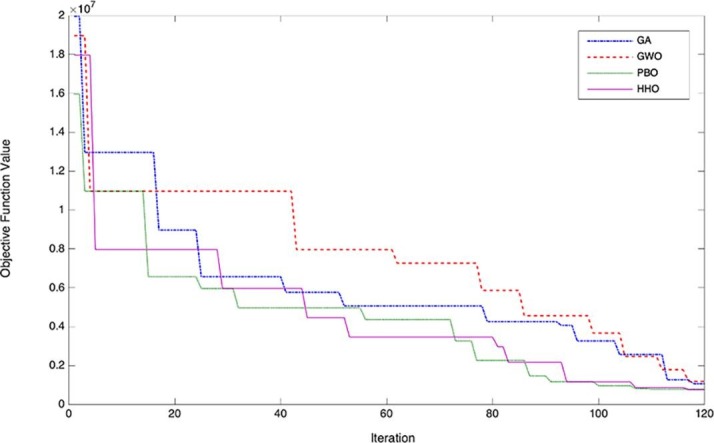
Fig. 6 shows the change of value in the objective function within 120 iterations. Due to the inability of GAMS software to solve the large-scale problem, we have compared the proposed algorithms in this figure. As shown in Fig. 6, the PBO algorithm performs better than other algorithms. However, the GWO algorithm could not find the optimal solution compared to other algorithms.

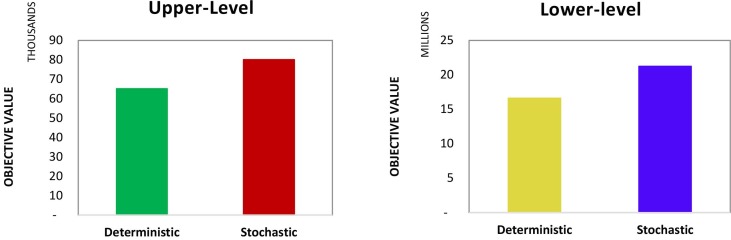
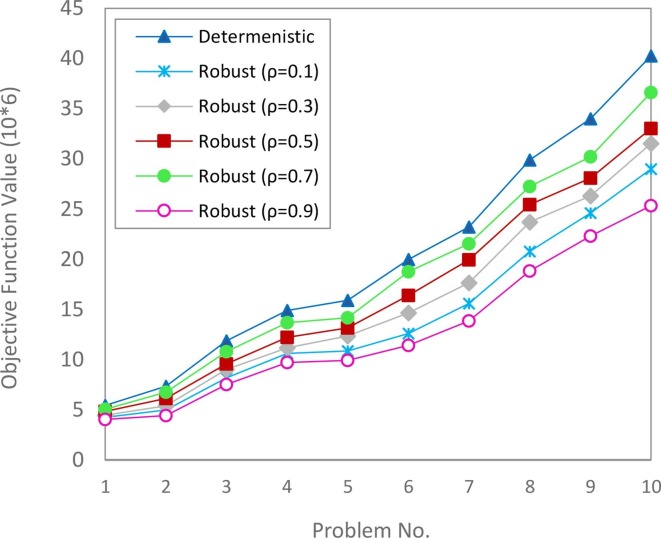
Fig. 7 shows the optimal values obtained for the two levels of the proposed model. Note that, according to the scenarios, the risks related to the distribution inequality of vaccines are more significant with the number of demands increasing. At the same time, the total costs will also increase. Fig. 7 compares the differences between the optimal solutions obtained in both deterministic and stochastic solutions for each of the levels of the proposed model. In comparison, it can be seen that the stochastic solution increases the total costs by 23 %. This increase is due to the consideration of demand in various scenarios. Moreover, at the upper level of the model, it can be seen that the risks of the VSC network in the stochastic model are 28 % more than the model in the deterministic case.

Fig. 7.

The results for the objective function values.

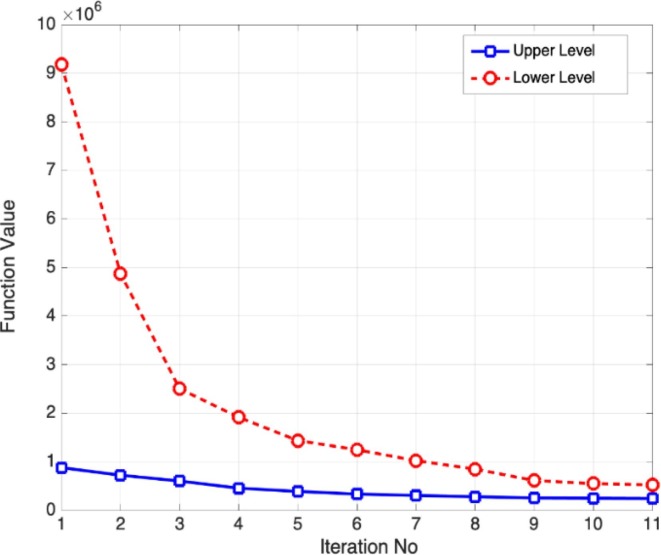
Fig. 8 shows that during ten iterations of the problem, the risks of the VSC network are significantly reduced. This result is due to the proper use of existing capacities to supply and distribute vaccines. In addition, in Fig. 8, it can be seen that the total cost is decreasing with a greater slope than the risk of mortality, and this shows that the proposed model has a greater impact on cost reduction than the risks of the VSC network.

Fig. 8.

Effect of changes in the value of the function.

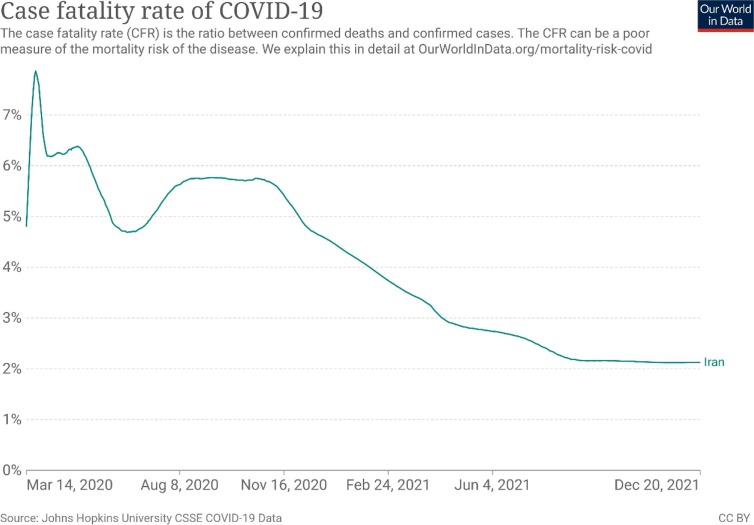
According to the results obtained from the analysis of the upper-level of the proposed model in comparison with the current status 1 (Fig. 9 ). It can be seen that the proposed model has calculated the mortality risk with a relatively accurate approximation. Based on this result, the proposed model will be able to reduce the risk of mortality due to not receiving the vaccine on time based on correct input data. Although the proposed model supports COVID-19 pandemic data, it can be used in similar situations in the future to obtain reliable results.

Fig. 9.

The measures the mortality risk of COVID-19 in Iran.

To achieve reliable results and evaluate the performance of the proposed model, it is necessary to assess the model's robustness and the solution's robustness. For this purpose, stochastic parameters are quantified in the model, and the obtained results are examined. Accordingly, sensitivity analysis has been carried out on the model parameters.

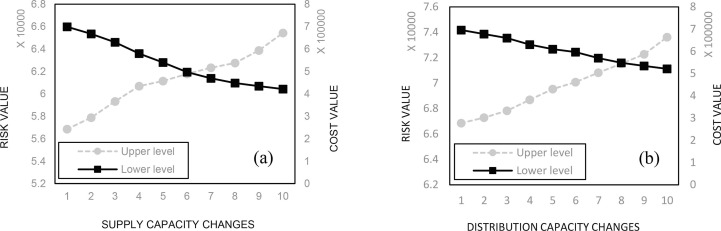
In this section, we will examine the effect of the weight of some variables on the model's performance. In this research, it was assumed that the number of suppliers and their capacity is limited. As shown in Fig. 10 (a), increasing the capacity of vaccine suppliers has caused the value of the risk objective function to decrease dramatically. Obviously, with more vaccine supply, the shortage of covered vaccines will increase their availability. But note that the value of the risk objective function also depends on other factors, such as the capacity of distributors. Therefore, even though the slope of the graph is high in the first iterations, the slope of the graph decreases gradually, showing the effect of the fair distribution of the vaccine. In addition, it is shown in Fig. 10(a) that with the increase in the capacity of vaccine suppliers, the network costs change and show an upward trend. In other words, increasing the capacity of vaccine suppliers has increased the flow of vaccine distribution and consequently increased the distribution costs.

Fig. 10.

Changes in the value of objective functions based on capacity.

On the other hand, the obtained values related to the changes in vaccine distribution capacity are shown in Fig. 10(b). As seen in Fig. 10(b), the value of the risk objective function decreases in different iterations while the value of the cost objective function grows. In other words, by increasing the capacity of the distributors, the risk of fair vaccine distribution decreases, and this effect is reflected in the final value of the risk objective function.

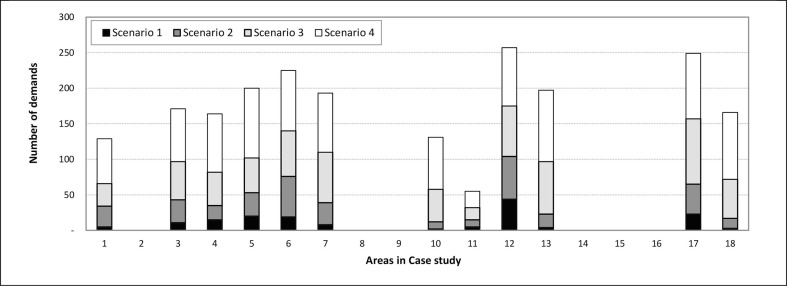
Fig. 11 shows the trend of unmet demands for vaccines in four possible scenarios. As Fig. 11 shows, the trend of vaccine shortage in scenarios 3 and 4 is upward, and the network is facing a large shortage. Obviously, to reduce the effect of the parameter (${\mathit{nh}}_{\mathit{ft}}$) on the performance of objective functions, suppliers should increase the value of this parameter and provide more vaccines. However, due to the vaccine supply limitations, it is impossible to increase the parameter (${\mathit{nh}}_{\mathit{ft}}$). Meanwhile, in some areas, the amount of excess vaccine has been allocated, which can be used to balance the inventory.

Fig. 11.

The vaccine shortage in four possible scenarios.

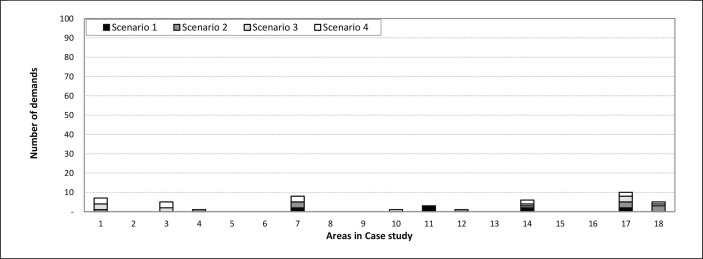
Fig. 12 shows the demand values after balancing the vaccine inventory in different areas. This fig shows that most demands are met in all four scenarios. One of the reasons for covering the vaccine shortage was the fair distribution of the vaccine among the areas. In other words, the previous fig shows no shortage in areas 2, 8, 9, 14, 15, and 16. This is even though there are a number of vaccines in these areas. Therefore, part of the shortage of vaccines in the network was covered by allocating additional vaccines to the shortage areas. But the main reason is that by referring to the capabilities of the robust model, it can be seen that the effect of stochastic parameters will significantly impact the performance of the objective functions. Therefore, the changes in stochastic parameters on the model's performance are evaluated in the following.

Fig. 12.

The demand values after balancing the inventory.

To bring supply and demand closer together, it can be helpful to adjust the stochastic parameters considered in the robust model. Fig. 13 shows the changes in the values of the objective functions in different scenarios when the variable significance coefficient parameter ($\omega$) and the model importance coefficient parameter ($\lambda$) are different. According to the explanations provided in the previous section, it is clear that by increasing the value of the ω parameter, the flexibility of the model can be increased, and the negative impact of vaccine shortage can be improved. Therefore, Fig. 13 shows how much increasing the parameter value ($\lambda$) can affect the value of the objective functions.

Fig. 13.

The changes of the objective functions based on weight $\lambda .$

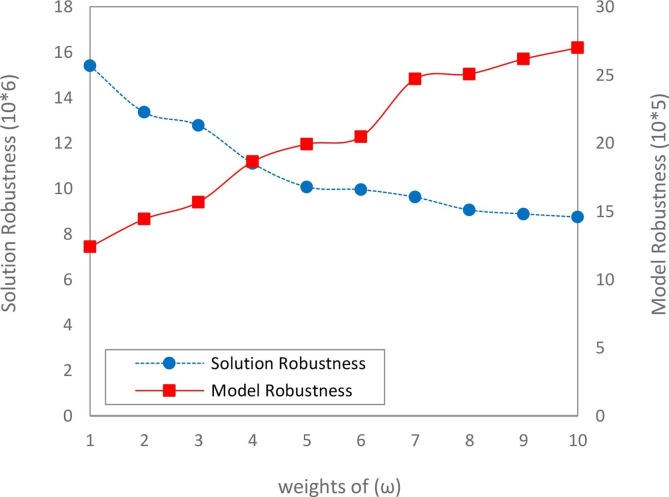
Evaluation of model robustness and solution robustness is based on the weight of $\omega$, which indicates the feasibility of the model (Valizadeh et al., 2021). As shown in Fig. 14 , the model robustness shows various values based on the different values $\omega$. The various values obtained for the model robustness show that the robust model's control constraints significantly impact the proposed model's performance. Fig. 14 also shows that as the weight $\omega$ increases, the solution robustness increases. But with increasing weight $\omega$, we see a downward trend in the model robustness, which is due to the nature of the problem minimization. In other words, with increasing weight $\omega$, although the model robustness is feasible, in each scenario, an increase in the cost objective function has occurred. Because the proposed model is bi-level, increasing the weight of $\omega$ each scenario (indicating increasing the number of demands for the vaccine) also increases the risks of distribution inequality.

Fig. 14.

The model robustness and the solution robustness based on weight..$\omega$.

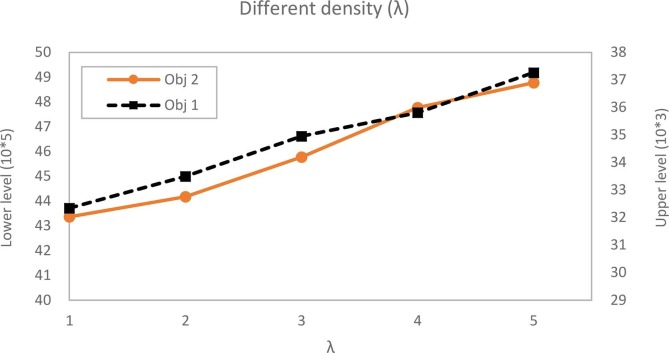
In addition, to examine the model's performance in more detail and investigate the feasibility based on the fluctuations of uncertain parameters, in Fig. 15 , the sensitivity analysis of the model based on the change in the parameter $\rho$ has been performed. According to the obtained results, it can be seen that the probability of occurrence of various scenarios has a significant impact on the results, and this effect is significant in the larger dimensions of the problem.

Fig. 15.

Sensitivity analysis for the proposed model.

6. Managerial insights

This paper proposed a BLP model for the VSC to reduce potential risks as governments' concerns at the upper level and minimize the operational costs of vaccination during the COVID-19 pandemic. The numerical results lead to some valuable managerial insights:

• It is challenging to maintain a system regardless of the risks. In other words, developing a model without considering the potential risks makes that model inefficient and impractical in the real world. This study proposes an efficient model regarding mortality risk due to the vaccines' untimely supply and distribution inequality. This result is in line with the findings of Kohli et al. (2021).

• Due to limited resources, high costs of public vaccination, and the economic crisis in most countries due to the COVID-19 pandemic, reducing the costs of the VSC network is one of the major concerns for health care network managers. Accordingly, the proposed model tried to minimize the costs of the VSCN, taking into account the existing capacity and the number of uncertain demands for the vaccine. As shown in Fig. 7, the total cost is reduced by 23 %. Therefore, managers can decide on VSC network costs by following the proposed model. This result is in line with the findings of Bozorgi and Fahimnia, 2021, Lee et al., 2016, Carvalho et al., 2019, Georgiadis and Georgiadis, 2021, Sazvar et al., 2021.

• In particular, designing mathematical models in applied problems reduces the model's flexibility in uncertain (real-world) conditions. Therefore, in the proposed model, considering various scenarios as well as considering the demand for vaccines indefinitely can be of great help in solving this problem. Although considering stochastic parameters in the proposed model increases costs (Fig. 7), the risks of the VSC network are reduced by up to 28 %. This result is derived exclusively from the findings of this study and cannot be generalized to other studies.

• According to the results of Fig. 10, it was found that as the number of demands for vaccines increases in various scenarios, the risk of mortality and the risk and the risk of distribution inequality of the vaccine also increase. Based on this, managers will be able to use the proposed model to make appropriate decisions to balance the capacity of vaccination centers and vehicles so that there is the least risk in the vaccination network during the COVID-19 pandemic. This result is also derived exclusively from this study's findings and cannot be generalized to other studies.

• A fascinating managerial insight can be gained by examining the relationship between the problem parameters. Eq. (56), which calculates the vaccine inequality rate, shows that if people in the community do not receive the vaccine or receive the vaccine later than others, the distribution inequality rate of the vaccine increases (this rate is firmly dependent on the vaccine shortage parameter). Due to the direct relationship between this parameter and the mortality risk in the proposed model, increasing the distribution inequality rate of the vaccine will increase the mortality risk. Therefore, managers should pay special attention to vaccines' equality and timely distribution. They should manage the vaccination planning if there is a shortage of vaccines so that their allocation is fair and among all demands. Finally, using a bi-level model helps managers manage the vaccination network better by simultaneously considering two concerns (risk and cost).

7. Conclusions

This paper proposed a decision support system for the VSC network during the COVID-19 pandemic. A robust BLP model is developed considering the government's concerns, including the risk of mortality due to untimely supply and the risk of unfair vaccine distribution, as the upper level in the proposed model. In addition, the concern of organizations involved in the vaccination network regarding the VSC operating costs has been considered as the lower level of the proposed model. Besides, considering the uncertain demand and various scenarios, an attempt was also made to propose a robust mathematical model for the vaccination program in Kermanshah as a case study.

Due to the complexity of the BLP model, KKT conditions were used to convert the bi-level model to a single-level model. The Epsilon constraint method was used in GAMS software to solve the model on a small scale. In addition, due to the complexity of the problem on medium and large scales, GA, GWO, PBO, and HHO algorithms were used. The results show that despite the high demand for vaccines during the COVID-19 pandemic, the proposed model was able to reduce total cost according to the four scenarios.

We have several suggestions for future research: (1) Given the different mutations of the virus in some countries, considering the vaccination failure rate in future models can be an exciting topic. (2) Given the relative effectiveness of general vaccination during the COVID-19 pandemic, predicting pandemic status after vaccination is another decent research area for future researchers. (3) Considering reliability and considering the components of stability in new models can be another focus for future research. (4) Finally, we suggest that some other parameters be considered, including the success rate of vaccination, other types of virus (or virus mutations), and the degree of resistance to the vaccine.

CRediT authorship contribution statement

Jaber Valizadeh: Conceptualization, Formal analysis, Methodology, Visualization, Writing – original draft. Shadi Boloukifar: Methodology, Software, Investigation. Sepehr Soltani: Software, Investigation. Ehsan Jabalbarezi Hookerd: Methodology, Writing – review & editing. Farzaneh Fouladi: Writing – review & editing. Anastasia Andreevna Rushchtc: Writing – review & editing. Bo Du: Formal analysis, Writing – original draft, Writing – review & editing. Jun Shen: Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.

$$\mathit{Min}Z1=\mathcal{A}+\sum _{s\in S}{\mathcal{B}}_s+\lambda \sum _{s\in S}{\rho }_s\left[\left({\mathcal{B}}_s\right)-\left({\mathcal{B}}_{s\prime }\right)+2{\theta }_s\right]+\omega \sum _{s\in S}\sum _{k\in K}{\rho }_s{\delta }_{\mathit{ks}}$$ (A.1)

$$\mathit{Min}Z2=\mathcal{H}+\mathcal{J}+\sum _{s\in S}{\mathcal{K}}_s+\sum _{s\in S}{\mathcal{L}}_s+\sum _{s\in S}{\mathcal{Q}}_s+\sum _{s\in S}{\mathcal{R}}_s+\lambda \sum _{s\in S}{\rho }_s\left[\left({\mathcal{K}}_s+{\mathcal{L}}_s+{\mathcal{Q}}_s+{\mathcal{R}}_s\right)-\left({\mathcal{K}}_{s\prime }+{\mathcal{L}}_{s\prime }+{\mathcal{Q}}_{s\prime }+{\mathcal{R}}_{s\prime }\right)+2{\theta \prime }_s\right]+\omega \sum _{s\in S}\sum _{k\in K}{\rho }_s{\delta \prime }_{\mathit{ks}}$$ (A.2)

$$\left({\mathcal{B}}_s\right)-\left({\mathcal{B}}_{s\prime }\right)+{\theta }_s\ge 0\forall s\in S$$ (A.3)

$$\left({\mathcal{K}}_s+{\mathcal{L}}_s+{\mathcal{Q}}_s+{\mathcal{R}}_s\right)-\left({\mathcal{K}}_{s\prime }+{\mathcal{L}}_{s\prime }+{\mathcal{Q}}_{s\prime }+{\mathcal{R}}_{s\prime }\right)+{\theta \prime }_s\ge 0\forall s\in S$$ (A.4)

$$R\left(Y\right)={\rho }_s\left({\mathcal{K}}_s+{\mathcal{L}}_s+{\mathcal{Q}}_s+{\mathcal{R}}_s\right)+\lambda \sum _{s\in S}{\rho }_s\left(\left({\mathcal{K}}_s+{\mathcal{L}}_s+{\mathcal{Q}}_s+{\mathcal{R}}_s\right)-\left({\mathcal{K}}_{s\prime }+{\mathcal{L}}_{s\prime }+{\mathcal{Q}}_{s\prime }+{\mathcal{R}}_{s\prime }\right)+2{\theta }_s\right)+\omega \sum _{s\in S}\sum _{k\in K}{\rho }_s{\mathrm{\delta }}_{\mathit{ks}}$$ (A.5)

$$-\sum _t\sum _s{\pi }_{\mathit{ts}}^1\left(\sum _r{\alpha }_{\mathit{rt}}^s-1\right)$$ (A.6)

$$-\sum _h\sum _t\sum _s{\pi }_{\mathit{hts}}^2\left(\left[d_{\mathit{ht}}^s+{\partial }_{\mathit{ht}}^s\right]-\sum _h\sum _f{U}_{\mathit{hft}}{\mathit{nh}}_{\mathit{ft}}\right)$$ (A.7)

$$-\sum _t\sum _s{\pi }_{\mathit{ts}}^3\left(\sum _h{\partial }_{\mathit{ht}}^s-1\right)$$ (A.8)

$$-\sum _k\sum _t\sum _s{\pi }_{\mathit{kts}}^4\left(\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkij}}^s-1\right)$$ (A.9)

$$-\sum _k\sum _t\sum _s{\pi }_{\mathit{kts}}^5\left(-\sum _{i,j/(i\ne j)}{\beta }_{\mathit{tkij}}^s\right)$$ (A.10)

$-{\sum }_k{\sum }_t{\sum }_s{\pi }_{\mathit{kts}}^6\left({\sum }_f{\mathrm{{\rm Y}}}_{\mathit{ktf}}^s-1\right)$(A.0.11).

$$-\sum _t\sum _s{\pi }_{\mathit{ts}}^7\left(\sum _h\sum _f{U}_{\mathit{hft}}-\sum _{i,j/(i\ne j)}\sum _k{\beta }_{\mathit{tkij}}^s{g}_k\right)$$ (A-12)

$$-\sum _{s\in S}{\pi }_s^8\left(\left({\mathcal{B}}_s\right)-\left({\mathcal{B}}_{s\prime }\right)+{\theta }_s\right)$$ (A.13)

$$-\sum _{s\in S}{\pi }_s^9\left(\left({\mathcal{K}}_s+{\mathcal{L}}_s+{\mathcal{Q}}_s+{\mathcal{R}}_s\right)-\left({\mathcal{K}}_{s\prime }+{\mathcal{L}}_{s\prime }+{\mathcal{Q}}_{s\prime }+{\mathcal{R}}_{s\prime }\right)+{\theta \prime }_s\right)$$ (A.14)

$$-\sum _{s\in S}{\pi }_s^{10}\left({\theta }_s\right)$$ (A.15)

$$-\sum _{s\in S}{\pi }_s^{11}\left({\theta \prime }_s\right)$$ (A.16)

$$-\sum _{k\in K}\sum _{s\in S}{\pi }_{\mathit{ks}}^{12}\left({\mathrm{\delta }}_{\mathit{ks}}\right)$$ (A.17)

Data availability

The authors do not have permission to share data.