Abstract
Enhanced sampling methodologies modifying underlying Hamiltonians can be used for the systems with a rugged potential energy surface that makes it hard to observe convergence using conventional unbiased molecular dynamics (MD) simulations. We present CHARMM‐GUI Enhanced Sampler, a web‐based tool to prepare various enhanced sampling simulations inputs with user‐selected collective variables (CVs). Enhanced Sampler provides inputs for the following nine methods: accelerated MD, Gaussian accelerated MD, conformational flooding, metadynamics, adaptive biasing force, steered MD, temperature replica exchange MD, replica exchange solute tempering 2, and replica exchange umbrella sampling for the method‐implemented MD packages including AMBER, CHARMM, GENESIS, GROMACS, NAMD, and OpenMM. Users only need to select a group of atoms via intuitive web‐implementation in order to define commonly used nine CVs of interest: center of mass based distance, angle, dihedral, root‐mean‐square‐distance, radius of gyration, distance projected on axis, two types of angles projected on axis, and coordination numbers. The enhanced sampling methods are tested with several biological systems to illustrate their efficiency over conventional MD. Enhanced Sampler with carefully optimized system‐dependent parameters will help users to get meaningful results from their enhanced sampling simulations.
Keywords: collective variables, enhanced sampling, molecular dynamics, rare events
1. INTRODUCTION
All‐atom molecular dynamics (MD) simulation becomes an essential tool to investigate complex molecular systems and provide a molecular‐level understanding of a target system with an accurate force field (FF). 1 , 2 With increasing system complexity, however, one might not be able to observe slow processes of interest within a typical simulation time. 3 Furthermore, biomolecular systems are known to have rugged free energy landscapes involving many local minima separated by high barriers. When the system falls into those metastable states, it could stay trapped for a long time with conventional MD simulations. Therefore, various enhanced sampling methods have been proposed and applied for MD simulations to resolve such issues by modifying the underlying Hamiltonian. 4 The modifications for a better sampling efficiency involve temperature variation, non‐equilibrium force addition to the subset of the system, or reshaping underlying potential energy functions. 5 , 6 , 7 Correction toward the equilibrium Boltzmann distribution is feasible using a replica exchange method or a post hoc reweighting scheme. 8 , 9 When altering Hamiltonian with additional biasing terms, defining and utilizing the reduced representations of molecular structure called collective variables (CVs) are often required to apply effective modifications along the chosen reaction coordinate. 10
Since its establishment in 2006, CHARMM‐GUI as a web‐based infrastructure has helped numerous academic users to prepare complex molecular simulation setup. In this study, we introduce Enhanced Sampler (https://www.charmm-gui.org/input/es), a new module in CHARMM‐GUI. Enhanced Sampler provides the input generation for nine different enhanced sampling methods with reasonable initial parameters accompanied with nine commonly used CVs. 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 These enhanced sampling methods are broadly categorized into (a) biasing potential energy function, (b) adaptively biasing potential energy function, (c) pulling, and (c) replica exchange methods.
Among the methods that directly modify a given potential energy function to lower the energy barrier and facilitate the transition between states, Enhanced Sampler supports accelerated MD (aMD), Gaussian accelerated MD (GaMD), and conformational flooding (CF). 19 , 20 , 21 These methods aim to increase the probability of observing rare events during the simulation. A set of parameters to control the amount of boost for aMD and CF solely depends on the user, and the methods are suitable for rare event observation within a short amount of simulation time. GaMD can be used to obtain an equilibrium distribution after reweighting with optimized parameters that are determined from two sequential pre‐runs of conventional MD and GaMD simulations.
Metadynamics (MTD) and adaptive biasing force (ABF) methods expedite the simulation with continuous modifications of potential or free energy surfaces. 22 , 23 , 24 Both methods retain memories of visited states along the chosen CV and promote the exploration toward the under‐sampled region by either depositing Gaussian hills to the visited states or flattening the free energy surface using the potential integrated from the average mean force. One can apply external forces to the subset of system using steered MD (SMD) with a constant force or velocity during the simulation. 25 , 33 For any system with two bodies of high binding affinities, SMD accelerates an unbinding process.
Enhanced Sampler also supports replica exchange MD (REMD) simulation setup for both temperature REMD (T‐REMD) and Hamiltonian REMD (H‐REMD). 26 , 27 , 28 Many copies of the system with different temperature or Hamiltonian are run simultaneously and exchanged at a fixed interval with a Metropolis criterion to expedite the sampling. As one of the earliest REMD applications, T‐REMD is still beloved by researchers interested in temperature‐dependent properties of their system. 5 Two types of H‐REMD, replica exchange solute tempering 2 (REST2) and replica exchange umbrella sampling (REUS), are available. 29 , 30 Instead of heating up the whole system, REST2 modifies only the interactions involving a subset of the system called solute for effective tempering. In REUS, biasing potentials along a reaction coordinate ensure thorough sampling and users can retrieve the unbiased potential of mean force (PMF) using weighted histogram analysis method or multistate Bennett acceptance ratio. 34 , 35 , 36 , 37 , 38
While the enhanced sampling methods have been developed and implemented in various MD packages, the simulation setup with a certain enhanced sampling method is often non‐trivial, being an entry barrier even for simulation experts. Especially, many found it difficult to set the initial parameters of the methods that are system‐dependent. The subsequent sections describe the implementation of Enhanced Sampler including CV selections, initial parameters for each method together with its brief theoretical background, and the exemplary practical usages of some enhanced sampling methods. We expect that careful setup of enhanced sampling simulations including initial parameters from Enhanced Sampler will be useful to study biological problems more effectively and accurately.
2. RESULTS AND DISCUSSION
2.1. Workflow of Enhanced Sampler
The workflow of Enhanced Sampler is shown in Figure 1. Enhanced Sampler utilizes Solution Builder and Membrane Builder to prepare user's system in solution or a lipid bilayer. 11 , 12 First, one can download a PDB structure from RCSB or upload their own while selecting the system type of solution, bilayer, or bilayer only. Through PDB Reader and Manipulator, users can model the segments (protein, ligand, RNA, etc) in the system. 39 Additionally, users can handle missing residues, mutate residues, protonate, glycosylate, and do many more. If a bilayer system type is selected, users will need to align the protein orientation with respect to the membrane (whose normal is the Z‐axis and center is at Z = 0), which is then followed by composing own bilayer using more than 600 different lipids. The common step would be solvating the system with the padding water thickness or box‐size and ions. Then, one may select the FF among CHARMM, AMBER, or OPLS‐AA utilizing FF‐Converter. 13 , 14 Hydrogen mass repartitioning (HMR) can be applied at this step, permitting a 4‐fs timestep. 40 , 41 Based on the selected FF, available enhanced sampling methods‐package combinations will be displayed. CV setup will be required for CV‐required methods (MTD, ABF, and REUS). Users may choose multiple method‐package combinations if willing to try different methods.
FIGURE 1.

Schematic overview of Enhanced Sampler in CHARMM‐GUI. FF, force field.
2.2. Supported collective variables
A CV is a subset of the system of interest or any measurable parameter based on the atomic coordinates. Certain enhanced sampling methods require a CV as a reaction coordinate, the target of one‐time or subsequent refinement. Table 1 summarizes the standardized CVs supported by Enhanced Sampler, utilizing PLUMED2 and COLVARS module. 10 , 32 The variables used in CV descriptions are as follows: a coordinate (), a mass (), a vector from to (, an axis (), a scalar part of quaternion (), and a vector part of quaternion ().
TABLE 1.
Collective variables supported in Enhanced Sampler
| Collective variables | Description | Required selections | Supported packages | |
|---|---|---|---|---|
| Distance |
|
Two sets of atoms, range (min/max) | All | |
| Angle |
|
Three sets of atoms, range (min/max) | All | |
| Dihedral |
|
Four sets of atoms, range (min/max) | All | |
| Root‐mean‐square deviation |
|
A set of atoms, range (min/max) | All | |
| Radius of gyration |
|
A set of atoms, range (min/max) | AMBER, CHARMM, NAMD, GROMACS, and OpenMM | |
| Distance on axis |
|
Two sets of atoms, range (min/max), axis (xyz vector) | NAMD | |
| Rotation on axis |
|
A set of atoms, range (min/max), axis (xyz vector) | AMBER and NAMD | |
| Tilt on axis |
|
A set of atoms, range (min/max), axis (xyz vector) | AMBER and NAMD | |
| Number of contacts |
|
Two sets of atoms, range (min/max), cutoff | NAMD, GROMACS, and OpenMM |
Enhanced Sampler presents an intuitive selection of groups of atoms based on a combination of a segment name (SEGID), a range of residue ID numbers (RESID‐from/to), and the name of atom or a certain groups of atoms (AtomName). When a user selects the SEGID, corresponding residue ID ranges of the segment become selectable. By setting up a range of residues, RESID‐from and RESID‐to that are inclusive, one may select numerous atoms at once. When RESIDs are set, available AtomNames are populated. AtomName selection has five default groups of atoms: All, Heavy atom, Backbone, Sidechain, and Alpha carbon. Single atom selection is also accessible if a single residue is chosen, that is, RESID‐from is equal to RESID‐to. Figure 2 shows an illustrative example, having three subsets of atoms for an angle CV. All CVs except for the number of contacts are center‐of‐mass (COM) based, and users can add or remove groups of atoms freely for each subset. An error‐prone job of writing many atom indices into CV file is done automatically and promptly in Enhanced Sampler.
FIGURE 2.

Collective variable (CV) selection web‐implementation, showing three subsets of atoms for an angle CV
2.3. Supported enhanced sampling methods and initial parameters
The enhanced sampling method‐package combinations available in Enhanced Sampler are summarized in Table 2 with the name of function or module used in the package (AMBER, CHARMM, GENESIS, GROMACS, NAMD, or OpenMM). 31 , 32 , 42 , 43 , 44 , 45 , 46 , 47 , 48 , 49 , 50 , 51 , 52 , 53 Figure 3 shows schematic representations of supported enhanced sampling methods: (a) biased potential energy (aMD, GaMD, and CF), (b) adaptively biased potential/free energy (MTD and ABF), (c) pulling (SMD), and (d) replica exchange based methods (T‐REMD, REST2, and REUS). The specific modifications of each method and system‐dependent initial parameter setup in Enhanced Sampler are elaborated in the following subsections.
TABLE 2.
Methods‐package combinations supported in Enhanced Sampler
| Enhanced sampling methods | AMBER | CHARMM | NAMD | GROMACS | OpenMM | GENESIS |
|---|---|---|---|---|---|---|
| Accelerated molecular dynamics | Iamd | accelMD | AMDIntegrator | |||
| Gaussian accelerated molecular dynamics | Igamd | accelMDG | GAMD | |||
| Conformational flooding | Flood | |||||
| Metadynamics | abmd flooding | metadynamics | Plumed | Plumed | ||
| Adaptive biasing force | abf | |||||
| Steered molecular dynamics | Jar rst | CONS PULL | SMD | Pull‐coord1 | SMD | SMD |
| Temperature replica exchange | Rem | REPD | Tcl script | Replex | OpenMMTools | REMD |
| Replica exchange umbrella sampling | Rem | REPD | Tcl script | Plumed | Plumed | REMD |
| Replica exchange solute tempering 2 | REPD/BLOCK | soluteScaling | Plumed | REST2 |
FIGURE 3.
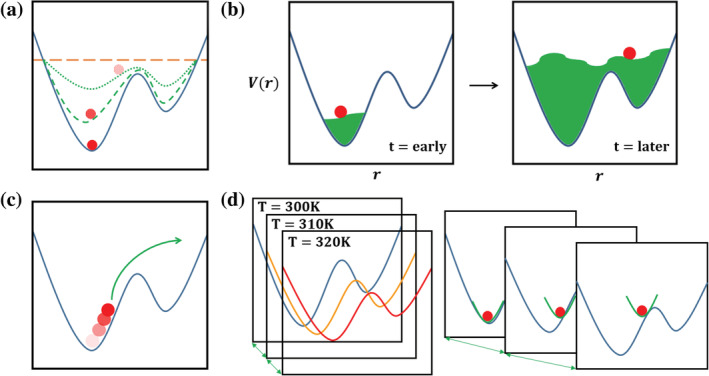
Schematic representations of categorized enhanced sampling methodologies in Enhanced Sampler: (a) biased potential energy, (b) adaptively biased potential energy, (c) pulling, and (d) replica exchange with temperature (left) and umbrella sampling (right). The red ball indicates the system of interest and the green lines indicate the characteristic behaviors of the method
2.3.1. Biased underlying potential energy functions
Accelerated molecular dynamics
For aMD, the modified potential is defined as
| (1) |
with a threshold energy E where boosting is only effective when the system potential is below E. 19 The boosting constant is to determine the depth of a modified potential energy basin. The boosting potential is carefully designed to make the derivative of a modified potential continuous. As a result, a new potential energy function echoes the underlying shape of potential energy, and a smoothened potential energy function raises an exchange rate between various conformational states (Figure 3a). Users can set the boosting potential to target dihedral, total potential, or both with different parameters by selecting a dihedral, total, or dual boosting mode.
Enhanced Sampler determines the initial parameters of aMD simulations based on the previous studies. 54 , 55 Average potential energies (dihedral and/or total based on boost modes) are detected from a short pre‐run, and system information including number of atoms, residues, and lipids is used to define two parameters E and .
| (2) |
where the subscript “d” and “t” represent dihedral and total, and , , , and are the average potential energy from the pre‐run and the numbers of residues, lipids, and atoms, respectively. The selection of initial parameters in Equation (2) ensures that the amount of boosts are in a reasonable range, preventing simulation failure.
Gaussian accelerated molecular dynamics
A long‐lasted post hoc reweighting problem that often results in discarded conformations with relatively high boosting is handled in GaMD. 20 The boosting potentials are designed to be a Gaussian distribution, making a second‐order cumulant expansion be an accurate approximation for the reweighting factor. For GaMD, the modified potential is similarly defined as in aMD, yet different in terms of the boosting potential being harmonic:
| (3) |
The GaMD initial parameters E and k are automatically selected from two sequential pre‐runs, a conventional MD followed by GaMD. Users can select the threshold energy E between lower and upper bounds, and , respectively, where and are detected during the first pre‐run. The boosting constant k for dihedral and for total potential) is defined as , and is calculated by
| (4) |
where is the standard deviation of the boosting potential and is the upper limit and its default value is 6.
The shell script provided by Enhanced Sampler can be used for minimization/equilibration, two GaMD pre‐runs for the parameter selection, and then GaMD production. To maximize the boost amount and efficiency, it is recommended to run the pre‐runs until reaches its own stable maximum or 1.
Conformational flooding
The multivariate Gaussian flooding potential in CF lifts the basin of the potential, permitting an acceleration of slow processes. 21 The boosting potential for CF is defined as
| (5) |
where and are the strength and the shape of the flooding potential, respectively. Enhanced Sampler strictly follows the procedure from flooding in GROMACS to generate the flooding input file containing flooding matrix and parameters from a short MD pre‐run. 56 The default is set to 12.0 kJ/mol.
2.3.2. Adaptively biased underlying potential energy functions
Metadynamics
A history‐dependent bias, continuously accumulated Gaussian potentials to the visited states, is added to the system for MTD simulations (Figure 3b). 22 , 23 The modified potential discourages repeated sampling of the same state, forcing the system out of the kinetic traps toward unexplored conformational spaces. The reaction coordinate must be defined using CVs to deposit potentials. The time‐dependent MTD bias is defined as
| (6) |
where is a reaction coordinate, W is a Gaussian hill height, and is a hill depositing frequency.
Enhanced Sampler let users select the hill height and width (0.2 kcal/mol and 1 as default) and the CV range of interest by specifying its minimum and maximum. For the CV range, the default depends on the CV types. A hill depositing frequency is set to every 500 timesteps, but it can be decreased for more accuracy at the cost of the simulation time.
Adaptive biasing force
With ABF's history‐dependent bias, one can rather crush the free energy landscape directly. Thus, the free energy surface is flattened with the gradients accumulated in the bins along the chosen reaction coordinate. 24 , 57 To achieve a zero mean force over the reaction coordinate , the progressively refined biasing force is defined as
| (7) |
where is the current estimate of the free energy and is the mean force at from averaging instantaneous forces, . For a CV, the sampling range of interest needs to be submitted. A parameter named FullSamples is required in order to avoid non‐equilibrium effects due to large deviations from initial estimates. The biasing force is multiplied by a scaling factor between 0 and 1, based on whether each bin has passed this threshold count or not. The default value of FullSamples is set to 200 and can be modified in the provided colvars file.
2.3.3. Pulling simulations
Steered molecular dynamics
A force to a biomolecule is applied in SMD (Figure 3c) to mimic in‐vivo biological events or in‐vitro atomic force experiments. 58 While an instantaneous force profile from SMD is already valuable enough, equilibrium properties such as the PMF can be acquired based on the Jarzynski's work that connects non‐equilibrium and equilibrium. 59 , 60 The moving potential of SMD is defined as
| (8) |
where is the spring constant, is the moving speed of the spring potentials (also called dummy atoms), r(t) is the current position of the selected COM, and is the pulling axis. For a CV, the subsets of atoms to be fixed and pulled must be defined. Users can set the pulling axis and the pulling velocity during the colvar selection. The default pulling velocity is set to 0.00005 Å/timestep.
2.3.4. Replica exchange based methods
Temperature replica exchange molecular dynamics
T‐REMD adopts running multiple replicas of the same system at different temperatures (Figure 3d). 26 The free energy barrier tends to be smoothened at high temperature, and the replica exchange based on the Metropolis criterion allows rigorous sampling. The general acceptance probability between T‐REMD replicas is
| (9) |
where represents the whole configurations of replica , equals , is the Boltzmann constant, and is temperature at replica .
Based on the previous work by Patriksson and Spoel, 61 Enhanced Sampler automatically provides a priori optimal temperature ladder based on user‐specific minimum and maximum temperatures and a desired exchange probability. This temperature ladder is carefully estimated with the number of degrees of freedom in the system, calculated from numbers of atoms, residues, water molecules, constraints, and virtual sites.
Replica exchange solute tempering 2
Rather than tempering the whole system, solute tempering methods selectively temper interactions involving subsets of the system. REST2 is a Hamiltonian replica exchange method, having all the replicas run at the same temperature while certain parts of potential energies are scaled to mimic the tempering. 30 The REST2 replica potential energy is defined as
| (10) |
where and are the interaction energies for solute–solute, solute–solvent, and solvent–solvent, respectively. , and is the target temperature. Thus, the acceptance criterion becomes
| (11) |
where represents the whole system configurations of replica .
For the REST2 temperature ladder, we provide the exponential temperature ladder based on user‐specific minimum and maximum temperatures and number of replicas. The temperature of replica becomes
| (12) |
Replica exchange umbrella sampling
With REUS, a thorough sampling along the chosen reaction coordinate is performed using multiple replicas with consecutive harmonic restraints (Figure 3d). The general acceptance probability of REUS between neighboring replicas is
| (13) |
where and represent the whole system configurations and the biased potential (original unbiased potential + replica‐specific biasing harmonic potential) of replica , respectively.
Based on the previous work by Park and Im, 62 Enhanced Sampler automatically provides a priori optimal REUS ladder of harmonic centers, assuming a flat free energy surface along the reaction coordinate.
| (14) |
where is the distance between neighboring centers of replicas, is the harmonic force constant of the umbrella, and is set to 0.8643 for the optimal window overlap that provides an average acceptance ratio of . It is unavoidable to self‐optimize the replica ladder based on the acceptance ratios from a simulation with the initial ladder, that is, adding or removing windows and/or adjusting if poor or overfull is observed. Users can also run pure US without replica exchange by setting an infinitesimal exchange frequency.
2.4. Benchmark test‐set simulations result
Five enhanced sampling methods were tested for their efficiency and accuracy for five different types of benchmark systems: (a) two peptides (Chignolin and K19), (b) a protein complex of human angiotensin‐converting enzyme 2 (ACE2) receptor and the receptor binding domain (RBD) of the spike protein of severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2), (c) Escherichia coli O176 lipopolysaccharide (LPS) O‐antigen, (d) two LPS membrane systems (E. coli and Burkholderia cepacia), and (e) a protein–lipid complex of MlaDE protein and POPG lipid. 41 , 63 , 64 , 65 , 66 , 67 , 68 , 69 Table 3 summarizes the simulation information. All enhanced sampling simulation inputs were generated by Enhanced Sampler.
TABLE 3.
Simulation details for five benchmark systems
| System | Methods | Package + force fields | Observations | Simulation time per method |
|---|---|---|---|---|
| Peptides (Chignolin and K19) | GaMD, MD | AMBER + ff19SB/OPC | Folding/unfolding |
Chig: 10 (1 μs × 10 reps) K19: 20 (2 μs × 10 reps) |
| ACE2–RBD | SMD (+HMR) | NAMD + c36m | Force profile | 800 ns (40 ns × 20 reps) |
| Glycan (O176) | REST2, MD | NAMD + c36 | Ramachandran | 800 ns (100 ns × 8 reps) |
| Lipopolysaccharide (Escherichia coli and Burkholderia cepacia) | aMD MD | OpenMM + c36 | Area per lipid | 1.5 (500 ns × 3 reps) |
| Mla–lipid | ABF | NAMD + c36m | Lipid movement | 450 ns (150 ns × 3 reps) |
2.4.1. Peptides (Chignolin and K19) with GaMD
An engineered fast‐folding 10‐residue peptide Chignolin and a 19‐residue peptide K19 are two well‐studied benchmark peptide systems. 63 , 64 For both peptides, the folded and unfolded structures are shown (Figure 4a). Folded into ‐hairpin structure in water, Chignolin has been frequently adopted for investigating folding‐nature of proteins and peptides as well as for developing sampling methods owing to its small size. 70 , 71 , 72 Likewise, the Ala‐rich Baldwin‐type peptide, K19, has been widely benchmark‐tested for FF developments. Recently proposed AMBER FFs were tested with K19, comparing with the nuclear magnetic resonance experimental results to model helical contents more accurately. 73 , 74
FIGURE 4.
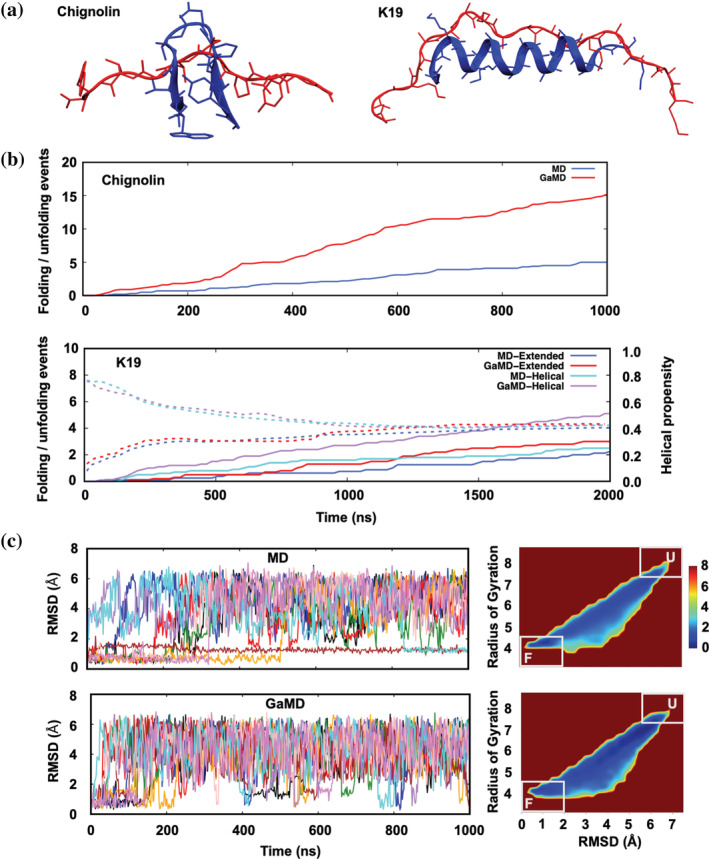
Gaussian accelerated molecular dynamics (GaMD) and molecular dynamics (MD) simulations of Chignolin and K19. (a) Folded (blue) and unfolded (red) conformations of Chignolin (left) and K19 (right). (b) Time‐series of the average number of folding/unfolding events for Chignolin (top) and K19 (bottom) from 10 independent simulations and time‐cumulative average helical propensity for K19 with dashed lines (bottom). (c) Time‐series of root‐mean‐square deviation for MD (top‐left) and GaMD (bottom‐left), and the definition of unfolded and folded states and the corresponding two‐dimensional free energy surfaces (right)
The average number of folding and unfolding events are greater in GaMD compared to the conventional MD for both Chignolin and K19 (Figure 4b). For Chignolin, the average number of folding/unfolding events during 2‐μs simulation is 15.2 with GaMD, eminently greater compared to 5.0 with MD. The conformational states are specified with the similar criterion from the previous study with root‐mean‐square deviation (RMSD) and radius of gyration (Rg), defining folded (RMSD <1.8 and Rg <4.8) and unfolded (RMSD >5.5 and Rg >7) with the reference coordinates based on PDB ID 1UAO. 20 The two dimensional free‐energy surface based on RMSD and Rg was generated after explicit reweighting, and defined folded and unfolded states on the surface are marked in Figure 4c. RMSD time‐series shows that a few trajectories with normal MD are stuck in the metastable states near the folded region, while swift escapes are notable with GaMD. For K19 peptide, similar analysis using RMSD was done with folded (RMSD <1.5) and unfolded (RMSD >6.5) states. For both helical and extended initial conformations, GaMD shows a greater number of transitions to MD counterpart. We did additional analysis for the helical propensity, assigning each residue to be helical if | −65° − ϕ| < 35° and | −37° − ψ| < 30°. 74 , 75 , 76 The average helical propensities, that is, a mean of all residues from all independent runs, for both MD and GaMD are converged to the reference over averaging 10 replicas of 2‐μs each (Figure 4b). However, we could not observe faster convergence for this equilibrium property and suspect if dihedral‐only boosting was not suitable for this purpose. Overall, we could observe faster folding and unfolding of two peptides with GaMD compared to conventional MD.
2.4.2. ACE2–RBD with SMD
SARS‐CoV‐2 reported in late 2019 emerged and spread out the entire world, causing the COVID‐19 pandemic. The RBD of spike glycoprotein of SARS‐CoV‐2 is known to bind with ACE2 for its entry to host cells. 65 , 77 , 78 Since the original strain (i.e., wild‐type [WT]) was identified in Wuhan, China, the virus has been evolved in ways that it can either strengthen the ACE2–RBD interaction or neutralize the antibody binding. 79 , 80 , 81 , 82 , 83 Such strategies have been developed by mutating multiple residues, especially ones located in the RBD. Thus, scientists have put much effort to characterize the effects of RBD mutations and their interaction with ACE2.
We ran SMD simulations for ACE2–RBDWT with inputs from Enhanced Sampler, reproducing the reference result that we reported previously. 84 , 85 , 86 Figure 5a shows the average instantaneous force profiles of 20 replicas during the pulling. Savitzky–Golay smoothing filter was applied to both the current and previous simulation results. 87 Figure 5b depicts three representative protein conformations during the dissociation. Note that both proteins were pulled to the opposite directions to each other in the reference simulations, but the pulling force was applied only to RBD in this study with doubled pulling speed to match the total simulation time. Despite a few differences in the simulation setup, the location and the height of the peak are reproduced well. Furthermore, the new simulations had 250 times more data points of instantaneous forces and COM coordinates with frequent outputting from COLVARS module, obtaining a finer force profile. This result validates the usefulness and the accuracy of SMD simulation setup provided by Enhanced Sampler.
FIGURE 5.

Steered molecular dynamics simulations of angiotensin‐converting enzyme 2–receptor binding domain system. (a) Instantaneous force profiles of reference simulation (black) and this study (red) with Enhanced Sampler. (b) Protein conformations at (1) initial, (2) highest force required, and (3) dissociated states. The correspondent points are marked in (a). COM, center‐of‐mass.
2.4.3. Glycan O176 with REST2
O‐antigen polysaccharides are the main component of the LPS molecules in the outer membrane of Gram‐negative bacteria. 88 , 89 In a previous study, Patel et al. investigated the conformational preferences of an E. coli O176 O‐antigen oligosaccharide at the atomic level through 1.2‐μs MD simulations. 67 The authors conducted a conformational analysis using a set of glycosidic torsion angles from MD trajectories. Due to the structural flexibility and complexity of the carbohydrate, overall exploration of conformational space required long timescale simulations.
We simulated O176 system with eight individual runs of conventional MD and 8‐replica REST2 using the inputs provided by Enhanced Sampler. Each individual run or replica was simulated for 100 ns, building a total of 800 ns per method for a fair comparison. The equilibrium properties from the previous study are used as references. While was highly populated near −55° due to the initial conformation as helical, the probability density became dominant around 100° after excessive samplings in the reference study. With REST2, we observed a faster conformational changes toward the preferred extended structure with a greater radius of gyration and a more analogous probability density profile of the glycosidic linkage (Figure 6). The average acceptance ratio was 0.36, ensuring adequate replica exchanges with effectively solute‐tempered states.
FIGURE 6.

Replica exchange solute tempering 2 (REST2) and molecular dynamics (MD) simulations of glycan O176. (a) Schematic representation of Escherichia coli O176 O‐antigen oligosaccharide (left) and its conformational change during REST2 simulation (right). (b) Probability distribution of radius of gyration (top) and that of key linkage dihedrals (bottom) for REST2 and MD simulations. The bars on the graphs indicate the standard errors from eight independent MD runs
2.4.4. LPS systems (E. coli and B. cepacia) with aMD
An LPS molecule is the main component of the Gram‐negative bacterial outer membrane. 90 LPS consists of lipid A, core oligosaccharide, and O‐antigen polysaccharide repeating units. The structural complexity of LPS molecules plays an essential role in providing protection against various types of chemical attack from the outside. 68 , 89 Despite of the protective advantage, this complication often causes less mobility within the LPS molecules, causing an additional relaxing time to obtain proper conformation for LPS‐containing MD simulations. 41 , 91
We employed two LPS systems, E. coli (Ec) and B. cepacia (Bc), which were not converged in the previous study with conventional MD simulations (Figure 7a). 41 Selected two systems had area‐per‐lipid (APL) differences of 15 Å2 between independent trajectories throughout a few‐microsecond‐long simulation. While such deviations arose from the beginning of the trajectories, we could prevent the divergence by starting with total potential boost aMD, then followed by conventional MD. Averaged APL time‐series for the two systems are shown (Figure 7b). For Ec and Bc, the average APLs are well‐converged among three independent trajectories as well as between different lengths of aMD usages: 181.94 Å2 (100‐ns aMD, Ec), 182.14 Å2 (200‐ns aMD, Ec), 198.35 Å2 (100‐ns aMD, Bc), and 198.41 Å2 (200‐ns aMD, Bc). The selected aMD parameters result in a substantial boost of ~0.12 per atom for each system. The boosted potentials with high variance complicate the reweighting when using a large amount of boost with aMD. However, we applied aMD only for fast lateral relaxation and equilibration, which do not require any post hoc reweighting. A greatly improved convergence of APL in LPS systems was achieved from the conventional MD followed by aMD simulation.
FIGURE 7.

Accelerated molecular dynamics (aMD) followed by conventional molecular dynamics (MD) simulation of lipopolysaccharide (LPS) membrane systems. (a) Two LPS systems, Escherichia coli (Ec, left) and Burkholderia cepacia (Bc, right). (b) Area‐per‐lipid (APL) convergence analysis of 100‐ns aMD followed by 400‐ns MD of Ec (left‐top) and Bc (right‐top), and 200‐ns aMD followed by 300‐ns MD of Ec (left‐bottom) and Bc (right‐bottom)
2.4.5. Mla–lipid system with ABF
Gram‐negative bacteria have an asymmetric outer membrane consisting of LPS in the outer leaflet and phospholipids in the inner leaflet. Phospholipids appearing at the outer leaflet are deleterious. 92 A delicate mechanism to maintain the asymmetry is the maintenance of lipid asymmetry (Mla) pathway, 93 spanning the two membranes. MlaA is located in the outer membrane, MlaC is in the periplasmic space to shuttle phospholipids, and MlaFEDB is located in the inner membrane. MlaE and MlaD are transmembrane protein, where phospholipids are found inside the pocket formed by MlaE and MlaD (Figure 8a). In the past few years, seven cryo‐electron microscopy (cryo‐EM) papers have reported MlaFEDB structures. 69 , 92 , 94 , 95 , 96 , 97 , 98 However, due to poor electron densities of the solved lipids inside Mla, the atomistic coordinates modeled by different research groups diverged (Figure 8a).
FIGURE 8.

Adaptive biasing force (ABF) simulations of Mla–phospholipid complex revealed a key lipid tail configuration and a lipid escape way. (a) Reported lipid configurations in the MlaDE pocket. PDB IDs 7CHA, 7CGE, 6VBD, 6ZY3 are shown. (b) Two lipid configurations from two independent ABF simulations both ended in a tail‐apart configuration that is the same as reported in PDB IDs 7CGE and 6XBD. (c) Phospholipid escaped to the MlaD crown at a position (red) similar to the detergent density (cyan) solved in the cryo‐EM structure (EMD‐11082, PDB 6Z5U). (d) Phospholipid flipping happens during one simulation. Green spheres indicate the phosphate group of bilayer lipids
We simulated the MlaDE complex in a bacterial membrane and modeled the initial lipid structure based on PDB ID 6XBD (Figure 8a). After 150‐ns equilibration, three replicas of ABF simulations were performed. The distance between the lipid‐binding pocket and the COM of the lipid was used as the CV. The lipids in the three systems all explored the pathway from the binding pocket between MlaE and MlaD to the crown region of MlaD. Once the lipid returns to the binding pocket, the lipid adopts a tail‐apart configuration (Figure 8b) as also reported in cryo‐EM structures (PDB IDs 7CGE, 6XBD). 94 , 96 When the lipid moves into the crown region, the lipid position overlaps with the detergent density in the cryo‐EM map of Mla (EMD‐11082) (Figure 8c). 92 This shows that the center of the crown region is a hydrophobic environment favorable for lipid and detergent. When we simulated the MlaDEBFG without a lipid or detergent in the crown region, we observed a collapse of the crown with a shrinking radius among the hexamer. The ABF results show that the MlaD crown region is indeed an important lipid‐residency site. When the phospholipid moves down back to MlaDE region, in one replica, the phospholipid exhibited flipping behavior (Figure 8d), similar to the observation from conventional MD simulations demonstrated by Mann et al. 92 With the ABF results, we demonstrate that the upward lipid escape pathway, the favorable tail‐apart configurations, and lipid flipping behavior inside the MlaDE pocket.
3. CONCLUSIONS
In this study, we have presented CHARMM‐GUI Enhanced Sampler that generates simulation systems and inputs for nine different enhanced sampling methods. The intuitive GUI interface allows users to go through a familiar road of Solution Builder or Membrane Builder to build their system, and then a few more clicks to generate multiple enhanced sampling method inputs at once. Also, users only need to select groups of atoms to define nine standardized CVs, which could be time‐consuming and error‐prone tasks.
To show the robustness of methods covered in Enhanced Sampler, we have generated and performed various enhanced sampling simulations and compared the results with the previous studies. The previous benchmarks are reproduced for the glycan system and the protein pulling simulation. The strength of enhanced sampling methods against the unbiased MD is demonstrated with frequent folding/unfolding of peptides and APL convergence in LPS systems. In addition, a common movement of lipid to the crown region is observed from independent simulations without giving specific directions, allowing us to deduce the potential lipid‐escaping pathway. We hope that Enhanced Sampler with carefully optimized system‐dependent parameters will be useful to get meaningful results from enhanced sampling simulations of various biological systems.
4. METHODS
Unless noted otherwise, a 1‐fs timestep and NVT (constant particle number, constant volume, and temperature) ensemble were used for minimization and equilibration. A 2‐fs timestep and NPT (constant particle number, pressure, and temperature) ensemble were used for the production. The SHAKE algorithm was applied to the bonds containing hydrogen atoms and the van der Waals (vdW) interactions were switched off smoothly over 10–12 Å through a force‐switching function. 99 , 100 The electrostatic interactions were calculated by the particle‐mesh Ewald method. 101 We performed minimization and equilibration of the systems using the CHARMM‐GUI default protocol of Solution Builder and Membrane Builder.
4.1. Peptides (Chignolin and K19) with GaMD
Chignolin peptide was modeled from PDB ID 1UAO, and a 19‐residue peptide with sequence of Ace‐GGG(KAAAA)3K‐NH2 called K19 was generated with LEaP module of AmberTools in AMBER‐v20 software. 63 , 64 , 102 Both systems were solvated using CHARMM‐GUI Solution Builder. AMBER ff19SB FF and OPC water model were used. 74 , 103 The constant temperature at 300 K and the constant pressure at 1 bar were controlled by Langevin dynamics with a friction coefficient of 1 ps−1 and a isotropic Monte Carlo (MC) barostat, respectively. 104 , 105 The vdW interactions were cut off at 9 Å. The system size was set for Chignolin (cubic, 41 × 41 × 41 Å 3 ) and for K19 (octahedron, 60 × 60 × 60 Å3).
The Chignolin and K19 systems were simulated with both MD and GaMD. We ran a 1‐μs (for Chignolin) and a 2‐μs (for K19) each of 10 individual simulations per method with AMBER simulation package. K19 had two initial starting points: a completely helical and an extended conformation. Thus, a total of 10 μs was simulated for Chignolin and a total of 40 μs was simulated for K19 per method. The time‐series of RMSD and Rg were post‐processed using CPPTRAJ from trajectories taken every 100 ps. 106 For GaMD simulations, Chignolin employed a dual boost while K19 used a dihedral boost mode. We ran two pre‐runs for both systems, 10 ns per each pre‐run for parameter selection and optimization. Chosen for Chignolin and for both systems were all set to 1.0, indicating that maximized boosts were applied. For a fair comparison, the production was 20 ns less for GaMD simulations compared to MD.
4.2. ACE2–RBD with SMD
The overall methods are the same as those in our previous studies. 84 , 86 The RBD and ACE2 complex model was obtained from COVID‐19 Protein Library in CHARMM‐GUI Archive. 107 The complex includes six N‐linked glycans: five glycans in ACE2 (Asn53, Asn90, Asn103, Asn322, and Asn546) and one glycan in RBD (Asn343). CHARMM‐GUI Solution Builder was used for system generation and parameter setup. The CHARMM36m FF and TIP3P water model were used with 150 mM K+ and Cl− ions. 75 , 108 , 109 The system size (cubic, 190 × 190 × 190 Å3) was large enough to let the proteins get fully solvated even after complete dissociation. HMR was applied and a 4‐fs timestep was employed for the production.
NAMD simulation software was utilized for all simulations with the COLVARS module. 10 , 46 In the reference system, 84 the SARS‐CoV‐2 RBD–ACE2 complex was aligned along the X‐axis and maintained during the pulling simulations, where external forces were applied to the COM of each protein. In the system reproduced by Enhanced Sampler, pulling forces were applied to the RBD only, while ACE2 was COM‐position restrained. The pulling speed of protein and the spring constant were set to 1 Å/ns and 5 kcal/(mol Å2), respectively. We ran 20 independent simulations to match with the number of reference simulations, each running for 40 ns, so that the RBD–ACE2 complex can be completely dissociated. Other simulation details such as non‐bonded interactions, ensemble, simulation temperature, and timesteps are the same as those in the previous study. 84 , 86
4.3. Glycan O176 with REST2
Glycan O176 system was prepared by Glycan Reader & Modeler in CHARMM‐GUI. 110 , 111 An initial structure of 10 repeating units of E. coli O176 O‐antigen structures was built using the topology information in the CHARMM36 additive FF for carbohydrates. 112 The glycan was immersed at the center of a box (cubic, 108 × 108 × 108 Å3) including 150 mM K+ and Cl− ions and TIP3P water molecules.
NAMD 3.0 simulation software was used for O176 simulations, especially with its GPU enforced replica‐exchange feature. 46 For normal MD simulations, eight replicas were built, and minimization and equilibration were done with a 2‐fs timestep. Then, a 100‐ns production simulation was performed for each replica at a temperature of 303.15 K and a pressure at 1.0 bar. For a REST2 simulation with eight replicas, the system was minimized and equilibrated with a 2‐fs timestep. A 100‐ns NPT production simulation per replica was followed with the temperatures ranged between 303.15 and 400 K for eight replicas. Replica exchanges were attempted every 10 ps. For comparison, we calculated the Rg and glycosidic torsion angles (, where n is the linkage position). 67
4.4. LPS systems (E. coli and B. cepacia) with aMD
Both Ec and Bc systems are composed of a symmetric bilayer membrane with 49 LPS molecules in each leaflet. The system was prepared by LPS Modeler and Membrane Builder in CHARMM‐GUI with an initial box size of 200 Å in X and Y. TIP3P water model and CHARMM36 FF for LPS, lipids, and carbohydrates were used, and the temperature was maintained at 310.15 K using Langevin dynamics with temperature coupling frequency of 1 ps−1. 112 , 113 , 114 , 115 , 116 The pressure was maintained at 1 bar using a semi‐isotropic MC barostat method with a pressure coupling frequency of 100 steps. The sequence of the Ec system includes lipid A with a protonation state (−2e) on the phosphate groups in the glucosamine dimer, K12 core oligosaccharides, and there is an additional protonation state (−1e) on Hep residue in the K12 core sequence. For the LPS sequence of the Bc system, Type 3 lipid A was used, including penta‐acylated tails with two phosphate groups with an additional 4‐amino‐4‐deoxy‐l‐arabinose at both phosphate groups.
OpenMM was used for the following LPS simulations. For the aMD system, we simulated each system up to 200 ns with a total‐boost parameter set of () for Ec (−1,460,000, 40,000) and Bc (−600,000, 40,000) in the unit of kJ/mol. After the aMD run, the conventional MD simulation was performed starting at the final coordinate of 100‐ns and 200‐ns points from the aMD simulation. Each replica was simulated up to 500 ns. The APL throughout the accelerated and conventional MD simulations was calculated using CHARMM for a convergence analysis.
4.5. Mla–lipid system with ABF
MlaDE protein and phospholipid POPG were modeled from PDB ID 7CHA and embedded into a complex membrane mimicking the bacterial membrane (33QMPE, 121PMPE, 27PMPG, 35POPE, 11OYPE, 25PYPG, 6PVCL2) using Membrane Builder. The system size was set to 107.5 × 107.5 × 148 Å3. The CHARMM36m FF and TIP3P water model were used. The temperature and the pressure were controlled at 303.15 K and at 1 bar by Langevin dynamics with a friction coefficient of 1 ps−1 and a semi‐isotropic MC barostat, respectively.
The MlaDE–POPG system was first simulated for 150 ns with a conventional MD simulation in OpenMM and then three replicas were created from this. We then ran 150‐ns ABF simulations with NAMD for each replica. The COM distance between heavy atoms of POPG and the binding pocket residue backbone atoms was defined as the CV. The ABF simulations used a bin size of 0.4 Å, lowerboundary and lowerwall of 0.5 Å, upperboundary and upperwall of 35 Å, wallconstant of 10.0 kcal/(mol Å2), and fullSamples of 100.
5. GENERAL STATEMENT
Various enhanced sampling methods have been proposed to observe slow processes of interest and to overcome high free‐energy barriers present in complex biomolecule systems. Enhanced Sampler generates enhanced sampling simulation inputs with system‐dependent initial parameters and CVs, freely available in CHARMM‐GUI (https://www.charmm-gui.org/input/es).
AUTHOR CONTRIBUTIONS
Donghyuk Suh: Conceptualization (equal); formal analysis (lead); investigation (equal); software (lead); visualization (equal); writing – original draft (lead); writing – review and editing (equal). Shasha Feng: Formal analysis (equal); investigation (supporting); software (supporting); visualization (equal); writing – original draft (supporting); writing – review and editing (supporting). Hwayoung Lee: Formal analysis (supporting); investigation (supporting); software (supporting); visualization (equal); writing – original draft (supporting); writing – review and editing (supporting). Han Zhang: Formal analysis (supporting); investigation (supporting); software (supporting); visualization (equal); writing – original draft (supporting); writing – review and editing (supporting). Sang‐Jun Park: Formal analysis (supporting); investigation (supporting); software (supporting); visualization (equal); writing – original draft (supporting); writing – review and editing (supporting). Seonghan Kim: Formal analysis (supporting); investigation (supporting); software (supporting); visualization (equal); writing – original draft (supporting); writing – review and editing (supporting). Sun Choi: Conceptualization (supporting); funding acquisition (lead); supervision (supporting); writing – review and editing (supporting). Jumin Lee: Software (equal); writing – review and editing (supporting). Wonpil Im: Conceptualization (equal); formal analysis (supporting); funding acquisition (lead); resources (lead); supervision (lead); writing – original draft (supporting); writing – review and editing (equal).
CONFLICT OF INTEREST
Wonpil Im is the co‐founder and CEO of MolCube INC. Jumin Lee is the co‐founder and CTO of MolCube INC.
ACKNOWLEDGMENTS
The authors thank to Jinan Wang and Yinglong Miao for useful discussion, suggestions, and feedback about GaMD. This work was supported in part by the grants from US National Institutes of Health (AI163708, GM126140, and GM138472 to Wonpil Im) and National Science Foundation (DBI‐1660380 and MCB‐1810695 to Wonpil Im), and from the National Research Foundation of Korea (NRF‐2020R1A2C2101636 and 2022M3E5F3080873 to Sun Choi).
Suh D, Feng S, Lee H, Zhang H, Park S‐J, Kim S, et al. CHARMM‐GUI Enhanced Sampler for various collective variables and enhanced sampling methods . Protein Science. 2022;31(11):e4446. 10.1002/pro.4446
Review Editor: Nir Ben‐Tal
Funding information National Institutes of Health, Grant/Award Numbers: AI163708, GM126140, GM138472; National Research Foundation of Korea, Grant/Award Numbers: 2020R1A2C2101636, 2022M3E5F3080873; National Science Foundation, Grant/Award Numbers: DBI‐1660380, MCB‐1810695
Contributor Information
Sun Choi, Email: sunchoi@ewha.ac.kr.
Wonpil Im, Email: wonpil@lehigh.edu.
REFERENCES
- 1. Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat Struct Biol. 2002;9(9):646–652. [DOI] [PubMed] [Google Scholar]
- 2. Neria E, Fischer S, Karplus M. Simulation of activation free energies in molecular systems. J Chem Phys. 1996;105(5):1902–1921. [Google Scholar]
- 3. Chen C, Huang Y, Xiao Y. Enhanced sampling of molecular dynamics simulation of peptides and proteins by double coupling to thermal bath. J Biomol Struct Dyn. 2013;31(2):206–214. [DOI] [PubMed] [Google Scholar]
- 4. Bernardi RC, Melo MCR, Schulten K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim BiophysActa ‐ Gen Subj. 2015;1850(5):872–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Earl DJ, Deem MW. Parallel tempering: Theory, applications, and new perspectives. Phys Chem Chem Phys. 2005;7(23):3910–3916. [DOI] [PubMed] [Google Scholar]
- 6. Isralewitz B, Gao M, Schulten K. Steered molecular dynamics and mechanical functions of proteins. Curr Opin Struct Biol. 2001;11(2):224–230. [DOI] [PubMed] [Google Scholar]
- 7. Huber T, Torda AE, van Gunsteren WF. Local elevation: A method for improving the searching properties of molecular dynamics simulation. J Comput Aided Mol Des. 1994;8(6):695–708. [DOI] [PubMed] [Google Scholar]
- 8. Arrar M, de Oliveira CAF, Fajer M, Sinko W, McCammon JA. W‐rexamd: A hamiltonian replica exchange approach to improve free energy calculations for systems with kinetically trapped conformations. J Chem Theory Comput. 2013;9(1):18–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Miao Y, Sinko W, Pierce L, Bucher D, Walker RC, McCammon JA. Improved reweighting of accelerated molecular dynamics simulations for free energy calculation. J Chem Theory Comput. 2014;10(7):2677–2689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Fiorin G, Klein ML, Hénin J. Using collective variables to drive molecular dynamics simulations. Mol Phys. 2013;111(22–23):3345–3362. [Google Scholar]
- 11. Jo S, Kim T, Iyer VG, Im W. Charmm‐gui: A web‐based graphical user interface for charmm. J Comput Chem. 2008;29(11):1859–1865. [DOI] [PubMed] [Google Scholar]
- 12. Jo S, Kim T, Im W. Automated builder and database of protein/membrane complexes for molecular dynamics simulations. PLOS ONE. 2007;2(9):e880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lee J, Cheng X, Swails JM, et al. Charmm‐gui input generator for namd, gromacs, amber, openmm, and charmm/openmm simulations using the charmm36 additive force field. J Chem Theory Comput. 2016;12(1):405–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Lee J, Hitzenberger M, Rieger M, Kern NR, Zacharias M, Im W. Charmm‐gui supports the amber force fields. J Chem Phys. 2020;153(3):035103. [DOI] [PubMed] [Google Scholar]
- 15. Jo S, Lim JB, Klauda JB, Im W. Charmm‐gui membrane builder for mixed bilayers and its application to yeast membranes. Biophys J. 2009;97(1):50–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Wu EL, Cheng X, Jo S, et al. Charmm‐gui membrane builder toward realistic biological membrane simulations. J Comput Chem. 2014;35(27):1997–2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lee J, Patel DS, Ståhle J, et al. Charmm‐gui membrane builder for complex biological membrane simulations with glycolipids and lipoglycans. J Chem Theory Comput. 2019;15(1):775–786. [DOI] [PubMed] [Google Scholar]
- 18. Park S, Choi YK, Kim S, Lee J, Im W. Charmm‐gui membrane builder for lipid nanoparticles with ionizable cationic lipids and pegylated lipids. J Chem Inf Model. 2021;61(10):5192–5202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hamelberg D, Mongan J, McCammon JA. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J Chem Phys. 2004;120(24):11919–11929. [DOI] [PubMed] [Google Scholar]
- 20. Miao Y, Feher VA, McCammon JA. Gaussian accelerated molecular dynamics: Unconstrained enhanced sampling and free energy calculation. J Chem Theory Comput. 2015;11(8):3584–3595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Grubmüller H. Predicting slow structural transitions in macromolecular systems: Conformational flooding. Phys Rev E. 1995;52(3):2893–2906. [DOI] [PubMed] [Google Scholar]
- 22. Laio A, Parrinello M. Escaping free‐energy minima. Proc Natl Acad Sci. 2002;99(20):12562–12566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Barducci A, Bussi G, Parrinello M. Well‐tempered metadynamics: A smoothly converging and tunable free‐energy method. Phys Rev Lett. 2008;100(2):020603. [DOI] [PubMed] [Google Scholar]
- 24. Darve E, Rodríguez‐Gómez D, Pohorille A. Adaptive biasing force method for scalar and vector free energy calculations. J Chem Phys. 2008;128(14):144120. [DOI] [PubMed] [Google Scholar]
- 25. Grubmüller H, Heymann B, Tavan P. Ligand binding: Molecular mechanics calculation of the streptavidin‐biotin rupture force. Science. 1996;271(5251):997–999. [DOI] [PubMed] [Google Scholar]
- 26. Swendsen RH, Wang J‐S. Replica Monte Carlo simulation of spin‐glasses. Phys Rev Lett. 1986;57(21):2607–2609. [DOI] [PubMed] [Google Scholar]
- 27. Sugita Y, Okamoto Y. Replica‐exchange molecular dynamics method for protein folding. Chem Phys Lett. 1999;314(1):141–151. [Google Scholar]
- 28. Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free‐energy estimation: Umbrella sampling. J Comput Phys. 1977;23(2):187–199. [Google Scholar]
- 29. Sugita Y, Kitao A, Okamoto Y. Multidimensional replica‐exchange method for free‐energy calculations. J Chem Phys. 2000;113(15):6042–6051. [Google Scholar]
- 30. Wang L, Friesner RA, Berne BJ. Replica exchange with solute scaling: A more efficient version of replica exchange with solute tempering (rest2). J Phys Chem B. 2011;115(30):9431–9438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Hénin J, Fiorin G, Chipot C, Klein ML. Exploring multidimensional free energy landscapes using time‐dependent biases on collective variables. J Chem Theory Comput. 2010;6(1):35–47. [DOI] [PubMed] [Google Scholar]
- 32. Tribello GA, Bonomi M, Branduardi D, Camilloni C, Bussi G. Plumed 2: New feathers for an old bird. Comput Phys Commun. 2014;185(2):604–613. [Google Scholar]
- 33. Lu H, Isralewitz B, Krammer A, Vogel V, Schulten K. Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation. Biophys J. 1998;75(2):662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Roux B. The calculation of the potential of mean force using computer simulations. Comput Phys Commun. 1995;91(1):275–282. [Google Scholar]
- 35. Hermans J, Shankar S. The free energy of xenon binding to myoglobin from molecular dynamics simulation. Israel J Chem. 1986;27(2):225–227. [Google Scholar]
- 36. Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The weighted histogram analysis method for free‐energy calculations on biomolecules. I. The method. J Comput Chem. 1992;13(8):1011–1021. [Google Scholar]
- 37. Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. J Comput Phys. 1976;22(2):245–268. [Google Scholar]
- 38. Shirts MR, Chodera JD. Statistically optimal analysis of samples from multiple equilibrium states. J Chem Phys. 2008;129(12):124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Jo S, Cheng X, Islam SM, et al. Charmm‐gui pdb manipulator for advanced modeling and simulations of proteins containing nonstandard residues. Adv Protein Chem Struct Biol. 2014;96:235–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Hopkins CW, Le Grand S, Walker RC, Roitberg AE. Long‐time‐step molecular dynamics through hydrogen mass repartitioning. J Chem Theory Comput. 2015;11(4):1864–1874. [DOI] [PubMed] [Google Scholar]
- 41. Gao Y, Lee J, Smith IPS, et al. Charmm‐gui supports hydrogen mass repartitioning and different protonation states of phosphates in lipopolysaccharides. J Chem Inf Model. 2021;61(2):831–839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Case DA, Cheatham TE 3rd, Darden T, et al. The amber biomolecular simulation programs. J Comput Chem. 2005;26(16):1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Brooks BR, Brooks CL 3rd, Mackerell AD Jr, et al. Charmm: The biomolecular simulation program. J Comput Chem. 2009;30(10):1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Jung J, Mori T, Kobayashi C, et al. Genesis: A hybrid‐parallel and multi‐scale molecular dynamics simulator with enhanced sampling algorithms for biomolecular and cellular simulations. Wiley Interdiscip Rev Comput Mol Sci. 2015;5(4):310–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Abraham MJ, Murtola T, Schulz R, et al. Gromacs: High performance molecular simulations through multi‐level parallelism from laptops to supercomputers. SoftwareX. 2015;1‐2:19–25. [Google Scholar]
- 46. Phillips JC, Braun R, Wang W, et al. Scalable molecular dynamics with namd. J Comput Chem. 2005;26(16):1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Eastman P, Swails J, Chodera JD, et al. Openmm 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput Biol. 2017;13(7):e1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Wang Y, Harrison CB, Schulten K, McCammon JA. Implementation of accelerated molecular dynamics in namd. Comput Sci Discov. 2011;4(1):015002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Pierce LCT, Salomon‐Ferrer R, Augusto F, de Oliveira C, McCammon JA, Walker RC. Routine access to millisecond time scale events with accelerated molecular dynamics. J Chem Theory Comput. 2012;8(9):2997–3002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Pang YT, Miao Y, Wang Y, McCammon JA. Gaussian accelerated molecular dynamics in namd. J Chem Theory Comput. 2017;13(1):9–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Moradi M, Babin V, Roland C, Sagui C. The adaptively biased molecular dynamics method revisited: New capabilities and an application. J Phys: Conf Ser. 2015;640:012020. [Google Scholar]
- 52. Yang M, Huang J, MacKerell AD. Enhanced conformational sampling using replica exchange with concurrent solute scaling and hamiltonian biasing realized in one dimension. J Chem Theory Comput. 2015;11(6):2855–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Jo S, Jiang W. A generic implementation of replica exchange with solute tempering (REST2) algorithm in NAMD for complex biophysical simulations. Comput Phys Commun. 2015;197:304–311. [Google Scholar]
- 54. de Oliveira CAF, Hamelberg D, McCammon JA. On the application of accelerated molecular dynamics to liquid water simulations. J Phys Chem B. 2006;110(45):22695–22701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Wang Y, Markwick PRL, de Oliveira CAF, McCammon JA. Enhanced lipid diffusion and mixing in accelerated molecular dynamics. J Chem TheoryComput. 2011;7(10):3199–3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Lange OF, Schäfer LV, Grubmüller H. Flooding in gromacs: Accelerated barrier crossings in molecular dynamics. J Comput Chem. 2006;27(14):1693–1702. [DOI] [PubMed] [Google Scholar]
- 57. Comer J, Gumbart JC, Hénin J, Lelièvre T, Pohorille A, Chipot C. The adaptive biasing force method: Everything you always wanted to know but were afraid to ask. J Phys Chem B. 2015;119(3):1129–1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Hsin J, Strümpfer J, Lee EH, Schulten K. Molecular origin of the hierarchical elasticity of titin: Simulation, experiment, and theory. Annu Rev Biophys. 2011;40(1):187–203. [DOI] [PubMed] [Google Scholar]
- 59. Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett. 1997;78(14):2690–2693. [Google Scholar]
- 60. Jarzynski C. Equilibrium free‐energy differences from nonequilibrium measurements: A master‐equation approach. Phys Rev E. 1997;56(5):5018–5035. [Google Scholar]
- 61. Patriksson A, van der Spoel D. A temperature predictor for parallel tempering simulations. Phys Chem Chem Phys. 2008;10(15):2073–2077. [DOI] [PubMed] [Google Scholar]
- 62. Park S, Kim T, Im W. Transmembrane helix assembly by window exchange umbrella sampling. Phys Rev Lett. 2012;108(10):108102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Honda S, Yamasaki K, Sawada Y, Morii H. 10 residue folded peptide designed by segment statistics. Structure. 2004;12(8):1507–1518. [DOI] [PubMed] [Google Scholar]
- 64. Song K, Stewart JM, Fesinmeyer RM, Andersen NH, Simmerling C. Structural insights for designed alanine‐rich helices: Comparing nmr helicity measures and conformational ensembles from molecular dynamics simulation. Biopolymers. 2008;89(9):747–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Shang J, Ye G, Shi K, et al. Structural basis of receptor recognition by sars‐cov‐2. Nature. 2020;581(7807):221–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Olsson U, Weintraub A, Widmalm G. Structural determination of the o‐antigenic polysaccharide from the verocytotoxin‐producing Escherichia coli O176. Carbohydr Res. 2008;343(4):805–809. [DOI] [PubMed] [Google Scholar]
- 67. Patel DS, Blasco P, Widmalm G, Im W. Escherichia coli o176 LPS structure and dynamics: A NMR spectroscopy and md simulation study. Curr Res Struct Biol. 2020;2:79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Simpson BW, Trent MS. Pushing the envelope: LPS modifications and their consequences. Nat Rev Microbiol. 2019;17(7):403–416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Kamischke C, Fan J, Bergeron J, et al. The Acinetobacter baumannii Mla system and glycerophospholipid transport to the outer membrane. eLife. 2019;8:e40171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Satoh D, Shimizu K, Nakamura S, Terada T. Folding free‐energy landscape of a 10‐residue mini‐protein, chignolin. FEBS Lett. 2006;580(14):3422–3426. [DOI] [PubMed] [Google Scholar]
- 71. Shaffer P, Valsson O, Parrinello M. Enhanced, targeted sampling of high‐dimensional free‐energy landscapes using variationally enhanced sampling, with an application to chignolin. Proc Natl Acad Sci. 2016;113(5):1150–1155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Kührová P, De Simone A, Otyepka M, Best RB. Force‐field dependence of chignolin folding and misfolding: Comparison with experiment and redesign. Biophys J. 2012;102(8):1897–1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Maier JA, Martinez C, Kasavajhala K, Wickstrom L, Hauser KE, Simmerling C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J Chem Theory Comput. 2015;11(8):3696–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Tian C, Kasavajhala K, Belfon KAA, et al. ff19SB: Amino‐acid‐specific protein backbone parameters trained against quantum mechanics energy surfaces in solution. J Chem Theory Comput. 2020;16(1):528–552. [DOI] [PubMed] [Google Scholar]
- 75. Huang J, Rauscher S, Nawrocki G, et al. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat Methods. 2017;14(1):71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Monera OD, Sereda TJ, Zhou NE, Kay CM, Hodges RS. Relationship of sidechain hydrophobicity and α‐helical propensity on the stability of the single‐stranded amphipathic α‐helix. J Peptide Sci: Off Publ Eur Peptide Soc. 1995;1(5):319–329. [DOI] [PubMed] [Google Scholar]
- 77. Wrapp D, Wang N, Corbett Kizzmekia S, et al. Cryo‐EM structure of the 2019‐nCoV spike in the prefusion conformation. Science. 2020;367(6483):1260–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Jackson CB, Farzan M, Chen B, Choe H. Mechanisms of SARS‐CoV‐2 entry into cells. Nat Rev Mol Cell Biol. 2022;23(1):3–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79. Deng X, Garcia‐Knight MA, Khalid MM, et al. Transmission, infectivity, and neutralization of a spike L452R SARS‐CoV‐2 variant. Cell. 2021;184(13):3426–3437.e38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Planas D, Veyer D, Baidaliuk A, et al. Reduced sensitivity of SARS‐CoV‐2 variant delta to antibody neutralization. Nature. 2021;596(7871):276–280. [DOI] [PubMed] [Google Scholar]
- 81. Grabowski F, Preibisch G, Giziński S, Kochańczyk M, Lipniacki T. SARS‐CoV‐2 variant of concern 202012/01 has about twofold replicative advantage and acquires concerning mutations. Viruses. 2021;13(3):392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Tegally H, Wilkinson E, Giovanetti M, et al. Detection of a SARS‐CoV‐2 variant of concern in South Africa. Nature. 2021;592(7854):438–443. [DOI] [PubMed] [Google Scholar]
- 83. Voloch Carolina M, da Silva FR, de Almeida Luiz GP, et al. Genomic characterization of a novel SARS‐CoV‐2 lineage from Rio de Janeiro, Brazil. J Virol. 2021;95(10):e00119‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Kim S, Liu Y, Lei Z, et al. Differential interactions between human ACE2 and spike RBD of SARS‐CoV‐2 variants of concern. J Chem Theory Comput. 2021;17(12):7972–7979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Cao W, Dong C, Kim S, et al. Biomechanical characterization of SARS‐CoV‐2 spike rbd and human ACE2 protein‐protein interaction. Biophys J. 2021;120(6):1011–1019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Kim S, Liu Y, Ziarnik M, Cao Y, Zhang XF, Im W. Binding of human ACE2 and RBD of omicron enhanced by unique interaction patterns among SARS‐CoV‐2 variants of concern. bioRxiv. 2022. 10.1101/2022.01.24.477633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Press WH, Teukolsky SA. Savitzky‐golay smoothing filters. Comput Phys. 1990;4(6):669–672. [Google Scholar]
- 88. Alexander C, Rietschel ET. Invited review: Bacterial lipopolysaccharides and innate immunity. J Endotoxin Res. 2001;7(3):167–202. [PubMed] [Google Scholar]
- 89. Ståhle J, Widmalm G. Lipopolysaccharides of gram‐negative bacteria: Biosynthesis and structural aspects. Trends GlycosciGlycotechnol. 2019;31(184):E159–E171. [Google Scholar]
- 90. Henderson JC, Zimmerman SM, Crofts AA, et al. The power of asymmetry: Architecture and assembly of the gram‐negative outer membrane lipid bilayer. Annu Rev Microbiol. 2016;70(1):255–278. [DOI] [PubMed] [Google Scholar]
- 91. Kim S, Patel Dhilon S, Park S, et al. Bilayer properties of lipid a from various gram‐negative bacteria. Biophys J. 2016;111(8):1750–1760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Mann D, Fan J, Somboon K, et al. Structure and lipid dynamics in the maintenance of lipid asymmetry inner membrane complex of a. Baumannii Commun Biol. 2021;4(1):817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Lundstedt E, Kahne D, Ruiz N. Assembly and maintenance of lipids at the bacterial outer membrane. Chem Rev. 2021;121(9):5098–5123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Chi X, Fan Q, Zhang Y, et al. Structural mechanism of phospholipids translocation by mlafedb complex. Cell Res. 2020;30(12):1127–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Tang X, Chang S, Qiao W, et al. Structural insights into outer membrane asymmetry maintenance in gram‐negative bacteria by mlafedb. Nat Struct Mol Biol. 2021;28(1):81–91. [DOI] [PubMed] [Google Scholar]
- 96. Coudray N, Isom GL, MacRae MR, Saiduddin MN, Bhabha G, Ekiert DC. Structure of bacterial phospholipid transporter MlaFEDB with substrate bound. eLife. 2020;9:e62518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Zhang Y, Fan Q, Chi X, Zhou Q, Li Y. Cryo‐EM structures of acinetobacter baumannii glycerophospholipid transporter. Cell Discov. 2020;6(1):86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98. Zhou C, Shi H, Zhang M, et al. Structural insight into phospholipid transport by the MlaFEBD complex from P. aeruginosa . J Mol Biol. 2021;433(13):166986. [DOI] [PubMed] [Google Scholar]
- 99. Steinbach PJ, Brooks BR. New spherical‐cutoff methods for long‐range forces in macromolecular simulation. J Comput Chem. 1994;15(7):667–683. [Google Scholar]
- 100. Ryckaert J‐P, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n‐alkanes. J Comput Phys. 1977;23(3):327–341. [Google Scholar]
- 101. Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh ewald method. J Chem Phys. 1995;103(19):8577–8593. [Google Scholar]
- 102. Case DA, Aktulga HM, Belfon K, et al. Amber 2021. San Francisco: University of California, 2021. [Google Scholar]
- 103. Izadi S, Anandakrishnan R, Onufriev AV. Building water models: A different approach. J Phys Chem Letters. 2014;5(21):3863–3871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Chow K‐H, Ferguson DM. Isothermal‐isobaric molecular dynamics simulations with Monte Carlo volume sampling. Comput Phys Commun. 1995;91(1):283–289. [Google Scholar]
- 105. Åqvist J, Wennerström P, Nervall M, Bjelic S, Brandsdal BO. Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chem Phys Lett. 2004;384(4):288–294. [Google Scholar]
- 106. Roe DR, Cheatham TE. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J Chem Theory Comput. 2013;9(7):3084–3095. [DOI] [PubMed] [Google Scholar]
- 107. Woo H, Park S‐J, Choi YK, et al. Developing a fully glycosylated full‐length SARS‐CoV‐2 spike protein model in a viral membrane. J Phys Chem B. 2020;124(33):7128–7137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Hatcher E, Guvench O, MacKerell AD. Charmm additive all‐atom force field for aldopentofuranoses, methyl‐aldopentofuranosides, and fructofuranose. J Phys Chem B. 2009;113(37):12466–12476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–935. [Google Scholar]
- 110. Park SJ, Lee J, Patel DS, et al. Glycan reader is improved to recognize most sugar types and chemical modifications in the protein data bank. Bioinformatics. 2017;33(19):3051–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Park S‐J, Lee J, Qi Y, et al. Charmm‐gui glycan modeler for modeling and simulation of carbohydrates and glycoconjugates. Glycobiology. 2019;29(4):320–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112. Guvench O, Mallajosyula SS, Raman EP, et al. Charmm additive all‐atom force field for carbohydrate derivatives and its utility in polysaccharide and carbohydrate‐protein modeling. J Chem Theory Comput. 2011;7(10):3162–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113. Jo S, Wu EL, Stuhlsatz D, et al. Lipopolysaccharide membrane building and simulation. Methods Mol Biol. 2015;1273:391–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114. Klauda JB, Venable RM, Freites JA, et al. Update of the charmm all‐atom additive force field for lipids: Validation on six lipid types. J Phys Chem B. 2010;114(23):7830–7843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Guvench O, Greene SN, Kamath G, et al. Additive empirical force field for hexopyranose monosaccharides. J Comput Chem. 2008;29(15):2543–2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Guvench O, Hatcher ER, Venable RM, Pastor RW, Mackerell AD. Charmm additive all‐atom force field for glycosidic linkages between hexopyranoses. J Chem Theory Comput. 2009;5(9):2353–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]


