Modeling Catalysis in Allosteric Enzymes: Capturing Conformational Consequences

Abstract

Greater understanding of enzymatic mechanisms aids the discovery of new targets for biologics, the development of biocatalytic transformations, and de novo enzyme design. Methods using quantum mechanical (QM) potentials, such as Density Functional Theory (DFT), have enabled complex multistep enzymatic mechanisms to be studied, often in quantitative detail. Nevertheless, the dynamic interconversion of enzyme conformations between active and inactive catalytic forms, involving length- and timescales inaccessible to QM treatments, presents a formidable challenge for the development of computational models for allosterically modulated enzymes. We present an overview of the key concepts underlying multistate models of enzyme catalysis, enzyme allostery, and the challenge that large-scale conformational changes pose for methods using QM, QM/MM, and MM potentials. Structural clustering is highlighted as a valuable approach to bridge molecular dynamics conformational sampling of MM potentials and quantum chemical cluster models of catalysis. Particularly relevant to this discussion is structural allostery, which serves as the exemplar of conformational consequences. Here, a well-characterized allosteric enzyme, Imidazole Glycerol Phosphate Synthase (IGPS), is used to showcase the importance of multiple conformations and guide a new direction for qualitative understanding and quantitative modeling in enzyme catalysis.

1. Introduction

Enzymes carry out the homogeneous catalysis of many essential biological transformations and industrial processes, yielding kinetic rate enhancements of up to 26 orders of magnitude [1]. The quantitative understanding of enzymes has expanded drastically, propelled by biophysical, biochemical, and theoretical studies. Fischer’s “lock and key” model became the foundation for understanding enzyme-substrate mechanics in 1894 [2]. Koshland modified this model in 1958, accounting for enzyme flexibility in developing the induced fit model [3]. The field of enzymatic catalysis has since evolved to account for critical contributions of conformational substates [4]. Additional current topics of interest are enzyme preorganization, reorganization, near attack conformations, desolvation effects, transition state stabilization (TSS), reactant state destabilization (RSD), and dynamic contributions [5–9]. The reader is directed towards reference [10] and references therein for a historical perspective on modeling enzyme catalysis. In this perspective, we focus on enzymes for which conformational changes are critical to (a) understanding the catalytic mechanism and (b) computing quantitatively accurate barriers and energy changes.

Three classes of potentials are commonly employed in computational studies of enzymes: quantum mechanics (QM) only, hybrid QM and molecular mechanics (QM/MM), and fully MM calculations. QM potentials are typically used to study stationary points on the potential energy surface, while computationally less-expensive MM potentials can be used to explore enzyme structure and motions across different timescales, such as in molecular dynamics (MD) simulations. QM-only approaches (Section 4.1), notably the cluster approach, are now routinely used to study reactions using a reduced active site model consisting of up to 200–300 atoms. The protein environment is accounted for by a continuum dielectric model, assuming the surrounding can be approximated as a homogeneous polarizable medium with a constant dielectric [11]. High levels of quantitative accuracy have been demonstrated with reduced active site models: for example, Himo and co-workers have successfully modeled competing enzymatic pathways leading to enantiomeric products (i.e., asymmetric biocatalysis), where energy differences on the order of 1–2 kcal/mol must be captured [12–14]. Cluster models have similarly been used to study how enzyme active sites control regioselectivity, for example, in facilitating intrinsically disfavored epoxide-opening pathways [15]. A related QM-only method, the theozyme approach, has been used to model a theoretical enzyme active site as a selection of functional groups directly involved in catalysis [16]. Houk and co-workers have used theozyme models to illustrate how side-chain motions are minimized in the multistep serine esterase catalytic cycle [7] and in the computational design of enzymes for abiological reactions [17].

To study enzymes where long-range interactions (e.g., electrostatic interactions in particular) play a fundamental role in the catalytic mechanism, the substrate and active site residues directly involved in the reaction can be described with QM, and the remaining protein and solvent can be modeled with classical (MM) force fields (Section 4.3). This QM/MM hybrid approach has yielded high quantitative accuracy of enzymatic reaction barriers. For example, Mulholland, Thiel, Werner, and co-workers have shown that systematic improvements to the QM level of theory, using LCCSD(T0) [18], provide near-quantitative results for the activation enthalpies and free energies of the reactions catalyzed by chorismate mutase and para-hydroxybenzoate hydroxylase [19]. MD simulations employing a QM/MM potential are more expensive than with classical force fields, although sampling times of nanoseconds are now attainable. While such timescales are insufficient to explore large and slow enzyme conformational changes, these may be addressed with classical simulations, as discussed in Section 5. As with the selection of a QM cluster model, the choice of QM/MM boundary and how MM partial point charges at the boundary are described should be handled with care and validated [20].

Classical MD (MD applied to classical force fields) can be used to study whole enzyme mechanics on timescales ranging from the nanosecond-microseconds regime. There may be many thermally accessible conformations sampled by a protein, one or more of which are essential to the catalytic mechanism and for which MD simulation provides one of the few ways to identify and quantify their involvement in atomistic detail. The ability of proteins to redistribute conformational populations to influence function in response to perturbations is a leading hypothesis in the fields of structural allostery [21–23] and, most recently, in directed evolution [24–26]. MD has proven to be especially apt at sampling “local” conformational diversity in enzymes such as the different rotamer states adopted by side-chains. However, some conformational changes necessary to achieve a catalytically competent active site, such as those involving loop and helix motions, occur on the millisecond timescale [27, 28]. In such cases, enhanced sampling MD methods can be used.

Of significance to enzyme catalysis is the ability of MD simulation to provide statistical details for catalytically relevant conformations. In general, this is aided by clustering the MD snapshots into structurally similar groups to yield populations of significant enzyme conformations (Section 5). While classical MD simulations excel in conformational sampling, conventional MM potentials do not describe the breaking and forming of bonds along a reaction pathway. In contrast, while low-cost QM potentials are gaining traction, high-accuracy QM approaches are illsuited to large-scale conformational analyses. Therefore, the combination of QM and classical MD approaches to study enzyme catalysis in the context of the conformational ensemble is of great interest to the community [29, 30].

A single enzyme conformation taken from an X-ray crystal structure might be an excellent starting point for the computational study of enzyme catalysis. However, it is vital to consider the assumptions being made. Mainly, that the single conformation is catalytically relevant, and no other conformations are important for catalysis [31]. The validity of these assumptions is difficult to test unless apriori knowledge or hypotheses regarding the catalytic mechanism exist. Thorough investigations of catalysis will evaluate mechanistic possibilities indicated in the literature and preliminary results. In Section 3, we discuss myriad enzymatic reactions now known for which these simplifying assumptions do not hold. These systems present challenges for computational chemistry to incorporate rigorous analyses of conformational ensembles alongside high-accuracy potentials to study reaction mechanisms. Improvements in conformational sampling techniques, accurate force field parameters, and quantum mechanical treatments have accelerated progress towards this goal. Section 6 describes how computational workflows based on macromolecular conformational sampling with MD, structural clustering to obtain ensemble populations, and QM calculations are poised to accelerate the study of enzyme catalysis further. The explicit consideration of multiple enzyme conformations to support mechanistic conclusions and calculate barrier heights has now been used in multiple studies [28, 32–35].

The main goal of perspective is to illustrate the role of conformational effects upon enzymatic catalysis. We provide a brief account of the main computational approaches, procedures, and limitations and discuss their relevance in modeling protein motions that occur across different timescales. We introduce fundamental concepts of protein allostery and discuss how these systems present a unique challenge for computational chemistry and conformational sampling. We suggest that a combination of cutting-edge techniques in MD sampling and QM modeling provides a particularly appealing approach to study enzyme catalysis. Clustering methods are discussed as a means to bridge the results of classical simulations with QM-cluster models. The final section outlines the case study of glutamine hydrolysis performed by the allosterically-regulated glutamine amidotransferase (GAT) imidazole glycerol phosphate synthase (IGPS). This system beautifully illustrates the importance of conformational changes in catalysis, the existence of inactive and active forms in the solid-state and solution, and the importance of computational sampling of the enzyme’s conformational space. The rate of glutamine hydrolysis in IGPS is critically dependent on the presence of the allosteric ligand over 25 Å away from the glutamine binding site [36]. Until recently, the atomic changes that yield the hydrolysis rate enhancement were not realized due to the absence of an observed catalytically active conformation.

2. Enzyme Catalysis: the Reaction Coordinate and Protein Dynamics

A fundamental understanding of enzyme mechanics has long been the goal of many chemical and biological scientists. Accomplishing this goal requires answering how the enzyme performs its function. To begin formulating an answer to this question, a simple enzyme mechanism can be considered:

$$E+S\underset{k_{-1}}{\stackrel{k_1}{\rightleftharpoons }}\mathit{\text{ES}}\stackrel{k_2}{\to }E+P,$$ (1)

where E indicates the enzyme, S the free substrate, ES the enzyme-substrate complex, and P the product after its release from the enzyme. In the steady-state approximation, where the substrate concentration is saturating and therefore negligible, there are two kinetic parameters used to describe enzyme performance: the maximum rate of product formation, k_cat, and the Michaelis-Menten constant, K_m. From Equation 1, the steady-state kinetic parameters are defined as k_cat = k₂ and K_m = (k₂ + k₋₁)/k₁.

However, a more realistic enzyme model to that presented above accounts for additional elementary mechanistic steps such as the following:

$$E+S\underset{k_{-1}}{\stackrel{k_1}{\rightleftharpoons }}\mathit{\text{ES}}\stackrel{k_2}{\to }\mathit{\text{EX}}\stackrel{k_3}{\to }E+P,$$ (2)

where EX is an intermediate state distinguished by a unique chemical species (i.e., involving a change in bonding relative to ES) or a kinetically significant conformation distinct from ES. With the expanded mechanistic scheme in Equation 2, the steady-state parameters are defined as k_cat = k₂k₃/k₂ +k₃ and K_m = (k₂ +k₋₁)k₃/(k₂ +k₃)k₁. Although the expressions for k_cat and K_m differ between Equations 1 and 2, laboratory observations of steady-state kinetics cannot distinguish between these two mechanistic scenarios. If the goal is to determine an enzyme’s substrate specificity, then simplification to Equation 1 is sufficient. However, computational analysis of individual reaction steps (including all relevant reactants, intermediates, and products) provides the basis to understand the enzyme’s mechanism and the atomistic factors influencing rate and selectivity. Importantly, a measured k_cat often reflects several elementary rate constants in the overall mechanism. Although, for example, in Equation 2, if k₂ >> k₃, simplification to k_cat = k₂ is justified. It is important to note that k_cat is not necessarily solely defined by “chemical” steps, such as where product inhibition occurs. However, we limit the scope of this perspective to examples for which the rate-determining step is associated with bond formation or cleavage.

One critical enzyme attribute missing from Equations 1 and 2 is conformational heterogeneity. Much of the focus of enzyme catalysis in the 21st century has been on the role of conformational changes involving both experimental and computational expertise [4, 10, 27, 30, 37]. The free energy landscape, a multi-dimensional construction of the intermediate and transition states available to an enzyme before, during, and after catalysis, is particularly useful to conceptualize the relationship between the conformational ensemble and the chemical reaction coordinate (Figure 1) [38].

Fig. 1.

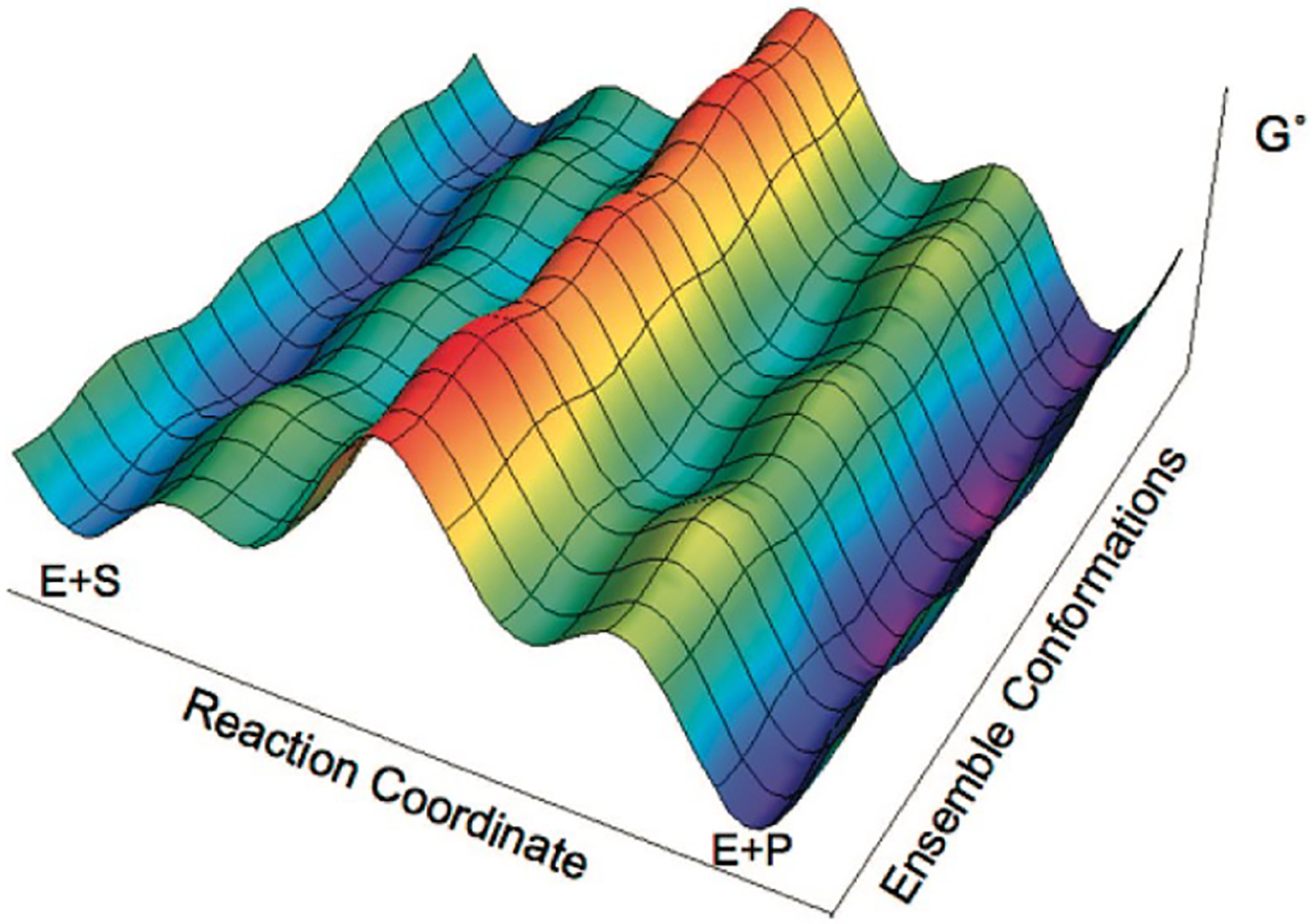
Enzyme free energy landscape projected onto the reaction and conformational coordinates. Adapted with permission from [38]. Copyright 2021 American Chemical Society.

Equations 1 and 2 do not account for the possibility of interconverting conformers (e.g., of the free enzyme, E) that may possess different reactivities along parallel reaction pathways, as described by Hammes-Schiffer and co-workers [38]. Consequently, quantitative agreement of computed reaction barriers with experiment may require explicit consideration of the enzyme’s conformational ensemble. In contrast to the weak coupling of the reaction and conformational coordinates depicted in Fig. 1, strong coupling can arise where even qualitative agreement with experiment requires consideration of the ensemble [27, 28]. Construction of the free energy landscape for large systems is a laborious task. As discussed above, such studies require computational methods in classical simulation techniques, while the reaction coordinate may be more amenable to QM approaches. As a result, a combination of distinct computational methodologies and expertise is often required.

2.1. The Enzymatic Reaction Coordinate

Catalytic mechanisms are often illustrated by (Gibbs) energy profiles, characterized by relative free energies of intermediate and transition state (TS) structures that culminate in the transformation of reactant into product within the enzyme complex (ES and EP, respectively), as illustrated in Figure 2. Multiple factors can influence the quality of the Gibbs energy profile and its mechanistic interpretation [39]. While computations can be used to provide evidence in favor of or against a particular reaction pathway, a reaction mechanism can never be conclusively proven, only experimentally corroborated [40]. With much success, contemporary QM approaches have been used to describe chemical reactions by calculating observables, such as energy barriers, kinetic isotope effects, and product selectivities that can be validated with experiments [41].

Fig. 2.

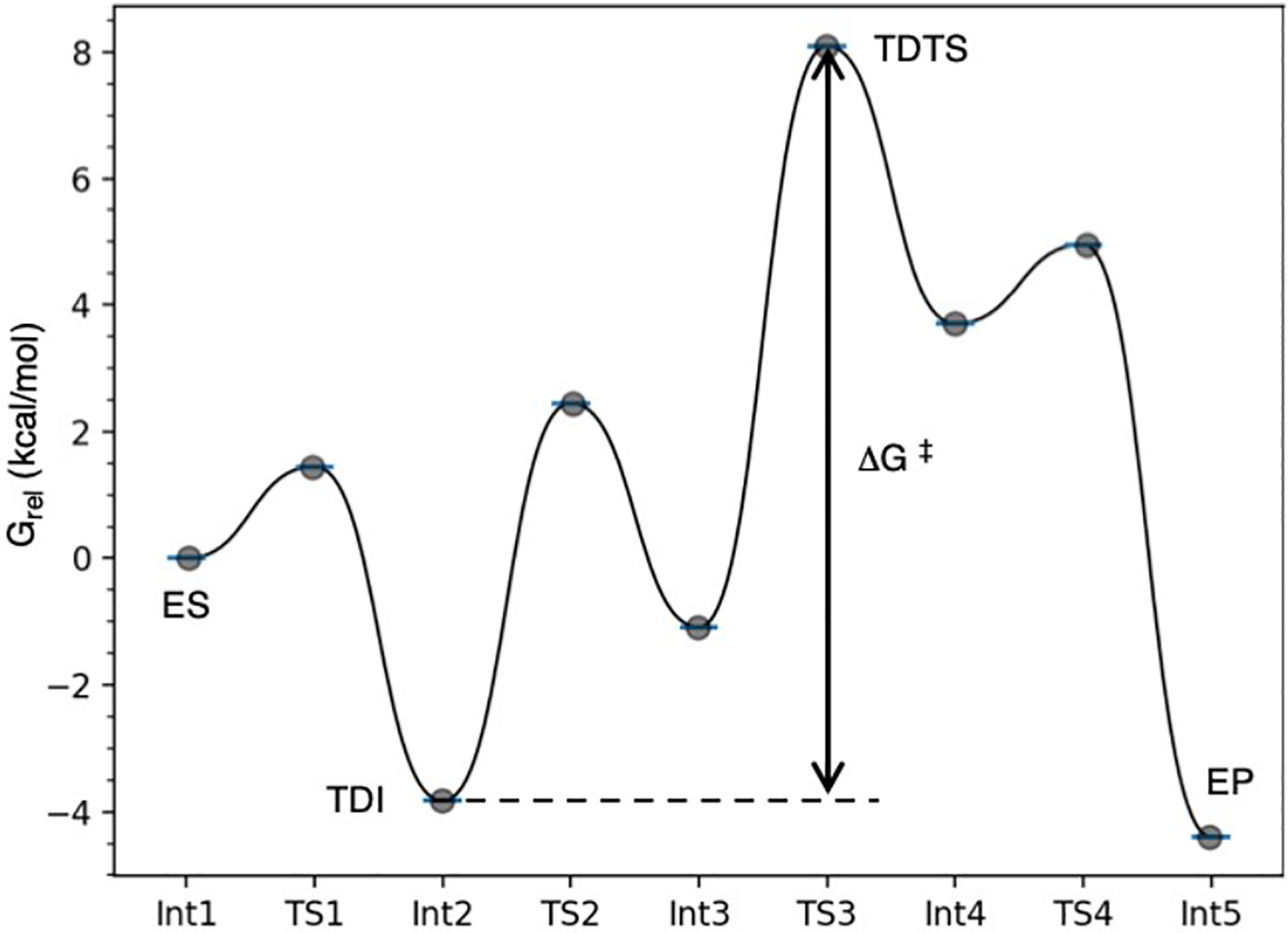
Example reaction coordinate, created with GoodVibes [42], for a multistep enzymatic chemical reaction showing several minima and transition structures proceeding from enzyme-substrate (ES) to enzyme-product complex (EP). Turnover determining intermediate (TDI), Int2, and transition state (TDTS), TS3, define the energetic span and apparent activation energy of the cycle, ΔG^‡.

In comparing the computed catalytic (Gibbs) energy with experiment, the concepts and language introduced by Kozuch and Shaik are both illuminating and influential [43]. In contrast to using rate constants to define a catalytic cycle (the k-representation), computational studies generate state energies (the E-representation). The apparent activation barrier is then represented by the energetic span of the catalytic cycle, defined by the difference (ΔG^‡) between the lowest energy, turnover determining intermediate (TDI), and the highest energy, turnover determining TS (TDTS) (Figure 2). The value of ΔG^‡ can then be used to calculate a theoretical rate constant based on Eyring’s transition state theory equation:

$$k_{\mathit{\text{cat}}}=\frac{\kappa k_{B}T}{h}\mathit{\text{exp}}\left(\frac{-\Delta G^{‡}}{\mathit{\text{RT}}}\right)$$ (3)

where κ is the transmission coefficient, k_B is Boltzmann’s constant, T is temperature, h is Planck’s constant, and R is the gas constant. It is common to set κ =1, but more advanced techniques have been developed to evaluate non-equilibrium effects and the contributions of recrossing and tunneling to enzymatic rate constants [44, 45]. In the case of enzyme models, computed activation barriers for catalytic cycles have reached impressive levels of accuracy. For example, by using relatively large QM regions optimized at the DFT (B3LYP-D3(BJ)/TZVP) level of theory and performing DLPNO-CCSD(T) single-point energy calculations, Neese and co-workers have demonstrated accuracies within 1 kcal/mol of experimental enzyme-catalyzed barriers. Even without high-level coupled-cluster corrections, B3LYP-D3 provides qualitatively correct results [46]. As cautioned by Kozuch and Shaik, care must be taken when calculating ΔG^‡ to be used in Eqn. 3. In some situations the internal energy can be a fair approximation for this value, however in other cases either additional methods or thermal and entropic corrections should be made.

Computational studies of enzyme catalysis are routinely performed using 1) QM-only approaches, which include cluster models [47] and theozyme [16] approaches, and 2) mixed QM/MM studies. These approaches are surveyed in Section 4. More detailed technical summaries of these approaches can be found elsewhere, e.g., in reference [31]. Herein, we focus on basic concepts to emphasize what information can be gained and how QM approaches can supplement a multiscale computational integration to model enzyme catalysis, particularly in the context of a conformational ensemble.

2.2. The Conformational Coordinate

Introductions to biochemistry emphasize that structure leads to function. However, this is an oversimplification, and there are many macromolecules where the interconversion between different structures influences overall biological function. Proteins are known to populate multiple metastable structures (the conformational ensemble) under typical physiological conditions [48]. Mounting evidence suggests that the ensemble nature of proteins is intricately tied to their function [49, 50]. From a statistical mechanics perspective, it is the probability and properties of the microscopic structural states that dictate the macroscopic properties of the protein. Consequently, the determination of the conformational ensemble, specifically the distribution of microscopic structural states, of enzymes is of utmost importance. One of the challenges in this field is the variety in timescales associated with motions, which ultimately dictates the most appropriate method used to study the underlying dynamics (Figure 3).

Fig. 3.

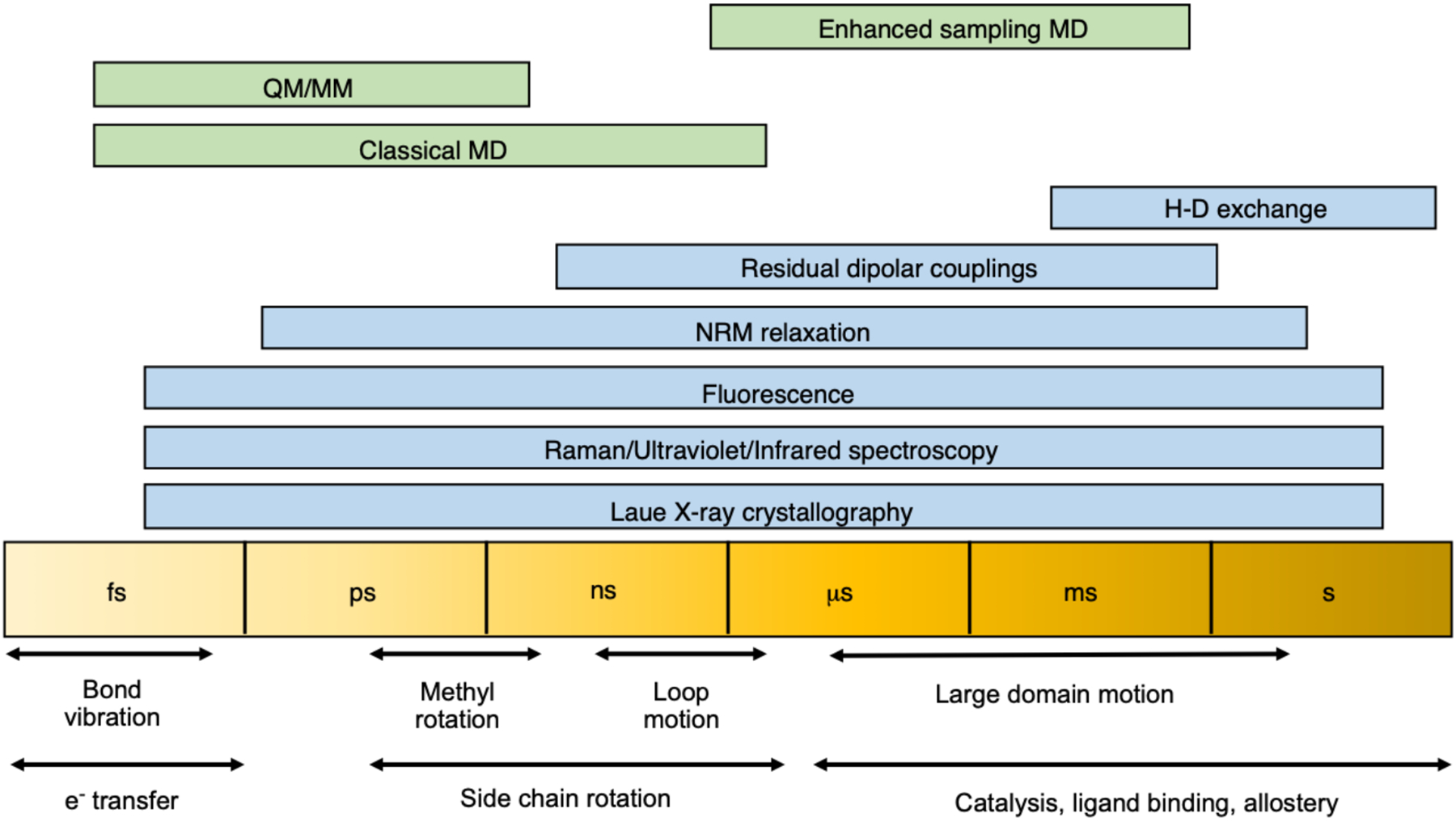
Methods for studying dynamic processes in proteins ranging from femtosecond to second timescales. Experimental and computational techniques are shown in blue and green, respectively.

Experimental techniques used to probe protein ensembles include X-ray crystallography, nuclear magnetic resonance (NMR) [50], small-angle X-ray scattering (SAXS), atomic force microscopy (AFM) [51–53], and more recently, cryogenic electron microscopy (cryoEM) [54–57]. Each of these methods has its own set of advantages and disadvantages. X-ray crystallography, for example, typically determines a single structure that represents a minimum energy structure under crystallization conditions. Recent advances in the field include the advent of room temperature crystallography [58] and recognition that a given crystal likely has multiple structures in the unit cell [59, 60]. Protein NMR is inherently an ensemble measurement that can be done under solution conditions. However, the measurement timescale of NMR dictates that the resulting values, for example, chemical shifts [61] and dipolar couplings [62], are ensemble averages over multiple metastable states. NMR has successfully been coupled to SAXS [63, 64], spectroscopic techniques, and molecular simulations [65–67] to tie the average values to the microscopic ensemble. AFM can provide structural trajectories of proteins but does not have atomic resolution. CryoEM stands out as one of the most promising approaches, with recent advances in image capturing hardware and software driving the resolution down to the atomic scale [54–57]. CryoEM is, however, devoid of temporal information.

Molecular modeling and in silico simulations can provide atomic-level protein ensemble data to complement experiment. A robust approach is to use all-atom force fields to model the protein and the solvent environment. MD simulations provide time-dependent trajectories of the system of interest. In the theoretical limit of infinite sampling and accurate force fields, these data would represent a complete atom-level picture of the protein ensemble. Practically, improvements to both force fields and sampling protocols continue to improve agreement between simulation and experiment, yet room for improvement still exists [68]. Other than reparametrization of standard functional forms, new directions in force field development include polarizable [69] and machine-learned force fields [70]. Regardless of the specific force field details, sufficient ensemble sampling is also an ongoing concern in the field. Typical timescales for conventional molecular-dynamics (cMD) on medium-sized proteins are in the tens of microseconds range. While this can adequately sample the conformational ensemble of small globular proteins near their native state, it is insufficient for large proteins and processes such as protein folding. Techniques to overcome this shortcoming include the development of specialized hardware [71] or enhanced sampling techniques. The latter is a more approachable solution and includes techniques such as replica exchange [72, 73], metadynamics [74], and adaptive sampling [75–77]. A recent study of the conformational ensemble of an intrinsically disordered protein demonstrated that cMD was adequate to reproduce the NMR chemical shifts (an ensemble property) but not the SAXS data (influenced by the distribution of molecular sizes). Enhanced sampling was shown to improve the agreement with SAXS data [78].

Characterizing the conformational ensemble is essential to fully understand the relationship between enzyme structure, dynamics, and the catalytic mechanism. Recently, consideration of the conformational ensemble has been pivotal in determining how the sampling of distinct conformations influences different catalytic properties in the directed evolution of various enzymes [24, 25, 79–81], and a direct correlation between reaction rate and active conformation population influenced by different allosteric ligands and enzyme mutations has been quantified [28].

Allosteric enzymes exemplify the importance of conformational ensembles [3]. Allosteric regulation occurs when a perturbation at a site distant from the primary active site modulates a protein’s function. As the simplest case, we can consider a two-state model (Figure 4), characterized by an active and inactive conformation. Although a variety of perturbations may influence the free energy landscape, such as mutations in directed evolution, in the context of allostery, we consider the binding of a small molecule distal from the enzyme’s primary active site as the perturbation. Upon binding the allosteric ligand, the energy landscape is altered, and the resulting inactive and active conformation populations are altered. This conformational shift phenomenon is often used in discussions of structural allostery but is not limited to such enzymes.

Fig. 4.

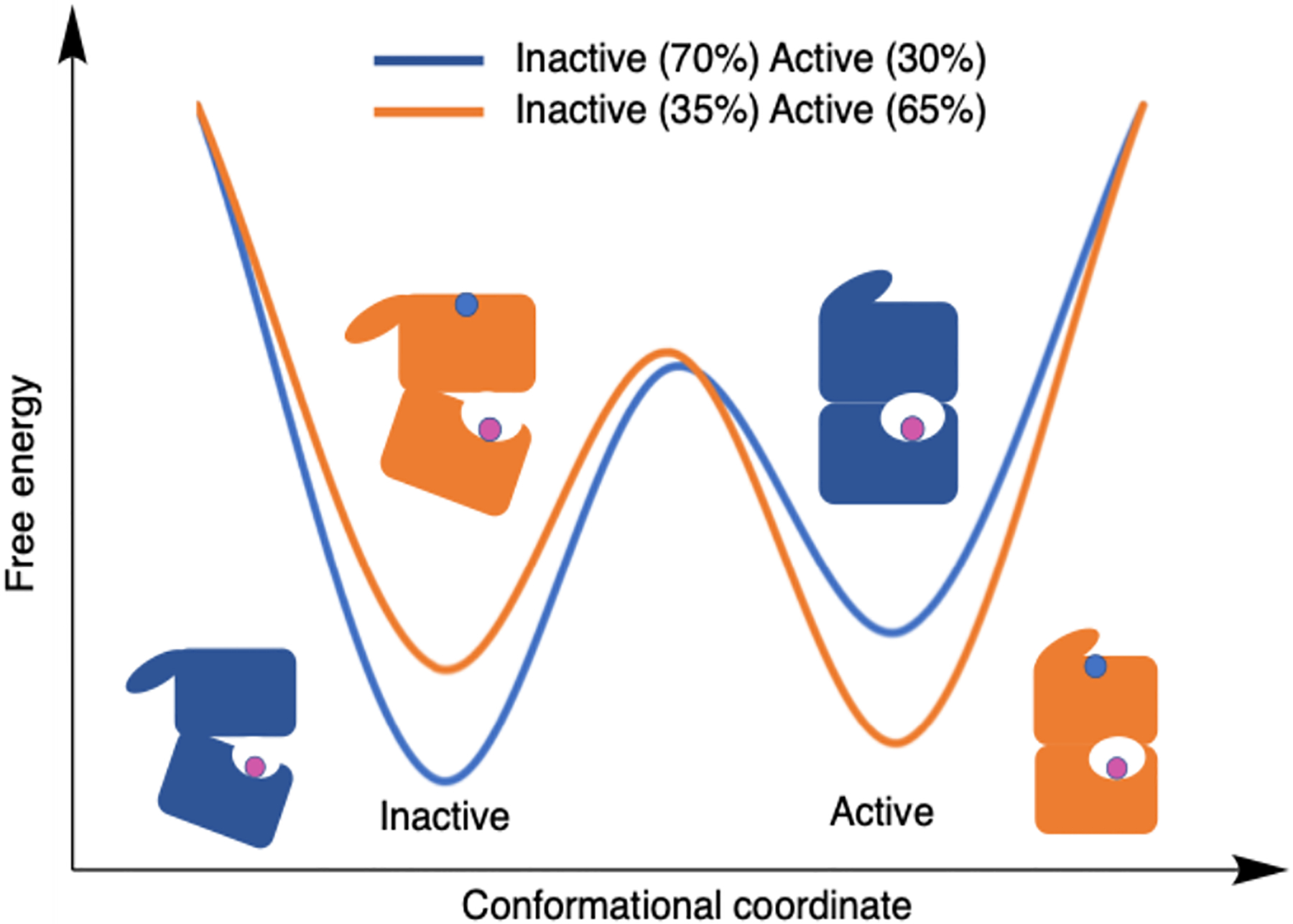
A free energy profile projected onto a two-state conformational coordinate. The blue line and toy enzyme model illustrate a system without the allosteric effector bound. Orange corresponds to a system with the allosteric effector bound. The legend shows relative populations of the active and inactive states that result from different ligand states.

3. Allostery in Enzyme Catalysis

The long-ranged coupling of sites in an allosteric system can be explained through short-range interactions linking the distant sites [82]. This mode of regulation has been referred to as the second secret of life, behind the central dogma that describes information transfer between DNA, RNA, and proteins [83]. Biological systems harness allostery to respond to changes in their environment. This is recognized in various biological processes such as signal transduction [84, 85], transcriptional regulation [86, 87] and metabolism [88]. It has been proposed that any system can be allosterically regulated; it becomes a matter of how to probe the interactions that couple binding sites [85]. In 2011, Huang and co-workers created the Allosteric Database (ASD) to provide a comprehensive collection of allosteric data [89]. Presently, the ASD contains 1,949 allosteric proteins and 82,070 allosteric modulators [90, 91]

3.1. Categorizing Allostery

In allosteric regulation, the binding of an effector molecule alters an enzyme’s activity towards its natural substrate. This is illustrated by the thermodynamic cycle shown in Figure 5. In the absence of the allosteric effector, X, the basal substrate-binding dissociation/affinity constant K_ia and rate constant k_cat are observed. Enzyme allostery is classified by the process of activity alteration. In K-type allostery, the allosteric response to effector binding is a change in the affinity, K_ia, for the substrate, A. This system is the most commonly studied, and an effective allosteric coupling constant, defined by the ratio of substrate binding affinity in the absence versus presence of the effector K_ix/K_ix/a, or equivalently K_ia/K_ia/x as defined in Figure 5, has been developed to quantify the allosteric effect of a K-type system [83]. There exist experimental and computational techniques to measure the allosteric coupling constant in a K-type system. In V-type allostery, binding of the effector causes a change in the catalytic activity, k_cat. An allosteric coupling metric analogous to a K-type system could be based on k_cat with and without the effector bound (k_cat/k_cat/x). Although there exist computational methods to measure k_cat, as previously mentioned, this is relatively unexplored in the context of allostery.

Fig. 5.

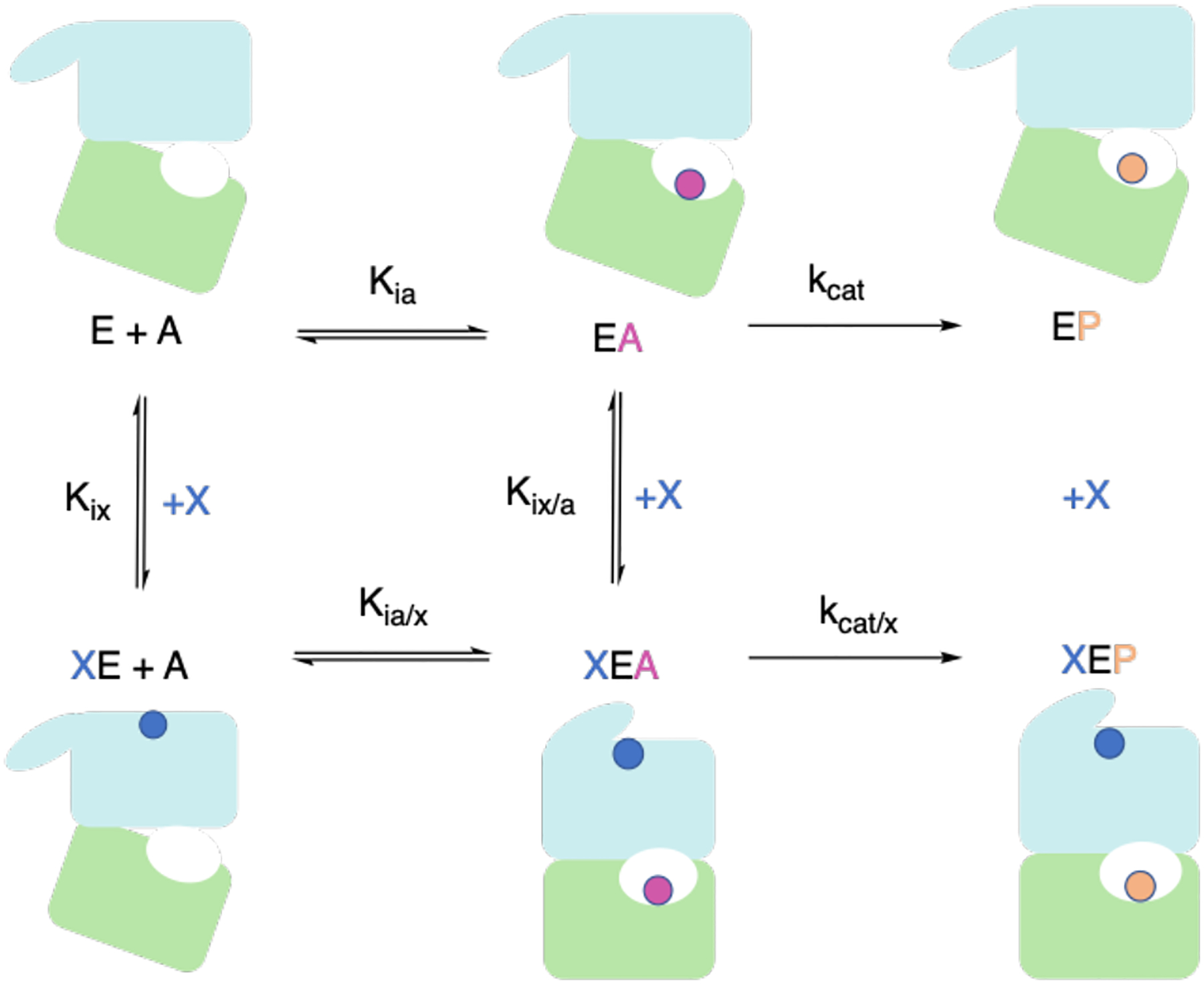
Complete thermodynamic cycle of an allosteric enzyme, E. The top row represents the enzyme in the presence of only substrate, A. The bottom row represents the enzyme in the presence of the substrate and allosteric effector, X. Binding of X modifies the activity of E by either altering the binding affinity of E for A, as in K-type allostery, or influencing the rate-determining step, as in V-type allostery. Nomenclature from Ref. [83] is used here for consistency.

3.2. The Ensemble Model of Allostery

The so-called ‘concerted’ Monod, Wyman and Changeux (MWC) model of allostery, established in 1965, states that most allosteric proteins are oligomers involving multiple identical protomers and thus have an axis of symmetry; the quaternary structures of such systems are altered by allosteric interactions; there exist at least two states that differ by the distribution and/or energy of interactions at the protomer interface(s); these interactions alter the affinity of the binding site towards its corresponding ligand, and the effector is not chemically identical to the substrate [92]. These statements were developed from observations of known allosteric systems at that time, with hemoglobin serving as the hallmark allosteric system, given that an X-ray structure was established for this protein [93]. It was observed that in apo-hemoglobin (absence of effector), there exists an equilibrium between two states, historically known as the constrained and relaxed states. The MWC model claims that effector binding shifts the equilibrium. In 1966, Koshland, Nemethy and Filmer (KNF) composed an alternative model [94]. This model favors an “induced fit” mechanism, whereby the apo-protein binds the effector, which induces a conformational transition to the holo-protein. The MWC and KNF model share a static view of allostery, dependent upon noticeable conformational differences in apo- and holo-structures.

A dynamic model of allostery was proposed in 1984 by Cooper and Dryden, which argues that large-scale conformational changes are not a requisite for allosteric regulation [95]. Instead, changes in thermodynamic fluctuations could mediate the coupling of binding sites. More recently, evidence has shown the importance of functional states unrelated to the so-called “tense” or “relaxed” states that belong to the MWC model [96]. In this more dynamics-driven view of allostery, a protein exists as an ensemble of states, and binding of an effector results in a global redistribution of protein fluctuations and thus alters the relative entropy of the ensembles. This ensemble model of allostery is favored in the literature today [23, 85, 88, 97, 98]. Allostery research, which traditionally emphasized static comparisons, is currently faced with the challenge of leveraging the ensemble nature of allostery [99]. Although this challenge is now considered fundamental in the field of allostery, it applies to enzymes in a general way. More recently, enzymes engineered through directed evolution have achieved higher catalytic efficiency by redistributing the energy landscape [25].

Restructuring of the energy landscape in response to allosteric ligand binding or a relevant mutation is expected to be the driving force that alters enzyme function, meaning multiple conformations and their populations are crucial to consider. Population shifts have been found to directly influence functional change in enzymes [28, 95]. The whole-scale enzymatic influence on the chemical rate in V-type allosteric systems is particularly intriguing in this regard.

Enzymatic catalytic activity is typically compared against the background reaction rate in (aqueous) solution to investigate catalytic origins [8]. Alternatively, one could compare the same reaction in enzymes with different activities. Such an approach can be adopted in evaluating V-type allosteric enzymes. To evaluate the source of an allosteric effect in catalysis, one must consider the reaction with and without the allosteric effect. In many cases, this means considering the enzyme in the presence and absence of the allosteric ligand and comparing the relative energy barriers resulting from the two systems. From a computational perspective, this is an attractive comparison of relative rather than absolute barrier heights. This, in addition to the biological relevance of allostery, makes allosteric systems ideal to explore and evaluate computational approaches for enzyme conformational ensemble modeling.

4. Quantum Mechanics for Enzyme Catalysis

4.1. The Cluster Approach

The quantum chemical cluster approach explicitly models the critical features of a biologically relevant active site using QM while typically accounting for the remainder of the protein with homogeneous dielectric continuum models [47]. This approach has been pioneered in the study of biologically relevant metal centers by Siegbahn and Blomberg, with model sizes around 60–70 atoms [100], and by Himo, who has used cluster models that can be much larger, even surpassing 300 atoms [11]. For more focused reviews on the quantum chemical cluster approach, we urge the interested reader to explore several excellent reviews [11, 47, 101]. Here, we summarize the steps taken in building a quantum chemical cluster model.

4.1.1. Model Selection

Once a biological target has been chosen, a deep dive into the literature is worthwhile to explore what is known, unknown, and theorized about the system. Most cluster models are designed from crystal structure coordinates. There may be attributes of the crystal structure that do not align with the system desired to be modeled, such as residue mutations, and alternative substrates bound. In some cases, it may be necessary to manually alter the structure to match the intended system of study, which will require longer MD simulation to allow the structure to properly relax. The primary literature may describe artifacts in the crystallographic model and whether specific residues are essential for catalytic activity (e.g., through the experimental study of enzyme mutants). Depending on the research goal, multiple crystal structures, sometimes with different ligand states, are important to consider. Additionally, the protonation states of some residues, particularly Glu, Asp, and His may be important to consider. If this information is not already available, it may be necessary to consider all the possibilities [102]. If crystallographic waters or ions are present in the active site, they may need to be explicitly included in the model as well [103]. It is typical to test various sizes of clusters, ranging from 100–300 atoms [11]. Convergence studies suggest that QM-cluster models give reliable energetics when the model size is large enough [47, 104–108]. Including additional residues beyond those immediately in contact with the substrate may be crucial to avoid unrealistic, extensive conformational reorganization of the active site following geometry optimization [109], however, it has been proposed that informed residue selection should take priority over a simple distance cutoff [110].

4.1.2. Model Truncation

The cluster approach requires cuts or truncations to be made since only a subset of the protein’s atoms will be included. The most common approach is to residues at the alpha carbon by removing all peptide bond atoms and capping the alpha carbon with hydrogens. The methyl-capping approach is performed when the N-C_α and C_α-CO peptide bonds on either side of the R chain are cut. There may be situations where peptide bond atoms are involved in the reaction, such as forming H-bonds to the substrate. In such cases, residues will be cut at either the N-terminus (N’), N-C_α bond or C-terminus (C’), C_α-CO bond, and the truncated ends will need an additional hydrogen to achieve saturation (“hydrogen-capping”). During this step, important considerations include atoms that influence catalysis to ensure the atom caps are neither artificially influencing the mechanism nor significantly altering the electronic structure, such as changing atomic hybridization or cutting across a highly polar bond. The effects of different truncation schemes are evaluated in Section 6.2.2.

4.1.3. Coordinate Locking

In most cluster models, it is necessary to lock or freeze certain atoms to preserve the active site geometry, maintain side-chain rotamer states along the reaction coordinate, and limit the model from accessing geometries that would not be possible inside the protein environment. As the structure is not fully optimized, evaluating the full QM partition function, including vibrational effects to thermochemistry, is challenging. Therefore, potential energies, rather than Gibbs energies, are often reported. There are methods to approximate entropic effects, such as projecting out the frozen coordinates from the Hessian [111]. The effects of coordinate locking have been explored in Ref. [112], where the authors studied phosphotriesterase using a cluster model of 82 atoms. The authors found locking induced significant strain, altering some geometric parameters. However, these did not influence the conclusions regarding the reaction mechanism and only altered the calculated barrier by 2 kcal/mol. The authors also noted that in this particular application, the truncation method resulted in a model that was too rigid. For example, a His residue in the cluster was modeled only as an imidazole ring, where one atom from the ring was locked, significantly hindering the motion of that group. However, the strain induced by coordinate locking is expected to reduce with larger models.

Freezing the alpha carbons of each truncated residue is a good choice. However, in some models, this might allow too many degrees of freedom resulting in inconsistent side-chain conformations along the pathway. Locking up to two hydrogens of the alpha carbon to restrict more degrees of freedom [11] or not locking residues that directly interact with the substrate [113] may be necessary. The more frozen atoms, the more rigid the model, which may influence energetics. Therefore, the coordinate locking scheme must be balanced, achieved through trial and error, between maintaining a reliable structure and allowing flexibility for energy minimization during geometry optimization.

4.1.4. Model Chemistry

In common with contemporary QM studies of organic and inorganic reactivity, dispersion-corrected density functionals such as B3LYP-D3 or ωB97XD are now commonly used for geometry optimizations of cluster models. In many cases, dispersion effects are expected to influence cluster geometry, such that Grimme’s zero-damped and Becke-Johnson damped (D3 and D3(BJ), respectively) corrections are recommended with typical GGA (generalized gradient approximation) or hybrid-GGA density functionals such as B3LYP [114]. While valence double-zeta basis sets are often suitable for geometry optimization, single-point energy corrections with solvent models and larger basis sets are generally employed to account for electrostatic effects and approach more accurate energies. A dielectric constant close to 4 (c.f. diethyl ether, for which ε = 4.24) is expected to mimic the relatively hydrophobic protein interior, although examples in the literature have evaluated cluster model energetics with multiple dielectrics to investigate their sensitivity to this value [47, 105]. Significant changes in relative energies at different dielectric values may indicate that the cluster is too small, and more residues or active site water molecules should be included.

4.2. Application of the Quantum Cluster Approach: Benzoylformate Decarboxylase

Benzoylformate decarboxylase (BFDC) is a thiamine diphosphate (ThDP)-dependent enzyme that catalyzes the decarboxylation of benzoylformate into benzaldehyde and carbon dioxide in a critical step of the mandelic acid degradation pathway [115, 116]. Additionally, BFDC can enantioselectively catalyze carboligation reactions, depending on the substrate. X-ray structures of enzymes in the ThDP-dependent decarboxylase family show common features such as the presence of ThDP, an almost invariant glutamate, two ionizable acidic residues, and two proximal histidine residues on an ordered loop termed the HH-motif. However, the first X-ray structure of BFDC contains serine (Ser26) as the only ionizable acidic residue in the active site, and the two proximal histidines (His70, His281) belong to separate monomers rather than an ordered loop.

Himo and co-workers used the cluster approach to study BFDC-catalyzed decarboxylation. Their model consisted of 307 atoms and an overall −1 charge. Geometry optimizations were performed at the B3LYP-D3(BJ)/6–31G(d,p) level of theory, with 6–311+G(2d,2p) single-point corrections using the SMD solvation model with a dielectric of ε = 4. While entropy changes along the reaction coordinate are often neglected in studies using cluster models, the release of CO₂ gas involves a significant increase in translational entropy. This was calculated to be 11.3 kcal/mol, and so this value was included in each step after CO₂ formation, in line with previous estimation methods [13, 117]. The key roles of active site residues were identified, and the authors also identified a kinetically relevant off-cycle species produced by intramolecular cyclization of the cofactor [118] .

In a subsequent study, Himo and co-workers focused on enantioselective catalysis by BFDC [119]. Following benzoylformate decarboxylation, the (Breslow) enamine intermediate can participate in a benzoin condensation with benzaldehyde or acetaldehyde electrophiles. Interestingly, these transformations proceed with an opposite sense of enantioselectivity. The computed energy difference between competing TSs in the enantioselectivity determining step for benzaldehyde addition (TS3, Figure 6) is 9.3 kcal/mol, consistent with complete stereocontrol observed experimentally. Steric interactions between substrate and multiple residues contribute to the higher energy of the disfavored pathway. For acetaldehyde, the energy difference (0.3 kcal/mol) favors the (S)-product, consistent with the contrast in selectivity observed for the two substrates. This, and other studies by Himo, illustrate the importance of a reasonably large cluster to capture the multiple steric and other noncovalent interactions influencing enantioselectivity in enzyme catalysis.

Fig. 6.

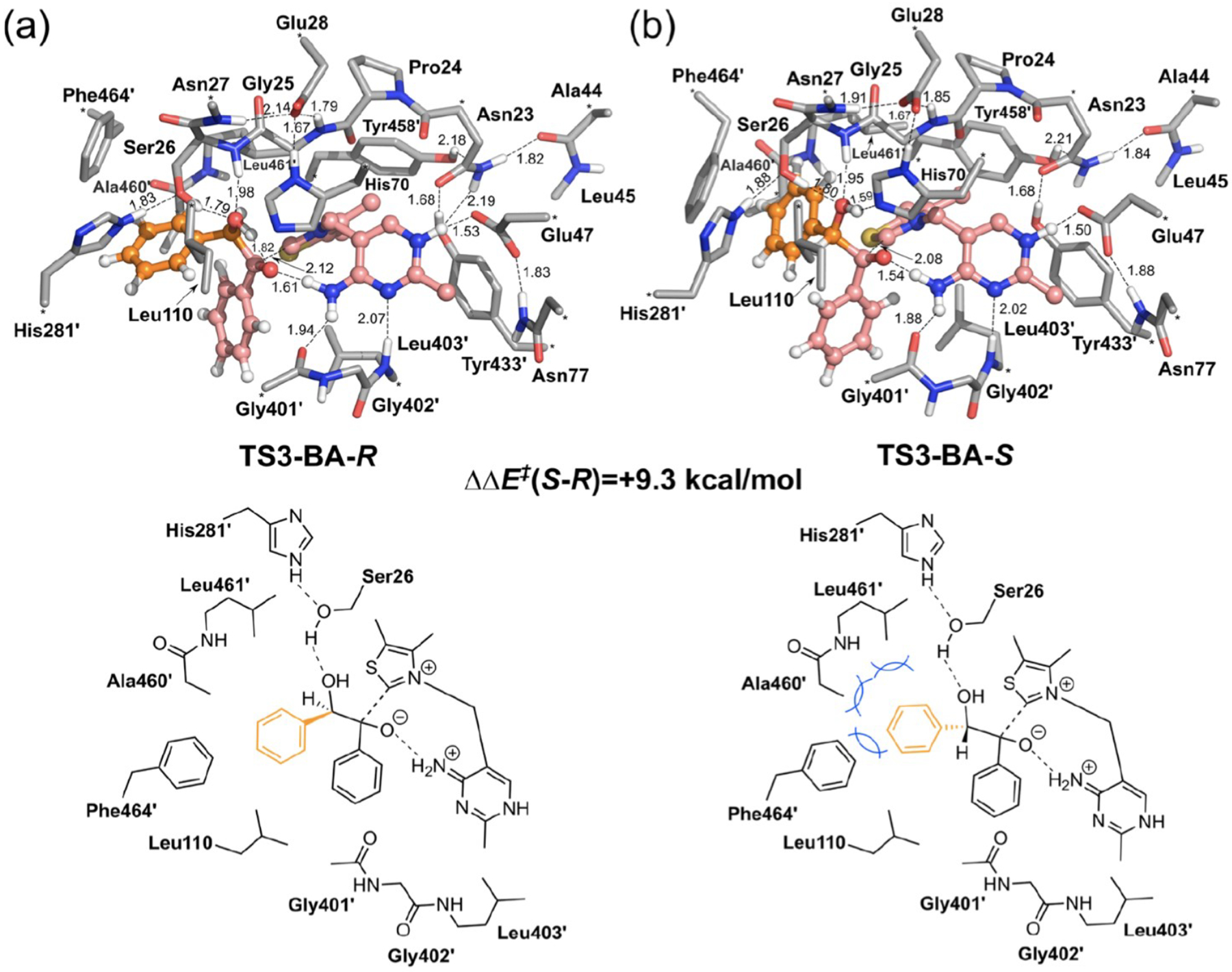
Optimized geometries of selectivity-determining transition state structures for (a) (R)-benzoin and (b) (S)-benzoin in the BFDC carboligation reaction. The benzaldehyde acceptor and enamine donor are shown in orange and pink, respectively. The blue lines in the lower panel of (b) indicate the steric clashes from Ala460, Leu461, Phe464 that drive stereoselectivity. Asterisks designate the atoms frozen during calculations. All non-polar hydrogens are hidden for simplicity. Figure adapted from [112].

4.3. QM/MM Approaches

Standing as an alternative to the truncation schemes discussed above, hybrid QM/MM approaches enable a small portion of the enzyme, typically in the active site region, to be treated by QM, while the remaining larger part of the system is described by MM. Compared to QM cluster models, the QM/MM approach explicitly represents the steric effects (e.g., via mechanical embedding) of an inhomogeneous protein, alongside noncovalent interactions such as long-range electrostatics between the QM and MM subsystems (e.g., via electronic embedding). QM/MM methods are widely-used across organic and organometallic chemistry, and are particularly well-established in the study of enzymatic reaction mechanisms [29, 120–128].

The explicit inclusion of the extended protein environment can quantitatively impact relative energetics, or indeed, fundamentally alter a computed energy profile. For example, electrostatic effects contribute several additional kcal/mol in QM/MM studies of dioxygen binding energies in JMJD2A [129]. Further, the role of protein reorganization along the reaction coordinate, which can be consequential, may also be captured and quantified [130]. Readers are referred to detailed reviews on the status of QM/MM approaches in modeling enzymatic catalysis [120, 127, 131, 132]. QM/MM models, which typically also include explicit solvent molecules as well as the enzyme and substrate, are much larger than those used in QM-only models. Geometry optimizations become more challenging for large system sizes and so may be performed with (partially) fixed surrounding atoms. Even so, more energy minima are possible with these larger models, and the importance of extensive configurational sampling becomes paramount.

For example, using energy minimization to generate potential QM/MM energy surfaces for an enzymatic reaction while starting from a single protein structure has been shown to produce severe errors in activation barrier heights and binding free energies. Averaging results over several protein configurations generated by long MD simulations has been recommended [120, 133, 134]. The computational demands of QM/MM simulations can be influenced by choice of the QM region’s size and by using low-cost semi-empirical QM (SQM) schemes in place of more expensive DFT calculations. In the first respect, many of the chemical and physical considerations relevant to the choice of cluster models stand; the QM region should be evaluated for convergence [135–138], and attention to the region definition is also required [139–142]. Although, compared to QM-only models, Warshel has demonstrated a relative lack of sensitivity to including more distal groups in the QM region [143]. The use of SQM methods generally requires careful benchmarking or parameterization against more expensive QM results [144]. Nevertheless, typical QM/MM simulations are run for timescales on the order of nanoseconds. Enhanced sampling techniques have been applied to compute the free energy profiles of reactions in QM regions, but, even in these cases, sampling of the rest of the protein is limited to the nanosecond timescale [145–147]. While this may be sufficient to sample side-chain rotamer preferences, protein conformational changes required to reach a catalytically active state (e.g., involving loop and helix motions) routinely take place on timescales several orders of magnitude slower [148]. Classical MD simulations over microsecond timescales, inaccessible while employing QM/MM potentials, have been necessary to observe binding site formation, for example, in bromodomains [149].

4.4. QM Approaches Using Multiple Conformations

In contrast to using an X-ray structure as a starting point for QM studies, a short MD simulation can be used (500–1000 ps) to generate an initial geometry [150]. This will relax the structure towards a local minimum, potentially reducing crystalline artifacts. However, this approach is unlikely to help when the X-ray structure is sufficiently far from the catalytically relevant conformation(s). QM/MM approaches often incorporate multiple conformations as initial geometries for modeling, usually taken as a series of random or evenly spaced snapshots from an MD simulation.

The question of how to combine the results from several QM or QM/MM models has been addressed by various approaches. An assortment of averaging techniques have been explained elsewhere [151]; however, questions continue to be raised, such as what is required to converge energies in this approach [104] and how to account for conformations with differing reactivities [30, 152, 153]. Alternatively, the Boltzmann ensemble can be evaluated with a combination of extended MD and structural clustering. In such an approach, the average structures and populations can be used to generate and weight energy barriers resulting from either the QM-only or QM/MM calculations. The details of this approach are outlined in the next section.

5. Structural Clustering with Molecular Dynamics

Structural clustering is a necessary and often overlooked component of describing the conformational ensemble of a protein. To illustrate the need for structural clustering, we consider a set, X, of N configurations of a protein system, $\mathbf{X}=\left\{{\overrightarrow{x}}_1,{\overrightarrow{x}}_2,\dots ,{\overrightarrow{x}}_N\right\}$, where ${\overrightarrow{x}}_i$ is the ith configuration of the system. The expected value of an observable, M, can be computed as an average over this set,

$$\langle M\rangle =\frac{{\sum }_i^{N}M\left({\overrightarrow{x}}_i\right)P_i}{{\sum }_i{P}_i}$$ (4)

where P_i denotes the probability of configuration i and is equivalent to $\frac{1}{N}$ in conventional MD sampling. The observable denotes any property of interest that depends on the conformation of the system, such as the electrostatic potential at the active site or the rate constant of a chemical reaction. If N is small and $M\left({\overrightarrow{x}}_i\right)$ is cheap to compute, Eq. 4 can be used directly to estimate the property of interest. When N gets large and/or $M\left({\overrightarrow{x}}_i\right)$ is expensive to compute, clustering approaches are employed to approximate Eq. 4. Clustering is particularly necessary and challenging for MD descriptions of protein ensembles due to the sheer size of the data sets: it is not uncommon to have millions of protein configurations in a trajectory [71] or combined trajectories [154]. Given a clustering of a conformational ensemble into K < N clusters with well-defined average (or mediod) structures, observable can be estimated as

$$\langle M\rangle \approx \frac{{\sum }_j^{K}M\left({\langle \overrightarrow{x}\rangle }_j\right)P_j}{{\sum }_j{P}_j}$$ (5)

where ${\langle \overrightarrow{x}\rangle }_j$ is the average structure and P_j is the probability of cluster j. The accuracy of Eq. 5 depends on several factors, including the conformational heterogeneity of clusters and the sensitivity of the observable to conformational heterogeneity.

The goal of structural clustering is to combine configurations into clusters that have similar values of the observable of interest. In the context of enzyme catalysis, the active site is an obvious focal point. Therefore consideration of only active site residues for structural clustering may be sufficient. The results of clustering are a set of K macrostates, made from MD snapshots, or microstates, and their associated populations, {P_j}. There are numerous clustering methods employed in the field and, unfortunately, no consistent best choice. Here, we describe five steps that most clustering protocols follow: (1) choosing a coarse-grained description of the protein, (2) picking features to describe the coarse-grained protein, (3) dimensionality reduction of the features, (4) clustering in reduced dimensions and (5) analysis of the results. We note that while this is a typical order of the steps, it is not unique. It is possible, for example, to cluster first and then perform dimensionality reduction (swapping steps 3 and 4).

5.1. Step 1: Choose a Coarse-Grained Description of the Protein

Atomistic descriptions of a protein and its environment must be coarse-grained to make the conformational ensemble a tractable object. In a typical aaMD simulation of a protein, there are ~ 100K total atoms and thus 300K degrees of freedom. It is intractable to consider each degree of freedom of the system, even with millions of frames. Luckily, many of these degrees of freedom are of the solvent and thus only implicitly important in determining the protein conformational ensemble. Thus, a natural coarse-graining of the system is to ignore the solvent degrees of freedom and only analyze the atoms of the protein. Even this yields exceptionally high-dimensional data sets that are intractable to analyze. Additional coarse-graining of a protein is almost always performed. Common examples of coarse-grained protein descriptions are backbone atoms, CA atoms, center-of-mass (COM) of residues, and/or secondary structural elements.

A good choice of the coarse-grained description of the protein depends on the application. For example, if one is interested in protein folding, the coarse-grained description should include all protein residues. Typical coarse-graining for this application includes all backbone atoms, only CA atoms, or COM of residues. A depiction of this type of coarse-graining is given in the first two panels of 7. The top-left panel depicts the folded state of a small, fast-folding protein (Trp-cage) in a box of water. The protein is coarse-grained in the top-middle panel by only choosing the CA atoms of each residue. The choice of all CA atoms is tractable for this small protein but will become intractable for larger proteins. In the case of enzymes will well-defined active sites, it is natural to choose a more detailed description of the active site while ignoring protein residues far away from the active site.

5.2. Step 2: Choosing Features

With a coarse-grained mapping chosen, one must then choose features or coordinates to describe these coarse-grained structures. A good set of features can discern between the important metastable conformations. For example, the features in a two-state protein folding problem must differentiate between folded and unfolded states. There are two natural choices for features: internal coordinates and positions. Each has its advantages and disadvantages that will be described below. There are also combinations of internal coordinates or positions called collective variables (CVs, e.g., helical content, RMSD of substructures, etc.) that we will not discuss in detail. Generally, these CVs have similar advantages and disadvantages to the internal coordinates or positions used to compute them.

Internal coordinates of a macromolecule include distances (two-body terms), angles (three-body terms), dihedral angles (four-body terms), and higher-order terms. Within the context of all-atom simulations of proteins, most force fields only include up to four body terms, and thus it is uncommon to consider terms higher than four bodies. Internal coordinates have the advantage of being the natural coordinates of the Hamiltonian of the system: they are rotationally invariant and can uniquely describe each structure. The downside of these features is feature space size, and the mixing of features can limit the types of clustering algorithms that can be employed. The choice of all pairwise distances for the Trp-cage example is depicted using blue lines between CA atoms in the top-right panel of Fig. 7. With 20 residues (and thus CA atoms) in the Trp-cage protein, there are 190 pairwise distances to consider.

Fig. 7.

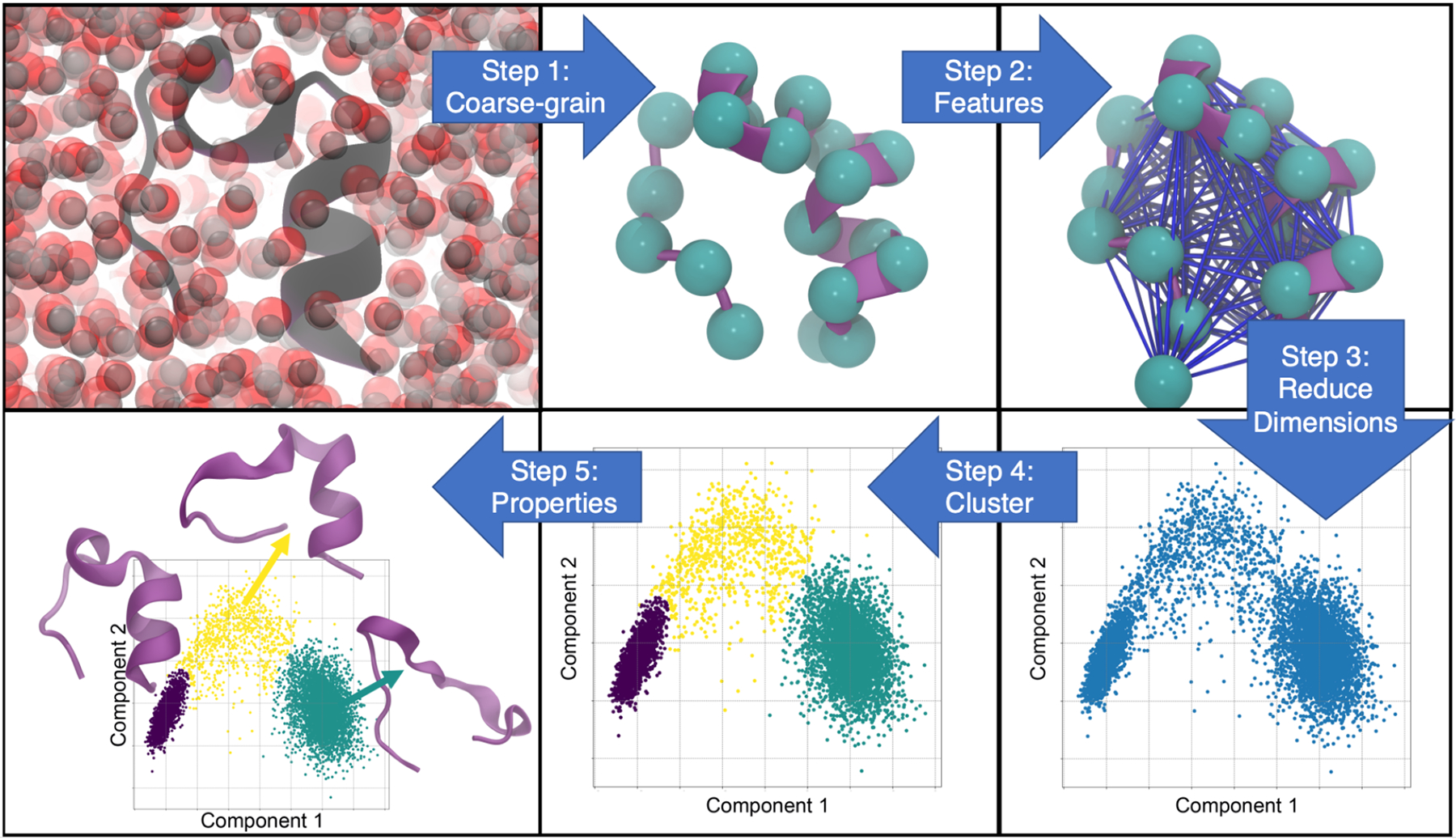
Five-step schematic for structural clustering from all-atom molecular dynamics trajectories. Starting from the top left, the first step is to choose a particle coarse-grained mapping and apply it to an explicit solvent all-atom trajectory. From there, a set of features to describe the system, such as all pairwise distances, are chosen. A trajectory of these features is then passed through an unsupervised dimensionality reduction algorithm (e.g., principal component analysis) and projected onto reduced dimensions. A clustering algorithm is applied in reduced dimensionality space to classify each frame of the trajectory. Finally, the structural clusters are analyzed (bottom left).

Particle positions are also a natural choice of features to cluster trajectory data of macromolecular systems. Advantages of these features include no significant over-determination of the system, coordinates are directly output by simulation software, and coordinates can differentiate between all configurations observed. A significant limitation of particle positions is that they are defined in the lab frame and thus are not immediately rotationally invariant. This leads to equivalences in particle positions that make them challenging to deal with [155].

5.3. Step 3: Dimensionality Reduction

Despite an initial particle coarse-graining (Step 1), the remaining degrees of freedom after featurization are often too large to consider in full-dimensional space. Take, for example, the folding and unfolding of an alpha helix coarse-grained into 12 beads. If we choose all pairwise distances as our features (Step 2), there are 66 degrees of freedom to describe each simulation frame. To make any sense of these dimensions that are often coupled, dimensionality reduction is performed. The goal is to determine a small subset of degrees of freedom that retain the essential information of the full-dimensional space.

Multiple dimensionality reduction methods have been used on MD data. These methods differ based on what they define as important information. Principal component analysis (PCA), for example, determines the linearly independent coordinates that retain the most variance in the data. It is not uncommon to see trajectory data projected onto the first two principal components with the largest variances. Time-lagged independent component analysis (tICA) determines the linear combination of coordinates that rank the timescale of collective motions [156]. tICA is often coupled with Markov State Modeling (MSM) to determine rates of transitions between metastable states [157]. Other dimensionality reduction methods have been employed, such as Sketch Map [158] and UMAP [159], to achieve specific properties in the reduced space. The outcome of any dimensionality reduction technique will be a description of each trajectory frame in reduced dimensions.

5.4. Step 4: Clustering Algorithm

Clustering algorithms are typically applied following dimensionality reduction methods to assign each frame to a conformational state. A variety of clustering algorithms have been applied in this context. The types of algorithms can be broken down into two categories: hierarchical and non-hierarchical. Both types have been used though more recent efforts have focused on non-hierarchical clustering algorithms.

Hierarchical clustering algorithms start with each frame in its own cluster and iteratively group similar frames together. This results in a dendrogram structure of the clustering. Different distances can be used to define similarity. Methods differ in how they join clusters together and the resulting distance used between clusters. Advantages of hierarchical methods include that the methods are fast, can be used to determine macroclusters and subclusters, and are easy to implement. The major disadvantage of hierarchical methods is that they are greedy: once clusters have been formed, they will not be broken apart to find a more global minimum. Examples of hierarchical methods include Ward, average linkage, and minimum linkage.

Non-hierarchical clustering methods are the most commonly employed for MD trajectory data. The most common example is k-means clustering and its variants. K-means determines the means and trajectory partitionings that minimize the summed distances between frames and associated means. This method works well for well-separated spherical distributions of points. Other density-based fitting algorithms include Gaussian mixture modeling (GMM) and DBSCAN, both of which have been employed to trajectory data projected onto reduced dimensional space with reasonable success [160]. These methods are not as greedy as hierarchical methods: frames can move from one cluster to another during the iterations until a (local) minimum in the algorithm metric is reached. A significant drawback to such methods is the computational cost and the difficulty in determining the appropriate number of clusters.

No single best method works for all trajectory data. An often overlooked aspect, however, is to consider the underlying assumptions of the clustering algorithm. GMMs, for example, work under the assumption that the probability of the density can be represented as a sum (mixture) of Gaussian functions. In a recent study of clustering algorithms, Westerlund and Delemotte showed that GMMs do not work well when the density in reduced dimensional space is non-Gaussian [160]. It is not immediately clear whether we should expect MD data to be Gaussian in these spaces and almost assuredly depends on the features chosen and dimensionality reduction technique employed.

5.5. Analysis of Resulting Data

The result of a clustering algorithm is an assignment of each frame into a conformational state. With this information in hand, one can analyze different aspects of the clusters. The specific analysis employed will depend on the application. For example, one might build an MSM based on conformational clustering and determine the rates and associated structural mechanisms if one cares about folding rates. If one cares about catalysis, it is relevant to compute the relative reaction rate in each conformational state. The implicit assumption is that the value of a macroscopic property does not vary significantly within a given cluster. This assumption can be tested to assess the validity of the clustering.

6. Unexplored Land in Computational Catalysis: A Case Study on IGPS

In this section, we focus on the mechanism of glutamine hydrolysis by the allosterically regulated enzyme IGPS. This system illustrates particular challenges for computation, such as catalytically-inactive crystal structures, the presence of active and inactive enzyme conformations, and allosteric rate enhancement.

6.1. Imidazole Glycerol Phosphate Synthase (IGPS)

Efficient transportation of a reaction product from one location to be used as a reactant in the next is a critical step in biological pathways. In some cases, the efficiency depends on whether or not that product must travel through bulk solvent to arrive at its next stop. The glutamine amidotransferase (GAT) family of enzymes produce ammonia through hydrolysis of glutamine and utilize the ammonia in a subsequent reaction, harnessing several traits to ensure their effectiveness in biochemical pathways. The bienzyme imidazole glycerol phosphate synthase (IGPS) is a GAT composed of glutaminase and cyclase subunits, nominally known as HisH and HisF in T. maritima (Fig. 8). It operates in histidine and purine biosynthesis in plants, fungi, bacteria, and archaea. In the glutaminase subunit, IGPS performs the hydrolysis of glutamine to form glutamate and ammonia, the latter of which goes on to react with the allosteric ligand (phosphoribulosyl-formimino-AICAR-phosphate, PrFAR) over 25 Å away in the cyclase active site. The binding of PrFAR results in a 4500-fold increase in glutamine hydrolysis, making IGPS a V-type allosteric system [36]. The mechanism of allosteric regulation in IGPS and how the two active sites are coupled through residue pathways has received intense interest from experimentalists and theoreticians alike [67, 82, 161, 162].

Fig. 8.

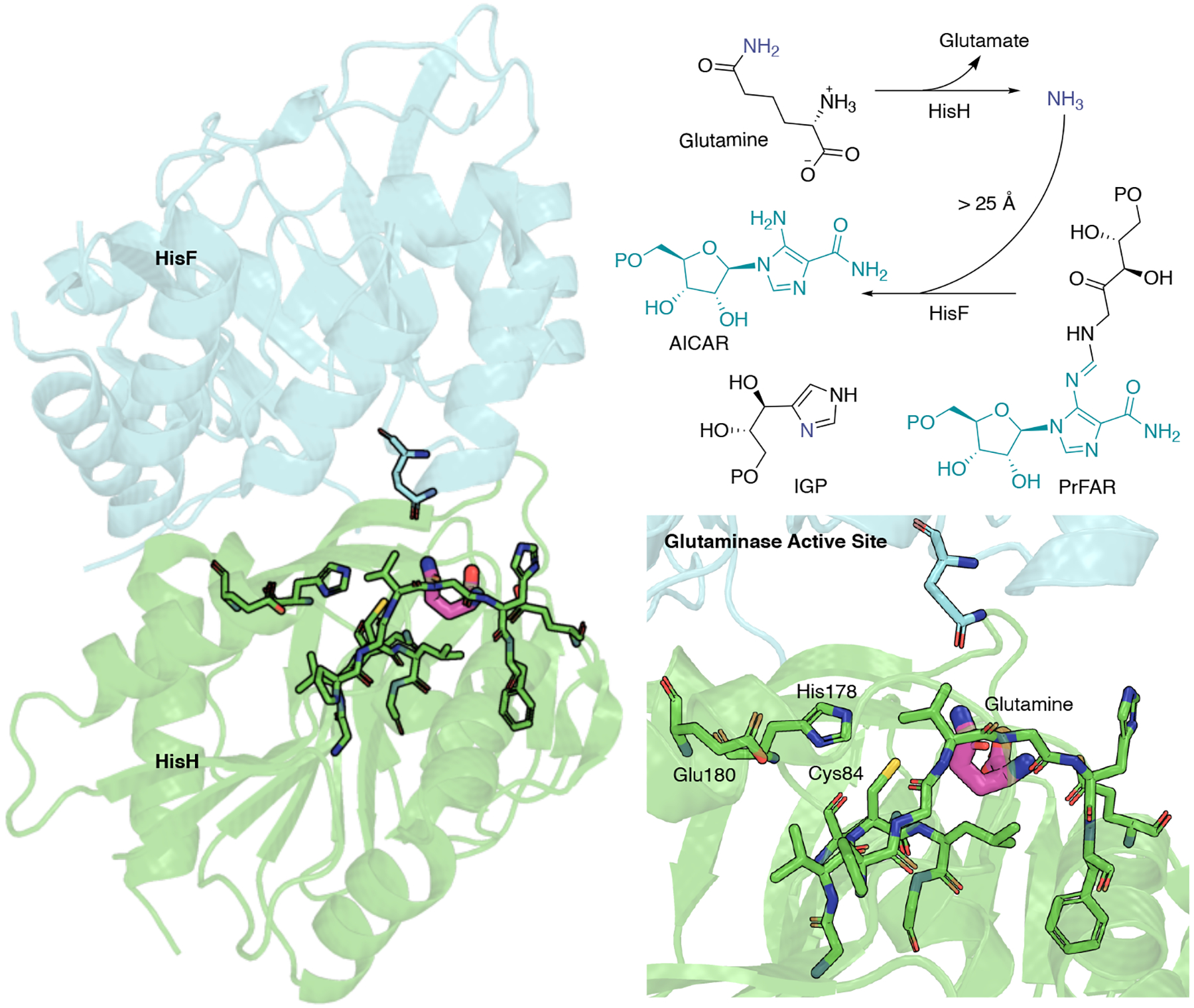
IGPS from T. maritima and overview of glutaminase and cyclase coupled reactions. HisH is shown in green, and HisF is shown in blue. In HisH, glutamine reacts with water to form glutamate and ammonia, which is shuttled over 25 Å to the cyclase active site in HisF, where it reacts with PrFAR to form AICAR and ImGP.

Until 2021, it was unclear how conformational ensembles impact allosteric regulation of IGPS and if changes to the conformational equilibrium occur when PrFAR binds. Furthermore, it was unknown whether PrFAR binding induces specific changes to catalytic residues involved in glutaminase activity. Comparison of IGPS to similar GATs suggested the conformation of a conserved oxyanion strand (P49 G50 V51 G52) to be critical to the rate enhancement. The formation of an oxyanion hole, a catalytic motif that stabilizes a substrate’s developing negative charge through hydrogen-bonding interactions, has been a leading theory to account for rate enhancement in GAT mechanisms. It has been proposed that for many GAT enzymes (e.g., pyridoxal 5’-phosphate synthase and IGPS from T. maritima) [65, 163], binding of the effector induces a backbone flip in the oxyanion strand, forming an emergent oxyanion hole that stabilizes an oxyanion tetrahedral intermediate. Visual inspection of the apo and ternary IGPS crystal structures, 3zr4 [164] and 1ox5 [165], respectively, shows the Val51 backbone has not flipped in either case, suggesting either the flip in the Val backbone is not induced by effector binding or the crystal structure with PrFAR bound is not in the catalytically enhanced state, as proposed from solution NMR and MD studies [65].

In 2021, an IGPS crystal structure from Sprangers and co-workers showed the oxyanion hole fully formed, with the Val51 amide flipped (Figure 9) [28]. Furthermore, the authors observed that both glutamine and PrFAR ligands must be present for the catalytically competent state to be reached. Numerous structural changes occur, breaking the hydrogen bond between P10 and V51 in HisH, a critical interaction stabilizing the backbone conformation of the oxyanion strand. Consequently, the V51 backbone is free to flip, accessing a conformation in which the backbone N-H is favorably oriented towards the carbonyl group of the substrate. The dynamic equilibrium between inactive and active IGPS conformations was found to occur on the millisecond timescale, explaining the difficulty of observing all conformational transitions in previous computational studies. Of particular importance, this study shows a direct correlation between the equilibrium of the active versus inactive states and glutamine turnover, just as the ensemble model of allostery predicts. The population of the active conformation can be manipulated experimentally by distant mutations. In these studies, a linear relationship is observed between destabilization of the active conformation and ln(k_cat), as predicted by the ensemble allostery model [28]. Furthermore, k_cat is directly influenced by the population of the active conformation.

Fig. 9.

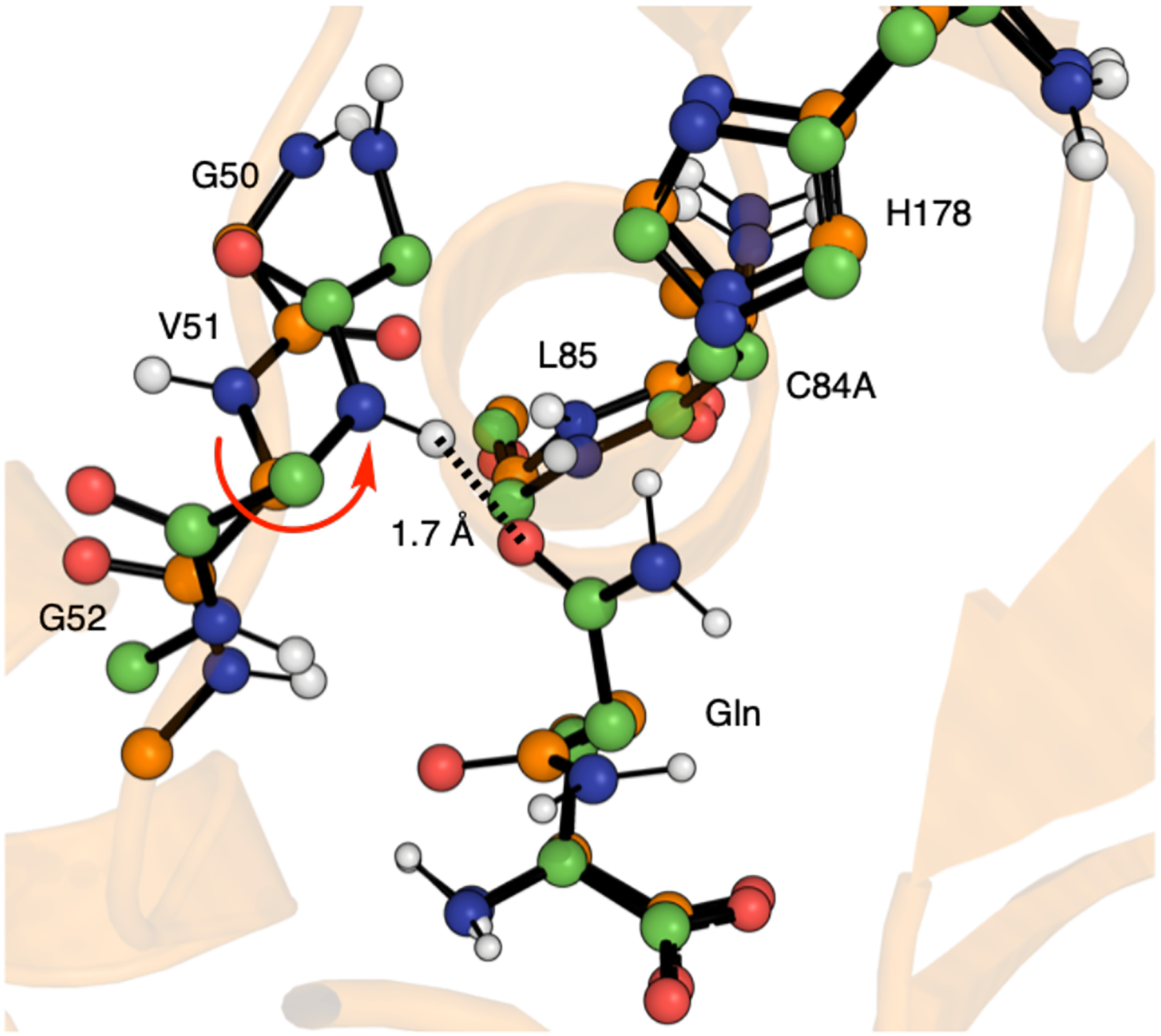
Aligned crystal structure conformations of IGPS in ball-and-stick representation. All oxygen, nitrogen, and polar hydrogen atoms are colored red, blue, and white. Orange carbons correspond to the catalytically inactive conformation, chains AB from crystal structure 7ac8. Green carbons correspond to the catalytically active conformation, chains EF from crystal structure 7ac8. The V51 backbone flip is highlighted with a red arrow. This dihedral flip leads to a strong hydrogen bond ( 1.7 Å) between the V51 amide and the oxygen atom of the bound Gln substrate.

6.2. Glutamine Hydrolysis in IGPS – Key Considerations for Future Computational Studies

Glutamine hydrolysis in IGPS occurs via a multistep mechanism; however, no previous quantum chemical or QM/MM studies have been conducted. Before 2021, the active enzyme conformation had not been captured crystallographically, and as outlined above, the millisecond timescale of conformational transitions between inactive and active states is challenging to sample with cMD simulations. In the following sections, we discuss current prospects for modeling glutamine hydrolysis in IGPS and identify the challenges ahead.

In IGPS, a catalytic triad (Glu180, His178, and Cys84) performs glutamine hydrolysis. These residues would be the minimal ingredients of a QM region. However, as outlined above, catalytic activity results from large-scale conformational changes leading to a backbone flip, and the substrate is in contact with several additional residues in the active site. For this reason, a physically realistic active site model of IGPS involves over 200 atoms. We suggest QM treatment of the following residues are necessary: f98D, f123Q, h10P, h11G, h12N, h50P, h51G, h52V, h53G, h84C, h85L, h88Q, h96E, h141H, h142T, h143Y, h176H, h178E, along with the glutamine substrate. Additionally, inactive (Chains A and B) and active conformations (Chains E and F) can be found from the 7ac8 crystal deposition. The overall charge of this 223-atom active site model is −3. For modeling via the QM-cluster approach, different truncation schemes (Section 4.1) can be considered for IGPS (Fig. 10), of which some illustrative examples are discussed below.

Fig. 10.

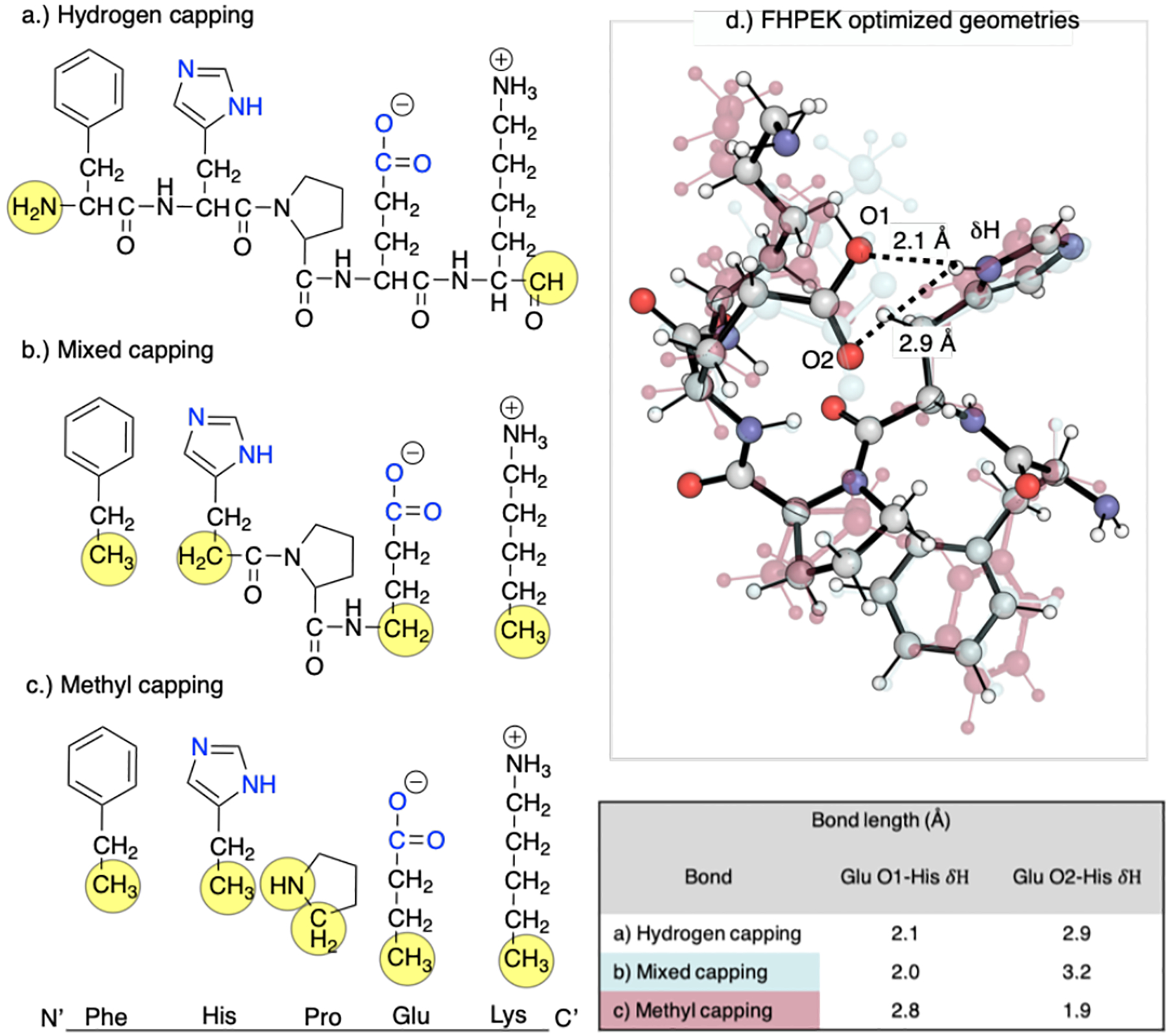
Truncation schemes applied to peptide sequence FHPEK from the IGPS HisH subunit. a) Hydrogen capping: the terminal ends are cut, and a single hydrogen is added to each end. b) Mixed capping: the peptide backbone atoms are removed from the terminal residues and the alpha carbons are capped, creating methyl groups, His and Glu are hydrogen capped at the N and C-terminus, respectively. c) Methyl capping: all peptide backbone atoms are removed from each residue and the alpha carbons methyl capped. d) Optimized geometries of each truncation scheme. The translucent red structure is the methyl capping scheme, the translucent blue is the mixed capping scheme, and the solid atom-colored model is the hydrogen capping scheme. The table shows O1 and O2 distances from the His δH resulting from different truncation schemes.

ωB97XD/6–31+G(d) optimizations of different truncated models of the FHPEK stand in the IGPS active site, in which all C_α atoms and capping hydrogens were frozen, reveal the importance of decisions made during this stage of the modeling process. Terminating the side-chains by methyl groups leads to much greater atomic displacement relative to a model in which the polypeptide backbone is preserved (Fig. 10 a–c). This disrupts an H-bond between His178 and Glu180, which is preserved in the more conservative capping scheme. While the impact of these structural differences upon the reaction mechanism has not been studied, various schemes may need to be examined in models of catalysis in the active site of IGPS.

6.3. Connecting Macroscopic Turnover Frequency to the Microscopic Conformational Ensemble

IGPS and other enzymes explore multiple conformations with different levels of catalytic activity. One such example is the acyltransferase, LovD, which is part of the lovastatin biosynthetic pathway. Exploring these conformational dynamics is essential to model reactivity. For example, the directed evolution of LovD produces a favorably mutated version (LovD9), whose catalytic performance can only be captured by microsecond MD simulations [32]. The overall catalytic activity is influenced by the populations of different conformational states and their interconversion, and the intrinsic reactivity (i.e., catalytic activation barrier) of these states. Therefore, a multistep computational workflow can be envisaged for modeling catalysis in allosteric enzymes such as IGPS (Fig. 11). First, explicitly-solvated aaMD simulation of the four different substrate states (E, E+X, E+X, E+X+S) is required. Statistically meaningful sampling of the dynamic equilibrium between inactive and active IGPS states is nontrivial and will undoubtedly require enhanced sampling techniques. Second, structural clustering of trajectories will be performed to yield representatives of each cluster, along with populations. Third, multistep reaction Gibbs energy profiles for glutamine hydrolysis will be generated for each conformational cluster from MD. Fourth, individual k_cat values are weighted according to conformational populations to predict overall turnover frequency according to Eq. 5.

Fig. 11.

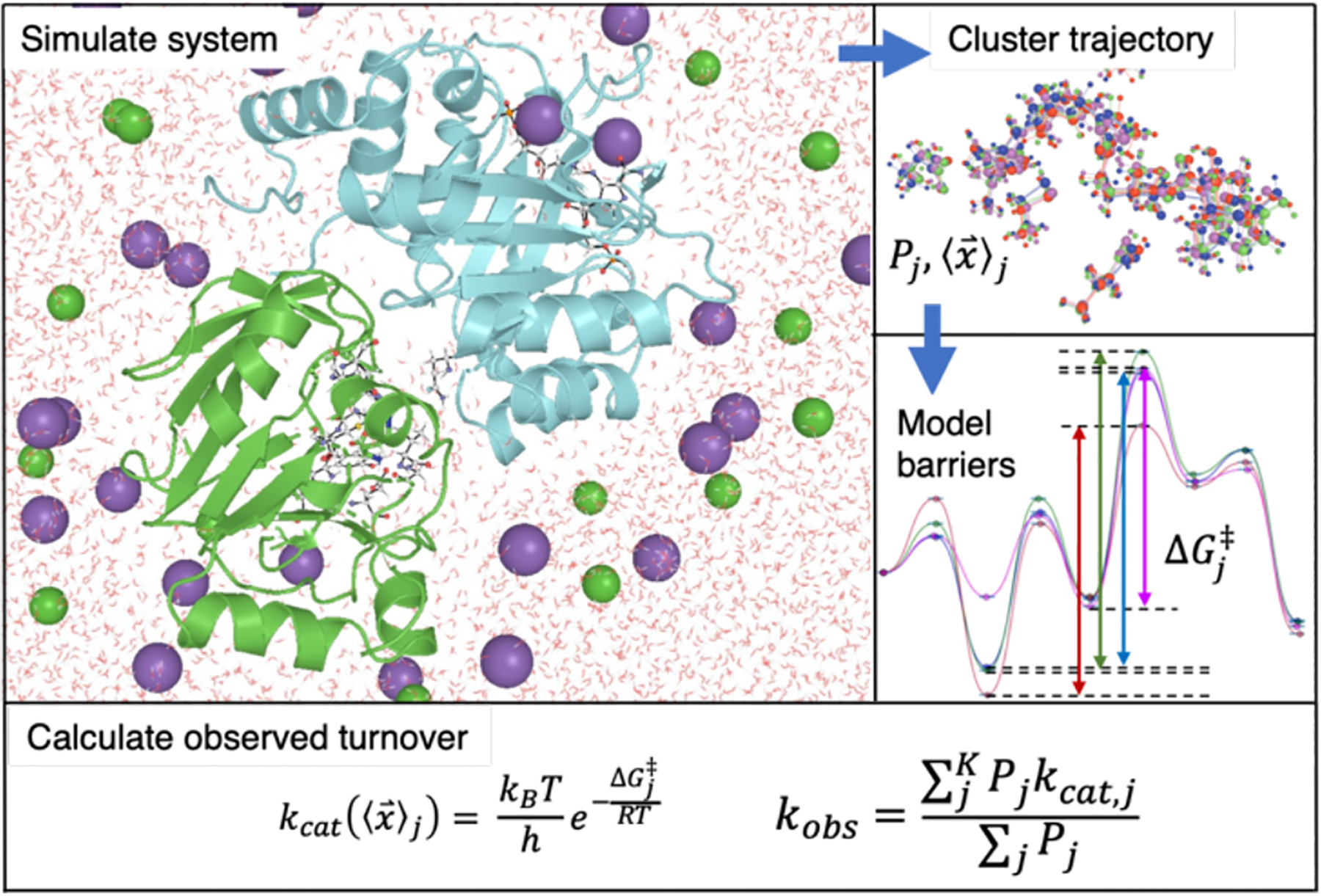
A stepwise workflow combining MD simulation, conformational clustering, and QM calculations to calculate catalytic turnover. The first step is to simulate the system with explicit solvent all-atom MD. Next, structural clustering of the trajectory yields populations, P_j and cluster average structure coordinates, ${\langle \overrightarrow{x}\rangle }_j$. These coordinates are used to generate models for QM calculations of barrier heights of each cluster, $\Delta G_j^{‡}$. The macroscopically observed turnover frequency, k_obs can be calculated as an expected value of k_cat,_j averaged over the conformational ensemble.

7. Conclusions and Future Directions

The combination of MD sampling of the protein conformational ensemble and QM modeling of the enzymatic reaction provides a practical framework for modeling enzymatic mechanisms. In particular, catalytically-inactive X-ray structures, long timescales associated with protein motions, and conformational landscapes influenced by allosteric ligands present challenges for QM-only approaches that require the intervention of protein sampling. In this perspective, we have emphasized that a bridge between MD simulations and QM cluster models comes in the form of conformational clustering and analysis since this generates a tractable number of states that could then be used in QM cluster models. This integrated approach is also suitable for use with QM/MM generated barriers. The choice of approach to calculate the reaction barriers may be based on user preference as well as attributes of the system of study. As the combination of MD sampling, conformational clustering, and subsequent energy barrier calculations are increasingly pursued, computational chemists will be able to access new mechanistic information about allosteric enzymes. Although the computational framework discussed herein applies to V-type allosteric systems, it can also be applied more generally to study the enzyme conformational ensemble and its importance for enzyme catalysis. While this approach is computationally demanding, the advent of GPU accelerated MD and QM approaches makes this tractable for numerous enzymes.

The empirical correlation between active conformation population and catalytic activity in IGPS shows the value in using MD and structural clustering to account for the influence of conformational heterogeneity on enzyme catalysis. This behavior is expected to be consistent among other enzymes that follow the ensemble model of allostery. Furthermore, the concept of free energy redistribution is a more general concept that numerous enzymes have exhibited as a way to regulate catalytic activity. Therefore, the workflow illustrated in Fig. 11 may be applicable across various enzymatic systems, although there may be cases where the results are consistent with single-conformation studies, particularly in more rigid systems.

Using a combined MD/QM conformational ensemble approach, computational studies of enzyme catalysis will address critical open questions. These include:

1. What are the relative rates of conformational sampling and enzymatic reactions for specific enzymes?

2. Can a single “active” conformation capture observed catalytic properties, or do enzymatic reactions proceed from various enzyme-substrate conformations?

3. Are there general mechanisms that can be applied to classes of enzymes? For example, do V-type allosteric enzymes all conform to the ensemble model of allostery?

Additionally, several assumptions underlying such approaches require further interrogation, such as (i) whether a single structure from a conformational cluster can be used to compute the energy barrier for a reaction, as in Eqn. 5; and (ii) whether different enzymatic reactions progress within the same conformational state, or whether in the limit of relatively fast conformational transitions, the Curtin-Hammett principle of chemical reactivity can be applied to enzyme catalysis. Further exploration of these questions will provide insightful results that propel the field of computational enzyme catalysis towards a land of opportunities.