Accuracy of angular displacements and velocities from inertial-based inclinometers

Abstract

The objective of this study was to evaluate the accuracy of various sensor fusion algorithms for measuring upper arm elevation relative to gravity (i.e., angular displacement and velocity summary measures) across different motion speeds. Thirteen participants completed a cyclic, short duration, arm-intensive work task that involved transfering wooden dowels at three work rates (slow, medium, fast). Angular displacement and velocity measurements of upper arm elevation were simultaneously measured using an inertial measurement unit (IMU) and an optical motion capture (OMC) system. Results indicated that IMU-based inclinometer solutions can reduce root-mean-square errors in comparison to accelerometer-based inclination estimates by as much as 87%, depending on the work rate and sensor fusion approach applied. The findings suggest that IMU-based inclinometers can substantially improve inclinometer accuracy in comparison to traditional accelerometer-based inclinometers. Ergonomists may use the non-proprietary sensor fusion algorithms provided here to more accurately estimate upper arm elevation.

1. Introduction

Measuring human motion with accuracy is critical for many applications in occupational ergonomics, such as estimating exposure to non-neutral working postures (Douphrate et al., 2012) and evaluating workplace designs (Fethke et al., 2011). Human motion is most accurately quantified using laboratory-based electromagnetic or optical motion capture systems (OMC). However, high equipment costs and constrained recording areas generally prevent such systems from use in field-based occupational research (Cuesta-Vargas et al., 2010; Sabatini, 2006).

Dual-axis and tri-axial piezoresistive accelerometers are commonly used as inclinometers in field-based applications to estimate posture and movements of the trunk and upper arm with respect to the gravity vector (Amasay et al., 2009; Bernmark and Wiktorin, 2002; Douphrate et al., 2012; Fethke et al., 2016; Wahlström et al., 2010). Accelerometer-based inclinometers, however, are (i) less accurate as motion speeds increase and (ii) cannot accurately capture rotation about the gravity vector (Amasay et al., 2009; Bernmark and Wiktorin, 2002; Korshøj et al., 2014). In theory, inertial measurement units (IMUs) overcome the limitations inherent to accelerometer-based measurement through the addition of gyroscopes, magnetometers, and sensor fusion algorithms (e.g., Kalman filter, complementary filter, or particle filter) to estimate body segment orientation in three-dimensional space (Madgwick et al., 2011; Roetenberg et al., 2005; Sun et al., 2013; Valenti et al., 2015; Yadav and Bleakley, 2014; Yun et al., 2008).

Previous research suggests that IMU-based motion capture can be highly accurate in controlled, laboratory settings (Bergamini et al., 2014; Faber et al., 2013; Kim and Nussbaum, 2013; Plamondon et al., 2007; Robert-Lachaine et al., 2016). However, local magnetic field disturbances can lead to joint angular displacement measurement errors of 180° (Bachmann et al., 2004). Strategies such as magnetic field rejection (Ligorio and Sabatini, 2016; Sabatini, 2006; Sun et al., 2013), zero velocity updating (Schiefer et al., 2014), and kinematic modeling (El-Gohary and McNames, 2012, 2015; Miezal et al., 2016) have been implemented with sensor fusion algorithms to improve IMU-based motion capture accuracy. Such approaches, however, can only compensate for magnetic field disturbances over short measurement durations (i.e., minutes) (El-Gohary and McNames, 2015; Ligorio and Sabatini, 2016). Consequently, and despite considerable research concerning IMU-based motion capture and continued improvements to IMU hardware, systems capable of recording full three-dimensional motion for longer time periods (i.e., hours) in unconstrained environments have been largely elusive. Given the current limitations of IMU-based motion capture systems, sensor fusion algorithms that focus on inclination estimates (i.e., IMU-based inclinometers) rather than spatial orientation have instead been used to improve the accuracy of trunk inclination and upper arm elevation measurements with promising results (Lee et al., 2012; Ligorio and Sabatini, 2015; Schall et al., 2015, 2016).

Few studies that have evaluated IMU-based inclinometers, however, have also reported the accuracy of (i) accelerometer-derived angular displacement measurements, (ii) angular velocity measurements, or (iii) posture and movement summary measures used for health-based decision making in the context of occupational ergonomics. Thus, the ability of IMU-based inclinometers to improve measurement accuracy relative to established accelerometer-based approaches remains unclear. Previous work compared accelerometer and IMU-based inclinometers to an electrogoniometer used to measure trunk motion (Schall et al., 2015) and to a biomechanical-based optical motion capture system (Schall et al., 2016). The results indicated (i) errors in the IMU measurements relative to the reference devices on the order of 5–9° depending on motion plane and body segment and (ii) marginal differences between accelerometer-based and IMU-based inclination measurements. However, error sources not reflective of sensor accuracy, such as measurement system misalignment (Mecheri et al., 2016) were not fully managed. Furthermore, the similarities in measurement accuracy between accelerometer and IMU-based inclinometers due to motion speed were not evaluated.

Acknowledging that field-based IMU measurement of full three-dimensional motion may not be achievable in many industrial environments due to magnetic field disturbances, we explored the potential benefits of intermediary solutions (IMU-based inclinometers) that forgo the use of magnetometer data and instead rely on accelerometer and gyroscope data. The specific objective of this laboratory study was to evaluate the effects of motion speed and upper arm elevation calculation method (i.e., no sensor fusion and a variety of sensor fusion approaches) on the error in measures of upper arm posture and movement. In particular, we aimed to isolate the error associated with the sensor (i.e., technological error) (Robert-Lachaine et al., 2016). To mimic methods commonly reported in field studies, a single IMU secured to the upper arm was used and upper arm elevation was calculated with respect to the gravity vector. We hypothesized that sensor fusion would improve measurement accuracy, particularly as motion speed increased.

2. Methods

2.1. Participants

Thirteen participants (11 male, mean age 27.2 ± 6.6 years, right-hand dominant) were recruited from the University of Iowa community. All participants were screened for any self-reported cases of: (i) physician-diagnosed musculoskeletal disorder in the past six months, (ii) pain during the previous two weeks prior to enrollment, and (iii) medical history of orthopedic surgery in the upper extremity (shoulder, elbow, wrist, hand). Each participant provided written informed consent. The University of Iowa Institutional Review Board approved all study procedures.

2.2. Task

Each participant completed six trials of a simulated work task that involved transferring wooden dowels (2 cm diameter x 8 cm length) from a waist-high container in front of the participant to a shoulder-height container located 45° diagonally from the participant (Fig. 1). Each transfer required the participant to (i) grasp the dowel, (ii) transfer the dowel to the unloading container, and (iii) return their hand to the material feed container. Each participant completed two trials at the given material transfer rate: slow (15 cycles/min), medium (30 cycles/min), and fast (45 cycles/min). The transfer rate was controlled using a metronome and experimental conditions were randomized to control for potential order effects. Each participant was given time to acclimate to the assigned motion speed before each trial was captured. In preliminary tests, it was difficult for the participants to maintain the fastest transfer rate (45 cycles/min) for longer than 1 min due to fatigue. Consequently, each trial was 1 min in duration and was followed by a rest period of 5 min.

Fig. 1.

Placement of the waist-height container holding the wooden dowels and the shoulder-height container.

2.3. Instrumentation

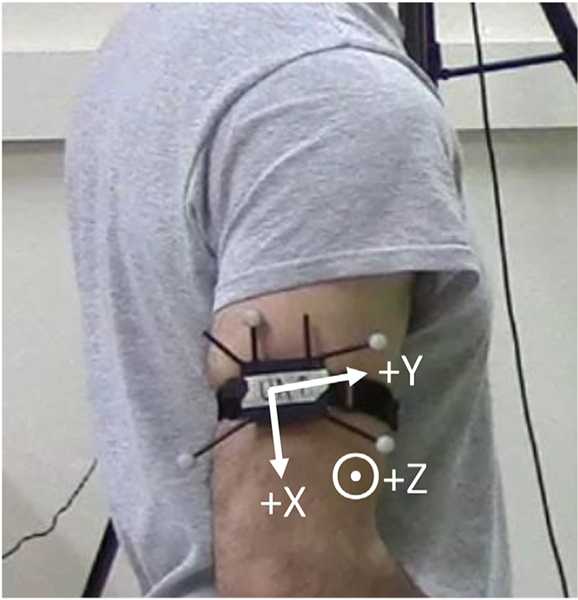
An IMU (series SXT, Nexgen Ergonomics, Inc., Pointe Claire, Quebec, CA) was secured to the lateral aspect of the dominant upper arm midway between the acromion and the lateral epicondyle (Fig. 2). The IMU was mounted to the upper arm with the x-axis oriented along the longitudinal axis (with positive x directed distally), the y-axis oriented along the anterior-posterior axis (with positive y directed anteriorly), and the z-axis oriented along the mediolateral axis (with positive z directed laterally). Raw accelerometer, gyroscope, and spatial orientation measurements (quaternions from an embedded Kalman filter) were captured from the IMU at 128 Hz.

Fig. 2.

IMU and its associated marker cluster attached to the upper arm of a participant.

Spatial orientation was also simultaneously recorded using a six-camera OMC system (Optitrack Flex 13, NaturalPoint, Inc., Corvallis, OR, USA) that tracked a cluster of four reflective markers mounted to the surface of the IMU with double-sided tape (Fig. 2). This was used in contrast to a biomechanical-based marker set to control for soft-tissue artifacts in order to isolate sensor error. The OMC measurements were recorded at 120 Hz. Initialization and calibration of the IMU and OMC instrumentation systems was performed using manufacturer-specified procedures. No additional (biomechanical) calibration procedures were performed as our goal was to compare the orientation of the IMU to the orientation of the marker cluster affixed to the IMU (i.e., sensor error was isolated).

2.4. Data processing

The spatial orientation derived from the OMC marker cluster was calculated using the quaternion output of the OMC system software. All post-processing was accomplished using MATLAB (2016a, Mathworks, Natick, MA). Data from both the IMU and OMC systems were recorded using the maximum available sampling rates. Therefore, the raw IMU data (128 Hz sampling rate) were down-sampled to 120 Hz (the OMC sampling rate) to maintain sample-to-sample temporal synchronization.

IMU inclination angles in the pitch (θ) and roll (ø) axes were calculated using five different approaches: (i) using accelerometer measurements without sensor fusion, (ii) using a first-order complementary filter, (iii) using a widely implemented second-order complementary filter, (iv) using modifications of a published, non-proprietary Kalman filter, and (v) using the quaternion output from the IMU’s embedded and proprietary Kalman filter.

The upper arm elevation displacement (α) was calculated by adding an offset of 90° to θ to orientate the local sensor coordinate frame. Upper arm angular velocity $\left(\dot{\alpha }\right)$ was calculated using the derivative of the upper arm elevation displacements with respect to time. IMU roll angles, which corresponded to upper arm internal/external rotation in this application, were not included in the final analysis due to issues associated with both soft tissue artifact (Cutti et al., 2006) and numerical instability when the roll axis approaches the gravity vector (i.e., when participants assume a neutral posture) (Pedley, 2013). However, we describe the intermediary calculations for the roll axis to provide a comprehensive description of the applied sensor fusion algorithms.

$$\alpha =\theta +{90}^{\circ }$$ (1)

$$\dot{\alpha }=\left({\alpha }_i-{\alpha }_{i-1}\right)/\text{Δ}t$$ (2)

2.4.1. Accelerometer-derived displacements

Pitch $\left({\theta }_{accel}\right)$ and roll $({\varphi }_{accel})$ angles were calculated from the accelerometer output $\left(a_x,a_y,a_z\right)$ as follows:

$${\theta }_{accel}={\tan }^{-1}\left(-a_x/\sqrt{a_y^2+a_z^2}\right)$$ (3)

$${\varphi }_{accel}={\tan }^{-1}\left(a_y/a_z\right)$$ (4)

The raw accelerometer data stream was low-pass filtered (2nd order Butterworth, 3 Hz corner frequency) prior to the angle calculations. Pitch and roll angles calculated without sensor fusion are described using the designation “Accel”.

2.4.2. First-order complementary filter

IMU pitch $\left({\theta }_{c,i}\right)$ and roll $\left({\varphi }_{c,i}\right)$ angles at sample i were calculated recursively using a first-order complementary filter that combines gyroscope measurements $\left({\omega }_{x,i},{\omega }_{y,i},{\omega }_{z,i}\right)$ with accelerometer measurements $\left(a_{x,i},a_{y,i},a_{z,i}\right)$ as follows:

$$\left[\begin{array}{c}{\theta }_{c,i}\\ {\varphi }_{c,i}\end{array}\right]=\left[\begin{array}{c}\left(1-{\beta }_{\theta }\right)\left({\theta }_{c,i-1}+\left({\omega }_{y,i}\cos {\varphi }_{c,i-1}-{\omega }_{z,i}\sin {\varphi }_{c,i-1}\right)\text{Δ}t\right)+{\beta }_{\theta }{\tan }^{-1}\left(-a_{x,i}/\sqrt{a_{y,i}^2+a_{z,i}^2}\right)\\ \left(1-{\beta }_{\varphi }\right)\left({\varphi }_{c,i-1}+\left({\omega }_{x,i}+{\omega }_{y,i}\sin {\varphi }_{c,i-1}\tan {\theta }_{c,i-1}+{\omega }_{z,i}\cos {\varphi }_{c,i-1}\tan {\theta }_{i-1}\right)\text{Δ}t\right)+{\beta }_{\varphi }{\tan }^{-1}\left(a_{y,i}/a_{z,i}\right)\end{array}\right]$$ (5)

where Δt is the sensor sampling period and β is the filter tuning parameter. β is assigned a value between 0 and 1 (0 would rely solely on gyroscope-derived inclination measurements, and 1 would rely solely on accelerometer-derived inclination measurements). For this study, both ${\beta }_{\theta }$ and ${\beta }_{\varphi }$ were assigned a value of 0.01, based on visual inspection of the complementary filter results and the OMC data. This value was chosen to sufficiently reduce motion-related artifacts without causing time-dependent errors. Pitch and roll angles calculated using the first-order complementary filter are described using the designation “Comp-1”. The derivation of (5) is provided in Appendix A. The MATLAB code is provided in Appendix C.

2.4.3. Second-order complementary filter

The design of the second-order complementary filter was a direct implementation of the filter developed by Madgwick et al. (2011). A detailed explanation can be found elsewhere (Madgwick et al., 2011; Mourcou et al., 2015). Equation (6) was used to convert the quaternion rotation vector output from the second-order complementary filter into heading, pitch, and roll angles. For this study, the filter parameter β was assigned a value of 0.13. The angles calculated in this manner are described with the designation “Comp-2.”

$$\left[\begin{array}{c}\psi \\ \theta \\ \varphi \end{array}\right]=\left[\begin{array}{c}{\tan }^{-1}(2\left(q_0{q}_3+q_1{q}_2\right)/\left(q_0^2+q_1^2-q_2^2-q_3^2\right)\\ {\sin }^{-1}\left(2\left(q_0{q}_2-q_1{q}_3\right)\right)\\ {\tan }^{-1}(2\left(q_0{q}_1+q_2{q}_3\right)/\left(q_0^2-q_1^2-q_2^2+q_3^2\right)\end{array}\right]$$ (6)

2.4.4. Kalman filter: non-proprietary

The Extended Kalman filter used in this study was designed to discriminate the direction of gravity (g^b) from the linear acceleration (a^b) in the local coordinate frame when gyroscope measurements ${\overrightarrow{\omega }}^b=\left({\omega }_x,{\omega }_y,{\omega }_z\right)$ and accelerometer measurements $\left(a_x,a_y,a_z\right)$ are provided. The process (7) and measurement (8) models are as follows:

$$\left[\begin{array}{c}{g}_i^b\\ a_i^b\\ b_{\omega ,i}\end{array}\right]=\left[\begin{array}{ccc}{I}_{3\times 3}-\left[\left({\omega }_{i-1}^b-b_{\omega ,i-1}\right)\times \right]\text{Δ}t& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& c_a{I}_{3\times 3}{a}_{i-1}^b& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& I_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_{i-1}^b\\ a_{i-1}^b\\ b_{\omega ,i-1}\end{array}\right]+\left[\begin{array}{ccc}\left[g_{i-1}^b\times \right]\text{Δ}t& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& c_b{I}_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& \text{Δ}t{I}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{w}_{i-1}^{\omega }\\ w_{i-1}^{gm}\\ {\dot{b}}_{\omega }\end{array}\right]$$ (7)

$$\left[\begin{array}{l}{a}_{x,k}\hfill \\ a_{y,k}\hfill \\ a_{z,k}\hfill \end{array}\right]=\left[\begin{array}{c}{I}_{3\times 3}{I}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_k^b\\ a_k^b\end{array}\right]+\left[\begin{array}{c}{I}_{3\times 3}{I}_{3\times 3}{0}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_k^b\\ a_k^b\\ b_{\omega ,k}\end{array}\right]v_k^a$$ (8)

Here, 0_3×3 is a 3 × 3 matrix with zeros, I_3×3 is a 3 × 3 identity matrix, $[\stackrel{\rightharpoonup }{u}\times ]$ is the skew symmetric matrix associated for a given vector $\left(\stackrel{\rightharpoonup }{u}\right)$, and c_a, c_b are the parameters of the first-order Gauss-Markov process used to account for external acceleration. The gyroscope white noise, w^ω, gyroscope bias, ${\dot{b}}_{\omega }$, and accelerometer noise, v^a, are each assumed to follow a normal distribution of $N\left(0,{\sigma }_{\omega }^2\right),N\left(0,{\sigma }_{{\omega }_b}^2\right)$, and $N\left(0,{\sigma }_a^2\right)$, respectively. The white Gaussian noise, w^gm, is assumed to be zero mean with an identity covariance matrix. The assigned filter parameters are shown in Table 1. The angles calculated in this manner are described with the designation “Accel-KF”. Pitch and roll measurements from this Kalman filter are calculated from g^b using (3) and (4), respectively.

Table 1.

Kalman filter parameters.

	Gyro White Noise	Gyro Bias	Accel White Noise	ca	cb
Accel-KF	0.005 rad/s	0.0005 (rad/s2)	0.005 m/s2	0.001	0.1

The derivation and implementation of (7) and (8) are provided in Appendix B. The MATLAB code is provided in Appendix C.

2.4.5. Kalman filter: embedded (proprietary)

Equation (6) was used to convert the quaternion rotation vector output from the IMU’s embedded Kalman filter to heading, pitch, and roll angles. The angles calculated in this manner are described with the designation “Em-KF.” The quaternion rotation vector output from the OMC system software was also converted to heading, pitch, and roll angles using (6).

2.4.6. Inclinometer accuracy

The offset between the local coordinate frames of the OMC and the IMU was calculated using angular rate measurements according to de Vries et al. (2010). After applying the local offset, the offset between the global coordinate frames of the OMC and the IMU was determined under static conditions using Accel-derived inclination measurements. OMC-derived upper arm elevation displacements and velocities were calculated after the offsets were added to OMC-derived orientation measurements.

Root-mean-square error (RMS) was calculated using (9) to quantify the average error of inclinometer measurements $\left({\alpha }_{INC}\right)$ relative to the OMC $\left({\alpha }_{OMC}\right)$. Peak error was calculated using the 99th percentile measurement of the rectified (absolute value) sample-to-sample difference between the OMC and inclinometer-derived measurements.

$$RMS=\sqrt{\frac{1}{n}\sum _n{\left({\alpha }_{OMC}-{\alpha }_{INC}\right)}^2}$$ (9)

2.4.7. Statistical analysis

A two-factor repeated measures analysis of variance (ANOVA) was used test the main and interactive effects of material transfer rate and upper arm elevation calculation method (i.e., Accel, Comp-1, Comp-2, Accel-KF, and Em-KF) on (i) RMS displacement error, (ii) peak displacement error, (iii) RMS velocity error, and (iv) peak velocity error. Pre-planned pairwise comparisons using Bonferroni corrections were used to test, at each level of motion speed, differences between RMS and peak errors (both for displacements and velocities) between (i) Accel and Comp-1, (ii) Accel and Comp-2, (iii) Accel and Accel-KF, and (iv) Accel and Em-KF. All statistical analyses were performed using SPSS (version 24, IBM Corporation, Armonk, NY).

3. Results

3.1. Angular displacements

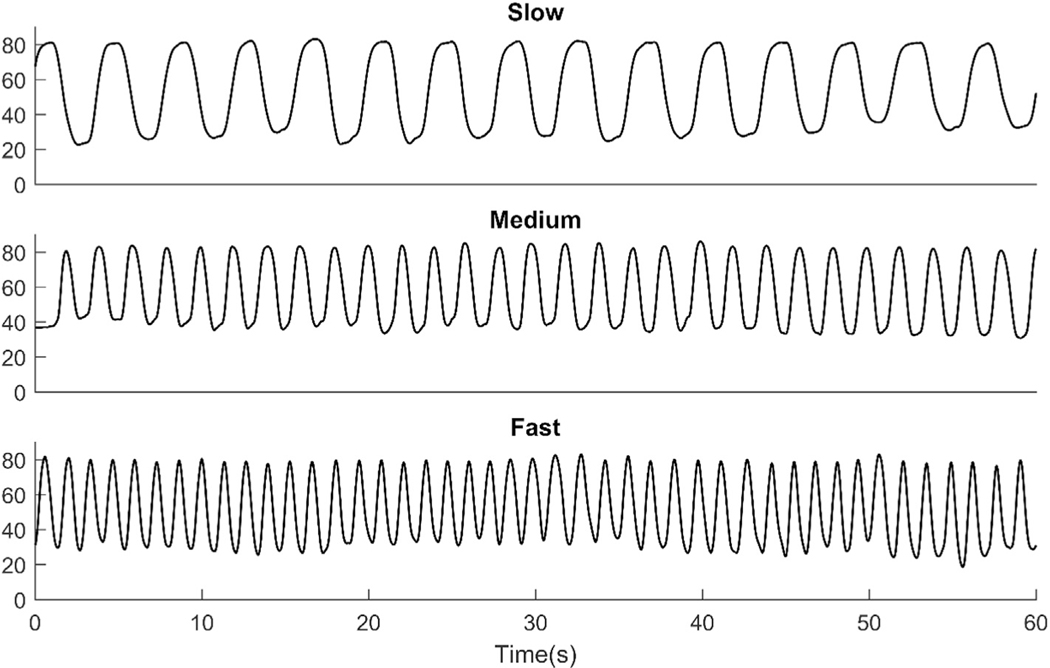
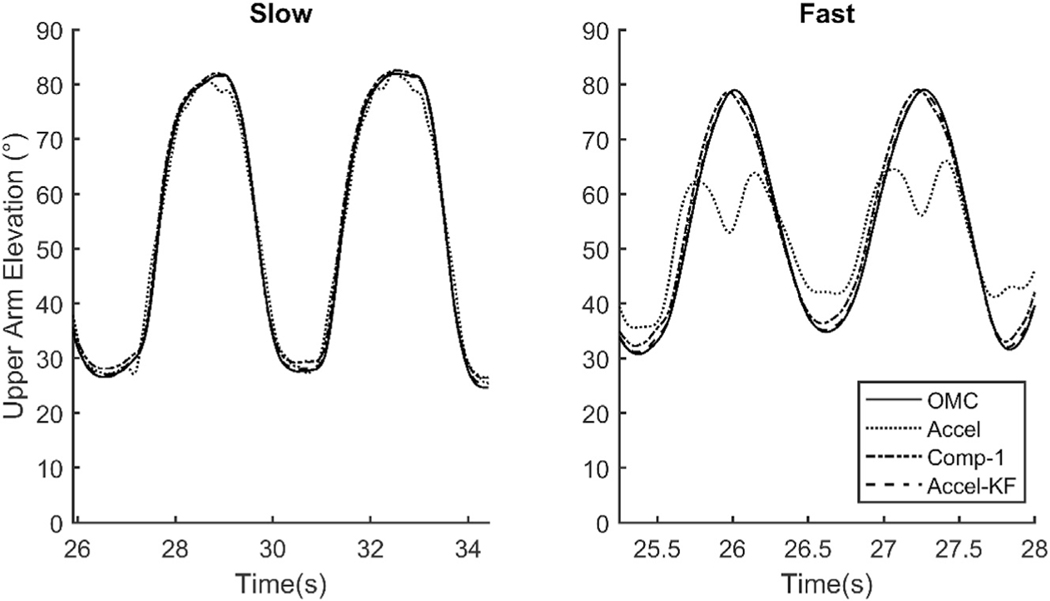
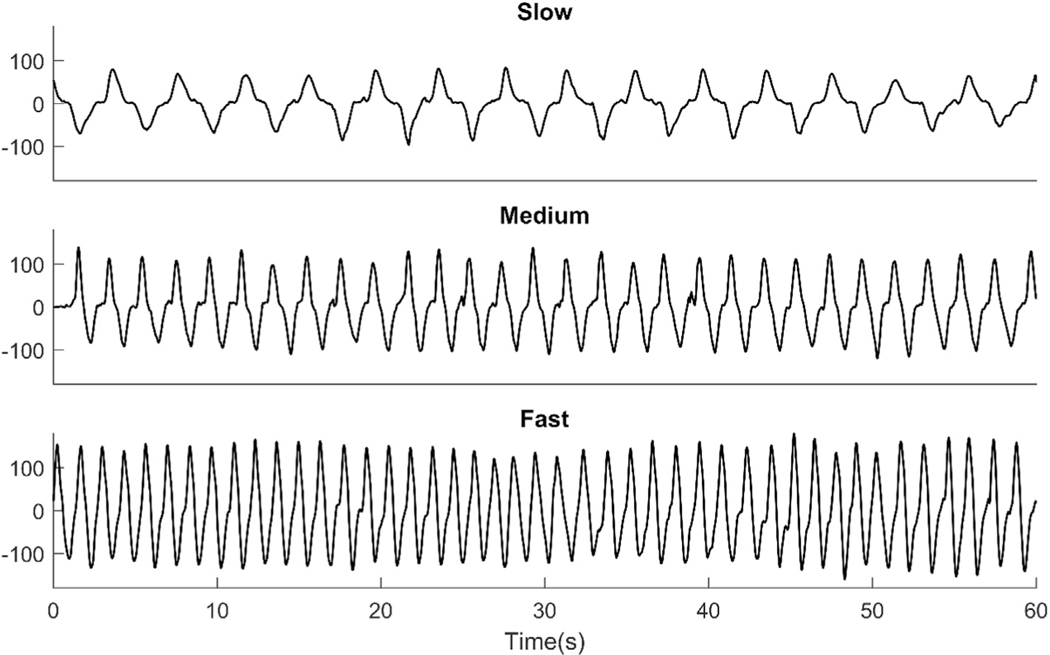
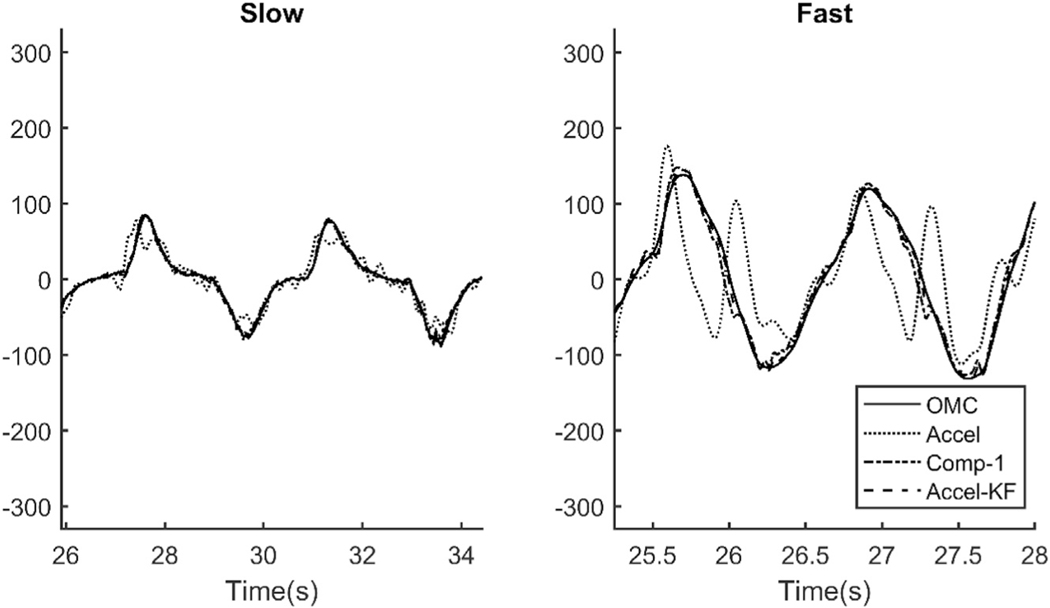
The cyclic motion pattern and the changes to movement frequency associated with increased transfer rates (15, 30, 45 cycles/min) can be observed through the OMC-derived angular displacement measurements (Fig. 3). The within-trial acceleration measurements (average and variation) across all testing conditions are shown in Table 2. Statistically significant (p < 0.01) main effects of material transfer rate, calculation method, and their interaction were observed for both RMS and peak displacement error. Regarding the interaction, both RMS and peak error magnitudes generally increased with increasing motion speed for all upper arm elevation calculation methods. However, the increases were substantially greater for the Accel approach compared to the Comp-1, Comp-2, Accel-KF, and Em-KF approaches (Table 3). All pre-planned pairwise comparisons within each transfer rate were statistically significant for RMS displacement error (p < 0.05) and peak displacement error (p < 0.01). As expected, the accelerometer-derived displacements were similar to the OMC-derived displacements for the slowest transfer rate, but deviated substantially for the fastest transfer rate (Fig. 4).

Fig. 3.

OMC-derived upper arm elevation displacements (°) for one participant across three different material transfer rates: slow (15 cycles/min), medium (30 cycles/min), and fast (45 cycles/min).

Table 2.

Mean(SD) within-trial acceleration measurements across all 13 participants and material transfer rates.

	Slow (15 cycles/min)	Medium (30 cycles/min)	Fast (45 cycles/min)
Average (m/s2)	9.9(0.3)	10.1(0.3)	10.4(0.2)
Standard Deviation (m/s2)	0.4(0.1)	1.0(0.2)	1.5(0.2)

Table 3.

Mean (SD) upper arm elevation displacement across 13 participants and three material transfer rates: slow (15 cycles/min), medium (30 cycles/min), and fast (45 cycles/min) that was maintained for a period of 1 min. Displacements were measured by the optical motion capture system (OMC) and calculated using an accelerometer (Accel), first-order complementary filter (Comp-1), a second-order complementary filter (Comp-2), a modified linear Kalman filter (Accel-KF), and an embedded Kalman filter (Em-KF).

Upper Arm Elevation Displacement	OMC	Accel	Comp-1	Comp-2	Accel-KF	Em-KF
‘Slow’ Transfer Rate
RMS error (°)	-REF-	2.3(0.4)	1.6(0.9)*	1.8(0.5)**	1.1(0.6)**	1.2(0.9)**
Peak error (°)	-REF-	6.8(1.7)	3.3(1.4)**	4.1(1.0)**	2.2(1.0)**	2.4(1.6)**
Mean (°)	47.4(7.7)	46.5(7.8)	46.9(8.2)	46.6(7.9)	46.7(7.8)	46.8(7.4)
10th Percentile (°)	20.5(6.4)	20.4(6.4)	21.0(6.9)	20.5(6.5)	20.4(6.6)	20.4(6.3)
50th Percentile (°)	46.1(8.9)	46.2(8.7)	45.5(9.2)	45.9(8.8)	45.4(8.8)	45.5(8.5)
90th Percentile (°)	75.4(8.7)	72.5(9.1)	74.2(9.2)	73.4(9.1)	74.2(8.8)	74.3(8.4)
Percentile Range (90th – 10th)(°)	54.9(4.4)	52.1(4.5)	53.2(4.1)	52.9(4.3)	53.7(4.0)	53.9(4.0)
Time in neutral posture (<20°) (%)	12.3(13.7)	12.0(12.9)	11.6(13.9)	12.2(13.4)	12.3(13.7)	12.1(13.2)
Time in extreme posture (≥45°)(%)	50.4(7.5)	50.6(8.3)	49.8(8.2)	50.2(8.1)	49.7(7.7)	49.9(7.2)
Time in extreme posture (≥60°)(%)	35.4(12.4)	33.4(13.7)	34.0(13.4)	33.8(13.4)	34.0(13.2)	34.7(11.8)
‘Medium’ Transfer Rate
RMS error (°)	-REF-	6.3(1.5)	2.4(1.0)**	2.4(0.6)**	1.3(0.6)**	1.4(1.0)**
Peak error (°)	-REF-	17.5(4.6)	5.7(4.4)**	5.3(1.2)**	2.7(1.1)**	2.5(1.5)**
Mean (°)	44.4(7.3)	42.9(7.4)	43.8(7.6)	44.2(7.8)	43.7(7.4)	43.5(7.5)
10th Percentile (°)	19.0(6.8)	20.8(6.9)	19.8(7.0)	20.1(7.3)	19.1(6.9)	18.9(6.8)
50th Percentile (°)	41.8(8.1)	43.9(7.6)	41.1(8.1)	41.5(8.2)	41.1(8.0)	40.9(8.2)
90th Percentile (°)	73.1(9.1)	63.3(8.6)	71.4(9.1)	71.8(9.4)	71.7(9.0)	71.5(9.2)
Percentile Range (90th – 10th)(°)	54.1(5.4)	42.5(4.7)	51.6(5.2)	51.7(5.0)	52.7(5.3)	52.7(5.2)
Time in neutral posture (<20) (%)	15.4(13.4)	11.7(11.9)	13.9(13.6)	13.6(13.9)	15.2(13.6)	15.5(13.7)
Time in extreme posture (≥45°)(%)	46.3(8.5)	46.9(12.3)	45.4(9.0)	45.8(9.1)	45.5(8.7)	45.2(8.8)
Time in extreme posture (≥60°)(%)	29.8(12.0)	21.0(15.8)	27.7(12.9)	28.0(13.0)	28.0(12.9)	27.6(13.2)
‘Fast’ Transfer Rate
RMS error (°)	-REF-	11.3(1.9)	3.2(0.8)**	2.9(1.1)**	1.5(0.5)**	1.2(0.8)**
Peak error (°)	-REF-	28.9(5.2)	6.5(1.8)**	5.7(1.6)**	3.2(1.0)**	2.4(1.2)**
Mean (°)	43.6(7.2)	40.7(6.9)	43.3(7.4)	44.1(8.4)	42.9(7.3)	43.3(7.4)
10th Percentile (°)	18.1(5.8)	23.0(6.4)	19.5(6.3)	19.4(6.9)	18.2(6.0)	18.5(5.9)
50th Percentile (°)	42.3(7.9)	43.7(7.2)	42.0(7.9)	42.4(8.9)	41.6(7.9)	42.0(8.2)
90th Percentile (°)	71.1(9.1)	54.8(7.8)	69.2(9.2)	71.3(10.2)	69.8(9.2)	70.2(9.1)
Percentile Range (90th – 10th)(°)	53.0(6.2)	31.8(4.3)	49.7(6.1)	51.9(6.2)	51.6(6.1)	51.7(5.9)
Time in neutral posture (<20) (%)	16.1(11.4)	8.0(9.6)	12.9(12.2)	14.2(13.3)	15.9(11.8)	15.5(12)
Time in extreme posture (≥45°)(%)	46.3(9.1)	41.1(20.9)	45.7(9.7)	46.5(10.3)	45.4(9.3)	45.9(9.5)
Time in extreme posture (≥60°)(%)	28.1(12.8)	8.3(10.2)	25.5(14.3)	27.7(14.6)	25.9(13.9)	26.7(13.9)

^*Statistically-significant (p < 0.05) pair-wise tests between the Accel and the sensor fusion method.

^**Statistically-significant (p < 0.01) pair-wise tests between the Accel and the sensor fusion method.

Fig. 4.

Upper arm elevation displacements across two cycles at two material transfer rates: slow (15 cycles/min), and fast (45 cycles/min). Displacements were measured by the optical motion capture system (OMC) and calculated using an accelerometer (Accel), first-order complementary filter (Comp-1), and a modified linear Kalman filter (Accel-KF).

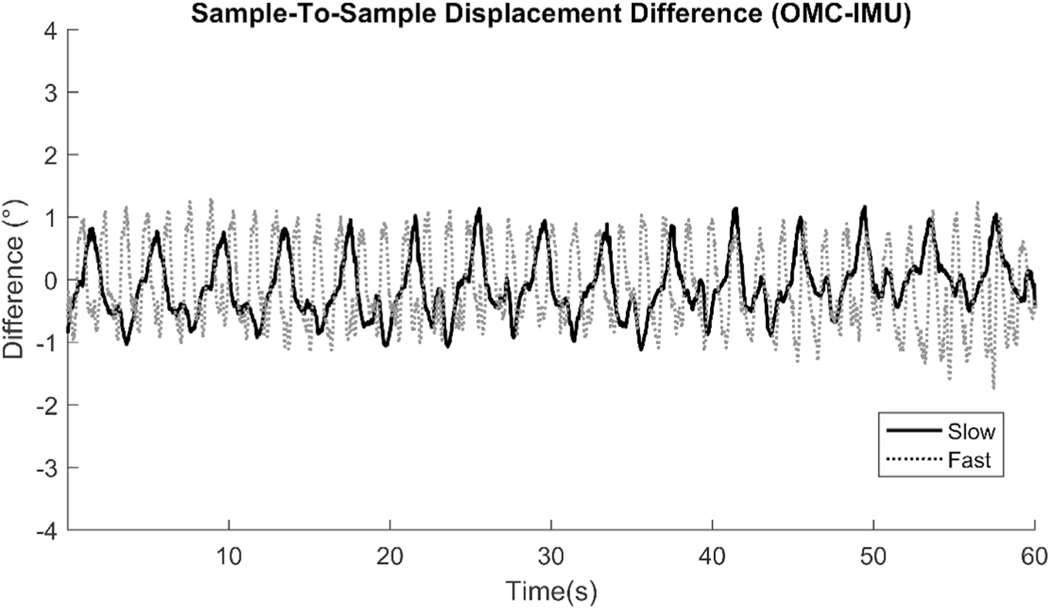
Although statistically significant pairwise comparisons were observed for the RMS and peak error measurements associated with the slowest transfer rate, the measurement errors were small (2.3° RMS, 6.8° peak for all calculation methods). Under the fastest transfer rate (maximum expected error), the errors associated with accelerometer-derived displacements were more apparent (11.3° RMS, 28.9° peak). The simple first-order complementary filter (Comp-1) reduced RMS error to 3.2°, while the Kalman filters reduced the RMS error to <1.5°. Similarly, a first-order complementary filter reduced peak error to 6.5°, while the Kalman filters reduced peak error to <3.2°. In general, the accelerometer-derived displacements underestimated upper arm elevation as transfer rates increased, as evidenced by the 90^th percentile measurements. This was mitigated by implementing a sensor fusion algorithm. Time-dependent errors were not observed for displacements calculated using sensor fusion algorithms (Fig. 5).

Fig. 5.

Sample-to-sample displacement difference between OMC and IMU using a modified linear Kalman filter across two material transfer rates: slow (15 cycles/min) and fast (45 cycles/min).

3.2. Angular velocities

The increase in amplitude and frequency of OMC-derived angular velocities associated with increased material transfer rates can be observed in Fig. 6. Statistically-significant (p < 0.01) main effects of material transfer rate, calculation method, and their interaction were observed for both RMS and peak velocity error. The nature of the interaction was identical to that observed for displacement error (i.e., while error magnitudes increased with increasing motion speed for all calculation methods, substantially greater increases were observed for the Accel approach compared to the sensor fusion approaches). All preplanned pairwise comparisons within each transfer rate were statistically significant for RMS velocity error (p < 0.01) and peak velocity error (p < 0.01). As expected, the accelerometer-derived velocities were similar to the OMC-derived velocities for the slow transfer rate, but deviated substantially for the fast transfer rate (Fig. 7).

Fig. 6.

OMC-derived upper arm elevation velocities (one participant) across three material transfer rates: slow (15 cycles/min), medium (30 cycles/min), and fast (45 cycles/min).

Fig. 7.

Upper arm elevation velocities (°/s) for one participant across two material transfer rates: slow (15 cycles/min), and fast (45 cycles/min). Angular velocities were derived using displacements measured from the optical motion capture (OMC) calculated using an accelerometer (Accel), first-order complementary filter (Comp-1), and a modified linear Kalman filter (Accel-KF).

Unlike the accelerometer-derived displacements, the RMS and peak angular velocity error associated with accelerometer-derived angular velocities were more noticeable (13.0°/s RMS and 42.7°/s peak). RMS and peak velocity error for accelerometer-derived measurements increased to 81.7°/s and 221.3°/s for the fastest motion condition. The first-order complementary filter reduced RMS error to 17°/s, while the Kalman filters decreased RMS error to ≤9.3°/s. Similarly, the first-order complementary filter reduced peak error to 46.2°/s, while the Kalman filters reduced peak error to ≤25.2°/s (Table 4).

Table 4.

Angular velocities of upper arm elevation across 13 participants and three material transfer rates: slow (15 cycles/min), medium (30 cycles/min), and fast (30 cycles/min) that was maintained for a period of 1 min. Angular velocities were calculated using displacement measurements obtained from an optical motion capture system (OMC) an accelerometer (Accel), first-order complementary filter (Comp-1), a modified linear Kalman filter (Accel-KF), and an embedded Kalman filter (Em-KF).

Velocity	OMC	Accel	Comp-1	Comp-2	Accel-KF	Em-KF
‘Slow’ Transfer Rate
RMS error (°/s)	-REF-	13.0(3.0)	4.4(1.1)**	9.9(0.8)**	3.1(0.9)**	2.8(1.0)**
Peak error (°/s)	-REF-	42.7(11.4)	14.1(4.4)**	19.9(2.1)**	9.7(3.4)**	8.7(3.3)**
Mean (°/s)	28.2(2.1)	28.6(2.3)	27.5(2.1)	28.7(2.4)	27.6(2.0)	27.7(2.0)
10th Percentile (°/s)	2.6(1.1)	4.0(1.3)	2.9(1.3)	4.4(0.7)	2.7(1.2)	2.6(1.2)
50th Percentile (°/s)	22.8(3.8)	25.9(2.7)	22.4(3.3)	23.8(2.0)	22.4(3.4)	22.5(3.5)
90th Percentile (°/s)	61.3(8.7)	56.6(7.0)	59.4(8.4)	59.6(7.7)	59.9(8.4)	60.1(8.5)
Percentile Range (90th – 10th)(°/s)	58.7(9.5)	52.6(7.7)	56.5(9.3)	55.2(7.8)	57.2(9.3)	57.4(9.4)
Time at low velocities (<5°/s)(%)	19.5(6.4)	13.2(3.7)	18.1(6.2)	11.5(1.9)	19.0(6.3)	19.6(6.3)
Time at high velocities (≥90°/s)(%)	1.0(1.5)	0.4(0.6)	0.8(1.3)	0.8(1.2)	0.9(1.4)	0.8(1.4)
‘Medium’ Transfer Rate
RMS error (°/s)	-REF-	39.8(10.9)	10.3(2.4)**	11.1(1.4)**	5.9(1.4)**	5.1(2.0)**
Peak error (°/s)	-REF-	112.5(29.1)	30.8(10.0)**	25.6(7.9)**	17.1(4.3)**	15.3(7.7)**
Mean (°/s)	56.0(5.3)	49.7(5.9)	54(5.4)	54.3(5.3)	54.8(5.3)	54.7(5.2)
10th Percentile (°/s)	7.5(2.8)	9.8(3.0)	7.8(2.9)	8.1(2.3)	7.8(2.8)	7.3(2.8)
50th Percentile (°/s)	52.6(6.1)	49.3(7.2)	50.0(5.5)	49.9(6.2)	51.3(5.8)	51.4(6.0)
90th Percentile (°/s)	109.7(17.3)	89.0(11.2)	106.4(16.4)	107.3(15.9)	107.4(16.8)	107.3(16.7)
Percentile Range (90th – 10th)(°/s)	102.2(19.0)	79.2(10.7)	98.6(17.7)	99.2(17.0)	99.6(18.4)	99.9(18.3)
Time at low velocities (<5°/s)(%)	7.9(3.8)	5.7(2.0)	7.5(3.6)	6.7(2.0)	7.6(3.7)	8.0(3.7)
Time at high velocities (≥90°/s)(%)	21.7(8.5)	9.8(6.0)	19(8.6)	19.5(8.1)	20.0(8.7)	20.2(8.7)
‘Fast’ Transfer Rate
RMS error (°/s)	-REF-	79.0(14.1)	17.0(2.7)**	13.8(3.7)**	9.3(1.7)**	7.3(3.9)**
Peak error (°/s)	-REF-	206.5(41.1)	46.2(8.4)**	36.2(18.6)**	25.2(5.8)**	21.4(13.8)**
Mean (°/s)	83.3(9.8)	62.5(7.2)	78.8(9.9)	81.9(10.2)	81.4(9.8)	81.6(9.4)
10th Percentile (°/s)	14.5(3.1)	11.4(2.5)	15.2(4.6)	13.5(4.0)	15.1(4.0)	15.0(3.6)
50th Percentile (°/s)	86.0(10.6)	57.6(7.6)	78.5(9.9)	82.6(10.8)	82.7(10.4)	83.5(9.9)
90th Percentile (°/s)	146.5(20.1)	118.5(16.6)	141.9(20.6)	148.5(19.7)	144.4(20.2)	144.0(19.7)
Percentile Range (90th – 10th)(°/s)	131.9(20.2)	107.1(16.2)	126.7(19.7)	135(18.9)	129.3(19.9)	128.9(19.8)
Time at low velocities (<5°/s)(%)	3.6(0.9)	4.6(1.3)	3.5(1.0)	4.0(1.3)	3.6(1.0)	3.5(1.0)
Time at high velocities (≥90/s)(%)	46.7(6.1)	24.1(6.9)	41.3(7.6)	44.9(6.1)	44.6(6.5)	45.3(6.1)

^*Statistically-significant (p < 0.05) pair-wise tests between the Accel and the sensor fusion method.

^**Statistically-significant (p < 0.01) pair-wise tests between the Accel and the sensor fusion method.

4. Discussion

The accelerometer-derived displacements were accurate (<2.5° RMS error, <7° peak error) for the slowest material transfer rates (15 cycles/min). This test condition corresponded to an acceleration average and standard deviation of 9.9 m/s² and 0.4 m/s² within each trial, respectively. The accelerometer-derived displacements were negatively affected by increased motion speeds. Under the fast motion condition, the RMS and peak displacement error increased to 11.3° and 28.9°, respectively. This observation was consistent with the expected increase in tangential and centripetal acceleration, which are both affected by increased angular velocities (Bernmark and Wiktorin, 2002). The results of this study indicate a range of displacement errors (RMS <2.5° to >11°) comparable to previous work that assessed (i) accelerometer-based inclinometers under a variety of tasks and arm swing frequencies (RMS 2.0° to >13°) (Korshøj et al., 2014) and (ii) accelerometer-derived displacements in static conditions (<2°) (Amasay et al., 2009). The accelerometer-based displacement RMS error for the medium material transfer rate (6.3°) was also consistent with previous work that reported an RMS error of 7.2° for upper arm elevation displacements during simulated dairy parlor work (Schall et al., 2016).

As expected, the sensor fusion algorithms improved measurement accuracy for upper arm elevation displacement. For every transfer rate tested, a statistically significant pairwise difference was observed between the accuracy of accelerometer-derived displacements and each of the sensor fusion algorithms. However, the improvements in measurement accuracy were more apparent with increased motion speeds. For the fast motion condition, a simple first-order complementary filter reduced the RMS displacement error from 11.3° to 3.2°. However, this filter design did not account for variability in gyroscope bias or non-gravitational acceleration. The Comp-2 filter, which reduced the RMS displacement error to <2.8°, accounted for gyroscope bias variability in the filter design. The modified linear Kalman filter accounted for both non-gravitational acceleration as well as gyroscope bias variability, which further reduced the error to <1.5°. In general, our errors were consistent with other studies (<4° RMS error) that provided inclination estimates using an identical comp-2 filter (Bergamini et al., 2014; Mourcou et al., 2015), an identical embedded Kalman filter (Lebel et al., 2013, 2015), and a similar linear Kalman filter (Bergamini et al., 2014; Ligorio and Sabatini, 2015, 2016).

Similar error trends appeared in velocity measurements since velocity was calculated by taking the derivative of the angular displacements with respect to time. As expected, accelerometer-derived angular velocities were unusable for the fast motion conditions (81.7°/s RMS error). This was mitigated considerably using a sensor fusion algorithm, which resulted in RMS errors between 7.3°/s and 17.0°/s for the fastest transfer rate, depending on the sensor fusion algorithm. Few studies have published accuracy of angular velocity measurements. In general, our results are consistent with previous studies. For the accelerometer-derived angular velocities, Schall et al. (2015) reported angular velocity errors <10°/s compared to measurements from a tri-axial lumbar spine electrogoniometer, which was consistent the current study (13°/s RMS) with regards to the slow transfer rate. For IMU-based angular velocity measurements, Kim and Nussbaum, 2013 reported errors <10°/s for the vast majority of joint angle velocities across all body segments through comparisons against an OMC (Kim and Nussbaum, 2013). Plamondon et al. (2007) reported angular velocity errors <13°/s (Plamondon et al., 2007) and Schall et al. (2015) reported RMS angular velocity errors <10.1°/s, which is consistent with our observations (<9.2°/s using a Kalman filter).

4.1. Study limitations

The relatively short sampling duration limits the extent to which the observed results can be applied to workplace exposure assessment practices. However, given the simplistic and cyclic motion (which was highly repeatable, as demonstrated in Figs. 3 and 6) and the absence of time-dependent error (which, if apparent, would be observed within a 1-min timeframe), it is unlikely that a longer sampling duration would influence the RMS and peak error magnitudes reported in the current study. Time-dependent errors were likely not observed due, in part, to the somewhat conservative tuning parameters that perhaps relied on accelerometer data to greater extent than necessary (and leading to increased error magnitudes at increased motion speeds). While several studies examining IMU accuracy have used similar sampling durations (Bergamini et al., 2014; Brodie et al., 2008; El-Gohary and McNames, 2012; Faber et al., 2013; Ligorio and Sabatini, 2016; Ricci et al., 2016), sampling durations for workplace exposure assessment are generally considerably longer (e.g., up to a full shift). While the influence of sampling duration on RMS and peak error, as calculated in this study, is difficult to predict, it is reasonable to expect larger error magnitudes in practice (particularly peak error as a consequence of transient, high-speed movements).

A cyclic task was chosen to provide the maximum influence of motion on error magnitudes. However, the nature of the cyclic task precludes rest/recovery metrics that are also used to quantify motion-related exposures (e.g., the percentage of time with neutral posture and low velocity [Kazmierczak et al., 2005]). Furthermore, this study focused on accuracy of inclinometers and disregarded the issue of magnetic disturbance. The use of relatively standard sensor fusion algorithms in this experiment facilitates comparisons across other studies. However, differences in sensor specifications and tuning parameters may provide different error magnitudes. Finally, this study considers strictly sensor error. A recent study, for example, demonstrated that accelerometer-based inclinometers may underestimate inclination measurements under static conditions, particularly at angles >60° (Jackson et al., 2015). Differences in error magnitudes due to measurement methodology, such as differences in the local coordinate frame defined using anatomical landmarks in comparison to the sensor local coordinate frame and errors due to soft tissue artifacts, were not considered.

4.2. Methodological considerations for future studies

In general, the findings of this study suggest that the dynamics associated with upper arm motion are more than capable of adversely affecting accelerometer-derived angular displacement and velocity measurements commonly reported in the occupational ergonomics literature. Importantly, we observed underestimation of the extreme upper arm postures and velocities (i.e., 90^th percentiles) at increased motion speeds. This result has meaningful implications for both researchers and practitioners when considering the use of accelerometers to identify and mitigate work activities that impose the greatest biomechanical loading. Moreover, in epidemiologic studies, underestimation of upper arm elevation during fast motion speeds may impact observed associations between summary measures of exposure to non-neutral posture and musculoskeletal health outcomes. If fast motion speeds are experienced randomly among those with and without outcomes, then any underestimation of upper arm elevation would lead to an attenuation of risk estimates. On the other hand, if those experiencing outcomes are more likely engaged in work with fast motion speeds in comparison to those not experiencing outcomes (or vice versa), then risk estimates become more difficult to interpret and operationalize.

5. Conclusion

The overall goal of this study was to evaluate the capability of IMU-based inclinometers to provide accurate measurements of upper arm elevation displacement and velocity. In general, the accelerometer-derived displacements were accurate (<2.5° RMS error, <7° peak error) for slow movement speeds. However, both accelerometer-derived displacements and velocities were negatively affected by increased motion speeds. Under the fast motion speeds, the RMS and peak displacement errors increased to 11.3° and 28.9°, respectively. More importantly, the RMS and peak errors associated with accelerometer-derived velocities were substantial (81.7°/s and 221.3°/s, respectively). A Kalman filter reduced peak displacement and velocity errors to <3.5° and <25.1°/s, respectively across all testing conditions. The results indicate that IMU-based inclinometers, in particular when implemented using a Kalman filter, can substantially improve inclinometer accuracy for the assessment of upper arm elevation during fast motion speeds.

APPENDIX

Appendix

Appendix A. First-order complementary filter design

The first-order complementary filter contains the following structure (Roan et al., 2012):

$${\vartheta }_{comp,i}=(1-\beta )\left({\vartheta }_{comp,i-1}+{\dot{\vartheta }}_i\text{Δt}\right)+\beta {\vartheta }_{accel,i}$$ (10)

where ${\vartheta }_{comp,i}$ is the angle derived from the complementary filter, ${\vartheta }_{accel,i}$ is the angle derived from the accelerometer measurements, ${\dot{\vartheta }}_i$ is the rotational velocity, Δt is the sensor sampling period, and α is the filter tuning parameter. The tuning parameter, α is assigned a value between 0 and 1 (0 would rely solely on gyroscope-derived inclination measurements, and 1 would rely solely on accelerometer-derived inclination measurements). Equation (10) is written in terms of pitch and roll measurements as follows:

$$\left[\begin{array}{l}{\theta }_i\hfill \\ {\varphi }_i\hfill \end{array}\right]=\left[\begin{array}{cc}1-{\beta }_{\theta }& 0\\ 0& 1-{\beta }_{\varphi }\end{array}\right]\left[\begin{array}{c}{\theta }_{i-1}+\dot{\theta }\text{Δt}\\ {\varphi }_{i-1}+\dot{\varphi }\text{Δt}\end{array}\right]+\left[\begin{array}{cc}{\beta }_{\theta }& 0\\ 0& {\beta }_{\varphi }\end{array}\right]\left[\begin{array}{l}{\theta }_{accel}\hfill \\ {\varphi }_{accel}\hfill \end{array}\right]$$ (11)

where $\dot{\theta }$ and $\dot{\varphi }$ are calculated using gyroscope measurements $({\omega }_x,{\omega }_y,{\omega }_z)$ and the complementary filtered inclination measurements, as shown in (12).

$$\left[\begin{array}{c}\dot{\theta }\\ \dot{\varphi }\end{array}\right]=\left[\begin{array}{c}{\omega }_y\cos \varphi -{\omega }_z\sin \varphi \\ {\omega }_x+{\omega }_y\sin \varphi \tan \theta +{\omega }_z\cos \varphi \tan \theta \end{array}\right]$$ (12)

The final equation of the first-order complementary filter (5) was obtained by substituting (3), (4), and (12) into (11).

Appendix B. Kalman filter design

The Extended Kalman Filter used in this study contains the generic process model (13) and measurement model (14). The process model estimates x_k, a column vector containing the parameters of interest, from prior estimate $x_{k-1}$ with a random variation of $w_{k-1}$. The matrices F and W relate $x_{k-1}$ and $w_{k-1}$ to x_k, respectively. The measurement model compares x_k to sensor measurements z_k, where G is a matrix that relates x_k to z_k, and v_k is the random variation within the measurement model. The random parameters w_k-1 and v_k are assumed to follow normal distributions of $p(w)\sim N(0,Q)$ and $p(v)\sim N(0,R)$, respectively.

$$x_k=F{x}_{k-1}+W_{k-1}{w}_{k-1}$$ (13)

$$z_k=G{x}_{k-1}+V_k{v}_k$$ (14)

The implementation of the Kalman filter consists of a series of five recursive equations:

$$x_k^{-}=F{x}_{k-1}$$ (15)

$$P_k^{-}=A{P}_{k-1}{A}^T+W_{k}Q{W}_k^T$$ (16)

$$K_k=P_k^{-}{H}^T{\left(H{P}_k^{-}{H}^T+V_k{Q}_k{V}_k^T\right)}^{-1}$$ (17)

$$x_k=x_k^{-}+K_k\left(z_k-G{x}_k^{-}\right)$$ (18)

$$P_k=\left(I-K_{k}H\right)P_k^{-}$$ (19)

where I is the identity matrix, P_k is the estimation error covariance, and K_k is the Kalman gain calculated from Q and R. Matrices A, W, H, and V are all Jacobin matrices. Matrix A contains the partial derivatives of F with respect x, W contains the partial derivatives of F with respect to w, H contains the partial derivatives of G with respect to x, and V contains the partial derivatives of G with respect to v.

The Kalman Filter implemented was modified from a validated Linear Kalman Filter (Ligorio and Sabatini, 2015). The filter was designed to discriminate the direction of gravity (g^b) from the linear acceleration (a^b) in the local coordinate frame when gyroscope measurements ${\overrightarrow{\omega }}^b=\left({\omega }_x,{\omega }_y,{\omega }_z\right)$ and accelerometer measurements $\left(a_x,a_y,a_z\right)$ are provided. The generic process (13) and measurement (14) models were provided by Ligorio and Sabatini (2015) as follows:

$$\left[\begin{array}{c}{g}_k^b\\ a_k^b\end{array}\right]=\left[\begin{array}{cc}expm\left(-\left[{\omega }_{i-1}^b\times \right]\text{Δ}t\right)& 0_{3\times 3}\\ 0_{3\times 3}& c_a{I}_{3\times 3}{a}_{i-1}^b\end{array}\right]\left[\begin{array}{c}{g}_{k-1}^b\\ a_{k-1}^b\end{array}\right]+\left[\begin{array}{cc}-\text{Δ}t\left[g_{i-1}^b\times \right]& 0_{3\times 3}\\ 0_{3\times 3}& c_b{I}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{w}_{k-1}^{\omega }\\ w_{k-1}^{gm}\end{array}\right]$$ (20)

$$\left[\begin{array}{l}{a}_{x,k}\hfill \\ a_{y,k}\hfill \\ a_{z,k}\hfill \end{array}\right]=\left[\begin{array}{c}{I}_{3\times 3}{I}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_k^b\\ a_k^b\end{array}\right]+I_{3\times 3}{v}_k^a$$ (21)

where 0_3×3 is a 3 × 3 matrix with zeros, I_3×3 is a 3 × 3 identity matrix, $[\stackrel{\rightharpoonup }{u}\times ]$ is the skew symmetric matrix associated for a given vector $\left(\stackrel{\rightharpoonup }{u}\right)$, and c_a, c_b are the parameters of the first-order Gauss-Markov process used to account for external acceleration. The gyroscope noise w^ω and accelerometer noise v^a are assumed to follow a normal distribution of $N\left(0,{\sigma }_{\omega }^2\right)$ and $N\left(0,{\sigma }_a^2\right)$, respectively. The white Gaussian noise w^gm is assumed to be zero mean with an identity covariance matrix.

This process model was modified into a first-order approximation (22) to reduce computation time. The gyroscope bias was also added to the process model (23) to improve measurement estimates, which is consistent with other Kalman Filter designs (Brigante et al., 2011; Chang et al., 2008; Gośliński et al., 2015 ). The gyroscope bias was modeled as a random walk, where ${\dot{b}}_{\omega }$ is assumed to follow a normal distribution of $N\left(0,{\sigma }_{{\omega }_b}^2\right)$.

$$expm\left(-\left[{\omega }_{i-1}^b\times \right]\text{Δ}t\right)\approx \left(I_{3\times 3}-\left[{\omega }_{i-1}^b\times \right]\text{Δ}t\right)$$ (22)

$$b_{\omega ,i}=b_{\omega ,i-1}+{\dot{b}}_{\omega }\text{Δ}t$$ (23)

Based on these changes, (20) and (21) becomes (24) and (25), respectively.

$$\left[\begin{array}{c}{g}_i^b\\ a_i^b\\ b_{\omega ,i}\end{array}\right]=\left[\begin{array}{ccc}{I}_{3\times 3}-\left[\left({\omega }_{i-1}^b-b_{\omega ,i-1}\right)\times \right]\text{Δ}t& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& c_a{I}_{3\times 3}{a}_{i-1}^b& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& I_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_{i-1}^b\\ a_{i-1}^b\\ b_{\omega ,i-1}\end{array}\right]+\left[\begin{array}{ccc}\left[g_{i-1}^b\times \right]\text{Δ}t& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& c_b{I}_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& \text{Δ}t{I}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{w}_{i-1}^{\omega }\\ w_{i-1}^{gm}\\ {\dot{b}}_{\omega }\end{array}\right]$$ (24)

$$\left[\begin{array}{l}{a}_{x,k}\hfill \\ a_{y,k}\hfill \\ a_{z,k}\hfill \end{array}\right]=\left[\begin{array}{c}{I}_{3\times 3}{I}_{3\times 3}\end{array}\right]\left[\begin{array}{l}{g}_k^b\hfill \\ a_k^b\hfill \end{array}\right]+\left[\begin{array}{c}{I}_{3\times 3}{I}_{3\times 3}{0}_{3\times 3}\end{array}\right]\left[\begin{array}{c}{g}_k^b\\ a_k^b\\ b_{\omega ,k}\end{array}\right]v_k^a$$ (25)

Given that F is non-linear, A is defined as follows:

$$A=\left[\begin{array}{ccc}{I}_{3\times 3}-\left[\left({\omega }_{i-1}^b-b_{\omega ,i-1}\right)\times \right]\text{Δ}t& 0_{3\times 3}& -\left[g_i^b\times \right]\text{Δ}t\\ 0_{3\times 3}& c_a{I}_{3\times 3}{a}_{i-1}^b& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& I_{3\times 3}\end{array}\right]$$ (26)

The process covariance matrix (Q) and the measurement covariance matrix (R) is defined as follows:

$$Q=\left[\begin{array}{ccc}{I}_{3\times 3}{\sigma }_{\omega }^2& 0_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& I_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& I_{3\times 3}{\sigma }_{{\omega }_b}^2\end{array}\right]$$ (27)

$$R=I_{3\times 3}{\sigma }_a^2$$ (28)

Appendix C. Source code

The MATLAB files for the filters in this paper are freely available using the following address:

https://github.com/how-chen/Biomech/tree/master/IMU/Inclination Other code within this git-hub are freely-available to use as well. However, they are in varying stages of development, and may not function properly at all times.