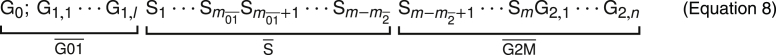CycleFlow simultaneously quantifies cell-cycle phase lengths and quiescence in vivo

Summary

Populations of stem, progenitor, or cancer cells show proliferative heterogeneity in vivo, comprising proliferating and quiescent cells. Consistent quantification of the quiescent subpopulation and progression of the proliferating cells through the individual phases of the cell cycle has not been achieved. Here, we describe CycleFlow, a method that robustly infers this comprehensive information from standard pulse-chase experiments with thymidine analogs. Inference is based on a mathematical model of the cell cycle, with realistic waiting time distributions for the G₁, S, and G₂/M phases and a long-term quiescent G₀ state. We validate CycleFlow with an exponentially growing cancer cell line in vitro. Applying it to T cell progenitors in steady state in vivo, we uncover strong proliferative heterogeneity, with a minority of CD4⁺CD8⁺ T cell progenitors cycling very rapidly and then entering quiescence. CycleFlow is suitable as a routine method for quantitative cell-cycle analysis.

Graphical abstract

Highlights

• •CycleFlow quantifies quiescence and cell cycling in heterogeneous populations in vivo
• •CycleFlow combines pulse chase with a thymidine analog with mathematical inference
• •Accounting for experimental uncertainty yields robust estimates of cell-cycle parameters
• •Application to T cell development quantifies thymocyte quiescence

Motivation

Assaying cell cycling with thymidine analogs in vivo is a standard method. However, the cell populations of interest are often heterogeneous, consisting of subpopulations of cycling and quiescent cells. Hence, the correct determination of the cell-cycle duration requires the simultaneous assessment of the quiescent fraction. Here, we show that a straightforward extension of the standard pulse-chase protocol, with a single thymidine analog, allows accurate determination of the quiescent cell fraction and of the cell-cycle phase durations in the proliferating subpopulation. Our method, CycleFlow, relies on measuring at several time points during the chase and interpreting the data with a realistic mathematical model of the cell cycle. CycleFlow yields robust estimates of the cell-cycle characteristics in the face of typical sources of experimental uncertainty.

The switching of cells between cycling and quiescence is a fundamental process in development, tissue homeostasis, and immune responses. Jolly et al. describe a broadly applicable method that combines thymidine-analog labeling with model-based inference to disentangle and quantify quiescence and cycle timing.

Introduction

The decision of cells to progress through the cell cycle or enter quiescence is fundamental for multicellular organisms. This decision is under strict control during development and tissue regeneration. Long-term quiescence of stem and progenitor cells is thought to be enabled by signals from niche or stroma cells or intrinsic developmental programs in the intact organism (van Velthoven and Rando, 2019), and it becomes deregulated in cancer (Aguirre-Ghiso, 2007; Li and Clevers, 2010). The proliferating fraction sustains cell production, and the proliferation rate can be regulated at various stages of the cell cycle, including the G₁ and S phases (Akinduro et al., 2018; Kretschmer et al., 2020; Gitlin et al., 2015). Hence, characterizing the proliferative activity of a cell population requires knowledge of the durations of the cell-cycle phases and the quiescent fraction. However, simultaneous quantification of long-term quiescence and proliferative activity in vivo remains challenging, thus also limiting mechanistic insight.

A major obstacle stems from the fact that inference of quiescence and cycle progression are interdependent. For instance, when estimating proliferative activity based on DNA content, the often-applied rule of thumb that low S and G₂/M fractions indicate slow cell cycles can be misleading: the low fractions may result from slow proliferation in a homogeneous population (i.e., a long G₁ phase) but also from a substantial subpopulation of quiescent cells (large G₀ fraction), or both, which cannot be distinguished based on DNA content. This example demonstrates that in order to obtain accurate cycle times, quiescent versus proliferating subpopulations need to be quantified.

Hitherto, pulse-chase techniques for quantifying cell cycling and methods that estimate the quiescent fraction have been applied separately. This is problematic, as pulse-chase techniques yield non-representative averages of cell-cycle time when neglecting quiescence. To estimate the quiescent fraction, proxy markers of cycling cells (Ki67, phosphorylated retinoblastoma protein [pRb]) have been used; how to combine such data with pulse-chase data in a statistically consistent manner is an open problem. Moreover, Ki67 continues to be expressed for some time after cells have stopped cycling (Miller et al., 2018), and pRB is absent from both transiently arrested (Spencer et al., 2013) and fully quiescent cells. Another approach, the long-term dilution of cell labels (thymidine analogs or fluorescently tagged histones), has been used in experiments demonstrating hematopoietic stem cell quiescence (Wilson et al., 2008; Foudi et al., 2009), but the quantitative interpretation of these data is not straightforward (Morcos et al., 2020).

The proliferative activity of cells and, in fact, the above-mentioned confounding effects are dynamic in nature. Hence, an adequate mathematical model of cell-cycle dynamics is needed to interpret the experimental data. Mathematical analysis has been applied to estimate cell-cycle progression from pulse-chase experiments, usually by estimating an overall proliferation rate (De Boer and Perelson, 2013; Lahoz-Beneytez et al., 2016) or by using sophisticated double-labeling techniques to estimate the duration of specific cell-cycle phases (Akinduro et al., 2018; Kretschmer et al., 2020). Thus far, these approaches have not considered quiescence. Typically, they also use exponential distributions for the lengths of the total cell cycle or its phases, which recent data show to be rather of Erlang type (Chao et al., 2019).

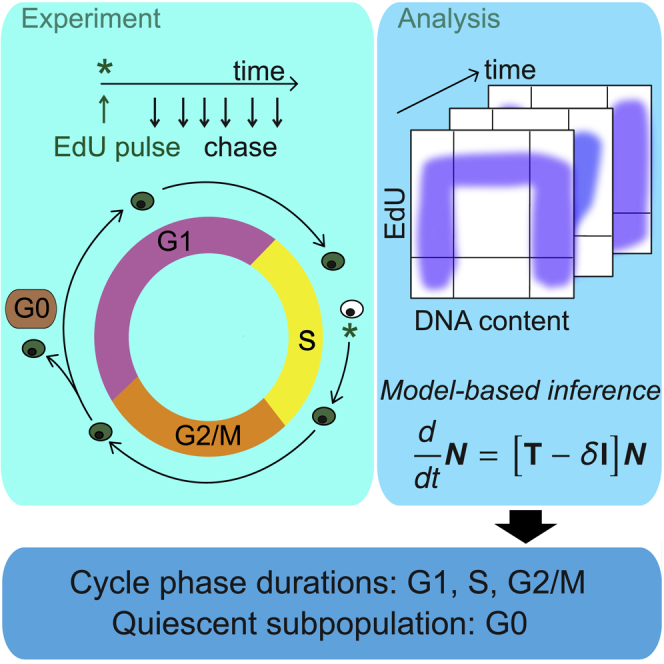
Here, we describe CycleFlow, an easy-to-use method that simultaneously quantifies proliferation and long-term quiescence in heterogeneous cell populations. Cells arrested transiently as a result of DNA damage (Spencer et al., 2013; Barr et al., 2016; Ryl et al., 2017; Yang et al., 2017; Arora et al., 2017) are considered proliferative, whereas the quiescent fraction comprises cells remaining out of the cell cycle for a longer period of time, at least several cycle durations. CycleFlow combines pulse chase of both a thymidine analog (e.g., 5-ethynyl-2′-deoxyuridine [EdU]) and a DNA stain, with Bayesian parameter inference. The key idea is to label a cohort of S phase cells with a brief pulse of a thymidine analog and then use DNA content as a coordinate to follow the labeled cells through the cell cycle, observing re-entry of divided cells into the cycle or transition into a quiescent state (Figure 1A). The experimental data are interpreted within a generic mathematical model of cell-cycle progression in heterogeneous populations, allowing us to infer simultaneously the fractions of quiescent (G₀) versus proliferating cells and the times that the latter spend in the G₁, S, and G₂/M phases of the cell cycle.

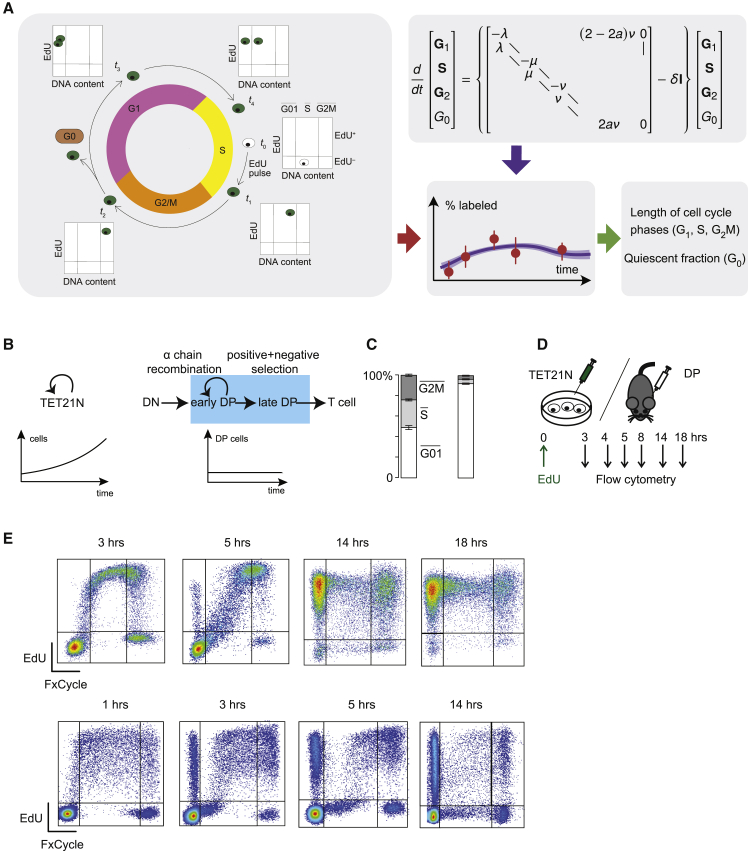
Figure 1.

Outline of CycleFlow

(A) Schematic of CycleFlow: the progression of EdU-labeled cells through the cell cycle is tracked over time, the mathematical model is fitted to the data, and cell-cycle parameters are estimated via Bayesian inference.

(B) Schematic of TET21N cells’ exponential growth in culture (left) and T cell differentiation in the thymus (right). The number of TET21N cells grow exponentially, while the number of cells in DP remains constant.

(C) Distribution of cells in the $\overline{\text{G}01}$, $\overline{\text{S}}$, and $\overline{\text{G}2\text{M}}$ gates as determined by DNA content averaged over all time points. For TET21N (left barplot, n = 25); for DP thymocytes (right barplot, n = 31). Error bars indicate SEM.

(D) EdU pulse-chase experiment for cells in culture or mouse.

(E) Progression of EdU-labeled TET21N (top row) and DP thymocytes (bottom row) through the cell cycle, as defined by DNA content. In each case, four representative flow cytometry snapshots are shown.

Results

Following a cell cohort labeled in S phase through the cycle

We applied CycleFlow in two standard settings: exponential population growth and population turnover at steady state. For exponential growth, we used a MYCN-driven cancer cell line (TET21N) in culture (Figure 1B, left panel). We had previously quantified cell-cycle parameters of these cells including cycle time and G₁ phase duration by time-lapse microscopy (Kuchen et al., 2020), which provided a “ground truth” to evaluate the results of CycleFlow. For steady-state turnover, we used developing T cells in the thymus in vivo (Figure 1B, right panel), a paradigm for studying cell differentiation in vertebrates (Yui and Rothenberg, 2014). We focused on the major thymocyte fraction consisting of cells at the CD4⁺CD8⁺ double-positive (DP) stage, which transition from proliferation to quiescence after successful recombination of the TCRA gene (Mingueneau et al., 2013). Quiescent DP thymocytes then further differentiate into single-positive CD4 and CD8 T cells. Although DPs are a key differentiation stage, it is not known how rapidly they cycle before becoming quiescent and how large the quiescent DP fraction is, with estimates in the literature ranging from 30% to 90% (Yates, 2014).

The proportions of cell-cycle phases, as determined by DNA content, were very different between the two populations; DP cells contained a much larger fraction with 2n DNA content than TET21N cells (Figure 1C). Importantly, 2n cells may be quiescent, which we refer to as G₀, or in the G₁ phase of the cell cycle; we denote the 2n flow cytometry gate by $\overline{\text{G}01}$. Naively, this observation might suggest that DP cells cycle more slowly than TET21N cells. However, this conclusion would be wrong if only a small fraction of DP cells were cycling, and most were in G₀.

We thus aimed to distinguish cells in G₀ from cells in ${\text{G}}_1$ within $\overline{\text{G}01}$ and thereby also determine the phase durations of the cycling fraction. To this end, we pulse labeled both cell types with EdU: for TET21N, we added EdU to the culture medium and washed after 1 h, and for DP, we injected a single EdU dose intraperitoneally into young adult mice (Figure 1D). In both cases, a cohort of EdU-labeled cells progressed from $\overline{\text{S}}$ to $\overline{\text{G}2\text{M}}$ and, after mitosis, back to $\overline{\text{G}01}$. Already after a few hours, unlabeled cells entered $\overline{\text{S}}$, while labeled cells in $\overline{\text{G}01}$ had not yet re-entered into a second cycle, producing a gap in the EdU-positive gate in early S phase (Figure 1E, 5 h time point for TET21N, 3 and 5 h time points for DP). At later time points, however, labeled cells started to re-enter into a second cycle, closing this gap again (Figure 1E, 14 and 18 h time points for TET21N, and 14 h time point for DP). Thus, EdU pulse labeling allows following a cohort of cells over one cycle.

CycleFlow models cycling and quiescent cell fractions

Notably, in DP, but not in TET21N, a large fraction of cells remained unlabeled (Figure 1E, final time points), which could mean either that these cells were quiescent, or that they were cycling but not in $\text{S}$ phase during the brief EdU pulse. To resolve this ambiguity, we designed the mathematical model underlying CycleFlow to infer the true quiescent fraction along with the cell-cycle phase durations of the cycling cells. Following Chao et al. (2019), we described the length of the cell-cycle phases by suitable Erlang distributions (Figure S1A; STAR Methods). We allowed cycling cells to transition irreversibly to ${\text{G}}_0$ after each cycle. This irreversibility reflects the long-term nature of quiescence (in an extended model, we also considered exit from quiescence; Figure S1C). To describe EdU labeling, we exploited the fact that the Erlang distribution can be modeled as a sequence of memoryless steps, allowing cells to acquire label at variable points in $\text{S}$ phase (Figure S1B; STAR Methods). As the precise duration of EdU availability cannot be directly measured, we estimate it as a free parameter from the experimental data. We also observed that the assignment of cell-cycle phases based on DNA content has limited resolution. For instance, at 3 h, some TET21N cells at the right-hand edge of $\overline{\text{G}01}$ were EdU positive, implying that these had already entered $\text{S}$ phase but were not identified as such by DNA staining (Figure 1E); likewise, it is possible that some labeled cells in $\overline{\text{G}2\text{M}}$ were still in late $\text{S}$ phase. Hence, CycleFlow also estimates the degree of misassignment of flow cytometry gates to cell-cycle phases from the data (see STAR Methods). After solving this model for the time course of the labeled population in the various gates, information on (1) the quiescent cell fraction, (2) the phase lengths for the cycling cells, and (3) the EdU labeling kinetics can be extracted from the experimental data within a Bayesian setting by sampling from the posterior distribution.

Accurate inference for both growing and steady-state populations

We fitted the model to both datasets, obtaining good agreement between model and data for all cell-cycle phases (Figures 2A, 2B, and S2). The model then also recovered the dynamics of the EdU-negative cell fractions, which were not used for fitting (Figure S3); this result implies that the fractions of cell-cycle phases remained constant throughout each experiment. To evaluate the accuracy of CycleFlow, we first considered the cell-cycle parameters inferred for the TET21N cells. We obtained approximately equal durations of ${\text{G}}_1$, $\text{S}$, and G₂/M and a very small quiescent fraction (Figure 2C). In particular, most labeled cells accumulating in the $\overline{\text{G}01}$ gate were identified as ${\text{G}}_1$ (Figure S4), implying that this cancer cell line proliferates homogeneously. Direct observation of TET21N cells expressing the FUCCI Cdt1 degron by time-lapse microscopy (Kuchen et al., 2020) indeed shows practically no quiescent cells. Moreover, the directly measured total cell-cycle duration and ${\text{G}}_1$ phase duration agrees with the inferred parameters (Figure 2D). Hence, CycleFlow yields correct estimates of the average duration of cell-cycle phases in a cell population containing a negligible fraction of quiescent cells.

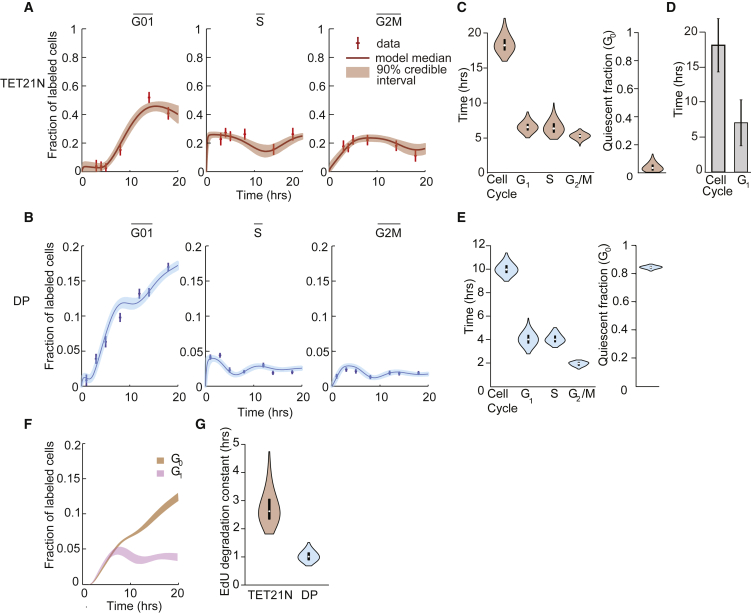
Figure 2.

Application of CycleFlow to determine quiescence and proliferation rate of TET21N cells and DP thymocytes in vivo

(A and B) Time courses of EdU-labeled TET21N cells (A) and DP thymocytes (B) in $\overline{\text{G}01}$, $\overline{\text{S}}$, and $\overline{\text{G}2\text{M}}$ gates compared between experimental data (error bars, pooled SEM; n = 3 to 6 per time point) and model fit. Population sizes are given as fractions of total cells.

(C) Duration of total cell cycle, G₁, S, and G₂/M phases of TET21N cells (left panel), and quiescent fraction (right panel) inferred by CycleFlow. Violin plot indicates parameter distributions; white dots, median values; black bars, interquartile ranges.

(D) Mean duration of cell-cycle and ${\text{G}}_1$ phase of TET21N, expressing the Cdt1 FUCCI degron, measured with time-lapse microscopy (data taken from Kuchen et al. [2020]). Error bars indicate standard deviation of the mean.

(E) Duration of G₁, S, and G₂/M phases (left panel) and fraction of quiescent cells (right panel) of DP thymocytes inferred by CycleFlow. Violin plot indicates parameter distributions; white dots, median values; black bars, interquartile ranges.

(F) Inferred time course of EdU-labeled G₀ and G₁ DP thymocytes in the $\overline{\text{G}01}$ gate.

(G) Samples of the posterior distribution of the EdU degradation time ${\tau }_E$ for TET21N cells (red) and DP thymocytes (blue). Violin plot; white dots, median values; black bars, interquartile ranges.

Next, we focused on DP thymocytes. Their much lower $\overline{\text{S}}$ and $\overline{\text{G}2\text{M}}$ fractions (Figure 1C) could be mistaken to indicate that DPs proliferate at a lower rate compared with the TET21N cells. However, CycleFlow inferred that the proliferating DP thymocytes actually cycle faster than TET21N cells, but this fact is masked by the high fraction of quiescent thymocytes in ${\text{G}}_0$ (Figure 2E); these constitute 84% (83%, 86%) (median and 90% credible interval) of DP cells. The remaining 16% of cells divide extremely rapidly, with a cycle length of 10 (9.3, 10.9) h. The transition of DP thymocytes into quiescence is seen by comparing the kinetics of labeled cells with TET21N: the key difference to TET21N cells is that in DP thymocytes, the labeled $\overline{\text{G}01}$ fraction increases during the entire experimental time course (Figure 2A). This continued increase is inferred to be due to labeled cells entering quiescence after division instead of progressing to $\text{S}$ phase. In this way, CycleFlow disentangles ${\text{G}}_0$ from ${\text{G}}_1$ subpopulations (Figure 2F) and reveals a pronounced proliferative heterogeneity in DPs. This finding is consistent with early DP cells first proliferating rapidly and soon becoming quiescent (Yates, 2014); quiescent DPs then constitute the vast majority of the heterogeneous DP compartment.

CycleFlow also infers the duration of EdU availability for labeling. For TET21N cells, which were washed after 1 h, the inferred EdU loss times correspond to a half-life of 1.8 (1.4, 2.8) h (Table S3; Figure 2G). For DP thymocytes in vivo, the EdU degradation half-life was 0.7 (0.5, 0.9) h, consistent with known pharmacokinetics of EdU in murine blood (Cheraghali et al., 1995).

Validation of thymocyte quiescence using single-cell transcriptomes

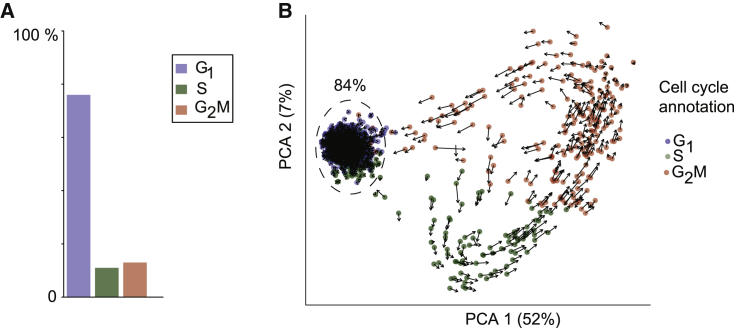
To further validate CycleFlow, we sought independent support for the inferred quiescent DP fraction. We began by performing single-cell RNA sequencing (RNA-seq) of freshly isolated DP cells. We assigned a cycle phase to each cell based on cycle-related transcripts (Stuart et al., 2019), which could not, however, disentangle ${\text{G}}_0$ and ${\text{G}}_1$. This procedure overestimated $\text{S}$ and ${\text{G}}_2$ fractions compared with the $\overline{\text{S}}$ and $\overline{\text{G}2\text{M}}$ gates defined by DNA content and, hence, underestimated $\overline{\text{G}01}$ (Figure 3A; cf. Figure 1C). The modest agreement of transcriptome-based phase assignment with measurement of DNA content is not surprising, as the gradual transcriptome changes cannot precisely pinpoint the transitions between cell-cycle phases (Hsiao et al., 2020). Recent work using proliferating cell lines in vitro has revealed a circular topology of transcriptomes due to cyclic expression (Schwabe et al., 2020). Using principal-component analysis and calculating RNA velocity based on a set of cell-cycle-associated genes for the DP thymocytes (see STAR Methods), we observed a circular flow, which, in contrast to the cell line data (Schwabe et al., 2020), entered a highly populated “sink” region with no apparent efflux (Figure 3B). Given that DP cells exit the cell cycle and enter quiescence, the sink region is likely made up of the quiescent DP cells. This conclusion is in line with these cells being annotated as ${\text{G}}_1$ by their transcriptome. These observations and the quantitative agreement we found between the fractions of quiescent cells estimated by CycleFlow and cells in the sink region (both 84%) support the validity of CycleFlow in cell populations that contain a quiescent subpopulation.

Figure 3.

Single-cell transcriptomic analysis of cycle progression

(A) Distribution of cell-cycle phases in DP thymocytes scRNA-seq dataset as estimated by the Seurat package; n =1.

(B) Principal-component analysis of DP scRNA-seq data performed on cell-cycle genes defined by the Seurat package; percentages on each axis denote the variability explained by the principal component. Cells are colored according to cell-cycle phase predicted by Seurat. Arrows indicate RNA velocities projected on the first and second principal components.

Distinguishing quiescent cells from transiently arrested cells

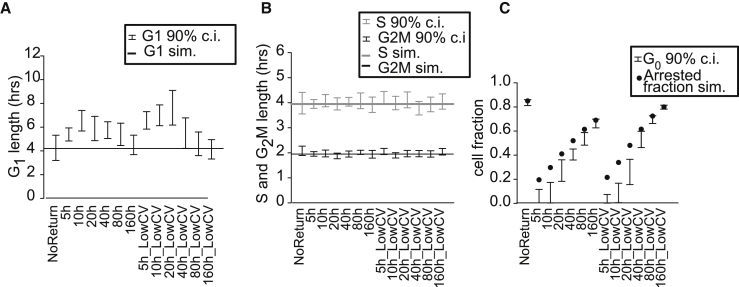
Finally, we studied the question whether CycleFlow can effectively distinguish transient cell-cycle arrest, which depends on DNA-damage and repair (Spencer et al., 2013; Barr et al., 2016; Ryl et al., 2017; Yang et al., 2017; Arora et al., 2017), from long-term quiescence as part of a developmental program. We generated synthetic EdU labeling data for a simulated population based on cell-cycle parameters as inferred for DP cells. Instead of entering quiescence irreversibly, the simulated population could now arrest the cycle at 2n DNA content for variable times and then re-enter into the cycle (Figure S1C). Applying CycleFlow to these data, we found that transient arrests (less than four unarrested cycle durations) were assigned as slow passages through ${\text{G}}_1$ (Figure 4A). Long-term arrests (exceeding 8 cycles) were assigned to ${\text{G}}_0$ and thus did not affect inferred ${\text{G}}_1$ duration (Figure 4C). Arrests between 4 and 8 cycles were split between ${\text{G}}_1$ and ${\text{G}}_0$, which reduced the quality of fit. Importantly, the inferred durations of $\text{S}$ and G₂/M phases were unaffected by cycle re-entry in all cases (Figure 4B). We conclude that CycleFlow robustly resolves heterogeneity between cycling cells (some of which may undergo transient arrest) and long-term quiescence.

Figure 4.

Parameters inferred by CycleFlow from synthetic data including cell-cycle arrest

(A) G₁ length versus mean cell-cycle arrest time used in simulation. “NoReturn” indicates that cells arrest irreversibly. The coefficient of variation (CV) of cell-cycle arrest was set to 1.0 except for the points annotated with “LowCV,” where it was 0.13. Error bars indicate 90% credible intervals; the G₁ length used in the simulations is shown as a solid line.

(B) Like (A) but for S (gray) and G₂/M (black) phase durations.

(C) G₀ fraction inferred by CycleFlow (90% credible intervals; bars) and simulated arrested fractions (dots).

Discussion

By exploiting joint information on DNA content and EdU label progression, CycleFlow determines the long-term quiescent fraction within a cell population along with all the cell-cycle phase durations of the proliferating cell fraction. Our approach overcomes practical problems, including the imperfect correspondence between cell-cycle phases and DNA content gates and the identification of the EdU removal kinetics. CycleFlow is equally applicable in vitro and in vivo as well as to growing or steady-state cell populations. In particular, CycleFlow enabled us to resolve the cycling characteristics of the DP thymocytes and the relative size of the quiescent subpopulation. Our finding that more than 80% of DP thymocytes are quiescent resolves a long-standing question in the immunological literature that is relevant for understanding the mechanisms of thymocyte selection (Yates, 2014). Application to other cell types is straightforward (e.g., Carvajal Ibañez et al., 2022): the measurements should extend over roughly one cell cycle with several (typically 4–8) time points. The model fitting and parameter inference are facilitated by a publicly available Python package.

Limitations of the study

As with any model-based inference method, the applicability of CycleFlow is limited by the validity of the underlying model assumptions. Specifically, all cycle phase durations are modeled as Erlang distributed, and exit from the cycle into ${\text{G}}_0$ is assumed to be effectively irreversible. While the Erlang shape of $\text{S}$ and ${\text{G}}_2$ is reasonable for a large class of mammalian cells (Chao et al., 2019), we found that the corresponding substep numbers cannot be identified from data. Here, CycleFlow resorts to fixing substep numbers in order to match typical observed coefficients of variation (Chao et al., 2019). The substep number for ${\text{G}}_1$ is identifiable from data, and CycleFlow infers it. In some cell populations, transient arrest after division may occur, with a duration similar to the cell cycle. In that situation, the effective distribution of the time until $\text{S}$ phase is poorly captured by an Erlang shape, CycleFlow will fit the data worse, and the inferred ${\text{G}}_1$ substep numbers and ${\text{G}}_0$ fractions may be distorted (cf. Figure 4). If transient arrest occurred in a large fraction of cycling cells, so that the Erlang assumption will be violated, an extension of the model, as well as additional data separating arrest from quiescence, may be warranted.

Loss of cells due to differentiation or death is modeled as uniform over all phases of the cycle, which is reasonable in absence of more detailed knowledge. If loss is known to be restricted to specific phases, this information can be incorporated straightforwardly by adapting the model. Moreover, CycleFlow could be extended to infer non-uniform loss rates for all phases, but whether these will be identifiable may depend on the particular dataset. Conversely, gain of cells by differentiation of a progenitor cell type is not included by the CycleFlow model, which describes an essentially self-sustaining population. Incorporating influx would require another extension of the model and additional data, for instance label kinetics of the upstream population. These possible extensions are an interesting avenue for future work.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
CD8a (clone 53–6.7) allophycocyanin (APC)	eBioscience	Cat#17–0081; RRID: AB_469335
TCRgd (clone GL3) BV421	BioLegend	Cat#118120; RRID: AB_2562566
CD4 (clone H129.19) phycoerythrin (PE)	BD Pharmingen	Cat#553652
Ter119 (clone Ter119) BV421	Biolegend	Cat#116234; RRID: AB_2562917
CD11b (clone: M1/70) BV421	BioLegend	Cat#101251; RRID: AB_2562904
CD19 (clone: 6D5) BV421	BioLegend	Cat#115549; RRID: AB_2563066
NK1.1 (clone PK136) BV421	BioLegend	Cat#108731; RRID: AB_10895916
Gr-1 (clone RB6-8C5) BV421	BioLegend	Cat#108445; RRID: AB_2562903
Critical commercial assays
Click-iT™ Plus EdU Alexa Fluor™ 488 Flow Cytometry Assay Kit	Invitrogen	Cat#C10632
Zombie Red™ Fixable Viability Kit	BioLegend	Cat#423109
FxCycle™ Violet Stain	Invitrogen	Cat#F10347
Deposited data
Raw and analysed scRNA-seq data	This paper	GEO: GSE196412
Thymocytes flow cytometry data	This paper	FlowRepository: FR-FCM-Z3D7
TET21/N flow cytometry data	This paper	FlowRepository: FR-FCM-Z3ER
Experimental models: Cell lines
TET21/N (Lutz et al., 1996)	DKFZ	RRID: CVCL_9812
Experimental models: Organisms/strains
mouse:C57BL/6-Tie2MCM/+ Rosa26YFP/+	Busch et al. (2015)	N/A
mouse: C57BL/6-Rosa26YFP	Srinivas et al. (2001)	N/A
mouse: C57BL/6-Cd45.1	In-house colony	N/A
Software and algorithms
CycleFlow	This paper	https://doi.org/10.5281/zenodo.7037488
Emcee (3.02)	Foreman-Mackey et al. (2013)	https://emcee.readthedocs.io

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Thomas Höfer (t.hoefer@dkfz.de).

Materials availability

This Study did not generate new unique reagents.

Experimental model and subject details

Mice

Mice of ages between eleven and sixteen weeks were used, both female and male. No randomization was done, no blinding was done and no animals were excluded from the analysis. Mice were kept in individually ventilated cages under specific pathogen-free conditions in the animal facility at the German Cancer Research Center (DKFZ, Heidelberg). All animal experiments were performed in accordance with institutional and governmental regulations, and were approved by the Regierungspräsidium (Karlsruhe, Germany).

Cell line

SH-EP TET21/N (TET21N) cells were grown in RPMI 1640 medium supplemented with 10% Fetal Calf Serum (FCS) at ${37}^{\circ }$ C, 5% CO₂ and 88% humidity. Versene was used for all harvesting steps. The Cell line was authenticated by the DKFZ in house facility.

Method details

Labeling and analysis of TET21N cells in vitro

For each sample, $1.5\times {10}^6$ cells were seeded on 15 cm Petri dishes one day before EdU treatment and then treated with EdU (Invitrogen) at a final concentration of 10 μM in the culture medium. Cells were then harvested and fixed in 4% paraformaldehyde solution in PBS and kept in 90% methanol 10% PBS solution at $-{20}^{\circ }$ C. For flow cytometry analysis, cells were washed in washing buffer (1% Bovine Serum Albumin(BSA), 0.1% TritonX in PBS) and resuspended in PBS supplemented with 1% BSA. Cells were then permeabilized and the Click-it reaction was performed using the Click-iT Plus EdU Alexa Fluor 488 flow cytometry Kit (Invitrogen) according to the manufacturer’s protocol. For total DNA staining, cells were resuspended in FxCycle Violet (Thermofisher Scientific) solution (1:1000 in Click-it permeabilization buffer) prior to flow cytometry measurement. Data were acquired on a MACSQuant VYB (Miltenyi Biotec) and cell populations were analyzed with FlowJo 10.

Labeling of thymocytes in vivo and analysis

Mice were injected intraperitoneally with 1 mg EdU (Invitrogen) diluted in sterile PBS. At several time points after injection mice were sacrificed and thymi harvested. Thymi were mashed in a 40 μm filter with the plunger of a syringe. To identify dead cells, cells were incubated in Zombie Red™ Fixable Viability dye (Biolegend) solution (1:1000 in PBS). Fc receptors were blocked by incubating cells in PBS supplemented with 5% FCS with 250 μg $/$ ml purified mouse IgG (Jackson ImmunoResearch Laboratories). Antibody stainings were performed in PBS/5% FCS on ice for 30 min with optimal dilutions of commercially-prepared antibodies. The following antibodies were used: CD8a allophycocyanin (APC) (53–6.7) from eBioscience; CD4 phycoerythrin (PE) (H129.19) from BD Pharmingen; CD11b BV421 (M1/70), CD19 BV421 (6D5), NK1.1 BV421 (PK136), Gr-1 BV421 (RB6-8C5), TCR gd BV421 (GL3) and Ter119 BV421 (Ter119) from Biolegend. The lineage cocktail was composed of CD11b, CD19, Ter119, NK1.1, Gr-1 and TCR gd. After antibody staining, cells were fixed, permeabilized and the Click-it reaction was performed using the Click-iT Plus EdU Alexa Fluor 488 flow cytometry kit (Invitrogen). For total DNA staining, cells were resuspended in FxCycle™ Violet solution (1:1000 in Click-it Permeabilization buffer) prior to flow cytometry measurement. Data was acquired on a BD LSRFortessa cell analyzer (Becton Dickinson) and cell populations were analyzed with FlowJo 10. Double-positive thymocytes were defined as lineage⁻ CD4⁺CD8⁺.

Cell sorting for single-cell RNA-seq

Thymocytes were isolated and stained with antibodies as in the above section. Double positive thymocytes were sorted (BDFACSAriaIII, 100 μm nozzle) into 500 μL PBS containing 50% FCS. The sorted cells were spun down at 300 g for 5 min at $4^{°}$C and resuspended in 35 μL FACS buffer. Single cells were captured using the Chromium System and single cell full transcriptome and targeted TCR transcriptome libraries were generated according to the Chromium Single Cell V(D)J and Reagent Kits protocols (10x Genomics). During the library preparation, reverse transcribed cDNA was amplified 14 times in accordance with 10x Genomics protocols. The full transcriptomes were sequenced on an Illumina HiSeq4000 platform (26 + 74 bp read-length).

Single-cell RNA-seq data analysis

Samples were aligned to mouse genome (mm10) and read counting per cell was performed using the software CellRanger3.0.1 from 10x genomics. The raw count matrix produced by CellRanger was then further processed with the Bioconductor pipeline. SingleCellExperiment R objects were generated and empty droplets were excluded using the function emptyDrops() from the package DropletUtils. Cells with low UMI counts, low number of expressed genes and/or high mitochondrial gene expression were also removed using isOutlier from the package scater. The data was then normalized using logNormCounts function from the package scran. Cell cycle annotation was performed using Seurat v3. We then performed principal component analysis (PCA) using exclusively cell cycle genes defined within the Seurat package. In order to perform RNA-velocity, spliced and unspliced matrices were generated using the function run10x from the python implementation of the software velocyto. We performed RNA velocity using the scVelo algorithm implemented in the R package velociraptor on a subset of 1354 genes annotated with Gene Ontology term ‟Cell Cycle”. The result of the RNA velocity analysis was embedded into the PCA using the function embedVelocity from velociraptor.

Parameter inference

CycleFlow addresses the most important challenges when interpreting thymidine-analog labeling time-course data by incorporating known sources of uncertainty into its dynamical model, as detailed below. For a summary, see Table S1.

Model for cell-cycle progression

Within a growing cell population, each cell progresses through the cycle phases ${\text{G}}_1$, $\text{S}$ and ${\text{G}}_2$/ $\text{M}$ (Figure S1A). Each phase requires a stochastic time to complete. We capture this variability by dividing the cycle phases into subphases: ${\text{G}}_{\mathrm{1,1}}$ through ${\text{G}}_{1,l}$, ${\text{S}}_1$ through ${\text{S}}_m$ and ${\text{G}}_{\mathrm{2,1}}$ through ${\text{G}}_{2,n}$, respectively (The ${\text{G}}_2$ subphases also comprise $\text{M}$ phase for simplicity of notation). The subphases track the approximate progress of a cell within the respective cycle phase. We model the transitions from one subphase to the next (and from the last subphase of a cycle phase to the first subphase of the next) as rate processes with rates λ, μ and ν, for ${\text{G}}_1$, $\text{S}$ and ${\text{G}}_2$, respectively. Within this model the times to complete each of the cycle phases are Erlang-distributed random variables, with means ${\tau }_{{\text{G}}_1}=l/\lambda$, ${\tau }_{\text{S}}=m/\mu$, and ${\tau }_{{\text{G}}_2}=n/\nu$, and coefficients of variation (CVs), $1/\sqrt{l}$, $1/\sqrt{m}$ and $1/\sqrt{n}$, respectively. At the end of the cycle, a cell divides to produce two daughters. Each individual daughter cell may then, with probability a, exit the cell cycle into the quiescent state ${\text{G}}_0$, or, with probability $1-a$, restart the cycle in phase ${\text{G}}_{\mathrm{1,1}}$. In the main text and in this section, we consider entry into ${\text{G}}_0$ to be irreversible on the time scale of the experiment, and therefore exclude any transition from ${\text{G}}_0$ back into the cycle. More generally, cells may be allowed to re-enter the cycle from ${\text{G}}_0$; the implications are discussed further below. Finally, cells may be lost from any cycle phase or ${\text{G}}_0$ with rate δ, due to cell death or differentiation. The parameter δ is an effective loss rate average over all stages of the cell cycle. In practice, we found that a uniform loss rate was sufficient to fit our data.

Within this model the dynamics of subpopulations is described by a linear system of ordinary differential equations. Written in matrix form,

$$\frac{d}{dt}\mathit{N}=\mathbf{T}\mathit{N}-\delta \mathit{N},$$ (Equation 1)

where the vector of cell numbers in the various cycle subphases is defined as

$$\mathit{N}={\left[{\text{G}}_{\mathrm{1,1}}\left(t\right)\text{,}\dots {\text{,G}}_{1,l}\left(t\right){\text{,S}}_1\left(t\right)\text{,}\dots {\text{,S}}_m\left(t\right),{\text{G}}_{\mathrm{2,1}}\left(t\right),\dots ,{\text{G}}_{2,n}\left(t\right),{\text{G}}_0\left(t\right)\right]}^{\mathsf{T}},$$

and the rate matrix

$$\mathbf{T}=\left[\begin{array}{lllllllllll}-\lambda \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & 2\left(1-a\right)\nu \hfill & 0\hfill \\ \lambda \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & ⋮\hfill \\ \hfill & \ddots \hfill & -\lambda \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \lambda \hfill & -\mu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \mu \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \ddots \hfill & -\mu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \mu \hfill & -\nu \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \nu \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \nu \hfill & -\nu \hfill & ⋮\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & 2a\nu \hfill & 0\hfill \end{array}\right].$$ (Equation 2)

CycleFlow presumes that the samples originate from a cell population deep in the exponential growth phase, where the total cell number $N\left(t\right)$ increases exponentially while the proportions of cells in the various subphases are constant; we call this regime steady growth. At steady growth, we can decompose the cell numbers into an exponentially growing population $N\left(t\right)$ and constant cycle fractions $\mathit{n}=\left[{\text{g}}_{\mathrm{1,1}},\dots ,{\text{g}}_0\right]$, that is,

$$\mathit{N}\left(t\right)=N\left(t\right)\mathit{n}=N\left(0\right)e^{\left(\kappa -\delta \right)t}\left[{\text{g}}_{\mathrm{1,1}},\dots ,{\text{g}}_{1,l},{\text{s}}_1,\dots ,{\text{s}}_m,{\text{g}}_{\mathrm{2,1}},\dots ,{\text{g}}_{2,n},{\text{g}}_0\right].$$ (Equation 3)

Here, we have introduced a new rate κ by denoting the net population growth rate as $\kappa -\delta$. The proportions of cells in the various subphases are given by the steady-growth distribution $\mathit{n}$, which is normalized: ${\mathit{1}}^T\mathit{n}=1$, where we use the abbreviation $\mathbf{1}={\left[1,\dots ,1\right]}^{\mathsf{T}}$. The dynamical Equation 1 then yields

$$\frac{d}{dt}\mathit{N}\left(t\right)=\left(\kappa -\delta \right)N\left(t\right)\mathit{n}=N\left(t\right)\left[\mathbf{T}\mathit{n}-\delta \mathit{n}\right],\text{which}\text{implies}\kappa \mathit{n}=\mathbf{T}\mathit{n}.$$ (Equation 4)

Thus κ is seen to equal the dominant eigenvalue of the matrix $\mathbf{T}$, and $\mathit{n}$ is the associated normalized (right) eigenvector. The rate κ is the growth rate the population would have in the absence of loss.

Steady-growth distribution

To find $\mathit{n}$, we start by normalizing Equation 4. Using Equation 2, we obtain

$$\kappa ={\mathbf{1}}^T\mathbf{T}\mathit{n}={\left[0,\dots ,0,\nu ,0\right]}^T\mathit{n}=\nu {\text{g}}_{2,n}.$$ (Equation 5a)

Equation 5a implies that the total rate of production of new cells $\kappa N$ equals the population in the final subphase ${\text{G}}_{2,n}$ times its rate of completion ν. Now consider steady growth with production of new cells, where ${\text{G}}_{2,n}$ and κ are positive. Starting from Equation 5a and backsubstituting using Equation 4, we compute the remainder of the cycle subphase distribution $\mathit{n}$ in steady growth as a function of κ:

$${\text{g}}_0={\text{g}}_{2,n}2a\nu /\kappa =2a$$ (Equation 5b)

$${\text{g}}_{2,n-j}={\text{g}}_{2,n}\frac{{\left(\kappa +\nu \right)}^j}{{\nu }^j}=\frac{\kappa }{\nu }{\left(\frac{\kappa +\nu }{\nu }\right)}^{j}0<j<n$$ (Equation 5c)

$${\text{s}}_m={\text{g}}_{\mathrm{2,1}}\frac{\kappa +\nu }{\mu }=\frac{\kappa }{\mu }{\left(\frac{\kappa +\nu }{\nu }\right)}^n$$ (Equation 5d)

$${\text{s}}_{m-j}={\text{s}}_m\frac{{\left(\kappa +\mu \right)}^j}{{\mu }^j}=\frac{\kappa }{\mu }{\left(\frac{\kappa +\nu }{\nu }\right)}^n{\left(\frac{\kappa +\mu }{\mu }\right)}^{j}0<j<m$$ (Equation 5e)

$${\text{g}}_{1,l}={\text{s}}_1\frac{\kappa +\mu }{\lambda }=\frac{\kappa }{\lambda }{\left(\frac{\kappa +\nu }{\nu }\right)}^n{\left(\frac{\kappa +\mu }{\mu }\right)}^m$$ (Equation 5f)

$${\text{g}}_{1,l-j}={\text{g}}_{1,l}\frac{{\left(\kappa +\lambda \right)}^j}{{\lambda }^j}=\frac{\kappa }{\lambda }{\left(\frac{\kappa +\nu }{\nu }\right)}^n{\left(\frac{\kappa +\mu }{\mu }\right)}^m{\left(\frac{\kappa +\lambda }{\lambda }\right)}^{j}0<j<l$$ (Equation 5g)

To complete the calculation, the dominant eigenvalue κ can be found numerically by solving Equation 4 for given transition rates and subphase numbers. For steady growth to be possible, $a\le 1/2$ is required, since otherwise each cell has less than one proliferating daughter cell on average. When $a\le 1/2$ then also ${\text{g}}_0\le 1$ as required, Equation 5b.

Steady-state distribution

To capture cell populations that are maintained at a fixed population size within the model Equation 1, we consider the loss rate δ to be subject to implicit homeostatic regulation. The regulation maintains $\delta \equiv \kappa$, so that proliferation and loss balance, and net growth is zero. In this way, homeostasis is treated as a marginal case of steady growth, Equation 3, with vanishing effective growth rate and subphase populations $\mathit{N}=N\mathit{n}$ that are constant in time. We can compute the steady-state distribution $\mathit{n}$ by (Equation 5a), (Equation 5b), (Equation 5c), (Equation 5d), (Equation 5e), (Equation 5f), (Equation 5g) as before. The homeostatic set point of δ is obtained numerically by solving the eigenvalue problem Equation 4, with $\kappa \to \delta$.

Kinetics of labeling

In order to relate the cycling model Equation 1 to experimental data, we include the dynamics of label incorporation and inheritance (Figure S1B). As long as EdU is available in the medium, unlabeled cells in $\text{S}$ phase incorporate it, thereby transitioning into a labeled state at a rate ε. The labeled states (denoted ${\text{S}}^{\text{∗}},{\text{G}}_{\mathrm{2,1}}^{\text{∗}}$ etc.) are defined operationally: Any cell that is gated above the background fluorescence level in the EdU fluorescence channel is considered labeled. In practice we find that transition to the labeled state requires only a small part of $\text{S}$ phase, in other words, the rate of label acquisition $\epsilon >\mu /m$. It is unclear if label acquisition is also faster than progress from one $\text{S}$ subphase to the next, $\epsilon \gtrless \mu$. We therefore consider $\text{S}$ phase progress and labeling to be parallel processes, as shown in Figure S1B. As the chase phase of the experiment remains shorter than two cell cycles, we do not observe nor include in the model any delabeling by dilution of EdU in cells.

Importantly, in experiments EdU supply is stopped at the end of an initial labeling pulse, and thereafter, the availability of free EdU decreases gradually as it is consumed by cells or otherwise degraded. We model this removal by an exponential decrease of the total labeling rate

$$\epsilon =\epsilon \left(t\right)={\epsilon }_0{e}^{-t/{\tau }_E}.$$

Both the initial labeling rate ${\epsilon }_0$ and label degradation time scale ${\tau }_E$ are adjustable parameters. In practical parameter inference from data, we find that these two parameters are negatively correlated, and that ${\epsilon }_0$ admits only a lower bound, but the label degradation time ${\tau }_E$ remains identifiable.

Labeled population dynamics

Finally, we collect the previous expressions into a system of linear ODEs for the dynamics of all, labeled or unlabeled, subpopulations. The vector of average labeled cell numbers is

$${\mathit{N}}^{\text{∗}}={[{\text{G}}_{1,1}^{\text{∗}}\left(t\right),\dots ,{\text{G}}_{2,n}^{\text{∗}}\left(t\right),{\text{G}}_0^{\text{∗}}\left(t\right)]}^T;$$

unlabeled cell numbers are denoted similarly by ${\mathit{N}}^{\circ }$. The two add up to the total cell numbers $\mathit{N}={\mathit{N}}^{\circ }+{\mathit{N}}^{\text{∗}}$.

We require that steady growth or steady state has been attained before labeling begins. Thus up to the label application at $t=0$, ${\mathit{N}}^{\circ }=\mathit{N}$ follows Equation 3, with a steady-growth distribution $\mathit{n}$ satisfying Equation 4. At times $t>0$, label acquisition transfers cells into the labeled populations, so that Equation 1 then still holds for $\mathit{N}$ but not for ${\mathit{N}}^{\circ }$ nor ${\mathit{N}}^{\text{∗}}$.

To describe the dynamics of the labeled population ${\mathit{N}}^{\text{∗}}$, we encode the labeling kinetics in matrix form:

$${\left(\mathbf{L}\right)}_{i,j}=\{\begin{array}{ll}\epsilon \hfill & \text{if}l<j=i\le l+m\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$

The labeling matrix $\mathbf{L}$ has the same dimensions as $\mathbf{T}$; its nonzero entries are ε on the diagonal for all subphases of $\text{S}$. It can be verified straightforwardly that $\mathbf{L}{\mathit{N}}^{\circ }$ is the flux from unlabeled to labeled compartments as shown in Figure S1B. Using this notation,

$$\frac{d}{dt}{\mathit{N}}^{\text{∗}}=\left(\mathbf{T}-\delta \right){\mathit{N}}^{\text{∗}}+\mathbf{L}{\mathit{N}}^{\circ }=\left(\mathbf{T}-\mathbf{L}-\delta \right){\mathit{N}}^{\text{∗}}+\mathbf{L}\mathit{N}$$ (Equation 6a)

$$=\left(\mathbf{T}-\mathbf{L}-\delta \right){\mathit{N}}^{\text{∗}}+N\mathbf{L}\mathit{n}.$$ (Equation 6b)

In Equation 6a, we have used the fact that already-labeled cells follow the undisturbed cycle progression ($\mathbf{T}-\delta$); in Equation 6b, we have inserted the undisturbed steady-growth expansion of the total population. Finally, we rewrite this system in terms of the dynamics of the (time-dependent, non-normalized) labeled fractions, ${\mathit{n}}^{\text{∗}}=\left[{\text{g}}_{\mathrm{1,1}}^{\text{∗}},\dots ,{\text{g}}_0^{\text{∗}}\right]={\mathit{N}}^{\text{∗}}/N$. From Equation 6b and using exponential growth of $N\left(t\right)$, we obtain

$$\frac{d}{dt}{\mathit{n}}^{\text{∗}}=\left(\mathbf{T}-\mathbf{L}-\kappa \right){\mathit{n}}^{\text{∗}}+\mathbf{L}\mathit{n}.$$ (Equation 7)

The appropriate initial condition is ${\mathit{n}}^{\text{∗}}\left(0\right)=\mathbf{0}$. The unlabeled fractions are then obtained as ${\mathit{n}}^{\circ }=\mathit{n}-{\mathit{n}}^{\text{∗}}$.

Parameter estimation

In experiment, cycle phase is assigned by DNA content. Thus, cells in ${\text{G}}_0$ or ${\text{G}}_1$ fall into a single experimental gate, $\overline{\text{G}01}$. Although most DNA-replicating cells are correctly counted in the corresponding $\overline{\text{S}}$ gate, the gating procedure inevitably assigns some cells that have started DNA replication to the $\overline{\text{G}01}$ gate, and some cells that have completed replication to the $\overline{\text{S}}$ gate rather than the $\overline{\text{G}2\text{M}}$ gate. When deriving model predictions, we account for this crosstalk by assigning the first $m_{\overline{01}}$ subphases of $\text{S}$ phase to $\overline{\text{G}01}$, and the last $m_{\overline{2}}$ subphases to $\overline{\text{G}2\text{M}}$, so that only the remaining innermost $m-m_{\overline{01}}-m_{\overline{2}}$ subphases ${\text{S}}_i$ are assigned to the gate $\overline{\text{S}}$, as shown in Equation 8.Conversely, misassignment of ${\text{G}}_0$, ${\text{G}}_1$ or ${\text{G}}_2$ cells to the $\overline{\text{S}}$ gate was not observed in our data: At the first time point after labeling, the $\overline{\text{S}}$ gate contained neglibigle amounts of unlabeled cells (Figure 1E).

In order to compute model predictions, we first solve Equation 4 for the constant steady-growth distribution $\mathit{n}$. From $\mathit{n}$ we obtain the time-independent total cell fractions in each experimental gate, e.g.

$${\overline{\text{g}2}}_{\text{pred}}=\sum _{i=m-m_{\overline{2}}+1}^m{\text{s}}_i+\sum _{i=1}^n{\text{g}}_{2,i}.$$

We then solve system Equation 7 numerically. From ${\mathit{n}}^{\text{∗}}\left(t\right)$, we obtain predictions for the time-dependent labeled fractions, e.g.

$${\overline{\text{g}01}}_{\text{pred}}^{\text{∗}}\left(t\right)={\text{g}}_0^{\text{∗}}\left(t\right)+\sum _{i=1}^l{\text{g}}_{1,i}^{\text{∗}}\left(t\right)+\sum _{i=1}^{m_{\overline{01}}}{\text{s}}_i^{\text{∗}}\left(t\right).$$

In order to then compare model predictions with experiments, we evaluate the negative log-likelihood function in a standard way, as

$${\chi }^2=\frac{1}{2}\sum _{\overline{\text{g}}=\overline{\text{g}01},\overline{\text{g}2}}\frac{{\left({\overline{\text{g}}}_{\text{pred}}-{\overline{\text{g}}}_{\text{obs}}\right)}^2}{{\sigma }_{\overline{\text{g}}}^2}+\frac{1}{2}\sum _{i=1\dots I}\sum _{{\overline{\text{g}}}^{\text{∗}}={\overline{\text{g}01}}^{\text{∗}},{\overline{\text{s}}}^{\text{∗}},{\overline{\text{g}2}}^{\text{∗}}}\frac{{\left({\overline{\text{g}}}_{\text{pred}}^{\text{∗}}\left(t_i\right)-{\overline{\text{g}}}_{\text{obs}}^{\text{∗}}\left(t_i\right)\right)}^2}{{\sigma }_{{\overline{\text{g}}}^{\text{∗}}}^2}.$$ (Equation 9)

Here, the first sum collects time independent terms; the experimental observations ${\overline{\text{g}}}_{\text{obs}}$ are averages over all time-points and experimental repeats, and the associated uncertainties ${\sigma }_{\overline{\text{g}}}$ are standard errors of these averages. Only two gates are included, since normalization fixes the third. The second (double) sum runs over the I experimental time points and is not constrained by normalization. The corresponding uncertainties are estimated as standard errors over experimental repeats of the mean labeled gate fractions; for robustness, we pool these errors and assign the same ${\sigma }_{{\overline{\text{g}}}^{\text{∗}}}$ for all time points.

Based on the log -likelihood Equation 9, we then perform Markov Chain Monte Carlo sampling to evaluate the posterior distribution over model parameters. The full set of model parameters and the allowed ranges of their uniform prior distributions are given in Table S2. As the substep numbers m and n of $\text{S}$ and ${\text{G}}_2$ phase, respectively, were only lower-bounded by this procedure, we fixed them to a value $n=m=15$, well above the lower bound. The credible intervals resulting from sampled posterior distributions for DP and TET21N are shown in Table S3.

The model assumes a cell population at steady growth, and we include the steady-state fractions directly as the first term in Equation 9. The steady-growth assumption can be checked for consistency by comparing total cycle fractions at successive time points. Only the labeled fractions are included directly in Equation 9, which implies that the residuals of the corresponding predicted unlabeled fractions $\left({\overline{\text{g}}}_{\text{pred}}^{\circ }\left(t_i\right)-{\overline{\text{g}}}_{\text{obs}}^{\circ }\left(t_i\right)\right)$ can provide another consistency check. If these residuals were to exceed the fitted residuals strongly, this would indicate a possible lack of steady growth.

Extended cell cycle model with transient arrest

We now consider an extension of the CycleFlow model where cells are allowed to arrest the cell cycle temporarily but then return into ${\text{G}}_{\mathrm{1,1}}$ (Figure S1C). We extend the transition scheme by introducing a reversible arrest phase $\text{A}$ with p subphases ${\text{A}}_1,\dots ,{\text{A}}_p$ in analogy to the other cycle phases, which replaces the irreversible entry into the quiescent state ${\text{G}}_0$. The vector of cell numbers becomes $\mathit{N}={\left[{\text{G}}_{\mathrm{1,1}}\left(t\right),\dots ,{\text{S}}_1\left(t\right),\dots ,{\text{G}}_{2,n}\left(t\right),{\text{A}}_1\left(t\right),\dots ,{\text{A}}_p\left(t\right)\right]}^{\mathsf{T}}$. The mean arrest time is $p/\pi$, where π is the transition rate between subphases of $\text{A}$. An exponential arrest time with a CV of 1 is achieved by setting $p=1$, and more controlled arrest times are achieved by higher p; high values $p>10$ resemble a fixed delay. The transition rate matrix is extended accordingly,

$$\mathbf{T}=\left[\begin{array}{llllllllllllll}-\lambda \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & 2\left(1-a\right)\nu \hfill & \hfill & \hfill & \hfill & \pi \hfill \\ \lambda \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & 0\hfill \\ \hfill & \ddots \hfill & -\lambda \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & ⋮\hfill \\ \hfill & \hfill & \lambda \hfill & -\mu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \mu \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \ddots \hfill & -\mu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \mu \hfill & -\nu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \nu \hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \ddots \hfill & -\nu \hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \nu \hfill & -\nu \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & 2a\nu \hfill & -\pi \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \pi \hfill & \ddots \hfill & \hfill & ⋮\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \ddots \hfill & -\pi \hfill & 0\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \hfill & \pi \hfill & -\pi \hfill \end{array}\right].$$

The steady state can be expressed as a function of the steady growth rate in a similar way as in the model without cycle re-entry. Equation 5a still holds unchanged in steady growth:

$$\kappa ={\mathbf{1}}^T\mathbf{T}\mathit{n}=\nu {\text{g}}_{2,n}.$$ (Equation 10a)

Indeed, the production rate of new cells $\kappa N$ still equals the population in subphase ${\text{G}}_{2,n}$ times its rate of completion ν, irrespective of return from $\text{A}$. Return from $\text{A}$ does increase growth as expected intuitively, because it leads to a higher influx back into ${\text{G}}_1$, which entails a higher population in ${\text{G}}_{2,n}$ and thereby higher growth rate κ. Again backsubstituting using Equation 4, one finds the general rule ${\phi }_{i-1}{r}_{\to i}={\phi }_i\left(r_{i\to }+\kappa \right)$. Here, ${\phi }_i$ for $2\le i\le l+m+n+p$ denotes a subphase with influx and outflux rates $r_{\to i}$ and $r_{i\to }$, respectively. Application of the rule then yields the steady state fractions

$${\text{a}}_1={\text{g}}_{2,n}\frac{2a\nu }{\kappa +\pi }=\frac{2a\kappa }{\kappa +\pi }$$ (Equation 10b)

$${\text{a}}_{1+j}={\text{a}}_1\frac{{\pi }^j}{{\left(\kappa +\pi \right)}^j}=\frac{2a\kappa {\pi }^j}{{\left(\kappa +\pi \right)}^{j+1}}0<j<p.$$ (Equation 10c)

The remaining steady state subphase fractions remain exactly as given in Equations 5c, 5d, 5e, 5f, and 5g, which shows that re-entry into the cycle affects the non-arrested cell cycle phases’ relative occupancies only through the change in the steady growth rate κ. (κ is be determined numerically, as before.)

Because $\kappa \lesssim 1/T_c$ where $T_c$ is the average cell cycle time, whereas the individual subphase transition rates $\lambda ,\mu ,\nu \sim \left(l+m+n+p\right)/T_c$, the factors $\kappa +\lambda$ etc. appearing in (Equation 5a), (Equation 5b), (Equation 5c), (Equation 5d), (Equation 5e), (Equation 5f), (Equation 5g) and (Equation 10a), (Equation 10b), (Equation 10c) are dominated by the subphase transition rates and change only slightly when κ is varied moderately. This fact explains our numerical observation that the relative subphase occupations among the cycling phases are not changed appreciably by the moderate increase in κ due to cycle re-entry.

Inference of cell cycle parameters from synthetic data including transient arrests

We performed stochastic simulations of the extended model with reentry of cells from $\text{A}$ to ${\text{G}}_1$. We chose an example population with $l=2$, $m=n=15$ cycle subphases and either $p=1$ $\text{A}$ subphase, corresponding to an exponential arrest time (with coefficient of variation (CV) 1), or $p=60$, corresponding to a nearly deterministic arrest time, with CV 0.13.

Each simulation was initalized with 10,000 EdU negative cells distributed according to steady state determined as above. We applied cell dilution with rate $\delta \equiv \kappa$ to ensure that the cell number remained constant on average. The transition rates λ, μ and ν were set to the median values inferred for the DP thymocytes; the label kinetics were given by ${\epsilon }_0=5/$h and $\tau =1$h. For each of the two cases (arrest time CV 0.13 or 1), we varied π to obtain mean arrest durations of 5h, 10h, 20h, 40h, 80h and 160h. We assigned the subphases to EdU positive and negative $\overline{\text{G}01}$, $\overline{\text{S}}$ and $\overline{\text{G}2\text{M}}$ gates with perfect gating, without misclassified S phase cells. For each set of parameters, from 6 simulation runs we computed the mean fractions and their standard errors at 3h, 5h, 8h, 12h, 14h and 18h, to reproduce the experimental data acquisition. We then carried out parameter inference using CycleFlow, i.e. without return from ${\text{G}}_0$. Here we assumed perfect gating, setting $m_{\overline{01}}=m_{\overline{2}}=0$.

Validation of steady state assumption

CycleFlow is applicable to biological systems a steady state or steady growth. This condition can be tested by measuring the total fraction of cells in each cell cycle phase over time; these must remain constant to satisfy the steady state condition.

Alternatively this condition can be tested by comparing the predicted time-dependent fraction of unlabeled cell to actual measurements not used for fitting. Figure S3 shows that for both Tet21N A and DP thymocytes B, the predicted fractions of unlabeled cells match the data, thereby confirming that the steady state condition is fulfilled.

Quantification and statistical analysis

The number of replicates (n) for each experiment and interpretation of error bars are given in the figure legends. Parameters were estimated by Markov chain Monte Carlo (MCMC) sampling from their respective posterior distributions; numerical values of parameter medians and credible intervals are listed in Table S3.

Implementation and software

The CycleFlow model was simulated using the Python programming language v.3.8.5 with the package Scipy v.0.13.0 and MCMC sampling was performed with the package Emcee v.3.02 with default settings. In accordance with the program’s documentation, a chain was deemed to have converged when the autocorrelation times for every parameters exceeded 50 times the length of the chain. Results of the MCMC sampling were then processed with Matlab R2013B (MathWorks) and R v.4.0.2 to produce graphical representations.

RNA-seq data count matrices were generated using CellRanger v3.0.1 and velocyto.py v0.17.17. The data was then analyzed with R v4.0.2 and the following R packages: DropletUtils v1.10, scater v1.18.6, scran v1.18.7, Seurat v3 and velociraptor v1.0.0.

Published: October 6, 2022

Data and code availability

• •Single-cell RNA-seq data have been deposited at GEO and are publicly available as of the date of publication. Flow Cytometry data have been deposited at FlowRepository and are publicly available as of the date of publication. The Accession numbers are listed in the key resources table.
• •All original code has been deposited at Zenodo and is publicly available as of the date of publication. the DOI is listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.