Summary
Family-based designs can eliminate confounding due to population substructure and can distinguish direct from indirect genetic effects, but these designs are underpowered due to limited sample sizes. Here, we propose KnockoffTrio, a statistical method to identify putative causal genetic variants for father-mother-child trio design built upon a recently developed knockoff framework in statistics. KnockoffTrio controls the false discovery rate (FDR) in the presence of arbitrary correlations among tests and is less conservative and thus more powerful than the conventional methods that control the family-wise error rate via Bonferroni correction. Furthermore, KnockoffTrio is not restricted to family-based association tests and can be used in conjunction with more powerful, potentially nonlinear models to improve the power of standard family-based tests. We show, using empirical simulations, that KnockoffTrio can prioritize causal variants over associations due to linkage disequilibrium and can provide protection against confounding due to population stratification. In applications to 14,200 trios from three study cohorts for autism spectrum disorders (ASDs), including AGP, SPARK, and SSC, we show that KnockoffTrio can identify multiple significant associations that are missed by conventional tests applied to the same data. In particular, we replicate known ASD association signals with variants in several genes such as MACROD2, NRXN1, PRKAR1B, CADM2, PCDH9, and DOCK4 and identify additional associations with variants in other genes including ARHGEF10, SLC28A1, ZNF589, and HINT1 at FDR .
Keywords: GWAS, family-based design, knockoff framework, causal variant identification
We introduce KnockoffTrio, a statistical method to identify putative causal genetic variants for the father-mother-child trio design built upon a recently developed knockoff framework. KnockoffTrio controls the false discovery rate, protects against confounding due to population stratification, and is more powerful than conventional methods that control the family-wise error rate.
Introduction
The father-mother-child trio design is a popular family-based design, especially for early-onset diseases. One important example is autism spectrum disorders (ASDs), where several prominent studies have successfully employed such a design.1, 2, 3 The main advantages of the family-based design are that it is robust to external confounders such as population structure4,5 and can help distinguish between direct and indirect effects.6 Although popular methods have been proposed to account for confounding effects of population structure in the context of population-based designs,7, 8, 9 a more reliable approach to eliminating such confounders is to use randomized experiments, and family-based designs provide an analogy to such experiments because of the randomness in transmission of genetic material from parents to offspring.10 However, a main limitation of genome-wide association studies (GWASs) with family-based designs is the modest sample sizes, which ultimately leads to reduced power.
Most of the existing studies have focused on controlling the family-wise error rate (FWER) to account for multiple testing in genome-wide association studies. Given the polygenic nature of many complex traits, with a large number of small-effect loci accounting for most of the trait heritability, a more meaningful and powerful strategy is to control the false-discovery rate (FDR) that quantifies the expected proportion of false discoveries. Control of FDR has been previously suggested in genome-wide association studies11,12 and has been successfully employed in genetic association studies of ASD.13,14 Valid control of FDR is, however, difficult to achieve using the standard Benjamini-Hochberg (BH) procedure due to possible complex correlations among genetic variants. The knockoff-based framework we employ here allows valid FDR control under arbitrary correlations.
The idea of the knockoff-based inference is to construct knockoff copies of the original features (genotypes) that preserve the correlation structure and are independent of the trait conditional on the original features.15 These knockoff features serve as negative controls and, when compared with the original features, help identify the truly causal ones. The knockoff-based inference provides rigorous control of FDR under arbitrary correlation structure and is thus more versatile than the BH procedure that requires independence or positive dependence16 for the FDR control. Several knockoff procedures have been proposed with applications to population-based designs, including KnockoffZoom17 for genome-wide association studies based on hidden Markov models and KnockoffScreen18 for whole-genome sequencing data based on the sequential conditional independent tuples (SCIT) algorithm. These methods, however, were designed for independent individuals in population-based studies, making them unsuitable for family-based studies as considered in this article. Likewise, KnockoffGWAS19 is a population-based knockoff procedure adjusting for possible relatedness among individuals in the study and is not based on a within-family test as proposed here. A related approach to construct synthetic offspring has been proposed before in order to perform causal inference with trio designs.10 Specifically, Bates et al. proposed a digital twin test based on the conditional randomization test,15 a method related to the knockoff but that can produce valid empirical p values. Computational cost is a concern for this test, especially in high-dimensional genome-wide settings where a large number of random drawings are needed to get small empirical p values.
In this paper we propose KnockoffTrio, a knockoff-based framework for the analysis of trio data in genome-wide association studies. Conventional association tests for family-based designs include the family-based association test (FBAT),5 a generalization of the transmission disequilibrium test (TDT)20 to handle various practical complexities such as missing parental data, covariate adjustment, and different types of phenotypes. Methods based on kernel machine regression under a generalized linear mixed model framework have also been proposed for family-based designs21,22 and for population-based designs adjusting for population structure and relatedness.8 Compared to these conventional testing strategies, KnockoffTrio enjoys several advantages of the general knockoff-based inference, such as higher statistical power, prioritization of causal variants over associations due to linkage disequilibrium, and robustness in controlling false positives in the presence of linkage disequilibrium between causal and non-causal variants,17,18 while providing protection against external confounders such as population stratification. Furthermore, KnockoffTrio can leverage more general machine learning models while increasing power and maintaining proper FDR control regardless of the validity of the assumed model.
Material and methods
Knockoff generation for trio design
We assume a study with n trios and p genetic variants. We denote the matrix of trio genotypes by . Our goal is to test the conditional null hypothesis
where Y are the phenotypes and is a continuous block. That is, variant(s) in group g (e.g., a gene or a region) are null if Y is independent of given variants outside g.
We describe a knockoff generation method for the trio design to capture sample relatedness and test the above hypothesis. Our method assumes knowledge of haplotype phase; most phasing algorithms are able to provide highly accurate estimates of haplotypes when applied to trio datasets.23 We first generate knockoff haplotypes for the parents, and then, conditional on them, we generate the knockoff haplotypes for the offspring. We describe the algorithm as follows:
Algorithm 1: Generation of knockoff trios
-
1.
Sample one haplotype from each father into a group; assign the remaining haplotypes to the second group.
-
2.
Repeat step 1 for mothers and obtain two additional groups of haplotypes.
-
3.
Apply the SCIP algorithm18 to each group of haplotypes and obtain the corresponding knockoffs (see below).
-
4.
Generate knockoff offspring haplotypes conditional on the knockoff parental haplotypes (see below).
Note that in steps 1 and 2, we assign an individual’s two haplotypes to two separate groups when generating their knockoffs so that the permutation-based SCIP algorithm below does not use the residual from one haplotype to generate the other haplotype’s knockoff. This is done to increase the contrast between the original and knockoff genotypes in an individual and, hence, to improve power.
SCIP algorithm to generate knockoff parental haplotypes
We adopt the residual permutation method proposed in KnockoffScreen18 to generate knockoff haplotypes for the parents. The residual permutation method is based on the general sequential conditional independent pairs (SCIP) algorithm15, defined as follows:
Algorithm 2: SCIP algorithm for knockoff haplotype generation
j = 1
while do
Sample independently from
end while
where and denote the original and knockoff parental haplotypes for the jth variant, respectively, and denotes the subset of variants in a neighborhood of the jth variant (±100 kb from the variant). Algorithm 2 has been shown to generate knockoffs that preserve the exchangeability conditions between the original and the knockoff genotypes necessary for controlling the FDR.18 In the context of genetic data, the exchangeability implies the invariance in the linkage disequilibrium structure when one swaps a subset S of genetic variants with their knockoffs, i.e., , in which is obtained from by swapping and , .
As in He et al.,18 we consider a semiparametric model for in KnockoffTrio:
where is a random error term with a mean of zero. We obtain , , fitted values , and residuals by minimizing the mean squared loss. We then obtain permuted residuals and define the parental knockoffs +.
Generating knockoff offspring haplotypes
Conditional on the knockoff parental haplotypes generated as above, we then proceed to generate the knockoff offspring haplotypes. Given the phased haplotypes of the original trio for a region, we first infer which parental haplotypes were transmitted to the offspring by matching parental haplotypes with offspring haplotypes. We assume that no recombination occurs in the transmission of haplotypes from parents to offspring in any small region. We then use the knockoff haplotypes that correspond to the transmitted haplotypes in the original trio as the offspring’s knockoff haplotypes.
Missing parental data
It is possible to accommodate missing parental data, i.e., one parent in a trio is completely missing. In such cases, one can still generate knockoff versions of such incomplete trios: the haplotype transmitted by the missing parent remains the same, while the other haplotype is obtained based on the knockoff haplotypes for the available parent. Because the FBAT test in the importance score can deal with missing parental data by design, the same feature importance score described below can be calculated.
Exchangeability property
As with independent samples, we need certain exchangeability properties to hold for the trio design in order for the FDR control to hold.15 We formally prove the exchangeability property and FDR control for the trio design in supplemental note 1.
Multiple knockoffs to improve power and stability
The knockoff generation algorithm described above generates one single knockoff haplotype for each original haplotype. However, the inference based on a single knockoff often has limited power due to the detection threshold of , i.e., the number of independent signals required for making any discoveries at the target FDR q. In particular, there is no power at the target FDR q if there are fewer than discoveries to be made, which is not uncommon when q is low and the signal is sparse. Moreover, the randomness in the sampling of a single knockoff makes the results unstable particularly for weak causal effects. Therefore, to further improve the stability and power at low target FDR, we extend the above single-knockoff algorithm to generating multiple knockoffs. For M knockoffs, the detection threshold decreases from to , making it more powerful to detect sparse signals even when the target FDR level q is low. Furthermore, multiple knockoffs help improve the stability and reproducibility of the results.
Algorithm 3: SCIT algorithm for multiple knockoffs
j = 1
while do
Sample independently from
end while
The semiparametric model for in the multiple-knockoff setting is:
where is a random error term with a mean of zero. We obtain , , fitted values , and the residuals and their permutations . We then define the mth knockoff = +.
KnockoffTrio: A knockoff framework for trio design
We describe here a knockoff-based test using a FBAT to compute the importance scores. Note that the use of FBAT to calculate feature importance statistics in KnockoffTrio helps protect against external confounders such as population stratification (see also supplemental note 1).
KnockoffTrio-FBAT
Once the knockoff generation for the father-mother-child trio data is completed, KnockoffTrio-FBAT performs a genome-wide scanning procedure with a window in both the original and the knockoff data. We consider several candidate window sizes (e.g., in our applications 1 bp and 1, 5, 10, 20, and 50 kb) for , with half of each window overlapping with neighboring windows of the same size. We employ the weighted burden FBAT,24 which is a generalization of the SNP-based FBAT for a set of variants. Let n denote the number of trios and p denote the number of variants in a window. When , the weighted burden FBAT is equivalent to the SNP-based FBAT. The weighted burden FBAT statistic for trio design is computed as:
in which is a weight associated with the jth variant, is a dichotomous or quantitative trait for the offspring in the ith trio, u is an offset parameter, is the offspring genotype, and are the parental genotypes, and is the expected value of the offspring genotype conditional on parental genotypes. Typically, for dichotomous traits and for quantitative traits. The choice of is flexible and can reflect any prior functional information on the variant; in this study we consider , in which n is the number of trios and is the minor allele frequency (MAF) for the jth variant. We can further obtain the variance of as
Therefore, the standardized test statistic approximately follows a standard normal distribution in large samples under the null hypothesis of no association between any of the p variants and the trait.
Aggregated Cauchy association test to compute importance scores
For a given window we compute an importance score as follows:
-
•
For a 1 bp window, KnockoffTrio-FBAT implements SNP-based FBAT for variants with a MAF and obtain and (for the mth knockoff).
-
•For a 1, 5, 10, 20, or 50 kb window, KnockoffTrio-FBAT implements:
-
1.Weighted burden FBAT for variants with MAF 0.01.
-
2.SNP-based FBAT for variants with MAF 0.01.
-
3.The aggregated Cauchy association test (ACAT)25 to combine the p values in steps 1 and 2 and obtain and .
-
1.
KnockoffTrio-X
The application of KnockoffTrio is not restricted to the FBAT test. Alternatively, p values can be obtained from different, more sophisticated methods that can help increase power in complex scenarios, e.g., the error terms for quantitative traits are not normally distributed. As a proof of concept, we investigate in simulations KnockoffTrio-iQRAT, in which we replace FBAT with the integrated quantile rank test (iQRAT), a gene-level association test that integrates quantile rank score process to accommodate more complex, non-linear associations.26 iQRAT considers a quantile model for quantitative trait Y:
where is the quantile level, is the quantile coefficient functions, is the intercept function, and is the adjusted offspring genotype where we subtract the conditional expectation (conditional on parental genotypes) so that it corresponds to FBAT formulation. iQRAT tests the null hypothesis . The iQRAT statistics that generalize the sequence kernel association tests (S) and burden tests (B) are computed, respectively, as:
where , , , is the weight function, is the estimated intercept via quantile regression under the null, and is the weight matrix. iQRAT considers four different weight functions and combines the results using ACAT. We use , the burden version of iQRAT, in KnockoffTrio-iQRAT so that it is comparable to the burden FBAT in KnockoffTrio-FBAT.
Knockoff filter procedure for FDR control
For each given window , KnockoffTrio calculates a feature statistic, defined as
| (Equation 1) |
in which and where and are the p values computed above for the original and the knockoff trios, respectively. KnockoffTrio then calculates a threshold τ and selects windows with while controlling the FDR at a target level q. The corresponding value of τ is computed as (see also KnockoffScreen18):
| (Equation 2) |
where is the largest importance score minus the median of the remaining importance scores, when is the largest importance score, and when for the mth knockoff is the largest importance score.
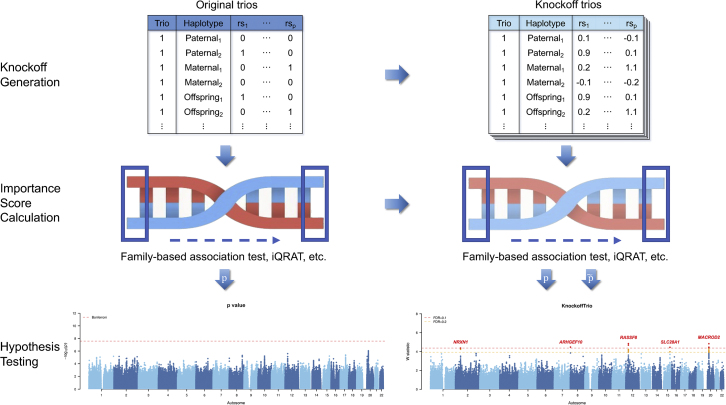
We show a schematic flowchart for KnockoffTrio in Figure 1.
Figure 1.
KnockoffTrio workflow
Knockoff generation based on original trios, calculation of importance scores using sliding windows, and examples of hypothesis testing using conventional association testing and KnockoffTrio.
Calculation of q values
We also calculate a q value for , which is the p value analogue in the FDR setting and unifies and τ for declaring significance. Specifically, the q value is the minimum FDR when all tests that show evidence against the null hypothesis at least as strong as the current test are declared as significant. Under the knockoff framework, we follow KnockoffScreen and define the q value for window ϕ as
where is the estimated FDR if we declare significant windows with feature statistics . We define for windows with so that they will not be selected. By definition, the windows selected by are equivalent to those selected by , where q is the target FDR.
Meta-analysis for KnockoffTrio
For a variant or set of variants, meta-analysis can be performed by integrating summary statistics from individual studies into a combined summary statistic. KnockoffTrio can be naturally extended to the meta-analysis setting because KnockoffTrio’s feature statistics are defined based on summary statistics for the original and the knockoff cohorts. Here, we implement the sample-size-based meta-analysis27 into KnockoffTrio. Specifically, KnockoffTrio’s meta-analysis procedure is defined as follows:
-
1.
For the ith study, obtain for a window in the original cohort and for the same window in the mth knockoff cohort; and are the standardized SNP-based FBAT statistics for a single-variant window or the set-based FBAT statistics for a multi-variant window.
-
2.
Calculate for the original cohort and for the mth knockoff cohort, in which is the weight and is the sample size (i.e., the number of trios) for the ith study.
-
3.
Calculate for the original cohort and for the mth knockoff cohort.
-
4.
Calculate and using Equations 1 and 2.
Results
Simulation studies
We simulate genetic data based on the Autism Genome Project (AGP) cohort. The AGP cohort consists of 798,961 common (MAF 0.05) and low-frequency (0.01 MAF 0.05) variants for 1,266 trio families of European ancestry. For a simulation replicate, we simulate 10,000 trios with common and low-frequency variants sampled from a 1-Mb region (chr20: 15,981,843–16,981,842; 495 variants with MAF 0.01) near MACROD2. In line with previous studies,18,28 we applied hierarchical clustering such that variants from different clusters have correlation no greater than 0.7 and then randomly selected one representative variant from each cluster to be included in the replicate. For a trio, we sampled four haplotypes from the phased AGP data for the parents and simulated the genotypes for the offspring using two of the four haplotypes, each randomly selected from a parent.
KnockoffTrio preserves exchangeability in trio studies
The rationale of the proposed algorithm is to augment the original trios with synthetic trios. The knockoff construction proposed here ensures the exchangeability property between the original and synthetic genotypes: i.e., if we swap any subset of variants with their synthetic counterparts, the joint haplotype distribution for the trio remains the same (see formal proof in supplemental note 1). This exchangeability property is a necessary condition for the FDR control. We verify the exchangeability for the offspring haplotypes using simulations. We generated a replicate of 10,000 trios with variants sampled from a 1-Mb region as described above. To validate the exchangeability, we generated the offspring knockoff haplotypes using the proposed algorithm in KnockoffTrio and evaluated whether the covariance between each pair of variants is exchangeable for the common variants in the region. As shown in Figure S1, the exchangeability property holds in simulations.
Empirical power and FDR in single-locus simulations
We performed simulations to evaluate the power and empirical FDR of KnockoffTrio. We simulated 500 replicates as described above. We generated the dichotomous trait for the offspring using a logit model:
and the quantitative trait using a linear model:
where , was set such that the disease prevalence is 1% and . We randomly selected three variants within a 1-kb signal window to be causal with the causal effect . For dichotomous traits, we include a trio only when to mimic the usual ascertainment in real trio design studies with dichotomous traits.
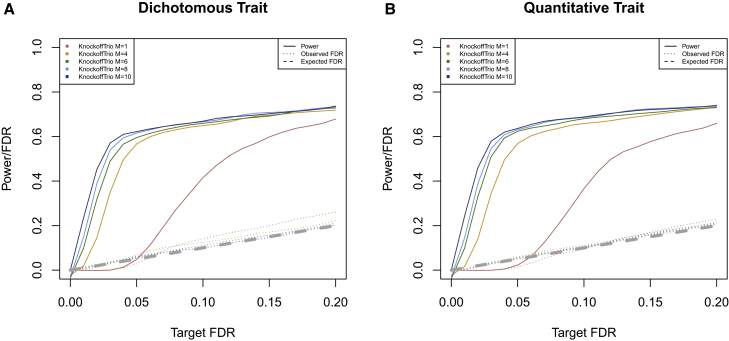
For each replicate, we generated multiple knockoffs (M = 1, 4, 6, 8, and 10) and used several window sizes to scan the region (1 bp and 1, 5, 10, 20, and 50 kb). We evaluated the performance of KnockoffTrio in terms of different numbers of knockoffs for both dichotomous and quantitative traits. For each replicate, the power is the proportion of detected causal windows (i.e., windows that contain at least one causal variant) among all causal windows, and the FDR is the proportion of non-causal windows among all detected windows. The power and FDR were averaged over the 500 replicates. As shown in Figure 2, KnockoffTrio with multiple knockoffs controls the FDR at the target level in all scenarios considered. A slightly inflated FDR for a single knockoff is observed especially for dichotomous traits, which is consistent with previous literature showing inflated FDR for dichotomous traits under highly correlated designs;15 see supplemental note 7 and Figure S7 for simulations where a single knockoff has no inflated FDR with lowered linkage disequilibrium. The power of KnockoffTrio increases when the number of knockoffs increases, especially at low target FDR levels as expected due to the detection threshold issue mentioned in the material and methods section.
Figure 2.
KnockoffTrio’s power and FDR in single-locus simulations
(A and B) The two panels show the power and FDR for dichotomous and quantitative traits. We evaluate KnockoffTrio’s power and FDR with a target FDR ranging from 0 to 0.2 and with different numbers of knockoffs. The solid lines indicate KnockoffTrio’s power, and the dotted lines indicate KnockoffTrio’s observed FDR. The different colors indicate different numbers of knockoffs. The gray dashed line indicates the expected FDR.
KnockoffTrio prioritizes causal variants over false-positive associations due to linkage disequilibrium
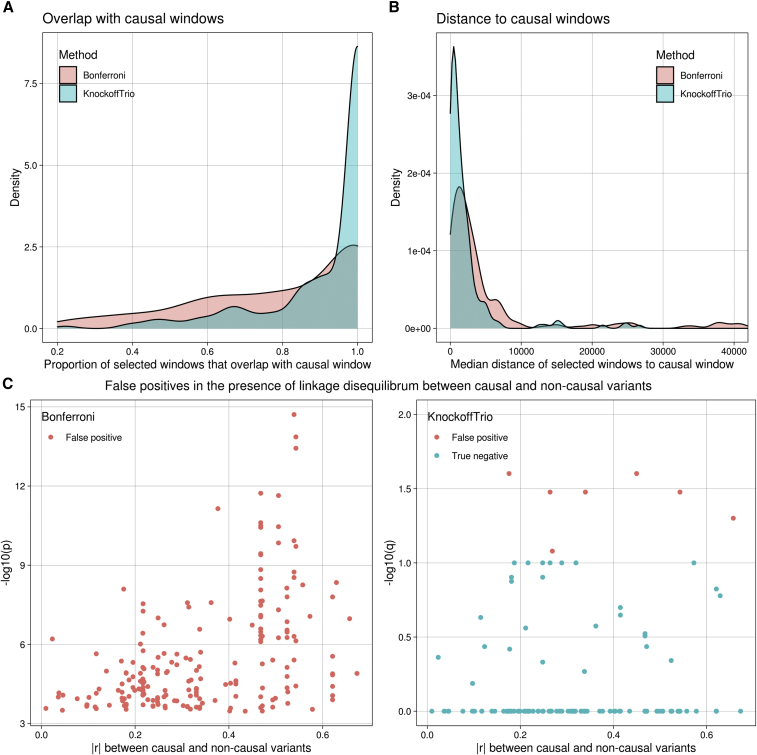
Based on the single-locus simulations, we further compared KnockoffTrio with the conventional association test that controls the FWER in terms of (1) the proportion of selected windows that overlap with the 1-kb signal window and (2) the median distance of selected windows to the 1-kb signal window. The distance was calculated as the absolute value of the difference between the middle point of a selected window and that of the signal window. For the conventional association test, we used the same aggregated Cauchy association test implemented in KnockoffTrio for each window and controlled the FWER using the Bonferroni correction. As shown in Figures 3A and 3B, the windows selected by KnockoffTrio have a substantially higher chance of overlapping with the signal window and a shorter distance to the signal window than the conventional method. We also randomly selected 200 false positives identified by the conventional association test with Bonferroni correction from all simulated replicates and showed the relationship between their significance and the maximum correlation with any causal variants in the left panel of Figure 3C. As the correlation increases, the conventional association test yields more significant p values for the false positives. On the other hand, for these same 200 variants, KnockoffTrio has a much higher chance of correctly identifying these non-causal variants as true negatives as shown in the right panel of Figure 3C, and thus is substantially more robust in controlling false positives in the presence of linkage disequilibrium between causal and non-causal variants.
Figure 3.
KnockoffTrio prioritizes causal variants over associations due to linkage disequilibrium
(A–C) Comparisons between KnockoffTrio and the conventional method in terms of (A) the proportion of selected windows that overlap with the signal window, (B) the median distance of selected windows to the signal window, and (C) the robustness in controlling false positives in the presence of linkage disequilibrium between causal and non-causal variants. The conventional method is the same aggregated Cauchy association test implemented in KnockoffTrio and controls the FWER using the Bonferroni correction. For KnockoffTrio, the target FDR is 0.1, and the number of multiple knockoffs is 10. The distance in (B) was calculated as the absolute value of the difference between the middle point of a selected window and that of the signal window. The in (C) is the maximum absolute correlation between the false positive and any causal variants. The variants in the right figure in (C) correspond to the variants in the left figure.
Empirical power and FDR in multi-locus simulations in the presence of noise loci
We additionally conducted multi-locus simulations to compare KnockoffTrio with conventional FDR and FWER control methods in the presence of multiple causal and non-causal (noise) loci. We adopted the same simulation method in single-locus simulations to randomly generate 100 1-Mb causal loci and 2,000 200-kb non-causal loci. A causal locus contains a 1-kb signal window, in which three variants were randomly selected to be causal.
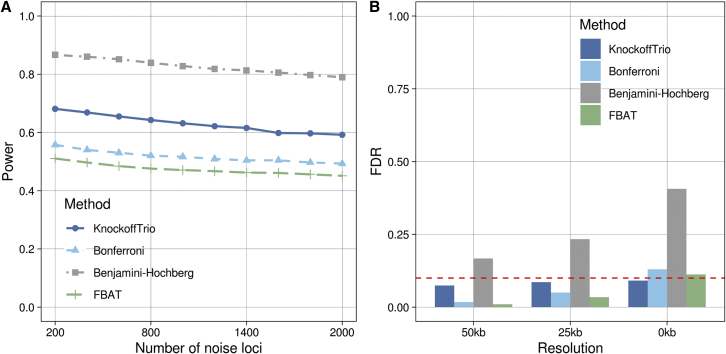
We compared KnockoffTrio with M = 10 to the Bonferroni correction that controls the FWER and the BH procedure that controls the FDR. Both the Bonferroni correction and the BH procedure were applied to the ACAT-combined p values used to compute importance scores in KnockoffTrio. We also applied the Bonferroni correction to the weighted burden FBAT, a commonly used test in family-based studies. A method’s power is the proportion of detected causal windows (i.e., windows that contain at least one causal variant) among all causal windows. We evaluated power at a target FDR of 0.1 for FDR-control methods or a target FWER of 0.05 for FWER-control methods. The empirical FDR is defined as the proportion of non-causal windows at least 50/25/0 kb away from the nearest signal windows among all detected windows. As shown in Figure 4, KnockoffTrio was more powerful than the Bonferroni correction, as expected given the more liberal FDR control, while preserving the FDR at the target level of 0.1. The BH procedure failed to control the FDR at the target level due to the complex correlations among genetic variants. We also note that the FDR for each method decreased as the distance to the signal windows increased. This is expected because the non-causal windows closer to the signal windows are more likely to be false positives due to stronger linkage disequilibrium with variants in the signal windows. Such decrease in FDR is particularly evident for the BH procedure, which is more affected by the correlation among tests.
Figure 4.
Genome-wide power and FDR in the presence of noise loci
The left panel presents each method’s power (target FDR 0.1), defined as the proportion of detected causal windows among all causal windows. A causal window is a window that contains any causal variants. The right panel presents each method’s false discovery rate (target FDR 0.1) at different resolutions, defined as the proportion of non-causal windows at least 50/25/0 kb away from the nearest signal windows among all detected windows. Note that KnockoffTrio and Benjamini-Hochberg have more liberal FDR control than Bonferroni and FBAT.
KnockoffTrio-iQRAT improves power in detecting complex associations
We performed simulations to compare the power of KnockoffTrio-iQRAT with KnockoffTrio-FBAT in complex scenarios where the normality of quantitative traits is violated. Specifically, we generated quantitative trait values using a location model:
where Cauchy( 0, 1), μ is the location parameter, and γ is the scale parameter for the Cauchy distribution. We generated 500 replicates, each of which consists of 1,000 trios and 500 variants near MACROD2, using the AGP cohort as above. We randomly selected three variants within a 1-kb window to be causal with the causal effect . We applied quantile and rank normalization to s before analysis. For KnockoffTrio-iQRAT, to make fair comparisons with FBAT, we only analyzed the offspring data, and we adjusted the offspring genotypes by subtracting the conditional expectation (conditional on parental genotypes), i.e., . As shown in Figure S5, KnockoffTrio-iQRAT is more powerful than KnockoffTrio-FBAT in the scenario with non-Gaussian errors as expected.
KnockoffTrio provides protection against external confounders such as population stratification
Population stratification is one of the most common confounders in genetic association studies and is often a source of spurious associations when a study cohort has individuals from different populations. We demonstrate KnockoffTrio’s robustness in controlling FDR in the presence of population stratification through simulations (see also discussion in supplemental note 1). For a replicate, we simulated 10,000 trios with 500 common and low-frequency variants randomly selected from a 1-Mb region (chr20: 15,981,843–16,981,842) near MACROD2 using the 1000 Genomes Phase III sequencing data,29 where haplotype data are available on 2,504 samples across 26 (sub)populations. For these analyses, we focus on 1,006 haplotypes of European origin and 1,096 haplotypes of African origin. In line with previous simulations, we applied hierarchical clustering such that variants from different clusters have correlation no greater than 0.7 and then randomly selected one representative variant from each cluster to be included in the replicate. For 70% of the trios, we sampled four haplotypes from the European population to obtain the parental data in a trio and simulated the offspring genotypes using two of the four haplotypes, each randomly selected from a parent. For the remaining 30% of the trios, we did the same except that we sampled parental haplotypes from the African population. We then generated a quantitative trait using a linear model:
where , if the ith trio is from the European population, and if the ith trio is from the African population. For dichotomous traits, we set to mimic the usual ascertainment in trio design studies with dichotomous traits.
We evaluated each method’s FDR, defined as the proportion of replicates where any window was detected among 500 replicates. As shown in Figure S2, both KnockoffTrio and the conventional family-based methods control the FDR in the presence of population stratification at a target FDR of 0.1 for both dichotomous and quantitative traits.
Applications to trio data on ASDs
To study the risk genetic variants for ASD, we applied KnockoffTrio with multiple knockoffs (M = 10) to several ASD cohorts, including the family trio data from the AGP (dbGaP: phs000267.v5.p2)30 and two cohorts collected by the Simons Foundation Autism Research Initiative (SFARI): the Simons Foundation Powering Autism Research (SPARK)31 and the Simons Simplex Collection (SSC).32 The details of the individual cohorts are described below. We have complied with the data-use agreements for each specific site. For comparisons, we also present results from the digital twin test and KnockoffGWAS (supplemental notes 4 and 5 and Tables S1 and S2).
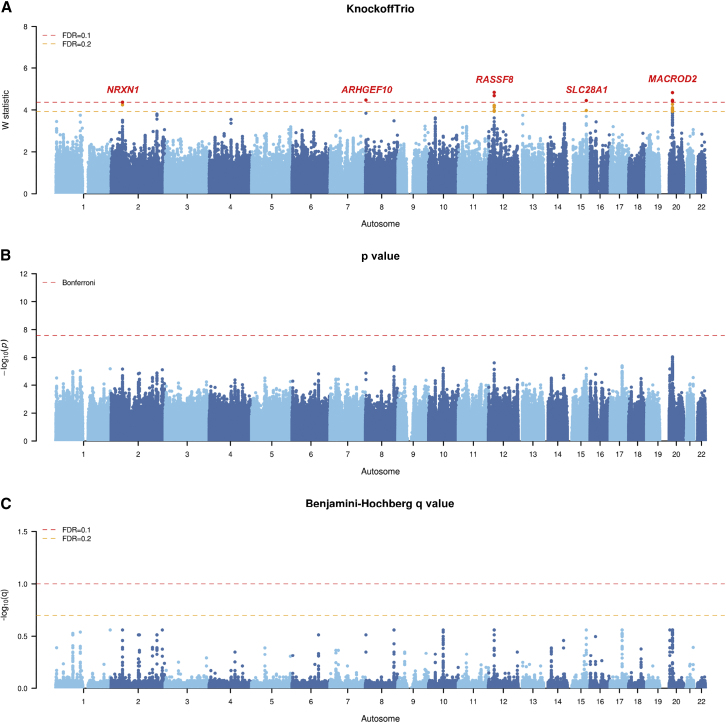
Figure 5.
Manhattan plots from KnockoffTrio analysis for the Autism Genome Project (AGP)
The Manhattan plots of the W statistics from KnockoffTrio, the p values from the conventional association tests with the Bonferroni correction for controlling the FWER, and the q values from the BH procedure for controlling the FDR. The FDR target level for KnockoffTrio and the BH procedure is 0.1 or 0.2. Each locus is annotated with the closest gene name.
Data descriptions
AGP
Our AGP analysis included 798,961 common (MAF 0.05) and low-frequency (0.01 MAF 0.05) variants for 1,266 trio families of European ancestry, each of which consists of two parents and their offspring diagnosed with strict ASD, i.e., met the criteria for autism on both the Autism Diagnostic Interview-Revised33 and the Autism Diagnostic Observation Schedule.34
SPARK
Our SPARK analysis included 10,540 trio families from the first three releases of the SPARK cohort. The probands in the two SFARI cohorts received a professional diagnosis of ASD from a physician, psychologist, or therapist. We have focused on 381,063 common and low-frequency variants.
SSC
Our SSC analysis included 2,394 trio families from the pilot and phases 1, 2, 3-1, and 3-2 studies of the SSC cohort, with whole-genome sequencing data available. We have focused on 5,772,421 common and low-frequency variants.
KnockoffTrio analyses
We adopted a quality control (QC) procedure that excluded variants with MAFs , missing call rates , Mendelian error rates , and Hardy-Weinberg equilibrium p values for all cohorts. For each cohort, we performed the QC procedure using all available individuals and then broke families into all possible trios (if they were not already trios) for analyses. Genotype data were phased using SHAPEIT2.35 The genomic coordinates in the AGP data were converted from hg18 to hg38 using the NCBI Genome Remapping Service. We adjusted for gender of offspring in all analyses. We present results from individual cohorts at a target FDR of 0.1 and 0.2 and compared them to the conventional association test with the Bonferroni correction and with the usual BH procedure for FDR control (Figures 5, 6, and 7 and Table 1). We also present results from meta-analyses of the three cohorts (Figure S11).
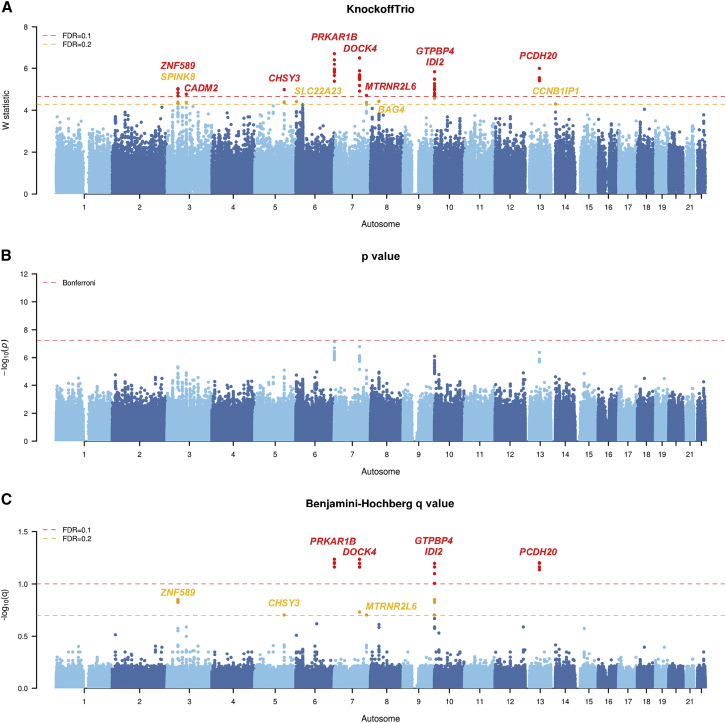
Figure 6.
Manhattan plots from KnockoffTrio analysis for the Simons Foundation Powering Autism Research (SPARK)
The Manhattan plots of the W statistics from KnockoffTrio, the p values from the conventional association tests with the Bonferroni correction for controlling the FWER, and the q values from the BH procedure for controlling the FDR. The FDR target level for KnockoffTrio and the BH procedure is 0.1 or 0.2. Each locus is annotated with the closest gene name.
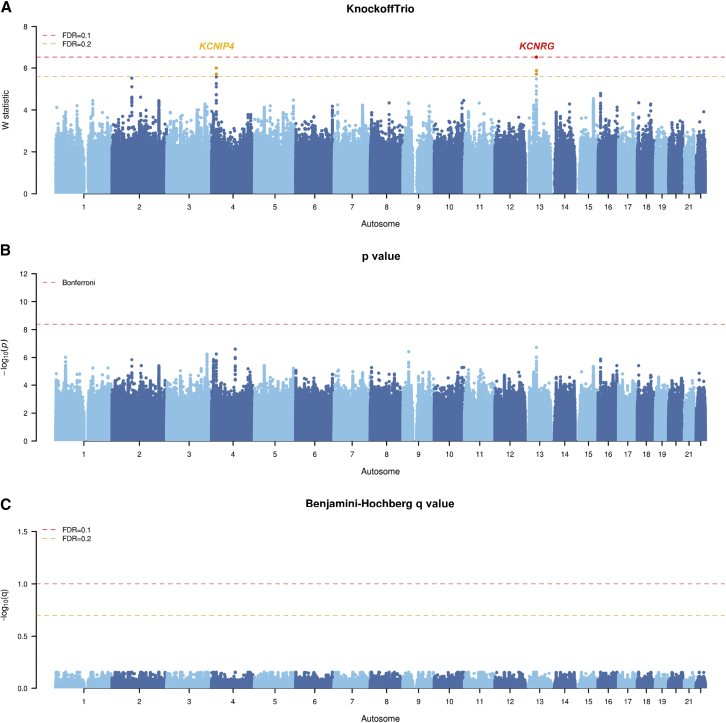
Figure 7.
Manhattan plots from KnockoffTrio analysis for the Simons Simplex Collection (SSC)
The Manhattan plots of the W statistics from KnockoffTrio, the p values from the conventional association tests with the Bonferroni correction for controlling the FWER, and the q values from the BH procedure for controlling the FDR. The FDR target level for KnockoffTrio and the BH procedure is 0.1 or 0.2. Each locus is annotated with the closest gene name.
Table 1.
Genome-wide significant loci from KnockoffTrio analysis
| Gene | Chr | Position | Variant | Allele | MAF | p | Z | W | q | BH q |
|---|---|---|---|---|---|---|---|---|---|---|
| AGP (FDR = 0.1) | ||||||||||
| NRXN1 | 2 | 50805721 | rs9284756 | A | 0.03 | 7.10E−6 | 4.49 | 4.37 | 0.10 | 0.28 |
| ARHGEF10 | 8 | 1920247–1920676 | rs17756915-rs11136442 | – | 0.41 | 1.38E−5 | – | 4.47 | 0.10 | 0.31 |
| LMNTD1-RASSF8 | 12 | 25946268 | rs4963941 | A | 0.10 | 2.56E−6 | 4.70 | 4.84 | 0.10 | 0.28 |
| ALPK3-SLC28A1 | 15 | 84881866 | rs12917429 | T | 0.21 | 6.19E−6 | −4.52 | 4.45 | 0.10 | 0.28 |
| MACROD2 | 20 | 14781064 | rs6074798 | A | 0.49 | 1.02E−6 | 4.89 | 4.83 | 0.10 | 0.28 |
| SFARI: SPARK (FDR = 0.1) | ||||||||||
| ZNF589 | 3 | 48262179 | rs11709691 | G | 0.28 | 4.87E−6 | −4.57 | 5.03 | 0.06 | 0.14 |
| CADM2 | 3 | 85395534–85410981 | rs75005531-rs1549979 | – | 0.22 | 1.30E−5 | – | 4.76 | 0.09 | 0.26 |
| CHSY3-HINT1 | 5 | 130661503 | rs17714209 | C | 0.28 | 8.25E−6 | 4.46 | 4.99 | 0.06 | 0.20 |
| PDGFA-PRKAR1B | 7 | 536383 | rs62431385 | C | 0.10 | 7.20E−8 | −5.39 | 6.71 | 0.02 | 0.06 |
| DOCK4 | 7 | 111986531 | rs73210911 | A | 0.12 | 1.59E−7 | −5.24 | 6.51 | 0.02 | 0.06 |
| MTRNR2L6-PRSS1 | 7 | 142688332 | rs13223009 | C | 0.02 | 8.42E−6 | −4.45 | 4.71 | 0.09 | 0.20 |
| LARP4B-GTPBP4 | 10 | 975370 | rs117732138 | A | 0.02 | 1.60E−6 | 4.80 | 5.48 | 0.02 | 0.07 |
| IDI2 | 10 | 1020654 | rs77782977 | C | 0.02 | 7.95E−7 | 4.94 | 5.84 | 0.02 | 0.06 |
| PCDH20-PCDH9 | 13 | 63204555 | rs12184522 | T | 0.23 | 4.21E−7 | 5.06 | 6.00 | 0.02 | 0.06 |
| SFARI: SPARK (FDR = 0.2) | ||||||||||
| SPINK8 | 3 | 48316110–48329279 | rs74735576-rs13090538 | – | 0.17 | 1.58E−5 | – | 4.39 | 0.17 | 0.28 |
| SLC22A23/PSMG4 | 6 | 3285062 | rs41301847 | G | 0.02 | 1.85E−5 | 4.28 | 4.41 | 0.17 | 0.31 |
| BAG4 | 8 | 38205717 | rs7836805 | A | 0.24 | 2.83E−5 | −4.19 | 4.43 | 0.17 | 0.40 |
| CCNB1IP1-PARP2 | 14 | 20334133 | rs72671266 | T | 0.02 | 2.45E−5 | −4.22 | 4.30 | 0.19 | 0.38 |
| SFARI: SSC (FDR = 0.1) | ||||||||||
| KCNRG-DLEU7 | 13 | 50197099 | rs2703087 | A | 0.04 | 1.88E−7 | 5.21 | 6.54 | 0.10 | 0.70 |
| SFARI: SSC (FDR = 0.2) | ||||||||||
| KCNIP4 | 4 | 20917151 | rs185413018 | T | 0.02 | 5.59E−7 | 5.00 | 6.00 | 0.13 | 0.70 |
Only the top signal is shown if multiple signals were identified for a locus. Gene: A single gene name indicates the signal is within or overlaps with the gene. “Gene1/Gene2” indicates the signal overlaps with two genes. “Gene1-Gene2” indicates the signal is between two genes. MAF: minor allele frequency of a variant, or average minor allele frequency if a signal contains multiple variants. p: KnockoffTrio’s ACAT-combined p values. For single variants, ACAT-combined p values are equivalent to FBAT p values. Z: FBAT Z scores for single variants. W: KnockoffTrio’s feature statistics. q: KnockoffTrio’s q values. BH q: Benjamini-Hochberg q values.
For the AGP cohort, the conventional association tests (Bonferroni and BH) did not identify any significant association, whereas KnockoffTrio identified five significant regions, including neurexin 1 (NRXN1), rho guanine nucleotide exchange factor 10 (ARHGEF10), lamin tail domain containing 1 (LMNTD1) - ras association domain family member 8 (RASSF8), alpha kinase 3 (ALPK3) - solute carrier family 28 member 1 (SLC28A1), and mono-ADP ribosylhydrolase 2 (MACROD2) at FDR = 0.1 (Figure 5). Among them, MACROD2 and NRXN1 have been reported in previous studies as risk genes associated with ASD.36, 37, 38, 39 ARHGEF10 has been associated with impaired social interaction in mice,40 one of the main features of ASD. SLC28A1 has a brain-biased expression and shows an excess of introgressed segments in European and East Asian populations.41 SLC28A1 also belongs to the SLC (solute carrier) family, several members of which have previously been associated with behavioral traits (depression, mood disorders, and smoking behavior), autism susceptibility, and attention-deficit/hyperactivity disorder.41 Furthermore, rs4842996, 8 kb upstream of SLC28A1, has been associated with ASD in a meta-analysis of GWAS findings from literature.42
For the SPARK cohort, KnockoffTrio identified nine significant loci, including zinc finger protein 589 (ZNF589), cell adhesion molecule 2 (CADM2), chondroitin sulfate synthase 3 (CHSY3) - histidine triad nucleotide binding protein 1 (HINT1), platelet derived growth factor subunit A (PDGFA) - protein kinase CAMP-dependent type I regulatory subunit beta (PRKAR1B), dedicator of cytokinesis 4 (DOCK4), MT-RNR2 like 6 (MTRNR2L6) - serine protease 1 (PRSS1), la ribonucleoprotein 4B (LARP4B) - GTP binding protein 4 (GTPBP4), isopentenyl-diphosphate delta isomerase 2 (IDI2), and protocadherin 20 (PCDH20) - protocadherin 9 (PCDH9) at FDR = 0.1 and, additionally, serine peptidase inhibitor kazal type 8 (SPINK8), solute carrier family 22 member 23 (SLC22A23)/proteasome assembly chaperone 4 (PSMG4), BAG cochaperone 4 (BAG4), and cyclin B1 interacting protein 1 (CCNB1IP1) - poly (ADP-ribose) polymerase 2 (PARP2) at FDR = 0.2 (Figure 6). PRKAR1B has been implicated in several neurodevelopmental disorders including ASD.43, 44, 45, 46 Similarly, CADM2 has been associated with ASD in multiple studies.47, 48, 49, 50 PCDH9 has been implicated as a genetic risk factor for multiple psychiatric disorders, including major depression51 and ASD.52 It is a cell adhesion molecule involved in neuronal migration, synaptic plasticity, and circuit formation. Previous studies have shown that homozygous knockout PCDH9-deficient mice have deficits in specific long-term social and object recognition.53 DOCK4 has been associated with ASD.54,55 Furthermore, DOCK4 knockout mice displayed a series of ASD-like behaviors, including impaired social novelty preference, abnormal isolation-induced pup vocalizations, elevated anxiety, and perturbed object and spatial learning.56 BAG4 resides at a locus that has been genome-wide significant in a combined ASD-schizophrenia GWAS.57 A deleterious variant, c.956T>A (p.Leu319His) (GenBank: NM_016089.3), in ZNF589 segregated with the phenotype (intellectual disability) and was identified as homozygous in two affected siblings in a consanguineous family from Northern Pakistan;58 the variant was absent from 200 ethnically matched control individuals. HINT1 regulates the function of protein kinase C (PKC), which is a prime gene to regulate regression in autism.59,60 SPINK8 resides at a GWAS-significant locus associated with multiple psychiatric disorders.61 In comparison, the conventional association test (BH) identified five loci (PDGFA-PRKAR1B, DOCK4, LARP4B-GTPBP4, IDI2, and PCDH20-PCDH9) at FDR = 0.1 and three loci (ZNF589, CHSY3-HINT1, and MTRNR2L6-PRSS1) at FDR = 0.2, all of which have been identified by KnockoffTrio as well.
For the SSC cohort, KnockoffTrio identified potassium channel regulator (KCNRG) - deleted in lymphocytic leukemia 7 (DLEU7) at FDR = 0.1 and, additionally, potassium voltage-gated channel interacting protein 4 (KCNIP4) at FDR = 0.2 (Figure 7). The finding of KCNRG, a gene in the potassium channel tetramerization domain (KCTD) family, provides further evidence for the role of KCTD family in neurodevelopmental and neuropsychiatric disorders.62 KCNIP4 is a gene with the largest number of differential RNA-editing sites that have been suggested for aberrant synaptic formation in ASD63; variants in KCNIP4 have also been associated with nonverbal communication and social skills in ASD twins.64 In comparison, the conventional association tests identified no significant loci.
Meta-analysis
We conducted meta-analysis of the AGP, SPARK, and SSC cohorts as a proof-of-principle because there are known differences across these studies in terms of phenotype definition (for example, AGP uses a very strict ASD definition) and study design (for example, SSC is expected to be enriched in de novo variants given its focus on discordant sibs), and such heterogeneity between cohorts makes it difficult to draw overall conclusions.65 KnockoffTrio identified one significant locus, DOCK4, at FDR = 0.2 and, additionally, RANBP2 like and GRIP domain containing 2 (RGPD2), KCNIP4, and CHSY3-HINT1 at FDR = 0.4 (Figure S11). In comparison, the conventional association tests identified no significant associations.
Replicability of analyses
Given the random nature of the knockoff procedure, we have attempted to assess the replicability of the results by re-analyzing the individual cohorts with different random seeds for knockoff generation. As shown in Figures S8–S10, the replications produced results that are in good concordance with the original results. For the AGP cohort, the replication analysis identified NRXN1, ARHGEF10, LMNTD1-RASSF8, and MACROD2, all of which were identified in the original analysis. For the SPARK cohort, the replication analysis identified ZNF589, SPINK8, CHSY3-HINT1, PDGFA-PRKAR1B, DOCK4, MTRNR2L6-PRSS1, LARP4B-GTPBP4, IDI2, and PCDH20-PCDH9, all of which were identified in the original analysis. For the SSC cohort, the replication analysis identified RGPD2, KCNIP4, and KCNRG-DLEU7, the latter two of which were identified in the original analysis. This shows the replicability of results from KnockoffTrio despite the randomness in knockoff generation.
Discussion
We propose KnockoffTrio, an association test with trio design for GWAS data built upon the knockoff framework. As an FDR-controlling procedure that accounts for arbitrary correlation structure, KnockoffTrio has been shown in both simulations and real data analyses to be more powerful than the conventional FWER-controlling methods while possessing better FDR control than the conventional FDR-controlling methods such as BH. We have also shown that KnockoffTrio protects against bias induced by population substructure using simulations and heuristic arguments. Furthermore, an important advantage of KnockoffTrio is that it can leverage more sophisticated machine learning methods to model the association between genotypes and phenotypes while maintaining valid FDR control and with potential increases in power. These properties make KnockoffTrio an appealing and promising strategy for the analysis of trio designs for which conventional methods are known to be underpowered.
Although we have focused the current manuscript on the complete trio design, the method can be naturally extended to more complex scenarios. In particular, KnockoffTrio can handle missing parental data and is robust to phasing errors in haplotypes as shown in supplemental note 6 and Figure S6. Furthermore, KnockoffTrio can be applied to large pedigrees by breaking each pedigree into all possible trios and applying KnockoffTrio on the individual trios. The method can also be extended to combine trios and population-based designs. For example, we can obtain the estimated coefficient for variant j from the external population-based GWAS and use it as weight in the weighted FBAT when constructing the importance scores. Alternatively, we can perform knockoff analysis for population-based data as in He et al.18 and use a meta-analysis approach as discussed in the material and methods section to combine the trio and population-based results. Note that this alternative approach is no longer robust to confounding due to population structure. Transfer learning methods that leverage information from such external population-based data could also be of interest.66
KnockoffTrio has been implemented in a computationally efficient R package. The runtime for completing the analyses of the AGP, SPARK, and SSC cohorts with 10 knockoffs is 8, 46, and 173 min, respectively, with 1,000 parallel jobs performed in a high-performance computing cluster environment of Intel(R) Xeon(R) CPU E5-2630 0 @ 2.30 GHz. In KnockoffTrio we have adopted the knockoff construction in KnockoffScreen, which has been shown to be a valid knockoff construction that is computationally efficient and can be applied to rare variants, but other, more sophisticated knockoff construction methods such as KnockoffZoom17 can be applied as well. This demonstrates that KnockoffTrio is a highly scalable method and can be effectively used for any large-scale datasets in whole-genome sequencing studies.
KnockoffTrio reduces the randomness in the knockoff generation by using a multiple-knockoff generation procedure. As shown in the simulations and real-data applications, KnockoffTrio with 10 knockoffs is more powerful at lower target FDR levels than using a single knockoff and has good replicability in terms of identifying significant loci. In our experience, stronger signals are more likely to be reproduced across different runs, though results can be more variable for weaker signals. Further increasing M would help with the reproducibility for weak signals at the cost of lowered computational efficiency, which is a tradeoff that researchers should be aware of. Although the gain in power diminishes as the number of knockoffs increases, especially at larger target FDR levels, given the computational efficiency of KnockoffTrio, we recommend that researchers generate multiple knockoffs for improved reproducibility and potentially better power at stricter FDR targets.
To simplify the inference about the transmission pattern, KnockoffTrio assumes no recombination events given a 200-kb region. However, KnockoffTrio can be extended to handle recombination events at the cost of more complex construction of offspring knockoffs, which may potentially help improve performance. In addition to the haplotype-based knockoff generation algorithm that KnockoffTrio adopts, another possible approach is to use summary statistics and apply knockoff-based methods for summary statistics directly instead of generating knockoffs for individual trio data.67 We leave these potential extensions to future studies.
GWASs with family-based designs are appealing due to their built-in robustness to population substructure, but they are underpowered due to limited sample sizes, much smaller than for GWASs with unrelated individuals. KnockoffTrio provides a more powerful alternative to classical FBATs in this setting while maintaining robustness to confounding due to population substructure. Furthermore, by design, KnockoffTrio reduces the confounding effect of linkage disequilibrium and prioritizes causal variants over associations due to linkage disequilibrium.
We have focused our applications to genetic studies of ASD, a highly heterogeneous and complex genetic disease. Despite these challenges, KnockoffTrio has identified some well-known (i.e., robustly identified in previous ASD studies) signals such as MACROD2, ARHGEF10, and NRXN1 in AGP; CADM2, PRKAR1B, DOCK4, and PCDH20 in SPARK; and KCNIP4 in SSC, suggesting that KnockoffTrio can have more power than conventional tests. Although the consistency across the different cohorts is low, that is not unexpected given the above-mentioned heterogeneity, the generally low power for each individual study with modest sample sizes, and inherent differences across studies in terms of phenotype definition (for example, AGP uses a very strict ASD definition) and study design (for example, SSC is expected to be enriched in de novo variants given its focus on discordant sibs).
In summary, KnockoffTrio provides a computationally efficient and more powerful association test for trio designs relative to commonly used family-based tests and has the added benefit of reducing confounding due to linkage disequilibrium. The method has been implemented in an R package.
Acknowledgments
This research was supported by NIH/National Institute of Mental Health Awards MH106910 and MH095797 (to I.I.-L.). We appreciate obtaining access to genetic and phenotypic data from dbGaP and SFARI Base and gratefully acknowledge the participants who provided data for the AGP, SPARK, and SSC projects.
Declaration of interests
The authors declare no competing interests.
Published: September 22, 2022
Footnotes
Supplemental information can be found online at https://doi.org/10.1016/j.ajhg.2022.08.013.
Supplemental information
Data and code availability
KnockoffTrio has been implemented in an R package available at https://cran.r-project.org/web/packages/KnockoffTrio. Researchers can apply for the AGP (dbGaP: phs000267.v5.p2) dataset at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000267.v5.p2 and the SPARK and the SSC datasets at https://base.sfari.org/.
References
- 1.Al-Mubarak B., Abouelhoda M., Omar A., AlDhalaan H., Aldosari M., Nester M., Alshamrani H.A., El-Kalioby M., Goljan E., Albar R., et al. Whole exome sequencing reveals inherited and de novo variants in autism spectrum disorder: a trio study from saudi families. Sci. Rep. 2017;7:5679–5714. doi: 10.1038/s41598-017-06033-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wassink T.H., Piven J., Vieland V.J., Huang J., Swiderski R.E., Pietila J., Braun T., Beck G., Folstein S.E., Haines J.L., Sheffield V.C. Evidence supporting wnt2 as an autism susceptibility gene. Am. J. Med. Genet. 2001;105:406–413. doi: 10.1002/ajmg.1401. [DOI] [PubMed] [Google Scholar]
- 3.O’Roak B.J., Deriziotis P., Lee C., Vives L., Schwartz J.J., Girirajan S., Karakoc E., MacKenzie A.P., Ng S.B., Baker C., et al. Exome sequencing in sporadic autism spectrum disorders identifies severe de novo mutations. Nat. Genet. 2011;43:585–589. doi: 10.1038/ng.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Laird N.M., Lange C. The role of family-based designs in genome-wide association studies. Stat. Sci. 2009;24:388–397. [Google Scholar]
- 5.Laird N.M., Lange C. Family-based designs in the age of large-scale gene-association studies. Nat. Rev. Genet. 2006;7:385–394. doi: 10.1038/nrg1839. [DOI] [PubMed] [Google Scholar]
- 6.Kong A., Thorleifsson G., Frigge M.L., Vilhjalmsson B.J., Young A.I., Thorgeirsson T.E., Benonisdottir S., Oddsson A., Halldorsson B.V., Masson G., et al. The nature of nurture: Effects of parental genotypes. Science. 2018;359:424–428. doi: 10.1126/science.aan6877. [DOI] [PubMed] [Google Scholar]
- 7.Price A.L., Zaitlen N.A., Reich D., Patterson N. New approaches to population stratification in genome-wide association studies. Nat. Rev. Genet. 2010;11:459–463. doi: 10.1038/nrg2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chen H., Huffman J.E., Brody J.A., Wang C., Lee S., Li Z., Gogarten S.M., Sofer T., Bielak L.F., Bis J.C., et al. Efficient variant set mixed model association tests for continuous and binary traits in large-scale whole-genome sequencing studies. Am. J. Hum. Genet. 2019;104:260–274. doi: 10.1016/j.ajhg.2018.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhou W., Zhao Z., Nielsen J.B., Fritsche L.G., LeFaive J., Gagliano Taliun S.A., Bi W., Gabrielsen M.E., Daly M.J., Neale B.M., et al. Scalable generalized linear mixed model for region-based association tests in large biobanks and cohorts. Nat. Genet. 2020;52:634–639. doi: 10.1038/s41588-020-0621-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bates S., Sesia M., Sabatti C., Candès E. Causal inference in genetic trio studies. Proc. Natl. Acad. Sci. USA. 2020;117:24117–24126. doi: 10.1073/pnas.2007743117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nelson C.P., Goel A., Butterworth A.S., Kanoni S., Webb T.R., Marouli E., Zeng L., Ntalla I., Lai F.Y., Hopewell J.C., et al. Association analyses based on false discovery rate implicate new loci for coronary artery disease. Nat. Genet. 2017;49:1385–1391. doi: 10.1038/ng.3913. [DOI] [PubMed] [Google Scholar]
- 12.Sesia M., Bates S., Candès E., Marchini J., Sabatti C. Controlling the False Discovery Rate in Gwas with Population Structure. bioRxiv. 2020 doi: 10.1101/2020.08.04.236703. Preprint at. [DOI] [Google Scholar]
- 13.Satterstrom F.K., Kosmicki J.A., Wang J., Breen M.S., De Rubeis S., An J.-Y., Peng M., Collins R., Grove J., Klei L., et al. Large-scale exome sequencing study implicates both developmental and functional changes in the neurobiology of autism. Cell. 2020;180:568–584.e23. doi: 10.1016/j.cell.2019.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.De Rubeis S., He X., Goldberg A.P., Poultney C.S., Samocha K., Cicek A.E., Kou Y., Liu L., Fromer M., Walker S., et al. Synaptic, transcriptional and chromatin genes disrupted in autism. Nature. 2014;515:209–215. doi: 10.1038/nature13772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Candès E., Fan Y., Janson L., Lv J., et al. Panning for gold: Model-x knockoffs for high-dimensional controlled variable selection. J. R. Stat. Soc. B. 2018;80:551–577. [Google Scholar]
- 16.Benjamini Y., Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001:1165–1188. [Google Scholar]
- 17.Sesia M., Katsevich E., Bates S., Candès E., Sabatti C. Multi-resolution localization of causal variants across the genome. Nat. Commun. 2020;11:1799. doi: 10.1038/s41467-020-14791-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.He Z., Liu L., Wang C., Le Guen Y., Lee J., Gogarten S., Lu F., Montgomery S., Tang H., Silverman E.K., et al. Identification of putative causal loci in whole-genome sequencing data via knockoff statistics. Nat. Commun. 2021;12:3152–3218. doi: 10.1038/s41467-021-22889-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Sesia M., Bates S., Candès E., Marchini J., Sabatti C. False discovery rate control in genome-wide association studies with population structure. Proc. Natl. Acad. Sci. USA. 2021;118 doi: 10.1073/pnas.2105841118. e2105841118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Spielman R.S., McGinnis R.E., Ewens W.J. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (iddm) Am. J. Hum. Genet. 1993;52:506–516. [PMC free article] [PubMed] [Google Scholar]
- 21.Chen H., Meigs J.B., Dupuis J. Sequence kernel association test for quantitative traits in family samples. Genet. Epidemiol. 2013;37:196–204. doi: 10.1002/gepi.21703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yan Q., Tiwari H.K., Yi N., Gao G., Zhang K., Lin W.-Y., Lou X.-Y., Cui X., Liu N. A sequence kernel association test for dichotomous traits in family samples under a generalized linear mixed model. Hum. Hered. 2015;79:60–68. doi: 10.1159/000375409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marchini J., Cutler D., Patterson N., Stephens M., Eskin E., Halperin E., Lin S., Qin Z.S., Munro H.M., Abecasis G.R., et al. A comparison of phasing algorithms for trios and unrelated individuals. Am. J. Hum. Genet. 2006;78:437–450. doi: 10.1086/500808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.De G., Yip W.-K., Ionita-Laza I., Laird N. Rare variant analysis for family-based design. PLoS One. 2013;8:e48495. doi: 10.1371/journal.pone.0048495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu Y., Chen S., Li Z., Morrison A.C., Boerwinkle E., Lin X. Acat: A fast and powerful p value combination method for rare-variant analysis in sequencing studies. Am. J. Hum. Genet. 2019;104:410–421. doi: 10.1016/j.ajhg.2019.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang T., Ionita-Laza I., Wei Y. Integrated quantile rank test (iqrat) for gene-level associations. Ann. Appl. Stat. 2022;16:1423–1444. [Google Scholar]
- 27.Willer C.J., Li Y., Abecasis G.R. Metal: fast and efficient meta-analysis of genomewide association scans. Bioinformatics. 2010;26:2190–2191. doi: 10.1093/bioinformatics/btq340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sesia M., Sabatti C., Candès E.J. Gene hunting with hidden Markov model knockoffs. Biometrika. 2019;106:1–18. doi: 10.1093/biomet/asy033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.1000 Genomes Project Consortium. Brooks L.D., Durbin R.M., Garrison E.P., Kang H.M., Korbel J.O., Marchini J.L., McCarthy S., McVean G.A., Abecasis G.R. A global reference for human genetic variation. Nature. 2015;526:68–74. doi: 10.1038/nature15393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Autism Genome Project Consortium. Szatmari P., Paterson A.D., Zwaigenbaum L., Roberts W., Brian J., Liu X.-Q., Vincent J.B., Skaug J.L., Thompson A.P., et al. Mapping autism risk loci using genetic linkage and chromosomal rearrangements. Nat. Genet. 2007;39:319–328. doi: 10.1038/ng1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.SPARK Consortium Electronic address pfeliciano@simonsfoundationorg Spark: A US cohort of 50, 000 families to accelerate autism research. Neuron. 2018;97:488–493. doi: 10.1016/j.neuron.2018.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fischbach G.D., Lord C. The simons simplex collection: a resource for identification of autism genetic risk factors. Neuron. 2010;68:192–195. doi: 10.1016/j.neuron.2010.10.006. [DOI] [PubMed] [Google Scholar]
- 33.Lord C., Rutter M., Le Couteur A. Autism diagnostic interview-revised: a revised version of a diagnostic interview for caregivers of individuals with possible pervasive developmental disorders. J. Autism Dev. Disord. 1994;24:659–685. doi: 10.1007/BF02172145. [DOI] [PubMed] [Google Scholar]
- 34.Lord C., Risi S., Lambrecht L., Cook E.H., Jr., Leventhal B.L., DiLavore P.C., Pickles A., Rutter M. The autism diagnostic observation schedule-generic: a standard measure of social and communication deficits associated with the spectrum of autism. J. Autism Dev. Disord. 2000;30:205–223. [PubMed] [Google Scholar]
- 35.Delaneau O., Marchini J., Zagury J.-F. A linear complexity phasing method for thousands of genomes. Nat. Methods. 2011;9:179–181. doi: 10.1038/nmeth.1785. [DOI] [PubMed] [Google Scholar]
- 36.Anney R., Klei L., Pinto D., Regan R., Conroy J., Magalhaes T.R., Correia C., Abrahams B.S., Sykes N., Pagnamenta A.T., et al. A genome-wide scan for common alleles affecting risk for autism. Hum. Mol. Genet. 2010;19:4072–4082. doi: 10.1093/hmg/ddq307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Grove J., Ripke S., Als T.D., Mattheisen M., Walters R.K., Won H., Pallesen J., Agerbo E., Andreassen O.A., Anney R., et al. Identification of common genetic risk variants for autism spectrum disorder. Nat. Genet. 2019;51:431–444. doi: 10.1038/s41588-019-0344-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gauthier J., Siddiqui T.J., Huashan P., Yokomaku D., Hamdan F.F., Champagne N., Lapointe M., Spiegelman D., Noreau A., Lafrenière R.G., et al. Truncating mutations in nrxn2 and nrxn1 in autism spectrum disorders and schizophrenia. Hum. Genet. 2011;130:563–573. doi: 10.1007/s00439-011-0975-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kim H.-G., Kishikawa S., Higgins A.W., Seong I.-S., Donovan D.J., Shen Y., Lally E., Weiss L.A., Najm J., Kutsche K., et al. Disruption of neurexin 1 associated with autism spectrum disorder. Am. J. Hum. Genet. 2008;82:199–207. doi: 10.1016/j.ajhg.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lu D.-H., Liao H.-M., Chen C.-H., Tu H.-J., Liou H.-C., Gau S.S.-F., Fu W.-M. Impairment of social behaviors in arhgef10 knockout mice. Mol. Autism. 2018;9:11. doi: 10.1186/s13229-018-0197-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gouy A., Excoffier L. Polygenic patterns of adaptive introgression in modern humans are mainly shaped by response to pathogens. Mol. Biol. Evol. 2020;37:1420–1433. doi: 10.1093/molbev/msz306. [DOI] [PubMed] [Google Scholar]
- 42.Lee J., Son M.J., Son C.Y., Jeong G.H., Lee K.H., Lee K.S., Ko Y., Kim J.Y., Lee J.Y., Radua J., et al. Genetic variation and autism: A field synopsis and systematic meta-analysis. Brain Sci. 2020;10:E692. doi: 10.3390/brainsci10100692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Marbach F., Stoyanov G., Erger F., Stratakis C.A., Settas N., London E., Rosenfeld J.A., Torti E., Haldeman-Englert C., Sklirou E., et al. Variants in prkar1b cause a neurodevelopmental disorder with autism spectrum disorder, apraxia, and insensitivity to pain. Genet. Med. 2021;23:1465–1473. doi: 10.1038/s41436-021-01152-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ruzzo E.K., Pérez-Cano L., Jung J.-Y., Wang L.-K., Kashef-Haghighi D., Hartl C., Singh C., Xu J., Hoekstra J.N., Leventhal O., et al. Inherited and de novo genetic risk for autism impacts shared networks. Cell. 2019;178:850–866.e26. doi: 10.1016/j.cell.2019.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Turner T.N., Hormozdiari F., Duyzend M.H., McClymont S.A., Hook P.W., Iossifov I., Raja A., Baker C., Hoekzema K., Stessman H.A., et al. Genome sequencing of autism-affected families reveals disruption of putative noncoding regulatory dna. Am. J. Hum. Genet. 2016;98:58–74. doi: 10.1016/j.ajhg.2015.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chen S., Zhou X., Byington E., Bruce S.L., Zhang H., Shen Y. Dissecting Autism Genetic Risk Using Single-Cell Rna-Seq Data. bioRxiv. 2020 doi: 10.1101/2020.06.15.153031. Preprint at. [DOI] [Google Scholar]
- 47.Casey J.P., Magalhaes T., Conroy J.M., Regan R., Shah N., Anney R., Shields D.C., Abrahams B.S., Almeida J., Bacchelli E., et al. A novel approach of homozygous haplotype sharing identifies candidate genes in autism spectrum disorder. Hum. Genet. 2012;131:565–579. doi: 10.1007/s00439-011-1094-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Namjou B., Marsolo K., Caroll R.J., Denny J.C., Ritchie M.D., Verma S.S., Lingren T., Porollo A., Cobb B.L., Perry C., et al. Phenome-wide association study (phewas) in emr-linked pediatric cohorts, genetically links plcl1 to speech language development and il5-il13 to eosinophilic esophagitis. Front. Genet. 2014;5:401. doi: 10.3389/fgene.2014.00401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gamsiz E.D., Viscidi E.W., Frederick A.M., Nagpal S., Sanders S.J., Murtha M.T., Schmidt M., Simons Simplex Collection Genetics Consortium. Triche E.W., Geschwind D.H., et al. Intellectual disability is associated with increased runs of homozygosity in simplex autism. Am. J. Hum. Genet. 2013;93:103–109. doi: 10.1016/j.ajhg.2013.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Calderoni S., Ricca I., Balboni G., Cagiano R., Cassandrini D., Doccini S., Cosenza A., Tolomeo D., Tancredi R., Santorelli F.M., Muratori F. Evaluation of chromosome microarray analysis in a large cohort of females with autism spectrum disorders: a single center italian study. J. Pers. Med. 2020;10:160. doi: 10.3390/jpm10040160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xiao X., Zheng F., Chang H., Ma Y., Yao Y.-G., Luo X.-J., Li M. The gene encoding protocadherin 9 (pcdh9), a novel risk factor for major depressive disorder. Neuropsychopharmacology. 2018;43:1128–1137. doi: 10.1038/npp.2017.241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Marshall C.R., Noor A., Vincent J.B., Lionel A.C., Feuk L., Skaug J., Shago M., Moessner R., Pinto D., Ren Y., et al. Structural variation of chromosomes in autism spectrum disorder. Am. J. Hum. Genet. 2008;82:477–488. doi: 10.1016/j.ajhg.2007.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bruining H., Matsui A., Oguro-Ando A., Kahn R.S., Van’t Spijker H.M., Akkermans G., Stiedl O., van Engeland H., Koopmans B., van Lith H.A., et al. Genetic mapping in mice reveals the involvement of pcdh9 in long-term social and object recognition and sensorimotor development. Biol. Psychiatry. 2015;78:485–495. doi: 10.1016/j.biopsych.2015.01.017. [DOI] [PubMed] [Google Scholar]
- 54.Maestrini E., Pagnamenta A.T., Lamb J.A., Bacchelli E., Sykes N.H., Sousa I., Toma C., Barnby G., Butler H., Winchester L., et al. High-density snp association study and copy number variation analysis of the auts1 and auts5 loci implicate the immp2l-dock4 gene region in autism susceptibility. Mol. Psychiatry. 2010;15:954–968. doi: 10.1038/mp.2009.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Pagnamenta A.T., Bacchelli E., de Jonge M.V., Mirza G., Scerri T.S., Minopoli F., Chiocchetti A., Ludwig K.U., Hoffmann P., Paracchini S., et al. Characterization of a family with rare deletions in cntnap5 and dock4 suggests novel risk loci for autism and dyslexia. Biol. Psychiatry. 2010;68:320–328. doi: 10.1016/j.biopsych.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Guo D., Peng Y., Wang L., Sun X., Wang X., Liang C., Yang X., Li S., Xu J., Ye W.-C., et al. Autism-like social deficit generated by dock4 deficiency is rescued by restoration of rac1 activity and nmda receptor function. Mol. Psychiatry. 2021;26:1505–1519. doi: 10.1038/s41380-019-0472-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.The Autism Spectrum Disorders Working Group of The Psychiatric Genomics Consortium Meta-analysis of gwas of over 16, 000 individuals with autism spectrum disorder highlights a novel locus at 10q24. 32 and a significant overlap with schizophrenia. Mol. Autism. 2017;8:1–17. doi: 10.1186/s13229-017-0137-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Agha Z., Iqbal Z., Azam M., Ayub H., Vissers L.E.L.M., Gilissen C., Ali S.H.B., Riaz M., Veltman J.A., Pfundt R., et al. Exome sequencing identifies three novel candidate genes implicated in intellectual disability. PLoS One. 2014;9:e112687. doi: 10.1371/journal.pone.0112687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bemben M.A., Nguyen Q.-A., Wang T., Li Y., Nicoll R.A., Roche K.W. Autism-associated mutation inhibits protein kinase c-mediated neuroligin-4x enhancement of excitatory synapses. Proc. Natl. Acad. Sci. USA. 2015;112:2551–2556. doi: 10.1073/pnas.1500501112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ji L., Chauhan A., Chauhan V. Reduced activity of protein kinase c in the frontal cortex of subjects with regressive autism: relationship with developmental abnormalities. Int. J. Biol. Sci. 2012;8:1075–1084. doi: 10.7150/ijbs.4742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schork A.J., Won H., Appadurai V., Nudel R., Gandal M., Delaneau O., Revsbech Christiansen M., Hougaard D.M., Bækved-Hansen M., Bybjerg-Grauholm J., et al. A genome-wide association study of shared risk across psychiatric disorders implicates gene regulation during fetal neurodevelopment. Nat. Neurosci. 2019;22:353–361. doi: 10.1038/s41593-018-0320-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Teng X., Aouacheria A., Lionnard L., Metz K.A., Soane L., Kamiya A., Hardwick J.M. Kctd: A new gene family involved in neurodevelopmental and neuropsychiatric disorders. CNS Neurosci. Ther. 2019;25:887–902. doi: 10.1111/cns.13156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Tran S.S., Jun H.-I., Bahn J.H., Azghadi A., Ramaswami G., Van Nostrand E.L., Nguyen T.B., Hsiao Y.-H.E., Lee C., Pratt G.A., et al. Widespread rna editing dysregulation in brains from autistic individuals. Nat. Neurosci. 2019;22:25–36. doi: 10.1038/s41593-018-0287-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hu V.W., Devlin C.A., Debski J.J. Asd phenotype-genotype associations in concordant and discordant monozygotic and dizygotic twins stratified by severity of autistic traits. Int. J. Mol. Sci. 2019;20:E3804. doi: 10.3390/ijms20153804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Higgins J.P.T., Thompson S.G. Quantifying heterogeneity in a meta-analysis. Stat. Med. 2002;21:1539–1558. doi: 10.1002/sim.1186. [DOI] [PubMed] [Google Scholar]
- 66.Li S., Ren Z., Sabatti C., Sesia M. Transfer learning in genome-wide association studies with knockoffs. arXiv. 2021 doi: 10.48550/arXiv.2108.08813. Preprint at. [DOI] [Google Scholar]
- 67.He Z., Liu L., Belloy M.E., Le Guen Y., Sossin A., Liu X., Qi X., Ma S., Wyss-Coray T., Tang H., et al. Summary statistics knockoff inference empowers identification of putative causal variants in genome-wide association studies. bioRxiv. 2021 doi: 10.1101/2021.12.06.471440. Preprint at. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
KnockoffTrio has been implemented in an R package available at https://cran.r-project.org/web/packages/KnockoffTrio. Researchers can apply for the AGP (dbGaP: phs000267.v5.p2) dataset at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000267.v5.p2 and the SPARK and the SSC datasets at https://base.sfari.org/.