Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Oct 10;7(42):37189–37200. doi: 10.1021/acsomega.2c03212

Tuning the Mechanical Behavior of Density-Graded Elastomeric Foam Structures via Interlayer Properties

Kazi Z Uddin †, Ibnaj A Anni †, George Youssef ‡, Behrad Koohbor †,§,*
PMCID: PMC9607669  PMID: 36312340

Abstract

graphic file with name ao2c03212_0013.jpg

The concept of density-graded foams has been proposed to simultaneously enhance strain energy dissipation and the load-bearing capacities at a reduced structural weight. From a practical perspective, the fabrication of density-graded foams is often achieved by stacking different foam densities. Under such conditions, the adhesive interlayer significantly affects the mechanical performance and failure modes of the structure. This work investigates the role of different adhesive layers on the mechanical and energy absorption behaviors of graded flexible foams with distinct density layers. Three adhesive candidates with different chemical, physical, and mechanical characteristics are used to assemble density-graded polyurea foam structures. The mechanical load-bearing and energy absorption performances of the structures are evaluated under quasi-static and dynamic loading conditions. Mechanical tests are accompanied by digital image correlation (DIC) analyses to study the local strain fields developed in the vicinity of the interface. Experimental measurements are also supplemented by model predictions that reveal the interplay between the mechanical properties of an adhesive interlayer and the macroscale mechanical performance of the graded foam structures. The results obtained herein demonstrate that the deformation patterns and macroscale properties of graded foam composites can be tuned by selecting different bonding agents. It is also shown that the proper selection of an adhesive can be a practical way to address the strength–energy dissipation dichotomy in graded structures.

1. Introduction

Polymeric foams are widely used in various applications due to their superior mechanical and thermal properties, including excellent energy absorption performance, specific strength, insulating properties, low structural weight, and low production cost. Cell architecture design and the use of flexible polymers as the base materials have facilitated the development of flexible polymeric foams with tunable mechanical properties and controlled degrees of deformation recovery, leading to the widespread use of this class of materials in applications where repeated loading events are common.1−3 However, one of the major drawbacks in the use of polymeric foams as protective structures stems from the dichotomy between specific mechanical strength and strain energy dissipation.4 It is understood that the mechanical load-bearing capacity of polymeric foams is directly correlated with their density: i.e., the presence of thinner cell walls in the structure results in lower strengths. On the other hand, the foam’s specific strain energy dissipation capacity is increased when the solid cell walls are thinner. A promising practical approach to addressing the strength–energy dissipation dichotomy in polymeric foams has been designing and developing density-graded structures.4−7 Each density layer serves a specific purpose in a carefully designed density-graded foam structure. In particular, the lower-density layers have an increased specific energy absorption, while higher-density foam layers improve the overall strength of the structure. Therefore, density gradation leads to a concurrent improvement of load-bearing and strain energy dissipation characteristics.

Recent advancements in flexible polymeric foams suggest tunable mechanical performances comparable to those of agile additively manufactured structures by controlling the architecture, geometry, and density.8−10 For example, the spatial variations of cell structure and density in functionally graded foam materials (FGFMs) make it possible to achieve higher strength and failure strains while simultaneously maintaining higher energy absorption properties at a lower overall structural weight.11−13

The fundamental premise in developing functionally graded structures is manipulating the mechanical response (i.e., cracking, damage, stiffness, strength) and tailoring the desired properties by controlling the spatial distribution of individual layers in specific geometric directions.14−17 However, the complication associated with the manufacturing of continuously graded FGFMs has limited their availability; thus, the impact mitigation applications mainly rely on the discretely graded FGFMs. In such cases, adhesives are widely used as interlayer materials to connect individual gradient layers. Adhesive bonding is facile, providing a larger connecting area than fastener joints, and in most cases possesses a lower elastic modulus than the main structural components.18,19 Theoretically, it has been proven that the nonuniformity at the interface between an adhesive and the adherend is controlled by their differences in mechanical properties, giving an increase in stress intensity.20,21 Depending on the stiffness of adhesives, the load distribution varies and creates a complex state of stress.22 In FGFMs, a uniformly distributed load throughout the foam laminate and adhesive joints can ensure integrity and prevent premature failure. Researchers have explored different lab-made or commercially available adhesive joints to understand the effect of the interlayer material on the structural behavior. Early research conducted by Sankactar et al.23 used toughened rubber epoxy as a lap joint with various chemical constituents (epoxy, adduct, and hardener); they observed distinguishable responses from the brittle adhesives. The use of multilayer adhesives as interlayers makes it possible to tune the adhesive stiffness and change the load propagation behavior all around the structure.24−28 In most cases, the adhesive between the functionally graded layers could have a physical range of viscoelastic to brittle nature and needs a comprehensive analysis. Researchers have followed different analytical and numerical approaches to investigate the design and analysis of adhesive joints as interlayer materials. The review carried out by Budhe et al.29 provides an extensive insight into the adhesive strength of joints using model predictions and experimental results.

The influence of adhesives and their diverse nature has motivated a careful and systematic study of the FGFM structure. The present study examines the role of interface adhesive properties on the mechanical response of bilayer density-graded polyurea foam structures. In recent years, polyurea foam has attracted a good amount of interest due to its hierarchical cellular network and semiclosed cellular structure in impact mitigation applications.14,30,31 Polyurea shows an extended plateau area in stress–strain response.9,32 The mechanical characterization of polyurea foams demonstrates a superior characteristic under both quasi-static and dynamic loading conditions.9,32,33 The outstanding mechanical performance of polyurea foam under different loading conditions distinguishes it from other elastomeric cellular solids.31,34

In this work, two different densities of cross-linked, thermoset semiclosed cell polyurea foams served as the main components of the bilayered functionally graded foam structures. Various adhesives with different mechanical properties were selected as bonding agents between the two densities of the polyurea foam stack. The mechanical properties of the entire structure (i.e., polyurea foam layers with an adhesive interlayer in between) were characterized under quasi-static and dynamic loading conditions. The mechanical tests were coupled with digital image correlation (DIC) analyses to reveal any local deformation anomalies within the structures and in the vicinity of the adhesive layers. The postprocessing of the data set provides a comprehensive and concise understanding of the impact mitigation behavior for different adhesives in the FGFM structure.

2. Materials and Methods

2.1. Sample Preparation

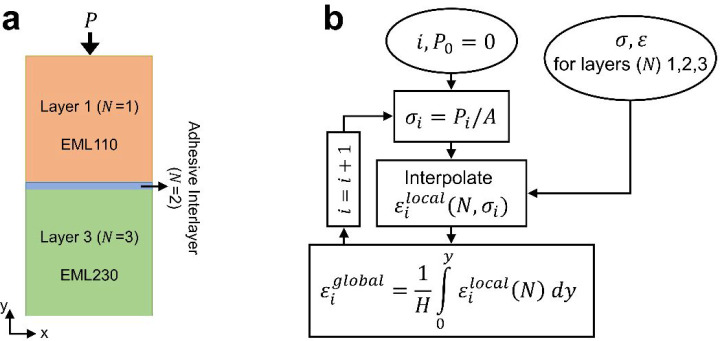
Hyperelastic polyurea foams with two densities of 110 and 230 kg/m3 (hereafter referred to as EML110 and EML230, respectively) were used to assemble bilayer density-graded foam structures. The manufacturing protocol of the foams has been discussed in detail in previous publications.9,32 The variations between the cell structures of the two foams (shown in the scanning electron (SEM) micrographs in Figure 1b,c) were attributed to the differences in their mechanical behaviors, as discussed in the forthcoming sections. Cubic samples with edge lengths of 18 mm were punched out of larger foam slabs. The graded foam structures were assembled using off-the-shelf adhesives selected primarily based on their mechanical properties, including (1) thermoplastic ethylene-vinyl acetate (EVA glue, Daikoye, USA), (2), thermosetting cyanoacrylate (Gorilla Glue, OH, USA), and (3) double-sided solid acrylic foam (VHB 5952 foam, 3M, Minnesota, USA), denoted hereafter as EVA, cyanoacrylate, and acrylic foam, respectively. The foam stacks were prepared using an ∼1 mm thickness interlayer of the aforementioned adhesives, as shown in Figure 1a (see the Supporting Information for a schematic of the fabrication process). The manufacturer-reported densities of the adhesives were 890, 1100, and 590 kg/m3 for EVA, cyanoacrylate, and acrylic foam, respectively. Therefore, the calculated effective densities of the bilayer foam stacks were ∼190, 195, and 181 kg/m3 for structures with EVA, cyanoacrylate, and acrylic foam interlayers, respectively. The difference between the lowest and the highest density foam stacks was only 7% and thus was deemed negligible.

Figure 1.

Figure 1

Open in a new tab

(a) Optical micrograph of the graded foam stack in the vicinity of the interface. (b, c) SEM micrographs of the base polyurea foams. (d) Test setup used for the mechanical characterization of the adhesives. Adhesive strips were inserted inside the grips of the tensile tester with the aid of aluminum tabs, shown schematically in (e).

2.2. Mechanical Testing

The compressive mechanical responses of the two foams were individually characterized under quasi-static compression at a nominal strain rate of 8 × 10–4 s–1. The dimensions of the tested foam samples were similar to those of a single layer in the density-graded structure (i.e., a cube with 18 mm edge lengths). Separately, the stress–strain behaviors of the three adhesive materials were also measured in-house under quasi-static tension. Since the adhesive layer is foreseen to undergo small deformations relative to the hyperelastic deformations of the foam layer, the adhesives were assumed to have even mechanical behavior. Here, tensile testing suffices to represent the mechanical response while overcoming the complications of producing representative compression samples. Mechanical testing of adhesives was performed on tensile strips (80 × 10 × 1 mm) prepared from each material. For the acrylic foam, the strips were extracted from a larger sheet using razor blades. For the other two adhesives, i.e., EVA and cyanoacrylate, samples were tape-cast and cured for 36 h under ambient conditions in a fume hood. Aluminum tabs (10 × 10 × 1 mm thick) were placed at the sample ends on both sides to eliminate the undesired damage imposed by the serrated grips of the tensile tester. Tensile samples were then tested at a nominal strain rate of 10–3 s–1 in a Shimadzu Universal Testing Machine with a 10 kN load cell capacity (Figure 1). Apparent elastic moduli of the five materials, including the two polyurea foams and three adhesives, were determined from the experimental stress–strain curves of each material.

In the essence of this research study, quasi-static and dynamic drop weight (impact) mechanical tests were performed on density-graded foam stacks under ambient conditions. For quasi-static tests, foam stacks were compressed at 5 mm/min (equivalent to a nominal strain rate of 2.2 × 10–3 s–1) using the same load frame mentioned above. Dynamic testing of the graded foam stacks was carried out using an instrumented drop weight tower (Figure 2a) by dropping a 723 g impactor from a height of 1000 mm. The utilized impact conditions subjected the graded samples to a nominal strain rate of ∼120 s–1, determined based on the impact velocity (discussed in refs (31 and 35)) and the original length of the foam stacks (∼37 mm). The transmitted impact force–time history was recorded using a sensor placed below the foam sample, which was then used to analyze the dynamic response of graded foam stacks. In dynamic tests, the foam stacks were oriented such that the lower density foam was impacted first, i.e., a positive gradient (see Figure 2b), to avoid the potential complexities due to the generation of double-shock deformation modes in negative density gradients.17

Figure 2.

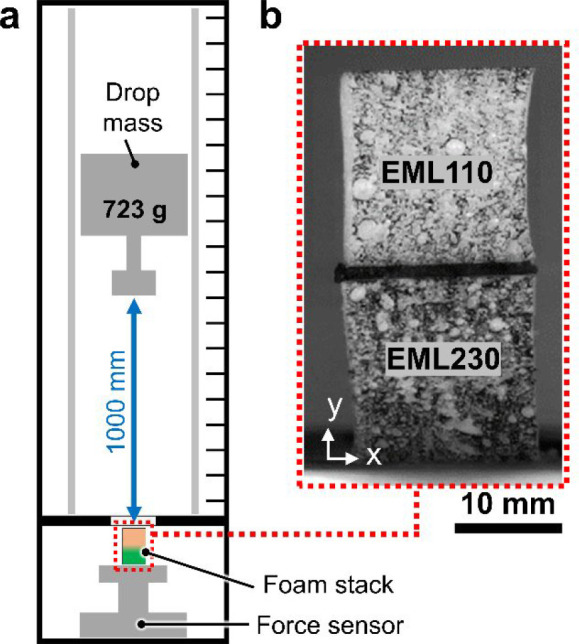
Figure 2

Open in a new tab

(a) Schematic of the impact test setup. (b) Speckle-patterned surface of the foam stack used in DIC analyses.

Image-based strain analyses augmented the aforementioned quasi-static and dynamic tests. Digital image correlation (DIC) was used to measure the full strain fields developed in the foam stacks during mechanical testing. The front surface of the foam stacks was coated with a random speckle pattern suitable for image correlation (see Figure 2b). In quasi-static tests, a 5 megapixel camera with an image acquisition rate of 1 Hz was used. A high-speed camera (Photron FASTCAM SA1.1) was utilized to capture images during low-velocity impact testing at a rate of 30000 fps. The recorded images were postprocessed using the commercial DIC software Vic-2D (Correlated Solutions Inc., SC, USA) with subset, step, and strain filter sizes optimized for each case. The DIC parameter optimization process has been reported in detail in refs (31 and 36).

2.3. Energy Absorption Metrics

The stress–strain curves obtained for the foam stacks under quasi-static and dynamic conditions were used to evaluate two impact mitigation performance metrics. The first is the specific strain energy (also known as strain energy density) dissipated by the structures (W), quantified by calculating the area under the stress–strain curve

2.3. 1

where ε and σ denote global uniaxial strain and stress, respectively, and εf is the final experimental uniaxial strain. Second, the energy absorption efficiency parameter (η) was also defined as the ratio between the specific energy and stress:

2.3. 2

The maximum value of energy absorption efficiency was used to identify the initiation of the global densification strain, εd.7,37

2.4. Modeling

A one-dimensional modeling approach was utilized to predict the mechanical performance of density-graded foam structures with different interlayer materials. The utilized model is based on a semianalytical algorithm that was developed previously for continuously graded and discretely layered cellular structures with seamless interfaces.5,7,14 In short, the model works based on the inverse identification of local (layerwise) strain as a function of global stress. The need for an inverse calculation of strain is due to the highly nonlinear stress–strain responses of the hyperelastic foams that prevent the direct correlation of the global strain of the entire stack to the local strain within each corresponding layer.14 The assumption of a one-dimensional stress state requires the base materials to possess zero (or at least near zero) Poisson ratios. This requirement was previously verified for the utilized foam materials through in situ experimental measurements whose details can be found elsewhere.31,34

First, a full-grid material data set is constructed based on the quasi-static stress–strain responses of the two polyurea foams and the adhesive material candidates. Instead of using the actual tensile stress–strain curves measured for the three adhesives in this work (see Section 3.1), the modeling approach utilized three artificial adhesive candidates with linear elastic behaviors but vastly different modulus values. The three artificial adhesives (denoted as low, medium, and high stiffness) were assigned elastic moduli of 30, 500, and 3000 kPa. These values were chosen due to their consistency with the experimentally measured values for the three actual adhesives. In addition, the choice of the aforementioned three moduli was also justified by their relative differences from the apparent elastic moduli of the two polyurea foam candidates, both of which had moduli in the range of 500–800 kPa, as detailed in later sections.

Second, a virtual three-layered foam stack (including two foam layers and a central 1 mm adhesive layer, as shown in Figure 3a) is created. The uniaxial compressive stress is incrementally applied on the graded foam stack. The layerwise local strain associated with the current stress increment is determined by interpolating through the material data grid. Once the local strains in each of the three layers are identified, the global strain in the entire structure is calculated by integrating the local strain values along the sample axis (i.e., y direction). This process is iterated until a complete stress–strain curve is extracted for the structure. Figure 3b shows the stepwise approach followed to identify the stress–strain curves for the three-layered structures with various interlayer properties.

Figure 3.

Figure 3

Open in a new tab

(a) Schematic of the foam stack, including the adhesive layer used in 1D modeling. (b) Flowchart showing the steps followed to predict the stress–strain response of the foam stack with different adhesive interlayers. H denotes the total height of the foam stack.

The limitations of the current modeling approach include its dimensionality: i.e., the model is only applicable to ideal uniaxial loading conditions with disregard to the interface quality. Furthermore, the model also does not take into account the strain rate sensitivity; therefore, it is not fully applicable to dynamic loading conditions. Nonetheless, the model predictions can be used as guidelines to assess and compare the behaviors of the foam stacks created using various interlayer adhesives.

3. Results and Discussion

3.1. Quasi-Static Behavior of Foams and Adhesives

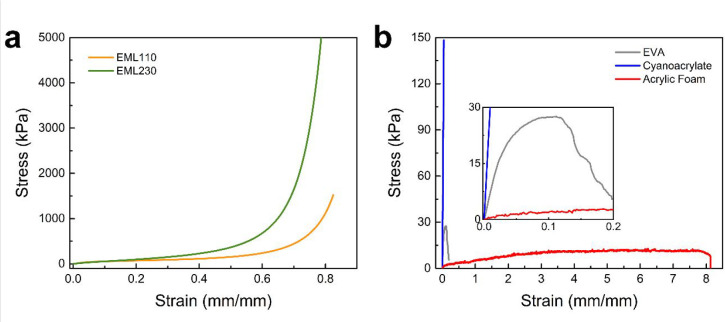
Stress–strain responses of the two polyurea foams, EML110 and EML230, under quasi-static compression are shown in Figure 4a. The general behavior is consistent with those of typical hyperelastic foams, exemplifying an initial linear region, followed by an extended stress plateau, which finally leads to a sharp increase in stress due to densification. The difference between the mechanical load-bearing capacities of the examined foams is primarily attributed to the difference in their densities and the average cell size.30 For example, the slope of the initial linear stress–strain region for EML110 and EML230 were determined to be 510 and 780 kPa, respectively, which are in good agreement with previous reports of polyurea foams.35

Figure 4.

Figure 4

Open in a new tab

Stress–strain curves for (a) the two base polyurea foams under quasi-static compression and (b) adhesive materials under quasi-static tension.

The tensile stress–strain behaviors of the three adhesives are shown in Figure 4b, elucidating the drastic differences among the mechanical responses of the examined materials. The thermoset cyanoacrylate adhesive shows a brittle tensile behavior with a low failure strain. On the other hand, the acrylic foam adhesive deforms at significantly lower stresses, showing extensively large tensile strain to failure, exceeding 800%. Finally, the thermoplastic EVA adhesive shows a typical ductile response, exemplified by an initial linear regime, followed by a maximum tensile strength. The apparent elastic moduli of the adhesives were determined to be 3224, 760, and 42 kPa for the thermoset cyanoacrylate, EVA, and acrylic foam, respectively.

3.2. Effect of Interlayer Modulus: Model Predictions

The predicted stress–strain curves for the three artificially graded structures with different interlayer stiffnesses are shown in Figure 5. The mechanical responses of the base polyurea foams are also included in the same figure for comparison. The densification onset strains for each case were determined by calculating the maximum value of energy absorption efficiency (see Section 2.3). The model predictions suggest that the response of a bilayered density-graded foam structure (with an equal thickness of each foam density) can be approximated as the average of the two base foams. While this observation agrees with previous reports,5 the unique difference between the present results and previous studies is the role of the interface material modulus. The model predictions in Figure 5 indicate that the modulus of a 1 mm thick interlayer can have considerable effects on the stress–strain and densification strain of density-graded foam stacks. In particular, a high modulus interlayer can lead to higher strength (especially at larger global strains) but at the cost of densification strain. On the other hand, lower modulus interlayers contribute to a comparably lower mechanical strength but in favor of an increased densification onset strain. These results justify further experimental investigations of the role of the interface material on the mechanical and energy absorption characteristics of density-graded foam stacks, as discussed in the following sections.

Figure 5.

Figure 5

Open in a new tab

Model predicted stress–strain curves of the foam stacks with three different artificial interlayer materials. The interlayers are classified by their mechanical stiffness as low, medium, and high modulus. Stress–strain responses of the base polyurea foams (EML110 and EML230) are included for comparison. The hollow circle markers indicate the onset of the densification point in each case.

3.3. Mechanical Performance of Foam Stacks in Quasi-Static Loading

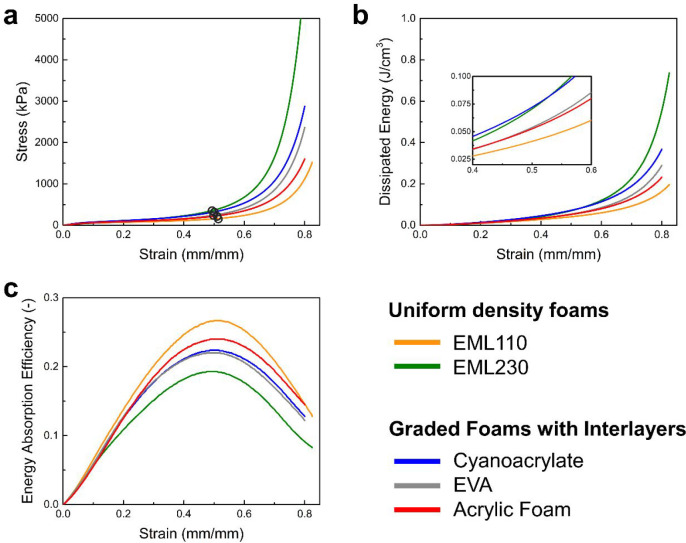
Load-bearing and energy absorption behaviors of the physical foam stacks were characterized under quasi-static compression. The stress–strain curves obtained from testing the graded foam stacks with different adhesives are shown in Figure 6a. For comparison, the mechanical responses of the uniform-density base polyurea foams, EML110 and EML230, are also included in this graph. First, the stress–strain responses of the foam stacks resemble those predicted by the model, where the behaviors of the graded foam structures lay between those of the uniform density foams. In addition, the effect of the interlayer adhesive is clearly shown in the form of an increased strength when higher modulus adhesives are used. Specifically, the foam structure fabricated using the thermoset cyanoacrylate adhesive is shown to outperform the other two structures in terms of compressive strength, especially at high compressive strains. On the other hand, the structure with acrylic foam adhesive shows the lowest mechanical performance among the three graded structures, primarily due to the negligible contribution of the foam interlayer as a load-bearing component.

Figure 6.

Figure 6

Open in a new tab

(a) Stress–strain, (b) specific dissipated energy, and (c) energy absorption efficiency of density-graded foam stacks with different adhesives (interlayers) under quasi-static conditions. Data for the uniform-density polyurea foams are included for comparison. Densification strains are marked with hollow circles in (a).

The performance improvement due to the application of the cyanoacrylate adhesive is also observed in the specific dissipated energy capacity of the structures (Figure 6b). Despite its overall lower strength and significantly lower density than EML230, the structure with cyanoacrylate adhesive shows energy absorption capacities similar to those of the high-density uniform foam, at least up to strains greater than 0.5. The latter observation is significant because it suggests the unique contribution of a stiff interlayer to the improvement of energy dissipation of the foam in the vicinity of densification strain—a metric of critical importance in the design of highly effective energy-mitigating protective structures.17,38

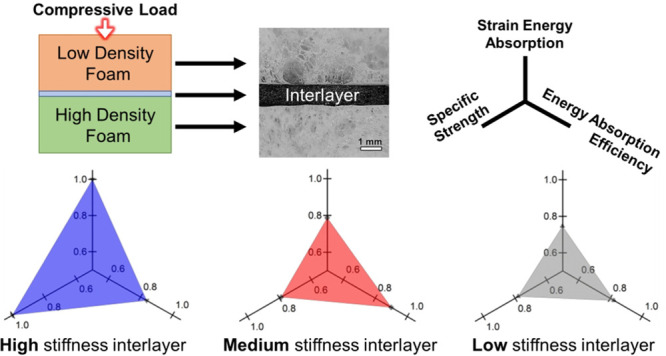
The combined effects of strength and energy dissipation are embedded in the energy absorption efficiency metric, shown in Figure 6c. The two extreme cases are the uniform-density foams, whose difference in the peak efficiency is primarily due to their inherent strengths. Among the three graded structures, that with acrylic foam adhesive shows higher energy efficiency due to its relatively lower stress in the vicinity of densification strain. The other two graded stacks show nearly identical efficiency responses, higher than that of EML230. To enable a more direct comparison between the load-bearing and energy absorption responses for all examined structures, the combined effects of energy dissipation at densification strain, W(εd), specific strength at densification strain, σ(εd)/ρ, and peak energy absorption efficiency, η, were examined. These additional metrics were determined for all structures and then normalized by their respective maximum values. Figure 7 shows the extent of each parameter for the five structures studied in this work. The radar graphs in this figure suggest that the graded foam stack with the cyanoacrylate adhesive outperforms the others in terms of combined specific strength and energy absorption performance metrics.

Figure 7.

Figure 7

Open in a new tab

Visual comparison between the uniform-density and graded structures in terms of specific energy dissipation at densification strain, W(εd), specific strength at densification, σ/ρ, and energy absorption efficiency, η. A unity value for each parameter indicates its maximum among all five structures.

3.4. Mechanical Performance of Foam Stacks in Dynamic Loading

The dynamic mechanical performance of the foam stacks was evaluated by releasing a 723 g mass from 1000 mm, imparting ∼7.1 J of impact energy. The same analysis approach employed in Section 3.3 was also used herein, where Figure 8 shows the dynamic stress–strain, dissipated energy, and efficiency performance of the three graded structures with different adhesives. The dynamic stress–strain behavior of the foam stacks mimics the quasi-static response except for the significantly higher levels of plateau stresses. The higher plateau stress under .dynamic testing conditions is attributed to the strong strain-rate-sensitive response of the base hyper-viscoelastic polyurea foams, where the viscoelasticity of the polymer adds to the material stiffness as the loading rate increases.35,39

Figure 8.

Figure 8

Open in a new tab

(a) Stress–strain, (b) dissipated energy (i.e., strain energy density), and (c) energy absorption efficiency of density-graded foam stacks with different adhesives (interlayers) under dynamic loading conditions. Densification strains are marked with hollow circles in (a).

Moreover, the dynamic mechanical behavior of the graded foam stacks departs from the quasi-static counterpart in two additional aspects. First, the plateau region dominates the dynamic response, where the stress remains nearly constant from the onset of the impact (quickly passed through the elastic region) to the onset of densification (shown by circles in Figure 8a). Such behavior was amplified when the acyclic foam interlayer was used as an adhesive, given its compliance compared to the other two adhesives and foam properties. As the stiffness of the adhesive increases, the dynamic stress–strain curve starts to resemble the combined and sequential contributions of the foam layers discussed in Section 3.3.17 This is further exemplified by the onset of densification, where the acrylic-based stack densifies at a higher strain, i.e., increasing the plateau region and improving the efficiency, as shown in Figure 8c. It is important to note that the densification onset strain for the impact testing was inferior to that reported based on quasi-static testing, irrespective of the stack configuration. The slower onset of densification in the dynamic regime is rooted in the rapid cell collapse, quickly engaging the cell-wall-entrapped base material in the overall response demonstrated by the significant increase in the stress in the densification region. Notably, polyurea is a shock-tolerant and impact-resistant material;40−42 hence, the significant rise in the stress as the foam stack densifies is associated with a negligible permanent set, as recently shown in a recent article.31

Second is the strain energy density, referred to herein as the dissipated energy, calculated as the area under the stress–strain curve, demonstrating contrasting behaviors between the dynamic and quasi-static cases: i.e., Figure 8b compared to Figure 6b. In the latter, the maximum dissipated energy was ca. 0.4 J/cm3 for the cyanoacrylate-bonded foam stacks, while the energies were ca. 0.3 and 0.2 J/cm3 when EVA and acrylic foam were used as interlayers, respectively. Furthermore, the values of the dissipated energy followed the same order throughout the strain history during quasi-static testing. On the other hand, the values and descending order have changed dramatically in the dynamic testing case, where the acrylic-bonded foam stacks outperformed the cyanoacrylate and EVA counterparts except within the densification region, as shown in Figure 8b. Below the onset of densification, the acrylic foam interlayer participates in the deformation from the beginning of the impact loading based on its low compliance. However, the stiffer interlayers appear to temporarily shield the bottom foam layer from the impact until the top layer reaches a critical strain that promotes the participation of the rest of the stack. During this temporary shielding period, the stiff interlayers undergo near-rigid body motion, where their contributions to impact mitigation are minimal. The sequential participation of the different layers, i.e., top lighter foam, interlayer, and bottom denser foam, is elucidated in the efficiency plots shown in Figure 8c via the superimposed oscillations. The number of superimposed oscillations before peak efficiency correlates with the sequential deformation of each layer in the stack.6,7,17 For example, the efficiency of the cyanoacrylate-bonded foam stack exhibits two pronounced slope changes, at ca. 0.075 and 0.32 strains, exemplifying the early participation of the low-density polyurea foam and late contributions of the higher-density foam layer. The EVA-based graded structure also shows two oscillations before the peak. On the other hand, the acrylic foam-based stack manifests three oscillations, leading to peak efficiency, associated with the significant contributions of each of the layers in the structure. As a result, higher energy-absorbing efficiency is reported for the acrylic foam stack, indicating that relaxing the stiffness of the interlayer influences the impact efficacy of elastomeric foams positively.

3.5. Characterizing Deformation Modes from Full-Field Strain Maps

Results obtained from quasi-static and dynamic testing of the foam stacks confirm the strain-rate sensitivity and the property-based contributions of each layer in the stack to the overall mechanical performance of the graded structures. However, the homogenized results from quasi-static and impact testing of the foam stacks fail to elucidate intricate insights into the dominant deformation patterns in the graded samples. As such, the previously discussed results were supplemented by full-field strain measurements facilitated by DIC with an emphasis on the role of the mechanical properties of the interlayer adhesive in the local deformation fields developed in the interface vicinity. Based on the discussion in the preceding sections, the full-field quasi-static and dynamic deformations are expected to exhibit distinct patterns, especially in the vicinity of the interface region. Therefore, the collective effects of the deformation fields are demonstrated and discussed here in terms of equivalent strain, εeq, defined as

3.5. 3

where εij are the in-plane logarithmic strain components of the finite strain tensor, obtained directly from DIC analyses. The development of equivalent strain fields in quasi-statically loaded foam stacks at various global strains is shown in Figure 9. These maps elucidate the asymmetric, quasi-homogeneous distribution of equivalent strain about the interlayer regions. Generally, the effective strains in the low- and high-density polyurea foam layers are analogous, demonstrating near mirror images of the strains above and below the interface region, except for a slight delay in developing strains in the high-density layer due to the difference in the stiffnesses.17 At the early stages of deformation, i.e., εeq ≤ 0.16, stiffer interlayers (e.g., cyanoacrylate and EVA) accumulated nearly zero strains since the compliant sandwiching foam layers gave in first to the applied load. This behavior persisted throughout the deformation history such that the equivalent strains in the interlayers significantly lagged behind those of the polyurea foam layers irrespective of the foam density. On the other hand, the acrylic foam based stacks resulted in a different behavior, where the interface region started to develop comparable strains from the early onset of the deformation. That is to say, the acrylic foam adhesive sample shows a smoother transition of strain from the more compliant top foam layer (EML110) to the stiffer bottom layer (EML230).

Figure 9.

Figure 9

Open in a new tab

Equivalent strain, εeq, fields in quasi-statically loaded foam stacks at various global strains, e, for samples with EVA (top), cyanoacrylate (middle), and acrylic foam (bottom) adhesives. The location of the interface layer at different strain levels is marked by a small arrow in each case.

The intensity of the equivalent strain distribution along the loading direction (Figure 10a–c) is further quantified by extracting the strain values along the normalized vertical axis (Figure 10d) at various global strains. As demonstrated earlier by contour maps, the strain jumps across the interlayers are more evident in the stacks with stiffer adhesive, while a smoother transition is observed for the acrylic foam-based graded structure. 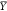In the latter case, the overall deformation of the foam stack occurs with higher strains developed in the top foam piece (0 < Inline graphic < 0.5) and relatively smaller strains in the bottom (0.5 < Inline graphic < 1). In the other two cases, i.e., where the adhesives are stiffer than the two foam parts, the strains in the foam layers are at comparable levels despite the apparent strain discontinuities in the vicinity of the adhesive interlayer. Interestingly, the strain anomalies seem to be more intense in the case of the stiffest adhesive (i.e., cyanoacrylate). The more severe strain gradient in the interface vicinity for the stiffer adhesives is directly correlated with the generation of strong shear deformations. Although they were not examined in detail in the present work, such strong local shear strain fields can serve as delamination initiation sites, thus increasing the propensity of the foam stack to slip and disintegrate.

Figure 10.

Figure 10

Open in a new tab

Distribution of equivalent strain along the vertical axis of foam stacks with (a) EVA, (b) cyanoacrylate, and (c) and acrylic foam adhesives under quasi-static compression. (d) Strain values plotted with respect to normalized length, Inline graphic. e denotes the global strain value. The location of the interface is marked by vertical green lines in (a–c).

Similar full-field strain analyses were extended to include dynamic (impact) loading experiments. Figure 11 shows the evolution of equivalent strain fields in the three foam stacks subjected to impact loading. Unlike quasi-static deformation, dynamic loading of the samples does not show any discernible differences among the mechanical behaviors of the foam stacks with different adhesives. Instead, all impact-loaded samples demonstrate an almost identical behavior, exemplified by the evolution of larger strains in the top, low-density foam layer. This observation is also supported by the line variation strain graphs shown in Figure 12. Although the overall strain distribution behavior is almost invariant for the three adhesive cases, the strain gradients across the cyanoacrylate adhesive (Figure 12b) show slightly higher slopes. In the case of acrylic foam based stacks (Figure 12c), the gradient extends over nearly the entire sample, substantiating the participation of all the layers in mitigating the incoming impact. Therefore, the reduction in the stiffness difference in impact loading leads to less intense property gradients across the interlayer, practically attributed to a lower likelihood of damage initiation from the interface. While beyond the scope of the present study, concepts involving the role of adhesive interlayer properties on the damage initiation and evolution in graded foams subjected to repeated impact conditions42,43 would be an interesting topic for future research. In such cases, an optimal interface layer may be identified by taking into account the interplay between mechanical and energy dissipation behaviors as well as the long-term use of foam stacks, especially considering repeated low-rate loading (e.g., for use in a walking shoe midsole14) or higher energy impact conditions (e.g., for use as helmet liners44). A possible avenue for the study of mechanical and energy dissipation behaviors after repeated loading is the estimation of apparent stiffness variations as a function of the adhesive properties. Mesomechanics characterizations similar to those reported by Koohbor et al.42 can be performed for this purpose.

Figure 11.

Figure 11

Open in a new tab

Equivalent strain, εeq, fields in impact-loaded foam stacks at various global strains for samples with EVA (top), cyanoacrylate (middle), and acrylic foam (bottom) adhesives. The location of the interface layer at different strain levels is marked by a small arrow in each case.

Figure 12.

Figure 12

Open in a new tab

Distribution of equivalent strain along the vertical axis of foam stacks with (a) EVA, (b) cyanoacrylate, and (c) and acrylic foam adhesives under impact loading. (d) Strain values plotted with respect to normalized length, Inline graphic. e denotes the global strain value. The location of the interface is marked by vertical green lines in (a–c).

4. Conclusions

Density-graded foam stacks with various interface adhesives were fabricated and characterized in terms of their mechanical load-bearing and energy dissipation capacities. The interface adhesive candidates were carefully selected to cover a wide range of base mechanical properties. Macroscale stress–strain responses of the foam stacks were characterized by quasi-static and dynamic loading conditions, supplemented by DIC strain field measurements. The results obtained herein indicate that the macroscale stress–strain and strain energy dissipation of a bilayer density-graded foam stack can be varied with respect to the properties of the adhesive interlayers. When it was subjected to a low rate of uniaxial compression, a stiff thermoset adhesive was shown to simultaneously improve the strength and energy dissipation capacities of the foam stack at the expense of energy dissipation efficiency. Similar behaviors were observed when the foam stacks were subjected to controlled-impact loading conditions. On the other hand, a mechanically compliant adhesive foam interlayer (with properties comparable to the base foam constituents) led to an enhanced energy absorption efficiency and a slightly increased densification strain. Full-field strain measurements suggest that the strain concentration due to sharp property gradients in the vicinity of the adhesive interlayers is more severe in the case of stiff thermoset adhesives. While not characterized herein, such strong strain gradients are likely to cause interface damage (in the form of delamination) when the foam stack is subjected to repeated loading. A detailed investigation of such interfacial failure mechanisms is only possible through the quantification of interfacial energy (or work of adhesion) in a progressively damaged interface.45 Nevertheless, the findings reported in this work highlight the significance of properly selected adhesives as a practical means for the simultaneous improvement of strength and energy dissipation characteristics in density-graded and functionally graded foam structures.

Acknowledgments

The authors wish to thank Yazeed Kokash, Jacob Porretta, and Damian Cuevas for assisting with experimental measurements.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c03212.

  • Schematic illustration of the fabrication process for graded foam structures (PDF)

Author Contributions

K.Z.U. and I.A.A. developed the methodology, performed experimental measurements, and carried out quasi-static experimental analyses and modeling. B.K. supervised the quasi-static measurements, performed the quasi-static analysis, and assisted in the analysis of the impact experiments. G.Y. supervised impact tests, performed dynamic analyses, and assisted in the quasi-static analyses. B.K. and G.Y. conceived the idea, acquired funding, and directed the research. All authors participated in writing the manuscript.

This material is based upon work supported by the National Science Foundation under Grant No. 2035660 (B.K.) and Grant No. 2035663 (G.Y.). This project has also been funded in part by Grant No. PC 46–22 (B.K.) from the New Jersey Health Foundation.

The authors declare no competing financial interest.

Supplementary Material

ao2c03212_si_001.pdf (124.9KB, pdf)

References

  1. Sun Y.; Li Q. M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. 10.1016/j.ijimpeng.2017.10.006. [DOI] [Google Scholar]
  2. Ousji H.; Belkassem B.; Louar M. A.; Reymen B.; Martino J.; Lecompte D.; Pyl L.; Vantomme J. Air-blast response of sacrificial cladding using low density foams: Experimental and analytical approach. Int. J. Mech. Sci. 2017, 128, 459–474. 10.1016/j.ijmecsci.2017.05.024. [DOI] [Google Scholar]
  3. Ouellet S.; Cronin D. S.; Moulton J.; Petel O. E. High rate characterization of polymeric closed-cell foams: challenges related to size effects. Dynam. Behav. Mater. 2013, 1, 21–28. [Google Scholar]
  4. Rahman O.; Uddin K. Z.; Muthulingam J.; Youssef G.; Shen C.; Koohbor B. Density-Graded Cellular Solids: Mechanics, Fabrication, and Applications. Adv. Eng. Mater. 2022, 24, 2100646. 10.1002/adem.202100646. [DOI] [Google Scholar]
  5. Koohbor B.; Kidane A. Design optimization of continuously and discretely graded foam materials for efficient energy absorption. Mater. Design 2016, 102, 151–161. 10.1016/j.matdes.2016.04.031. [DOI] [Google Scholar]
  6. Bates S. R.G.; Farrow I. R.; Trask R. S. Compressive behaviour of 3D printed thermoplastic polyurethane honeycombs with graded densities. Mater. Design 2019, 162, 130–142. 10.1016/j.matdes.2018.11.019. [DOI] [Google Scholar]
  7. Rahman O.; Koohbor B. Optimization of energy absorption performance of polymer honeycombs by density gradation. Compos. Part C 2020, 3, 100052. 10.1016/j.jcomc.2020.100052. [DOI] [Google Scholar]
  8. Traugutt N. A.; Mistry D.; Luo C.; Yu K.; Ge Q.; Yakacki C. M. Liquid-crystal-elastomer-based dissipative structures by digital light processing 3D printing. Adv. Mater. 2020, 32 (28), 2000797. 10.1002/adma.202000797. [DOI] [PubMed] [Google Scholar]
  9. Youssef G.; Reed N.. Scalable manufacturing method of property-tailorable polyurea foam. U.S. Patent 10,899,903, 2021.
  10. Pagliocca N.; Uddin K. Z.; Anni I. A.; Shen C.; Youssef G.; Koohbor B. Flexible planar metamaterials with tunable Poisson’s ratios. Mater. Design 2022, 215, 110446. 10.1016/j.matdes.2022.110446. [DOI] [Google Scholar]
  11. Zhang W.; Zhao S.; Scarpa F.; Wang J.; Sun R. In-plane mechanical behavior of novel auxetic hybrid metamaterials. Thin Wall Struct 2021, 159, 107191. 10.1016/j.tws.2020.107191. [DOI] [Google Scholar]
  12. Gupta N. A functionally graded syntactic foam material for high energy absorption under compression. Mater. Lett. 2007, 61 (4–5), 979–982. 10.1016/j.matlet.2006.06.033. [DOI] [Google Scholar]
  13. Sun G.; Wang E.; Wang H.; Xiao Z.; Li Q. Low-velocity impact behaviour of sandwich panels with homogeneous and stepwise graded foam cores. Mater. Design 2018, 160, 1117–1136. 10.1016/j.matdes.2018.10.047. [DOI] [Google Scholar]
  14. Uddin K. Z.; Youssef G.; Trkov M.; Seyyedhosseinzadeh H.; Koohbor B. Gradient optimization of multi-layered density-graded foam laminates for footwear material design. J. Biomech 2020, 109, 109950. 10.1016/j.jbiomech.2020.109950. [DOI] [PubMed] [Google Scholar]
  15. Uddin K. Z.; Koohbor B. Gradient optimization of transversely graded Ti-TiB structures for enhanced fracture resistance. Int. J. Mech. Sci. 2020, 187, 105917. 10.1016/j.ijmecsci.2020.105917. [DOI] [Google Scholar]
  16. Li S.; Li Q. Response of functionally graded polymeric foam under axial compression. Int. J. Mech. Sci. 2021, 210, 106750. 10.1016/j.ijmecsci.2021.106750. [DOI] [Google Scholar]
  17. Koohbor B.; Ravindran S.; Kidane A. In situ deformation characterization of density-graded foams in quasi-static and impact loading conditions. Int. J. Impact Eng. 2021, 150, 103820. 10.1016/j.ijimpeng.2021.103820. [DOI] [Google Scholar]
  18. Guin W. E.; Wang J. Theoretical model of adhesively bonded single lap joints with functionally graded adherends. Eng. Struct 2016, 124, 316–332. 10.1016/j.engstruct.2016.06.036. [DOI] [Google Scholar]
  19. Wu P.; Yang Z.; Huang X.; Liu W.; Fang H. Exact solutions for multilayer functionally graded beams bonded by viscoelastic interlayer considering memory effect. Compos. Struct 2020, 249, 112492. 10.1016/j.compstruct.2020.112492. [DOI] [Google Scholar]
  20. Volkersen O. Rivet strength distribution in tensile-stressed rivet joints with constant cross-section. Luftfahrtforschung 1938, 15 (1), 41–47. [Google Scholar]
  21. Liu J. L.; Xia R.; Zhou X. A new look on wetting models: continuum analysis. Sci. China Phys. Mech 2012, 55 (11), 2158–2166. 10.1007/s11433-012-4895-2. [DOI] [Google Scholar]
  22. Durodola J. Functionally graded adhesive joints–A review and prospects. Int. J. Adhes. Adhes 2017, 76, 83–89. 10.1016/j.ijadhadh.2017.02.008. [DOI] [Google Scholar]
  23. Sancaktar E.; Kumar S. Selective use of rubber toughening to optimize lap-joint strength. J. Adhes. Sci. Technol. 2000, 14 (10), 1265–1296. 10.1163/156856100742195. [DOI] [Google Scholar]
  24. Pires I.; Quintino L.; Durodola J.; Beevers A. Performance of bi-adhesive bonded aluminium lap joints. Int. J. Adhes. Adhes 2003, 23 (3), 215–223. 10.1016/S0143-7496(03)00024-1. [DOI] [Google Scholar]
  25. Fitton M. D.; Broughton J. Variable modulus adhesives: an approach to optimized joint performance. Int. J. Adhes. Adhes 2005, 25 (4), 329–336. 10.1016/j.ijadhadh.2004.08.002. [DOI] [Google Scholar]
  26. Vallée T.; Tannert T.; Murcia-Delso J.; Quinn D. J. Influence of stress-reduction methods on the strength of adhesively bonded joints composed of orthotropic brittle adherends. Int. J. Adhes. Adhes 2010, 30 (7), 583–594. 10.1016/j.ijadhadh.2010.05.007. [DOI] [Google Scholar]
  27. Carbas R.; Da Silva L.; Critchlow G. Adhesively bonded functionally graded joints by induction heating. Int. J. Adhes. Adhes 2014, 48, 110–118. 10.1016/j.ijadhadh.2013.09.045. [DOI] [Google Scholar]
  28. Kumar S.; Wardle B. L.; Arif M. F. Strength and performance enhancement of bonded joints by spatial tailoring of adhesive compliance via 3D printing. ACS Appl. Mater. Inter 2017, 9 (1), 884–891. 10.1021/acsami.6b13038. [DOI] [PubMed] [Google Scholar]
  29. Budhe S.; Banea M.; De Barros S.; Silva Da An updated review of adhesively bonded joints in composite materials. Int. J. Adhes. Adhes 2017, 72, 30–42. 10.1016/j.ijadhadh.2016.10.010. [DOI] [Google Scholar]
  30. Do S.; Huynh N. U.; Reed N.; Mohammad Shaik A.; Nacy S.; Youssef G. Partially-Perforated Self-Reinforced Polyurea Foams. Appl. Sci. 2020, 10 (17), 5869. 10.3390/app10175869. [DOI] [Google Scholar]
  31. Koohbor B.; Blourchian A.; Uddin K. Z.; Youssef G. Characterization of Energy Absorption and Strain Rate Sensitivity of a Novel Elastomeric Polyurea Foam. Adv. Eng. Mater. 2021, 23 (1), 2000797. 10.1002/adem.202000797. [DOI] [Google Scholar]
  32. Reed N.; Huynh N. U.; Rosenow B.; Manlulu K.; Youssef G. Synthesis and characterization of elastomeric polyurea foam. J. Appl. Polym. Sci. 2020, 137 (26), 48839. 10.1002/app.48839. [DOI] [Google Scholar]
  33. Youssef G.; Nacy S.; Huynh N. U. Mechanics of Microspheres Reinforced Hollow Microcells. J. Appl. Mech 2021, 88 (4), 041009. 10.1115/1.4049329. [DOI] [Google Scholar]
  34. Koohbor B.; Pagliocca N.; Youssef G. A multiscale experimental approach to characterize micro-to-macro transition length scale in polymer foams. Mech. Mater. 2021, 161, 104006. 10.1016/j.mechmat.2021.104006. [DOI] [Google Scholar]
  35. Youssef G.; Reed N.; Huynh N. U.; Rosenow B.; Manlulu K. Experimentally-validated predictions of impact response of polyurea foams using viscoelasticity based on bulk properties. Mech. Mater. 2020, 148, 103432. 10.1016/j.mechmat.2020.103432. [DOI] [Google Scholar]
  36. Koohbor B.; Ravindran S.; Kidane A. Experimental determination of Representative Volume Element (RVE) size in woven composites. Opt. Laser. Eng. 2017, 90, 59–71. 10.1016/j.optlaseng.2016.10.001. [DOI] [Google Scholar]
  37. Avalle M.; Belingardi G.; Montanini R. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact Eng. 2001, 25 (5), 455–472. 10.1016/S0734-743X(00)00060-9. [DOI] [Google Scholar]
  38. Zhang J.; Lu G.; Ruan D.; Huang X. Experimental observations of the double shock deformation mode in density graded honeycombs. Int. J. Impact Eng. 2019, 134, 103386. 10.1016/j.ijimpeng.2019.103386. [DOI] [Google Scholar]
  39. Youssef G.Applied Mechanics of Polymers – Properties, Processing, and behavior Elsevier: 2022. [Google Scholar]
  40. Gupta V.; Crum R.; Gámez C.; Ramirez B.; Le N.; Youssef G.; Citron J.; Kim A.; Jain A.; Misra U.. Adhesive and ultrahigh strain rate properties of polyurea under tension, tension/shear, and pressure/shear loadings with applications to multilayer armors. Elastomeric Polymers with High Rate Sensitivity: Applications in Blast, Shockwave, and Penetration Mechanics; Elsevier: 2015; Vol. 1, pp 71–92. [Google Scholar]
  41. Gupta V.; Youssef G. Orientation-dependent impact behavior of polymer/EVA bilayer specimens at long wavelengths. Exp. Mech 2014, 54, 1133–1137. 10.1007/s11340-014-9854-6. [DOI] [Google Scholar]
  42. Koohbor B.; Youssef G.; Uddin K. Z.; Kokash Y. Dynamic behavior and impact tolerance of elastomeric foams subjected to multiple impact conditions. J. Dynam. Behav. Mater. 2022, 8, 359–370. 10.1007/s40870-022-00340-z. [DOI] [Google Scholar]
  43. Youssef G.; Kokash Y.; Uddin K. Z.; Koohbor B. Density-dependent impact resilience and auxeticity of elastomeric polyurea foams. Adv. Eng. Mater. 2022, 2200578. 10.1002/adem.202200578. [DOI] [Google Scholar]
  44. Forero Rueda M. A.; Cui L.; Gilchrist M. D. Optimisation of energy absorbing liner for equestrian helmets, Part I: Layered foam liner. Mater. Design 2009, 30 (9), 3405–3413. 10.1016/j.matdes.2009.03.037. [DOI] [Google Scholar]
  45. Liu J. -L; Xia R. A unified analysis of a micro-beam, droplet and CNT ring adhered on a substrate: Calculation of variation with movable boundaries. Acta Mech. Sinica 2013, 29 (1), 62–72. 10.1007/s10409-012-0202-8. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c03212_si_001.pdf (124.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES