Summary
When validating a risk model in an independent cohort, some predictors may be missing for some subjects. Missingness can be unplanned or by design, as in case-cohort or nested case–control studies, in which some covariates are measured only in subsampled subjects. Weighting methods and imputation are used to handle missing data. We propose methods to increase the efficiency of weighting to assess calibration of a risk model (i.e. bias in model predictions), which is quantified by the ratio of the number of observed events,  , to expected events,
, to expected events,  , computed from the model. We adjust known inverse probability weights by incorporating auxiliary information available for all cohort members. We use survey calibration that requires the weighted sum of the auxiliary statistics in the complete data subset to equal their sum in the full cohort. We show that a pseudo-risk estimate that approximates the actual risk value but uses only variables available for the entire cohort is an excellent auxiliary statistic to estimate
, computed from the model. We adjust known inverse probability weights by incorporating auxiliary information available for all cohort members. We use survey calibration that requires the weighted sum of the auxiliary statistics in the complete data subset to equal their sum in the full cohort. We show that a pseudo-risk estimate that approximates the actual risk value but uses only variables available for the entire cohort is an excellent auxiliary statistic to estimate  . We derive analytic variance formulas for
. We derive analytic variance formulas for 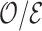 with adjusted weights. In simulations, weight adjustment with pseudo-risk was much more efficient than inverse probability weighting and yielded consistent estimates even when the pseudo-risk was a poor approximation. Multiple imputation was often efficient but yielded biased estimates when the imputation model was misspecified. Using these methods, we assessed calibration of an absolute risk model for second primary thyroid cancer in an independent cohort.
with adjusted weights. In simulations, weight adjustment with pseudo-risk was much more efficient than inverse probability weighting and yielded consistent estimates even when the pseudo-risk was a poor approximation. Multiple imputation was often efficient but yielded biased estimates when the imputation model was misspecified. Using these methods, we assessed calibration of an absolute risk model for second primary thyroid cancer in an independent cohort.
Keywords: Case-cohort study, External validation, Missing, Model calibration, Nested case–control study, Pseudo-risk model, Survey calibration, Weight adjustment
1. Introduction
Statistical models that predict risk of disease incidence or mortality following disease onset have applications in clinical and public health settings. They are used to inform decisions for preventive interventions or treatments and to identify high-risk individuals for intensive screening for early detection of disease.
Once a risk model is developed, before recommending it for broader use, one needs to assess how valid model predictions are, ideally in independent data. Two popular measures of predictive performance of a risk model are calibration and discrimination. Calibration assesses bias in model predictions, and discrimination quantifies how different the predicted risks are in individuals with events compared to those without events. Discrimination is typically measured by the area under the receiver operator characteristics curve (AUC) (Pepe, 2003, p. 67). Here, we focus on calibration, as unbiased predictions are a key model feature for clinical and public health applications. We estimate calibration using the ratio of the number of events  predicted by the risk model, to the number of observed events,
predicted by the risk model, to the number of observed events, 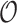 , that arise in an independent validation cohort, overall or in subgroups defined by predictors in the model or by risk deciles (Pfeiffer and Gail, 2017, Chapter 6). Other goodness of fit tests have been proposed, e.g., by Gong and others (2014). However, such comparisons are impeded when data on some of the model predictors are missing in the validation cohort. The example that motivated our work is an absolute risk model for second primary thyroid cancer (SPTC), developed using data from the Childhood Cancer Survivor Study (CCSS) in the USA, Canada, and Norway (Kovalchik and others, 2013). Validation of this model in the only two other such cohorts worldwide, the French and British childhood cancer survivors, was hampered by missing model predictors. In this article, we thus propose and study various approaches to accommodate missing data in the validation of risk prediction models. We assume the independent validation data arise from a two-phase sampling design from a well-defined cohort. In phase 1, the validation cohort is sampled from a superpopulation but not all model predictors are measured on all cohort members. Specifically, we consider data missing completely at random or at random due to phase 2 subsampling based on two common designs for epidemiologic studies, the case-cohort design (Prentice, 1986) and the nested case–control design (Langholz and Thomas, 1990). Some model predictors are observed on everyone in the cohort (phase 1), while others are only observed on individuals sampled into a second phase. A standard approach is to weigh the phase 2 sample back to the whole cohort, based on inverse probability of sampling weights (also called “design weights”). This method yields Horvitz–Thompson estimates of
, that arise in an independent validation cohort, overall or in subgroups defined by predictors in the model or by risk deciles (Pfeiffer and Gail, 2017, Chapter 6). Other goodness of fit tests have been proposed, e.g., by Gong and others (2014). However, such comparisons are impeded when data on some of the model predictors are missing in the validation cohort. The example that motivated our work is an absolute risk model for second primary thyroid cancer (SPTC), developed using data from the Childhood Cancer Survivor Study (CCSS) in the USA, Canada, and Norway (Kovalchik and others, 2013). Validation of this model in the only two other such cohorts worldwide, the French and British childhood cancer survivors, was hampered by missing model predictors. In this article, we thus propose and study various approaches to accommodate missing data in the validation of risk prediction models. We assume the independent validation data arise from a two-phase sampling design from a well-defined cohort. In phase 1, the validation cohort is sampled from a superpopulation but not all model predictors are measured on all cohort members. Specifically, we consider data missing completely at random or at random due to phase 2 subsampling based on two common designs for epidemiologic studies, the case-cohort design (Prentice, 1986) and the nested case–control design (Langholz and Thomas, 1990). Some model predictors are observed on everyone in the cohort (phase 1), while others are only observed on individuals sampled into a second phase. A standard approach is to weigh the phase 2 sample back to the whole cohort, based on inverse probability of sampling weights (also called “design weights”). This method yields Horvitz–Thompson estimates of 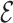 (Horvitz and Thompson, 1952). This approach, however, does not use any information available for individuals who were not in the phase 2 sample.
(Horvitz and Thompson, 1952). This approach, however, does not use any information available for individuals who were not in the phase 2 sample.
Deville and Särndal (1992) introduced weight adjustment methods to incorporate such information, referred to as phase 1 information, by adjusting weights to improve efficiency. The adjusted weights are computed such that the weighted-total of auxiliary statistics in phase 2 equals their total in the entire cohort. Auxiliary statistics are functions of variables that measured on everyone in phase 1 and thus can be computed for all cohort members. Most important for gains in efficiency are the specific choices of auxiliary statistics. Using all available phase 1 data directly as auxiliary statistics is often computationally burdensome and not efficient. Thus, only selected variables should be used, and additionally, the specific functional form through which these variables are used in the auxiliary statistics impacts improvements in efficiency through its relation with the design weights (Wu and Sitter, 2001; Breidt and Opsomer, 2017). We propose to use pseudo-risk estimates which we compute based on full cohort (phase 1) information, for efficiently calibrating the design weights. Our approach is compared to multiple imputation, which is also popular for handling missing data (Rubin, 2004; White and Royston, 2009). The remainder of the article is organized as follows. After introducing notation and the general set-up (Section 2), we present three approaches, classical sampling probability weighting, weight adjustment, and multiple imputation, when covariates in validation data are missing completely at random, or missing by design due to case-cohort or nested case–control subsampling (Section 3). In Section 4, we derive the variance estimators for weight adjusted estimates of the  calibration measure. We compare these approaches in various simulated scenarios (Section 5) and for a real data example (Section 6), before closing with a discussion (Section 7). To avoid semantic confusion, the reader should distinguish “survey (or weight) calibration,” which is a method to improve efficiency of estimates, from “model calibration,” which assesses the degree of bias in a risk prediction model.
calibration measure. We compare these approaches in various simulated scenarios (Section 5) and for a real data example (Section 6), before closing with a discussion (Section 7). To avoid semantic confusion, the reader should distinguish “survey (or weight) calibration,” which is a method to improve efficiency of estimates, from “model calibration,” which assesses the degree of bias in a risk prediction model.
2. Notation and missing data set-up
2.1. Notation
The risk model  estimates the probability of a dichotomous event,
estimates the probability of a dichotomous event, 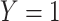 , occurring in the time interval of length
, occurring in the time interval of length 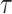 given the predictors
given the predictors  . Otherwise,
. Otherwise, 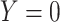 . Unless needed for clarity, we also denote the model by
. Unless needed for clarity, we also denote the model by 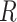 . This simple formulation applies to several important problems in clinical medicine and public health. A model
. This simple formulation applies to several important problems in clinical medicine and public health. A model  could be an absolute risk model, when
could be an absolute risk model, when 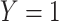 denotes developing a specific disease in a defined age interval,
denotes developing a specific disease in a defined age interval,  , in the presence of competing risks. An absolute risk model is also relevant when, following diagnosis,
, in the presence of competing risks. An absolute risk model is also relevant when, following diagnosis, 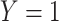 represents death in
represents death in 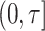 from the diagnosed disease in the presence of competing causes of death. Absent competing risks,
from the diagnosed disease in the presence of competing causes of death. Absent competing risks,  could refer to a pure risk model, for example when
could refer to a pure risk model, for example when 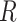 models overall survival after disease onset. We regard the risk model as fixed and assume that the data used to develop the model and those used for validation are independent.
models overall survival after disease onset. We regard the risk model as fixed and assume that the data used to develop the model and those used for validation are independent.
We assume that a cohort of  individuals is available to assess calibration (bias) of the risk model
individuals is available to assess calibration (bias) of the risk model  . For each individual
. For each individual  , we observe the outcome,
, we observe the outcome,  , and the time to event or censoring,
, and the time to event or censoring, 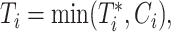 where
where 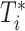 and
and 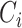 denote the event time and the censoring time, respectively. Here,
denote the event time and the censoring time, respectively. Here, 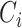 is assumed to be independent of
is assumed to be independent of 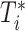 given
given  .
.
We call a model  well calibrated in the cohort if
well calibrated in the cohort if  for every value
for every value  . If the model is well calibrated, then
. If the model is well calibrated, then 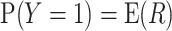 , overall or in subgroups (Pfeiffer and Gail, 2017, Chapter 6). Assuming that the model predictors
, overall or in subgroups (Pfeiffer and Gail, 2017, Chapter 6). Assuming that the model predictors 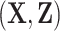 are available for all subjects in the validation cohort, measures of model calibration thus typically compare the observed number of events in
are available for all subjects in the validation cohort, measures of model calibration thus typically compare the observed number of events in 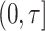 ,
,  and the expected number of events computed from the model,
and the expected number of events computed from the model, 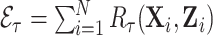 for a given risk projection period
for a given risk projection period 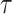 .
.
In the presence of censoring, 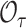 is well defined as above, but the computing of
is well defined as above, but the computing of  needs to be modified, and for individuals who are censored before
needs to be modified, and for individuals who are censored before  (for absolute risk models only administrative censoring or loss to follow-up need to be considered), risk is projected up to the censoring time
(for absolute risk models only administrative censoring or loss to follow-up need to be considered), risk is projected up to the censoring time 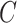 . As the outcome for censored individuals is also only observable until time
. As the outcome for censored individuals is also only observable until time 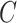 , this approach leads to unbiased assessment of calibration. The statistic we focus on in this article is the observed-to-expected ratio,
, this approach leads to unbiased assessment of calibration. The statistic we focus on in this article is the observed-to-expected ratio,
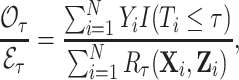 |
(2.1) |
which estimates the corresponding superpopulation quantity,  . When all risk model predictors
. When all risk model predictors 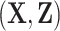 are observed, inference on
are observed, inference on 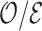 derives from i.i.d. phase 1 sampling of
derives from i.i.d. phase 1 sampling of  from the superpopulation. For rare outcomes
from the superpopulation. For rare outcomes  can be regarded as fixed and
can be regarded as fixed and 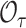 as a Poisson random variable. With missing data however, additional variation in estimates of
as a Poisson random variable. With missing data however, additional variation in estimates of 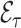 arises from phase 2 sampling. We next describe settings with missingness and the impact on inference when
arises from phase 2 sampling. We next describe settings with missingness and the impact on inference when  has to be estimated. We emphasize that
has to be estimated. We emphasize that  and
and 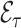 are parameters of the sampled validation cohort
are parameters of the sampled validation cohort 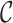 whereas
whereas  and
and 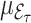 are the corresponding means in the superpopulation.
are the corresponding means in the superpopulation.
2.2. Patterns of missing model predictors and inclusion probability
We divide the model predictors into two categories: predictors  that are available on everybody in the validation cohort (phase 1), and predictors
that are available on everybody in the validation cohort (phase 1), and predictors 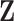 that are only observed for a subsample of individuals, those included in phase 2. We let
that are only observed for a subsample of individuals, those included in phase 2. We let 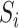 denote a sampling indicator that is 1 if subject
denote a sampling indicator that is 1 if subject 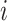 is included in phase 2 and 0 otherwise, for a given cohort
is included in phase 2 and 0 otherwise, for a given cohort 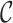 .
.
The inclusion probabilities 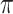 depend on the missingness mechanisms for
depend on the missingness mechanisms for  . Under missing completely at random (MCAR), missingness of
. Under missing completely at random (MCAR), missingness of  does not depend on any other information and
does not depend on any other information and  is constant for all
is constant for all  where
where 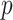 is the Bernoulli sampling inclusion probability. Under missing at random (MAR), the patterns of the missing covariates
is the Bernoulli sampling inclusion probability. Under missing at random (MAR), the patterns of the missing covariates 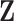 depend on other observed quantities. We consider the two most popular subsampling strategies for cohorts that fall into the MAR category, the case-cohort (CC) design (Prentice, 1986) and the nested case–control (NCC) design (Langholz and Thomas, 1990), where missingness of
depend on other observed quantities. We consider the two most popular subsampling strategies for cohorts that fall into the MAR category, the case-cohort (CC) design (Prentice, 1986) and the nested case–control (NCC) design (Langholz and Thomas, 1990), where missingness of  depends on outcome status,
depends on outcome status, 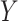 . These designs are particularly relevant for large cohorts and rare outcomes, where it is more cost-effective to measure expensive covariates on all subjects who experience the event of interest during follow-up (cases), but only on a small subset of individuals who have not experienced the event (controls). For the CC design, a random subcohort is selected at the beginning of the follow-up with a constant inclusion probability
. These designs are particularly relevant for large cohorts and rare outcomes, where it is more cost-effective to measure expensive covariates on all subjects who experience the event of interest during follow-up (cases), but only on a small subset of individuals who have not experienced the event (controls). For the CC design, a random subcohort is selected at the beginning of the follow-up with a constant inclusion probability 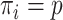 and all cases (
and all cases ( ) that develop outside the subcohort are included with
) that develop outside the subcohort are included with  . For the NCC design, every time a case develops during follow-up
. For the NCC design, every time a case develops during follow-up 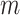 individuals from those at risk are selected, and
individuals from those at risk are selected, and  are measured for all cases (
are measured for all cases ( if
if  ) and those selected controls. Following Samuelsen (1997),
) and those selected controls. Following Samuelsen (1997),  for
for 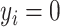 is
is 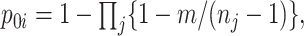 where the product is taken over all
where the product is taken over all 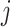 ’s with
’s with 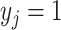 and
and  ;
;  is the cohort entry time of subject
is the cohort entry time of subject 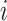 ,
, 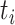 is the time to event or censoring, and
is the time to event or censoring, and 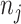 is the number of those at risk at
is the number of those at risk at 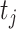 . For MAR settings other than CC and NCC the methods we develop here can be applied as well, assuming that the inclusion probabilities are known or can be estimated under the MAR assumption.
. For MAR settings other than CC and NCC the methods we develop here can be applied as well, assuming that the inclusion probabilities are known or can be estimated under the MAR assumption.
In summary, the inclusion probabilities for individuals  are
are
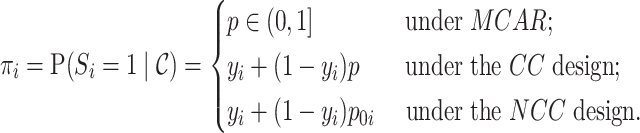 |
(2.2) |
3. Estimation of the expected number of events with missing covariates
3.1. Adjusted inclusion probability weighting
As the model predictors 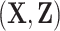 are completely observed for all individuals in phase 2, an estimate of
are completely observed for all individuals in phase 2, an estimate of 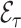 , the expected number of events that occurred in the follow-up period
, the expected number of events that occurred in the follow-up period 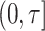 , is
, is
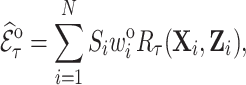 |
(3.3) |
where 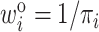 is the inverse of the inclusion probability defined in (2.2).
is the inverse of the inclusion probability defined in (2.2).
However, 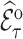 , also known as the Horvitz–Thompson estimate (Horvitz and Thompson, 1952), only uses phase 2 information. We thus use survey calibration to incorporate information on the variables
, also known as the Horvitz–Thompson estimate (Horvitz and Thompson, 1952), only uses phase 2 information. We thus use survey calibration to incorporate information on the variables  and possibly additional variables that are available on everyone in the cohort into the weights, to increase the efficiency of the weighted estimate
and possibly additional variables that are available on everyone in the cohort into the weights, to increase the efficiency of the weighted estimate 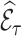 . Survey calibration adjusts the inclusion probability weights
. Survey calibration adjusts the inclusion probability weights 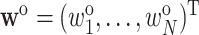 via auxiliary statistics, denoted by
via auxiliary statistics, denoted by 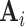 , which are based on the phase 1 variables, so that the weighted sum of
, which are based on the phase 1 variables, so that the weighted sum of  equals the total sum of
equals the total sum of  in the cohort, which is known (Deville and Särndal, 1992). The new adjusted weights
in the cohort, which is known (Deville and Särndal, 1992). The new adjusted weights 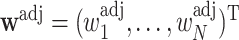 satisfy
satisfy
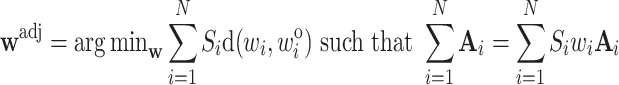 |
(3.4) |
for some distance measure 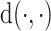 . After weight adjustment,
. After weight adjustment, 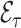 is estimated by
is estimated by
 |
(3.5) |
The constrained optimization problem (3.4) is solved by applying Newton’s method to a Lagrangian function. Here, we use the distance measure 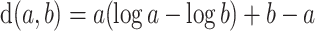 (Case 2 of Deville and Särndal (1992)), which is called raking or exponential tilting. This choice is appealing as it always leads to a solution of the form
(Case 2 of Deville and Särndal (1992)), which is called raking or exponential tilting. This choice is appealing as it always leads to a solution of the form  , where
, where 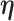 is a vector of Lagrangian multipliers. In other words, the adjusted weight is a positive multiple of the original weight. See Appendix A of the Supplementary material available at Biostatistics online for further details on the computation. To avoid confusion, we henceforth call survey calibration weight adjustment while “calibration” refers to model calibration.
is a vector of Lagrangian multipliers. In other words, the adjusted weight is a positive multiple of the original weight. See Appendix A of the Supplementary material available at Biostatistics online for further details on the computation. To avoid confusion, we henceforth call survey calibration weight adjustment while “calibration” refers to model calibration.
The weighted estimator (3.3) is design unbiased by the definition of the inclusion probability weights, i.e., 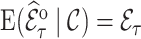 and therefore unbiased for
and therefore unbiased for  as
as 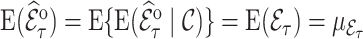 . The weight-adjusted estimator defined in (3.5) is asymptotically design unbiased and
. The weight-adjusted estimator defined in (3.5) is asymptotically design unbiased and 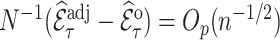 , if (3.4) has a solution
, if (3.4) has a solution 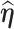 , and
, and 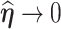 as
as 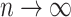 , where
, where  is the phase 2 sample size. Thus the weight adjusted estimator is also asymptotically unbiased for
is the phase 2 sample size. Thus the weight adjusted estimator is also asymptotically unbiased for 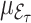 . See the result 4 and remark of Deville and Särndal (1992, p. 379) for more details.
. See the result 4 and remark of Deville and Särndal (1992, p. 379) for more details.
The key in gaining efficiency is choosing auxiliary statistics 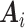 whose sum is strongly correlated with a target estimator that one would use if there were no missing data, in our case
whose sum is strongly correlated with a target estimator that one would use if there were no missing data, in our case 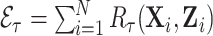 . The weight-adjusted estimator is asymptotically equivalent to an estimator (Deville and Särndal, 1992, Result 5) constructed by weighted linear regression of
. The weight-adjusted estimator is asymptotically equivalent to an estimator (Deville and Särndal, 1992, Result 5) constructed by weighted linear regression of  on
on 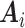 in phase 2. Larger correlations between
in phase 2. Larger correlations between 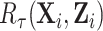 and
and  lead to a smaller variance of
lead to a smaller variance of 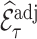 , as the residual error from the regression is reduced. Note that the choice of
, as the residual error from the regression is reduced. Note that the choice of  does not impact the consistency of
does not impact the consistency of  but can affect its variance.
but can affect its variance.
For our target estimator, 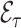 , we suggest
, we suggest 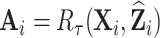 as auxiliary statistics, where
as auxiliary statistics, where  denotes a predicted value. We call
denotes a predicted value. We call 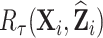 pseudo-risk estimates, that can be viewed as the first term in a Taylor expansion of the true risk
pseudo-risk estimates, that can be viewed as the first term in a Taylor expansion of the true risk  around
around 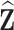 :
:  . Better prediction of
. Better prediction of  results in smaller values of
results in smaller values of  and therefore higher correlations between
and therefore higher correlations between 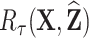 and
and  and more precise estimates of
and more precise estimates of 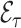 . In Section 4.1 where we derive the analytic variance of
. In Section 4.1 where we derive the analytic variance of  , we discuss this point further.
, we discuss this point further.
To predict a univariate 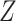 , one can use a generalized linear model (GLM) weighted by
, one can use a generalized linear model (GLM) weighted by  , e.g., weighted logistic or weighted linear regression in the phase 2 data, with predictors
, e.g., weighted logistic or weighted linear regression in the phase 2 data, with predictors 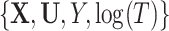 that are available in phase 1. Here,
that are available in phase 1. Here, 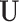 denotes a vector of other ancillary predictors for
denotes a vector of other ancillary predictors for 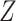 . For multivariate
. For multivariate 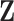 , one can fit marginal GLMs to each component of
, one can fit marginal GLMs to each component of 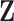 or use a multivariate linear regression model. As alternatives to
or use a multivariate linear regression model. As alternatives to  , estimates of the cumulative baseline hazard,
, estimates of the cumulative baseline hazard, 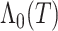 , or the cumulative hazard,
, or the cumulative hazard, 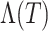 , could be used. We then compute pseudo-risk estimates
, could be used. We then compute pseudo-risk estimates 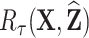 using the predicted values
using the predicted values 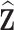 for all individuals in the cohort, even for those included in phase 2.
for all individuals in the cohort, even for those included in phase 2.
The inclusion weights are then calibrated using  to improve the estimation of
to improve the estimation of 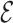 . The first component of
. The first component of 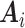 is
is  for all observations, leading to the constraint
for all observations, leading to the constraint  and thus standardizing the adjusted weights. For example, when
and thus standardizing the adjusted weights. For example, when 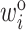 is constant (e.g., under MCAR) and adjusted using only
is constant (e.g., under MCAR) and adjusted using only 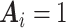 , then one would obtain
, then one would obtain 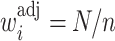 for all
for all 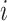 where
where  . These
. These 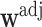 are also known as empirical weights (Robins and others, 1994, Section 6.1).
are also known as empirical weights (Robins and others, 1994, Section 6.1).
Figure 1 summarizes the weight adjustment methods based on pseudo-risk estimates.
Fig. 1.
Diagram of obtaining design weights and adjusted weights for estimating  , where
, where 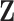 are partially missing in a validation cohort. Without loss of generality we assume that
are partially missing in a validation cohort. Without loss of generality we assume that 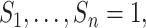 and
and 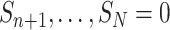 . The estimator of
. The estimator of 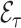 with adjusted weights,
with adjusted weights,  , which incorporate all available information in a full cohort via pseudo-risk estimates, is
, which incorporate all available information in a full cohort via pseudo-risk estimates, is 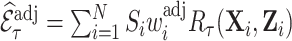
3.2. Multiple imputation
As an alternative to weighting, 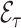 can also be estimated using multiple imputation for the missing predictors (Rubin, 2004). In the first step one creates
can also be estimated using multiple imputation for the missing predictors (Rubin, 2004). In the first step one creates 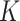 complete copies of a dataset, where each is based on imputed missing values from an imputation model for their predictive distribution given the observed data. Such models are implemented in many statistical packages, e.g., mice in R uses multivariate imputation by chained equations (van Buuren and Groothuis-Oudshoorn, 2011). In the second step, one computes the statistic of interest for each of the
complete copies of a dataset, where each is based on imputed missing values from an imputation model for their predictive distribution given the observed data. Such models are implemented in many statistical packages, e.g., mice in R uses multivariate imputation by chained equations (van Buuren and Groothuis-Oudshoorn, 2011). In the second step, one computes the statistic of interest for each of the 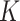 complete datasets, and uses their empirical mean as the final estimate.
complete datasets, and uses their empirical mean as the final estimate.
Using this approach, we estimate 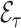 as
as
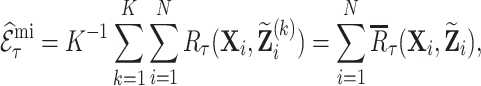 |
(3.6) |
where 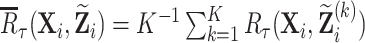 is the mean of risks that are evaluated at imputed values
is the mean of risks that are evaluated at imputed values  for the
for the  th imputation. For phase 2 individuals whose
th imputation. For phase 2 individuals whose 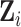 are observed (i.e., for individuals
are observed (i.e., for individuals  with
with 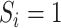 ),
), 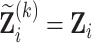 for
for 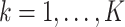 .
.
We use all observed data 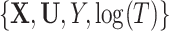 in the imputation, including survival information, as recommended by White and Royston (2009). If the sampling pattern is related to missing covariates, the inclusion probability weights,
in the imputation, including survival information, as recommended by White and Royston (2009). If the sampling pattern is related to missing covariates, the inclusion probability weights,  , should be used for the imputation as well.
, should be used for the imputation as well.
When the imputation model is misspecified however, estimates of 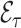 can be biased (Keogh and others, 2018). Unlike weight adjustment, the multiple imputation approach directly uses the imputed
can be biased (Keogh and others, 2018). Unlike weight adjustment, the multiple imputation approach directly uses the imputed 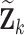 ’s to estimate
’s to estimate  so that
so that 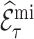 is susceptible to bias if the imputed values of
is susceptible to bias if the imputed values of  are biased due to misspecification of the imputation model. We confirmed this observation in simulations (Scenario II in Section 5.2).
are biased due to misspecification of the imputation model. We confirmed this observation in simulations (Scenario II in Section 5.2).
4. Variance estimation
4.1. Variance of 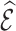
To ease the notational burden, we assume that the projection period 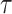 is fixed, and omitting the subscript
is fixed, and omitting the subscript 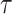 , use the notations
, use the notations 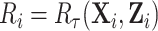 . We decompose the variance by conditioning on the cohort
. We decompose the variance by conditioning on the cohort 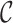 as
as
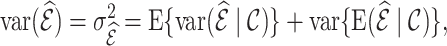 |
(4.7) |
where the first term presents the variance due to phase 2 sampling from 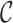 , and the second term presents the variance from sampling
, and the second term presents the variance from sampling 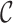 itself from an infinite superpopulation.
itself from an infinite superpopulation.
Conditionally on the cohort 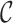 , the weights,
, the weights,  or
or  , and risk values,
, and risk values, 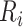 , are fixed, and only the inclusion indicators
, are fixed, and only the inclusion indicators  are random. For the weighted estimators (3.3) and (3.5) of
are random. For the weighted estimators (3.3) and (3.5) of 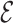 ,
, 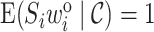 as
as 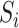 has a Bernoulli distribution with
has a Bernoulli distribution with 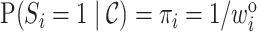 . Thus,
. Thus, 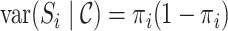 and
and  for
for 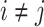 , where
, where 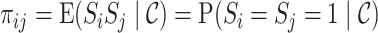 is a joint inclusion probability.
is a joint inclusion probability.
Letting 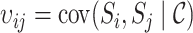 , the variance of inverse probability weighted estimator (3.3) is
, the variance of inverse probability weighted estimator (3.3) is
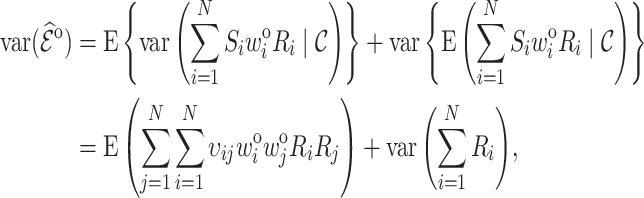 |
(4.8) |
which is estimated by
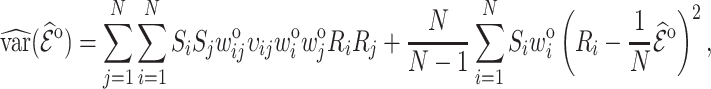 |
(4.9) |
where 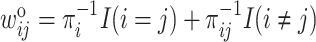 . Both
. Both  and
and 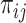 depend on the missingness mechanism: MCAR or CC samples are independent, and thus
depend on the missingness mechanism: MCAR or CC samples are independent, and thus 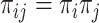 . NCC samples are dependent and
. NCC samples are dependent and  where the product is taken over all
where the product is taken over all 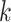 such that
such that  ,
, 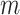 denotes the number of controls selected for each case, and
denotes the number of controls selected for each case, and 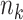 is the number of subjects at risk at
is the number of subjects at risk at  (Samuelsen, 1997).
(Samuelsen, 1997).
The variance of the weight-adjusted estimator (3.5) is obtained following similar steps, with further details given in Appendix B of the Supplementary material available at Biostatistics online, as
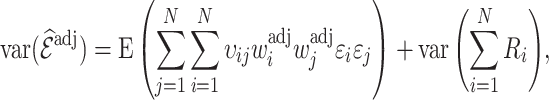 |
(4.10) |
where 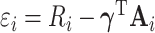 denotes a residual of the adjusted-weighted linear model that regresses
denotes a residual of the adjusted-weighted linear model that regresses 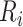 on
on  with a regression coefficient
with a regression coefficient 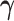 . Stronger correlation of the auxiliary statistic
. Stronger correlation of the auxiliary statistic 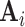 with
with  leads to smaller residuals, and thus a smaller first term in (4.10). Therefore, choosing the pseudo-risk estimate as an auxiliary statistic as suggested in Section 3.1 can lead to large improvements in efficiency of
leads to smaller residuals, and thus a smaller first term in (4.10). Therefore, choosing the pseudo-risk estimate as an auxiliary statistic as suggested in Section 3.1 can lead to large improvements in efficiency of  . An estimate of (4.10) is
. An estimate of (4.10) is
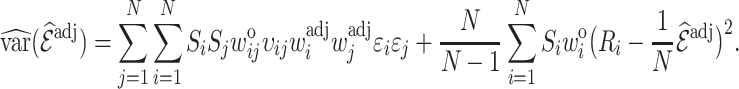 |
(4.11) |
Note that we weigh each term using the inclusion probability weights  , not
, not  , in (4.9) and (4.11) because the adjusted weights are tailored to estimate
, in (4.9) and (4.11) because the adjusted weights are tailored to estimate  efficiently, but not the variance of its estimator. Comparing the variance formulas in (4.8) and (4.10) shows that weight adjustment only affects the first term by replacing
efficiently, but not the variance of its estimator. Comparing the variance formulas in (4.8) and (4.10) shows that weight adjustment only affects the first term by replacing  with
with 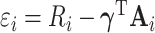 ; the second terms in both formulas are identical. See also Appendix B of Supplementary material available at Biostatistics online for the variance estimation when
; the second terms in both formulas are identical. See also Appendix B of Supplementary material available at Biostatistics online for the variance estimation when  is unknown and needs to be estimated.
is unknown and needs to be estimated.
The variance for the multiple imputation estimate (3.6), that accommodates the additional variation resulting from the imputations follows from Rubin’s formula (Rubin, 2004),
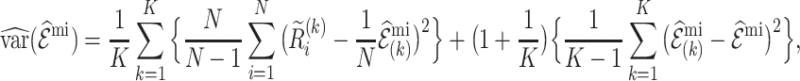 |
(4.12) |
where  and
and 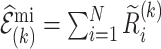 . Formula (4.12) can also be viewed as arising from the variance decomposition in (4.7) with conditioning on multiple imputed cohorts,
. Formula (4.12) can also be viewed as arising from the variance decomposition in (4.7) with conditioning on multiple imputed cohorts, 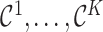 , where
, where 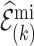 is an estimate of
is an estimate of 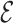 for each
for each 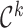 . The first term in (4.12) estimates the mean of the variances of
. The first term in (4.12) estimates the mean of the variances of 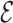 for each imputed dataset, and the second term estimates the variance between the imputed datasets.
for each imputed dataset, and the second term estimates the variance between the imputed datasets.
4.2. Variance of 
The variance of the target estimate, the ratio of observed and expected number of events,  , also depends on the variability of the observed number of events,
, also depends on the variability of the observed number of events, 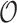 . When the outcome is rare, it is reasonable to assume that
. When the outcome is rare, it is reasonable to assume that  has a Poisson distribution with rate
has a Poisson distribution with rate  (Cameron and Trivedi, 2013, Chapter 1.1). We let
(Cameron and Trivedi, 2013, Chapter 1.1). We let  and
and 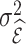 denote the mean and variance of the estimator
denote the mean and variance of the estimator 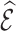 , respectively, and the covariance between
, respectively, and the covariance between 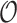 and
and 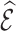 is denoted by
is denoted by  .
.
Using Taylor linearization,
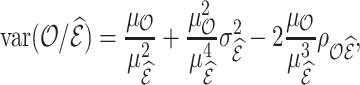 |
(4.13) |
which is estimated by
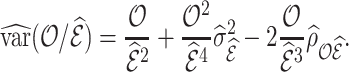 |
(4.14) |
For each approach,  is given in (4.9), (4.11), and (4.12), and
is given in (4.9), (4.11), and (4.12), and  is
is
 |
Note that the first term of the covariance, 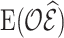 , is estimated by the sum of cases’ risk values. For
, is estimated by the sum of cases’ risk values. For 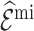 , (4.14) holds only when the imputation model is correctly specified and the estimate is unbiased.
, (4.14) holds only when the imputation model is correctly specified and the estimate is unbiased.
4.3. Remark on efficiency of  compared to
compared to 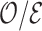
As already commented on in Section 3.1, 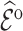 (or
(or 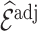 ) is (asymptotically) design unbiased (Section 3.1), and
) is (asymptotically) design unbiased (Section 3.1), and 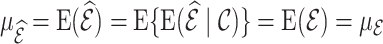 . Similarly, by the law of iterated expectations,
. Similarly, by the law of iterated expectations, 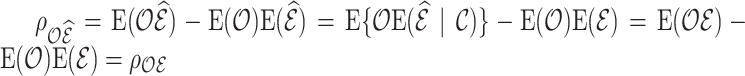 . As a result, the variance decomposition (4.7) can be simplified to
. As a result, the variance decomposition (4.7) can be simplified to  , and the variance expression in (4.13) is reduced to
, and the variance expression in (4.13) is reduced to  . If cohort data are fully available,
. If cohort data are fully available, 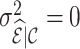 and
and  .
.
For longer projection periods 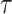 , the expected number of events
, the expected number of events 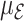 increases and leads to more precise estimates
increases and leads to more precise estimates 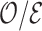 because
because 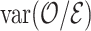 gets smaller. We confirm this in simulation studies.
gets smaller. We confirm this in simulation studies.
On the other hand, the relative efficiency (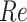 ) of
) of 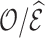 compared to
compared to 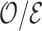 expressed as the ratio of their variances,
expressed as the ratio of their variances,
 |
(4.15) |
decreases as 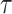 increases due to the increase in the conditional variance,
increases due to the increase in the conditional variance, 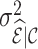 . Nevertheless, weight adjustment mitigates this increase in
. Nevertheless, weight adjustment mitigates this increase in  so that efficiency losses are smaller than those seen for inclusion probability weighting; that is,
so that efficiency losses are smaller than those seen for inclusion probability weighting; that is, 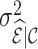 for
for 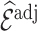 is smaller than
is smaller than  for
for 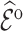 . We confirm these observations in simulation studies (e.g., Figure 2).
. We confirm these observations in simulation studies (e.g., Figure 2).
Fig. 2.
Empirical relative efficiency (ratio of the empirical variance from full cohort to that from the two-phase estimate) of observed-to-expected ratios over 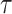 ; weight adjustment using pseudo-risk is the most efficient for all projection periods, compared to the other approaches using design weights and adjusted weights by phase 1 variables.
; weight adjustment using pseudo-risk is the most efficient for all projection periods, compared to the other approaches using design weights and adjusted weights by phase 1 variables.
5. Simulations
We conducted two sets of simulations, the first to investigate the performance of the proposed pseudo-risk estimate as an auxiliary statistic for weight adjustment (Section 5.1) and the second to compare weight adjustment with multiple imputation (Section 5.2).
5.1. Efficiency of weight-adjusted calibration estimators using pseudo-risk as auxiliary statistic
We investigated the performance of weight adjustment compared to inverse probability weighting method for estimating 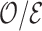 . We also assessed the proposed auxiliary statistic, pseudo-risk estimates, by comparing to another choice of auxiliary statistics, namely all phase 1 covariates.
. We also assessed the proposed auxiliary statistic, pseudo-risk estimates, by comparing to another choice of auxiliary statistics, namely all phase 1 covariates.
5.1.1. Risk model and data generation
We validated a pure risk model (that treats competing risks as random censoring), 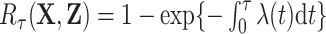 , developed from the United States and Canada childhood cancer survivor (CCSS) cohort, comprised of
, developed from the United States and Canada childhood cancer survivor (CCSS) cohort, comprised of 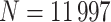 5-year survivors of a childhood cancer. The hazard function is
5-year survivors of a childhood cancer. The hazard function is 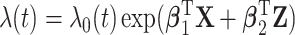 , where
, where 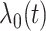 is a baseline hazard function, and
is a baseline hazard function, and 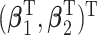 are log-hazard ratios associated with the covariates
are log-hazard ratios associated with the covariates 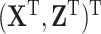 . We assumed that
. We assumed that 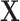 includes the following binary risk factors: female gender (yes/no), “birth after 1970 (yes/no),” “age at the first primary cancer
includes the following binary risk factors: female gender (yes/no), “birth after 1970 (yes/no),” “age at the first primary cancer 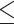 15-year-old (yes/no),” “any thyroid nodule in life time (yes/no),” “any alkylating agents (yes/no)” and “any radiation treatment (yes/no),” and
15-year-old (yes/no),” “any thyroid nodule in life time (yes/no),” “any alkylating agents (yes/no)” and “any radiation treatment (yes/no),” and 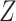 was the binary risk factor “any radiation to the neck (yes/no).” Table 1 shows the corresponding hazard ratio estimates, obtained from the CCSS cohort for the predictors of model 2 of Kovalchik and others (2013) where the outcome of interest was diagnosis of a second primary thyroid cancer (SPTC). The baseline hazard function
was the binary risk factor “any radiation to the neck (yes/no).” Table 1 shows the corresponding hazard ratio estimates, obtained from the CCSS cohort for the predictors of model 2 of Kovalchik and others (2013) where the outcome of interest was diagnosis of a second primary thyroid cancer (SPTC). The baseline hazard function 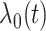 was estimated by the Breslow estimate (see Figure A1, Appendix D in Supplementary material available at Biostatistics online). We treated death from competing causes as a censoring event. The observed number of SPTCs in the CCSS cohort for projections lengths
was estimated by the Breslow estimate (see Figure A1, Appendix D in Supplementary material available at Biostatistics online). We treated death from competing causes as a censoring event. The observed number of SPTCs in the CCSS cohort for projections lengths 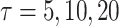 , and
, and  years were
years were 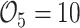 ,
, 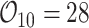 ,
, 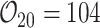 , and
, and  . This model was regarded as fixed.
. This model was regarded as fixed.
Table 1.
Hazard ratio estimates from the childhood cancer survival study (CCSS) cohort in the USA and Canada for the second primary thyroid cancer (SPTC) model predictors; all risk predictors are binary (yes = 1 or no = 0); “Radiation to neck” is considered to be a missing variable (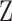 ) in a simulation study using resampled cohorts.
) in a simulation study using resampled cohorts.
| Risk predictor | Hazard ratio from CCSS | |
|---|---|---|

|
Birth year after 1970 | 1.69 |
Age at first primary cancer  -year -year |
3.05 | |
| Female | 2.32 | |
| Thyroid nodule in life time | 7.05 | |
| Any alkylating agent | 1.63 | |
| Any radiation | 1.40 | |
|
Radiation to neck | 6.01 |
We generated 500 validation cohorts of size 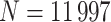 by resampling subjects with replacement from the CCSS cohort. For each cohort, we used the following phase 2 sampling schemes: MCAR, MAR/CC, and MAR/NCC. To allow for comparisons across the designs, we first created the MAR/NCC subsample, with
by resampling subjects with replacement from the CCSS cohort. For each cohort, we used the following phase 2 sampling schemes: MCAR, MAR/CC, and MAR/NCC. To allow for comparisons across the designs, we first created the MAR/NCC subsample, with  controls matched on time to each case, corresponding to a sample of
controls matched on time to each case, corresponding to a sample of  unique individuals (
unique individuals (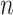 varies between simulated cohorts because the number of cases is random and some controls are sampled repeatedly). We then created an MCAR subsample using Bernoulli sampling with
varies between simulated cohorts because the number of cases is random and some controls are sampled repeatedly). We then created an MCAR subsample using Bernoulli sampling with 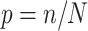 where
where 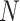 is the size of a full cohort (phase 1). The MAR/CC samples were the same individuals as used as MCAR samples, but in addition we included all cases with
is the size of a full cohort (phase 1). The MAR/CC samples were the same individuals as used as MCAR samples, but in addition we included all cases with 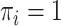 , and therefore the phase 2 CC sample size was slightly bigger than that of NCC or MCAR.
, and therefore the phase 2 CC sample size was slightly bigger than that of NCC or MCAR.
We assumed that  “Radiation to neck,” a predictor with high hazard ratio (
“Radiation to neck,” a predictor with high hazard ratio ( ), was only available for phase 2 samples. We created a binary ancillary predictor
), was only available for phase 2 samples. We created a binary ancillary predictor 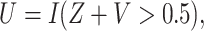 where
where 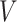 had a uniform distribution on the interval
had a uniform distribution on the interval  and was independent of
and was independent of 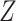 , so that
, so that 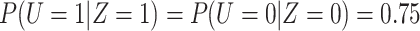 and
and 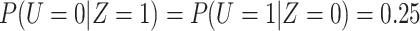 .
.
5.1.2. Estimation of 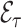
We estimated 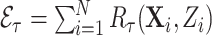 by the weighted sums with three different weights: design weights,
by the weighted sums with three different weights: design weights, 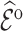 ; adjusted weights using the model covariates
; adjusted weights using the model covariates 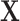 and the ancillary predictor
and the ancillary predictor 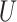 that are available in phase 1 as the auxiliary statistic,
that are available in phase 1 as the auxiliary statistic, 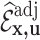 ; and adjusted weights using the pseudo-risk as the auxiliary statistic,
; and adjusted weights using the pseudo-risk as the auxiliary statistic, 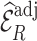 . To predict
. To predict  for the computation of the pseudo-risk estimates,
for the computation of the pseudo-risk estimates, 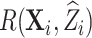 , we used design-weighted logistic regression with predictors,
, we used design-weighted logistic regression with predictors,  ,
, 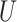 ,
, 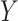 , and
, and  .
.
We assessed the efficiency of estimates 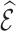 based on adjusted design weights when phase 1 variables
based on adjusted design weights when phase 1 variables  , and ancillary predictors of
, and ancillary predictors of 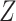 , namely,
, namely,  , are used as auxiliary statistics, denoted by
, are used as auxiliary statistics, denoted by  , and when pseudo-risk estimates,
, and when pseudo-risk estimates,  , are used as auxiliary statistics, denoted by
, are used as auxiliary statistics, denoted by 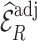 .
.
5.1.3. Results
Table 2 summarizes 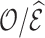 estimates from
estimates from 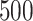 validation cohorts resampled from the CCSS cohort. All estimates were unbiased with Means close to the true
validation cohorts resampled from the CCSS cohort. All estimates were unbiased with Means close to the true  ratios computed from CCSS; 0.89, 0.88, 1.10, and 1.04 for
ratios computed from CCSS; 0.89, 0.88, 1.10, and 1.04 for 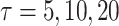 and
and 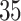 , respectively. The weight-adjusted estimates had smaller mean absolute deviations (Mads) and standard deviations (Sds) than the design weighted estimates for all designs and all values of
, respectively. The weight-adjusted estimates had smaller mean absolute deviations (Mads) and standard deviations (Sds) than the design weighted estimates for all designs and all values of 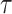 . The estimates
. The estimates 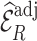 using adjusted weights based on the pseudo-risk improved the estimation efficiency more than those using
using adjusted weights based on the pseudo-risk improved the estimation efficiency more than those using  directly for weight adjustment. This supports that efficiency gains depend on the choice of auxiliary statistics for weight adjustment, and pseudo-risk is a good choice because it is strongly correlated with the actual risk, as discussed in Section 3.1. Figure 2 shows the relative efficiencies (Res) compared to the full cohort analysis. While Re decreased with increasing
directly for weight adjustment. This supports that efficiency gains depend on the choice of auxiliary statistics for weight adjustment, and pseudo-risk is a good choice because it is strongly correlated with the actual risk, as discussed in Section 3.1. Figure 2 shows the relative efficiencies (Res) compared to the full cohort analysis. While Re decreased with increasing 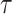 for all missingness mechanisms and approaches, the decreases were mitigated by weight adjustment, especially when using pseudo-risk as the auxiliary statistic.
for all missingness mechanisms and approaches, the decreases were mitigated by weight adjustment, especially when using pseudo-risk as the auxiliary statistic.
Table 2.
Summary of observed-to-expected ratio estimates, the precision of the variance estimates, and 95% confidence interval coverage, based on  resampled cohorts from the CCSS cohort;
resampled cohorts from the CCSS cohort; 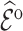 denotes the design-weighted estimates;
denotes the design-weighted estimates;  denotes the weight-adjusted estimates using
denotes the weight-adjusted estimates using 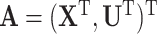 ;
; 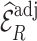 denotes the weight-adjusted estimates using
denotes the weight-adjusted estimates using 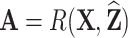 .
.
+
|
FULL | MCAR | MAR/CC | MAR/NCC 
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
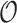 /
/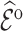
|
 /
/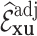
|
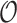 /
/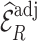
|
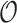 /
/
|
 /
/
|
 /
/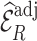
|
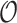 /
/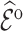
|
 /
/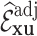
|
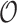 /
/
|
||
| 5 | Mean | 0.88 | 0.89 | 0.88 | 0.88 | 0.89 | 0.88 | 0.88 | 0.91 | 0.88 | 0.89 |
| Mad | 0 | 0.061 | 0.048 | 0.028 | 0.058 | 0.047 | 0.027 | 0.106 | 0.079 | 0.049 | |
| Sd | 0.283 | 0.293 | 0.286 | 0.284 | 0.293 | 0.286 | 0.284 | 0.324 | 0.304 | 0.294 | |
| Se | 0.276 | 0.288 | 0.283 | 0.278 | 0.287 | 0.282 | 0.279 | 0.308 | 0.287 | 0.281 | |
| Cr | 0.92 | 0.93 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.93 | 0.91 | 0.93 | |
| 10 | Mean | 0.88 | 0.88 | 0.88 | 0.87 | 0.88 | 0.88 | 0.88 | 0.89 | 0.86 | 0.88 |
| Mad | 0 | 0.061 | 0.047 | 0.029 | 0.059 | 0.046 | 0.027 | 0.084 | 0.071 | 0.041 | |
| Sd | 0.161 | 0.175 | 0.168 | 0.163 | 0.174 | 0.168 | 0.163 | 0.192 | 0.183 | 0.174 | |
| Se | 0.165 | 0.182 | 0.174 | 0.168 | 0.181 | 0.174 | 0.169 | 0.195 | 0.178 | 0.172 | |
| Cr | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.92 | 0.94 | |
| 20 | Mean | 1.10 | 1.10 | 1.10 | 1.09 | 1.10 | 1.10 | 1.10 | 1.11 | 1.06 | 1.10 |
| Mad | 0 | 0.086 | 0.066 | 0.040 | 0.084 | 0.065 | 0.038 | 0.091 | 0.093 | 0.045 | |
| Sd | 0.106 | 0.148 | 0.130 | 0.115 | 0.147 | 0.130 | 0.114 | 0.154 | 0.151 | 0.122 | |
| Se | 0.108 | 0.153 | 0.135 | 0.117 | 0.151 | 0.134 | 0.117 | 0.152 | 0.139 | 0.119 | |
| Cr | 0.96 | 0.96 | 0.95 | 0.96 | 0.96 | 0.95 | 0.96 | 0.95 | 0.90 | 0.94 | |
| 35 | Mean | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.05 | 1.01 | 1.04 |
| Mad | 0 | 0.086 | 0.066 | 0.038 | 0.085 | 0.064 | 0.038 | 0.080 | 0.087 | 0.042 | |
| Sd | 0.090 | 0.139 | 0.120 | 0.101 | 0.138 | 0.118 | 0.099 | 0.132 | 0.132 | 0.104 | |
| Se | 0.094 | 0.140 | 0.121 | 0.104 | 0.139 | 0.120 | 0.104 | 0.134 | 0.124 | 0.106 | |
| Cr | 0.96 | 0.95 | 0.94 | 0.96 | 0.94 | 0.94 | 0.96 | 0.95 | 0.90 | 0.95 | |
Mean, mean of estimates; Mad, mean absolute deviation of estimates; Sd, standard deviation of estimates; Se, mean of estimated standard errors; Cr, coverage rate of 95% confidence intervals.
The coverage rates (Crs) of the 95% confidence intervals (CIs) for weighting approaches were near the nominal 95% level, except for  . When few events are observed (
. When few events are observed (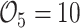 ), the normal approximation may not be fully appropriate. A 95% CI based on 500 simulations around an estimate of
), the normal approximation may not be fully appropriate. A 95% CI based on 500 simulations around an estimate of  is
is 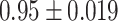 , which includes almost all the coverages shown. The mean of the estimated standard errors (Ses) based on the variance formulas were close to the empirical Sds, indicating that the variance formulas given in Section 4 yield unbiased estimates.
, which includes almost all the coverages shown. The mean of the estimated standard errors (Ses) based on the variance formulas were close to the empirical Sds, indicating that the variance formulas given in Section 4 yield unbiased estimates.
5.2. Comparison of weight adjustment with multiple imputation
We compared the bias and efficiency in 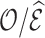 for weight adjustment and multiple imputation when the prediction models for
for weight adjustment and multiple imputation when the prediction models for 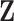 used in the auxiliary statistic and the imputation models for
used in the auxiliary statistic and the imputation models for  are correct (Scenario I) and misspecified (Scenario II).
are correct (Scenario I) and misspecified (Scenario II).
5.2.1. Risk model and data generation
We generated univariate covariates for a validation cohort of 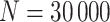 subjects as follows. For Scenario I (correctly specified prediction/imputation model), each of
subjects as follows. For Scenario I (correctly specified prediction/imputation model), each of  was sampled from a multivariate normal distribution with mean
was sampled from a multivariate normal distribution with mean  , variances
, variances 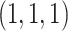 , and
, and  and
and  . For Scenario II (misspecified prediction/imputation model),
. For Scenario II (misspecified prediction/imputation model), 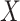 and
and 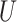 came from a bivariate normal distribution with variances
came from a bivariate normal distribution with variances 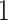 and
and 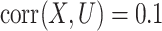 , and
, and  where
where 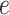 followed a normal distribution with mean 0 and variance 1. Given
followed a normal distribution with mean 0 and variance 1. Given 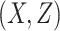 , the event time
, the event time  for each cohort member was generated from an exponential distribution with parameter
for each cohort member was generated from an exponential distribution with parameter  with
with  ,
, 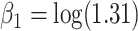 and
and 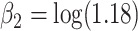 . We assumed there is administrative censoring and thus observed
. We assumed there is administrative censoring and thus observed  , and the event indicator,
, and the event indicator, 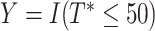 . Under these parameter choices,
. Under these parameter choices,  . We sampled individuals into phase 2 using three missing mechanisms, MCAR, MAR/CC, and MAR/NCC, as described in Section 5.1. For the NCC design, we selected
. We sampled individuals into phase 2 using three missing mechanisms, MCAR, MAR/CC, and MAR/NCC, as described in Section 5.1. For the NCC design, we selected 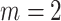 controls per case.
controls per case.
5.2.2. Estimation of 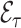
We estimated 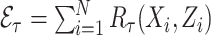 by
by 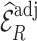 and
and 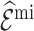 . For both scenarios, we predicted and imputed
. For both scenarios, we predicted and imputed 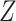 under the assumption that
under the assumption that  is linear in
is linear in 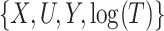 , which is correct for Scenario I but not for Scenario II. The prediction for
, which is correct for Scenario I but not for Scenario II. The prediction for  for pseudo-risk computations was based on design-weighted linear regression, and we created
for pseudo-risk computations was based on design-weighted linear regression, and we created  imputed data sets with
imputed data sets with 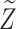 .
.
5.2.3. Results
Table 3 summarizes results for  simulated validation cohorts. When the model for
simulated validation cohorts. When the model for  was correctly specified for prediction and imputation (Scenario I), all Means were near
was correctly specified for prediction and imputation (Scenario I), all Means were near 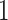 , suggesting that the
, suggesting that the  estimates are unbiased. Using
estimates are unbiased. Using 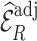 in the
in the 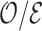 estimation was more efficient than
estimation was more efficient than 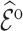 , as shown in Section 5.1, and was almost equally efficient as
, as shown in Section 5.1, and was almost equally efficient as  ; both
; both  and
and 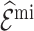 led to smaller Mad and Sd for all missingness mechanisms.
led to smaller Mad and Sd for all missingness mechanisms.
Table 3.
Summary of observed-to-expected ratio estimates, the precision of the estimates, and 95% confidence interval coverage, based on 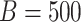 simulated validation cohorts.
simulated validation cohorts.
| FULL | MCAR | MAR/CC | MAR/NCC 
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
 /
/
|
 /
/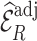
|
 /
/
|
 /
/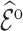
|
 /
/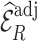
|
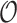 /
/
|
 /
/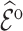
|
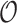 /
/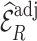
|
 /
/
|
|
| Scenario I: when the model for missing data is correct. | ||||||||||
| Mean | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Mad | 0.030 | 0.036 | 0.030 | 0.031 | 0.036 | 0.030 | 0.031 | 0.032 | 0.030 | 0.030 |
| Sd | 0.037 | 0.046 | 0.037 | 0.037 | 0.045 | 0.037 | 0.037 | 0.039 | 0.037 | 0.037 |
| Se | 0.038 | 0.045 | 0.038 | 0.038 | 0.045 | 0.038 | 0.038 | 0.041 | 0.038 | 0.039 |
| Cr | 0.96 | 0.95 | 0.96 | 0.95 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 |
| Scenario II: when the model for missing data is misspecified. | ||||||||||
| Mean | 1.00 | 1.00 | 1.00 | 0.94 | 1.00 | 1.00 | 0.94 | 1.00 | 1.00 | 0.94 |
| Mad | 0.030 | 0.035 | 0.032 | 0.073 | 0.035 | 0.031 | 0.077 | 0.032 | 0.031 | 0.078 |
| Sd | 0.037 | 0.044 | 0.039 | 0.101 | 0.044 | 0.039 | 0.108 | 0.040 | 0.038 | 0.109 |
| Se | 0.038 | 0.046 | 0.039 | 0.075 | 0.045 | 0.039 | 0.077 | 0.041 | 0.039 | 0.076 |
| Cr | 0.96 | 0.96 | 0.96 | 0.92 | 0.96 | 0.95 | 0.92 | 0.96 | 0.96 | 0.93 |
Mean, mean of estimates; Mad, mean absolute deviation of estimates; Sd, standard deviation of estimates; Se, mean of estimated standard errors; Cr, coverage rate of 95% confidence intervals.
When the model for predicting and imputing  was misspecified (Scenario II), both
was misspecified (Scenario II), both 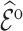 , and
, and 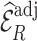 were unbiased, but
were unbiased, but 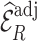 was more precise than
was more precise than 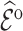 , although its standard deviation (Sd = 0.039) was not reduced as much as in Scenario I (Sd = 0.037). However,
, although its standard deviation (Sd = 0.039) was not reduced as much as in Scenario I (Sd = 0.037). However, 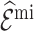 was biased, leading to biased estimates of
was biased, leading to biased estimates of  (Mean
(Mean 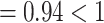 ). Moreover, Sds of
). Moreover, Sds of 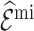 (
(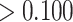 ) were more than twice as big as those of
) were more than twice as big as those of 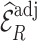 (
(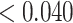 ) for all missingness mechanisms. This confirmed that weight adjustment is more robust to model misspecification than multiple imputation.
) for all missingness mechanisms. This confirmed that weight adjustment is more robust to model misspecification than multiple imputation.
The variance formula (4.14) for the weight adjustment approach worked well regardless of the correctness of the prediction model specification, as the coverages (Crs) of the 95% CIs for all approaches were near the nominal 95% level. A 95% CI based on 500 simulations around an estimate of 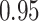 is
is 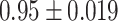 , which includes almost all the coverages shown. However, for multiple imputation, the variance formula (4.14) worked well only when the imputation model was correctly specified; 95% CI coverage for Scenario II was slightly subnominal, at 0.92.
, which includes almost all the coverages shown. However, for multiple imputation, the variance formula (4.14) worked well only when the imputation model was correctly specified; 95% CI coverage for Scenario II was slightly subnominal, at 0.92.
6. Data example
To illustrate our methods, we assessed the calibration of an absolute risk model for second primary thyroid cancer (SPTC) (Kovalchik and others, 2013, Model 2), developed from the CCSS data and two nested case-control studies, the Late Effects Study Group and the Nordic CCSS, implemented in the R package ‘thyroid’ (https://dceg.cancer.gov/tools/risk-assessment/tcrat).
For validation, we used the independent cohort of  French childhood cancer survivors, also used by Kovalchik and others (2013) for assessing model performance, who give the following details. During follow-up,
French childhood cancer survivors, also used by Kovalchik and others (2013) for assessing model performance, who give the following details. During follow-up,  SPTCs were observed in the French cohort. Censoring events were loss to follow-up and end of study. The predictors female gender (yes/no), “birth after 1970 (yes/no),” “age at the first primary cancer
SPTCs were observed in the French cohort. Censoring events were loss to follow-up and end of study. The predictors female gender (yes/no), “birth after 1970 (yes/no),” “age at the first primary cancer  15-year-old (yes/no),” “any alkylating agents (yes/no),” and “any radiation treatment (yes/no)” are fully observed in the cohort (
15-year-old (yes/no),” “any alkylating agents (yes/no),” and “any radiation treatment (yes/no)” are fully observed in the cohort ( ). The predictors “any thyroid nodule in life time (yes/no)” and “any radiation to the neck (yes/no)” (
). The predictors “any thyroid nodule in life time (yes/no)” and “any radiation to the neck (yes/no)” (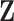 ) had
) had  values missing completely at random (MCAR). To better assess the performance of the methods, we further created a
values missing completely at random (MCAR). To better assess the performance of the methods, we further created a 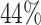 missing MCAR rate. To predict
missing MCAR rate. To predict 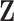 for the pseudo-risk computation, we separately regressed the components of
for the pseudo-risk computation, we separately regressed the components of 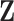 on the phase 1 variables (
on the phase 1 variables (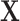 ), the two ancillary predictors “Hodgkin diagnosis (yes/no)” for the first primary cancer, and “radiation absorbed dose to thyroid (in Gy)” (
), the two ancillary predictors “Hodgkin diagnosis (yes/no)” for the first primary cancer, and “radiation absorbed dose to thyroid (in Gy)” (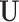 ), and the survival information (times to event or censoring,
), and the survival information (times to event or censoring, 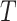 , and outcome variables,
, and outcome variables,  ), using inclusion probability weighted logistic regression in phase 2. The same variables were used to impute
), using inclusion probability weighted logistic regression in phase 2. The same variables were used to impute 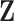 in the multiple imputation with
in the multiple imputation with 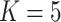 imputed datasets.
imputed datasets.
Table 4 summarizes the calibration estimates from the French CCSS. The model underestimated the true risk in the validation cohort by 12% based on inverse probability weighting and the weight adjusted estimates of 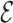 , and by 9% based on multiple imputation, albeit not significantly. The weight adjustment based on pseudo-risk was much more efficient than using MCAR sampling weights, with standard errors of 1.24 for
, and by 9% based on multiple imputation, albeit not significantly. The weight adjustment based on pseudo-risk was much more efficient than using MCAR sampling weights, with standard errors of 1.24 for  and 1.52 for
and 1.52 for 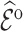 . This was also reflected in the standard errors of the calibration estimates,
. This was also reflected in the standard errors of the calibration estimates,  . Multiple imputation resulted in larger standard errors for
. Multiple imputation resulted in larger standard errors for 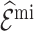 and
and  .
.
Table 4.
Summary of calibration estimates from validating the absolute risk model for second primary thyroid cancer (Kovalchik and others, 2013, Model 2) where the covariates “Any radiation” and “Thyroid nodule in life time” are 44% missing completely at random (MCAR) in the independent validation cohort, French CCSS. Standard errors are in parentheses.
| Method |
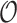
|
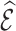
|
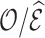
|
|---|---|---|---|
Inverse probability weighting 
|
35 | 31.26 (1.52) | 1.12 (0.191) |
Weight adjustment via pseudo-risk 
|
35 | 31.28 (1.24) | 1.12 (0.188) |
Multiple imputation 
|
35 | 32.18 (2.27) | 1.09 (0.194) |
7. Discussion
In this article, we proposed efficient auxiliary statistics for weight adjustment to estimate the number of events 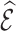 predicted from a risk model used to compute the ratio of observed to expected events,
predicted from a risk model used to compute the ratio of observed to expected events, 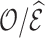 as a measure for calibration in an independent validation cohort in which some model covariates are missing. Our focus was to efficiently estimate the expected number of events from a risk model in an independent validation cohort, treating the risk model as fixed, while Shin and others (2020) used weight calibration to improve the efficiency of the risk estimates.
as a measure for calibration in an independent validation cohort in which some model covariates are missing. Our focus was to efficiently estimate the expected number of events from a risk model in an independent validation cohort, treating the risk model as fixed, while Shin and others (2020) used weight calibration to improve the efficiency of the risk estimates.
Weighting and multiple imputation are widely used to handle missing variables, and both methods require assumptions on the missingness mechanism. We considered three common missingness mechanisms encountered in cohort studies: missing completely at random and missing due to sampling individuals based on the case-cohort design and the nested case–control design. For each setting, the data can be viewed as arising from two-phase sampling. In phase 1, we measure certain variables on the entire cohort that is sampled from a superpopulation. Phase 2 consists of a subsample of the subjects for whom additional variables that were not available in phase 1 are obtained. The phase 2 sample thus has complete data on the risk model predictors. With weighting methods, the missingness mechanism defines the probabilities of inclusion in phase 2. Applying inverse probability of inclusion weights (Horvitz and Thompson, 1952) to the subjects with complete data reweights them to represent the entire validation cohort, but these weights can be inefficient. We used survey sampling methods (also called weight calibration, regression calibration, or model-assisted survey estimation) (Breidt and Opsomer, 2017) to obtain more efficient weights by utilizing phase 1 information. The key in improving efficiency is to find auxiliary statistics of the phase 1 data that are highly correlated with the statistic of interest that we would use if complete data were available in phase 1. We proposed a “pseudo-risk” as an auxiliary statistic, which can be computed from phase 1 data and which is highly correlated with the actual risk one would use with complete cohort data. We showed that using this “pseudo-risk” as an auxiliary statistic led to large improvements in the precision of estimates of 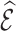 obtained from the model. As a result, the precision of estimates
obtained from the model. As a result, the precision of estimates 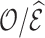 was also improved.
was also improved.
In our analytic computations, we focused on the setting of rare outcomes, and assumed that the observed number of events follows a Poisson distribution. This is a practically relevant situation. However, when the Poisson assumption on  cannot be made, one can estimate its variance from the phase 1 data as
cannot be made, one can estimate its variance from the phase 1 data as 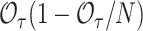 , which reduces to
, which reduces to  for rare outcomes.
for rare outcomes.
We handled censoring by shortening the projection period to the actual observation time, which leads to unbiased estimates of 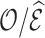 over an average follow-up duration. An alternative approach is to add to the observed number of events the number expected to occur among censored individuals, e.g., as suggested by Li and others (2018). This approach allows one to base calibration assessment on the expected number of events for risks computed up to
over an average follow-up duration. An alternative approach is to add to the observed number of events the number expected to occur among censored individuals, e.g., as suggested by Li and others (2018). This approach allows one to base calibration assessment on the expected number of events for risks computed up to  for all individuals (including censored subjects). It thus assesses
for all individuals (including censored subjects). It thus assesses 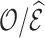 over the full interval
over the full interval 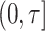 but requires estimating the conditional survival function given the risk estimates.
but requires estimating the conditional survival function given the risk estimates.
Multiple imputation had similar efficiency gains as weight adjustment when the model for imputing the missing data was correctly specified. However, when the imputation model was misspecified, multiple imputation leads to biased estimates, which was also observed by Keogh and others (2018) and Seaman and others (2012). In contrast, weight-adjusted estimates are asymptotically consistent, provided the design-based inclusion probabilities are known (Breidt and Opsomer, 2017; Deville and Särndal, 1992), even when the auxillary statistics (such as the pseudo-risk) are biased.
Some related literature should be mentioned. Ganna and others (2012) used inverse probability weighting to estimate pure covariate-specific risks from case-cohort and nested case–control designs, but they did not attempt to improve efficiency by weight adjustment or study estimates of the  calibration measure. Whittemore and Halpern (2016) discussed a two-phase design, which is similar to a stratified case-cohort design, for comparing mean projected risks with observed risks. They used inverse probability weighting and discussed efficient stratification (partitioning) for sampling, but they did not consider weight adjustment for improving the efficiency of estimation for a given two-phase design.
calibration measure. Whittemore and Halpern (2016) discussed a two-phase design, which is similar to a stratified case-cohort design, for comparing mean projected risks with observed risks. They used inverse probability weighting and discussed efficient stratification (partitioning) for sampling, but they did not consider weight adjustment for improving the efficiency of estimation for a given two-phase design.
Our approach for the nested case–control and case-cohort designs can also be extended to estimate the expected number of events in risk deciles for the whole population, extending e.g., Chambers and Dunstan (1986). However, more work is needed to derive the variance estimates of the corresponding calibration statistic for that setting. Moreover, when data are MCAR and covariates are missing on cases, then it is not clear which quantile to put a case with missing covariates in.
In summary, we found that weight adjustment based on pseudo-risks is a convenient and effective way to improve the precision of estimates of expected counts and observed-to-expected ratios in validation cohorts with missing risk factor information. In the examples we studied, such weight calibration yielded estimates at least as precise as multiple imputation and was robust to model misspecification.
Supplementary Material
Acknowledgements
We thank Florence de Vathaire for access to the data of the French CCSS cohort.
Conflict of Interest: The authors declare no conflicts of interest.
Contributor Information
Yei Eun Shin, Biostatistics Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, 9609 Medical Center Drive, Rockville, MD 20850, USA.
Mitchell H Gail, Biostatistics Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, 9609 Medical Center Drive, Rockville, MD 20850, USA.
Ruth M Pfeiffer, Biostatistics Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, 9609 Medical Center Drive, Rockville, MD 20850, USA.
Software
The R package rmodcal for assessing risk model calibration with missing covariates introduced in this paper is available at https://github.com/syeeun/rmodcal. Example code using a simulated data set is also provided in the package.
Supplementary materials
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
The Intramural Research Program of the National Cancer Institute, Division of Cancer Epidemiology and Genetics.
References
- Breidt, F. J. and Opsomer, J. D. (2017). Model-assisted survey estimation with modern prediction techniques. Statistical Science 32, 190–205. [Google Scholar]
- Cameron, A. C. and Trivedi, P. K. (2013). Regression Analysis of Count Data, Vol. 53. Cambridge, UK: Cambridge University Press. [Google Scholar]
- Chambers, R. L. and Dunstan, R. (1986). Estimating distribution functions from survey data. Biometrika 73, 597–604. [Google Scholar]
- Deville, J.-C. and Särndal, C.-E. (1992). Calibration estimators in survey sampling. Journal of the American Statistical Association 87, 376–382. [Google Scholar]
- Ganna, A., Reilly, M., de Faire, U., Pedersen, N., Magnusson, P. and Ingelsson, E. (2012). Risk prediction measures for case-cohort and nested case-control designs: an application to cardiovascular disease. American Journal of Epidemiology 175, 715–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong, G., Quante, A. S., Terry, M. B. and Whittemore, A. S. (2014). Assessing the goodness of fit of personal risk models. Statistics in Medicine 33, 3179–3190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvitz, D. G. and Thompson, D. J. (1952). A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association 47, 663–685. [Google Scholar]
- Keogh, R. H., Seaman, S. R., Bartlett, J. W. and Wood, A. M. (2018). Multiple imputation of missing data in nested case-control and case-cohort studies. Biometrics 74, 1438–1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovalchik, S. A., Ronckers, C. M., Veiga, L. H. S., Sigurdson, A. J., Inskip, P. D., De Vathaire, F. and others. (2013). Absolute risk prediction of second primary thyroid cancer among 5-year survivors of childhood cancer. Journal of Clinical Oncology 31, 119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langholz, B. and Thomas, D. C. (1990). Nested case-control and case-cohort methods of sampling from a cohort: a critical comparison. American Journal of Epidemiology 131, 169–176. [DOI] [PubMed] [Google Scholar]
- Li, L., Greene, T. and Hu, B. (2018). A simple method to estimate the time-dependent receiver operating characteristic curve and the area under the curve with right censored data. Statistical Methods in Medical Research 27, 2264–2278. [DOI] [PubMed] [Google Scholar]
- Pepe, M. S. (2003). The Statistical Evaluation of Medical Tests for Classification and Prediction. Medicine. Oxford, U.K.: Oxford University Press. [Google Scholar]
- Pfeiffer, R. M. and Gail, M. H. (2017). Absolute Risk: Methods and Applications in Clinical Management and Public Health. Chapman & Hall/CRC Monographs on Statistics & Applied Probability. New York: CRC Press. [Google Scholar]
- Prentice, R. L. (1986). A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika 73, 1–11. [Google Scholar]
- Robins, J. M., Rotnitzky, A. and Zhao, L. P. (1994). Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association 89, 846–866. [Google Scholar]
- Rubin, D. B. (2004). Multiple Imputation for Nonresponse in Surveys, Volume 81. Hoboken, NJ: John Wiley & Sons. [Google Scholar]
- Samuelsen, S. O. (1997). A pseudolikelihood approach to analysis of nested case-control studies. Biometrika 84, 379–394. [Google Scholar]
- Seaman, S. R., Bartlett, J. W. and White, I R. (2012). Multiple imputation of missing covariates with non-linear effects and interactions: an evaluation of statistical methods. BMC Medical Research Methodology 12, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin, Y. E., Pfeiffer, R. M., Graubard, B. I. and Gail, M. H. (2020). Weight calibration to improve the efficiency of pure risk estimates from case-control samples nested in a cohort. Biometrics 76, 1087–1097. [DOI] [PubMed] [Google Scholar]
- van Buuren, S. and Groothuis-Oudshoorn, K. (2011). mice: multivariate imputation by chained equations in R. Journal of Statistical Software 45, 1–67. [Google Scholar]
- White, I. R. and Royston, P. (2009). Imputing missing covariate values for the Cox model. Statistics in Medicine 28, 1982–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittemore, A. S. and Halpern, J. (2016). Two-stage sampling designs for external validation of personal risk models. Statistical Methods in Medical Research 25, 1313–1329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu, C. and Sitter, R. R. (2001). A model-calibration approach to using complete auxiliary information from survey data. Journal of the American Statistical Association 96, 185–193. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




