A Comprehensive Introduction to Magnetic Resonance Imaging Relaxometry and Contrast Agents

Abstract

The development of imaging technologies allowing noninvasive observation through solid bodies has represented a breakthrough in medical diagnosis, facilitating the comprehension of biomolecular events underlying disease and the development of more efficient therapeutic approaches. Some of the traditional limitations of these techniques are nowadays fading away thanks to the combination of imaging with nanotechnology, allowing the development of novel functional biomaterials that increase the sensitivity of detection, enable sensitivity to specific targets, and facilitate the combination of therapeutic and diagnostic functions (theragnosis) with molecular platforms functioning simultaneously as imaging probes and drug delivery carriers. The design of such functional biomaterials requires a comprehensive understanding of the principles that govern the generation of signal and modulation of contrast for a given imaging modality to exploit its capabilities to the maximal level. In this sense, magnetic resonance imaging (MRI) is a technique that presents a complex relationship between the detected signal and the physical–chemical properties of its sourcing matter, allowing the generation of multiple image contrasts. Thus, while magnetic resonance imaging is a highly versatile imaging modality, it requires specific knowledge of its physical principles to take advantage of all of its possibilities. This work reviews the origin of the image signal and contrast in MRI and the concepts of relaxometry and MRI contrast agents.

1. Introduction

The development of imaging technologies allowing noninvasive observation through solid bodies has represented a breakthrough in disease diagnosis, fostering a better understanding of biomolecular mechanisms underlying disease and the development of more efficient therapeutic approaches.

In recent years, the development of new biomaterials has helped to advance medical imaging technologies and applications, transcending the mere acquisition of anatomical images. Nanotechnology facilitates increased sensitivity of detection (increasing resolution to the cellular level), high selectivity for specific targets, capability to detect function (from the cellular scale to systems level), and the combination of therapeutic and diagnostic functions in common molecular platforms (a discipline named theragnosis). Thus, by combining nanotechnology and imaging technologies, molecular imaging is emerging as a multidisciplinary key enabling technology in the field of biomedicine.

The development of effective functional and biomimetic materials for molecular imaging requires a comprehensive understanding of image generation, and the rules that govern signal and contrast on those images. Only in this way one could completely exploit all of the opportunities that a particular imaging modality offers. In this sense, imaging modalities such as positron emission tomography (PET) or optical imaging (OI) make use of probes to generate a signal, the signal intensity being proportional to the concentration and physical–chemical characteristics of the emitting probe. Others, like X-ray computerized tomography (CT), rely on the absorption of energy depending on the nature of substructures of the observed object (e.g., bone vs soft tissue density). The situation is totally different in magnetic resonance imaging (MRI), a multimodal imaging technique with a complex relationship between the image signal and the physical–chemical properties of matter that generates such a signal, allowing the generation of multiple image contrasts and making MRI a very versatile while complex image modality. This work reviews the origin of the image signal and contrast in MRI, and the concepts of relaxometry and MRI contrast agents. While a detailed analysis of fundamentals of this technique is out of the scope of this work, we present instead a comprehensive introduction to the main concepts. Scientific definitions and concepts may be presented in an generous descriptive, fairly rigorous (scientifically speaking) simplified way, but we intend to facilitate the comprehension of the concepts for multidisciplinary readers, rather than provide an extensive description of physical or chemical concepts that would require deeper knowledge of these fields. Further reading is highly recommended to help the reader to gain a deeper knowledge of these concepts to exploit the real potential of MRI as a molecular imaging technique.

2. Principles of the MRI Signal and Image Contrast

In imaging, contrast can be defined as the difference in signal intensity (SI) between a region of interest (ROI) and its surroundings, within the field of view (FOV) under observation. Contrast can be treated as a qualitative concept, describing a particular ROI as hypointense (lower intensity) or hyperintense (higher intensity), depending on the visual perception of such a region with respect to its surroundings. On the other hand, contrast can be quantified, by measuring numerical differences in the signal intensity of a pixel (or its three-dimensional equivalents, voxel), which may not always be appreciable by the naked eye. Thus, contrast may be expressed as a signal ratio, a percentage of signal change, a contrast to noise ratio (CNR), or similar user-defined parameters, with no gold standard existing in this sense.

In general, signal intensity in a given image pixel, voxel, or ROI is determined by a series of intrinsic parameters, reflecting the physicochemical properties and environmental conditions of matter in that region under analysis (including pH, T, tissue organization, etc.), which may eventually include the influence of present imaging probes of different nature, properties, and concentrations. On the other hand, SI will also depend on a series of extrinsic parameters, reflecting the particularities of image acquisition (equipment characteristics, operational procedures, pulse sequences and imaging parameters selected by the user, etc.). In general, knowing the intrinsic characteristics of the matter under observation and adjusting the image acquisition parameters (extrinsic parameters) properly, one can govern the signal and contrast for specific ROIs.

With MRI, images are obtained by processing signals emitted by radiofrequency (RF) excited protons (mostly water protons for in vivo applications). Thus, the signal intensity in a particular pixel (or voxel, or ROI) reflects the contribution of various intrinsic parameters (longitudinal and transverse relaxation times, proton density, flow and molecular diffusion related parameters, etc.) and extrinsic parameters (type of acquisition schemes, timing parameters of pulse sequences, magnetic field strength, etc.).¹ In practice, the contribution of all of these parameters are included in a single equation:

1

where S represents the signal intensity for a given pixel or ROI, ρ represents the proton density, and 0 ≤ F1, F2, F3 ≤ 1 are weighting factors related to the intrinsic and extrinsic parameters. In particular:

2

represents the so-called T₁-weighting factor, which depends on the longitudinal or spin–lattice relaxation time (T₁, an intrinsic parameter) and the repetition (or recycling) time (TR) and the flip angle of the excitation RF pulse (θ), both extrinsic parameters.

The repetition time is a parameter that represents the time lapse between two consecutive image acquisition (between two consecutive RF pulses are applied to excite protons). This time is employed to influence image contrast, by means of the T₁ weighting mechanism.On the other hand, F2 (alternatively F2*, as we will discuss later) is the T₂-weighting factor, dependent on the transverse or spin–spin relaxation time (T₂, an intrinsic parameter) and the echo (or encoding) time (TE, extrinsic parameter), as described by

3

The echo time is a parameter that represents the time lapse between protons that are excited, by the RF pulse, and the signal is recorded. This time is usually employed for space encoding of the signal and to influence image contrast, by means of the T₂ weighting mechanism.

Finally, the factor F3 is given by

4

which is a weighting factor related to the diffusion of water molecules, dependent on the apparent diffusion coefficient of water (D) and the gyromagnetic ratio of protons (both D and γ are intrinsic parameters), and the diffusion gradients’ strength, duration, and pulsation periods (G, δ, Δ), which are extrinsic parameters.

In this work, we will not discuss in detail the so-called magnetization transfer effects (such as chemical exchange saturation transfer (CEST), nuclear Overhauser effect (NOE), etc.), which also can be used to manipulate the image contrast and to extract physical and chemical information from the matter under observation but are more advanced concepts, and out of the scope of this work.

In general, the intrinsic parameters are fixed parameters determined by the nature and physical and chemical environment of water molecules under observation. The intrinsic parameters T₁, T₂, and D usually depend on other parameters, such as the nature and concentration of chemical species, temperature, pH, structure, organization of tissues, etc. Many factors influence these parameters, which is why MRI is a very versatile technique.

In this sense, an MR image can be much more than a mere picture. MRI data can be presented in the form of parametric maps that contain encoded physicochemical information on the ROI under analysis. Thus, the molecular environment (pH, T, presence of macromolecules, etc.), changes of state, and other important information can be extracted from MR images, when properly acquired and processed.

The equations presented here include a series of extrinsic parameters such as the repetition and echo times, the flip angle of the excitation pulse, or the use of diffusional gradients. The user can modify these parameters on-demand, thus modulating the different weighting factors and influencing signal intensity in MRI. This is what MRI scientists do when selecting a particular pulse sequence and set of imaging parameters; they play around with the extrinsic parameters to modulate the weighting factors and thus modulate signal intensities of different ROIs in an MR.

Considering only the three main mechanisms of image contrast in MRI (T₁, T₂ and diffusion), one can yield four main sorts of images or combinations of these four (Figure 1):

• Proton density images: (F1 ≈ F2 ≈ F3 ≈ 1)

• T₁ weighted images: (F1 < 1, F2 ≈ F3 ≈ 1)

• T₂ weighted images: (F2 < 1, F1 ≈ F3 ≈ 1)

• Diffusion weighted images: (F3 < 1, F1 ≈ F2 ≈ 1)

Figure 1.

MR images of a rat brain with an ischemic lesion, obtained at 9.4 T with different image contrasts. (a) Proton density image (F1 ≈ F2 ≈ F3 ≈ 1), (b) T₁-weighted image (F1 = 0.125; F2 ≈ F3 ≈ 1), (c) T₂-weighted image (F2 = 0.135; F1 ≈ F3 ≈ 1), and (d) diffusion weighted image (F3 = 0.464; F1 ≈ F2 ≈ 1).

Figure 1 shows the versatility of MRI and how the signal intensity can be modulated to generate a good contrast between regions of different intrinsic properties (lesion vs healthy tissue). Depending on such intrinsic properties, conditioned by the biological process under study, some image modalities show higher contrast than others, or even contrast in opposite directions (hyper- vs hypointensity). Contrast between ROIs can be quantified by separating the individual contributions of the four different contrast mechanisms (proton density, T₁, T₂, and diffusion) implicated in the modulation of the SI.

The interpretation of biomedical MR images requires prior knowledge of the influence of the different weighting parameters in the image under observation, the pulse sequence used for image acquisition, and the values of the corresponding set of extrinsic parameters used. This provides a thorough understanding of the correlation between the corresponding signal contrast and the underlying pathophysiology of tissues under observation. For example, a clearly defined ischemic lesion (like the hyperintense region observed in the rat brain in Figure 1c) may not be appreciable by unsuitable management of the weighting factors (i.e., acquisition parameters), resulting in a masked lesion (Figure 1b).

On top of the acquisition parameters, there are extrinsic factors like the main magnetic field of the MRI scanner (B₀), the hardware configuration (design and performance of RF coils, magnetic field gradients, adjustment of shimming coils, local disturbances of the magnetic fields, etc.) that influence signal intensities, and contrast on MR images. Thus, direct comparison of images across different experimental setups is complex, resulting in typical evaluation of MR images at a qualitative and subjective level, usually restricted to descriptions of relative contrast between different anatomical regions (the use of sentences like “presence of a hypo- or a hyperintense signal in the region” are common in medical literature). For quantitative and cross-setup comparison of MRI data, it is crucial to extract the contributions of the different contrast mechanisms, to provide absolute-scaled information on tissue structure and function, independent of hardware and sequence related parameters.

3. MR Relaxation Times

The quantitative nature of the MR signal can be used to extract very useful absolute measurements of biophysical parameters, if one understands and decouples the contrast mechanisms that contribute to the overall MR signal, which can be essentially achieved through the use of eqs 1–4.

Relaxation times (T₁, T₂, or T₂^*) and apparent diffusion coefficients (ADC or D) are the most influential MRI parameters used in quantitative biomedical applications of MRI. These parameters reflect the local nature and physicochemical properties of tissue environments that are directly correlated to the biological properties of such tissues (a correspondence that will be discussed later in this work).

The term “relaxometry” is used in MRI to describe the process of measuring signal decay (relaxation) after excitation of protons by radiofrequency (RF) pulses, and the extraction from such measurement of absolute values for the relaxation times (the intrinsic properties of matter under study). Images representing the spatial distribution of the relaxation times are called relaxation maps (Figure 2). Similarly, images representing the spatial distribution of ADC are called ADC maps (Figure 2).

Figure 2.

Parametric MR mapping. Color-coded T₁ (left), T₂ (center), and ADC (right) parametric maps on which each pixel represents the absolute value of the longitudinal (T₁) and transverse (T₂) relaxation times, or the apparent diffusion coefficient (ADC), calculated for a rat brain with an ischemic lesion.

Although relaxation times vary with the external magnetic field used for acquisition (see ref (2) for a practical study),²T₁ and T₂ maps acquired at the same field should be absolute, facilitating the comparison of data irrespective of the system and pulse sequence used for their acquisition. However, not controlled experimental conditions (temperature of the subject, degree of hydration of tissues, percentage of fat or presence of macromolecules in tissues, etc., all representing biological variables that differ from one individual to another) may yield different T₁ and T₂ values across experimental setups. The direct comparison of ADC absolute values across experimental setups is even more complex since diffusion is an anisotropic property, and obtained values depend on the direction of the diffusion gradients applied during acquisition (this is the origin of the word “apparent” in the term ADC). In fact, it is common practice to estimate ADC values in multiple directions of space (as many as 30 or more) for diffusion tensor imaging (DTI) acquisition schemes,³ yielding a mean value for ADC, termed as mean diffusivity (MD), to facilitate the comparison of data from different studies.

As we have already mentioned, relaxation times can be calculated by decoupling the different contrast mechanisms that contribute to the overall MR signal. For example, if one acquires a series of MR images with a constant value for F1 (by fixing TR and θ) and F3 (by making diffusional gradients equal to zero or fixing their amplitude and duration), the signal intensity in those images will only depend on the extrinsic parameter TE, according to eq 1:

5

This equation can be linearized as

6

Thus, the transverse or spin–spin relaxation time T₂ can be calculated by acquiring a series of N images of increasing echo time (TE), fitting the decay of the signal intensity versus TE to an exponential function, or its logarithm to a linear function (Figure 3).

Figure 3.

Calculation of T₂. Fitting the signal intensity decay on a series of images acquired with different TE values (at fixed TR and θ values) provides the absolute value of the transverse relaxation time T₂.

It is crucial to notice that the fitting parameter S₀ represents the proton density (ρ) of the pixel under analysis, and we can obtain purely T₂-weighted images only when the weighting factors F1 and F3 are equal to 1. The later condition (F3 = 1) is met using no diffusional gradients (G = 0); however, strictly speaking, it is not possible to fulfill the (F1 = 1) condition for the T₁ weighting factor since we would need to set a repetition time of TR = ∞, or a flip angle of θ = 0 (no excitation pulse, meaning no signal creation). Nevertheless, it is usually assumed that when F1 ≥ 0.995 (F1 weighting factor <0.5%), the T₁ effect on the signal can be considered negligible. Mathematically speaking, this is achieved when the repetition time is set to at least 5.3 times the T₁ value (TR≥ 5.3 T₁) when using a flip angle of θ = 90:

7

In practice, there are several experimental approaches to measure transverse relaxation times (T₂) based on the relaxation process described by eq 5 and Figure 3. The most common one relies on the use of a multispin echo sequence (Figure 4), in which a series of signal echoes are acquired at regular intervals of TE (ΔTE = i × TE) by using a series of N consecutive “refocusing pulses” (180 deg pulses) following a single excitation pulse (a 90° pulse). This approach is faster than acquiring a series of N single images of increasing TE value (an alternative approach to measure T₂). However, it requires a good calibration of the 180° pulse and high B1 field homogeneity profile of excitation RF coils to avoid that poor refocusing pulses yield in systematic errors propagated through the N image series.

Figure 4.

Schematic representation of the multi-spin–echo experiment to measure T₂ relaxation. Following the generation of a signal (S₀) by an excitation (90°) RF pulse, the signal decays due to defocusing of spins (process explained later in section 3). If a refocusing RF pulse (180° pulse) is applied after a period of (TE/2), a so-called echo is generated at the same interval of time (at TE/2 from the refocusing pulse or a total TE period from the excitation pulse). The process is repeated N times to generate N echo images. Signal decays exponentially from echo to echo with a time constant of T₂ (transverse or T₂ relaxation time).

An alternative to use refocusing pulses, signal echoes can be generated by magnetic field gradients (see ref (4) for further details).⁴ In this case, the calculated transverse relaxation times are susceptible to local magnetic field inhomogeneities, and T₂ is then termed T₂^* (which can be substantially smaller than T₂). This constant includes not only the relaxation due to the pure T₂ effects but also the influence of the so-called susceptibility effects (that we will discuss later). In the case of T₂ relaxation, a train of N echoes may also be acquired after a single excitation pulse (multigradient echo sequence), or a series of N single-gradient echo images can be acquired using increasing TE values to acquire each one of an N series of images. The first approach is much faster, but the minimum TE difference between consecutive steps of an echo train (ΔTE) is limited by the hardware (short ΔTE requires high gradient strengths, not always available in all scanners). Detailed information about the issues discussed in the previous paragraph can be found in the specialized bibliography.⁴⁻⁶

Likewise, estimation of longitudinal relaxation times (T₁) can be achieved by making constant the weighting factors F2 and F3, and playing around with the factor F1 (as expressed by eq 2). In this case, F1 depends on two extrinsic parameters that can be independently varied. Therefore, there are two experimental procedures to determine T₁ values (Figure 5). In the first approach (the most common one), the flip angle, θ, and TE are fixed for the acquisition of images of variables repetition time (TR). Under these conditions, eq 1 becomes

8

Figure 5.

Calculation of T₁. On the top, the evolution of signal intensity with the flip angle (θ) for three different TR/T₁ fixed ratios. On the bottom, signal intensity evolution with the parameter TR, at a fixed pulse angle of θ = 90. In practice, full relaxation is achieved when TR = 5.3 × T₁ (F1 = 0.995). By fitting experimental data to eqs 8 or 9, the longitudinal relaxation times (T₁) can be estimated.

Alternatively, one can opt for fixing the repetition time and vary the excitation pulse angle according to

9

Again, S₀ represents the proton density only when F2 = 1, and no diffusion gradients are used (G = 0 → b = 0 → F3 = 1), a situation that is only achievable when TE = 0. Like in the previous case, this last requirement is virtually impossible to achieve from an experimental point of view, and it is generally agreed that when (TE ≤ 0.005 × T₂), the T₂ weighing factor is negligible (F2 < 0.5%), according to

10

This condition is still challenging to achieve for most conventional pulse sequences, and proton densities are usually assessed by using the strategy previously described through eqs 5 and 7, or by estimating the F1 value prior to the use of eqs 8 and 9.

Situations described by eqs 8 and 9, shown in Figure 5, correspond to the so-called saturation–recovery experimental setup. There are other experimental approaches to calculate T₁ values based on the use of an inversion pulse of 180 in front of the image acquisition schemes (inversion–recovery experimental setup) or more complex approaches such as look-locker sequences, SSFP (steady-state free precession) approach, etc., designed for fast acquisition of T₁ values. However, their description is out of the scope of this work, and deeper discussion about different techniques for the determination of T₁ and T₂ relaxation times can be found in specialized literature.⁵

Finally, with respect to the diffusional weighting factor F3, the apparent diffusion constants can be estimated according to eqs 11 or 12, by fitting the decay of the signal intensity versus variable b values, while keeping F1 and F2 constant (fixed TE, TR, and θ):

11

or its linearized version:

12

Plots of S or ln S versus b are like those presented in Figure 3 for T₂ decay. In practice, different b values are achieved by using different diffusion gradient strengths, G, in eq 4 for the acquisition of images with different F3 weighting factor values, used to extract D (or ADC) values from the fitting of experimental data.

Having disclosed the influence of the most common contrast mechanisms in biomedical applications of MRI (see refs (5 and 6) for details about other specific contrast mechanisms such as magnetization transfer (MT), T₁ρ, chemical exchange saturation transfer (CEST), etc.),^5,6 the advantages of quantitative imaging is more evident. The most prominent advantage is the removal of influences unrelated to tissue properties, like operator or MR system dependencies, differences in scan parameters, spatial variation in the magnetic field, and image scaling. Thus, absolute quantification allows the comparison of data across different laboratories and experimental protocols, enabling longitudinal and large-scale multicenter studies on patient cohorts, accounting only for intraindividual evolution and interindividual differences.

4. Physical Meaning of the Relaxation Constants

From a physical point of view, the relaxation times T₁, T₂ (or T₂^*) are time constants that describe how fast an MR signal, generated by an excitation RF pulse, decays over time. Their values are determined by the intrinsic physicochemical properties of matter under study. It is important to understand that the longitudinal (T₁) and the transverse (T₂ or T₂) relaxation processes are independent and always occur simultaneously.

The longitudinal relaxation time (T₁) is a time constant describing the return of observed nuclei from an excited (higher energy) state, achieved by an excitation RF pulse, to its equilibrium (lower energy state), by dissipating the received energy to the surrounding molecular lattice (T₁ is also called spin–lattice relaxation time).

If one considers the exited protons of a single water molecule, their return to the equilibrium state (recovery) is basically influenced by neighboring molecules in the surroundings, which behave as fluctuating magnetic fields. In bulk water, the surrounding water molecules of the one under observation behave as “little magnets” in permanent movement, tumbling as well at different rates (characterized by different rotational correlation times, τ_c) (Figure 6a). These moving and tumbling molecules around the observed one generate magnetic fluctuations that induce the relaxation (loss of energy) of the observed nucleus.

Figure 6.

Schematic representation of the T₁, longitudinal, or spin–lattice relaxation mechanism. Because of the tumbling of their magnetic moments (represented by arrows), the MR active nuclei (blue spheres) in the vicinity of an excited proton (red sphere) produce magnetic fluctuations that facilitate the dissipation of energy, when tumbling at the adequate frequency. The chance of finding MR active nuclei that tumble at the right frequencies (faster relaxation, shorter T₁) is higher when the nuclei are in the presence of a large macromolecule (right) than when they are surrounded by free-moving small molecules (left).

More precisely, when a molecule or series of molecules in the neighborhood tumble with a τ_c value equal to (1/ω), ω being the resonance frequency of the excited (observed) nucleus, the resonance condition is met, dissipating the acquired energy in these interactions. In general, in bulk water, it is not easy for the observed excited molecule to meet this condition (many “molecular encounters” have to take place until sufficient water molecules of appropriate τ_c interact with the observed molecule), and therefore, energy is dissipated slowly (with a large T₁ time constant value). Conversely, in more complex environments, with the presence of large macromolecules in the surroundings (for example, lipids or proteins, see Figure 6b), it is statistically more likely to meet the condition or resonance, and energy is dissipated much faster (with a short T₁ constant time). In this way, T₁ reflects the amount, structure, and mobility of surrounding molecules, and it is generally used to study water and macromolecular contents and water binding states with the variables that influence them (pH, T, etc.).

The transverse relaxation time (T₂) is a time constant describing the decay of the MR signal by the building-up of incoherence in the phase of the magnetization of the excited nuclei. To understand this concept, we will briefly explain how the incoherence of the phase of a series of waves leads to a loss of signal, and then we will use this concept to explain how the MR signal is lost by this phenomenon.

To describe a sinusoidal signal, we need three magnitudes, the amplitude (A), the oscillation frequency (ω), and the phase (α) of the wave (Figure 7). When multiple sinusoidal signals oscillate with the same phase and frequency and are simultaneously recorded, the total amplitude of the recorded signal is the addition of the individual amplitudes of each contributing wave (Figure 7, left). If some of the signals suffer a change in their phase, coherence is lost, and the total amplitude is reduced (Figure 7).

Figure 7.

Signal lost by incoherence. Left, a sinusoidal signal of amplitude A1 (purple line) built up from three coherent sinusoidal signals of amplitude A1/3 ((blue, red, and green lines). Middle, the amplitude of the overall signal is reduced (A2 < A1) when a signal oscillates out of phase. Right, when all signals lose their coherence, the amplitude of the global signal is further decreased (A3 < A2 < A1).

Protons excited by an RF pulse inside a magnetic field (B₀) build up a magnetic moment that precesses at the so-called Larmor frequency, which depends on an intrinsic parameter (the gyromagnetic ratio, γ) and the magnitude of the externally applied magnetic field (B₀). Such precession may be represented by a sinusoidal signal of specific amplitude, frequency, and phase, and this is valid for each individual MR active nuclei present in the matter under observation. In principle, all protons on a specific pixel (voxel, or ROI) submitted to the same magnetic field will oscillate at the same frequency and phase (coherent signal). Thus, the amplitude of the global signal detected in such pixel is the addition of the individual amplitudes of all excited nuclei within the pixel.⁴

However, fluctuations over time of the Larmor frequency of the individual nuclei present in the matter under observation lead to a situation in which phase is no longer accumulated at the same rate, losing the coherence among the individual components of the signal, leading to a global signal amplitude decay (Figure 7). The faster the coherence is lost, the faster the MR signal is lost (short T₂).

This mechanism of signal loss is called T₂ or spin–spin relaxation. Contrary to what happens with T₁ relaxation, in T₂ relaxation there is no loss of energy involved, and all individual components of the signal maintain their amplitude (contrary to what the term relaxations may suggest). The assimilation of this concept is crucial to understanding that T₁ and T₂ are unrelated but simultaneously occurring mechanisms of signal destruction.

In theoretical terms, the signal lost by T₂ relaxation can be regained by rephasing the signals from the individual nuclei, generating a signal echo. An echo should have, in theory, the same amplitude as the originally generated signal (just after the excitation pulse). However, in practice, signal coherence is partially lost permanently, any time an echo is generated, and therefore a portion of the global amplitude is definitely lost over time (that is why the term relaxation is used).

This phenomenon is a consequence of the existence of two different contributions to the T₂ effect. The surroundings of each observed nucleus contain fixed or permanent elements and random elements (for example, another molecule that “passes by” at a specific moment). Fluctuations of magnetic fields that are fixed over time can be reversed, while random fluctuations of the local magnetic field cannot, contributing to a permanent loss of phase coherence. This is reflected in the following equation:

13

Thus, the effective spin–spin or effective transverse relaxation time (T₂^*) includes the contribution of the transverse relaxation time (T_2 random, generally referred to as T₂) and the so-called “magnetic field inhomogeneities” that reflect the influence of local, constant influences on the magnetic field (T_2 fixed). In a perfectly homogeneous magnetic field, T₂ = T₂, this condition is complicated to meet when the matter under observation is not a pool of bulk water, due to the presence of magnetic microdomains in solid matter.

Figure 8.

T₂ vs T₂* signal decay. Top, at a given instant, the static magnetic field acting over an excited proton (red sphere) is reinforced by the random presence of another proton (blue sphere) with a magnetic moment aligned with the principal field. This causes the proton to slightly increase its Larmor frequency, dephasing its signal from the rest of the unaffected protons, reducing the signal intensity (red line in the plot on the right). Successive instantaneous influences of other randomly oriented magnetic moments will cause successive dephasing of the proton. (Bottom) Plot showing the evolution of an MR signal suffering T₂ (green curve) or T₂* (red curve) decays. T₂* decay is faster than T₂ since it includes a term related to “static” or “fixed” contributions to the dephasing of the spins, which can be reversed by generating an echo. Signal loss due to a T₂* effect can be only partially refocused.

In general, protons from water molecules confined in rigid environments (solids) and protons belonging to, or under the influence of, nuclei belonging to large and slow tumbling molecules (macromolecules in general) are more prone to suffer random influences from nearby active nuclei, showing a faster T₂ decay of the signal (shorter T₂). In contrast, the signal generated by relatively mobile protons (e.g., free water) decay much more slowly because rapid fluctuations tend to average out, yielding a smaller net phase dispersion over time.

The presence of super-paramagnetic or paramagnetic substances in the observed matter is a source of strong local magnetic field fluctuations and has a strong T₂^* effect. This is an important concept that we will discuss further in section 6 of this manuscript.

We know that T₁ and T₂ relaxation processes are complex phenomena to understand without going deeper into MR physics. However, a simple conceptual discussion like the one presented here may help introduce the reader to important concepts for understanding the nature of these two independent and simultaneous processes and understand why they are closely related to the nature of the matter under observation. Composition, concentration, presence of macromolecules, temperature, pH, and many other variables have an influence on these parameters, and therefore, measurement of T₁ and T₂ (or T₂^*) time constants can provide important information on the matter under observation.

5. Biomedical Meaning of the Relaxation Times

So far, we have learned that relaxation times are susceptible to the local environment of the nuclei that produce the MR signal, reflecting their influence as shorter or longer T₁, T₂, and T₂^* values. In practice and considering that the local environment of observed protons is directly related to tissue composition and functional status, quantitative MR relaxometry allows the characterization of the nature and functional status of a wide range of healthy and pathological tissues in biomedicine. This section provides a simple but straightforward interpretation of the influence of several fundamental physiological and pathophysiological properties of tissues on the relaxation times T₁ and T₂ (or T₂).

In the absence of super-paramagnetic or paramagnetic substances (we will discuss later the presence of the so-called contrast agents), the relaxation time T₁ is mostly sensitive to the macromolecular content, water content, presence of dissolved oxygen, and temperature. Any difference in tissue composition or condition that involves a difference in these parameters will be reflected in the T₁ value. Thus, T₁ has proven value in evaluating the loss of myelin and axonal alterations in brain tissue, loss of proteoglycan in cartilage, changes in collagen and methemoglobin content in the heart, edema in the brain and heart, fat content in the liver, etc. When an exogenous gadolinium T₁-reducing vascular contrast agent (a concept that will be discussed in detail in the next section) is intravenously injected, changes in T₁ values and distribution in tissues enable assessment of tumor vessel blood flow and leakiness, breakdown of the blood–brain barrier, infarct or gray zone regions in the heart, and fibrosis, among other applications.¹

The relaxation time T₂ is sensitive to tissue composition and structure, water content, and iron levels. It has been used to assess myelin content in the brain, collagen content and organization in cartilage and heart muscle, edema (inflammation), hemorrhage, and iron content in the liver and heart. The relaxation time T₂^* is sensitive to deoxyhemoglobin and water content and has even better sensitivity than T₂ to iron levels. It has been used to assess brain function (altered deoxyhemoglobin levels), myocardial oxygenation, tumor hypoxia, hemorrhage, angiogenesis, calcification in the heart (low water content), liver and cardiac iron.¹

This is only a simplistic view of some biomedical applications of T₁ and T₂ relaxometry, and many different applications can be found in the literature.

6. Contrast Agents

MRI is a very versatile imaging technique with multiple mechanisms available to generate contrast. However, there are situation on which exploitation of those mechanisms is not efficient in generating the desired contrast between tissues or ROIs because the intrinsic properties (relaxation times) of those tissues are very similar, and extrinsic parameters cannot enhance their differences.

When the selection of pulse sequence and tuning of extrinsic parameters are not enough to enhance contrast, it is possible to use a so-called “contrast agent”. Such an agent is generally a nanoparticle, a small molecule, a macromolecule, or a supramolecular complex that alters the intrinsic properties of water molecules in the tissue under its influence (alters T₁ or T₂), enabling the possibility to generate a contrast. A graphical explanation of this phenomenon is presented in Figure 9.

Figure 9.

Generation of contrast by a CA. (a) T₂ decay plots for two brain regions that are easy to differentiate (A: CSF at ventricle, B: white matter of corpus callosum) due to their different T₂ values. Subtracting the two decay plots makes it easy to see how contrast between the two tissues changes with the extrinsic parameter TE, and find the value of TE at which contrast is maximal. (b) A brain tumor (orange plot) presents a very similar T₂ value to gray matter (red plot), being virtually impossible to generate contrast between these two tissues. (c) Administration of a contrast agent into the brain parenchyma induces a substantial reduction of the T₂ value on the injected area (changes the intrinsic properties of the tissue), generating a strong contrast where there was no contrast before.

A possibility to generate contrast in tissues is the induction of a change in the properties of the surrounding media (pH, T, density, etc.), a process that is not always possible without disturbing the natural conditions that allow cells to survive and perform their functions with normality. Alternatively, we can add a contrast agent in the surroundings of the observed nuclei, which affects the relaxation processes and their characteristic relaxation times (by shortening them). Thus, a contrast agent is an entity (small molecule, macromolecule, supramolecular aggregates, nanoparticles, etc.) that influences the intrinsic properties of MR active nuclei, altering the contrast in the signal. It is important to mention that MR contrast agents are usually not active in MRI (they do not produce a signal), but they influence the signal produced by other molecules (surrounding water, in most cases) instead (again, we exclude from the discussion heteronuclear based imaging probes, such as ¹⁹F-containing materials, which indeed generate a signal distinguished from the background by themselves).

In this work, we will focus on the concept of a contrast agent as a material that alters the magnetic properties of protons, in ¹H based MRI. Materials containing other MRI active nuclei, such as ¹⁹F or ¹³C, that can be used as imaging probes in heteronuclear MRI, and that are also referred as “contrast agents” in the literature, will not be discussed here. Other options to generate contrast as the exploitation of magnetization transfer mechanisms by suing the so-called CEST contrast agents will be briefly introduced. Hyperpolarization is another alternative to generate contrast in MRI, but the discussion of this phenomenon is beyond the scope of this work (see ref (7) for a review on this subject).⁷

When the action of the contrast agent results in an increase of the signal produced by water (by reduction of T₁ times as a result of a positive longitudinal relaxivity r₁), they are called positive contrast agents (generally paramagnetic materials), while when their action results in a decrease of the signal (by reduction of T₂ times, as a result of a positive transverse relaxivity r₂), they are called negative contrast agents (mostly super-paramagnetic materials).

The magnitude of the signal enhancement induced by a contrast agent (i.e., its efficiency) depends on intrinsic and extrinsic parameters. In general, the variation of the relaxation times suffered by water molecules (or any other MR detectable substances) in the presence of a contrast agent can be quantified by the following expressions:

14

15

where T_1,0 and T_2,0 (or T_2,0*) are the relaxation times of observed molecules in the absence of contrast agent, r₁ and r₂ are the longitudinal and transverse relaxivities of the contrast agent (intrinsic properties, in units of mM^–1 s^–1), and [CA] is the concentration of contrast agent (in mM). It is common to express the same relationships in terms of relaxation rates R_i = (1/T_i) instead of relaxation times, as

16

17

The longitudinal (r₁) and transverse (r₂) relaxivities of a contrast agent are defined as the capacity of the agent to enhance the relaxation rate constants (R₁ or R₂, respectively) of water, normalized to the contrast agent’s concentration. The values of r₁ and r₂ are the main physicochemical parameters that are considered for the development of an effective magnetic resonance imaging probe (their ratio, and not just their absolute values, is also important as we will discuss later). They depend on the size and chemical structure of the contrast molecule, and on the accessibility of water molecules to the magnetic center.⁷

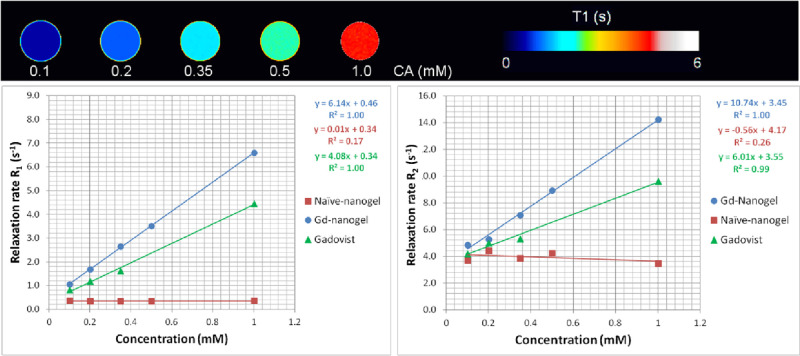
Experimentally, the relaxivities of a contrast agent can be estimated by preparing a series of solutions of the contrast agent at different concentrations and measuring the R₁ and R₂ (or R₂^*) values of those solutions using the relaxometry methods described in section 3. Then, relaxivities are calculated as the slope of the linear regressions of the relaxation rates versus the concentration of the solutions (Figure 10). For a very precise quantification of relaxivity values, samples should be analyzed by inductively coupled plasma (ICP)-MS or other precise analytical means to estimate accurately the contrast agent concentration. It is important to remember that relaxivities depend on the external magnetic field and temperature, when comparing absolute values from different experimental setups.

Figure 10.

Determination of magnetic relaxivities for a CA. On top, R₁ parametric maps of five tubes filled with water doped with a gadolinium-based contrast agent at different concentrations. Bottom, characteristic linear regressions of the longitudinal (R₁) and transverse (R₂) relaxation rates vs the concentration of three different materials. Two of them (Gadovist and Gd-nanogel) behave as contrast agents, reducing T₁ and T₂ values of water (increasing the relaxivities R_i). The third substance does not behave as a contrast agent in MR, not affecting the relaxation behavior of water at any concentration.

It should be emphasized that the relaxivity of the agent and its concentration in the tissue are not the only parameters that contribute to its efficiency. The distribution of the agent within the image voxel (or ROI), the proton density, and the potential diffusion of the agent, as well as the chemical environment of the surroundings, and of course the applied magnetic field, are also contributors to the efficiency of signal enhancement that need to be considered (see ref (8) for extended explanation).⁸

Finally, it should be also mentioned that contrast agents for MRI should fulfill several additional requirements for biomedical applications, including adequate relaxivity and susceptibility effects, tolerance, low toxicity, stability, optimal biodistribution, elimination from the body, or metabolization. The design and applications of MR contrast agents is a very active field of research that involves multiple disciplines such as nanotechnology, biomaterial science, and biomedicine. Tuning their structure, properties, functionality, biocompatibility, and in vivo behavior is a complex task that requires a wide range of skills, but in general, all of them work following the basic principles presented here.

7. MR Contrast Agent Types and Applications

We will finish this work with a brief discussion of the different types of MR contrast agents and some of their biomedical applications. This is not a simple task since every day new MR contrast agents of different natures, mechanisms of action, and functionality are presented in the literature. Despite the numerous families of contrast agents, they can be classified, in general, based on three different criteria: (1) the magnetic properties of the contrast agents, (2) the in vivo biodistribution behavior of the contrast agent, and (3) the type of contrast enhancement produced by the agent (see Figure 11).

Figure 11.

Classification of contrast agents.

7.1. Magnetic Properties

According to their magnetic properties, contrast agents can be classified as follows.

7.1.1. Agents Based on Paramagnetic Relaxation

Most MR contrast agents used in human clinical applications are based on paramagnetic substances which are metal ions with unpaired electrons in the outer orbital shells (transition and lanthanide metal ions), giving rise to magnetic dipoles when exposed to an external magnetic field. Since the electron’s magnetic moment is ca. 700 times higher than the nuclear magnetic moment of a proton, paramagnetic ions induce large fluctuating magnetic fields that affect nearby protons. If the frequency of such a fluctuation has components close to the Larmor frequency of the observed nuclei, their relaxation will be significantly enhanced, resulting in shorter relaxation times. Many paramagnetic metal ions could be used as MR contrast agents, but gadolinium or manganese ions (linked to chelating molecules of different nature and functionality) are the most used ones because of the seven unpaired electrons of Gd³⁺ ions (five for manganese), combined with long electron spin relaxation times. Paramagnetic agents affect both the T₁ and the T₂ values but are generally used to exploit their effects on the longitudinal relaxation times (T₁ contrast agents). For further details on paramagnetic-based contrast agents, see Peter Caravan’s work.^10,11

7.1.2. Agents Based on Superparamagnetic Relaxation

Super-paramagnetic agents are based on iron oxides, mostly magnetite (Fe₃O₄) or maghemite (γ-Fe₂O₃). These are water-dispersible crystals with a core diameter in the range 5–10 nm, made of several thousands of iron nuclei that are usually coated by a polymeric shell (in the initial applications, it used to be a dextran coating, but nowadays, composition is very variable) with typical sizes around 100 nm. This shell aims to stabilize the particles, facilitate their dispersibility in water and their biocompatibility, and allow their functionalization. When iron ions are magnetically ordered within the crystal, the net magnetic moment of the whole nanoparticle is so large that it greatly exceeds that of typical paramagnetic metal ions. This effect is called super-paramagnetism and is characterized by a large magnetic moment in an external magnetic field but no remnant magnetic moment in the absence of such a field. Super-paramagnetic agents strongly reduce both T₁ and T₂ relaxation times of surrounding water molecules, but their dominant effect is on the transverse relaxation times (T₂ or T₂^*). Thus, super-paramagnetic contrast agents are usually referred as T₂ contrast agents. For further details on iron oxide-based contrast agents, see the work of Muller and co-workers.¹²

7.1.3. Agents Based on Magnetization Transfer Effects

A novel family of contrast agents has been defined in the past decade to introduce contrast enhancement in MR by saturation transfer effects. Using RF pulses of appropriate frequency, the magnetization of solid/semisolid protons (belonging to macromolecules) can be transferred to mobile protons of surrounding water molecules, inducing a marked reduction in the signal intensity of mobile water molecules, which interact with bound protons in the macromolecules. This mechanism, known as magnetization transfer contrast (MTC), can be applied in imaging applications using the so-called CEST contrast agents. The amount of MTC will depend on the macromolecules’ concentration, surface chemistry, and biophysical dynamics. Thus, a CEST agent is a system containing one or more mobile protons in slow/intermediate exchange with water proton resonances. Thus, on irradiation of the absorption of the exchanging protons, saturated magnetization is transferred to the water signal, thereby causing a decrease in signal intensity. This approach is becoming popular because it allows the use of specific radiofrequency pulses to introduce contrast, and it allows the activatable and selective excitation of different contrast agents at the same time (multifrequency imaging), providing the opportunity to perform multiplex detection of different contrast agents in the same anatomical region. This feature is very appealing for in vivo applications. For a further details on CEST-based contrast agents, see the work of Aime and co-workers.¹³

7.2. Biodistribution Behavior

In parallel, contrast agents can be classified according to their biodistribution patterns:

7.2.1. Intravascular Contrast Agents

Intravascular contrast agents are molecules administered intra-arterially or intravenously and have a sufficient size (in terms of molecular weight or hydrodynamic radius) to prevent their leakage from the vascular bed to the extravascular space. Intravascular contrast agents present a half-life in blood of minutes to several hours and are eventually eliminated from the blood by the Kupffer cells of the liver, spleen, and lymphatic system, or by the kidneys.

Since these agents remain in the blood for a certain time, their main applications are as vascular agents in angiography, contrast agents for perfusion (e.g., in tumors), and for the study of the integrity and permeability of the blood–brain barrier. Since they are finally taken up by the liver, accumulating into larger particulate clusters in the Kupffer cells, they are also used to study liver diseases.⁹

7.2.2. Extracellular Fluid Contrast Agents

When paramagnetic contrast agents present a small molecular weight, they may be small enough to diffuse from the plasma into the interstitium, being distributed to the extracellular fluid by mechanisms dominated by diffusion. These agents are therefore often referred to as extracellular fluid contrast agents. They are not taken up by cells and are eliminated by renal excretion, with a half-life determined by the glomerular filtration rate.⁹

7.2.3. Tissue-Specific Contrast Agents

Tissue-specific agents are molecules specifically designed to accumulate in a given organ or tissue. An example of this type of agent is iron oxide nanoparticles, which generally accumulate in the liver (liver-specific contrast agents). Another example is HDL-based contrast agents that can target atherosclerotic plaques¹⁴ or nanoparticles tagged with antibodies against specific cells, such as tumors or ischemic tissue.¹⁵

7.3. Contrast Type

Contrast agents are also classified according to the type of contrast that they induces.

In this regard, contrast agents can be generally classified as “positive contrast agents” when they act as T₁ contrast agents, enhancing the signal intensity on ROIs under observation. A good T₁ or positive contrast agent should present a high value for r₁ relaxivity and a low r₂/r₁ ratio. Iron oxide nanoparticles have elevated r₁ and r₂ values, but they are not ideal for T₁ contrast because of their elevated r₂/r₁ ratio, which causes the T₂ effect (signal destruction) to prevail over (or “quench”) T₁ effect (signal enhancement). Therefore, they are designated as negative contrast agents.

Most positive contrast agents are based on paramagnetic substances, such as gadolinium and manganese ions, while most negative contrast agents are based on super-paramagnetic substances (iron oxides).

A particularly interesting group of contrast agents are the so-called “dual contrast agents”, which are materials able to exploit both sorts of contrasts simultaneously. These contrast agents present the particularity of presenting moderate values for both r₁ and r₂ relaxivities. Thus, depending on the pulse sequence used for imaging, they will appear as positive, in T₁ weighted images, and as negative, in T₂ (or T₂^*) weighted images.

It is known that the presence of endogenous contrast agents in the body, such as ferritin, deoxyhemoglobin, etc. or the existence of confounding effects like those caused by small deposits of fat, air bubbles, calcifications, etc., can cause signal variations that may be misinterpreted as the presence of positive or negative exogenous contrast agents. These sources of contrast can be differentiated from a truly exogenous contrast agent by using dual contrast agents, since the later will show both positive and negative contrast (depending on the image acquisition parameters), while endogenous sources of contrast will behave as only positive or only negative contrast sources, as graphically explained in Figure 12 (see ref (14) for an extended explanation).¹⁶

Figure 12.

Dual T₁/T₂ contrast agents. A dual T₁/T₂ contrast agent produces a different contrast in both T₁-weighted and T₂-weighted images, facilitating their ability to distinguish potential endogenous substances of the body that can act either as T₁ or T₂ contrast agents.

7.4. Advanced Contrast Agents

In recent years, novel and more sophisticated contrast agents have been developed to generate contrast in MR images, beyond the relaxivity concepts, adding functionalities to the agents that are very useful to study different biomedical issues. To conclude this work, we would like to mention that despite the numerous examples of MR contrast agents reported in the literature, recent advances in the fields of MRI and nanotechnology are enabling the design of novel and more sophisticated contrast agents, searching for specific magnetic, biological or structural properties and functions. On top of that, thousands of publications report particular biomedical applications of those agents and techniques. It is a simplification to classify all existing contrast agents in the categories presented here, since this is a fast-changing field of research, but we intended to introduce the basic principles of image contrast, and it remains out of the scope of this mini-review to describe in detail the whole field of contrast agent design and uses. Some references are provided instead, to introduce the reader to this fascinating research field, hoping that this work can be used as a starting point for further reading on the subject. Among the most interesting types of contrast agents falling in the category of “advanced contrast agents” we should mention the following.

7.4.1. Responsive, Activatable or “Smart” Contrast Agents

Most contrast agents described in the literature, and used in clinical applications are passive and nonspecific, but advances achieved in the fields of material sciences and nanotechnology are boosting the development of imaging probes that respond to external stimuli (such as changes of pH, temperature, oxidation states, enzyme activity, etc.). The possibility of change contrast upon external stimuli allows the study of function at the cellular or subcellular level, which is a very useful feature for the definition of imaging biomarkers of disease.¹¹ References (18 and 19) are reviews on the matter.^17,18

7.4.2. Ratiometric Contrast Agents

The absolute amounts of contrast agent concentrated in a particular region of interest is difficult to quantify in in vivo applications of MRI since, as already discussed, the signal intensity depends not only on the concentration of contrast agent but in the imaging sequence used of image acquisition, image artifacts, endogenous alteration of contrast, even the oxygenation level of the blood.¹⁹ Therefore, there is a current trend to develop so-called “ratiometric contrast agents”, self-calibrating materials that allow absolute quantification by measuring two or more signal changes inducing the same single entity. One of the signal changes is used as a calibrating or normalizing signal for the other. For a detailed description of this phenomenon and the characteristics of these contrast agents, we suggest the reading of a review on the matter presented by Genicio et al.¹⁷

7.4.3. Multimodal and Theragnostic Contrast agents

The advancing of key enabling technologies such as nano- and biotechnology has resulted in the development of advanced multifunctional nanomaterials with important applications in biomedicine. Nanotechnologists have used the advances achieved during decades in the field of drug delivery for designing advanced imaging probes with specific functions such as targeting capacity, responsiveness to external stimuli, biocompatibility, biodistribution and bioavailability properties, etc.

Since most of the objectives of advanced drug delivery and targeted imaging are common, the field of theragnosis, the combined function of a nanomaterial as a therapeutic (drug delivery) and as a diagnostic tool (contrast agent for imaging), has emerged in the past decade, facilitating the development of the concept of personalized medicine. Thus, novel nanomaterials presenting both functions simultaneously have systematically been described in the literature, with multiple biomedical applications, although treatment of cancer has been the most popular field of application.

Since all imaging modalities present advantages and disadvantages, it is also common practice to include more than one sort of imaging probe to overcome individual limitations and profit from synergistic capacities of multiple imaging modalities. Thus, the development of multimodal imaging contrast agents is also a very active field of research. For further details on these concepts, we suggest the reading of the work of Lee et al.²⁰

8. Conclusions

This review provides some comprehensive concepts of the origins of contrast in MRI, how contrast depends on intrinsic properties of matter, and how contrast can be manipulated by tuning MR experimental conditions and using MR active biomaterials, attempting to facilitate further exploration of the reader in the field. This is an introductory manuscript rather than a rigorous and extended presentation of the fundamentals of MRI. We hope that the background presented here will facilitate the reader in further exploration of the extensive specific literature existing in the field of MR relaxometry and contrast agents.

Biographies

Saioa Alzola-Aldamizetxebarria has an M.Sc. in molecular biology and biomedicine. She is graduated in pharmacy at the University of the Basque Country, Spain. Her main research interests are neurological diseases, development of genetic tools for the study of brain circuits, and magnetic resonance imaging.

Laura Fernández-Méndez graduated in material sciences studies at the University Complutense of Madrid, Spain. Her current research interests include the development of new nanomaterials as contrast agents and drug delivery systems for neurological and pulmonary diseases by microfluidic techniques.

Daniel Padro has a Ph.D. in physics (University of Warwick, UK, 2002). He is specialist in NMR and MRI techniques. His current interests include the development of novel techniques in NMR and MRI and their applications in the fields of material sciences, chemistry, biology and biomedicine.

Prof. Jesus Ruiz-Cabello received his PhD in Physicochemistry in 1990 at the University Complutense Madrid, Spain. He is specialized in MR and molecular imaging of the lung and heart. His current research interests include studying molecular and functional biomarkers of vascular diseases for early diagnosis and monitoring novel therapies.

Prof. Pedro Ramos-Cabrer received his Ph.D. in chemistry in 2000 at the University of Santiago de Compostela, Spain. He specializes in MRI and theranostic applications for the study of the central nervous system. His current research interests include the use of animal models of neurological diseases, development of imaging biomarkers of disease, and the development of drug delivery systems for the brain.

Author Contributions

^# S.A.-A. and L.F.-M. contributed equally to this work.

The authors declare no competing financial interest.