A Cross-validated Ensemble Approach to Robust Hypothesis Testing of Continuous Nonlinear Interactions: Application to Nutrition-Environment Studies

Abstract

Gene-environment and nutrition-environment studies often involve testing of high-dimensional interactions between two sets of variables, each having potentially complex nonlinear main effects on an outcome. Construction of a valid and powerful hypothesis test for such an interaction is challenging, due to the difficulty in constructing an efficient and unbiased estimator for the complex, nonlinear main effects. In this work we address this problem by proposing a Cross-validated Ensemble of Kernels (CVEK) that learns the space of appropriate functions for the main effects using a cross-validated ensemble approach. With a carefully chosen library of base kernels, CVEK flexibly estimates the form of the main-effect functions from the data, and encourages test power by guarding against over-fitting under the alternative. The method is motivated by a study on the interaction between metal exposures in utero and maternal nutrition on children’s neurodevelopment in rural Bangladesh. The proposed tests identified evidence of an interaction between minerals and vitamins intake and arsenic and manganese exposures. Results suggest that the detrimental effects of these metals are most pronounced at low intake levels of the nutrients, suggesting nutritional interventions in pregnant women could mitigate the adverse impacts of in utero metal exposures on children’s neurodevelopment.

1. Introduction

Investigation of the interplay between multiple lifestyle, biological, and environmental factors contributing to disease risk is a major goal in public health. Classic gene-environment and nutrition-environment studies focus primarily on the interaction between discrete factors (31; 8), or between discrete factors and the linear effect of a few continuous measurements (e.g. (28)). In recent years, however, recognizing the fact that populations are exposed to combinations of continuously-measured chemical and non-chemical factors that potentially have a nonlinear effect on outcome, there has been increasing interest in the best ways to statistically quantify the complex interplay of these continuous, nonlinear effects on health.

In this work we analyze data from a birth cohort study on the interaction between in utero exposure to a metal mixture and maternal nutrition intake during pregnancy on children’s neurodevelopment in rural Bangladesh (13; 21). Bangladesh has been experiencing unparalleled levels of arsenic (As) other toxic metal poisoning through contaminated groundwater (33). Bangladesh also has rates of undernutrition that are among the highest in the world (42). A recent study (43) assessed the relationships between the arsenic (As), manganese (Mn), and lead (Pb) metal pollution mixture and infant neurodevelopment in Bangladesh, and has detected nonlinear, inverted-U shaped exposure–response relationships that differ among population subgroups. Its findings suggested a role of additional cultural/behavioral factors in affecting the impact of this metal mixture on children’s health. One possible factor impacting these environmental effects is maternal nutrition during pregnancy. At vulnerable stages of fetal development, mother’s overall nutrition intake may exacerbate adverse effects of chemical stressors. Specific nutrients may modify chemical effects because of their influence on the metabolism of the chemicals, on epigenetic programming in response to the chemicals, or through other mechanisms that vary by metal or by outcome. To answer this question, a companion nutritional study (26) was conducted to collect data on mother’s nutrition intake during pregnancy, measuring the level of nutrition intake of 27 nutrients grouped in five nutrition categories (macronutrient, minerals, (pro-)vitamin As, vitamin Bs, and other vitamins), thereby providing an unique opportunity for researchers to quantitatively investigate the effect modification between nutrition intake during pregnancy and in utero metal exposures on infant development.

The Bangladesh study posed two challenges that are common in many modern data science applications: (1) high dimensionality of the interaction, as the interaction term contains second- and higher-order interactions between 27 nutrients and 3 metal exposures, and (2) the nonlinearity of the underlying exposure-response relationship, whose mathematical properties are unknown a priori. In such a scenario, linear-model based methods are known to suffer from misspecification of the main effects model for nutrients (that include nutrient-nutrient interactions) and metals (including metal-metal interactions) even under the null of no nutrient-metal interactions, leading to inflated Type I error and reduced test power (40; 8; 46). To boost efficiency and incorporate nonlinearities in the exposure-response relationship, a recent line of research has focused on constructing interaction tests based on kernel machine regression (KMR) (36; 34). Building on the success of previous kernel testing literature (29; 47), these tests model the main-effect and interaction-effect functions as elements in reproducing kernel Hilbert spaces (RKHS) generated by pre-specified kernel functions, and build the hypothesis test by re-parametrizing the kernel machine regression as a linear mixed model (29). In this framework, the interaction term is an additional random effect term controlled by an univariate garrote parameter, on which one can construct a variance-component score test (27) for a test of the null hypothesis of no interaction. Successful applications of such tests include targeted gene effect identification in genetic pathway analysis (30), gene–gene interaction detection in genome-wide association study (24), and also in gene-environment interaction studies with discrete factor such as gender (4) and risk indicators of cardiovascular disease (12).

Applications of interaction tests involving sets of multiple continuous measurements with nonlinear effects, however, remain rare. The key challenge impeding the success of interaction tests in continuous settings lies in designing a proper kernel function for the multi-dimensional, nonlinear main-effect functions of unknown form. The kernel functions for the main effect terms need to generate a RKHS that is rich enough to contain the main-effect functions under the null, while at the same time be sufficiently structured to maintain power for detecting interactions. Earlier work (29; 30) approached this problem by selecting the kernel from an assumed parametric family (e.g. the Gaussian radial basis functions (RBF)) through maximum likelihood estimation, risking the specification of overly strong assumptions for these nonlinear functions. More recent approaches alleviate assumptions on the data-generation mechanism by incorporating multiple candidate kernels into the analysis, treating the kernel function as a weighted combination of candidate kernels, and learning kernel weights by maximizing various objective functions such as centered kernel alignment (10) or by an L₁-regularized model likelihood (37). However, designed primarily to maximize predictive accuracy, such procedures can be overly flexible under the alternative and potentially result in hypothesis tests with low power (49). Permutation tests are another popular approach for alleviating the issue of kernel misspecification (7; 49); however, constructing a permutation procedure for an interaction test is usually not possible in observational studies, since the gene-environment independence condition tends to not hold (6).

In this article, we propose a new approach to test for the interaction effect between groups of continuous features, each having potentially complex main effect functions relating outcome to that set of exposures. Built under the framework of kernel machine regression, we address the issue of kernel misspecification by deploying an ensemble of candidate kernels, and carefully design the ensemble strategy so that it minimizes the generalization error of the overall ensemble (11). Consequently, the proposed test automatically estimates the form of the kernel under the null from the data and guards against overfitting the interaction effect under the alternative, resulting in a powerful test that is robust under a wide range of data generation mechanisms. As we discuss in Section 3, such a strategy results in an estimator that enjoys an oracle property for ensemble selection and good generalization performance in limited samples, thereby achieving a powerful null-model estimator especially suitable for hypothesis testing in epidemiology studies. We term our method the Cross-Validated Ensemble of Kernels (CVEK). In Section 4, we illustrate the robustness of our method by conducting simulation studies that evaluate the finite-sample performance (Type-I error and power) under a range of data-generating scenarios and compare the performance of the proposed approach with other popular interaction tests. Finally, in Section 5, we apply our method to data from the Bangladesh reproductive cohort study (13; 21) to investigate the interaction between mother’s daily nutrient intake and in-utero exposure to an environmental metal mixture (As, Mn and Pb) on children’s neurodevelopment.

2. Model and Inference

Assume we observe data from n independent subjects. For the i^th subject, let y_i be a continuous response, x_i be the set of p baseline covariates that can be entered into the model linearly, and z_i be the set of q continuous covariates that have a nonlinear effect on y_i. Furthermore, we assume that there exists a grouping structure among the z_i covariates such that z_i = {z_1,i, z_2,i}, where the m^th group ${\text{z}}_{m,i}\in {ℝ}^{q_m}$ contains q_m covariates, m = 1, 2. We discuss the generalization to the case of more than two groups in z_i in Section 2.2.

We assume that the outcome y_i depends on covariates x_i, z_i through the model:

$$y_i={\mathbf{x}}_i^T\mathit{\beta }+h\left({\mathbf{z}}_i\right)+{ϵ}_i\hspace{1em}\hspace{1em}\text{where}\hspace{0.17em}{ϵ}_i\stackrel{iid}{~}N\left(0,{\sigma }^2\right),$$ (1)

where β is a p × 1 vector of unknown coefficients for background covariates, $h\left({\mathbf{z}}_i\right):{ℝ}^q\to ℝ$ is an unknown continuous function describing the effect of z_i, and ϵ_i is random noise that is independently and identically distributed as N (0,σ²). For identifiability purpose, h is assumed to be square-integrable and subject to the constraint ${\int }_{{ℝ}^q}h\left(\mathbf{z}\right)d\mathbf{z}=0$.

Our main objective in this work is to test for the interaction between two chosen sets of covariates in z_i = {z_1,i z_2,i}, while accounting for interactions within each covariate set. Without loss of generality, consider testing for the interaction between z_1,i and z_2,i. Then our hypothesis is:

$$H_0:h\in {{\mathcal{H}}_{12}}^{\perp },$$ (2)

where ${\mathcal{H}}_{12}$ is the functional space of ”pure interaction” functions that contain only the interaction effect between (z_1,i, z_2,i). That is, under the null hypothesis, h(z) may depend on the individual main effects of z_1,i, z_2,i, but does not depend on the interaction effect of the set pair (z_1,i, z_2,i).

We take the penalized likelihood approach to estimate parameters (β, h). Namely, we first specify $\mathcal{H}$ the candidate space and $\lambda$ the penalty parameter, then estimate parameters $\mathit{\theta }=\left(\mathit{\beta },\widehat{h}\right)$ by minimizing the penalized negative log likelihood:

$$\left(\mathit{\beta },\widehat{h}\right)=\underset{\mathit{\beta }\in ℝ,h\in \mathcal{H}}{argmin}{L}_{\lambda }\left(\mathit{\beta },h\right),\hspace{1em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}_{\lambda }\left(\mathit{\beta },h\right)=\sum _{i=1}^n{\Vert y_i-{\mathbf{x}}_i\mathit{\beta }-h\left(z_i\right)\Vert }^2+\lambda {\Vert h\Vert }_{\mathcal{H}}^2.$$ (3)

We model $\mathcal{H}$ using Kernel Machine Regression (KMR) (36). Specifically, we assume $\mathcal{H}$ to be a Reproducing Kernel Hilbert Space (RKHS) generated by a positive-definite kernel function k(z_i, z_i′), such that any $h\in \mathcal{H}$ can be expressed in terms the kernel function as $h\left({\mathbf{z}}_i\right)={\langle h,k\left({\mathbf{z}}_i,.\right)\rangle }_{\mathcal{H}}$. Then by the Representer theorem (5), if we define ${\mathbf{y}}_{n\times 1}={\left[y_1,\dots ,y_n\right]}^T$, ${\mathbf{X}}_{n\times p}={\left[{\mathbf{x}}_1^T,\dots ,{\mathbf{x}}_n^T\right]}^T$, $\mathit{\alpha }={\left[{\alpha }_1,\dots ,{\alpha }_n\right]}^T$ and also denote K_n×n the kernel matrix with its (i, j)^th element to be $\delta =I\left(T\le C\right)$, then (3) can be re-written as

$$\left(\mathit{\beta },\mathit{\alpha }\right)=\underset{\mathit{\beta }\in ℝ,\mathit{\alpha }\in {ℝ}^n}{argmin}{L}_{\lambda }\left(\mathit{\beta },\mathit{\alpha }\right),\hspace{1em}\hspace{1em}\text{where}\hspace{0.17em}{L}_{\lambda }\left(\mathit{\beta },\mathit{\alpha }\right)={\Vert \mathbf{y}-\mathbf{X}\mathit{\beta }-\mathbf{K}\mathit{\alpha }\Vert }^2+\lambda {\mathit{\alpha }}^T\mathbf{K}\mathit{\alpha }$$ (4)

Furthermore, if we define $\tau =\frac{{\sigma }^2}{\lambda }$, $\mathbf{h}={\left[h\left({\mathbf{z}}_1\right),\dots ,h\left({\mathbf{z}}_n\right)\right]}^{\top }$ can arise exactly from a linear mixed model (LMM) (29)

$$\mathbf{y}=\mathbf{X}\mathit{\beta }+\mathbf{h}+ϵ\hspace{1em}\hspace{1em}\text{where}\hspace{1em}\hspace{1em}\mathbf{h}~N\left(\text{0},\tau \mathbf{K}\right)\hspace{1em}\hspace{1em}ϵ~N\left(\text{0},{\sigma }^2\mathbf{I}\right).$$ (5)

2.1. A Variance Component Test for Kernel Interaction

Under the LMM formulation of the kernel machine regression model in (5), Maity and Lin (30) built a general test for the hypothesis $H_0:h\in {\mathcal{H}}_0$ by assuming that h lies in a RKHS generated by a garrote kernel function k_δ(z, z′), which is constructed by attaching an extra garrote parameter δ to a regular kernel function. When δ = 0, the garrote kernel function $k_0\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)={k_{\delta }\left(\mathbf{z},\mathbf{z}\right)|}_{\delta =0}$ generates exactly ${\mathcal{H}}_0$ the space of functions under the null hypothesis. The authors further proposed a REML-based variance component score test for H₀.

In order to adapt the above approach to the hypothesis for interaction $H_0:h\in {{\mathcal{H}}_{12}}^{\perp }$, we construct the garrote kernel function K_δ(z, z′) by building its corresponding RKHS for the main-effect and interaction spaces using the tensor-product construction (15; 16). Briefly, for the two sets of covariates ${\mathbf{z}}_m\in {ℝ}^{q_m}$, where m = 1, 2, let μ_m be the probability measure of z_m on $k\in \mathcal{D}$, let ${\mathbf{1}}_m=\left\{f:{ℝ}^{q_m}\to ℝ|f\propto 1\right\}$ be the RKHS of constant functions with kernel function P_max,k, and let ${\mathcal{H}}_m$ be the RKHS of centered and square-integrable functions on z_m (i.e. $\int h\left({\mathbf{z}}_m\right)d\mu \left({\mathbf{z}}_m\right)=0$ and $\int h^2\left({\mathbf{z}}_m\right)d\mu \left({\mathbf{z}}_m\right)<\infty$). Now consider the space ${\mathbf{1}}_m\oplus {\mathcal{H}}_m$. Any function h in this space can be decomposed as $h=P_{c}h+\left(h-P_{c}h\right)$ with a constant component $P_{c}h=\int h\left({\mathbf{z}}_m\right)d\mu \left({\mathbf{z}}_m\right)\in {\mathbf{1}}_m$ and a centered non-constant component $\left(h-P_{c}h\right)\in {\mathcal{H}}_m$. As a result, the tensor product space $\mathcal{H}=\left\{{\mathbf{1}}_1\oplus {\mathcal{H}}_1\right\}\otimes \left\{{\mathbf{1}}_2\oplus {\mathcal{H}}_2\right\}$ adopts the following orthogonal decomposition:

$$\begin{gathered} \mathcal{H}=\left\{{\mathbf{1}}_1\otimes {\mathbf{1}}_2\right\}\oplus \left\{{\mathcal{H}}_1\otimes {\mathbf{1}}_2\right\}\oplus \left\{{\mathbf{1}}_1\otimes {\mathcal{H}}_2\right\}\oplus \left\{{\mathcal{H}}_1\otimes {\mathcal{H}}_2\right\} \\ =\left\{\mathbf{1}\right\}\oplus \left\{{\mathcal{H}}_1\oplus {\mathcal{H}}_2\right\}\oplus \left\{{\mathcal{H}}_1\otimes {\mathcal{H}}_2\right\}, \end{gathered}$$

where 1 is the space of constant functions with support on z = {z₁, z₂} (24). This decomposition is shown to be unique under mild regularity conditions (i.e., the probability measures μ_m’s are absolutely continuous and bounded away from zero and infinity) (39; 20). In the equation above, ${\mathcal{H}}_0={\mathcal{H}}_1\oplus {\mathcal{H}}_2$ is the space of main-effect functions that does not contain the (z_1,i, z_2,i) interaction, and ${{\mathcal{H}}_{12}}^{\perp }={\mathcal{H}}_1\otimes {\mathcal{H}}_2$ is the space of “pure interaction” function whose elements describe only the interaction effect between (z_1,i, z_2,i) and are orthogonal to the main-effect functions. Consequently, we can construct the garrote kernel function for the tensor product space $\mathcal{H}$ as

$$k_{\delta }\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)=k_0\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)+{\delta }^{\ast }{k}_{12}\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)$$ (6)

where k₀ (z, z′) = k₁ (z, z′) + k₂ (z, z′) is the kernel function for ${\mathcal{H}}_0={\mathcal{H}}_1\oplus {\mathcal{H}}_2$ that corresponds to the null hypothesis of no interaction, and $k_{12}\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)=k_1{\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)}^{\ast }{k}_2\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)$ is the kernel function for space of interaction-effect functions ${\mathcal{H}}_{12}^{\perp }={\mathcal{H}}_1\otimes {\mathcal{H}}_2$. Finally, notice that k_δ does not include the kernel function for the space of the constant functions 1 since this is already modeled by the intercept term.

Under the above form of the garrote kernel function, the derivative of the kernel function with respect to the garrote parameter is $\frac{\partial }{\partial \delta }{k}_{\delta }\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)=k_{12}\left(\mathbf{z},{\mathbf{z}}^{\prime }\right)$, i.e., the kernel function that corresponds to ${\mathcal{H}}_{12}^{\perp }$. Therefore given n data points ${\left\{y_i,{\mathbf{x}}_i,{\mathbf{z}}_i\right\}}_{i=1}^n$, the derivative kernel matrix ∂K₀ under the null is simply the n × n kernel matrix K₁₂ whose (i, j)^th element is k₁₂ (z_i, z_j), and the score test statistic is:

$$\begin{gathered} {\widehat{T}}_0=\widehat{\tau }*{\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right)}^T{\text{V}}_0^{-1}\partial {\mathbf{K}}_0{\text{V}}_0^{-1}\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right) \\ =\widehat{\tau }*{\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right)}^T{\text{V}}_0^{-1}{\mathbf{K}}_{12}{\text{V}}_0^{-1}\left(\mathbf{y}-\mathbf{X}\mathit{\beta }\right). \end{gathered}$$ (7)

where ${\text{V}}_0={\widehat{\sigma }}^2{\mathbf{I}}_{n\times n}+\lambda {\mathbf{K}}_0$ is the marginal covariance matrix of y_n×1, K₀ is the n × n kernel matrix whose (i, j)^th element is k₀(z_i, z_j), and $\left(\widehat{\beta },{\widehat{\sigma }}^2,\widehat{\tau }\right)$ are the model parameters estimated under the null hypothesis (30). The null distribution of ${\widehat{T}}_0$ is a mixture of chi-squares that can be approximated using a scaled chi-square distribution $\kappa {\chi }_{\nu }^2$ using either Satterthwaite-Welch method (48) or other higher-moment approximations (3).

2.2. Generalization to Multiple Groups with Nuisance Interaction

Our description so far assumes there exists no nuisance interaction terms in the model $y={\mathbf{x}}^T\mathit{\beta }+h\left(\mathbf{z}\right)+ϵ$. However, in more realistic scenario, z usually exhibits complex hierarchical structure subsuming multiple groups, and it is often of interest to test only for the interaction between two small subgroups of z, leaving other interactions as nuisance effect to be accounted for by the null model. For example, consider the case of nutrition-environment interaction in Bangladesh birth cohort, z_i is the 30 × 1 vector of during-pregnancy exposure to 27 nutrients and 3 metal pollutants, corresponding the grouping structure z_i = {z_metal, z_nutr}, where z_nutr is further divided into z_{nutr =} {z_macro, z_mineral, z_vitA, z_vitB, z_vitO}. Therefore, when testing for the interaction between metal mixture exposures and a specific nutrient group of interest, care should be given to formulate h(z_i) such that it not only explicitly characterizes the interaction of interest, but also account for all nuisance interactions among other z_i subgroups.

More specifically, assume z_i = {z₁, z₂, z₃}, when testing for the interaction between z₁ and z₂, the nuisance interactions between z₁ and z₃, as well as between z₂ and z₃, should also be included in the null model. To this end, following the tensor-product construction in Section 2.1 and under the same regularity conditions, h(z) adopts an unique orthogonal decomposition:

$$h\left({\mathbf{z}}_1,{\mathbf{z}}_2,{\mathbf{z}}_3\right)=\left[h_1\left({\mathbf{z}}_1\right)+h_2\left({\mathbf{z}}_2\right)+h_3\left({\mathbf{z}}_3\right)\right]+\left[h_{12}\left({\mathbf{z}}_1,{\mathbf{z}}_2\right)+h_{13}\left({\mathbf{z}}_1,{\mathbf{z}}_3\right)+h_{23}\left({\mathbf{z}}_2,{\mathbf{z}}_3\right)\right]+h_{123}\left({\mathbf{z}}_1,{\mathbf{z}}_2,{\mathbf{z}}_3\right),$$ (8)

where for ${\mathcal{H}}_m$ the RKHS of centered and square-integrable functions, h_m are the main-effect functions such that $h_m\in {\mathcal{H}}_m$, and $h_{m_1{m}_2}$ and $h_{m_1{m}_2{m}_3}$ are the higher-order interaction functions that belong to ${\mathcal{H}}_{m_1{m}_2}={\mathcal{H}}_{m_1}\otimes {\mathcal{H}}_{m_2}$ and ${\mathcal{H}}_{m_1{m}_2{m}_3}={\mathcal{H}}_{m_1}\otimes {\mathcal{H}}_{m_2}\otimes {\mathcal{H}}_{m_3}$, respectively. Under such construction, the null hypothesis of no interaction between z₁ and z₂ corresponds to h₁₂ and h₁₂₃ equaling zero, i.e.

$$H_0:\hspace{1em}\hspace{0.17em}\hspace{0.17em}h=h_1+h_2+h_3+h_{13}+h_{23}$$

$$H_a:\hspace{1em}\hspace{0.17em}\hspace{0.17em}h=h_1+h_2+h_3+h_{13}+h_{23}+h_{12}+h_{123},$$

and the corresponding garrote kernel for the null hypothesis is k_δ(z, z′) = k₀ (z, z′) + δ*k_a(z, z′), where k₀ = k₁ + k₂ + k₃ + k₁₃ + k₂₃ and k_a = k₁₂ + k₁₂₃. Here k_m is the reproducing kernels for the main-effect space $H_m$, and the higher-order interaction kernels are constructed as $\forall \left(i,j\right),k_{ij}=k_i*k_j$ and k₁₂₃ = k₁ *k₂ *k₃ similar to Section 2.1. Consequently, denoting K_m as the n × n kernel matrix corresponding to k_m, the null kernel matrix K₀ and the interaction kernel matrix K₁₂ are n × n matrices that are computed as:

$$2{\mathbf{K}}_0={\mathbf{K}}_1+{\mathbf{K}}_2+{\mathbf{K}}_3+{\mathbf{K}}_1°{\mathbf{K}}_2+{\mathbf{K}}_2°{\mathbf{K}}_3$$

$${\mathbf{K}}_{12}={\mathbf{K}}_1°{\mathbf{K}}_2+{\mathbf{K}}_1°{\mathbf{K}}_2°{\mathbf{K}}_3.$$

where ° indicates the Hadamard (i.e., element-wise) product. As a result, the test statistic can be constructed as in (7).

3. Robust Effect Estimation using Cross-validated Ensemble

We motivate the importance of robust null model estimation by considering the possible impact of a misspecified null kernel function k₀ on the performance of the resulting hypothesis test. Specifically, we express the test statistic ${\widehat{T}}_0$ in (7) in terms of the model residual ϵ =y – μ – h:

$${\widehat{T}}_0\propto {ϵ}^T{\mathbf{K}}_{12}ϵ,$$ (9)

where we have used the fact ${\text{V}}_0^{-1}\left(\mathbf{y}-\mathit{\mu }\right)={\left({\widehat{\sigma }}^2\right)}^{-1}\left(ϵ\right)$ (17). Therefore, the test statistic ${\widehat{T}}_0$ is a scaled quadratic-form statistic that is a function of the model residual. If k₀ is too restrictive, model estimates will underfit the data under the null hypothesis, introducing extraneous correlation among the ${\widehat{ϵ}}_i$‘s that yield inflated ${\widehat{T}}_0$ values and deflated p-values under the null. Therefore, this approach will yield an invalid test having inflated Type I error. On the other hand, if k₀ is too flexible, model estimates will likely overfit the data in small samples, producing underestimated residuals, which leads to underestimated test statistics and overestimated p-values. Accordingly, the resulting test will have low power.

The above observations motivate a kernel estimation strategy that is flexible in that it does not underfit under the null, yet stable so that it does not overfit under the alternative. To this end, we propose estimating h using the convex ensemble of a library of fixed base kernels ${\left\{k_d\right\}}_{d=1}^D$:

$$\widehat{h}\left(\mathbf{x}\right)=\sum _{d=1}^D{u}_d{\widehat{h}}_d\left(\mathbf{x}\right)\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{u}\in \mathrm{\Delta }=\left\{\mathbf{u}|\mathbf{u}\ge \text{0,}{\mathbf{1}}^T\mathbf{u}=1\right\},$$ (10)

where ${\widehat{h}}_d$ is the kernel predictor generated by d^th base kernel k_d. In order to maximize model stability, we divide data $\mathcal{D}={\left\{\left(y_i,{\mathbf{x}}_i,{\mathbf{z}}_i\right)\right\}}_{i=1}^n$ into a training and validation set ${\mathcal{D}}_{\text{train}}$, ${\mathcal{D}}_{\text{valid}}$ and estimate the ensemble weights u to minimize the overall cross-validation error of $\widehat{h}$ on ${\mathcal{D}}_{\text{valid}}$. We term this method the Cross-Validated Ensemble of Kernels (CVEK). The exact algorithm proceeds in three stages as follows (see Algorithm 1 for summary):

Stage 1: Candidate Kernel Predictors

For each basis kernel in the library ${\left\{k_d\right\}}_{d=1}^D$, we first standardize the kernel matrix by its trace K_d = K_d / tr(K_d), and then estimate the prediction based on each kernel as ${\mathbf{h}}_{d,{\widehat{\lambda }}_d}={\mathbf{K}}_d{\left({\mathbf{K}}_d+{\widehat{\lambda }}_d\mathbf{I}\right)}^{-1}\mathbf{y}$, $d\in \left\{1,\dots ,D\right\}$ where the tuning parameter ${\widehat{\lambda }}_d$ is selected by minimizing the k–fold cross-validation error on ${\mathcal{D}}_{\text{train}}$, and compute the validation cross-validation error on ${\mathcal{D}}_{\text{valid}}$ for the d^th kernel as ${\widehat{ϵ}}_d=CV\left({\widehat{\lambda }}_d|{\mathbf{K}}_d\right)$.

Stage 2: Cross-validated Ensemble

Using the estimated validation cross-validation errors ${\left\{{\widehat{ϵ}}_d\right\}}_{d=1}^D$, estimate the ensemble weights $\mathbf{u}={\left\{u_d\right\}}_{d=1}^D$ by minimizing the overall cross-validation error ${ϵ}_{\mathbf{u}}=\sum _{d=1}^D{u}_d{\widehat{ϵ}}_d$:

$$\mathbf{u}=\underset{\mathbf{u}\in \mathrm{\Delta }}{argmin}{\Vert \sum _{d=1}^D{u}_d{\widehat{ϵ}}_d\Vert }^2,\hspace{1em}\hspace{1em}\text{where}\hspace{0.17em}\hspace{0.17em}\mathrm{\Delta }=\left\{\mathbf{u}|\mathbf{u}\ge 0,{\mathbf{1}}^T\mathbf{u}=1\right\},$$

and produce the final ensemble prediction $\mathbf{h}=\sum _{d=1}^D{\widehat{u}}_d{\mathbf{h}}_d=\sum _{d=1}^D{\widehat{u}}_d{\text{A}}_{d,{\widehat{\lambda }}_d}\mathbf{y}=\text{Ay}$, where $\text{A}=\sum _{d=1}^D{\widehat{u}}_d{\text{A}}_{d,{\widehat{\lambda }}_d}$ is the ensemble hat matrix.

Stage 3: Ensemble Kernel Matrix

Using the ensemble hat matrix A, estimate the ensemble kernel matrix K by solving K(K + λI)⁻¹ = A. Specifically, if we denote U_A and ${\left\{{\delta }_{A,k}\right\}}_{k=1}^n$ as the eigenvector and eigenvalues of A, respectively, then the ensemble kernel matrix K adopts the form:

$$\mathbf{K}={\lambda }_{\mathbf{K}}*\left[{\mathbf{U}}_A\text{diag}\left(\frac{{\delta }_{A,k}}{1-{\delta }_{A,k}}\right){\mathbf{U}}_A^T\right],$$ (11)

where we recommended setting ${\lambda }_{\mathbf{K}}=min\left(1,{\left(\sum _{k=1}^n\frac{{\delta }_{A,k}}{1-{\delta }_{A,k}}\right)}^{-1}\right)$ (see Supplementary Section A).

We remind readers that the CVEK’s ensemble form (Stage 2) belongs to the general class of model aggregation method known as convex aggregation (41), whose oracle property in model selection has been established both asymptotically and in finite-sample (44; 23). It can be also considered as a special case of ensemble of kernel predictors (EKP) (9), whose generalization behavior is well characterized in terms of the rate of eigenvalue decay of the base kernels. Consequently, under the null hypothesis, with a diverse set of base kernels, the CVEK ensemble converges in $O\left(\frac{1}{n}\right)$ rate to the “oracle ensemble” made by an oracle that has access to infinite amount of validation data, thereby resulting in correct Type I error by mitigating null model misspecification. Under the alternative, by setting the diverse kernel library to be a mix of parametric kernels (linear, polynomial) and smooth kernels of exponential eigendecay rate (e.g. a collection of Gaussian RBF kernel with different fixed spatial smoothness parameters), CVEK converges to its asymptotic counterpart in $O\left(\frac{1}{n}\right)$ rate if the data-generation function is indeed parametric, and in the ”near-parametric” rate of $O\left(\frac{log\left(n\right)}{n}\right)$ if the data-generation function is complex and nonlinear, thereby encouraging good test power by not overfitting the interaction effect due to fast generalization rate. The resulting ensemble kernel is therefore a strong candidate for a null model estimator that is suitable for hypothesis testing. We refer readers to Supplementary Section B for detailed discussion.

4. Numeric Studies

We evaluate the finite-sample performance of the proposed interaction test in a simulation study that mimics a small-sample nutrition-environment interaction study. We generate the fixed-effect covariates ${\mathbf{x}}_i\in {ℝ}^{p_x}$ and the input features $\left({\mathbf{z}}_{i,1},{\mathbf{z}}_{i,2}\right)\in {ℝ}^{p_1}\times {ℝ}^{p_2}$ independently from a standard multivariate Gaussian distribution. Here, (z_i,1, z_i,2) reflects each subject’s level of exposure to p₁ environmental pollutants and the levels of a subject’s intake of p₂ nutrients during the study. We generate the outcome y_i as:

$$y_i={\mathbf{x}}_i\mathit{\beta }+h_1\left({\mathbf{z}}_{i,1}\right)+h_2\left({\mathbf{z}}_{i,2}\right)+\delta *h_{12}\left({\mathbf{z}}_{i,1},{\mathbf{z}}_{i,2}\right)+{ϵ}_i,$$ (12)

where the fixed-effect coefficients ${\mathit{\beta }}_{p_x\times 1}$ is sampled from a standard Gaussian distribution. The nonlinear functions h₁, h₂, h₁₂ are sampled from RKHSs ${\mathcal{H}}_1$, ${\mathcal{H}}_2$ and ${\mathcal{H}}_1\otimes {\mathcal{H}}_2$, generated using a ground-truth kernel k_true. We standardize all sampled functions to have unit norm, so that δ represents the strength of interaction relative to the main effect. For the main section of the numeric study, we consider sample size n = 200, data dimension p_x = 5, p₁ = p₂ = 3 and ${ϵ}_i\stackrel{i.i.d.}{~}N\left(0,{\sigma }^2=0.1\right)$. For each simulation scenario, we first generate data using δ and and k_true, and then use a k_model to estimate the null model and obtain p-value using the proposed test. We repeat each scenario 200 times, and evaluate the test performance using the empirical probability $\widehat{P}\left(p\le 0.05\right)$.

In this study, we vary k_true to produce data-generating functions h_δ(z_i,1, z_i,2) with different smoothness and complexity properties, and vary k_model to reflect different common modeling strategies for the null model in addition to using CVEK. We then evaluate how these two aspects impact the hypothesis test’s Type I error and power. More specifically, we sample the data-generating function using k_true from Matérn kernel family (34):

$$k\left(\mathbf{r}|\nu ,\sigma \right)=\frac{2^{1-\nu }}{\Gamma \left(\nu \right)}{\left(\sqrt{2\nu }\sigma \Vert \mathbf{r}\Vert \right)}^{\nu }{K}_{\nu }\left(\sqrt{2\nu }\sigma \Vert \mathbf{r}\Vert \right),\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{r}=\mathbf{x}-{\mathbf{x}}^{\prime },$$

with two non-negative hyperparameters (ν, σ). For a function h sampled using a Matérn kernel, v determines the function’s smoothness (i.e. degree of mean-square differentiability), and σ determines the function’s complexity in terms of spectral frequency (34).

In this work, we vary $\nu \in \left\{\frac{3}{2},\frac{5}{2},\infty \right\}$ to generate once-, twice, and infinitely-differentiable functions, and vary σ ∊{0.5,1,1.5} to generate functions with varying degree of complexity.

We consider 12 k_model ‘s that are grouped into five model families (See Table 1 for a complete summary): (1) Polynomial Kernels that is equivalent to polynomial ridge regression. In this work, we use the linear kernel $k_{linear}\left(\mathbf{x},{\mathbf{x}}^{\prime }|p\right)={\mathbf{x}}^T{\mathbf{x}}^{\prime }$ and quadratic kernel $k_{\text{quad}}\left(\mathbf{x},{\mathbf{x}}^{\prime }|p\right)={\left(1+{\mathbf{x}}^T{\mathbf{x}}^{\prime }\right)}^2$. (2) Gaussian RBF Kernels: $k_{RBF}\left(\mathbf{x},{\mathbf{x}}^{\prime }|\sigma \right)=exp\left(-{\Vert \mathbf{x}-{\mathbf{x}}^{\prime }\Vert }^2/{\sigma }^2\right)$ is a general-purpose kernel family that generates nonlinear, but very smooth (infinitely differentiable), functions. Under this kernel, we consider two hyperparameter selection strategies commonly seen in application: RBF-Median where we set σ to the sample median of ${\left\{\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\Vert \right\}}_{i\ne j}$, and RBF-MLE, which estimates σ by maximizing the model likelihood. (3) Matérn and (4) Neural Network Kernels are two flexible kernel families both containing a rich space of candidate functions. For Matérn kernel, we use Matern 1/2, Matern 3/2 and Matern 5/2, corresponding to flexible models that is capable of approximating non-differentiable, once-differentiable, and twice-differentiable functions. Neural network kernels (34), on the other hand, represent a 1-layer Bayesian neural network with σ being the prior variance on the hidden weights, and it is theoretically capable of approximate arbitrary continuous functions on the compact domain (19). In this work, we let NN 0.1, NN 1 and NN 10 denote Bayesian neural networks with different prior constraints σ ∊{0.1,1,10}. Finally, we evaluate the performance of the (5) Cross-validated Kernel Ensemble estimator we propose here. Specifically, we consider a CVEK estimator based on a Gaussian RBF kernel with log(σ) ∊{−2, −1, 0,1, 2}, which we label CVEK-RBF. Furthermore, to evaluate the consequence of more flexible kernel families on ensemble behavior, we also consider CVEK-NN, which is a ensemble of neural network kernels with σ ∊{0.1,1,10,50} ).

Table 1.

List of k_model’s considered in the numeric study

Kernel Family	Kernel Function	Model Name	Parameter Value
Polynomial	${\left(1+{\mathbf{x}}^T\mathbf{x}\text{'}\right)}^d$	Linear	d = 1
		Quadratic	d = 2
Gaussian RBF	$exp\left(-{\Vert \mathbf{\text{x-x}}\text{'}\Vert }^2/{\sigma }^2\right)$	RBF-MLE	σ = argmax(ML(σ))
		RBF-Median	σ = median({|| xi – xj ||}i≠j)
Matérn	$\frac{2^{1-\nu }}{\Gamma \left(v\right)}{\left(\sqrt{2v}\Vert \mathbf{r}\Vert \right)}^v{K}_v\left(\sqrt{2v}\sigma \Vert \mathbf{r}\Vert \right)$	Matérn 1/2	v = 1/2
		Matérn 3/2	v = 3/2
		Matérn 5/2	v = 5/2
Neural Network	$\frac{2}{\pi }\ast si{n}^{-1}\left(\frac{2\sigma {\mathbf{x}}^T\mathbf{x}\text{'}}{\sqrt{\left(1+2\sigma {\mathbf{x}}^T\mathbf{x}\right)\left(1+2\sigma \mathbf{x}{\text{'}}^T\mathbf{x}\text{'}\right)}}\right)$	NN 0.1	σ = 0.1
		NN 1	σ = 1
		NN 10	σ = 10
CVEK	$\text{K=}{\lambda }_{\mathbf{K}}*\left[{\mathbf{U}}_{A}diag\left(\frac{{\delta }_{A,k}}{1-{\delta }_{A,k}}\right){\mathbf{U}}_A^T\right]$	CVEK-RBF	log(σ) ∊{−2, −1, 0,1, 2}
		CVEK-NN	σ ∊{0.1,1,10,50}

The results of our primary simulation scenario (n = 200 and p₁ = p₂ = 3 ) are presented graphically in Figure 1. We first observe that for reasonably specified values of k_model, the proposed hypothesis test with CVEK estimator always has the correct Type I error and reasonable power. We also observe that the complexity of the data-generating function h_δ (12) plays a role in test performance, in the sense that the power of the hypothesis tests increases as the Matérn k_true ‘s complex parameter σ becomes larger, which corresponds to functions that put more weight on the simpler, slow-varying eigenfunctions in Bochner’s spectral decomposition (34).

Fig. 1.

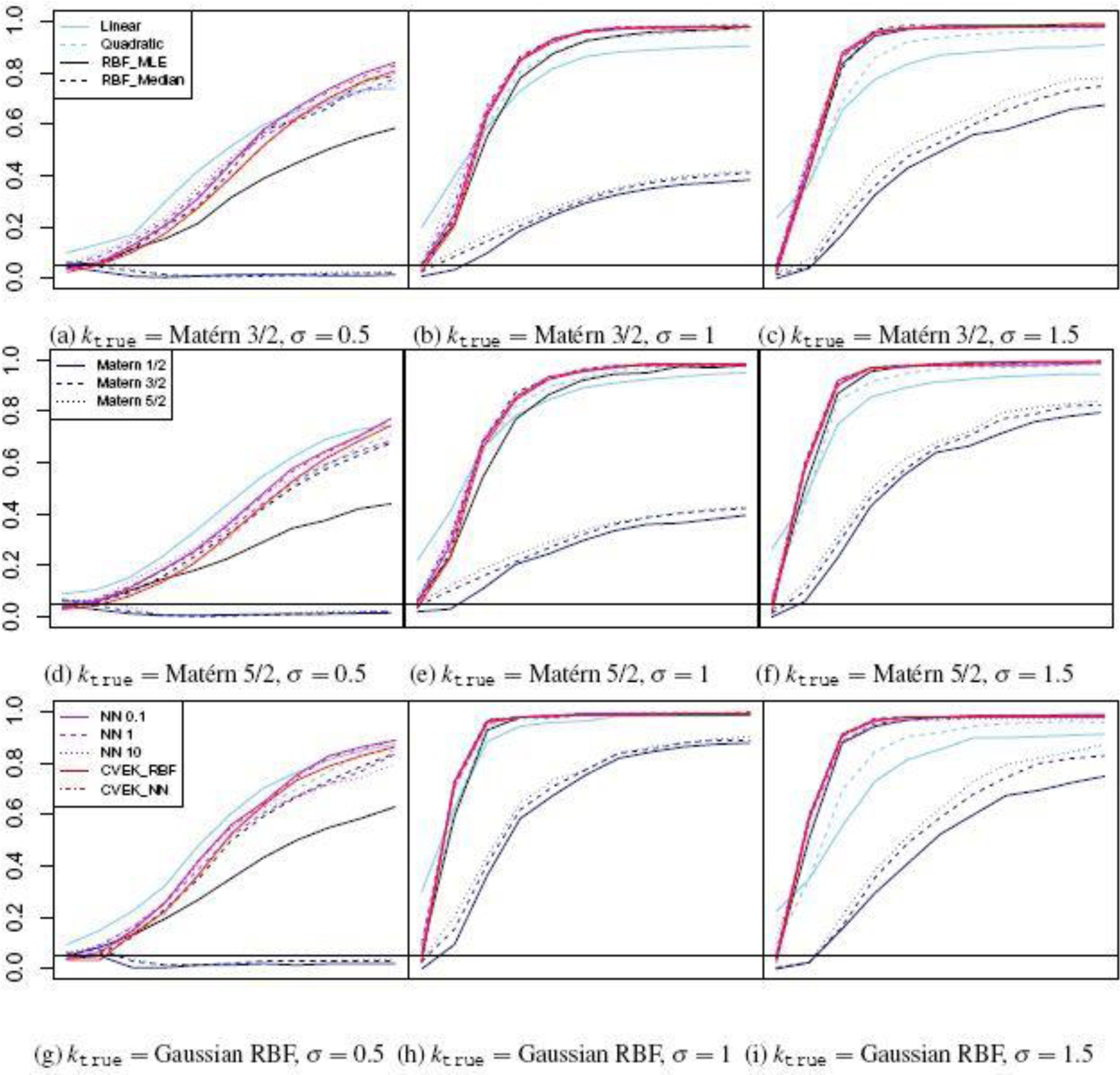
Estimated $\widehat{P}\left(p<0.05\right)$ (y-axis) as a function of Interaction Strength δ∊ [0,1] (x-axis) for n = 200 and p₁ = p₂ = 3. Sky Blue: Linear (Solid) and Quadratic (Dashed) Kernels, Black: RBF-Median (Solid) and RBF-MLE (Dashed), Dark Blue: Matérn Kernels with $\nu =\frac{1}{2},\frac{3}{2},\frac{5}{2}$, Purple: Neural Network Kernels with σ = 0.1,1,10, Red: CVEK based on RBF (Solid) and Neural Networks (Dashed). Horizontal line marks the test’s significance level (0.05). When δ = 0, $\widehat{P}$ should be below this line.

There exist clear differences in test performance between different model families. In general, polynomial models (linear and quadratic) appear to be too restrictive and underfit the data under both the null and the alternative, producing inflated Type I error and diminished power. On the other hand, lower-order Matérn kernels (Matérn 1/2 and Matérn 3/2, dark blue lines) appear to be too flexible, due to their slow eigenvalue decay. Whenever data are generated from similarly or smoother k_true, Matérn 1/2 and 3/2 overfit the data and produce deflated Type I error and severely diminished power, even if the hyperparameter σ is fixed at its true value. Comparatively, Gaussian RBF works well for a wider range of k_true ‘s but only if the hyperparameter σ is selected carefully. Specifically, RBF-Median (black dashed line) works generally well, despite being slightly conservative (i.e. lower power) when the data-generation function is smooth and of low complexity. RBF-MLE (black solid line), on the other hand, tends to overfit the data and exhibits weak power especially in higher dimension and for complex data generation functions (45). Neural Network kernels also perform well for a wide range of k_true and with the Type I error more robust to the specification of hyperparameters. Finally, the two ensemble estimators CVEK-RBF and CVEK-NN perform as well or better than the non-ensemble approaches for all k_true ‘s, despite being slightly conservative under the null.

To understand how the performance of CVEK depends on the dimension of the inputs, we conduct additional studies for p₁ = p₂ = 6 and p₁ = p₂ = 10, and report the results in Figure C.1–C.2 in the Supplementary Material (Section C). Briefly, there is a clear effect of the data dimension and the complexity of the data generation mechanism on the test power. As the dimension p₁ = p₂ = p increases, we observe a consistent pattern of power degradation in test performance that strongly depends on the complexity of the data-generating function h_δ. For example, consider the test power of CVEK-NN at an interaction strength δ = 1 for k_true = Gaussian RBF. As data dimension increases from p = 3 (Figure 1) to p = 10 (Figure C.2), test power degrades to as low as 0.2 for highly complex data-generating functions (σ = 0.5 ), around 0.6 for moderately complex data-generating functions σ = 1, yet remains close 1.0 for smooth data-generating functions ( σ = 1.5). Comparing different model families in high dimensions (p = 10; Figure C.1–C.2), we find that the polynomial models either have difficulty maintaining the correct Type I error, or have weak power under the alternative. Among the nonlinear models, the RBF-MLE model’s test power degrades particularly quickly due to overfitting. Interestingly, we also observe that the hypothesis test based on NN-based models (e.g., CVEK-NN) becomes more powerful than the RBF-based models in higher data dimension, which is consistent with the recent theoretical observations on the effectiveness of neural network models in high-dimensional scenarios (1).

5. Nutrition-Environment Analysis for Child Neurodevelopment in Bangladesh Birth Cohort

We use the proposed methods to test for nutrition-environment interactions for the child neurodevelopment in the Bangladesh birth cohort study. Section 5.1 presents a detailed description of the Bangladesh birth cohort study, and the Section 5.2 present the analysis. Our aim is to detect whether mother’s nutrient intake during pregnancy modifies the effect of metal mixture exposures on children’s early-stage fine motor BSID-III scores in the district of Pabna (n = 351).

5.1. Study Background

The Bangladesh Reproductive Cohort Study (Project Jeebon) was initiated in 2008 to investigate the effects of prenatal and early childhood exposure to As, Mn and Pb on early childhood development. During 2008–2011, pregnant female participants (with gestational age < 16 weeks) were recruited from two rural health clinics operated by the Dhaka Community Hospital Trust (DCH) in the Sirajdikhan and Pabna Sadar upazilas of Bangladesh. During 2008–2013, data were collected at five time points spanning the entire perinatal and early childhood period, including: initial clinic visit (gestational age < 16 weeks, Visit 1); pre-delivery clinic visit (gestational age = 28 weeks, Visit 2), time of delivery (Visit 3), post-delivery clinic visit (infant age less than 1 month, Visit 4), and a postnatal follow-up visit (infant age between 20–40 weeks, Visit 5). Our central hypothesis is that children born from mother who had lower nutrient intake will be the most susceptible to adverse effects of metal exposures.

Detailed procedures for data collection and measurement protocols have been documented previously (13; 21; 43). Briefly, background information on parent’s demographic status, including age, education, smoking history and socioeconomic status were collected through structured questionnaires at the two clinic visits during pregnancy (Visits 1–2). Information on infant’s biometric measurements, including sex, birth weight, length, head circumference, birth order and gestational age, were recorded at birth. Information on maternal medical history, maternal depression status (in Edinburgh Depression scale), maternal IQ (assessed using the Raven’s Progressive Indices (35)) were measured during the pregnancy visits (Visits 1–2), and an infant’s early childhood development, medical history, and quality of home environment (in terms of emotional, social, and cognitive stimulation, measured by Home Observation Measurement of Environment (HOME) instrument score (2) were measured during the follow-up visits (Visits 4–5), respectively.

Each infant’s exposure to multiple metals As, Mn and Pb (concentrations in µg / dL ) during pregnancy were measured using blood samples from infant’s umbilical cord venous blood collected at the time of the birth. Mother’s overall nutrition intake status during pregnancy was measured for 27 nutrients derived from semi-quantitative Food Frequency Questionnaires (FFQs) specially adapted to Bangladeshi diet (25) at both the pre- and post-delivery visits (Visit 2 and 4). This instrument derives data on these 27 nutrients from measures of the consumption frequency (amount per week) of 42 food items during the 12-month period preceding delivery. The nutrients measured can be grouped into 5 categories including macro-nutrients (5 nutrients: protein, fat, carbohydrate, dietary fiber and ash), minerals (7 nutrients: calcium, magnesium, phosphorus, potassium, sodium, zinc and copper), vitamin A and provitamin As (6 nutrients: vitamin A, retinol, beta-carotene equivalents, alpha-carotene, beta-carotene, and cryptoxanthin), vitamin B (5 nutrients: thiamin (B1), riboflavin (B2), niacin (B3), vitamin B6 and folate (B9)), and other vitamins (3 nutrients: vitamin C (i.e. L-ascorbic acid), vitamin D, and vitamin E). Finally, infant’s neurodevelopmental outcomes were assessed at 20–40 months of age (Visit 5) using a translated and culturally-adapted version of the Bayley Scales of Infant and Toddler Development, Third Edition (BSID-III) including five cognitive domains: cognitive, receptive language, expressive language, fine motor and gross motor.

We compare our method with three existing approaches for testing high-dimensional interaction. The (1) Interaction Sequence Kernel Association Test (iSKAT)(28) is a baseline approach that assumes linear relationship between exposures and outcome. It estimates the null model using ridge linear regression and corresponds to the linear model in simulation. (2) The Gaussian Kernel Machine test (GKM) (30) estimates the null model using kernel machine regression with Gaussian RBF kernels and tunes the kernel hyperparameter by maximizing REML. It correspondes to the RBF-MLE model in simulation. Finally, the (3) GE-spline test (18) which uses the generalized additive regression to model the nonlinear effect of environmental exposures using spline sieves. It can be considered as a special case of kernel machine regression with the kernel matrix constructed adaptively using spline basis functions (22). In order to visualize the identified interaction and thereby provide interpretable findings, we graphically summarize the multivariate interaction effects by examining the joint exposure-response surface between the principal components of the pollutant mixture and those for each nutrient group.

5.2. Data Analysis

In this nutrition-environment interaction study, our interest concentrates on the interaction between the mixture of As, Mn and Pb, and five major nutrient groups: macro-nutrient, mineral, vitamin A, vitamin B and the other vitamins (denoted as vitamin, other). For each of the five nutrient groups, we test for the overall interaction between the selected group and the joint effect of the As, Pb, Mn mixture. We adjust for parent’s demographic status (age, education, smoking history), infant’s biometric measurements at birth (sex, birth weight, length, head circumference, birth order and gestational age), and quality of early-childhood home environment (HOME score, maternal depression scale, maternal IQ).

5.2.1. Nutrient - Mixture Interactions

Table 2 presents p–values for the interaction between the overall metal mixture and each of the five nutrient groups. We conducted the proposed test using two types of CVEK models: an ensemble of seven RBF kernels with bandwidth parameter set between log(σ²) ∊{−3, −2, −1, 0,1, 2,3} (denoted as CVEK-RBF), and an ensemble of seven neural network kernels with prior parameters set between log(σ²) ∊{−3, −2, −1, 0,1, 2,3} (denoted as CVEK-NN). We compared the results of each to those generated by iSKAT, GKM, and GE-Spline. As shown in the table, most tests yielded strong evidence of interaction (p < 0.05) for the vitamin A and the vitamin, other groups, as well as weak-to-moderate evidence of interaction ( p <≈0.1) for the mineral and the vitamin B groups. There was no evidence of an interaction between metal exposures and macro-nutrients.

Table 2.

p – value for Nutrient - Environment interaction test with joint As, Pb, Mn mixture

Model	Nutrient Group
	macro	mineral	vitamin A	vitamin B	vitamin, other
CVEK-NN	0.1442	0.0456	0.0135	0.0672	0.0315
CVEK-RBF	0.1257	0.0270	0.0124	0.0541	0.0288
iSKAT	0.2530	0.0905	0.0442	0.1299	0.0459
GKM	0.2081	0.0707	0.0297	0.1075	0.0391
GE-spline	0.1167	0.2080	0.0745	0.2562	0.2133

Comparing the performance across different tests, we observed similar patterns for p-values for CVEK-NN and CVEK-RBF, suggesting robustness in test performance with respect to the choice of the family of the base kernels. We also observed higher values of p-values for the iSKAT (linear kernel) and GKM, the latter of which used a single RBF kernel with REML-based hyperparameter tuning. The statistical conclusions from these two tests are similar to those from the CVEK tests for vitamin A and vitamin, other groups of nutrients (at the significance level of 0.05). However, they are less powerful in detecting the interaction for the mineral and the vitamin B groups. This is consistent with our observation in Section 4 that, when the true effect is smooth, nonlinear and exhibits a moderate level of complexity (a scenario that is likely to hold for the effect of environmental exposures, see Figure 1 (h)), the hypothesis test based on GKM is slightly more powerful than that based on the iSKAT but is less powerful than the CVEK-based test. This reduction in power is possibly due to the overly strong smoothness assumption imposed by these two models. Finally, we notice that the performance of the test from the GE-spline model appears sub-optimal when compared to that of the other methods. GE-spline produced much higher p–values for all nutrient groups, failing to detect the interaction for the A vitamins and the other vitamins. We hypothesize that the observed instability of GE-spline is likely caused by the lack of fit of the null model, due to the difficulty in estimating multivariate splines in high dimensions.

5.2.2. Visualization of Exposure-Response Surface

To better understand the nature of the multivariate interactions between the environmental exposures and nutrition, in Figure 2 and 3, we visualize the fitted exposure-response surface relating the mean normalized fine motor BSID-III score and the principal components (PCs) of the pollution mixture and of the nutrient groups. Every panel in Figure 2 and 3 depicts the joint effect of a pollutant PC and a nutrient PC for a selected nutrient group on the fine motor score, holding all the other PCs at their median. For each joint-effect term, the strength of evidence of an interaction between metal exposure and nutrition is driven by the ”importance” of the corresponding PCs, i.e. the amount of variation the corresponding PCs explain in their respective pollutant/nutrient group. For example, in Figure 2, the pollutant PCs account for 42.6%, 37.3% and 20.1% of the total variation in pollutant mixture, and the nutrient PCs account for 63.5%, 28.5% and 7.4% of the total variation in the macronutrient group. Consequently, the strength of the signal of the interaction between the 1^st PCs (e.g. Figure 2 (a)) in the overall interaction is expectedly much stronger than that between the 3^rd PCs (e.g. Figure 2 (i)). This explains the lack of significant evidence of overall interaction for the macronutrients in Table 2, since the joint effect between the PCs accounting for more variance (e.g. Figure 2 (a),(b) and (d)) do not display strong evidence of interaction. In comparison, for the other four nutrient groups, evidence of interaction can be observed between at least two nutrient-pollutant PC pairs among their leading PCs (Figure 3), thereby suggesting evidence of overall interaction between nutrients and the pollutant mixture, and consequently providing additional evidence for the findings from the CVEK tests in Table 2. Finally, we observe that across all nutrient groups, the nutrient PCs interacts the most often with the 1^st pollutant PC, which is strongly associated with As, and also with the 3^rd pollutant PC, which is strongly associated with Mn, suggesting that As and Mn are the two main pollutants driving the overall interaction. Furthermore, the pattern of interaction between nutrient and pollutant PCs are observed to be similar across nutrient groups: at lower levels of nutrients (x-axis), higher levels of metal exposure (y-axis) is associated with lower neurodevelopment scores. At intermediate or high levels of the nutrient, however, this negative association either disappears (see, e.g. Figure 3 (c), (d), (h)) or even becomes positive (see, e.g. Figure 3 (a), (b), (f)).

Fig. 2.

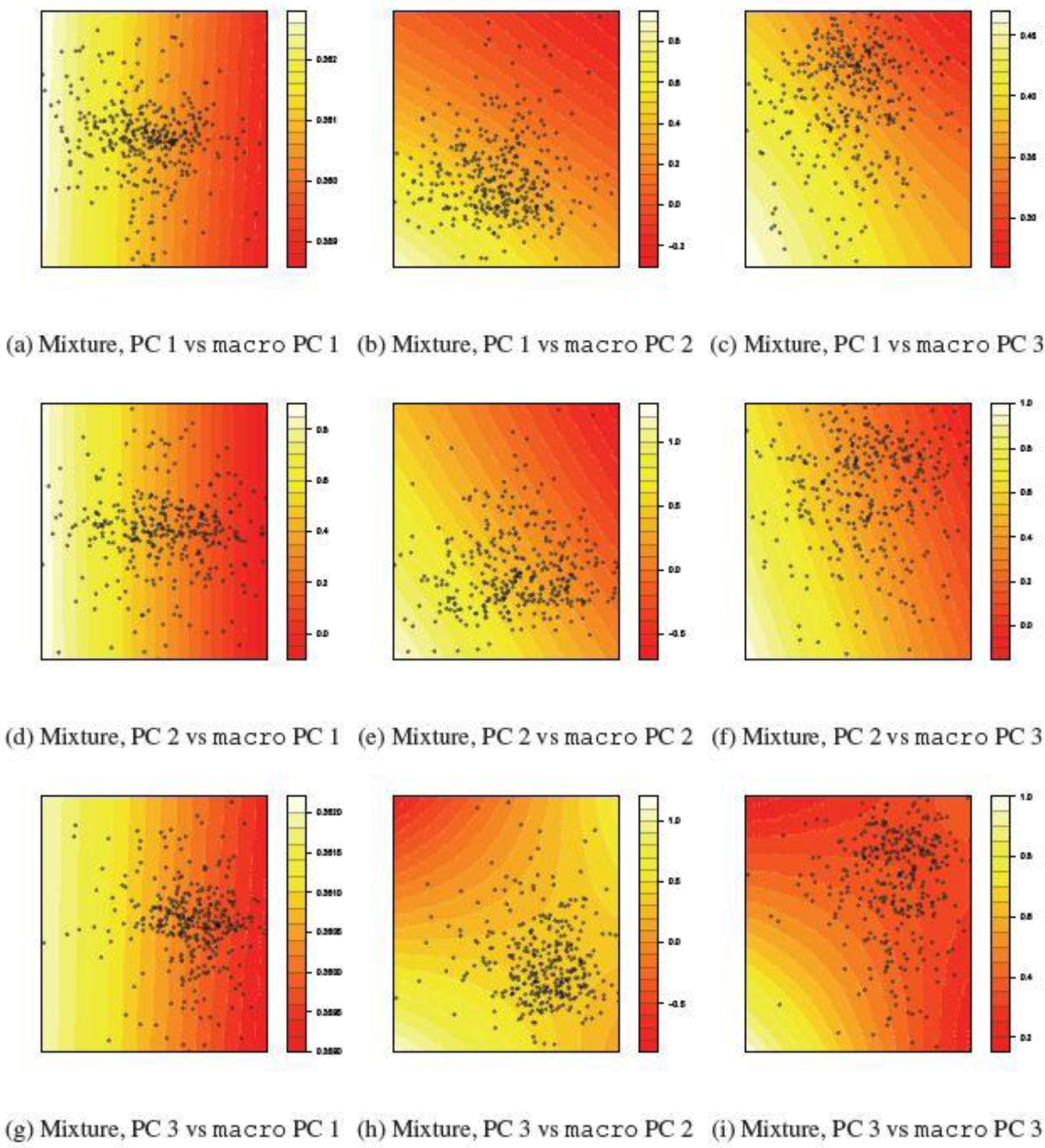
Interaction between joint mixture and macronutrient by principal components The top 3 PCs for pollutants accounts for 42.60%, 37.34%, 20.05% of total variation, The top 3 PCs for macro accounts for 63.54%, 28.46% and 7.36% of total variation.

Fig. 3.

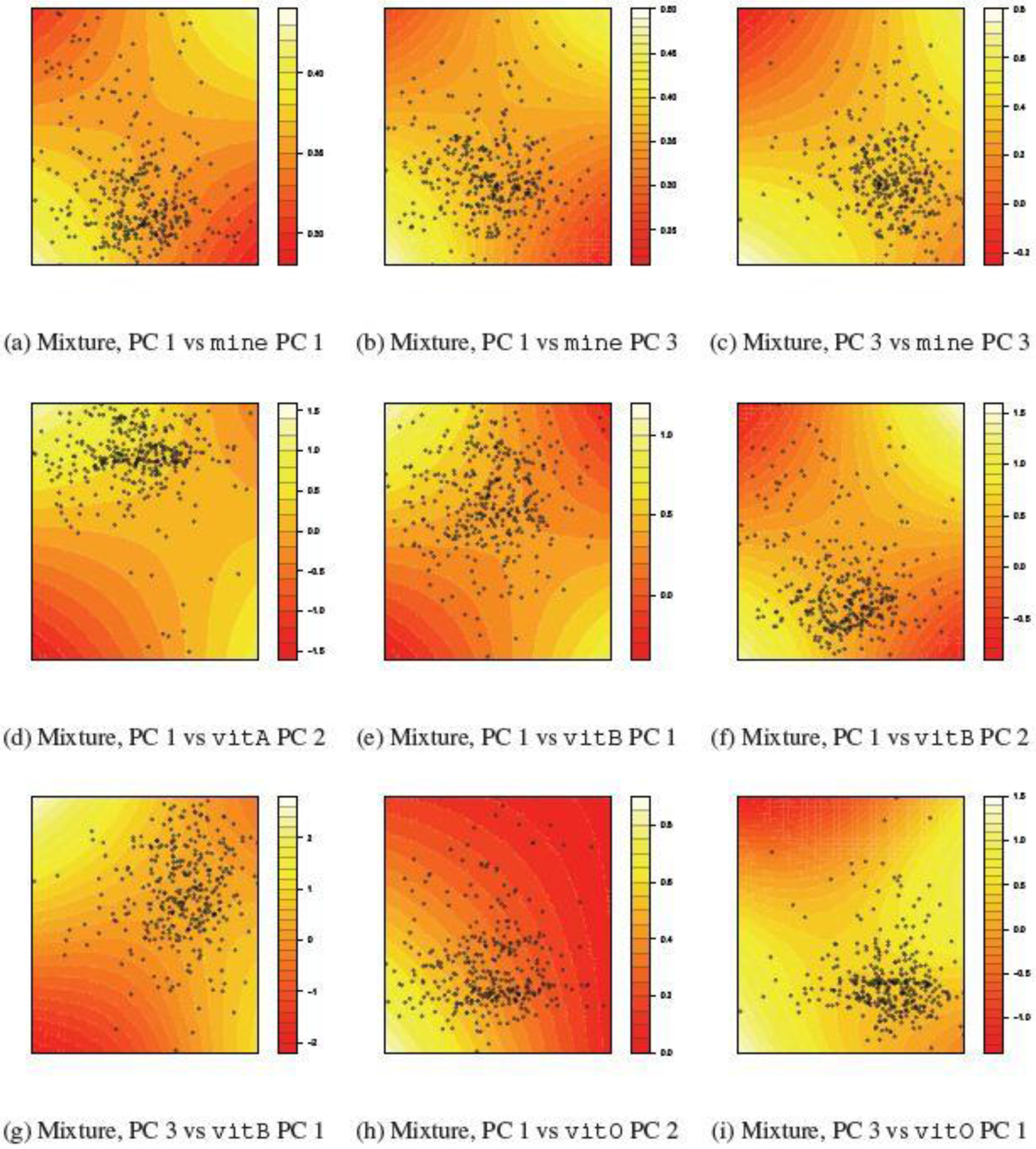
Interactions between joint mixture and selected principal components in other four nutrition groups (i.e. Mineral, Vitamin A, Vitamin B and Other Vitamins).

6. Discussion

Under the framework of kernel machine regression, we have developed a hypothesis testing procedure for detecting nonlinear interactions between groups of continuous covariates. In this context, we identified the unique challenge of possible kernel misspecification for the main-effect terms in the model, and illustrated the negative consequences of misspecified main effect kernels both in terms of Type I error and power. Specifically, we showed that an overly smooth model, even when including all causal covariates, can still underfit the data under the null and thereby produce inflated Type I error rates. On the other hand, an overly flexible model tends to overfit the data under both the null and the alternative, resulting in deflated Type I error and weak power. While these observations motivate careful selection of the form of the main effect kernels, we also observe that choice of regularization parameters via a likelihood-based model selection strategy (for example, estimating the bandwidth parameter in a Gaussian RBF kernel via REML (30)) can also over-smooth the main-effect terms under the null. This situation appears to be especially severe in limited sample sizes and for misspecified kernel functions (Figure 1 (a)–(c)). Our work addresses this challenge by estimating the main-effect model using a flexible ensemble of carefully selected base kernels, which we term Cross-validated Ensemble of Kernels (CVEK), coupled with a hyperparameter selection strategy based on cross validation. This approach avoids kernel misspecification under the null and mitigates overfitting under the alternative, resulting in tests that are powerful yet maintain nominal Type I error rates. We validated the approach through extensive numerical studies. Under a wide variety of data-generation mechanisms, CVEK consistently produced correct Type I error and reasonable power.

We applied the proposed method to estimate nutrition-environment interactions between exposure to a metal mixture and multiple nutrient groups on neurodevelopment in Bangladeshi children. Challenges presented by the analysis included the presence of nonlinear within-group interactions within the effect of the metal mixture, the high-dimensionality for the between-group interaction terms (d_{N×E ≥} 9 ), and the limited sample size (n = 351).

The proposed test identified evidence of interaction between the metal mixture and four nutrient groups, and we observed differences between the CVEK-based results and those from existing approaches for the mineral group. Visualization of bivariate exposure-response surfaces based on nutrient and metal PCs allowed us to visualize the direction of these interactions. The application is important in that identification of nutritional factors that can effectively mitigate the impact of adverse effects of environmental exposures can inform recommendations for pregnant women to improve the health of children across the lifespan.

An important extension of the proposed method would be to incorporate variable selection methods (e.g., shrinkage estimators) to further improve the effectiveness of the proposed approach in the high-dimensional settings. As shown in the numerical studies presented in Section 4, for complex and non-smooth data-generation functions (e.g., k_true = Matérn 3/2 or σ = 0.5 in Figure 1), the proposed method may have weak power even in moderate data dimension. Consequently, it is desirable to identify methods that prune out the effect of irrelevant main effect and nuisance interactions during estimation and inference, rather than fitting all possible nuisance terms. To this end, one particular interesting direction is to combine the sparseness-inducing penalties (e.g., L₁ penalty on the nuisance-effect functions h₁, h₂, h₃, h₁₃, etc in (8)) with a post-selection inference procedure that handles high-dimensional nuisance parameters. One possible avenue to pursue is the de-correlated score test, where the test statistic is made to be orthogonal to the score statistic of the high-dimensional nuisance parameters (32).

A second important extension is to improve the method’s robustness to the non-normality of the residual distributions. Although the kernel ensemble approach is designed to be robust against the mis-specification of the mean functions, the inference procedure employed in this work is consistent with that of the classic variance component test. Under heavier-tailed distributions, the variance component test is known to overestimate the spread of its null distribution, leading to an overly conservative test with weak power (38). To verify this empirically, we conducted a simulation study in which the residual follow a t-distribution with degrees of freedom equal to either 5 and 10. (Supplementary Figure C.3–C.4). These results showed that the test is able to maintain Type I error, but has extremely weak power. Consequently, it is of great practical interest to explore combining kernel ensemble methods with a hypothesis testing procedure based on flexible distributional assumptions, thereby improving the method’s performance in non-Gaussian scenarios.

Finally, the ensemble weights ${\left\{u_d\right\}}_{d=1}^D$ (see (10)) in CVEK were estimated to maximize the estimator’s cross-validation stability. The optimality of such method in terms of the power of the hypothesis test has not been fully investigated. It is desirable to develop an optimal estimation procedure for the ensemble weights ${\left\{u_d\right\}}_{d=1}^D$ that maximizes the power of the hypothesis test, in a manner similar to (14). Given such a procedure, it is also of theoretical interest to compare the difference between the ensemble weights generated by maximizing cross-validation stability to those generated by maximizing the power of the test in both finite samples and asymptotically.

$$\begin{array}{l}\mathbf{\text{Algorithm 1}}\text{ Cross Validated Ensemble of Kernels (CVEK)}\\ \text{1:}\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{procedure}}\text{ CVEK}\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{Input:}}\text{ A library of kernels}\hspace{0.17em}{\left\{k_d\right\}}_{d=1}^D,\hspace{0.17em}\text{Data}\hspace{0.17em}\left(\mathbf{y},\mathbf{X},\mathbf{x}\right)\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{Output:}}\text{ Ensemble Kernel Matrix }\mathbf{K}\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\# \text{Stage} 1: \text{Estimate} \lambda \hspace{0.17em}\text{and}\hspace{0.17em}\text{CV}\hspace{0.17em}\text{error}\hspace{0.17em}\text{for}\hspace{0.17em}\text{each}\hspace{0.17em}\text{kernel}\\ \hspace{0.17em}\\ 2:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}} d=1\text{ to }D \mathbf{\text{do}}\\ \hspace{0.17em}\\ 3:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{K}}_d={\mathbf{K}}_d/tr\left({\mathbf{K}}_d\right)\\ \hspace{0.17em}\\ 4:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\lambda }}_d=argmin\hspace{0.17em}\text{CV}\left(\lambda |{\mathbf{K}}_{\text{d}}\right)\\ \hspace{0.17em}\\ 5:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{ϵ}}_d=\text{CV}\left({\widehat{\lambda }}_d|{\mathbf{K}}_d\right)\\ \hspace{0.17em}\\ 6:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{for}}\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\# \text{Stage} 2: \text{Estimate} \text{ensemble} \text{weights}\hspace{0.17em}{\mathbf{u}}_{D\times 1}=\left\{u_1,\dots ,u_D\right\}\\ \hspace{0.17em}\\ 7:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{u}=\underset{\mathbf{u}\in \mathrm{\Delta }}{argmin}{\Vert \sum _{d=1}^D{u}_d{\widehat{ϵ}}_d\Vert }^2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\mathrm{\Delta }=\left\{\mathbf{u}|\mathbf{u}\ge 0,{\Vert \mathbf{u}\Vert }_2^2=1\right\}\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\# \text{Stage} 3: \text{Assemble} \text{the} \text{ensemble} \text{kernel} \text{matrix}\hspace{0.17em}\hspace{0.17em}{\mathbf{K}}_{ens}\\ \hspace{0.17em}\\ 8:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{A}=\sum _{d=1}^D{\widehat{\mu }}_d{\mathbf{A}}_{{\widehat{\lambda }}_d,k_d}\\ \hspace{0.17em}\\ 9:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathbf{U}}_A,{\mathit{\delta }}_A=\mathrm{spectral}\_\mathrm{decomp}\left(\mathbf{A}\right)\\ \hspace{0.17em}\\ 10:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\lambda }_{\mathbf{K}}=min\left(1,{\left(\sum _{k=1}^n\frac{{\delta }_{A,k}}{1-{\delta }_{A,k}}\right)}^{-1},min\left({\left\{{\widehat{\lambda }}_d\right\}}_{d=1}^D\right)\right)\\ \hspace{0.17em}\\ 11:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{K}={\lambda }_{\mathbf{K}}*{\mathbf{U}}_A\hspace{0.17em}diag\left(\frac{{\delta }_{A,k}}{1-{\delta }_{A,k}}\right){\mathbf{U}}_A^T\\ \hspace{0.17em}\\ 12:\\ \hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{end}}\hspace{0.17em}\mathbf{\text{procedure}}\end{array}$$