Detection of Immunologically Significant Factors for Chronic Fatigue Syndrome Using Neural-Network Classifiers

Abstract

Neural-network classifiers were used to detect immunological differences in groups of chronic fatigue syndrome (CFS) patients that heretofore had not shown significant differences from controls. In the past linear methods were unable to detect differences between CFS groups and non-CFS control groups in the nonveteran population. An examination of the cluster structure for 29 immunological factors revealed a complex, nonlinear decision surface. Multilayer neural networks showed an over 16% improvement in an n-fold resampling generalization test on unseen data. A sensitivity analysis of the network found differences between groups that are consistent with the hypothesis that CFS symptoms are a consequence of immune system dysregulation. Corresponding decreases in the CD19⁺ B-cell compartment and the CD34⁺ hematopoietic progenitor subpopulation were also detected by the neural network, consistent with the T-cell expansion. Of significant interest was the fact that, of all the cytokines evaluated, the only one to be in the final model was interleukin-4 (IL-4). Seeing an increase in IL-4 suggests a shift to a type 2 cytokine pattern. Such a shift has been hypothesized, but until now convincing evidence to support that hypothesis has been lacking.

Chronic fatigue syndrome (CFS) is a medically unexplained illness characterized by over 6 months of fatigue producing a substantial decrease in usual activity and occurring in association with infectious, rheumatological, and neuropsychiatric symptoms. Because CFS often begins acutely with a virus-like presentation, one major idea for its cause is an immune system-activated state, a hypothesis supported by reports of alterations in some activated T-cell populations (9) and by increases in certain subpopulations of “memory” T cells (14). However, other groups have not been able to replicate these findings (15), and we have recently completed a large study in which we were unable to confirm any immune system abnormalities at all in a group of CFS patients (18).

One reason for the apparent discrepancy may be statistical. No study besides our own has controlled for multiple comparisons. Moreover, because activity can affect immunological function, we compared our CFS data to data from sedentary healthy people, an effort to match on activity, which had not been done by others. Of interest was the fact that we found immunological differences between Gulf War veterans with CFS and healthy Gulf War veterans. The data suggest that those differences emerged because the veteran population was more immunologically homogeneous than the nonveteran population. Rather than make a type 1 error and reject the immunological hypothesis for CFS in nonveterans based on our analysis, which had employed classical statistical methods, we decided to reevaluate the immunological data from our nonveteran sample using a nonlinear-neural-net method to determine if immunological differences between patients and controls did in fact exist.

Neural networks as nonlinear classification schemes are good candidates for this type of medical classification problem and have been shown to be productive in the past in other types of medical classification cases. Previously it has been shown (1, 10) that networks under fairly weak conditions can provide optimal classification for unknown separation surfaces and for unspecified distributions (6). Neural networks work by creating separable partitions of the data at the feature level and then, often, productively combine the results of the linear surfaces into more complex decision surfaces at the next layer, sometimes called the “hidden” layer. The hidden layer of a neural network in fact is critical for its classification performance under nonlinear conditions, and considerable theory and experimental work prescribing the relationship between classification performance and the complexity of the network exists (3, 5). Nonetheless, out-of-sample validity testing is critical for selecting the model and assessing the level of complexity in the data, which is ultimately responsible for the classification performance achieved. In the present study, given the potentially large number of immunologically relevant variables, modular networks, which allow for opportunisitic partitioning of variables into smaller clusters rather than requiring them to be processed at once in parallel as single hidden-layer networks, were tested as possible classifiers. These model classes were compared to perceptron (logit regression) and to combinatorics/single-layer-neural-net classifiers. n out of k bootstraps (2) were used to form a conservative test of the classifier once acceptable results were obtained with a given parametrization of the models. Sensitivity analysis of the classification surface conditioned on each variable was used to estimate the contribution of each immunological factor.

Methods (subjects).

The subjects were 103 women and 24 men (mean age ± standard deviation [SD], 36.1 ± 8.6 years; 118 Caucasians) who on history, physical examination, and elimination of known medical causes of fatigue by laboratory testing fulfilled the 1994 case definion for CFS. The mode of onset of illness and its severity were determined for 125 and 109 patients, respectively. Seventy-four patients reported a sudden, flu-like onset occurring in 1 to 2 days, while 54 reported a gradual onset taking days to weeks. Sixty-nine patients fulfilled the 1988 case definition and, in addition, reported symptom severities of ≥3 on 0-to-5 Likert scales, where 0 is none, 3 is substantial, and 5 is very severe. Seventy-six women and 11 men (mean age ± SD, 35.9 ± 8.5 years; 79 Caucasians) who did not exercise regularly and who were not taking medications besides birth control pills served as a healthy, matched comparison group.

Following signing informed consent, subjects underwent venipuncture, and blood was collected in EDTA-anticoagulated tubes and was coded to prevent knowledge of subject group. Peripheral blood lymphocytes (PBLs) were labeled within 6 h of collection with commercially available combinations of monoclonal antibodies to the following cell surface markers: CD45 and CD14, CD3 and CD8, CD3 and CD4, CD3 and CD19, CD3 and CD16 and -56 (Simulset reagents; Becton Dickinson [BDIS], San Jose, Calif.), CD8 and CD38, CD8 and HLA-DR, CD8 and CD11b, CD8 and CD28, CD4 and CD45RO, and CD4 and CD45RA (antibodies to CD11b were from DAKO, Carpinteria, Calif.; all other antibodies were from BDIS). The preparations were fixed in 0.5 ml of 1% formalin (methanol free) and kept overnight at 4°C until flow-cytometric analysis was performed. This analysis was done using a FACscan cytometer (BDIS) equipped with a 15-mW air-cooled 488-nm argon-ion laser (for details see reference 8). Thus the following were quantified for each group of subjects and used in the modeling: total white blood cell (WBC) count; number (and percentage of total WBCs) of lymphocytes; number (and percentage of total lymphocyte count) of CD3⁺ CD19⁻ (total T cells), CD3⁺ CD4⁺ (major histocompatibility complex class II [MHC II]-restricted T cells), and CD3⁺ CD8⁺ (MHC I-restricted T cells) cells and the arithmetic sum of the latter two; CD3⁻ CD19⁺ (B cells) and CD3⁻ CD16⁺ and CD56⁺ (NK cells) cells; percentage of class II-restricted T cells expressing CD45RO and CD45RA; and the percentage of class I-restricted T cells expressing CD28, HLA-DR, and CD38 but not CD11b.

PBLs harvested from additional aliquots of blood were homogenized in RNA-zol (Cinna/Biotecs, Friendswood, Tex.) at 50 mg per 0.2 ml (10⁶ cells). The quantitative reverse transcriptase PCR (RT-PCR) cytokine assay was used as previously described (4, 8). RNA samples were reverse transcribed with Superscript RT (Bethesda Research Laboratories, Rockville Md.), and cytokine-specific primers were used to amplify the following cytokines: alpha interferon, tumor necrosis factor alpha, interleukin-2 (IL-2), IL-4, IL-6, IL-10, and IL-12. Amplified PCR product was detected by Southern blot analysis, and the resultant signal was quantified with a phosphorimager (Molecular Dynamics, Sunnyvale, Calif.) as described in detail previously (4, 8).

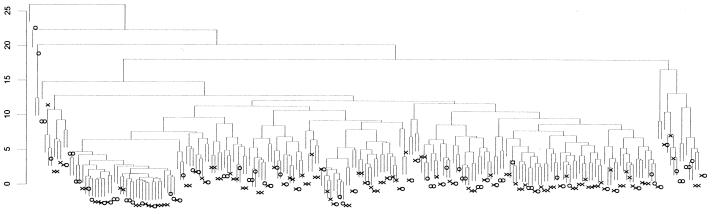
Variable selection based on minimum variance and potentially high immunological relevance resulted in 29 predictor variables. These variables were examined for correlation and means and SDs were produced. Strong off-diagonal correlations and covariance implied that data reduction and subspace projections would be profitable in the present case. An initial cluster analysis (hierarchical, Euclidean, agglomerative clustering) was performed on all subjects over the candidate predictors, and the resultant dendrogram can be seen in Fig. 1. Clearly the underlying separation surface is complex. Although small separable clusters of CFS or control groups appear in the dendrogram (Fig. 1), the overall clustering diagram indicates that the problem is highly nonlinearly separable. This encouraged us to explore more-complex nonlinear classification schemes such as neural networks. We first looked at the linear (Fisher's discriminant analysis) case to see what to expect in the form of a lower bound of classification performance.

FIG. 1.

Clustering dendrogram of CFS (X) and control (O) cases on 29 immunologically defined features.

In the neural-network literature a perceptron neural-network model is similar to Fisher's discriminants in that local hyperplanes are fit to the decision surface of the classes in order to minimize the classification error per case. These types of models cannot account for nonlinearity of class membership either in terms of relationship between variables or in terms of nonconvexity of the concept class.

Using the immunological features and 128 CFS and 87 control subjects as described earlier, a linear perceptron was used to create a discrimination function on n/2 bootstraps resampled with replacement 100 times. This effectively created over 11,000 independent cases for classification. Of these, 5,381 cases were correctly classified as CFS and 1,675 cases were correctly identified as control, while 1,578 CFS cases were incorrectly classified as control (misses) and 3,029 control cases were incorrectly classified as CFS (false alarms). The percent correct for CFS was 77%, showing significant classification performance, while marginal-to-poor classification performance for control subjects near the decision surface (36%) was observed. The overall percentage of correct classification was near 60%. These values provide a benchmark set for other more-complex classification methods. Below we consider the case of multilayer networks and modular networks.

Multilayer neural networks are standard nonlinear classifiers using a logit output. These networks are the logical increment in classification power above the linear discriminant or perceptron type classifier. Consequently, such models are referred to many times as multilayer perceptrons. Network training is accomplished by the back-propagation method and appears to converge in a few hundred training epochs (where an epoch was using every subject to reestimate each parameter in the model). These models can recognize extremely complex patterns in the feature space and can be used to construct decision surfaces that can have high generalization potential. Presently, it is unknown how to predict whether a given neural-network classifier will have significant generalization performance on unseen or out-of-sample cases, even if it is performing with perfect accuracy for the training or sample cases. Partly this could be due to “overfitting,” meaning that the network is unable to extract general patterns and is in effect “storing” random patterns that provide little similarity to the population from which the cases have been drawn.

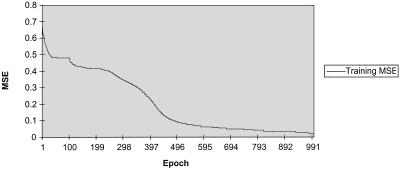
Typical learning curves.

A learning curve for a multilayer network with approximately 500 weights is shown in Fig. 2. Convergence of the classification error usually occurred within 400 to 600 epochs over all patients. As is typical for most such error curves there is an early resolution of some locally best gradient direction and then a fairly rapid decline toward minimum error values on both classification units (CFS and control, coded as <1 0> and <0 1>, respectively). Two classification units were used to determine the rate of false alarms and misses in the final learned classification function.

FIG. 2.

Overall MSE over epochs.

Model selection: sizes of hidden-layer and modular networks.

The size of the hidden layer was determined by systematic cross-validation of the network trained on one sample and tested on a held-out sample. Hidden-layer sizes from 2 to 120 were tested using 100 replications per hidden-unit size. Between 12 and 18 hidden units, the network error reached a minimum and seemed to decrease very slowly to a marginally different value near 80 to 100 hidden units. All network simulations were thereafter fixed at 12.

Alternative network architectures were also explored using “modular-style” networks. These types of networks isolate processing from either input clusters or output clusters or both. Various possibilities were tested using 12 hidden units at various layers (at most two layers of hidden units were tested) and cases where 12 was the total number of hidden units, which were distributed in patterns of <4 4> <2 2> for the first and second hidden layers, respectively. Split half tests provided no better, and in larger modular networks considerably worse, generalization performance. Consequently, for the final tests and analysis all networks were fixed at 12 hidden units in a multilayer perceptron.

In-sample testing.

In a typical result for an in-sample test for a single network, all 107 cases (63 CFS and 44 control) randomly sampled from the total cases were correctly classified. Shown in Table 1 is a summary of the mean square error (MSE), a normalized MSE, mean average error, minimum absolute error within the sample, maximum absolute error, and correlation coefficient of output value with classification code. This was fairly typical of all 100 resampled tests; each independent network correctly classified all of the in-sample cases, nothwithstanding nonzero MSE.

TABLE 1.

Summary of variables for in-sample test for a single network^a

Classification	MSE	NMSE	Mean avg error	Absolute error	r	% Correct
CFS	0.0076	0.0314	0.0390	0.0000–0.4810	0.9865	100.0000
Control	0.0076	0.0314	0.0390	0.0000–0.4847	0.9864	100.0000

^aNMSE, normalized MSE; r, correlation coefficient of output value with classification code. 

Out-of-sample testing.

Similar to the out-of-sample tests with the linear discriminant classifier out-of-sample tests with the multilayer perceptron were performed on over 11,000 independent samples. The CFS cases were correctly classified at a rate similar to that for the linear discriminant (4,550 of 6,037 [75%] correctly classified); however, the control cases were correctly classified at a 16% higher rate, with 51% (2,084 of 4,128) correct. With larger training sets, the out-of-sample generalization increased very rapidly to 80 to 90% with, consequently, fewer out-of-sample test cases (<20) and therefore less reliability for the classification estimate.

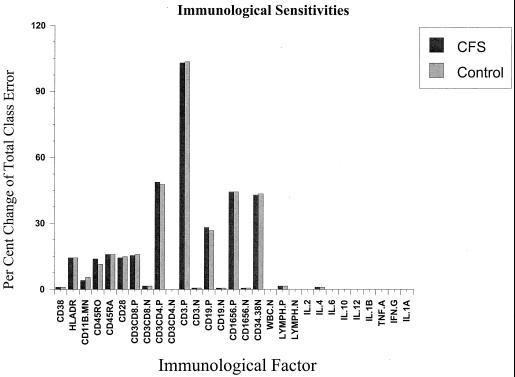
With the given neural-network classifier, we can determine the specific contribution of each variable to the classification performance. This is accomplished by perturbing each input line and observing its effect on the classification performance. Shown in Fig. 3 is the result of this procedure for all 29 variables. While all other variables were held constant, each variable was perturbed by 2 SDs and the classification output units were recorded. Each bar in the histogram shows a normalized response on each classification variable (CFS and control). The height of the bar indicates the effect on the remaining classification error; the maximum sensitivity indicates a 102% increase in classification error, while the minimum change was a 1% increase in classification error. The maximum change in classification error would completely disrupt the classification function, while a 1 to 2% change reduces the classification error toward the linear perceptron performance. With this threshold there were 10 to 14 variables identified as making significant contributions to classification. Shown in Table 2 are the 14 variables found by the sensitivity analysis to be the most significant.

FIG. 3.

Sensitivity analysis for network classifier, showing relative contributions of each immunological factor. TNF. A, tumor necrosis factor alpha; IFN. G, gamma interferon; lymph. lymphocytes; P, percent; N, number.

TABLE 2.

Immunological sensitivities for the 14 most significant factors

Factor(s)	% Change of classification error
CD38	−1.0
HLA-DR	−14.2
CD11b	+3.9
CD45RO	+13.8
CD45RA	−15.8
CD28	+14.2
CD3, CD8	+15.3
CD3, CD4	+48.8
CD3	+102.9
CD19	−28.0
CD16, CD56	+44.3
CD34, CD38	−42.8
Lymphocytes	−1.5
IL-4	+1.0

When we used classical statistical methods to search for immunological differences between nonveterans with CFS and healthy, sedentary controls, we found no major differences (18). Obviously one limitation of our earlier work was that we may not have studied all the correct domains of immune system variables (e.g., we never studied soluble-cytokine receptors). Despite this possible deficiency, however, using these neural-network models, we did find that important immunological differences emerged. Of interest was the fact that, of all the cytokines evaluated, the only one to be in the final model was IL-4. Seeing an increase in IL-4 suggests a shift to a type 2 cytokine pattern. Such a shift has been hypothesized (17), but convincing evidence to support that hypothesis has been lacking. The neural networks in these studies are able to detect and represent nonlinear decision surfaces and can therefore in principle be sensitive to factors and the interaction of factors that linear methods would overlook. Moreover the resampling techniques in these studies provide high reliability for the more-complex kinds of classifiers that neural networks can detect and approximate.

The cell surface marker data provide evidence that T cells are selectively activated in CFS patients, resulting in their expansion relative to other mononuclear cell populations. A proportional increase in memory/effector CD45RO cells relative to naive CD45RA cells and an increase in CD28 T cells both accompany an overall increase in CD3 T cells. The positive interaction with IL-4 suggests the possibility that this Th2 cytokine is associated with this expansion. These findings are consistent with the hypothesis that CFS symptoms are a consequence of immune system dysregulation. A corresponding decrease in the CD19⁺ B-cell compartment and the CD34⁺ hematopoietic progenitor subpopulation is also detected, consistent with the T-cell expansion.

If the symptoms of CFS were caused by immune system activation, one would expect to find an increase in CD45RO memory cells. Although this result has not been found prior to this report (11, 14), Straus et al. did find a suggestion of immune system activation in the form of an increased number of activated CD45RO subpopulations. In contrast to the expected result, two groups have found decreases in CD45RA, the naive cell (11, 14), a result quite different from the one reported here and one which we did not find. Inconsistent immunological results across laboratories have been the rule (for examples, see references 7, 11, and 18). An association of this disease with IL-4 may provide insights into the basis of chronic fatigue since IL-4 can promote allergy-associated inflammatory responses resulting from activation of mast cells and other effector cell types triggered during the Th2 response. These immunological changes could explain some of the clinical picture seen in CFS. We believe that controlling for illness-related inactivity and using newer statistical techniques such as the one used here should provide the field a methodological template for future studies designed to replicate and extend earlier results.