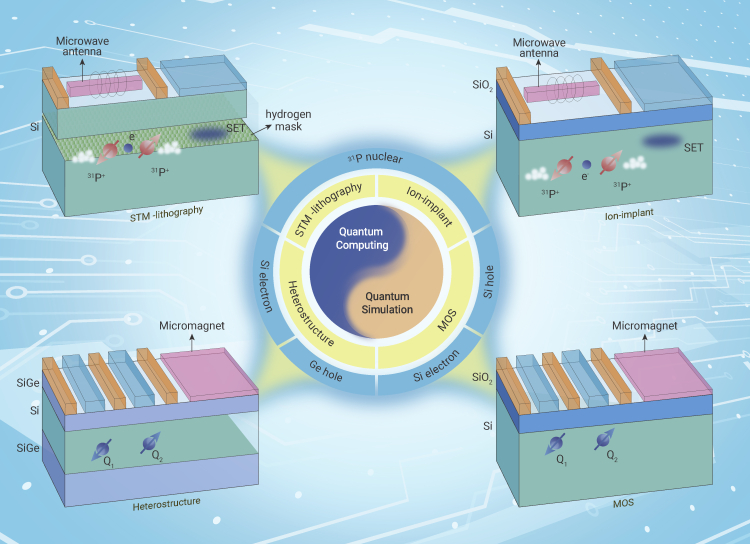
Silicon-based quantum dots are considered a promising platform for large-scale quantum computing because of their compatibility with the mature complementary metal-oxide-semiconductor (CMOS) fabrication technology and long spin lifetime (Figure 1). The spins of an electron confined in gate-defined quantum dots or the nuclear spins of donor-doped atoms embedded in the Si matrix can be used as the basic unit of quantum computing, i.e., quantum bit (qubit), and the exchange interactions between spins serve to couple different qubits and thus generate two-qubit logic operations. These two features ensure that semiconductors can be constructed as universal quantum computers, which means that the same machine can solve different problems. Theoretically, any system can be simulated using a universal quantum computer, since the system’s unitary transformation can be decomposed into a set of single- and two-qubit gates, which is known as digital quantum simulation (DQS).1 However, the implementation of universal quantum computing with quantum dots still faces a great challenge to achieve long-range coupling between different qubits. Therefore, an alternative approach that many studies have turned to for simulating quantum systems is analog quantum simulation (AQS), in which the system’s Hamiltonian is mapped directly onto the simulator’s Hamiltonian without the need for a quantum computer and thus is free from long-range coupling limit.1 AQS is more fault tolerant than DQS because in many cases only the qualitative results of the simulated "toy model" are needed, but since each simulator is built specifically for a particular system of interest, their use is limited compared with the more versatile DQS.
Figure 1.
Schematic diagram of various silicon-based quantum dots
(Top left) donor-based Si qubits fabricated by STM-lithography. (Top right) donor-based Si qubits fabricated by ion implantation. (Bottom left) gate-defined quantum dots fabricated on Si/SiGe heterostructures. (Bottom right) gate-defined quantum dots fabricated on Si MOS.
The analog simulation of the strongly correlated electron systems using quantum dots is straightforward because an array of quantum dots is exactly described by the Hubbard model. The intrinsic properties of quantum dots, such as long-range Coulomb interactions and interdot tunneling coupling, are key elements for simulating solid-state electronic systems. Despite these obvious advantages over other quantum systems (such as neutral ultracold atoms and superconducting circuits), precise tuning of each quantum dot’s parameters remains a huge engineering challenge. Recently, Kiczynski et al.2 demonstrated simulations of the interacting many-body Su-Schrieffer-Heeger (SSH) model using an array of ten phosphorus-doped quantum dots in silicon. By using scanning-tunneling-microscopy (STM) lithography, they achieved atomic-precision control of quantum dot positions (Figure 1). Thus, the strength of the tunneling coupling, which is also the hopping amplitudes in the SSH model, can be regulated by the interdot separation distance. With different staggered hopping amplitudes, the quantum dot array will enter either topologically trivial or topologically non-trivial regimes, which can be distinguished by measuring the conductance. Compared with gate-defined GaAs quantum dots, the quantum dots based on phosphorus impurities possessing the inherently Coulomb confining potential can greatly simplify the device design by allowing the control of a 10-quantum dot array utilizing only six electrostatic gates, thus avoiding unnecessary cross-talk. This work demonstrates the superiority of donor-doped quantum dot structures in AQS and represents an important step toward a large-scale quantum dot simulator for strongly correlated electron systems.
Besides the application in AQS, the donor-doped quantum dot is originally proposed as a platform for quantum computing since the nuclear spins of donor atoms have extremely long coherence times.3 While adopting donor-doped quantum dots as an analog quantum simulator can greatly simplify device design, this advantage is no longer available when used for quantum computing, as the initialization, manipulation, and readout of qubits will inevitably increase the complexity of devices. For example, the initialization and readout of a nuclear spin involve measuring the electron spin resonance spectrum of its bound donor electron, which requires a single-electron transistor (SET) as a charge sensor to read the electron spin through spin-to-charge conversion.3 The control of qubits also requires external magnets to generate oscillating magnetic fields to implement nuclear magnetic resonance and electron spin resonance (ESR), which is not conducive to large-scale integration [3].
Another serious challenge of donor-based qubits for quantum computing is that, unlike the easily accessible Coulomb interactions in AQS, it is difficult to achieve an effective exchange interaction between two qubits, which oscillate with atomic placement due to intervalley interference. This sensitivity to the position of donor atoms limits the fidelity of two-qubit gates, and for the donor-doped quantum dot devices fabricated by STM, there are currently no experiments to quantitatively characterize the two-qubit exchange gate through randomized benchmarking.3 However, a recent breakthrough in two-qubit gate fidelity has been achieved with ion-implanted donor-doped quantum dots (Figure 1), an alternative method for doping. A pair of 31P donor nuclear were linked via a shared electron, and the two-qubit average gate fidelity reaches 99.37(11) % exceeding the threshold for quantum error correction (QEC).3 As a critical tool in the standard silicon foundry processing, ion implantation is more beneficial in integration than the newly developed and immature STM-lithography approach. The bottleneck of ion implantation is that the donor atoms are placed stochastically, and how to achieve deterministic ion implantation will be essential to solving the scaling problem.
Employing gate-defined quantum dots for quantum computing can circumvent some problems of donor-based qubits. With the electrostatic gates placed on top of two-dimensional electron gas, the locations of qubits can be well defined, and the spin-spin exchange interactions can be easily tuned by the interdot gate voltage, allowing fast two-qubit gate operations. Like the donor-based qubit fabricated by ion implantation, two-qubit gates above the QEC threshold were also demonstrated in gate-defined quantum dots fabricated on isotopically enriched 28Si/SiGe heterostructures (Figure 1).3 The reduced 29Si content and the low disorder of the epitaxial barrier enable long spin decoherence times. Considering that the alternating magnetic field used for ESR leads to device heating and is non-local, they used micromagnets to generate a magnetic field gradient and, thus, can control the spin through the alternating electric field, i.e., electric dipole spin resonance (EDSR) with Rabi frequency typically below 10 MHz.3 The main challenge for Si/SiGe heterostructures is that the valley splitting is too small, around 35 to 270 μeV, which will lead to leakage of quantum information.4
Another type of gate-defined quantum dot is to trap electrons at the Si/SiO2 interface (Figure 1). This metal-oxide-semiconductor (MOS) quantum dot has a large vertical electric field, which enhances valley splitting compared with SiGe heterostructures. The valley splitting of MOS quantum dots can range from 300 to 800 μeV, but its magnitude is uncontrollable and varies between different quantum dots randomly.4 The limitation of MOS quantum dots is the presence of defects at the Si/SiO2 interface, which generate 1/f noise and consequently reduce the fidelity of the qubit.
Regardless of the quantum dot structure or manufacturing process, as long as the qubit is encoded on electron or nuclear spins, the use of external magnets cannot be avoided, which severely limits scaling. As a result, some studies turned to the single-hole spins confined in group IV quantum dots as qubits. Due to the strong spin-orbit coupling (SOC) of the hole, EDSR can be used to control qubits by an alternating electric field alone, eliminating the need for an alternating magnetic field or a magnetic field gradient. This all-electrical manipulation of the hole qubit is suitable for large-scale integration. Experimentally, MOS quantum dots can also be used to confine Si holes, and single-qubit gate operations have been demonstrated.3
Compared with Si holes, Ge holes, also belonging to group IV, are developing rapidly. After achieving the all-electrical control of a single-hole-spin qubit confined in Ge/SiGe quantum wells, significant progress has been made in increasing the number of coupled qubits, doubled every year.3 The strong SOC allows the qubit to be driven at Rabi frequencies over 100 MHz, which is 10 times that of the Si electron qubits. The in-plane effective mass of Ge holes is very light, allowing the formation of larger quantum dots and thus relaxing the fabrication constraints of devices. For this reason, the demonstration of a four-qubit quantum processor and a 16-quantum dot crossbar array reported at American Physical Society (APS) March Meeting 2022 both show the extraordinary scalability of Ge hole quantum dots. Compared with electrons, the 4-fold degeneracy of the valence band makes hole physics in low-dimensional nanostructures more complex, with the most significant feature being the heavy-hole (HH) and light-hole (LH) mixing, which has important effects on the qubit, such as the electrical tunability of Si and Ge hole g-factors and decoherence time. The strength of direct Rashba SOC used to control hole qubits is also proportional to the magnitude of HH-LH mixing at the zone center.5 All these inherent properties of the hole will bring new advantages to the qubit operations.
In summary, silicon-based quantum dots have emerged as a promising platform for both quantum computing and quantum simulation, and there are various appealing device designs to explore. Actually, not only does each structure, material, or qubit type of silicon has its advantages and limitations, but so do different quantum computing platforms. Future developments in quantum technology are therefore more likely to be complementary between different approaches. For example, photonic connections or superconducting resonators can facilitate long-range coupling between semiconductor qubits to achieve QEC.
Acknowledgments
Declaration of interests
The authors declare no competing interests.
Published Online: September 28, 2022
References
- 1.Georgescu I.M., Ashhab S., Nori F. Quantum simulation. Rev. Mod. Phys. 2014;86:153–185. [Google Scholar]
- 2.Kiczynski M., Gorman S.K., Geng H., et al. Engineering topological states in atom-based semiconductor quantum dots. Nature. 2022;606:694–699. doi: 10.1038/s41586-022-04706-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burkard G., Ladd T.D., Nichol J.M., et al. Semiconductor spin qubits. arXiv. 2021 doi: 10.48550/arXiv.2112.08863. Preprint at. [DOI] [Google Scholar]
- 4.Zhang X., Li H.O., Cao G., et al. Semiconductor quantum computation. Natl. Sci. Rev. 2019;6:32–54. doi: 10.1093/nsr/nwy153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Liu Y., Xiong J.X., Wang Z., et al. Emergent linear Rashba spin-orbit coupling offers fast manipulation of hole-spin qubits in germanium. Phys. Rev. B. 2022;105:075313. [Google Scholar]