Selection-Corrected Statistical Inference for Region Detection With High-Throughput Assays

Abstract

Scientists use high-dimensional measurement assays to detect and prioritize regions of strong signal in spatially organized domain. Examples include finding methylation enriched genomic regions using microarrays, and active cortical areas using brain-imaging. The most common procedure for detecting potential regions is to group neighboring sites where the signal passed a threshold. However, one needs to account for the selection bias induced by this procedure to avoid diminishing effects when generalizing to a population. This paper introduces pin-down inference, a model and an inference framework that permit population inference for these detected regions. Pin-down inference provides non-asymptotic point and confidence interval estimators for the mean effect in the region that account for local selection bias. Our estimators accommodate non-stationary covariances that are typical of these data, allowing researchers to better compare regions of different sizes and correlation structures. Inference is provided within a conditional one-parameter exponential family per region, with truncations that match the selection constraints. A secondary screening-and-adjustment step allows pruning the set of detected regions, while controlling the false-coverage rate over the reported regions. We apply the method to genomic regions with differing DNA-methylation rates across tissue. Our method provides superior power compared to other conditional and non-parametric approaches.

1. Introduction

Due to the advent of modern measurement technologies, several scientific fields are increasingly relying on data-driven discovery. A prominent example is the success of high-throughput assays such as microarrays and next generation sequencing in biology. While the original application of these technologies depended on predefined biologically relevant measurement units, such as genes or singe nucleotide polymorphisms (SNPs), more recent applications attempt to use data to identify and locate genomic regions of interest. Examples of such application include detection of copy number aberrations (Sebat et al., 2004), transcription binding sites (Zhang et al., 2008), differentially methylated regions (Jaffe et al., 2012b), and active gene regulation elements (Song and Crawford, 2010). Neuroscientists also use data to identify regions affected by variations in cognitive tasks, when analyzing functional imaging data (Friston et al., 1994, Hagler et al., 2006, Woo et al., 2014). As these technologies mature, the focus of statistical inference shifts from individuals to populations. Instead of searching for regions different from baseline in an individual sample, we instead search for differences between two or more populations (cancer versus normal, for example). In population inference, region detection methodology needs to account for between-individual biological variability, which is often non-stationary, and for technical measurement noise. Furthermore, sample size is usually small due to high costs, so variability in the estimates remains considerable.

An inherent risk of data-driven discovery is selection bias, the bias associated with using standard inference procedures on results that were chosen preferentially. In the context of population inference, the most common approach for detecting regions is to compute marginal p-values at each site, correct for multiplicity, and then combine contiguous significant sites. Publications in the high-profile biology journals have implemented these ad-hoc analysis pipelines (Kundaje et al., 2015, Becker et al., 2011, Pacis et al., 2015, Lister et al., 2013). However, there is no theoretical justification for extrapolating inferences from the single sites to the region. In particular, using the average of the observed values at the selected sites as an estimate for the region will result in a biased estimate. Kriegeskorte et al. (2009) coined the term circular inference for such practices in neuroscience, highlighting the reuse of the same information in the search and in the estimation. Furthermore, the power of such methods to detect regions is limited by the power to detect at the individual sites, which are noisier and require a-priori stronger multiplicity corrections compared to regions: a region consisting of several almost-significant sites will be overlooked by such algorithms. Finally, there is no clear way how to prioritize regions of different sizes and different correlation structures without more refined statistical methods. Here we describe a general framework that permits statistical inference for region detection in this context.

Although high-profile genomic publications have mostly ignored it, the statistical literature includes several publications on inference for detected regions within large statistics maps. Published methods differ in how they summarize the initial information into a continuous map of statistics: smoothing or convolving the measurements with a pre-specified kernel, forming point-wise Z maps, p-value maps, or likelihood maps (Pedersen et al., 2012, Siegmund et al., 2011, Hansen et al., 2012). Regions of interest can be identified around local maxima, by thresholding the signal, or by model based segmentation(Jaffe et al., 2012b, Kuan and Chiang, 2012, Zhang and Siegmund, 2012). (See Cai and Yuan, 2014, for asymptotic analysis). Multiplicity corrections for individual detected regions can be employed assuming true signal locations are well separated (Schwartzman et al., 2011, 2013, Sun et al., 2015). Alternatively, non-parametric methods use sample-assignment permutation to simulate the null distribution, without requiring stationarity or knowing the distribution (Jaffe et al., 2012b, Hayasaka and Nichols, 2003).

However, current methods fail to address two important aspects: the first is non-null inference such as effect-size estimation and intervals. Non-null inference requires stronger modeling assumptions and a more sophisticated treatment of nuisance parameters, in comparison to tests of a fully specified null. In genomics, irrelevant confounders can create many small differences between the groups, which can reach strong statistical significance in highly powered studies but are not biologically interesting (Leek et al., 2010). Estimates and intervals for effect size, rather than just p-value, permit the practitioner to discern biological significance. Work on confidence intervals in large processes include Zhong and Prentice (2008) and Weinstein et al. (2013) for individual points rather than regions, and Sommerfeld et al. (2015) for globally bounding the size of the non-null set. We consider providing estimates of the effect in biologically meaningful units and quantification of the uncertainty in these estimates an important contribution.

The second challenge is non-stationarity: in most genomic signals, both the variance and the auto-correlation change considerably along the genome. This behavior is due to uneven marker coverage, and biochemical properties affecting DNA amplification (Bock et al., 2008, Benjamini and Speed, 2012, Jaffe et al., 2012a). Non-stationarity makes it harder to compare the observed properties of the signal across regions: a region of k adjacent positive sites is more likely to signal a true population difference if probe correlation is small.

In this paper, we introduce pin-down inference, a comprehensive approach for inference for region detection that produces selection-corrected p-values, estimators and confidence intervals for the population effect size. We focus on detection algorithms that, after preprocessing, apply a threshold-and-merge approach to region detection: the map of statistics is thresholded at a given level, and neighboring sites that pass the threshold are merged together. The difficulty in inference for these detection algorithms is that choosing local null and alternative models around the detected region introduces selection bias. The key idea of pin-down inference is to identify for each potential region its selection event – the necessary and sufficient set of conditions that lead to detection of the region; for threshold-and-merge, this selection event can be described as a set of coordinate-wise truncations. Selection bias is then corrected by using the distribution of the test statistic conditional on the selection event (Fithian et al., 2014). Because inference is local, it can be tailored for each region according to the local covariance. When further selection is needed downstream, standard family wise corrections can be applied to the list of detected regions.

The paper is structured as follows. First, we introduce a specific genomic signal – DNA-methylation – that will be used to demonstrate our method. In Section 2 we present a model for the data generation, define the threshold-and-merge selection, and describe the selection bias. In Section 3 we review the conditional approach to selective-inference, and specify the conditional distribution associated with a detected region. When the data is approximately multivariate normal, the conditional distribution follows a truncated multivariate normal (TMN, Section 3.3). In Section 4 we describe the sampling based tests and interval estimates for a single region. If only a subset of the detected regions is eventually reported, a secondary adjustment is needed (Section 5). Sections 6 and 7 evaluate the performance of the method on simulated and measured DNA-methylation data, followed by a discussion.

Motivating example: differentially methylated regions (DNA)

DNA methylation is a biochemical modification of DNA that does not change the actual sequence and is inherited during mitosis. The process is widely studied because it is thought to play an important role in cell development (Razin and Riggs, 1980) and cancer (Feinberg and Tycko, 2004). Unlike the genomic sequence, methylation differs across different tissues of the same individual, changes with age, environmental impacts, and disease (Robertson, 2005). Of current interest is to associate changes in methylation to biological outcomes such as development and disease. Current high-throughput technologies measure the proportion of cells in a biological specimen that are methylated giving a value between 0 and 1 for each measured site. The most widely used product, the Illumina Infinuim array, produces these proportion measurements at approximately 450,000 sites (Bibikova et al., 2011). Reported functionally relevant findings have been generally associated with genomic regions rather than single sites (Jaenisch and Bird, 2003, Lister et al., 2009, Aryee et al., 2014) thus our focus on differentially methylated regions (DMRs). Because DNA methylation is also susceptible to several levels of stochastic variability (Hansen et al., 2012), inference for DMRs needs to take into account the unknown but variable and often strong local correlation between nearby methylation sites.

2. Model for the effects of selection

2.1. Population model

Suppose the collected data consists of n samples of D measurements each, Y₁,…, Y_n. We model the i’th sample as a random process composed of a mean effect that is linear in known covariates, and an additive random individual effect. Each sample is annotated by the covariate of interest X_i ∈ R, and by a vector of nuisance covariates W_i ∈ R^p−1. Then the i’th observed vector is:

$$\begin{array}{ccc}{Y}_i=\Theta X_i+\Gamma W_i+{\epsilon }_i,& E\left[{\epsilon }_i\right]=\mathbf{0},& i=1,\dots ,n.\end{array}$$ (1)

Here Θ = (θ₁,…, θ_D)′ ∈ R^D is the fixed process of interest, Γ ∈ R^D×p−1 are fixed nuisance processes, and ε_i ∈ R^D captures both the individual sample effect and any measurement noise. ε_i can further be characterized by a positive-definite covariance matrix C_jj′ := E[ε_i(j)ε_i(j′)], 1 ≤ j, j′ ≤ D. In matrix notation, let $Y={(Y_1^{\prime },\dots ,Y_n^{\prime })}^{\prime }\in R^{n\times D}$ be the matrix of measurements and $\mathbf{X}={[(X_1,W_1^{\prime }),\dots ,(X_n,W_n^{\prime })]}^{\prime }\in R^{n\times p}$ be the design matrix organized so the covariate of interest is in the first column.

For a concrete example of our notation, consider a two-group design comparing samples from two tissue-types. Each sample would be coded in a vector Y_i ∈ R^D. X_i would code the tissue type, 1 for group A and 0 for group B. W_i can encode such demographic variables as age and gender, as well as a bias term. Then θ_j would code for the mean difference between groups on the j’th site. We expect the Θ process $\Theta ={\left({\theta }_j\right)}_{j=1}^D$ to be almost zero in most sites, and to deviate from zero in short connected regions.

Regions of interest

A region of interest (ROI) corresponds to a range a : b = (a, a + 1,…, b) where Θ_a:b = (θ_a, θ_a+1,…, θ_b) is large in absolute value. A sufficient representation for an ROI is a triplet r = (a, b, d), where a ≤ b ∈ 1,…, D are indices and d ∈ {−, +} represents the direction of deviation from 0. Depending on context, we would usually restrict our analysis to indices b, a that are not too far apart. These restrictions are coded into the set $\mathcal{B}$ of all interesting ROIs. Note that $\mathcal{B}$ is redundant, with many ROIs that are almost identical; in any realization of the model, only a small subset of $\mathcal{B}$ will be selected for estimation.

Vector of estimators Z

Our procedure focuses on a vector of point-wise unbiased normal estimators $Z=\widehat{\Theta }$. The assumptions for Z are:

• Unbiasedness: E[Z] = Θ.

• Estimable covariance: Σ := Cov (Z) is estimable, and the estimator $\widehat{\Sigma }$ is unbiased and independent of Z.

• Local normality: For indices a ≤ b that define a potential ROI, meaning (a, b, +) or (a, b, −) are in $\mathcal{B}$, vector Z_a−1:b+1 is multivariate normal

  $$Z_{a-1:b+1}\sim N\left({\Theta }_{a-1:b+1},{\Sigma }_{a-1:b+1}\right).$$

• Here, Θ_a−1:b+1 , Σ_a−1:b+1 are the R^b−a+3 and R^{(b−a+3)×(b−a+3)} subsets of Θ and Σ.

Specifically, we can take Z to be the least-squares estimator for Θ

$$Z=\widehat{\Theta }:={\left[{\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\prime }Y\right]}_1.$$ (2)

With well behaved data, the region Z_(a−1:b+1) would be approximately multivariate normal even with a moderate number of samples n. Furthermore, with enough samples compared to covariates (n > p)¹, the local covariance C = Cov(ε_i) is estimable from the linear model residuals, resulting in Ĉ. Furthermore, for each 1 ≤ j, j′ ≤ D, $\mathrm{Var}\left(Z_j\right)={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}_{11}^{-1}\mathrm{Var}\left({ϵ}_{.j}\right)$ and $\mathrm{Cov}\left(Z_j,Z_{j^{\prime }}\right)={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}_{11}^{-1}\mathrm{Cov}\left({ϵ}_{.j},{ϵ}_{.j^{\prime }}\right)$. Hence,

$$\begin{array}{ccc}\Sigma =\mathrm{Cov}\left(Z\right)={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}_{11}^{-1}C,& \mathrm{and}& \widehat{\Sigma }={\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}_{11}^{-1}\widehat{C}\end{array}.$$ (3)

This is extendable to a two-group design where each group is allowed a different covariance.

Effect size and population effect size

A commonly used summary for the effect size in a region is the area under the curve (AUC) of the observed process, which is the sum of the estimated effects in the region (Jaffe et al., 2012b). To decouple the region length and the magnitude of the difference, we define the observed effect size as the average rather than the sum of the effect:

Definition 1 The observed effect size of region a : b is

$$t\left(Z_{a:b}\right)={\overline{Z}}_{a:b}:=\frac{1}{b-a+1}\sum _{j=a}^b{Z}_j.$$

We will associate the observed effect size t(Z_a:b) for each potential region a : b with the population parameter representing its unconditional mean

Definition 2 The (population) effect size of region a : b is

$${\overline{\theta }}_{a:b}:=\frac{1}{b-a+1}\sum _{j=a}^b{\theta }_j.$$

We prefer ${\overline{\theta }}_{a:b}$ to AUC because it decouples two different sources of information: the region length and the effect magnitude. Either way, it is easy to covert between the two parameters because for $\left(a,b,+\right)$ , $AUC=\left(b-a+1\right){\overline{\theta }}_{a:b}$. The methods described here are easily extendible for other linear statistics.

Note that in our setup, each parameter ${\overline{\theta }}_{a:b}$ is well-defined regardless of the data-dependent decision whether to estimate it. We do not assume that there is a “correct” selection decision; rather, we view selection as a technical step that prunes and disambiguates the set of ROIs.

2.2. Selection

A common way to identify potential ROIs is to screen the map of statistics at some threshold, and then merge sites that passed the screening into regions (Jaffe et al., 2012b, Siegmund et al., 2011, Schwartzman et al., 2013, Woo et al., 2014). This procedure ascertains a minimal biological effect-size in each site, while increasing statistical power to detect regions and controlling the computational effort. After preprocessing and smoothing the responses, these algorithms run a version of the following steps:

1. Produce an unbiased vector of linear estimates $\widehat{\Theta }=Z$.

2. Identify the set of indices exceeding a fixed threshold c, {j : Z_j > c}.

3. Merge adjacent features that pass the threshold into regions.

4. Filter (or split) regions that are too large.

The procedure is illustrated in Figure 2. The output of such algorithms is a random set of (positive) detected ROIs ${\widehat{\mathcal{B}}}^{+}$. Step 4 ascertains that ${\widehat{\mathcal{B}}}^{+}\subset \mathcal{B}$. Comments:

• Typically, we are also interested in the similarly defined set of negative ROIs ${\widehat{\mathcal{B}}}^{-}$. For ease of notation we deal only with ${\widehat{\mathcal{B}}}^{+}$, understanding that ${\widehat{\mathcal{B}}}^{-}$ can be analyzed in the same way. It is important to note that each region is selected either to the positive set or to the negative set, and this choice will instruct the hypothesis test.

• Local adjustment of the threshold can also be incorporated into this framework, as long as this adjustment is fixed or independent of the estimate vector Z.

• In most applications, the measurement vectors or the estimated process are smoothed to produce larger coherent regions with less interference due to noise. Our framework accommodates smoothing as a preprocessing step, meaning that each sample Y_i is smoothed separately. The degree of smoothing will therefore affect the inference target Θ, as defined by the linear model in (1). For example, for a two group design and a linear smoother, inferences after smoothing apply to regions of the smoothed mean process. See more in Section 8.

Figure 2: Cartoon of the statistical setup.

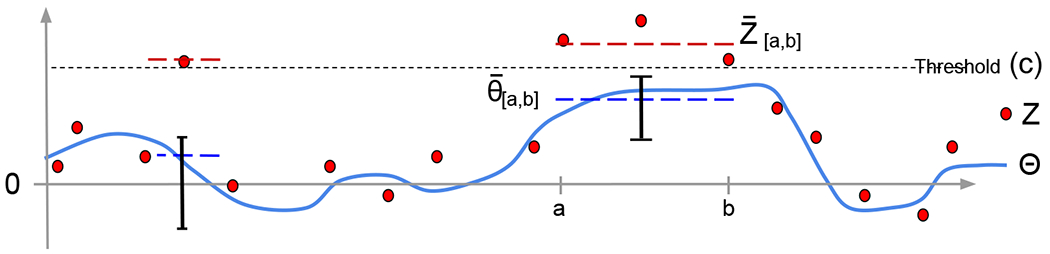
The parameter vector of interest Θ (solid blue) is unobserved; we observe an unbiased estimate vector Z (full red os). The thresholds (dotted line) are at c and −c, and the excursion set {j : Z_j > c} is clustered into two regions. (No regions {j : Z_j < −c} are shown). Due to this selection, the two parameters to be estimated are ${\overline{\theta }}_{4:4}={\theta }_4$ on the left and ${\overline{\theta }}_{a:b}=av{g}_{j=a}^b\left({\theta }_j\right)$, marked with a blue dashed line (here a = 10, b = 12). The observed effect sizes (red dashed line) are biased because of the selection. Our goal is to form confidence intervals for ${\overline{\theta }}_{4:4}$ and ${\overline{\theta }}_{10:12}$.

Distribution after selection

It is important to distinguish between inference for predefined regions based on previous biological knowledge, such as exons or transcription start sites, and inference for regions detected with the same data from which we will construct inferential statements. For a predefined region, the linear estimator ${\overline{Z}}_{a:b}$ is an unbiased estimator for ${\overline{\theta }}_{a:b}$, and its uncertainty can be assessed using classical methods. Moreover, ${\overline{Z}}_{a:b}$ would be approximately normal, so the sampling distribution of ${\overline{Z}}_{a:b}-{\overline{\theta }}_{a:b}$ would only depend on a single parameter for the variance. In particular, the correlation between measurements would affect the distribution of ${\overline{Z}}_{a:b}$ only through this variance parameter $\mathrm{Var}\left({\overline{\theta }}_{a:b}\right)={{\mathbf{1}}^{\prime }}_{a:b}\sum {\mathbf{1}}_{a:b}$, and can be accounted for in studentized intervals.

In contrast, when the ROI (a, b, +) is detected from the data, ${\overline{Z}}_{a:b}$ becomes biased (Berk et al., 2013, Fithian et al., 2014, Kriegeskorte et al., 2009). We will tend to observe extreme effect sizes compared to the true population mean. If $\left(a,b,+\right)\in {\widehat{\mathcal{B}}}^{+}$, the observed effect size ${\overline{Z}}_{a:b}$ would always be greater than the threshold c. Furthermore, the distribution of ${\overline{Z}}_{a:b}$ would be right-skewed, so normal-based inference methods are no longer valid. Our goal will be to remove these biases and to make inferential statements on the population parameter ${\overline{\theta }}_{a:b}$.

For non-stationary processes, evaluating the observed regions poses an even greater challenge. Due to variation in the dependence structure, it is no longer straightforward to compare different regions found on the same map. The bias and skewness depend not only on a single index of variance, but rather on the local inter-dependence of Z in a neighborhood of a : b. In Figure 3, we show that changes in correlation affect the bias, the spread and the skewness of the conditional distribution.

Figure 3: Effects of selection.

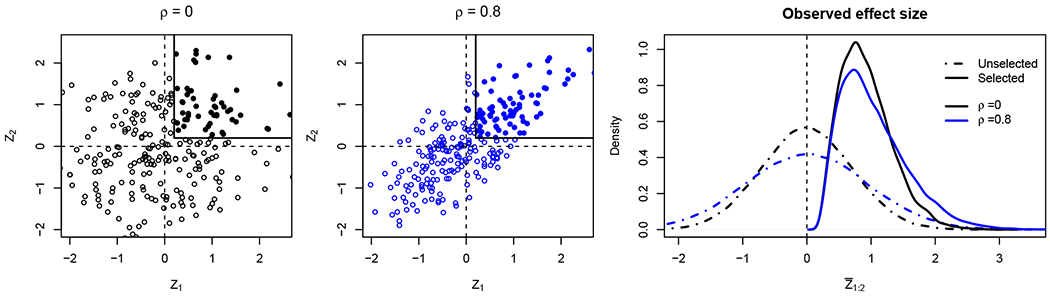
Simulation to illustrate the bias and skewness of selected distributions with different correlation parameters. For D = 2 and c = 0.2, we simulate data from Z = (Z₁, Z₂) ~ N ((0, 0), (1, ρ; ρ, 1)), and separate cases where the region 1 : 2 was selected (full circle). The left plots show the bivariate distributions for ρ = 0 and ρ = 0.8. The right plot displays the density of the observed effect-size ${\overline{Z}}_{a:b}$ for all data (dash-dot) versus the selected data (full). Although ${\overline{\theta }}_{a:b}=0,{\overline{Z}}_{a:b}$ is biased away from 0 in the case of selection. Furthermore, the conditional distribution and the selection bias are different for each correlation regime. Without selection there is no bias and the effect of correlation amounts to rescaling.

2.3. Inference goals

For a set of K detected regions ${\widehat{\mathcal{B}}}^{+}={\left(a_k,b_k,+\right)}_{k=1,\dots ,K}$, we would like to make selection-corrected inferential statements about each ${\overline{\theta }}_{a_k:b_k}$ k = 1,…, K, including:

1. a hypothesis test for $H_1:{\overline{\theta }}_{a_k:b_k}>0$ against the null $H_0:{\overline{\theta }}_{a_k:b_k}\le 0$, and a high-precision p-value for downstream multiplicity corrections;

2. an estimate for ${\overline{\theta }}_{a_k:b_k}$;

3. a confidence interval for ${\overline{\theta }}_{a_k:b_k}$.

We would also like to be able to prune the detected set ${\widehat{\mathcal{B}}}^{+}$ based on the hypotheses tests, while continuing to control for the false coverage statements in the set.

3. Conditional approach to selective inference

Because we are only interested in inference for selected ROIs in ${\widehat{\mathcal{B}}}^{+}$, a correction for the selection procedure is needed. Most such corrections are based on evaluating, ahead of selection, the potential family of inferences. In hypothesis testing, this requires to evaluate all potential ROIs and transform them into a common distribution (e.g. calculate the p-value). Instead, we adapt here a solution proposed for meta-analysis and model selection problems in regression: adjust inference to hold for the conditional distribution of the data given the selection event (Lee et al., 2016, Fithian et al., 2014). First we review the premise of selective inference, and then specify the selection event and selective distribution for region detection.

3.1. Selective inference framework

Recall that $\mathcal{B}$ denotes the set of potential ROIs, and the random set ${\widehat{\mathcal{B}}}^{+}(Z)\subset \mathcal{B}$ denotes the random set of selected ROIs. Assume that for ROI $r=(a,b,+)\in \mathcal{B}$ we associate a null hypothesis $H_0^r$ that will be evaluated if and only if $r\in {\widehat{\mathcal{B}}}^{+}$. A hypothesis test controls for the selective error if it controls for the probability of error given that the test was conducted. Formally, denote by $A_r=A_{\left(a,b,+\right)}$ the event that r was selected for ${\widehat{\mathcal{B}}}^{+}$. Then:

Definition 3 (Control of selective type 1 error, Fithian et al. 2014) The hypothesis test ${\varphi }_r\left(Z\right)\in \left\{0,1\right\}$, which returns 1 if the null is rejected and 0 otherwise, is said to control the selective type 1 error at level α if

$$P_F\left[{\varphi }_r\left(Z\right)=1|A_r\right]\le \alpha \mathit{for\; any}F\in H_0^r.$$ (4)

In a frequentist interpretation, the relative long-term frequency of errors in the tests of r that are carried out should be controlled at level α.

Selective confidence intervals are defined in a similar manner. Denote by F the true distribution of Z, so that F belongs to a model $\mathcal{F}$. Associate with each r a functional η_r(F) of the true distribution of Z, and again let A_r be the event that the confidence interval I_r(Z) for η_r(F) is formed. Then I_r(Z) is a selective 1 − α confidence interval if:

$$P\left[{\eta }_r\left(F\right)\in I_r\left(Z\right)|A_r\right]\ge 1-\alpha \mathrm{for\; any}F\in \mathcal{F}.$$

Correcting the tests and intervals to hold over the selection criteria removes most biases that are associated with hypothesis selection. If no additional selection is performed, the selective tests are not susceptible to the “winner’s curse”, whereby the estimates of the selected parameters tend to display over-optimistic results. If each individual test ϕ_r controls selective error at level a, then the ratio of mean errors to mean selected is also less than α. In a similar manner, the proportion of intervals not covering their parameter (False Coverage Rate, FCR) is controlled at α (Fithian et al., 2014, Weinstein et al., 2013). This strong individual criterion allows us to ignore the complicated dependencies between the selection events; as long as the individual inference for the selected ROIs is selection controlled, error is also controlled over the family.

Note that when the researcher decides to report only a subset of the selected intervals or hypotheses, a secondary multiplicity correction is required. A likely scenario is reporting only selective intervals that do not cover 0 (Benjamini and Yekutieli, 2005). The set of selective intervals behaves like a standard interval family, so usual family-wise or false coverage corrections can be used. See Section 5.

3.2. Selection event in region detection

For region detection, we can identify the selection event A_r = A_(a,b,+)(Z) as a coordinate-wise truncation on coordinates of Z. Selection of (a, b, +) occurs only if all estimates within the region exceed the threshold. These are the internal conditions:

$$Z_a>c,Z_{a+1}>c,\dots ,Z_b>c.$$ (5)

Furthermore, unless Z_a or Z_b are on a boundary, the selection of (a, b, +) further requires external conditions that do not allow the selection of a larger region, meaning:

$$Z_{a-1}\le c,Z_{b+1}\le c.$$ (6)

3.3. Truncated multivariate normal distribution

Assume the observations are distributed approximately as a multivariate normal distribution Z ~ N(Θ, Σ) with Σ known. According to (4), to form selective tests or intervals based on a statistic t_(a,b,+)(Z), we need to characterize the conditional distribution of t_(a,b,+)(Z) given the selection event A_(a,b,+).

Conditioning the multivariate normal vector Z on the selection event results in coordinate-wise truncated multivariate normal (TMN) vector with density

$$f_{Z|A_{a,b};\Theta ,\Sigma }\left(\mathbf{z}\right)=\frac{\exp \left\{{\left(\mathbf{z}-\Theta \right)}^{\prime }{\Sigma }^{-1}\left(\mathbf{z}-\Theta \right)\right\}}{{\int }_{A_{\left(a,b,+\right)}}\exp \left\{{\left(u-\Theta \right)}^{\prime }{\Sigma }^{-1}\left(u-\Theta \right)\right\}d\mathbf{u}}1\left(\mathbf{z}\in A_{\left(a,b,+\right)}\right),$$ (7)

where A_(a,b,+) is seen as a subset of R^D. The TMN distribution has been studied in many contexts, including constructing instrumental variables (Lee, 1981), Bayesian inference (Pakman and Paninski, 2014), and lately post selection inference in regressions (Lee et al., 2016). In contrast to the usual multivariate normal, linear functionals of the truncated normal cannot be described analytically (Horrace, 2005). We will therefore resort to Monte Carlo methods for sampling TMN vectors, and empirically estimate the functional distribution from this sample. Naively, one can sample from this distribution using a rejection sampling algorithm: produce samples from the unconditional multivariate normal density of Z, and reject samples that do not meet the criteria A_(a,b,+). In practice, we will use more efficient samplers; these are further discussed in the Supplementary.

Note that there is no need to sample the full Z; for each ROI, it is sufficient to sample Z at the vicinity of a : b. Coordinates of the parameters or of Z that are outside the selection range a − 1 : b + 1 do not affect the distribution of t_(a,b,+)(Z), as described in the following lemma. Proof is in the supplementary information.

Lemma 1 Let $Z\sim MVN\left(\Theta ,\Sigma \right)$ and $Z^{\prime }\in R^{a-b+3}\sim MVN\left({\Theta }^{\prime },{\Sigma }^{\prime }\right)$, with ${\Theta }^{\prime }={\Theta }_{a-1:b+1}$ and ${\Sigma }^{\prime }={\Sigma }_{a-1:b+1}$. Then

$${\left\{Z|A_{\left(a,b,+\right)})\right\}}_{a-1:b+1}\underset{=}{d}\left\{Z^{\prime }|A_{\left(2,a-b+2,+\right)}\right\}.$$

Therefore, if region (a, b, +) is detected, we model a vector of size b − a + 3. Nevertheless, for consistency we continue indexing the vector with its original coordinates a − 1 : b +1.

4. Inference for the effect size

With a specific region pinned-down, we can now design statistical algorithms that allow inference for the effect size of the region, while accounting for selection. In Section 4.1, we propose a selective test and p-value for the fully specified null hypothesis against a directional-shift alternative. In Section 4.2, we propose a selective confidence interval for $\overline{\theta }$, assuming that the true mean vector belongs to a linear family parameterized by $\overline{\theta }$. We then show theoretical and simulation results on how the choice of linear family affects the behavior of the intervals. Finally, in Section 4.3 we introduce plug-in estimators for several ancillary parameters. With these choices, the conditional distribution for each value of $\overline{\theta }$ is fully specified and sampling based tests can be run in practice. Efficient sampling strategies are discussed in the supplementary information.

Remarks:

1. Throughout the section we focus on a single selected region r = (a, b, +), and use a statistic t(Z) = t_a:b(Z) that is supported on a : b. Per Lemma 1, we can restrict the analysis to the coordinates a − 1 : b + 1. We therefore use the notation:

   $$\begin{array}{ccc}Z=Z_{a-1:b+1},& \Theta ={\Theta }_{a-1:b+1}=\left({\theta }_{a-1},{\Theta }_{a:b},{\theta }_{b+1}\right),& \Sigma ={\Sigma }_{a-1:b+1}\end{array}.$$

2. When analyzing the positively detected regions ${\widehat{\mathcal{B}}}^{+}$, a region a : b is associated with a single selection event (a, b, +). We therefore adopt the shorthand A_a:b = A_(a,b,+). Negatively detected regions would be analyzed separately, in a similar manner.

3. The distribution of the unconditional estimators for θ_a−1, θ_b+1 and Σ = Σ_a−1:b+1 changes less under the selection event compared to the estimators for the internal mean vector Θ_a:b.² In Sections 4.1 and 4.2, we develop the inference procedures assuming these parameters are known, and denote them ${\theta }_{a-1}^{\ast },{\theta }_{b+1}^{\ast }$ and Σ*. In Section 4.3, we suggest plug-in estimators for these parameters. This procedure is validated in simulations in Section 6.

4. Because we are interested primarily in the effects of the internal mean vector Θ_a:b on the distribution of Z and t(Z) = Z_a:b, we use the shorthand

   $$f_{{\Theta }_{a:b}}:=f_{Z|A_{a:b};\left({\theta }_{a-1}^{\ast },{\Theta }_{a:b},{\theta }_{b+1}^{\ast }\right),\Sigma \ast ,}{g}_{t,{\Theta }_{a:b}}:=f_{t\left(Z\right)|A_{a:b};\left({\theta }_{a-1}^{\ast },{\Theta }_{a:b},{\theta }_{b+1}^{\ast }\right),\Sigma \ast }$$

   for the TMN density with mean vector $\Theta =\left({\theta }_{a-1}^{\ast },{\Theta }_{a:b},{\theta }_{b+1}^{\ast }\right)$ and the univariate density of t(Z) = Z ~ f_Θa:b.

4.1. Test for a full mean vector

Consider a vector Z that follows a TMN density f_Θa.b. Suppose we want to test a strong (fully specified) hypothesis $H_0:{\Theta }_{a:b}={\Theta }_{a:b}^0$ for some ${\Theta }_{a:b}^0=\left({\theta }_a^0,\dots ,{\theta }_b^0\right)$ against $H_1:{\Theta }_{a:b}\ge {\Theta }_{a:b}^0$. A case in point is the strong null ${\Theta }_{a:b}^0=\mathbf{0}=\left(0,\dots ,0\right)$. For the test to be powerful against a shift in multiple coordinates, we consider the test

$${\varphi }_{\alpha }\left(Z\right)=1\left(t\left(Z\right)>q\right),$$

where t(Z) is a non-negative linear combination of the a : b coordinates in $Z:t\left(Z\right)=t_{a:b}\left(Z\right)={\eta }^{\prime }{Z}_{a:b}$. By (4), q should be set to be the 1 − α quantile of $\left\{t\left(Z\right)|A_{a:b}\right\}$ under the null so the test will hold at a selective level of 1 − α. This conditional null distribution is fully specified given ${\theta }_{a-1}^{\ast },{\theta }_{b+1}^{\ast }$, and ${\Sigma }^{\ast }$,

$$\left\{t\left(Z\right)|A_{a:b}\right\}\stackrel{H_0}{\sim }{g}_{t,{\Theta }_{a:b}^0}.$$

and we can denote the 1 − α quantile of $g_{t,{\Theta }_{a:b}^0}$ by q_1−α. However, because the analytic form of $g_{t,{\Theta }_{a:b}^0}$ is unknown, q_1−α cannot be directly obtained.

Instead, q_1−α can be estimated with Monte Carlo methods. We can sample from $f_{{\Theta }_{a:b}^0}$, and use these samples to empirically estimate the 1 − α quantile of $g_{t,{\Theta }_{a:b}^0}$, or q_1−α. Explicitly, the algorithm would:

1. Use a TMN sampler to generate a Monte Carlo sample from $H_0{\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\sim f_{{\Theta }_{a:b}^0}$.

2. Compute the statistic for each example t₁,…, t_N, t_i = t(z_i).

3. Estimate q_1−α under H₀ by taking the ⌊N(1 − α)⌋ order statistic of t_i

   $${\widehat{q}}_{1-\alpha }^{\left(N\right)}:=t_{\left(\lfloor N\left(1-\alpha \right)\rfloor \right)}$$

Theorem 1 Consider the test ϕ_α(Z) for $H_0:{\Theta }_{a:b}={\Theta }_{a:b}^0$ against $H_1:{\Theta }_{a:b}\ge {\Theta }_{a:b}^0$, which is conducted only if (a, b, +) is selected. Given an iid sample ${\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\sim f_{{\Theta }_{a:b}^0}$, define $\widehat{q}{\left({\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\right)}_{1-\alpha }=t_{\left(\lfloor N\left(1-\alpha \right)\rfloor \right)}$. Then the selective type 1 error of the test

$${\varphi }_{\alpha }\left(Z\right)=1\left(t\left(Z\right)>{\widehat{q}}_{1-\alpha }^{\left(N\right)}\right)$$

converges to α as N → ∞.

Comments:

• z₁,…, z_N are in R^b−a+3, whereas Θ and Z can be larger.

• The sample z₁,…, z_N does not have to be iid, or exactly from $f_{{\Theta }_{a:b}^0}$. We only need $\widehat{q}{\left({\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\right)}_{1-\alpha }$ to converge to $q_{1-\alpha }=q_{1-\alpha }(g_{{\Theta }_{a:b}^0;t})$ as N increases.

This approach can be extended to produce p-value estimates and two sided tests. The estimated p-value of an observed vector z_obs is

$$p-\widehat{\mathit{va}}\mathit{lue}={\widehat{P}}_{H_0}\left(t\left(Z\right)>t\left({\mathbf{z}}_{obs}\right)\right)=\frac{1}{N}\sum 1\left(t_i>t\left({\mathbf{z}}_{obs}\right)\right).$$

A two sided test ${\varphi }_{2\alpha }^{\prime }$ can be constructed by setting

$${\varphi }_{2\alpha }^{\prime }\left(Z\right)=1(t\left(Z\right)<{\widehat{q}}_{\alpha }^{\left(N\right)}\mathrm{or}t\left(Z\right)>{\widehat{q}}_{1-\alpha }^{\left(N\right)})$$

where ${\widehat{q}}_{\alpha }^{\left(N\right)},{\widehat{q}}_{1-\alpha }^{\left(N\right)}$ are Monte Carlo estimates for $q_{\alpha },q_{1-\alpha }$.

4.2. A single parameter family for the mean

Confidence intervals for $\overline{\theta }=\frac{1}{b-a+1}{\sum }_{j=a}^b{\theta }_j$ require more care than the null tests, because even after specifying $\overline{\theta }$ the model has b − a additional degrees of freedom. Approaches to non-parametric inference include plugging-in the maximal-likelihood values of the ancillary parameters for every value of $\overline{\theta }$ (profile-likelihood, see review in DiCiccio and Romano, 1988), or conditioning on the ancillary directions in the data as in Lockhart et al. (2014), Lee et al. (2016). We take an approach similar to the least favorable one-dimensional exponential family (Efron, 1985), in proposing a linear trajectory from $\overline{\theta }$ to the mean vector Θ_a:b. Figure 4 shows the main steps of our approach.

Figure 4: Pin-down inference algorithm.

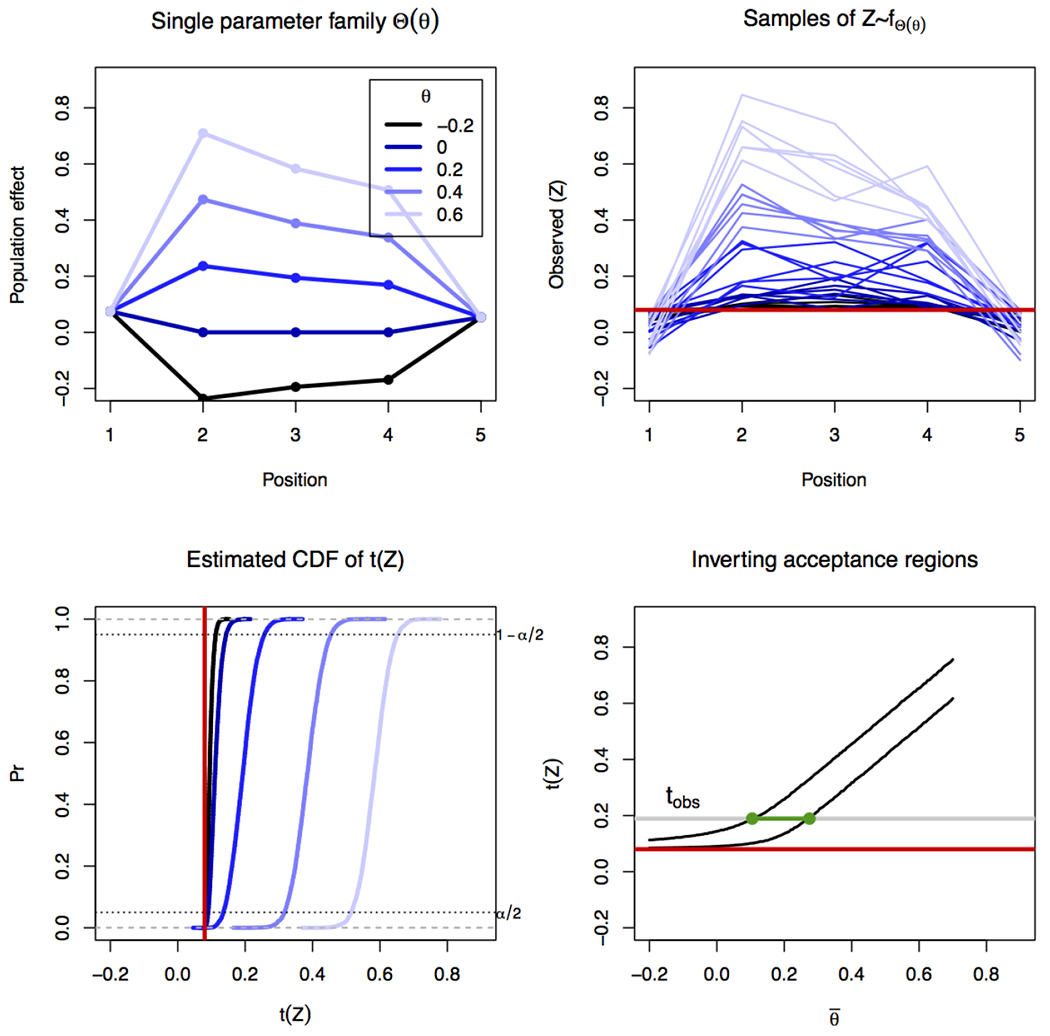
For the region 2 : 4 the plots show steps in the inference. The top left displays the unconditional mean vectors Θ_s(θ) for 5 values of θ. The profile used is s_Σ. The top right panel displays 6 examples from the Monte Carlo sample of the conditional density $f_{{\Theta }_s\left(\theta \right)}=f_{Z|A;\Theta \left(\theta \right),\Sigma }$, color coded by the value of θ. Empirical CDFs are estimated for each value of θ (bottom left), and $\alpha /2,1-\alpha /2$ quantiles extracted. The acceptance regions are inverted (bottom right) based on the observed statistic (t(z_obs)) to generate a two-sided 1 − α interval. Plots based on a simulated region with a true mean effect of $\overline{\theta }=0.14$ and an observed effect of $t\left({\mathbf{z}}_{obs}\right)={\overline{\mathbf{z}}}_{a:b}\approx 0.19$. The true (known) covariance of Z is used.

Conceptually, we form the confidence interval by inverting a set of tests for the average parameter $\overline{\theta }$. Recall that a random interval I(Z) is a 1 − 2α level confidence interval for $\overline{\theta }$ if $P_{\Theta }\left(\overline{\theta }\left(\Theta \right)\in I\left(Z\right)\right)\ge 1-2\alpha$ for any Θ. Given a family of 2α level two-sided tests for $\overline{\theta }=\theta$, the set of non-rejected parameter-values forms a 1 − 2α confidence set (Inversion lemma, Lehmann and Romano, 2005).

The family of tests we use are based on a one-dimensional sub-family of the TMN, produced by the linear (or affine) mapping ${\Theta }_s:\theta \mapsto \theta \cdot s$. The vector $\mathbf{s}=\left(s_a,\dots ,s_b\right)\in R_{+}^{b-a+1}$ represents the non-negative profile (shape) of the mean, which is scaled linearly by θ. For now we will assume s is known, though in practice the user needs to specify a profile s; in Section 4.2.1 we offer several generic suggestions. For identifiability, we set $\frac{1}{b-a+1}\sum s_j=1$. For any value of θ ∈ R, we write $f_{{\Theta }_s\left(\theta \right)}$ for the conditional density associated with the internal mean vector Θ_s(θ) = θ · s:

$$f_{{\Theta }_{\text{s}}\left(\theta \right)}\left(\mathbf{z}\right):=f_{Z|A_{a:b};\left({\theta }_{a-1}^{\ast },\theta \cdot \mathbf{s},{\theta }_{b+1}^{\ast }\right),\Sigma \ast }\left(\mathbf{z}\right).$$

At θ = 0, we get the strong null hypothesis ${\Theta }_{a:b}=\mathbf{0}$. For other values of θ we get different TMN distributions. Note that the condition $\frac{1}{b-a+1}\Sigma s_j=1$ ascertains that $\overline{\theta }\left({\Theta }_s\left(\theta \right)\right)=\theta$, because ${\Theta }_s\left(\theta \right)=\theta \cdot s$, and $\overline{\theta }\left({\Theta }_s\left(\theta \right)\right)=\frac{1}{b-a+1}{\sum }_{j=a}^b\theta s_j=\theta \frac{1}{b-a+1}\Sigma s_j$. Notationally, let $q_{1-\alpha }\left(\theta \right)$ denote the 1 − α quantile of $g_{t,{\Theta }_s\left(\theta \right)}$.

We derive confidence intervals and point estimators for $\overline{\Theta }$ based on the one-parameter family $f_{{\Theta }_s\left(\theta \right)}$. Each value of $\overline{\theta }=\theta$ identifies a specific mean vector (panel A), and a conditional distribution for the vector Z and the statistic t(Z) (panels B, C). Therefore, for each value of θ, we can construct the two-sided test ${\varphi }_{\theta ,2\alpha }^{\prime }\left(Z\right)$ by following the recipe in 4.1. That is, we can sample from $f_{{\Theta }_s\left(\theta \right)}$, estimate empirically the distribution and quantiles of t(Z) under this null, and reject if not ${\widehat{q}}_{1-\alpha }\left(\theta \right)>t\left({\mathbf{z}}_{obs}\right)>{\widehat{q}}_{\alpha }\left(\theta \right)$. By repeating this process for a fine grid of θ values, we can invert the sequence of tests (panel D) and get a high-resolution confidence interval I.

More generally, for a given Z vector we define the quantities

$$\begin{array}{cc}l\left(Z\right)=\sup \left\{{\theta }_l:t\left(Z\right)>\underset{\theta <{\theta }_l}{\sup }\left\{q_{1-\alpha }\left(\theta \right)\right\}\right\},& u\left(Z\right)=\inf \left\{{\theta }_u:t\left(Z\right)<\underset{\theta <{\theta }_u}{\inf }\left\{q_{\alpha }\left(\theta \right)\right\}\right\},\end{array}$$ (9)

and use a truncated MVN sampler to form consistent estimators for these quantities. If the true ${\Theta }_{a:b}$ vector is a member of the one parameter family ${\left\{{\Theta }_{a:b}\left(\theta \right)\right\}}_{\theta \in R}={\left\{\theta \cdot s\right\}}_{\theta \in R}$, this procedure forms intervals that converge to the valid selective confidence intervals.

Theorem 2 Let $Z\sim MVN\left(\Theta ,\Sigma \right)$, where ${\Theta }_{a:b}=\overline{\theta }·\mathbf{s}$ for a pre-specified profile vector s and an unknown mean parameter $\overline{\theta }$. A confidence interval for $\overline{\theta }$ is estimated if A_a:b occurs. For a Monte Carlo sample ${\mathbf{z}}_1,\dots ,{\mathbf{z}}_N$, let $l^{\left(N\right)}\left(Z\right)=l\left({\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\right)$ and $u^{\left(N\right)}\left(Z\right)=u\left({\mathbf{z}}_1,\dots ,{\mathbf{z}}_N\right)$ be consistent estimators of l(Z) and u(Z), as defined in (9).

Then the selective coverage of the interval $I^{\left(N\right)}\left(Z\right)=\left(l{\left(Z\right)}^{\left(N\right)},u{\left(Z\right)}^{\left(N\right)}\right)$ converges to at least 1 − 2 · α

$$\underset{N\to \infty }{\lim }P\left(\overline{\theta }\in I^{\left(N\right)}\left(Z\right)|A_{a:b}\right)\ge 1-2\cdot \alpha$$

Comments:

• Due to the linear structure of the single parameter family, consistent estimators of u(Z) and l(Z) can be computed from a single Monte Carlo sample. Details are in the supplementary information.

• If the quantile functions q_α(·) are increasing in θ then the estimation of u(Z) and l(Z) can be made more robust to noise. In the next section we discuss conditions that assure such monotonicity. In simulations, for θ ≥ 0, we have yet to encounter non-monotone cases.

• A point estimator for $\overline{\theta }$ can be derived from the same procedure:

  $$\widehat{\theta }=\theta s.t.{\mathbf{P}}_{\theta }\left(t\left(Z\right)>t\left({\mathbf{z}}_{obs}\right)\right)=\mathrm{0.5.}$$

  This corresponds to the intersection of the median function ${\widehat{q}}_{0.5}\left(\theta \right)$ with t(z_obs), and does not require extra calculations when computing intervals.

Applying Theorems 1 and 2 to data requires making several assumptions. First, we do not know the true shape of the profile s, so we need to assume its structure. In the next subsection we show that the interval is somewhat robust to different choices of profile s and discuss some theoretical properties related to this choice. Second, specific values for the unknown parameters θ_a−1, θ_b+1 and Σ are required to generate the confidence intervals. We propose plug-in estimators for θ_a−1, θ_b+1 and Σ in 4.3. Finally, we need to assume that Z can locally be well approximated as a MVN, which will depend on the original distribution of the data and the number of samples (n) used for estimating Z.

4.2.1. Choice of profile and monotonicity

For the statistic ${\overline{Z}}_{a:b}=\frac{1}{b-a+1}{\left(1,\dots ,1\right)}^{\prime }{Z}_{a:b}$, we propose to use one of the following profiles:

1. The uniform profile s_u induces a uniform increase in each coordinate

   $${\mathbf{s}}_u=\left(1,\dots ,1\right).$$ (10)
2. The natural profile s_Σ induces an increase in each coordinate proportional to the sum of the columns in Σ

   $${\mathbf{s}}_{\Sigma }=\left(b-a+1\right)\cdot \frac{{\left(1,\dots ,1\right)}^{\prime }{\Sigma }_{a:b}}{{\left(1,\dots ,1\right)}^{\prime }{\Sigma }_{a:b}\left(1,\dots ,1\right)}.$$ (11)

We call s_Σ the natural profile because for Z_a:b ~ T M N(θ_sΣ, Σ), ${\overline{Z}}_{a:b}$ is the natural statistic³. Due to this relation, using s_Σ will admit monotone quantile functions (see Lemma 2). In practice, the methods appear not sensitive to a choice between these two profiles, as seen in Figure 5, but sampling for larger regions sometimes converges better for the uniform profile. We discuss the choice of the profile in 4.2.1; some readers may prefer to skip directly to 4.3.

Figure 5: Comparison of profiles vectors and covariances.

Conditional mean of $t\left(Z\right)={\overline{Z}}_{1:3}$ as a function of θ for different covariances (panels) and profiles (colors). Threshold is c = 1. In all panels, we use the following profiles: s_Σ ∝ (1, 1, 1)′Σ in black, s_u = (1, 1, 1) in red, s₂ = (1.5, 0, 1.5) in blue, and s₁ = (3, 0, 0) in grey. In the top-left and bottom-right panels, s_u ≡ s_Σ). All covariances have unit variance, and the number of correlated variables decrease from Σ_A (ρ = 0.4 between every pair), through Σ_B (as before but ρ₁₃ = 0), Σ_C (ρ₁₂ = 0) and uncorrelated Σ_D. We observe method is not very sensitive to small differences in the profile, as s_Σ, s_u give almost identical curves for Σ_B and Σ_C. The figure shows that although s_Σ ensures E_Θs(θ)[t(Z)] strictly increases with θ (monotonicity, Lemma 2), monotonicity is not guaranteed for s₂ or s₁. For Σ_C, s₁ satisfies the conditions of Lemma 3 and displays monotonicity, whereas s₂ does not. When the covariance is iid, any non-negative profile satisfies Lemma 3. Under all covariances, the curves for s₁, s₂ are greater than s_Σ; this is a potential source for coverage error if s_Σ is used.

Intuitively, we would expect functionals of the distribution of t(Z) to increase as Θ_s(θ) increases. Monotonicity is an important conceptual prerequisite for the method: measuring θ using t(Z) makes sense only if t(Z) indeed increases with θ. Furthermore, monotonicity guarantees that the acceptance region of the family of tests would be an interval, simplifying the parameter searches. Indeed, for a non-truncated multivariate normal with mean θ · s and s positive, the distribution of t(Z) is monotone increasing in every coordinate of Θ (and does not depend s).

Unfortunately, after conditioning, monotonicity is no longer guaranteed. In Figure 5 we show some examples where E_Θs(θ)[t(Z)] does not increase θ ⁴. We therefore introduce two lemmas discussing conditions that guarantee monotonicity. Lemma 2 we show that for every non-negative covariance, using the profile s_Σ ∝ (1,…, 1)′Σ ensures that E_Θs(θ)]t(Z)] increases in θ. This result is tailored for the statistic t(Z) ∝ (1,…, 1)′. In Lemma 3, we identify a subset of the non-negative covariances and, for each covariance, a set of profiles that ensure monotonicity for any non-negative statistic. Examples are shown in Figure 5. Proofs are in the supplementary information.

Denote by $g_{\theta ;s,t}$ the family of densities $\left\{t\left(Z\right)|A\right\}$ for t(Z) ∝ (1,…, 1)′Z parametrized by θ where $Z\sim N\left(\theta \cdot s,\Sigma \right)$, and let s_Σ as in (11). The following lemma proves that for s = s_Σ and $t={\left(1,\dots ,1\right)}^{\prime }Z,g_{\theta ,\mathbf{s},t}$ is a monotone likelihood ratio family in θ.

• Lemma 2 1. $g_{\theta ,{\mathbf{s}}_{\Sigma },t}$ is a monotone likelihood ratio family.

• 2. EΘ_sΣ [t(Z)] is an increasing function of θ.

• 3. The confidence set for θ obtained by inverting two sided tests is an interval.

(1) is a consequence of identifying t(Z) as the natural statistic of the family (see Fithian et al., 2014). (2,3) are direct consequences of the monotone likelihood ratio family property.

The lemma further allows a classical approach to the problem of choosing the statistic after the model. If we choose a specific deviation from 0, e.g. setting the profile to be uniform s_u = (1,…, 1)′, then the most efficient statistic would be the exponential-family natural statistic $t^{\ast }\left(Z\right)\propto {\mathbf{s}}_u^{\prime }{\Sigma }^{-1}$. Lemma 1 implies that t*(Z) would be monotone in θ.

A stronger result of monotonicity of g_θ;s,t can be derived from properties of the multivariate distribution f_Θ if the covariance of Z_a:b belongs to a restrictive class of positive-covariance matrices.

Definition 4 An M-matrix is a positive-definite matrix in which all off-diagonal elements are non-positive.

Lemma 3 Suppose Σ⁻¹ is an M-matrix, and the profile s can be written as a non-negative sum of columns of Σ, then g_θ;s,t is a monotone likelihood ratio family.

The condition on Z is sufficient to show a strong enough association condition on Z (second-order multivariate total positivity property, MTP-2) that continues to hold after conditioning. The lemma is based on theory developed by Rinott and Scarsini (2006).

4.3. Estimating external means and covariance

For the distribution $f_{\Theta }$ to be fully specified, we need to set values for the external mean parameters ${\theta }_{a-1},{\theta }_{b+1}$ and for the covariance Σ.

4.3.1. External means

We propose plugging-in the unconditional estimators for θ_a−1, θ_b+1 based on the observed values Z_a−1, Z_b+1:

$$\begin{array}{cc}{\widehat{\theta }}_{a-1}=Z_{a-1},& {\widehat{\theta }}_{b+1}=Z_{b+1}\end{array}.$$

Without selection, these would be consistent unbiased estimators for the respective parameters. Note that after selection, these estimators are not affected as strongly as the parameters of the interior mean: $\left\{Z_i<c\right\}$ is a high-probability event for typical θ_i, and therefore $\left\{Z_i|Z_i<c\right\}$ has relatively little bias. (This is in contrast to $\left\{Z_i\ge c\right\}$ which is a rare event, and so the bias of $\left\{{\widehat{\theta }}_i|Z_i\ge c\right\}$ can be considerable).

Alternatives, such as assuming ${\theta }_{a-1}={\theta }_{b+1}=0$ or scaling the external mean with θ, sometimes lead to bad fit or otherwise ill behaved intervals. This problem is particularly acute when the variance of Z_a−1 and Z_b+1 are small and when Z_a−1 or Z_b+1 are strongly correlated with (Z_a, …, Z_b).

To summarize, an affine model for the mean is:

$$\begin{array}{cc}{\Theta }_{a-1:b+1}\left(\theta \right)={\left(Z_{a-1},0,\dots ,0,Z_{b+1}\right)}^{\prime }+\theta \cdot {\tilde{\mathbf{s}}}_{\Sigma },& {\tilde{\mathbf{s}}}_{\Sigma }={\left(0,{\mathbf{s}}_{\Sigma },0\right)}^{\prime }\end{array}.$$

4.3.2. Estimated covariance

The unbiased estimator $\widehat{\Sigma }$ is a natural candidate for estimating Σ, because it is independent of Z and therefore its distribution is unchanged by selection.

When the number of samples is small, the estimation may be sensitive to the covariance that is used. We therefore propose using an inflated estimate of the sample covariance in order to reduce the probability of underestimating the variance of individual sites and of overestimating the correlation between internal and external variables.

Call $\widehat{\Sigma }$ the sample estimator for Cov(Z). Then the 1 + λ diagonally inflated covariance ${\widehat{\Sigma }}^{\lambda }$ is defined as follows:

$${\widehat{\Sigma }}_{j{j}^{\prime }}^{\lambda }=\{\begin{array}{ll}\left(1+\lambda \right){\widehat{\Sigma }}_{j{j}^{\prime }}& \hfill \mathrm{if}j=j^{\prime }\hfill \\ {\widehat{\Sigma }}_{j{j}^{\prime }}& otherwise.\end{array}$$ (12)

As a heuristic, we can select λ so that ${\widehat{\Sigma }}_{jj}^{\lambda }$ approximates a fixed quantile of the distribution of ${\widehat{\Sigma }}_{jj}$. For example, if ${\widehat{\Sigma }}_{jj}\stackrel{.}{\sim }{\Sigma }_{jj}\cdot {\chi }_d^2/d$ for d degrees of freedom, we can set λ so that $1+\lambda =\mathit{quantile}({\chi }_d^2,0.75)$, giving an approximate 75% quantile.

5. Controlling false coverage on the set of intervals

When the threshold is selected liberally, the result of running the threshold-and-merge algorithm is a large set of detected regions. If only a subset of these regions is reported, this selection could lead to low coverage properties over the selected set. In our framework, because the confidence intervals are conditioned on the initial selection, the problem does not arise (Fithian et al., 2014). However, if we use the new p-values (or intervals) to screen regions that are not separated from 0, a secondary adjustment is needed.

Applying an iterative algorithm similar to Benjamini and Yekutieli (2005) can control FCR for the pruned interval set at a specified level. Formally, if the test statistics are dependent, At each iteration, the set of intervals is pruned so that only intervals separated from 0 are kept in the set. Then, the BH procedure is run on the subset of p-values, selecting the q-value threshold that controls the false discovery rate at α. Selective 1 − q confidence would control the rate of false coverage on the new set. If any of the intervals cover 0 after this inflation, the set can be further pruned, and another BH algorithm run on the smaller set. Computationally, note that re-estimating the intervals does not require resampling. Here is a review of the full algorithm:

1. Run a threshold-and-cluster algorithm to generate the bump candidates.

2. For each bump, test the selective hypothesis that the effect is greater than 0.

3. Find the p-value for $H_0:{\overline{\theta }}_{a:b}\le 0$.

4. Run the BH procedure on the (sorted) p-value list. Find a value q that controls the FDR at level α. Filter the list of regions.

5. For region that passed, re-estimate selective intervals with coverage 1 − q

Technically, FCR control by this procedure requires an additional assumption on the joint distribution of the conditional test-statistics. The algorithm is valid under independence of the region test-statistics; furthermore, if the test statistics are dependent, it is sufficient that they adhere to positive regression dependence over subsets (PRDS), because selection is one-sided (Benjamini and Yekutieli, 2005).

6. Simulation

We conducted three simulation experiments to verify that the coverage properties of the confidence intervals are robust, and to investigate the power of our method. Data for all experiments sets followed the two-group model. Briefly, in the first experiment we sampled Normal vectors and selected for the same region repeatedly (D=5, b-a+1=3, e.g. Figure 4). We varied the number of samples, covariance shape, effect size, and the shape of the mean vector. We show results for both known and estimated covariance. Note that increasing the number of samples both reduces the variance of the Z vector, as well as improves the estimation of the covariance (scaling the variances is equivalent to inverse scaling of both the threshold and the mean).

In the second experiment, both the length and the shape of the selected region were randomly generated. We sampled la onger (D=50) non-stationary processes with a random non-null between-group difference vector. In each run of the process, we randomly selected one of the detected ROIs and estimated a confidence interval for that region. We sampled normal and logistic-transformed normal vectors. We chose parameters similar to the DNA-methylation data.

In a third experiment, we sampled regions of different sizes to investigate the effect of region size on the probability of detection. We expect the power to increase and coverage to stay constant as region-size increases. We compared the power of our method to the pivot estimator. Detailed description of the three simulation settings are found in the Supplementary.

Summary of the results are in Table 1 and Figures 6 and 7. For the known covariance, coverage rates are approximately nominally correct under both covariance regimes, for different samples sizes and effect sizes. For the estimated covariance, coverage is less than the nominal rate, but this error decreases as the number of samples increases. Note that although for n = 16 with estimated Σ the two-sided coverage is almost correct, for θ = 0 the lower bound is too liberal. The results are similar when the process is a continuous Normal – correct intervals for the known covariance liberal results for the estimated covariance and small samples. This is indicative that the misspecified mean is less a problem than the estimation of Σ. For the logistic-transformed process, intervals are found to be conservative, perhaps due to the short tails. Figure 6 (right) plots the power of the selective intervals, as the probability of not covering 0 with increasing true effects θ. We calculate power only for the known Σ, for which coverage is accurate.

Table 1:

Coverage of nominal α = 0.9 confidence interval for fixed regions (experiment 1) and for continuous-processes (experiment 2). Experiment 1 values are based on averages of 20 values of θ (displayed on left of Figure 6). Each value was repeated 250 times, for a total of 5000. Experiment 2 values were based on 1000 repeats. Variance in estimators decreases linearly with number of samples, as well as accuracy of estimating Σ in the unknown case.

		Σ Known			Estimated
		na = 16	8	4	16	8	4
Experiment 1	Independent	.916	.908	.908	.903	.867	.770
	Correlated	.913	.902	.907	.896	.870	.794
Experiment 2	Normal	.914	.912	.904	.921	.925	.900
	Logistic	.941	.937	.922	.951	.934	.885

Figure 6: Coverage and Power (Experiment 1):

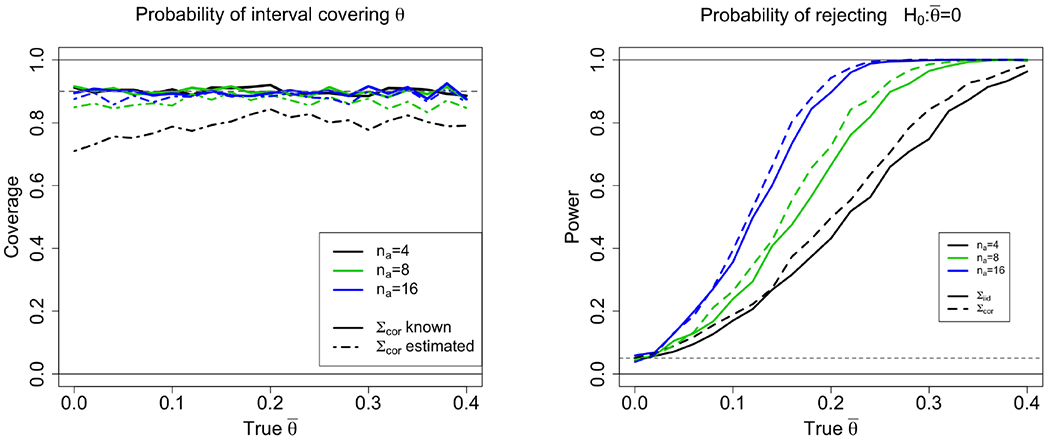
On left, coverage probability of nominal α = 0.9 confidence intervals for different true effect size $\overline{\theta }$ (x-axis), group size (color), and estimation of covariance (line-type). Group size affects the variance of Z and, if Σ is estimated, the samples available for this estimation. We see that coverage is approximately correct for the known covariance and for estimated covariance with n_a = 16. On right, power is plotted for different true effect size (x-axis), group size (color), and known covariance type (Σ_iid or Σ_cor). Power is computed as the proportion of intervals not covering the null for non-zero true effects. Results for estimated Σ not shown, because coverage in-exact for small n’s. Each point averages 1000 runs. See details in the supplementary information.

Figure 7: Increasing Regions (Experiment 3):

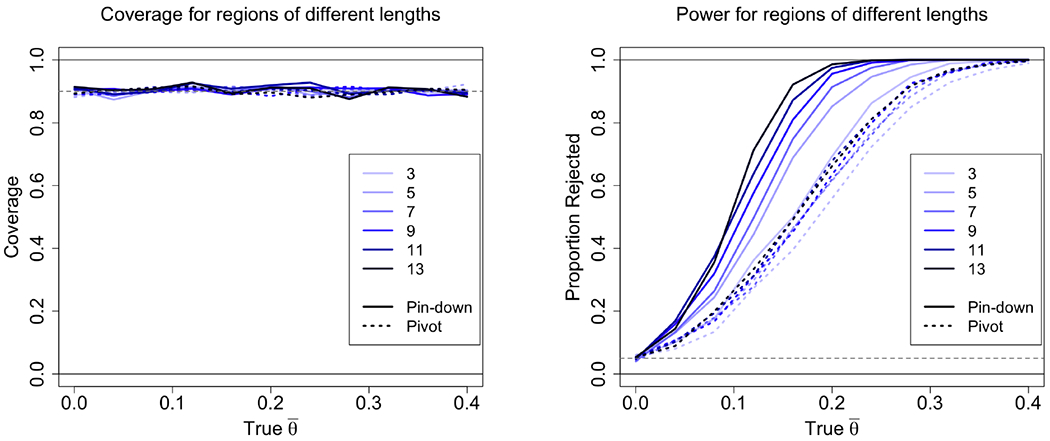
Coverage (left) and power (right) is plotted for regions of different lengths (line color) and true effect size (x-axis). The pin-down conditional interval (continuous line) is compared to the pivot-based conditional interval of Lee et al. (2016) (dotted line). Power increases with region size. The increase is much more pronounced in the pin down algorithm, whereas for the pivot there is little increase in coverage with growing region size. Coverage for both algorithms is similar to the nominal rate. Each point averages 1000 runs.

For the growing region experiment, we compared the results of the algorithm to the pivot-based conditional inference described in Lee et al (Figure 7). We see that the both methods give correct coverage. However, for the pivot method, power increases much slower as a function of region size compared to the our estimator.

7. DNA methylation data

Region detection and inference was run on 36 DNA-methylation samples from two healthy human tissue types (D ≈ 450000). We ran two analyses of the data:

• The two-tissue analysis compares 19 lung samples with 17 colon samples. We expect many true differences between the two groups.

• For the one-tissue data, we randomly partitioned the 19 lung samples into two groups of 9 and 10 samples. Regions found on here are considered false-positive.

For each dataset, we thresholded the estimated difference to produce a list of candidate regions. We estimated selective p-values and 90% intervals for each region. We then used multiplicity corrections to reevaluate the set of regions (see Section 5). For comparison, we computed non-parametric p-values by permuting the sample labels, and corrected for family-wise error (Jaffe et al., 2012b). More details are found in supplementary information.

Results show that the pin-down method has greater sensitivity than the permutation method. At the same time, it hardly reduces specificity. See Table 2 for results summary. Examples for regions detected by selective inference and not by permutation FWE are shown in Figure 8. For the one tissue design, the nominal coverage of the intervals is conservative (3% of regions are rejected at the 0.05 level). No region is significant after multiplicity corrections with either method. If no covariance inflation is used (λ = 0), 5.5% of the regions are rejected at the 0.05 level, and 11 regions pass the BH procedure.

Table 2:

Number of regions detected on the two-tissue and one-tissue designs, for one-sided α/2 = 0.05 tests. Data in the one-tissue were split randomly into two groups, so we consider all detections to be false positives. Estimated covariance ${\widehat{\Sigma }}^{\lambda }$ were used with λ = 0.15.

		Permutation	Pin-down
	Regions found	$\mathit{FW\; E}<\frac{\alpha }{2}$	$\mathit{p}<\frac{\alpha }{2}$	$p_{\mathit{Bon\; f}}<\frac{\alpha }{2}$	$p_{\mathit{BH}}<\frac{\alpha }{2}$
Two tissue	58298	61 (.07%)	51598 (89%)	36513 (63%)	51394 (88%)
One tissue	1578	0	49 (3%)	0	0

Figure 8: Examples undetected by non-parametrics.

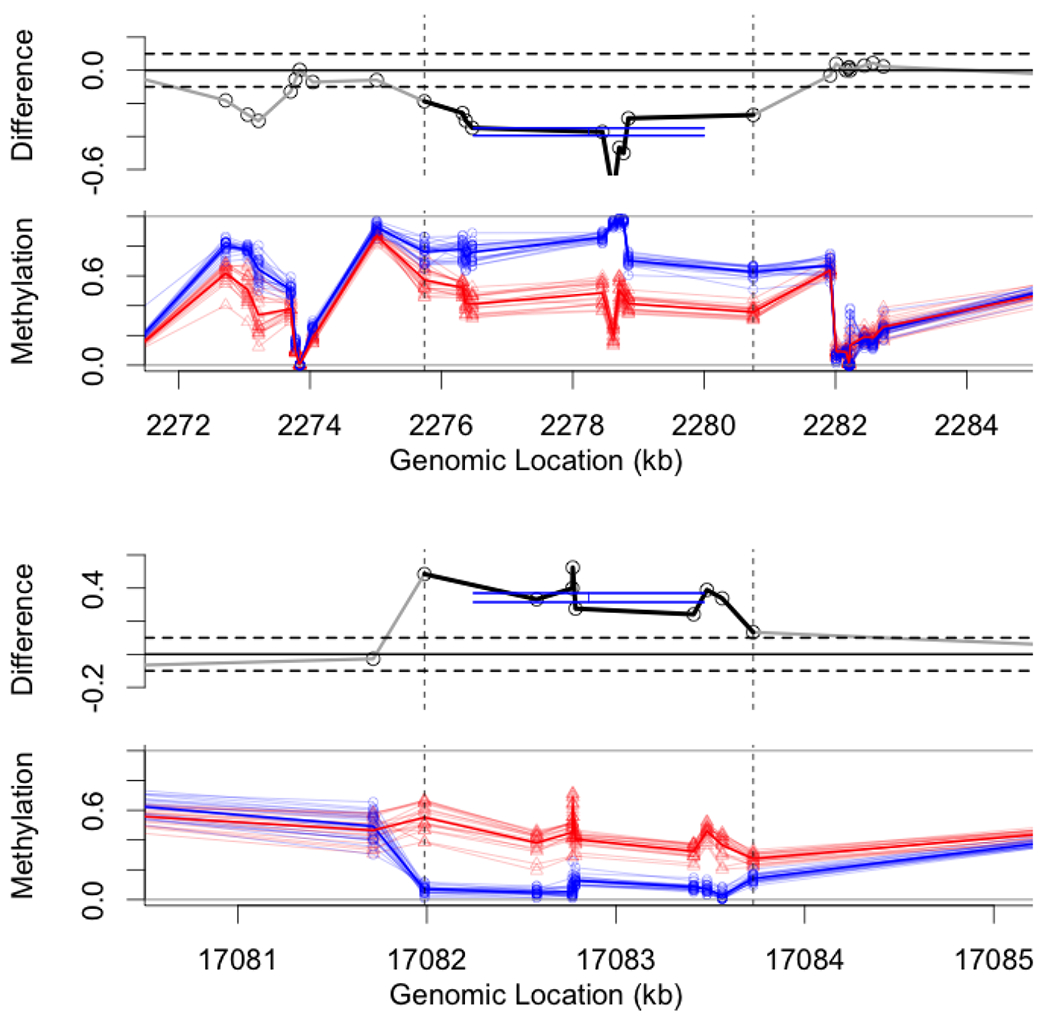
Two example regions that are detected using our method, but not detected using the non-parametric FWE approach at α = 0.05 level. On left is a 10-site region from chromosome 19: we estimate $\widehat{\theta }=0.375$ with interval Î = [0.35, 0.4] and p_BH < 10⁻¹⁰; non-parametric FWE was 0.06. On right is a 9-site region from chromosome 22: we estimate $\widehat{\theta }=0.345$ with interval Î = [0.32, 0.375] and p_BH < 10⁻¹⁰; non-parametric FWE was 0.1. Data is from TCGA; see details in text.

There are several factors that explain this difference in power. First, familywise error controlling methods can be very conservative compared to FDR controlling methods when many hypotheses are rejected. Second, non-parametric p-values tend to be larger than parametric ones. Finally, in our case, a region is rejected by the permutation method only if it exceeds the strongest region of 95% of permutations. Therefore, regions with relatively weak signal can be masked by traces of (true positive) regions with large signal or (false-positive) regions with high variance. Note that the longer the original process, the more likely a high-variance region will exceed true-positive regions.

8. Discussion

We present a method of generating selection corrected p-values, estimates and confidence intervals for the effect size of individual regions detected from the same data. The method allows for non-stationary individual processes, as each region is evaluated according to its own covariance. For a two group design under non-negative correlation, the coverage of the tests and lower-bounds of the intervals hold at the nominal level when the covariance is known, or for moderate sample-sizes (group size ≥ 16). For genomic data sets, we show that the method has considerably better power than non-parametric alternatives, and the resulting intervals are often short enough to aid decision making.

Setting the threshold

The threshold c has considerable sway over the size and the number of regions detected. Setting c too high “conditions away” all the information at the selection stage, and too little information is left for the inference. Setting c threshold too low allows many regions to pass, requiring stronger multiplicity corrections to control the family-wise error rates. This tradeoff should be further explored. Furthermore, the assumption that c is determined before the analysis can probably be relaxed, as the threshold is weakly dependent on any individual region. For example, the threshold for each chromosome can be set using data from other chromosomes. Robust functions of the data such as the median or non-extremal quantiles may also be used for adaptive thresholding (Weinstein et al., 2013).

Smoothing

The threshold-and-merge algorithm is sensitive to high-frequency noise that can split regions. Smoothing the data can reduce these unwanted partitions, as well as highlight lower frequency variations that are previously hidden under the noise. The expected size for regions of interest, and subsequent smoothing bandwidth, typically depend on both the scientific questions as well as the distributional properties of the measurement noise. For methylation, for example, different size-scales of DMRs are found between tumors, compared to DMRs between healthy tissues (Hansen et al., 2012, Knijnenburg et al., 2014). Our method currently allows for a single smoothing procedure as part of the preprocessing. The window size will have a large effect on the results, but will need to be decided based mostly on the biology of interest.

Region size information

Information regarding the size of the detected region is discarded when we condition on the region. Instead, inference is based only on the vertical distance between the observations and the threshold: if observations are sufficiently greater than the threshold, the p-value will be small. Discarding the size of the region is perhaps counterintuitive. Hypothetically, we may detect a large enough region (with P(A_a:b) small enough) to be significant regardless of the effects of selection, but still get selective p-value that are large. In practice, however, this is unlikely; both the probability of the event A_a:b and the selective p-value become smaller as the size of the unconditional mean vector (Θ_a:b) increases. Long regions would usually be detected because the mean was larger than 0 in most of the region. This would usually also manifest in smaller p-values and less uncertainty in the confidence interval. We may be able to recover the probability of selection from the Monte Carlo sample. It is tempting to reintegrate the probability of selection into the inference: under a strong null (Θ_a:b = 0), the likelihood of the data is the product of these two probabilities. The caveat, of course, is that the p-values associated with region size – P(A_a:b) – are not corrected for selection. Hence, we are back to the problem we wanted to initially solve.

Difference between our approach and pivot-based methods

The methods we propose are different from exact pivot-based inference (Lockhart et al., 2014, Lee et al., 2016). In those methods, the statistic t(Z) is conditioned not only on the selection event, but also on the subspace orthogonal to t(Z). The result is a fully-specified single parameter conditional distribution. The model produces exact p-values and intervals, without requiring sampling and without nuisance parameters. However, in simulations, the fully-conditional approach has less power to separate true effects from nulls, in particular for longer regions. For exact pivot inference, inference is conducted within a single segment ${\left\{Z_{a:b}+\alpha \left(1,\dots ,1\right)\right\}}_{\alpha }$; if the estimate of any of the points in the region is very close to the threshold, there will be no separation and the p-value obtained would be high. In contrast, our method is not sensitive to having individual points which are close to the threshold, because it aggregates outcomes over the set $Z:{\sum }_a^b{Z}_i\le t$. We pay a price in having an inexact method that leans on sampling and a misspecified choice of mean vector.

Additional applications and future work

The importance of accurate regional inference extends from only genomics. Threshold-and-merge is the most common method for region detection in neuroscience for the analysis of fMRI data (“cluster inference”). The standard parametric methods used for cluster inference rely on approximations for extreme sets in stationary Gaussian processes (Friston et al., 1994). Recently, the high-profile study of (Eklund et al., 2016) showed these methods to be too liberal by testing them on manufactured null; also, the distribution of detections was not uniform along the brain suggesting the process was non-stationary. The alternative offered were non-parametric permutations of subject assignment (Hayasaka et al., 2004), similar to those used in Section 7. As we observe, these non-parametric methods can be grossly over-conservative in their model, in particular when multiple regions are detected. Adapting our method for functional data may allow a powerful parametric model that relaxes the stationarity and strong thresholding requirements, without sacrificing power.

These applications require an expansion of the method for two-dimensional or three-dimensional data and for larger regions. In particular, our samplers are still sensitive, in larger regions, to initial parameters and to mixing time of the Markov chains. Better samplers, or perhaps approximations of t(Z)|A, would be needed. Furthermore, local covariance estimates might require too many samples to stabilize, and rigorous methods should be employed to deal with the unknown covariances. Using the truncated multivariate T instead of multivariate normal would account for the uncertainty in estimating the variances; however, the correlation structure also has uncertainty which we currently do not take into account. We suggest in (12) an inflation parameter to give a conservative estimate of the correlation, leaving to the user the choice of λ. It is more likely that for each application, specific models for covariance estimation can be developed. In genomics, external annotation including probe-distance and sequence composition can give a prior model for shrinkage.

Figure 1: Intervals for differential methylation regions.

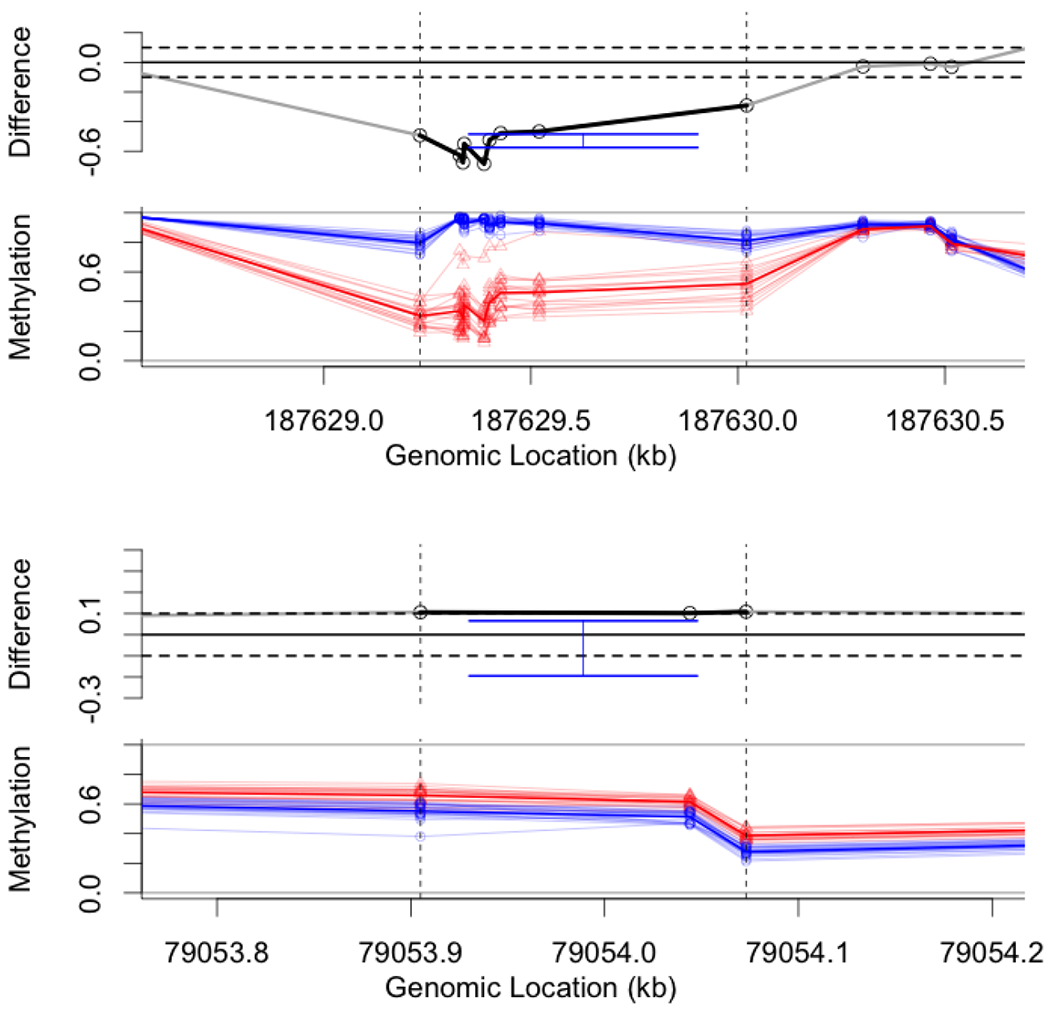
Confidence intervals for the mean between-tissue difference in two genomic regions. Top pair: the figures show a nine-site region in chromosome 4 (within the vertical dashed lines). The mean-difference (top) is considerably below the negative threshold. Individual samples are plotted below, colored by tissue type, and show relatively small within group variance. Hence, the estimated 90% confidence interval (blue, top) is relatively short and the estimate for the effect, $\widehat{\Theta }=-0.535$, is close to the observed mean. Bottom pair: the figures show a three-site region in chromosome 17 which is just above the threshold. Although the observed average is $\widehat{\Theta }=0.105$, after correcting for selection the estimated confidence interval covers 0. Data was collected by The Cancer Genome Atlas consortium (TCGA).