Archetype tasks link intratumoral heterogeneity to plasticity and cancer hallmarks in small cell lung cancer

SUMMARY

Small cell lung cancer (SCLC) tumors comprise heterogeneous mixtures of cell states, categorized into neuroendocrine (NE) and non-neuroendocrine (non-NE) transcriptional subtypes. NE to non-NE state transitions, fueled by plasticity, likely underlie adaptability to treatment and dismal survival rates. Here, we apply an archetypal analysis to model plasticity by recasting SCLC phenotypic heterogeneity through multi-task evolutionary theory. Cell line and tumor transcriptomics data fit well in a five-dimensional convex polytope whose vertices optimize tasks reminiscent of pulmonary NE cells, the SCLC normal counterparts. These tasks, supported by knowledge and experimental data, include proliferation, slithering, metabolism, secretion, and injury repair, reflecting cancer hallmarks. SCLC subtypes, either at the population or single-cell level, can be positioned in archetypal space by bulk or single-cell transcriptomics, respectively, and characterized as task specialists or multi-task generalists by the distance from archetype vertex signatures. In the archetype space, modeling single-cell plasticity as a Markovian process along an underlying state manifold indicates that task trade-offs, in response to microenvironmental perturbations or treatment, may drive cell plasticity. Stifling phenotypic transitions and plasticity may provide new targets for much-needed translational advances in SCLC. A record of this paper’s Transparent Peer Review process is included in the supplemental information.

Graphical Abstract

In brief

Groves et al. revisit small cell lung cancer intra-tumor heterogeneity by applying archetypal analysis and produce actionable insights into functional task trade-offs as drivers of cancer cell plasticity.

INTRODUCTION

Small cell lung cancer (SCLC) is a neuroendocrine (NE) malignancy of the airway epithelium that accounts for ~15% of lung cancer, characterized by early metastasis and recalcitrance to treatment. SCLC tumors have long been considered homogeneous due to their histological appearance as a carpet of uniform “small blue round cells” and the virtually ubiquitous biallelic inactivation of tumor suppressors RB1 and TP53 (Semenova et al., 2015). However, in recent years, accumulating evidence has led to the identification of distinct SCLC NE and non-NE transcriptional subtypes across several experimental systems, including cell lines, human tumors, and genetically engineered mouse models (GEMMs) (Borromeo et al., 2016; Gazdar et al., 1985; Huang et al., 2018; Mollaoglu et al., 2017).

The discrete subtype classification has spurred investigations into intra- and inter-tumor SCLC heterogeneity, with the hope to achieve much-needed translational insights to improve the 5-year survival rate of 7%. It is possible that SCLC subtypes may be differentially sensitive to therapy and that alignment with subtypes may improve treatment outcomes (Polley et al., 2016; Wooten et al., 2019). Indeed, both genetic and non-genetic heterogeneity are studied across all cancer types due to their perceived impact on progression, acquired resistance, and relapse (Altschuler and Wu, 2010; Gupta et al., 2011; Howard et al., 2018; Jia et al., 2017; Pisco and Huang, 2015; Sáez-Ayala et al., 2013; Su et al., 2019). Dynamics of intratumoral heterogeneity are especially relevant for SCLC because cooperativity and transitions among SCLC subtypes have been postulated to underlie its aggressive features, such as early metastatic spread and inevitable relapse after initial response to the chemoradiation standard of care (Ireland et al., 2020; Lim et al., 2017; Rudin et al., 2019).

The classification of SCLC into three NE and two non-NE subtypes has been provisionally defined by the enriched expression of one of the four transcription factors (TFs) ASCL1 (A and A2), NEUROD1 (N), YAP1 (Y), and POU2F3 (P) (Rudin et al., 2019). These canonical subtypes are of great value to anchor research results and to benchmark comparisons among various groups investigating SCLC heterogeneity. However, one limitation of this classification is that stark clustering into these transcriptional subtypes is at times problematic because multiple or none of the eponymous TFs are expressed in SCLC cell lines or tumors. Other TFs such as ATOH1 and MYC family genes may be involved in subtype definition as well (Borromeo et al., 2016; Mollaoglu et al., 2017; Rudin et al., 2019; Simpson et al., 2020; Wooten et al., 2019).

A second limitation is that SCLC tumors can be a composite of multiple subtypes, so stark delineation of tumors into subtypes may be impractical. For instance, CIBERSORT decomposition showed all tested SCLC tumors are composed of multiple NE and non-NE subtypes, and several studies have reported changes in subtype prevalence during tumor progression or in response to treatment (Newman et al., 2015; Ireland et al., 2020; Stewart et al., 2020; Wooten et al., 2019). Bulk RNA sequencing (RNA-seq) and immunohistochemistry confirm tumors can be positive for more than one TF, such as ASCL1 and NEUROD1 (Simpson et al., 2020; Zhang et al., 2018). In bulk data, it is unclear if this is due to a mix of discrete NE and non-NE cells or due to intermediate states, the presence of which is supported by single-cell data (Udyavar et al., 2017). Deconvolving subtype mixtures and recognizing intermediate cells are substantial challenges for subtype-directed treatment.

A third limitation, perhaps most relevant to this study, is that current classification schemes say little about the functional phenotypes of cancer cells and the task trade-offs that may occur in response to selective pressure from changing microenvironments and treatments. The limitations of such schemes have been discussed extensively by Alon and collaborators (Shoval et al., 2012; Korem et al., 2015; Hart et al., 2015; Hausser and Alon, 2020). In the case of SCLC, tumor evolution reflected by shifts in subtype composition (Ireland et al., 2020; Stewart et al., 2020) may be due to adaptive cell state transitions in response to selective pressure operating on SCLC phenotypes. A proper understanding of SCLC tasks may therefore engender precise targeting of such tasks as a strategy to hinder state transitions and to prevent SCLC tumor adaptability to microenvironmental perturbations or treatment.

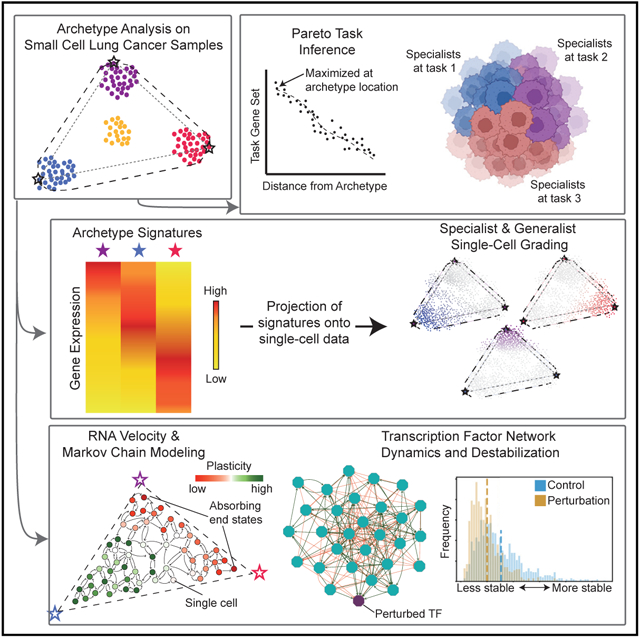
To overcome these limitations, here we view subtype definition as the starting point to build a comprehensive understanding of the phenotypic drivers for SCLC heterogeneity and plasticity, which are likely responsible for tumor adaptability, evolution under selective pressure, and ultimately resistance to treatment. Toward this goal, we apply multi-task evolutionary theory using archetype analysis (AA), which has been proposed as an avenue to produce systems frameworks of tumor heterogeneity (Hausser et al., 2019; Shoval et al., 2012). Briefly, we apply AA to gene expression data from SCLC cell lines and tumors to uncover a convex polytope with low-dimensional five-vertex geometry representing the SCLC phenotypic space. Gene set enrichment at the five vertices identifies phenotypic tasks that are consistent with cancer hallmarks (e.g., proliferation or migration) and are reminiscent of the proper functions of the SCLC normal counterpart, the pulmonary neuroendocrine cells (PNECs) (Garg et al., 2019; Gu et al., 2014; Van Lommel, 2001). Experimental data and prior knowledge support the validity of task assignments. We then use archetypal transcriptomics signatures to position bulk or single-cell transcriptomics of cell lines or tumors in the SCLC phenotypic space. Where each cell falls with respect to the archetypes determines how specifically it optimizes a single task (specialists near an archetype) or how it has generalized to complete several tasks (near the center of the polytope or along an edge or face between two or more tasks). According to multi-task evolutionary theory, the low-dimensional polytope, with specialists at the vertices and generalists between them, arises in response to selective pressure that requires the optimization of competing tasks, such as proliferation and migration, in the face of limited energy resources and metabolic constraints. Cells then fall along a Pareto front (a line, triangle, or higher dimensional polytope) between archetypes in gene expression or trait space (Gallaher et al., 2019; Hatzikirou et al., 2012). Thus, multi-task trade-off considerations can produce insights into the microenvironmental conditions that may cause state transitions in SCLC tumors and provide a theoretical basis for the existence of dual-positive intermediate cells (e.g., ASCL1+/NEUROD1+ cells) (Simpson et al., 2020; Zhang et al., 2018).

Clustering methods, which identify prototypical gene expression profiles of cluster centers, are often used to characterize SCLC subtypes. Such clusters are often too rigidly defined in the case of mixed or intermediate samples, effectively obscuring proper consideration of cell states between subtypes, a limitation overcome by AA (Mørup and Hansen, 2012; Shoval et al., 2012). Using a set of SCLC human cell lines regarded as exemplars for each subtype, we show that placing individual cells within a cell line or tumor sample in archetype space provides a more accurate view of SCLC heterogeneity, particularly for samples with uncertain or mixed subtype assignment. The continuum of transcriptomic states between archetypal extremes suggests that SCLC cells may diversify and shift between archetypes in efforts to optimize fitness by task trade-off. To analyze the dynamics of these phenotype transitions, we model single-cell dynamics as a Markovian process along an underlying state manifold (Teschendorff and Feinberg, 2021) from which we can calculate metrics of plasticity. We quantify the average change in expression over the phenotypic transition from source states to terminal states, which we term cell transport potential (CTrP). Using this metric, we delineate plasticity across archetype space within SCLC human cell lines. In mouse and human tumors, NE cells can acquire plasticity de novo due to MYC overactivity. We then quantify the multipotency of MYC-driven NE cells and show they can transition toward either Archetype Y or a previously unrecognized cell state, which we term Archetype X.

Taking these findings together, we propose that SCLC tumors should be viewed as a complex heterogeneous ecosystem of plastic NE and non-NE cells, which can evolve under selective pressure by task trade-offs. A key point is that task optimization takes place within a phenotypic space (a polytope) that can be derived from SCLC transcriptomics data by the AA. Thus, the AA of tumor gene expression or proteomics data may shed light on the dynamics of SCLC tumor evolution and hopefully uncover points of attack for SCLC’s aggressive and recalcitrant properties.

RESULTS

Archetype analysis defines a five-vertex polytope for SCLC

SCLC subtypes have recently been classified into discrete NE and non-NE subtypes by the expression of eponymous transcription factors: ASCL1+ (NE), NEUROD1+ (NE), POU2F3+ (non-NE), and triple-negative non-NE subtypes, often but not always YAP1+ (Baine et al., 2020; Lim et al., 2017; Rudin et al., 2019; Simpson et al., 2020). To examine relationships between these discrete subtypes, we analyzed a dataset of bulk RNA-seq on 120 human SCLC cell lines from two sources: the cancer cell line encyclopedia (CCLE) and cBioPortal (Barretina et al., 2012; Cerami et al., 2012; Gao et al., 2013). This transcriptomics dataset includes cell lines with the overexpression of each of the subtype-driving TFs, suggesting it adequately covers the relevant phenotypic space for SCLC. We defined the SCLC phenotypic space on bulk transcriptomics data from cell lines rather than tumors, which may contain extraneous cell types like inflammatory infiltrate.

Previously, we showed that the analyses of gene expression profiles (RNA-seq) from human SCLC cell lines by weighted gene co-expression network analysis (WGCNA) captures canonical SCLC subtype gene programs (modules) enriched in distinct cellular functions, such as immune response or neuronal differentiation (Wooten et al., 2019). Here, we update this characterization to include virtually all human cell lines available and the SCLC-P subtype (Figures S1A-S1C) and show that gene module expression is coordinated across five subtypes, with a subset of gene modules and associated enrichment in cellular functions corresponding to each SCLC subtype (Figure S1D; Table S1). According to multi-task evolutionary theory, the diversity of functions across subtypes in a normal or neoplastic cell population may arise when selective pressure forces cells to optimize survival by functional task trade-off (Hausser et al., 2019; Shoval et al., 2012). To investigate this possibility, we applied AA, which allows for a flexible characterization of gene expression space constrained by functional phenotypic features (Mørup and Hansen, 2012).

Briefly, AA approximates the cell phenotype space as a low-dimensional polytope that envelops gene expression data. The vertices of this multi-dimensional shape represent archetypes, constrained to be linear mixtures of some set of data points each optimal for a specific functional task. To determine the optimal number and location of the archetype vertices in the SCLC gene expression space, we applied the MATLAB package ParTI (Hart et al., 2015) and the principal convex hull analysis (PCHA) algorithm (Mørup and Hansen, 2012), which finds k points on the convex hull, or bounding envelope, enclosing as much of the data as possible (see STAR Methods) (Korem et al., 2015). Using this method, we determined whether it was possible to fit the SCLC cell line data within a low-dimensional polytope and compared the fit with randomized datasets to calculate statistical significance.

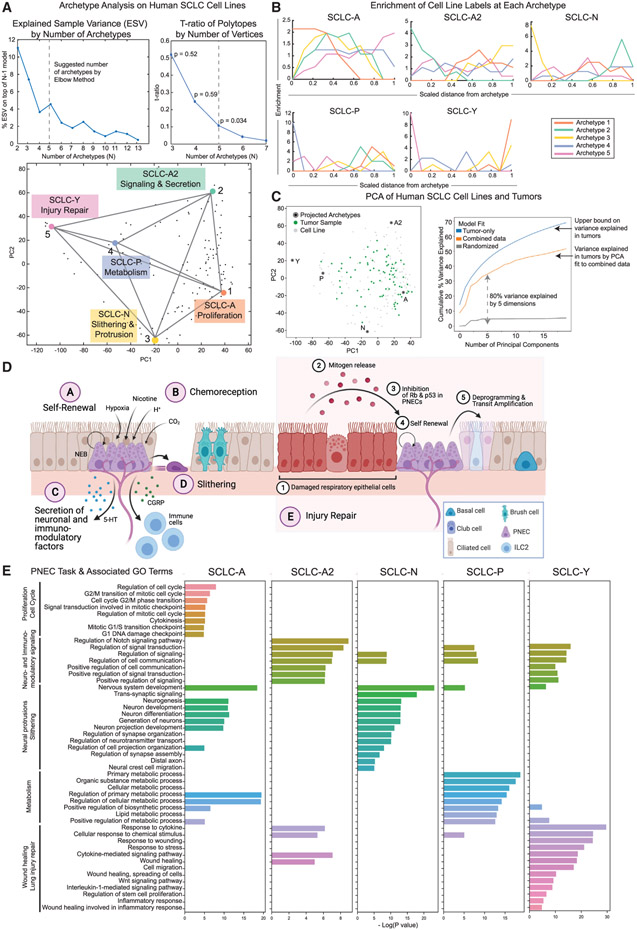
First, to determine how well the data is fit by polytopes of varying dimensionality, we computed the variance in the data that is explained (explained variance [EV]) by polytopes with different possible numbers of k vertices (k = 2–15). We found that EV saturates around 5 archetypes, such that the variance explained by additional archetype vertices was minimal (Figure 1A). This was confirmed by identifying the elbow, k*, in the EV versus k curve, which suggested k* = 4, 5, or 6 (Figure S1E; see STAR Methods). Therefore, we fit the data to polytopes of each order (4, 5, or 6 vertices) and computed the t-ratio, a measure comparing the volume enclosed by the data with that of a polytope. As described in Korem et al. (2015), a larger t-ratio suggests that the data is more similar to the polytope. The t-ratio of the data can be compared with that of randomly shuffled datasets to quantify the significance of the fit as a p value. To avoid overfitting, the lowest number of archetypes that reached significance was chosen. Therefore, a polytope with five archetypes best fits the data (Figures 1A and S1E; Table S2, p value = 0.034, t-ratio test; see STAR Methods).

Figure 1. Archetype analysis on bulk RNA-seq data from human SCLC cell lines shows archetypes are enriched for PNEC-related gene programs.

(A) Archetype analysis of bulk RNA-seq from 120 human cell lines shows that 5 archetypes fit the cell line data well (p = 0.034). Explained sample variance increases for 5 archetypes compared with 4, and 5 archetypes is the lowest number with a significant p value by a t-ratio test.

(B) Subtype label enrichment. Data were binned by distance from archetype (x axis), and enrichment of each subtype label (y axis) was computed. Enriched subtypes are highest at x = 0, in the bin closest to one of the archetypes, and lowest near all other archetypes. Each archetype shows enrichment in one of the five SCLC subtypes from the literature.

(C) PCA of full human RNA-seq dataset (tumors and cell lines). Projection of 5 archetypes by this PCA shows that tumors are mainly contained within the same archetype space as cell lines. Variance explained by this combined-data PCA, a tumor-data PCA, and a randomized model shows that the top 5 components of the combined-data PCA explain a large percentage, around 80%, of the variance explained by the tumor-only PCA.

(D) Pulmonary neuroendocrine cell (PNEC) related tasks. PNECs can trade-off between these tasks to regenerate injured lung epithelium, respond to chemical signals in the microenvironment, affect the nervous and immune systems, and migrate to new regions of the lung airways.

(i) A subset of PNECs has been shown to act like stem cells that can proliferate under lung injury (Ouadah et al., 2019).

(ii) PNECs and brush cells both respond to chemicals and cytokines in the lung (Van Lommel, 2001).

(iii) PNECs are innervated and can send neuronal signals by releasing neurotransmitters and peptides such as serotonin (5-HT) (Van Lommel, 2001). They also have been shown to interact with the immune system by releasing proteins such as CGRP, which can activate IL2 cells (Branchfield et al., 2016).

(iv) A subset of PNECs can “slither,” or migrate, by transiently downregulating epithelial genes to move toward and form neuroendocrine bodies (NEBs), or clusters of PNECs (Kuo and Krasnow, 2015).

(v) After injury to the lung epithelium (ablation of club cells), PNEC stem cells can deprogram into a transit-amplifying cell type that can then differentiate into other lung types to regenerate the epithelium (Ouadah et al., 2019).

(E) Each archetype is enriched in gene ontology terms related to PNEC tasks.

Mathematically, each of the five consensus SCLC subtypes (Wooten et al., 2019; Rudin et al., 2019) was enriched at an archetype (Figure 1B, p < 10⁻⁶ for each subtype) such that there is a one-to-one correspondence between archetypes and consensus subtypes and the nomenclature is interchangeable. Fitting the data to a polytope with fewer vertices, such as a tetrahedron (four-vertex polytope) did not achieve a statistically significant t-ratio (p value = 0.059, Figure S1F; Table S2). Furthermore, the only difference between the four- and five-vertex polytopes was the SCLC-P archetype, previously recognized as a distinct subtype (Huang et al., 2018). When we compared the archetypes of the five- and six-vertex polytopes (see STAR Methods), we found that the six-vertex polytope did not identify any plausible additional archetypes, since two archetypes matched one in the five-vertex polytope, and the other four vertices matched the remaining four, one-to-one, between five- and six-vertex polytopes (Table S3; Figure S1F). We used bootstrapping tests where we resampled the data with replacement 1,000 times to evaluate the robustness of the detected archetypes. Five archetypes were robust to data sampling and not dependent on any extreme points in the dataset (Figure S1E).

To determine if cell-line archetypes could adequately describe the inter-sample variance of human tumors, we batch-corrected 81 human SCLC tumor samples (George et al., 2015) to the cell line data (Figure S1G). Since tumors are likely to be heterogeneous subtype mixtures, they may not span the phenotypic space (Figure 1C) to the same extent as the cell lines. However, when we project the 5 archetypes (Figure 1C) by a principal-component analysis (PCA) fit to the combined dataset of cell lines and tumors, virtually all tumors are contained by the same phenotypic space as cell lines (Figure 1C). Furthermore, the variance explained by this PCA is a large proportion of the variance explained in a tumor-only PCA, with the top five components explaining 80% of the tumor variance (Figure 1C). In addition, the polytope best fit to the combined dataset of cell lines and tumors also resulted in 5 archetypes (p = 0.09), and each archetype matched at least one of the cell line archetypes (Figure S1H; Table S4).

In summary, AA explained SCLC heterogeneity in bulk transcriptomics data as a low-dimensional phenotypic space between five archetype vertices corresponding to five major SCLC phenotypes (SCLC-A, -A2, -N, -P, and -Y). Because the archetype space is continuous, any bulk transcriptome profile can be placed within the polytope rather than be forced into a discrete cluster not fully reflective of their transcriptomic profile. For example, samples that are ill-defined by classical subtyping methods due to a lack of eponymous TF expression (Rudin et al., 2019) can be classified in the polytope based on archetype distance. In addition, since functional tasks are optimal at archetypes, distance from archetype vertices can be used to infer whether an SCLC cell population is a specialist at one task, a generalist for multiple suboptimal tasks, or both.

The SCLC phenotypic polytope is bounded by functional tasks reminiscent of PNECs

Pulmonary neuroendocrine cells (PNECs), the counterpart of SCLC in normal lungs, are plastic cells that can trade off between functions in response to microenvironmental conditions, including lung epithelium repair in response to injury, self-renewal, and secretion of neuro- and immunomodulatory peptides (Figure 1D) (Garg et al., 2019; Song et al., 2012). We hypothesized that SCLC cells may be innately programmed to fulfill similar tasks, albeit in a dysregulated manner, geared toward optimizing tumor fitness and survival.

To define functional tasks optimized by each archetype, we evaluated the enrichment of genes at each SCLC archetype location (Table S5, Bonferroni-Hochberg-corrected q < 0.1). We then used ConsensusPathDB on the most enriched genes to find enriched gene ontologies (GO terms) (Table S6) and used the molecular signatures database (MSigDB) to evaluate the enrichment of cancer hallmarks (Table S7; see STAR Methods) Kamburov et al., 2013; Liberzon et al., 2011; Zhang et al., 2020). As shown in Figure 1E and Table 1, each archetype optimized a task previously associated with PNECs and performed cancer hallmark-related functions to promote tumor survival.

Table 1.

Archetypes with associated PNEC-related tasks and the cancer hallmark functions they optimize^a

Archetype	Associated PNEC task	Optimized function for increased tumor fitness
SCLC-A	Proliferation	Increased cell proliferationb
SCLC-A2	Neuro- and immuno-modulatory signaling	Evading immune destruction and tumor-promoting inflammation
SCLC-N	Slithering and axon-like protrusions	Activating invasion and metastasisb
SCLC-P	Chemosensation and metabolism	Reprogramming energy metabolism
SCLC-Y	Transdifferentiation to non-NE state in response to injury	Inducing angiogenesis and resisting cell death

^aAll enriched Cancer Hallmark Gene Sets are shown in Table S4.

^bCancer hallmark is inferred from GO term enrichment rather than the enrichment of Cancer Hallmark Gene Sets.

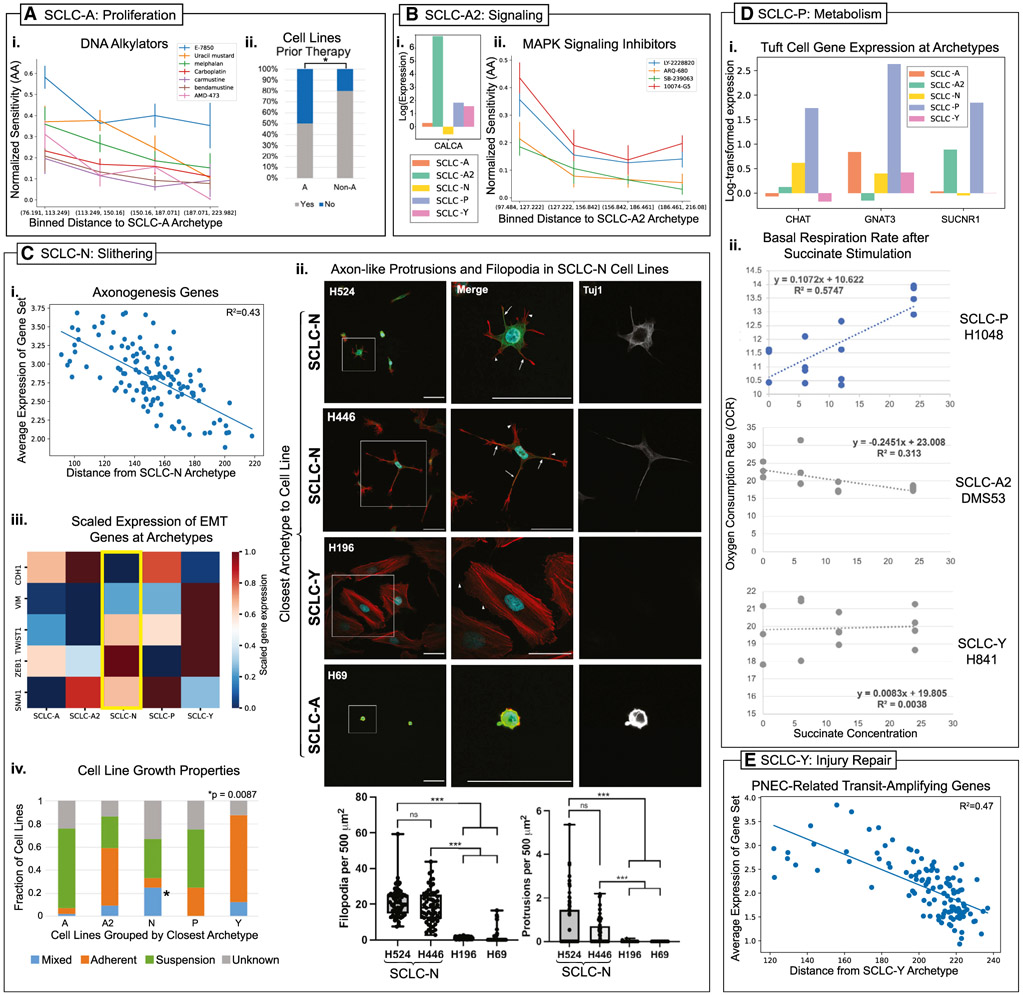
Archetype 1, related to the SCLC-A subtype by transcriptomics (Figure 1B), is enriched in cell cycle GO terms. This enrichment may reflect the self-renewal potential of PNECs, which proliferate after lung injury and/or chronic hypoxia (McGovern et al., 2010; Noguchi et al., 2020). Previous studies on ASCL1+, HES1− cells similar to the SCLC-A archetype have shown them to be more proliferative than other SCLC cell types (Lim et al., 2017). This archetype task is consistent with the highly proliferative nature of the SCLC-A subtype, evidenced by its often-larger proportion in primary tumors (Alam et al., 2020; Carney et al., 1985). Furthermore, classic tumors containing mostly proliferative SCLC-A cells are initially sensitive to DNA damaging agents that selectively kill fast-growing cells (Sen et al., 2018). Accordingly, ASCL1 expression is reduced in post-chemotherapy tumors and chemoresistant cell lines (Wagner et al., 2018). Analysis of drug sensitivity to DNA alkylators and cell cycle inhibitors shows that cell lines closest to SCLC-A are indeed more sensitive to these drug classes (Figures 2Ai and S1I). This is reflected in the archetype space: cell lines near the SCLC-A archetype are more likely to be derived from untreated tumors than cell lines near other archetypes (p = 0.019). Conversely, cell lines from treated tumors are less likely to be near SCLC-A (p = 0.03, one-tailed binomial tests on treatment status of cell lines; see STAR Methods; Figure 2Aii). Together, this evidence suggests that the SCLC-A archetype optimizes the cancer hallmark of increased cell proliferation (Table 1).

Figure 2. SCLC cell line archetypes optimize PNEC-related tasks.

(A) SCLC-A is enriched for proliferation.

(i) Normalized activity area (AA, a measure of sensitivity) to DNA alkylators. Cell lines in the bin closest to the SCLC-A archetype are more sensitive (p < 0.05). Error bars show standard error of the mean (SEM) of AA for cell lines in each bin by distance.

(ii) Cell lines closest to A are less likely to have had prior therapy (p = 0.019, hypergeometric test).

(B) SCLC-A2 is enriched for signaling.

(i) CALCA expression is highest at the SCLC-A2 archetype.

(ii) Cell lines closest to SCLC-A2 are most sensitive to MAPK signaling inhibitors (p < 0.05). Error bars show SEM for cell lines in bin.

(C) SCLC-N is enriched for slithering-related tasks.

(i) Average expression of an axonogenesis gene set from Yang et al. (2019) as a function of distance from the SCLC-N archetype, showing a correlation between expression and closeness to the SCLC-N archetype.

(ii) Axon-like (Tuj1+) protrusions and filopodia are more prevalent in SCLC-N cell lines, as shown by arrows (Tuj1+ protrusions) and arrowheads (filopodia) and quantified using a one-way ANOVA (***p < 0.001, n = 3 replicates, 20 cells quantified per replicate). All scale bars are 50 mm. A representative of 6, 9, 9, and 2 individual cells are shown for four cell lines (left column), with a higher resolution image of a single representative cell shown for each cell line (middle and right column). DAPI channel for H69, H524, and H196 is brightened in the final images and no other digital adjustments were made.

(iii) EMT gene expression rescaled by gene (rescaled log-normalized expression) is shown by color in a heat map across archetypes. SCLC-N cells express some mesenchymal markers (ZEB1, SNAI1, and TWIST1) at intermediate levels and downregulate CDH1.

(iv) SCLC-N cell lines are more likely to be mixed (3/12 cell line) than non-N cell lines (3/80 cell lines) with p = 0.0087 (hypergeometric test).

(D) SCLC-P is enriched for tuft cell-like features and metabolism tasks.

(i) Genes upregulated in the SCLC-P archetype that is expressed in tuft cells. CHAT, GNAT3, and SUCNR1 are part of the pathway by which succinate stimulation affects the metabolism of intestinal tuft cells and the stimulation of type 2 immunity (Banerjee et al., 2020).

(ii) Basal respiration rate (OCR) after overnight (12 h) stimulation by succinate. H1048, which is closest to the SCLC-P archetype, increases OCR after stimulation, whereas SCLC-A2 and SCLC-Y cell lines do not.

(E) SCLC-Y is enriched in injury repair tasks. The average expression of genes related to the transit-amplifying subpopulation of PNEC stem cells from Ouadah et al. (2019) under lung injury is correlated with closeness to the SCLC-Y archetype.

Archetype 2 (SCLC-A2), also driven by NE gene programs, is enriched for stimulus-response, cytokine-mediated signaling, and signal transduction, suggesting these cells specialize in the PNEC task of neuronal and immune-modulatory signaling and secretion (Figure 1E). This is consistent with SCLC-A2 subtype enrichment in GO terms related to neuronal secretion and response to environmental signals (Wooten et al., 2019). In particular, the SCLC-A2 archetype is enriched for CALCA transcripts (Figure 2Bi) encoding the vasodilating and immunomodulatory peptide, Calcitonin gene-related peptide (CGRP) (Branchfield et al., 2016). SCLC-A2 cell lines are also preferentially sensitive to mitogen-activated protein kinase (MAPK) signaling inhibitors (Figure 2Bii). Together, the optimization of these signaling and secretion tasks may allow SCLC-A2 cells to interact with the tumor microenvironment quickly and effectively by sensing and responding to external signals. This suggests the SCLC-A2 archetype optimizes the cancer hallmarks tumor-promoting inflammation and evading immune destruction (Tables 1 and S7).

Archetype 3 (SCLC-N) is enriched in neurogenesis terms, including synapse and distal axon terms (Figure 1E). These functions may enhance tumor spreading by specifying a protruding, axon-like morphology. Accordingly, Yang et al. (2019) reported that the disruption of axon-like protrusions in certain SCLC cells impairs cell movement. Moreover, we determined that the expression of axon guidance-related genes across cell lines is inversely correlated to the distance from the SCLC-N archetype (Figure 2Ci). Confocal imaging experimentally confirmed that filopodia and neuronal protrusions, identified by staining with the specific marker Tuji (Yang et al., 2019), were observed in cell lines close to the SCLC-N archetype (H524 and H446) but not in distant ones (H69, close to SCLC-A, and H196, close to SCLC-Y) (Figure 2Cii). This morphology may be related to the slithering movements observed in PNECs, whereby cells transiently downregulate adhesion genes and use axon-like protrusions to migrate across epithelial layers (Kuo and Krasnow, 2015; Osborne et al., 2013). We therefore considered the expression of adhesion, migration, and epithelial-to-mesenchymal transition (EMT) genes and found that the EMT-promoting genes ZEB1, SNAI1, and TWIST1, but not VIM, are upregulated in SCLC-N, suggesting a hybrid E/M or non-canonical/incomplete M phenotype (Figure 2Ciii). This is reflected in growth patterns of cultured SCLC cell lines, whereby cell lines close to the SCLC-N archetype are significantly more likely to display a mixed adherent/floating morphology than distant ones (p = 0.0087, Figure 2Civ). Thus, our data suggest that Archetype 3 may optimize the hallmark activating invasion and metastasis to promote tumor spreading by performing the PNEC task of slithering (Table 1).

Archetype 4 (SCLC-P) is enriched in metabolic GO terms (Figure 1E). The cell of origin of SCLC-P cells remains uncertain, but the eponymous POU2F3 TF is a landmark for tuft cells in other organs, and SCLC-P has been described as tuft-like with remarkable similarity to brush cells in the lung (Huang et al., 2018), possible precursors for PNECs (Goldfarbmuren et al., 2020). Chemosensory tuft cells respond to the metabolite succinate through the receptor SUCNR1, promoting type 2 inflammation through ILC2 activation (Nadjsombati et al., 2018). SUCNR1 and gustducin (GNAT3) are uniquely upregulated in the SCLC-P archetype (Figure 2Di). In response to experimental overnight stimulation by succinate, SCLC-P cells (but not SCLC-A2 or -Y) adapted their metabolism by increasing basal respiration rate (Figure 2Dii). We tested a SUCNR1+ SCLC-P cell line (H1048) for G-alpha-q-mediated calcium signaling response via SUCNR1, a G-protein coupled receptor (GPCR) (Figure S1K). While we did not find signaling activity in this cell line, further experiments will be necessary to determine how the response to succinate is being mediated in SCLC-P cell lines. Together, these results indicate that SCLC cells close to the SCLC-P archetype respond to metabolites like succinate, similar to the function of chemosensory tuft cells, though most likely not through G-alpha-q-mediated GPCRs.These functions are consistent with our findings that the SCLC-P archetype enriched the cancer hallmark reprogramming energy metabolism (Tables 1 and S7).

Archetype 5 (SCLC-Y) was enriched in GO terms such as stress response, wound healing, and cell migration (Figure 1E). This archetype showed broad enrichment in most cancer hallmark gene sets, corroborating previous findings that it may be key to understanding resistance (Cai et al., 2021; Lim et al., 2017; Wagner et al., 2018). The cancer hallmarks of inducing angiogenesis and resisting cell death showed the greatest enrichment in SCLC-Y cell lines (Tables 1 and S7). Notably, normal PNECs transdifferentiate to a transit-amplifying (TA) state to repair the lung epithelium after injury (Ouadah et al., 2019). Although data on the PNEC TA state are limited, there is a clear correspondence between the SCLC-Y archetype distance and TA gene signature (Figure 2E; Table S8). We propose that this archetype is an SCLC version of the TA state whose task is lung injury repair. The upregulation of genes in the Notch and Wnt pathways, also involved in lung injury repair, provides further supporting evidence (Lim et al., 2017; Shi et al., 2015; Wagner et al., 2018).

In summary, these data indicate that SCLC archetype tasks in cell lines and tumors are reminiscent of dysregulated versions of normal PNEC functional tasks. Moreover, these dysregulated functions can be tied to the enrichment of cancer hallmark tasks, illustrating how SCLC cells may utilize PNEC functions for fueling tumor recalcitrance (Table 1).

Intra-sample heterogeneity is aligned with inter-sample diversity

By considering bulk RNA-seq data, we framed the diversity of SCLC cell line and tumor samples at a population level within an archetype-bounded phenotypic space and identified five archetypal gene programs enriched at the extremes (vertices) of this space. As mentioned previously, cell populations close to an archetype vertex are specialists for that archetype task, whereas more distant populations are generalists that perform multiple tasks. Thus, inter-sample diversity between cell populations is contained within the Pareto front bound by archetypes, where populations may occupy intermediate states continuously throughout the polytope.

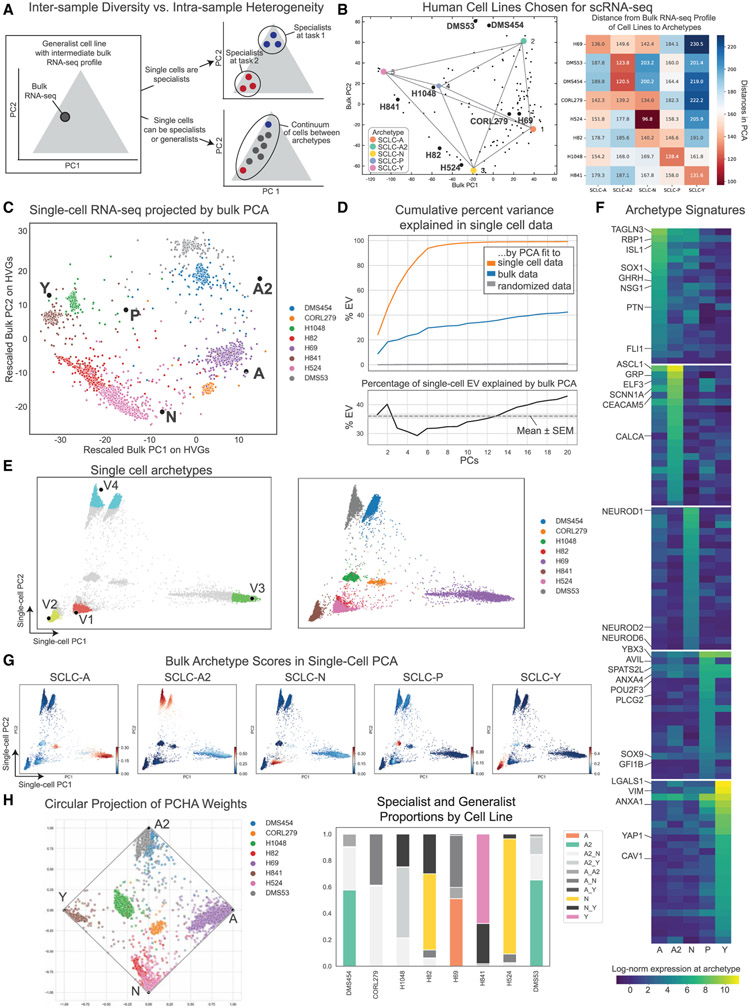
However, it is unclear to what degree a cell population (e.g., a tumor or a cell line) can or does comprise both generalists and specialists at the single-cell level. Although specialist populations are presumably composed largely of specialist single cells, a generalist cell line (or tumor) could comprise multiple specialists and generalists alike (Figure 3A). To consider relationships between inter- and intra-sample diversity, we analyzed single-cell RNA sequencing (scRNA-seq) data from a panel of eight cell lines, selected to maximally span the archetype space defined by the bulk data AA (see STAR Methods; Figures 3B and S2A-S2D). The axes of maximal variance among single cells from these 8 cell lines can be defined with a PCA fit to the single-cell expression data. We compared the variance explained by this single-cell-fit PCA model with the variance explained by projecting the single-cell data onto the space defined by the bulk data-derived archetypes (Figure 3C). If intra-sample heterogeneity were perfectly aligned with inter-sample diversity, we would expect the single-cell variance explained by inter-sample diversity to equal the single-cell variance explained by the single-cell PCA. In other words, the percentage of variance explained by the single-cell PCA is an upper bound on the variance explained by inter-sample diversity.

Figure 3. SCLC archetype gene signatures reveal generalists and specialists in cell lines at the single-cell level.

(A) Inter-sample diversity is supported by intra-sample heterogeneity. Generalist cell lines may comprise several specialist subpopulations or both specialists and generalists in a continuum of single cells.

(B) To investigate intra-sample heterogeneity, human cell lines for scRNA-seq were chosen to span the phenotypic space of SCLC. Two cell lines from each neuroendocrine subtype (A, A2, and N) were chosen, and one from each non-neuroendocrine subtype (P and Y) was chosen. Left: chosen cell lines in bulk PCA space. Right: the distance of each bulk cell line gene expression profile to each archetype in PCA.

(C) Single-cell RNA-seq on sampled human SCLC cell lines projected by PCA fit to bulk RNA-seq on cell lines in (A). Each sample occupies a distinct region in this space, and many samples fall in between archetypes.

(D) Top: variance explained in single-cell data by PCA fit to bulk cell line data. Orange: upper bound of variance explained for each number of components is given by PCA fit to single-cell data. Blue: the variance explained by the bulk PCA is a large proportion of this, as compared with a randomized model (gray). Bottom: inter-sample diversity explains a large percentage of the intra-sample variance, around 36%. This fraction stays relatively constant for varying numbers of PCs. Black line: intra-sample variance explained by inter-sample diversity as a percentage of upper bound. Gray dotted line: mean ± SEM (gray box).

(E) Left: single-cell archetypes from PCHA on imputed cell line scRNA-seq data for human cell lines in single-cell PCA. The 5% of cells closest to each archetype are colored; generalists are shown in gray. Right: cell lines labeled in single-cell PCA.

(F) Gene signature used for single-cell subtyping. Expression of genes at archetype location is shown by color (log-normalized expression), with genes of interest highlighted. A full list of genes and numerical values can be found in Table S6.

(G) Using least-squares approximation, we score single cells by 5 bulk archetype signatures in (F). The color shows archetype signature scores on human cell line scRNA-seq data (linear scale, arbitrary units).

(H) Left: using a permutation test (see STAR Methods), we compare average archetype scores of each single-cell specialist subpopulation with background distributions from non-specialists to label archetypes. Circular a posteriori (CAP) plot of single-cell archetype weights for each cell, with archetypes labeled by enriched bulk signature. Right: specialist and generalist proportions shown for each cell line in bar plots.

The projection of the single cells onto the archetype-defined space suggests that inter-sample diversity in human SCLC cell lines explains 36% of the intra-sample variance (Figure 3D). This level of alignment is likely not due to random chance, since PCA models fit to shuffled bulk data only explained about 0.26% ± 0.008% of the single-cell variance (50 shuffles, see STAR Methods). The remainder of the unexplained single-cell variation may be due to the intrinsic stochasticity of RNA expression (Hayford et al., 2021). These findings indicate that intra- and inter-sample variations in SCLC are well aligned.

Single cells in SCLC cell lines can be task specialists or generalists

Based on the analyses in the previous section, single SCLC cells fit into the phenotypic space defined by population-level measurements. We next sought to independently grade single cells along a continuum of specialists and generalists in the bulk-derived archetype space. To this end, we compared a polytope fit to single-cell data with the bulk data-derived archetypes. We first applied PCHA to the single-cell data directly to determine if the geometry of the data was bounded by a polytope. We found the sampled cell lines fall in a shape with four vertices with a t-ratio test p value of 0.001 (Figures 3E, S2E, and S2F; see note about SCLC-P in STAR Methods). The presence of a low-dimensional polytope in the single-cell data suggests that cancer cells trade-off between multiple functions at the individual, not just population, level.

To align these single-cell archetypes with our previously defined bulk archetype space, we asked whether each single-cell archetype was enriched for a bulk archetypal gene signature. We generated gene expression signatures characteristic of each bulk archetype location by finding genes enriched in the bulk expression profiles of cell lines closest to each archetype (Mann-Whitney test, q < 0.1, Table S9; see STAR Methods). We then performed feature selection by considering the condition number of the gene signature matrix, which measures the sensitivity of the matrix to changes, or errors, in input (i.e., the bulk RNA-seq profiles). A well-conditioned matrix with a low condition number is better able to discriminate between archetypes and therefore can be used to project other data into this lower dimensional space more accurately. By minimizing the condition number, we found a small signature matrix of 105 genes that can sufficiently define archetype space (Figure 3F).

The resulting signatures contain several NE and non-NE genes that have previously been associated with consensus SCLC subtypes (Figure 3F). For example, Transgelin 3 (TAGLN3), growth-hormone-releasing hormone (GHRH), and gastrin-releasing peptide (GRP) are all neuropeptides previously associated with neuroendocrine tumors including SCLC (Bepler et al., 1988; Bostwick and Bensch, 1985; Gola et al., 2006; Ratié et al., 2014; Wang and Conlon, 1993; Zhang et al., 2018), whereas ASCL1, ISL1, ELF3, and FLI1 are NE transcription factors that drive distinct transcriptional programs in SCLC-A and SCLC-A2 subtypes, respectively (Agaimy et al., 2013; Borromeo et al., 2016; Li et al., 2017; Wooten et al., 2019). Several NEUROD family genes are enriched at the SCLC-N archetype, as expected (Borromeo et al., 2016; Osborne et al., 2013; Wooten et al., 2019). The top genes for the SCLC-P archetype have previously been associated with this SCLC subtype and tuft cells (Huang et al., 2018). The top two genes enriched in the SCLC-Y archetype, LGALS1 and VIM, are associated with a mesenchymal phenotype and have previously been implicated with SCLC chemoresistance (Krohn et al., 2014; Tripathi et al., 2017).

We therefore used the 105-gene signature matrix to score single cells by least-squares approximation and tested enrichment of these scores near each single-cell archetype (see STAR Methods; Figures S3G and S3H). The bulk archetype with the greatest significant enrichment (family-wise error rate q < 0.1) labeled each single-cell archetype (Figure S3H). Each single-cell archetype was enriched in one of four SCLC signatures: A, A2, N, or Y (Figure 3G; see note in STAR Methods regarding SCLC-P). We visualized the location of the single cells in relationship to these archetypes in two-dimensional space by a circular A posteriori projection (Figure 3H).

Each cell line occupies a distinct region in archetype space, as expected from the bulk transcriptomes (Figure 3B). Although each cell line comprised predominantly specialists for a respective archetype, some included generalists, as they fell in between multiple archetypes (Figure 3H). A scrublet analysis (Wolock et al., 2019) showed that these cells are not predicted to be doublets, a technical artifact of scRNA-seq, suggesting they have a truly intermediate cell type (Figure S3C). For example, CORL279 forms a continuum of A/N and A2/N generalists, consistent with its dual positivity for ASCL1 and NEUROD1 at the bulk expression level (Figure S3I). H841 is composed entirely of SCLC-Y specialists and non-NE generalists (between Y and another archetype), consistent with its sole expression of YAP1. Our classification was consistent with the bulk expression of the canonical TFs (ASCL1, NEUROD1, POU2F3, and YAP1) in each cell line (Figures 3H and S3I). Some intermediate cell types were more common, such as A-N and N-Y generalists, whereas others were not found or were extremely rare, such as A-Y. H82 spanned states between the A, N, and Y archetypes, which has been shown to be a possible transition path in mouse models (Ireland et al., 2020) and is consistent with its bulk expression of ASCL1, NEUROD1, and YAP1 (Figure S3I).

In conclusion, SCLC cell lines may each comprise archetypal specialists and generalists at the single-cell level. The relative proportion of specialists and generalists varies in each cell line, and generalist cell types may represent intermediate phenotypes or cells transitioning between two archetypes.

Specialist and generalist cells are detectable in SCLC tumors

To determine whether generalists exist in tumors as well, we applied AA to scRNA-seq data from SCLC human and GEMM tumors and evaluated enrichment of the bulk archetype gene signature (Figure 3F) at single-cell archetypes (Figure 4).

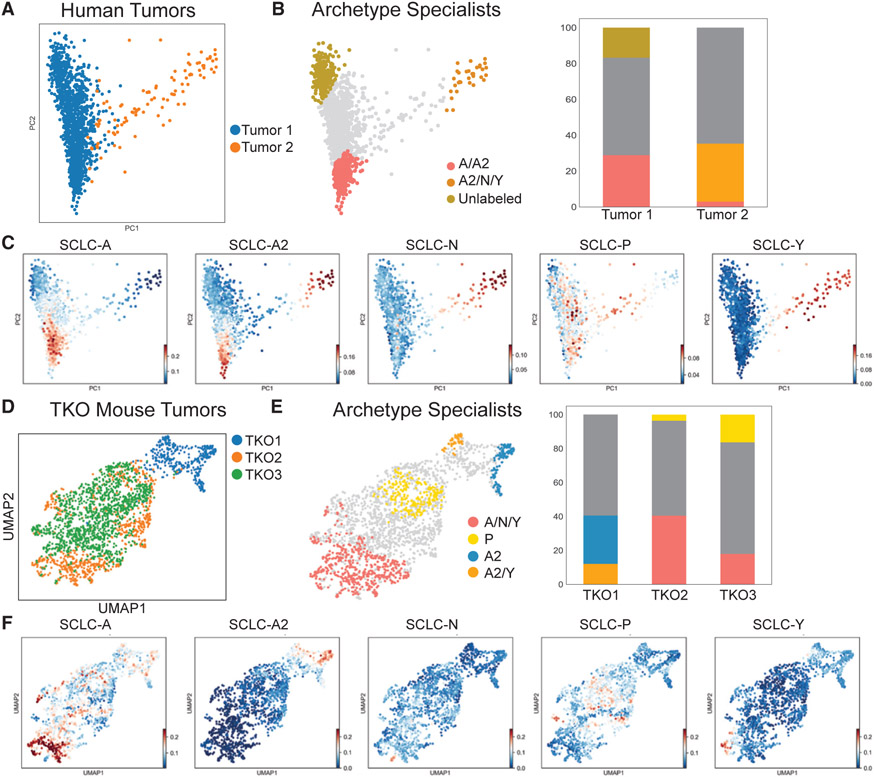
Figure 4. Archetype analysis of human tumors and triple knockout (TKO) mouse models.

(A) PCA of imputed scRNA-seq from two human tumors.

(B) Two human tumors shown in PCA with archetype specialists labeled. Three archetypes best fit the data. Specialists with scores > 0.9 are shown on the PCA projection. Bar plots show the proportions of specialists and generalists in each tumor.

(C) Bulk archetype scores used to label specialists in (B).

(D) Three TKO mouse tumors in a UMAP projection (GSE137749). TKO2 and TKO3 are from the same mouse, contributing to their overlap in the UMAP.

(E) Four archetypes fit the three TKO tumors. Archetype specialists are shown by color; generalists are shown in gray. Bar plots show the proportions of specialists and generalists in each tumor.

(F) Bulk archetype scores used to label specialists in (E). Archetype signature scores shown by color (linear scale, arbitrary units).

We sequenced single cells from human tumors from the lungs of two patients who had been treated with and relapsed from the standard-of-care therapy (etoposide and a platinum-based agent, EP; patient 1 also received prophylactic cranial irradiation; see STAR Methods; Figure S3). After filtering non-tumor cells, such as immune subpopulations (Figures S3A-S3D), we found that the single-cell variance could be explained by a low number of dimensions (PC1 explained over 60% of the variance), and this variance was partially explained by the bulk archetype space, as expected (see above sections) (Figure S3B). We therefore applied AA to the low-dimensional data and found that the tumors fit within a triangle polytope (p = 0.008, Figures S3E and S3F). Tumor 1 spanned two of the archetypes, one of which was enriched for ASCL1 expression (p = 4.19e–6) and the NE subtypes SCLC-A and SCLC-A2 (Figures 4A-4C). Of note, the second archetype did not show significant enrichment in any bulk archetype signatures (see below). Tumor 2 spanned the region between the same A/A2 archetype and an archetype most enriched in the SCLC-Y signature and YAP1 (p = 2.1e–49). This is also reflected in the projection of the tumors using the bulk archetype space: tumor 2 is closer to the SCLC-Y archetype, whereas most of the variance in tumor 1 spans the NE archetypes (Figures S3G-S3I). In both samples, subpopulations of generalist cells spanned space between the archetypes to different degrees (Figures 4B and 4C), supporting the possibility of intermediate cell states and task trade-offs in vivo, possibly as an adaptation to treatment.

We next analyzed single-cell transcriptomics from three tumors triple knockout (TKO1, 2, and 3) isolated from an Rb1^fl/fl/Tp53^fl/fl/Rbl2^fl/fl GEMM (Figures 4D-4F). TKO1 and TKO2 were primary tumors from independent replicates, and TKO3 was a metastatic tumor from the same mouse as TKO2. AA showed that the transcriptomics of all three tumors fit within a four-vertex polytope (p = 0.001, Figures S3J-S3M). In both the primary and metastatic tumors, archetype signatures revealed a large proportion of SCLC-A2 (TKO1) or SCLC-A (TKO2 and TKO3) specialists (Figure 4E). TKO2 and TKO3 also comprised specialists with a high signature score for SCLC-P (Figure 4F). In each mouse tumor analyzed, regardless of relative specialist composition, a large proportion of cells were generalists (Figure 4E). Thus, in GEMM tumors, generalists aligned along a polytope-defined Pareto front, further supporting the notion of an SCLC cell-state continuum.

Taken together, single-cell gene expression data indicated that SCLC cell lines, human, and GEMM tumors each comprise specialist and generalist cells. This characterization of single cells into a phenotypic continuum between archetypes reveals critical facets of cellular identity that may not be captured by discrete clustering frameworks. Furthermore, the assignment of phenotypic tasks and associated trade-offs in archetype space provides insights into the adaptive, dynamic nature of SCLC tumors, as addressed in the next section.

Task trade-offs drive transitions in SCLC tumors

Intra-tumoral heterogeneity spanning specialists and generalists in mouse and human tumors may have arisen due to the phenotypic plasticity of single cells. Phenotypic plasticity, in the context of SCLC archetype space, is tantamount to dynamics of task trade-offs, i.e., transitions across archetypal functional states. We previously showed that a highly plastic non-NE subpopulation emerges from NE cells after treatment in human tumors (Gay et al., 2021), raising the possibility of a trade-off between the proliferation task of NE SCLC-A specialists, which is susceptible to chemotherapy, and the injury repair/metabolic detoxification task optimized by non-NE, SCLC-Y specialists (Figure 1).

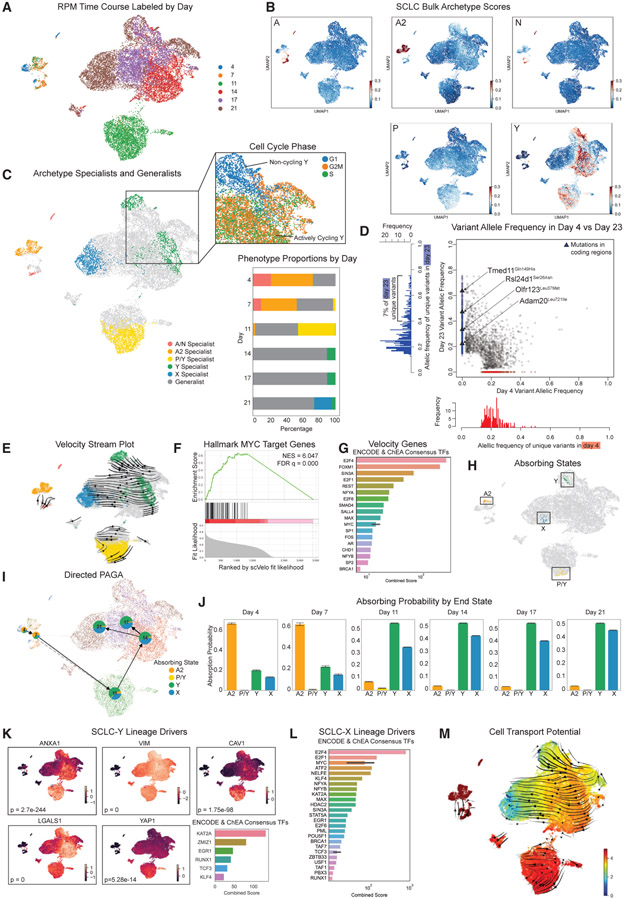
To test this possibility in independent datasets, we focused on task trade-offs along the SCLC-A and SCLC-Y axis, using cell plasticity as a proxy. Previous studies from our co-authors and others showed that SCLC cells transition between A and Y subtypes under certain perturbations, such as Notch pathway activation (Lim et al., 2017) and MYC hyperactivation (Ireland et al, 2020; Patel et al., 2021). In these studies, classical NE cells (i.e., SCLC-A, -A2, and -N) acquire non-NE properties such as variant morphology and expression of non-NE markers (such as YAP1). Furthermore, the studies on MYC suggest NE subtypes could exhibit increased plasticity under MYC activation. To investigate whether task trade-offs associated with these dynamics, we analyzed a time course of progression in a GEMM tumor with the hyperactivation of MYC (Rb1^fl/fl;TP53^fl/fl;Lox-Stop-Lox [LSL]-Myc^T58A, RPM tumors, six time points, Figures 5A and S4A-S4C) (Ireland et al., 2020). To align the previous subtyping of these time points based on key transcription factors, we tested the enrichment of bulk archetypal signatures in the single-cell time series dataset (Figure 5B). Using PCHA, we found that a six-vertex polytope best fit the combined data from all time points (p = 0.001, Figures S4D and S4E), and 5 of the 6 archetypes were enriched for SCLC signatures (Figure 5C; Table S10).

Figure 5. MYC increases the plasticity of NE specialists (SCLC-A, A2, and N) in GEMM tumor progression.

(A) UMAP of the RPM time course (GSE149180) with time points labeled. Days 4 and 7 fall in the same region of the UMAP; day 11 is mostly distinct; and days 14–21 fall in the same large cluster.

(B) Bulk archetype signature scores (linear scale, arbitrary units) shown as color for single cells in RPM time course. Days 4 and 7 are enriched in the NE SCLC-A, -A2, and -N archetype signatures; day 11 is slightly enriched for the non-NE SCLC-P and -Y signatures; and a subpopulation of days 14–21 is enriched in the SCLC-Y signature.

(C) Left: specialists for 6 archetypes are shown by color on UMAP, with generalists in gray. The 5 of 6 archetypes are enriched in SCLC signatures; the sixth archetype (blue) is labeled as X. Top right: two archetypes are enriched for the SCLC-Y signature. One of these archetypes is actively cycling, with cells in the G2M and S phases of the cell cycle. The other is non-cycling. Bottom right: stacked bar plots show overall subtype composition change.

(D) Variant allele frequency for beginning (day 4) and end (day 23) of an independent RPM time course. Only 4 variants unique to day 23 are in coding regions (triangles), and less than 7% of variants are high frequency, suggesting minimal clonal evolution. This supports the notion that phenotype transitions, rather than clonal selection, drive movement from NE to non-NE archetypes.

(E) RNA velocity shows transition across the time course in UMAP projection.

(F) Hallmark gene set of MYC targets is enriched in gene set with high fit likelihoods for dynamical RNA velocity model.

(G) ENCODE and ChEA consensus TFs from EnrichR analysis of top fit likelihood genes (likelihood > 0.3). The consensus score from EnrichR shown. For genes from both sources (i.e., ENCODE and ChEA both have the TF), a black bar shows 95% confidence interval on the mean consensus score. E2F family genes and MYC are key drivers of the transition.

(H) Using CellRank, we fit a Markov transition matrix to these dynamics using a weighted kernel of the RNA velocity (weight = 0.8) and diffusion pseudotime (DPT) calculated in Ireland et al. (2020) (weight = 0.2). Using the CellRank implementation of a GPCCA estimator, we find end states for the Markov chain model and display the top 30 most likely cells for each absorbing (end) state.

(I) PAGA plot shows transitions between time points. Pie plots overlaid on PAGA show aggregate lineage probabilities by time point.

(J) Aggregate lineage probabilities by time point shown as a bar plot, with absorption probability on the y axis.

(K) Lineage drivers of the SCLC-Y lineage. Genes correlated to absorption probabilities for the SCLC-Y lineage are considered drivers of that lineage. UMAP of select lineage drivers from the SCLC-Y archetype signature is shown, with normalized gene expression shown by color (rescaled log-normalized expression). EnrichR analysis shows TF regulators, ranked by consensus score, of the top 40 significant lineage drivers sorted by correlation with lineage (p < 0.05). TCF3 is in the SCLC network described in Wooten et al. (2019); RUNX1 was predicted to regulate an intermediate osteogenic state in an RPM mouse model with inactivated ASCL1 (Olsen et al., 2021).

(L) TF regulators of lineage drivers for the X absorbing state. As in (K), EnrichR was used to rank regulators by consensus score. E2F family genes, MYC, and RUNX1 are regulators of the X lineage. For genes found in both sources (ENCODE and ChEA), 95% confidence interval shown as black bar around mean of scores from each source.

(M) Cell transport potential (shown by color, linear scale, arbitrary units) shows most plastic subtypes across the time course. Cells closer to the NE archetypes SCLC-A and -A2 have higher plasticity in earlier time points. CTrP decreases over time, consistent with cells that transition from NE phenotypes to non-NE phenotypes with lower plasticity.

At the earliest time points (days 4 and 7), tumors were largely composed of SCLC-A/N and SCLC-A2 specialist cells (>50%), forming a continuum of specialists and generalists near the NE archetypes. By day 11, the population of cells was near an SCLC-P/Y archetype (Figures 5C and S4F-S4G). Two archetypes in the dataset were enriched in the SCLC-Y signature (green in Figure 5C) but differed markedly in cell cycle gene representation: one was dominated by G2M and S genes, whereas the other contained cells mostly in the G1 phase. From days 14 to 21, cells moved toward these SCLC-Y archetypes, consistent with the increase in YAP1 expression found in Ireland et al. (2020). By day 21, cells fall near a new 6th archetype with a distinctive gene expression profile not enriched in any of the SCLC signatures (X specialists, blue in Figure 5C). Gene set enrichment analysis (GSEA) showed that Archetype X is enriched for the following hallmark gene sets: MYC targets, oxidative phosphorylation, reactive oxygen species (ROS) pathway, and glycolysis (Figure S4H). Archetype X is significantly depleted in hallmark gene sets related to cell cycle terms (mitotic spindle and G2M checkpoint, false discovery rate [FDR] q val = 0.000 for each term) and hypoxia (FDR q val = 0.000) (Figure S4H). Further research will be necessary to characterize this new non-NE archetype. In summary, the changing proportions of archetypal subpopulations over the time course suggest that cells may be trading off between the NE and non-NE archetypal tasks.

We sought to validate that cell-state transitions, rather than clonal selection, were responsible for the observed shift in phenotype from NE to non-NE. To this end, we performed whole-genome sequencing on independent samples from days 4 and 23 (Figures 5D and S4I). We filtered variants by read depth and compared the frequency of variants across the two time points. If the clonal selection of a preexisting non-NE rare subpopulation was driving the dynamics of the time course, we would expect to see a substantial number of subclonal variants from day 4 increase in allelic frequency at day 23. Instead, we found that only 7% of the total somatic variants were unique to and had high allelic frequencies (greater than 0.4) on day 23. Furthermore, only four of the variants unique to day 23 are in coding regions (triangles in Figure 5D). None of the four genes are associated with SCLC phenotype identity and show low to no expression dynamics in the scRNA-seq data, suggesting these variants do not drive phenotypic evolution (Figure S4J). Thus, there is minimal genetic evolution between days 4 and 23, and the transformation of cell state over this time course is most likely due to phenotypic transitions rather than clonal selection. Together, these results indicate that RPM tumor cells can transition between NE and non-NE states, possibly as a result of MYC-driven archetype task trade-offs.

Plasticity analysis identifies regulators of task trade-offs

We next sought a method that could deconvolve two aspects of plasticity, reflecting two distinct qualities of the underlying phenotypic landscape: containment and drift potential Weinreb et al., 2018). Containment potential should be reflected in the multipotency of cells. Therefore, we examined whether cells progressed along multiple lineages using CellRank (Lange et al., 2022). To approximate drift potential, we calculated an expected distance of transition for every single cell, here termed CTrP, to reflect movement across phenotypic space (see STAR Methods).

First, to determine the transition paths of cells along the time course, we applied RNA velocity analysis using scVelo (Figures 5E and S5A-S5C) (Bergen et al., 2020; La Manno et al., 2018). We fit each gene using a dynamical model and investigated the genes with top fit likelihoods (see STAR Methods; Figures S5D and S5E). GSEA shows that genes ranked by their fit likelihood were enriched for MYC target genes (q = 0.000), corroborating that MYC is critical for driving the transitions across time points (Figure 5F). We next used EnrichR (Chen et al., 2013) to investigate TFs that regulate the top fit genes (fit likelihood > 0.3), and we found it validated MYC as an important regulator of the velocity dynamics (Figure 5G). E2F family proteins, REST, and SMAD4 were also identified as regulators, consistent with previous reports implicating them in SCLC progression (Lim et al., 2017; Wang et al., 2017; Wooten et al., 2019).

Using CellRank (Lange et al., 2022), we fit a Markov chain model by combining two sources of dynamic information: diffusion pseudotime calculated in Ireland et al. (2020) and RNA velocity. We find four regions of end states (absorbing states, Figure 5H), two in earlier (days 7 and 11) and two in later time points (days 17 and 21). Of note, all of the absorbing states are in specialist regions rather than generalists (SCLC-A2, P/Y, Y, and X specialists). A coarse-grained PAGA graph shows transitions between time points as expected, with varying proportions of cells in each time point transitioning toward each end state (Figure 5I). About two-thirds of the cells in days 4 and 7 transition toward the A2 end state, whereas the remaining third transitions toward the Y and X end states. The remaining time points (11–21) are split between the SCLC-Y and X lineages (Figure 5J).

We then correlated the probabilities of absorption at either end state with gene expression to find potential lineage drivers for SCLC-Y and X and applied EnrichR to investigate TFs that regulate these genes (Figures 5K, 5L, S5F, and S5G). VIM and LGALS1 were two of the top SCLC-Y lineage drivers, consistent with their presence in our SCLC-Y archetype signature (Figure 5K). In fact, 19 of 24 genes from the SCLC-Y signature (Figure 3F) were identified as significant lineage drivers (q < 0.05), confirming their role in driving this phenotype. The top SCLC-Y lineage drivers were regulated by TCF3 and RUNX1, which we previously showed may be important in SCLC progression (Figures 5K and S5G) (Olsen et al., 2021; Wooten et al., 2019).

SCLC-X lineage drivers are regulated by MYC, RUNX1, and E2F family genes, suggesting MYC activation is key to reaching this archetype (Figures 5L and S5G). Furthermore, ChEA identified as X lineage regulators several TFs that maintain pluripotent stem cells, such as OCT4, NANOG, and SOX2 (Figure S5G). To determine if the TF regulators of the SCLC-Y and X lineages interact, we used STRING to construct a regulatory network (Figure S5H) (Snel et al., 2000; Szklarczyk et al., 2021). Twelve of the 86 drivers regulated both lineages, including SOX2, RUNX1, and KLF and E2F family genes. An analysis of node centrality demonstrated that p300, which is often mutated in SCLC (George et al., 2015) and may be associated with poor prognosis (Gao et al., 2014; Hou et al., 2018; Jia et al., 2018), regulates the most child nodes (38) in the network. Other central TFs include MYC, as expected; JUN, which is important for the SCLC-to-NSCLC transition (Risse-Hackl et al., 1998; Shimizu et al., 2008); and CEBP family genes, which have been shown to play a vital role in inflammatory diseases, including cancer (Chi et al., 2021).

Finally, as a proxy for drift potential, we calculated CTrP in this dataset (see above, top of this section). As expected for a time course of phenotype-transitioning cells, CTrP decreased steadily over the time course (Figure 5M). Despite the presence of early time point end states (A2 and P/Y, Figure 5H), all specialist cells in early time points had higher CTrP than later time points (Figure S5I). Together, our plasticity analysis indicates that MYC increases the plasticity of early time point cells (NE specialists) allowing them to transition to the non-NE SCLC-Y archetype and the new Archetype X, which may be regulated by multipotency TFs.

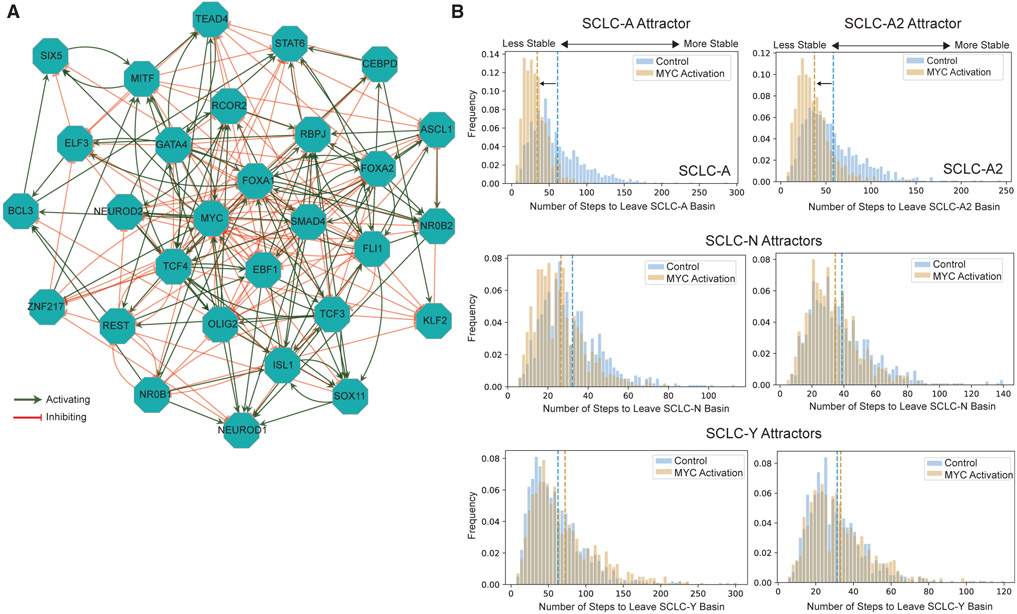
Network analysis validates the role of MYC in driving SCLC plasticity

To gain mechanistic insights into the effects of MYC on plasticity, we introduced MYC into an SCLC-specific TF network (Figure 6A). As we described (Wooten et al., 2019), computer simulations of this TF network dynamics reveal attractors (i.e., network equilibrium states) that correspond well to the experimentally defined SCLC subtypes. The stability of these attractors (i.e., subtypes) can be quantified with the BooleaBayes algorithm (Wooten et al., 2019). To mirror the experimental conditions of Ireland et al., 2020, we imposed constitutive activation to the MYC node in the simulations of the dynamics of the modified SCLC TF network. This modification decreased the number of steps needed to leave the NE attractors; that is, MYC activation destabilized the SCLC-A and SCLC-A2 attractors but did not destabilize the SCLC-N or the non-NE SCLC-Y attractors (Figure 6B). The in silico perturbations suggest that the activation of MYC and the subsequent epigenetic regulations may be able to shift NE cells to non-NE by destabilizing the NE attractor (cell state). Further experiments will determine whether MYC activation is necessary and sufficient for this phenotype shift to occur.

Figure 6. MYC activation destabilizes NE states.

(A) Transcription factor network adapted from Wooten et al. to incorporate MYC activity.

(B) In silico destabilization of NE specialists by MYC activation. Using BooleaBayes simulations (Wooten et al., 2019), we performed random walks with activated MYC and found that SCLC-A and SCLC-A2 states are destabilized; i.e., MYC activation is capable of increasing plasticity of these subtypes in RPM tumors. SCLC-N and SCLC-Y attractors were not destabilized.

The above independent lines of evidence indicate the following: (12) MYC overactivity can drive phenotype transitions from NE to non-NE states, as confirmed by whole-genome sequencing showing little clonal evolution, and () MYC may be capable of increasing the plasticity of NE subtypes, as demonstrated by in silico simulations and RNA velocity analysis. Together, this suggests that the upregulation or activation of MYC can increase NE cell plasticity to promote cell-state transitions toward a non-NE state, which may help cancer cells overcome treatment.

DISCUSSION

The goal of this study was to produce insights into the role SCLC heterogeneous subtype dynamics and phenotypic plasticity may play in supporting aggressive and recalcitrant features of SCLC (Ireland et al., 2020; Lim et al., 2017; Stewart et al., 2020). Our study is timely in view of the recent consensus on SCLC classification into transcriptional subtypes (Rudin et al., 2019), which compels much-needed new lines of research in SCLC and provides impetus to investigate in depth the sources of SCLC heterogeneity.

In analyzing SCLC datasets from diverse sources (i.e., human tumors and cell lines, GEMM tumors), we realized that current subtypes, admittedly still a work in progress (Rudin et al., 2019), are insufficient to capture SCLC heterogeneity dynamics because they are based on discrete clusters, whereas SCLC cells from cell lines and tumors often fall between distinct subtypes by customary transcriptomics analyses. Here, we propose an alternative, continuous view of SCLC heterogeneity based on SCLC archetypes defined by functional tasks.

Although there was a high concordance between archetypes and consensus subtypes, the archetype-bounded phenotypic space paradigm presented several advantages that better represent SCLC heterogeneity. First, the transcriptional profile of every single cell can be evaluated based on distance from archetypes and graded as a specialist or generalist (e.g., a cell between archetypes N and Y has a generalist phenotype with a high degree of N and Y character). Second, our flexible pipeline can determine how the five SCLC archetypes from our bulk analysis relate to single-cell AA for any new sample, such as the human tumor archetype enriched in both A and A2 signatures, or the new Archetype X found in the RPM time series data. Third, cell-state transitions are rooted in multi-task evolutionary theory such that movement across the phenotypic continuum fulfills the goal of trading off between tasks, providing a functional interpretation of SCLC phenotypes as they adapt to microenvironmental selective pressures.

Cooperation of SCLC archetypal tasks

Using GSEA, we were able to relate tasks optimized by each SCLC specialist cell type in archetype space to tasks fulfilled by normal PNECs, itself a plastic cell. We then projected single-cell data into an archetype-defined polytope and found intratumoral heterogeneity aligns with inter-sample diversity. Batch and technical effects can make the comparison across data platforms, such as scRNA-seq and bulk RNA-seq, difficult. Therefore, additional technical replicates may be necessary to confirm the relationship between the bulk archetype space and the variability of single cells. Even so, our results suggested that SCLC cell lines and tumors comprise specialist and generalist cells, with single cells optimizing various tasks within a single tumor, demonstrating a high degree of both intra- and inter-tumoral heterogeneity. This palette of biological tasks within a cell line or tumor agrees with recent reports indicating that lung tumors are capable of building their own microenvironment, where SCLC cell types (NE and non-NE) were found to interact in a way that is mutually beneficial to the growth of the tumor (Calbo et al., 2011; Huch and Rawlins, 2017; Kwon et al., 2015; Lim et al., 2017). Similarly, we expect SCLC cells optimizing archetypal functions to cooperate in vivo by performing PNEC-related tasks that contribute to the growth of a tumor in the face of changing external conditions, such as treatment. It remains to be seen whether the normal functions of PNECs represent an actionable constraint for SCLC cells.

Our analysis suggests that multi-task optimization under Pareto theory shapes SCLC phenotypic space, supported by the enriched gene programs and experimentally tested tasks of each archetype. However, a polytope could result from other phenomena. For example, each archetype could correspond to a weighted average of five transcriptional profiles. Although we show preliminary experimental evidence that each archetype optimizes a specific task, further work is needed to validate the task trade-offs characteristic of Pareto optimality. Phenotypic perturbation experiments may help determine the cost trade-off between archetypes and uncover the relationship between archetypal task optimization and tumor fitness. For example, Archetype 1 (SCLC-A) cells optimize proliferation (function) and, therefore, are highly chemosensitive (cost). By contrast, a transition to Archetype 5 (SCLC-Y) under chemotherapy may decrease the rate of growth of a tumor (cost) but are better able to respond to cell injury and may therefore better survive treatment (function). The optimization of two tasks may be a key to establishing resistance to treatment. The emergence of Archetype X in RPM tumors may reflect the ability of SCLC to expand the Pareto front to new phenotypes under MYC hyperactivation, and experimental validation will be necessary to determine this.

In this respect, the similarity between SCLC and PNEC tasks should be adjusted to reflect the neoplastic nature of SCLC. Thus, a comparison between SCLC archetypal tasks and cancer hallmarks is also relevant. As we describe in the Results section, there are uncanny relationships between PNEC tasks and cancer hallmarks. The virtually ubiquitous biallelic inactivation of Rb and p53 tumor suppressors in SCLC suggests that PNEC functions are enacted in SCLC cells in the absence of negative feedback to regulate cell division (see SCLC and PNEC plasticity for additional details).

SCLC and PNEC plasticity

Multi-task evolutionary theory suggests that the source of the heterogeneous ecosystem of phenotypes arises in SCLC tumors due to cell state transitions driven by task trade-offs. By quantifying multipotency and CTrP, we uncovered subpopulations of high plasticity, capable of transitioning to multiple other phenotypes. We speculate that the plasticity of SCLC cells may derive from the dysregulation of the innate plasticity in normal PNECs. After injury to the lung epithelium, “specialist” stem-like PNECs can transdifferentiate to perform repair tasks and regenerate specialist club cells, whose main task is the secretion of protective proteins, most likely through non-genetic mechanisms (Oudah et al., 2019). As shown in the tumors analyzed here, SCLC cells can likewise transition between NE and non-NE phenotypes.

It is tempting to speculate that such levels of adaptability may be responsible for the highly aggressive and recalcitrant features of SCLC tumors. For instance, an altered balance in favor of the wound-healing SCLC-Y specialists may be expected in tumors immediately after treatment, as supported by treated human tumor data reported here, and could be further tested experimentally in GEMM or PDX tumors. These dynamics could explain the initial exceptional response to chemotherapy seen in patients, which is inevitably followed by relapse as cells transition to generalist and non-NE specialist cells better equipped to overcome chemotherapy by ROS detoxification, and still be suboptimal at cell division.

Controlling plasticity in SCLC

Previously, a subset of SCLC cells has been shown to be capable of the long-term propagation of tumors (tumor propagating cells [TPCs]) (Jahchan et al., 2016), and it is unclear how these cells relate to the archetypes described here, as well as to our definition of plastic potential. Although SCLC-A cells express markers for TPCs (positive for EPCAM, MYCL, and CD24 and negative for CD44), it remains to be seen whether SCLC-A cells correspond to TPCs functionally or if TPCs can span archetype space. Similarly, a PLCG2-expressing stem-like subpopulation was recently reported in a survey of human SCLC tumors (Chan et al., 2021). This stem-like cell may be consistent with a diverse, stem-like functional state since it is present across SCLC-A, -N, and -P tumors. PLCG2, enriched in SCLC-P, was present in our archetype signature. Further work is needed to understand the relationship between this archetype and stemness.

Plasticity is dependent on the underlying genetics that determine the shape of the phenotypic landscape, the particular cellular state in which a cell resides due to epigenetic regulation, and any external conditions that may transiently distort the landscape. For this reason, epigenetic methods may directly target plasticity, such as gene regulatory network perturbations. Furthermore, previous research suggests that MYC may play a role in genome-wide transcriptional upregulation, allowing cells to change expressed gene programs and thus phenotype (Lin et al., 2012). In other words, MYC may allow cells to “move further” in gene expression space, as shown here by increased CTrP. However, future studies, such as using an inducible MYC model in GEMMs or PDXs, will be necessary to determine the complete mechanism underlying the relationship between MYC and phenotype plasticity.

Task trade-offs and acquired resistance

The current standard of care for SCLC is predicated upon targeting highly proliferative cells. However, this treatment inevitably results in resistant relapse. Highly plastic cells detected in SCLC cell lines and tumors suggest that plasticity may drive resistance in SCLC, consistent with a recent study showing increased intratumoral heterogeneity upon chemotherapy relapse (Stewart et al., 2020). The archetype continuum shows that plasticity enables SCLC cells to trade off PNEC-related tasks, which translates to a high level of adaptability to diverse microenvironments. Thus, plasticity may also be responsible for SCLC aggressive traits, such as local invasion and early metastatic spread. Therefore, our work suggests two strategies for treatment. First, the placement of transcriptomics data from a patient into the archetypal framework can identify targetable cancer cell functions individualized for that patient’s tumor. For example, the SCLC-A archetype is preferentially sensitive to DNA alkylating agents, and numerous alkylating agents have been evaluated in the context of SCLC (e.g., cytoxan and bendamustine) and are included in professional guidelines (such as the National Comprehensive Care Network guidelines) for treatment. Further work is needed to show that the archetypal framework could identify patients preferentially sensitive to alkylating agents. Second, our analyses suggest strategies to target plasticity directly, by simulation of TF network dynamics, as suggested by our result that MYC inhibition may prevent transitions from the A subtype. Given the primary role of TFs in driving SCLC phenotype (Wooten et al., 2019), SCLC should be a prime candidate for plasticity-targeted therapy.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Vito Quaranta (vito.quaranta@vanderbilt.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• Sequencing data for human cell lines and tumors are deposited in GEO: GSE193961. Other sequencing data was obtained from the NCBI GEO database deposited at GEO: GSE149180 (RPM scRNA-seq and WGS) and GEO: GSE137749 (TKO scRNA-seq).

• The data analyzed in this study was performed using custom Python and R code, as well as open-source software packages and previously published software (BooleaBayes) (Wooten et al., 2019). The code generated during this study has been deposited in a Github repository and is available at https://zenodo.org/badge/latestdoi/426287007.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Human SCLC cell lines

Eight SCLC human cell lines were used for single-cell RNA-sequencing and were obtained from ATCC. We chose two cell lines from each NE subtype (A: NCI-H69 and CORL279, A2: DMS53 and DMS454; N: NCI-H82 and NCI-H524) and one cell line from each non-NE subtype (P: NCI-H1048; Y: NCI-H841). Cell lines were grown in the preferred media by ATCC in incubators at 37 degrees Celsius and 5% CO2. SCLC human cell lines were validated by matching transcript abundance in scRNA-seq to the bulk RNA-seq data from Cancer Cell Line Encyclopedia (CCLE).

Human tumors

Patients with SCLC were prospectively identified and consented using an Institutional Review Board (IRB, #030763) approved protocol for collection of tissue plus clinical information and treatment history. All samples were de-identified and protected health information was reviewed according to the Health Insurance Portability and Accountability Act (HIPAA) guidelines. The two human SCLC tumors were collected in collaboration with Vanderbilt University Medical Center. Tumor #1 was a relapsed tumor collected via bronchoscopy with transbronchial needle aspiration of a left hilar mass. The patient had completed carboplatin and etoposide and then prophylactic cranial irradiation. The tissue was immediately washed in an RBC lysis buffer, passed through a 70 μm filter, and washed in PBS to prepare for single-cell sequencing. Human tumor #2 was a stage 1B SCLC tumor with a mixed large cell NE component treated with etoposide and cisplatin and was surgically removed via right upper lobectomy. The tumor was immediately placed in cold RPMI on ice in preparation for single-cell sequencing.

Mouse tumors

The Rb1/p53/Myc (RPM) mice are available at JAX#029971; RRID: IMSR_JAX:029971 and all experiments with RPM cells were previously performed as in Ireland et al. (2020). TKO mouse lines used were the triple-knockout (TKO) SCLC mouse model bearing deletions of floxed (fl) alleles of p53, Rb, and p130 as previously described (PMID: 20406986). For in vivo SCLC tumor studies with this model, 8 to 12 weeks old mice were used for cancer initiation, and tumors were collected 6-7 months later.

METHOD DETAILS

Bulk SCLC Cell Line RNA-seq Data Preprocessing

Bulk RNA sequencing expression data on SCLC cell lines were taken from two sources: 50 cell lines were taken from the Cancer Cell Line Encyclopedia and 70 cell lines (not including H69 variants) were taken from cBioPortal (Cerami et al., 2012; Gao et al., 2013) deposited by Minna Lab (Data from McMillan et al. [2018]. Data available in dbGaP [PHS001823.v1.p1]). Access to data from cBioPortal was provided by participation in the NCI SCLC Consortium. 29 cell lines overlapped between the datasets, so a “c” (CCLE) or “m” (Minna) was used to denote the source of each cell line. Each dataset was filtered and normalized independently and then batch corrected together. For each source, genes and cell lines with all NAs were removed, as well as mitochondrial genes. The counts data is then normalized by library size and transcript abundance to TPM values. The two datasets were combined using overlapping genes and log-transformed, and genes with low expression across all samples were removed (cutoff of log(TPM) >= 1). The two datasets were then batch corrected using the sva R package, which includes a ComBat-based integration method (Johnson et al., 2007; Leek and Storey, 2007). SVA, or surrogate variable analysis, uses a null model and a full model to derive hidden variables, such as batch, that may contribute to gene expression variance across samples. The four SCLC TF factors that define broad subtypes— ASCL1 (A), NEUROD1 (N), YAP1 (Y), and POU2F3 (P)— were used to align the two datasets to each other. Batch-corrected distributions of gene expression are shown in Figures S1A and S1B. The resulting dataset contained 120 samples and 15,950 genes.

Initial clustering of cell line RNA-seq

For labeling cell lines by subtype cluster (Figures S1B and S1C), hierarchical clustering with the Spearman distance metric was calculated using the R function hclust and cluster cutoffs were determined manually. Cell lines previously characterized as SCLC-A in Wooten et al. (2019) comprised two branches of the dendrogram separated by SCLC-N cell lines, most likely due to the dual positivity of ASCL1 and NEUROD1 in some SCLC-A cell lines. Cell line H82 (from both data sources) was considered “unclustered,” as it has previously been considered an SCLC-N cell line (with positive expression of NEUROD1) but was clustered with SCLC-Y cell lines here. As shown in Figure 3B, H82 falls in between SCLC-Y and SCLC-N archetypes, corroborating our conclusion that clustering cannot adequately describe all cell lines. Principal Component Analysis (PCA) was run on the bulk RNA-seq dataset using the R prcomp function. The R package factoextra was used to visualize the percentage explained variance for each principal component up to 30. The elbow method on explained variance per component was used to choose 12 principal components for downstream analysis (Figure S1E). The top 12 principal components were able to explain ~50% of the variance in the dataset, suggesting a low-dimensional representation of the data was possible.

Weighted Gene Co-expression Network Analysis (WGCNA) of human cell line bulk RNA-seq

To identify gene programs associated with the five SCLC phenotypes found with clustering, we performed weighted gene co-expression network analysis (WGCNA) on the same RNA-seq data (Figure S1D (Langfelder and Horvath, 2008)). First, we generated an unsigned network adjacency matrix from the gene expression data and then calculated a topological overlap matrix (TOM). Hierarchical clustering on 1-TOM using method = ‘average,’ and the function sampledBlockwiseModules was used to generate stable gene modules, with parameters: minModuleSize = 50, corType = ‘bicor’, deepSplit = 1.5, and pamRespects Dendro = False. We then fed these module labels into the blockwiseModules function as stabilityLabels, with minStabilityDissim = 0.45. This resulted in robust gene modules that could describe the RNA-seq data. We used WGCNA’s GOenrichmentAnalysis function to find enriched GO terms associated with each module, as shown in Figure S1D.

Archetypal Analysis using PCHA

Using an AA method known as Principle Convex Hull Analysis (PCHA) we found a low-dimensional Principal Convex Hull (PCH) for the cell line dataset (Mørup and Hansen, 2012). The convex hull is the minimal convex set of data points that can envelop the whole dataset. The PCH is a subset of the convex hull comprising a set of vertices, or archetypes, that form a polytope able to capture the shape of the data. The vertices are constrained to be a weighted average of the data points, and the data points are then approximated as a weighted average of the vertices. The algorithm solves the optimization problem of minimizing the norm of the approximated data subtracted from the original data. The algorithm constraints can be relaxed such that the vertices can be found within a certain volume around the convex hull; i.e. relaxing the constraint that the vertices must fall on the convex hull. By comparing the convex hull to the PCH, we can determine how well a low-dimensional shape fits the dataset with a statistical test, and thus ascertain the optimal number of vertices, or archetypes, that best define the shape.

Determining the number of archetypes in the human cell line data

Archetypal Analysis was done using the Matlab package ParTI (Hart et al., 2015). To determine the best k, we found the explained variance (EV) for each number of archetypes k, which is computed by the PCHA algorithm (in the function ParTI_lite) as previously described (Cutler and Breiman, 1994; Korem et al., 2015) Then, we chose a number of archetypes, k*, for which the EV doesn’t increase by much when adding additional archetypes (Figure 1A). In practice, this is done by finding the “elbow” of the EV versus k curve, which is the most distant point from the line that passes through the first (k=2) and the last (k = k_max= 15) points in the graph. Because this could be dependent on our choice of k_max, we varied k_max between 8 and 15 and found k* in each case. K* = 5 for 6 of 8 EV versus k plots; k* = 4 when k_max =12, and k* = 6 when k_max = 11. Therefore, we proceeded with our analysis using k* = 4, 5, or 6 (Figures S1E and S1F).

Finding the best fit polytope and evaluating significance with a t-ratio test

The function ParTI was then used for the full analysis for each k* with parameters dim = 12 (dimensions) and algNum = 5 (PCHA) to find the location of the archetypes in gene expression space. To measure the similarity between the data and a polytope is its t-ratio. This was calculated by comparing the ratio of the polytope volume to that of the convex hull. For PCHA, a bigger t-ratio suggests the polytope is more similar to the data (and thus a better fit). Empirical p-values were calculated by comparing the t-ratio of the data to that of 1000 sets of shuffled data, as described in Korem et al. (2015). The p-value was defined as the fraction of sets for which the t-ratio is equal to or larger than that of the data. P-values for different numbers of archetypes are reported in Table S2. The p-value for 5 archetypes, p = 0.034, suggests the polytope fits the data well. We also tested k* = 3, even though it was not suggested by ParTI software. We found this polytope has an insignificant p-value of 0.58, suggesting it does not fit the data well. We therefore do not show the results for this polytope, but we show 4, 5 and 6 vertices, in Figures S1E and S1F.

We adapted a method from Hausser et al. (2019) to compare the archetypes found for 4, 5, and 6-vertex polytopes. Briefly, we compare the significantly enriched (FDR <10% and log₂ fold change > 0.1) gene sets at each archetype (described below in “Gene and ontology enrichment at archetype locations”) using a hypergeometric test. This allows us to test if the number of overlapping enriched sets for the two archetypes is significantly higher than expected, given the null hypothesis of random sampling from the union of gene sets found at any archetype in a given polytope. The results of these tests are shown in Table S3.

Errors were then calculated on each archetype location by sampling the data with replacement and calculating the archetypes on the bootstrapped data sets (1000 times, Figures S1E and S1F). Error on the archetypes gives an idea of the variance in archetype position expected, and a smaller variance suggests the archetype is robust to outlier samples. In the 5-vertex polytope, the errors on each archetype are relatively small, suggesting none are dependent on outliers in the data.

Enrichment of hierarchical clustering subtype labels at each archetype

Enrichment of subtype labels was determined using the ParTI function DiscreteEnrichment. Cell lines were binned into 10 bins according to distance from each archetype. For each subtype label (from hierarchical clustering above), the percentage of labels in the bin closest to the archetype was compared to the percentage in the rest of the data using a hypergeometric test. Enrichment was considered significant, as it was for all five subtypes, if the bin closest to the archetype was maximal for that label and the FDR-corrected p-value for the hypergeometric test was significant (Benjamini-Hochberg, q < 0.1). After binning the data into ten bins by distance to archetype, we found that each archetype was enriched in cell lines from one of the five SCLC subtypes (Figure 1B). For example, canonical SCLC-A-labeled cell lines were enriched in the bin closest to archetype 1 (orange line), but no SCLC-A cell lines were found in bins closest to the other four archetypes. Likewise, bins closest to the remaining 4 archetypes each contained cell lines from the remaining 4 canonical subtypes (Figure 1B).

Gene and ontology enrichment at archetype locations

To find genes enriched by each archetype, we tested the enrichment of each feature on the bin closest to archetypes versus the rest of the data. For each archetype, data were separated into 10 bins according to the distance from the archetype (12 samples in each bin). The ParTI function ContinuousEnrichment was used to analyze gene expression of all 15,950 genes (Table S5) and Cancer Hallmark Gene Sets (Table S7). Cancer hallmark gene sets were transformed into a matrix using the function MakeGOMatrix such that each row is a sample, each column represents an MSigDB category, and expression values represent the average expression of genes belonging to that MSigDB category. Data were binned into 10 bins according to distance from each archetype. The expression of each feature was compared between the closest bin to each archetype and the rest of the data using a Mann-Whitney test (FDR-corrected p-value, q<0.1). To determine PNEC functions enriched at each archetype, we used ConsensusPathDB (Kamburov et al., 2013) on the top 300 most enriched genes for each archetype, as well as for PNECs and other airway cell types from Montoro et al (2018). (using Scanpy’s function rank_genes_groups, Table S6). As described in Wooten et al. (2019) we used t-SNE to cluster the GO terms, using distances from GOSemSim (Yu et al., 2010). We then chose clusters with GO terms related to PNEC tasks and evaluated enrichment of these terms at each archetype.

Archetype analysis on bulk RNA-seq from 81 human tumors

Batch correction of cell line and tumor datasets

We chose to define archetypes on cell lines because cell lines are generally thought to be less heterogeneous than tumor samples, and therefore may better represent extreme, pure phenotypes rather than mixed (averaged) phenotypes of tumors. To test whether it is true that cell lines better represent extreme phenotypes in our particular SCLC samples, we combined our dataset of 120 cell lines with an independent dataset of 81 human SCLC tumors (George et al., 2015) and analyzed the relationships between the cell lines and tumor samples. First, we batch corrected this data using SVA as described in our methods to ensure that technical variation was not driving the differences between the cell line and tumor datasets. Cell line RNA-seq datasets were preprocessed as described above. Similar to cell line datasets, for an RNA-seq dataset of 81 human tumors from George et al. (2015), genes and cell lines with all NAs were removed, as well as mitochondrial genes. The counts data was then normalized by library size and transcript abundance to TPM values. The cell line and tumor datasets were combined using overlapping genes and then log-transformed, and genes with low expression across all samples were removed (cutoff of log(TPM) >= 1). The two datasets were then batch corrected using the sva R package. A ComBat model (Johnson et al., 2007; Leek and Storey, 2007), implemented in the sva package, best aligned the distributions of log-transformed expression (Figure S1G). The resulting dataset contains 14,545 genes and 201 samples.

The variance between human cell lines is aligned with variance between human tumors

We next fit a principal components analysis (PCA) model to this combined dataset. We find that the tumor samples tend to be contained within the same archetype space as defined by cell lines, as shown in Figure 1C. Next, we compared a PCA model fit to tumor samples only to this PCA on the combined dataset, to determine how variance in the cell lines differs from variance in the tumors. We find that the top PCs of the tumor-only model match the top PCs in the combined-dataset model, as shown by the correlation coefficients between the top PC loadings from each model (see Figure S1H). This suggests that the variance, and thus extreme phenotypes, seen in cell lines is similar to the variance seen in tumor samples.

Once we determined that the variance in SCLC cell lines and tumors is aligned, we applied archetype analysis directly to the tumor data. We use the ParTI MATLAB package to run PCHA and find archetypes associated with (a) the combined dataset and (b) the tumor data only, and used a method described in Hausser et al. (2019) to match the archetypes to our 5 cell-line archetypes.

AA on a combined dataset of cell lines and tumors

We adapted a method from Hausser et al. (2019) to find ‘SCLC universal’ archetypes associated with both cell line and tumor samples. To find the best number of archetypes k* that explains this combined dataset, we found the “elbow” of the Explained Variance (EV) versus k curve, which is the most distant point from the line that passes through the first (k=2) and the last (k = k_max= 15) points in the graph. Because this could be dependent on our choice of k_max, we varied k_max between 8 and 15 and found k* in each case. The Elbow method on the EV vs k plot suggests k* = 4 (when k_max = 8), 5 (k_max = 9, 10, 11, or 15) or 6 (k_max = 12, 13, or 14) archetypes best fit the tumor data. We ran ParTI for k* = 4, 5, or 6 and found that 5 archetypes gave the most significant p-value (p = 0.59 for k*=4; p = 0.09 for k*=5; p =0.33 for k* = 6).

AA on tumor samples only

We then performed our analysis on tumor samples and compared the tumor-only archetypes to the archetypes defined by cell lines alone. Using the elbow method and varying k_max between 8 and 15, PCHA suggested k* = 3 (k_max = 8, 10), k* = 4 (k_max = 9, 12), k* = 5 (k_max = 11, 13), or k* = 6 (k_max = 14, 15). Interestingly, no best fit polytope with 3 to 7 vertices was significant according to its t-ratio. We wondered if this was due to our hypothesis that tumors are more mixed than cell lines. As described in Note S2 of Hausser et al. (2019), “mixing cell types in different proportions should produce tumors that describe polyhedra in linear gene expression space (Shen-Orr et al., 2010), but not log gene expression space.” We, therefore, looked for polytopes in linear gene expression space by exponentiating gene expression and subtracting 1 (inverse operation of log(x+1)) before mean-centering the data and performing a PCA. In linear space, the elbow method suggested k* = 5 for all k_max between 8 and 15. To ensure k* = 5 is the best fit polytope, we tested k* between 3 and 7. We found k*= 5, 6, or 7 were all significant with p-values of 0.021, 0, and 0.002 respectively. Therefore, while no polytope was significant in the log-transformed dataset, at least 3 polytopes significantly fit the tumor samples in linear space; generally, the lowest number of vertices that reach significance is chosen, which would mean that a 5-vertex polytope best fit the tumor samples in linear space.

While these results do not preclude the possibility that a polytope in linear space best fits the tumor data due to technical variation, as described in the ParTI Manual Caveats, the two analyses together (combined data and tumor samples only) suggest the tumor samples may be linear mixtures of cell types, defined by the original cell-line-based archetype analysis and the combined-data analysis.

Comparing human cell line and human tumor archetypes using functional enrichment

We then found the enriched gene sets (GO Biological Processes v7.2) for the combined dataset, as described above for cell lines. We compared the combined dataset archetypes to the original cell line archetypes using a hypergeometric test, as described in “Finding the best fit polytope and evaluating significance with a t-ratio test,” above. We found that each cell-line archetype matches at least one combined-dataset archetype, and each combined-dataset archetype matches at least one cell-line archetype. These relationships are shown in Table S4.

Pareto Task Inference

Drug Sensitivity Analysis

Our drug sensitivity analysis used the freely available drug screen data from Polley et al. (2016). This screen included 103 Food and Drug Administration-approved oncology agents and 423 investigational agents on 63 human SCLC cell lines and 3 NSCLC lines. As described previously (Wooten et al., 2019), we subsetted the data to the cell lines we analyzed here. Curve fitting was implemented by Thunor Web, a web application for managing, visualizing and analyzing high throughput screen (HTS) data developed by our lab at Vanderbilt University (Lubbock et al., 2021). As described in Wooten et al. (2019), we used activity area (AA) to measure sensitivity. Briefly, AA is the area (on a log-transformed x-axis) between y = 1 (no response) and linear extrapolations connecting the average measured response at each concentration. A larger activity area indicates greater drug sensitivity, characterized either by greater potency or greater efficacy, or both.

We scored each drug using an adapted version of the method described in Hausser et al. (2019). Briefly, for each archetype x, we binned the cell lines into 4 bins by distance to x. We then calculated a score as a product over the difference between bins:

$$S=\prod _i^{3}A{A}_i-A{A}_{i+1}+2\ast S{E}_i$$

Where i is the bin, AA_i, is the median activity area for bin i, and SE is the standard error of the median of bin i. This method gives us a way to rank drugs for each archetype x where cell lines closest to x are most sensitive to the drug, and there is an inverse relationship between sensitivity and distance to x. If the difference between consecutive bins increases by more than twice the SE of the first bin, such that AA_{i + 1} − AA_i > 2 * SE_i the product is set to 0. Using the standard error of the mean for each bin in this way allows for small increases in consecutive bins, but if the increase between bins is too large, the score will be set to 0. Positive scores can then be ranked to find drugs for which archetype x is most sensitive. Using the drug-archetype combinations with positive scores, we then ran a one-tailed Mann Whitney test comparing AA of the closest bin to AA of the remaining bins to determine which drug sensitivity was significantly higher for the bin closest to an archetype. An FDR (Bonferroni-Hochberg) correction to these tests showed that no corrected q-values were lower than 0.18. This may be due to the large number of comparisons being made with relatively low numbers of samples (37 total cell lines). Keeping this in mind, we report drugs for each archetype with a p-value <0.05, which suggest trends in drug sensitivity that should be further confirmed by additional experiments. We grouped drugs by target class and show the counts of drugs in each class with sensitivity enriched at an archetype in Figures S1I and S1J.

Binomial test on treatment of SCLC-A cell lines

To determine if there was a relationship between chemotherapy treatment status of cell lines and the SCLC-A archetype, we ran two binomial tests. First, we mined the ATCC and CCLE databases, and past literature, to determine the treatment status of as many cell lines in our dataset as possible. We found this information for 43 cell lines near the SCLC-A archetype, and 49 non-SCLC-A cell lines. Of the 43 SCLC-A cell lines, 6 had prior therapy and 6 did not. Of the 49 non-A cell lines, 16 had prior therapy and 4 did not. We therefore tested the hypothesis that SCLC-A cells are more likely to be untreated with the logic that, if chemotherapy selectively kills SCLC-A cells, we would be more likely to see SCLC-A cell lines from tumors prior to treatment. We compared the probability of being untreated given an A cell line (6 out of 12) to the expected distribution of untreated cell lines from non-A cell lines (4 out of 20, or p = 0.2). A one-tailed binomial test with an alternative hypothesis that the probability of SCLC-A cells being untreated is greater than non-A cells showed that we can reject the null with a p-value = 0.019.

Similarly, we asked whether an untreated cell line is more likely to have a phenotype near the SCLC-A archetype. We compared the probability of being SCLC-A given an untreated cell line (6 out of 10) to the expected distribution of SCLC-A from treated cell lines (6 out of 22). Again, we reject the null of a one-tailed binomial test with a p-value of 0.03, suggesting that untreated cell lines are more likely to be near SCLC-A.

Filopodia staining

SCLC human cell lines—H446 (N), H524 (N), H69 (A), and H196 (Y)—were maintained in RPMI+10% FBS. Glass coverslips were sterilized and then coated with 5 μg/mL Laminin (mouse, Corning Cat# 354232) diluted in PBS overnight at 4 degrees in a 12 well plate. PBS/Laminin solution was aspirated from the coverslips the next day and cells were seeded into the wells at a concentration of 5x10^4 cells per well for H524, H446, and H69, and 1x10⁴ cells per well for H196 (due to their larger size). 24 hours post-seeding, cells were fixed with 4% paraformaldehyde, permeabilized with 0.2% saponin, and blocked for 1 hour with 5% BSA + 0.1% saponin, with PBS washes in between. Cells were incubated with anti-Tubulin beta 3 (TUBB3 Clone TUJ1, Cat# 801213, Biolegend) diluted 1:500 in Blocking solution for 1 hour at room temperature. Cells were washed with PBS and then incubated for 1 hour in the dark at room temperature with secondary antibodies diluted 1:1000 in Blocking solution as follows: Hoechst 33342, Rhodamine phalloidin (Cat# R415, Invitrogen), and donkey anti-mouse Alexa Fluor 488 (Cat# A-21202, Invitrogen). Finally, cells were washed with PBS and mounted onto glass slides for imaging. Images were acquired using a Nikon-A1R-HD25 confocal microscope (ran by NIS-Elements) equipped with an Apo TIRF 60x/1.49 NA oil immersion lens. 20 images of each cell type were acquired per experiment, and each cell analyzed was isolated and not directly touching another cell, to ensure accurate filopodia and protrusion counts per cell. Analysis was done using Fiji software by manually tracing the cell border and using Analyze tab/Measure to quantify cell area. “Filopodia” were counted manually and are defined as the slender protrusions from the cell body involved in cell polarization in migrating cells that are phalloidin-positive and TUBB3-negative. “Protrusions” were counted manually and are defined as long slender protrusions of the cell body that are TUBB3-positive. Data was graphed in GraphPad Prism as the number of filopodia or protrusions per 500 μm² cell area. Box and whisker plots show the box extending from the 25^th to 75^th percentile with a line denoting the median. Whiskers extend from the minimum to the maximum values with all points shown. Statistics were calculated in GraphPad Prism using Kruskal-Wallis one-way ANOVA nonparametric tests.

Seahorse XF Cell Mito Stress Test

Response to succinate was tested by incubating 25,000-50,000 living cells per well onto Seahorse cell culture plates. Sodium succinate dibasic hexahydrate was diluted into water at 0.25 M (6.75 g/mL), and HCl and KOH were added until the pH was between 7.2 and 7.4. Succinate was then added to cell culture plates at three different concentrations (6mM, 12mM, and 24mM, plus control) and left to incubate overnight for 12 hours. Oxygen consumption rate testing was performed as described in the Seahorse XF Cell Mito Stress test kit User Guide. Cells were then imaged using Hoechst and propidium iodide to count live cells for normalization.

Calcium Flux Experiments

To test if cells respond to succinate through GPCRs that activate calcium signaling, cytoplasmic calcium imaging was recorded on a kinetic imager (WaveFront Biosciences Panoptic) before and after stimulation with a concentration curve of succinate or control compounds. H1048 cells were grown in DMEM/F12 media + 10% FBS in T75 flasks (Corning, Ref 430720U) in a humidified incubator at 37 degrees Celsius and 5% CO2. Cells were grown to 70-90% confluency before the day of experimentation to maintain health and viability. To transfer cells into tissue culture treated 384 well imaging plates (Corning, Ref 3764), flasks were treated with TrypLE express (Thermo Fisher Scientific, Ref 12604013) for 6 minutes before inactivation with cell culture media to generate single cell suspensions. Cell suspensions were diluted to 1000 cells/uL before 20,000 cells/well were plated onto the 384 well plates; Cells were allowed to recover overnight in a humidified incubator at 37 degrees Celsius and 5% CO2 before calcium flux assays were performed. A Chem-1 cell line engineered to express SUCNR1/GRP91 (succinate receptor) and respond to succinate via calcium signaling (Millipore, Ref HTS241RTA) was handled in the same way above and used as a positive control for all experiments. Both cell lines were plated on the same plate and loaded with the calcium responsive dye, Fluo-8-AM (AAT Bioquest, Ref 21080), at a concentration of 4 uM in HBSS (Gibco, Ref 14025-092) for 1 hour in a humidified incubator at 37 degrees Celsius and 5% CO2. Dye was flicked out, cells were washed with HBSS before 20 uL of HBSS was added back to the wells and the plate was loaded onto the kinetic imager. Data were acquired at 5 Hz (excitation 482 ± 35 nm, emission 536 ± 40 nm) for 340 s after 20 uL/well of succinate or control (vehicle or Cyclopiazonic Acid) solutions in HBSS were added to each well. Next, 10 uL/well of 5 uM ionomycin (calcium ionophore) in HBSS was added to validate strong calcium signal was detectable given the experimental conditions. Data was generated in technical triplicate and biological triplicate. The Chem-1 control cell line responded strongly to succinate with a concentration response curve to be expected. H1048, however, did not have any detectable signal above vehicle control at any concentration of succinate, including 2.5 mM. Both cell lines did demonstrate robust calcium signals in response to cyclopiazonic acid and ionomycin, demonstrating that the experimental conditions could capture physiologically relevant and extreme amounts of calcium flux, respectively, in both cell lines.

Gene signature matrix generation

After testing each gene with a Mann-Whitney test as described above, genes that are not maximized in the bin closest to an archetype or with a p-value higher than 0.05 are considered insignificant and are removed from the analysis. The remaining genes are assigned to the archetype for which the mean difference (log-ratio) of log-transformed gene expression in the closest bin to the archetype compared to the rest is highest. The matrix (with size [G, n], where G = total number of genes and n = number of archetypes) is populated with the archetype gene expression profiles (i.e. the average location in gene expression space after bootstrapping the archetype analysis). To reduce the size of the gene matrix and choose the most salient genes for each archetype, an algorithm is used to optimize the condition number, or stability, of the matrix. The condition number of the matrix, κ(A), is the value of the asymptotic worst-case relative change in output for a relative change in input:

$$A(x+\delta x)=b+\delta b$$

$$\frac{\Vert \delta x\Vert }{\Vert x\Vert }\le \kappa (A)\frac{\Vert \delta b\Vert }{\Vert b\Vert }$$

Where A is the signature matrix, b is the input expression matrix, x is the output signature score, and δ is the error. The condition number κ thus gives an upper bound on the output error given a perturbation to the input. Minimizing this value ensures that genes that do not well-distinguish between the archetypes are not included in the matrix. With genes sorted by mean difference for each archetype, the top g genes are chosen for each archetype, with g ranging from 20 to 200. For each g, the condition number of the matrix is calculated using the Python function cond from numpy.linalg (Oliphant, 2006) using the 2-norm (largest singular value, p = 2). The gene signature matrix size with the lowest condition number, which includes g* genes, is chosen. For our archetypes, g* = 21, so the resulting size of the gene signature matrix is [g* x n, n] = [105, 5] (Table S9). This method can be extended to other sorted lists of genes, such as genes sorted by adjusted p-value in an ANOVA test between archetypes. For SCLC, the gene signature included the four consensus TFs: ASCL1, NEUROD1, POU2F3, and YAP1 (Figure 3F).

Single-cell RNA sequencing of SCLC cell line and tumor samples

Human cell line scRNA-seq

Eight SCLC human cell lines from the bulk data above were chosen for single-cell RNA-sequencing. SCLC human cells lines were obtained from ATCC. We chose two cell lines from each NE subtype (A: H69 and CORL279, A2: DMS53 and DMS454; N: H82 and H524) and one cell line from each non-NE subtype (P: H1048; Y: H841; Figure 3B). This approximates the distribution of subtypes seen in bulk tumor data, where most tumors are largely NE. We also aimed to pick cell lines that ranged in their distance from their “assigned” archetype, to better understand intermediate samples as compared to ones close to an archetype location.

Cell lines were grown in the preferred media by ATCC in incubators at 37 degrees Celsius and 5% CO2. In preparation for single-cell RNA-sequencing, cells were dissociated with TrypLE, washed with PBS three times, and then the cells were counted, and concentration was adjusted to 100 cells/μL. Droplet-based single-cell encapsulation and barcoding were performed using the inDrop platform (1CellBio), with an in vitro transcription library preparation protocol (Klein et al., 2015). After library preparation, the cells were sequenced using the NextSeq 500 (Illumina). DropEst pipeline was used to process scRNA-seq data and to generate count matrices of each gene in each cell (Petukhov et al., 2018). Specifically, cell barcodes and UMIs were extracted by dropTag, reads were aligned to the human reference transcriptome hg38 using STAR (Dobin et al., 2013) and cell barcode errors were corrected and gene-by-cell count matrices and three other count matrices for exons, introns, and exon/intron spanning reads were measured by dropEst. Spliced and unspliced reads were annotated and RNA expression dynamics of single cells were estimated by velocyto (La Manno et al., 2018). SCLC human cell lines have been validated by matching transcript abundance to the bulk RNA-seq data from CCLE.

Human and mouse tumor scRNA-seq

Patients with SCLC were prospectively identified and consented using an Institutional Review Board (IRB, #030763) approved protocol for collection of tissue plus clinical information and treatment history. All samples were de-identified and protected health information was reviewed according to the Health Insurance Portability and Accountability Act (HIPAA) guidelines. The two human SCLC tumors were collected in collaboration with Vanderbilt University Medical Center. Tumor #1 was a relapsed tumor collected via bronchoscopy with transbronchial needle aspiration of a left hilar mass. The patient had completed carboplatin and etoposide and then prophylactic cranial irradiation. The tissue was washed in an RBC lysis buffer, passed through a 70 μm filter, and washed in PBS. Cells were dissociated with cold DNAse and proteases and titrated every 5-10 minutes to increase dissociation. Library preparation for scRNA-seq was performed according to previous protocols (Banerjee et al., 2020), and cells were sequenced using BGI MGI-seq. Human tumor #2 was a stage 1B SCLC tumor with a mixed large cell NE component treated with etoposide and cisplatin and was surgically removed via right upper lobectomy. The tumor was immediately placed in cold RPMI on ice for dissociation. Library preparation for scRNA-seq was performed as described previously (Banerjee et al., 2020). Cells were prepared for sequencing using TruDrop (Southard-Smith et al., 2020) and sequenced on Nova-seq. As with cell lines, the DropEst pipeline was used to process scRNA-seq data and to generate count matrices of each gene in each cell (Petukhov et al., 2018).

The Rb1/p53/Myc (RPM) mice are available at JAX#029971; RRID: IMSR_JAX:029971 and all experiments with RPM cells were previously performed as in Ireland et al. (2020). TKO mouse lines used were the triple-knockout (TKO) SCLC mouse model bearing deletions of floxed (fl) alleles of p53, Rb, and p130 as previously described (PMID: 20406986). For in vivo SCLC tumor studies with this model, 8 to 12 weeks old mice were used for cancer initiation, and tumors were collected 6-7 months later.

Preprocessing of single-cell RNA-seq data

Single-cell RNA-seq counts matrices were primarily analyzed using the Python packages Scanpy and scVelo (Bergen et al., 2020; Wolf et al., 2018). First, the scRNA-seq read counts, including both spliced and unspliced counts, for each of the samples in each dataset were generated using the command line interface (run_dropest) from velocyto on the BAM files generated from DropEst, as described above. This tool generates loom files that can be used with Scanpy and scVelo for preprocessing and velocity calculations. We then used Scanpy to read in the loom files as an AnnData object (anndata.readthedocs.io).

Preprocessing of human cell line data

Filtering and Normalization.

We used a combination of Scanpy and Dropkick v1.2.6 (https://github.com/KenLauLab/dropkick) to label and filter out low-quality cells from each sample. Dropkick considers total UMI distribution, ambient genes, and percent mitochondrial reads to give a sense of data quality for each sample. Empty droplets have low counts and gene number, so high-quality samples should have a large proportion of cells with high counts and genes. By considering dropout rate, we find ambient genes, or RNA molecules that have been released in the cell suspension during droplet-based scRNA-seq that may be due to cross-contamination and contribute to background noise in the sequencing data. As described in the tutorial, Dropkick then trains “a glmnet-style logistic regression model to determine scores and labels for each barcode in the dataset describing the likelihood of being a real cell (rather than empty droplet).” Once each sample has dropkick scores and labels (using dropkick score > 0.5 to identify high-quality cells), we then concatenate the datasets with a batch key for each cell line. In downstream analyses, we can analyze the dataset as a whole (such as in the PCA reduction) or we can analyze each batch independently (such as in calculating RNA velocity by batch). Where applicable, we note in the analyses below if we analyzed each batch independently (if unspecified, we ran the analysis on the whole dataset).

We hierarchically perform the filtering, following the recipe_dropkickfunction from the Dropkick package, We initially filter out cells with < 100 genes using scanpy.pp.filter_cells with min_genes = 100. This reduces the total number of cells (in all 8 samples) from 86,492 to 86,349. We remove genes found in < 3 total spliced counts across all samples with scanpy.pp.filter_genes with min_counts < 3. This reduces the number of genes from 63,677 to 22,475. These filtering steps ensure we remove any cells or genes with low or no reads, to prepare for further filtering steps below.

We normalize the data using scanpy.pp.normalize_total, which removes any biases due to varying total counts per cell. We used default arguments for this normalization (as described in the Scanpy API v 1.8), such that after normalization, each cell has a total count equal to the median of total counts for cells before normalization. Next, numpy.log1p is used to log transform the data (+1, which keeps zeroes from being transformed to negative infinity). Finally, the log-transformed, normalized counts are then scaled using scapy.pp.scale, which rescales the data to unit variance and mean-centers each gene. We then use scanpy.tl.pca to compute a 50-component PCA embedding of the data, using all genes, and use scvelo.pp.neighbors and scvelo.tl.umap to generate a UMAP dimensionality reduction. This is shown in Figure S2A. As shown by the dropkick labels, a large number of cells are low-quality cells. We filter these out and recompute the PCA embedding, neighborhood calculation, and UMAP on the reduced dataset of 16,108 cells. After removing so many cells, we re-filter the genes with a low threshold (min_cells = 3) to remove any genes that were only expressed in the low-quality cells. This reduces the number of genes from 22,475 to 20,446.

Cell Cycle Scoring, and Doublet Detection.

Often, the location of a cell in gene expression space can be dependent on where it is in the cell cycle. To determine the extent of this relationship, we use scvelo.tl.score_genes_cell_cycle, which scores a list of cell cycle genes from Tirosh et al. (2016). 43 genes in this list are associated with the S phase, while 54 genes are associated with G2M. The score is the average expression of each set of genes subtracted by the average expression of a reference set of genes, randomly sampled from all genes for each binned expression value. Each cell is then assigned a phase: if S_score > G2M_score, the cell is given the phase S and vice versa. If both scores are negative, the phase is assigned G1. The attribute cell_cycle_diff is calculated by subtracting the G2M_score from the S_score. As shown in Figure S2B, there is some variability within each cell line by cell cycle phase. We elect not to remove this variability, as there is no consensus in the field on regressing out this effect (Luecken and Theis, 2019). For example, we can identify cell populations that proliferate based on cell cycle scores. We, therefore, include these scores in our analysis as a possible source of informative biological signal and interpret later results in light of this variability.

We do, however, wish to remove any possible doublets in the dataset and use the Python package Scrublet to do so (Wolock et al., 2019). We follow the best practices for using Scrublet at github.com/swolock/scrublet and apply the tool on each sample independently. We run Scrublet directly on the raw data, including both spliced and unspliced counts, using the ‘matrix’ layer of the AnnData object. We run Scrublet with default parameters, which expects a doublet ratio of 10% and calculates the number of neighbors as half the square root of the number of cells. The scrub_doublets function is run with the default parameters as well, including mean_center = True, normalize_variance = True, log_transform = False, and 30 principal components. Interestingly, in all samples except CORL279, the detected doublet rate was exactly or near 0%, with less than 10 total doublets detected across all 7 samples. In CORL279, however, Scrublet detected 20.8% of the cells as doublets (3148 cells). We analyzed this cell line further by plotting the histograms of the doublet scores for the observed data and the simulated data (Figure S2C). As described in best practices, the doublet score threshold should separate two peaks of a bimodal simulated doublet score histogram. Because the histograms did not look bimodal, we followed the demuxlet_example.ipynb example notebook, which compares mean-centered, variance-normalized results to mean-centered, variance-normalized, log-transformed results. When we log-transform the data and rerun Scrublet on the CORL279 sample, we find that the histogram for the simulated cells is more bimodal, with a threshold separating the two peaks. Furthermore, predicted doublets should mostly co-localize in a 2D embedding, and we find that the predicted doublets for the log-transformed CORL279 data co-localize more than without the log transformation. We thus use the doublet prediction from the log-transformed data, which detected doublets at a rate of 28.6% (4328 cells).

MAGIC imputation and batch correction.

Imputation of single-cell data with a tool such as MAGIC has been shown to improve archetype detection (Van Dijk et al., 2018). We, therefore, use MAGIC to build a model with the default parameters (knn =5, decay = 1, t= 3). We fit this operator with solver = ‘approximate’ and genes = ‘all_genes’ and transform the preprocessed data after the filtering and normalization described above (16,108 cells and 20,446 genes). As shown in Figure S2D, the first few components of the PCA fit to the imputed data explain a high percentage of the variance in the data (11 PCs explain over 85% of the variance).

For most of the following analyses, we use this imputed dataset or the normalized, log-transformed counts. However, spurious archetypes may arise in cases where batch effects can add unwanted technical variance. Therefore, we also try batch-correcting the data using Scanorama (Hie et al., 2019) to determine if any archetypes found in the single-cell data are likely due to batch effects (as described below in Single-cell archetype analysis using PCHA). We used default parameters for Scanorama’s correct_scanpy function, which returns both an integrated matrix (low dimensional embedding of the datasets) and a corrected matrix (with transformed gene expression profiles in a gene-by-cell matrix). We use the corrected data in the single-cell archetype analysis, as described below.

Preprocessing of human tumor data

Initial filtering and normalization.

Similar to human cell lines, we then use Dropkick v1.2.6 (https://github.com/KenLauLab/dropkick) to label and filter out low-quality cells from each sample. Once each sample has dropkick scores and labels (using dropkick score > 0.5 to identify high-quality cells), we then concatenate the datasets with a batch key for each tumor.

Human tumor datasets were preprocessed using the same tools as described above, including Scanpy and scVelo. We initially filter out cells with < 100 genes using scanpy.pp.filter_cells with min_genes = 100. This reduces the total number of cells (in both tumors) from 8,649 to 4,863. We remove genes found in < 3 total spliced counts across all samples with scanpy.pp.filter_genes with min_counts < 3. This reduces the number of genes from 43,306 to 15,344. These filtering steps ensure we remove any cells or genes with low or no reads, to prepare for further filtering steps below.

We normalize the data using scanpy.pp.normalize_total and used default arguments for this normalization (as described in the Scanpy API v 1.8), such that after normalization, each cell has a total count equal to the median of total counts for cells before normalization. Next, numpy.log1p is used to log transform the data (+1, which keeps zeroes from being transformed to negative infinity). Finally, the log-transformed, normalized counts are then scaled using scapy.pp.scale, which rescales the data to unit variance and mean-centers each gene. We filter out the low-quality cells that have low Dropkick scores. We then use scanpy.tl.pca to compute a 50-component PCA embedding of the data, using all genes, and use scvelo.pp.neighbors and scvelo.tl.umap to generate a UMAP dimensionality reduction. This is shown in Figure S3A.

Removal of non-cancer cells, doublets, and low-quality cells.

We use Scrublet to determine the number of possible doublets in the data. One tumor had 6 predicted doublets (out of 7741 original cells before filtering); the other had 3 (out of 580 original cells), which were removed.

Because these samples may contain non-tumor cells, we annotated clusters by cell type based on the expression of tissue compartment markers. First, we clustered cells by the Leiden algorithm and then analyzed the expression of markers across these clusters. To remove immune cells, we filtered clusters by expression of PTPRC. To remove fibroblasts, we filtered cells using COL1A1 expression, and we used CLDN5 expression to remove endothelial cells. We also used EPCAM to identify epithelial cells. We found several small clusters of immune cells and a single small population of likely fibroblasts. A single cluster had a few cells with low expression of CLDN5, and higher average expression of EPCAM, so we chose not to remove this cluster. Removing the other non-cancer cells reduced the number of cells from 4,863 to 4,463. The expression of these markers is shown in Figure S3A.

As shown by the dropkick labels, a large number of cells are low-quality cells. We filter these out and recompute the PCA embedding, neighborhood calculation, and UMAP on the reduced dataset of 1,596 cells.

After removing so many cells, we re-filter the genes with a low threshold (min_cells = 3) to remove any genes that were only expressed in the low-quality cells. This reduces the number of genes from 15,344 to 13,593. Therefore, we moved forward with the analysis with 1,596 cells and 13,593 across two tumors.

MAGIC Imputation.

We use MAGIC to build a model with the default parameters (knn =5, decay = 1, t= 3). We fit this operator with solver = ‘approximate’ and genes = ‘all_genes’ and transform the preprocessed data after the filtering and normalization described above (1,596 cells and 13,593 genes). We use the MAGIC imputed dataset for archetype analysis. Imputation does not affect the spliced and unspliced layers of the AnnData object, which are used in downstream analyses to calculate velocity dynamics.

Cell Cycle Regression.

Initially, we scored cell cycle genes using Scanpy, but did not regress out the effect using the same reasoning as for human cell lines. However, single cell archetype analysis showed that one of the archetypes was enriched for G2M cells. While we are interested in preserving the differences between cycling and non-cycling cells, such a strong dependence of location in gene expression space on location in the cell cycle can result in spurious archetypes. Therefore, we chose to regress out the difference between the G2M and S scores (cell_cycle_diff). While this removed the dependence on location in the cell cycle (Figure S3C), it did not change our other conclusions (for example, a three-vertex polytope still fits the data well).

Preprocessing of mouse tumor (TKO) data

Initial Filtering and Normalization.

TKO tumors were filtered using the same steps as human cell lines. Initial filtering using Scanpy reduced the number of cells from 12,228 to 12,220 (removing cells with <100 genes) and genes from 27,998 to 15,443 (removing genes with < 3 spliced counts). Removing low-quality cells using Dropkick further reduced the number of cells from 12,220 to 2,310. As above, we normalize the data using scanpy.pp.normalize_total with default arguments. Next, we log transform the data (+1). Finally, the log-transformed, normalized counts are then scaled using scapy.pp.scale. We then use scanpy.tl.pca to compute a 50-component PCA embedding of the data, using all genes, and use scvelo.pp.neighbors and scvelo.tl.umap to generate a UMAP dimensionality reduction.

Doublet Detection.

We used Scrublet the determine the number of possible doublets in the data. Scrublet was run on the raw (unprocessed) data before filtering above. TKO1 was predicted to have 11 doublets, which were removed with the filtering above. TKO2 was predicted to have 0 doublets. TKO3 was predicted to have 1,052 doublets, or 27% of the samples, using the default parameters for scrub_doublets. We, therefore, investigated this sample further and found that the observed and simulated doublet score histograms were not bimodal, which would be expected if there were true doublets in the data. Furthermore, the minimum between the two modes of the simulated histogram is used to pick a threshold for scoring doublets, and the lack of bimodality meant that the threshold chosen automatically was arbitrary. This may be due to the homogeneity of the sample because Scrublet can only detect neotypic doublets, “which are generated by cells with distinct gene expression (e.g., different cell types) and are expected to introduce more artifacts in downstream analyses” (from scrublet_basics tutorial). Log-transforming the data, as suggested by the demuxlet_example tutorial, gave a doublet percentage of 0.3% (12 cells). Therefore, we removed only these 12 doublets from the dataset.

After removing these cells and low Dropkick scoring cells, we re-filter the genes with a low threshold (min_cells = 3) to remove any genes that were only expressed in the low-quality cells. This reduces the number of genes from 15,443 to 12,751. Therefore, we moved forward with the analysis with 2305 cells and 12,751 genes across three tumors.

MAGIC Imputation.

We use MAGIC to build a model with the default parameters (knn =5, decay = 1, t= 3). We fit this operator with solver = ‘approximate’ and genes = ‘all_genes’ and transform the preprocessed data after the filtering and normalization described above (12,305 cells and 12,751 genes). We use the MAGIC imputed dataset for archetype analysis. Imputation does not affect the spliced and unspliced layers of the AnnData object, which are used in downstream analyses to calculate velocity dynamics.

Preprocessing of mouse tumor (RPM) time-series data

Initial Filtering and Normalization.

While RNA velocity requires realignment to the genome (as described above) and therefore the counts matrices are slightly different from those deposited by Ireland et al. (2020), we chose preprocessing steps and parameters to be as consistent as possible with the original publication of the data (Figure S4). Therefore, we first filtered out cells from the RPM time-series samples with < 100 genes using scanpy.pp.filter_cells with min_genes = 100. This reduces the total number of cells from 31,514 to 30,365. We remove genes found in < 3 total spliced counts across all samples with scanpy.pp.filter_genes with min_counts < 3. This reduces the number of genes from 32,385 to 21,288. These filtering steps ensure we remove any cells or genes with low or no reads, to prepare for further filtering steps.

Filtering Doublets, Immune and Stromal Subpopulations, and Low-Quality Cells.

We ran Scrublet to determine if any doublets were present in the samples. For these samples, we found that log-transformation before detection gave simulated doublet histograms with bimodal distributions, and UMAP projections of doublet scores for each sample show doublets localized to distinct regions/clusters, as expected for detection of true doublets.

Because stringent filtering was already done in Ireland et al. (2020) to remove low-quality cells and non-cancer populations such as immune and stromal cells, we filtered to the same cells. We also removed cells that did not have inferred pseudotime coordinates in Ireland et al. (2020). This resulted in 15,138 cells. 2,175 of these remaining cells were predicted to be doublets. To ensure consistency with the original publication, we did not remove these potential doublets but used the doublet score in downstream analyses to ensure that no spurious archetypes are enriched for doublets.

Cell Cycle Scoring and MAGIC Imputation.

Ireland et al. (2020) regressed out cell cycle effects to remove variation due to the cell cycle phase, so we repeat this preprocessing step here. We use scvelo.tl.score_genes_cell_cycle to determine the extent of this effect. As above, each cell is given a score that is the average expression of each set of genes (S genes and G2M genes) subtracted by the average expression of a reference set of genes, randomly sampled from all genes for each binned expression value. The attribute cell_cycle_diff is calculated by subtracting the G2M_score from the S_score. Because we want to preserve the difference between cycling and non-cycling cells, we remove variability due to location in the cell cycle by regressing out the cell_cycle_diff attribute. We then rescale the data with scanpy.pp.scale, and we re-filter the genes with a low threshold (min_cells = 3) to remove any genes that were only expressed in the low-quality, non-cancer, and doublet cells. This results in 19,455 genes and 15,138 cells for downstream analysis.

We use MAGIC to build a model with the default parameters (knn =5, decay = 1, t= 3). We fit this operator with solver = ‘approximate’ and genes = ‘all_genes’ and transform the preprocessed data after the filtering and normalization described above (15,138 cells and 19,455 genes) (Figure S4C).

Comparing intra-sample heterogeneity and inter-sample diversity

Projection of single-cell data on principal components of bulk RNA-seq

We sought to assess whether variation across SCLC samples (cell lines in the bulk RNA-seq data) is aligned to variation within SCLC samples (scRNA-seq on cell lines and tumors). To do this, we utilize the preprocessed scRNA-seq data on human cell lines described above (with doublets removed and without Scanorama batch correction). We analyze the single-cell data both before and after gene imputation, to ensure that imputation is not leading to spurious relationships between bulk and single-cell data. We adapt the method described in Hausser et al. (2019) for comparing intra-tumor heterogeneity and inter-tumor diversity. In Hausser et al. (2019), genes are reduced to those expressed in at least 50% of the single cancer cells “so that gene expression could be quantified in most cells, allowing projection of these cells on the space defined by the first three PCs of the [bulk expression data from] tumors.” However, we expect each cell line to comprise different subpopulations, and reducing genes to those expressed in over half of the cells may miss important variance in minority subpopulations. Instead, we reduce the dimensionality of the data by focusing on the genes that are profiled in the bulk cell line data and are highly variable in the single-cell data. This reduces the dataset down to 3033 genes and 13,945 cells. We then project the single-cell data (both before and after imputation) into the space defined by the bulk data-fitted PCA, focusing on the top 7 principal components due to an elbow in the explained variance curve for this number of components.

If intra-sample heterogeneity were perfectly aligned with inter-sample diversity, we would expect the single-cell variance explained by the principal components computed on the bulk data to equal the single-cell variance explained by the principal components computed on the single-cell data. In other words, the percentage of variance explained by the single-cell PCA is an upper bound on the variance explained by inter-sample diversity. We, therefore, computed each of these fractions for the single-cell data (with and without imputation) and compared them. For the non-imputed data, we find that the variance explained by the single-cell PCA has an elbow around 6 or 7 components, explaining ~25% of the variance. In comparison, the same number of components in the bulk data-fitted PCA explains about 6% of the variance in the data, which amounts to 23.47% of the variance explained by the first 7 single-cell PCs. To determine if this percentage variance explained could be explained by a PCA fit to randomized data, we shuffled the bulk data 50 times and fit a PCA to each shuffled dataset. We found that these shuffled models explained only 1.02 +/−0.0098% of the single-cell variance, suggesting 23.47% explained by the data is larger than random. If we consider different numbers of PCs (1 to 20), the percentage of intra-sample heterogeneity explained by inter-sample diversity stays stable at 25.36 +/−0.52%.

Some of the remaining variance may be attributed to stochasticity, noise, and measurement error that commonly plagues single-cell data. To remove some of this noise in the single-cell data, we then applied the same analysis to the imputed dataset generated by MAGIC, which denoises high-dimensional data. We again compare the fraction of variance explained by the bulk PCA to the upper bound of variance explained by the single-cell PCA. When we investigate this ratio for the top 7 components, we find that inter-sample diversity explains 32% of the variance explained by the first 7 single-cell PCs, while a PCA fit to shuffled data explains about 0.28 +/− 0.009% of this variance (50 shuffles). If we consider varying numbers of PCs (1 to 20), the percentage of intra-sample heterogeneity explained by inter-sample diversity stays stable at 36 +/− 0.94%.

Bulk gene signature scoring of single cells using archetype signature matrix

To score the gene signature matrix (Table S6) in single cancer cells, we first subset the single-cell data to the genes in the archetype signatures. Due to dropouts, the intersection of genes from the signatures and the single-cell data may be less than the full signature (105 genes), and we refer to this intersection as “shared genes.” We scale the gene signature and the single-cell gene expression data by the L2 norm for each archetype and cell, respectively, to remove differences caused by different platforms (bulk vs. single-cell sequencing). Each archetypal gene expression vector and each cell’s gene expression vector were therefore scaled to have a length of 1 so that the archetype space has basis vectors of length 1. We then transformed each cell signature into archetype space using the least-squares approximate solution to Ax = b, where A is the signature matrix (shared genes g by subtypes s) and b is the single-cell matrix (shared genes g by cells c). This is solved using numpy.linalg.lstsq to generate a “pattern matrix” x (subtypes s by cells c). These scores could then be visualized on PCA, UMAP, and CAP projections (see visualization of single-cell RNA-seq). For PCA and UMAP plots, the scores were smoothened using scVelo’s plotting functions with smooth = True.

Archetype analysis on single-cell datasets using the Principal Convex Hull Algorithm (PCHA)

PCHA on Human Cell Lines

We used the R package ParetoTI (Kleshchevnikov, 2019), which we found to be more computationally efficient than the original MATLAB package ParTI for the high-dimensional single-cell datasets. ParetoTI uses a fast python implementation of PCHA and includes tests for statistical significance and enrichment of genes and gene sets, as in the ParTI package. The package recommends doublet removal before analysis. As described in STAR Methods, we used Scrublet to remove doublets from the human cell line data—a large number of doublets were only found in CORL279. ParetoTI suggests doublets can result in spurious archetypes, so we run the complete PCHA analysis on the cell line data with doublets removed.

As described in Van Dijk et al. (2018), imputation of the single-cell data (using MAGIC) is an essential step into finding meaningful archetypes. Before imputation, the single-cell data is dominated by noise and lacks apparent extreme states. Imputation can uncover extreme states, or vertices, in the data and increase the robustness of the archetypes. Notably, “since PCA is a linear transformation, the convex hull of the data in PCA-dimensions is a subset of the convex hull of the original data, and therefore the archetypes obtained are indeed extreme points of the original data” (Van Dijk et al., 2018). Therefore, we run PCHA on the data after imputation.

To reduce the dimensionality of the data, we fit a PCA model to the single-cell data. We consider the explained variance per PC and find the number of PCs where the additional explained variance (variance explained on top of n-1 model) is less than 0.1%. We find that 11 components represent the imputed data well, explaining over 85% of the variance in the imputed data. We fit k* = 2 to 8 vertices to the 11-component PCA of the imputed data, with delta = 0. Looking at the variance explained vs. the number of archetypes k, we find that k* = 4 or k* = 6 based on the elbow method. We also considered the mean variance in position of vertices upon bootstrapping (200 iterations with data downsampled to 75%). We find that k* = 4 and k* =6 give variances close to 0, while k* = 5 gives the highest mean variance, suggesting that k* = 5 is not fitting the data geometry well.

Therefore, we move forward with k* = 4 and k* = 6 for t-ratio tests. We randomized the data 1000 times as described in STAR Methods to generate a background distribution of t-ratios. We find four archetypes give significant polytopes using the t-ratio test as described in STAR Methods (t-ratio = 0.3743, p = 0.001). Six archetypes were not significant with a t-ratio of 0.0012 and p = 0.940. Based on these results, it seems k*=4 best fits the cell line data. As shown in Figures S2D-SDI, these archetypes correspond to the following cell lines and associated bulk archetypes:

• Archetype 1: H69, SCLC-A

• Archetype 2: DMS53 and DMS454, SCLC-A2

• Archetype 3: H524, SCLC-N

• Archetype 4: H841, SCLC-Y

H82, CORL279, and H1048 are all more central in the polytope, suggesting they may comprise single-cell generalists.

These results validate that the human cell lines can be fit by a polytope, suggesting Pareto optimality applies to single cancer cells in these cell lines.

SCLC-P Archetype

Interestingly, we did not find an SCLC-P archetype. Even using k* = 6 did not result in an archetype by the cell line expressing POU2F3 (H1048), but instead gives two SCLC-A archetypes and two SCLC-A2 archetypes. This suggests that the lack of an SCLC-P archetype is not due to the number of archetypes chosen. A few explanations exist for why there is not a POU2F3 enriched archetype:

1. Bulk RNA-seq profiles of SCLC-P cell lines may give a spurious archetype in our analysis that is actually a mixture of the other four archetypal transcriptomic profiles in varying proportions. We discuss this possibility in the discussion. Proving task trade-offs exist between SCLC-P and other subtypes (i.e., SCLC-P cells are optimal at a specific task) will be necessary to prove it is not an intermediate or mixed phenotype.

2. Due to our small sample size, we may miss an SCLC-P archetype in this single-cell data. Sequencing single cells from more cell lines near the SCLC-P bulk archetype may be necessary to unveil the fifth archetype.

3. SCLC-P cell lines and tumors may represent a valid subtype that does not fit within the Pareto theoretical polytope found here. In other words, the SCLC-P subtype may be a distinct subtype not confined by the Pareto front of the other four SCLC subtypes. This may be supported by SCLC-P phenotype similarity with normal lung tuft cells rather than normal PNECs, and their alternative cell type of origin found in RPM mouse models driven by the general promoter Ad-CMV-Cre (Ireland et al., 2020). If SCLC-P tumors are derived from an alternative cell of origin, we would not expect the functional tasks to trade off with the others found here. This does not explain how some tumors may contain markers for multiple subtypes, including SCLC-P, such as NEUROD1 (SCLC-N, Ireland et al., 2020).

PCHA on Human Tumors

We followed the same preprocessing steps as described for human cell lines above. Filtering, normalization, and MAGIC imputation are also described above. After MAGIC imputation, we fit a PCA to the data and found that 8 PCs explain over 85% of the variance (Figure S3D). The knee of the explained variance vs. PC plot is 7, suggesting a low dimensional representation of the data is possible. We also consider the number of PCs where the additional explained variance is less than 0.1%; this gives 11 components. We, therefore, use the first 11 PCs for downstream analyses. We fit k* = 2 to 8 vertices to the 11-component PCA of the imputed data with delta = 0. We find that three or more archetypes explain over 80% of the variance in the reduced dimensional data (2 archetypes explain less than 70% of the variance). When considering the mean variance in position of vertices, we find that K* = 2-4 archetypes show little variance (less than.05), suggesting the archetype locations are robust to bootstrapping. K* = 5 gives the highest mean variance in position, at 0.8. Furthermore, the t-ratio of the polytope dips significantly for k*= 5 (where a higher t-ratio close to 1 is a better fit). Therefore, k* = 3 or 4 seems most likely to fit the data (Figure S3E).

We move forward with these k* for t-ratio tests, where the data is randomized 1000 times as described above to generate a background distribution of t-ratios under random noise. As expected, we find k*= 3 is the smallest number of archetypes that significantly fits the data, with a t-ratio of 0.596 (closer to 1 is better) and p = 0.008. K* = 4 had a much lower t-ratio of 0.396 (p = 0.001) and k* = 5 was insignificant, with a p-value of 0.753. Based on these results, k* = 3 best fits the data.

PCHA on scRNA-seq from TKO mouse tumors

We wanted to ensure that mouse tumors could also be well described by Pareto theory and applied archetype analysis to TKO mouse tumors. In this dataset of three tumors, nine principal components explain over 85% of the variance in the imputed data. Furthermore, 16 PCs are needed for the variance explained by additional components to be less than 0.1%. We, therefore, reduced the dataset dimensionality to 16 dimensions for archetype analysis. We fit k* = 2 to 8 vertices to this PCA with delta = 0 and found that three archetypes can explain over 65% of the variance in the dataset. Using a bootstrapping method, we found that the mean variance in position of the vertices increases greatly after four archetypes; 4 archetypes have a mean variance of less than 0.025, while 5 gives over 0.25, and 6 gives over 0.175. Lastly, the t-ratio drops dramatically after four archetypes, from over 0.2 to under 0.05. These results suggest that the number of archetypes that best fit the data is k* = 3 or 4.

We then performed a t-ratio test with the same parameters as above to determine which was the better fit. Three archetypes were insignificant, with a t-ratio of 0.33 and p = 0.999. Contrarily, four archetypes gave a significant polytope with p = 0.001 and t-ratio = 0.21. Therefore, four archetypes best fit the data. Two of these archetypes form the main axis of variation in TKO1, while the other two archetypes form the main axis of variation in TKO2 and TKO3 (which tended to overlap) (Figures S2J-S2M).

PCHA on scRNA-seq from RPM tumors

We next analyzed the time course of RPM tumor cells. We found that the top 9 PCs explain over 90% of the variance in the data, and the top 22 PCs are needed for the variance explained by an additional PC to be less than 0.1%. We therefore run PCHA on the 22-dimensional data. We fit K* = 2-8 vertices with delta = 0 and found a knee in the EV vs. number of archetypes plot at k* = 3. Using a bootstrapping method, we found that the mean variance in position of the vertices increases for k* = 4 and k* =5, and decreases for k* = 6, suggesting k* = 3 or 6 are the most robust number of archetypes. We therefore ran a t-ratio test on k* = 3-6 to determine the best number of archetypes. We found that k* = 6 was the only polytope with a significant t-ratio (p-value = 0.001) and had a larger t-ratio than fewer archetypes (k*=5). Therefore, k* = 6 archetypes best fits the data. This is shown in Figures S4D and S4E.

Alignment of bulk and single-cell archetypes

We use archetype analysis to find the closest single cells to each archetype and label these as specialists. PCHA constrains the archetype vertices to be a weighted average of the data points and approximates the data points by a weighted average of the archetypes. Therefore, each cell has archetypal weights given by a matrix S, such that the weights for each cell sum to 1. We can use these weights to directly “score” the single cells and label them by archetype. Each cell is given weights summing to 1, and we consider the cells with a score above 0.95 for a single archetype to be a specialist.

In order to align the single-cell archetypes with our predefined archetype space, we consider the scores for each cell described in the STAR Methods section “Bulk gene signature scoring of single cells using archetype signature matrix” above. For each bulk signature x and for each single-cell archetype a, we ran the following significance test:

1. Find the mean bulk score x for a specialists, m.

2. Choose a random sample of size n_a, where n_a is the number of a specialists, with replacement from the remaining cells (i.e. cells that are not a specialists, including generalists and other specialist cells). Find the mean bulk score for this sample. N.B. Because some time points have very few cells, we sample evenly from each time point to ensure adequate representation across the time points.

3. Repeat this random selection 1000 times.

4. Generate a p-value, which is equal to the percentage of means from this random distribution above m.

5. Using statsmodels.states.multitest, correct p-values for multiple tests. We used the Bonferroni-Holm method to control the family-wise error rate. Consider q < 0.1 significant.

GSEA on Archetype X in RPM dataset

To understand the functional state of Archetype X in the RPM time series dataset, we used gene set enrichment analysis (GSEA). We compared the expression of genes in the Archetype X specialists to the remaining cells to determine relative expression. We then ran GSEA on the ordered gene list by log fold change in expression with 1000 permutations for hallmark gene sets from MSigDB (h.all.v7.5.1.symbols.gmt). Results in Figure S4H show a subset of the gene sets that were statistically higher or lower in the X specialist cells.

Visualization of single-cell RNA-seq

PCA and UMAP Projections

To visualize single cells in lower-dimensional space, we use PCA and UMAP projections. UMAP plots, we used Scanpy’s implementation of UMAP (McInnes et al., 2018) using the default parameters such as n_components = 2 found at scanpy.readthedocs.io/en/stable/generated/scanpy.tl.umap.html. A random seed was used (random_state = 0) for the reproducibility of plots.

Visualization by Circular A Posteriori (CAP) Projection Plots

To display archetype scores or probabilities p_i, of archetype labels for each cell, we used a method based on circular a posteriori (CAP) projection adapted from Jaitin et al. (2014) and Velten et al. (2017). For the five-dimensional vectors p of archetype scores (shape of p is the number of cells C X number of bulk archetypes N), we first arrange the archetypes on the edge of a circle such that each archetype k is assigned an angle a_k. The class probabilities p_ik for cell i are transformed to Cartesian coordinates by

$$x_i=\sum _k{p}_{ik}cos{a}_k$$

and

$$y_i=\sum _k{p}_{ik}sin{a}_k$$

Because the archetypes could be arranged in several different orders around the circle, we wish to find the best arrangement such that the most similar archetypes are placed next to each other. In practice, this is done by calculating the proximity between archetypes, given for archetypes l and k by

$$D_{lk}=\sum _i{p}_{il}\times p_{ik}$$

We calculate the proximity for each arrangement of archetypes as the sum of the proximity for each pair of neighboring archetypes; for example, the arrangement of archetypes A B C D E gives the proximity

$$D_{ABCDE}=D_{AB}+D_{BC}+D_{CD}+D_{DE}+D_{EA}$$

We test all possible arrangements (N! for N archetypes) and choose the arrangement with the highest proximity.

RNA Velocity Calculation and Analysis

RNA Velocity using scVelo

We interrogated the dynamics of SCLC cells and tumors by analyzing RNA velocity with the Python packages scVelo and CellRank (Bergen et al., 2020; Lange et al., 2022). RNA velocity uses a splicing model to predict directionality and magnitude of gene expression change in the near future for each cell sampled. Using the data without MAGIC imputation (because there are no standardized ways to incorporate imputation and RNA velocity in the field), we used scVelo packages to fit a neighborhood graph (adjacency matrix) and first-order moments with scvelo.pp.neighbors and scvelo.pp.moments, respectively. We then used scVelo’s dynamical modeling pipeline as described in https://scvelo.readthedocs.io/DynamicalModeling/, with the velocity calculation grouped by time-point. We then computed velocity graphs, confidences (coherence of velocities), and velocity lengths, which indicate how coherent and large the velocity vectors are across gene expression space. This gives an idea of how much movement is in the dataset.

Velocity genes and regulators of dynamics

The dynamical model also reports fitting parameters and fit likelihoods for each gene. We used the fit likelihood to rank-order the velocity genes, and visualizing investigated the top genes for each dataset to determine if the fit could be used to make predictions about transitions. As described in the scVelo tutorial, the plots of unspliced versus spliced counts for each gene should have a characteristic “almond” shape.

To determine possible regulators of the highly fit genes that are driving transitions, we used EnrichR on the genes with a fit likelihood > 0.3 and report the significant transcription factors from the “ENCODE and ChEA Consensus TF” list (Chen et al., 2013; Kuleshov et al., 2016).

CellRank

For the RPM dataset, the data samples span 17 days, and therefore the dynamics of the data cover a longer timescale than that of splicing dynamics, which typically occurs on the timescale of a few hours (La Manno et al., 2018). To overcome this challenge, we use CellRank. CellRank is capable of incorporating velocity information fit to each timepoint and alternative measures of temporal dynamics such as pseudotime. We therefore use a previously calculated diffusion pseudotime (Ireland et al., 2020) which adds information about the longer timescale dynamics across days. We adapted the CellRank tutorial on “Kernels and estimators” to combine these two sources of dynamical information into a combined kernel. We use the same weights as in the tutorial—0.8 for the velocity kernel and 0.2 for the DPT kernel—though our results were robust to this parameter. The combined kernel is used to compute a cell-cell transition matrix as a representation of the Markov chain underlying the dynamics. We used the Generalized Perron Cluster Analysis (GPCCA) estimator, which computes aggregate dynamics based on the Markov chain transition matrix by projecting the Markov chain onto a small set of macrostates. We computed a Schur decomposition with 20 components and default parameters. Finally, we computed the macrostates and terminal states on the phenotype clusters (specialists and generalists).

We use the “gmres” solver to compute absorption probabilities using the solvers from petsc4py. We computed driver genes for the Archetype X and SCLC-Y lineages (Figures S5D-S5F). Because the significance of the driver genes is quantified by a CellRank-derived q-value, we used this to determine whether genes in the SCLC-Y bulk archetype signature were drivers of the SCLC-Y lineage, including only genes with a positive correlation to the lineage. We then used EnrichR to investigate the regulators of the top 40 drivers for each lineage (Figure S5G). In order to ensure we capture all possible connections between TFs, we used two lists of enriched regulators for each lineage found in EnrichR: ChEA (2016) and the ENCODE and ChEA Consensus TFs (Figures 5G, 5L, and S5G). We combined these lists and used STRING to determine the relationships between these TFs that regulate the Y and X lineages, as shown in Figure S5H, with the following settings: physical subnetwork (edges indicate proteins are part of a physical complex); confidence-based network edges; active interaction sources = textmining, experiments, and databases; minimum required interaction score of 0.4 medium confidence; hide disconnected nodes. Finally, we applied Cell Transport Potential analysis (Figures 5M and S5I) described below.

Cell Transport Potential Calculation and Analysis

In quantifying plasticity, we wanted to capture the local likelihood of phenotypic transition (that is, change in gene expression profile) for each transcriptional state sampled. Furthermore, we would like to consider size and variance of the phenotypic change. Colloquially, “plastic” cells, such as stem cells, generally are considered plastic because they have at least these two characteristics: they are poised to change their gene expression profile by a large amount (differentiation potency), and they are able to change into multiple different end states (multipotency). Weinreb et al. (2018) showed that single cell transitions could be quantified via the velocity field of a phenotypic landscape, which is the gradient of a potential function. This potential can be decomposed into two terms: a “transport” term and a “constraint” term. The deterministic transport term counteracts sources and sinks in the landscape to keep the cell density in dynamic equilibrium, assuming the population is at steady state. As a proxy for this potential term, we calculate the Cell Transport Potential (CTrP). CTrP is the expected value for the movement of each individual cell. More formally, it is the expected distance of travel for a cell, weighted by the time spent in each other cell state before absorption (reaching an end state). The method is detailed below.

CTrP is a measure of the average distance a cell may travel according to its RNA velocity. For each independent sample (untreated or treated), we ran the following pipeline:

Using RNA velocity calculated as described above, and for each category (‘treatment’), compute a Markov Chain Model transition matrix

This is calculated using an adapted version of ScVelo’s transition_matrix function, in which transition probabilities between each two cells, i and j, is calculated from the velocity graph pairwise. Each entry is a probability describing the likelihood of moving from state i to state j, and each row is the probability distribution of transitions from state i. RNA velocity is compared to distances between other cells to get a pairwise cosine correlation matrix (velocity graph). A scale parameter (default 10) is used to scale a Gaussian kernel applied to the velocity graph, restricted to transitions in the PCA embedding. This transition matrix, P, has dimensions nxn, where n = number of cells. It is then normalized to ensure each row adds to 1 (because each row is the probability of cell i transitioning to any other cell j, which should total 1). Diffusion for P is scaled to 0 (i.e., ignored). Alternatively (for RPM time course), we used CellRank to compute a transition matrix as described above in “RNA Velocity Calculation and Analysis.”

Calculate absorbing states (end states) using eigenvectors

Eigenvalues are calculated for the transition matrix. Any eigenvalue l = 1 (here, with a tolerance of 0.01), is associated with an end state distribution (eigenvector v); i.e., P(v) = lv implies that a distribution of states v will not change under further transformation (transitions) from P. If the Markov Chain is an absorbing Markov Chain, it will contain both transient states (t = number of transient states, where P(i,i) < 1), and absorbing states (r = number of absorbing states, where P(i,i) = 1). For every absorbing state in the matrix, there will be an associated eigenvalue/vector pair, with I =1, because any initial configuration of states will continue to evolve until every cell has reached an absorbing state. Therefore, the multiplicity of l = 1 is equal to the number of end states (absorbing states, or irreducible cycles). The associated eigenvectors v thus correspond to the absorbing states in the Markov Chain, within the tolerance of 0.01.

Calculate the fundamental matrix

In an absorbing Markov Chain, it is possible for every cell to reach an absorbing state in a finite number of steps. Let us rewrite P, the transition matrix, that has t transient states and r absorbing states, as:

$$P=\left[\begin{array}{cc}\hfill Q\hfill & \hfill R\hfill \\ \hfill 0\hfill & \hfill I_r\hfill \end{array}\right]$$

where Q is a t x t matrix, R is a non-zero t x r matrix, 0 is an r x t zero matrix, and I_r is an r x r identity matrix. Thus, Q describes the probability of transitioning between transient states, and R describes the probability of transitioning from a transient state to an absorbing state. The fundamental matrix N of P describes the expected number of visits to a transient state j from a transient state i before being absorbed. Because the Markov Chain is absorbing, this number is the sum for all k of Q^kfor k in {0,1,2,…}:

$$N=\sum _{k=0}^{inf}{Q}^k=(I_t-Q{)}^{-1}$$

Because Q^k eventually goes to the zero matrix (all cells are absorbed), this sum converges for all absorbing chains. Furthermore, each row of the fundamental matrix describes the expected amount of time (i.e. number of steps in the Markov random walk) spent in state j starting from state i, and thus the row can be thought of as a distribution of weights associated with each state j for each starting state i. N is calculated as written above: the inverse of Q subtracted from the identity matrix. In practice, Numpy’s function numpy.linalg.inv(I-Q) is used to calculate N.

Calculate a distance matrix

A distance matrix D (n x n) is then calculated using scipy’s function scipy.spatial.distance.cdist (Virtanen et al., 2020). Here, we calculate the Euclidean distance on the PCA embedding of each sample. Distance may also be calculated directly on the high dimensional data; alternatively, it may be calculated on nonlinear dimensionality reduction techniques, such as UMAP and tSNE, but these distances tend to break down for samples that are highly discontinuous (discrete clusters) and should only be applied to continuous data that falls on a single manifold.

Calculate Cell Transport Potential

Finally, CTrP is calculated as the inner product of each row in fundamental matrix N, and each row in distance matrix D. This gives an expected distance (sum of distances to j from i, weighted by time or number of steps spent in j before absorption).

The advantage of this metric over similar techniques, such as pseudotime and other trajectory inference metrics, is that CTrP is an expected distance in linear (PCA) space, which can be compared across samples (assuming they have been embedded in the same PCA). In other words, unitless measures such as pseudotime cannot be compared between samples because their values are rescaled to [0,1] for each sample. Alternatively, CTrP has a scale set across all samples, dependent only on transformations of the data itself (such as log-normalization and PCA). In future implementations of this method, we plan to include the effect of differences in cell number between states.

Whole Genome Sequencing (WGS)

As described previously in Ireland et al. (2020), “30X WGS data was collected from Day 4 and Day 23 samples, as well as from a blood sample from RPM mice as the normal control. Genomic DNA was extracted from flash frozen cell pellets of Day 4 and 23 cells along with whole blood from the same RPM mouse using Qiagen’s DNeasy Blood and Tissue kit (Qiagen cat#69504). Libraries were prepared using the Nextera DNA Flex Library Prep Kit (Illumina cat#20018705). Libraries were sequenced on a NovaSeq 6000 instrument targeting 300 million read-pairs on a 2 x 150 bp run (30x coverage of whole genome). Sequencing reads were aligned to mouse genome mm10 by BWA 0.7.17-r1188 (Li and Durbin, 2009). Rb1 and Trp53 deletions were examined in the Integrated Genome Viewer (IGV) software v2.5.0. SNVs were jointly called by Freebayes 1.2.0.” Somatic SNVs were filtered by the following criteria: DP >15 and AO =0 in the normal sample. Somatic SNVs were further filter by AO>15 and AO<110 in day 4 and day 23 samples as shown in Figure S4I. Variants were annotated by SnpEff 4.3 (Cingolani et al., 2012).

Network Inference using BooleaBayes

In order to explain our expanded dataset analyzed here, we updated the network structure from the transcription factor network generated in Wooten et al. (2019) to include MYC and NEUROD1. As described previously, the ChEA database was queried to add connections between all TFs, in addition to connections found in the literature. The updated network structure included these 2 new TFs with 43 new edges between them. Therefore, the edges in the network comprise connections from the literature that are verified in ChEA, and addition connections from the ChEA database directly. The network was built using NetworkX software (Hagberg et al., 2008).

We refit the human cell line data used in Wooten et al. (2019) (CCLE RNA-seq data) to generate new rules for this updated network. As described previously, these rules are inferred using BooleaBayes, a method developed in Wooten et al. (2019). This method gives the probability that a specific TF will turn on given the Boolean state of its parent nodes in the network. With one rule for each transcription factor in the network, we can simulate the network asynchronously by picking an initial state (either a random or a predetermined state), randomly pick a TF (with equal probability), and update the state of the TF based on its rule and parent node states. Further information about rule inference and simulations is detailed in Wooten et al. (2019).

We find pseudo-attractors for the updated network, which are states with a higher probability of moving towards than away (i.e. if state A is a pseudo-attractor and state B is its neighbor, then P(B A) > P(A B)). Importantly, with the two additional TFs in the updated network, we find similar pseudo-attractors that match our expected archetypes (1 SCLC-A state, 1 SCLC-A2 state, 2 SCLC-N states, and 2 SCLC-Y states). As in Wooten et al. (2019) we do not find an SCLC-P state, which may be due to the low number of samples near the P archetype in the CCLE data. To analyze the stability, we perform random walks on the network with MYC stably turned on (MYC = 1). We repeated the random walks for 1000 iterations to generate a distribution of the number of steps it takes to leave each basin around each pseudo-attractor, which gives a quantitative change in stability with the in silico MYC perturbation (compared to no perturbation). Fewer steps to leave the basin around a pseudo-attractor suggests that the perturbation has a destabilizing effect, while more steps to leave suggests a stabilizing effect.

QUANTIFICATION AND STATISTICAL ANALYSIS

Details about statistical methods can be found in Method details. For Mann-Whitney tests used in identification of archetype tasks, we considered Bonferroni-Hochberg-corrected q < 0.1 as significant. The ParTI package functions ContinuousEnrichment and DiscreteEnrichment were used for these tests. To determine PNEC functions enriched at each archetype, we used ConsensusPathDB (Kamburov et al., 2013) and Scanpy’s function rank_genes_groups. Details regarding center and dispersion measures (mean and confidence intervals) are in associated Figure legends. n of at least 3 samples was used in experiments when possible. For exploratory analysis of single cell data, preprocessing did not involve estimating sample sizes by power calculations for specific statistical testing. For single cell analysis, cells were excluded based on filtering described in the Method details section. Single cells serve as replicates for detecting subtype heterogeneity in each sample. For human tumor data, patients with SCLC were prospectively identified.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Biological samples
Human SCLC bronchoscopy (Tumor #1)	Vanderbilt University Medical Center	236D
Human SCLC biopsy (Tumor #2)	Vanderbilt University Medical Center	3359-PK
Chemicals, peptides, and recombinant proteins
Sodium succinate dibasic hexahydrate, ReagentPus, ≥99%	Sigma Aldrich	Cat# S2378
Mouse anti-Tubulin beta 3 (TUBB3) Clone TUJ1	BioLegend	Cat# 801213; RRID:AB_2728521
Rhodamine phalloidin	Invitrogen	R415
Donkey anti-mouse Alexa Fluor 488	Invitrogen	Cat# A-21202; RRID:AB_141607
Mounting medium: Aqua-Poly/Mount	Polysciences Inc.	18606-20
Mouse laminin 5% in PBS	Corning	354232
Critical commercial assays
Seahorse XF Cell Mito Stress Test	Agilent	103015-100
Deposited data
Raw and analyzed single cell data (human cell lines and tumors)	This paper	GEO: GSE193961
RPM scRNA-seq and WGS	Ireland et al., 2020	GEO: GSE149180
TKO scRNA-seq	Wooten et al., 2019	GEO: GSE137749
Experimental models: Cell lines
Human: H69 cell line	ATCC	NCI-H69; RRID:CVCL_1579
Human: H82 cell line	ATCC	NCI-H82; RRID:CVCL_1591
Human: H524 cell line	ATCC	NCI-H524; RRID:CVCL_1568
Human: H1048 cell line	ATCC	NCI-H1048; RRID:CVCL_1453
Human: DMS53 cell line	ATCC	CRL-2062; RRID:CVCL_1177
Human: DMS454 cell line	Sigma Aldrich	RRID:CVCL_2438
Human: H841 cell line	ATCC	NCI-H841; RRID:CVCL_1595
Human: CORL279 cell line	Sigma Aldrich	COR-L279; RRID:CVCL_1140
Human: Ready-to-Assay™ SUCNR1 / GPR91 Succinate Receptor Chem-1 cell line	Millipore	HTS241RTA
Experimental models: Organisms/strains
Mouse: Rb1 fl/fl;p53 fl/fl;Myc (RPM)	Oliver laboratory	RRID: IMSR_JAX:029971
Mouse: RB1 fl/fl; P53 fl/fl; P130 fl/fl	Stanford Research Animal Facility	TKO mouse model: PMID: 20406986
Software and algorithms
R version 3.6.3	The R Foundation	http://r-project.org
Factoextra version 1.0.7	The R Foundation	https://cran.r-project.org/web/packages/factoextra
WGCNA version 1.70-3	Langfelder and Horvath, 2008	https://horvath.genetics.ucla.edu/html/CoexpressionNetwork/Rpackages/WGCNA/
ParTI	Hart et al., 2015	https://www.weizmann.ac.il/mcb/UriAlon/download/ParTI
Python version 3.7.6	Python Software Foundation	http://python.org
matplotlib version 3.0.3	Hunter, 2007	http://matplotlib.org
Seaborn version 0.10.1	Waskom, 2021	https://seaborn.pydata.org/
scanpy version 1.8.0	Wolf et al., 2018	https://github.com/theislab/scanpy
scVelo version 0.2.3	Bergen et al., 2020	https://github.com/theislab/scvelo/
Velocyto version 0.17	La Manno et al., 2018	http://velocyto.org/
Scrublet version 0.2.1	Wolock et al., 2019	https://github.com/swolock/scrublet
Numpy version 1.17.0	Oliphant, 2006	http://numpy.org
STAR	Dobin et al., 2013	https://github.com/alexdobin/STAR
DropEst version 0.8.6	Petukhov et al., 2018	https://github.com/kharchenkolab/dropEst
BooleaBayes	Wooten et al., 2019	N/A
Scipy version 1.5.3	Virtanen et al., 2020	https://www.scipy.org/
Cell Transport Potential algorithm	This paper	https://zenodo.org/badge/latestdoi/426287007
CellRank 1.5.1	Lange et al., 2022	https://github.com/theislab/cellrank
Code generated in this manuscript	This paper	https://zenodo.org/badge/latestdoi/426287007

Highlights.

• SCLC intra-tumor heterogeneity is explained by functional tasks of normal PNECs

• Archetypes matching cancer hallmarks constrain SCLC phenotypic heterogeneity

• Task trade-offs along the Pareto front in archetype space drive single-cell plasticity

• MYC reshapes TF network dynamics to drive formation of new SCLC archetypes

INCLUSION AND DIVERSITY

We worked to ensure that the study questionnaires were prepared in an inclusive way. One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in science. One or more of the authors of this paper self-identifies as a member of the LGBTQ+ community. One or more of the authors of this paper received support from a program designed to increase minority representation in science. The author list of this paper includes contributors from the location where the research was conducted who participated in the data collection, design, analysis, and/orinterpretation of the work.