How directed evolution reshapes energy landscapes in enzymes to boost catalysis

Abstract

The advent of biocatalysts designed computationally and optimized by laboratory evolution provides an opportunity to explore molecular strategies for augmenting catalytic function. Applying a suite of NMR, crystallographic, and stopped-flow techniques to an enzyme designed for an elementary proton transfer reaction, we show how directed evolution gradually altered the conformational ensemble of the protein scaffold to populate a narrow, highly active conformational ensemble and achieve a nearly billionfold rate acceleration. Mutations acquired during optimization enabled global conformational changes, including high-energy backbone rearrangements, that cooperatively organized the catalytic base and oxyanion stabilizer, thus perfecting transition-state stabilization. Explicit sampling of conformational sub-states during design, and specifically stabilizing productive over all unproductive conformations, could speed up the development of protein catalysts for many chemical transformations.

One Sentence Summary:

Altered sampling of conformational sub-states on multiple time scales was critical for optimization of a designer enzyme.

Computational enzyme design has afforded catalysts for chemical reactions ranging from ester hydrolysis to abiological cycloadditions (1, 2). Although starting activities are usually low, they can be increased to levels approaching those of natural enzymes through laboratory evolution (3-6). This process mimics the natural selection of enzymes in biology, with the advantage that individual intermediates along the evolutionary pathway can be characterized to deduce how function was enhanced. A comprehensive understanding of the molecular changes that confer better activity could improve design protocols as well as guide the development of smarter mutagenesis and screening strategies.

Here, we investigate the molecular origins of the nearly billionfold rate enhancement achieved by directed evolution of the computationally designed Kemp eliminase HG3 (7). The Kemp elimination (Fig. 1A) is a well-studied model for proton transfer from carbon (8) that has served as a benchmark for de novo design (7, 9-11). Although the first-generation HG3 design is significantly more efficient than an “off-the-shelf” catalyst like bovine serum albumin (12), its specific activity was further increased 200-fold over 17 rounds of mutagenesis and screening (3). The resulting catalyst HG3.17, which exhibits improved alignment of the substrate and the catalytic base (Asp127) and possesses a newly acquired H-bond donor for oxyanion stabilization (Gln50), approaches the efficiency of natural enzymes that promote metabolically important proton transfers (13). Characterization of HG3, the evolutionary intermediate HG3.7, and optimized HG3.17 by a combination of NMR spectroscopy, cryo- and high-temperature crystallography, and stopped-flow fluorescence experiments shows that altered sampling of conformational sub-states on different temporal and spatial scales was crucial for attaining the evolved enzyme’s superior catalytic power.

Fig. 1. Inactivation of Kemp eliminase variants is due to sampling of an alternative, folded conformation.

(A) The Kemp elimination reaction (8) with the structure of the transition-state analog shown on the right. (B) Temperature- and pH-dependent NMR experiments for free HG3.17 display peak duplication for many residues (Fig. S2A) as exemplified here for Gly263. The cross peak of the minor, inactive (I) species increases with temperature and/or pH, indicative of a slow interconversion process between two folded conformations. (C) Directed evolution greatly increased catalytic efficiency (k_cat/K_M) from HG3 to HG3.17 (3), but for evolved enzymes a clear temperature-dependent inactivation is observed. (D) Protein stability measurements using thermal-shift assays indicate that inactivation above ~25 °C is not due to global unfolding, but the smaller transition at lower temperatures suggests the presence of another state.

We first obtained NMR backbone assignments for HG3.17 (Fig. S1) and recorded data at different temperatures and pH values (Fig. 1B and Fig. S2). Unexpectedly, peak duplication spanning a large portion of the protein was detected (Fig. S2A), indicating that the resting enzyme exists in two different folded states undergoing a global conformational exchange that is slow on the NMR timescale. Upon raising either temperature or pH, the cross-peak intensity of one set of peaks increased relative to the other (Fig. 1B and Fig. S2B-D). Based on the independent observation that HG3.17 undergoes inactivation above ~25 °C (Fig. 1C), well below the melting temperature (T_m ≥ 50 °C; Fig. 1D), we hypothesized that the species observed at high temperature corresponds to a less active (or fully inactive) conformational sub-state. An additional transition observed in thermal-shift assays (Fig. 1D and Fig. S3), not seen in circular dichroism melting curves (3), provides further evidence for a pre-existing equilibrium between active (A) and inactive (I) forms of the enzyme.

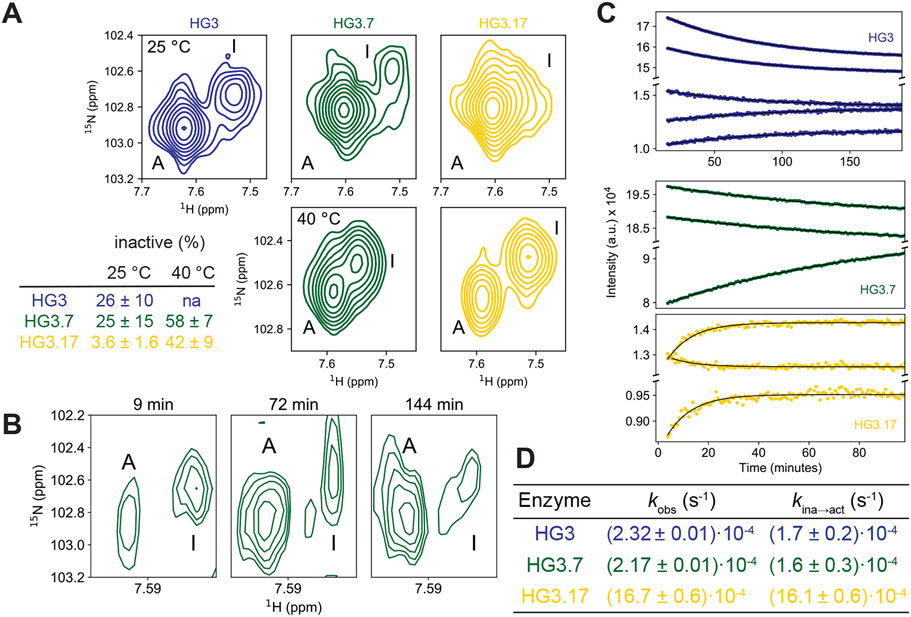
Importantly, the NMR spectra of HG3 and HG3.7 show analogous features, although their inactive sub-states are populated to a greater extent than in HG3.17 (Fig. S2C,D). Estimating the respective populations from the volumes of duplicated cross peaks (Fig. 2A) shows that the inactive species comprises ~25% of the HG3 and HG3.7 samples at 25 °C, but only 5% of HG3.17. At 40 °C, though, the fraction of inactive state increases to 42% and 58% for HG3.17 and HG3.7, respectively (Fig. 2A). Activity-based pH-jump assays (Fig. S4) confirmed that the inactivation process is fully reversible, and repopulation of the active species could be monitored in real time by recording two-dimensional NMR spectra after a rapid change from pH 10 to 7 (Fig. 2B). Trp fluorescence (Fig. S5) and one-dimensional NMR (Fig. 2C) experiments allowed extraction of quantitative rate constants (k_ina→act; Fig. 2D) and show that the interconversion between the two states is slow for all variants (k_obs ~10⁻³-10⁻⁴ s⁻¹). We note that in addition to this slow process, millisecond motions are detected for many residues in the form of line-broadening or complete loss of amide signals for several residues in the core β-strands (Fig. S1D). We hypothesize that these faster, more localized motions underlie the slower collective global rearrangements we observe.

Fig. 2. Characterization of the inactive/active interconversion of Kemp eliminase variants.

(A) Active and inactive conformations are observed for all HG3 variants as exemplified by the NMR cross peaks of Gly229 at pH 7. At 25 °C the inactive population is small for HG3.17, but sizeable for HG3 and HG3.7, and the inactive species increases with temperature. (B-D) Detection of interconversion kinetics at 25 °C by real-time NMR using a pH-jump from proteins equilibrated at pH 10.0 to 7.0. (B) pH-jump experiment for HG3.7 followed by 2D HSQC spectra confirm that the interconversion from the inactive (at high pH) to active (at lower pH) conformation indeed occurs, but the quality of the data is insufficient to extract reliable rate constants. (C, D) The measurements were repeated using 1D proton NMR experiments and time-dependent changes of selected peak areas are shown (C). Observed rate constants (k_obs) in (C), combined with the populations from NMR (A), yielded the activation rate constant (k_ina→act; D).

Taken together, these data show that: (i) the HG3 variants all exhibit a slow, pre-existing equilibrium between active and inactive conformational sub-states; (ii) the last 10 rounds of directed evolution (HG3.7→G3.17) substantially reduced the population of inactive species present under ambient conditions; and (iii) moving away from the conditions employed for selection (i.e., higher temperatures or pH) increases the fraction of enzyme in the inactive state.

To provide structural information on these conformational sub-states, we turned to X-ray crystallography. Cryogenic structures of HG3 and HG3.7 in the absence of a ligand revealed that β-strands 6 and 7 (located adjacent to the binding pocket), adopt two distinct backbone conformations whereas only a single conformer is observed for HG3.17 (Fig. 3A-C, Fig. S6, and Table S1). One conformation matches that seen in the corresponding complexes with a transition-state analog (TSA), and presumably represents the active sub-state. The almost identical positioning of the catalytic residues in the free and the TSA-bound forms of HG3.7 (Fig. 3E and Table S1) indicates that the active site of this sub-state is already primed for catalysis. In the inactive sub-state, however, a backbone flip creates a steric clash between the carbonyl group of Leu236 and the nitro group of the TSA that would block ligand binding (Fig. 3D). Interestingly, this inactive backbone conformation is the only one present in the original xylanase scaffold used for design (PDB 1gor (14); Fig. 3F).

Fig. 3. X-ray data reveal extensive structural changes between the active and inactive conformations of the Kemp eliminases.

(A-E) Crystal structures in the absence of TSA show two conformations for residues near the active site of HG3 (A) and HG3.7 (B), but not of HG3.17 (C). The active state (light colors) makes favorable interactions with the modeled TSA (transparent gray; A-C), whereas the inactive state (dark colors) is a binding-incompetent conformation as the carbonyl-group of Leu236 would clash with the TSA (D). (E) The active conformation of free HG3.7 is nearly superimposable with its TSA-bound form. (F) The inactive backbone conformation is the only one observed in the xylanase scaffold (red, PDB 1gor (14)). (G) X-ray structure of inactive conformation of HG3.17, obtained by calcium (green) binding at a surface-exposed site. Residues with NMR peak duplication (Fig. 1B) are shown in blue, unassigned residues in grey, and prolines in black. (H) Superposition of the active (yellow) and inactive, calcium-bound (orange) conformation of HG3.17 shows the propagation of backbone changes from the calcium-binding site extending to the active site with modeled TSA. (I) The mFo-DFc-polder map (green mesh, contoured at 3σ) for crystallographic data recorded at 70 °C for free HG3.17 can only be explained by modeling both the active (yellow) and inactive (orange) conformations (see also Fig. S7H).

Because the sparsely populated inactive sub-state of HG3.17 was not detected in the cryogenic X-ray structure, we set up crystal screens under conditions favoring this conformation (pH 10 and 37 °C). Crystals obtained with calcium in the crystallization solution yielded a structure of this inactive species (Fig. 3G,H and Table S1). A weak, surface-exposed calcium-binding site stabilizes the inactive form, with substantial backbone changes propagating to the active site, including the backbone flip in strand 7 that impedes substrate binding (Fig. 3G,H and Fig. S7A-E). The 270-282 loop, which contains four of the 10 mutations introduced in the last rounds of directed evolution, also differs in the two conformational sub-states. This segment is ordered in the active state, likely stabilized by a cation-π interaction between protonated His209 and Phe276 (Fig. 3H and Fig. S8A), but disordered in the inactive state. We conjecture that disrupting the His209-Phe276 interaction by raising either temperature or pH, or mutation of His to Ala (Fig. S8B,C), shifts the equilibrium toward the inactive conformation. NMR spectra of HG3.17 with 100 mM Ca²⁺ confirm that the conformational sub-state captured crystallographically is the same as the inactive species in solution, as the positions of the corresponding cross peaks are virtually unaltered but their intensities relative to the ‘active’ signal increase (Fig. S7F,G). Independent kinetic measurements show that the enzyme is 80% inhibited in the crystallization buffer. Remarkably, a HG3.17 structure obtained at 70 °C in the absence of calcium enabled simultaneous observation of both the inactive and active conformations (Fig. 3I, Fig. S7H, and Table S1) as observed in solution by NMR. At this temperature, the complete global rearrangement is permitted within the crystal lattice.

Considering that an enzyme’s affinity to an ideal transition-state analogue is directly proportional to the rate enhancement for the chemical step (15, 16), we dissected the TSA binding mechanism to probe changes in the activation barrier of the chemical step through directed evolution. The minimal binding scheme involves a conformational-selection step for the binding-competent state plus the physical binding step, and—for HG3.17 only—an additional induced-fit step (Fig. 4A and Fig. S9). We hypothesize that the induced-fit step involves a slow ring flip of Trp44 at the bottom of the binding pocket (Fig. S9E), but this does not likely affect activity significantly. The microscopic rate constants were obtained by combining stopped-flow binding kinetics and NMR experiments (Figs. 2 and 4A and Figs. S10-S13); the agreement between the measured macroscopic K_D and their calculated values (Fig. S13E and Equations 11 and 12) confirm our binding schemes. As expected for a good TSA, its affinity increases over the course of evolution (K₂ values of 276, 16.5, and 4.4 μM). For a quantitative comparison of these values with improvements in catalytic efficiency, reliable steady-state parameters are paramount. Previously, k_cat and K_M values were extracted from initial rates, but our new insights into these enzymes reveal that a simple Michaelis-Menten model is not sufficient to describe the system. We therefore monitored the enzymatic conversion of 5-nitrobenzisoxazole to completion and numerically fit the data to a scheme that includes the conformational-selection step and product inhibition (Fig. S14A). This approach enables a more reliable determination of k_cat and K_M even if substrate saturation cannot be achieved (17), as is the case for 5-nitrobenzoisoxazole due to its limited solubility (Fig. 4B and Fig. S14). The extracted values show excellent agreement with the previously published steady-state parameters after correction for the fraction of enzyme in the active state, and the increase in (K_S/k_cat)·k_uncat through the evolutionary rounds indeed correlates remarkably well with the change in K₂ (Fig. 4C). Notably, as TSA affinity increased during evolution, product affinity decreased, minimizing product inhibition and guaranteeing efficient enzyme turnover (Fig. 4B).

Fig. 4. Transition-state analogue binding as a proxy for probing the chemical activation barrier over evolution.

(A) Mechanism and microscopic equilibrium constants (reported as dissociation constants) for TSA binding to the HG3 variants. (B) Kinetic parameters obtained by numerically fitting the progress curves for substrate conversion at 25 °C to an extended Michaelis-Menten model (Fig. S14A). (C) The increase in (K_S/k_cat)·k_uncat through the evolutionary rounds correlates remarkably well with the change in K₂, as expected from transition-state theory. (D) Ensemble refinements (see also Fig. S16-S17) of cryogenic X-ray structures of HG3 variants bound to TSA reveal extensive conformational sampling for HG3 and HG3 K50Q, whereas in evolved enzymes the side chain orientations become more ordered leading to optimal positioning of the catalytic base Asp127 and the oxyanion stabilizer Gln50 (see also Fig. S15-S16). The apparent order for residues Lys50, Trp87, Ser89, and Gln90 in HG3 is explained by crystal contacts in that region (Fig. S16D) that are specific to HG3. HG3 K50Q is thus better suited for comparison of the ensembles as it forms similar crystal contacts as HG3.7 and HG3.17. (E) k_cat values for all Kemp eliminase variants (Fig. S18) highlight the major boost in k_cat by the K50Q/M84C substitutions.

Although reducing the fraction of inactive sub-states in the apo protein improved overall catalysis, the maximum change in the active population of 20% between variants only accounts for a small fraction of the observed 200-fold increase in catalytic efficiency from HG3 to HG3.17 (Fig. 1C). However, ensemble refinement of crystal structures (18) for all the variants in complex with the TSA points to progressive increase of the active configuration as the key contributor to the catalytic enhancement (Figs. 3A-F and 4D and Figs. S15-S17). Increased ordering of the Met172 and Met237 side chains, which interact with one face of the TSA and likely stabilize the charge delocalized transition state through London dispersion forces (19-21), illustrates this trend (Fig. 4D and Figs. S15E,F and S16C). Although relatively flexible in HG3, Met172 becomes better ordered in HG3.7 due to shortening of residue 84 through the M84C mutation, which enabled a stabilizing interaction between the terminal methyl group of Met172 and the π-face of Trp87. The resulting conformation helps to position the catalytic base (Asp127), which samples many unreactive conformations in HG3, in a single orientation with the geometry required for proton abstraction (Figs. 3A-F and 4D and Figs. S15 and S16). Furthermore, HG3.7’s acquisition of the oxyanion stabilizer Gln50 constrains the TSA in a productive pose through hydrogen bonding, which is accompanied by ordering of Met237. In principle, Lys50 in HG3 could act as an effective oxyanion stabilizer and constrain the ligand in a reactive pose, but its side chain points away and forms a hydrogen bond with Gln90 instead (Fig. S15A,B). Further tuning of active site conformations by second- and third-shell mutations from subsequent evolutionary rounds ultimately yielded the highly preorganized HG3.17 binding pocket (Fig. 4D and Figs. S15 and S16).

To disentangle the catalytic contributions of M84C and K50Q from those of more distant mutations, we introduced them singly and together into the original computational design. K50Q increased HG3 activity only 1.5-fold (Fig. 4E and Fig. S18), in marked contrast to the 40-fold loss in efficiency seen when Gln50 was reverted to Lys in HG3.17 (22). The maximum likelihood X-ray structure of HG3 K50Q shows that the Gln50 side chain is properly oriented to hydrogen-bond with the TSA (Fig. S15E), but it shows significant disorder in the ensemble refinement, as do Asp127 and adjacent residues (Fig. 4D and Fig. S16). Similarly, M84C provides no catalytic benefit to HG3 on its own. Together, however, these two mutations boost catalytic efficiency substantially, increasing the rate of the chemical step ~30-fold and overall catalytic efficiency 10-fold (Fig. 4E and Fig. S18). Epistasis is indicated by the synergistic effect of these two mutations. This striking result highlights the serendipitous paths that directed evolution takes, and offers a bright outlook for rational enzyme design: only two of the 17 mutations introduced by directed evolution (Fig. S19) account for a major fraction of the catalytic enhancement. Crucially, these two mutations were predicted from a structural analysis within a protein dynamics framework, underscoring the potential for improved success in enzyme design by focusing on counterselection against sampling of alternative, catalytically unproductive states. The other 15 mutations in HG3.17 had a relatively small effect on k_cat (3-fold), but increased k_cat/K_M 10-fold by lowering K_M; they also largely eliminated the inactive conformational sub-state and decreased product inhibition (Fig. 4B).

Kemp eliminase HG3.17 is among the most efficient artificial enzymes described to date. Analysis of its evolutionary trajectory has revealed how changes in conformational sampling were critical to its success. All HG3 variants have an inactive conformational sub-state, rooted in the original protein scaffold, which was gradually supplanted with a catalytically competent sub-state as evolution progressed. Although conformational selection has been observed in the optimization of other designed enzymes (23, 24), including Kemp eliminases (4, 25-28), what is striking in the HG3 system is that the active conformational sub-state was not explicitly engineered into the xylanase scaffold but only emerged upon introduction of the 11 design mutations due to a serendipitous backbone flip. Instead, design created two “energetically frustrated” enzyme conformations. Drastically decreased sampling of unreactive conformations within the catalytically-competent state provided the second major mechanism for improving efficiency. While distant mutations contributed to this fine-tuning, two active-site residues played an outsized role in sculpting a steric and electrostatic environment conducive to transition-state stabilization. These findings speak to the ongoing debate on the role of protein dynamics in enzyme catalysis (29-34), providing a direct, quantitative demonstration of how modulating a protein conformational landscape, something not optimized by current design protocols but which evolution perfects, can speed up a simple chemical reaction. Proper modeling of conformational dynamics and selective stabilization of productive sub-states over all unproductive conformations during design, for example by explicit energy landscape optimization (35), may open the door to substantially better biocatalysts.