Conformational transitions in BTG1 antiproliferative protein and their modulation by disease mutants

Abstract

B cell translocation gene 1 (BTG1) protein belongs to the BTG/transducer of ERBB2 (TOB) family of antiproliferative proteins whose members regulate various key cellular processes such as cell cycle progression, apoptosis, and differentiation. Somatic missense mutations in BTG1 are found in ∼70% of a particularly malignant and disseminated subtype of diffuse large B cell lymphoma (DLBCL). Antiproliferative activity of BTG1 has been linked to its ability to associate with transcriptional cofactors and various enzymes. However, molecular mechanisms underlying these functional interactions and how the disease-linked mutations in BTG1 affect these mechanisms are currently unknown. To start filling these knowledge gaps, here, using atomistic molecular dynamics (MD) simulations, we explored structural, dynamic, and kinetic characteristics of BTG1 protein, and studied how various DLBCL mutations affect these characteristics. We focused on the protein region formed by α2 and α4 helices, as this interface has been reported not only to serve as a binding hotspot for several cellular partners but also to harbor sites for the majority of known DLBCL mutations. Markov state modeling analysis of extensive MD simulations revealed that the α2-α4 interface in the wild-type (WT) BTG1 undergoes conformational transitions between closed and open metastable states. Importantly, we show that some of the mutations in this region that are observed in DLBCL, such as Q36H, F40C, Q45P, E50K (in α2), and A83T and A84E (in α4), either overstabilize one of these two metastable states or give rise to new conformations in which these helices are distorted (i.e., kinked or unfolded). Based on these results, we conclude that the rapid interconversion between the closed and open conformations of the α2-α4 interface is an essential component of the BTG1 functional dynamics that can prime the protein for functional associations with its binding partners. Disruption of the native dynamic equilibrium by DLBCL mutants leads to the ensemble of conformations in BTG1 that are unlikely structurally and/or kinetically to enable productive functional interactions with the binding proteins.

Significance

B cell translocation gene 1 (BTG1) antiproliferative protein regulates many vital cellular processes. Mutations in BTG1 are found in up to 70% of a particularly aggressive and disseminated form of diffuse large B-cell lymphoma (MCD-DLBCL). BTG1 activity has been linked to its ability to associate with transcriptional cofactors and enzymes. However, molecular mechanisms underlying these interactions and how disease-linked mutations in BTG1 affect these mechanisms are unknown. Here, using molecular dynamics simulations and Markov state modeling, we address this knowledge gap by providing detailed mechanistic description of how DLBCL mutants modify the conformational equilibrium of BTG1. The emerging insights open doors for future studies of functional BTG1 complexes to address how protein-protein interactions are mechanistically modulated by BTG1 disease mutations.

Introduction

B cell translocation gene 1 (BTG1) (1) is a soluble protein of the BTG/transducer of ERBB2 (TOB) family of antiproliferative proteins, which also includes BTG2, BTG3, BTG4, TOB1, and TOB2 (2). All six members of the family have been associated with regulation of key cellular processes, such as cell-cycle progression, apoptosis, and differentiation (2,3). Alterations in the expression pattern of BTG1 and BTG2 are commonly observed in cancer (4, 5, 6, 7, 8). Furthermore, somatic variants of these proteins, and of BTG1 in particular, have been identified with relatively high frequency in non-Hodgkin’s lymphoma (9). Indeed, somatic missense mutations in BTG1 are found in up to ∼70% of a particularly malignant and disseminated subtype of diffuse large B cell lymphoma (DLBCL) called MCD-DLBCL (10).

Antiproliferative activity of BTG/TOB proteins has been linked to their ability to regulate gene expression and/or to control messenger RNA (mRNA) stability through association with transcriptional cofactors and various enzymes (9,11, 12, 13, 14, 15, 16). For example, both BTG1 and BTG2 have been reported to associate with HOXB9, a homeobox transcription factor (16), and interactions of BTG1 with transcription cofactors and enzymes such as PRMT1 have been reported to regulate transcriptional activation (11,13,14,16, 17, 18, 19). Furthermore, BTG1 (and other BTG/TOB proteins) can form a complex with CNOT7 (Caf1 catalytic subunit of the Ccrt4-Not deadenylase complex) to promote mRNA degradation (9,15,20, 21, 22, 23, 24, 25, 26). Studies have proposed classification of BTG1 lymphoma mutations based on the severity of their impact on CNOT7 binding (9), but how these mutations affect BTG1 structure and yield functional phenotypes remains unresolved. Indeed, there is scant information on structure-function relations of the BTG/TOB proteins and BTG1 specifically, which precludes evaluations of the mechanisms of disease-linked mutations in BTG1 and how they affect functional protein interactions in cells.

The existing biochemical and structural data provide important but still limited insights regarding structure-function relationships in BTG/TOB family proteins. Recent X-ray structures of BTG2 and TOB1 proteins (27) revealed a structurally conserved 104–106-residue-long N-terminal domain in the BTG/TOB proteins. Furthermore, the studies have established that this region is the major locus for functional protein-protein interactions. Within this domain, the distal end (residues 1–38), and the structurally conserved loci termed Box A and Box B, as well as the two hydrophobic LxxLL regions (Figs. 1 A, C, D), have been implicated specifically in such interactions (9,12,13,27,28). Importantly, most BTG1 lymphoma mutations are found within this N-terminal BTG domain, and specifically in the α2 helix (residues 35–53; Fig. 1 B) (9,10), but how they affect BTG1 structure, conformational dynamics, and functional interactions is unknown.

Figure 1.

Structural features of BTG1 protein. (A) Sequence of human BTG1 from Uniprot P62324 with important functional regions highlighted. (B) Sites of selected clinical mutations along the α2/α4 interface of BTG1. Colormap shows the frequency of clinical mutations observed in each residue of the protein. (C) Selected residues constituting the hydrophobic core of the protein behind the α2/α4 interface. (D) Zoomed view from above of the hydrophobic core behind α2/α4. The LxxLL regions in H2 and H4 are highlighted in orange in (C) and (D). To see this figure in color, go online.

As a first step toward enabling evaluations of the way(s) in which the disease-linked mutations in BTG1 affect functional interactions with target proteins in cells, it is important to identify structural, dynamic, and kinetic characteristics of BTG1 protein that mechanistically underly its functional activity and to establish how the disease mutations affect these characteristics. To address these goals, here we explored, using computational modeling and atomistic molecular dynamics (MD) simulations, conformational transitions in the wild-type (WT) BTG1 protein, and studied how these transitions are affected by various DLBCL mutations.

Kinetic Markov state model (MSM) and transition path theory (TPT) analyses of the extensive MD dataset revealed that, under the equilibrium condition, the WT BTG1 protein rapidly interconverts between two stationary states that are different in the mutual arrangement of α2 and juxtaposed α4 helix. In one state, the two helices are close to each other to form a tightly packed hydrophobic interface. In the other state, the α4 segment is shifted relative to α2, resulting in more loosely packed α2/α4 interface. Importantly, we show that the DLBCL mutations in this region, such as Q36H, E50K, F40C (all in α2), or A83T (in α4), overstabilize one of these states and significantly affect kinetic rates of transitions between them. Moreover, several other clinical mutations, such as Q45P (in α2) and A84E (in α4), lead to additional metastable states, not detectable in the WT system, in which not only α2 and α4 helices are repositioned with respect to each other but also their helical structure is distorted either through a helical kink (Q45P) or unfolding (A84E).

Based on these results and given that the α2/α4 interface in BTG1 represents one of the key structural regions on the protein involved in functional interactions with several cellular partners, we propose that the rapid rates of interconversion between the two metastable states of the WT BTG1 (BTG1^WT) are essential mechanistic characteristics that prime the protein for functional associations with its binding partners. Disruption of this native dynamic equilibrium, as seen here upon introduction of the DLBCL mutations along the α2/α4 interface, gives rise to the ensemble of conformations in BTG1 that are unlikely structurally and/or kinetically to enable productive functional interactions with the binding proteins. Together, our studies offer detailed mechanistic understanding of how disease mutants modify the conformational landscape of BTG1 protein and lay the groundwork for future structural modeling and investigations of functionally defined protein complexes involving BTG1 and how the protein-protein interactions are modulated by the disease mutations in BTG1.

Results

α2 and α4 helices of BTG1 protein harbor multiple sites of DLBCL mutations (Fig. 1 B) (9,10). While functional phenotypes for some of these mutants are starting to emerge (9,10), it remains unclear how these mutations affect BTG1 structure and conformational dynamics to yield functional phenotypes. In the 3D molecular model of human BTG1^WT protein we built (see section “methods”), α2 and α4 helices form a tight interface that protects the hydrophobic core of the protein from solvent exposure (Figs. 1 C and D). Additionally, the α2/α4 interface of BTG1 was shown to be involved in functional interactions with several other proteins, such as HOXB9 transcription factor (16)). Based on these inferences, we hypothesized that the disease mutations located at the α2/α4 interface would induce structural modifications in this region (and potentially in other distal regions of the protein as well), giving rise to new structural states and/or triggering changes in the distribution of the conformational states as compared with the WT equilibrium ensemble.

To test this premise, we have conducted a rigorous comparative molecular modeling study of the BTG1^WT protein and its six mutant analogs carrying different DLBCL mutations—Q36H, F40C, Q45P, E50K, A83T, and A84E—that are located in different parts of the α2/α4 region (Fig. 1 B). For each construct, all-atom MD simulations were carried out using multi-stage adaptive sampling procedure (see section “methods”) to enhance the conformational sampling. The effect of each mutation was assessed quantitatively by comparing the kinetic and structural characteristics of mutants’ conformational ensembles with that of the BTG1^WT. To this end, the data from MD trajectories for each system were used to build system-specific MSMs (29,30), as described in section “methods.”

The first step in building an MSM is construction of a reduced-dimensionality conformational space that captures relevant dynamics of the α2/α4 region. To construct such a space, we first implemented the time-independent component analysis (tICA) procedure on a set of collective variables (CVs) extracted from the MD trajectories that describe time evolution of the relative positioning of α2 and α4 helices. The nine selected CVs were (1) the distances between the C_α atoms of residues His36, Phe40, Leu44, Leu48 (α2), and Ala83, Ile87 (α4), and (2) the dihedral angle between the two helices, α2 and α4, computed as the angle formed by the C_α atoms of Phe40, Leu47, Arg86, Gln82 (see Figs. S1 A and B). Implementation of the tICA method to construct the conformational space of α2/α4 dynamics provides an accurate way to reduce the dimensionality of the system to the largest space vectors of the slowest transitions, thus producing a space that preserves the relevant kinetic information from the initial dataset (31,32). The tICA dimensionality approach with these CV parameters was applied to all but the BTG1^A84E system. The latter was treated separately since, in the MD simulations, the A84E mutation was seen to induce partial unfolding of the α4 region, a conformational change that required a different set of CVs for structural quantification (see below).

In the combined tICA space built from the MD trajectories of the WT and the other mutant systems (Q36H, F40C, Q45P, E50K, A83T), six components of the tICA decomposition yielded >95% of the changes observed in the dataset (Figs. S1 C and D). Projection of the simulation data onto each of the six time-independent component (tIC) eigenvectors showed only the first two (tIC 1 and tIC 2) to produce non-Gaussian distributions suitable for data discretization (Fig. S2). All the higher-order tIC components exhibited gaussian-like distributions, i.e., they did not show dataset separation into distinguishable states, thus indicating that the first two tIC components are sufficient to capture the relevant dynamic transitions observed in the α2/α4 region of BTG1 during the MD simulations. We also found that the cumulative eigenvalue sum of tIC 1 and tIC 2 accounts only for 54% of the changes observed along the CVs (see Fig. S1 D), implying that the remaining 46% of the motion along the CVs is not related to the slowest conformational transitions. This could be additionally illustrated by evaluating instantaneous correlations between the mean-free values of the CVs and the eigenvalues of the tICA space (Fig. S1 C). The correlation values indicate that each of the CVs contribute the most either to tIC 1 or to tIC 2 among the first six tICA components (Fig. S1 C). Considering these results, all the subsequent analyses were carried out on the 2D tICA space composed of the first two tIC vectors, while the higher tIC contributions were ignored.

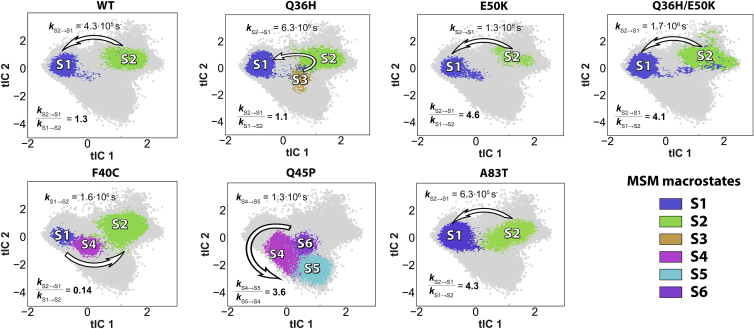
Per-system sampling of the resulting 2D tICA space during the MD simulations is shown in Fig. S3 (see also section “methods”). To facilitate comparative analysis of the structural and kinetic characteristics of the WT and the mutant systems, the tICA landscapes were clustered into kinetically similar macrostates (Fig. 2). This cluster assignment was based on per-system MSMs and was used to calculate corresponding kinetic constants and reactive fluxes (33,34), following the protocols described in section “methods.”

Figure 2.

Kinetic model of conformational transitions in the WT and mutant BTG1 constructs. MSM analysis carried out on the 2D tICA spaces of the individual BTG1 systems (see Fig. S3) identified locations of kinetically distinct macrostates on the tICA surface (color coded; the gray cloud represents the entire 2D tICA conformational space sampled by all the protein systems within the entire MD dataset). The arrows show the direction of the reactive fluxes evaluated with the transition path theory (TPT) approach, as described in Methods. To see this figure in color, go online.

α2/α4 region of the BTG1^WT system samples two metastable states

Our analysis revealed that BTG1^WT exists in an equilibrium between two metastable states: S1 (initial) and S2 (Figs. 2 and 3 A). In S1 state, α2 and α4 helices are held closely against each other (distance between the C_α atoms of Q36 and I87 residues measuring 6Å,;see Figs. 3 B and C, upper panels) and their mutual orientation deviates from the parallel arrangement by about −40° tilt angle (Figs. 3 B and C, lower panels). This closed conformation is stabilized by tightly packed cluster of hydrophobic residues along the α2/α4 interface (Figs. 1 B and C), which includes residue F40 on α2 with its phenyl ring facing into the protein interior and approaching residue L26 on H1 (Figs. 4 A and F), as well as residue I87 on α4 with its side chain positioned near F40 (Figs. 1 B and C). The closed S1 conformation is additionally stabilized by a couple of hydrophilic interactions formed between residues located on the two helices: a hydrogen bond between the Nε atom of Q36 on α2 and I87 backbone oxygen atom (Figs. 4 C and F) and a salt bridge between residues E46 on α2 and R86 on α4 (Figs. 4 D and F). The importance of the latter will be specifically addressed below in view of its direct impact on the sidechain orientation of E50 and conformational dynamics of the E50K mutant.

Figure 3.

Metastable states identified from the MSM analysis and their structural properties. (A) The populations of the kinetic states of the MSM. Each color corresponds to a particular state (see the legend). (B) The violin plot of distributions of the Ca distance between the residues Q36 and I87 (top), and of the distribution of the dihedral angle between α2 and α4 (bottom). (C) The representative conformations of each of the identified kinetic metastable states with two of the CVs highlighted. Top row: the average values of the C_α distance between residues Q36 and I87. Bottom row: the average values of the dihedral angle between α2 and α4. To see this figure in color, go online.

Figure 4.

Key molecular interactions stabilizing various metastable states. Distribution of hydrophobic and polar interactions behind the α2/α4 interface in the identified MSM macrostates from all the BTG1 variants studied, including L26-F40 (A), L26-I87 (B), Q/H36-I87 (C), E46-R86 (D), and Q36-F40 (E). The apolar interaction between a pair of residues (for A, B, and E) was assumed if the minimum distance between any heavy sidechain atoms was no longer than 5 Å. The cutoff radius for the polar interactions (for C and D) was set to 3.5 Å. (F) Structural representation of the hydrophobic core in S1 (left) and S2 (right) metastable states. To see this figure in color, go online.

In the S2 state, the tight packing of the α2-α4 interface is disrupted with the distance between the C_α atoms of Q36 and I87 increasing up to ∼9 Å (Figs. 3 B and C, upper panels) while α2 and α4 helices become nearly parallel to each other (the relative angle about −10°) (Figs. 3 B and C, lower panels). Concomitantly, the hydrophobic core along the α2/α4 interface is reorganized: the sidechain of F40 switches from facing the protein interior to protruding away from the α2/α4 interface where it is stabilized by amino-π interactions with Q36 sidechain (Figs. 4 A, E, and F). At the same time, the sidechain of I87 becomes buried deeper into the hydrophobic core (Figs. 4 C and F). Accompanying this large rearrangement of the α2/α4 hydrophobic core, the position of L31 residue (9), mutation of which to Leu is one of the most frequent phenotypes of DLBCL, located on the loop adjacent to α2, shifts from being exposed to the solvent in S1 state to permeating the center of the hydrophobic core behind the α2-α4 interface (Fig. S4). Quantification of the stationary probabilities and kinetic characteristics of the two states in the BTG1^WT system revealed that the S1 state is more populated than the S2 state (by ∼20%; Fig. 3 A), with the ratio between the rate constant close to 1.3 creating the reactive flux from S2 to S1 state (Fig. 2).

Q36H mutation leads to redistribution of S1 and S2 states and gives rise to a new metastable state

The most common DLBCL mutation occurring in BTG1 is a substitution of Q36 by His residue (Q36H) (10). In the BTG1^WT, as described above, Q36 forms a hydrogen bond with I87 that is crucial for stabilization of S1 state. Thus, we hypothesized that substitution of Q36 with a shorter sidechain of His imidazole group would weaken this hydrogen bond and thus result in destabilization of S1 state. Indeed, the MSM analysis of the MD data for BTG1^Q36H revealed reduction of population of S1 state so that the two states, S1 and S2, become equally populated (Figs. 2 and 3 A). Furthermore, the kinetic MSM model of BTG1^Q36H also identified a new low (3%) population S3 state (Figs. 2 and 3 A) in which the protein adopts somewhat different opened conformation of the α2/α4 region: similar to the S2 state, the S3 state is characterized by shifted position of α4 (i.e., distance between the C_α atoms of Q36 and I87 remains large, ∼9–10 Å); however, the relative tilt between α2 and α4 mimics the one observed in S1 conformation (Figs. 3 B and C).

Overall, our data suggest that Q36H mutation shifts the protein conformations toward wider α2-α4 interface, and the stationary distribution ratio between S1 and S2 drops by ∼20%, becoming equal (Fig. 3 A). In addition, our kinetic analysis reveals that the transitions between S1 and S2 states in BTG1^Q36H occur more rapidly than in the WT system, with the ratio between the transition rate constants decreasing to ∼1.1 (Fig. 2). We hypothesized that this difference is due to the weakening of the hydrogen bond between Q36 and I87 in S1 state and by additional stabilization of both S2 and S3 states with the π-π interactions between the phenyl ring of F40 and imidazole of H36 (Figs. 4 E and F, see occupancy of non-polar interactions between H36 and F40). To test this premise and generally to assess the role of Q36 residue in conformational dynamics of the α2/α4 region, we have computationally designed and explored additional in silico mutations at Q36 position in BTG1.

Mutations at Q36 position affect conformational dynamics of F40 residue to favor the closed state of the α2/α4 interface

We carried out MD simulations of BTG1 constructs in which Q36 was mutated to a small (Q36A) or large (Q36L) hydrophobic sidechain, as well as to the shorter but otherwise similar Asn sidechain (Q36N). Interestingly, all three substitutions resulted in a single S1-state kinetic model (Fig. S5 A), as the distance between Q36A/L/N and I87 largely sampled small values, with only occasional excursions to distances exceeding 8 Å for Q36L and Q36N systems (see Fig. S5 B, left panel). The mutual orientation of α2 and α4 was similar to that in the S1 state of the WT system (Fig. S5 B, right panel). Thus, the absence of the hydrogen bond between Q36A/L/N and I87 is sufficient to abolish the S2 state and, at the same time, does not appear to be necessary for stabilization of the S1 state (Figs. 5 A and C).

Figure 5.

Effects of mutations at Q36 position on the interactions along the H2/H4 interface. (A) The extent of hydrophobic interactions behind the α2/α4 interface, including F40-L26, I87-L26, and Q/H36-F40, quantified as a fraction of MD trajectory frames the residue pairs formed apolar interactions. The latter was defined as formed if the minimum distance between any heavy sidechain atoms was no longer than 5 Å. (B) Fraction of MD trajectory frames in which polar interactions between the sidechain of a residue in 36 position and the sidechains (T32, S33) or the backbone (I87) of its neighbors. The cutoff radius for the polar interactions was set to 3.5 Å. (C) Visual snapshots showing the polar interactions formed between Q/H/N36, T32, S33, and L87 residues in BTG1 WT, Q36H, and Q36N, respectively. To see this figure in color, go online.

However, our results suggest that the introduced mutations at the Q36 position affect the dynamical properties of the above-described hydrophobic network of interactions along the α2-α4 interface. Specifically, as described above, in the WT and Q36H systems, the sidechain of F40 occasionally leaves the hydrophobic core behind the α2-α4 interface and engages in π interactions with either Q36 or H36, thus disturbing the tight packing of the α2 and α4 (S2 state in Figs. 4 A and C). This leads to a formation of the new hydrophobic interactions between the deeply buried L26 and I87 sidechains that favor stabilization of the S2 conformation (Fig. 4 B). On the other hand, the mutant sidechains in Q36/A/L/N BTG1 systems cannot form stable non-bonded interactions with F40 due to either their apolar nature (Q36A, Q36L) or shorter sidechain (Q36N) (Figs. 5 A and C). Therefore, the sidechain of F40 remains within the hydrophobic core behind the closed α2/α4 interface, close to L26 (Fig. 4 A). At the same time, N36 can form stable hydrogen bonds with juxtaposed T32 and S33 sidechain oxygens that were only scarcely populated in both the WT and Q36H (Figs. 5 B and C). The consequence of these new interactions in the Q36N mutant is stabilization of the position of N36 sidechain away from F40 preventing the formation of the S2 state (Fig. 5 C).

The structural effects of the Q36A/L mutations are also found to be confined to the hydrophobic core region. Substitutions of Q36 with these hydrophobic residues favor the tight packing of the region as they result in additional stabilization of the F40 sidechain inside the protein core through its interactions with residue L26 (Fig. 5 A). This reorganization impedes emergence of the S2 state by preventing the formation of the π-stack interactions between F40 and residue in 36 position that stabilize the state (Fig. 5 A).

E50K and Q36H have opposite effects on populations and inter-transition rates of the S1 and S2 states

As described above, apart from the hydrogen bond between Q36 and the backbone of I87, another polar interaction contributing to the stabilization of both S1 and S2 states in BTG1^WT is a salt bridge formed between residues E46 and R86 (the frequency of this interaction is ∼30% in S1 and S2 states for BTG1^WT or BTG1^Q36H; Fig. S5 C). This interaction is completely abolished in S3 state of BTG1^Q36H (Figs. 4 D and S5 C). Notably, E46 resides one helical turn away from E50, which is one of the charge-reversal disease mutation sites, E50K. We thus hypothesized that residue E50, through its electrostatic effect on the E46-R86 salt bridge, may play a mechanistic role in conformational transitions between the S1 and S2 states observed in the WT and Q36 systems, and specifically in stabilizing the shifted conformation of α4 seen in the S2 state. Indeed, the presence of positively charged K50 in the close proximity to E46 would create an electrostatic barrier for the R86 to form the salt bridge with E46 in the shifted S2 conformation. To test this hypothesis, we first collected and analyzed MD trajectories of BTG1 with the clinical E50K mutation. Our MSM results show that, in BTG1^E50K, the S1 state is over-stabilized compared with the WT (Figs. 3 A and S5 A), while the population of the E46-R86 salt bridge exhibits almost twofold increase (Fig. 4 D, BTG1^WT; Fig. S5 C, BTG1^E50K). Moreover, the transition rate constant $k_{S2\to S1}$ is significantly (?3-fold) increased compared with the WT (Fig. 2), further strengthening the flow toward the S1 state.

As Q36H and E50K mutations seem to have a somewhat opposite effect on the WT equilibrium between the S1 and S2 states, we hypothesized that Q36H/E50K double mutations would in part mitigate the effect of Q36H mutation. To test this, we performed MD simulations of the BTG^Q36H/E50K construct. The MSM model build for this system shows that, when paired with Q36H, E50K indeed mitigates the effect of the latter. Thus, the double mutation eliminates the S3 state observed in Q36H mutant, and significantly reduces the population of the S2 state, shifting the ensemble distribution in the direction of the WT system (albeit not completely; compare Figs. 3 A and S5 A). These findings suggest that formation of the E46-R86 salt bridge is essential for the stability of the α2/α4 interface and that this interaction supports the fast interconversion between the S1 and S2 states observed in the WT.

F40C and A83T DLBCL mutations have opposite effects on the stability of the S1 and S2 states

To further assess the importance of the hydrophobic interactions along the α2/α4 interface, we have performed MD simulations and subsequent analysis of F40C and A83T DLBCL mutations located on the α2/α4 interface. F40 is situated inside the hydrophobic core of BTG1 (Figs. 1B and C and 4 E), and, as was shown above, its sidechain motion plays a key role in the conformational transitions between the S1 and S2 states. Introduction of the polar Cys residue at the F40 position leads to the predominance of the opened S2 state (Figs. 2 and 3 A). Indeed, analysis of the BTG1^F40C simulations revealed disruption of the hydrophobic core, as C40 becomes exposed to the solution in the majority of the macrostates observed in the MD trajectories (in Fig. 5 A see decrease in L26-C40 occupancy compared with L26-F40 in the WT system). The population of the S1 in F40C is low (below 4%; Fig. 3 A) and is only observed in the microstates corresponding to the initial stages of the MD simulations (Fig. S6), suggesting that the S1 state is scarcely visited in equilibrium. Interestingly, F40C exhibits a new metastable state S4 (8% population; Fig. 3 A), characterized by even shorter distance between the C_α atoms of Q36 and I87 than that in the WT system (Figs. 4 C and 5 B), and by mostly tilted (about −40°) orientation of α2 and α4 (Figs. 3 B and C) with less than 5% of occupancy for −20° conformation. The reactive flow calculated from the trajectories of the BTG1^F40C system suggests that S4 is a transition state between S1 and S2 (Fig. 2) and thus unlikely to be populated in the equilibrium. Overall, the MD data for BTG1^F40C strongly suggest that this mutation favors S2 state with its loosened conformation of the α2-α4 interface.

On the opposite α4 helix, the A83 residue is located directly at the α2-α4 interface. The MD simulations of the A83T DLBCL mutant construct revealed that this system strongly favored S1 state (85% population; Fig. 3 A). The aliphatic group of threonine at position 83 becomes constrained by the hydrogen bond formed between the alcohol group of T83 and the backbone of L79 (Fig. 6 A, left). This hydrogen bond is preserved throughout the entire MD simulations and leads to overstabilization of S1 state (Figs. 2 and 3 A), which, in turn, results in significant increase in $k_{S1\to S2}$ rate constant, producing the reactive flux from S2 to S1 states, similar to the E50K system (Fig. 2). Altogether, these changes lead to a closer positioning of T83 to α2 helix in BTG1^A83T, as illustrated by the reduced distance between T83 and the center of mass of the Q36-E50 segment of α2 compared with the WT (Fig. 6 A, center and right).

Figure 6.

The effects of A83T, A84E, and Q45P BTG1 DLBCL mutations on the structure of the H2/H4 region. (A) The formation of the hydrogen bond (H-bond) between the mutated T83 and the backbone of L79 (left), the minimum distance between heavy atoms of T83 sidechain and Q36-E50 residues of H2 (center), and aligned conformations of the WT (pale green) and A83T (royal blue) S1 states (right). (B) Fraction of trajectory frames from BTG1^A84E MD simulations a residue in the 78–87 segment is in the helical (deep purple) or coil (light blue) secondary structure conformation (left); selected frames from MD simulations of A84E representing unfolded conformation of H4 helix (right). (C) Violin plot showing distributions of the backbone dihedrals of the residues neighboring Q45P from MD simulations of BTG1^Q45P system (left). The horizontal lines represent the mean values (solid lines) and their standard deviations (dashed lines) of the φ (hot pink) and ψ (gray) peptide dihedrals in α helix; representative conformations of the S4, S5, and S6 states from MD simulations of Q45P BTG1 system aligned to α2 (right). To see this figure in color, go online.

A84E and Q45P DLBCL BTG1 mutations create distortions in the secondary structure of the α4 and α2 helices, respectively, leading to emergence of new metastable states in the BTG1 protein.

Neighboring A83, residue A84 in α4 helix is situated with its sidechain inside the hydrophobic cavity. As mentioned above, dynamics of BTG1^A84E system in our simulations could not be described in terms of relative orientation of α2/α4 α helices, as A84E mutation leads to nearly full unfolding of the α4 helix, with fractions of stable secondary structure observed only for a small N-terminal part of the helix (residues 78–82; Figs. 6 B and S7). In the WT system, A84 is surrounded by several hydrophobic sidechains (I80, I87, L89, and L94; Figs. 1 B and C) that stabilize the Ala sidechain inside the hydrophobic core. Introduction of the polar charged Glu residue in this position, however, exposes it to the solvent, thus destroying the helical structure of α4.

Finally, to assess the importance of α2 secondary structure for the stability and conformational dynamics of the α2/α4 region, we have performed MD simulations of Q45P, another DLBCL mutant of BTG1. In BTG1^WT, Q45 residue resides in the middle of α2, is part of one of the LxxLL functional motifs in the protein, and is exposed to the solvent (Fig. 1 A). We reasoned that introduction of Pro in place of Q45 would alter the α -helical structure of α2. Accordingly, in the simulations, BTG1^Q45P visits three metastable states (S4 state, and two new kinetic states, S5 and S6), with the majority of the conformational space equally distributed between two states: S4 and S5 state (Figs 3 A and C). The main distinguishing feature of S5 and S6 states is the kink in α2 helix around the mutated P45 residue (Fig. 3 C). This helical kink is quantified in Fig. 6 C, which shows that the backbone dihedral angles in the residues neighboring P45 diverge from the canonical α-helical structure (Fig. 6 C). Also, evaluation of the bend angle of α2 helix around P45 residue reveals that this angle in S4, S5, and S6 states is gradually shifting from 0° to 1°, characteristic of an intact α helix, to about −15° (Fig. 6 C, left, and Fig. S8), indicative of a helical kink. We note that S5 and S6 states also differ from each other in that the distance between Q36 and I87 is somewhat larger in S6 state, and α2/α4 helices form larger dihedral angles in this state (Figs. 3 B and C). The reactive flux evaluated for this BTG1 construct follows the direction from S6/S4 states to S5 with reaction constants ratio of ∼3 (Fig. 2), indicating that the lowest energy minimum in the Q45P system is the S5 metastable state.

Discussion

The emergence of experimental data suggesting the involvement of the α2/α4 interface region of BTG1 protein in functional interactions with transcriptional cofactors and enzymes together with the finding that the same region harbors multiple sites of lymphoma-associated mutations has necessitated detailed molecular-level investigation of conformational landscape of this region of the protein and mechanistic understanding of how the disease mutants modify this landscape. To address these goals, here we explored computationally the modes of the conformational mobility of the α2/α4 interface in the WT BTG1 as well as in a number of DLBCL mutations in the α2/α4 region of the protein. Comparison of the structural, dynamic, and kinetic properties of the mutants and WT BTG1 constructs enabled us to identify mechanistic characteristics of the protein that may underly its functional activity.

Distinctive characteristics of the BTG1^WT conformational ensemble arise from the equilibrium interconversion between two stationary states, S1 and S2, that represent tightly packed and loosened/shifted conformations of the α2/α4 interface populated ∼60% and ∼40% of the time, respectively. We propose that the equilibrium between these two states and the rapid rates of interconversion between them are critical to mechanistically enable functional associations of BTG1 with the binding proteins. This hypothesis is supported by our results from MD simulations on DLBCL mutant BTG1 constructs. The mutations along the α2/α4 interface lead to overpopulation of one of the two metastable states observed in the WT system. Specifically, E50K and A83T DLBCL mutants strongly favor the closed S1 conformation of the α2/α4 interface, boosting the population of this state by 1.5 times, while F40C and Q36H (the most frequent DLBCL mutation in BTG1) exhibit 2- and 1.2-fold increase in the population of the S2 state, respectively, compared with the WT protein. While systematic functional characterization of these and other DLBCL mutants in BTG1 is still lacking, in their recent work, Almasmoum et al. (9) proposed classification of a number of BTG1 lymphoma mutations, including F40C and Q36H variants, based on the severity of their impact on CNOT7 protein binding and mRNA degradation in HEK293 cell expression systems. According to the classification, F40C, one of the mutants we found to significantly alter conformational landscape of BTG1, belonged to the group of variants that most severely interfered with BTG1 activity: their binding to CNOT7 was completely abolished and they were unable to induce mRNA degradation. Interestingly, Q36H mutant, which in our studies showed relatively modest changes from the WT construct, was classified along with the variants that did not interfere with BTG1 activity under the experimental conditions used. Indeed, the HEK293 cell expression system might not fully recapitulate the context in which BTG1 mutations naturally occur and associate with disease progression (that is, the B cell and derived B cell lymphomas). It is also important to note that BTG1 somatic mutations are exclusively found in mature B cell neoplasm, pointing to potential BTG1 functions that are specific to B cells. Indeed, Q36H mutation in mature B cells confers a massive fitness advantage to these cells and drives the development of highly aggressive lymphomas that are similar in nature to human MCD-DLBCLs, as we recently showed (10).

Remarkably, our simulations show that alternative mutations at the Q36 position, such as modifications to residues with hydrophobic (Q36A and Q36L) or polar but shorter sidechain (Q36N) completely abolish the open conformation of the α2/α4 interface and, unlike Q36H variant, which shifted the native equilibrium toward wider α2-α4 interface, stabilize the closed S1 state. These phenotypes are directly related to the dynamics of the network of hydrophobic interactions in the protein core behind the α2/α4 helices and centered on the F40 residue. Thus, we find that the integrity of the tightly packed interface observed in the S1 state is in large part dependent on these hydrophobic interactions. Indeed, loosening of this interface (i.e., S1→S2 transition) was accompanied by conformational switch in the sidechain of F40 from facing inside the core to protruding outside where it was stabilized by amino-π (in the WT) or π-π (in Q36H) interactions with Q36 or H36 sidechains, respectively. Furthermore, F40C mutation practically eliminated the closed α2/α4 conformation and was the only variant studied that exhibited the reactive flow reversed toward the open α2/α4 state. When the hydrophobic sidechains of Ala and Leu were introduced at position 36, they provided additional stability to the hydrophobic core. The polar sidechain of Asn at this position was unable to stabilize the outward positioning of F40, likely because it is too short for engaging in amino-π interactions with F40 phenyl ring. Thus, all three Q36A/L/N mutants favored closed S1 state.

An additional mode of regulation of the conformational flexibility of the α2/α4 region is provided by polar interactions between E46/E50 (in α2) and R86 (in α4). In the closed S1 state, E46 and R86 residues are engaged in salt-bridge interactions that are maintained when the system transitions to the open S2 state, in which α4 is shifted “upward” relative to α2 helix. Importantly, this salt bridge appears to be modulated by juxtaposed residue E50. Thus, in the conformational ensemble of E50K mutant, we find significant decrease in the population of the shifted state. This is likely due to electrostatic repulsion between K50 and R86 that influences the ability of the latter residue to form a salt bridge with E46 in the shifted conformation. As a result, E50K mutation leads to the overstabilization of the closed S1 state.

Our simulations of two additional DLBCL mutants, Q45P in α2 and A84E in α4, show another mode of restructuring of the α2/α4 interface that involves not only repositioning of the two helices but also changes to their helical structure. Indeed, we find that Q45P mutation introduces a helical kink distortion to the α2 helix. This finding is especially important as this residue is situated within one of the conserved LxxLL sites on the protein that has been implicated in functional protein-protein interactions. Even more dramatic structural change is found in the simulations of A84E mutant, which almost entirely unfolds the α4 helix. Together, these two DLBCL variants dramatically alter the conformational landscape of the α2/α4 interface and stabilize new metastable states not visited by the WT protein.

Overall, our computational studies reveal how various DLBCL mutations along the α2/α4 interface can disrupt native conformational equilibrium in the BTG1 protein. We propose that the structural and/or kinetic characteristics of the new conformational landscape that emerges as the result of such disruptions will be unable to prime BTG1 protein for functional interactions with the cellular partners. By providing detailed mechanistic understanding of how disease mutants modify conformational equilibrium in BTG1 protein, our work lays the groundwork for future studies of functionally defined protein complexes involving BTG1 to address how the protein-protein interactions are mechanistically modulated by the disease-related mutations in BTG1.

Methods

Molecular constructs

The homology model of the WT human BTG1 protein (residues 1–129) was built with Modeller (6) from the available structure of BTG2 (PDB: 3DJU; (27)) with its high sequence similarity to BTG1 (74% identity, 96% similarity). One-hundred models were created in Modeller and ranked according to the molpdf energy score. The structure with the lowest energy score was chosen for the subsequent computational investigations. The same modeling protocol was used for creating models of the following mutant BTG1 protein constructs: BTG1^Q36H, BTG1^Q36A, BTG1^Q36L, BTG1^Q36N, BTG1^F40C, BTG1^Q45P, BTG1^A83T, and BTG1^A84E. To build molecular models for BTG1^E50K and BTG1^E50K/Q36H double-mutant constructs the corresponding mutations were introduced to the lowest-energy Modeller structure of the BTG1^WT using VMD Mutator Plugin.

Atomistic MD simulations

The WT and the mutant BTG1 constructs were embedded into a rectangular solution box of the size 88 Å × 83 Å × 103Å which also included 150 mM K⁺Cl⁻ ion concentration. The resulting systems contained ∼71,250 atoms.

The systems were equilibrated with NAMD version 2.12 (35) following a multi-step protocol during which the backbone atoms of the BTG1 protein in the solution were first harmonically constrained and subsequently gradually released in four steps (totaling 5 ns), changing the restrain force constants k_F from 1, to 0.5, to 0.1 kcal/(mol Ų), and 0 kcal/(mol Ų). These simulations implemented “all” option for rigidbonds, 1 fs (for k_F of 1, 0.5, and 0.1 kcal/(mol Ų)) or 2 fs (for k_F of 0) integration time step, PME for electrostatics interactions (36), and were carried out in NPT ensemble under isotropic pressure coupling conditions, at a temperature of 310 K. The Nose-Hoover Langevin piston algorithm (37) was used to control the target p = 1 atm pressure with the LangevinPistonPeriod set to 200 fs and LangevinPistonDecay set to 50 fs. The van der Waals interactions were calculated applying a cutoff distance of 12 Å and switching the potential from 10 Å.

After this initial equilibration phase, the velocities of all the atoms in the system were reset and ensemble MD runs were initiated with ACEMD software (38), during which the systems were simulated in five independent replicates, each for ∼1 μs (i.e., cumulative time of ∼5 μs per construct). These runs implemented the PME method for electrostatic calculations and were carried out according to the protocol developed at Acellera and implemented by us previously (38,39) with 4-fs integration time step and the standard mass repartitioning procedure for hydrogen atoms. The computations were conducted under the NVT ensemble (at T = 310 K), using the Langevin thermostat with Langevin damping factor set to 0.1.

To enhance conformational transitions in the BTG1^WT, BTG1^Q36H, BTG1^E50K, and BTG1^E50K/Q36H BTG1 constructs, we selected six frames (per system) from the above-described MD trajectories of the respective systems that represented the S2 state of the protein (with the C_α distance between Q/H36 and I87 spanning from 8.5 Å to 11.5 Å; see section “results”). We then initiated new set of MD runs from these selected structures (simulated in six replicates, each for 1 μs). These simulations were carried out with OpenMM software version 7.4 (40) and using the same run parameters as in the above-described ACEMD runs.

For all the simulations, the latest CHARMM36 force field parameters for proteins, lipids, and ions (35,41) were used.

Dimensionality reduction with tICA

To build a tICA space on the collected MD data from all the trajectories simulated for all the BTG1 constructs, we applied the PyEMMA 2.7 python package (42). The tICA lag time was set to 40 ns (see Fig. S9) and the cumulative kinetic variance cutoff (var_cutoff) was set to 95%. The output tICA space contained nine dimensions. The tICA projection of MD-generated microstates for each individual system can be seen in Fig. S3.

K-means clustering

The 2D tICA projections of MD microstates were subjected to k-means clustering with PyEMMA k-means protocol (42) to further reduce the dimensionality of the space.

To estimate the optimal number of clusters, we evaluated VAMP-2 scores for the Markov models built with varying number of cluster centers (42). The VAMP-2 score measures the kinetic variance contained in the CVs used to build a reduced tICA space. Multiple rounds of clustering were conducted followed by construction of MSM using different number of cluster centers (5, 10, 25, 50, 100, 200, 400, 800, 1000), and a lag time of 30 ns. From the graph shown in Fig. S9 A, the value of VAMP-2 score begins to saturate at n = 100 (95% of variance), thus we used the next value in the row (n = 200, providing more than 98% of VAMP-2 score saturation) for discretization of the tICA space and subsequent MSM analysis. The distribution of the 200 cluster centers on the 2-D tICA space for the BTG1^WT is shown in Fig. S9 B.

MSM construction

To select the lag time ($t_{lag}$) for MSM construction, we have evaluated the implied timescales for a set of lag times: [5, 10, 20, 40, 60, 80, 100, 120]. For the lag times $t_{lag}$ = 30 ns or longer, the implied timescales were time independent in all the BTG1 systems (Fig. S10), indicating Markovian behavior of the systems. Therefore 30-ns lag time was chosen for the MSM building. Reversible MSMs were constructed individually for WT, Q36H/A/L/N, F40C, Q45P, E50K, E50K/Q36H, and A83T BTG1 constructs with the estimate_markov_model package of PyEMMA 2.7 (42). Using the Perron cluster cluster analysis (PCCA⁺⁺) (43), we identified the metastable macrostates of resulting MSMs. To calculate the mean first-passage times (MFPTs) between PCCA metastable macrostates, first, we applied TPT to identify the flux between the states, and then evaluated corresponding MFPTs.

Secondary structure analysis of α2/α4 region in BTG1^A84E

We applied the DSSP algorithm (44) implemented in the MDTraj 1.9.3 software package (45) to estimate the secondary structure of α4 based on the five ∼1-μs MD trajectories of BTG1^A84E. The DSSP algorithm estimates electrostatic energies of hydrogen bonds formed between oxygen and nitrogen atoms of the protein backbone and, based on the value obtained, assigns the secondary structure to the region. The bend angle of the α2 helix around residue P45 in the BTG1^Q45P mutant was calculated using ProKink algorithm (46).

Author contributions

G.K., A.M., C.M., and E.K. conceived the project. E.K. and G.K. designed the experiments, performed the computational simulations, and analyzed the data. E.K. and G.K. wrote the manuscript. E.K., C.M., and G.K. edited the manuscript. All the authors read and approved the final version of the manuscript.

Editor: Alemayehu A. Gorfe.