Validation of and Demographically Adjusted Normative Data for the Learning Ratio Derived from the RAVLT in Robustly Intact Older Adults

Abstract

Background

The learning ratio (LR) is a novel learning slope score that was developed to identify learning more accurately by considering the proportion of information learned after the first trial of a multi-trial learning task. Specifically, LR is the number of items learned after trial one divided by the number of items yet to be learned. Although research on LR has been promising, convergent validation, clinical characterization, and demographic norming of this LR metric are warranted to understand its clinical utility when derived from the Rey Auditory Verbal Learning Test (RAVLT).

Method

Data from 674 robustly cognitively intact older participants from the Alzheimer’s Disease Neuroimaging Initiative (aged 54– 89) were used to calculate the LR metric. Comparison of LR’s relationship with standard memory measures was undertaken relative to other traditional learning slope metrics. In addition, retest reliability at 6, 12, and 24 months was examined, and demographically adjusted normative comparisons were developed.

Results

Lower LR scores were associated with poorer performances on memory measures, and LR scores outperformed traditional learning slope calculations across all analyses. Retest reliability exceeded acceptability thresholds across time, and demographically adjusted normative equations suggested better performance for cognitively intact participants than those with mild cognitive impairment.

Conclusions

These results suggest that this LR score possesses sound retest reliability and can better reflect learning capacity than traditional learning slope calculations. With the added development and validation of regression-based normative comparisons, these findings support the use of the RAVLT LR as a clinical tool to inform clinical decision-making and treatment.

Introduction

Learning slopes represent the extent to which an individual learns after the initial trial of a learning task and provide insight into the benefit of repeated exposure to information over multiple trials. Poor learning slopes have been consistently shown in neurodegenerative conditions like mild cognitive impairment (MCI; Hammers, Suhrie, et al., 2021a) and dementia due to Alzheimer’s disease (AD; Gifford et al., 2015; Hammers, Suhrie, et al., 2021b), and reflect a tool available to clinicians for the diagnosis and treatment of patients. Learning slope data can be found throughout the neuropsychology literature, with the most common calculation being the difference between the first learning trial and the final/best learning trial (Bender et al., 2020; Benedict, 1997; Bonner-Jackson, Mahmoud, Miller, & Banks, 2015; Brandt & Benedict, 1997; Wehling, Lundervold, Standnes, Gjerstad, & Reinvang, 2007). This value has been described as the “Raw Learning Slope” (RLS). An additional slope metric—“Learning Over Trials” (LOT)— has frequently been associated with the Rey Auditory Verbal Learning Test (RAVLT; Schmidt, 1996) and represents incremental learning after factoring out trial one performance of the task (Morrison et al., 2018; Thomas et al., 2020).

However, research has shown that using traditional learning slope scores tend to produce counterintuitive findings. For example, learning slope data from the manuals of some of the most commonly used memory measures suggest that older adults display better learning capacity than younger individuals (Benedict, 1997; Brandt & Benedict, 1997), which is opposite to the known effects of age on learning and memory (Salthouse, 2009, 2010). Partly in response to these idiosyncrasies, there has been increased focus recently on creating a novel learning slope metric that more accurately quantifies learning capacity over trials. In particular, Spencer and colleagues (Spencer, Gradwohl, Williams, Kordovski, & Hammers, 2020) found that by dividing the RLS by the number of items yet to be learned after Trial 1, the resultant learning slope—termed the “Learning Ratio” (LR)—follows a more expected declining trajectory in older adults. Please see the Methods for a more detailed equation of LR. This expected finding is because, unlike other learning slope metrics, LR controls for the competition between Trial 1 and subsequent trial performance by representing the proportion of still-to-be-learned information obtained over successive trials. Consequently, this metric incorporates the opportunity for future learning in its calculation of learning slope, which varies depending upon an individual’s success at Trial 1 (e.g., individuals obtaining higher scores at Trial 1 have fewer items available for subsequent learning). To highlight this effect, suppose two individuals engage in a 15-item learning test over five trials. Further suppose Patient 1 recalls 4 words at Trial 1 and 7 words at Trial 5 (his/her highest performance), whereas Patient 2 recalls 11 words at Trial 1 and 14 words at Trial 5 (his/her highest performance). According to the traditional RLS (i.e., highest trial score minus Trial 1), both patients obtained a learning slope score of 3 (i.e., in both cases the difference between words recalled at Trials 5 and 1 is 3), though this does not appear to accurately predict Patient 2’s stronger learning ability. Conversely, as Patient 1 had 11 words remaining to learn after Trial 1 and Patient 2 had 4 words remaining, their LR scores would be 0.27 (3/11; words learned between Trials 1 and 5 divided by the number of words in the to-be-learned pool after Trial 1) for Patient 1 and 0.75 (3/4) for Patient 2. In essence, Patient 1 learned 27% of information left to learn after Trial 1, and Patient 2 learned 75%, which fits much closer to the learning capacities of these two patients.

Although this LR equation was developed relatively recently, it has been shown to be advantageous to the traditional RLS calculation across several memory measures. Spencer and his associates (2020) originally developed the LR equation from the List Learning and Story Memory subtests of the Repeatable Battery for the Assessment of Neuropsychological Status (RBANS; Randolph, 2012) and validated its performance among standard memory measures relative to RLS in a sample of 289 older veterans from an outpatient memory disorders clinic. Hammers and colleagues (Hammers et al., 2021) additionally validated LR when derived from the Hopkins Verbal Learning Test – Revised (HVLT-R; Brandt & Benedict, 1997) and the Brief Visuospatial Memory Test – Revised (BVMT-R; Benedict, 1997) in an independent sample of 56 memory clinic patients. Furthermore, in a series of studies on a sample of 123 participants across the AD continuum administered the HVLT-R, BVMT-R, and RBANS, Hammers and colleagues have also shown that LR scores were smaller for MCI and AD participants than those with normal cognition (Hammers, Suhrie, et al., 2021a), and that lower LR values were associated with greater levels of hippocampal atrophy, β-amyloid burden, and apolipoprotein ε4 carrier status (Hammers, Suhrie, et al., 2021b). For each of these aforementioned studies, effects observed for LR were greater than those observed for RLS. The use of this learning slope metric as a clinical tool has additionally been advanced by the creation of demographically adjusted normative comparisons for LR derived from the HVLT-R and BVMT-R (Hammers, Duff, et al., 2021a) and the RBANS (Hammers, Duff, et al., 2021b) in 200 robustly intact older adults.

Even though LR has been applied to the HVLT-R, BVMT-R, and RBANS memory measures, to date no investigation of LR derived from the RAVLT has taken place. This represents a gap in the literature because in addition to the common usage of this measure clinically, the RAVLT is administered in conjunction with some of the largest and most comprehensive late-onset and early onset observational studies in the field of AD (e.g., the Alzheimer’s Disease Neuroimaging Initiative [ADNI; Weiner et al., 2017], the National Alzheimer’s Coordinating Center [Besser et al., 2018], and the Longitudinal Early Onset Alzheimer’s Disease Study [Apostolova et al., 2021] multi-center longitudinal trials). Therefore, validating LR in this memory measure represents an opportunity to more accurately assess learning slopes in large cohorts of clinical and research populations. Consequently, the primary aim of the current study was to examine the convergent validity of the LR in a large and well-characterized sample of cognitively intact older adults. As greater emphasis is being placed on the use of cognitively “clean” or “robustly intact” samples recently (Goodwill et al., 2019; Harrington et al., 2017), all study participants possessed intact and stable cognition over 24 months. Specifically, the current study compared LR learning slope performance relative to traditional learning scores (RLS, LOT, and Trial 1 performance) when assessed against standard measures of immediate and delayed memory. It was hypothesized that by accounting for Trial 1 learning, LR would be more strongly associated with tasks of immediate and delayed memory than other markers of learning. The study also assessed the incremental validity of LR above and beyond the impact of the traditional learning scores and examined test characteristics of the metric (e.g., means, retest reliability coefficients). This latter aspect of the study will be particularly important considering that questions have previously been raised about the use of individual trial data in a learning acquisition metric – given the historically low retest reliability of learning trial performance (Hammers, Duff, et al., 2021b). As such, it was anticipated that LR would predict RAVLT total learning performance above and beyond the contribution of Trial 1 performance and possess better retest reliability coefficients than other learning slope metrics. The final purpose of this study was to develop and validate demographically adjusted normative data for the RAVLT LR in this large sample of robustly intact older adults. Given the relationships observed between the RAVLT and demographic variables of age, education, and sex (Gale, Baxter, Connor, Herring, & Comer, 2007; Stricker et al., 2021), it was expected that these variables would be associated with LR metrics from the RAVLT and would be predictive of these LR scores in an older adult sample. Overall, should our hypotheses be correct, our results would provide support that this RAVLT LR metric is better at characterizing learning capacity than traditional learning slope calculations. In addition, by creating demographically adjusted norms, we hope to enhance LR’s utility as a tool for the assessment of learning slopes in older adults administered the RAVLT for either clinical or research purposes. Such use of LR may permit a more nuanced and accurate understanding of trial-by-trial learning capacity in older adults administered the RAVLT than either a total recall score or the currently used raw learning score calculations, and may subsequently allow for more personalized treatment recommendations for some patients.

Methods

All participant data in the current study were obtained from ADNI’s multi-center longitudinal study. Please see the ADNI website (http://adni.loni.usc.edu) for a thorough review of the study resources and data publicly available. ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. For up-to-date information, see www.adni-info.org. Institutional Review Board approval has been obtained for each of the multi-center sites, and informed consent was obtained in written form from study participants or their authorized representatives.

As of April 26, 2021, cognitive data were available for 2,366 ADNI participants across various ADNI protocols, with enrolled participants being followed cognitively for up to 180 months. The earliest participant data collected was from August 23, 2005. Inclusion for ADNI involved being between the ages of 55–90 at baseline; having at least 6 years of education and having a reliable study partner; being free of significant head trauma, depression, or neurologic disease; being stable on permitted medications; and being fluent in either English or Spanish (ADNI2, 2008; ADNI3, 2017). Due to recent critique of ADNI’s classification of participants into diagnostic categories (Duff & Alzheimer's Disease Neuroimaging Initiative, 2021), for the current study ADNI participants were reclassified using a modified version of Jak/Bondi and colleagues’ (Bondi et al., 2014; Jak et al., 2009) actuarial model of diagnosis for MCI. Briefly, age-, education-, and sex-adjusted normative scores were generated for Logical Memory I and II (“Story A”) from the Wechsler Memory Scale – Revised (WMS-R; Wechsler, 1987), Trail-Making Test Parts A and B (Reitan, 1992), Category Fluency – Animals (Morris et al., 1989), Boston Naming Test (Kaplan, Goodglass, & Weintraub, 1983), and Multi-Lingual Naming Test (Gollan, Weissberger, Runnqvist, Montoya, & Cera, 2012) using published normative data from the National Alzheimer’s Coordinating Center neuropsychological battery (Shirk et al., 2011; Weintraub et al., 2018). Specifically, the domain of memory was accounted for by Logical Memory I and II, the domain of speed/executive functioning was accounted for by Trail-Making Test Parts A and B, and the domain of language was accounted for by Category Fluency – Animals and either Boston Naming Test or Multi-Lingual Naming Test (depending on the ADNI protocol the participant received). Note that this is described as a modified version of Jak/Bondi criteria because Logical Memory was used in the place of RAVLT to avoid diagnostic circularity with RAVLT learning slopes. Participants were classified as having MCI if any of the following criteria were met: (1) impaired scores (>1 SD below the normative mean) were present on both measures within at least one cognitive domain (i.e., memory, speed/executive function, or language); (2) one impaired score (>1 SD below the normative mean) was present in each of the three cognitive domains; or (3) a score on the Functional Activity Questionnaire (FAQ; Pfeffer, Kurosaki, Harrah Jr., Chance, & Filos, 1982) ≥ 9 was present. If no criteria were met, then the participants were classified as being cognitively intact.

For the current study, 402 participants were excluded for possessing an ADNI diagnosis of AD. An additional 120 participants were excluded for having missing baseline cognitive data, and a further 1,167 participants were excluded for not being classified as cognitively intact at both baseline and 24-month assessments. As a result, the current sample reflected 674 robustly cognitively intact participants over 24 months, which was the sample for this study for all primary RAVLT LR analyses and the development of demographically adjusted LR norms. Note that the aforementioned 1,167 participants were later incorporated into a validation sample for the demographically adjusted LR norms, as will be described in the Data Analysis section.

Procedure

All participants underwent an extensive clinical and neuropsychological battery at a baseline visit as a result of their enrolment in ADNI. Readers are encouraged to review respective test manuals or ADNI protocols (ADNI2, 2011; ADNI3, 2016) for details of measures only currently used in Jak/Bondi actuarial classification (Trail-Making Test Parts A and B, Category Fluency – Animals, Boston Naming Test, and the Multi-Lingual Naming Test) for the present study. Learning slope scores (as will be described subsequently) were additionally obtained at 6-month, 12-month, and 24-month assessments. For the current study, the neuropsychological and clinical measures used were as follows:

• RAVLT (Schmidt, 1996) is a verbal memory task with 15 words learned over five trials, with the number of correct words summed for the Total Recall score (range = 0–75). The Delayed Recall score is the number of correct words recalled after a 30-min delay (range = 0–15). For descriptive purposes, T score values (M = 50, SD = 10) were generated for Total Recall and Delayed Recall using age-, education-, and sex-adjusted normative comparisons (Stricker et al., 2021). Learning slope performances were evaluated by raw data from individual trials. For both raw scores and T scores, higher values indicate better performance.

• Immediate and delayed memory abilities were also assessed using Logical Memory I and II from the WMS-R (Wechsler, 1987) and the Word Recall subtest from the Alzheimer’s Disease Assessment Scale – Cognitive Subscale (ADAS-Cog; Rosen, Mohs, & Davis, 1984). Specifically, Logical Memory I is a verbal immediate memory task asking patients to learn a verbally presented short story (“Story A”), with the number of story details correctly recalled as the total score (range = 0–23). Logical Memory II is the number of story details correctly recalled after a 20–30-min delay (range = 0–23).

• In addition, the ADAS-Cog is a neuropsychological test battery comprising 13 subtests that are used to assess learning and memory, language production and comprehension, constructional praxis, ideational praxis, and orientation. The Word Recall subtest (Question 1) is a verbal memory task with 10 words learned over three trials, and the Delayed Recall subtest (Question 4) requests participants to recall those words after a 10-min delay. For the purpose of the current study, the Total Recall score is the number of correct words over trials being summed for the Total Recall score (range = 0–30), and the Delayed Recall score is the number of correct words recalled after delay (range = 0–10). Although this scoring deviates from test developer’s protocols, it was instituted for consistency with all other memory measures in the study. As a result, higher values indicate better performance.

• American National Adult Reading Test (AMNART; Grober & Sliwinski, 1991) is used as an estimate of premorbid verbal intellect, in which an individual attempts to pronounce 50 words for which the pronunciation does not follow common phonetic rules. The total number of errors made is entered into a regression equation with years of education to yield the estimate of verbal intelligence in standard scores (M = 100, SD = 15). Higher values indicate better estimates of higher baseline intellectual functioning.

• Mini-Mental State Examination (MMSE); (Folstein, Folstein, & McHugh, 1975) is an 11-item screening instrument that assesses the domains of orientation to time and place, registration and subsequent recall of three unrelated words, attention and calculation, language, and visual construction. Scores range from 0 to 30, with higher values indicating better performance.

• Clinical Dementia Rating (CDR) scale (Morris, 1993) is an informant/participant-based questionnaire assessing performance over the domains of memory, orientation, judgment and problem solving, community affairs, home and hobbies, and personal care. Each domain is rated on a 5-point scale of functioning as follows: 0, no impairment; 0.5, questionable impairment; 1, mild impairment; 2, moderate impairment; and 3, severe impairment. The CDR – Sum of Boxes (CDR-SB) was the variable of interest in the current study, which is a summation of the six individual domain scores. The range of the CDR-SB is 0–18, with higher scores indicating worse performance.

• The FAQ (Pfeffer et al., 1982) is a 10-item self-report questionnaire that was used to assess activities of daily functioning. The range of scores is from 0 to 30, with higher scores indicating greater self-reported functional difficulties.

• The 15-item Geriatric Depression Scale (GDS); (Sheikh & Yesavage, 1986) was used to assess self-reported depression. The range of scores is from 0 to 15, with higher scores indicating greater self-reported depression. The cutoff for this measure is a score ≥ 5.

Calculation of Learning Slopes

For the RAVLT, RLS scores were computed as the highest number of items learned on Trials 2 through 5, relative to Trial 1. LOT scores were computed as the sum of Trials 1 through 5 minus the value of Trial 1 multiplied by 5 (Morrison et al., 2018). The LR score is represented as a proportion as follows: the difference in performance between the highest trial score (of Trials 2 through 5) and Trial 1 in the numerator, and the difference between the maximum possible trial score and Trial 1 performance in the denominator (Spencer et al., 2020). Please note that the “Total Points Available for a Trial” for the RAVLT is 15, though the equations below are written broadly to apply to both the RAVLT and other learning measures. The formulas for RLS, LOT, and LR derived from the RAVLT are as follows:

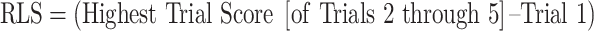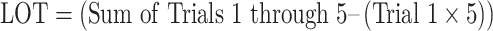Data Analysis

For the convergent validity analyses, partial correlation coefficients were calculated comparing learning slope performances to standard immediate and delayed memory measures. To determine appropriateness of covariates, bivariate correlation coefficients were calculated between continuous demographic variables (e.g., age, education) and LR scores, and one-way analyses of variance (ANOVA) were calculated for categorical demographic variables (e.g., sex and ethnicity) and LR scores. Next, hierarchical linear regression analyses were conducted to determine the incremental validity of LR in predicting RAVLT immediate and delayed memory performance at baseline after accounting for demographics (age, education, and sex; Step 1) and RLS, LOT, or Trial 1 (Step 2). Furthermore, retest reliability was calculated for LR, RLS, LOT, Trial 1, RAVLT Total Recall, and RAVLT Delayed Recall at 6-, 12-, and 24-month assessments using intraclass correlation coefficients (ICCs). As indicated earlier, these analyses were conducted on the 674 robustly cognitively intact participants over 24 months. As additional exploratory analyses, an ethnicity-, age-, and education-matched subsample of participants were selected to consider differences in LR findings between Caucasian/Non-Hispanic participants and Non-Caucasian/Hispanic participants (n = 53/group).

Finally, to generate demographically adjusted normative data, hierarchical linear regression analyses were conducted for the RAVLT LR scores (Cherner et al., 2007; Duff, 2016; Hammers, Duff, et al., 2021a, 2021b; Norman et al., 2011). Specifically, the individual LR scores were the criterion variable, and demographic variables of age, sex (male = 1, female = 2), and education were the predictor variables entered individually within each model. These demographically adjusted normative equations were subsequently applied to the 1,167 participants who were not classified as being robustly intact over 24 months (n = 439 cognitively intact participants at baseline only, and n = 728 MCI participants) for criterion validity analysis.

Measures of effect size for our partial correlation and hierarchical regression analyses were expressed as r² values, and as Cohen’s d values for group comparisons. Comparisons between r values were examined using Fisher r to z transformations. To protect against multiple comparisons, a two-tailed alpha level was set at 0.01 for all primary analyses.

Results

Demographics and Memory Testing

The primary sample was composed of 674 participants classified as being robustly cognitively intact over 24 months. As seen in Table 1, the mean age was 71.86 (SD = 6.4) years old and the sample averaged 16.43 (SD = 2.4) years of education. The sample of participants was slightly more female predominant (54.7% female) and the majority of participants were Caucasian (92.1%). Mean intellect at baseline was estimated to be superior according to the AMNART Verbal Intellect standard score (M = 120.76, SD = 7.2). Regarding participant global cognitive status, the participants’ mean performance on the MMSE was 29.00 (SD = 1.2), mean CDR-SB score was 0.34 (SD = 0.6), and mean FAQ score was 0.40 (SD = 1.0). The sample performed on average at the upper limit of the average range for RAVLT Total Recall (T score = 55) and in the average range for RAVLT Delayed Recall (T score = 47). Self-reported depression was generally low (M = 1.02, SD = 1.3) according to the 15-item GDS (cutoff for depression <5).

Table 1.

Demographic, neuropsychological, and behavioral variables across the robustly cognitively intact sample (n = 674) and validation samples (ns = 439 and 728)

	Robustly cognitively intact sample		Validation sample
			Cognitively Intact		MCI
n	674		439		728
Variable	Mean (SD)	Range	Mean (SD)	Range	Mean (SD)	Range
Age (years)	71.86 (6.4)	55–89	72.00 (7.1)	55–88	73.11 (7.4)	54–89
Education (years)	16.43 (2.6)	6–20	16.23 (2.6)	7–20	16.03 (2.9)	4–20
Sex (% female)	54.7%		53.3%		36.7%
Race (% Caucasian)	92.1%		84.1%		86.8%
GDS	1.02 (1.3)	0–6	1.17 (1.3)	0–6	1.62 (1.5)	0–6
AMNART VIQ	120.76 (7.2)	86–131	119.25 (9.2)	86–131	115.86 (9.8)	84–131
MMSE	29.00 (1.2)	23–30	28.62 (1.5)	19–30	27.35 (1.9)	19–20
CDR-SB	0.34 (0.6)	0–3.5	0.56 (0.8)	0–4	1.57 (1.0)	0–6
FAQ	0.40 (1.0)	0–8	0.90 (1.8)	0–8	3.84 (4.58)	0–24
RAVLT LR score	0.68 (0.2)	0.00–1.00	0.60 (0.2)	0.00–1.00	0.39 (0.2)	0.00–1.00
RAVLT RLS score	6.40 (2.2)	1–12	5.84 (2.3)	1–12	4.13 (2.2)	1–11
RAVLT LOT score	18.36 (7.5)	−3 – 39	16.32 (7.7)	−3 – 46	10.60 (6.9)	−7 – 39
RAVLT Trial 1 score	5.49 (1.7)	1–13	5.09 (1.9)	0–13	4.23 (1.6)	0–10

Note: MCI = mild cognitive impairment, SD = standard deviation, GDS = Geriatric Depression Scale, AMNART VIQ = American National Adult Reading Test Verbal Intellectual Quotient, MMSE = Mini-Mental State Examination, CDR-SB = Clinical Dementia Rating scale-Sum of Boxes, FAQ = Functional Activity Questionnaire, RAVLT = Rey Auditory Verbal Learning Test, LR = learning ratio, RLS = Raw Learning Score, LOT = learning over trials. AMNART VIQ Mean score listed as a Standard Score. LR calculated using the equation (Highest Trial Score [of Trials 2 through 5] – Trial 1)/(Total Points Available for a Trial – Trial 1). RLS calculated using the equation (Highest Trial Score [of Trials 2 through 5] – Trial 1). LOT calculated using the equation (Sum of Trials 1 through 5 – (Trial 1 × 5)). Note, the Robustly Cognitively Intact sample was used for all primary analyses, and the Validation sample was used to validate the demographically adjusted normative equations.

The mean value for LR derived from RAVLT in the current sample was 0.68 (SD = 0.2). This equates to the sample, on average, learning 68% of the available information after Trial 1. The mean value for RLS was 6.40 (SD = 2.2), and the mean value for LOT was 18.36 (SD = 7.5). The bivariate correlation coefficient between LR and age was significant, r = −0.23, p < .001, as was the correlation coefficient between LR and education, r = 0.14, p < .001. One-way ANOVA indicated that LR was significantly associated with sex (women performing better than men; p < .001), but not ethnicity (p = .46). Consequently, age, education, and sex were used as covariates in the subsequent learning slope comparisons.

Convergent Validity Analyses

After accounting for age, education, and sex, RAVLT LR was significantly and positively related to immediate and delayed memory performances for not only RAVLT, but also for additional verbal memory measures (all ps < .001; see Table 2). Similarly, RLS was significantly and positively related to most immediate and delayed memory performances, as were LOT and Trial 1. When comparing across learning slopes, LR score correlations were consistently larger than RLS, LOT, and Trial 1 score correlations. Specifically, Fisher r to z transformations indicated that partial correlations were significantly greater for LR than all other learning slope calculations (e.g., RLS, LOT, and Trial 1) for RAVLT Total Recall (zs = 4.17–12.00, ps < .001), RAVLT Delayed Recall (zs = 6.19–9.56, ps < .001), and ADAS-Cog Word Recall Delayed Recall (zs = 2.73–6.54, ps < .01). Partial correlations were significantly greater for LR than RLS and LOT for ADAS-Cog Word Recall Immediate Recall (zs = 3.58–4.36, ps < .01).

Table 2.

Partial correlation coefficients between standard memory measures and learning slope metrics, after controlling for age, education, and sex (n = 674)

Measure	RAVLT LR		RAVLT RLS		RAVLT LOT		RAVLT Trial 1
	r	r  2	r	r  2	r	r  2	r	r  2
RAVLT
Total Recall 1,2,3	0.77**	0.60	0.35**	0.12	0.48**	0.23	0.66**	0.43
Delayed Recall 1,2,3	0.71**	0.50	0.45**	0.21	0.50**	0.25	0.35**	0.13
Logical Memory
Immediate memory	0.20**	0.04	0.09	0.01	0.13*	0.02	0.18**	0.03
Delayed memory	0.26**	0.07	0.16**	0.03	0.19**	0.04	0.15**	0.02
ADAS-Cog Word Recall
Immediate Recall 1,2	0.44**	0.20	0.23**	0.05	0.27**	0.07	0.34**	0.12
Delayed Recall 1,2,3	0.50**	0.25	0.36**	0.13	0.38**	0.14	0.19**	0.04

Note: RAVLT = Rey Auditory Verbal Learning Test, LR = Learning Ratio, RLS = Raw Learning Score, LOT = Learning Over Trials, ADAS-Cog Word Recall = number of words learned across trials (Immediate) and after a delay (Delayed) on the Word Recall (and delay) subtests from the Alzheimer’s Disease Assessment Scale – Cognitive Subscale. Effect Sizes were measured using r² values. ¹ Denotes significant difference between LR and RLS partial correlation values, p < .01. ² Denotes significant difference between LR and LOT partial correlation values, p < .01. ³ Denotes significant difference between LR and Trial 1 partial correlation values, p < .01. ^* Denotes significant partial correlation value, p < .01. ^** Denotes significant partial correlation value, p < .001.

Table 3 shows the results of a series of incremental validity analyses for RAVLT LR using hierarchical linear regression, after accounting for age, education, and sex. All total models significantly predicted RAVLT Total Recall and Delayed Recall baseline performances (ps < .001, r²s = 0.56–0.91). Specifically, LR consistently predicted RAVLT Total Recall and RAVLT Delayed Recall performances above and beyond the contribution of RLS, LOT, or Trial 1 performances. For example, when RLS scores were entered into Step 2 of a model predicting RAVLT Total Recall scores, they accounted for 9.8% of the variance, whereas LR scores accounted for an additional 59.3% of the variance at Step 3 (change p < .001). Across analyses, LR accounted for an additional 33.2%– 59.3% of the variance when predicting RAVLT Total Recall, and an additional 22.6%– 38.2% of the variance when predicting RAVLT Delayed Recall.

Table 3.

Incremental validity of LR predicting RAVLT Total Recall and Delayed Recall beyond other learning metrics (n = 674)

	Total model F(df), p, r  2	Incremental r  2 change, p
RAVLT Total Recall	F(5, 668) = 859.95, p < .001, r2 = 0.87
Step 1: Demographics		r  2 = 0.17, p < .001
Step 2: RLS		r  2 = 0.10, p < .001
Step 3: LR		r  2 = 0.59, p < .001
RAVLT Total Recall	F(5, 668) = 307.00, p < .001, r2 = 0.68
Step 1: Demographics		r  2 = 0.17, p < .001
Step 2: LOT		r  2 = 0.19, p < .001
Step 3: LR		r  2 = 0.33, p < .001
RAVLT Total Recall	F(5, 668) = 1317.31, p < .001, r2 = 0.91
Step 1: Demographics		r  2 = 0.17, p < .001
Step 2: Trial 1		r  2 = 0.36, p < .001
Step 3: LR		r  2 = 0.38, p < .001
RAVLT Delayed Recall	F(5, 668) = 195.69, p < .001, r2 = 0.59
Step 1: Demographics		r  2 = 0.12, p < .001
Step 2: RLS		r  2 = 0.18, p < .001
Step 3: LR		r  2 = 0.30, p < .001
RAVLT Delayed Recall	F(5, 668) = 107.97, p < .001, r2 = 0.56
Step 1: Demographics		r  2 = 0.12, p < .001
Step 2: LOT		r  2 = 0.22, p < .001
Step 3: LR		r  2 = 0.23, p < .001
RAVLT Delayed Recall	F(5, 668) = 206.89, p < .001, r2 = 0.61
Step 1: Demographics		r  2 = 0.12, p < .001
Step 2: Trial 1		r  2 = 0.11, p < .001
Step 3: LR		r  2 = 0.38, p < .001

Note: RAVLT = Rey Auditory Verbal Learning Test – Revised, LR = Learning Ratio, RLS = Raw Learning Score, and LOT = learning over trials. Demographics reflects participant age, education, and sex.

Table 4 displays the retest reliability—as measured by ICCs—for RAVLT LR at 6, 12, and 24 months relative to the other learning slope metrics and RAVLT total scores. Specifically, retest reliability coefficients for LR ranged from 0.75 to 0.79 over that time frame (95% confidence intervals [CIs] of 0.68–0.82). When comparing LR versus RLS, LOT, and Trial 1 ICCs for each assessment period, retest reliability was consistently stronger for the respective LR metrics; relatedly, 95% CIs did not overlap for any of the comparisons, suggesting that all ICC differences between LR and RLS, LOT, and Trial 1 were significant across 6, 12, and 24 months. Conversely, no differences in retest reliability were observed between LR and either RAVLT Total Recall or Delayed Recall, based on overlap of 95% CIs for each of the comparisons.

Table 4.

Retest reliability coefficients for RAVLT learning slope metrics and total scores at 6, 12, and 24 months (n = 674)

	ICC	95% CI
LR
6 month	0.75	0.68–0.79
12 month	0.79	0.75–0.82
24 month	0.79	0.75–0.82
RLS
6 month	0.57	0.49–0.64
12 month	0.57	0.49–0.64
24 month	0.60	0.53–0.63
LOT
6 month	0.56	0.48–0.63
12 month	0.58	0.50–0.65
24 month	0.59	0.52–0.65
Trial 1
6 month	0.59	0.51–0.65
12 month	0.61	0.54–0.67
24 month	0.62	0.56–0.67
Total Recall
6 month	0.83	0.78–0.87
12 month	0.83	0.80–0.86
24 month	0.82	0.80–0.85
Delayed Recall
6 month	0.79	0.74–0.82
12 month	0.80	0.77–0.84
24 month	0.76	0.72–0.79

Note: RAVLT = Rey Auditory Verbal Learning Test, LR = learning ratio, ICC = intraclass correlation coefficient, CI = confidence interval, RLS = Raw Learning Score, LOT = learning over trials.

When exploring learning slope analyses across ethnicities (Caucasian/Non-Hispanic versus Non-Caucasian/Hispanic participants), there were no differences in mean value for any learning slope (ps = .41–.71, Cohen’s d = 0.07–0.16). In addition, no differences between groups were observed in partial correlations for LR with traditional memory measures (zs = 0.52–2.22, ps = .03–.60). Furthermore, no differences were observed between groups when examining incremental validity analyses for RAVLT LR over other learning slope metrics using hierarchical linear regression to predict RAVLT Total Recall and Delayed Recall baseline performances (zs = 0.41–0.42, ps = .67–.68). Finally, when comparing retest reliability—as measured by ICCs—for RAVLT LR at 6, 12, and 24 months across ethnicity groups, no differences were observed based on overlap of 95% CIs for each of the comparisons.

Demographically Adjusted Normative Comparison Analyses

Before conducting hierarchical linear regression analyses to develop normative data for the RAVLT LR, we examined the assumptions of regression pertaining to independence, homoscedasticity, and normality of the standardized and unstandardized residuals. Using regression standardized residual × predicted scatterplots, the residuals appeared to be independent and homoscedastic. Based on a combination of both normal probability plots of regression standardized and unstandardized residuals, along with skewness/kurtosis data (−0.02 and −0.50, respectively) and Kolmogorov–Smirnov test results (p = .20), we can assume that the residuals were normally distributed.

Finally, Table 5 displays the results of the hierarchical linear regression analyses for RAVLT LR as the criterion variable, and age, sex, and education as the predictor variables. The model containing all three demographic variables (Model 3) predicted LR better than with just age (Model 1) or age and sex alone (Model 2; all ps < .001). When applying these demographically adjusted normative data to RAVLT LR performances for the validation sample, as seen in Table 1 significant differences existed in the resultant LR T score values for the cognitively intact (M = 45.2, SD = 10.6) and MCI (M = 36.3, SD = 10.0) samples (p < .001, Cohen’s d = 18.68).

Table 5.

Regression equation for demographically corrected scores on the RAVLT LR (n = 674)

	F(df), p, r2	Equation	SEest
Model 1	F(1, 672) = 38.43, p < .001, r2 = 0.05		0.22
Model 2	F(2, 671) = 38.17, p < .001, r2 = 0.10		0.21
Model 3	F(3, 670) = 34.60, p < .001, r2 = 0.13	0.77 – (age×0.007) + (sex×0.116) + (education×0.016)	0.21

Note: RAVLT = Rey Auditory Verbal Learning Test, LR = learning ratio. Model 1 contains age as the predictor variable, Model 2 contains age and sex as predictor variables, and Model 3 contains age, sex, and education as predictor variables. Age and education are both in years, sex is coded male = 1, female = 2. SE_est = standard error of the estimate.

Discussion

The results of the current study suggest that LR performance on the RAVLT was positively and significantly related to learning and memory both the RAVLT and memory tasks that were not related to LR (e.g., Logical Memory and ADAS-Cog Word Recall; see Table 2). As such, after accounting for age, education, and sex, lower LR performance was associated with worse performance on learning and memory tests. These results are consistent with previous research in cognitively intact samples, including Hammers and colleagues (Hammers, Suhrie, et al., 2021) observing correlations for LR scores with Total Recall aspects of the same measure (e.g., HVLT-R LR with HVLT-R Total Recall) ranging from 0.61 to 0.76, relative to 0.77 in the current study. Hammers and his associates correlations between LR and both other word-list-learning tasks (rs = 0.41–0.47) and other story memory tasks (rs = 0.29–0.38) were also comparable with our current findings (rs = 0.50 and 0.26, respectively). These comparable results occurred despite differences in the measures used between studies related to semantic clustering, and trial length and/or number. For example, the HVLT-R word list uses themes for semantic clustering of stimuli (e.g., types of jewels, animals; Brandt & Benedict, 1997), whereas the RAVLT does not. Semantic clustering strategies have been suggested to improve learning and recall (Manning & Kahana, 2012), though our result suggests that the original learning measure’s use of clustering may not greatly influence LR. In addition, the RBANS List Learning includes 10 words presented over 4 trials and HVLT-R includes 12 words presented over 3 trials, whereas RAVLT assesses learning of 15 items over 5 trials. Together, these results appear to provide evidence of convergent validity for LR from the RAVLT and also support the notion that trial length and number of the original learning measure have limited impact on the subsequent LR score.

In addition, across a variety of analyses, LR consistently outperformed other traditional learning slope metrics (RLS and LOT) and learning scores (Trial 1). For example, the correlations between LR and RAVLT Total Recall, RAVLT Delayed Recall, and ADAS-Cog Word Recall Delayed Recall were significantly stronger than those for RLS, LOT, and Trial 1, and also stronger than RLS and LOT for ADAS-Cog Word Recall Total Recall (Table 2). Similarly, LR consistently displayed a high degree incremental validity beyond these other learning markers when predicting performance on RAVLT Total Recall and Delayed Recall (Table 3). In particular, LR accounted for an additional 33.2%–59.3% of the variance beyond RLS, LOT, or Trial 1 when predicting RAVLT Total Recall, and an additional 22.6%– 38.2% of the variance when predicting RAVLT Delayed Recall. Furthermore, retest reliability (ICCs) was statistically stronger for LR than RLS, LOT, or Trial 1 at 6, 12, and 24 months, as seen by the lack of overlap in 95% CIs. These results are consistent with Spencer et al. (2020) suggesting support for the use of LR over RLS as a measure of learning slope in the RBANS. They also coincide with Hammers and his associates prior findings of LR’s superiority to RLS from the RBANS, HVLT-R, and BVMT-R when discriminating cognitive impairment (2021) and predicting AD biomarkers (2021). However, our findings additionally represent the first documentation of LR’s superiority over the LOT metric. This is important because the LOT metric from the RAVLT has been used in the literature as a “process score” to identify cognitive disfunction across a variety of settings (e.g., comparing computerized and traditional cognitive testing, Morrison et al., 2018; using objective subtle cognitive difficulties to predict amyloid accumulation and neurodegeneration, Thomas et al., 2020). Our findings suggest that future research on the RAVLT may benefit from using LR as the learning slope metric of choice.

Of note, of all the learning slope metrics assessed from the RAVLT, only LR (ICC = 0.75–0.79) surpassed the ICC > 0.70 cutoff widely used as the minimum acceptable level of reliability for psychological measures (Shieh, 2016) across 6-, 12-, and 24-month assessments. In fact, ICCs for RLS, LOT, and Trial 1 were all appreciably below this cutoff (ICC = 0.57–0.60 for RLS, 0.56–0.59 for LOT, and 0.59–0.62 for Trial 1). Relatedly, the ICCs for RAVLT Total Recall and Delayed Recall were comparable to LR in this sample (ICC = 0.82–0.83 for Total Recall, 0.76–0.80 for Delayed Recall). As anecdotal and published (Hammers, Duff, et al., 2021b) critique of LR has previously questioned its usefulness given its calculation from (often low reliability) individual learning trial data, these results represent the first evidence that LR possesses sound retest reliability over time.

Finally, the current study aimed to advance clinical use of RAVLT-based LR by developing demographically adjusted normative data from this sample of robustly cognitively intact older adults. Table 5 shows the final hierarchical regression-based prediction equation developed for the RAVLT LR, with predicted LR scores being generated from a model containing the demographic variables of age, sex, and education (Model 3). When examining the r² values closely, the final model accounted for a relatively small proportion of variance across predictors (13%). This is not surprising given the small bivariate correlations with LR for age and education in the results (rs = −0.23 and 0.14, respectively), and the lower magnitude of the beta weights in the prediction equations in Table 5. These findings were also consistent with prediction equations for LR values from HVLT-R and RBANS List Learning that observed age and education only accounted for 6%–7% of the variance with scores (Hammers, Duff, et al., 2021a, 2021b). However, unlike the norms for HVLT-R and RBANS List Learning, in the current study sex was also a significant predictor of LR performance – with performance on LR being stronger for women (M = 0.73, SD = 0.21) than men (M = 0.62, SD = 0.22). This is consistent with long-standing findings of sex differences on the RAVLT (e.g., Bleecker, Bolla-Wilson, Agnew, & Meyers, 1988), along with multiple sets of demographically adjusted normative comparisons for RAVLT that factor in sex in test prediction (Gale et al., 2007; Stricker et al., 2021). Exploratory analyses suggested that minimal LR differences were present based on ethnicity. Overall, regardless of their degree of variance accounted for, the addition of these demographic variables permits more accurate prediction of LR performances – and greater specificity of the resultant normative comparisons.

To better highlight the use of this LR prediction equation for an individual, an example is provided in Table 6. Please note, however, that the interested reader can also contact the first author to obtain an Excel spreadsheet that will automatically calculate these demographically adjusted values. First, after entering in demographic information for an individual, the equation in Table 5 will generate a predicted LR performance. Second, this predicted value can be compared with the observed LR value to inform the degree of deviation an individual displays from his/her same-age, -sex, and -education-matched peers (i.e., observed LR – predicted LR/Standard Error of the Estimate [SE_est]). Finally, the resulting calculation yields a demographically adjusted LR Discrepancy z score value that can be translated into an age-, sex-, and education-adjusted T score (mean of 50, SD of 10; achieved by multiplying the z-score by 10 and adding 50). Specifically, for our example of a 71-year-old woman with 16 years of education who obtained an observed RAVLT LR value of 0.75 and had a predicted LR value of 0.76, the difference between the predicted and observed LR value was −0.01. When divided by 0.21 (the SE_est from Table 5), this led to a z value of −0.06. Translating this LR Discrepancy, z score value resulted in a T score of 49, which is consistent with a learning slope performance within the average range. Interestingly, it is notable that this LR T score of 49 tells a different story about the individual’s learning than her RAVLT Total Recall T score alone. In particular, her Total Recall suggested borderline impaired learning abilities (T score of 36), whereas her LR and individual trial performances describe someone with poor Trial 1 learning but a subsequently steep learning curve upon repeated stimulus exposure. Consequently, these LR results portray a clinical picture of an individual with weaker learning upon initial exposure, but a strong capacity to benefit from repeated exposure. This suggests that this normative information can therefore be helpful to provide greater nuance and accuracy to understanding an individual patient’s trial-by-trial learning acquisition capacity when administered the RAVLT than either a total recall score or the currently used raw learning score calculations. As a consequence, this may allow for more personalized treatment recommendations for some patients.

Table 6.

Case Example of a 71-year-old woman with 16 years of education

	RAVLT
Trial 1	3
Trial 2	6
Trial 3	7
Trial 4	9
Trial 5	11
Total Recall T Score	36
Observed LR value	0.75
Predicted LR value	0.76
Observed – predicted scaled score LR value	−0.01
SEest	0.21
Demographically adjusted LR discrepancy z score value	−0.06
Demographically adjusted LR T score value	49

Note: RAVLT = Rey Auditory Verbal Learning Test, LR = learning ratio, SE_est = standard error of the estimate of the regression equations. Predicted LR values are derived from the regression formula from Table 5. Demographically adjusted LR discrepancy z score value = observed – predicted LR Value/ SE_est.

For the reader seeking to calculate normative values for LR scores using observed LR performance, participant age, participant sex, and participant education in a single step, the equation is as follows: (((Observed LR – (0.77 – (age×0.007) + (sex×0.116) + (education×0.016))) / 0.21) × 10) + 50).

The current study is not without limitations. First, these results are specific to the LR metric derived from the RAVLT, using the equations from Spencer and his associates (2020). Although it appears that convergent validity for LR may generalize across memory measures, the normative data developed in our sample are unique to the RAVLT. Future investigation on normative comparisons for the LR from other memory measures like the California Verbal Learning Test - II (Delis, Kramer, Kaplan, & Ober, 2000) is advised. In addition, this examination of LR in the RAVLT has been conducted within cognitively intact samples, consequently future work investigating RAVLT LR in MCI and AD populations is warranted to better understand its sensitivity across disease states. Third, our hierarchical regression-based prediction equation suggested that demographic factors of age, sex, and education accounted for a limited level of variance in LR performance. Although these demographic variables were selected based on (1) ease of accessibility and (2) convergence with normative data for the RAVLT in the literature, future investigation should consider additional demographic information to possibly improve the accuracy of prediction. Fourth, the nature of ADNI recruitment resulted in our sample being mostly Caucasian and highly educated, therefore the generalizability of these findings in more heterogeneous participants regarding ethnicity and education is unknown. As such, future work should consider replication of these findings in more diverse populations. Another limitation to the current study is that ADNI employs rigorous exclusion criteria typical of clinical trials, therefore our study cohort might not be representative of the general population. Finally, as the presence of depression is an exclusion in ADNI, the current study was unable to examine the potential role of mood on learning slope capacity. Given the previous connections between mood and learning (Eysenck, Derakshan, Santos, & Calvo, 2007), future investigation should examine the impact of mood on the LR metric.

These limitations notwithstanding, the current study appears to provide evidence of convergent validity for the learning slope metric LR (Spencer et al., 2020) derived from the RAVLT in large sample of robustly cognitively intact participants. This LR score consistently outperformed other traditional learning slope calculations—RLS, LOT, and Trial 1—across all analyses and displayed acceptable retest reliability coefficients over 6, 12, and 24 months. Finally, we calculated and validated normative comparisons for the LR based on demographic characteristics of age, sex, and education, which now permit the RAVLT LR to be used to inform clinical decision-making and treatment.

Funding

Data collection and sharing for this project were funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer’s Association; Alzheimer’s Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org).

Conlict of Interest

None declared.