Abstract
We leveraged nationally representative data from the Panel Study of Income Dynamics-Child Development Supplement (N = 3,562) and the Early Childhood Longitudinal Study (N = 18,174), to chart the development of working memory, indexed via verbal forward and backward digit span task performance, from 3 to 19 years of age. Results revealed non-linear growth patterns for forward and backward digit span tasks, with the most rapid growth occurring during childhood followed by a brief accelerated period of growth during early adolescence. We also found similar developmental trajectories on digit span task performance for males and females across the U.S. population. Together, this study highlights the relative importance of the childhood period for working memory development and provides researchers with a reference against which to compare the developmental changes of working memory in individual studies. From a practical perspective, clinicians and educators can also use this information to understand important periods of working memory growth using national developmental trends.
Keywords: Working memory development, Childhood, Adolescence, Sex differences
Working memory (WM) refers to a complex cognitive system involved in the storage, maintenance and manipulation of information in immediately accessible memory systems (Cowan, 2008). The fundamental ability to actively maintain information in the presence of ongoing cognitive processing plays an essential role in everyday cognitive functions such as learning, reasoning, and problem solving (Baddely & Hitch, 1974). The significance of WM for a range of cognitive functions and behaviors has made it one of the most widely studied constructs in cognitive psychology and neuroscience (Miyake & Shah, 1999). In fact, WM has been referred to as the “hub of cognition” (Haberlandt, 1997, p. 212) and hailed as “perhaps the most significant achievement of human mental evolution” (Goldman-Rakic, 1992, p. 11).
Although ubiquitous in cognitive psychology, WM research has become common in almost all branches of psychology, given its foundational role in active information maintenance, which underpins virtually all complex thought and behavior (Moser et al., 2018). In the past two decades, there has been a sharp rise in WM research in areas such as clinical psychology - as an endophenotype for neurological and psychiatric disorders (Forbes et al., 2009; Kasper et al., 2012), developmental and educational psychology - in the context of learning and social functioning (Ahmed et al, 2019; McQuade et al., 2013), and social psychology, given its role in decision-making and personality traits (Finn, 2002; Hinson et al., 2003). WM research has also been heavily studied in the areas health psychology and gerontology (e.g., Coppin et al., 2014), most notably in context of Alzheimer’s’ disease (Huntly & Howard, 2010) and recently in areas of public health and medicine (Gunstand et al., 2020; Xie et al., 2020).
Despite its widespread use as a psychological construct, several fundamental questions about the development of WM remain unanswered. First, although the developmental progression of WM has been extensively studied across various developmental stages, much of the research in this area relies on cross-sectional data or short-term longitudinal studies to chart WM growth over time (Alloway et al., 2006; Conklin, 2007; Gathercole et al., 2004; Luciana et al., 2005; Simmering, 2012). For example, Alloway and colleagues (2006) reported gradual increases in WM capacity from age 4 to age 11. Further, Luciana and colleagues (2006) found that aspects of spatial WM continue to develop during adolescence and early adulthood in a sample of 10–20-year-old participants. However, the functional form of WM development spanning early childhood through adulthood has not been extensively examined. This fragmented understanding of the growth and progression of WM across discrete developmental stages has resulted in an incomplete picture of WM development across a wide developmental timespan. Not only would extending the developmental window provide a more comprehensive understanding of WM growth, but can also reveal periods of relative calm and rapid growth across important developmental stages (e.g., early childhood and adolescence) which would otherwise be masked in cross-sectional or short-term longitudinal studies.
Second, the overwhelming use of homogenous and convenience samples in charting WM growth limits our understanding of the developmental trends of WM across the national population. As WM research becomes increasingly widespread in educational, clinical, and medical settings, providing information about normative development at the population level becomes increasingly important, as a way to provide researchers and practitioners with a national standard of WM development across childhood and adolescence. Although recent studies have used nationally representative samples to chart WM development during early childhood (e.g., Finch, 2019; Reynolds et al., 2022; Willoughby et al., 2019), few studies have examined population growth from early childhood into adolescence and early adulthood. An archetype of WM development across a wide age range can be useful from a clinical perspective (akin to national height or weight standards in medical settings) and provide researchers with a foundation to understand the effects of interventions independent of age-related changes in WM.
Finally, examining WM growth across a wide age range at the population level can also clarify sex differences that are presently under debate in the WM literature. Sex differences in WM are generally small, domain-specific, and vary across age. For example, meta-analyses indicate a small, but significant female advantage in auditory WM in children and adolescents, but not during adulthood (Lynn & Irwing, 2008). Conversely, there is also evidence supporting a male advantage in visuospatial WM; however, these sex differences are small and first appear during adolescence (Voyer, 2016). Differences in WM performance across biological sex might be due to underlying neurobiological differences (e.g., circulating sex hormones; Zilles et al., 2016) or due to differences in how males and females approach and process WM tasks (e.g., differences in attentional biases; Weiss et al., 2006). However, there is limited, and mixed evidence for sex differences in WM. When disparities emerge, they depend on the developmental stage of assessment and are almost always examined cross-sectionally. Therefore, understanding the nature of WM sex differences, when they emerge, and the extent to which they persist over time using longitudinal data remains an important and underexplored topic of inquiry.
Current study
We leveraged data from the Panel Study of Income Dynamics-Child Development Supplement (PSID-CDS) to chart the development of verbal forward and backward digit span task performance from 3 to 19 years of age. The PSID-CDS, an accelerated longitudinal design, includes counting span tasks measured from 3 to 19 years of age, which will allow us to examine the development of verbal WM across a wide developmental window. Given research demonstrating rapid WM growth during childhood and relative stabilization during adolescence (e.g., Gathercole et al., 2004; Luna et al., 2004; Thaler et al, 2013), we expect nonlinear functional forms to best characterize WM development.
Despite being a rich national data set, the PSID-CDS lacks the prospective longitudinal design necessary to characterize intraindividual change of WM at the person-level (e.g., Nesselroade, 1991). Therefore, we will also chart the functional form of WM development in the ECLS-K:2011, a prospective longitudinal population sample of over 18,000 individuals, albeit sampled across a narrower timeframe from 5 to 11 years of age. Both the PSID-CDS and the ECLS-K:2011 include counting span tasks measured multiple times across the studies, making it possible to examine developmental trends and compare findings across the two data sets. Counting span tasks measure verbal WM, one of two core WM systems outlined in Baddeley and Hitch’s (1974) WM model (i.e., phonological loop and visuospatial sketchpad). Verbal counting span tasks are widely used in both academic and clinical settings given their ease of administration, developmental stability, and suitability for a wide range of populations, including young children and non-native English speakers (e.g., Conway et al., 2005; Waters & Kaplan, 2003). Finally, both the PSID-CDS and ECLS-K:2011 are nationally-representative, making them ideal to examine whether developmental trajectories differ across biological sex, which can provide patterns of normative WM development generalizable to the U.S. population.
Method
Participants, PSID-CDS:
We examined public use data from the PSID, a longitudinal household study of over 5,000 U.S. families that began in 1967 (Johnson, et al., 2018). The PSID used a probability sampling design to achieve a sample representative of U.S. households in 1967 (see Table 1 for sample demographics). Data for the PSID-CDS were collected in three waves: 1997, 2002/2003, and 2007/2008. The PSID-CDS employed an accelerated longitudinal design. That is, a single cohort consisting of children of different ages was tested in 1997 (age range 2.78 years to 13.64 years), and was tested again across two subsequent waves; 2002/2003 (age range 5.25 years to 19.33 years), and 2007/2008 (age range 10.33 years to 19 years). This sampling design allowed the PSID-CDS to collect data from participants spanning a wide age range (i.e., 3–19 years of age) in a shorter period of time than would be possible with a prospective longitudinal design. The 1997 cross-sectional family weight was applied to make the sample representative of the U.S. population during 1997. The total sample size of our analytic sample in the PSID-CDS was 3,562.
Table 1.
Descriptive Statistics of Study Variables.
| PSID-CDS | ECLS-K 2010–11 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| N | % | M | SD | % Missing | N | % | M | SD | % Missing | ||
|
| |||||||||||
| Child Sex Male, 1997 | 1813 | 50.90 | 0.00 | Child Sex, Male, F2010 | 9288 | 51.22 | 0.21 | ||||
| Child Disability, 1997 | 129 | 3.63 | 0.36 | Child Disability, S2011 | 10473 | 80.32 | 28.25 | ||||
| Unemployed, 1997 | 97 | 5.13 | 46.88 | Unemployed, F2010 | 1034 | 10.27 | 44.59 | ||||
| Unemployed, 2007 | 59 | 3.71 | 56.15 | Child Race, F2010 | 0.24 | ||||||
| Child Race | White | 8488 | 46.81 | ||||||||
| White | 1642 | 46.20 | Black | 2396 | 13.21 | ||||||
| Black | 1455 | 40.94 | Hispanic | 4207 | 23.20 | ||||||
| Hispanic | 267 | 7.51 | Asian | 385 | 2.12 | ||||||
| Asian | 64 | 1.80 | American Indian | 1543 | 8.51 | ||||||
| American Indian | 19 | 0.53 | Hawaiian | 117 | 0.65 | ||||||
| Other | 107 | 3.01 | Multiracial | 168 | 0.93 | ||||||
| Maternal Education | Other | 827 | 4.56 | ||||||||
| Household Income, 1997 | 44,531.31 | 44,328.97 | 0.06 | Guardian Education, F2010 | 4.60 | 1.90 | 11.93 | ||||
| Passage Comprehension, 1997 | 30.56 | 5.50 | 23.10 | Household Income, S2011 | 10.48 | 5.60 | 25.55 | ||||
| Passage Comprehension, 2002 | 24.31 | 7.50 | 28.66 | Child Math Score, F2010 | −1.12 | 0.70 | 14.19 | ||||
| Passage Comprehension, 2007 | 27.13 | 5.04 | 57.72 | Child Reading Score, F2010 | −1.22 | 0.80 | 13.78 | ||||
| Letter-Word, 1997 | 27.41 | 16.43 | 37.76 | Child Age, F2010 | 67.45 | 4.48 | 13.20 | ||||
| Letter-Word, 2002 | 41.22 | 11.03 | 26.08 | Numbers Reversed, F2010 | 433.01 | 30.21 | 14.17 | ||||
| Letter-Word, 2007 | 46.12 | 6.19 | 57.57 | Numbers Reversed, S2011 | 449.68 | 30.52 | 5.65 | ||||
| Applied Problems, 1997 | 24.37 | 11.69 | 38.01 | Numbers Reversed, F2011 | 456.96 | 28.74 | 71.27 | ||||
| Applied Problems, 2002 | 34.89 | 9.27 | 26.31 | Numbers Reversed, S2012 | 469.33 | 25.82 | 16.88 | ||||
| Applied Problems, 2007 | 39.27 | 6.53 | 57.89 | Numbers Reversed, S2013 | 473.24 | 24.33 | 73.99 | ||||
| Child Age at Testing, 1997 | 8.12 | 2.96 | 38.27 | Numbers Reversed, S2014 | 480.68 | 23.28 | 23.89 | ||||
| Child Age at Testing, 2002 | 12.17 | 3.73 | 25.77 | Numbers Reversed, S2015 | 489.80 | 22.21 | 29.15 | ||||
| Child Age at Testing, 2007 | 14.44 | 2.18 | 57.72 | Numbers Reversed, S2016 | 497.24 | 21.70 | 33.50 | ||||
| Forward Digit Span, 1997 | 7.54 | 3.04 | 38.27 | Numbers Reversed, S2017 | 503.31 | 22.36 | 37.11 | ||||
| Forward Digit Span, 2002 | 9.43 | 2.62 | 26.25 | ||||||||
| Forward Digit Span, 2007 | 9.11 | 2.30 | 63.64 | ||||||||
| Backward Digit Span, 1997 | 3.20 | 2.54 | 38.74 | ||||||||
| Backward Digit Span, 2002 | 5.12 | 2.51 | 26.36 | ||||||||
| Backward Digit Span, 2007 | 5.44 | 2.05 | 62.61 | ||||||||
Note: In the ECLS-K:2011, household income was measured in 18 categories, ranging from $5,000 or less to $200,001 or more. In the ECLS-K:2011 math, reading, and digit span scores are standardized. In the PSID-CDS, child age at testing is in years; in the ECLS-K:2011, child age in 2010 is in months. In the ECLS-K:2011, guardian education was measured in categories, ranging from 1 (first grade) to 8 (doctoral). In the ECLS-K:2011, F=fall, S=spring.
Working Memory, PSID-CDS:
The Digit Span Task from the Wechsler Intelligence Scale for Children, Revised (Wechsler, 1974) was administered to measure participants’ verbal working memory capacity. Participants were asked to accurately recite a string of numbers that began with two-number sequences and increased in length until eight digits, including two trials for each length. In Digit Span Forward, participants were asked to accurately recall the string of numbers in the same order they were presented, and in Digit Span Backward, to recall the numbers in the reverse-order. Although there is some debate in the WM literature (see Conway et al., 2005 for review), forward and backward span tasks capture distinct aspects of the broader working memory construct. Forward span includes storage and maintenance components, whereas backward span also requires participants to manipulate and update the information stored in short-term memory, and is often described as capturing working memory capacity because of the additional processing demand (Conway et al., 2005; Cowan, 2008). Participants completed both Forward and Backward Span tasks in 1997, 2002/2003, and 2007/2008. Items were scored by summing the number of correctly answered sequences (digit span score range: 0-16). The Digit Span Task demonstrates excellent reliability (α = .93; Wechsler, 2008) and good test-retest reliability (r = .73; Lipsey et al., 2017).
Covariates and Missing Data, PSID-CDS:
Child covariates used in missing data analysis included child sex, child age at the time of digit span testing measured in years, race, whether the child had ever been diagnosed with a learning disability in 1997, reading scores in 1997, 2002, and 2007; and math scores in 1997, 2002, and 2007. Family covariates included maternal unemployment in 1997 and 2007, household income in 1997, and maternal educational attainment measured in years in 1997. Descriptive statistics of study variables and percentages of missing data in the PSID-CDS can be found in Table 1. Missing data for digit span forward ranged from 26.25% to 63.64% and for backward span from 26.36% to 62.61% (Table 1 displays missing rates for all study variables). To account for the high levels of missingness, missing data were imputed using multiple imputations (Rubin, 1987) by chained equations procedures implemented in Stata (StataCorp., 2019) to create 70 complete data sets. Using the covariates mentioned above, we conducted missing data analyses, where missing data on the digit span variables were dichotomously coded (0=non-missing, 1=missing) and t-tests and chi-square tests were conducted. Variables that were related to missingness on the outcome variables of interest were entered in our imputation models as covariates to adhere to MAR assumptions (Enders, 2010). Specific details about covariates and missing data analysis for the PSID-CDS can be found in the online supplemental materials.
Participants, ECLS-K:2011.
We examined public-use data from the Early Childhood Longitudinal Study, Kindergarten Class of 2010–2011 (ECLS-K:2011), a prospective longitudinal study of 18,174 children sponsored by the National Center for Education Statistics (NCES). Participants in the ECLS-K:2011 were a nationally representative sample of public and private school students, their families, teachers, schools, and care providers (Tourangeau et al., 2015). Sample characteristics for the ECLS-K:2011 are displayed in Table 1. The baseline sampling weights provided by NCES were applied to make the sample representative of the U.S. population during the 2010–2011 school year.
Working memory, ECLS-K:2011.
The Numbers Reversed subtest of the Woodcock Johnson Tests of Achievement (WJ-NR) is a measure of working memory where children are presented with lists of numbers and are asked to repeat the numbers back in reverse order (Mather & Woodcock, 2001). Students begin with five two-number sequences; if a student incorrectly repeats three consecutive two-number sequences, the assessment is discontinued. In each subsequent round, the number sequences increase by one digit, up to a maximum of eight-number sequences. The discontinue rule of three consecutive incorrect answers applies in each round, or until a student completes all number sequences. W-scores, a score metric on an equal-interval scale sensitive to longitudinal change, were used for the present study (Mather & Jaffe, 2016; McGrew & Woodcock, 2001).
Covariates, ECLS-K:2011.
Parents reported their children’s sex, age (in months), race and ethnicity, and family socioeconomic status. Information regarding child’s sex, age, disability status, guardian education level, and employment status was gathered from parents during interviews conducted in the fall of kindergarten, and household income was reported by parents during the spring kindergarten interview. Children’s Math and Reading achievement was measured during the fall of Kindergarten (i.e., first wave) using theta scores based on the National Assessment of Educational Progress (NAEP) math and reading frameworks (Tourangeau et al., 2015).
Missing data – Longitudinal Attrition and Planned Missingness, ECLS-K:2011:
Table 1 displays missing rates for all study variables from the ECLS-K:2011. Using the covariates mentioned above, we conducted missing data analyses, where missing data on the digit span variable was dichotomously coded (0=non-missing, 1=missing) and t-tests and chi-square tests were conducted. To account for longitudinal attrition and planned missingness across the study’s waves, missing data were imputed using multiple imputations (MI; Rubin, 1987) by chained equations procedures implemented in STATA (StataCorp., 2019) to create 40 complete data sets. Further, and to adhere to MAR assumptions, variables significantly related to the outcome of interest were entered in our imputation models as covariates (Enders, 2010). Specific details about covariates and missing data analysis for the ECLS-K:2011 can be found in the online supplemental materials.
Analytic Plan
PSID-CDS and ECLS-K:2011:
Longitudinal mixed-effects modeling was used to examine the functional form of children’s working memory development (Singer & Willett, 2003). Using this framework, time was nested within persons, where level 1 variables included child age and digit span performance, with a random intercept (level 2) that varied across individuals. We estimated the intraclass correlation (ICC), which conveys the percent variation in the dependent variable that can be attributed to difference between and within individuals. In supplementary analyses not included in our preregistration plan, we also tested whether the random slope at level 2 was statistically significant; tested whether there were a statistically significant covariance between the intercept and random slope; and plotted individual trajectories of a random subsample of 100 participants in the ECLSK:2011 in order to understand individual variation in the development of digit span performance across time. In the PSID-CDS, the primary independent variable was child age (which ranged from 3–19 years), and the dependent variable was the raw score of digit span. Because the ECLS-K:2011 numbers reversed variable was standardized based, partially, on child age, the primary independent variable in the ECLS-K:2011 was study-wave. The ECLS-K:2011 had 9 study waves: Fall 2010, Spring 2011, Fall 2011, Spring 2012, Spring 2013, Spring 2014, Spring 2015, Spring 2016, and Spring 2017. Therefore, the study wave variable was re-coded to mirror the unequal distances in measures (.5=wave 1, 1=wave 2, 1.5=wave 3, 2=wave 4, 3=wave 5, 4=wave 6, 5=wave 7, 6=wave 8, 7=wave 9). When dealing with an independent variable that is time-unstructured (such as child age in the PSID-CDS), or when dealing with a time variable that has unequal distances (as in the ECLS-K:2011), mixed effects modeling is preferred over other methods, such as latent growth-curve modeling (McNeish & Matta, 2018).
Four functional forms were tested: linear, quadratic, logarithmic, and cubic. The best fitting model was determined by comparing AIC and BIC across models as well as the functional-form regression estimates and corresponding p-values. Smaller AIC and BIC values and significant parameter estimates were used to identify the best fitting model (e.g. Rafferty, 1995; Singer & Willett, 2003). We first examined the functional forms of Forward Digit Span and Backward Digit Span using the entire child age range of the PSID-CDS (i.e., ages 3–19). Then, for the comparison analyses, we examined the functional form of Backward Digit Span in the PSID-CDS and ECLS-K:2011 datasets, wherein PSID-CDS data were restricted to the ages examined in the ECLS-K:2011. More specifically, PSID-CDS data were restricted to the mean age of children in the ECLS-K:2011 in 2010 and 2017 (i.e., ages 6–11). Next, we conducted subgroup analyses based on child sex to determine whether the functional forms of children’s Forward Digit Span and Backward Digit Span were the same for boys and girls. These subgroup analyses were conducted on the full age range of the PSID-CDS Forward Digit Span, the full age range of the PSID-CDS Backward Digit Span, the restricted age range of the PSID-CDS, and the ECLS-K:2011. To adjust for multiple testing, we used a Bonferroni correction, such that only p-values < .001 were considered statistically significant. This study used publicly available and deidentified data and, therefore, Institutional Review Board (IRB) approval was not obtained. Data from the ECLS-K: 2010–11 are publicly available at https://nces.ed.gov/ecls/dataproducts.asp. Data from the PSID-CDS are publicly available at https://psidonline.isr.umich.edu/cds/default.aspx. All study analyses were preregistered on OSF: https://osf.io/szvmx/ (Ellis et al., 2021).
Results
Functional form model parameters and fit statistics of Forward and Backward Digit Span in the full PSID-CDS sample (i.e., ages 3–19) can be found in Table 2. The ICC suggested that 27% of the variation in Forward Digit Span could be attributed to differences between persons, with 73% being attributed to differences within persons. The ICC suggested that 26% of the variation in Backward Digit Span could be attributed to differences between-persons, with 74% being attributed to differences within persons. For Forward Digit Span, model fit statistics suggested that a cubic functional form best characterized development on both Forward (AIC = 503165648; BIC = 503165692; b = 0.002, p < .001) and Backward Digit Span tasks (AIC = 462856581; BIC = 462856628; b = 0.002, p < .001). The random slopes for the Forward and Backward Digit Span models were statistically significant, but extremely small (Forward: b = 0.011, SE = .005, 95% CI = [0.005, 0.026]; Backward: b = 0.020, SE = .002, 95% CI = [0.016, 0.024]). The covariance between the intercept and slope had a confidence interval that included 0 for Forward Digit Span (b = −0.081, SE = .057, 95% CI = [−0.194, 0.033]). The covariance between the intercept and slope for Backward Digit span was small, but statistically significant (b = −0.056, SE = .014, 95% CI = [−0.084, −0.028]1. It is important to note that the PSID-CDS only had three waves of data collection; therefore, the random slope models and covariances between the intercept and slope in this data set should be interpreted with caution.
Table 2.
Estimates and Model Fit of Digit Span Functional Form in the Full PSID-CDS Sample
| PSID-CDS, Forward Digit Span | PSID-CDS, Backward Digit Span | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Functional Form | Model 1 | Model 2 | Model 3 | Model 4 | Model 1 | Model 2 | Model 3 | Model 4 | |
|
| |||||||||
| Linear | b | 0.355 | 1.214 | 2.121 | 0.405 | 1.166 | 1.701 | ||
| SE | 0.009 | 0.048 | 0.168 | 0.008 | 0.036 | 0.115 | |||
| Lower CI | 0.337 | 1.119 | 1.792 | 0.390 | 1.096 | 1.475 | |||
| Upper CI | 0.373 | 1.309 | 2.451 | 0.420 | 1.237 | 1.927 | |||
| p-value | <.001 | <.001 | <.001 | <.001 | <.001 | <.001 | |||
| AIC | 512736363 | 473110830 | |||||||
| BIC | 512736391 | 473110858 | |||||||
| Quadratic | b | −0.038 | −0.128 | −0.034 | −0.087 | ||||
| SE | 0.002 | 0.016 | 0.002 | 0.012 | |||||
| Lower CI | −0.043 | −0.159 | −0.037 | −0.110 | |||||
| Upper CI | −0.034 | −0.097 | −0.031 | −0.064 | |||||
| p-value | <.001 | <.001 | <.001 | <.001 | |||||
| AIC | 503916653 | 463232157 | |||||||
| BIC | 503916689 | 463232196 | |||||||
| Cubic | b | 0.003 | 0.002 | ||||||
| SE | 0.000 | 0.000 | |||||||
| Lower CI | 0.002 | 0.001 | |||||||
| Upper CI | 0.004 | 0.002 | |||||||
| p-value | <.001 | <.001 | |||||||
| AIC | 503165648 | 462856581 | |||||||
| BIC | 503165692 | 462856628 | |||||||
| Logarithmic | b | 3.738 | 4.154 | ||||||
| SE | 0.087 | 0.064 | |||||||
| Lower CI | 3.567 | 4.028 | |||||||
| Upper CI | 3.908 | 4.280 | |||||||
| p-value | <.001 | <.001 | |||||||
| AIC | 505770650 | 464665537 | |||||||
| BIC | 505770679 | 464665565 | |||||||
Note: Missing data were handled using multiple imputation, and baseline cross-sectional sampling weights were used. PSID-CDS child age range: 3–19 years. Bolded values indicate best fitting models.
As shown in Figure 1, the most rapid growth for Forward Digit Span occurred across childhood (i.e., ages 3–10), followed by a brief period of growth during early adolescence (i.e., ages 13–16). Also displayed in Figure 1, the most rapid growth for Backward Digit Span also occurred during childhood; however, the onset of performance did not begin until the age of 5, with childhood growth leveling off at age 11. Similar to Forward Digit Span, we observed a brief period of growth during early adolescence (i.e., ages 14–17). Means, standard errors, and 95% confidence intervals of the point estimates for Forward and Backward Digit Span in the full PSID-CDS sample (i.e., ages 3–19) are reported in tables 3 and 4, respectively. Sample means, standard deviations, and ranges for Forward and Backward Digit Span in the full PSID-CDS sample (i.e., ages 3–19) can be found in tables S5 and S6 in the supplementary materials.
Figure 1.
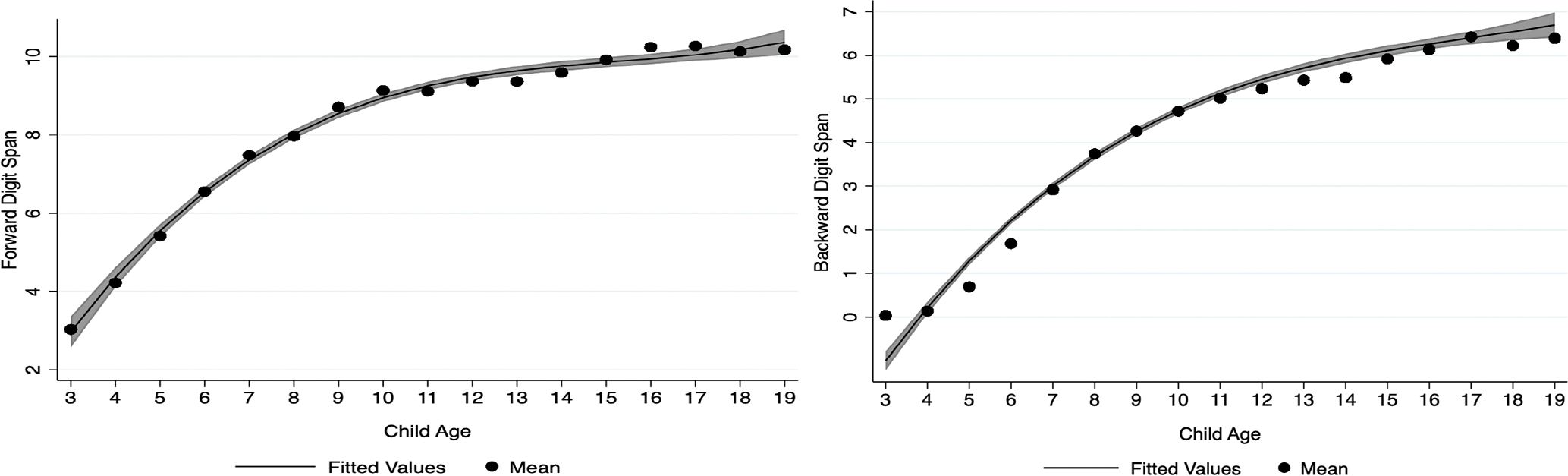
Functional forms of forward and backward digit span tasks in the PSID-CDS.
Note: Fitted values for forward and backward spans are cubic functions based on observed means; 95% confidence intervals are in gray. Values shown are non-imputed.
Table 3.
Predicted Means for Forward Digit Span in the PSID-CDS.
| Age | Mean | SE | LCI | UCI |
|---|---|---|---|---|
|
| ||||
| 3 | 3.09 | .19 | 2.72 | 3.46 |
| 4 | 4.41 | .13 | 4.17 | 4.66 |
| 5 | 5.55 | .08 | 5.38 | 5.71 |
| 6 | 6.50 | .07 | 6.37 | 6.63 |
| 7 | 7.30 | .06 | 7.18 | 7.42 |
| 8 | 7.96 | .06 | 7.84 | 8.07 |
| 9 | 8.48 | .06 | 8.37 | 8.59 |
| 10 | 8.90 | .05 | 8.79 | 9.00 |
| 11 | 9.22 | .05 | 9.12 | 9.32 |
| 12 | 9.46 | .05 | 9.36 | 9.57 |
| 13 | 9.64 | .06 | 9.53 | 9.75 |
| 14 | 9.78 | .06 | 9.66 | 9.89 |
| 15 | 9.88 | .06 | 9.76 | 10.00 |
| 16 | 9.97 | .06 | 9.84 | 10.09 |
| 17 | 10.06 | .08 | 9.91 | 10.21 |
| 18 | 10.17 | .11 | 9.95 | 10.38 |
| 19 | 10.31 | .16 | 9.98 | 10.64 |
Note: Estimates were calculated by running a weighted multilevel model where age was a cubic function. Missing data were handled using multiple imputation.
Table 4.
Predicted Means for Backward Digit Span in the PSID-CDS.
| Age | Mean | SE | LCI | UCI |
|---|---|---|---|---|
|
| ||||
| 3 | −0.90 | .10 | −1.11 | −0.70 |
| 4 | 0.25 | .07 | 0.11 | 0.38 |
| 5 | 1.26 | .05 | 1.17 | 1.36 |
| 6 | 2.15 | .04 | 2.07 | 2.24 |
| 7 | 2.93 | .04 | 2.84 | 3.01 |
| 8 | 3.59 | .04 | 3.50 | 3.68 |
| 9 | 4.16 | .04 | 4.08 | 4.24 |
| 10 | 4.64 | .04 | 4.56 | 4.72 |
| 11 | 5.04 | .04 | 4.96 | 5.12 |
| 12 | 5.37 | .04 | 5.28 | 5.46 |
| 13 | 5.64 | .05 | 5.54 | 5.74 |
| 14 | 5.86 | .05 | 5.76 | 5.96 |
| 15 | 6.04 | .05 | 5.93 | 6.15 |
| 16 | 6.19 | .06 | 6.07 | 6.31 |
| 17 | 6.32 | .07 | 6.18 | 6.46 |
| 18 | 6.43 | .10 | 6.23 | 6.64 |
| 19 | 6.55 | .15 | 6.24 | 6.85 |
Note: Estimates were calculated by running a weighted multilevel model where age was a cubic function. Missing data were handled using multiple imputation.
Results from the comparison analyses can be found in Table 5 and Figure 2. Although inspection of the model fit indices in the age-restricted PSID-CDS data suggested that a cubic functional form best fit the data, the cubic coefficient was non-significant (b = 0.015, p = .208). Therefore, the best fitting model was the quadratic functional form, which had the next-lowest model fit indices and a statistically significant growth coefficient (AIC =104487838; BIC =104487868; b =−0.101, p <.001). In the ECLS-K:2011 data, the ICC suggested that 15% of the variability in number reversed can be attributed to differences between individuals, with 85% of the variability being attributed to differences within person. A logarithmic functional form best fit growth in numbers reversed performance in the ECLS-K:2011 data (AIC =348702742; BIC =348702778; b = 20.714, p < .001), suggesting that growth begins to grow quickly during early childhood and decelerates over time. The random slope was statistically significant (b = 7.749, SE = .174, 95% CI = 7.414, 8.100). The covariance between the intercept and slope was also statistically significant (b = −0.489, SE = .014, 95% CI = [−0.517, −0.461]). Means, standard errors, and 95% confidence intervals of the point estimates for Numbers Reversed in the ECLS-K:2011 sample are reported in table 6. Sample means, standard deviations, and ranges for Numbers Reversed in the ECLS-K:2011 sample can be found in tables S7 in the supplementary materials.
Table 5.
Functional Form of Backward Digit Span in the ECLS-K:2011 and Restricted-range PSID-CDS.
| PSID-CDS, Backward Digit Span | ECLS-K:2011, Numbers Reversed | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Functional Form | Model 1 | Model 2 | Model 3 | Model 4 | Model 1 | Model 2 | Model 3 | Model 4 | |
|
| |||||||||
| Linear | b | 0.620 | 2.360 | 5.577 | 7.307 | 18.051 | 38.796 | ||
| SE | 0.023 | 0.280 | 2.529 | 0.053 | 0.196 | 0.551 | |||
| Lower CI | 0.575 | 1.810 | 0.619 | 7.203 | 17.666 | 37.711 | |||
| Upper CI | 0.664 | 2.909 | 10.534 | 7.410 | 18.435 | 39.880 | |||
| p-value | <.001 | <.001 | 0.027 | <.001 | <.001 | <.001 | |||
| AIC | 105055483 | 351071978 | |||||||
| BIC | 105055507 | 351072019 | |||||||
| Quadratic | b | −0.101 | −0.488 | −1.461 | −8.266 | ||||
| SE | 0.016 | 0.305 | 0.027 | 0.170 | |||||
| Lower CI | −0.134 | −1.086 | −1.514 | −8.602 | |||||
| Upper CI | −0.069 | 0.110 | −1.408 | −7.930 | |||||
| p-value | <.001 | 0.110 | <.001 | <.001 | |||||
| AIC | 104487838 | 349613642 | |||||||
| BIC | 104487868 | 349613692 | |||||||
| Cubic | b | 0.015 | 0.605 | ||||||
| SE | 0.012 | 0.015 | |||||||
| Lower CI | −0.008 | 0.576 | |||||||
| Upper CI | 0.039 | 0.635 | |||||||
| p-value | 0.208 | <.001 | |||||||
| AIC | 104463551 | 348801730 | |||||||
| BIC | 104463586 | 348801784 | |||||||
| Logarithmic | b | 5.250 | 20.714 | ||||||
| SE | 0.186 | 0.126 | |||||||
| Lower CI | 4.886 | 20.466 | |||||||
| Upper CI | 5.615 | 20.962 | |||||||
| p-value | <.001 | <.001 | |||||||
| AIC | 104704659 | 348702742 | |||||||
| BIC | 104704683 | 348702778 | |||||||
Note: The age range for the PSID-CDS is restricted to ages 6–11 to mirror the ages in the ECLS-K:2011. Missing data were handled using multiple imputation, and baseline cross-sectional sampling weights were used. Bolded values indicate best fitting models.
Figure 2.
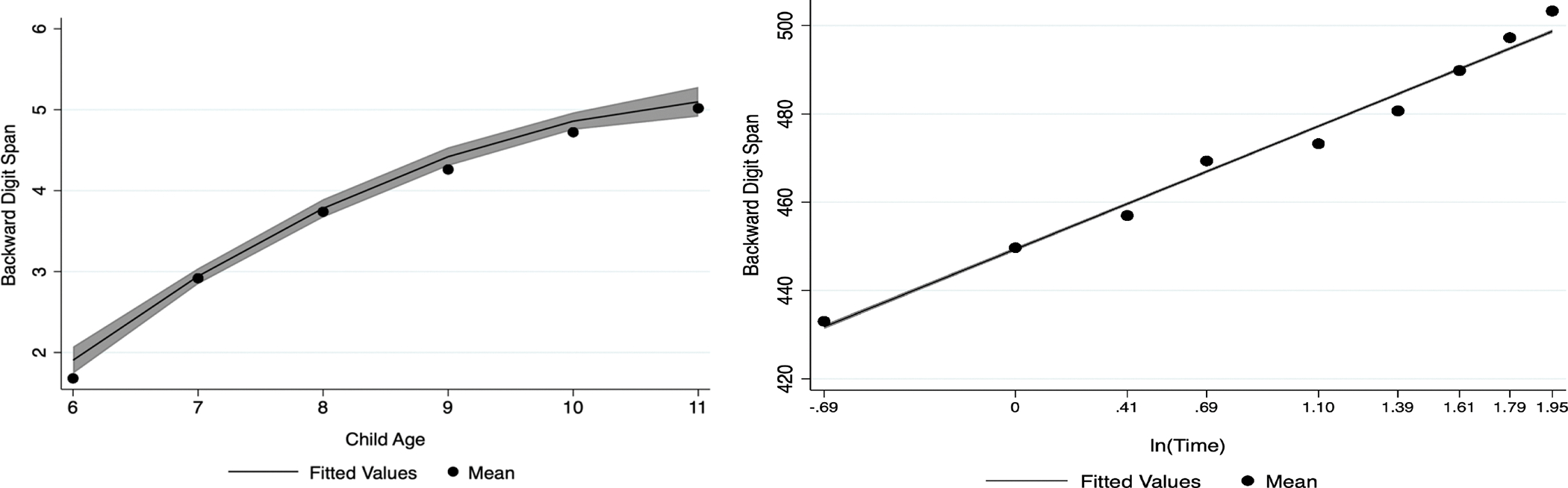
Functional forms of backward digit span tasks in the restricted-range PSID and the full ECLS-K:2011.
Note: 95% confidence intervals are in gray. Values shown are non-imputed. Time in the ECLS-K:2011 was coded as .5=wave 1, 1=wave 2, 1.5=wave 3, 2=wave 4, 3=wave 5, 4=wave 6, 5=wave 7, 6=wave 8, 7=wave 9; the x-axis displays the log of Time. Means depicted are raw, unadjusted means.
Table 6.
Predicted Means for Numbers Reversed in the ECLS-K:2011.
| Time | Mean | SE | LCI | UCI |
|---|---|---|---|---|
|
| ||||
| 1 | 436.77 | .26 | 436.27 | 437.27 |
| 2 | 451.13 | .20 | 450.74 | 451.51 |
| 3 | 459.53 | .17 | 459.19 | 459.87 |
| 4 | 465.49 | .16 | 465.16 | 465.81 |
| 5 | 473.88 | .16 | 473.56 | 474.21 |
| 6 | 479.84 | .17 | 479.51 | 480.19 |
| 7 | 484.47 | .19 | 484.10 | 484.83 |
| 8 | 488.24 | .20 | 487.86 | 488.63 |
| 9 | 491.44 | .21 | 491.02 | 491.85 |
Note: Estimates were calculated by running a weighted multilevel model where time was a logarithmic function. Missing data were handled using multiple imputation.
Results from the biological sex subgroup analyses conducted with the full age range of the PSID-CDS can be found in Tables S1 and S2 of the supplementary materials. For the Forward Digit Span, the cubic functional form was the best fitting model for boys and for girls. However, the cubic coefficient was not statistically significant for boys after adjusting for multiple comparisons (girls: b = 0.002, p < .001; boys: b = 0.001, p = .005). For the Backward Digit Span, the cubic functional form was the best fit model for boys and for girls. However, the cubic coefficient was not statistically significant for boys after adjusting for multiple comparisons (girls: b = .002, p < .001; boys: b = .001, p = .035). The subgroup analysis for the restricted age range of the PSID-CDS can be found in Table S3 of the supplementary materials. Although inspection of model fit indices alone suggested that a cubic functional form best fit the data, the cubic coefficient was non-significant for girls (b = 0.035, p = .036) and boys (b = −0.003, p = .843). Therefore, the best fitting model for boys and girls was the quadratic functional form, which had the next-least model fit indices and statistically significant growth coefficients (girls: b = −0.116, p < .001; boys: b = −0.087, p < .001). The subgroup analysis for the ECLS-K:2011 can be found in Table S4 in the supplementary materials. The logarithmic functional form was the best fit model for girls (b = 20.446, p < .001) and boys (b = 20.959, p < .001).
As a robustness check, we conducted an interaction between biological sex and age to determine whether the growth in task performance differed by sex. We observed non-significant interaction coefficients for the cubic functional form of the Forward Digit Span (b = 0.001, SE = .001, p = .217; see Figure 3) and Backward Digit Span (b = 0.001, SE = .001, p = .224; see Figure 3) in the full PSID-CDS dataset. We also observed non-significant interaction coefficients (i.e., child ages 6–11) for the cubic functional form of Backward Digit Span (b = −0.029, SE = .033, p = .372; see Figure 3) in the restricted PSID-CDS dataset (i.e., child ages 6–11), and the logarithmic functional form of Numbers Reversed in the ECLS-K:2011 (b = −0.520, SE = .250, p = .041; see Figure 3) after the multiple comparison correction. Finally, individual trajectories of a random subsample of 100 participants in the ECLSK:2011 can be found in Figure S1 of the supplementary materials.
Figure 3.
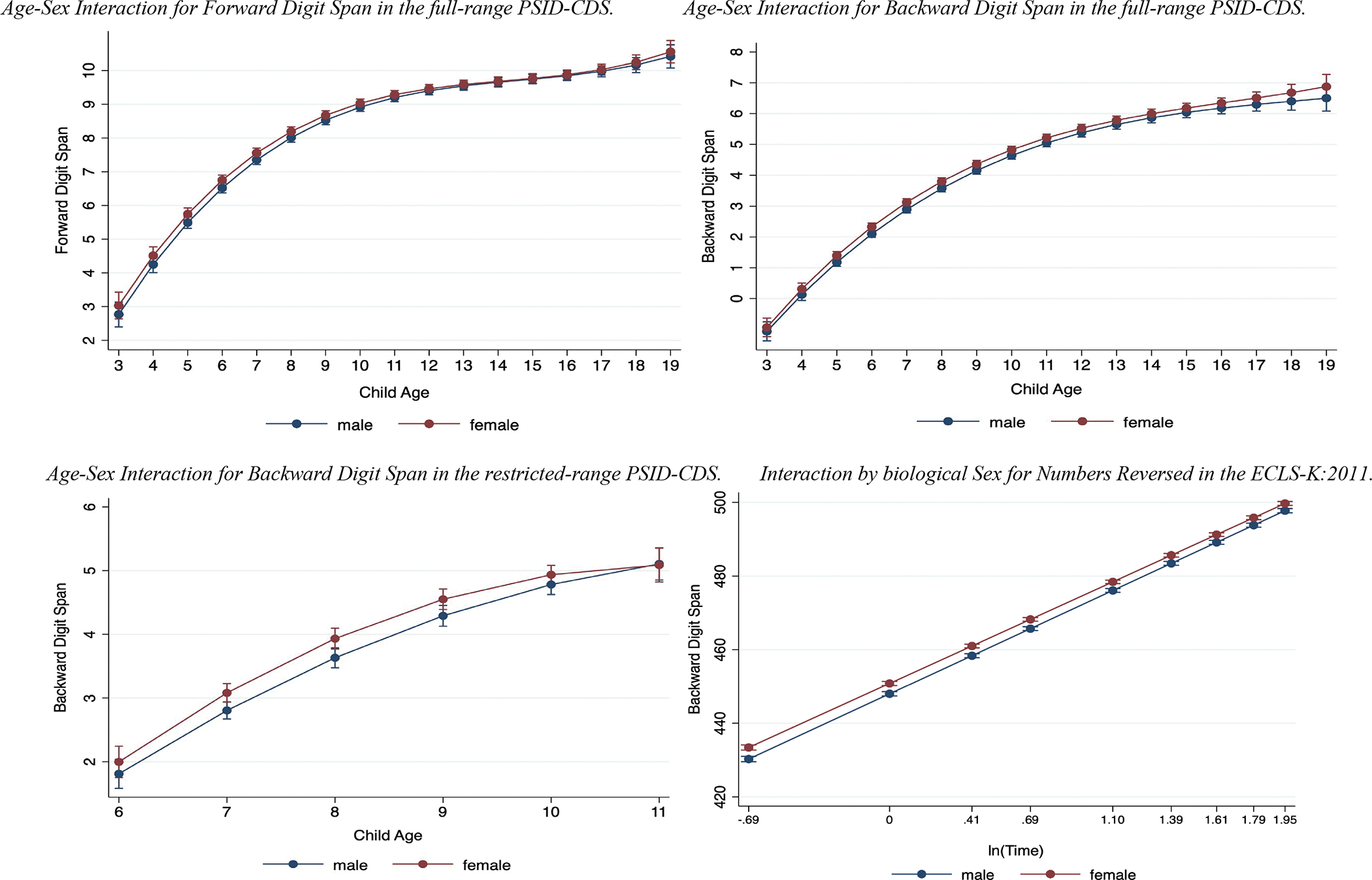
Working memory functional forms across biological sex.
Discussion
The purpose of the present study was to chart the functional form of working memory (WM) development using verbal counting span tasks in two samples representative of the U.S. population. Four main findings emerged. First, we observed non-linear growth patterns for both forward and backward digit span tasks from 3 to 19 years of age, with the most rapid growth occurring across childhood, followed by a brief accelerated period of growth during early adolescence. Second, the age of onset differed for forward and backward span tasks–children as young as 3 years of age were able to complete the forward span task, whereas performance on backward span did not emerge until 5 years of age. Third, we observed a non-linear growth pattern of WM in a separate prospective longitudinal sample of 6–11-year-old participants. Finally, results from subgroup analyses indicated that males and females developed WM at similar rates across the population.
Non-linear growth functions best characterized development on both forward and backward span tasks. Specifically, we observed rapid age-related changes in WM capacity across childhood and to a lesser degree during early adolescence, and two periods of relative calm: late childhood and late adolescence. These findings are consistent with previous research demonstrating rapid increases in WM across childhood and relative stabilization during late adolescence (Alloway et al., 2006; Gathercole et al., 2004; Luna et al., 2004; Thaler et al, 2013). The rapid development of WM during childhood also coincides with the dramatic physical and neurological changes that take place during childhood, as well as with important contextual transitions (e.g., start of formal schooling) that have been shown to influence the maturation of executive systems (Kim et al., 2021; Finch, 2019). This pattern of WM growth highlights the relative importance of the early childhood period for normative WM development, which may provide a window of opportunity during which the effects of interventions might be the most effective. Conversely, from a clinical perspective, these findings also suggest that children’s WM development might be particularly vulnerable to the effects of negative environmental settings during childhood. As such, an important future direction of this research would be to understand the contextual predictors of WM growth to identify the factors that promote or impede normative WM development at the population level.
We also observed a brief acceleration in WM performance during early adolescence, which aligns with previous studies examining adolescent WM development (Anderson, 2001; Brocki & Bohlin, 2004; Lensing & Elsner, 2018; Vuontela et al., 2012). Like childhood, there are also contextual and biological changes occurring during this time that might explain this acceleration in WM development, such as the onset and progression of puberty, adolescent neural differentiation, and transitions in educational and social contexts, which have been shown to influence the maturation of executive systems (see Blakemore, & Choudhury, 2006, for review). However, future research carefully examining the brief uptick in WM performance during adolescence is necessary to help elucidate the causes and nature of this developmental pattern and to rule out age-related measurement artifacts, such as motivation or task persistence, that might partially explain these findings. For example, it is possible that a subgroup of low-performing participants during late childhood could be driving the apparent acceleration of WM performance during early adolescence. Therefore, a promising future direction of this research would be to model different WM performance classifications over time. This would help illuminate heterogeneity in WM trajectories at the population level while also allowing researchers to understand whether the brief accelerated period of growth during early adolescence is present across classes of WM trajectories.
The PSID-CDS sample used in the present study was an accelerated longitudinal design, however, we were also able to characterize intraindividual change of WM using a prospective longitudinal sample, which lends further support to the non-linearity of WM growth across childhood. However, the difference in scaling of counting span across the two data sets warrants caution in directly comparing the results across the PSID-CDS and ECLS-K:2011. Moreover, given the narrower window of development in the ECLS-K:2011, a truly developmental account of WM trajectories from early childhood to late adolescence at the population level is still needed. Therefore, future research, including intensive, prospective measurement during the adolescent period, should be undertaken to replicate these findings and clarify the scope and non-linearity of WM development at the within-person level. A particularly fruitful avenue of future longitudinal research would be to also extend the measurement occasions of WM past late adolescence and emerging adulthood. Given that research with aging populations suggests a marked decline in WM capacity during later adulthood (Ferguson et al., 2021), longitudinal data during middle adulthood could shed light on the normative development of WM across the lifespan.
A notable finding that emerged from these analyses is the lack of meaningful sex differences in the overall functional form and rate of growth of WM. Specifically, we observed a non-significant biological sex-age interaction for growth on both Forward and Backward Digit Span tasks from 3–19 years of age. Although prior research in this area has been mixed (Lynn & Irwing, 2008; Voyer, 2016), our findings suggest that when modeled at the population level, WM sex differences are minimal at any given developmental stage and entirely disappear when examining growth patterns over time. The inconsistent sex differences found in the literature could be attributed to the lack of studies charting the growth of WM across development. That is, when WM sex disparities are found, they depend on the developmental stage of assessment and are almost always examined cross-sectionally.
There are several limitations of the present research that are important to note. First, this study focused solely on verbal WM development - however, the extent to which these developmental trends extend to visuospatial WM development remains unclear. An important future direction of this work would be to chart the functional form of visuospatial WM development to understand whether the two core WM systems outlined in Baddeley and Hitch’s (1974) WM model (i.e., phonological loop and visuospatial sketchpad) develop at similar rates at the population level. Second, it is important to note that the observed decelerating growth pattern can be, in part, due to scale shrinkage, or the tendency of growth rates to decline as item complexity increases (Bolt et al., 2014; Yen, 1985). As a result, it is possible that task performance is not increasing as quickly as true WM capacity over time. Finally, although these findings are representative of the U.S. population, they are only generalizable to a small fraction of the human population. As such, longitudinal data from non-western societies and populations historically underrepresented in psychological science are needed to gain a fuller understanding of the development of working memory.
Together, the present study provides national trends of working memory development from preschool to late adolescence. Despite its ubiquity in psychological science, researchers often do not have a reference against which to compare the developmental changes of working memory in individual studies. Not only do these findings offer information about normative development of working memory at the population level, they can also provide researchers with a foundation to understand the effects of interventions independent of normative age-related changes in working memory. From a practical perspective, clinicians and educators can also use this information to understand important periods of working memory growth using national developmental trends.
Supplementary Material
Acknowledgments:
We would like to thank Adrienne D. Woods, Brady West, and Josh Errickson for their feedback on the analytic methods used in the present study. We would also like to thank Josh Errickson for his assistance in building a Stata program that allowed us to conduct our analyses.
Funding:
The present research was supported by grants from the National Science Foundation (grant #1749294 awarded to Purdue University; 1519686 awarded to University of Texas at Austin), and the Eunice Kennedy Shriver National Institute of Child Health and Human Development (grant #T32 HD007109 awarded to University of Michigan).
Footnotes
The random slope models for the PSID-CDS with the multiple imputation dataset yielded standard errors and a 95% CI that were so close to zero that Stata would not show exact estimates; therefore, the random slope results for the PSID-CDS are with non-imputed data. Further, the random slopes model would not converge for the cubic function, therefore, the random slopes models were run on the linear function.
Contributor Information
Sammy F. Ahmed, Michigan State University.
Alexa Ellis, Purdue University.
Kaitlin P. Ward, Natasha Chaku
Pamela E. Davis-Kean, University of Michigan
Data Availability:
Data from the ECLS-K: 2010–11 are publicly available at https://nces.ed.gov/ecls/dataproducts.asp. Data from the PSID-CDS are publicly available at https://psidonline.isr.umich.edu/cds/default.aspx. All study analyses were preregistered on OSF and can be found at: https://osf.io/szvmx/.
References
- Anderson VA, Anderson P, Northam E, Jacobs R, & Catroppa C (2001). Development of executive functions through late childhood and adolescence in an Australian sample. Developmental neuropsychology, 20(1), 385–406. [DOI] [PubMed] [Google Scholar]
- Ahmed SF, Tang S, Waters NE, & Davis-Kean P (2019). Executive function and academic achievement: Longitudinal relations from early childhood to adolescence. Journal of Educational Psychology, 111(3), 446. [Google Scholar]
- Alloway TP, Gathercole SE, & Pickering SJ (2006). Verbal and visuospatial short-term and working memory in children: Are they separable?. Child development, 77(6), 1698–1716. [DOI] [PubMed] [Google Scholar]
- Baddeley AD, & Hitch G (1974). Working memory. In Psychology of learning and motivation (Vol. 8, pp. 47–89). Academic press. [Google Scholar]
- Blakemore SJ, & Choudhury S (2006). Development of the adolescent brain: implications for executive function and social cognition. Journal of child psychology and psychiatry, 47(3–4), 296–312. [DOI] [PubMed] [Google Scholar]
- Bolt DM, Deng S, & Lee S (2014). IRT model misspecification and measurement of growth in vertical scaling. Journal of Educational Measurement, 51(2), 141–162. [Google Scholar]
- Brocki KC, & Bohlin G (2004). Executive functions in children aged 6 to 13: A dimensional and developmental study. Developmental neuropsychology, 26(2), 571–593. [DOI] [PubMed] [Google Scholar]
- Conklin HM, Luciana M, Hooper CJ, & Yarger RS (2007). Working memory performance in typically developing children and adolescents: Behavioral evidence of protracted frontal lobe development. Developmental neuropsychology, 31(1), 103–128. [DOI] [PubMed] [Google Scholar]
- Conway AR, Kane MJ, Bunting MF, Hambrick DZ, Wilhelm O, & Engle RW (2005). Working memory span tasks: A methodological review and user’s guide. Psychonomic bulletin & review, 12(5), 769–786. [DOI] [PubMed] [Google Scholar]
- Coppin G, Nolan-Poupart S, Jones-Gotman M, & Small DM (2014). Working memory and reward association learning impairments in obesity. Neuropsychologia, 65, 146–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan N (2008). What are the differences between long-term, short-term, and working memory?. Progress in brain research, 169, 323–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellis A, Davis-Kean P, Ward KP, Ahmed SF, & Chaku N (2021, June 29). Functional Form of Working Memory. 10.17605/OSF.IO/SZVMX [DOI] [Google Scholar]
- Finch JE (2019). Do schools promote executive functions? Differential working memory growth across school-year and summer months. AERA Open, 5(2), 2332858419848443. [Google Scholar]
- Finn PR (2002). Motivation, working memory, and decision making: A cognitive-motivational theory of personality vulnerability to alcoholism. Behavioral and cognitive neuroscience reviews, 1(3), 183–205. [DOI] [PubMed] [Google Scholar]
- Diamond A (2002). Normal development of prefrontal cortex from birth to young adulthood: Cognitive functions, anatomy, and biochemistry. In Stuss DT & Knight RT (Eds.), Principles of frontal lobe function (pp. 466–503). Oxford University Press. [Google Scholar]
- Enders CK (2010). Applied missing data analysis. Guilford press. [Google Scholar]
- Ferguson HJ, Brunsdon VE, & Bradford EE (2021). The developmental trajectories of executive function from adolescence to old age. Scientific reports, 11(1), 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forbes NF, Carrick LA, McIntosh AM, & Lawrie SM (2009). Working memory in schizophrenia: a meta-analysis. Psychological medicine, 39(6), 889. [DOI] [PubMed] [Google Scholar]
- Gathercole SE, Pickering SJ, Ambridge B, & Wearing H (2004). The structure of working memory from 4 to 15 years of age. Developmental psychology, 40(2), 177. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS (1992). Working memory and the mind. Scientific American, 267(3), 110–117. [DOI] [PubMed] [Google Scholar]
- Graham JW (2003). Adding missing-data-relevant variables to FIML-based structural equation models. Structural Equation Modeling, 10(1), 80–100. [Google Scholar]
- Haberlandt K (1997). Cognitive psychology. Allyn & Bacon. [Google Scholar]
- Hinson JM, Jameson TL, & Whitney P (2003). Impulsive decision making and working memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 29(2), 298. [DOI] [PubMed] [Google Scholar]
- Hofferth S, Davis-Kean PE, Davis J, & Finkelstein J (1997). The child development supplement to the Panel Study of Income Dynamics: 1997 user guide. Ann Arbor: Survey Research Center, Institute for Social Research, University of Michigan. [Google Scholar]
- Huntly & Howard (2010). Working memory in early Alzheimer’s disease: A neuropsychological review. International Journal of Geriatric Psychiatry, 25(2), 121–132. [DOI] [PubMed] [Google Scholar]
- Jaffe LE (2009). Development, interpretation, and application of the W score and the relative proficiency index(Woodcock-Johnson III Assessment Service Bulletin No. 11). Rolling Meadows, IL: Riverside Publishing. [Google Scholar]
- Johnson DS, McGonagle KA, Freedman VA, Sastry N (2018). Longitudinal research on social dynamics: the PSID at 50 years. Ann. Am. Acad. Political Soc. Sci. 680(1):1–259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasper LJ, Alderson RM, & Hudec KL (2012). Moderators of working memory deficits in children with attention-deficit/hyperactivity disorder (ADHD): a meta-analytic review. Clinical psychology review, 32(7), 605–617. [DOI] [PubMed] [Google Scholar]
- Kim M, Ahmed SF, & Morrison FJ (2021). Kindergarten and first grade schooling effects on executive function and academic skill development: Evidence from a school cutoff design. Frontiers in Psychology, 11:607973. doi: 10.3389/fpsyg.2020.607973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lensing N, & Elsner B (2018). Development of hot and cool executive functions in middle childhood: three-year growth curves of decision making and working memory updating. Journal of experimental child psychology, 173, 187–204. [DOI] [PubMed] [Google Scholar]
- Lipsey MW, Nesbitt KT, Farran DC, Dong N, Fuhs MW, & Wilson SJ (2017). Learning-related cognitive self-regulation measures for prekindergarten children: A comparative evaluation of the educational relevance of selected measures. Journal of Educational Psychology, 109(8), 1084–1102. [Google Scholar]
- Lynn R, & Irwing P (2008). Sex differences in mental arithmetic, digit span, and g defined as working memory capacity. Intelligence, 36(3), 226–235. [Google Scholar]
- Luciana M, Conklin HM, Hooper CJ, & Yarger RS (2005). The development of nonverbal working memory and executive control processes in adolescents. Child development, 76(3), 697–712. [DOI] [PubMed] [Google Scholar]
- Mather N, and Woodcock RW (2001). Woodcock-Johnson III Tests of Cognitive Abilities: Examiner’s Manual. Itasca, IL: Riverside Publishing. [Google Scholar]
- McNeish D, & Matta T (2018). Differentiating between mixed-effects and latent-curve approaches to growth modeling. Behavior Research Methods, 50, 1398–1414. [DOI] [PubMed] [Google Scholar]
- McQuade JD, Murray-Close D, Shoulberg EK, & Hoza B (2013). Working memory and social functioning in children. Journal of experimental child psychology, 115(3), 422–435. [DOI] [PubMed] [Google Scholar]
- Miyake A, & Shah P (Eds.). (1999). Models of working memory: Mechanisms of active maintenance and executive control. Cambridge University Press. [Google Scholar]
- Moser DA, Doucet GE, Ing A, Dima D, Schumann G, Bilder RM, & Frangou S (2018). An integrated brain–behavior model for working memory. Molecular psychiatry, 23(10), 1974–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nesselroade JR (1991). Interindividual differences in intraindividual change. In Collins LM & Horn JL (Eds.), Best methods for the analysis of change(pp. 92–105). Washington, DC: American Psychological Association. [Google Scholar]
- Raftery AE (1995). Bayesian model selection in social research. Sociological methodology, 111–163. [Google Scholar]
- Reynolds MR, Niileksela CR, Gignac GE, & Sevillano CN (2022, April 7). Working Memory Capacity Development Through Childhood: A Longitudinal Analysis. Developmental Psychology. Advance online publication. 10.1037/dev0001360 [DOI] [PubMed] [Google Scholar]
- Rubin DB (1988). An overview of multiple imputation. In Proceedings of the survey research methods section of the American statistical association (pp. 79–84). [Google Scholar]
- Simmering VR (2012). The development of visual working memory capacity during early childhood. Journal of experimental child psychology, 111(4), 695–707. [DOI] [PubMed] [Google Scholar]
- Singer JD, Willett JB, & Willett JB (2003). Applied longitudinal data analysis: Modeling change and event occurrence. Oxford university press. [Google Scholar]
- StataCorp. 2019. Stata Statistical Software: Release 16. College Station, TX: StataCorp LLC. [Google Scholar]
- Tourangeau K, Nord C, Lê T, Sorongon AG, Hagedorn MC, Daly P, & Najarian M (2015). Early Childhood Longitudinal Study, Kindergarten Class of 2010–11 (ECLS-K: 2011). User’s Manual for the ECLS-K: 2011 Kindergarten Data File and Electronic Codebook, Public Version. NCES 2015–074. National Center for Education Statistics. [Google Scholar]
- Voyer D, Voyer SD, & Saint-Aubin J (2017). Sex differences in visual-spatial working memory: A meta-analysis. Psychonomic bulletin & review, 24(2), 307–334. [DOI] [PubMed] [Google Scholar]
- Vuontela V, Carlson S, Troberg AM, Fontell T, Simola P, Saarinen S, & Aronen ET (2013). Working memory, attention, inhibition, and their relation to adaptive functioning and behavioral/emotional symptoms in school-aged children. Child Psychiatry & Human Development, 44(1), 105–122. [DOI] [PubMed] [Google Scholar]
- Wechsler D (2008). Wechsler Adult Intelligence Scale–Fourth edition: Technical and interpretive manual. San Antonio, TX: Pearson Assessment. [Google Scholar]
- Wechsler D (1974). Wechsler Intelligence Scales for children Revised. New York: The Psychological Corporation. [Google Scholar]
- Weiss EM, Ragland JD, Brensinger CM, Bilker WB, Deisenhammer EA, & Delazer M (2006). Sex differences in clustering and switching in verbal fluency tasks. Journal of the International Neuropsychological Society, 12, 502–509. doi:10.10170S1355617706060656 [DOI] [PubMed] [Google Scholar]
- Woodcock RW & Johnson MB (1989). Woodcock-Johnson Psycho-Educational Battery – Revised. Allen, TX: DLM Teaching Resources. [Google Scholar]
- Willoughby MT, Wylie AC, & Little MH (2019). Testing longitudinal associations between executive function and academic achievement. Developmental psychology, 55(4), 767. [DOI] [PubMed] [Google Scholar]
- Xie W, Campbell S, & Zhang W (2020). Working memory capacity predicts individual differences in social-distancing compliance during the COVID-19 pandemic in the United States. Proceedings of the National Academy of Sciences, 117(30), 17667–17674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yen WM (1985). Increasing item complexity: A possible cause of scale shrinkage for unidimensional item response theory. Psychometrika, 50(4), 399–410. [Google Scholar]
- Zilles D, Lewandowski M, Vieker H, Henseler I, Diekhof E, Melcher T, ... & Gruber O (2016). Gender differences in verbal and visuospatial working memory performance and networks. Neuropsychobiology, 73(1), 52–63. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data from the ECLS-K: 2010–11 are publicly available at https://nces.ed.gov/ecls/dataproducts.asp. Data from the PSID-CDS are publicly available at https://psidonline.isr.umich.edu/cds/default.aspx. All study analyses were preregistered on OSF and can be found at: https://osf.io/szvmx/.


