The NIST REFPROP Database for Highly Accurate Properties of Industrially Important Fluids

Abstract

The NIST REFPROP software program is a powerful tool for calculating thermophysical properties of industrially important fluids, and this manuscript describes the models implemented in, and features of, this software. REFPROP implements the most accurate models available for selected pure fluids and their mixtures that are valid over the entire fluid range including gas, liquid, and supercritical states, with the goal of uncertainties approaching the level of the underlying experimental data. The equations of state for thermodynamic properties are primarily of the Helmholtz energy form; a variety of models are implemented for the transport properties. We document the models for the 147 fluids included in the current version. A graphical user interface generates tables and provides extensive plotting capabilities. Properties can also be accessed through third-party apps or user-written code via the core property subroutines compiled into a shared library. REFPROP disseminates international standards in both the natural gas and refrigeration industries, as well as standards for water/steam.

1. Introduction

Modeling and simulation are the foundation of modern design, including in the chemical process industry. The accuracy, and thus utility, of such simulations can be no better than the accuracy of the underlying materials property data employed. Here we are concerned with fluid property data, encompassing gas, liquid, and supercritical states. The required accuracy varies among applications, with the highest accuracy required for (1) fluids requiring accurate data due to their sheer scale in the economy, such as natural gas and other fuels, (2) working fluids in power and refrigeration cycles, where accurate data are needed to optimize the energy efficiency of equipment, (3) flow metering applications, (4) calibration fluids and other standards, and (5) thermodynamic research, including the development and verification of property models. It is no longer sufficient to present accurate property data merely as tabulations (e.g., “steam tables”)—they must be integrated into process models. But the most accurate property models can be quite complex, and the difficulties of implementing these models hinders their wider use. Thus, there is a need for tools that remove the burden of coding the property models from the engineer analyzing data from a lab experiment or designing a process and transfer that burden to thermodynamic specialists. Here, we describe one such tool—the NIST REFPROP database from the National Institute of Standards and Technology.

REFPROP (formally known as NIST Standard Reference Database 23: REference Fluid Thermodynamic and Transport PROPerties—REFPROP)¹ is a computer program distributed by NIST that provides thermophysical properties for a variety of industrially important fluids and their mixtures. The acronym REFPROP provides a clue to the history of the program, as it once stood for REFrigerant PROPerties² but now it is applicable to many common industrial fluids including cryogens, common hydrocarbon and natural gas constituent fluids, solvents, siloxanes, biodiesel constituents, lubricants, alcohols, glycols, and water, etc., in addition to refrigerants. It contains models for the thermophysical properties of a wide variety of fluids with the goal of representing the properties to near or within the uncertainty of available experimental data. Unlike other databases distributed by NIST,³ it does not contain critically evaluated experimental data, but rather it is a computational database. It is distributed as a computer program with a graphical user interface (GUI) designed to run under the Windows⁴ operating system, but also supplied is a dynamic link library (DLL) enabling users to interface with other programs or languages including Excel, Python, C++, Matlab, LabView, and Mathematica, etc. The source code for the property calculations, in FORTRAN, is also distributed with the program. It has become a useful tool in the refrigeration, natural gas, and aerospace industries, among others. In addition to directly using the NIST REFPROP program, researchers have also accessed properties from REFPROP indirectly from its inclusion in commercial simulation software such as ANSYS⁵ and aspenONE,⁶ or by reading input files created from REFPROP as is done by NASA’s GFSSP fluid system simulation program.⁷ This article summarizes some of the models, features, and limitations of the program.

In this manuscript we will first briefly discuss the history of REFPROP, and then discuss the models used for calculating the thermodynamic properties of pure fluids. We next discuss the pure-fluid models used for the calculation of the transport properties viscosity and thermal conductivity, and additional properties surface tension and the dielectric constant. Following that, the corresponding models for mixture properties are summarized. Finally, we briefly describe the features of the program and future directions.

2. Models for Thermodynamic Properties of Pure Fluids

2.1. Historical Background

The first version of REFPROP was released in 1989 and was in response to the need for thermophysical properties of new refrigerants and their mixtures that were proposed to replace the ozone-damaging chlorofluorocarbon (CFC) refrigerants in use at the time. A more detailed history of refrigerants can be found in ref (2). Rather than have a collection of separate correlations for thermophysical properties, such as individual correlations for vapor pressure, saturated liquid density, enthalpy of vaporization, etc., REFPROP takes the equation of state approach where all thermodynamic properties are obtained from an equation of state (EOS), thereby ensuring thermodynamic consistency among thermodynamic properties.

In the late 1980s when REFPROP first appeared, the Martin-Hou equation of state⁸ was widely used in the refrigerants community, as discussed by Downing.⁹ This model has significant limitations, namely it is not valid in the liquid region, and requires ancillary equations for vapor pressure and saturated liquid density. NIST instead opted for an approach based on a modification¹⁰ of the Carnahan–Starling–DeSantis EOS.¹¹ There were several reasons for this: (1) the CSD EOS has a theoretical basis and requires minimal data to obtain parameters, (2) it can represent both liquid and vapor phases, and (3) it is applicable to mixtures. The modified CSD EOS proposed by Morrison and McLinden¹⁰ required only six parameters, which were usually obtained by fitting experimental data for vapor pressures and saturated liquid and vapor volume.

Lack of availability of accurate property data continued to be an issue during the early research on alternative refrigerants, and a second modeling approach, the extended corresponding states (ECS) model, was added to REFPROP. Technically ECS is not an equation of state, but rather a model that incorporates properties from an equation of state for a “reference” fluid. The model was proposed by Leland and co-workers,^12,13 used at NIST for the properties of hydrocarbons and their mixtures,^14,15 applied in 1994 to refrigerants,¹⁶ and then incorporated into early versions of REFPROP. The basic premise is to represent the properties of the fluid of interest in terms of scaling factors applied to a fluid for which the properties are well characterized, called the reference fluid. Typically, the reference fluid was R-134a for refrigerants and propane for simple hydrocarbons since these fluids were well-characterized and accurate equations of state were available. The major advantage of this method was that refrigerants or simple hydrocarbons could be represented with minimal data, usually just a few saturated liquid density points and vapor pressures. ECS also can be used for transport properties, as discussed in section 3. For thermodynamic properties, it has largely been replaced by more accurate multiparameter EOS discussed in the following paragraphs, although there still are some recent applications to the very new hydrofluoroolefin (HFO) refrigerants in cases where sufficient data for more accurate EOS development are not yet available.¹⁷

The two models mentioned thus far, the modified Carnahan–Starling–DeSantis EOS and extended corresponding states, were attractive because they could be applied in situations in which few reliable data were available, and both were capable of covering the entire fluid region from the gas to the liquid and including supercritical states. Both have some basis in theory and do not give unphysical behavior. For the case of ECS, we assume that the reference fluid EOS has realistic behavior—if one chooses a reference fluid with unphysical behavior, the ECS model will show the same behavior as the reference fluid. These methods typically could represent density to within a few percent. As more and better data became available, it was desirable to represent the experimental data to nearly within the experimental uncertainty, often on the order of a tenth of a percent or better for density. For example, the density data for pentafluoroethane (R-125) of Defibaugh and Morrison,¹⁸ published in 1992, had an estimated uncertainty of 0.05%, except in the near-critical region. The ECS model of Huber and Ely,¹⁶ implemented in an early version of REFPROP, represents the compressed liquid density from this data set (which extend to 6.3 MPa) with an uncertainty at the k = 2 level of 2.3%. This clearly is not adequate if one is trying to represent the data to within the experimental uncertainty.

In 1993, the Modified Benedict–Webb–Rubin (MBWR) EOS was added to REFPROP to address some of the deficiencies of the ECS model and the CSD EOS. This form of equation of state, introduced by Jacobsen and Stewart¹⁹ for nitrogen, is considerably more complex than the six-parameter CSD EOS. It contains 32 parameters that are obtained by fitting multiple types of experimental thermodynamic data, such as (T, p, ρ), isochoric and isobaric heat capacities, second virial coefficients, coexistence properties, etc. It also can be applied to polar fluids that caused difficulties with the CSD EOS, and it is capable of representing experimental data for multiple thermodynamic properties to near the experimental uncertainty. For the example of compressed liquid data for R-125 of Defibaugh and Morrison¹⁸ mentioned above, the MBWR EOS developed by Outcalt and McLinden²⁰ represents the compressed liquid density data with an average absolute deviation (AAD) of 0.092%, a significant improvement over ECS or CSD, but requiring more data in its development. The MBWR EOS also is superior in its representation of other thermodynamic properties, even those not used in its development. Taking R-125 again as an example, Takagi²¹ measured the speed of sound in the liquid phase of R-125 with an estimated uncertainty of 0.2%. The performance of several models for this data set is shown in Figure 1. The MBWR EOS of Outcalt and McLinden²⁰ represents this data set with an average absolute deviation (AAD) of 0.5% and a bias of 0.5%. The ECS model, however, represents this data set with an AAD of 7.8% and also a bias of −7.8%. The Takagi²¹ data were not used in the development of either the MBWR EOS or the ECS model; the MBWR EOS represents the data much better than the ECS model, suggesting that it would better represent other properties, as well. However, it still does not represent the experimental data to within the uncertainty of the data. A different form of equation of state, called a Helmholtz form, is discussed in section 2.2. As shown in Figure 1, the Helmholtz equation of state of Lemmon and Jacobsen²² is superior to both the MBWR and ECS models; the AAD is 0.27% with a bias of −0.11%; approaching the experimental uncertainty²¹ of 0.2%.

Figure 1.

Deviations in the representation of the sound speed data of Takagi²¹ for R-125.

The MBWR and CSD equations of state are explicit in pressure, p, that is, are written in the form p = f(T, ρ) whereT is temperature and ρ is the molar density. Any equation of state written in this form may be combined with an expression for the molar heat capacity of the ideal gas at constant pressure, C_p⁰(T), to compute all thermodynamic properties,²³ including speed of sound, enthalpy, entropy, etc. Equations of state in this form are quite natural since they involve quantities that are easily measured and follow a tradition that started with the ideal gas law. Although one can compute all thermodynamic properties with this form, integration is necessary to obtain caloric properties. It is not a serious problem to obtain the necessary analytical expressions for thermodynamic properties from the MBWR or other pressure-explicit EOS, but it does impose some restrictions on the types of mathematical terms that can be used.²⁴

2.2. Fundamental Equations of State

A different approach is the so-called “fundamental EOS” meaning that all thermodynamic properties can be obtained using only derivatives (not integrals). Because of this, there is more flexibility in the types of mathematical expressions that can be incorporated. A fundamental EOS can be developed in terms of the Helmholtz energy [a = f(T, ρ)], Gibbs energy [g = f(T, p)], enthalpy [h = f(s, p)], or internal energy [u = f(s, ρ)]. Here we use lower case variables for the properties to indicate that they are on a specific or a molar basis. Of these, the Helmholtz energy is the most commonly used. The properties h and u are difficult to implement practically because entropy, s, is not experimentally accessible. Both g and a involve easily obtainable variables T, p, and ρ.T and p are intensive thermodynamic variables, meaning that their magnitude is not dependent on the size of the system.²⁵ Volume and mass however are extensive properties that do depend on the size (or extent) of the system; density is mass/volume and is an intensive property. Across any phase boundary (liquid–vapor, liquid–liquid, liquid–solid, etc.) the temperature and pressure are the same, and the Gibbs energy is equal in both phases. Thus, one cannot uniquely specify a thermodynamic state point on the phase boundary or in the 2-phase region using only T and p. Although the temperature across a phase boundary is the same, the density of the phases in equilibrium are different and the Helmholtz energy is different as well, allowing one to distinguish between the phases. Thus, formulating a fundamental EOS in terms of Helmholtz energy as a function of the variables T and ρ allows one to uniquely specify the thermodynamic state across the 2-phase region in addition to along the saturation boundary and is the preferred formulation.

Application of the Helmholtz-form approach to developing reference-quality EOS began in the mid-1980s with publications from the groups of Wagner²⁶ and of Jacobsen,²⁷ who used multiproperty fitting to develop new equations that were not possible with pressure-explicit formulations. This type of EOS is the current state-of-the-art in equation of state development for which accuracy is paramount, and they comprise the vast majority of EOS incorporated into REFPROP. An excellent detailed discussion of multiparameter EOS, covering both the MBWR and Helmholtz forms, is presented in the book by Span.²⁴

The Helmholtz energy form for a fundamental EOS is often written as^24,28

1

where α is the reduced molar Helmholtz energy, α^id is the ideal gas contribution, and α^r is the residual, or real-fluid, contribution. The first summation term in eq 1 is called the polynomial-like term, and the second is referred to as the exponential term. The temperature and density are expressed in reduced variables τ = T*/T and δ = ρ/ρ* where T* and ρ* are reducing parameters that often are the critical parameters. N_k is coefficients obtained by fitting experimental data, and the exponents d_k, t_k, and l_k are also determined by regression. The values of t_k should be greater than zero, and d_k and l_k should be integers greater than zero.²⁹ In these formulations a total of 4 to 20 terms are used in each summation, and the index k points to each individual term.

To better represent properties in the critical region, additional terms have been added to eq 1 yielding²⁹

2

The additional terms, referred to as Gaussian bell-shaped terms, were introduced by Setzmann and Wagner³⁰ and incorporated into their equation of state for methane. Some of these equations can be extremely complex, such as the equation of state for water,³¹ which contains 56 terms.

To recover the more familiar expression p = f(T, ρ) the following thermodynamic relationship is used:

3

A complete listing of expressions for other thermodynamic properties expressed as derivatives of the Helmholtz energy can be found in ref (24) and the Appendix of ref (22).

Originally, the fitting started with a set of mathematical expressions selected from a large bank of fixed terms, and terms were added and eliminated until an optimal form was found. With faster computers, a fully nonlinear, least-squares fit was implemented, which allowed incorporation of terms of an arbitrary form. The resulting fitting process is quite complex as discussed by Lemmon and Jacobsen.²² Due to the empirical nature of the equation, care must be taken to control the behavior in the two-phase region as well as the extrapolation behavior; this is done by including constraints in the regression process²² and examining the behavior of characteristic curves (the Boyle curve, the Joule-Thomson inversion curve, and the Joule inversion curve)^22,32.

The major strength of the Helmholtz-form EOS is the ability to represent multiple types of thermodynamic data—(T, p, ρ), sound speed, isobaric and isothermal heat capacity, second virial coefficients, vapor pressures, saturated liquid and vapor densities, enthalpy of vaporization, Joule-Thomson coefficient, isothermal throttling coefficients, etc.—to within the estimated uncertainty of the underlying data. The fact that multiple types of properties are used to develop a Helmholtz-form EOS serves as a powerful consistency check on the data—if all of the data are fitted well that is an indication that the data are accurate. The Helmholtz-based EOS are superior to any other form of EOS in this respect, and thus are used in applications of custody transfer and calibrations, and they are at the heart of the REFPROP program. Due to their complexity, considerable expertise is required to develop these equations to ensure that they behave in a physically reasonable manner when extrapolated to conditions for which there are no experimental data, behave well in the two-phase region, and that data are not overfit with an excessive number of coefficients. They are, however, computationally slow compared to simpler equations of state^33,34 and require a large amount of accurate experimental data for their development.

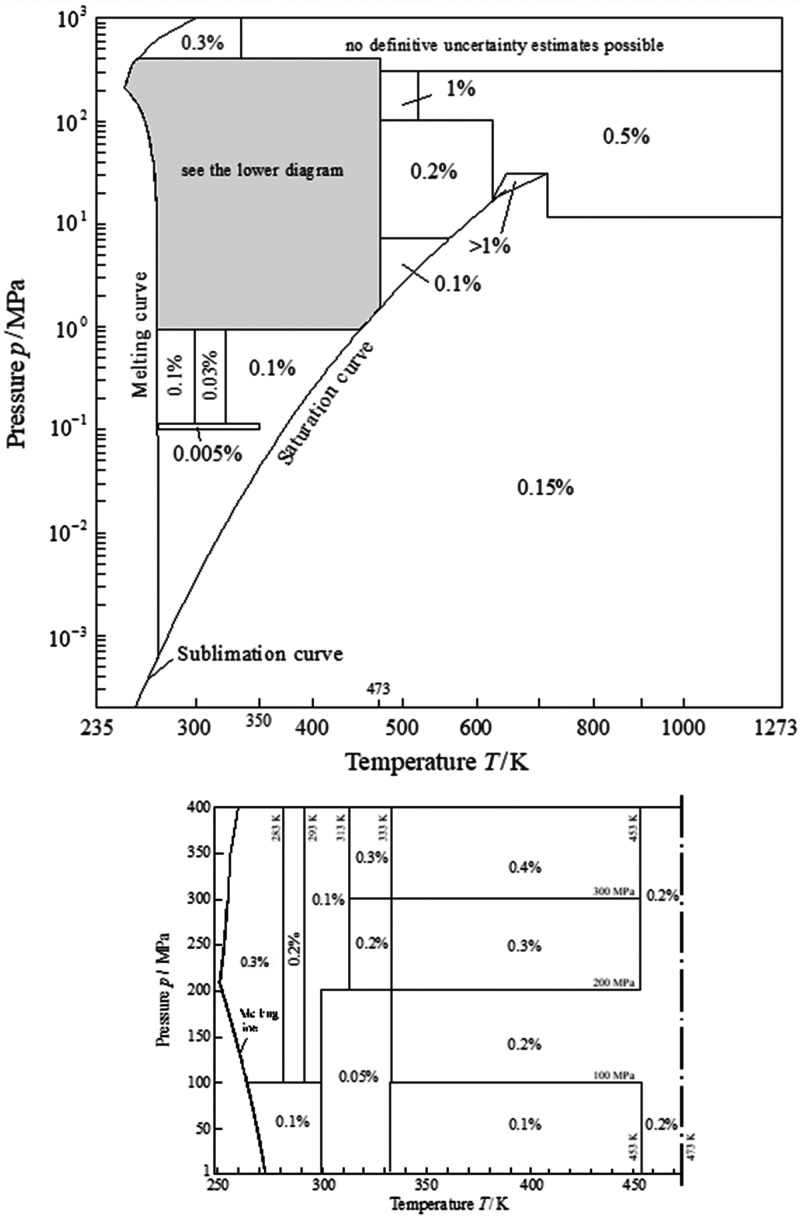
As an example of the capability of the Helmholtz-form EOS, Figures 2, 3, and 4 show the uncertainties in density, sound speed, and specific isobaric heat capacity for the Helmholtz EOS of Wagner and Pruß³¹ for water, which was adopted as an international standard by IAPWS.³⁵ The experimental data set for water (considering accuracy, range of temperature and pressure, and types of properties available) is the most extensive for any fluid. Thus, Figures 2, 3, and 4 represent the best case for an EOS.

Figure 2.

Relative uncertainties in density, Δρ/ρ, for the Helmholtz EOS for water from IAPWS R6-95(2018).³⁵

Figure 3.

Relative uncertainties in speed of sound, Δw/w, for the Helmholtz EOS for water from IAPWS R6-95(2018).³⁵

Figure 4.

Relative uncertainties in specific isobaric heat capacity, Δc_p/c_p, for the Helmholtz EOS for water from IAPWS R6-95(2018).³⁵

2.3. Equations of State Implemented in REFPROP

Table 1 summarizes the recommended equations of state for the fluids implemented in version 10.0 of REFPROP.¹ Displayed are the short name, the full name, chemical formula, and CAS number to assist with proper identification. In addition, REFPROP also makes available the standard InChI string and standard InChI key. For the equation of state column, EOS, in Table 1, all equations are of the Helmholtz form except those for F₃N, R-13, R-123, and R-152a, which are of the MBWR type. There also are three legacy EOS³⁶ (for R-14, R-114, and RC-318), formulated as the Bender^37,38 EOS, which also is a pressure-explicit EOS and very similar to the MBWR EOS. However, for inclusion in REFPROP they have been converted to a Helmholtz formulation. We also note that in addition to the recommended EOS that are listed in Table 1 and used by default in REFPROP, for many fluids there are additional EOS that may be optionally used, including older MBWR forms and also the simple cubic Peng-Robinson³⁹ EOS. However, to obtain the most accurate results we recommend the use of the default EOS. Also note that since the release of v10.0 in 2018, additional EOS correlations have been published,⁴⁰⁻⁴³ and these will be included in future releases. Table 1 also includes references for the surface tension, σ, thermal conductivity, λ, and viscosity, η, models that will be discussed in more detail later in this document. Finally, for some fluids there are additional types of information available as denoted in the column labeled “other”, such as dielectric constants, sublimation lines, and melting lines.

Table 1. Summary of Recommended Pure Fluid Models in REFPROP v10.0.

short name	full name	short formula	CAS no.	EOS	σa	λa,b,c	ηa,b,c,d	othera,e
1,3-Butadiene	Buta-1,3-diene	C4H6	106-99-0	(44)	(45)	ECS45	ECS45	na
1-Butyne	But-1-yne	C4H6	107-00-6	(46)	(45)	ECS45	ECS45	na
1-Pentene	Pent-1-ene	C5H10	109-67-1	(47)	(45)	ECS45	ECS45	na
2,2-Dimethylbutane	2,2-Dimethylbutane	C6H14	75-83-2	(48)	(45)	ECS45	ECS45	na
2,3-Dimethylbutane	2,3-Dimethylbutane	C6H14	79-29-8	(48)	(45)	ECS45	ECS45	na
3-Methylpentane	3-Methylpentane	C6H14	96-14-0	(48)	(45)	ECS45	ECS45	na
Acetone	Propanone	C3H6O	67-64-1	(49)	(50)	ECS45	ECS45	na
Acetylene	Ethyne	C2H2	74-86-2	(51)	(45)	ECS45	ECS45	na
Ammonia	Ammonia	NH3	7664-41-7	(52)	(50)	FS53	FS54	M,55 S56,f
Argon	Argon	Ar	7440-37-1	(57)	(50)	FS58	FS58	D,59 M,57 S60
Benzene	Benzene	C6H6	71-43-2	(61)	(50)	FS62	FS63	na
Butane	n-Butane	C4H10	106-97-8	(64)	(50)	FS65	FS66	na
Butene	1-Butene	C4H8	106-98-9	(67)	(50)	ECS45	ECS45	na
Carbon dioxide	Carbon dioxide	CO2	124-38-9	(68)	(50)	FS69	FS70	D,59 M,68 S68
Carbon monoxide	Carbon monoxide	CO	630-08-0	(49)	(50)	ECS45	ECS45	M,71 S72,f
Carbonyl sulfide	Carbon oxide sulfide	COS	463-58-1	(49)	(50)	ECS45	ECS45	na
Chlorine	Chlorine	Cl2	7782-50-5	(73)	(45)	ECS45	ECS45	na
Chlorobenzene	Chlorobenzene	C6H5Cl	108-90-7	(74)	(45)	ECS45	ECS45	na
cis-Butene	cis-2-Butene	C4H8	590-18-1	(67)	(75)	ECS45	ECS45	na
Cyclobutene	1-Cyclobutene	C4H6	822-35-5	(76)	(45)	ECS45	ECS45	na
Cyclohexane	Cyclohexane	C6H12	110-82-7	(77)	(50)	FS78	FS79	M77
Cyclopentane	Cyclopentane	C5H10	287-92-3	(80)	(75)	FS81	ECS45	na
Cyclopropane	Cyclopropane	C3H6	75-19-4	(82)	(75)	ECS45	ECS45	na
D4	Octamethylcyclotetrasiloxane	C8H24O4Si4	556-67-2	(83)	(75)	ECS45	ECS45	na
D5	Decamethylcyclopentasiloxane	C10H30O5Si5	541-02-6	(84)	(75)	ECS45	ECS45	na
D6	Dodecamethylcyclohexasiloxane	C12H36O6Si6	540-97-6	(85)	(75)	ECS45	ECS45	na
DEA	2,2′-Iminodiethanol	C4H11NO2	111-42-2	(86)	(45)	ECS45	ECS45	na
Decane	Decane	C10H22	124-18-5	(49)	(50)	FS87	FS88	D59
Deuterium	Deuterium	D2	7782-39-0	(89)	(50)	FS90,e	FS91a,e	na
Dichloroethane	1,2-Dichloroethane	C2H4Cl2	107-06-2	(92)	(45)	ECS45	ECS45	na
Diethyl ether	Diethyl ether	C4H10O	60-29-7	(93)	(75)	ECS45	ECS45	na
Dimethyl carbonate	Dimethyl ester carbonic acid	C3H6O3	616-38-6	(94)	(75)	ECS45	ECS45	na
Dimethyl ether	Methoxymethane	C2H6O	115-10-6	(95)	(50)	ECS45	FS96	na
Docosane	Docosane	C22H46	629-97-0	(97)	(45)	ECS45	ECS45	na
Dodecane	Dodecane	C12H26	112-40-3	(98)	(50)	FS99	FS99	na
Ethane	Ethane	C2H6	74-84-0	(100)	(50)	FS101	FS102	na
Ethanol	Ethyl alcohol	C2H6O	64-17-5	(103)	(104)	FS105	FS106	na
Ethylene glycol	1,2-Ethandiol	C2H6O2	107-21-1	(107)	(45)	ECS45	ECS45	na
Ethylbenzene	Phenylethane	C8H10	100-41-4	(108)	(75)	FS109	FS110	na
Ethylene	Ethene	C2H4	74-85-1	(111)	(50)	FS112	FS113	D,59 M,114 S72,f
Ethylene oxide	Ethylene oxide	C2H4O	75-21-8	(115)	(75)	ECS45	ECS45	na
Fluorine	Fluorine	F2	7782-41-4	(116)	(50)	ECS45	ECS45	M,116 S72,f
Heavy water	Deuterium oxide	D2O	7789-20-0	(117)	(118)	FS119	FS119	M,117 S117
Helium	Helium-4	He	7440-59-7	(120)	(50)	FS121	FS122	D,59 M123
Heptane	Heptane	C7H16	142-82-5	(124)	(50)	FS125	FS126	D59
Hexadecane	Hexadecane	C16H34	544-76-3	(97)	(45)	FS127	FS128	na
Hexane	Hexane	C6H14	110-54-3	(129)	(50)	FS130	FS131	na
Hydrogen (normal)	Hydrogen (normal)	H2	1333-74-0	(132)	(50)	FS90	FS91	D,59 M,133 S134
Hydrogen chloride	Hydrogen chloride	HCl	7647-01-0	(135)	(75)	ECS45	ECS45	na
Hydrogen sulfide	Hydrogen sulfide	H2S	7783-06-4	(49)	(50)	ECS45	FT136	D,137 S56,f
Isobutane	2-Methylpropane	C4H10	75-28-5	(64)	(50)	FS138	FS139	na
Isobutene	2-Methyl-1-propene	C4H8	115-11-7	(67)	(50)	ECS45	ECS45	na
Isohexane	2-Methylpentane	C6H14	107-83-5	(49)	(50)	ECS45	ECS45	na
Isooctane	2,2,4-Trimethylpentane	C8H18	540-84-1	(140)	(75)	ECS45	ECS45	na
Isopentane	2-Methylbutane	C5H12	78-78-4	(49)	(50)	FS81	ECS45	D,59 M141
Krypton	Krypton	Kr	7439-90-9	(49)	(50)	ECS45	ECS45	D,59 M,142 S143
MD2M	Decamethyltetrasiloxane	C10H30O3Si4	141-62-8	(144)	(75)	ECS45	ECS45	na
MD3M	Dodecamethylpentasiloxane	C12H36O4Si5	141-63-9	(84)	(75)	ECS45	ECS45	na
MD4M	Tetradecamethylhexasiloxane	C14H42O5Si6	107-52-8	(84)	(75)	ECS45	ECS45	na
MDM	Octamethyltrisiloxane	C8H24O2Si3	107-51-7	(144)	(75)	ECS45	ECS45	na
MEA	Ethanolamine	C2H7NO	141-43-5	(145)	(45)	ECS45	ECS45	na
Methane	Methane	CH4	74-82-8	(30)	(50)	FS146	FT147	D,59 M,30 S148
Methanol	Methanol	CH4O	67-56-1	(149)	(50)	FS150,151	FS152	M149
Methyl linoleate	Methyl (Z,Z)-9,12-octadecadienate	C19H34O2	112-63-0	(153)	(75)	FS154	ECS45	na
Methyl linolenate	Methyl (Z,Z,Z)-9,12,15-octadecatrienoate	C19H32O2	301-00-8	(153)	(45)	ECS45	ECS45	na
Methyl oleate	Methyl cis-9-octadecenoate	C19H36O2	112-62-9	(153)	(75)	FS154	ECS45	na
Methyl palmitate	Methyl hexadecanoate	C17H34O2	112-39-0	(153)	(75)	ECS45	ECS45	na
Methyl stearate	Methyl octadecanoate	C19H38O2	112-61-8	(153)	(75)	ECS45	ECS45	na
Methylcyclohexane	Methylcyclohexane	C7H14	108-87-2	(155)	(75)	FS156	ECS45	na
MM	Hexamethyldisiloxane	C6H18OSi2	107-46-0	(157)	(75)	ECS45	ECS45	na
m-Xylene	1,3-Dimethylbenzene	C8H10	108-38-3	(108)	(75)	FS109	FS158	na
Neon	Neon	Ne	7440-01-9	(159)	(50)	ECS45	ECS45	na
Neopentane	2,2-Dimethylpropane	C5H12	463-82-1	(49)	(75)	ECS45	ECS45	na
Nitrogen	Nitrogen	N2	7727-37-9	(160)	(50)	FS58	FS58	D,59 M,160 S161
Nitrogen trifluoride	Nitrogen trifluoride	F3N	7783-54-2	(162)	(75)	na	na	na
Nitrous oxide	Dinitrogen monoxide	N2O	10024-97-2	(49)	(50)	ECS45	ECS45	S163
Nonane	Nonane	C9H20	111-84-2	(49)	(50)	FS87	FS88	D59
Novec 649, 1230	1,1,1,2,2,4,5,5,5-Nonafluoro-4-	C6F12O	756-13-8	(164)	(165)	FS166	FS167	na
	(trifluoromethyl)-3-pentanone							na
Octane	Octane	C8H18	111-65-9	(168)	(50)	FS87	FS88	D59
Orthohydrogen	Orthohydrogen	H2		(132)	na	na	na	na
Oxygen	Oxygen	O2	7782-44-7	(26)	(50)	FS58	FS58	D,59 M,26 S169
o-Xylene	1,2-Dimethylbenzene	C8H10	95-47-6	(108)	(75)	FS109	FS170	na
Parahydrogen	Parahydrogen	H2		(132)	(50)	FS90	FS91	D,59 M,162 S72,f
Pentane	Pentane	C5H12	109-66-0	(171)	(50)	FS81	ECS45	D,59 M172
Perfluorobutane	Decafluorobutane	C4F10	355-25-9	(173)	(50)	ECS45	ECS45	na
Perfluorohexane	Tetradecafluorohexane	C6F14	355-42-0	(173)	(45)	ECS45	ECS45	na
Perfluoropentane	Dodecafluoropentane	C5F12	678-26-2	(173)	(50)	ECS45	ECS45	na
Propadiene	1,2-Propadiene	C3H4	463-49-0	(174)	(45)	ECS45	ECS45	na
Propane	Propane	C3H8	74-98-6	(29)	(50)	FS175	FS176	D,59 M177
Propylcyclohexane	n-Propylcyclohexane	C9H18	1678-92-8	(178)	(75)	FS156	ECS45	na
Propylene	Propene	C3H6	115-07-1	(179)	(50)	FS112	ECS45	M180
Propylene oxide	1,2-Epoxypropane	C3H6O	75-56-9	(181)	(45)	ECS45	ECS45	na
Propyne	Propyne	C3H4	74-99-7	(82)	(50)	ECS45	ECS45	na
p-Xylene	1,4-Dimethylbenzene	C8H10	106-42-3	(108)	(75)	FS109	FS182	na
R11	Trichlorofluoromethane	CCl3F	75-69-4	(183)	(50)	ECS184	ECS185	na
R1123	Trifluoroethylene	C2HF3	359-11-5	(186)	(45)	ECS45	ECS45	na
R113	1,1,2-Trichloro-1,2,2-trifluoroethane	C2Cl3F3	76-13-1	(187)	(50)	FS188	FS188	na
R114	1,2-Dichloro-1,1,2,2-tetrafluoroethane	C2Cl2F4	76-14-2	(36)	(50)	ECS45	ECS45	na
R115	Chloropentafluoroethane	C2ClF5	76-15-3	(189)	(50)	ECS190	ECS190	na
R116	Hexafluoroethane	C2F6	76-16-4	(49)	(50)	FS191	FS191	na
R12	Dichlorodifluoromethane	CCl2F2	75-71-8	(187)	(50)	ECS184	ECS185	na
R1216	Hexafluoropropene	C3F6	116-15-4	(192)	(75)	ECS45	ECS45	na
R1224yd(Z)	(Z)-1-Chloro-2,3,3,3-tetrafluoropropene	C3HClF4	111512-60-8	(193)	(45)	ECS45	ECS45	na
R123	2,2-Dichloro-1,1,1-trifluoroethane	C2HCl2F3	306-83-2	(23)	(50)	FS194	FS195	na
R1233zd(E)	trans-1-Chloro-3,3,3-trifluoro-1-propene	C3H2ClF3	102687-65-0	(196)	(197)	FS198	ECS45	na
R1234yf	2,3,3,3-Tetrafluoroprop-1-ene	C3F4H2	754-12-1	(199)	(50)	FS200	FS201	na
R1234ze(E)	trans-1,3,3,3-Tetrafluoropropene	C3F4H2	29118-24-9	(202)	(75)	FS200	FS201	na
R1234ze(Z)	cis-1,3,3,3-Tetrafluoropropene	C3F4H2	29118-25-0	(203)	(197)	ECS45	ECS45	na
R124	1-Chloro-1,2,2,2-tetrafluoroethane	C2HClF4	2837-89-0	(204)	(50)	ECS205	ECS205	na
R1243zf	3,3,3-Trifluoropropene	C3H3F3	677-21-4	(203)	(197)	ECS45	ECS45	na
R125	Pentafluoroethane	C2HF5	354-33-6	(22)	(50)	FS206	FS207	na
R13	Chlorotrifluoromethane	CClF3	75-72-9	(208)	(50)	ECS209	ECS209	na
R1336mzz(Z)	(Z)-1,1,1,4,4,4-Hexafluoro-2-butene	C4H2F6	692-49-9	(210)	(45)	ECS45	ECS45	na
R134a	1,1,1,2-Tetrafluoroethane	C2H2F4	811-97-2	(211)	(50)	FS212	FS213	na
R13I1	Trifluoroiodomethane	CF3I	2314-97-8	(189)	(50)	ECS45	ECS45	na
R14	Tetrafluoromethane	CF4	75-73-0	(36)	(50)	ECS214	ECS214	na
R141b	1,1-Dichloro-1-fluoroethane	C2H3Cl2F	1717-00-6	(49)	(50)	ECS215	ECS215	na
R142b	1-Chloro-1,1-difluoroethane	C2H3ClF2	75-68-3	(49)	(50)	ECS216	ECS216	na
R143a	1,1,1-Trifluoroethane	C2H3F3	420-46-2	(217)	(75)	ECS45	ECS45	na
R152a	1,1-Difluoroethane	C2H4F2	75-37-6	(218)	(50)	FS219	ECS185	na
R161	Fluoroethane	C2H5F	353-36-6	(220)	(50)	FS221	FS221	na
R21	Dichlorofluoromethane	CHClF	75-43-4	(36)	(50)	ECS222	ECS222	na
R218	Octafluoropropane	C3F8	76-19-7	(49)	(50)	ECS45	ECS45	na
R22	Chlorodifluoromethane	CHClF2	75-45-6	(223)	(50)	ECS184	ECS185	na
R227ea	1,1,1,2,3,3,3-Heptafluoropropane	C3HF7	431-89-0	(189)	(50)	ECS224	ECS224	na
R23	Trifluoromethane	CHF3	75-46-7	(225)	(50)	FS226	FS226	na
R236ea	1,1,1,2,3,3-Hexafluoropropane	C3H2F6	431-63-0	(227)	(50)	ECS45	ECS45	na
R236fa	1,1,1,3,3,3-Hexafluoropropane	C3H2F6	690-39-1	(228)	(50)	ECS45	ECS45	na
R245ca	1,1,2,2,3-Pentafluoropropane	C3H3F5	679-86-7	(229)	(50)	ECS45	ECS45	na
R245fa	1,1,1,3,3-Pentafluoropropane	C3H3F5	460-73-1	(230)	(50)	FS231	FS231	na
R32	Difluoromethane	CH2F2	75-10-5	(232)	(50)	FS233	ECS234	na
R365mfc	1,1,1,3,3-Pentafluorobutane	C4H5F5	406-58-6	(189)	(50)	ECS45	ECS45	na
R40	Methyl chloride	CH3Cl	74-87-3	(93)	(75)	ECS45	ECS45	na
R41	Fluoromethane	CH3F	593-53-3	(49)	(50)	ECS184	ECS185	na
RC318	Octafluorocyclobutane	C4F8	115-25-3	(36)	(50)	ECS45	ECS45	na
RE143a	Methyl trifluoromethyl ether	C2H3F3O	421-14-7	(235)	(45)	ECS45	ECS45	na
RE245cb2	Methyl pentafluoroethyl ether	C3H3F5O	22410-44-2	(236)	(75)	ECS45	ECS45	na
RE245fa2	2,2,2-Trifluoroethyl-difluoromethyl-ether	C3H3F5O	1885-48-9	(237)	(75)	ECS45	ECS45	na
RE347mcc (HFE-7000)	1,1,1,2,2,3,3-Heptafluoro-3-methoxypropane	C4H3F7O	375-03-1	(238)	(75)	ECS45	ECS45	na
Sulfur dioxide	Sulfur dioxide	O2S	7446-09-5	(239)	(50)	ECS45	ECS45	D137
Sulfur hexafluoride	Sulfur hexafluoride	SF6	2551-62-4	(240)	(50)	FS241,242	FT243	D,137 M,244 S240
Toluene	Methylbenzene	C7H8	108-88-3	(49)	(50)	FS245	FS246	na
trans-Butene	trans-2-Butene	C4H8	624-64-6	(67)	(75)	ECS45	ECS45	na
Undecane	Undecane	C11H24	1120-21-4	(247)	(75)	FS248	FS248	na
Vinyl chloride	Chloroethylene	C2H3Cl	75-01-4	(249)	(45)	ECS45	ECS45	na
Water	Water	H2O	7732-18-5	(31)	(250)	FS251	FS252	D,253 M,254 S254
Xenon	Xenon	Xe	7440-63-3	(49)	(50)	ECS45	ECS45	D,59 M,142 S255

^ana, not available.

^bECS, extended corresponding states model; FS, fluid-specific model.

^cH₂ correlations scaled for D₂.

^dFT, friction theory model.

^eM, melting line; S, sublimation line; D, dielectric constant.

^fModified to match triple point of EOS.

3. Models for Transport and Miscellaneous Properties of Pure Fluids

3.1. Viscosity

In addition to providing thermodynamic properties obtained through an equation of state, REFPROP also provides values for the viscosity, thermal conductivity, and surface tension. Although there are models that link transport properties directly with an equation of state through entropy,^256,257 traditionally models for viscosity and thermal conductivity were developed separately from the EOS and written as a function of density and temperature. They do require an accurate EOS to provide the density when given a p, T state point. The first version of REFPROP did not provide transport properties at all. Version 3, released in 1991, introduced an extended corresponding states (ECS) model for viscosity and thermal conductivity. This particular model was originally developed by Ely and Hanley^14,15,258 in the early 1980s; it had already been successfully used at NIST for modeling hydrocarbons.²⁵⁹ It was modified slightly and adapted for refrigerants.^16,260,261 This type of model has the advantage that it covers the entire fluid region and is valid for gas, liquid, and supercritical states, and it can be used in a predictive mode when data are unavailable. The minimum information required is the molar mass, the critical parameters T_c, p_c, and ρ_c, the normal boiling point, and an expression for the ideal gas heat capacity.²⁵⁹ Any additional information about the fluid, such as the acentric factor, vapor pressure, saturated liquid density, liquid thermal conductivity, or liquid viscosity values, can be used to refine the model and improve predictions. In the late 1990s and early 2000s, improvements were made to the model,^184,185 and REFPROP basically retains this same model today,^45,262 and it is still useful for cases for which there are limited experimental data.²⁶³

The uncertainties vary for each fluid and the data used for development, but a very general assessment is that an ECS model can represent the viscosity and the thermal conductivity of a pure fluid to within 5–10%.^260,261 For refrigerant fluids with sufficient data to tune the ECS model, results were on the order of 4% for viscosity¹⁸⁵ and ranged from 1 to 5.6% for thermal conductivity.¹⁸⁴ With careful tuning, the uncertainties of viscosity and thermal conductivity may even be reduced to 2% and 1%, respectively, as was done for the new low-GWP refrigerant R-1234ze(Z).²⁶³

For fluids where sufficient data exist (covering a wide range of T, ρ conditions— not just along the saturation boundary), the ECS model has largely been replaced by fluid-specific models that are fitted to experimental data, as they have lower uncertainties than an ECS model and have more flexibility to better fit the data. For viscosity, there is no general form of model that has been used for all fluids; many different approaches have been taken. However, often the viscosity is expressed as a function of T and ρ arising from independent contributions,

4

Equation 4 is used in conjunction with an equation of state to provide densities at a given T and p.

Expressing the viscosity as the sum of these terms allows one to incorporate theory to guide the development of some of the terms. Instead of appearing as additive terms such as in eq 4, the terms may be combined multiplicatively as was done for water²⁶⁴ and heavy water.²⁶⁵ The first term, η₀(Τ) = η(T,0), is the contribution to the viscosity in the zero-density limit, where only two-body molecular interactions occur; it is only a function of temperature. If there are sufficient low-density data along isotherms, extrapolation to zero density can be made and the data can be fit to a convenient form.²⁶⁴ Alternatively, the Chapman-Enskog theory for dilute gases²⁶⁶ can be used to formulate a term for the zero-density limit. Often, an engineering formulation for this term is used, such as that presented in Chung et al.²⁶⁷ when few or no low-density data are available. When sufficient data are available, the approach used by Vogel et al.²⁶⁸ can be used in which experimental data can be fit to obtain an effective cross section. However, there now are ab initio calculations of the zero-density viscosity and thermal conductivity from the group of Hellmann^269−278 that can also be used to develop an expression for the zero-density term²⁶⁵ for a limited number of small, rigid molecules.

The second term, Δη, is a function of both T and ρ and is sometimes called the residual contribution. It represents the contributions at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer. Sometimes a linear-in-density term is broken out as a separate term, as this can be treated with guidance from theory, and the residual viscosity is represented as

5

6

where B_η is the second viscosity virial coefficient, and η_h represents terms resulting from higher densities. Vogel et al.²⁶⁸ present a methodology to calculate B_η that is based on the Rainwater-Friend theory^279,280 and has been used successfully in many reference correlations.

Traditionally the residual contribution Δη in eq 4 or the higher density term η_h in eq 5 are found by fitting data to an entirely empirical form. A wide variety of functional forms have been used for this term. Only two examples will be given here; for more examples consult Table 1 for a list of reference correlations for all of the fluids in REFPROP.

One particular methodology for determining the residual contribution to viscosity is one used by Vogel and co-workers,^{66,102,176,281,282} which incorporates a sophisticated fitting procedure, similar to that used for EOS development, with a large bank of initial terms with optimal terms selected based on regressing a critically evaluated set of data. Typical mathematical expressions included in the bank are double polynomials in reduced temperature and density, and also exponential factors of the reduced density, again very similar to terms in an equation of state approach. Other terms could also be added, for example a modified Batchinski-Hildebrand term^139,268,283 or a free-volume type term,^213,284 although these are now generally not used as they can have bad extrapolation behavior at high density.

A completely different approach, used for a variety of fluids,^{54,63,126,131,201,221,246,248,285} determines the form of the residual contribution using symbolic regression. Symbolic regression is a type of genetic programming that allows the exploration of arbitrary functional forms. The types of terms are not known ahead of time—they are found during the regression. The functional form is obtained by the use of a set of operators, parameters, and variables as building blocks. These two methods are totally empirical and depend on having a large amount of high-quality, critically evaluated data for development, which can be problematic. Care must also be taken to ensure that extrapolation behavior is physically reasonable in regions for which there are no data. Symbolic regression in particular may encounter problems with overfitting and the introduction of spurious terms.

Thus far, the approaches discussed for determining the high-density contribution to the viscosity have been empirical. However, there also are methods that use theory to develop the residual term, namely the entropy-scaling approach^256,257 and the friction-theory approach.²⁸⁶ These have not yet been extensively used in developing reference correlations^{136,147,243,287} but may play a larger role in the future.

The last term in eq 4, Δη_c, is used to represent the behavior in the critical region. For viscosity, this term affects only a very small region in the immediate vicinity of the critical point,²⁸⁸ and with the exception of relatively few fluids^{66,70,102,176,264,265,281,282} is usually set to zero as there are not sufficient data for its evaluation. As an example, the critical enhancement for the viscosity of water contributes an amount greater than 2% to the total viscosity only with the narrow region²⁶⁴ 645.91 K < T < 650.7 K, 245.8 kg m^–3 < ρ < 405.3 kg m^–3.

The goal of a reference correlation for viscosity is the same as that for a reference EOS—to represent the available experimental data to within their estimated uncertainty. The data for viscosity typically are of higher uncertainty than the densities and sound speeds encountered in equation of state development. Water is one of the most-studied fluids, and there are large amounts of high-quality data. An uncertainty plot for the reference correlation for the viscosity of water^252,264 is presented in Figure 5. The uncertainty shown in Figure 5 is the combined expanded uncertainty with a coverage factor of 2.

Figure 5.

Relative uncertainties in viscosity, Δη/η, for the reference correlation for water from IAPWS R12-08.²⁵²

3.2. Thermal Conductivity

The models incorporated in REFPROP for thermal conductivity are very similar to those for viscosity. An ECS model described in refs (184 and 185) is implemented in REFPROP, and as in the case for viscosity, is useful when few data are available. However, it is preferable to use fluid-specific models when possible as they generally have lower uncertainty. Table 1 lists the thermal conductivity models implemented in REFPROP.

As was the case for viscosity, the fluid-specific models for thermal conductivity are often expressed as a function of T and ρ arising from three independent contributions,

7

Equation 7 is used in conjunction with an equation of state to provide densities when T and p are the input variables. Instead of appearing as additive terms such as in eq 7, the terms may alternatively be combined multiplicatively as was done for water²⁸⁹ and heavy water.²⁹⁰

The first term, λ₀(Τ) = λ(T,0), is the contribution to the thermal conductivity in the zero-density limit, where only two-body molecular interactions occur; it is only a function of temperature. Again, if there are sufficient low-density data along isotherms, extrapolation to zero density can be made and the data fit to a convenient form.²⁸⁹ Alternatively, Chapman-Enskog theory for dilute gases²⁶⁶ can be used to guide formulations for the zero-density limit. The method proposed in Chung et al.²⁶⁷ can be useful when few or no data are available. A modified Eucken correlation for polyatomic gases may also be used, as discussed in refs (15, 184, and 261). An alternative expression using kinetic theory and an approach by Thijsse et al.²⁹¹ and Millat et al.²⁹² was implemented in a correlation for the thermal conductivity of ammonia.⁵³ And as was mentioned in the viscosity section, new theoretical ab initio calculations from the group of Hellmann^269−278 are available for a limited number of fluids, and these may be fit to convenient functional forms.²⁹⁰

The second term, Δλ, sometimes called the residual contribution, represents the contributions at elevated densities including many-body collisions, molecular-velocity correlations, and collisional transfer. As was the case for viscosity, the residual contribution has traditionally been found by fitting data to an entirely empirical form without any theoretical guidance. Unlike viscosity, most researchers use the same form to express the residual term,

8

where n, the number of terms in the summation, is six or less and the B coefficients are determined by regressing experimental data. Many of the formulations in REFPROP are of this type, for example in refs (65, 69, 81, 112, 166, 194, 198, 200, 206, and 231).

The last term in eq 7, Δλ_c, is used to represent the behavior in the critical region. Unlike viscosity, this term affects a much larger region around the critical point and should be considered in a thermal conductivity correlation. Figure 6 shows the significance of the contribution of the critical enhancement term to the thermal conductivity of water.^251,289 The critical temperature of water is 647.096 K, the critical density is 322.0 kg m^–3, and the region where the enhancement is 5% or larger is shown in Figure 6 to extend from densities of 100 to almost 600 kg m^–3 at temperatures extending to almost 780 K.

Figure 6.

Contours in the temperature–density plane for water where the contribution from the critical enhancement Δλ_c to the total thermal conductivity of water λ equals 5%, 1%, 0.5%, and 0.1%.²⁵¹

To calculate the critical enhancement term, the theoretically based, simplified crossover model of Olchowy and Sengers²⁹³ is used in the models in REFPROP. In addition to the temperature and density, it requires the viscosity, the isobaric and isochoric heat capacity, and the partial derivative (∂ρ/∂ρ)_T. The viscosity is obtained from a separate model, and the other quantities are calculated from the EOS. The Olchowy-Sengers model also requires three fluid-specific parameters. When data are not available for the evaluation of the fluid-specific parameters, the generalized model of Perkins et al.²⁹⁴ is used.

It is once again useful to see an uncertainty diagram for a reference correlation for thermal conductivity. An uncertainty plot for the reference correlation for the thermal conductivity of water^251,289 is shown in Figure 7, where the uncertainty shown is the combined expanded uncertainty with a coverage factor of 2.

Figure 7.

Uncertainty in thermal conductivity, Δλ/λ, for the reference correlation for water from IAPWS R15-11.²⁵¹

3.3. Surface Tension

Most of the correlations for surface tension, σ, incorporated into REFPROP have the general form

9

where s_i and n_i are coefficients obtained from fitting experimental data, and k usually is between 1 and 3. The surface tension approaches zero at the critical point, and this form correctly reproduces that behavior. As shown in Table 1, the majority of the correlations are from the group of Mulero.^50,75,104 A more recent paper from the Mulero group²⁹⁵ revisited many of the fluids in REFPROP and gives detailed information on the deviations from the data used in the development of the correlations. The uncertainty of the correlation is dependent on the quality of the data used in its development; we use water again as an example of a very well-studied fluid. The uncertainty in the surface tension of the IAPWS recommended formulation for water²⁵⁰ varies from 0.38 mN m^–1 at 0.01 °C to 0.10 mN m^–1 at 370 °C.

3.4. Dielectric Constant

As indicated in Table 1, for a limited number of fluids that are mostly of interest to the natural gas community, REFPROP provides the dielectric constant. We refer the reader to the original publications, refs^{59, 137, and 253}, for details.

4. Mixture Models for Thermodynamic Properties

Just as there are many different EOS and approaches to modeling the thermodynamic properties of a pure fluid, there also are many different approaches to modeling the thermodynamic properties of a mixture. A general discussion of methods can be found in ref (296). Here we will give a very condensed discussion that focuses on the models incorporated in REFPROP.

Among the various ways to model mixtures, one method is to apply mixing and combining rules to the parameters of an EOS. For a very simple cubic EOS such as the Peng-Robinson EOS³⁹ (available as a calculation option in REFPROP and used internally to provide starting guesses for some calculations)

10

there is a mixing rule for the parameters a and b, and combining rules for the cross term a_ij,

11

12

where the δ_ij is empirically determined binary interaction parameters for each binary pair. This approach can also be extended to the MBWR EOS, but it can be very complex due to the large number of coefficients involved.

Instead of applying mixing rules to the individual parameters of an EOS, one can apply mixing rules to a property. Lemmon²⁹⁷ and Tillner-Roth²⁹⁸ each independently developed mixture models based on modeling the reduced molar Helmholtz energy of the mixture,

13

where the first summation is the contribution from the EOS of each of the constituent pure fluids, the x ln x term accounts for the entropy of mixing, and the second summation is often called the departure function. The F_pq is generalizing parameters that relate the behavior of one binary pair with that of another. The α_pq^excess is empirical functions that are fit to binary mixture data. The terms α_j and α_pq are not evaluated at the temperature and density of the mixture, T_mix and ρ_mix, but rather at a scaled or reduced temperature and density τ = T_red/T_mix and δ = ρ_mix/ρ_red. It should be noted that α_pq^excess is not the same as the excess Helmholtz energy. Mixing rules are used to determine the reducing values T_red and ρ_red. For example, one set that was used for mixtures containing R-32, R-125, R-134a, R-143a, and R-152a is²⁹⁹

14

The parameters ζ_ij and ξ_ij are used to define the shapes of the reducing temperature and density curves. These reducing parameters are not the same as the critical parameters of the mixture and may be found by fitting experimental data or from a predictive model.³⁰⁰ Other models of this type were formulated for binary mixtures of ammonia and water,³⁰¹ dry air,³⁰² and hydrocarbons.³⁰³ Other developments, such as having a temperature-dependent departure function, have been applied to model mixtures of helium-4, neon, and argon.³⁰⁴ Very recently, improved Helmholtz mixture models have been developed for environmentally friendly refrigerant mixtures containing R-134a, R-152a, R-227ea, R-1234yf, and R-1234ze(E).³⁰⁵

In particular, the Helmholtz mixing model^306,307 has been used as an international standard for the properties of natural gas. The original GERG (Groupe Européen de Recherches Gazières or European Gas Research Group) 2004³⁰⁷ model is a multifluid Helmholtz model for calculation of the thermal and caloric properties of natural gases and has 18 components: methane, nitrogen, CO₂, ethane, propane, n-butane, isobutane, n-pentane, isopentane, n-hexane, n-heptane, n-octane, H₂, O₂, carbon monoxide, H₂O, helium, and argon. An update, known as GERG 2008,³⁰⁶ added n-nonane, n-decane, and H₂S, and is the basis for an ISO Standard (ISO 20765-2/3),³⁰⁸ a method to calculate the volumetric and caloric properties of natural gases, manufactured fuel gases, and similar mixtures, at conditions at which the mixture may be in either the homogeneous (single-phase) gas state, the homogeneous liquid state, or the homogeneous supercritical (dense-fluid) state. This formulation represents the most accurate experimental mixture data to the level of experimental uncertainty. For example, the uncertainties in gas-phase density and speed of sound for a broad variety of natural gases and related mixtures are 0.1% over the temperature range from 250 to 450 K at pressures up to 35 MPa, while in the liquid phase the uncertainty for density is generally in the range of 0.2% to 0.5%.³⁰⁶ Research continues on improving this model, such as recent improvements in the representation of the binary mixtures H₂/CH₄, H₂/N₂, H₂/CO₂, and H₂/CO.³⁰⁹

The development of these very accurate models depends upon the availability of binary interaction parameters for the various mixture pairs. (The properties of ternary and higher-order mixtures are calculated in terms of the constituent binary pairs.) Bell and Lemmon³¹⁰ published an automatic evolutionary optimization algorithm that was used in conjunction with a large database of experimental vapor–liquid equilibrium data to obtain binary interaction parameters for more than 1100 mixtures. Many of these have been implemented into REFPROP v10.0. When binary interaction parameters have not been obtained by fitting experimental data, methods can be used to predict them. One predictive method developed by Lemmon and McLinden³⁰⁰ is available that works reasonably well for refrigerant mixtures. It is formulated in terms of properties such as the dipole moment, acentric factor, and critical temperature and pressure for each refrigerant pair. Another predictive method, applicable only to mixtures of nitrogen with selected halogenated refrigerants, incorporates the normal boiling point, the critical pressure, and the number of fluorine atoms in the molecule.³¹¹ REFPROP also estimates interaction parameters based on chemically similar pairs, for example the mixture of R-32/1234ze(Z) (which has no experimental data available) is treated the same as the mixture R-32/1234ze(E) (for which binary interaction parameters have been fitted to data). Research is currently underway to develop additional predictive models for the binary interaction parameters in Helmholtz mixture models in REFPROP.

Finally, there is an additional way of modeling mixtures in REFPROP. A mixture at a fixed composition can be treated as a pseudopure fluid. In REFPROP, this has been done for the refrigerant mixtures³¹² R-404A, R-410A, R-507A, and R-407C and also CO₂-free dry air.³⁰² The advantage of using this type of model is computational speed, especially for saturation properties, but this approach cannot account for variations in properties as a function of composition and may not be used for two-phase inputs inside the vapor–liquid-equilibrium region.

5. Mixture Models for Transport and Miscellaneous Properties

In this section we discuss the mixture models implemented in REFPROP for viscosity, thermal conductivity, surface tension, and the dielectric constant. A more general treatment can be found in ref (296).

5.1. Viscosity of Mixtures

Currently there is a single viscosity mixture model implemented in REFPROP. The viscosity of a mixture is treated as it was for a pure fluid: as a sum of a dilute-gas contribution and a residual contribution. The critical contribution is set to zero, and all terms are now functions of composition,

15

The dilute-gas contribution is found from kinetic theory^313−315 assuming a Lennard-Jones potential applies with collision integrals as given by Neufeld et al.;³¹⁶ however, the sinusoidal term is omitted. The dilute-gas contribution for a mixture in REFPROP is always calculated with the Lennard-Jones potential; however, some of the pure-fluid correlations in REFPROP use different formulations. A scaling factor is used in REFPROP so that in the limit of the pure fluid, the recommended pure fluid formulation is exactly reproduced.

The residual contribution is modeled using a one-fluid extending corresponding states (ECS) approach,^185,213,262

16

The mixture is represented by a hypothetical pure fluid, the properties of which are found by evaluating a single (“one-fluid”) reference fluid (denoted by subscript ref) that is evaluated not at the mixture T and ρ but rather at a conformal temperature and molar density T_ref and ρ_ref. In REFPROP v10.0, nitrogen is used as the reference fluid in all mixture calculations. The conformal temperature and density are found using the relationships T_ref = T/f_x and ρ_ref = ρh_x and the quantities f_x and h_x are determined through the use of mixing and combining rules that involve the individual pure fluid f_i and h_i. Binary interaction parameters may also be used if data are available for a specific binary pair. The pure fluid f_i and h_i are called equivalent substance reducing ratios and relate the reference fluid (which can be different for each pure fluid and are not necessarily the same as the reference fluid for the mixture) to the fluid of interest using a ratio of critical parameters and functions of temperature and density called “shape factors”. There are various methods that can be used to determine the shape factors,^185,258,260 and in REFPROP the “exact shape factor method” is used.²⁵⁸ This is an iterative procedure that can at times be complicated; the equations to be solved are described in ref (185) and care is needed to avoid obtaining incorrect roots in regions where there are multiple roots. The factor F_η in eq 16 is a function of the quantities f_x and h_x and an additional factor g_x that involves the f_i and h_i functions and also the molar masses M_i of the fluids in the mixture as described in refs (185, 213, and 262). The ECS model as implemented in REFPROP is adequate for representing the viscosity of many refrigerant and hydrocarbon mixtures, typically representing viscosity of refrigerant mixtures to within about 4%¹⁸⁵ and to within 5% to 10% for some other binary pairs.²⁶² However, not all mixtures can currently be represented with this model. For example, it presently cannot be used for mixtures with associating fluids such as water or alcohols. The ECS model also has large deviations if the constituent fluids have very large size differences, as pointed out recently by Thol and Richter.³¹⁷

5.2. Thermal Conductivity of Mixtures

The model implemented in REFPROP for mixture thermal conductivity is also an ECS model. The treatment is similar to that of viscosity; however, the thermal conductivity is first divided^{15,184,213,262} into contributions from internal motions of the molecule, λ^int, (which are only functions of temperature) and translational contributions, λ^trans, which are due to collisions between molecules and are a function of both temperature and density, along with an additional term for the critical enhancement,

17

The translational contribution is further divided into a dilute-gas contribution, λ*, and a residual contribution λ^r,

18

The internal contribution and translational dilute-gas contributions for the mixture are found using the empirical mixing rule¹⁸⁴

19

with

20

The pure-fluid dilute gas-viscosity for fluid j, η_0,j is computed from the recommended pure fluid model implemented in REFPROP, and the k_ij,λ are optional binary interaction parameters for thermal conductivity of a given binary ij pair. As in the case for viscosity, extended corresponding states are applied to the residual contribution,

21

where the thermal conductivity of the reference fluid for the mixture, again denoted by subscript ref, is evaluated at the conformal temperature and density T_ref and ρ_ref described in the mixture viscosity discussion. Similarly, F_λ is a function of the quantities f_i, h_i, and M_i.^184,262

The remaining contribution in eq 17, due to the critical enhancement, is calculated by applying mixing rules to the parameters in the Olchowy-Sengers model^293,294 as described in ref (262).

There are fewer data for mixture thermal conductivity than for mixture viscosity, but limited testing indicates that the ECS mixture model for thermal conductivity can represent the data (excluding the critical region) to within about 5–10%.²⁶² The same limitations noted for the ECS model for viscosity, namely inability to model mixtures containing associating fluids and difficulties with asymmetric mixtures, also apply to the thermal conductivity mixture model. The mixture model also significantly underpredicts the thermal conductivity in the critical region,²⁶² and additional research is necessary in this area.

5.3. Surface Tension of Mixtures

To compute the surface tension of a mixture, REFPROP implements a parachor-based model,^318,319 where the parachor for pure fluid Ρ_i is defined as

22

with the surface tension σ_i obtained from the pure fluid correlation implemented in REFPROP, and the pure component saturated liquid ρ_L,i and saturated vapor molar densities ρ_V,i are obtained from the EOS for the pure fluid at the temperature of interest. We use m = 3.87, and if T ≥ 0.9T_c the parachor is calculated at T = 0.9T_c. Next, the liquid and vapor densities of the mixture at saturation are computed with the Helmholtz energy mixture model and the surface tension of the mixture is found using

23

with mixing and combining rules

24

25

where δ_ij is an optional binary interaction parameter, and x_i and y_i are the molar compositions of the liquid and gas phases, respectively. This method works best if the fluids are chemically similar, although the use of binary interaction parameters can improve results. The uncertainties involved will be greater than those for the pure fluid constituents.

5.4. Dielectric Constant of Mixtures

As mentioned in section 3.4, REFPROP provides the dielectric constant of a number of fluids of interest to the natural gas community. Details on how to calculate the dielectric constant of a mixture of these fluids can be found in ref (59).

6. REFPROP Features

Using the models described above, REFPROP calculates a wide range of thermophysical properties, as outlined in Table 2. For definitions of some of the more obscure properties in Table 2, such as the supercompressibility factor F_pv, see ref (320). In addition to any of the pure fluids listed in Table 1, mixtures of up to 20 components may be constructed. However, not all mixtures are available. For example, REFPROP cannot provide calculations for some mixtures with associating compounds (e.g., water) for which an adequate model is not yet available. Users may create custom natural gas mixtures and perform calculations with international standard models including the GERG-2008³⁰⁶ model as well as the older AGA-8 model.³²¹ There are also a wide variety of predefined mixtures including the zeotropic and azeotropic mixtures designated by ASHRAE Standard 34³²² and the five pseudopure fluid mixtures discussed earlier.

Table 2. Properties Computed by REFPROP.

thermodynamic properties	transport, misc. prop.	derivatives	mixture
Temperature, T	Thermal conductivity	Isothermal compressibility	Fugacity
Pressure, p	Viscosity	Volume expansivity	Fugacity coeff.
Density, ρ	Kinematic viscosity	Isentropic expansion coef.	Chemical potential
Volume, V	Thermal diffusivity	Isothermal expansion coef.	K value
Internal Energy, U	Prandtl Number	Adiabatic compressibility	Molar mass
Enthalpy, H	Surface tension	Adiabatic bulk modulus	B12
Entropy, S	Dielectric constant	Isothermal throttling coeff.	Excess Volume
Isochoric Heat Capacity, Cv	Gross heating value (HV)	∂p/∂ρ|T	Excess Helmholtz
Isobaric heat capacity, Cp	Gross HV, liquid	∂2p/∂ρ2|T	Excess Gibbs
Ideal Gas Cp0	Gross HV, volume basis	∂p/∂T|ρ	Composition
The ratio Cp/Cv	Net Heating Value	∂2p/∂T2|ρ
Csat	Net HV, liquid	∂2p/∂ρ∂T
Speed of sound, w	Net HV, volume basis	∂p/∂T|sat
Compressibility Factor, Z	Heat of Formation	∂H/∂Z|sat
Joule-Thomson Coefficient	Acentric factor	∂ρ/∂T|p
Quality	Relative density (air)	∂ρ/∂P|T
Phase	Relative density (water)	∂2ρ/∂T2|p
2nd virial coefficient, B	API gravity	∂2ρ/∂p2|T
3rd virial coefficient, C	2nd acoustic virial	∂2ρ/∂p∂T
4th virial coefficient, D	3rd acoustic virial	dB/dT
Helmholtz energy	–1/T	∂H/∂T|ρ
Gibbs energy	Flow exergy	∂H/∂T|p
Heat of vaporization	Closed system exergy	∂H/∂ρ|T
Cv, 2-phase	Critical flow factor	∂H/∂ρ|p
Internal pressure	Throat mass flux	∂H/∂p|T
Repulsive pressure	Fpv	∂H/∂p|ρ
Attractive pressure
p–pideal

A graphical user interface (GUI) provides access to the models and properties here mentioned. The interface provides a convenient means to calculate and display calculated properties. It accesses the core property subroutines via a dynamic link library. The program is controlled through the use of the following pull-down menus as seen across the top of Figure 8, which shows two representative tables:

• File provides commands to save and print generated tables and plots. Individual items or entire sessions with multiple windows may be saved or recalled. The standard “print setup” and “exit” commands are also present.

• The Edit menu provides copy and paste commands which allow selected data to be exchanged with other applications.

• The Options menu provides commands for selecting the unit system, properties of interest, and the reference state. These options may be stored for recall at a later time. A user-defined set of preferences is loaded upon program startup.

• The pure fluid or mixture of interest is specified with commands in the Substance menu. New mixtures can be specified and saved. The refrigerant mixtures having an ASHRAE R-400 or R-500-series designation in ASHRAE Standard 34³²² are predefined. Dry air and five predefined natural gas mixtures are also available.

• The Calculate menu initiates the calculations that generate a property table. Each property selected for display is shown in a separate column of the table. Two types of tables are provided. The first type provides properties at saturation or with a property (such as temperature or pressure) held constant with another selected property varying over a specified range. For mixtures, one can calculate the liquid and vapor at the same composition, or liquid at the bubble point with its coexisting vapor, or the vapor at the dew point with its coexisting liquid. The second type of table allows the user to select the independent variables. Values of the independent variables may then be entered with the keyboard, read from a file, or pasted from another application.

• The Plot menu provides x–y plots of any variables appearing in a table. In addition, temperature–entropy, pressure–enthalpy, temperature–composition, and a large number of additional diagrams may be generated automatically, as outlined in Table 3. Controls are provided to modify the plot size, axis scaling, plot symbols, line type, legend, and other plot features. Figure 9 shows an example of an automatically generated pressure–enthalpy diagram.

• Each table or plot appears in a separate window and can be accessed, resized, or retitled with commands in the Window menu. The number of windows is limited only by available memory.

• The Help menu provides access to online documentation, while the Cautions menu takes the user directly to that section of the documentation.

Figure 8.

Screen shot of table output.

Table 3. Plotting Options in REFPROP.

Temperature vs Entropy	Temperature vs Enthalpy	Temperature vs Density
Pressure vs Enthalpy	Pressure vs Density	Pressure vs Volume
Pressure vs Temperature	Compressibility Factor vs Pressure	Enthalpy vs Entropy
Isochoric Heat Capacity vs T	Isobaric Heat Capacity vs T	Sound Speed vs T
Exergy vs Enthalpy	Isothermal Compressibility vs T	Viscosity vs T
Thermal Conductivity vs T

Figure 9.

Automatically generated pressure–enthalpy plot for ammonia.

A typical session would start by specifying the desired properties, units, etc. in the Options menu; the fluid or mixture of interest would be defined in the Substance menu; table(s) of properties would be generated in Calculate and/or plots would be generated in Plot.

While the property models are written with temperature and density as the independent variables, REFPROP supports a wide range of inputs to accommodate the variables that would be known in a particular situation. These are called “flash” calculations, and REFPROP supports 15 combinations of variables: the first property can be any of (T, p, ρ, or s) and the second can be (p, ρ, s, h, or u). These involve iterative calculations to solve for the corresponding temperature and density, which are then input to the core property routines to solve for any other desired quantities. Temperature and pressure are easily measured in a process, and this is the most common flash calculation. REFPROP employs the cubic Peng–Robinson EOS (which can be solved explicitly for ρ as a f(T, p)) to generate an initial guess for the iteration.

Instead of using the Windows-based GUI, many users prefer to access the core REFPROP routines directly, either from apps such as Excel or from their own custom programs. Such programmatic access to REFPROP is possible with wrappers available on all operating systems. The core of REFPROP is a set of FORTRAN routines compiled into a shared library (a DLL on Windows). To use REFPROP in other environments such as C++, Python, MATLAB, Excel, etc., wrappers are used which allow the user to call into the REFPROP shared library. Native wrappers of REFPROP are available on github³²³ for the most popular programming languages. A modern CMake build system is available³²⁴ to assist with the compilation of REFPROP on non-Windows platforms.

Further user support is provided via several Github and other websites maintained by NIST.^325,326 These provide a mechanism for users to report bugs and share tips and instructions for using REFPROP on different platforms. A number of mini-tutorials and additional documentation³²⁷ on thermodynamic topics are also included.

7. Future Directions

REFPROP has changed significantly since its first release in 1989 and will continue to evolve to address the changing needs of industry. There will be improvements to the models, the code, the interface, and additions to the fluid component library as described below.

7.1. Models

Equations of state will continue to evolve as we improve our understanding of the “correct” form for an EOS. New EOS may increasingly incorporate the results of molecular simulations in their development, but this would be largely hidden from the end user. While new or modified terms may appear in future EOS, we anticipate that the Helmholtz energy form will continue to be the basis for the vast majority of new and revised EOS in the foreseeable future. Work also is underway on improving the regression algorithms with additional constraints to enable future development with fewer data.

On the transport property side, entropy scaling approaches represent a new way of understanding the link between transport and thermodynamic properties. A semirigorous theory forms the basis of the approach. Applying this technique to viscosity has shown promise,³²⁸ so long as the equation of state yields the correct values for the residual entropy and so long as entropy scaling should apply for the given fluid(s). Entropy scaling has shown results competitive with ECS for refrigerant mixtures,^329,330 and the model can be concisely implemented. Furthermore, the entropy scaling approaches avoid the computational speed penalty of ECS introduced by the exact conformal state solver.³³¹ The theoretical understanding of entropy scaling approaches continues to develop, and these entropy-scaling-based models will start making their way into REFPROP. The friction-theory approach for viscosity²⁸⁶ and thermal conductivity³³² may also see increasing application. A lack of mixture data for both viscosity and thermal conductivity has hindered model development, and the availability of high-quality data in the future can aid in model development. Simulation data can aid in this effort, but there will continue to be a need for experimental data to validate and test new models.

7.2. Code and Interface

The world is moving toward web-based technologies, and REFPROP is too. A web-based interface of REFPROP is currently under development. It includes tabular outputs in a form very similar to the desktop application. All calculations are carried out on the REFPROP server, allowing users access to a GUI without installing anything on their own computer. This will avoid problems with increasingly strict computer security policies restricting the installation of third-party software. This will be an additional way to access REFPROP; it will not replace the current forms.

While the computational efficiency of REFPROP is sufficient for many use cases, its architecture (heavy use of global state and blocking file reads) is not optimal for our multithreading world in which computer processor clock speeds are stagnating, but parallelism is continuing to increase. Therefore, an effort is underway to rewrite the entirety of REFPROP with a modern C++-based architecture. The motivations for this campaign, which is part of a multiyear effort, are

• to improve the modularity of models and algorithms so that the code of REFPROP is thread-safe by design

• to better leverage open-source libraries (e.g., Eigen³³³ for matrix math, nlohmann::json³³⁴ for working with data encoded in strings, algorithms from the C++ standard library and boost, ChebTools³³⁵ for Chebyshev expansions, etc.)

• to allow for other thermodynamic models. The focus of REFPROP is and will remain the highest accuracy models possible, but other models are needed where data availability is very poor. It is also desirable to easily prototype different models or EOS terms.

• to enable the use of new algorithms, such as for density rootfinding,³³⁶ for tracing phase boundaries for mixtures,^337,338 for tracing critical loci,³³⁹ and for obtaining vapor–liquid–liquid equilibria³⁴⁰

• to speed up pure fluid saturation properties by a factor of at least a few hundred through the use of superancillary equations³⁴¹

• to migrate toward self-documenting interoperable data files (fluid files, mixture files, etc.) that are stored in an international standard file format (here, JSON)

Some of these techniques have already been incorporated in open-source software,³⁴² and lessons learned from that will inform decisions for future versions of REFPROP. For example, hardcoding transport property models (as was done in versions of REFPROP prior to v10.0) does not make for a flexible piece of software. In REFPROP 10.0, a reverse-Polish-notation means of defining transport property models was added. Although this approach gives a tremendous amount of flexibility and hardcoded transport property models are no longer needed, it is not a particularly straightforward way of defining mathematical expressions. In the future, REPROP will incorporate a more comprehensible math parsing approach that should be accessible to a broader set of model developers.

The core of the new REFPROP will be built around the open-source teqp library³⁴ for EOS evaluation. The teqp library does not use analytical derivatives of the Helmholtz energy of the EOS—rather automatic differentiation is used to calculate the derivatives. This results in a tremendous increase in flexibility such that implementing a new thermodynamic model goes from taking weeks (or years!) to hours.

As much as possible, the future versions of REFPROP will strive to maintain backward compatibility. There will be necessary changes to the interface to allow for multithreading and the adoption of a completely encapsulated internal structure. A key design constraint is that all models in the library will be immutable; once a model is initialized, it may not be changed. All options (equation of state, reference states, etc.) must be selected at model initialization. Aside from the thermodynamic and transport property calculations described above, there are plans to include other types of calculations, such as combustion-related quantities, in the future.

7.3. Component Library

As REFPROP has evolved over the years, additional classes of chemical compounds have been added. Version 1.0 included just 15 refrigerants (with only two-component mixtures supported), while the current version 10.0 includes multiple types of fluids comprising 147 pure fluids and mixtures with up to 20 components. The motivation for adding fluids arises from several sources. The most important is industrial importance based on user feedback. REFPROP often serves as the vehicle for delivering the research outputs of the Thermophysical Properties of Fluids Group of NIST, and the inclusion of many fluids traces to this source. The criteria for adding new fluids will continue to be guided by the “REF” of REFPROP—namely the provision of highly accurate reference data on well-characterized fluids.

8. Conclusions

The NIST REFPROP database is a powerful tool for calculating thermophysical properties of industrially important fluids, with a focus on incorporating the most accurate models available. We will continue to develop the program so that it may evolve to serve the needs of industry.

The authors declare no competing financial interest.

Notes

Contribution of the National Institute of Standards and Technology. Not subject to copyright in the United States.