Efficient Inner-to-Outer Wall Energy Transfer in Highly Pure Double-Wall Carbon Nanotubes Revealed by Detailed Spectroscopy

Abstract

The coaxial stacking of two single-wall carbon nanotubes (SWCNTs) into a double-wall carbon nanotube (DWCNT), forming a so-called one-dimensional van der Waals structure, leads to synergetic effects that dramatically affect the optical and electronic properties of both layers. In this work, we explore these effects in purified DWCNT samples by combining absorption, wavelength-dependent infrared fluorescence–excitation (PLE), and wavelength-dependent resonant Raman scattering (RRS) spectroscopy. Purified DWCNTs are obtained by careful solubilization that strictly avoids ultrasonication or by electronic-type sorting, both followed by a density gradient ultracentrifugation to remove unwanted SWCNTs that could obscure the DWCNT characterization. Chirality-dependent shifts of the radial breathing mode vibrational frequencies and transition energies of the inner and outer DWCNT walls with respect to their SWCNT analogues are determined by advanced two-dimensional fitting of RRS and PLE data of DWCNT and their reference SWCNT samples. This exhaustive data set verifies that fluorescence from the inner DWCNT walls of well-purified samples is severely quenched through efficient energy transfer from the inner to the outer DWCNT walls. Combined analysis of the PLE and RRS results further reveals that this transfer is dependent on the inner and outer wall chirality, and we identify the specific combinations dominant in our DWCNT samples. These obtained results demonstrate the necessity and value of a combined structural characterization approach including PLE and RRS spectroscopy for bulk DWCNT samples.

Ultramanipulable quantum materials with properties-on-demand are viewed as the basis for the generation of electronic and photonic devices¹ and as quantum simulation platforms for studying strongly correlated physics and new physical phenomena.^1,2 The best-known example is a two-dimensional (2D) van der Waals (VDW) heterostructure consisting of stacked atomically thin layers, for example, graphene or hexagonal boron nitride, whose physical properties are widely tunable by various external parameters such as gating, strain, and the composition, stacking order, and relative orientation of the layers.² This high level of tunability is further expanded when the scale is reduced to one dimension (1D).³ More specifically, by confinement of a graphene sheet into a cylinder with a diameter d and roll-up (or chiral) angle θ, one obtains a metallic (M) or semiconducting (S) single-wall carbon nanotube (SWCNT), both showing excitonic optical resonances due to quantum confinement effects.⁴ Coaxial stacking of two such SWCNT layers defines a double-wall carbon nanotube (DWCNT).^5,6 Homoatomic in nature, a DWCNT can exist in four electronic forms with either M or S inner and outer walls (i.e., S@S, M@S, S@M, and M@M, where the “@” sign refers to “encapsulated in”).^5,6 The exact combination of inner and outer (n,m) chiral structure is important, since the interlayer distance and the specific moiré potential arising from the chiral angle mismatch between the inner and outer walls controls the VDW coupling⁷⁻¹⁰ and strongly modulates the optoelectronic^9,10 and vibrational^7,8,11 properties of the DWCNTs compared to those of the constituent SWCNT walls. Recently, an efficient method to grow 1D VDW heterostructures with a different composition of walls was demonstrated by Xiang et al.,¹² which allows for the development of 1D VDW heterostructures as materials with properties on-demand.¹³

Due to the complexity of possible structures and the impact to their properties, further progress in the SWCNT-based 1D VDW heterostructure synthesis and applications requires the development of reliable characterization procedures. For SWCNTs, optical spectroscopy has proven to be a versatile structural characterization technique. Fluorescence–Excitation (PLE) spectroscopy, mapping the fluorescence (PL) over an extensive range of excitation wavelengths, and ultraviolet–visible–near-infrared (UV–vis–NIR) absorption spectroscopy have been the metrological standards for structural characterization of SWCNTs for over a decade.¹⁴ Resonant Raman spectroscopy (RRS) is also widely used to assess SWCNT diameter, electronic type, chiral structure, doping, and strain.¹⁵ However, for SWCNT-based VDW heterostructures the VDW interaction-induced synergetic effects influence the results of the optical characterization. As recently demonstrated for individual suspended DWCNTs¹⁶ and SWCNT@BNNT@MoS₂ heterostructures,¹⁷ the PL of the inner resp. outer wall becomes strongly quenched. This makes PLE spectroscopy in its original form highly complicated because some signatures will entirely disappear from the optical maps while shifts of the optical transition energies,⁹ the appearance of interlayer transitions^18,19 and modified vibrational modes^7,8,20 can occur, which obfuscate the interpretation of the spectroscopic data.

Due to these challenges, most progress in accounting for VDW-coupling in optical characterization has been made on individual free-standing DWCNTs, as their exact chiral structure can be cross-characterized by high-resolution transmission electron microscopy (HRTEM) and electron diffraction (ED).^8,21 Characterizing bulk DWCNT samples, on the contrary, has, until recently, led to mainly ambiguous results due to sample processing issues, for example, contamination with SWCNT impurities or difficulties in analyzing the largely overlapping spectroscopic signals from different DWCNT combinations. The former can originate from either synthesis²² or ultrasonication processing that extracts SWCNTs from DWCNTs^23,24 and can thus unwittingly obscure the DWCNT characterization. Due to the latter, previously reported wavelength-dependent RRS measurements on macroscopic DWCNT samples focused mainly on the limited spectroscopic region of sub-nanometer inner walls of DWCNTs.^25,26 Raman signals overlap less in this region because of the reduced number of possible inner@outer wall combinations.²⁷ These studies reported the appearance of radial breathing mode (RBM) clusters originating from the same inner walls encapsulated in different outer tubes, where each DWCNT combination has a different interwall interaction and, hence, different RBM frequency and electronic excitation energy.^25,28 More recent and thorough reports by Li et al.²⁹ and Gordeev et al.³⁰ further advanced such measurements by studying DWCNTs sorted by both the inner and outer wall’s electronic type, thereby demonstrating the effect of both the interlayer distance and the moiré potential on the electronic and vibrational properties of the inner DWCNT walls. However, both studies^29,30 employed ultrasonication to disperse sorted DWCNTs and, thus, contained extracted SWCNTs,²⁴ complicating the DWCNT characterization and interpretation.

For PLE studies on macroscopic DWCNT samples, a majority of the literature has focused on whether the inner walls of DWCNTs fluoresce or not. Contradicting studies exist either concluding that the inner wall’s PL was heavily quenched^16,31−33 or claiming the observation of a relatively bright PL.³⁴⁻³⁷ However, since ultrasonication was employed in the latter case,³⁴⁻³⁷ this observation is now generally attributed to the unanticipated presence of SWCNTs in the nominal DWCNT samples.^24,33 Although quenching of the inner wall PL is now broadly established,^16,24,33 the nature of the quenching remains largely unknown. Shen et al.⁵ hypothesized that it is associated with a charge or energy transfer (ET) from the inner to the outer wall of the DWCNTs, which in case of ET could result in the observation of emission from the outer wall after excitation of the inner wall. Postupna et al.³⁸ theoretically predicted that the contribution of dark states, for example, crossover transitions between nonsymmetric van Hove singularities or intertube electronic states, should also be accounted for. Measuring the outer wall PL can shed light on this issue, but is technically challenging, as the large diameter of the outer walls results in emission at longer wavelengths in the infrared (beyond the detection limit of a normal InGaAs detector, >1650 nm). Only two studies have reported PL from outer DWCNT walls,^34,35 although again for ultrasonication dispersed samples that possibly include PL contributions from extracted SWCNTs.²⁴

Together, the remaining uncertainty and lack of specificity for attributing the observations to VDW physics highlights the continued need for well-controlled, high-purity DWCNT samples for fundamental spectroscopic characterization studies. In this work, we perform such measurements, demonstrating that combined detailed PLE and RRS experiments and meticulous two-dimensional fitting of the spectroscopic data can allow for direct measurement of the energy transfer from the inner to the outer walls of the DWCNT, and for the identification of the specific inner@outer chirality combinations, even in macroscopic mixed-chirality DWCNT samples.

Results and Discussion

For a detailed ensemble investigation of the optical properties of DWCNTs, we prepared two distinct purified DWCNT samples as well as several reference SWCNT samples (as detailed in the Methods section and Supporting Information, section S1 and Figures S1–S3). In short, the first DWCNT sample was prepared by gentle solubilization of as-synthesized DWCNTs, that is, without sonication to prevent inner wall extraction and shortening of the DWCNTs, followed by two subsequent density gradient ultracentrifugation (DGU) steps to purify them from any cosynthesized²² or extracted SWCNTs, as detailed in ref (24). We will further denote this sample as “P-DWCNT”, with the “P” referring to the DGU purification step (see also the table in Figure 1). The second DWCNT sample was first sorted by the aqueous two-phase extraction (ATPE) methodology to select only S@S DWCNTs, as described in detail in refs (29, 39, and 40), and was subsequently DGU purified to remove a large fraction of the remaining SWCNTs (further denoted as “P-S@S-DWCNT”). In this case, a single DGU separation step was used, and two fractions were selected from the ultracentrifuge tube after DGU with slightly different diameter distributions, which are further denoted as “P-S@S-DWCNT-1” and “P-S@S-DWCNT-2”. In parallel, we also prepared SWCNT samples with different diameter distributions matching those of the DWCNT inner and outer walls; they will be referred to as the “small-SWCNT” and the “large-SWCNT” samples, where “small” and “large” refer to their respective diameter distribution. In addition, to take into account the possible effect of the inner environment, we prepared an empty (“large-E-SWCNT”) and a water-filled (“large-WF-SWCNT”) variant of the large-SWCNT sample based on a DGU separation of sonicated large-SWCNT samples, as in ref (41). For the small-SWCNT sample no additional DGU separation was performed, therefore making it a mixture of empty and water-filled SWCNTs. Finally, all samples were dialyzed to the same external environment, namely, a 10 g/L sodium deoxycholate (DOC) solution in deuterated water (D₂O), thereby removing all polymers and gradient media from the different sorting steps.

Figure 1.

(left) Background-corrected and normalized absorption spectra of the small-SWCNT sample (bright green), the large-E-SWCNT sample (black), the large-WF-SWCNT sample (blue), the P-DWCNT sample (red), the P-S@S-DWCNT-1 (dark green), and the P-S@S-DWCNT-2 sample (magenta), shown with a vertical offset from each other. The black star denotes the wavelength range where the baseline correction is difficult due to the saturated D₂O absorption, and the dashed lines indicate the expected wavelength ranges for the first van Hove transitions of the inner and outer walls (see Figure S4 for the uncorrected absorption spectra). (right) Overview table of the samples studied in this work.

Absorption Spectroscopy

The normalized absorption spectra of all samples are shown in Figure 1, after subtracting a Lorentzian profile for the π-plasmon band around 270 nm and in addition subtracting the overall scattering background, which is modeled by an inverse power law, c/λ, where c is a fitting parameter and λ is the absorption wavelength⁴² (see Figure S4 in the Supporting Information for the raw absorption spectra and the fitted backgrounds). This subtraction is done to account for the much larger scattering background in the DWCNT samples with respect to that in the SWCNT reference samples. Based on the optical transitions in these spectra, we estimate the diameter distributions of the reference SWCNT samples to range from 0.7 to 1.3 nm for the small-SWCNT sample and from 1.2 to 1.8 nm for the large-SWCNT sample. A similar approximation of the diameter distribution for the DWCNT samples is not straightforward because of the intricate absorption spectrum that consists of peaks originating from both the inner and outer walls of the DWCNTs as well as additional peaks that arise from possible intertube transitions.^18,19 The absorption spectra of the DWCNT samples show that the P-DWCNT and P-S@S-DWCNT-1 samples have similar diameter distributions, except for the presence of M tubes in the P-DWCNT sample (absorption in the 600–800 nm range). One can note that the P-S@S-DWCNT-2 sample has slightly larger outer DWCNT walls, which agrees with the larger density of this fraction in the DGU tube (see Figure S2 in the Supporting Information). The diameters of the outer DWCNT walls in the DWCNT samples that are spectroscopically detectable can be roughly estimated to range from 1.3 to 2.0 nm, as their first-order absorption peaks are well-separated from the absorption of the smaller diameter inner DWCNT walls.⁴³ A previous statistical HRTEM study on DWCNTs of the same synthesis batch as the P-DWCNT sample showed that the diameter distribution of the inner and outer DWCNT walls ranges from 0.53 to 2.53 nm and from 1.23 to 3.23 nm,²² respectively, but diameters larger than 2.0 nm are typically not observable with optical spectroscopy. Hence, the chosen reference SWCNT samples have approximately similar diameter distributions as the optically detectable inner and outer DWCNT walls. Note also that all samples are solubilized in heavy water (D₂O) for its optical transparency in the IR, but still, the absorption spectra (taken with an optical path length of 3 mm) are dominated by the strong D₂O absorption band in the range of 1850–2100 nm (cut out in Figure 1, see also Figure S4 for the spectrum of the D₂O baseline).

Wavelength-Dependent Resonant Raman Scattering Spectroscopy

In Figure 2, a detailed wavelength-dependent RRS measurement of the P-DWCNT sample is compared with that of the reference SWCNT samples. Since the diameter distribution of the P-S@S-DWCNT-1 and P-DWCNT samples are very similar (see above), and the larger diameter outer walls of the P-S@S-DWCNT-2 sample have an intrinsically lower Raman cross-section,⁴⁴ the P-DWCNT can be used as a representative DWCNT sample for these RRS studies. The 2D RRS maps are measured from 90 to 450 cm^–1 over the extensive wavelength range from 400 nm (3.1 eV) to 870 nm (1.425 eV) in 5 nm steps. By doing so, we should simultaneously detect the RBMs of the inner and outer walls of the DWCNTs within the diameter range of 0.5–2.0 nm. For better visualization of the RBMs of the thinnest CNTs, the color scale of the area within the white dashed rectangles is locally enhanced in Figure 2 by the factor denoted on each color map. The additional solid white lines overlaid on the 2D color maps subdivide the maps in several ranges that correspond to the first (S₁₁) and second (S₂₂) van Hove transitions of the S CNTs, the two branches of the M CNTs, and the higher-order transitions (E_ii), based on known relationships for the higher order SWCNT transitions.⁴⁵

Figure 2.

Wavelength-dependent RRS maps of the (a) small-SWCNT, (b) large-E-SWCNT, (c) large-WF-SWCNT, and (d) P-DWCNT samples. The color scale in the bottom right part of the maps, indicated by the dashed white lines, is enhanced by the denoted factor. Each of the RRS maps was first drawn by setting the maximum intensity to 100 and, subsequently, zoomed in on the color axis to visualize also the weaker RRS modes. Therefore, the absolute intensities between the color maps of different samples cannot be compared, but the relative intensities within a single color map can be compared, as they are calibrated to CCl₄ (acting as an internal standard). The solid white lines subdivide the maps into groups of RBMs depending on their excitation level, as indicated by S₁₁ and S₂₂ for, respectively, the first- and second-order semiconducting transitions, M for the first order metallic transitions and E_ii for any higher-order transitions.

Based on the comparison between the diameter distribution of the SWCNT samples with that of the inner and outer walls of the DWCNTs, the RBMs of the inner and outer walls are expected at frequencies greater and smaller than approximately 200 cm^–1, respectively. Hence, the complex 2D RRS map of the P-DWCNT sample, shown in panel (d) of Figure 2, can be split up into two parts, a figure comprising the RBMs of the outer DWCNT walls (Figure S5 in the Supporting Information) and a part detailing the different RBM families of the inner DWCNT walls (Figure S7 in the Supporting Information).

Due to the many different CNT chiralities occurring in close spectral proximity of each other, a detailed analysis of the RBMs of the outer DWCNT walls with frequencies less than 200 cm^–1 is heavily complicated; however, a direct comparison with the RBMs of the SWCNTs in the large-E-SWCNT and large-WF-SWCNT samples highlights shifts of both the RBM frequencies and electronic transitions of the outer DWCNT walls (see Supporting Information, Figure S6). In contrast, for the inner DWCNT walls a more detailed analysis of the RBMs is feasible, with individual peaks quantifiable through means of a two-dimensional fit. The 2D fit model is described in detail in the Supporting Information, section S3, and is based on a previous model used to fit wavelength-dependent RRS data of empty and water-filled SWCNTs.⁴⁶ In brief, the 2D fit model consists of a set of 2D basis functions, each corresponding to the 2D RRS spectrum of a single chiral species, such that a linear combination of these individual contributions leads to a full 2D RRS map. Each individual 2D RRS spectrum is a product function of a Lorentzian in the Raman frequency direction, which represents the RBM mode, and a resonance profile for the excitation direction, as used previously in ref (46). Importantly, to unambiguously discriminate between RBM signals of inner walls of the DWCNTs and peaks that arise from the RBMs of a very small fraction of remaining SWCNTs (despite the thorough purification process), the 2D RRS maps of the P-DWCNT sample and the small-SWCNT sample are fitted simultaneously. This means that the same set of parameters for the SWCNT peaks are optimized to fit both maps at the same time, while only their amplitudes are allowed to vary for each map. Consequently, the weaker RBM signals of the remaining SWCNTs in the P-DWCNT sample are determined by the more prominent RBM peaks in the small-SWCNT sample, while the DWCNT peaks are solely optimized to fit the 2D RRS map of the P-DWCNT sample and are omitted in the fit of the small-SWCNT maps. Before fitting, the experimental data are divided into different ranges, each around a particular family of RBMs, while any overlapping signals from other CNTs are cut out to allow even the weakest contributions to be accurately fitted while accounting for varying background signals.

Figure 3 presents the fitting results of the P-DWCNT sample for two such ranges, each focusing on a discrete set of inner-wall chiralities. All other fit ranges and the fits of the corresponding small-SWCNT samples are presented in the Supporting Information Figures S8–S11. The resulting fitted RBM and excitation energy positions and line widths are presented in Figure 4a and can be found in the Supporting Information, Table S1. Where given, uncertainty and fit errors in this contribution are reported as one standard deviation. Figure S7 presents an overview of the fitted peak positions superimposed on the 2D RRS maps of the small-SWCNT sample and the P-DWCNT sample in the small-diameter range.

Figure 3.

Fit results for the 2D RRS map of the P-DWCNT sample in two distinct wavelength ranges (all other ranges and simultaneous fits for small-SWCNTs can be found in Figures S8–S11). Panels (a,e) and (b,f), respectively, show the experimental data and fit after zooming in on specific ranges of inner DWCNT walls. (c,g) and (d,h) show horizontal and vertical slices, obtained by summation of the Raman maps either between two different excitation ranges (c,g) or between two Raman shifts (d,h). The slices are each time normalized over the width of the range, and, where necessary, multiplied by the provided factor. The experimental data are presented with black circles, the total fit in red, and the individual components in green. Fitted RBM maxima are denoted on the fitted Raman maps by white filled circles and open triangles for SWCNT and DWCNT peaks, respectively, and magenta open squares account for weak background peaks or unassigned species. For clarity, we plot the RBM fitted peak positions at the maxima of the RBM intensity, not at the electronic transition energies. These differ by an energy offset corresponding to half of the RBM frequency, since the Raman excitation profile is composed of a resonance with the ingoing and scattered photon energy.

Figure 4.

(a) Overview of all the fitted RBM peaks for the various RBM clusters assigned to specific inner DWCNT wall chiralities. A varying redshift in transition energy and a varying Raman up- and downshift of the inner wall RBMs (dots) are revealed compared to the fitted RBM positions of the same water-filled SWCNT chiralities solubilized using a surfactant (circles). The error bars (in gray) represent the uncertainties of the fitted peak positions. The gray rectangle highlights the data analyzed further in panel (b). (b) Results of theoretical calculations of RBM frequencies and E₂₂ energies for different combinations of (6,4)@(n,m) DWCNTs. S and M outer walls are represented by filled circles and triangles, respectively. The color of the circles (see colorbar) represents the ET amplitudes, which are derived further on from 2D PLE experiments and are presented in Figure 9, normalized over all ET amplitudes for the different observed (6,4)@(n,m) combinations, while the gray color is used to show those DWCNT combinations for which ET was not measured. The open circles correspond to the fitted data of (6,4)@(n,m) DWCNTs from (a), with size proportional to the fitted Raman intensities. Dashed and dash-dot gray lines show two dependencies between RBM frequency and E₂₂ transition energy previously reported by Gordeev et al.³⁰ and Pfeiffer et al.,²⁵ respectively.

Figures 3, 4a, and S7–S11 visualize two main differences between the RBM features of inner walls of the DWCNTs and the small-diameter SWCNTs. First, instead of a single RBM peak, a cluster of RBM frequencies is detected for each inner DWCNT chirality.²⁵ Second, each of these clusters is strongly red-shifted in electronic transition energy compared to the RBMs of the SWCNTs. Taking these two differences into account, an assignment of each cluster to an inner tube chirality can be unambiguously made, as presented by the different colors in Figure 4a. For small-diameter inner walls, like the (7,5), (8,3), and (9,1) chiralities, the individual peaks are indeed well-resolved in the cluster, as is shown by the individual components in Figure 3. However, the larger the diameter becomes, the more difficult it is to identify and fit these individual peaks. For example, for the (10,2) chirality, the broadened line width prevents individual contributions from being resolved and thus accurately fitted. In such instances, RBM clusters were fitted with the fewest possible individual components (e.g., Figure S10).

While the clusters are roughly centered around the RBM frequencies of the corresponding SWCNT RBMs of the small-SWCNT sample, shifts to both lower and higher frequencies are observed and are attributable to the environmental differences of the individual chirality combinations. More precisely, the RBM frequency shift of each individual peak in the cluster depends on the interlayer distance between the inner and outer DWCNT wall with larger upshifts occurring for smaller interwall distances as the walls enter into the more repulsive part of the VDW potential, but it is expected to be always positive relative to the RBM frequency of free-standing empty SWCNTs.⁴⁷ Nevertheless, since we are comparing with the small-SWCNT sample containing surfactant-coated and water-filled SWCNTs, we observe both blue- and redshifts of the inner wall RBMs depending on the exact DWCNT combination due to the changing attractive or repelling force between the two walls with respect to the interaction of the same SWCNT chirality with its inner and outer environment.²⁵

The strong electronic shifts observed agree with earlier reported experimental results by Pfeiffer et al.²⁵ and are attributable to the electronic interlayer VDW interaction that depends on the exact inner and outer wall combination as investigated experimentally⁹ and theoretically.^19,48 We show this dependence in Figure 4a, where the fitted excitation energies and Raman frequencies of all the components in each chirality-identified cluster of DWCNT inner wall RBMs (dots) are plotted and compared with those of the matching, mostly water-filled, SWCNTs in surfactant solution (circles). Due to the high spectral resolution of our Raman spectrometer combined with the accurate fits of these peaks, we reveal a complicated relation between the electronic energy and the RBM frequency, as shown by example for (6,4)@(n,m) DWCNTs in Figure 4b (open circles with size proportional to the observed Raman intensity). In general, the E₂₂ transition energy changes gradually with increasing RBM frequency of (6,4)@(n,m) DWCNTs, but has occasional significant deviations from this trend for particular combinations. Pfeiffer et al.²⁵ concluded that each peak in an RBM cluster has a monotonically increasing electronic redshift of 2 meV/cm^–1 (indicated by the dash-dot line in Figure 4b) due to an increasing radial pressure induced by the DWCNT outer wall. Such a model agrees reasonably well with most of our observations. In addition, we also compare with the results of Gordeev et al.,³⁰ who report a much stronger slope of 11 meV/cm^–1 (dashed line in Figure 4b).

To clarify the observed discrepancy in slope between our experimental results and the latter literature data, we calculate the E₂₂ optical transition energies and out-of-phase RBM frequencies for all geometrically possible DWCNTs with inner (6,4) or (6,5) tubes within the nonorthogonal tight-binding model (NTB).⁴⁸ The details of these calculations are discussed in detail in the Supporting Information, section S6. The results of the calculations for (6,4)@(n,m) DWCNTs with outer S and M walls are shown in Figure 4b by filled circles and triangles, respectively (only DWCNTs having interlayer distance between 0.31 and 0.39 nm are considered). These calculations report a variation in E₂₂ energies in different DWCNT combinations that correspond quite well to the experimental data of (6,4)@(n,m) DWCNTs measured on the P-DWCNT sample in this work and allow us to propose a partial identification of the outer walls of the (6,4)@(n,m) combinations. Table S2 in the Supporting Information provides a comparison between the experimentally observed and calculated RBM-frequencies and E₂₂ optical transition energies, which allows the assignment of a few outer wall chiralities to each experimental data point. For most data points, one to three options for an outer wall chirality exist, highlighted by vertical lines and labels in Figure 4b. The outlier experimental data point observed at an energy of 1.94 eV does not correspond to any of the calculated data points and can be due to excitonic contributions or interactions between the excitons on the inner and outer wall, which are not accounted for by the theoretical model. Similar assignments can also be done for the inner (6,5) chirality (Supporting Information section S6 and Figure S13). Further on, we will show that we can decrease the number of possible outer wall chiralities for each point by observing an ET from the inner (6,4) chirality to particular outer wall chiralities.

The results in Figure 4 also demonstrate, in agreement with the results of Liu et al.⁹ and Popov et al.,⁴⁸ that the magnitude of the redshift in electronic transition energy is dominated by highly chirality-specific moiré coupling^9,10 instead of the previously postulated varying radial pressure.²⁵ However, we note that the observed discrepancy of our data with the reported trend of Gordeev et al.³⁰ can be explained by different sample composition, for example, differences in abundance of outer wall (n,m)s in their respective samples or due to the presence of SWCNT impurities from using sonication in their sample preparation,²⁴ or the wrapping of the DWCNTs with a polymer instead of a surfactant solution.

Given the excellent agreement between the experimental results and theory, we last note that the simultaneous 2D RRS fit of SWCNTs and inner walls of DWCNTs now firmly establishes the chirality identification of several inner DWCNT chiralities (see Figure 4a and Table S1 in the Supporting Information for a list of the fitted parameters for the RBMs of the SWCNTs and inner-wall DWCNTs). Even though the exact number of peaks within a single cluster is expected to vary depending on the diameter distribution of the DWCNT production method used, this table will allow for a correct identification using 2D RRS or for identifying the best laser energies to access particular inner DWCNT walls if a complete laser tunability is not accessible.

PLE Spectroscopy of DWCNTs

The modulated optoelectronic properties of the inner and outer DWCNT walls are furthermore thoroughly characterized with respect to the various SWCNT reference samples by performing extensive 2D PLE measurements. Figure 5 presents the 2D PLE maps of the DWCNT samples in panels (a–c), which show a notable fluorescence signal above an emission wavelength of 1600 nm. This is due to absorption and PL of the outer walls of the DWCNTs. Once again, the PLE signals from the P-DWCNT and the P-S@S-DWCNT-1 samples are similar due to the similar diameter distribution selected by the in situ DGU characterization, while the P-S@S-DWCNT-2 sample shows emission from even larger outer walls, in agreement with the conclusions from absorption spectroscopy. Note, however, that the signal-to-noise ratio for the P-DWCNT sample is much lower than that of the P-S@S-DWCNT samples. This can be explained by the much higher absolute concentration for the latter. Moreover, the presence of M species in the P-DWCNT sample could also result in lower emission efficiencies, although this effect is estimated to be very low as the DWCNTs are all isolated in a surfactant environment and, hence, interaction between DWCNTs will be small. The greaterabsolute concentration of the P-S@S-DWCNT samples originates from the fact that the P-DWCNT sample was purified with a sequence of two DGU steps to remove remaining SWCNTs, while for the P-S@S-SWCNT only one DGU step was applied for the reason of absolute concentration, at the cost of remaining SWCNT impurities, which are visible in the emission wavelength range below 1500 nm. Note that, because of the strong D₂O absorption band, only the thinnest outer wall DWCNTs can be reliably detected (that is, those showing emission below 1850 nm).

Figure 5.

Overview of the 2D PLE maps of the (a) P-DWCNT, (b) P-S@S-DWCNT-1, (c) P-S@S-DWCNT-2, (d) large-E-SWCNT, (e) small-SWCNT, and (f) large-WF-SWCNT samples, showing the electronic transitions within the range of both the inner DWCNT walls (emission below approximately 1500 nm) as well as outer DWCNT walls (emission above approximately 1500 nm). The data in the top-left corner of the 2D PLE maps is cut to eliminate the excitation light and the inaccessible ranges due to the different filters used. The step in the signal-to-noise ratio at an emission wavelength of 1220 nm arises from the changeover in excitation grating (see Supporting Information, section S2). Note that the absolute PL intensities of the different samples cannot be compared across samples due to differences in concentration, and normalization over the absorption is not possible due to strongly varying diameter distributions.

The direct comparison between the emission of the outer DWCNT walls in the DWCNT samples and the emission from the larger diameter SWCNTs allows for further insights into the optical properties of the DWCNTs. For instance, in comparison to the signals of the large-SWCNT samples, the PL of the outer walls of the DWCNTs is significantly red-shifted in both emission and resonance excitation, and the PL peaks are also broadened. This can be illustrated by summing the DWCNT PLE maps in the emission direction (e.g., between 1600 and 1850 nm) to yield an excitation slice, or, likewise, summing the PLE maps in the excitation direction (e.g., between 980 and 1030 nm) resulting in an emission slice. When doing this for the DWCNT and large-SWCNT samples, Figure 6 is obtained, which clearly demonstrates the shifts and broadening for the outer DWCNT walls with respect to the empty and water-filled SWCNTs.

Figure 6.

(a) Emission slices of the 2D PLE maps obtained by summing the PL intensities over the excitation range of 980–1030 nm for the large-E-SWCNT (black trace), the large-WF-SWCNT (blue trace), the P-DWCNT sample (red trace), the P-S@S-DWCNT-1 (green), and the P-S@S-DWCNT-2 samples (magenta). (b) Excitation slices of the 2D PLE maps summing the PL intensities over an emission range of 1600–1850 nm (same color coding as in (a)).

Before analyzing the shifts of the electronic transitions of the outer DWCNT walls in more detail, we first discuss the emission signals in the range of the inner DWCNTs. According to the 2D PLE map of the small-SWCNT sample (Figure 5e), PL of the inner DWCNT walls is expected at emission wavelengths less than 1500 nm. In the P-DWCNT sample, no significant fluorescence signals are detected in this emission range (Figure 5a), except for a few imperceptible peaks within the noise level; the P-S@S-DWCNT-2 and, in particular, the P-S@S-DWCNT-1 sample, however, clearly show emission signals from such thin-diameter CNTs. Note however that according to our RRS fits (Figure 4a) the PL of the inner DWCNT walls should be significantly shifted with respect to the small-SWCNTs, while in this case no shift is observed (see Supporting Information section S7, Figures S14–S16). As demonstrated previously,^24,33 these signals do not originate from inner DWCNT walls but from remaining SWCNTs, which are more present in the P-S@S-DWCNT samples because only one DGU purification step was applied to reduce less thoroughly the amount of SWCNTs while maintaining a greaterabsolute concentration of DWCNTs. Since the P-S@S-DWCNT-1 sample has a much lower absolute concentration of DWCNTs as it was extracted from the centrifuge tube just above the dark colored band that is associated with the DWCNTs (see Figure S2 in the Supporting Information), the PLE maps of this sample show relatively more PL from the remaining SWCNT impurities. Sample P-S@S-DWCNT-2 was extracted at a slightly greater density and contains relatively more DWCNTs than remaining SWCNT impurities. We therefore emphasize that even a small fraction of SWCNTs, despite intensive DGU purification, can lead to PL signals that are easily misinterpreted as PL arising from inner DWCNT walls.

Inner-to-Outer Wall Energy Transfer

A possible explanation for this drastically quenched fluorescence of the inner DWCNT walls is the earlier postulated ET from the inner to the outer wall of the DWCNTs.^38,49 This transfer occurs because the larger outer walls naturally have a smaller band gap compared to those of the inner walls. In 2D PLE, such an ET would express itself as an additional peak at the crossing point of the excitation wavelength of the inner DWCNT wall and the emission wavelength of the corresponding outer DWCNT wall, similarly to the observed ET from encapsulated dye molecules to surrounding SWCNTs.^50,51Also in SWCNT bundles, efficient and ultrafast energy transfer to the smallest band gaps has been observed previously.^52,53 In our samples, where extensive DGU sorting was applied, the presence of such bundles can be neglected. In Figure 7, we therefore present the 2D PLE maps of the P-S@S-DWCNT-1 and P-S@S-DWCNT-2 samples, with a zoomed-in intensity color scale as compared to Figure 5, to search for such cross peaks. In addition, we sum the experimental PLE maps between two emission wavelengths of the outer DWCNT walls and plot these so-called excitation spectra together with the average E₂₂ excitation energies of the chirality-identified inner DWCNT walls obtained from the detailed RRS fits (horizontal colored lines with labels; the average E₂₂ of each cluster is taken for simplicity).

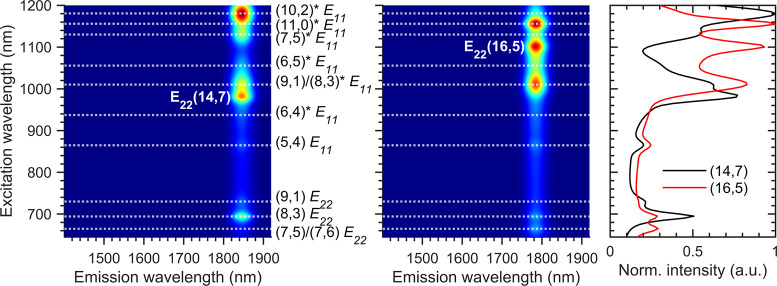
Figure 7.

PLE maps of the P-S@S-DWCNT-1 and P-S@S-DWCNT-2 samples (previously shown in Figure 5, but now zoomed in on the color scale and the outer DWCNT range to highlight the ET peaks) together with excitation slices obtained by summing the PL intensities over a certain emission range. The P-S@S-DWCNT-1 slice, summed over the range of 1600–1720 nm (in red), is compared with the P-S@S-DWCNT-2 slice (range: 1780–1840 nm, in blue) and the large-WF-SWCNT sample (range: 1600–1850 nm, in black). The excitation slices have been normalized after subtraction of a linear background, in order to directly compare the slices. Expected excitation energies for different inner DWCNT walls are also presented by horizontal lines, taking the mean excitation energy obtained from the previous RRS fits.

For the P-S@S-DWCNT-1 sample (summed between 1600 and 1720 nm, red trace), we clearly observe a peak in the excitation slices corresponding to the excitation energy of the (5,4) inner DWCNT wall and also a weaker peak corresponding to the (6,4)/(6,5) inner walls that are not present in the large-WF-SWCNT reference sample (summed between 1600 and 1850 nm, black trace). Similarly, for the P-S@S-DWCNT-2 sample (blue trace, summed between emission wavelengths 1780 and 1840 nm), additional peaks can be directly observed corresponding to the excitation energies of the (8,3) and (7,5)/(7,6) chiralities. Since these excitation slices thus indicate the absorption of photons at energies corresponding to the inner DWCNT walls and subsequent emission by the outer DWCNT walls, they are a direct proof of ET from the inner to the outer DWCNT walls.

When studying these PLE maps in more detail by, for example, selecting different emission ranges and again comparing with the expected excitation wavelengths of the inner DWCNT walls obtained from the RRS fits, other ET peaks appear in the excitation slices, but they are more hidden in the noise. Interestingly, we also observe additional peaks in the PLE maps at longer excitation wavelengths, for example, at approximately 1150 or 1170 nm, which are not present in the reference SWCNT samples (see Figure 5), which we postulate to originate from ET from inner walls to outer walls after optical excitation in the first optical transition (E₁₁) of the inner DWCNT walls. Unfortunately, we do not have information from excitation wavelengths above 800 nm from RRS spectroscopy, but assuming similar red shifts of the E₁₁ transitions of about 60 to 80 meV, as observed for the second optical transition (E₂₂) of the inner DWCNT walls with respect to the water-filled SWCNT transitions, these ET positions can also be assigned tentatively to other inner DWCNT chiralities (see Supporting Information Figure S23).

To assess these ET peaks in more detail, we fitted all the PLE maps using our previously developed 2D fit model for SWCNT PLE maps.^{40,41,50,51,54,55} While for the SWCNT PLE maps (see results in Figures S17 & S18) the previous model could be directly employed, we adapt the model to also fit the ET peaks of particular inner@outer wall combinations in the PLE map. In this respect, for each inner DWCNT chirality that shows a well-resolved ET peak within the measured excitation range, we added a Voigt line shape in the excitation profile of the outer DWCNT wall, corresponding to the excitation of the inner DWCNT chirality (see Supporting Information section S3 for more details). This adaptation of the model is quite similar to what was employed in refs (50 and 51) for the fitting of the ET of encapsulated dyes inside SWCNTs but different in the sense that now, for each outer DWCNT chirality, multiple inner DWCNT chiralities could show an ET peak (because of the different inner@outer wall combinations). To accurately fit these ET peaks, the PLE maps of the DWCNT samples were fitted simultaneously, with shared peak positions and line widths for the outer wall emission peaks.

Most importantly, the relative amplitude of a specific ET peak with respect to the outer wall emission (after direct excitation of this outer wall in its E₂₂) depends on three factors: (i) the abundance of a specific inner wall inside that outer wall, (ii) the ET efficiency for that specific inner@outer wall combination, and (iii) the relative absorption cross-section of the inner DWCNT wall at its excitation wavelength (either E₁₁ or E₂₂) with respect to that of the outer wall at its direct excitation at E₂₂. First, the ET efficiency is expected to be close to 100% as the emission of the inner DWCNT walls is found to be completely quenched,¹⁶ and also for other encapsulants, such as dyes, the ET efficiency to the surrounding SWCNTs is found to be nearly complete.⁵⁰ Second, we can assume that the relative absorption cross-section for a given inner@outer wall combination is the same across the three samples. Finally, the different abundances of inner@outer wall combinations could, in theory, be very different across the different samples, which implies that we should add three different ET amplitudes for each ET peak in the fit. However, this resulted in an overparametrized fit. For the sake of simplicity we positto take the relative ET amplitudes the same in the three samples, thereby reducing the number of ET amplitudes by a factor of 3 in the fit. In this way, we assume that, for a given outer DWCNT, the ratio of specific inner DWCNT chiralities is constant. This assumption, even though it is very limiting, already gives very good fits of the experimental PLE maps. If single-chirality DWCNTs become available in the future, the inner@outer wall ratio can of course be studied in more detail.

The resulting fits are presented in Figure 8 for the P-S@S-DWCNT-2 sample and in Figures S19 & S20 for the other DWCNT samples. In addition, Figures S21 & S22 in the Supporting Information show the fit either with ET amplitudes included or without the ET peaks included, allowing one to present the contribution of the ET peaks in a residuals plot. Finally, Figure S24 shows the shifted E₁₁ and E₂₂ transition energies of the outer DWCNT walls with respect to the empty and water-filled SWCNTs. On top of the fitted PLE map in Figure 8, we highlight the fitted ET peak positions with white dashed lines. While the ET positions associated with the E₂₂ of the inner DWCNT walls (and the E₁₁ of the (5,4) inner chirality) can be directly assigned by comparison with the RRS fits, the ET positions of the E₁₁ of other chiralities are tentatively assigned by using the above assumption that the E₁₁ peaks have similar shifts as those observed for the E₂₂ transitions (presented by (n,m)* in Figure 8 and beyond; see also Figure S23).

Figure 8.

PLE map and fit for the P-S@S-DWCNT-2 sample. (a) Experimental PLE map zoomed in on the fitted data range, (b) fitted PLE map overlaid with the fitted outer wall peak positions with their respective error bars (in white with magenta labels) and fitted ET peak positions indicated by white horizontal dashed lines, each assigned to a different inner wall transition. The (*) marks indicate tentatively assigned chiralities, while the other chiralities are taken from the RRS fits. (c) Emission and (d) excitation spectra by summing the PLE maps between the indicated excitation wavelengths or emission wavelengths, respectively (black: experimental data, red: fit). See also Figures S17–S20 for PLE fit and residuals plots of the other samples.

It should be noted that not all observed inner DWCNT walls in RRS result in a distinguishable ET peak in the DWCNT PLE maps. A likely explanation is that the ET exists, but we do not observe it due to experimental limitations constraining the observation of PLE from larger outer DWCNT walls and fitting constraints aimed to exclude possible E₃₃ excitations. Specifically, PLE collection is limited to wavelengths ⩽ 1870 nm due to strong absorption of the D₂O solvent, the maximum excitation wavelength is 1200 nm (limited by our setup), and, for the fits we needed to restrict ourselves to the minimal excitation wavelength range of ∼630 nm. The latter is due to the overlap with the E₃₃ excitation range of the outer DWCNT walls, which prevents proper fitting of some ET peaks in the 2D fit (e.g., (6,4) and (6,5) E₂₂, which visually seem to be present in the red curve in Figure 7). The strong D₂O absorption furthermore limits the observed ET peaks to the thinnest outer walls of the DWCNT diameter distribution. Hence, we suspect that, if this hindering absorption band could be overcome, many more and possibly stronger ET peaks due to the higher DWCNT abundance can be detected.

Finally, we look at the fitted amplitudes of the ET peaks for each inner@outer DWCNT wall combination. In Figure 9, for each inner DWCNT chirality (see top-left parts of the panels) found in the three DWCNT samples, the fitted ET amplitude as a function of the outer DWCNT diameter is presented. Previously, Ghedjatti et al.⁵⁶ conducted a statistical HRTEM study on DWCNTs from the same batch of parent soot from which the P-DWCNT sample was prepared, revealing an experimentally determined range of interlayer distances between inner and outer walls. Based on a Gaussian fit of this normal distribution (see Figure S25), the interlayer distance ranges from 0.304 to 0.397 nm based on the 95% confidence interval with an average of 0.351 ± 0.033 nm. Hence, not all combinations of inner and outer walls are expected to occur in practice. We highlight this with the red lines in Figure 9 obtained by calculating the Gaussian interlayer distribution function based on the given diameter of the inner DWCNT wall. Interestingly, for most of the probed chiralities, we find a suggestive correspondence between the ET amplitudes and the expected outer wall diameters in which each inner wall naturally fits, except for the (11,0)* and (10,2)* chiralities; however, their E₁₁ assignment might not be correct.

Figure 9.

Fitted relative amplitude of the ET presented for each inner chirality (shown in top-left part of each panel) as a function of the diameter of the corresponding outer wall. The relative ET amplitudes include the ET efficiency, the relative abundance of a specific inner@outer wall combination, and the inner-wall extinction coefficient. The red curve provides the expected outer-wall diameter range, assuming a Gaussian distribution of the interlayer distance (see Figure S25). Chiral indices for the most relevant outer-wall chiralities are also provided by labels in the panels. The (*) marks indicate tentatively assigned chiralities, while the other chiralities could be identified from the RRS fits.

This approach also reveals various inner@outer wall combinations that show a significant ET amplitude relative to the directly excited emission in the E₂₂ of the outer tube. For example, for the (5,4) inner tube chirality, ET is mainly observed to the (13,6), (11,9), (15,4), and (14,6) outer walls. For the (6,4)* inner wall chirality, where the (*) indicates the tentative assignment of the specific chirality, the main ET peaks are observed for (16,3), (11,10), (17,3), and (13,8), likely evidencing that those chiral combinations are the most prevalent in the sample. Note that error bars represent 1σ fit errors of the amplitude determinations. Typically, outer wall chiralities that are less abundant correspond to larger error bars for the amplitude determinations (see, e.g., the (11,10) outer wall). These possible combinations of DWCNT inner and outer walls for which an ET is detected in Figure 9 will be further on referred to as the ET-DWCNTs. In future studies, it would be very helpful to sort specific inner@outer wall combinations such that these fits become much easier to perform due to fewer overlapping chiralities. Nevertheless, we identified ET peaks for seven different inner DWCNT chiralities, occurring after excitation in the first or second electronic transitions of those inner DWCNTs.

It is important to note that, even though in the color maps of the PLE data the ET peaks look small and often close to the noise level, it can be demonstrated from the fit that the relative ET amplitudes (i.e., corresponding to the integrated intensity of the peaks) are comparable to or sometimes even stronger than the directly excited outer-wall emission (i.e., directly excited in E₂₂). For instance, we plot in Figure 10 the basis functions from the fit for two individual outer-wall chiralities (the overall fit being a sum of these basis functions with different amplitudes corresponding to the outer wall abundancies). Each basis function contains multiple ET peaks originating from the different inner@outer wall combinations, with their relative amplitudes with respect to the direct excitation of the outer walls, as presented in Figure S26. While this direct excitation of the E₂₂ of the outer wall is highlighted by the chirality label right next to it, the different ET peak positions are again marked with white dashed lines in Figure 10. It is clear that some ET amplitudes can be close to or even larger than the directly excited outer wall emission (for instance, see the peak corresponding to (10,2)@(14,7) DWCNT combination in Figure 10).

Figure 10.

PLE fit basis function for two different outer wall chiralities (14,7) and (16,5) showing the intrinsic, directly excited emission of the outer walls and the fitted ET peaks (at the positions of the dashed lines) with their relative amplitudes. The panel on the right shows the excitation profile for both outer wall chiralities to better highlight the relative amplitudes of the different ET peaks. The two peaks labeled (14,7) and (16,5) correspond to the direct excitation of the outer walls in their second optical transition.

Since the relative amplitude of the ET peaks with respect to the directly excited outer wall emission intensity depends on three factors, namely, the ET efficiency, the relative abundances of the specific inner@outer wall chiralities, and the specific relative absorption cross sections of the inner and outer walls, which are both unknown, an absolute measure of the ET efficiency cannot easily be provided. However, to get a rough estimate, we find the ratio of the total integrated outer wall emission intensity measured after exciting at the E₁₁ of all inner DWCNT walls (i.e., summing over all inner wall ET peaks corresponding to the E₁₁ excitation) and the directly excited outer wall emission intensity obtained after excitation at the E₂₂ of the outer walls. To do so, we split our fit function up into a part that only includes the directly excited outer wall emission obtained after excitation at the E₂₂ of the outer walls (see Figure S26b) and a part that only includes the ET peaks corresponding to the E₁₁ or E₂₂ excitation of the inner walls (Figure S26c). We then integrate the latter only over the E₁₁ excitation range and the former over the full E₂₂ excitation range, obtaining a ratio of ET peaks over direct excitation of the outer walls ranging from 0 to 10, as presented in Figure S27 for the different outer wall chiralities. This factor of 0–10 can be easily understood from the different absorption cross sections of the smaller-diameter inner walls with respect to the larger-diameter outer walls and the different optical transitions probed (E₁₁ for the inner walls and E₂₂ for the outer walls). In section S11 in the Supporting Information we derive this difference in absorption cross sections from literature predictions⁵⁷ to be in the range of 4.8–9.9, exactly in the same order of magnitude of the ratios found in the PLE maps and, thus, consistent with a nearly 100% efficiency of ET from the inner to the outer walls.

In general, we observe the relative ET amplitudes of the inner walls to be stronger after E₁₁ excitation compared to E₂₂ excitation. This is in agreement with the fact that the absorption cross-section of the E₁₁ is typically a factor of 2–4 greater than for E₂₂, as observed for single-chirality sorted SWCNTs in the diameter range of the inner DWCNT walls.^40,58,59

These results indicate that the energy absorbed by the inner walls is efficiently transferred to the outer walls. This efficient ET is also in line with the ultraefficient ET (close to 100%) in porphyrin-nanotube compounds⁶⁰ and in dye-filled SWCNTs⁵⁰ where comparable PL intensities of ET and intrinsic SWCNT peaks have been reported. It also agrees with the near-to-complete quenching of the emission from the inner DWCNT walls, as previously observed for individual index-identified DWCNTs.¹⁶ Lastly, it should be noted that previous time-domain ab initio simulations of photon-induced exciton relaxation in both inner and outer shell semiconducting DWCNTs³⁸ emphasized the role of ET to other nanotube states, including crossover transitions between nonsymmetric van Hove singularities and dark interwall states where the electron and the hole are located on different walls of the DWCNT. Such ET would then not result in outer wall emission, which if present, could result in a lower than 100% ET efficiency observed in our PLE studies.

Observation of ET-DWCNTs in RBM Raman Maps

Finally, we are able to confirm the presence of ET-DWCNTs in the 2D RRS maps (Figure 2d) of the P-DWCNT sample by analyzing, in particular, the region of the RBMs of the outer walls. To this end, we calculate the VDW-modulated electronic transition energies and RBM frequencies of the outer DWCNT walls for all possible DWCNT combinations, including the identified ET-DWCNTs from Figure 9, within the model of Chalin et al.¹⁹ and the coupled-harmonic oscillator model,²¹ respectively (for details on the calculations, see Section S12 in the Supporting Information, and for comparison with experimental data see Figure S28). For those ET-DWCNTs that are abundant and possess a sufficiently high Raman cross-section, the theoretically predicted RBMs match very well with the experimentally observed RBM peaks in Figure 2d, further evidencing the presence of these particular inner@outer wall combinations in our samples.

In an orthogonal strategy, we can observe ET-DWCNTs also in the region of the inner walls of the 2D RRS map. This can be illustrated by the experimental and calculated Raman data of (6,4)@(n,m) DWCNTs in Figure 4b, where we chose the color of the calculated data points (filled circles and triangles) to represent the ET amplitude in the 2D PLE maps (see the top right panel for (6,4)@(n,m) DWCNTs in Figure 9). The DWCNT combinations for which ET was not observed, for example, all metallic and some semiconducting outer layers, are plotted in gray. Comparing the results of NTB calculations with the experimental 2D RRS data (see also Tables S2 & S3 and Figure S13 in Section S6 of the Supporting Information), we show that (6,4)@(n,m) and (6,5)@(n,m) DWCNTs with the strongest ET amplitudes are similarly observed as the most intense peaks in the 2D RRS map. These results serve as independent confirmation of the observation and identification of ET-DWCNTs in the studied DWCNT samples.

Conclusion

In this work, we explored the VDW-coupling effects on the optical properties of purified DWCNT samples obtained by careful solubilization or metallic/semiconducting sorting by ATPE, followed by a DGU sorting procedure to remove as much as possible the contaminating SWCNTs. In addition, we prepared three SWCNT samples for reference measurements with diameters matching those of the inner and the outer walls of the DWCNTs.

First, detailed fitting of wavelength-dependent RRS maps allows us to establish accurate values of the vibrational and electronic shifts induced by VDW coupling between small-diameter inner walls and various outer walls. Second, through fitting the 2D PLE and RRS maps to great detail we demonstrate that the fluorescence of the outer walls of the DWCNTs is chirality-dependently shifted with respect to both empty and water-filled SWCNTs as a result of the intricate interlayer VDW coupling. Additionally, no PL of the inner walls of DWCNTs was detected, which is in line with the inner-wall PL quenching expected from previous single-tube measurements. Most importantly, we detect ET peaks from specific combinations of inner and outer wall chirality-identified DWCNTs via a combination of detailed 2D fitting of PLE maps in which both the different ET peaks and their relative amplitude and the directly excited outer wall emission are fitted, in particular, for those inner@outer wall combinations with a matching interlayer distance, demonstrating efficient ET. These structural assignments were then independently confirmed by observing corresponding DWCNT combinations in the inner and outer wall regions of the RBM RRS maps. In future work, PL and ET peaks from larger-diameter DWCNTs currently concealed by D₂O absorption should be detectable through measurements made on film samples of purified DWCNTs or using DWCNTs dispersed in a more transparent solvent such as deuterated toluene. Measuring ET peaks is expected to be exceptionally efficient after chiral sorting of the outer walls, to avoid overlap of ET peaks with emission from other outer walls, as such allowing the particular DWCNT combinations with various inner walls to be better resolved.

Finally, comparison with theoretical calculations allows one to also identify specific inner@outer wall combination in the RRS maps. Our assignments of DWCNT chiralities based on the observation of ET peaks in the PLE maps establish an approach for DWCNT characterization. Detection of an ET peak allows direct estimation of factors such as the transition energy of the inner wall, which are otherwise inaccessible in the PLE maps, and the knowledge of the transition energy propagates to subsequent Raman measurements, giving additional structural information about the probed ET-DWCNT.

Methods

Certain equipment, instruments, or materials are identified in this paper in order to adequately specify the experimental details. Such identification does not imply recommendation by the National Institute of Standards and Technology (NIST), nor does it imply the materials are necessarily the best available for the purpose. Where specified, uncertainty in this contribution is reported as one standard deviation.

Sample Preparation

A detailed sample preparation description is provided in the Supporting Information, section S1. An overview of the different samples with their most important parameters is presented in Figure 1. In brief, DWCNT samples²² are solubilized in a surfactant solution of sodium deoxycholate and further purified by either a two-step DGU procedure²⁴ or an ATPE sorting to obtain only S@S DWCNTs²⁹ with a subsequent one-step DGU purification. Reference SWCNT samples are prepared with similar diameter distributions matching inner or outer walls and with different endohedral content (empty or water-filled) according to previously accomplished procedures in literature.^41,61

Experimental Setups

The experimental setups for absorption, wavelength-dependent RRS and PLE spectroscopy are described in detail in the Supporting Information, section S2. In brief, absorption spectra were recorded using a Cary 5E and Cary 5000 UV–vis–IR spectrometer from 200 to 2500 nm, in a 60 μL quartz microcell with a 3 mm optical path length. Wavelength-dependent RRS experiments were acquired with a Dilor XY800 triple Raman spectrometer in backscattering geometry, after excitation by different tunable lasers. Any laser power variations among the spectra are corrected by using a tetrachloromethane (CCl₄) reference sample, which is transparent throughout the entire wavelength range and thus exhibits nonresonant Raman scattering. To measure the wavelength-dependent infrared PLE, we used a dedicated in-house developed setup equipped with a liquid nitrogen cooled extended InGaAs photodiode array detector with a sensitivity up to 2.2 μm (more details in Supporting Information Section S2). The sample in PLE is contained in a 60 μL quartz microcell with a 3 mm path length. The samples are diluted to an absorbance of less than 0.3 before measuring PLE to be in the linear correctable reabsorption regime, except for wavelengths in the range of 1850–2100 nm due to the saturated D₂O absorption peak.

Fitting Models

The fitting models are based on previously developed fitting models for wavelength-dependent RRS⁴⁶ and PLE^40,41,50,54 and are described in detail in the Supporting Information section S3.

Glossary

Abbreviations

SWCNT

single-wall carbon nanotube

DWCNT

double-wall carbon nanotube

RRS

resonant Raman spectroscopy

RBM

Radial Breathing Mode

PLE

fluorescence–excitation spectroscopy

2D

two-dimensional

1D

one-dimensional

PL

fluorescence

ET

energy transfer

VDW

van der Waals

M

metallic

S

semiconducting

HRTEM

high-resolution transmission electron microscopy

ED

electron diffraction

DGU

density gradient ultracentrifugation

ATPE

aqueous two-phase extraction

NTB

nonorthogonal tight-binding model

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.2c03883.

• The SI contains further details and additional figures on (1) sample preparation, (2) experimental setups, (3) 2D fit models for RRS and PLE (4) absorption spectroscopy, (5) RRS spectroscopy, fits and table with all fitted peak positions, (6) theoretical calculation of RBM and E₂₂-shifts for (6,4) and (6,5) inner DWCNT walls, (7) PLE spectroscopy and fits, (8) assignment of ET peaks for excitation in the E₁₁ range of the inner DWCNT walls, (9) comparison of fitted transition energies for empty SWCNTs, water-filled SWCNTs and outer DWCNT walls (10) estimation of interlayer distance distribution in P-DWCNTs, (11) efficiency estimation of the ET and (12) observation of ET-DWCNTs in the outer wall RBM Raman maps (PDF)

Author Contributions

M.E. prepared the P-DWCNT sample and SWCNT reference samples, which he has consequently spectroscopically investigated using absorption, RRS, and PLE spectroscopy. S.F. helped with a part of these RRS experiments. M.E. further processed and analyzed the data, including the RRS fits and first PLE fits. S.C. analyzed the ET and incorporated the ET in the PLE fit model, which was previously developed for fitting SWCNT PLE spectra by S.C. and W.W.; D.L. investigated P-S@S-DWCNT samples by absorption and PLE spectroscopies and calculated VDW-induced RBM frequency and transition energy shifts for outer walls of the DWCNTs. M.A. performed and analyzed the DGU separations of the P-S@S-DWCNT sample. W.W. developed the PLE setup. W.W. and S.C. supervised the work at the University of Antwerp. E.F. synthesized the DWCNTs used to prepare the P-DWCNT sample. H.L., J.A.F., and B.S.F. prepared the P-S@S-DWCNT samples. V.N.P. performed the calculations of RBM and transition energies for the DWCNTs. M.E., D.L., and S.C. wrote the manuscript, with contributions of all authors.

The authors declare no competing financial interest.