Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Sep 23;16(10):16314–16321. doi: 10.1021/acsnano.2c05333

Energy Dissipation from Confined States in Nanoporous Molecular Networks

Philipp D’Astolfo †, Xing Wang ‡, Xunshan Liu ‡, Marcin Kisiel †, Carl Drechsel †, Alexis Baratoff †, Ulrich Aschauer ‡, Silvio Decurtins ‡, Shi-Xia Liu ‡, Rémy Pawlak †,*, Ernst Meyer †,*
PMCID: PMC9620977  PMID: 36150702

Abstract

graphic file with name nn2c05333_0005.jpg

Crystalline nanoporous molecular networks are assembled on the Ag(111) surface, where the pores confine electrons originating from the surface state of the metal. Depending on the pore sizes and their coupling, an antibonding level is shifted upward by 0.1–0.3 eV as measured by scanning tunneling microscopy. On molecular sites, a downshifted bonding state is observed, which is occupied under equilibrium conditions. Low-temperature force spectroscopy reveals energy dissipation peaks and jumps of frequency shifts at bias voltages, which are related to the confined states. The dissipation maps show delocalization on the supramolecular assembly and a weak distance dependence of the dissipation peaks. These observations indicate that two-dimensional arrays of coupled quantum dots are formed, which are quantitatively characterized by their quantum capacitances and resonant tunneling rates. Our work provides a method for studying the capacitive and dissipative response of quantum materials with nanomechanical oscillators.

Keywords: supramolecular assembly, artificial atoms, energy dissipation, quantum capacitance, scanning tunneling microscopy, atomic force microscopy, density functional theory

Introduction

Since the quantum corral built in 1993 in IBM Almaden,1 atomic structures capable of confining Shockley surface states (SS) of noble metals into discrete energy levels (also referred to as artificial atoms) are achieved by atom-by-atom manipulation with a scanning tunneling microscope (STM)2,3 or by spontaneous assembly of molecules into nanoporous networks.4 When a two-dimensional array of artificial atoms is formed, its geometry and symmetry as well as the interaction between the confined states—all depending on the precursor forming the network5—are key factors in determining the final topology of the band structure. To date, this strategy has been successfully utilized to generate quantum states in artificial lattices such as dispersive electronic bands,4,5 Dirac fermions,6 fractional behavior in fractal systems,7 topological edge states,8 and flat bands.9−11 Interestingly, a partial filling of flat electronic bands can result in a variety of interesting many-body phenomena, including Wigner crystallization12 and topological insulating transitions.13 However, the control of designer quantum states in artificial lattices with a local external electric field has not yet been reported.

Recent progress in dynamic frequency-modulated (FM) atomic force microscopy (AFM)14 has enabled researchers to obtain spatial resolution at the atomic scale15 and electrostatic force measurements with single-electron sensitivity. The latter has been used to demonstrate single-electron tunneling in individual QDs16,17 or the charge-state control of single adatoms18 and molecules at surfaces.19,20 Experimentally, such charging/discharging phenomena are manifested in force spectroscopic measurements versus bias voltage V as drops (peaks) in the cantilever’s resonance frequency shift Δf (damping) at a constant tip–sample separation Z.16 In addition to ascertaining tunneling processes in individual QDs, Δf(Z) spectroscopy can quantify energy loss subsequent to lateral charge transfers between quantized levels19,21,22 or tunneling into quantum states in the vicinity of the surface.23,24 Recently, Stilp et al.3 also measured the bonding interaction of an artificial atom made in a quantum corral on Cu(111) with an atomic force microscope, making AFM an appealing technique for probing the “force” of an artificial atom. Similarly, one could envision controlling its charge state or even filling of a mini-band developed in an artificial superlattice using force versus voltage spectroscopy.18

In principle, Δf(Z) spectroscopy conducted at low temperature probes the tip–sample capacitance including the quantum capacitance CQ(25) arising from a finite and low density of states near the Fermi level EF,26 where CQ = ρ(E)e2 relates to the density of states (DOS) ρ(E) = dn/dE with n being the carrier concentration and e the electronic charge. 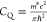On noble metals, the Shockley surface state provides a canonical 2D quasi-free electron gas (2DEG) with a quadratic energy dispersion E(k∥) = Inline graphic, where ℏ is the reduced Planck constant, k∥ the wave vector parallel to the surface, and m* the electron’s effective mass. Upon confining surface electrons in two dimensions, the DOS takes the form of a staircase as a result of the formation of dispersive ”minibands” in reciprocal space.5,27 The contribution of the quantum capacitance in AFM measurements of a 2D lattice thus scales as Inline graphic, which not only directly encodes the k-dispersion relation of the quantized states (i.e. m*) but also reflects the interaction between artificial atoms.

Results and Discussion

Synthesis of Nanoporous Molecular Networks

Our aim is to employ a low-temperature atomic force microscope (AFM) as a local gate capable of probing the capacitance of engineered quantum states in artificial superlattices (Figure 1a). We created two molecular networks through the thermal evaporation under ultrahigh vacuum (UHV) of 2,7-dihydroxypyrene (DHP) on the Ag(111) surface. These precursors are oxidized to pyrene-2,7-dione (PO; Figure 1b) species under the experimental conditions as verified by DFT calculations (Figure 2b in the Supporting Information). PO molecules spontaneously form nanoporous self-assemblies as a function of the substrate temperature (see the Experimental Section). The topographic STM image of Figure 1c shows the molecular assemblies, denoted α and β, where detailed insights are derived from the STM images of Figures 1d,e and Figure 1 in the Supporting Information. The α-network consists of a hexagonal arrangement with lattice parameter aα ≈ 2.9 nm (Figure 1d). The assembly is governed by cooperative intermolecular hydrogen bonds (Figure 2a in the Supporting Information), leading to identical hexagonal cavities of 0.95 nm diameter that are separated from the surrounding ones by two precursors (∼1.5 nm). The β-assembly is a hexagonal lattice of parameter aβ ≈ 6.7–8.7 nm that is composed of trigonal, hexagonal, octagonal, and nonagonal cavities. While both networks coexist at the surface, they do not intermix (Figure 1c).

Figure 1.

Figure 1

Open in a new tab

Coupling an AFM to an artificial superlattice. (a) Schematic of the experiment. An oscillating AFM probe is capacitively coupled to the confined state of surface electrons in a nanoporous molecular network. Ctip and Csub refer to the capacitance of the tip and substrate, respectively. CQ is the quantum capacitance of the “minibands” emerging in the artificial superlattice. (b) Surface oxidation of 2,7-dihydroxypyrene (DHP) into pyrene-2,7-dione (PO). (c) STM overview of the α- and β-assemblies of PO molecules on Ag(111) (scan parameters: V = −0.3 V, I = 1 pA). (d, e) STM images of the α- and β-structures, respectively (scan parameters: V = −0.13 V, I = 1 pA). (f) Bond-resolved STM images of the α network (Amod = 1.5 mV). (g) AFM image with a CO-terminated tip of the β-network displaying hexagonal and octagonal pores (Aosc = 50 pm).

An atomic understanding of the α- and β-structures is obtained via constant-height AFM and bond-resolved STM imaging15 with CO-terminated tips (Figures 1f,g) combined with calculations based on a deep-learning neural network (DPNN) potential model (see the Experimental Section and Text 1 in the Supporting Information). Our calculations (Figure 2b in the Supporting Information) reveal DHP molecules to be oxidized to pyrene-2,7-dione (PO) species under the experimental conditions. While molecules lie flat in both structures, neighboring PO molecules of the α-network interact through C–H···O–C hydrogen bonds between carbonyl groups and peripheral ortho hydrogens, leading to chiral trimers of PO molecules (plain triangle, Figure 1g, and Figure 2a in the Supporting Information). A similar bonding motif is observed for hexagonal pores in the β-assembly (Figure 1g), whereas trigonal, octogonal, and nonagonal cavities result from different H-bonding motifs between PO molecules. As a result, the β-structure contains four cavity geometries as reproduced by our DPNN-based calculations (Figure 2c in the Supporting Information).

Electronic Structure of the Superlattices

We next employed scanning tunneling spectroscopy (STS) to probe the local density of states (LDOS) and wave functions of both superlattices (Figures 2 and 3). On Ag(111), the unperturbed surface state appears at −67 meV (Figure 1g in the Supporting Information) with the quadratic energy dispersion m* = 0.397 × m0; the wave vector k is parallel to the surface with a Fermi wave vector of kF = 2π/λF ≈ 0.8 nm–1 and λF ≈ 7.8 nm. The top of the valence band is located at E0 = −400 meV. Figure 2c shows dI/dV spectra acquired at the center of an α-pore and above a PO molecule of the assembly (see inset). A resonance peak is observed at ψ6,1 = +300 meV corresponding to the first eigenstate ψi=6,n=1 (i is the edge number of the polygonal cavity and n is the quantization integer) due to quantum confinement of surface electrons in the cavity. The resonance peak near 0 V is attributed to a signature of the electronic state of the tip atom.28 Below EF, a resonance state at −130 meV denoted ψα* is observed at molecule sites (black spectra in Figure 2c and dI/dV map of Figure 2b), which is attributed to the formation of a molecule-induced bound state lowering the surface state energy.29 The ψα and ψα* resonance peaks persist at the molecule and pore sites (gray and black spectra in Figure 2c), respectively, which indicates the concomitant formation of filled (ψα*) and unoccupied (ψα) minibands in the superlattice upon the quantum confinement of surface electrons in cavities. We also conclude that the strong hybridization between artificial atoms of the superlattice leads to the splitting of the confined states into a bonding (ψα*) and antibonding states (ψα) similar to that found in refs (30−32). A gap of ΔU = 430 meV is thus deduced throughout the α-lattice. The dI/dV mapping at the ψ6 energy reveals the spatial localization of the ψ6 wave function (Figure 1c) as bright contrasts at the center of the cavities. Figure 2d shows a LDOS(X,V) cross-section taken along two neighboring cavities (see dashed line of inset of Figure 2, demonstrating the high fidelity of both ψ6,α and ψα* states throughout the porous array.

Figure 2.

Figure 2

Open in a new tab

Electronic structure of the α superlattice. (a) Structure of the α-lattice on Ag(111) obtained by DPNN calculations and (b) LDOS(X,Y) maps at ψα* = −103 mV and ψ6,1 = 303 mV showing the spatial localization of the molecule-induced bound state and confined states in the superlattice (Amod = 6 mV). (c) dI/dV(V) spectra acquired at the center of a pore (gray) and above a molecule (black) (see inset; scan parameters V = −0.15 V and I = 1 pA). Resonance peaks at 302 and −102 mV corresponds to the ψ6 and ψα* states separated by the gap ΔU = 430 mV. (d) dI/dV(X,V) cross-section acquired along two α-pores as marked by the dashed lines. (e) Schematic of the projected electronic band structure of the α-QD superlattice. The E(k) dispersion considering the α-lattice in the form of a Kronig–Penney model is plotted in gray.

Figure 3.

Figure 3

Open in a new tab

Electronic structure of the β superlattice. (a) Structure of the β-superlattice on Ag(111) obtained by DPNN calculations containing trigonal, hexagonal, and octagonal cavities colored in pale blue, gray and dark blue, respectively. (b) Series of LDOS(X,Y) mapping revealing the spacial confinement of the confined states at the corresponding energies (Amod = 6 mV). Resonance states of the 3-, 6-, 8-, and 9-member pores are ψ3 = 389 mV, ψ6 = 294 mV, ψ8 = 207 mV, and ψ9 = 144 mV, respectively. (c) dI/dV(V) point spectra acquired at the center of hexagonal (gray), octogonal (blue) pores and above a molecule (black). (d) LDOS(V,X) cross-section taken along hexagonal and octagonal pores (see the dashed lines; scan parameters V = −0.15 V, I = 1 pA). (e) Schematic of the projected electronic band structure of the β-superlattice on Ag(111). The E(k) relation considers each pore dimension in the Kronig–Penney model with m* = 0.45.

Figure 2d depicts the projected band structure of the α-array considering the ψ6 single-particle levels as compared to the top of the valence band (VBAg marked by an arrow at −0.4 eV), the bottom of the conduction band (CBAg marked by an arrow at +4.0 eV),33 the surface state (SS at −67 meV), and the image potential state (IPS at 3.9 eV) of Ag(111). The last is located at +3.9 eV, as confirmed by measuring field-emission resonance states by tunneling dZ/dV spectroscopy (Figure 9 and Text 3 in the Supporting Information). We reproduce the E(k) dispersion relation of the eigenstates by taking into account the dimensions of the α-lattice in an one-dimensional array of finite quantum wells in the form of the Kronig–Penney potential U(X), whose value is 0.8 eV at the top of the well and the SS energy is for the well bottom. As shown in Figure 2e, ψ6 emerges at +0.30 eV with a gap opening at the Brillouin zone boundaries kα. The ψ6 extends in k-space between ±kα = π/aα = 1.09 nm–1 states with a dispersion arbitrarily approximated to m* = 0.45 in relative agreement with ARPES measurements on similar porous systems on silver.5

We also investigated the confined states induced by the polygonal cavity (i.e. i = 3, 6, 8) of the β-superlattice, which are depicted in pale blue, gray, and dark blue in the structure obtained by DPNN calculations (Figure 3a), respectively. The four pore sizes and geometries modulate the confinement landscape, leading to four different eigenenergies ψ identified by dI/dV spectra acquired in each cavity (Figure 3c and Figure 7 in the Supporting Information) at ψ3 = 389 meV, ψ6 = 295 meV, ψ8 = 205 meV, and ψ9 = 145 meV, respectively. Figure 3b shows the wave function mapping of these eigenenergies ψ, again demonstrating a high fidelity of the confined states throughout the nanoporous assembly. This observation is further confirmed by the LDOS(X,V) cross-section (Figure 3d) acquired along hexagonal and octogonal cavities (see inset). In analogy to the α-lattice, a molecule-induced bound state ψβ* emerges at V = −190 mV (Figures 3c,d), where its shift compared to ψα* likely results from different bonding motifs in the β-phase. The gap ΔU = 335 meV is estimated between the ψβ* band and the lowest confined eigenstate ψ9. The corresponding projected band structure of the β-superlattice (Figure 3e) is approximated by the lowest ψ8 eigenvalues (= +200 meV) and extends in k-space according to a 1D Kronig–Penney (KP) model between ±kβ = π/aβ = 0.5 Å–1 with m* = 0.45m0.

Quantum Capacitance and Mechanical Dissipation Probed by Force Spectroscopy

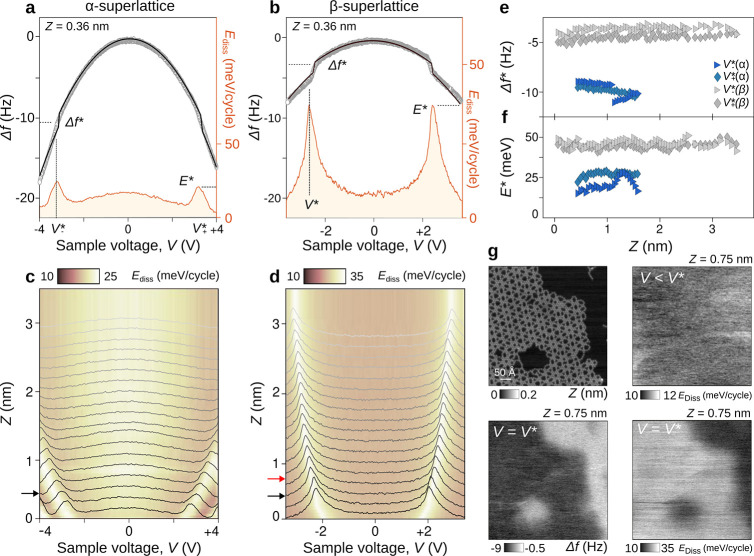
Next we discuss the detected mechanical dissipation above the artificial lattices using force-voltage spectroscopy with silver-coated tips.16,17Figures 4a,b shows exemplary Δf(V) (gray) and Ediss(V) (orange) point-spectra at the fixed tip–sample separation Z = 0.36 nm above the α- and β-superlattices, respectively. Both Δf and Ediss curves show abrupt transitions denoted Δf* and E* at positive and negative threshold voltages ±V*, which are absent on the pristine Ag(111) sample (Figure 10 in the Supporting Information). At first glance, the Δf* steps and E* peaks resemble charging/discharging events as encountered in a single QD such as molecules,19,20,22 indicating a charge injection/extraction in the minibands of the superlattices similar to that in ref (24). To better rationalize this, we reproduce the Δf(V) parabolas (black curves in Figures 4a,b) using a model that accounts for the quantum capacitance CQ and the tip and substrate capacitance, Ctip and Csub (Text 4 in the Supporting Information). CQ(V) is expressed as a Heaviside function which reflects the staircase LDOS of the 2D-superlattice with steps at −ψ* and +ψi,1 (see Figures 12 and 13 in the Supporting Information) as determined by tunneling spectroscopy. The fit agreement allows us to infer that CQ is equal to 2.2 and 18.3 aF/nm2 for the α- and β-QD superlattice, respectively.

Figure 4.

Figure 4

Open in a new tab

Dissipation spectroscopy above the α- and β-superlattices. (a, b) Δf(V) point spectra (gray) and associated dissipation Ediss(V) (orange) spectra of the α- and β-arrays for a relative tip–sample distance of Z = 0.36 nm (Aosc = 70 pm). The jump position in Δf(V), denoted as Δf*, are associated with dissipation peaks E* at threshold voltage V*. (c, d) Dissipation map Ediss(V,Z) acquired above the α- and β-superlattice. The bright lines correspond to the evolution of E* peaks as a function of Z. Single Ediss(V) spectra are superimposed in gray as a guide for the eye. Black arrows show the relative tip–sample distance Z of the spectra shown in (a) and (b). The red arrow in (d) refers to the tip–sample distance at which dissipation maps of (g) were acquired. (e, f) Δf* and E* magnitudes for increasing Z. Blue and gray markers refers to the α- and β-superlattices, respectively. Diamonds and triangles correspond to positive and negative voltage V, respectively. (g) Topographic STM images of the β-superlattice as compared to Δf(X,Y) and Ediss(X,Y) maps at V = V* . The maps show that force/dissipation signals are only detected above the molecular network. The Ediss(X,Y) map obtained for V ≠ V* at the same tip–sample distance and Z = 0.5 nm shows no mechanical dissipation (Aosc = 80 pm).

The Δf* jumps are accompanied by an increase of E* up to 20 meV/cycle and 40 meV/cycle for the α- and the β-assemblies, as compared to the unperturbed oscillator (15 meV/cycle) recorded at the compensated contact potential difference (CPD). This minute amount of dissipation detected by the small oscillation amplitude of the actuator34 suggests electron charging/discharging events from the superlattices,17,24 which is absent on pristine Ag(111) (Figure 10 in the Supporting Information). Note also that the dissipation magnitude is likely overestimated because of a possible apparent dissipation from the nonlinear behavior of our instruments, which was not corrected in our experiments, as described in ref (35). The Ediss(Z,V) cross-section (Figures 4c,d) shows bright lines associated with the E* peaks as a function of tip–sample separation Z. The E*(Z) dependence results from the tip (Ctip) and sample (Csub) capacitances, as typically observed in force spectroscopic measurements. The values of the threshold voltage V* depends on the lever arm defined as κ = Ctip/(Csub + Ctip) such as V = ψ/κ (Text 4 in the Supporting Information).17 Note also that the maximum voltage Vtip applicable to the tip in our experiments is ±4 V, which corresponds to the energetic position of the image potential state (IPS) identified by field-emission resonance tunneling spectra (Figure 9 in the Supporting Information) that is known to induce mechanical dissipation by charge injection between the tip and sample, thus possessing a strong distance dependence.36

In Figures 4e,f, Δf* and E* (triangle vs square) of α (blue markers)- and β (gray marker)-superlattices are plotted as a function of tip–sample distance Z. Their magnitudes are constant for both V polarities as Z increases. This observation is in stark contrast with previous works assessing Coulomb blockade in 0D systems (such as quantum dots or single molecules),17,19−22 where both Δf* jumps and E* peaks are dictated by single-electron tunneling between the tip and quantized levels. There, the dissipation directly scales with the tunneling rate Γ and decays with increasing Z,22 which is in contrast to our observation. This suggests that the tip gating in our system induces charge fluctuations between the quantum states of the artificial lattice (i.e., the bonding or the antibonding states) and the electron reservoir of the substrate but no direct charge transfers between tip and sample. This is followed by a variation of the quantum capacitance of the system detected by our probe and a dissipative response. Another difference is that the DOS in 0D systems adopts a fully discretized Δ distribution, resulting in the observation in constant-height Δf*/E* maps of Coulomb rings,17,20−22 whose diameter depends on the local (X,Y,Z) position of the AFM tip with respect to the QD.

Figure 4g shows a series of exemplary Δf*/E* maps acquired at the constant height Z = 0.75 nm (position which is marked by a red arrow in Figure 4d) above the β-superlattice. The dissipation map at V = V* (bottom right panel) reveals no ring features but instead a strong homogeneous dissipation background above the molecular assembly that vanishes on the Ag(111) surface, implying that the dissipation arises from charging/discharging states induced by the molecular lattice. When Vtip ≠ V*, no site-dependent dissipation is observed between the tip and sample (top right panel), which proves that any dissipation signal detected at such a large tip–sample distance is not related to topographic variations in the molecular lattice. The absence of Coulomb rings at V = V* further confirms the two-dimensional nature of the electron confinement in the α- and β-lattices, giving rise to delocalized wave functions throughout both superlattices (Figure 8 in the Supporting Information), in contrast to an array of weakly coupled quantum dots. This is in strong analogy to our previous work reporting energy dissipation above a reduced reconstruction of SrTiO3, where the observed dissipation peaks were attributed to tip-induced charge and spin state transitions in an ensemble of quantum-dot-like entities formed by oxygen vacancies.24

From the dissipation data, we also inferred the charge transfers between the superlattice’s eigenstates and the substrate, resulting in the filling (unfilling) of the ψ (ψ*) minibands. As charges may switch back and forth at the voltage threshold V*, we estimated the tunneling rate Γ to be on the orders of about 65 and 420 kHz for the α- and β-superlattices, respectively (see the Experimental Section and Text 5 and Figure 14 in the Supporting Information). Note also that the overestimation of the dissipation magnitude in our experiments might lead to a substantial decrease of these extracted tunneling rates (eq 17 in Text 5 in the Supporting Information). We assume that these values might refer to a resonant tunneling between artificial atoms or between the minibands of the superlattice. Since electrons are more confined in the α-lattice, the frequency of fluctuating currents is expected to decrease as compared to the β-lattice.

Conclusions

In summary, we characterized using low-temperature (4.8 K) scanning tunneling microscopy (STM) and atomic force microscopy (AFM) combined with density functional theory (DFT) and a deep-learning neural network (DPNN) potential model two crystalline nanoporous networks formed on a Ag(111) surface by self-assembling pyrene-2,7-dione molecules. Scanning tunneling spectroscopy shows the confinement of the surface electrons into the pores of the molecular networks, leading to levels shifted upward by 0.1–0.3 eV above the Fermi level. As a result of the strong coupling between these artificial atoms, the confined levels form bonding/antibonding states, leading to the formation of an occupied and an unoccupied band delocalized over the lattice.31,32 Force (dissipation) versus voltage spectroscopy acquired above the lattices systematically shows steps (peaks) at both voltage polarities similar to charging/discharging events in 0D quantum dots by local tip gating. We interpret this phenomenon as a change of the band occupancy induced by electrostatic gating from the AFM tip, which is rationalized using a capacitance model that includes the capacitance of the substrate and tip as well as the quantum capacitance of the confined states. While STM is known to be very useful for the design and spectral characterization of designer quantum states in artificial lattices,2 our results thus demonstrate that AFM could serve as a complementary technique enabling the investigation of exotic electronic effects induced by electrostatic gating and quantify their quantum capacitance. We foresee that AFM spectroscopy will not only allow the local gating of artificial lattices on metals but also induce a quantum phase transition in dual-gated heterostructure devices where a back-gate voltage can be additionally applied.37

Experimental Section

Molecule Synthesis

2,7-Dihydroxypyrene (DHP) was prepared according to literature procedures.38

Sample Preparation

An Ag(111) single crystal purchased from Mateck GmbH was cleaned by several sputtering and annealing cycles under ultrahigh vacuum (UHV). DHP molecules were evaporated from a quartz crucible onto the silver substrate annealed at ∼500 K. The evaporation rate was controlled using a quartz microbalance.

STM/AFM Experiments

STM/AFM experiments were carried out at 4.8 K with an Omicron GmbH low-temperature STM/AFM instrument operated with Nanonis RC5 electronics. We used commercial tuning fork sensors in the qPlus configuration (f0 = 26 kHz, Q = 7000–25000, nominal spring constant k = 1800 N m–1). The constant-height AFM images were acquired with CO-terminated tips using the noncontact mode with an oscillation amplitude Aosc of 50 pm. The AFM spectroscopy has been carried out with oscillation amplitudes of about 70 pm using silver-coated tips, which we obtain by gently indenting the tip apex to the silver substrate prior to experiments. Differential conductance measurements were carried out with the lock-in technique (lock-in frequency f = 540 Hz, modulation amplitude Amod = 6 mV).

DFT Calculations

Density functional theory (DFT) calculations were performed with the Quickstep code39 within the CP2K package, using a mixed Gaussian and plane waves basis set, the Goedecker, Teter, and Hutter (GTH) pseudopotentials,40 and a GGA-PBE41 exchange-correlation functional including self-consistently the van der Waals (vdW) interaction. We used a plane-wave basis energy cutoff of 500 Ry. To deal with the metallic configurations, we adopted a 0.22 eV Fermi Dirac smearing of the occupation number (electronic temperature 2500 K) around the Fermi energy. The Ag(111) substrate was modeled as a periodically repeated slab of four layers, adding a vacuum gap of 15 Å between the adsorbed molecule and the bottom layer of the slab above. Structural relaxations were considered completed when the atomic forces reached 0.02 eV/Å. Depending on the lateral dimension of the slab cell (a), we used k-point grids of k × k × 1 to sample the Brillouin zone and made sure that k × a > 50.

The relative stability of the supported molecules compared to their gas-phase counterparts is given by (taking DHP as an example)

graphic file with name nn2c05333_m003.jpg 1

where GDHP/(111), G(111), and GDHP are the free energies of the surface with an adsorbed DHP molecule, a clean Ag (111) surface, and a gas-phase DHP molecule, respectively.

The phase diagram of adsorbed trimers was calculated based on the method of ab initio atomistic thermodynamics.42 The Gibbs free energy in gas phase at temperature T and partial pressure P is given by

graphic file with name nn2c05333_m004.jpg 2

where EDFT is the energy calculated by DFT at 0 K, EZPE is the zero-point energy, P0 is the standard pressure, and ΔG(T, P0) includes the contributions from translational, rotational, vibrational and electronic free energy terms of the species under consideration. The detailed derivation for ΔG(T, P0) can be found elsewhere.43 These were implemented in the Atomic Simulation Environment (ASE) Python package.44 The change of the Gibbs free energy of the solid phase with T and P is much smaller compared to the gas phase, and it is therefore neglected in this study.

Deep-Learning NN Potential Model

In the present work, the deep-learning neural network (DPNN) potential was constructed using the DeepPot-SE model proposed by Zhang et al.45 In this model, the total potential energy (E) of a system is the sum of atomic energies (Ei) depending on the local environment of atom i within a smooth cutoff radius Rc. Ei is constructed in two steps. First, for each atom a set of symmetry-preserving descriptors is constructed. Next, this information is given as input to a DNN, which returns Ei as the output. The additive form of E naturally preserves the extensive character of the potential energy. The NN potential was trained with the DeepMD-kit package.45 The cutoff radius smoothly decays from 5.5 to 6.5 Å. We used three hidden layers with (25, 50, 100) nodes/layer for the embedding network and three hidden layers with (240, 240, 240) nodes/layer for the fitting network. The learning rate decays from 1.0 × 10–3 to 3.5 × 10–8. The prefactors of the energy and the force terms in the loss function change from 0.02 to 1 and from 1000 to 10, respectively.

Dissipation Spectroscopy

We simultaneously acquired the frequency shift Δf(V) and the excitation amplitude Aexc required to constantly keep the oscillation amplitude of the tip in interaction with the sample above the α- and β-lattices at the tip–sample separation Z. The dissipated energy per oscillation cycle Ediss is extracted from Aexc with the formula

graphic file with name nn2c05333_m005.jpg 3

where k is the tuning fork stiffness, A the oscillation amplitude of the tip, and Q the intrinsic quality factor.46Aexc,0 refers to the excitation amplitude at the contact potential difference far from the surface. The dissipation maps Ediss(Z,Vtip) consist of 58 × 512 and 72 × 512 pixels2, respectively. We extract the tunneling rates Γ from the Ediss(Δf) plots using the formula17,47

graphic file with name nn2c05333_m006.jpg 4

where δf is the full width at half-maximum of the Ediss(Δf) curve and Ediss the maximum dissipation (Text 5 and Figure 14 in the Supporting Information).

Acknowledgments

We thank the Swiss National Science Foundation (SNF) and the Swiss Nanoscience Institute (SNI). E.M. and R.P. acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ULTRADISS grant agreement no. 834402 and supports as a part of NCCR SPIN, a National Centre of Competence (or Excellence) in Research, funded by the Swiss National Science Foundation (grant no. 51NF40-180604)O. S.-X.L. acknowledges the grant from the SNF (200021_204053). X.W. and U.A. acknowledge funding by the SNF Professorship (grant no. PP00P2_187185/2). Calculations were performed on UBELIX (http://www.id.unibe.ch/hpc), the HPC cluster at the University of Bern. X.L. acknowledges grants from the Natural Science Foundation of Zhejiang Province (LQ22B040003) and the National Natural Science Foundation of China (22105172).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.2c05333.

  • Additional STM images and STS data of the α- and β-superlattices, molecular assemblies obtained using DFT and a deep-learning neural network (DPNN), field-emission resonance tunneling spectra, mechanical dissipation above the pristine Ag(111), simulation of a 1D-periodic array of quantum wells using a periodic Kronig–Penney model, details on the fit procedure of the Δf(V) spectra considering the quantum capacitance, extraction of the tunneling rates from the dissipation data, determination of the lever arm, and additional references (PDF)

Author Present Address

§ Key Laboratory of Surface & Interface Science of Polymer Materials of Zhejiang Province, Department of Chemistry, Zhejiang Sci-Tech University, 928 Second Street, Hangzhou 310018, People’s Republic of China

Author Contributions

R.P., S.D., S.-X.L., and E.M. conceived the experiments. X.L., S.-X.L., and S.D. synthesized the monomer. P.D. and R.P. performed the STM/AFM measurements. U.A. and X.W. performed the DFT calculations. R.P., M.K., A.B., and E.M. analyzed the data. R.P. wrote the manuscript. All authors discussed the results and revised the manuscript.

The authors declare no competing financial interest.

Supplementary Material

nn2c05333_si_001.pdf (19.4MB, pdf)

References

  1. Crommie M. F.; Lutz C. P.; Eigler D. M. Confinement of Electrons to Quantum Corrals on a Metal Surface. Science 1993, 262, 218–220. 10.1126/science.262.5131.218. [DOI] [PubMed] [Google Scholar]
  2. Khajetoorians A. A.; Wegner D.; Otte A. F.; Swart I. Creating designer quantum states of matter atom-by-atom. Nat. Rev. Phys. 2019, 1, 703–715. 10.1038/s42254-019-0108-5. [DOI] [Google Scholar]
  3. Stilp F.; Bereczuk A.; Berwanger J.; Mundigl N.; Richter K.; Giessibl F. J. Very weak bonds to artificial atoms formed by quantum corrals. Science 2021, 372, 1196–1200. 10.1126/science.abe2600. [DOI] [PubMed] [Google Scholar]
  4. Lobo-Checa J.; Matena M.; Müller K.; Dil J. H.; Meier F.; Gade L. H.; Jung T. A.; Stöhr M. Band Formation from Coupled Quantum Dots Formed by a Nanoporous Network on a Copper Surface. Science 2009, 325, 300–303. 10.1126/science.1175141. [DOI] [PubMed] [Google Scholar]
  5. Piquero-Zulaica I.; Lobo-Checa J.; Sadeghi A.; El-Fattah Z. M. A.; Mitsui C.; Okamoto T.; Pawlak R.; Meier T.; Arnau A.; Ortega J. E.; Takeya J.; Goedecker S.; Meyer E.; Kawai S. Precise engineering of quantum dot array coupling through their barrier widths. Nat. Commun. 2017, 8, 787. 10.1038/s41467-017-00872-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gomes K. K.; Mar W.; Ko W.; Guinea F.; Manoharan H. C. Designer Dirac fermions and topological phases in molecular graphene. Nature 2012, 483, 306–310. 10.1038/nature10941. [DOI] [PubMed] [Google Scholar]
  7. Kempkes S. N.; Slot M. R.; Freeney S. E.; Zevenhuizen S. J. M.; Vanmaekelbergh D.; Swart I.; Smith C. M. Design and characterization of electrons in a fractal geometry. Nat. Phys. 2019, 15, 127–131. 10.1038/s41567-018-0328-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Drost R.; Ojanen T.; Harju A.; Liljeroth P. Topological states in engineered atomic lattices. Nat. Phys. 2017, 13, 668–671. 10.1038/nphys4080. [DOI] [Google Scholar]
  9. Slot M. R.; Gardenier T. S.; Jacobse P. H.; van Miert G. C. P.; Kempkes S. N.; Zevenhuizen S. J. M.; Smith C. M.; Vanmaekelbergh D.; Swart I. Experimental realization and characterization of an electronic Lieb lattice. Nat. Phys. 2017, 13, 672–676. 10.1038/nphys4105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gardenier T. S.; van den Broeke J. J.; Moes J. R.; Swart I.; Delerue C.; Slot M. R.; Smith C. M.; Vanmaekelbergh D. p Orbital Flat Band and Dirac Cone in the Electronic Honeycomb Lattice. ACS Nano 2020, 14, 13638–13644. 10.1021/acsnano.0c05747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Telychko M.; Li G.; Mutombo P.; Soler-Polo D.; Peng X.; Su J.; Song S.; Koh M. J.; Edmonds M.; Jelínek P.; Wu J.; Lu J. Ultrahigh-yield on-surface synthesis and assembly of circumcoronene into a chiral electronic Kagome-honeycomb lattice. Sci. Adv. 2021, 7, eabf0269. 10.1126/sciadv.abf0269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Li H.; Li S.; Regan E. C.; Wang D.; Zhao W.; Kahn S.; Yumigeta K.; Blei M.; Taniguchi T.; Watanabe K.; Tongay S.; Zettl A.; Crommie M. F.; Wang F. Imaging two-dimensional generalized Wigner crystals. Nature 2021, 597, 650–654. 10.1038/s41586-021-03874-9. [DOI] [PubMed] [Google Scholar]
  13. Ugajin R. Mott metal-insulator transition driven by an external electric field in coupled quantum dot arrays and its application to field effect devices. J. Appl. Phys. 1994, 76, 2833–2836. 10.1063/1.357518. [DOI] [Google Scholar]
  14. Giessibl F. J. The qPlus sensor, a powerful core for the atomic force microscope. Rev. Sci. Instrum. 2019, 90, 011101. 10.1063/1.5052264. [DOI] [PubMed] [Google Scholar]
  15. Gross L.; Mohn F.; Moll N.; Liljeroth P.; Meyer G. The chemical structure of a molecule resolved by atomic force microscopy. Science 2009, 325, 1110–1114. 10.1126/science.1176210. [DOI] [PubMed] [Google Scholar]
  16. Stomp R.; Miyahara Y.; Schaer S.; Sun Q.; Guo H.; Grutter P.; Studenikin S.; Poole P.; Sachrajda A. Detection of Single-Electron Charging in an Individual InAs Quantum Dot by Noncontact Atomic-Force Microscopy. Phys. Rev. Lett. 2005, 94, 056802. 10.1103/PhysRevLett.94.056802. [DOI] [PubMed] [Google Scholar]
  17. Cockins L.; Miyahara Y.; Bennett S. D.; Clerk A. A.; Studenikin S.; Poole P.; Sachrajda A.; Grutter P. Energy levels of few-electron quantum dots imaged and characterized by atomic force microscopy. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 9496. 10.1073/pnas.0912716107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gross L.; Mohn F.; Liljeroth P.; Repp J.; Giessibl F. J.; Meyer G. Measuring the Charge State of an Adatom with Noncontact Atomic Force Microscopy. Science 2009, 324, 1428. 10.1126/science.1172273. [DOI] [PubMed] [Google Scholar]
  19. Steurer W.; Fatayer S.; Gross L.; Meyer G. Probe-based measurement of lateral single-electron transfer between individual molecules. Nat. Commun. 2015, 6, 8353. 10.1038/ncomms9353. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kocić N.; Weiderer P.; Keller S.; Decurtins S.; Liu S.-X.; Repp J. Periodic Charging of Individual Molecules Coupled to the Motion of an Atomic Force Microscopy Tip. Nano Lett. 2015, 15, 4406–4411. 10.1021/acs.nanolett.5b00711. [DOI] [PubMed] [Google Scholar]
  21. Scheuerer P.; Patera L. L.; Repp J. Manipulating and Probing the Distribution of Excess Electrons in an Electrically Isolated Self-Assembled Molecular Structure. Nano Lett. 2020, 20, 1839–1845. 10.1021/acs.nanolett.9b05063. [DOI] [PubMed] [Google Scholar]
  22. Berger J.; Ondráček M.; Stetsovych O.; Malý P.; Holý P.; Rybáček J.; Švec M.; Stará I. G.; Mančal T.; Starý I.; Jelínek P. Quantum dissipation driven by electron transfer within a single molecule investigated with atomic force microscopy. Nat. Commun. 2020, 11, 1337. 10.1038/s41467-020-15054-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Langer M.; Kisiel M.; Pawlak R.; Pellegrini F.; Santoro G. E.; Buzio R.; Gerbi A.; Balakrishnan G.; Baratoff A.; Tosatti E.; Meyer E. Giant frictional dissipation peaks and charge-density-wave slips at the NbSe2 surface. Nat. Mater. 2014, 13, 173–177. 10.1038/nmat3836. [DOI] [PubMed] [Google Scholar]
  24. Kisiel M.; Brovko O. O.; Yildiz D.; Pawlak R.; Gysin U.; Tosatti E.; Meyer E. Mechanical dissipation from charge and spin transitions in oxygen-deficient SrTiO3 surfaces. Nat. Commun. 2018, 9, 2946. 10.1038/s41467-018-05392-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Giannazzo F.; Sonde S.; Raineri V.; Rimini E. Screening Length and Quantum Capacitance in Graphene by Scanning Probe Microscopy. Nano Lett. 2009, 9, 23–29. 10.1021/nl801823n. [DOI] [PubMed] [Google Scholar]
  26. Luryi S. Quantum capacitance devices. Appl. Phys. Lett. 1988, 52, 501–503. 10.1063/1.99649. [DOI] [Google Scholar]
  27. Piquero-Zulaica I.; Lobo-Checa J.; El-Fattah Z. M. A.; Ortega J. E.; Klappenberger F.; Auwärter W.; Barth J. V.. Engineering interfacial quantum states and electronic landscapes by molecular nanoarchitectures. 2021, 2107.10141v1. arXiv. https://arxiv.org/abs/2107.10141 (assesed July 21, 2021).
  28. Kwapiński T.; Jałochowski M. Signature of tip electronic states on tunneling spectra. Surf. Sci. 2010, 604, 1752–1756. 10.1016/j.susc.2010.06.026. [DOI] [Google Scholar]
  29. Limot L.; Pehlke E.; Kröger J.; Berndt R. Surface-State Localization at Adatoms. Phys. Rev. Lett. 2005, 94, 036805. 10.1103/PhysRevLett.94.036805. [DOI] [PubMed] [Google Scholar]
  30. Sperl A.; Kröger J.; Berndt R.; Franke A.; Pehlke E. Evolution of unoccupied resonance during the synthesis of a silver dimer on Ag(111). New J. Phys. 2009, 11, 063020. 10.1088/1367-2630/11/6/063020. [DOI] [Google Scholar]
  31. Seufert K.; Auwarter W.; Garcia de Abajo F. J.; Ecija D.; Vijayaraghavan S.; Joshi S.; Barth J. V. Controlled Interaction of Surface Quantum-Well Electronic States. Nano Lett. 2013, 13, 6130–6135. 10.1021/nl403459m. [DOI] [PubMed] [Google Scholar]
  32. Peng X.; Mahalingam H.; Dong S.; Mutombo P.; Su J.; Telychko M.; Song S.; Lyu P.; Ng P. W.; Wu J.; Jelínek P.; Chi C.; Rodin A.; Lu J. Visualizing designer quantum states in stable macrocycle quantum corrals. Nat. Commun. 2021, 12, 5895. 10.1038/s41467-021-26198-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Cui X.; Wang C.; Argondizzo A.; Garrett-Roe S.; Gumhalter B.; Petek H. Transient excitons at metal surfaces. Nat. Phys. 2014, 10, 505–509. 10.1038/nphys2981. [DOI] [Google Scholar]
  34. Kawai S.; Glatzel T.; Such B.; Koch S.; Baratoff A.; Meyer E. Energy dissipation in dynamic force microscopy on KBr(001) correlatedwith atomic-scale adhesion phenomena. Phys. Rev. B 2012, 86, 245419. 10.1103/PhysRevB.86.245419. [DOI] [Google Scholar]
  35. Labuda A.; Miyahara Y.; Cockins L.; Grütter P. H. Decoupling conservative and dissipative forces in frequency modulation atomic force microscopy. Phys. Rev. B 2011, 84, 125433. 10.1103/PhysRevB.84.125433. [DOI] [Google Scholar]
  36. Yildiz D.; Kisiel M.; Gysin U.; Gürlü O.; Meyer E. Mechanical dissipation via image potential states on a topological insulator surface. Nat. Mater. 2019, 18, 1201–1206. 10.1038/s41563-019-0492-3. [DOI] [PubMed] [Google Scholar]
  37. Kim S.; Schwenk J.; Walkup D.; Zeng Y.; Ghahari F.; Le S. T.; Slot M. R.; Berwanger J.; Blankenship S. R.; Watanabe K.; Taniguchi T.; Giessibl F. J.; Zhitenev N. B.; Dean C. R.; Stroscio J. A. Edge channels of broken-symmetry quantum Hall states in graphene visualized by atomic force microscopy. Nat. Commun. 2021, 12, 2852. 10.1038/s41467-021-22886-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Crawford A. G.; Liu Z.; Mkhalid I. A. I.; Thibault M.-H.; Schwarz N.; Alcaraz G.; Steffen A.; Collings J. C.; Batsanov A. S.; Howard J. A. K.; Marder T. B. Synthesis of 2- and 2,7-Functionalized Pyrene Derivatives: An Application of Selective C-H Borylation. Chem. - A Eur. J. 2012, 18, 5022–5035. 10.1002/chem.201103774. [DOI] [PubMed] [Google Scholar]
  39. VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
  40. Goedecker S.; Teter M.; Hutter J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. 10.1103/PhysRevB.54.1703. [DOI] [PubMed] [Google Scholar]
  41. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  42. Reuter K.; Scheffler M. First-Principles Atomistic Thermodynamics for Oxidation Catalysis: Surface Phase Diagrams and Catalytically Interesting Regions. Phys. Rev. Lett. 2003, 90, 046103. 10.1103/PhysRevLett.90.046103. [DOI] [PubMed] [Google Scholar]
  43. Reuter K.; Stampf C.; Scheffler M.. Handbook of Materials Modeling: Methods; Springer Netherlands: 2005; pp 149–194. [Google Scholar]
  44. Larsen A. H.; et al. The atomic simulation environment—a Python library for working with atoms. J. Phys. Condens. Mater. 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  45. Zhang L.; Han J.; Wang H.; Car R.; Weinan E. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett. 2018, 120, 143001. 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
  46. Anczykowski B.; Gotsmann B.; Fuchs H.; Cleveland J. P.; Elings V. B. How to measure energy dissipation in dynamic mode atomic force microscopy. Appl. Surf. Sci. 1999, 140, 376–382. 10.1016/S0169-4332(98)00558-3. [DOI] [Google Scholar]
  47. Zhu J.; Brink M.; McEuen P. L. Single-Electron Force Readout of Nanoparticle Electrometers Attached to Carbon Nanotubes. Nano Lett. 2008, 8, 2399–2404. 10.1021/nl801295y. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn2c05333_si_001.pdf (19.4MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES