Full Body Musculoskeletal Model for Simulations of Gait in Persons with Transtibial Amputation

Abstract

This paper describes the development, properties, and evaluation of a musculoskeletal model that reflects the anatomical and prosthetic properties of a transtibial amputee using OpenSim. Average passive prosthesis properties were used to develop CAD models of a socket, pylon, and foot to replace the lower leg. Additional degrees of freedom (DOF) were included in each joint of the prosthesis for potential use in a range of research areas, such as socket torque and socket pistoning. The ankle has three DOFs to provide further generality to the model. Seven transtibial amputee subjects were recruited for this study. 3D motion capture, ground reaction force, and electromyographic (EMG) data were collected while participants wore their prescribed prosthesis, and then a passive prototype prosthesis instrumented with a 6-DOF load cell in series with the pylon. The model’s estimates of the ankle, knee, and hip kinematics comparable to previous studies. The load cell provided an independent experimental measure of ankle joint torque, which was compared to inverse dynamics results from the model and showed a 7.7% mean absolute error. EMG data and muscle outputs from OpenSim’s Static Optimization tool were qualitatively compared and showed reasonable agreement. Further improvements to the muscle characteristics or prosthesis-specific foot models may be necessary to better characterize individual amputee gait. The model is open-source and available at (https://simtk.org/projects/biartprosthesis) for other researchers to use to advance our understanding and amputee gait and assist with the development of new lower limb prostheses.

Introduction

Computational musculoskeletal models of human walking are valuable tools to study the biomechanics and neuromuscular coordination of gait. These models, when paired with an appropriate simulation environment, mimic walking with rigid bodies linked by joints that are actuated by dynamic, force producing muscles (Anderson and Pandy, 2001; Zajac et al., 2002). Musculoskeletal simulations can provide noninvasive estimates of physical quantities that are difficult to measure in vivo, e.g., muscle and bone contact forces during walking (Lerner et al., 2015; Trinler et al., 2019). Insights enabled by these models have allowed clinicians and engineers to design novel medical devices, better understand muscle function in clinical populations, and optimize assistive wearable devices (Arnold et al., 2006; Dembia et al., 2017; Homayouni et al., 2015). One clinical population of interest to the musculoskeletal modeling community is people with transtibial limb loss.

Musculoskeletal models have been used to study a variety of research questions relating to transtibial amputee gait. Some researchers have used musculoskeletal models to investigate muscle and bone contact forces during walking and running with a prosthesis (Pickle et al., 2017; Sepp et al., 2021; Silverman and Neptune, 2012; Zmitrewicz et al., 2007). These types of studies aim to link altered muscle and joint function with clinical outcomes like knee osteoarthritis and chronic lower back pain (Silverman and Neptune, 2014; Yoder et al., 2015) and have the potential to inform clinical practice. Others have used modeling techniques to design, optimize, and assess novel prosthetic devices (LaPre et al., 2014; Willson et al., 2021). Another class of modeling studies uses predictive simulation and optimal control theory to study how people with transtibial limb loss coordinate gait in the presence of altered joint and muscle mechanics (Falisse et al., 2019; Miller and Esposito, 2021). For each type of study, access to a high fidelity musculoskeletal model enables novel insights that unavailable to researchers via other experimental methods.

Building a musculoskeletal model of a transtibial amputee is a process that can be subjective and requires significant expertise. Before conducting a modeling study of transtibial amputee gait, researchers usually modify the lower limb of an existing musculoskeletal model by removing the ankle musculature, shortening the shank segment, and replacing the foot and distal shank with a prosthesis model. Inertial properties of the affected limb and prosthesis are also modified to match values reported in the literature (Mattes et al., 2000; Smith and Martin, 2013). However, this process is usually not described in detail, and the resulting model outputs are rarely validated against external measurements.

Few amputee models are publicly available and adequately described to allow other researchers to adopt them with confidence. To date, one open-source transtibial amputee model has been provided to the research community by LaPrè et al (LaPrè et al., 2018) . The model was created for use in OpenSim (Delp et al., 2007) to specifically investigate the interface between the prosthetic socket and residual limb, but the altered mass and inertial properties of the limb were not described and its inverse dynamics outputs were not validated. There still remains a demonstrated need for open-source amputee specific musculoskeletal models for use in inverse dynamics and muscle-driven simulations of amputee gait with detailed descriptions and validations.

The aim of this paper is to provide a detailed explanation to an OpenSim transtibial amputee model we have developed and made open-source (https://simtk.org/projects/biartprosthesis). We provide a detailed description of the model development process and justify our modeling decisions. We also present data from a motion capture experiment with seven transtibial amputee participants intended to validate our model. We compare our model’s joint moment estimates to those computed by in instrumented load cell in-line with the prosthetic pylon, and qualitatively compare our model’s muscle force activations to measured electromyography data.

Model Development

A. Full-body model by Rajagopal et al

The goal of this study was to develop an OpenSim musculoskeletal model of transtibial amputees. To this end, we started with a well-validated full-body OpenSim model, developed by Rajagopal et al (Rajagopal et al., 2016). This model is an improvement on the “gait2354” that comes with the OpenSim package and was used by LaPrè et al (LaPrè et al., 2018). The primary improvements Rajagopal et al. made include cylindrical wrapping to improve computation time, and basing musculotendon parameters not only on cadaveric measurements but also in vivo measurements of muscle (Rajagopal et al., 2016). This model has 37 degrees of freedom (DOF), 20 of which are in the lower body. 80 Hill-type muscles actuate the lower body, and 17 ideal torque actuators drive the upper body. The muscle properties were based on 21 cadavers and MRI images of 24 young healthy subjects. The model represents a 75 kg, 170 cm tall male but can be scaled to match subject-specific measurements.

The Rajagopal model consists of 22 rigid body segments, each defined with a local coordinate system and its joint DOFs. Each muscle is modeled as a massless linear actuator with wrapping and path points to define the line of action for each muscle (Rajagopal et al., 2016). For muscles that fan out anatomically and don’t have a precise line of action, such as gluteus maximus, multiple massless linear actuators were used (Rajagopal et al., 2016). Muscle parameters, such as maximum isometric force, optimal fiber length, and pennation angle were defined using experimentally determined values. Additional musculotendon parameters were defined based on cadaver and MRI imaging studies (Rajagopal et al., 2016).

The Rajagopal model was tested in simulation for both walking and running (Rajagopal et al., 2016). To validate the model’s muscle outputs, Rajagopal et al performed a qualitative comparison of the model’s muscle force outputs and experimentally measured electromyographic (EMG) signals over a single gait cycle. The OpenSim muscle activations matched well with experimental data (Perry et al., 2010), and many of the major features of the EMG signals were represented in the simulated muscle force estimates.

B. Modifications for Transtibial Amputee Model

i. Body Geometry and Joint Definitions.

In OpenSim, each body has its own center of mass (COM) defined in its own local coordinate frame. The intact model has four segments that make up the foot and shank, and the prosthesis model has three (Figure 1) as the foot is one segment in the prosthesis model.

Figure 1.

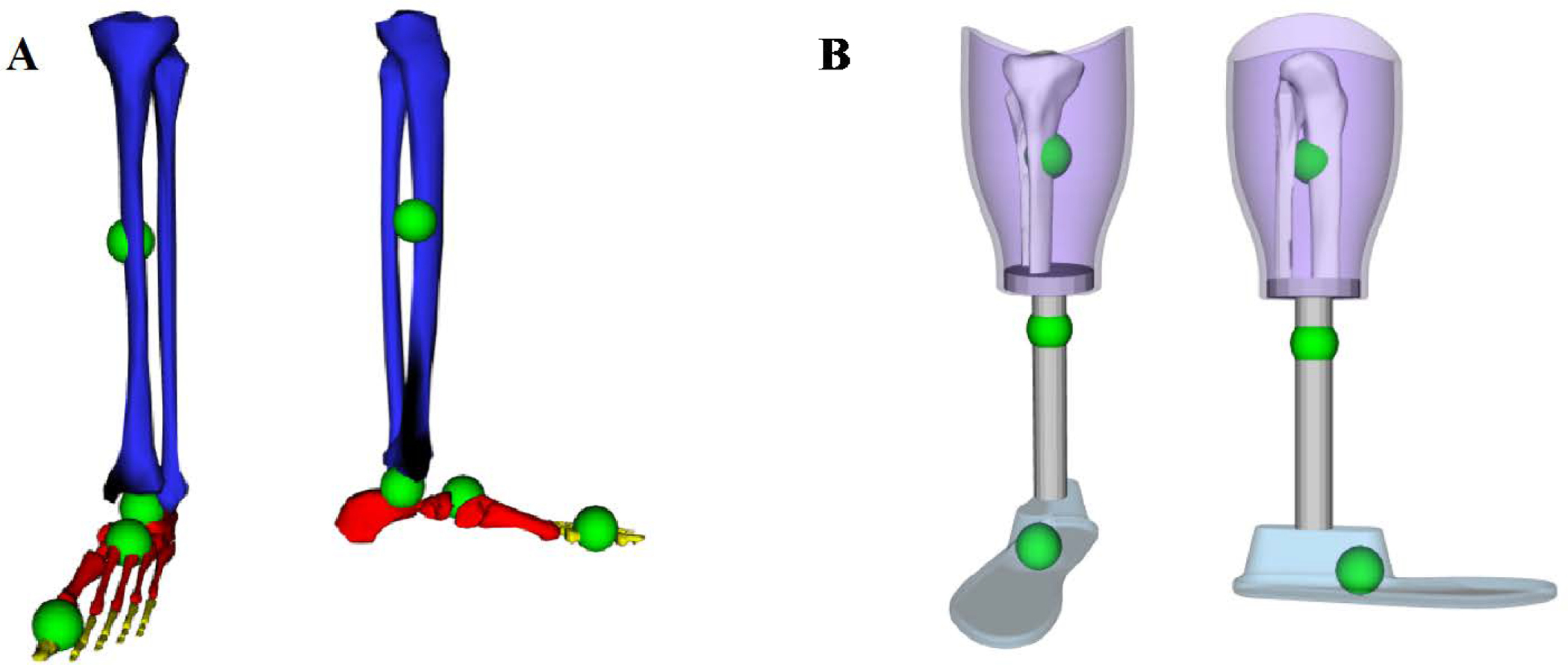
A: Bodies and centers of mass defined as in Rajagopal et al (Rajagopal et al., 2016) for the intact lower limb. Blue is the tibia body, calcn (heel and mid-foot bones) is in red, and the toes body is in yellow. Not visible is talus, which articulates with the tibia and the calcaneus. Green spheres show the center of mass for each body. B: Bodies and centers of mass as defined for the prosthesis. Purple is the socket, gray is the pylon (which includes the transverse plate at the socket-pylon interface), and light blue is the foot. Green spheres show the center of mass for each prosthesis body. Residual tibia and fibula are also shown.

To create a transtibial amputee model in OpenSim, changes were made to the Rajagopal model’s lower leg. SolidWorks (Dassault Systèmes SOLIDWORKS Corp., Waltham MA) CAD models of a generic socket, pylon, and foot were built to match the size of the full body model and dimensioned to represent an amputation at the midpoint of the tibia. The default foot size was set at 27 cm, which is a common foot size for amputees, but can also be scaled to individual subjects like any other body segment. The OpenSim geometry files for the tibia and fibula were modified to resemble a mid-tibia amputation.

To accommodate as many future research interests as possible without making the model unnecessarily complex, additional coordinates were defined between the prosthesis components. The joint between the socket and the residual tibia was given two DOFs: socket internal-external rotation with respect to the tibia, and socket pistoning (superior-inferior translation). Both were locked for this study, but researchers looking at transverse socket torque (Childers and Siebert, 2016; Pew and Klute, 2017) and socket pistoning (Gholizadeh et al., 2014; Noll et al., 2015) may use these DOFs in the future. The pylon is connected to the socket with a single DOF joint that allows the pylon to rotate about the vertical axis with respect to the socket (internal-external rotation), which may also be a DOF of interest in other prosthesis designs (Pew and Klute, 2017). For our study, the socket-pylon joint was locked, as would be standard for most prostheses. Finally, the ankle was defined with three DOF: plantar flexion-dorsiflexion, internal-external rotation, and inversion-eversion. During level walking, prosthesis motion is primarily plantar flexion-dorsiflexion, but these other DOFs have been included for their potential to help answer other research questions (Yeates et al., 2018). Additionally, foot external rotation is a key setting for prosthetists to fit devices to amputees (Fridman et al., 2003). This DOF should generally remain locked, but, as we did in this study, it can be locked to a subject-specific external rotation angle. These modifications were repeated on a second full body model using the other limb, to create both a generic left amputee model and a generic right amputee model.

ii. Mass Properties.

The mass properties of the bodies at the distal leg are substantially different for amputated limbs than intact limbs. Prostheses are lighter weight than intact limbs, and studies into prosthesis mass distribution have found that adding weight to the distal limb, even to match the intact side, have adverse effects (Lin-Chan et al., 2003; Smith and Martin, 2013). As such, it is important to have a model that represents the average mass properties of current prostheses.

To estimate generic residual limb and prosthesis mass properties, we conducted a literature search to obtain population averages across transtibial amputees to inform the final model design. From our literature search, we found the following facts regarding COM and moment of inertia (MOI). The COM for the entire below-knee segment (residual tibia, socket, pylon, and foot) is roughly 30% closer to the knee joint than in intact limbs (Lin-Chan et al., 2003; Mattes et al., 2000; Smith et al., 2014; Smith and Martin, 2013). The COM for the residual limb alone is about 25% of the knee-to-ankle distance below the knee (Silverman and Neptune, 2012). The mass of the residual limb is 50% of the original tibia segment mass, and the total mass for the entire below-knee segment is about 65% that of non-amputees (Silverman and Neptune, 2012). The MOI about the transverse axis through the knee joint is roughly 55% of a non-amputee’s MOI (Lin-Chan et al., 2003; Mattes et al., 2000; Smith et al., 2014; Smith and Martin, 2013).

A series of calculations were performed in MATLAB (The Mathworks, Inc. Natick, MA) to define mass properties for the amputee model. All model COMs below the knee were translated into the same reference frame with the knee at the origin. Once all COM values were in a global reference frame, COMs for all below-knee bodies were combined to obtain the total intact below-knee COM. This location was then moved 30% closer to the knee joint (Lin-Chan et al., 2003; Mattes et al., 2000; Smith et al., 2014; Smith and Martin, 2013). The residual limb mass was set to be half that of the intact tibia body mass, and the residual limb COM was set to 25% of the model’s knee-to-ankle distance (Silverman and Neptune, 2012). The masses and COMs of the socket and pylon were estimated based on SolidWorks models. The necessary mass of the foot segment was then calculated and is comparable to commercially available prostheses (Venture foot, College Park Industries, Warren, MI).

With the new masses and COMs calculated for the amputee model, the MOIs were re-computed to match using the following method. First, the intact MOIs, reported about the center of mass, were translated to moments of inertia about the knee joint center (I_knee), using the Parallel Axis Theorem:

$${\mathit{I}}_{\mathit{k}\mathit{n}\mathit{e}\mathit{e}}={\mathit{I}}_{\mathit{C}\mathit{O}\mathit{M}}+\mathit{M}\mathbf{*}{\mathit{d}}^2$$ (Eq. 1)

where I_COM is the given MOI about the COM, M is the body mass, and d is the distance from the COM to the knee joint center. These MOIs were then reduced by 45% (Lin-Chan et al., 2003; Mattes et al., 2000; Smith et al., 2014; Smith and Martin, 2013). Finally, the Parallel Axis Theorem was used in the reverse direction to resolve for the MOI about the COM, using the calculated masses and COMs for the amputated limb:

$${\mathit{I}}_{\mathit{C}\mathit{O}\mathit{M},\mathit{a}\mathit{m}\mathit{p}}={(0.55\mathrm{*}\mathit{I}}_{\mathit{k}\mathit{n}\mathit{e}\mathit{e}})-{\mathit{M}}_{\mathit{a}\mathit{m}\mathbf{p}}*{{\mathit{d}}_{\mathit{a}\mathit{m}\mathit{p}}}^2$$ (Eq. 2)

These body masses, centers of mass, and moments of inertia were input to the generic amputee OpenSim model files so that the mass properties of the model’s residual limb and prosthesis match best possible estimates of amputated limb mass properties (Figure 1, Table 1).

Table 1.

Segment Mass Properties of OpenSim Model

	Full-Body Model			Amputee Model
Segment Mass (kg)		Tibia		Tibia	Socket	Pylon
		3.71		1.85	0.811	0.180
Segment Mass (kg)	Talus	Caln	Toes		Foot
	0.1	1.25	0.217		0.583

^*Grey denotes segments of the lower leg, white denotes foot segments

iii. Muscle Properties.

Amputees experience several muscle imbalances compared to non-amputees, but these differences vary greatly across individuals with amputation. A study by Nolan et al. looked at the hip flexor and hip extensor strength in active and sedentary amputees and found that active amputees were 8–14% stronger in their residual limb than their intact, but that sedentary amputees were up to 49% weaker in the residual limb compared to the intact limb (Nolan, 2009). Another study investigating transtibial amputee strength found that the residual limb quadriceps were 35–51% weaker than contralateral, and hamstrings were 42–60% weaker (Isakov et al., 1996). Researchers also found no significant differences in strength asymmetries compared across time since amputation. Ryser et al. found a 27% reduction in strength of the residual limb hip abductors of transfemoral amputees, compared to both the intact limb and matched non-amputee subjects (Ryser et al., 1988).

This high variation makes it difficult to settle on a scheme of muscle imbalance for a generic amputee model. Therefore, the default muscle strengths from Rajagopal’s model (Rajagopal et al., 2016) were left unchanged. However, users can change these properties based upon their research question, new data, or patient specific data. For example, ongoing research to improve simulations for heterogeneous populations like CP patients are being investigated that use MRI, muscle synergies, continuum descriptions of muscle, hand-held dynamometers, and other methods (Kainz et al., 2018; Meyer et al., 2016; Sartori et al., 2017).

At the point of amputation, there are also a variety of differences in muscle reattachments. The level of amputation as well as other complications in amputation surgeries affect where and how the residual limb muscles can be reattached. Aside from perhaps the gastrocnemius (GAS), these reattached lower-leg muscles cannot produce functional torques as they no longer span a joint. However, they still contract and can be measured by surface EMG recordings. We were interested in including the GAS in the model, as it can produce a flexion moment at the knee if reattached. However, not enough information was available about the residual muscle specifics of the amputee population or our subject population, so all below-knee muscles were excluded from the amputee model. This leaves the amputee model with 72 Hill-type muscles. The full musculoskeletal amputee model is shown in Figure 2.

Figure 2.

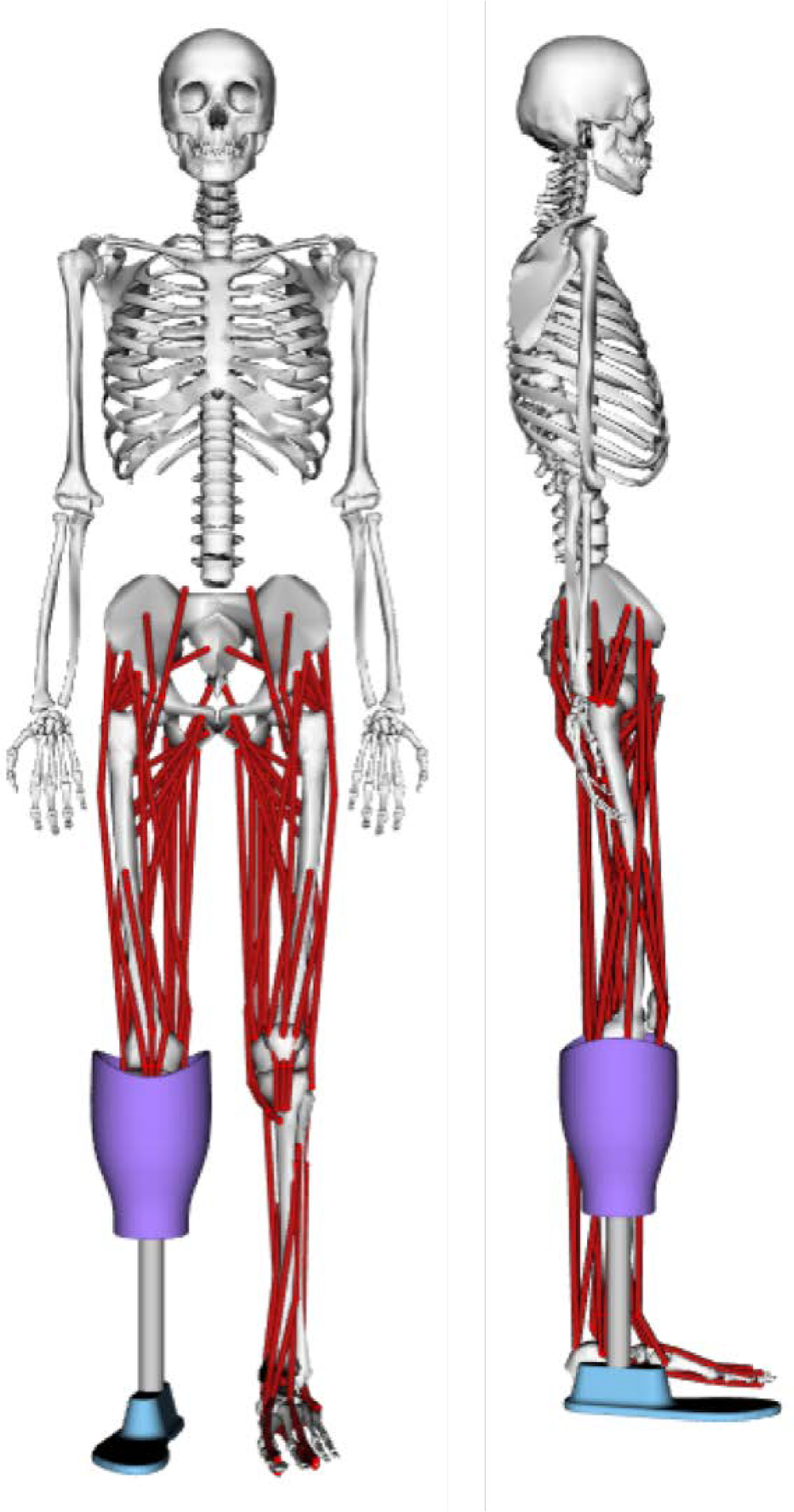
Final amputee musculoskeletal model for OpenSim

C. Guidelines for Other Users

This section aims to highlight a few features and possibilities of the new generic amputee model to aid other researchers. First, because the pylon and socket are included as separate bodies, it is possible to scale them separately. By positioning a marker at the base of the socket, where it meets the pylon, separate scaling factors can be assigned to the residual limb and the pylon. This will allow the scaled model to match the specific subject’s level of amputation and make the scaled mass properties more accurate. An example of this marker placement is shown in Figure 3. The bodyweight of the participant including the prosthesis should be used during model scaling.

Figure 3.

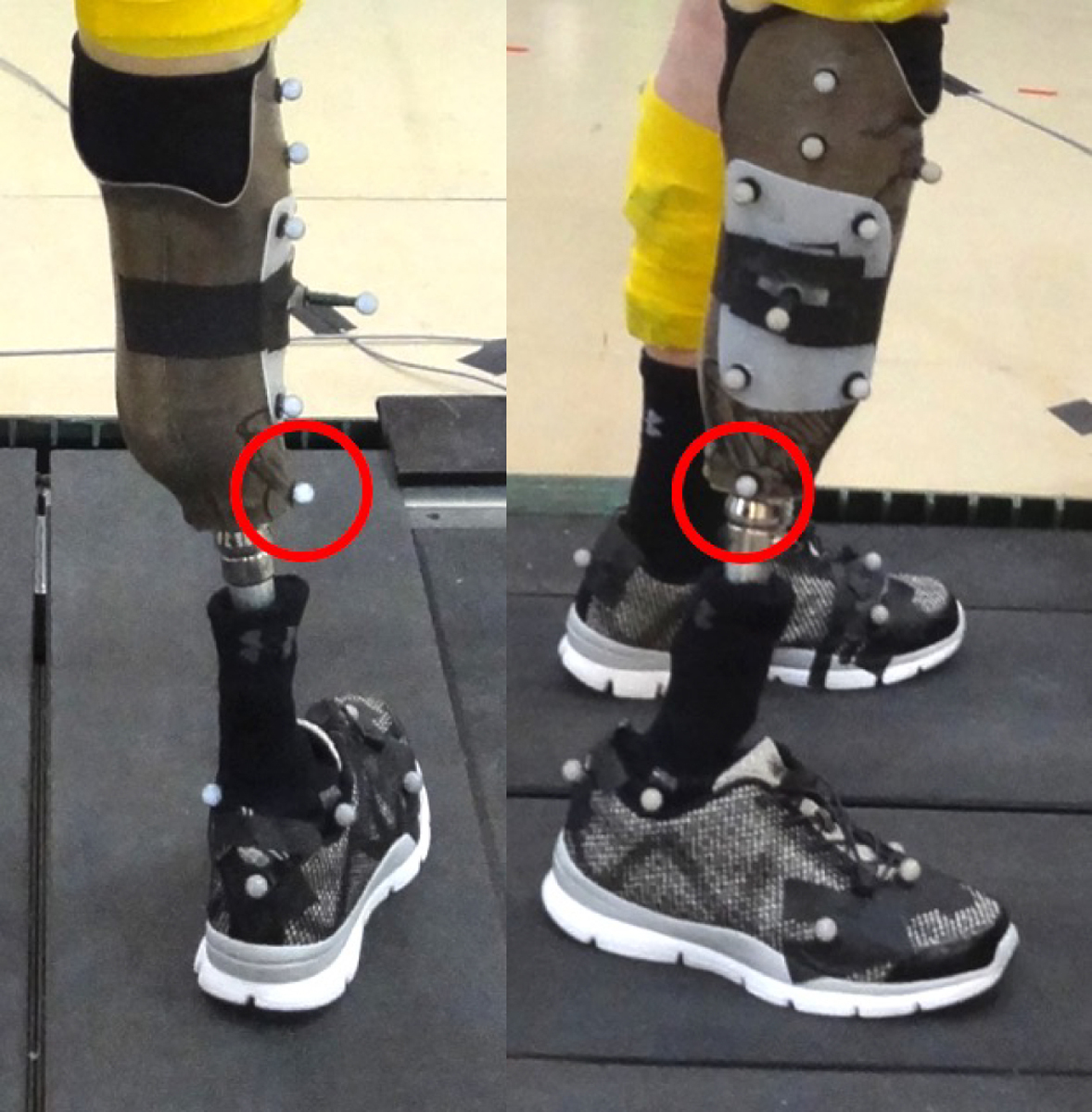
Static trial images showing the placement of the pylon marker. This marker is used in scaling the model to separately scale the residual limb and pylon segments

It is also possible to set a subject-specific ankle external rotation angle using this model. To do so, the external rotation between the pylon and prosthesis could be measured during data collection and manually set as a model parameter. Alternatively, the external rotation angle could be set in the model by unlocking this degree of freedom during the least-squares model scaling procedure. This would allow OpenSim to estimate the external rotation angle based on the marker positions from a static trial. However, the scaling algorithm will minimize global error, so errors from all markers on the body could affect estimates of ankle angle with this method. Once set, the ankle external rotation should be locked at the static pose angle for analysis of the dynamic trials, as this DOF is typically set by the prosthetist and then locked with set screws.

Experimental Methods

A. Subject Demographics

With VA Puget Sound Health Care System and University of Washington IRB approval, seven subjects with unilateral transtibial amputation were recruited through the VA Puget Sound Health Care System. Demographic data for the subjects are summarized in Table 2. Six subjects were male, and one was female. The mean plus/minus one standard deviation (SD) age was 51 ± 12.3 years, height was 1.78 ± 0.06 m, and weight was 91.5 ± 15.3 kg. Participants chose a comfortable treadmill walking speed (held constant across conditions), with a mean ± SD self-selected walking speed of 0.84 ± 0.22 m/s.

Table 2.

Demographic data for study participants

Subject	Sex	Age	Height (m)	Weight (kg)	Walking Speed (m/s)	Prescribed Prosthesis
1	M	45	1.75	111.6	1	College Park Soleus
2	F	55	1.77	89.4	0.5	not recorded
4	M	63	1.75	87.1	0.9	Ossur Variflex
5	M	59	1.83	105.9	0.8	Ossur Variflex
6	M	63	1.69	74	0.6	College Park Velocity
7	M	31	1.87	100.7	1	Ossur Proflex XC
8	M	41	1.81	71.9	1.1	Ossur Re-flex

B. Data Collection

Subjects wore tight fitting clothing and appropriate footwear for the data collection. Fifteen EMG sensors (Noraxon USA, Inc., Scottsdale, AZ) were placed on major lower-leg muscles on both the intact and amputated limb (Table 3) according to Seniam.org guidelines (Hermens et al., 2000). Low-profile electrodes were used for muscles inside the socket (residual GAS and TA). These muscles are not included in the model and therefore cannot be used in the model evaluation, but the data on in-socket EMG activity may inform future prosthesis designs (Huang and Ferris, 2012; Seyedali et al., 2012). Most EMG sensors were placed with subjects prone and supine on a table with their prosthesis removed, and then subjects stood while wearing their prescribed device as the pairs of gluteus maximus and gluteus medius sensors were placed. Because the muscle reattachments in amputation surgery and the level of amputation on the tibia were not consistent between subjects, soleus on the residual limb was not measured. Location of the medial GAS and TA varied more on the residual limb than the intact limb. As the EMG sensors were placed, voluntary contraction exercises were performed to check the signal-to-noise ratios of each sensor.

Table 3.

EMG placement locations

Sensor Number	Limb	Muscle
1	Residual	Gluteus maximus (GMAX)
2	Residual	Gluteus medius (GMED)
3	Residual	Biceps femoris long head
4	Residual	Rectus femoris (RF)
5	Residual	Vastus medialis origin
6	Residual	Tibialis anterior (TA)
7	Residual	Medial gastrocnemius
9	Intact	Gluteus maximus (GMAX)
10	Intact	Gluteus medius (GMED)
11	Intact	Biceps femoris long head
12	Intact	Rectus femoris (RF)
13	Intact	Vastus medialis origin
14	Intact	Tibialis anterior (TA)
15	Intact	Medial gastrocnemius
16	Intact	Solees (SOL)

Once EMG placement was completed, subjects donned a safety harness, that would later be attached to an overhead rope to prevent falling while walking on the treadmill. The subject was then instrumented with 74 reflective markers in a modified full-body Plug-in Gait marker set. Modifications to the Plug-in Gait set included: clusters on the femur, shank, and humerus (Cappozzo et al., 1997), markers on the tibial tuberosity and fibular head, and additional medial joint markers at the elbow, knee, and ankle. Anthropometric measurements of the shoulder, elbow, wrist, knee, and ankle widths, as well as leg length (anterior superior iliac spine to medial malleolus of the tibia) were measured and recorded.

Motion capture data were collected using a 12-camera Vicon system (Oxford Metrics, Oxford UK) and a side-by-side split belt instrumented treadmill (Bertec Corp., Columbus, OH). A static motion capture trial was collected by having the participant stand in anatomic position, with their arms slightly abducted at the shoulder and their palms facing forward in the middle of the data collection volume. This static trial was used to help label motion capture markers, as well as to scale OpenSim models to match each subject.

To determine self-selected walking speed, participants walked on the treadmill with their prescribed prosthesis at 0.5 m/s and then increased or decreased speed in increments of 0.1 m/s at the subject’s request. The final speed chosen by the participant was used for the rest of the study. Data was collected until we had five 10-second trials where subjects appeared to be walking in steady-state and were centered on the treadmill such that each foot only contacted one force plate.

In addition to their prescribed prosthesis, each subject also walked on a prototype prosthesis. This device uses a College Park Venture foot (College Park, Warren MI) that has a defined axis of plantar-dorsiflexion at the ankle and is equipped with an iPecs load cell (RTC Electronics, Inc., Dexter, MI) in the pylon. This setup allows us to experimentally measure net ankle joint torque and compare it to the OpenSim results (Hicks et al., 2015). After walking on the prescribed prosthesis, participants donned the prototype foot. Several markers on the affected limb had to be removed and replaced for the new device. This device was then tuned by a prosthetist before gait trials were collected. An additional five 10-second trials were collected at self-selected walking speed while wearing the instrumented prototype.

C. OpenSim

After labelling markers in Vicon and preparing files in MATLAB, the amputee musculoskeletal model was used to analyze each participant’s gait data in OpenSim. First, the model was scaled to match each specific subject using OpenSim’s Scale Tool (Delp et al., 2007). Ankle and knee joint centers were included during scaling. Joint kinematics for each trial were calculated using OpenSim’s Inverse Kinematics Tool, with the metatarsophalangeal, subtalar, socket pistoning, socket rotation, and socket-pylon joint coordinates locked in neutral position. The Inverse Dynamics Tool in OpenSim was used to calculate net joint moments, and then SO was run to estimate muscle activations and force outputs from the model.

D. iPecs 6-DOF Force/Torque Processing

When walking with the prototype prosthesis, an iPecs 6-DOF force/torque sensor was placed in series with the pylon and recorded the forces and torques that passed through the 6-DOF sensor. A voltage proportional to the strain gauge voltage for each gauge within the iPecs was streamed wirelessly from the iPecs to the Vicon DAQ, temporally synced with the motion capture data and saved to file. During MATLAB post-processing, a locally calibrated scale factor and offset were applied to convert the logged data to strain gauge volts. Next, a manufacturer calibration matrix was applied to convert strain gauge volts to 6-DOF forces and moments. Finally, a free body diagram was used to convert forces and moments at the iPecs load cell to moments at the ankle joint.

E. EMG Processing

Raw EMG signals were high-pass filtered at 40 Hz using a fourth order, zero-lag Butterworth filter. Any DC offset was then removed using MATLAB’s detrend function. The absolute value of the detrended data was taken, and then a low-pass filter (fourth order, zero-lag Butterworth) with a 10 Hz cutoff frequency was applied. For comparison between EMG data and SO results, both data sets were normalized between 0–1 using the maximum respective signal values during walking with the prescribed prosthesis. Post analysis of the processed EMG signal was performed to confirm good signal-to-noise ratio. Signals that qualitatively look erroneous because of bad contact with the skin or excessive movement artifact where selectively removed from further analysis.

Results

The model produced joint kinematics that are generally consistent with published amputee gait data (Ferris et al., 2012) (Figure 4). There are some small differences in all-subject average kinematics for the prescribed and passive prototype conditions, but these are not significant.

Figure 4.

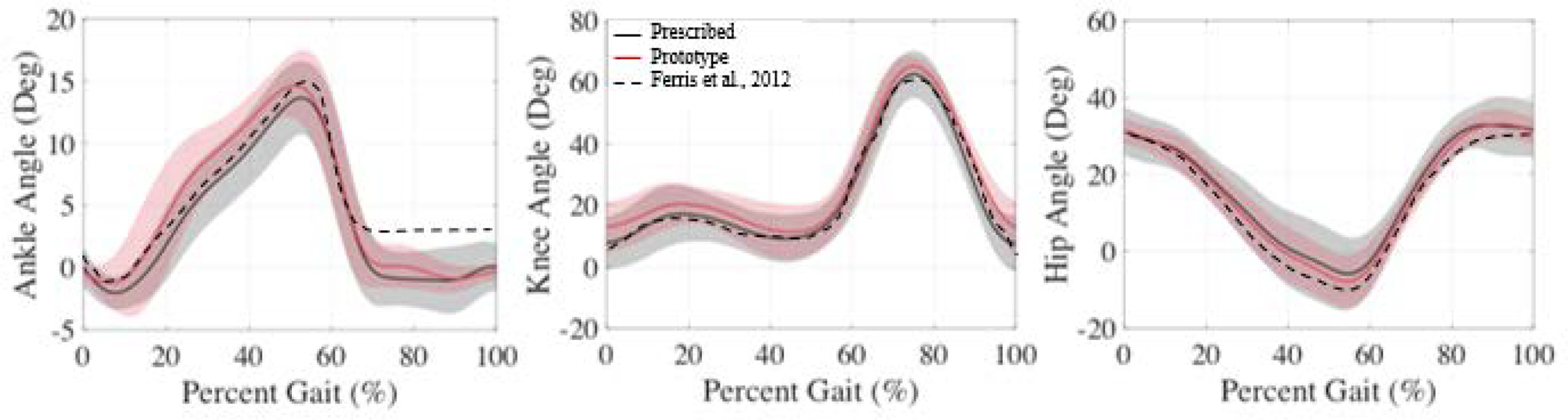
Average affected limb joint kinematics for the prescribed (black), prototype (red), and from (Ferris et al., 2012) for reference. Shaded regions show the standard deviation.

The model’s estimate of ankle torque and the experimental measure of ankle torque via the iPecs sensor were similar for all subjects (Figure 5). The largest errors between OpenSim and iPecs results occurred near maximum ankle plantarflexion torque, at roughly 50% of the gait cycle. Across all subjects, the mean absolute error (Chai and Draxler, 2014) in the OpenSim model’s ankle torque was 0.116 Nm/kg (or 7.7%).

Figure 5.

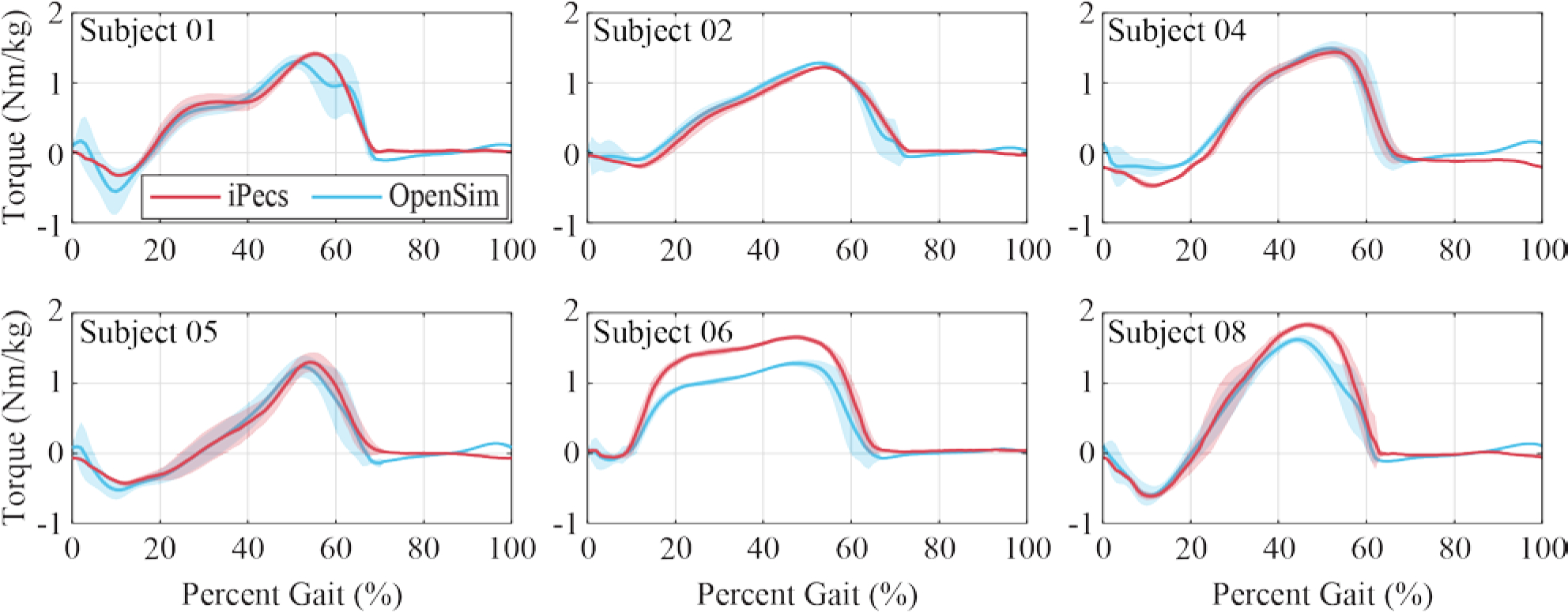
OpenSim inverse dynamics ankle torque calculation, in comparison with the experimentally measured iPecs torque transformed to the ankle joint, for each subject walking on the prototype prosthesis. Shaded regions represent the standard deviation. Subject 7 is not shown because an iPecs malfunction prevented this data from being collected during their session

Similar to prior studies (Rajagopal et al., 2016; Voinescu et al., 2012), a qualitative comparison of the experimentally measured EMG signals and the muscle force outputs from SO in OpenSim was performed to evaluate the amputee musculoskeletal model. Figure 6 shows the average EMG and SO traces over the gait cycle for a representative subject for muscles on the affected limb. Similar plots for all other subjects are provided in supplemental material.

Figure 6.

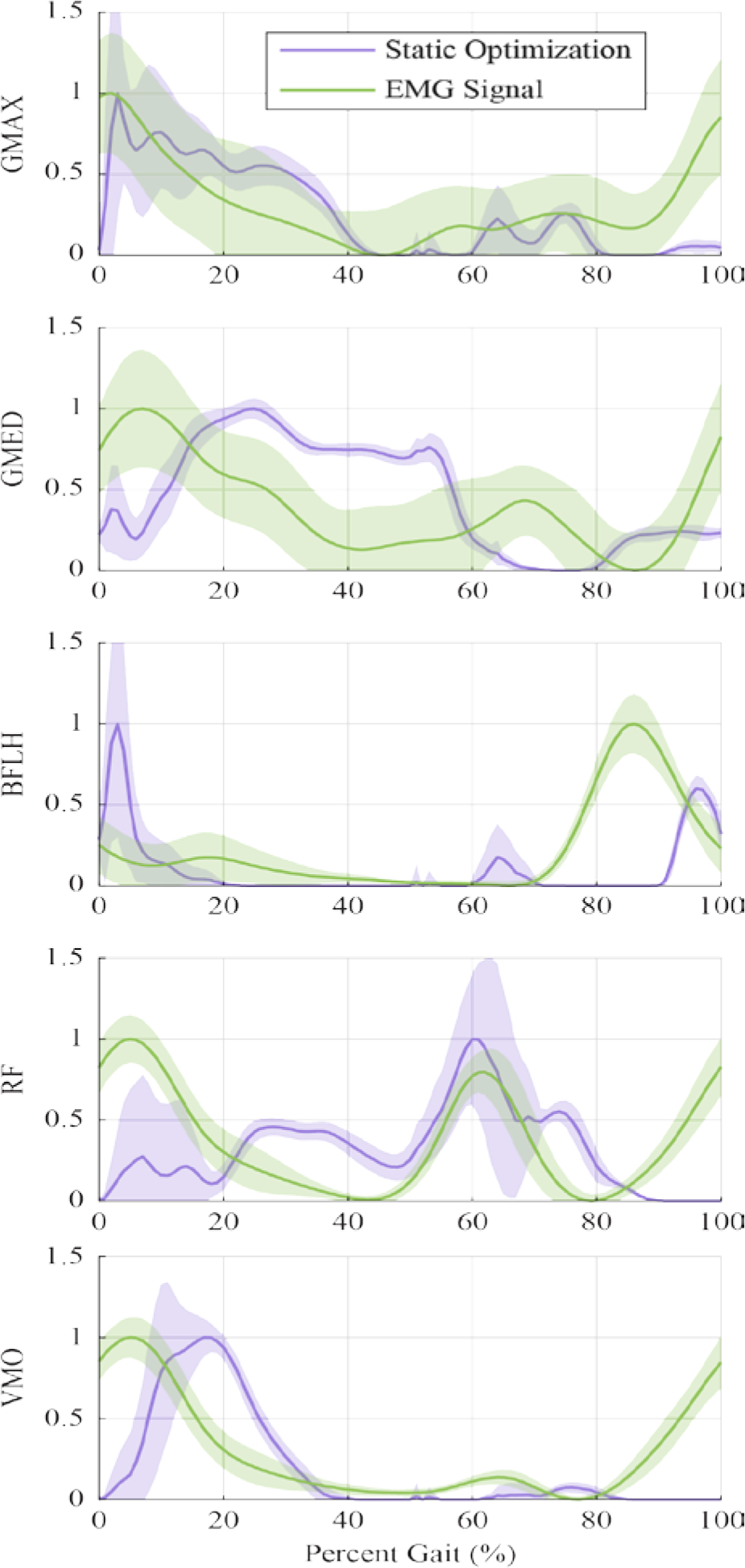
Normalized Static Optimization and EMG outputs of Subject 01 for qualitative comparison, showing only the muscles of the affected limb. Shaded regions represent the standard deviation. Static Optimization outputs for GMAX and GMED were summed across the individual sub-muscle models before normalizing. Similar plots for other subjects can be found in Supplemental Figures.

Overall, the SO results represent many of the large features found in the EMG signals, with a delay commonly seen in this type of comparison (Hicks et al., 2015). Some subjects had low quality EMG signals from muscles such as GMAX, likely because of thicker layers of subcutaneous fat, and thus the comparison for these signals was difficult. There was generally more variability in the EMG measurements between gait cycles than the SO results (Figure 6).

The amputated and intact TA muscles showed similar activation profiles over the gait cycle, while GAS showed more variation when comparing the intact to the amputated muscle (Figure 7). In the GAS measurements, the peak activation of the amputated limb was after 60% of the gait cycle, while the intact limb peaked around 40%. This trend was true for 5 of our 7 subjects, while two subjects showed peak GAS activation at about 40% of the gait cycle for both the intact and amputated limbs. This explains the large standard deviation for the normalized GAS signal in the amputated limb.

Figure 7.

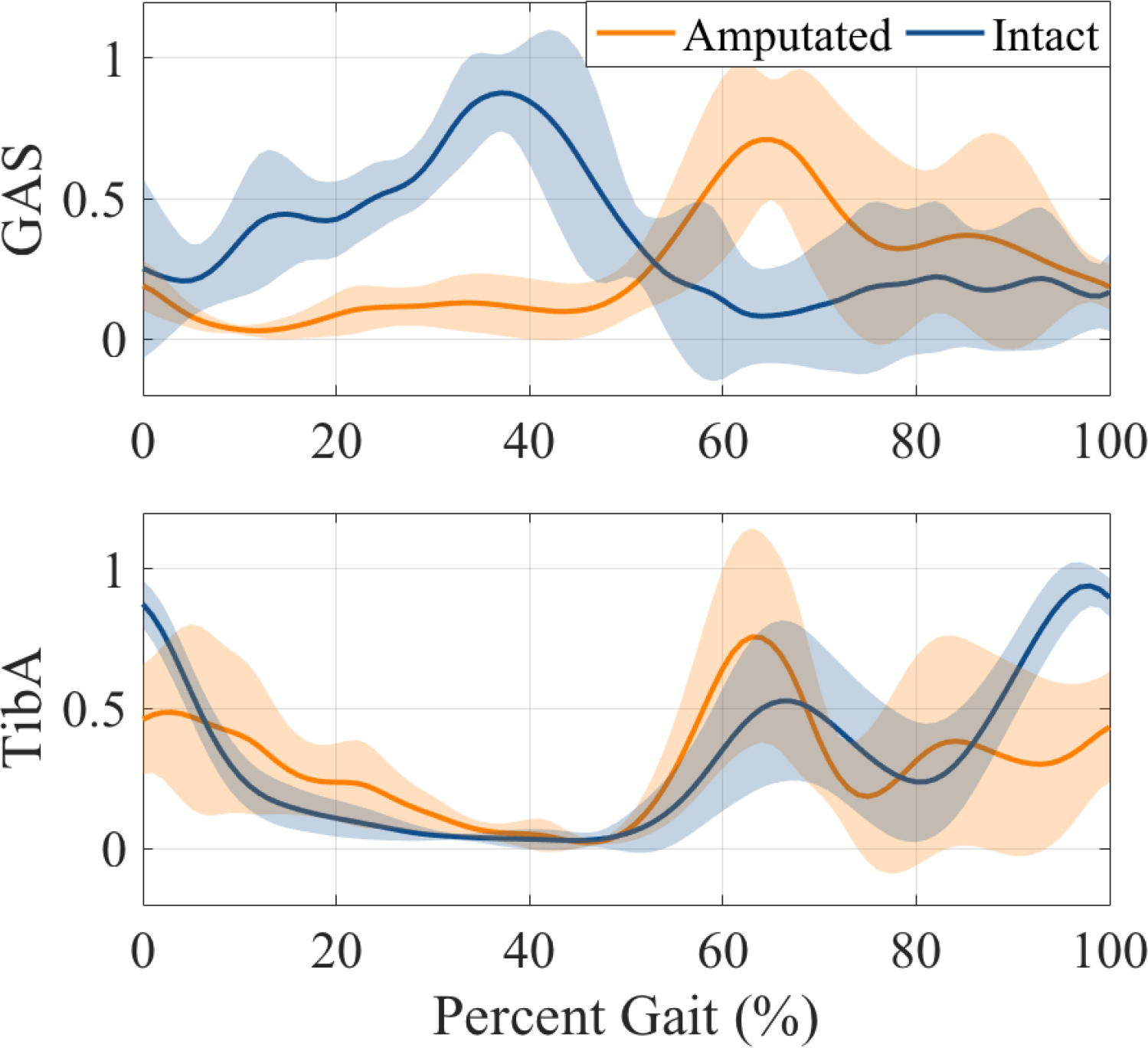
All-subject averages of normalized medial GAS and Tibialis Anterior EMG signals for amputated and intact limbs. Shaded regions show the standard deviation.

Discussion

The ankle torque and EMG data showed reasonable agreement between the OpenSim model outputs and the experimentally measured data. The iPecs-measured torque and the inverse dynamics results from the OpenSim model compare well. The average error was 7.7%, and Figure 5 shows that the two torque curves match well in shape and timing. When validated against traditional inverse dynamic gait analysis methods, the iPecs had a reported RMS error of 5.2% (Koehler et al., 2014). As such, the iPecs cannot be considered a ground truth for comparison of the OpenSim model outputs, but our comparison result of 7.7% error still shows a reasonable correlation. Some of this difference can also be explained by the fact that we do not model soft tissue losses (Zelik and Kuo, 2010). The iPecs validation also notes a particular sensitivity to errors in defining the axes when interpreting iPecs data in another reference frame, as was done here. There was likely some error in translating the iPecs-measured data from the iPecs axis to the ankle for comparison to inverse dynamics results. Subject 06 showed a particularly high mean absolute error (Figure 5), and a misalignment of axes could explain this result.

The comparison of experimental EMG measurements to SO results show that the model adequately simulates many of the dominant features of the measured EMG signals. The higher variation in EMG signals were expected and can be attributed to measurement noise with surface EMG electrodes. While there were distinct features that differed between the EMG data and simulated activations, such as activation of the GMED in early stance, these discrepancies are similar to prior studies of musculoskeletal simulations of unimpaired individuals and likely reflect short-comings of the optimization methods used to estimate muscle activations or muscle length properties (Hamner et al., 2010; Hamner and Delp, 2013; Hicks et al., 2015; Pasdar et al., 2012; Rajagopal et al., 2016). Some of the discrepancies in timing of muscle activations are also likely explained by the high variability of muscle strengths and weaknesses within the amputee population, which were not reflected in our subject-specific models. Identifying appropriate maximum isometric muscle forces for the model also poses a challenge. Given the difficulties of quantifying subject-specific muscle strength variation, we elected to use the maximum isometric muscle forces from the original Rajopagol model. This is a source of model error. Future work will aim to improve upon these muscle parameters, where possible. Other research groups are currently working to improve muscle simulation in other clinical populations like using MRI, strength assessments, or other methods (Kainz et al., 2018; Meyer et al., 2016; Sartori et al., 2017). These works may give insight into modeling the amputee population as well.

Previous EMG studies have shown higher variability in amputee EMG activity, and one study found that residual limb plantar flexors are generally inactive in mid-terminal stance, which is different than the intact limb, or limbs of non-amputees (Huang and Ferris, 2012; Silver-Thorn et al., 2012). This was true for in-socket EMG measurements of the medial GAS in many of our subjects, but not all (Figure 7). This discrepancy between normal GAS activation timing and residual GAS timing may have implications for the development of myoelectric or other electromechanical prosthesis designs, and the variability across individuals with lower limb amputation merits consideration.

Another amputee model for OpenSim was recently published by LaPrè et al. (LaPrè et al., 2018), who explored residuum kinematics and kinetics using up to 6 DOFs at the tibia-socket interface. Notable differences in the structure of this model are the handling of foot bending with a midfoot DOF, their inclusion of the GAS muscle, and their use of the “gait2354” full-body model as a base, as opposed to our use of the Rajagopal model. The model presented here does not separately account for the flexibility of the foot, and this flexion is part of the ankle joint motion. This approach is similar to previous gait studies of non-amputees, where the entire foot segment is considered rigid with locked MTP and subtalar joints (Rajagopal et al., 2016; Steele et al., 2012). Additionally, as mentioned in the Model Development section, GAS reattachment and functionality after amputation is largely unknown, and thus GAS was not included in our model. The in-socket measurements of GAS EMG may contribute to understanding of GAS functionality in transtibial amputees in the future. Additionally, the Rajagopal model used as the foundation of our model features improved computational fidelity and updated muscle force estimates from the “gait2354” used by LaPrè (Rajagopal et al., 2016). Inverse dynamics results at the ankle, knee, and hip compare well between LaPrè et al. and our work. LaPrè et al. do not include full ankle, knee, and hip kinematics or muscle-driven simulations in their work, but the kinematic and muscle driven simulation results presented here do align well with previous work (Ferris et al., 2012; Hamner et al., 2010; Hamner and Delp, 2013). Additionally, we believe the inclusion of the mass and inertial calculations provides valuable transparency to the model to be as easily understood and adopted by other researchers as possible.

There were some limitations to the current functionality of this model. As described previously, the model’s muscle parameters were unaltered from healthy estimates, but individuals with lower-limb amputation exhibit muscle weakness heterogeneously in a variety of muscle groups. Furthermore, this generic amputee model was not analyzed using any running-style prosthetic feet, such as the Flex-Foot Cheetah (Össur Americas, Inc., California USA). Some research has shown that modeling prosthetic ankles as pin joints can be inaccurate and sensitive to marker placement (Fey et al., 2013; Rigney et al., 2016). Although some feet do have a physical pin joint, such as the College Park Venture foot used here, other researchers will need to consider how the model’s ankle pin joint could affect their results, and potentially alter the model for their specific purposes. Additionally, the model in its present form could not be used for forward simulations because the specific energy storage and return characteristics of the foot have not been modeled. Rather, this model generalizes the dynamics of the foot such that inverse dynamics and SO procedures are now available to all researchers of amputee gait.

Conclusion

Computational models are valuable tools for understanding gait, and an amputee-specific model can provide insights within this population. This model has been tested with roughly 35 gait cycles from each of seven individuals with transtibial amputation, both in joint dynamics and estimated muscle activations. Additional testing and analysis by the community is encouraged. Further refinement of the model’s muscle properties is also needed. The model is freely available on our SimTK project page (https://simtk.org/projects/biartprosthesis), and others are invited to make modifications and share them with the community.