The Timing, the Treatment, the Question: Comparison of Epidemiologic Approaches to Minimize Immortal Time Bias in Real-World Data Using a Surgical Oncology Example

Abstract

Background:

Studies evaluating the effects of cancer treatments are prone to immortal time bias that, if unaddressed, can lead to treatments appearing more beneficial than they are.

Methods:

To demonstrate the impact of immortal time bias, we compared results across several analytic approaches (dichotomous exposure, dichotomous exposure excluding immortal time, time-varying exposure, landmark analysis, clone-censor-weight method), using surgical resection among women with metastatic breast cancer as an example. All adult women diagnosed with incident metastatic breast cancer from 2013–2016 in the National Cancer Database were included. To quantify immortal time bias, we also conducted a simulation study where the “true” relationship between surgical resection and mortality was known.

Results:

24,329 women (median age 61, IQR 51–71) were included, and 24% underwent surgical resection. The largest association between resection and mortality was observed when using a dichotomized exposure [HR, 0.54; 95% confidence interval (CI), 0.51–0.57], followed by dichotomous with exclusion of immortal time (HR, 0.62; 95% CI, 0.59–0.65). Results from the time-varying exposure, landmark, and clone-censor-weight method analyses were closer to the null (HR, 0.67–0.84). Results from the plasmode simulation found that the time-varying exposure, landmark, and clone-censor-weight method models all produced unbiased HRs (bias −0.003 to 0.016). Both standard dichotomous exposure (HR, 0.84; bias, −0.177) and dichotomous with exclusion of immortal time (HR, 0.93; bias, −0.074) produced meaningfully biased estimates.

Conclusions:

Researchers should use time-varying exposures with a treatment assessment window or the clone-censor-weight method when immortal time is present.

Impact:

Using methods that appropriately account for immortal time will improve evidence and decision-making from research using real-world data.

Introduction

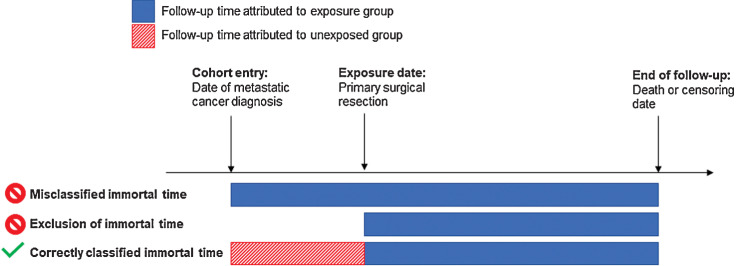
The volume and availability of real-world data (RWD; refs. 1, 2) present unique opportunities to study effects of medical interventions in large and heterogenous populations. However, these opportunities come with distinct challenges that can threaten the validity of RWD evidence. Immortal time arises in studies when treatment occurs after cohort entry, precluding the individual from experiencing the outcome and rendering the time “immortal” or “immune” (Fig. 1) (3–5). If unaddressed, immortal time can lead to bias exaggerating the effect of treatment, making it seem more beneficial than it is. Several epidemiologic and statistical approaches can be used to avoid immortal time bias, including using a time-varying exposure (4), landmark analyses (6, 7), and clone-censor-weight methods that emulate randomized clinical trials (8–10); however, they remain underutilized in many RWD analyses.

Figure 1.

Depiction of immortal time bias in observational studies. Hypothetical data from a longitudinal observational study for an individual who received an exposure (e.g., surgical resection) following the cohort entry date (e.g., date of metastatic cancer diagnosis). The “Misclassified immortal time” and “Exclusion of immortal time” approaches do not appropriately categorize time into “exposed” and “unexposed” periods. The “Correctly classified immortal time” correctly assigns time between cohort entry and exposure to the unexposed group and time after the exposure to the exposed group.

Studies evaluating the effects of cancer treatments are often prone to immortal time bias. Studies typically identify patients at time of cancer diagnosis, yet treatment often occurs after the start of follow-up. One setting for which there is a clear potential for immortal time bias is in evaluating the effect of surgical resection for the treatment of metastatic breast cancer. While several retrospective studies using cancer registries report substantial benefits among women who underwent surgical resection (11–18), prospective studies and randomized trials largely found no effect of treatment (19–21).

To date, there have been no formal efforts to quantify immortal time bias in studies evaluating the effect of surgical resection in this patient population. We aimed to demonstrate the impact of immortal time bias on the observed treatment effect of surgical resection among women with metastatic breast cancer. We hypothesized that treatment effect estimates would be overestimated when immortal time was unaddressed (e.g., when using a standard dichotomous exposure [yes/no resection]) or inappropriately addressed (e.g., when excluding immortal time from the exposed group). To further demonstrate the potential impact of immortal time bias and different analytic approaches on treatment effect estimates, we also conducted a simulation study where the “true” relationship between surgical resection and all-cause mortality was known (i.e., set by the researcher) and bias could be quantified.

Materials and Methods

Data source and study design

We used the National Cancer Database (NCDB) 2017 Participant Use File, a clinical database sourced from over 1500 commission-accredited cancer facilities in the US (22, 23). Importantly, NCDB captures time to treatment, which allows researchers to measure time between cancer diagnosis and surgical resection. Our study included adult women (≥18 years) diagnosed with incident metastatic breast cancer from 2013–2016. Women with cT0/x, cNx, missing cTNM, prior cancer history, or missing surgery information were excluded (Supplementary Fig. S1). Patients were followed from cancer diagnosis until death, last contact, or the end of study follow-up (December 31, 2017).

The primary exposure was surgical resection, defined as a total or partial mastectomy. Individuals who did not undergo resection, including those who only underwent breast biopsies for tissue diagnosis, were categorized as not having surgery. Time to surgery was calculated as the time from diagnosis to the date of the most definitive surgical resection. The outcome of interest was 3-year all-cause mortality, consistent with randomized trials and prospective studies in similar populations (19–21, 24).

Statistical analysis

We estimated the association between surgical resection and mortality using several approaches to define surgical status. Brief descriptions of each are provided below, with additional details (and sample SAS code) in the Supplementary Methods and Materials. Multivariable Cox proportional hazards regression was used for all analyses.

Approaches that fail to account for immortal time

We first estimated the association between surgical resection and mortality using two commonly used methods that do not appropriately address immortal time—using a dichotomous exposure and using a dichotomous exposure but excluding immortal time. Dichotomous exposures classify women who underwent surgery at any time during follow-up as exposed for the entire study period, thus creating a period of immortal time. Alternatively, excluding immortal time shifts the start of follow-up to the date of surgical resection among exposed patients, but starts follow-up at diagnosis for the unexposed, which will not fully ‘fix’ the immortal time bias (25). A more in-depth overview of these approaches, as well as time-varying exposures and landmark analyses, has been previously described (26).

Time-varying exposure(s)

The time-varying exposure allows treatment status to vary over time and treated patients contribute both ‘exposed’ and ‘unexposed’ time (3, 4). In our study, the time between cancer diagnosis and surgical resection was attributed to the unexposed group and the time after surgery was attributed to the exposed group. The HR from this model is interpreted as the average effect of undergoing surgical resection at any time after diagnosis, compared with no resection (Table 1).

Table 1.

Summary of analytic techniques that can address immortal time, using surgical resection among women with metastatic breast cancer as an example.

Analytic approach	Description	Interpretation
Time-varying exposure (yes/no surgery) (3, 4), ever/never treated	Included: All women with metastatic cancer	Effect of ever undergoing resection, compared to never, on mortality.
	Treatment status: Surgical resection during any point during follow-up. Women are classified as being ‘unexposed’ until the date of surgery; after the date of surgery they are classified as exposeda.
	Follow-up: Starts at date of diagnosis. Women are followed until death, loss to follow-up, or end of study period.
Time-varying exposure (yes/no surgery) (3, 4) with specified treatment window	Included: All women with metastatic cancer	Effect of undergoing resection within 8 months of diagnosis, compared to never or undergoing resection later, on mortality.
	Treatment status: Surgical resection within a specified treatment window (e.g., 8 months after diagnosis). Women are classified as being ‘unexposed’ until the date of surgery; after the date of surgery they are classified as exposeda. Women who undergo resection after the treatment window are classified as unexposed.
	Follow-up: Starts at date of diagnosis. Women are followed until death, loss to follow-up, or end of study period.
Landmark approach (6, 7)	Included: All women with metastatic cancer and who are alive and not lost to follow-up before landmark	Effect of undergoing resection within 8 months of diagnosis, compared to never or undergoing resection later, on mortality, among women who survive at least 8 months after diagnosis.
	Treatment status: Women who undergo resection prior to the landmark are considered exposed, and individuals who do not are unexposed.
	Follow-up: Starts at a landmark time-point (e.g., 8 months) following cancer diagnosis. Women are followed until death, loss to follow-up, or end of study period.
Clone-censor-weight method (8–10)	Included: All women with metastatic cancer are included twice; once in each treatment arm (surgical resection and no resection)	Effect of undergoing resection within 8 months of diagnosis, compared to never or undergoing resection later, on mortality.
	Treatment status: Assigned. Treatment is defined to occur within a specified time frame (e.g., 8 months)
	Follow-up: Starts at date of diagnosis. Patients are followed until their treatment is no longer compatible with the treatment assignment (e.g., “unexposed” women are censored at the time of resection and “exposed” women are censored at 8 months if they do not undergo resection), death, loss to follow-up, or end of study period.

^aWhile in our analyses we assumed a ‘once exposed, always exposed’ approach given that our treatment of interest was surgery, these methods allow for individuals to be switched from unexposed to exposed and vice versa across the entire study period; studies on medication adherence or other treatments may want to reclassify individuals as unexposed as treatment is discontinued; lag effects of treatments can also be incorporated.

However, the time between diagnosis and surgical resection can vary widely between women, due to other treatments, prognosis, and other clinical decision-making factors. This variation can make the ‘ever’ versus ‘never’ undergoing resection approach difficult to interpret. One way to address this issue is to create a “treatment assessment window”. To illustrate this, we fit two additional time-varying exposure models that only considered surgical resection that occurred within specific time windows, 8 and 12 months from diagnosis, respectively. Women were able to change exposure status (from unexposed to exposed) if they underwent surgery during the treatment assessment window. The HRs from these models can be interpreted as effect of undergoing surgery within 8 (or 12) months of diagnosis on mortality, compared to never undergoing surgery or undergoing surgery after 8 (or 12) months.

Landmark analysis

In this approach, instead of using a time-varying exposure, you instead begin follow-up for individuals at the end of the treatment assessment window (i.e., landmark; refs. 6, 7). Patients who died or who were censored before the end of the treatment assessment window are excluded. The HR from these models is also interpreted similarly: the effect of undergoing surgery within 8 (12) months, compared to no surgery or later surgery, among patients who survived for at least 8 (12) months after diagnosis.

Clone-censor-weight method

The clone-censor-weight method emulates a hypothetical clinical trial by creating two copies of each patient at cohort entry and allocating one copy or “clone” to each treatment arm (i.e., exposed/treated and unexposed/no treatment) (8–10). Copies/clones are censored when they deviate from their assigned treatment. This means that in the exposed/treatment arm, copy/clones are censored if they do not undergo treatment by the end of a treatment assessment window. In the no treatment arm, copy/clones are censored when they undergo treatment. Otherwise, patients are followed normally and administratively censored at the end of the study or loss to follow-up. In our analyses, we used the same treatment assessment windows as our prior analyses: 8 and 12 months. The interpretation of the HRs is the same as those from the time-varying exposure model with treatment assessment windows.

Because women are assigned to each exposure group at baseline, there is no baseline confounding (covariates are balanced across groups). However, informative censoring (i.e., selection bias) must be accounted for since women may deviate from their assigned treatment strategies during the assessment window. In our analysis, we accounted for informative censoring by calculating inverse-probability of censoring weights (e.g., when a woman undergoes surgical resection when assigned to the unexposed group) (27). Additional details on methods to address confounding and estimation of censoring weights are provided in the Supplementary Methods and Materials (28, 29).

Plasmode simulation

To further demonstrate the differences between the aforementioned approaches, we conducted a plasmode simulation where we were able to set the ‘true’ relationship between surgical resection and mortality (30). Plasmode simulations are useful for emulating RWD, since the distribution of patient characteristics and other variables are derived from actual clinical databases. We extracted patient demographic and cancer characteristics from the original NCDB cohort of women with metastatic breast cancer, and simulated treatment (surgical resection) and patient outcomes (mortality).

We created 1,000 plasmode datasets by drawing 10,000 women with replacement from the metastatic breast cancer cohort. In each plasmode dataset, time to surgical resection and time to mortality were separately simulated using Weibull distributions. For demonstration purposes, we assumed that surgery had no impact on mortality (HR = 1). Additional details on the simulation methods are provided in the Supplementary Methods and Materials.

We estimated the association between surgical resection and all-cause mortality using the methods above in each of the 1,000 plasmode datasets, and then averaged the results to estimate the HR. SEs were estimated as the mean standard deviation across plasmode datasets and 95% confidence interval coverage (CIC) was estimated as the proportion of 95% confidence intervals that contained the true HR. Bias was estimated for each approach as the log average HR across the 1,000 datasets minus the true log HR.

All analyses were conducted using SAS version 9.4 (SAS Inc.). This study was determined to be exempt by the University of North Carolina Institutional Review Board (IRB# 20-1493).

Data availability

The American College of Surgeons National Cancer Database (NCDB) were used under license and not publicly available. However, all SAS programming for the study are included in the Supplementary Methods and Materials.

Results

NCDB analyses

Overall, 24,329 women with metastatic breast cancer met study inclusion criteria, of which 5,847 underwent surgical resection at some time during their follow-up. Median time to resection, among women who underwent surgical resection, was 160 days (interquartile range 35–215, full range 0–1,016). Demographic and tumor characteristics, stratified by ever undergoing resection, are provided in Supplementary Table S1.

The estimated associations between resection and mortality using the different analytic approaches are presented in Table 2. The biggest association between resection and mortality was observed when using a dichotomous exposure (HR, 0.52; 95% CI, 0.49–0.55). The observed association was slightly attenuated when we excluded immortal time (HR, 0.62; 95% CI, 0.58–0.65). Results from the time-varying exposure, landmark, and clone-censor-weight analyses were all closer to the null, although all three analyses showed some protective association between resection and all-cause mortality (HR, 0.65–0.88). Varying the treatment assessment window did not meaningfully change results.

Table 2.

Results from analysis of NCDB data using various methods to account for immortal time.

	Surgical resection				No resection
Model	Deaths	Na	Time (Months)	IRb	Deaths	Na	Time (Months)	IRb	HR (95% CI)
Dichotomous exposure with misclassified immortal timec	1,569	4,795	131,226	12.0	7,534	14,453	291,752	25.8	0.52 (0.49–0.55)
Dichotomous exposure with exclusion of immortal person-timec	1,569	4,795	107,887	14.5	7,534	14,453	291,752	25.8	0.62 (0.58–0.65)
Time-varying exposurec
Ever/never treated	1,569	4,795	107,887	14.5	7,534	14,453	315,091	23.9	0.65 (0.62–0.69)
8-month treatment window	1,364	3,994	92,603	14.7	7,736	15,243	330,375	23.4	0.67 (0.64–0.72)
12-month treatment window	1,542	4,609	104,873	14.7	7,558	14,628	318,105	23.8	0.66 (0.63–0.70)
Landmark modelc
8-month landmark	1,053	3,633	76,416	13.8	4,372	11,212	212,982	20.5	0.68 (0.63–0.73)
12-month landmark	1,027	3,993	73,015	14.1	3,273	9,500	159,742	20.5	0.67 (0.62–0.72)
Clone-censor-weight methodd
8-month treatment window	4,728	19,237	209,995	22.5	7,736	19,237	330,375	23.4	0.86 (0.83–0.90)
12-month treatment window	5,827	19,237	263,236	22.1	7,558	19,237	318,105	23.8	0.88 (0.85–0.91)

Abbreviations: IR, incidence rate; NCDB, National Cancer Database.

^aIndividuals with missing covariate information were excluded from all analyses (n = 5,081).

^bCrude IR per 1,000 person-months.

^cHRs were calculated by fitting inverse-probability of treatment weighted Cox regression models. Inverse probability of treatment weights were estimated using a logistic regression model with surgery as the dependent variable and the following patient characteristics as independent variables: age, race, insurance, comorbidity index, median income quartile, year of diagnosis, histology, clinical T stage, clinical N stage, and cancer subtype and interaction terms for age and comorbidity index. Facility type and region were not adjusted for since they are restricted in the NCDB in women <40.

^dHRs were calculated by fitting inverse-probability of censoring weighted Cox regression models. Models to estimate weights included the same covariates listed in footnote c.

Plasmode simulation

Results from the plasmode simulation are presented in Table 3. As expected, when using a dichotomous exposure (HR, 0.84; bias, −0.177), even when immortal time was excluded (HR, 0.93; bias, −0.074) produced biased estimates. Notably, none of the dichotomous exposure simulations produced confidence intervals that included the true effect (95% CIC = 0%). Alternatively, the time-varying exposure, landmark, and clone-censor-weight models all produced unbiased HRs (bias = −0.003 to 0.016). Precision (range log SE = 0.028–0.038) and CIC (range = 0.919–0.955) were similar across the three approaches that accounted for immortal time.

Table 3.

Results from analyses of plasmode simulation using various methods to account for immortal time.

Model	HRa	log SE	95% CICb	Bias (log scale)c
Dichotomous exposure with misclassified immortal time	0.84	0.029	0.000	−0.177
Dichotomous exposure with exclusion of immortal person-time	0.93	0.030	0.348	−0.074
Time-varying exposure
Ever/never treated	1.02	0.030	0.919	0.016
8-month treatment window	1.01	0.032	0.946	0.012
12-month treatment window	1.01	0.031	0.938	0.014
Landmark model
8-month landmark	1.00	0.038	0.946	−0.001
12-month landmark	1.00	0.038	0.955	−0.001
Clone-censor-weight method
8-month treatment window	1.00	0.029	0.949	0.001
12-month treatment window	1.00	0.028	0.948	−0.003

Abbreviation: CIC, confidence interval coverage.

^aMean HR across all 1,000 plasmode simulation datasets.

^bProportion of 95% CIs that include the true HR of 1.00.

^cDifference between the log average HR across the 1,000 plasmode datasets and the true log HR (0); larger absolute numbers indicate more bias. Negative bias makes surgical resection appear more protective, positive bias makes surgical resection appear more harmful. In our example, since the true log HR is 0, bias equals the log of the average HR. In simulations where the true HR is not null (1.00), this will not be the case.

Discussion

Our study demonstrates the impact of immortal time on the estimated treatment effect of surgical resection on mortality in women with metastatic breast cancer using both a case study and plasmode simulation. In the case study, our findings suggest that analyses that do not appropriately account for immortal time are overestimating the protective association between surgical resection and mortality among women with metastatic breast cancer. This is further supported by the simulation results, which found that using a dichotomous exposure, even when immortal time was excluded, produced biased results, while the time-varying exposure, landmark, and clone-censor-weight analyses produced unbiased estimates.

Our study partially explains why studies using observational RWD found that surgical resection was associated with improved survival among patients with metastatic breast cancer, while subsequent randomized studies did not. Published results from studies assessing the surgery-survival association in women with metastatic breast cancer using Surveillance, Epidemiology, and End Results (SEER) data have estimated HRs ranging from 0.53 to 0.63, suggesting a large protective benefit of surgery (11, 15–17). However, information on treatment timing is not captured in SEER, meaning that immortal time cannot be accounted for even if researchers wanted to use appropriate methods. Other studies using NCDB have also found similar, strong protective associations, suggesting that appropriate methods to account for immortal time were not used (12–14, 18).

We found that the estimated HR for resection on survival was substantially attenuated when immortal time was appropriately handled (HR, 0.65–0.88), suggesting that immortal time bias partially explains the discrepancies between the clinical trials and observational study findings. Notably, a recent study using NCDB that accounted for immortal time bias found similar results to our clone-censor-weight analysis (HR, 0.82; 31). If resection truly has no impact on outcomes, as clinical trials and prospective studies have found (HR, 1.04–1.09; refs. 19–21), then residual confounding may also partially explain the persistent discrepancies. For example, fitness for surgery is generally unavailable in limited observational datasets and may confound these associations. Selection/exclusion criteria in clinical trials and prospective studies may also play a role.

It is important to note that the hazard ratios using the clone-censor-weight approach (8-month: HR, 0.86, 12-month: HR, 0.88) were higher than the hazard ratios using time-varying exposures (8-month: HR, 0.67, 12-month: HR, 0.66) and landmark analysis (8-month: HR, 0.68, 12-month: HR, 0.67). While all three of these approaches can be used to address immortal time bias, they produce different estimands, which may explain the differences in findings. In addition, landmark analyses draw inference for a less generalizable study population since they restrict to survivors of the landmark period. A key advantage of the clone-censor-weight method is that it operates under a target trial emulation framework, which may explain why results from this analysis were more similar to those reported in RCTs. This approach ensures no baseline confounding, although confounding is replaced by selection bias due to informative censoring, which can be accounted for using censor weights.

As RWD become more commonplace in clinical research, a more in-depth understanding of study design and analytic approaches is needed to ensure researchers are generating robust and valid estimates of treatment effects. While confounding and selection bias are relatively well understood (32, 33), immortal time bias has historically not been widely discussed, despite its potential to substantially bias results. Who can forget the famous study that erroneously found that Oscar winners had improved survival in the early 2000s? (34, 35) Even more recently (2018–2019) papers have had to be retracted in high impact, peer-reviewed journals after readers pointed out potential immortal time bias; when the authors went back and used appropriate methods, they found the treatment actually had no effect (36–39). These events have prompted journals to publish additional guidance on immortal time bias (40) and calls for more effective use of reporting guidelines for observational research (41), such as STrengthening the Reporting of OBservational studies in Epidemiology (STROBE; refs. 42, 43), REporting of studies Conducted using Observational Routinely collected health Data (RECORD; ref. 44), and RECORD for Pharmacoepidemiology (RECORD-PE; refs. 40, 41, 45). We hope that these events, in addition to our results, increase awareness of the need for rigorous peer review of potential immortal time bias prior to publication and the use of appropriate analytic methods.

Choosing the appropriate dataset and analytic approach to avoid immortal time bias (as well as other forms of bias) when using RWD can be challenging. We encourage researchers to avoid studying treatments where immortal time is a concern in databases where dates or timing of treatment cannot be captured (e.g., SEER). When timing is known, there are still decisions to be made about which analytic approach to use. As we show in our plasmode simulation, only methods that address immortal time are expected to produce unbiased estimates. However, these approaches each have strengths and limitations. The landmark approach may be the most straight-forward to implement and exact dates are not needed, so long as researchers can verify that an exposure occurred during a pre-specified treatment assessment window. However, using a landmark can impact generalizability, especially if the treatment assessment window is long or if early mortality is high (e.g., lung cancer). Results from landmark analyses do not apply to individuals who die or are lost to follow-up prior to the landmark.

Choice of the treatment assessment window also changes the causal effect being estimated and the population of inference (i.e., the target population) (46). In all of the approaches that incorporate a treatment assessment window, clinical expertise should be used to determine the treatment assessment window and/or landmark, and sensitivity analyses using different windows (or landmarks) should be conducted to ensure the cut point doesn't impact results.

Time-varying exposures have the advantage that they do not require dropping patients who die early. However, interpreting and implementing findings into clinical practice can be difficult since treatment received at any time during follow-up is compared to no treatment. Incorporating a treatment assessment window into these analyses (e.g., resection within 8 months versus no resection or resection after 8 months) is an easy way to solve this issue. However, when using time-varying exposures, researchers must also consider how to appropriately adjust for time-varying confounders. While outside the scope of this study, marginal structural models or g-methods can be used to address time-varying confounding and have been described in detail elsewhere (47–49).

The clone-censor-weight method, which has recently gained traction in epidemiologic research, allows researchers to emulate a trial using observational data (9). This has several strengths, including the ability to ask causal research questions and removal of confounding since treatment is “assigned”. However, because clones are censored based on their actual, observed treatment, informative censoring due to assigned treatment deviation must be accounted for by applying inverse-probability of censoring weights. Maringe and colleagues published a tutorial with R and Stata code using surgery among older adults with early-stage lung cancer as an example (10). We are adding to the literature of this approach by providing a SAS code tutorial in our Supplementary Methods and Materials.

As with all studies that use RWD, analyses can still be subject to bias from unmeasured confounding, missing data, and selection. Using the clone-censor-weight method to emulate a target trial may help elucidate some of these potential biases, especially selection bias, for researchers. Overall, given the strengths and limitations of each analysis approach, we recommend using either a time-varying exposure with a treatment assessment window or the clone-censor-weight method when immortal time is a concern. Both of these approaches appropriately minimize immortal time bias.

Results from our comparison of analytic approaches using the NCDB cohort should be interpreted in light of several limitations. First, our analysis was restricted to a single dataset and results may not be generalizable to all women with metastatic breast cancer. However, NCDB captures 70% of all incident cancers in the US and is one of the largest and most comprehensive datasets that captures incident cancer and timing of treatment. We followed individuals for up to three years and individuals diagnosed later in the study period did not have the opportunity for full follow-up. We accounted for this by administratively censoring individuals at the end of their data availability. If loss to follow-up is differential with respect to the exposure, this can induce selection bias. Although not demonstrated in this paper, selection bias due to informative censoring can be dealt with using inverse probability of censoring weights, similar to those employed in our clone-censor-weight analyses (48). We recommend that researchers who use censoring weights to apply the clone-censor-weight method and to account for differential loss to follow-up use separate models for each of these types of censoring. In addition, studies using NCDB, including ours, may be subject to residual confounding due to variables that are not captured in the database, like frailty and other factors associated with survival and clinical decision-making. Unlike our NCDB analyses, the plasmode simulation can quantify bias since the true relationship between surgery and mortality is set by the researchers. However, simulations are limited to the scenario that they present, and alternate strategies for generating the exposure or outcome data can lead to different results. Finally, our simulation only considered a simplified example in which the proportional hazards assumption was met. Future simulations should assess how these approaches to handle immortal time perform in more complex scenarios, for example when the hazard ratio is time-varying. Researchers should also consider other methods when proportional hazards assumptions do not hold (e.g., piecewise proportional hazards models, linear time functions, accelerated failure time models) (50, 51). The methods outlined in our paper to deal with immortal time bias can be extended to cases where proportionality fails.

In conclusion, immortal time and immortal time bias are serious concerns in studies that use RWD to estimate the effects of cancer treatment on patient outcomes. These concepts also at least partially explain why RCTs and observational studies evaluating the impact of surgical resection in metastatic breast cancer patients present such conflicting results. As the availability of RWD increases (1, 2), it is critical for healthcare researchers to be aware of immortal time and use methods that account for potential bias.

Authors' Disclosures

E.D. Duchesneau reports grants from National Cancer Institute during the conduct of the study; other support from AbbVie outside the submitted work. M. Webster-Clark reports other support from Johnson & Johnson outside the submitted work. J.L. Lund reports other support from GlaxoSmithKline, grants from Roche, and grants from AbbVie outside the submitted work. K.E. Reeder-Hayes reports grants from Pfizer Foundation outside the submitted work. No disclosures were reported by the other authors.

Disclaimer

The contents and views in this manuscript are those of the authors and should not be construed to represent the views of the National Institutes of Health.

Authors' Contributions

E.D. Duchesneau: Conceptualization, data curation, formal analysis, visualization, methodology, writing–original draft, writing–review and editing. B.E. Jackson: Conceptualization, writing–original draft, writing–review and editing. M. Webster-Clark: Methodology, writing–review and editing. J.L. Lund: Supervision, writing–review and editing. K.E. Reeder-Hayes: Writing–review and editing. A.M. Nápoles: Writing–review and editing. P.D. Strassle: Conceptualization, data curation, supervision, methodology, writing–original draft, project administration, writing–review and editing.