Mechanics of diffusion-mediated budding and implications for virus replication and infection

Abstract

Budding allows virus replication and macromolecular secretion in cells through the formation of a membrane protrusion (bud) that evolves into an envelope. The largest energetic barrier to bud formation is membrane deflection and is trespassed primarily thanks to nucleocapsid-membrane adhesion. Transmembrane proteins (TPs), which later form the virus ligands, are the main promotors of adhesion and can accommodate membrane bending thanks to an induced spontaneous curvature. Adhesive TPs must diffuse across the membrane from remote regions to gather on the bud surface, thus, diffusivity controls the kinetics. This paper proposes a simple model to describe diffusion-mediated budding unravelling important size limitations and size-dependent kinetics. The predicted optimal virion radius, giving the fastest budding, is validated against experiments for coronavirus, HIV, flu and hepatitis. Assuming exponential replication of virions and hereditary size, the model can predict the size distribution of a virus population. This is verified against experiments for SARS-CoV-2. All the above comparisons rely on the premise that budding poses the tightest size constraint. This is true in most cases, as demonstrated in this paper, where the proposed model is extended to describe virus infection via receptor- and clathrin-mediated endocytosis, and via membrane fusion.

1. Introduction

Enveloped viruses are ubiquitous in nature. They have covered a fundamental role in the evolution of the living kingdom and can have a tremendously disruptive impact on human health and economy, as observed in recent times. While subject to intense study from the biochemical point of view, the physical mechanisms involved in virus replication and infection have comparatively received rather limited attention [1,2]. Despite the controversy around the definition of a virus as a form of life, it is commonly observed that viruses replicate and evolve to optimize replication at the planetary scale [2]. Replication is preceded by the infection of a host cell [2], thus, infection must occur for a virus to replicate itself. This explains why infection has been the centre of attention in recent times. However, as demonstrated in this paper, and in agreement with observations in the literature, replication is a much slower biophysical process than infection. Hence, it can cover a more significant role in the life cycle of a virus.

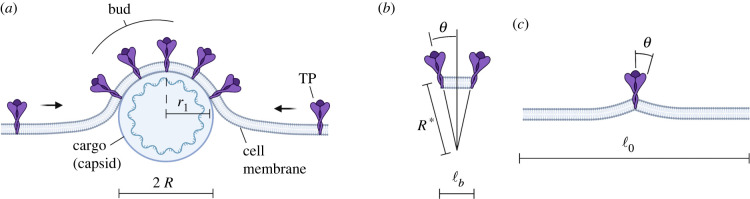
Enveloped viruses are characterized by a lipid membrane wrap (envelope) surrounding the nucleocapsid, which encapsulates genetic material [2] (RNA). The membrane is decorated with transmembrane proteins (TPs), of which the most important ones are virus ligands (spike proteins). Virus ligands are macromolecular assemblies that protrude from the virion (virus particle) and anchor to the receptors of the host cell to prompt infection. The latter involves RNA delivery inside the cytosol of the infected cell (host). The virulent RNA can hijack the host's protein-duplication mechanism to replicate the components of the virus. The new components then assemble into new nucleocapsids inside the cytosol, while the new TPs are delivered to the host membrane. Virus replication concludes with budding, the process by which the nucleocapsid wraps around the host membrane, equipped with virus ligands, and is ultimately expelled from the mother cell into a new enveloped virion [2,3] (figure 1). Budding requires significant membrane deflection, and this constitutes the main energetic barrier to the process. Because TPs protrude from the cell membrane, pointing outward, they create a local spontaneous curvature [4–7], which facilitates wrapping. The energetic barrier becomes then a function of the radius of the capsid, relative to the spontaneous membrane curvature, with the latter defining the optimal capsid radius for fast replication. This also provides minimum and maximum radii ensuring the spontaneity of budding. To accommodate membrane bending, the TPs have to diffuse in the location of the bud. Their diffusion is promoted by their high affinity with the nucleocapsid (cargo); thus, TP diffusion controls the kinetics of the process [8]. Lerner et al. [8] developed the first theoretical model to describe budding from an energetic analysis. The free energy of the bud includes the bending energy of the membrane and the binding energy with the nucleocapsid, mediated by spike proteins. The authors also speculated on the possibility of the spike proteins accommodating non-zero spontaneous curvature in the membrane, thereby lowering the energetic barrier for bud formation. They estimated the budding time as between 10 and 20 min, in agreement with prior measurements. However, they did not explore the influence of virion size in the process. Tzlil et al. [9] continued this investigation by providing a steady state model for budding incorporating the many-body interaction among multiple forming buds. Here, the free energy of the system includes membrane bending, spike adhesion and the line energy of the bud rim. They provided the energetic landscape of the multi-bud system and discussed the implications of size and spike density in budding, but did not consider the spontaneous membrane curvature induced by the TPs, nor the kinetics of TP diffusion.

Figure 1.

Schematics of the (virus) budding process: (a) The cell membrane adheres with the cargo (virus capsid) through TP interaction; (b) TPs induce a spontaneous curvature 1/R* to the budding membrane, which is function of the conical TP angle θ and TP spacing ℓ_b on the bud surface; (c) The TP also induces local bending in the rest (flat) membrane of the cell due to the angle θ, with ℓ₀ the TP spacing in the resting membrane.

Both the above-discussed investigations provided important basic principles to better understand the physics of virus replication; however, none provided a quantitative investigation of the role of virion size on budding spontaneity and kinetics. This paper provides a simple model to describe the process, inspired by a simple model for diffusion-mediated endocytosis [3]. It provides virion size limitations via energetic analysis and size-dependent budding kinetics. The model ultimately finds the optimal virion size at which budding is fastest. This optimum is compared against experiments for several virus species, namely SARS-CoV-1 and 2 [10–12] (coronavirus), HIV-1 (HIV type 1) [13], flu (influenza) [14,15] and HCV (hepatitis type C) [16,17]. Using an exponential replication model based on size hereditariness, the proposed budding model can predict the size polydispersity of a virus population. This prediction is then compared against experiments for SARS-CoV-2 (novel coronavirus) [11] as an example. The reader will find it easy to create such a comparison for all other virus species. The above comparisons are based on the hypothesis that budding is the most size-limiting process in the life cycle of a virus. This hypothesis is later validated by investigating the size limitations of virus infection; finding that, for the majority of biologically relevant cases, budding imposes the tightest size constraints on the virion. Virus infection is studied considering the two main infection mechanisms, namely, receptor- and clathrin-mediated endocytosis [3,18] and membrane fusion.

The model can predict size constraints and the polydispersity of a virus population from molecular-scale properties such as TP adhesion, spontaneous membrane curvature and TP availability. It can be also used in reverse, where virus size polydispersity can be used to predict molecular-scale properties. This is particularly useful to extrapolate the value of parameters that are difficult to measure, such as TP–capsid adhesion.

2. Budding mechanics model

As sketched in figure 1a, in the proposed model, the kinetics of the process is controlled by TP diffusion (also observed in [8]). The free energy of the system ψ, in its dimensionless form, is

$$\begin{array}{rl}{\displaystyle \frac{\psi }{kT}=}& \left[-g_m-{\rho }_b{e}_T+\sigma {\epsilon }_S+{\rho }_b\ln \left({\displaystyle \frac{{\rho }_b}{{\rho }_0}}\right)+2B{\left({\displaystyle \frac{1}{R}-{\displaystyle \frac{1}{R^{\ast }}}}\right)}^2\right]S_b\\ & +2\pi {\int }_r^{\mathrm{\infty }}\rho \hspace{0.17em}\ln \left({\displaystyle \frac{\rho }{{\rho }_0}}\right)r\hspace{0.17em}\mathrm{d}r,\end{array}$$

where k is the Boltzmann's constant; T is temperature; g_m is the adhesion surface energy between the cargo surface (CS, the virus nucleocapsid) and the cell membrane; e_T is the energy released by a TP joining the bud; σ is the surface tension of the cell membrane, here considered constant for simplicity albeit dependent on membrane curvature [7]; ${\epsilon }_S=\mathrm{\Delta }S/S_b$ is the surface strain of the membrane, with $\mathrm{\Delta }S$ the change in membrane surface and S_b the bud surface; ρ is the TP density in the membrane, with ρ₀ and ${\rho }_b\approx l_b^{-2}$ [18] that in the resting membrane and in the bud (i.e. the ligand density in the virion), respectively, and l_b the TP (ligand) spacing in the bud (virus particle); B is the bending modulus of the membrane; R is the radius of curvature of the CS, i.e. that of the wrapping membrane, with R* the spontaneous radius of curvature of the membrane; r₁ is the distance between the axis of symmetry and the bud rim (the point of contact between the cargo and the membrane, figure 1a). Equation (2.1) neglects the bending energy of the membrane outside the bud and the line energy of the bud rim. A full elastic solution would provide completeness [19]; however, [4] showed that the cell membrane in that region assumes a zero-energy catenoid-like configuration. This is also proven by the calculations of [20], where the energy of the system is nearly constant during wrapping. ε_S > 0 constitutes an additional energy penalty due to stretching of the cell membrane, i.e. the diffusion of amphiphiles to compensate for the surface area change during budding. ε_S < 0 provides an energetic driving force due to an excess of amphiphiles in the membrane, which can be removed by expelling a vesicle (membrane buckling).

The spontaneous radius of curvature R* is given by the conical angle θ created by the TPs located in the bud, as shown in figure 1b, giving

$${\displaystyle \frac{1}{R^{\ast }}=2\theta \sqrt{{\rho }_b}.}$$ 2.2

The energy released by one TP joining the bud is

$$e_T=e_{T_a}+e_{Tm},$$ 2.3a

with $e_{T_a}$ the adhesion energy between a TP and the CS, and

$$e_{Tm}=\hspace{0.17em}B2\pi {\theta }^2{\displaystyle \frac{d_{TP}^2}{{\ell }_0^2-d_{TP}^2\hspace{0.17em}},}$$ 2.3b

the bending energy associated with the local curvature created by the TP in the resting membrane, as depicted in figure 1c [4]. This energy is released once the TP joins the bud, hence it proves a driving force. In equation (2.3b), d_TP is the diameter of the TP and ℓ₀ is the TP spacing in the resting membrane.

Appendix A provides the solution to the transient problem, where the bud rim moves following the kinetic law

$$r_1=2\alpha \sqrt{Dt},$$ 2.4

with α a kinetic constant called ‘speed factor’ [3], D the diffusivity of a TP in the membrane and t time. D can be calculated using the bidimensional Stokes–Einstein relation [21], assuming the lipid membrane behaves like a fluid mosaic, giving D = kT/1.69πη. Here, η = 10⁻⁵ N s m⁻¹ is the viscosity of the membrane measured via rheology [22]. Also note that in the above relation, D is independent of d_TP. The value of D, obtained via bidimensional Stokes–Einstein relation, is provided in table 1 and is in agreement with the value adopted in [3].

Table 1.

Parameters adopted in the model, together with their source, value range and adopted median value.

Parameter	source	value (range; adopted median)
kT	[23]	4 · 10−21 J
ρb	[3]	3 · 10−3−20 · 10−3 nm−2; 5 · 10−3 nm−2
lb	${\rho }_b^{-1/2}$, [18]	7−18 nm; 14 nm
σ	[24]	5 · 10−3 nm−2
B	[3]	10−25; 20
θ	[11]	θ ≈ 8.2° = 0.14 rad
R*	equation (2.2)	50 nm
dTP	[12]	4 nm
D	[3]	104 nm2 s−1
$\tilde{\rho }={\rho }_0/{\rho }_b$	[3,18]	0.01−0.1
$\tilde{B}$	equation (2.7b)	1.64
$e_{b0}/2\tilde{B}$	figure 3	0.03−0.2; 0.05
eb0		0.1−0.66; 0.16
eRL	[3]	10−25; 20
Bc	[25]	255−315; 300
Bc/B		10.2−31.5; 15
ρc	[25]	1.25 · 10−3 nm−2
${\tilde{\rho }}_c={\rho }_c/{\rho }_b$		0.25
ec	[25]	5−30; 23
Rc	[25]	32.5−90 nm; 50 nm

Equation (2.4) can be inverted to give the time required for budding completion (budding time), t_b, from the relation $S_b=\pi r_1^2=4\pi R^2$, thus

$$t_b={\displaystyle \frac{R^2}{D{\alpha }^2}.}$$ 2.5

To calculate t_b, one has to compute α. This is reported in appendix A from the condition

$$e_b\ge F_{\tilde{\rho }}(\alpha ),$$ 2.6a

where e_b is the budding energy, i.e. the driving force for budding, and

$$F_{\tilde{\rho }}(\alpha )=(1-\tilde{\rho })f(\alpha )-\ln \left[1+\left({\displaystyle \frac{1}{\tilde{\rho }}-1}\right)f(\alpha )\right],$$ 2.6b

is the kinetic function of the process, with $\tilde{\rho }={\rho }_0/{\rho }_b$ the dimensionless equilibrium density of TPs in the resting membrane, and

$$f(\alpha )={\displaystyle \frac{{\alpha }^{2}E({\alpha }^2)}{{\alpha }^{2}E({\alpha }^2)-\exp (-{\alpha }^2)},}$$ 2.6c

with $E({\alpha }^2)={\int }_{{\alpha }^2}^{\mathrm{\infty }}{e}^{-u}\mathrm{d}u/u\hspace{0.17em}$ the exponential integral function. The budding energy in equation (2.6a) is given by

$$e_b=e_{b0}-2\tilde{B}{\left(1-{\displaystyle \frac{R^{\ast }}{R}}\right)}^2,$$ 2.7a

where

$$\tilde{B}={\displaystyle \frac{B}{{\rho }_b{R}^{\ast 2}}=4B{\theta }^2,}$$ 2.7b

is the dimensionless bending rigidity of the membrane, and

$$e_{b0}=e_{T_a}+e_{Tr}+e_{Tm}+{\tilde{g}}_m-\tilde{\sigma }{\epsilon }_S,$$ 2.7c

is the budding input energy, independent of the cargo size (R), with

$$e_{Tr}=1-\tilde{\rho }+\ln \tilde{\rho },$$ 2.7d

the energetic cost of TP relocation, and e_Tm the released bending energy given by equation (2.3b) and rewritten as

$$e_{Tm}=\tilde{B}{\displaystyle \frac{\pi }{2}{\displaystyle \frac{\xi \tilde{\rho }}{1-\xi \tilde{\rho }\hspace{0.17em}},}}$$ 2.7e

with

$$\xi ={\displaystyle \frac{\sqrt{3}}{2}{d}_{TP}^2{\rho }_b.}$$ 2.7f

Equations (2.7e,f) are derived by adopting a hexagonal distribution of TP in the resting membrane, for which $1/{\rho }_0=\sqrt{3}{\ell }_0^2/2$.

From equations (2.6) and (2.7), it should be noted that α is proportional to e_b, so that a higher driving force e_b can produce faster budding or smaller t_b. Conversely, α = 0, i.e. t_b → ∞, provides the critical condition for budding spontaneity. From equation (2.6a), we have that $F_{\tilde{\rho }}(0)=0$ for any $\tilde{\rho }$, thus e_b ≥ 0 gives the necessary condition for spontaneous budding. This condition, applied to equation (2.7a), provides the size constraints

$$R_{\min }\le R\le R_{\max },$$ 2.8a

with

$${\displaystyle \frac{R_{\max }}{R^{\ast }}={\displaystyle \frac{1}{1-\sqrt{e_{b0}/2\tilde{B}}}\hspace{0.17em}}}$$ 2.8b

and

$${\displaystyle \frac{R_{\min }}{R^{\ast }}={\displaystyle \frac{1}{1+\sqrt{e_{b0}/2\tilde{B}}}.}}$$ 2.8c

It should be noted that equation (2.8b) only applies for $e_{b0}<2\tilde{B}$, whereas for higher input energy R_max → ∞ and equations (2.8) only provides a constraint for minimum radius.

The inequality in equation (2.8a) ensures budding spontaneity. The next section reports the size constraints from equations (2.8) in the absence of TPs, and the budding time as a function of e_b0, $\tilde{\rho }$ and R in the presence of TPs.

Table 1 reports the parameter values adopted in this investigation and their source.

3. Results and discussion

3.1. Budding in absence of transmembrane proteins

In the absence of TPs, the kinetics of the process is controlled by the relaxation time of the membrane. Here, the model is simply used to define the size constraints for budding spontaneity, neglecting the kinetics of budding. In this case, ρ, ρ_b, ρ₀, 1/R* all vanish to zero, thus, equations (2.6)–(2.8) rewrite as

$$g_m-\sigma {\epsilon }_S\ge {\displaystyle \frac{2B}{R^2}.}$$ 3.1

From this, one can obtain the minimum (dimensionless) bud radius as

$${\displaystyle \frac{R_{\min }}{\sqrt{2B/\sigma }}={\displaystyle \frac{1}{\sqrt{g_m/\sigma -{\epsilon }_S}}.}}$$ 3.2

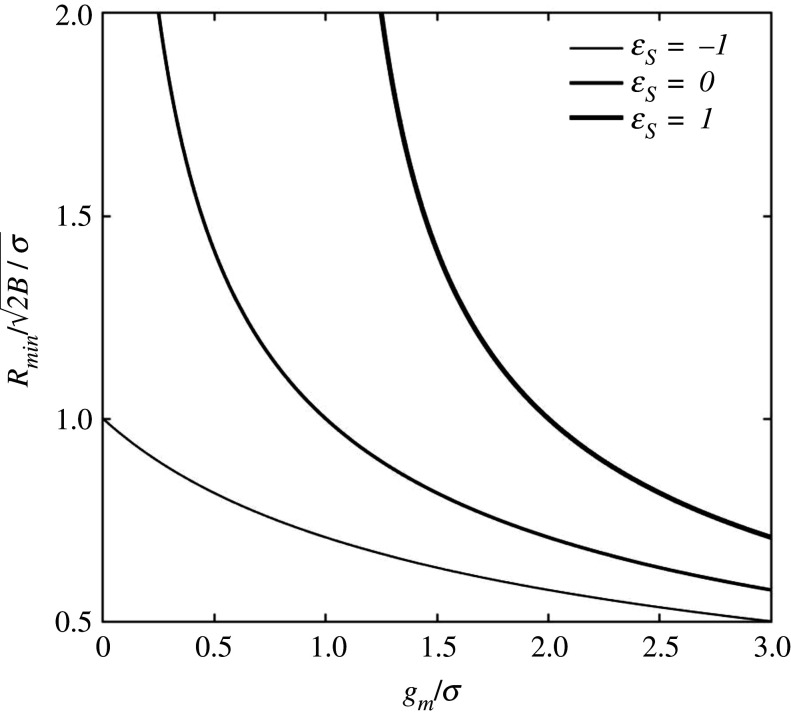
Figure 2 plots $R_{\min }/\sqrt{2B/\sigma }$ versus the dimensionless adhesion energy g_m/σ and surface strain ε_S, from equation (3.2). All plots show a horizontal asymptote for very strong adhesion, leading to a zero minimum radius. I.e. in the case of very strong adhesion, compared with membrane tension, or g_m ≫ σε_S, we have that $R_{\min }\ll \sqrt{2B/\sigma }$. The minimum radius also appears to be highly sensitive to the surface strain ε_S. When ε_S > 0, e.g. in the case of ε_S = 1, the energy of surface stretch, together with bending energy, has to be compensated by adhesion. In the case of ε_S = −1, the surface energy in excess is equivalent to the surface of the bud. In the absence of adhesion, the latter case is the only one that can favour budding since for g_m = 0, all other plots give R_min → ∞ (i.e. no budding spontaneity for any size). The case of g_m = 0 and ε_S = −1 is also that in which the cargo can be absent, i.e. vesiculation, where $R_{\min }=\sqrt{2B/\sigma }$. In this case, the excess surface energy is released in the form of bending energy, i.e. membrane buckling. Taking the values reported in table 1 for B and σ, the minimum vesicle radius computes to R_min = 60–100 nm, in agreement with experimental observations [26].

Figure 2.

Budding in the absence of TPs. The plots report dimensionless minimum bud radius versus dimensionless adhesion energy at various surface strains, from equation (3.2).

3.2. Transmembrane protein-mediated budding

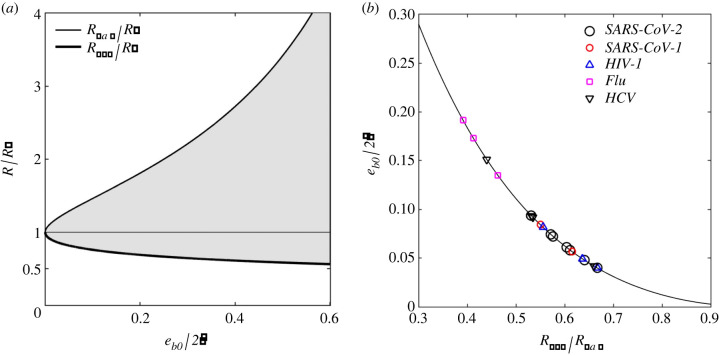
In the presence of TPs one can compute the minimum and maximum radii of curvature of the cargo allowing spontaneous budding (i.e. the size constraints of the virion), from equation (2.8). Figure 3a plots these radii as a function of the ratio $e_{b0}/2\tilde{B}$. $\tilde{B}$ is estimated from equation (2.7b) and the parameter values in table 1, and its value is reported in the same table. To the author's knowledge, e_b0 has never been measured and is here estimated from the observed minimum/maximum radii. Figure 3b reports the predicted $e_{b0}/2\tilde{B}$ as a function of the ratio R_min/R_max, from equations (2.8), and from the minimum/maximum radii extracted from experimental observations of several virus species. These are SARS-CoV-1 & 2 (coronavirus) [10–12], HIV-1 (human immunodeficiency virus type 1) [13], flu (influenza) [14,15] and HCV (hepatitis C virus) [16,17]. As evidenced in this figure, the proposed model predicts the range $e_{b0}/2\tilde{B}=0.03-0.2$, while the majority of data points suggest a median value of 0.05. From equations (2.7), one can deduce that the variability of input energy within the same virus species is likely to be attributed to the stochastic variation of TP concentration (variable $\tilde{\rho }$) and/or the stochastic presence of excess amphiphiles (variable ε_S).

Figure 3.

Bud size constraints as a function of input energy e_b0, from equations (2.8): (a) size constraints R_max and R_min, relative to the spontaneous radius of curvature R*, versus input energy ratio $e_{b0}/2\tilde{B}$; (b) predicted $e_{b0}/2\tilde{B}$ as a function of the ratio R_min/R_max from the reported minimum/maximum virion size for virus species: SARS-CoV-1 & 2 [10–12], HIV-1 [13], flu [14,15] and HCV (hepatitis C) [16,17].

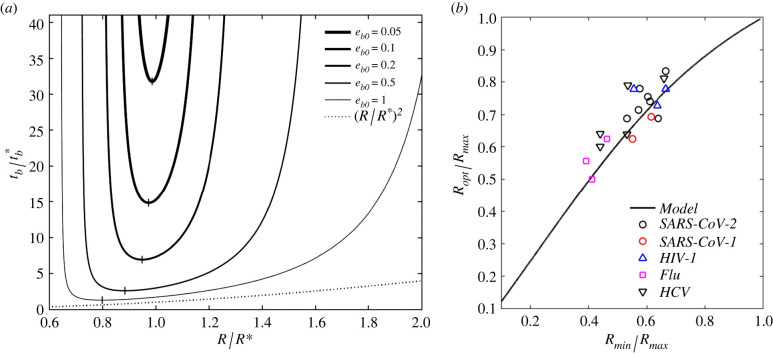
Figure 4a plots the dimensionless budding time $t_b/t_b^{\ast }$, with $t_b^{\ast }$ the characteristic budding time, as a function of the dimensionless radius R/R* at various input energy e_b0. Equation (2.5) reports the budding time t_b as function of the speed factor α, where the latter is then calculated numerically as function of the budding energy e_b from equations (A 8)–(A 10) in appendix A. The characteristic budding time is

$$t_b^{\ast }={\displaystyle \frac{R^{\ast 2}}{D{\alpha }_{\mathrm{\infty }}^2},}$$ 3.3

with α_∞ the maximum speed factor obtained for e_b → ∞ and reported in table 2 in appendix A. The plots in figure 4a are obtained for $\tilde{\rho }=0.01$, where $\tilde{\rho }=0.1$ gives nearly identical plots, hence omitted. Note that, albeit $t_b/t_b^{\ast }$ appears not to be directly affected by $\tilde{\rho }$ within the explored range, $\tilde{\rho }$ affects the input energy e_b0, via equations (2.7), and $t_b^{\ast }$, via equation (3.3), where α_∞ depends on $\tilde{\rho }$ through appendix A, table 2. Each plot shows a minimum and maximum radius, calculated from equation (2.8), giving t_b → ∞, as well as an optimal radius R_opt, for which t_b = t_b,min, the minimum budding time (vertical bar symbol). Larger e_b0 provide smaller t_b, intuitively, following the simple scaling law $t_{b,min}/t_b^{\ast }\approx 1.5/e_{b0}$ within the observed range. For e_b0 ≥ 5, the curves approach the simple scaling law $t_b/t_b^{\ast }\simeq {(R/R^{\ast })}^2$ (dashed line in figure 4a) for R > R_min, where R_opt ≃ R_min. This case, however, involves much higher input energy than the values extracted in figure 3b, rendering this simple scaling inapplicable to the reported experimental observations.

Figure 4.

(a) Dimensionless budding time $t_b/t_b^{\ast }$ versus dimensionless bud radius R/R* for various input energy e_b0, from equations (2.5), and (A 8)–(A 10) in appendix A; the dashed line indicates $t_b/t_b^{\ast }={(R/R^{\ast })}^2$, valid for e_b0 ≥ 5; (b) predicted optimal-to-maximum radii R_opt/R_max versus minimum-to-maximum radii R_min/R_max. The input energy is extracted from figure 3b, and the predictions are compared against the observed median virion sizes for SARS-CoV-1 & 2 [10–12], HIV-1 [13], flu [14,15] and HCV (hepatitis C) [16,17].

From the values in table 1 and the median value $e_{b0}/2\tilde{B}\approx 0.05$, we have e_b0 ≈ 0.16 giving $t_{b,opt}\approx 10\hspace{0.17em}{t}_b^{\ast }$ from figure 4a. From tables 1 and 2, we then have $t_b^{\ast }\approx 0.15$–2.93 min, for $\tilde{\rho }=$ 0.01–0.1, respectively, from which t_b,opt ≈ 1.5−29.3 min. This range includes the experimentally observed 10−20 min budding time [8].

Figure 4b reports the predicted ratio R_opt/R_max, extracted from figure 4a, as a function of R_min/R_max, where e_b0 is extracted from figure 3b. This figure compares the theoretical prediction with the observed optimal virion radius (from median values) for the species reported in figure 3b. The close agreement between theory and experiments validates the proposed model under the assumption that budding provides the tightest constraint to virus size. This hypothesis is discussed in the next subsections.

The model considers the ideal condition of a fully formed capsid at the onset of budding. In some cases, the capsid is still forming when the first CS-TP binding occurs. This is particularly the case in retroviruses like HIV, where the capsid develops from the agglomeration of gags. In these cases, the attractive/repulsive forces between gags, and/or other capsid components, might affect e_b0. Thus, additional energetic terms may be needed in equation (2.7c) to account for it. Repulsive forces will reduce the effective e_b0, while attractive forces will increase it. Additionally, the diffusion of capsid components within the cytosol to reach the bud might also affect the kinetics of the process. The proposed model assumes that the process of capsid assembly is much faster than TP diffusion. This idealization could explain the larger deviation in figure 4b for HIV-1.

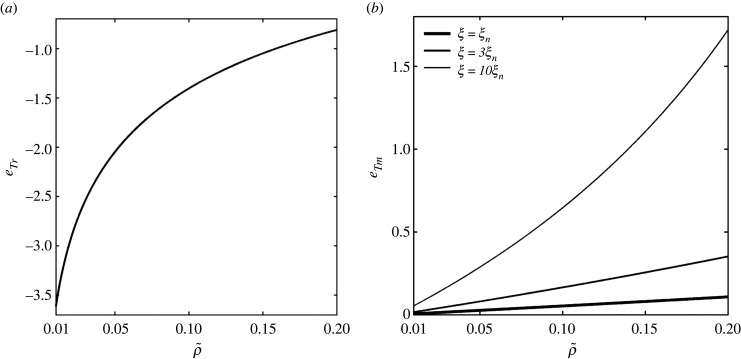
Figure 5a reports the energy of TP relocation e_Tr, from equation (2.7d), as a function of $\tilde{\rho }$, for $\tilde{\rho }=0.01-0.2$. This energy is negative as it constitutes a cost, with smaller $\tilde{\rho }$ requiring higher relocation costs due to the higher density gap between the bud and the resting membrane. This figure shows a logarithmic correlation between $\tilde{\rho }$ and e_Tr, within the observed range, evidencing the predominance of the third term on the right-hand side of equation (2.7d) over the others. Figure 5b reports the membrane bending energy released by a TP joining the bud, e_Tm, from equation (2.7e), as a function of $\tilde{\rho }$ for the same value range, and for ξ = ξ_n, 3ξ_n, and 10ξ_n, with ξ_n = 0.2 a nominal parameter value based on equation (2.7f) and table 1. e_Tm is positive since the release of this energy promotes budding. Figure 5b shows that e_Tm is proportional to $\tilde{\rho }$ (TPs availability) and ξ, with the sensitivity of e_Tm with respect to $\tilde{\rho }$ significantly amplified by ξ. From equation (2.7f) one can deduce that large d_TP and ρ_b (large and densely distributed TPs) yield higher e_Tm. For the median values of the parameters adopted in table 1, we can see in figure 5b that the contribution of e_Tm is relatively small (< 0.1) compared with e_Tr. Take now, for simplicity, ${\tilde{g}}_m=0$, ε_S = 0, $\tilde{\rho }=0.1$ (0.01), e_b0 = 0.16 and ξ = 0.2. We have then e_Tr = −1.4 (− 3.62) and e_Tm = 0.053 (0.0052), so that we can finally estimate the TP–capsid binding energy (in kT units) as $e_{T_a}=1.51$ (3.77).

Figure 5.

(a) TP relocation energy e_Tr (change in configurational energy) versus $\tilde{\rho }={\rho }_0/{\rho }_b$ from equation (2.7d); (b) membrane bending energy released by a TP joining the bud as a function of $\tilde{\rho }$ and ξ from equation (2.7e), with ξ_n = 0.2.

3.3. Exponential replication and virion size polydispersity

Let us assume that virion size is hereditary, i.e. if a virion of radius R infects the host, this will reproduce n* copies of itself having a radius that is very close to R.

Let us introduce the function n(t, R) giving the number of virions having radius R in the population at time t. Assuming that budding provides the tightest size constraint, the reproduction rate of virions having radius R, at the time t, becomes

$${\displaystyle \frac{\mathrm{\partial }n(t,R)}{\mathrm{\partial }t}=n^{\ast }{\displaystyle \frac{n(t,R)}{t_b(R)}.}}$$ 3.4a

By integrating equation (3.4a) with time, we have

$$n(t,R)=n_0(R)\exp \left({\displaystyle \frac{n^{\ast }\hspace{0.17em}t}{t_b(R)}}\right),$$ 3.4b

where n₀(R) = n(0, R). Consider now n₀(R) = n₀, $\mathrm{\forall }R$, i.e. before any virus reproduction occurs the population has equal number of virions for any size. Now the total number of virions at the time t is $N(t)={\int }_{R_{\min }}^{R_{\max }}n(t,R)\hspace{0.17em}\mathrm{d}R$, via numerical integration, and the statistical frequency of virions having radius R is f(t, R) = n(t, R)/N(t), giving finally

$$f(t,R)={\displaystyle \frac{n_0}{N(t)}\exp \left({\displaystyle \frac{n^{\ast }\hspace{0.17em}t}{t_b(R)}}\right).}$$ 3.5

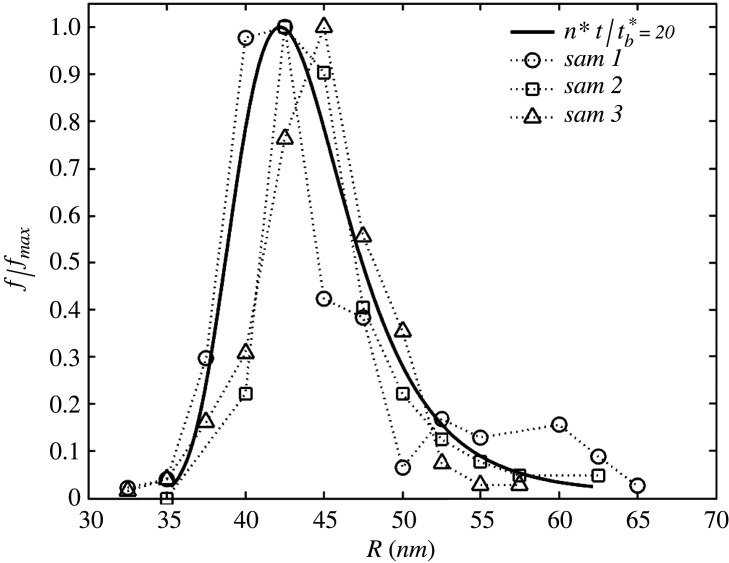
From equation (3.5), we can now compare the statistical distribution of virion size with experimental observations. Figure 6 reports this comparison by taking three virus population samples (sam 1, 2 and 3) from [11], where the vertical axis reports the normalized frequency with respect to its maximum in the population, f/f_max. Here, f = f_max if R = R_opt. In the proposed model, one has to define the time of observation t, which here is taken as $t=20\hspace{0.17em}{t}_b^{\ast }/n^{\ast }$. The parameter values used in this figure are e_b0 = 0.2 and R* = 45 nm, estimated from the ratio R_min/R_max of the samples [11], following the same procedure as in figure 3b.

Figure 6.

Distribution of the normalized statistical frequency f/f_max versus virion radius R. The theoretical prediction (solid line) is generated with the proposed model, assuming hereditary size and exponential replication from equation (3.4) and (3.5). Taking $n^{\ast }t/t_b^{\ast }=20$ as a fitting parameter, the prediction is compared against experimental observation on virion size polydispersity for SARS-CoV-2 [11], on three virus populations samples (sam 1, 2, and 3).

In the model here described, the virus population evolves toward the ideal condition at which all virions have radius R_opt, at t → ∞, hence no polydispersity and f(∞, R) = δ(R − R_opt), with δ the Dirac delta. This condition is never reached in real virus populations, and this is probably due to the imperfect hereditariness of size, by which a virion might replicate itself into virions having slightly different radii, or due to finite availability of building blocks. A more comprehensive model should consider these aspects, but this is beyond the present scope.

3.4. Size constraints of virus infection

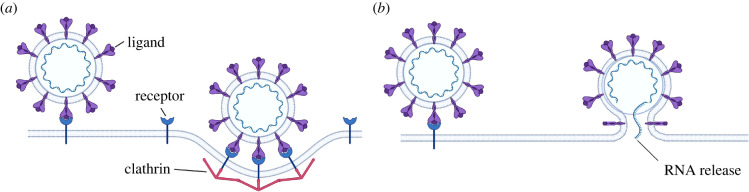
The experimental comparisons presented in the previous sections rely on the hypothesis that budding provides the tightest constraint to virion size. The other most important size-limiting process, in the life of a virion, is infection. This section discusses the size limitations introduced by infection, a process occurring via two main mechanisms, (i) receptor- and clathrin-mediated endocytosis, and (ii) membrane fusion. (i) requires the membrane of the host cell to wrap around the envelope to produce an endosome (figure 7a), which later fuses with the enveloped membrane inside the cytosol to release RNA [3,27]; (ii) involves the fusion of the envelope membrane with that of the host cell prior to the creation of the endosome (figure 7b) [27].

Figure 7.

Infection mechanisms of enveloped viruses: (a) receptor- and clathrin-mediated endocytosis; (b) membrane fusion.

3.4.1. Endocytosis

The kinetics of the process is here controlled by the diffusion of receptors [3], and the proposed model applies by considering that now TPs stand for receptors (instead of virus ligands). In this case, equation (2.6) is rewritten to

$$e_e\ge F_{\tilde{\rho }}(\alpha ),$$ 3.6a

where

$$e_e=e_{e0}-2\tilde{B}{\left({\displaystyle \frac{R^{\ast }}{R}}\right)}^2-2{\tilde{B}}_c{\left({\displaystyle \frac{R^{\ast }}{R}-{\displaystyle \frac{R^{\ast }}{R_c}}}\right)}^2,$$ 3.6b

is the endocytosis energy (the driving force for wrapping), with

$$e_{e0}=e_{RL}+{\tilde{\rho }}_c\hspace{0.17em}{e}_c-\tilde{\sigma }{\epsilon }_S+1-\tilde{\rho }+\ln \tilde{\rho },$$ 3.6c

the input endocytosis energy, and $F_{\tilde{\rho }}(\alpha )$ the kinetic function described in equations (2.6b,c). As previously discussed, TP diffusion is size independent, thus the value of D is here again given in table 1. In equation (3.6), ${\tilde{B}}_c$ is the bending rigidity of the clathrin coat (taken to be zero in the absence of clathrin), R_c is its spontaneous radius of curvature, e_RL is the receptor–ligand binding energy, $\tilde{\rho }={\rho }_{r0}/{\rho }_b$, with ρ_r0 the surface density of receptors in the resting membrane, ρ_b the density of receptors in the wrap (equivalent to the ligand density [3]), e_c is the binding energy of the clathrin pit with the backing of the receptor [18] and ${\tilde{\rho }}_c={\rho }_c/{\rho }_b$, with ρ_c the surface density of clathrin pits.

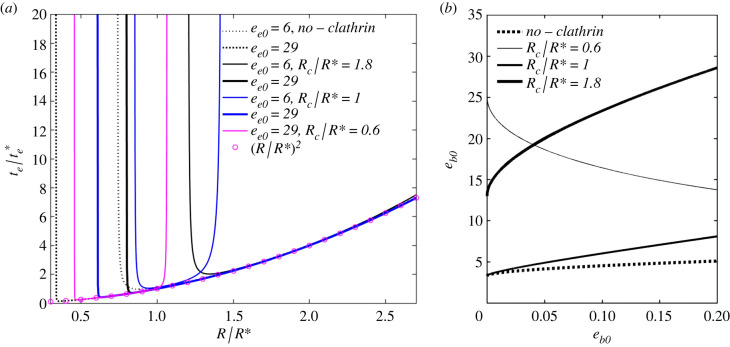
Figure 8a provides the dimensionless endocytosis (wrapping) time $t_e/t_e^{\ast }$, with $t_e^{\ast }=t_b^{\ast }$, versus dimensionless virion radius R/R*, at various input energy e_e0, and normalized spontaneous curvature of clathrin R_c/R*. The results are obtained in the same way as in figure 4a, with e_b substituted with e_e, from equation (3.6b). The dashed black lines represent the plots in the absence of clathrin (${\tilde{B}}_c=0$ and ${\tilde{\rho }}_c=0$), while the solid black, blue and magenta lines represent the plots in the presence of clathrin. For all these cases, the parameter values are taken from table 1, with ε_S = 0 and the median values for e_c. In the absence of clathrin (receptor-mediated endocytosis), this gives e_e0 = 6.4−23.6 and a median of e_e0 = 17.5 (taking the median for e_RL and averaged over $\tilde{\rho }=0.01$–0.1). In the presence of clathrin, we have e_e0 = 12.13−29.3 with a median of e_e0 = 23.24. This is then rounded to e_e0 = 6−29 in the figure. For R_c/R* = 0.6, e_e0 = 6 gives negative e_e, thus equation (3.6a) is violated and endocytosis cannot occur. For this reason, this plot is omitted. All the reported plots can be approximated by $t_e/t_e^{\ast }\approx {(R/R^{\ast })}^2$ (magenta circles) for R_min < R < R_max. Also, the plots consider $\tilde{\rho }=0.01$, where $\tilde{\rho }=0.1$ gives nearly identical plots, hence omitted. As observed by [3] and confirmed in this figure, endocytosis provides size limitations, where virions having a radius smaller than R_min are denied entry due to the excessive (bending) energy barrier. The same authors also predicted a maximum radius R_max due to receptor depletion. However, as calculated by [18], and shown in this figure, the presence of clathrin also creates an R_max and generally provides a tighter constraint to the minimum and maximum virion radii. The input energy e_e0 appears here not to affect the dimensionless endocytosis time significantly, so long that the virion size R is within its limits. However, e_e0 has a strong influence on virion size limitations, particularly in the presence of clathrin, and more so for R_c ≤ R*.

Figure 8.

(a) Dimensionless endocytosis (wrapping) time $t_e/t_e^{\ast }$ ($t_e^{\ast }=t_b^{\ast }$) versus virion size R/R*, at various input endocytosis energy e_e0 and normalized spontaneous radius of curvature R_c/R*. The results are obtained in the same way as in figure 4a, with e_b substituted with e_e from equation (3.6b). The clathrin bending modulus is B_c = 15B (table 1). (b) Minimum e_e0 versus budding input energy e_b0, for which the highest selective pressure is provided by budding, with clathrin (solid line), at various R_c/R*, and with no clathrin (dashed line), from equation (3.8).

Taking R ≈ 50 nm, we have R/R* ≈ 1, from which $t_e\approx t_b^{\ast }\approx 0.15$–2.93 min. This is in qualitative agreement with the 2−58 s optimal wrapping time calculated in [3].

Let us now analyse the condition for which budding provides the tightest selective pressure to the size of the virions. Let us assume that we are at the limit for budding spontaneity, i.e. α = 0 and t_b → ∞, giving e_b = 0. From equation (2.7a), this condition gives that R = R_min or R = R_max from equation (2.8b,c), i.e.

$${\displaystyle \frac{R^{\ast }}{R}=1\pm \sqrt{{\displaystyle \frac{e_{b0}}{2\tilde{B}}}}.}$$ 3.7

Substitution of equation (3.7) into (3.6b), with condition (3.6a) under α = 0, gives

$${\displaystyle \frac{e_{e0}}{2\tilde{B}}\ge {\left(1\pm \sqrt{{\displaystyle \frac{e_{b0}}{2\tilde{B}}}}\right)}^2+{\displaystyle \frac{B_c}{B}{\left(1\pm \sqrt{{\displaystyle \frac{e_{b0}}{2\tilde{B}}}}-{\displaystyle \frac{R^{\ast }}{R_c}}\right)}^2,}}$$ 3.8

where the tightest limitation comes with ± substituted with +.

Figure 8b reports the minimum input energy e_e0 satisfying equation (3.8) as a function of e_b0 and R_c/R*, and with B_c = 0 and B_c = 15B from table 1. The dashed lines report the case of no clathrin. In the range of the parameter values reported in table 1, the range of e_e0 discussed in figure 8a, and in the absence of clathrin, equation (3.8) is always satisfied. In the presence of clathrin, equation (3.8) is satisfied for all cases apart from that of R_c/R* = 0.6 and 1.8 for certain values of e_b0. For the adopted median parameter values and R_c/R* = 1, equation (3.8) is always satisfied. Thus, we can conclude that, for the most representative cases of infection via endocytosis, the tightest size constraint is dictated by budding.

3.4.2. Membrane fusion

This process involves virus unwrapping, as shown in figure 7b and figure 9c, where the membrane of the virion fuses with that of the host and transits from a spherical envelope to a flat configuration. In this case, the ligands of the virion, one by one, detach from the nucleocapsid and then diffuse away toward remote regions in the host membrane. It starts with the formation of a fusion pore, via molecular reconfiguration of receptor–ligand bonds (proteolytic cleavage). In this case, TP stands for the ligands of the virus. The propagation of the fusion pore is described by the solution to the transient problem reported in appendix B, under the assumption of a diffusion-limited regime, where the process continues thanks to the detachment and diffusion of TPs. This is described by

$$e_f\ge F_{{\tilde{\rho }}_f}(\alpha ),$$ 3.9a

with

$$e_f=e_{\hspace{0.17em}f0}+2\tilde{B}{\left(1-{\displaystyle \frac{R^{\ast }}{R}}\right)}^2,$$ 3.9b

the fusion energy,

$$e_{\hspace{0.17em}f0}=e_{RL}\gamma -{\tilde{g}}_m-e_T+\tilde{\sigma }{\epsilon }_S-(1+{\tilde{\rho }}_f+\ln {\tilde{\rho }}_f),$$ 3.9c

the input fusion energy and

$$F{(\alpha )}_{\tilde{\rho }}=({\tilde{\rho }}_f+1)f(\alpha )+\ln \left[1+\left(1+{\displaystyle \frac{1}{{\tilde{\rho }}_f\hspace{0.17em}}}\right)f(\alpha )\right],$$ 3.9d

the kinetic function of fusion, with ${\tilde{\rho }}_f={\rho }_{\hspace{0.17em}f0}/{\rho }_b$, where ρ_f0 is the equilibrium TP density in the host membrane, and f(α) is given by equation (2.6c). In equations (3.9), γ = S_f/S_b with S_f the area of the nucleated fusion pore and S_b = 4πR² the surface of the envelope. The speed factor α identifies the velocity of the fusion process. As specified in appendix B, for e_f → ∞ we have that α → ∞, i.e. TP diffusion can be indefinitely fast (unlike budding and endocytosis). Due to the unlimited speed factor, TP diffusion can become faster than membrane relaxation or equally fast. In this case, the fusion time t_f calculated in appendix B is inaccurate since the proposed model relies on the assumption that viscoelastic relaxation is much faster than TP diffusion. This model neglects again the bending energy of the membrane outside the envelope and, thus, also the line energy of the rim. This approximation is again based on the hypothesis that the membrane outside the wrap assumes a catenoid-like configuration [4].

Figure 9.

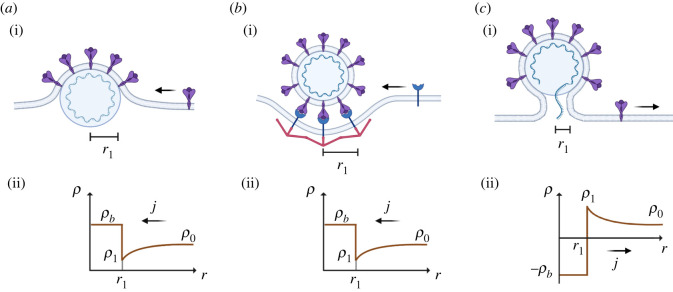
Schematic (i) of budding (a), endocytosis (b) and fusion (c), with corresponding TP density distribution (ii). The density distribution promotes the TP flux from remote regions toward the bud, for budding and endocytosis, and from the bud toward remote regions for fusion.

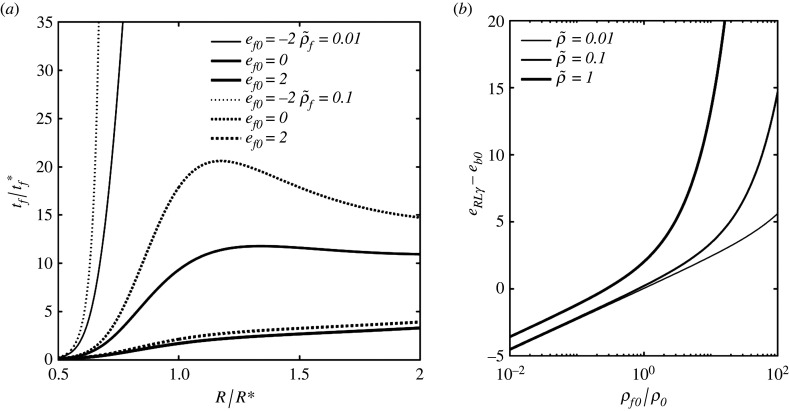
Figure 10a plots the dimensionless fusion time $t_f/t_f^{\ast }$, with $t_f^{\ast }$ the characteristic fusion time, versus R/R*, at various e_f0 and ${\tilde{\rho }}_f$. The fusion time is given by equation (2.5), with t_b substituted with t_f, as function of the speed factor α. The latter is then calculated numerically as function of the fusion energy e_f from equation (3.9) and (B 6) in appendix B. The characteristic fusion time is

$$t_f^{\ast }={\displaystyle \frac{R^{\ast 2}}{D}.}$$ 3.10

Figure 10.

(a) Dimensionless fusion (unwrapping) time $t_f/t_f^{\ast }$ versus virion size R/R* at various e_f0 and ${\tilde{\rho }}_f$, from equations (2.5) (with t_b substituted with t_f) and (3.9) and from equation (B 6) from appendix B; (b) Minimum fusion pore energy e_RLγ required to promote membrane fusion at the limiting conditions of budding, as described in equation (3.11), versus ρ_f0/ρ_f (ratio of TP densities host-to-mother) for various equilibrium TP densities $\tilde{\rho }$ in the mother cell.

As shown in this figure, t_f is smallest for R ≈ R_min or R ≈ R_max, and largest for R near R*, showing an opposite correlation compared with t_b and t_e. This is intuitive since the bending energy is now a promoter of fusion, rather than an energy barrier. Also, the fusion time and size-dependent kinetics appear here to be highly sensitive to the input energy e_f0.

It is important to notice that virus infection only requires the injection of RNA, which can occur as soon as the pore is large enough, compared with the envelope size. Albeit completed unwrapping is far from necessary for infection, we can still assume that the infection time is proportional to t_f. It is interesting to notice that fusion can occur with negative e_f if R ≪ R*. From the parameter values in table 1 and equation (3.10), we can obtain $t_f^{\ast }=0.25\hspace{0.17em}\hspace{0.17em}\mathrm{s}$. The relaxation time of the cell membrane is t_r = 0.5−0.75 s (measured on a red blood cell [28]), thus the prediction reported in figure 10a is reliable only for e_f ≤ 0 and R/R* ≥ 0.7. That is, for the reported smallest values of $t_f/t_f^{\ast }$ (for R → 0.5), TP diffusion is faster than membrane relaxation, hence, the latter controls the kinetics of the process and the proposed model is inapplicable.

From figure 10a, we can deduce that $t_f/t_f^{\ast }\approx 0$–100, for the observed parameter values, thus t_f ≈ 1−10 s.

Let us now analyse the hypothesis of budding as the tightest size constraint. Because the statistical size frequency of virions has the median at an intermediate radius, and lower virion count for larger and smaller radii, it is intuitive to consider that membrane fusion has limited influence on the size polydispersity of a virus population by looking at figure 10a. However, it is useful to analyse the critical conditions required for the spontaneity of membrane fusion. By equating equations (2.7) with (3.9), under α = 0, this condition becomes

$$e_{RL}\gamma -e_b\ge \tilde{\rho }\left(1+{\displaystyle \frac{{\tilde{\rho }}_f}{\tilde{\rho }}}\right)+\ln \left({\displaystyle \frac{{\tilde{\rho }}_f}{\tilde{\rho }}}\right).$$ 3.11

Because e_b ≤ e_b0, from equations (2.7), we can deduce that R = R* produces the worst-case scenario in equation (3.11) so that one can simply substitute e_b with e_b0 in this equation.

Figure 10b reports the minimum e_RLγ − e_b0 required to favour fusion, from the right-hand side of equation (3.11) and for various values of $\tilde{\rho }$ and ${\tilde{\rho }}_f/\tilde{\rho }={\rho }_{\hspace{0.17em}f0}/{\rho }_0$. Noteworthy, ρ₀ is the equilibrium density of ligands in the mother cell, where the virion is generated, while ρ_f0 is that in the infected (host) cell. We can observe that a larger ρ_f0/ρ₀ raises the bar for spontaneous fusion, while a smaller ρ_f0/ρ₀ can facilitate fusion. That is, according to this model, the first infection of a cell is far more likely to succeed and proceed at a high rate than the infection of a cell that has already been infected multiple times. Considering now ρ_f0 = ρ₀, equation (3.11) reduces to $e_{RL}\gamma -e_{b0}\ge 2\tilde{\rho }$. For the range of parameter values adopted in table 1, for e_b0 and e_RL, one can estimate γ ≥ 0.0048−0.086, with median values giving γ ≥ 0.014. That is, the spontaneous formation and propagation of the fusion pore can require up to 8.6% of the envelope surface to be covered with receptor–ligand bonds. Take now the fusion pore surface $S_f=\pi r_f^2$, with r_f its radius, and S_f = γ S_b = γ 4πR², with R ≈ 50 nm from table 1. We can then estimate the pore radius as $r_f=2R\sqrt{\gamma }=6.93$–29.33 nm, with median value at r_f = 11.62 nm. By comparing this with the ligand spacing l_b = 14 nm in table 1, we can deduce that the fusion pore requires commonly only one receptor–ligand bond to nucleate, and in some cases, it can require up to three–four bonds.

4. Conclusion

The proposed simple model provides an energetic analysis to derive size constraints and size-dependent budding time for an enveloped virus. This compares well with experimental observations on the optimal size (statistical median), giving fastest budding, in virus populations for SARS-CoV-1 & 2 (coronavirus), HIV-1, flu and HCV (hepatitis C). The model also shows a good prediction of the size polydispersity for a virus population, via a simple exponential replication model based on perfect size hereditariness, for SARS-CoV-2. The same comparison can be simply extended to the other species of enveloped virus analysed. These comparisons rely on the assumption that budding provides the tightest size constraint. This hypothesis is verified by analysing the size and energy limitations introduced by infection via receptor- and clathrin-mediated endocytosis, and via membrane fusion. Furthermore, as discussed in this article, the timescale for virus replication (via budding) is approximately 10 min, while that of virus infection goes from approximately 10 s, for membrane fusion, to approximately 1 min, for endocytosis. From this, one can observe that the life cycle of a virus can be much more impacted by the kinetics of replication than that of infection. This observation could shed light on the biophysical mechanisms involved in virus infectivity. The experimental validation presented in this paper also suggests that, for the analysed virus species, budding is mediated by TP diffusion. The model is constructed to organize its parameters in a hierarchical fashion, so that the dimensionless budding time $t_b/t_b^{\ast }$ only depends on a small number of dimensionless parameters, namely, the virion size R/R*, the availability of TPs $\tilde{\rho }$ and the input energy e_b0. While R/R* varies across a small range, $\tilde{\rho }$ and e_b0 are observed to span across at least one order of magnitude. This paper also provides a simple scaling between the budding time and these quantities. The proposed model provides a valuable tool to correlate molecular-scale properties (e.g. TP–capsid binding energy) of a single enveloped virion with the size polydispersity of a virus population. Because molecular-scale properties are often difficult to measure (e.g. to the author's knowledge, no experimental data is available for TP–capsid adhesion), this model can be used in reverse to extrapolate these properties from statistical observations on size polydispersity. Finally, the proposed model can inspire biomolecular strategies to limit virus replication by reducing the budding energy, thereby increasing the budding time of a virus population.

Appendix A. Diffusion-mediated budding (and endocytosis)

The proposed model assumes that TP diffusion controls the kinetics of the process, as discussed by [8]. In axial symmetry, the radial diffusion j is described by Fick's second law as

$$j=-D{\rho }_{,r}$$ A 1a

or

$$j=-\rho D{\mu }_{,r}$$ A 1b

with r the distance from the axis of symmetry, and D, ρ and μ = 1 + ln(ρ/ρ₀) the diffusivity, surface density and (dimensionless) chemical potential of TPs in the membrane, respectively. In this case, TP conservation imposes

$$\dot{\rho }=-{\displaystyle \frac{1}{r}{(rj)}_{,r}}$$ A 2

everywhere in the membrane, where $\dot{\rho }=\mathrm{\partial }\rho /\mathrm{\partial }t$ is the local rate of change of TP concentration, with t time. Substitution of (A 1) into (A 2) provides a partial differential equation in the function ρ(t, r), subjected to the boundary conditions ρ(t, ∞) = ρ₀ and initial conditions ρ(0, r) = ρ₀, with ρ₀ the equilibrium TP density in the unperturbed membrane (prior to budding or far away from the bud). The solution to this problem is given in [3]

$$\rho ={\rho }_0+C\hspace{0.17em}E\left({\displaystyle \frac{r^2}{4Dt}}\right),$$ A 3

with C an integration constant and $E(x)={\int }_x^{\mathrm{\infty }}\exp (-u)\hspace{0.17em}\mathrm{d}u/u$ the exponential integral function.

The total number of TPs in the system is

$$n_{TP}={\rho }_b{S}_b+2\pi {\int }_r^{\mathrm{\infty }}\rho r\hspace{0.17em}\mathrm{d}r,$$ A 4

with ρ_b the (constant) TP density on the bud, S_b the surface of the bud and r₁ the distance between the bud rim and the axis of symmetry (figure 1a). The assumption of constant ρ_b (and spacing, $l_b={\rho }_b^{-1/2}$, [18]) derives from observations on ligand density and spacing for influenza-A virus [29] and SARS-CoV-2 [30]. In this case, TP conservation imposes ${\dot{n}}_{TP}=0$ on equation (A 4), which, considering ${\dot{S}}_b=2\pi r_1{\dot{r}}_1$ and (A 1–A 3), gives

$$({\rho }_b-{\rho }_1){\dot{r}}_1+j_1=0,$$ A 5

where ρ₁ and j₁ are the TP density and flux at the bud rim r = r₁, respectively. Because the condition at equation (A 5) must be satisfied at any instant, the substitution of (A 3) into (A5) gives the kinetic law for the moving boundary at equation (2.4).

By substituting (A 1), (A 3) and (2.4) into (A 5), the integration constant computes to

$$C={\displaystyle \frac{{\alpha }^2({\rho }_b-{\rho }_0)}{{\alpha }^{2}E({\alpha }^2)-\exp (-{\alpha }^2)}.}$$ A 6

To calculate α, one has to define the thermodynamics of the problem. The free energy of the system is described by equation (2.1), and its rate of change, from the substitution of (A 1), (A 2) and (A 5) into it, gives

$$\begin{array}{rl}{\displaystyle \frac{\dot{\psi }}{2\pi kT}}& =\left[-{\rho }_b{e}_T-g_m+\sigma {\epsilon }_S+{\rho }_1-{\rho }_b+{\rho }_b\ln \left({\displaystyle \frac{{\rho }_b}{{\rho }_1}}\right)+2B{\left({\displaystyle \frac{1}{R}-{\displaystyle \frac{1}{R^{\ast }}}}\right)}^2\right]\\ & r_1{\dot{r}}_1-{\displaystyle \frac{\dot{q}}{2\pi kT},}\end{array}$$ A 7a

with

$${\displaystyle \frac{\dot{q}}{2\pi kT}={\int }_{r_1}^{\mathrm{\infty }}D\rho {({\mu }_{,r})}^{2}r\hspace{0.17em}\mathrm{d}r.}$$ A 7b

The term in equation (A 7b) is the energy dissipation due to the diffusive transport of TP across the membrane, from remote locations to the bud rim. To ensure the spontaneity of the process, one needs to ensure a continuous free energy reduction, i.e. $\dot{\psi }\le 0$ (second law of thermodynamics).

Figure 9a gives the distribution of ρ across the membrane, from equation (A 6) substituted into (A 3) and with ρ_b > ρ₀. For budding and endocytosis (figure 9b,c), ρ₁ < ρ₀ is required to prompt the flux of TP toward the bud. From equation (A 7b) one can deduce that $\dot{q}\ge 0$ is always satisfied. At this point, budding spontaneity requires that the term in [ ], in equation (A 7a), satisfies [ ] ≤ 0. This condition, from the substitution of equation (A 6) into (A 3) and the result into (A 7a), ultimately provides equation (2.6).

The kinetic constant is then obtained from $\alpha =F_{\tilde{\rho }}^{-1}(e_b)$, by inverting equation (2.6a). This is here done numerically, giving

$$\alpha ={\alpha }_{\mathrm{\infty }}\tilde{\alpha }(e_b),$$ A 8

with ${\alpha }_{\mathrm{\infty }}=F_{\tilde{\rho }}^{-1}(\mathrm{\infty })$ the maximum speed factor, and $\tilde{\alpha }(e_b)$ the normalized speed factor giving $\tilde{\alpha }(0)=0$ and $\tilde{\alpha }(\mathrm{\infty })=1$. The latter is fitted to the function

$$\tilde{\alpha }(e_b)=1-\exp \left(-k_1\hspace{0.17em}{e}_b-k_2\sqrt{e_b}\right).$$ A 9

The values for α_∞ and the fitting constants k₁ and k₂ are given in table 2 for $\tilde{\rho }=0.01$ and $\tilde{\rho }=0.1$.

Table 2.

Fitting parameters for equation (A 9).

$\tilde{\rho }$	α∞	k1	k2
0.01	0.0415	0.7443	0.7002
0.1	0.1846	0.8043	0.6326

The fitting accuracy of equation (A 9), with the coefficients in table 2, is R² = 1 for both the adopted values of $\tilde{\rho }$.

The budding time t_b, expressed in equation (2.5) as a function of α, can be rewritten in dimensionless form as

$${\displaystyle \frac{t_b}{t_b^{\ast }}={\left({\displaystyle \frac{R}{R^{\ast }}}\right)}^2{\displaystyle \frac{1}{\tilde{\alpha }{(e_b)}^2},}}$$ A 10

with $t_b^{\ast }$ the characteristic budding time taken from equation (3.3), and $\tilde{\alpha }(e_b)$ from equation (A 9). The dimensionless budding time in equation (A 10) is finally reported in figure 4a.

Appendix B. Diffusion-mediated membrane fusion

Assuming TP diffusion controls again the kinetics of the process, in axial symmetry, the radial diffusion j is described by Fick's second law as in equation (A 1), with (A 2) giving again TP (ligand) conservation. The TP density distribution ρ_f(t, r) is again given by (A 3) with ρ and ρ₀ substituted with ρ_f and ρ_f0.

The total number of TP now is

$$n_{TP}=-{\rho }_v{S}_v+2\pi {\int }_{r_1}^{\mathrm{\infty }}{\rho }_{f}r\hspace{0.17em}\mathrm{d}r,$$ B 1

where ρ_v and S_v are the TP density and surface of the virion, and the minus on the first term on the right-hand side is due to the extraction of TPs from the envelope to then join the resting membrane (figure 9). TP conservation imposes again ${\dot{n}}_{TP}=0$ on equation (B 1), which, considering ${\dot{S}}_b=2\pi r_1{\dot{r}}_1$ and (A 1)–(A 3), gives

$$-({\rho }_v+{\rho }_1){\dot{r}}_1+j_1=0,$$ B 2

where ρ₁, r₁ and j₁ are now associated with the rim of the fusion pore. The latter advances again according to the kinetic law given by equation (2.4)

By substituting (A 1), (A 3) and (2.4) into (B 2), the integration constant computes to

$$C={\displaystyle \frac{{\alpha }^2({\rho }_{\hspace{0.17em}f0}+{\rho }_v)}{\exp (-{\alpha }^2)-{\alpha }^{2}E({\alpha }^2)}.}$$ B 3

To calculate α, one has to again define the thermodynamics of the problem. The free energy of the system is now described by

$$\begin{array}{rl}{\displaystyle \frac{\psi }{kT}=}& \left[g_m+{\rho }_v{e}_T-\sigma {\epsilon }_S-{\rho }_v\ln \left({\displaystyle \frac{{\rho }_v}{{\rho }_0}}\right)-2B{\left({\displaystyle \frac{1}{R}-{\displaystyle \frac{1}{R^{\ast }}}}\right)}^2\right]S_v\\ & +2\pi {\int }_{r_1}^{\mathrm{\infty }}{\rho }_f\ln \left({\displaystyle \frac{{\rho }_f}{{\rho }_{\hspace{0.17em}f0}}}\right)r\mathrm{d}r,\end{array}$$ B 4

and its rate of change, from the substitution of (A 1), (A 2) and (B 2) into it, gives

$$\begin{array}{rl}{\displaystyle \frac{\dot{\psi }}{2\pi kT}=}& \left[g_m+{\rho }_v{e}_T-\sigma {\epsilon }_S-2B{\left({\displaystyle \frac{1}{R}-{\displaystyle \frac{1}{R^{\ast }}}}\right)}^2+{\rho }_1+{\rho }_v+{\rho }_v\ln \left({\displaystyle \frac{{\rho }_1}{{\rho }_v}}\right)\right]r_1{\dot{r}}_1\\ & -{\displaystyle \frac{\dot{q}}{2\pi kT},}\end{array}$$ B 5

with $\dot{q}$ the energy dissipated by TP transport, given by equation (A7b). To ensure the spontaneity of the process, one needs to again ensure continuous free energy reduction, i.e. $\dot{\psi }\le 0$ (second law of thermodynamics). Here, one can again ensure spontaneity by imposing [ ] ≤ 0 for the terms within [ ] in equation (B5). This then provides the condition in equation (3.9).

The fusion time t_f, similarly to the budding time, can be written in dimensionless form as

$${\displaystyle \frac{t_f}{t_f^{\ast }}={\left({\displaystyle \frac{R}{R^{\ast }}}\right)}^2{\displaystyle \frac{1}{\alpha {(e_f)}^2},}}$$ B 6

and plotted in figure 10a, with $t_f^{\ast }$ the characteristic fusion time given by equation (3.10). Here, the relation α(e_f) in equation (B 6) is calculated from the numerical solution of equation (3.9d).

Data accessibility

This article has no additional data.

Authors' contributions

M.B.: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, validation and writing—original draft.

Conflict of interest declaration

I declare I have no competing interests.

Funding

This work was supported by the New Frontiers in Research Funds – Exploration (grant no. NFRFE-2018-00730) and the Natural Sciences and Engineering Research Council of Canada (NSERC) (grant nos. RGPIN-2017-04464 and ALLRP554607-20).