Abstract
The learning process and hyper-parameter optimization of artificial neural networks (ANNs) and deep learning (DL) architectures is considered one of the most challenging machine learning problems. Several past studies have used gradient-based back propagation methods to train DL architectures. However, gradient-based methods have major drawbacks such as stucking at local minimums in multi-objective cost functions, expensive execution time due to calculating gradient information with thousands of iterations and needing the cost functions to be continuous. Since training the ANNs and DLs is an NP-hard optimization problem, their structure and parameters optimization using the meta-heuristic (MH) algorithms has been considerably raised. MH algorithms can accurately formulate the optimal estimation of DL components (such as hyper-parameter, weights, number of layers, number of neurons, learning rate, etc.). This paper provides a comprehensive review of the optimization of ANNs and DLs using MH algorithms. In this paper, we have reviewed the latest developments in the use of MH algorithms in the DL and ANN methods, presented their disadvantages and advantages, and pointed out some research directions to fill the gaps between MHs and DL methods. Moreover, it has been explained that the evolutionary hybrid architecture still has limited applicability in the literature. Also, this paper classifies the latest MH algorithms in the literature to demonstrate their effectiveness in DL and ANN training for various applications. Most researchers tend to extend novel hybrid algorithms by combining MHs to optimize the hyper-parameters of DLs and ANNs. The development of hybrid MHs helps improving algorithms performance and capable of solving complex optimization problems. In general, the optimal performance of the MHs should be able to achieve a suitable trade-off between exploration and exploitation features. Hence, this paper tries to summarize various MH algorithms in terms of the convergence trend, exploration, exploitation, and the ability to avoid local minima. The integration of MH with DLs is expected to accelerate the training process in the coming few years. However, relevant publications in this way are still rare.
Keywords: Deep learning (DL), Artificial neural networks (ANN), Meta-heuristics (MH), Hyper-parameters optimization, Training, And gradient-based back propagation (BP) learning algorithm
Introduction
Artificial Intelligence (AI) was first introduced in the ideas and hypotheses of Gottfried Leibniz [1]. In 1943, McCulloch and Pitts proposed an evolutionary model of the human brain that began research on the artificial neural network (ANN) [2]. ANNs can learn and recognize and solve a wide range of complex problems. Today, ANNs and deep learning (DL) techniques are the most popular and main methods of machine learning (ML) algorithms [3–10]. Figure 1 compares the accuracy of a typical machine learning algorithm and a deep neural network (DNN). As can be seen, if sufficient data and computational power are available, DL techniques perform better (in terms of accuracy) than conventional machine learning approaches [2].
Fig. 1.
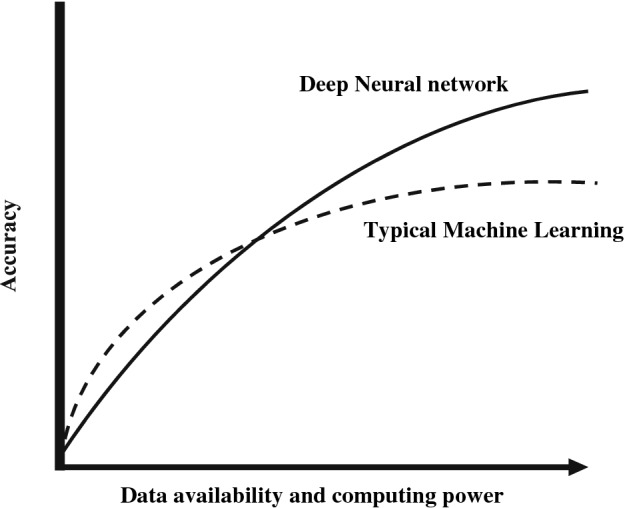
Comparison of the accuracy of a typical machine learning algorithm and a deep neural network [2]
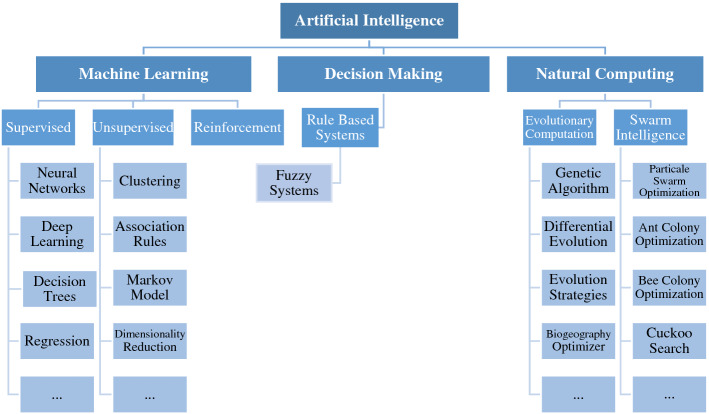
Since 2006, DL has become a popular topic in machine learning. Its position in AI and data science has been shown in Fig. 2 [10]. DL techniques are superior to traditional ML algorithms due to data availability and systems processing power development [10, 11]. In smaller databases and simple applications, traditional ML algorithms perform better because they are easier to implement. This is one of the most important reasons that neural networks and DL techniques had not grown much in the early years [1, 2, 12]. With the advent of the Big Data era, much faster data collection, storage, updating, and management advances have become possible. In addition, the development of GPU has made efficient processing in large data sets. These dramatic advances have led to recent advances in DL techniques [2, 10]. Additionally, reducing the computation time and increasing the convergence process have increased the popularity of these algorithms [3, 4]. Moreover, the position of DL and ANNs in the taxonomy of artificial intelligence approaches has been shown in Fig. 3.
Fig. 2.
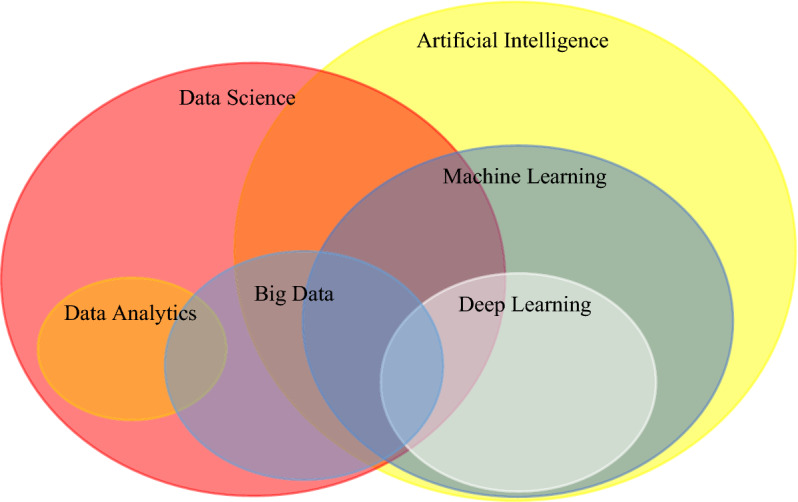
The position of deep learning in artificial intelligence and data science [10]
Fig. 3.
Taxonomy of artificial intelligence approaches: Machine learning, natural computing, and decision making
ANNs have been used in various applications, including function approximation [13, 14], classification [15–20], feature selection [21, 22], medical image registration [6], pattern recognition [23–26], data mining [27], signal processing [28], Nonlinear system identification [29, 30], speech processing [31], etc. In addition, different DL methods have been used in various applications, including classification [32–36], prediction [37–39], Phoneme recognition [40], hand-written digit recognition [41–46], etc.
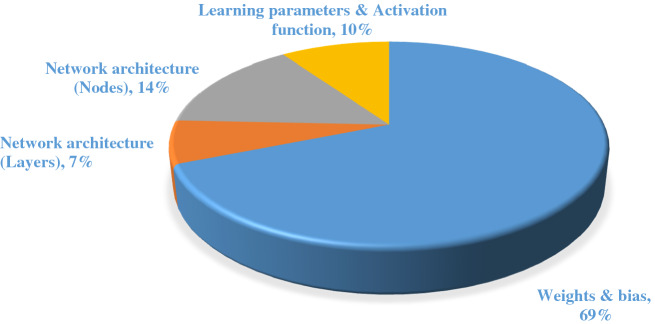
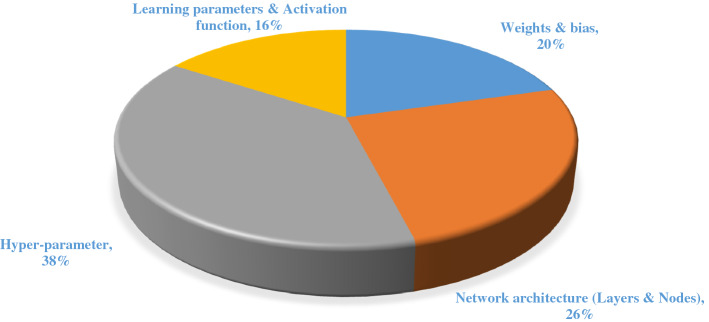
Given the importance of using ANNs and DL methods in various applications, identifying weaknesses and improving these algorithms is one of the current issues in machine learning. The learning process of ANNs and DL architectures is considered one of the most difficult machines learning challenges. Over the past two decades, optimizing the structure and parameters of ANNs and DLs has been one of the main interests of researchers [8–10]. Optimization of ANNs and DLs is often considered from several aspects: optimization of weights, hyper-parameters, network structure, activation nodes, learning parameters, learning algorithm, learning environment, etc. [9].
Optimizing weights, biases, and hyper-parameters is one of the most important parts of neural networks and DL architectures. In fact, ANNs and DLs are distinguished by two pillars of structure and learning algorithm. In many past studies, gradient-based methods have been used for architecture training. However, due to the limitations of gradient-based algorithms, the need to use optimization algorithms has been identified [8–10]. For example, in back propagation (BP) learning algorithm, the goal of learning is to optimize the weights and thresholds of the network to minimize the cost function.
In gradient-based learning algorithms, the cost function must be derivative to use BP. This is also one of the weaknesses of gradient-based learning algorithms. Because, in many cases, the activation function (and the cost function) is not derivative. Sigmoid activation functions are commonly used in these algorithms. In the literature, several gradient-based methods, such as Back Propagation (BP) and Levenberg Marquardt (LM) methods, have been developed to teach neural network-based systems [29]. But gradient-based methods have the following major drawbacks.
For multi-objective cost functions, they may be stuck at local minimums.
The execution time of these algorithms is very expensive due to the calculation of gradient information with thousands of iterations.
If there are several local minimums in the problem search space, the learning algorithm reaches error = 0 in the first local minimum. As a result, the learning algorithm converges in the first local minimum and will not achieve the optimal solution. MH algorithms easily escape the local minimum using exploitation and exploration and are a good alternative for gradient-based algorithms.
In gradient-based learning algorithms, the cost function must be derivative. As a result, the cost function must be continuous. This is also one of the weaknesses of gradient-based learning algorithms. Because, in many cases, the activation function is not derivative. For example, if a step function were used instead of the sigmoid function, all backward calculations in gradient-based learning algorithms would be useless.
At first, Conjugate Gradient Algorithm [47], Newton's Method [48], Stochastic Gradient Descent (SGD) [49], and Adaptive Moment Estimation (Adam) [50] were developed to improve gradient-based learning algorithms, which have better generalizability and convergence than the BP algorithm. However, these methods' neural networks and DL architectures are considered "black boxes" [8]. Because it cannot be interpreted with human intuition. Evolutionary and swarm intelligence algorithms have provided a generalized and optimal network [51–54].
Since training the ANNs and DLs is an NP-hard optimization problem, their structure and parameters optimization using the meta-heuristic (MH) algorithms has been considerably raised. As an optimization problem, MH algorithms formulate the optimal estimation of DL components (such as hyper-parameter, weights, number of layers/neurons, learning rate) [8]. The existence of multiple objectives in optimizing ANNs and DLs, such as error minimization, network generalization, and model simplification, has increased the need for multi-objective MH algorithms. Using MH algorithms to optimize ANNs and DL architectures is still challenging, and more research is needed. Using MH algorithms to train DLs improves the learning process. This increases the accuracy of the algorithm and reduces its execution time.
The rest of the paper is organized as follows: Sect. 2 shows the research methodology. In Sect. 3, first the concept of deep learning models is discussed, then some well-known and state-of-the-art competitive meta-heuristic algorithms are introduced. In Sect. 4, a comprehensive review of the training ANNs and DLs using MH algorithms has been collected. In Sect. 5, the analysis of statistical results from the literature review, challenges and future perspectives are reviewed. Finally, in Sect. 6, the conclusion of this paper is presented.
Methodology
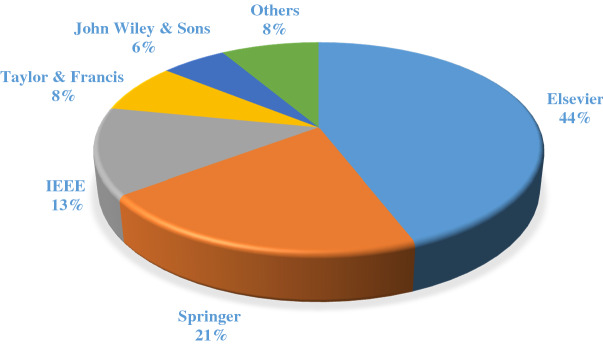
This paper has used 440 papers from different journals and publishers in the field of training ANNs and DL architectures (by MH algorithm) for a systematic literature review. First, 627 papers were reviewed, and after reading all the papers, 440 papers entered the next stage. This study systematically searched Google Scholar, Web of Science, and Scopus databases to find related papers. In particular, a thorough search was conducted in Elsevier, IEEE, Springer, Taylor & Francis, John Wiley & Sons, MDPI, Tech Science Press, and other journals. Some conference papers were also selected. In addition, we searched for papers sources to find missing papers. In this paper, only the papers published in English were selected. The following keyword combinations have been used to search for papers:
‘Deep learning’, ‘Artificial neural networks’, ‘Meta-heuristics’, ‘Parameters optimization’, ‘Optimized, ‘Training’, ‘Learning algorithm’, ‘Deep Autoencoder’, ‘Adaptive Network Fuzzy Inference System’, ‘Convolutional Neural Network’, ‘Deep Boltzmann Machine’, ‘Deep Belief Network’, ‘Deep Neural Networks’, ‘Evolutionary Deep Networks’, ‘Feed Forward Neural Network’, ‘Generative Adversarial Network’, ‘Long Short-Term Memory’, ‘Machine Learning’, ‘Radial Basis Function Neural Network’, ‘Recurrent Neural Network’, ‘Artificial Bee Colony’, ‘Ant Colony Optimization’, ‘Artificial Intelligence’, ‘Bat Algorithm’, ‘Biogeography-Based Optimization’, ‘Chimp Optimization Algorithm’, ‘Cuckoo Search’, ‘Differential Evolution’, ‘Evolutionary Algorithm’, ‘Evolutionary Computation’, ‘Evolutionary Deep Learning’, ‘Evolution Strategy’, ‘Firefly Algorithm’, ‘Genetic Algorithm’, ‘Gravitational Search Algorithm’, ‘Grasshopper Optimization Algorithm’, ‘Grey Wolf Optimizer’, ‘Harmony Search’, ‘Jaya Algorithm’, ‘Memetic Evolution Algorithm’, ‘Multi-objective Optimization’, ‘Non-dominated Sorting Genetic Algorithm’, ‘Particle Swarm Optimization’, ‘Quantum-Based Algorithm’, ‘Simulated Annealing’, ‘Swarm Intelligence’, ‘Trajectory-Based Optimization’, ‘Tabu Search’, and etc.
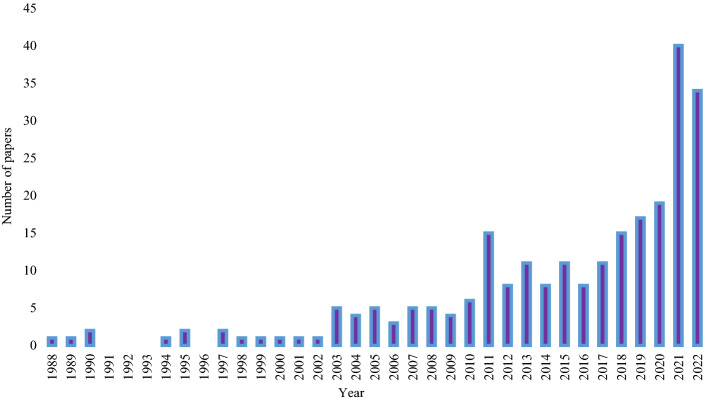
In this paper, we have tried to collect and discuss all research from the beginning of 1988 to 2022 (September), and therefore 627 articles were selected. The bibliometric tool in this paper was such that first, all papers' titles and the abstract quality of journals based on JCR were reviewed. After this initial review, 187 papers were deleted. Then, the papers that entered the next phase were thoroughly reviewed, and all the discussions and challenges related to this literature review were presented in the next sections.
After analyzing the candidate papers, we found that optimizing the parameters of artificial neural networks and deep learning architectures is a major challenge, and meta-heuristic algorithms are a promising way to solve this challenge. We also noticed that by the mid-2022, there would be a big gap in collecting all papers in this field. Finally, the research questions that need to be answered are as follows:
Why is the optimization of ANNs and DL parameters important?
Which MH algorithms are more used to optimize ANNs and DL architectures?
Which of the ANN and DL parameters are optimized by meta-heuristic algorithms?
Which applications (and dataset) are solved by DLs optimized by meta-heuristic algorithms?
Which ANN and DL architectures are optimized by meta-heuristic algorithms?
What is the effect of using meta-heuristic algorithms to optimize ANNs and DL architectures?
What is the effect of improving meta-heuristic algorithms (and combination of MHs) to optimize ANNs and DL architectures?
Background
In the late 1990s, two events created a new challenge in neural networks that marks the beginning of DL today. Long short-term memory (LSTM) was introduced by Hochreiter and Schmidhuber in 1997 and is still one of the most popular DL architectures [55]. In 1998, LeCun et al. developed the first convolutional neural network (CNN), LeNet-5, which yielded significant results in the MNIST dataset [56]. Neither CNN nor LSTM attracted the attention of the large AI community at the time. The last event in the return of deep neural networks (DNNs) was a paper by Hinton et al. in 2006 that introduced deep belief networks (DBN) and produced far better results in the MNIST dataset [57, 58]. After this paper, the renaming of deep neural networks to DL was completed, and a new era in the history of AI began. Figure 4 shows common DL architectures, which are: Long short-term memory (LSTM), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBN), Recurrent Neural Networks (RNN), Deep Boltzmann Machines (DBM), Deep Auto Encoder (DAE), and Deep Neural Networks (DNN).
Fig. 4.
Common deep learning architectures
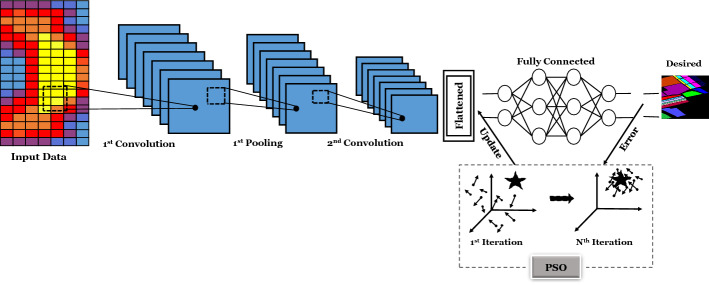
Much more research is needed to train and optimize the parameters and structure of ANNs and DL architectures. The learning process of ANNs and DLs is one of the most difficult machines learning challenges and has recently attracted the attention of many researchers [8, 10]. Figure 5 shows an example of the evolutionary deep learning architecture (PSO-DCNN) for classification problem.
Fig. 5.
An example of the evolutionary deep learning architecture (PSO-DCNN) for classification problem
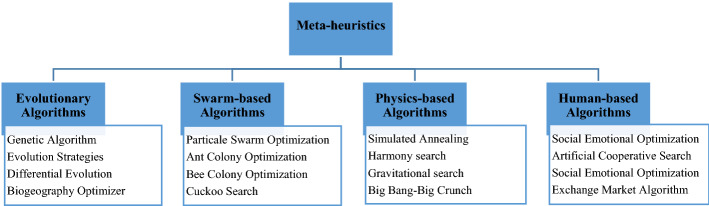
In recent years, MH algorithms have emerged as a promising method for training ANNs and DLs. The term MH was first introduced in 1986 by Glover [59]. MH methods have become very popular in the last two decades. In designing the MH algorithm, two contradictory criteria are considered: Exploration in the search space and exploitation of the best solutions. In exploration, unsearched areas are visited to ensure that all areas of the search space are searched uniformly. Potential areas are explored more fully in exploitation to find a better solution. Unlike exact methods, MHs solve large-scale problems in a reasonable time. Figure 6 shows the different types of MHs, which include four main categories.
Fig. 6.
Different types of meta-heuristic algorithms
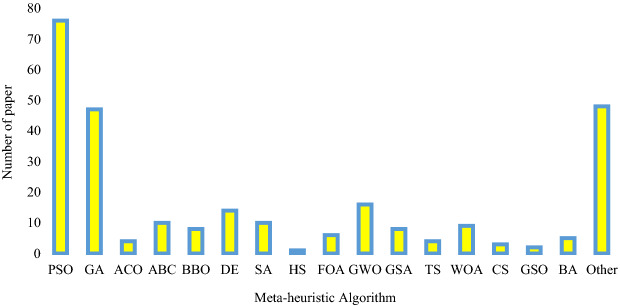
Since a few decades ago, a few nature-inspired meta-heuristic algorithms, such as genetic algorithm (GA) [60], ant colony optimization (ACO) [61], particle swarm optimization (PSO) [62], simulated annealing (SA) [63], and differential evolution (DE) [64] have been introduced and used for different optimization problems. Afterward, many studies concentrated on the improvement or adaptation of these MH algorithms for new applications. Other researchers tried to introduce new meta-heuristic algorithms by taking inspiration from nature. Some newer algorithms such as the grey wolf optimization (gwo) [65], black widow optimization (BWO) [66], chimp optimization algorithm (ChOA) [67], red fox optimization (RFO) [68], and gannet optimization algorithm (GOA) [69] are the results of such efforts. Table 1 presents general information about some of the more popular algorithms. In the following, five well-known algorithms called particle swarm optimization (PSO), genetic algorithm (GA), artificial bee colony (ABC), differential evolution (DE), biogeography-based optimization (BBO), and two state-of-the-art competitive algorithms called grey wolf optimization (GWO), and chimp optimization algorithm (ChOA) are introduced.
Table 1.
General information of some meta-heuristic algorithms
| Authors and references | Algorithm’s name and abbreviation | Year |
|---|---|---|
| Holland [60] | Genetic algorithm (GA) | 1975 |
| Kirkpatrick et al. [63] | Simulated annealing (SA) | 1983 |
| Glover [59] | Tabu search (TS) | 1986 |
| Srinivas and Deb [70] | NSGA for multi-objective optimization | 1994 |
| Eberhart and Kennedy [62] | Particle swarm optimization (PSO) | 1995 |
| Dorigo et al. [61] | Ant colony optimization (ACO) | 1996 |
| Storn and Price [64] | Differential evolution (DE) | 1997 |
| Rubinstein [71] | Cross entropy method (CEM) | 1997 |
| Mladenovic and Hansen [72] | Variable neighborhood search (VNS) | 1997 |
| Hansen and Ostermeier [73] | CMA-ES | 2001 |
| Geem et al. [74] | Harmony search (HS) | 2001 |
| Hanseth and Aanestad [75] | Bootstrap algorithm (BA) | 2001 |
| Larranaga and Lozano [76] | Estimation of distribution algorithms (EDA) | 2001 |
| Pham et al. [77] | Bees algorithms (BA) | 2005 |
| Karaboga [78] | Artificial bee colony algorithm (ABC) | 2005 |
| Krishnanand and Ghose [79] | Glowworm swarm optimization (GSO) | 2006 |
| Haddad et al. [80] | Honey-bee mating optimization (HMO) | 2006 |
| Mucherino and Seref [81] | Monkey search (MS) | 2007 |
| Atashpaz-Gargari and Lucas [82] | Imperialist competitive algorithm (ICA) | 2007 |
| Simon [83] | Biogeography-based optimization (BBO) | 2008 |
| Teodorović [84] | Bee colony optimization (BCO) | 2009 |
| He et al. [85] | Group search optimizer (GSO) | 2009 |
| Yang and Deb [86] | Cuckoo search (CS) | 2009 |
| Rashedi et al. [87] | Gravitational search algorithm (GSA) | 2009 |
| Kashan [88] | League championship algorithm (LCA) | 2009 |
| Kadioglu and Sellmann [89] | Dialectic search | 2009 |
| Shah-Hosseini [90] | Intelligent water drops (IWD) | 2009 |
| Yang [91] | Firefly algorithm (FA) | 2009 |
| Battiti and Brunato [92] | Reactive search optimization (RSO) | 2010 |
| Yang [93] | Bat algorithm (BA) | 2010 |
| Shah-Hosseini [94] | Galaxy-based search algorithm (GbSA) | 2011 |
| Tamura and Yasuda [95] | Spiral optimization (SO) | 2011 |
| Alsheddy [96] | Guided local search (GLS) | 2011 |
| Rajabioun [97] | Cuckoo optimization algorithm (COA) | 2011 |
| Gandomi and Alavi [98] | Krill Herd (KH) algorithm | 2012 |
| Civicioglu [99] | Differential search algorithm (DS) | 2012 |
| Sadollah et al. [100] | Mine blast algorithm (MBA) | 2013 |
| Hatamlou [101] | Black hole (BH) | 2013 |
| Gandomi [102] | Interior search algorithm (ISA) | 2014 |
| Cheng and Prayogo [103] | Symbiotic organisms search (SOS) | 2014 |
| Mirjalili et al. [65] | Grey wolf optimizer (GWO) | 2014 |
| Kashan [104] | Optics inspired optimization (OIO) | 2015 |
| Kaveh and Mahdavi [105] | Colliding bodies optimization (CBO) | 2015 |
| Salimi [106] | Stochastic fractal search (SFS) | 2015 |
| Zheng [107] | Water wave optimization (WWO) | 2015 |
| Dogan and olmez [108] | Vortex search algorithm (VSA) | 2015 |
| Wang et al. [109] | Elephant herding optimization (EHO) | 2015 |
| Kashan et al. [110] | Grouping evolution strategies (GES) | 2015 |
| Mirjalili [111] | Dragonfly algorithm | 2016 |
| Liang et al. [112] | Virus optimization algorithm (VOA) | 2016 |
| Mirjalili [113] | Sine cosine algorithm (SCA) | 2016 |
| Ebrahimi and Khamehchi [114] | Sperm whale algorithm (SWA) | 2016 |
| Mirjalili et al. [115] | Salp swarm algorithm (SSA) | 2017 |
| Baykasoğlu and Akpinar [116] | Weighted superposition attraction (WSA) | 2017 |
| Mortazavi et al. [117] | Interactive search algorithm (ISA) | 2018 |
| Heidari et al. [118] | Harris Hawks optimization (HHO) | 2019 |
| Yapici and Cetinkaya [119] | Pathfinder algorithm (PFA) | 2019 |
| Kaur et al. [120] | Tunicate swarm algorithm (TSA) | 2020 |
| Hayyolalam and Kazem [66] | Black widow optimization (BWO) | 2020 |
| Khishe and Mosavi [67] | Chimp optimization algorithm (ChOA) | 2020 |
| Braik et al. [121] | Capuchin search algorithm (CapSA) | 2021 |
| Talatahari et al. [122] | Crystal structure algorithm (CryStAl) | 2021 |
| Połap and Woźniak [68] | Red fox optimization (RFO) | 2021 |
| Pan et al. [69] | Gannet optimization algorithm (GOA) | 2022 |
| Eslami et al. [123] | Aphid–Ant mutualism (AAM) | 2022 |
| Hashim et al. [124] | Honey Badger algorithm (HBA) | 2022 |
Genetic Algorithm (GA)
Genetic algorithm is an exploratory search inspired by Charles Darwin’s theory of natural evolution, first introduced by Holland in 1975 [60]. This algorithm reflects the natural selection process in which the best individuals for reproduction are selected to produce offspring. This algorithm repeatedly changes the population of individual solutions. In each generation, GA randomly selects individuals from the current population and uses them as parents to produce offspring for the next generation. Over successive generations, the population "evolves" toward an optimal solution. Four phases are considered in a GA.
Initial Population This process begins with a group of chromosomes called a population. Each chromosome is a solution to the problem you want to solve. A chromosome is characterized by a set of variables called genes.
Selection Two pairs of chromosomes (parents) are selected based on their fitness scores. Chromosomes with high fitness have more chance to be selected for reproduction.
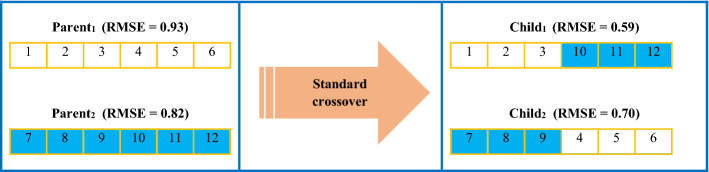
Crossover This operator is the most significant step in a GA algorithm. For each pair of parents to be mated, a crossover point is randomly selected from within the genes. Offspring are created by exchanging the genes of parents. The crossover operator is applied to improve the exploitation of algorithm. This operator actually searches the space around a chromosome.
Mutation In some newly formed offspring, some of their genes can be subjected to a mutation. The mutation operator is applied to enhance exploration.
Today in many applications, GA is used to train the deep learning architectures such as convolutional neural network (GA-CNN). In this proposed architectures, GA optimizes the weights and biases of the CNN. In the following, GA modeling for this problem is presented. For GA modeling, one of the main tasks is to define a solution in the form of a chromosome. Figure 7 shows the definition of a chromosome in GA.
Fig. 7.

Chromosome definition in GA
Figure 8 shows the single point crossover operator of standard GA. As can be seen, in a single-point crossover, only two chromosomes are combined. Figure 9 illustrates the mutation process of GA.
Fig. 8.
An example of single point crossover
Fig. 9.
Example of the mutation operator in GA
Differential Evolution (DE)
Differential evolution (DE) is a global optimization algorithm developed by Storn and Price in the year 1997 [64]. Similar to other popular approaches, such as genetic algorithm and evolutionary algorithm, the differential evolution starts with an initial population of candidate solutions. These candidate solutions are iteratively improved by introducing crossover, mutation, and selection into the population, and retaining the fittest candidate solutions. Due to its several competitive advantages, DE is one of the most popular MH algorithm used by researchers and practitioners to tackle a diverse set of real-world applications. First, the implementation of DE is simpler than most other MHs. This feature enables those practitioners who may not have strong coding skills to make simple adjustments to the DE coding to solve problems. Second, despite its simplicity, DE can show a more promising optimization ability than other MHs in solving different types of optimization problems such as nonlinearity and multimodality. Third, various DE algorithms have appeared as the top three best-performing optimizers in most CEC competitions since 2005. Figure 10 shows the flowchart of the DE algorithm.
Fig. 10.
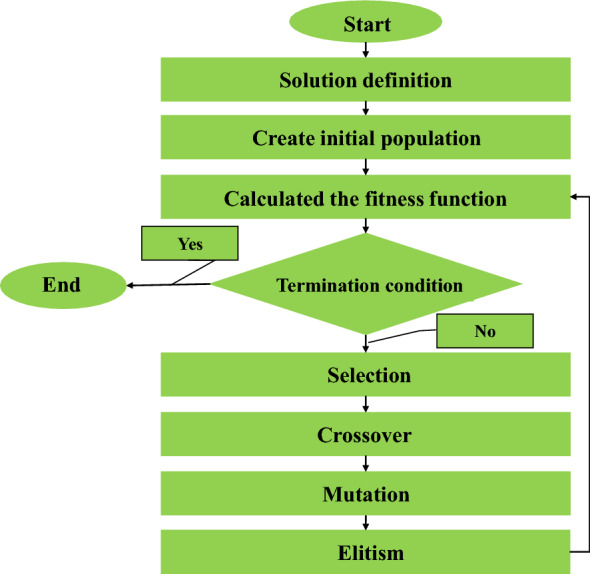
The flowchart of DE algorithm
Particle Swarm Optimization (PSO)
Particle Swarm Optimization (PSO) algorithm is one of the most important intelligent optimization algorithms in the field of Swarm Intelligence. This algorithm was introduced by Kennedy and Eberhart in 1995, inspired by the social behavior of animals such as fish and birds that live together in small and large groups. PSO is suitable for a wide range of continuous and discrete problems and has performed very well in different optimization problems [62].
In PSO, all possible solutions are mapped to corresponded particles, and every particle is assigned an initial velocity that deputes a position change. For calculating the next velocity of the particles in the solution space, an optimization function is utilized. Particle velocity is made of three main movements: a) the percentage of the previous movement's continuation, b) the movement toward the best personal experience, and c) the movement toward the best global experience. Equations (1) and (2) are respectively expressing the update of velocity and position of the particles.
| 1 |
| 2 |
Artificial Bee Colony (ABC)
Artificial bee colony (ABC) is a swarm based meta-heuristic algorithm that was introduced by Karaboga in 2005. ABC was inspired by the intelligent search behavior of honey bees [78]. In ABC algorithm, the colony contains three types of artificial bees (Fig. 11):
Scout bees Solutions that are randomly generated to discover new spaces are called scout bees. Scout bees are responsible for exploring the search space.
Employed bees A number of scout bees with good fitness function become employed bees. Employed bees are responsible for advertising quality food sources.
Onlooker bees The onlooker bees are responsible for searching the neighborhood for employed bees. Onlooker bees receive information about food sources and search around these sources. The role of these bees is both exploitation and exploration of algorithm.
Fig. 11.
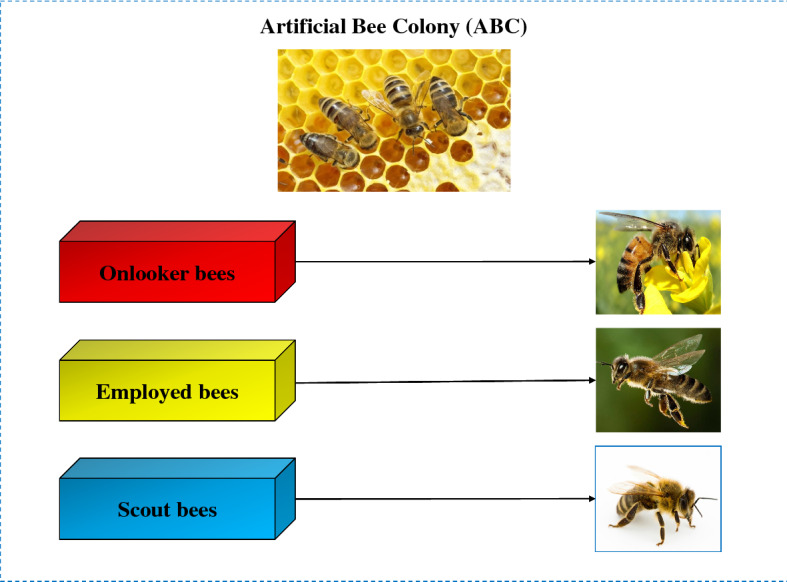
Three types of artificial bees in ABC
In ABC, scout bees randomly discover a population of initial solution vectors and then repeatedly improve them by onlooker and employed bees (using neighbor search method to move towards better solutions while eliminating poor solutions). In general, ABC uses two main methods (neighbor search and random search) to get the optimal answer: Random search by scout and onlooker bees and neighbor search by employed and onlooker bees. In ABC, each candidate answer indicates the position of food source, and the quality of the nectar is used as a fitness function. In this algorithm, first, all initial populations are explored by scout bees. Scout bees with best fitness functions are selected as the employed bees. Employed bees exploit the solution positions and then onlooker bees are created. The higher the quality of the employed bee, the more onlooker bees will be created around it. The onlooker bee also select new food positions (using the employed bee information) and exploit around these positions. In the next step, random scout bees are created to find new random food positions. ABC algorithm can be formulated as Eq. (3)-(5).
| 3 |
| 4 |
| 5 |
where.
= Probability of selecting employed bees by onlooker bees.
= Fitness function of the solution.
= Onlooker bee.
= Scout bees.
= Low limit of search space.
= High limit of search space, = Number of employed bees.
{1, 2, …, SN}.
= Dimension {1, 2, …, D}.
= Onlooker bee number.
is the random number
= Scout bee number.
Biogeography-Based Optimization (BBO)
Biographical-based optimization is a population-based evolutionary algorithm first proposed by Dan Simon in 2008 [83]. The answer in BBO is called habitat and habitat is considered as a vector of its habitant. In addition, the value of each habitat is defined by the habitat suitability index (HSI). The high value of HSI shows high fitness function of habitat. Three main operators of BBO include migration, mutation and elitism. In BBO, each habitat has its own emigration rate, immigration rate, and mutation rate. The emigration () rate and immigration rate () are defined as Eq. (6) and Eq. (7).
| 6 |
| 7 |
In which, represents the rank of the jth habitat after sorting accordance to their HSI and is the highest rank in the total habitat (population size). The rank is related to the habitat suitability index (fitness function). In addition, represents the highest emigration rate and represents the highest immigration rate. Migration, mutation and elitism are the main operators of this algorithm. By assuming as the host habitat and as the guest habitat, the migration process for the standard BBO will be as the Eq. (8):
| 8 |
According to the Eq. (8), the host habitat (selected based on the immigration rate and roulette wheel method) receives information only from the guest habitat (selected based on the emigration rate and roulette wheel method) and itself.
Grey Wolf Optimization (GWO)
GWO is a swarm-based MH algorithm inspired by the the gray wolf’s hunting policies [65]. GWO divide the population into four levels: alpha, beta, delta, and omega. Alphas are the leaders that make decisions about living, hunting, and moving wolfs, while the beta act as an advisor to the alpha. The delta is responsible for warning when there is danger and protecting the pack, providing food and caring for sick or injured wolves. In the end, Omega is the last wolve that has to obey leaders. They follow four phases: hunting, searching, encircling, and then attacking the prey. GWO is one of the state-of-the-art competitive MH algorithm, which has attracted great attention of researchers. GWO is simple to set parameters, flexible and has a good trade-off between exploration and exploitation.
Chimp optimization Algorithm (ChOA)
ChOA algorithms is one of the new MH algorithm introduced by Khishe and Mosavi in 2020. ChOA is inspired by the chimps’ movement in group hunting and their sexual motivations [67]. In the ChOA, prey hunting is utilized to reach the optimal solution in the optimization problem. ChOA divides hunting into four main phases: driving, blocking, chasing, and attacking. In the first, ChOA is initialized by the generating a random chimps’ population. Chimps are then randomly classified into four groups: attacker, chaser, barrier, and driver. In order to model driving and chasing the prey, Eqs. (9)–(13) have been proposed.
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
where, is the prey position vector, denote the chimp position vector, present the current iteration, are the coefficient vectors, is the dynamic vector , are the random vectors , and denote a chaotic vector.
The chimps first detect the prey’s position in the hunting step using driver, blocker, and chaser chimps. In the exploitation process, the hunting process is done by attackers. For this purpose, the prey’s position is estimated by the attacker, barrier, chaser, and driver chimps, and other chimps update their position through the prey. This process is formulated as Eqs. (14)–(16).
| 14 |
| 15 |
| 16 |
where, denotes the best search agent, is the second-best search agent, presents the third-best search agent, is the fourth-best search agent, and is the updated position of each chimp.
Also, to set up the exploration process, parameter is applied such that and is the cause of diverging chimps and preys. As well, parameter with the values between + 1 and − 1, help the chimps and preys to be converged and will lead to improved exploitation. In addition, parameter helps the algorithm to have the exploration process. Finally, all chimps attack their prey to achieve social rights (sexual incentive) after prey hunting regardless of their duties. In order to formulate social behavior, chaotic maps are used as Eq. (17).
| 17 |
Memetic Algorithms (Hybridization)
It is complicated to find the best possible solution in the search space in large-scale optimization problems. Moreover, changing algorithm variables does not have much influence on the algorithm convergence. Therefore, for massive dataset with high complexity, even if the researchers have determined accurate initial parameters, the algorithm will not be able to perform adequate exploration and exploitation. Consequently, to achieve comprehensive global and local searches, we need to apply powerful operators to make better exploration and exploitation. MH algorithms can be combined with others and overcome this problem by using the advantages and operators of other algorithms [125]. Despite promising results achieved by MHs over the past years, many successful attempts have been made that do not pursue a single inspiration from nature but compound various MHs exploiting their complementarity. This is particularly important for challenging optimization applications where combination methods show promising performance, leading to further intensification of the research. Generally, High-level hybridization of MHs is achieved by running algorithms in a sequence where all factors changed by one MH are transferred to the other algorithm [125]. According to the literature review, most hybridization models are designed for specific optimization problem, including clustering, feature selection, and image segmentation. Since modelling a hybrid model that would be able to improve more than one MH is challenging, available solutions mostly use two competitive algorithms to an optimization problem. In recent decades, researchers have utilized a combination of algorithms to improve the performance of the optimization process.
Modification of MH (Devoted Local Search and Manipulating the Solutions Space)
The increasing discovery of alternative methods to solve optimization problems makes it necessary to parallelize and modify available algorithms. Achieving a suitable solution using a MH algorithms may need a long runtime, iterations, or population. The first one is to use the neighborhood search method in order to minimize the exploration of the solution space. In addition, powerful CPU can affect the convergence speed of the MH algorithm and therefore work more efficiently. In the proposed neighborhood search approach, smaller populations called groups may formed. Suppose the number of computer cores is specified at the beginning of the algorithm. In comparison with the standard version of MH algorithms, an initial population consisting of N individuals is generated randomly. From this population, suitable individuals are selected. Each individual in population will be the best adapted solution in the smaller group that will be created under his leadership. The second proposed approach involves manipulating the solutions space to minimize the number of calculations. In this proposition, the multi-threading approach plays a big role because dividing the space and selecting the best areas does not cost extra. In addition, the third proposed approach is the combination of the previous two methods. While the proposed approach of parallelization and manipulation of solution space improves the performance of classical algorithms, they are so flexible that can be improved with different ideas. In addition, it achieves better results in different applications [126].
Review of the Training DL and AANs by MH Algorithms
This section provides an overview of the optimization of neural networks and DL architectures using MH algorithms. The review of papers is divided into two parts: ANN optimization and DL optimization.
Review1: Training the AANs by MH Algorithms
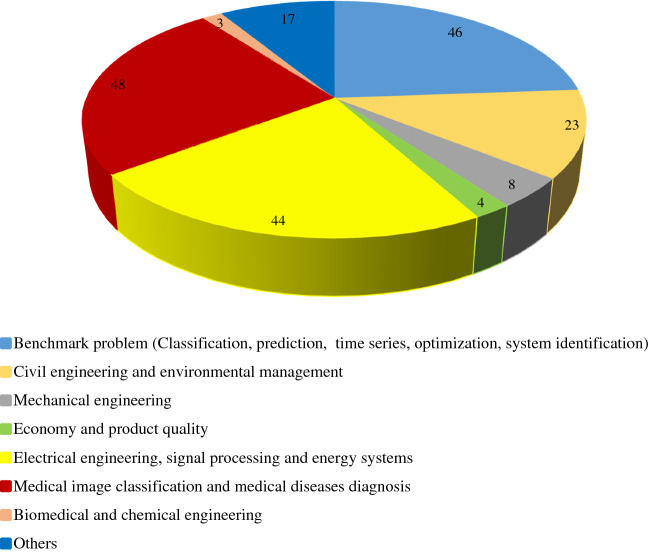
This section provides a comprehensive overview of the optimization of different types of ANNs using MH algorithms. Optimization of ANNs is often considered from several aspects: optimization of weights, hyper-parameters, network structure, activation nodes, learning parameters, learning algorithm, learning environment, etc.
Eberhart and Kennedy [62] used the PSO algorithm to optimize the weights of an MLPNN. The proposed architecture performed very well on a benchmark data set. Storn and Price [64] used a differential evolution algorithm to optimize the weights of an FFNN. Experiments on the nonlinear optimization problem indicated the superiority of the proposed DE-FFNN algorithm. PSO algorithm was used by Chunkai et al. [127] to optimize the weights and architecture of MLPNN. This hybrid approach was introduced to model the quality estimation of a product. The results showed that the performance of PSO-MLPNN is better than other algorithms. Li et al. [128] used the genetic algorithm to train the parameters and weights of an ANN. The proposed architecture (GA-ANN) showed good performance for the pollutant emissions problem.
Leung et al. [129] used the improved genetic algorithm (IGA) to optimize the architecture and weights of an ANN. This study compared the proposed architecture (IGA-ANN) with other architectures and presented better results. Meissner et al. [130] used an improved PSO algorithm to optimize the number of neurons, parameters, and weights of an ANN. The developed architecture showed good results in benchmark datasets. Geethanjali et al. [131] used the PSO algorithm to train the ANN (MLFFNN). The results showed that the PSO- MLFFNN architecture was more accurate and faster than the BP- MLFFNN architecture. Yu et al. [132] used PSO and DPSO algorithms to optimize the architecture and parameters (weight and bias) of a three-layer FFANN network. The proposed algorithm was named ESPNet. A self-adaptive evolutionary strategy was used to improve PSO and DPSO. Experimental results from two real-world problems show that ESPNet can generate compact neural networks with good generalizability.
Khayat et al. [133] used GA and PSO algorithms to optimize the weights of a SOFNN. The results showed that the optimized SOFNN architecture based on GA and PSO performs well. Lin and Hsieh [134] used the improved PSO algorithm to optimize the weights of a three-layer neural network. The proposed approach provided good performance for the classification data. Cruz-Ramírez et al. [135] used the Pareto Memetic Differential Evolution Algorithm (MPDA) to optimize the structure and weights of a neural network. The proposed approach performed well in benchmark problems. Subudhi and Jena [29] used the combination of the memetic differential evolution (MDE) algorithm and BP algorithm (DEBP) to train a multilayer neural network to identify a nonlinear system. DEBP performance was compared with six other algorithms such as Back Propagation (BP), Genetic Algorithm (GA), PSO, DE, Back Propagation genetic algorithm (GABP), and Back Propagation Particle Swarm Optimization (PSOBP). The results of different algorithms showed that the proposed DEBP has better identification compared to other cases.
Malviya and Pratihar [136] used PSO, BP, and two clustering algorithms (including Fuzzy C-means) to train the RBFNN and MLFFNN networks for the MIG welding process problem. In this research, connection weights and learning parameters are optimized. Zhao and Qian [137] used the CPSO algorithm to optimize the weights and architecture of a three-layer FFNN. The performance of CPSO-FFNN was compared with the existing architectures in the research literature, and the results showed the superiority of the proposed architecture. Green II et al. [138] used the CFO algorithm to optimize the weights of an ANN. The performance of the CFO was compared with the PSO algorithm, which shows the superiority of CFO-NN.
Vasumathi and Moorthi [139] used the PSO algorithm to optimize the weights of an ANN. The results showed that the proposed PSO-ANN architecture performs well in the harmonic estimation problem. Yaghini et al. [140] used a combination of the improved particle swarm optimization (IOPSO) and the BP algorithm to train an ANN. The developed architecture was implemented on eight benchmark datasets. IOPSO-BPA-ANN also performed better than the other 10 algorithms. Dragoi et al. [141] used the differential evolutionary self-adaptation algorithm (SADE) to optimize the weights, architecture, and learning parameters of an ANN. The developed approach for the aerobic fermentation process was proposed and presented good results. Ismail et al. [142] used a combination of PSO and BP algorithms to train the product unit neural network (PUNN). The PSO-BP-PUNN architecture performed better than the PSO-PUNN and BP-PUNN architectures.
Das et al. [143] used the PSO algorithm to train ANN. In this study, all four parameters of weight, number of layers, number of neurons and learning parameters were optimized simultaneously. According to the results, the PSO-ANN architecture performed better than other architectures in the literature. Mirjalili et al. [144] used the BBO algorithm to optimize the weights of an MLPNN for classification and function approximation problems. They compared the BBO algorithm with five other metaheuristic algorithms and the BP and ELM algorithms. BBO results were better than other algorithms in terms of accuracy and convergence speed. Jaddi et al. [145] used the improvement of the bat algorithm to optimize an ANN. Where both the ANN structure and the network weights are optimized. Statistical analysis showed that the bat algorithm with Ring and Master-Slave strategies for the classification problem performed better than other methods in the literature.
Jaddi et al. [146] used the improved bat algorithm (MBA) to optimize the weights, architecture, and active neurons of an ANN. The hybrid algorithm showed high performance in six classification problems, two-time series problems and one real-world problem. González et al. [147] used the fuzzy gravitational search algorithm (FGSA) to train a neural network's modules, layers and nodes. The proposed FGSA-NN architecture was implemented for the pattern recognition problem and provided acceptable results. Gaxiola et al. [148] used particle swarm optimization and a genetic algorithm to optimize the weights of type-2 fuzzy inference systems. The developed architectures were implemented on time series benchmark datasets. According to the results, NNT2FWGA and NNT2FWPSO algorithms performed better than NNT2FW. Karaboga and Kaya [149] used the hybrid artificial bee colony algorithm (aABC) to train ANFIS. The performance of aABC-ANFIS was compared with 14 other architectures on four nonlinear dynamic systems, which showed its superiority in accuracy.
Jafrasteh and Fathianpour [150] used an improved artificial bee colony algorithm (SPABC) to train the LLRBF neural network. The results of the proposed algorithm were compared with six other MH algorithms that show the superiority of SPABC-LLRBFNN. Khishe et al. [19] used the improved migration model of the biogeography-based optimization to optimize the weights and biases of an MLPNN. They developed the exponential-logarithmic migration model to improve BBO performance. Additionally, the performance of the proposed algorithm was compared with six other MH algorithms for sonar data classification, which showed the superiority of IBBO-MLPNN. Ganjefar and Tofighi [151] used a combination of GA and GD algorithms to train an ANN. The proposed HGAGD-NN approach has yielded good results for several benchmark problems.
Aljarah et al. [152] used the whale optimization algorithm (WOA) to train the weights of an MLPNN. They implemented the proposed WOA-MLP algorithm on 20 benchmark problems, which produced better accuracy and speed than the BP, GA, PSO, ACO, DE, ES, and PBIL algorithms. Heidari et al. [153] used the grasshopper optimization algorithm (GOA) to train an MLPNN. The performance of GOA-MLPNN was evaluated with eight other algorithms on five medical identification classification datasets. Finally, the proposed GOA-MLPNN algorithm gave better results in different criteria. Hadavandi et al. [154] proposed an MLPNN simulator based on the gray wolf optimizer (GWO) to predict the tensile strength of Siro-Spun yarn. The gray wolf optimizer algorithm was applied to train the neural network weights. Finally, proposed hybrid architecture GWO-MLPNN performed better than a traditional learning-based neural network (BP-MLPNN).
Haznedar and Kalinli [155] used the SA algorithm to train an ANFIS. The SA-ANFIS architecture was compared with GA, BP algorithms and various architectures from the research literature, which showed the superiority of SA-ANFIS. Pham et al. [156] used biogeography-based optimization to optimize the weights and parameters of an MLPNN to predict the soil composition coefficient. This study used BP-MLPNN, RBFNN, Gaussian Process (GP) and SVR algorithms to compare with BBO-MLPNN. According to the results, the BBO-MLPNN algorithm excelled in three criteria: RMSE, MAE and correlation coefficient. Han et al. [157] used the improved mutation model of the DE algorithm to optimize the neural network. The DE-BPNN model has been implemented to predict the performance of pre-cooling systems, which has yielded far better results than other networks.
Rojas-Delgado et al. [158] used particle swarm optimization (PSO), firefly algorithm (FA), and cuckoo search (CS) to train the ANN. The various neural network architectures trained by meta-heuristic algorithms were implemented on six benchmark problems that performed very well compared to traditional methods. Khishe and Mosavi [159] used the chimp optimization algorithm to optimize the weights and biases of an MLPNN. In that study, the performance of the MLPNN-ChOA algorithm was compared with the performance of IMA, GWO and a hybrid algorithm on the underwater acoustic dataset classification problem, which showed the superiority of the MLPNN-ChOA. Wang et al. [160] used the PSO and CA algorithms to optimize the neural network weights. The combined particle swarm optimization (HPSO) algorithm was first developed in that research. The HPSO algorithm was combined with CA, and finally, the HPSO-CA algorithm was implemented for network training (HPSO-CA-ANN). The developed algorithm and five other MH algorithms were implemented on 15 benchmark datasets that performed better than the others.
Al-Majidi et al. [161] used the PSO algorithm to optimize the weights and architecture of FFNN. The results showed that the optimized FFNN architecture based on the PSO accurately predicts the maximum power point. Ertuğrul [54] used the differential evolution algorithm (DE) to optimize the nodes and learning parameters of RaANN. The results showed that the differential evolution algorithm for 48 synthetic datasets performed better than other methods. Ansari et al. [162] used the magnetic optimization algorithm (MOA) & PSO to optimize the weights of the back-propagation neural network. According to the results, the proposed approach (MOA-BBNN) performed well in the bankruptcy prediction problem.
Zhang et al., [163] used the chicken swarm optimization (CSO) algorithm to optimize the weights, biases, and number of layers of the Elman neural network (ENN). According to the results, the proposed hybrid approach (CSO-ENN) performed well in the Air pollution forecasting. Also, the performance of the proposed hybrid architecture has been better than other algorithms. Li et al., [164] used the biogeography-based optimization (BBO) algorithm to optimize the weights of MLPNN for medical image classification. The results showed that the proposed hybrid architecture (BBO-MLPNN) performs better than the other original architectures.
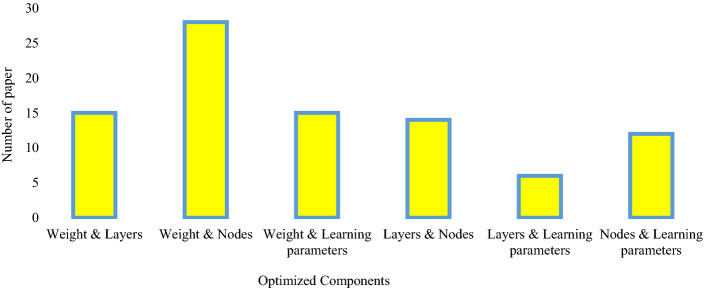
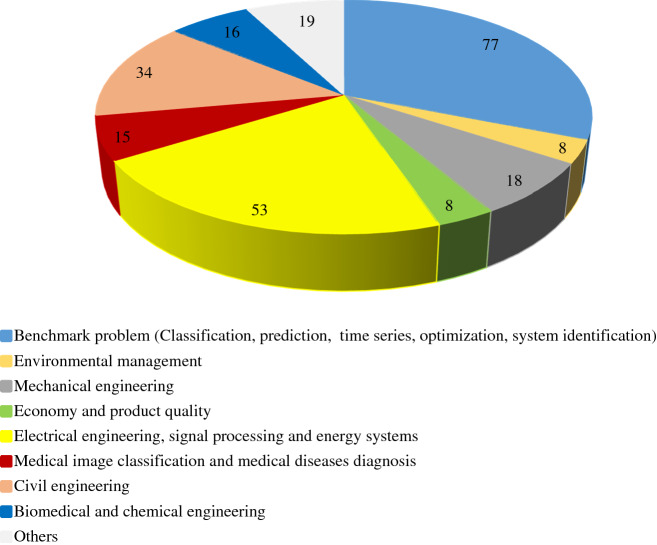
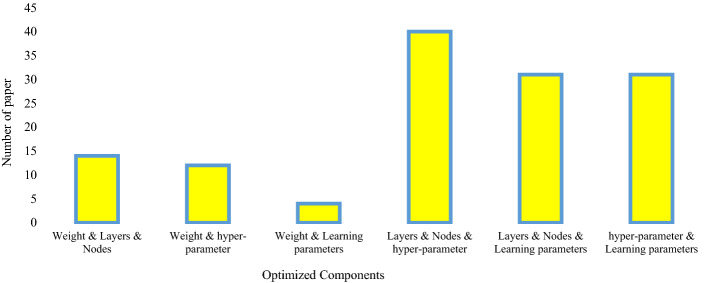
Table 2 summarizes the above research as well as many other studies. As can be seen, for each research, the author's name, year of publication, type of neural network, optimized components in the network, type of MH algorithm used, application and data set used are listed. In the following, for a more comprehensive review, some statistical analysis of the research collected in Table 2 is presented.
Table 2.
A summary of meta-heuristic algorithms developments for training/optimization of ANNs
| Authors & dates | Neural network categories | Optimized components: 1. Weights & bias, 2. Layers 3. Nodes 4. Activation function and learning parameters |
The meta-heuristic algorithm used for training neural networks | Application / dataset | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| Engel [165] | FFNN | ✓ | Simulated annealing (SA) | The parity and "clump-recognition" problems | |||
| Montana and Davis [166] | FFNN | Genetic algorithm (GA) | Sonar data from arrays of underwater acoustic receivers | ||||
| Whitley et al. [167] | FFNN | ✓ | Genetic algorithm (GA) | Benchmark problems for Training NN | |||
| Belew et al. [168] | FFNN | ✓ | Genetic algorithm (GA) | Benchmark optimization problems and classification | |||
| Kitano [169] | ANN | ✓ | ✓ | Genetic algorithm (GA) | Benchmark optimization problems and classification | ||
| Eberhart and Kennedy [62] | MLPNN | ✓ | Particle swarm optimization (PSO) | Systematic benchmark optimization problems | |||
| Battiti and Tecchiolli [170] | FFNN | ✓ | Reactive tabu search (RTS) algorithm | Training sub-symbolic systems | |||
| Storn and Price [64] | FFNN | ✓ | Differential evolution (DE) algorithm | Non-linear optimization problems | |||
| Yao and Liu [171] | FFNN | ✓ | ✓ | Evolutionary programming (EP) | The Parity and Medical Diagnosis Problems | ||
| Sexton et al. [172] | FFNN | ✓ | Tabu search (TS) | Mackey–Glass chaotic time series & Benchmark problems | |||
| Sexton et al. [173] | FFNN | ✓ | Simulated annealing (SA) | Monte Carlo study on seven test functions | |||
| Chunkai et al. [127] | MLPNN | ✓ | ✓ | Particle swarm optimization (PSO) | Modelling product quality estimator problem | ||
| Arifovic and Gencay [174] | FFNN | ✓ | ✓ | Genetic algorithm (GA) | The long-term behavior of dissipative systems | ||
| Alvarez [175] | FFNN | ✓ | Genetic programming (GP) | The problem domain of time series prediction | |||
| Li et al. [128] | ANN | ✓ | ✓ | Genetic algorithm (GA) | Human supervisory control, pollutant emission | ||
| Sarkar and Modak [176] | FFNN | ✓ | Simulated annealing (SA) algorithm | Nonlinear optimal control problems | |||
| García-Pedrajas et al. [177] | ANN | ✓ | Cooperative coevolution | Three real problems of classification | |||
| Ilonen et al. [178] | FFNN | ✓ | Differential evolution (DE) algorithm | Continuous optimization problems | |||
| Leung et al. [129] | FFNN | ✓ | ✓ | Improved genetic algorithm (IGA) | Some benchmark optimization functions | ||
| Augusteijn and Harrington [179] | FFNN | ✓ | Evolutionary programming (EP) | Four benchmark classification problems | |||
| Abraham [180] | ANN | ✓ | ✓ | ✓ | Evolutionary algorithm & meta-learning evolutionary | Three different well-known chaotic time series | |
| Lahiri and Chakravorti [181] | ANN | ✓ | ✓ | ✓ | Genetic algorithm (GA) | Electrode-spacer contour optimization | |
| Shen et al. [182] | MLFFNN | ✓ | ✓ | Particle swarm optimization (PSO) | QSAR studies of bioactivity of organic compounds | ||
| Kim et al. [183] | FFNN | ✓ | Genetic algorithm (GA) | Mathematical optimization and set covering problem | |||
| Chatterjee et al. [184] | FNN | ✓ | Particle swarm optimization (PSO) | Optimization voice-controlled robot systems | |||
| Feng et al. [185] | FFNN | ✓ | Guaranteed convergence PSO (GCPSO) | Noise Identification and Classification Problem | |||
| Da and Xiurun [186] | FFNN | ✓ | Modified PSO with simulated annealing (PSOSA) | Triaxial compression tests (rock engineering) | |||
| Salajegheh and Gholizadeh [187] | RBF | ✓ | Improved genetic algorithm (IGA) | 25-bar space tower,-bar grid space dome, | |||
| Tsai et al. [188] | FFNN | ✓ | ✓ | Hybrid Taguchi-genetic algorithm (HTGA) | Forecasting the sunspot numbers | ||
| García-Pedrajas et al. [189] | ANN | ✓ | Genetic algorithm (GA) | 25 real-world optimization problems | |||
| Meissner et al. [130] | ANN | ✓ | ✓ | ✓ | Optimized particle swarm optimization (OPSO) | Benchmark datasets | |
| Ye et al. [190] | FFNN | ✓ | Tabu search (TS) | Several typical non-linear optimization functions | |||
| Socha and Blum [191] | FFNN | ✓ | Ant colony optimization (ACO) algorithm | Discrete optimization problems | |||
| Lin et al. [192] | MLFFNN | ✓ | Particle swarm optimization (PSO) | Application in QSAR studies of bioactivity | |||
| Ulagammai et al. [193] | WNN | ✓ | Bacterial foraging technique (BFT) | Identification of the non-linear characteristics of power system | |||
| Zhang et al. [194] | FFNN | ✓ | Hybrid particle swarm optimization (HPSO) | Three bits parity problem | |||
| Yu et al. [132] | 3LFFANN | ✓ | ✓ | Discrete particle swarm optimization (DPSO) & PSO | Two real-world problems | ||
| Geethanjali et al. [131] | MLFFNN | ✓ | Particle swarm optimization (PSO) | Modeling power transformers problems | |||
| Lin et al. [195] | FLNFN | ✓ | Cooperative particle swarm optimization (CPSO) | Prediction Applications | |||
| Tsoulos et al. [196] | FFNN | ✓ | ✓ | Grammatical evolution (GE) | 9 known classification and 9 known regression problems | ||
| Goh et al. [197] | FFNN | ✓ | Microhybrid genetic algorithm (µHGA) | Real-world medical data sets | |||
| Lin and Hsieh [134] | 3LNN | ✓ | Improved particle swarm optimization (IPSO) | Classification of mental task from EEG data | |||
| Bashir and El-Hawary [198] | ANN | ✓ | Particle swarm optimization (PSO) | Modeling hourly load forecasting problem | |||
| Kiranyaz et al. [199] | FFNN | ✓ | ✓ | Particle swarm optimization (PSO) | Synthetic problems | ||
| Khayat et al. [133] | SOFNN | ✓ | Particle swarm optimization (PSO) & GA | Three tested examples | |||
| Tong and Mintram [21] | FFNN | ✓ | Genetic algorithm (GA) | Real-world applications (feature selection) | |||
| Slowik [200] | FFNN | ✓ | Differential evolution (DE) algorithm | Continuous optimization problems | |||
| Kordík et al. [201] | FFNN | ✓ | Meta-heuristic algorithms (MH) | Several real-world problems and benchmark data sets | |||
| Lian et al. [202] | ANN | ✓ | ✓ | Particle swarm optimization (PSO) | Non-linear system identification | ||
| Cruz-Ramírez et al. [135] | ANN | ✓ | ✓ | Memetic pareto differential evolution (MPDE) | Growth multi-classes in predictive microbiology | ||
| Zhao et al. [203] | RBFNN | ✓ | ✓ | Particle swarm optimization (PSO) | Melt Index modeling and Prediction problems | ||
| Subudhi and Jena [29] | MLPNN | ✓ | Memetic differential evolution (MDE) | Nonlinear system identification | |||
| Ma et al. [204] | ANN | ✓ | Genetic algorithm (GA) | Modeling chemical oxygen demand removal | |||
| Ding et al. [205] | FFNN | ✓ | Genetic algorithm (GA) | Real-world applications (The UCI data set) | |||
| Subudhi and Jena [206] | FFNN | ✓ | Opposition based differential evolution (ODE) | Nonlinear system identification | |||
| Ghalambaz et al. [207] | MLPNN | ✓ | Gravitational search algorithm (GSA) | Wessinger's Equation | |||
| Irani and Nasimi [208] | FFNN | ✓ | Genetic algorithm (GA) | Permeability estimation of the reservoir | |||
| Li and Liu [209] | RBFNN | ✓ | Modified PSO simulated annealing (MPSOSA) | Melt index prediction model | |||
| Sun et al. [210] | NN | ✓ | Genetic algorithm (GA) | Dynamic prediction of financial distress | |||
| Ozbakır and Delice [211] | MLPNN | ✓✓ | Binary particle swarm optimization (BPSO) | Exploring comprehensible classification rules | |||
| Carvalho et al. [212] | FFNN | ✓ | VNS, SA, GEO, and GA algorithms | Identification and estimation of pollution sources | |||
| Han et al. [213] | FFNN | ✓ | Gaussian particle swarm optimization (GPSO) | Predictive control and system identification | |||
| Zhao and Qian [137] | 3LFFNN | ✓ | ✓ | Cooperative particle swarm optimization (CPSO) | The application of predicting the sunspot numbers | ||
| Zanchettin et al. [214] | MLPNN | ✓ | ✓ | ✓ | Simulated annealing (SA), Tabu search (TS) and GA | Data classification | |
| Vadood et al. [215] | ANN | ✓ | ✓ | ✓ | Genetic algorithm (GA) | Optimization of acrylic dry spinning production line | |
| Malviya and Pratihar [136] | RBFNN | ✓ | ✓ | Particle swarm optimization (PSO) | Metal inert gas (MIG) welding process | ||
| Vasumathi and Moorthi [139] | ANN | ✓ | Particle swarm optimization (PSO) | power engineering optimization problem | |||
| Mirjalili et al. [216] | FFNN | ✓ | Hybrid PSO &gravitational search algorithm (GSA) | Three benchmark problems | |||
| Khan and Sahai [217] | FFNN | ✓ | Bat algorithm (BA), GA & PSO | Standard dataset (in the field of Medicine) | |||
| Huang et al. [218] | RBF | ✓ | Improved chaos optimization (ICO) | Melt index prediction | |||
| Green II et al. [138] | FFNN | ✓ | Central force optimization (CFO) & PSO | Data classification | |||
| Irani and Nasimi [219] | BPNN | ✓ | Ant colony optimization (ACO) | Permeability Estimation of the Reservoir | |||
| Kulluk et al. [220] | FFNN | ✓ | Self-adaptive global best harmony search (SGHS) | six benchmark classification problems | |||
| Nandy et al. [221] | FFNN | ✓ | Firefly optimization algorithm (foa) | Iras dataset, Wine dataset and Liver dataset | |||
| Yaghini et al. [140] | ANN | ✓ | Improved particle swarm optimization (IPSO) | Eight benchmark datasets | |||
| Han and Zhu [222] | FFNN | ✓ | Improved particle swarm optimization (IPSO) | Function approximation and classification problems | |||
| Sharma et al. [223] | FFNN | ✓ | Ant colony optimization (ACO) algorithms | Bankruptcy prediction in banks | |||
| Li et al. [224] | GRNN | ✓ | ✓ | Fruit fly optimization algorithm (FOA) | Annual power load forecasting | ||
| Ismail et al. [142] | PUNN | ✓ | Particle swarm optimization (PSO) | Load–deformation analysis of axially loaded piles | |||
| Wang et al. [225] | ANN | ✓ | Group search optimization (GSO) | Spatiotemporal prediction for nonlinear system | |||
| Lu et al. [226] | QNN | ✓ | ✓ | Quantum-based algorithm (QBA) | Several Benchmark Classification problem | ||
| Askarzadeh and Rezazadeh [227] | FFANN | ✓ | Bird mating optimizer (BMO) | Three real-world classification problems | |||
| Li et al. [228] | FFNN | ✓ | Convex combination algorithm (CCA) | Several computational experiments | |||
| Dragoi et al. [141] | ANN | ✓ | ✓ | ✓ | Self-adaptive differential evolution algorithm (SADE) | An aerobic fermentation process | |
| Parra et al. [229] | ANN | ✓ | ✓ | Evolutionary strategy (ES) | Time series, classification and biometric recognition | ||
| Mirjalili et al. [144] | MLPNN | ✓ | ✓ | ✓ | Biogeography-based optimization (BBO) | 5 classification and 6 function approximation datasets | |
| Piotrowski [230] | MLPNN | ✓ | Differential evolution (DE) | Real-world regression problem & Benchmark problems | |||
| Nasimi and Irani [231] | ANN | ✓ | Particle swarm optimization (PSO) | Identification and modeling of a yeast fermentation bioreactor | |||
| Tapoglou et al. [232] | FFNN | ✓ | Particle swarm optimization (PSO) | Groundwater-level forecasting under climate change scenarios | |||
| Raja et al. [233] | DENN | ✓ | Particle swarm optimization (PSO) | Bratu equation arising in the fuel ignition model | |||
| Beheshti et al. [234] | MLPNN | ✓ | Centripetal accelerated PSO (CAPSO) | Medical diseases diagnosis | |||
| Ren et al. [235] | BPNN | ✓ | Particle swarm optimization (PSO) | Wind speed forecasting (WSF) problem | |||
| Das et al. [143] | ANN | ✓ | ✓ | ✓ | ✓ | Particle swarm optimization (PSO) | Non-linear channel equalization problem |
| Jaddi et al. [145] | ANN | ✓ | ✓ | Multi-population cooperative bat algorithm | Classification and time series prediction benchmark datasets | ||
| Svečko and Kusić [236] | FFNN | ✓ | BAT search algorithm | The precise positional controls of piezoelectric actuators | |||
| Kumaran and Ravi [237] | ANN | ✓ | Biogeography-based optimization (BBO) | Long-term sector-wise electrical energy forecasting | |||
| Cui et al. [238] | SMRNNN | ✓ | Improved glowworm swarm optimization (IGSO) | Time series prediction | |||
| Chen et al. [239] | NFN | ✓ | ✓ | Improved artificial bee colony (IABC) | Approximation of the Piecewise Function | ||
| Mirjalili [240] | MLPNN | ✓ | Grey Wolf optimizer (GWO) | Five classification and three function-approximation DB | |||
| Agrawal and Bawane [241] | ANN | ✓ | Swarm optimization (PSO) | Pixel classification in satellite imagery | |||
| Gharghan et al. [242] | ANN | ✓ | ✓ | Particle swarm optimization (PSO) | Indoor and outdoor track cycling problem | ||
| Vadood et al. [243] | ANN | ✓ | ✓ | Genetic algorithm (GA) | Prediction of resilient modulus of polyester | ||
| González et al. [147] | NN | ✓ | ✓ | Fuzzy gravitational search algorithm (FGSA) | Particular pattern recognition application (medical images) | ||
| Jaddi et al. [146] | ANN | ✓ | ✓ | ✓ | Modified bat-inspired algorithm (MBA) | classifications and time series datasets | |
| Gaxiola et al. [148] | T2FNN | ✓ | Particle swarm optimization (PSO) & genetic algorithm | Mackey–Glass time series problem | |||
| Razmjooy and Ramezani [30] | WNN | ✓ | Hybrid PSO & gravitational search algorithm | System identification | |||
| Yazdi et al. [244] | NN | ✓ | Artificial bee colony (ABC) | Optimization of geometrical parameters | |||
| Jia et al. [245] | RBFNN | ✓ | ✓ | Genetic algorithm (GA) | Classification of Small Samples (benchmark) | ||
| Leema et al. [246] | FFANN | ✓ | Differential evolution (DE) & PSO | Three benchmark clinical datasets | |||
| Karaboga and Kaya [149] | ANFIS | ✓ | Hybrid artificial bee colony (aABC) | Nonlinear dynamic systems | |||
| Xia et al. [247] | RBFNN | ✓ | Bare‐bones particle swarm optimization (BBPSO) | Starch foam material performance prediction | |||
| Melo and Watada [248] | FFNN | ✓ | ✓ | Gaussian-particle swarm optimization (GPSO) | The Iris data classification problem | ||
| Chidambaram et al. [249] | ANN | ✓ | ✓ | ✓ | Genetic algorithm (GA) | Prediction of the base plate temperature of the fin | |
| Khishe et al. [19] | MLPNN | ✓ | Improved biogeography-based optimization (IBBO) | Sonar dataset classification | |||
| Pradeepkumar and Ravi [250] | QRNN | ✓ | Particle swarm optimization (PSO) | Forecasting Financial Time Series Volatility | |||
| Islam et al. [251] | ANN | ✓ | Chaotic genetic algorithm-simulated annealing (SA) | Electrical energy demand prediction in smart grid | |||
| Emary et al. [252] | FFNN | ✓ | Grey Wolf optimizer (GWO) | Feature Selection and classification problems | |||
| Taheri et al. [253] | ANN | ✓ | Hybrid artificial bee colony (HABC) | Forecasting the blast‑produced ground vibration | |||
| Chatterjee et al. [254] | MLPFFNN | ✓ | Particle swarm optimization (PSO) | Structural failure prediction of multistoried RC buildings | |||
| Song et al. [255] | DNN | ✓ | Particle swarm optimization (PSO) | Transient probabilistic analysis of flexible mechanism | |||
| Yan et al. [256] | BRNN | ✓ | Particle swarm optimization (PSO) algorithm | Stock prediction | |||
| Ganjefar and Tofighi [151] | QNN | ✓ | Hybrid genetic algorithm (HGA) | Function approximation problem | |||
| Jafrasteh and Fathianpour [150] | LLRBFNN | ✓ | Artificial bee colony (SPABC) | Ore grade estimation | |||
| Aljarah et al. [152] | MLPNN | ✓ | Whale optimization algorithm (WOA) | Benchmark datasets | |||
| Mansouri et al. [257] | ANN | ✓ | Grey Wolf optimizer (GWO) | Anomaly recognition in industrial sensor networks | |||
| Rukhaiyar et al. [258] | ANN | ✓ | Particle swarm optimization (PSO) | Predicting factor of safety of slope problem | |||
| Semero et al. [259] | FFNN | ✓ | Particle swarm optimization (PSO) & GA | Short-term wind power forecasting | |||
| Bohat and Arya [260] | FFNN | ✓ | Gbest-guided gravitational search algorithm (GSA) | Real-Parameter Optimization | |||
| Mostafaeipour et al. [261] | MLPNN | ✓ | BA & firefly optimization algorithm (FOA) | Prediction of air travel demand | |||
| Camci et al. [262] | T2FNN | ✓ | PSO-sliding mode control (PSOSMC) | Agricultural robots, or agrobots | |||
| Hadavandi et al. [154] | MLPNN | ✓ | Grey wolf optimizer (GWO) | Modeling the strength of siro-spun yarn in spinning mills | |||
| Huang and Liu [263] | RBF | ✓ | ✓ | ✓ | Particle swarm optimization (PSO) | Price Forecasting Method of Carbon Trading Market | |
| Nayak and Misra [264] | CPNN | ✓ | Genetic algorithm (GA) | The estimating stock closing indices problem | |||
| Agrawal et al. [265] | RBFNN | ✓ | Fuzzy particle swarm optimization (PSO) | Multi-label classification & real-world datasets | |||
| Mao et al. [266] | T2FNN | ✓ | Grey wolf optimizer (GWO) | Single input/output and multi-input/output systems | |||
| Tian et al. [267] | ANN | ✓ | Genetic algorithm (GA) | Detection of loss of nuclear power plants | |||
| Tang et al. [268] | FFANN | ✓ | ✓ | ✓ | Dynamic group optimisation (DGO) | Approximation testing function | |
| Haznedar and Kalinli [155] | ANFIS | ✓ | Simulated annealing (SA) | Dynamic systems identification problems | |||
| Xu et al. [269] | FFANN | ✓ | Modified artificial bee colony (MABC) | Benchmark functions | |||
| Heidari et al. [153] | MLPNN | ✓ | Grasshopper optimization algorithm (GOA) | Medical diagnosis classification datasets | |||
| Karkheiran et al. [270] | FFBPNN | ✓ | Particle swarm optimization (PSO) & GA | Precise estimation of the local scour at bridge piers | |||
| Ong and Zainuddin [271] | WNN | ✓ | Modified cuckoo search algorithm (MCS) | Multi-step ahead chaotic time series prediction | |||
| Harandizadeh et al. [272] | ANFIS | ✓ | ✓ | Particle swarm optimization (PSO) | Prediction of pile bearing capacity problem | ||
| Pham et al. [156] | MLPNN | ✓ | ✓ | Biogeography-based optimization (BBO) | Predicting coefficient of consolidation of soil | ||
| Han et al. [157] | FFNN | ✓ | Differential evolution (DE) | Prediction of cooling efficiency of forced-air systems | |||
| Jiang et al. [273] | BPNN | ✓ | Genetic algorithm (GA) | Power Grid Investment Risk (PGIR) problem | |||
| Xu et al. [274] | BPNN | ✓ | Grey wolf optimizer (GWO) | Prediction of mobile multiuser communication networks | |||
| Djema et al. [275] | MLPNN | ✓ | Grey wolf optimizer (GWO) | Adaptive direct power control problem | |||
| Li et al. [276] | GRNN | ✓ | Cuckoo search algorithm (CS) | Power transformer fault diagnosis problem | |||
| Zhao et al. [277] | MLPNN | ✓ | Selfish herd optimization algorithm (SHO) | UCI machine learning repository | |||
| Faris et al. [278] | FFNN | ✓ | ✓ | Grey wolf optimizer (GWO) | Twenty-three standard classification datasets | ||
| Rojas-Delgado et al. [158] | ANN | ✓ | PSO & FOA & cuckoo search (CS) | Six classification benchmark datasets | |||
| Bui [279] | ANN | ✓ | BBO, GSA and GWO | Forest fire susceptibility mapping in Dak Nong | |||
| Yu and Zhao [280] | BPNN | ✓ | Genetic algorithm (GA) | Prediction of critical properties of biodiesel fuels | |||
| Ma et al. [281] | NCLNN | ✓ | Particle swarm optimization (PSO) | Forecasting short-term wind speed of wind farms in China | |||
| Wang et al. [160] | MLFFNN | ✓ | Human-behavior PSO & cellular automata (CA) | 15 benchmark complex and real-world datasets | |||
| Son et al. [53] | NNARX | ✓ | Jaya algorithm (JA) | Uncertain nonlinear system identification | |||
| Raval and Pandya [282] | NNFS | ✓ | ✓ | Particle swarm optimization (PSO) | Extra High Voltage Transmission lines | ||
| Kuntoji et al. [283] | ANN | ✓ | ✓ | Particle swarm optimization (PSO) | Prediction of wave transmission | ||
| Al-Majidi et al. [161] | FFNN | ✓ | ✓ | Particle swarm optimization (PSO) | Predicting the maximum power point of a photovoltaic array | ||
| da Silva Veloso et al. [284] | FFNN | ✓ | ✓ | Particle swarm optimization (PSO) | The spouted bed drying of deformable solid materials | ||
| Yadav and Satyannarayana [285] | FFNN | ✓ | ✓ | ✓ | Multi-objective genetic algorithm (MOGA) | Estimating suspended sediment yield | |
| Wu et al. [286] | ANN | ✓ | ✓ | ✓ | Particle swarm optimization (PSO) | Prediction of Endpoint Sulfur Content in KR Desulfurization | |
| Ertuğrul [54] | RaANN | ✓ | ✓ | Differential evolution algorithms (DE) | 48 synthetic datasets | ||
| Khishe and Mosavi [159] | MLPNN | ✓ | Chimp optimization algorithm (ChOA) | Classification of underwater acoustical dataset | |||
| Shen et al. [287] | BPNN | ✓ | Particle swarm evolution (PSE) | Microchananel resistance factor prediction | |||
| Huang et al. [288] | BPNN | ✓ | Improved particle swarm optimization (IPSO) | Air Quality Prediction | |||
| Shen et al. [289] | BPNN | ✓ | Genetic algorithm (GA) | Forecasting Model for the Velocity of Robotic Fish | |||
| Ghanem et al. [290] | BPNN | ✓ | ABC and dragonfly algorithm (DA) | Efficient Intrusion Detection Model | |||
| Ansari et al. [162] | BPNN | ✓ | Magnetic optimization algorithm (MOA) & PSO | Bankruptcy Prediction problem | |||
| Gong et al. [291] | ANN | ✓ | Whale optimization algorithm (WOA) | Brain tumor diagnosis | |||
| Zeng et al. [292] | ANN | ✓ | Fruit fly optimization algorithm (FOA) | User equipment association in wireless sensor | |||
| Supraja et al. [293] | ANN | ✓ | GA & Shuffled frog‐leaping algorithm (SFLA) | Prediction of free spectrum in cognitive radio | |||
| Fang et al. [294] | MLPNN | ✓ | Whale optimization algorithm (WOA) | Automatic breast cancer detection | |||
| Zafar et al. [295] | ANN | ✓ | Particle swarm optimization (PSO) | Internet of Things (IOT) | |||
| Darabi et al. [296] | ANN | ✓ | Grey Wolf optimizer (GWO) | Spatial prediction of urban flood-inundation | |||
| Qiao et al. [297] | MLPNN | ✓ | Whale optimization algorithm (WOA) | Underwater targets classification | |||
| Zheng et al. [298] | FFNN | ✓ | Salp swarm optimization (SalpSO) | Resources Policy | |||
| Bahiraei et al. [299] | ANN | ✓ | Ant lion optimizer (ALO) algorithm | Predicting heat transfer rate | |||
| Zhang et al. [163] | Elman NN | ✓ | ✓ | ✓ | Chicken swarm optimization (CSO) | Air pollution | |
| Njock et al. [300] | ANN | ✓ | ✓ | ✓ | Differential evolution (DE) | Mechanics and Geotechnical Engineering | |
| Khatir et al. [301] | ANN | ✓ | Arithmetic optimization algorithm (AOA) | Damage assessment in FGM composite plates | |||
| Yeganeh and Shadman [302] | ANN | ✓ | ✓ | ✓ | GA & PSO | Monitoring binary and polytomous logistic profiles | |
| Guo et al. [303] | RBFNN | ✓ | JAYA optimization algorithm | Energy storage systems problems | |||
| Korouzhdeh et al. [304] | ANN | ✓ | ✓ | Biogeography-based optimization (BBO) | Construction and Building Materials | ||
| Li et al. [305] | RBFNN | ✓ | Fruit fly optimization algorithm (FOA) | Vegetable price forecasting | |||
| Cui et al. [306] | BPNN | ✓ | Biogeography-based optimization (BBO) | Multiple-criteria inventory classification | |||
| Bai et al. [307] | BPNN | ✓ | Improved particle swarm optimization (PSO) | Reliability prediction in engineering | |||
| Ghersi et al. [308] | ANN | ✓ | Genetic algorithm (GA) | Optimization of power and generation engines by biogas | |||
| Luo et al. [309] | FFNN | ✓ | Spotted hyena optimizer (SHO) | Three function-approximations | |||
| Fetimi et al. [310] | ANN | ✓ | Particle swarm optimization (PSO) | Environmental Chemical Engineering | |||
| Yibre and Koçer [311] | FFNN | ✓ | Artificial algae algorithm (AAA) | Semen quality predictive model | |||
| Sun et al. [312] | Elman NN | ✓ | Quantum water strider algorithm (QWSA) | Energy estimation | |||
| Sheelwant et al. [313] | ANN | ✓ | Genetic algorithm (GA) | Communications (aluminum metal matrix composites) | |||
| Medi and Asadbeigi [314] | NNARX | ✓ | Genetic algorithm (GA) | Nonlinear chemical and biochemical processes | |||
| Zhang et al. [315] | BPNN | ✓ | Chaotic adaptive gravity search algorithm (CAGSA) | Fault diagnosis of electrical machine drive system | |||
| Zhao et al. [316] | BPNN | ✓ | Whale optimization algorithm (WOA) | Prediction of the deflection of reinforced concrete beams | |||
| Garcıa-Rodenas et al. [317] | FFNN | ✓ | Memetic chaotic gravitational search algorithm (MCGSA) | Approximation of a continuous function | |||
| Uzlu [318] | ANN | ✓ | Grey wolf optimizer (GWO) | Estimates of greenhouse gas emission | |||
| Saffari et al. [319] | MLPNN | ✓ | Chimp optimization algorithm (ChOA) | Marine mammal classification | |||
| Liu et al. [320] | FNN | ✓ | Particle swarm optimization (PSO) | Path planning problem | |||
| Bui et al. [321] | ANN | ✓ | Cuckoo search optimization (CSO) | Predicting Ground Vibrations | |||
| Raei et al. [322] | BPNN | ✓ | Whale optimization algorithm (WOA) | Soil wind erodibility | |||
| Cui et al. [323] | BPNN | ✓ | Genetic algorithm (GA) | Applications in prediction of foundation pit deformation | |||
| Sağ and Abdullah Jalil [324] | FFNN | ✓ | Vortex search (VS) Optimization algorithm | Classification Dataset | |||
| Wang et al. [325] | ANN | ✓ | Genetic algorithm (GA) | Prediction of parameters of shot peen forming | |||
| Wang et al. [326] | BPNN | ✓ | Whale optimization algorithm (WOA) | Image denoising | |||
| Turki and Shammari [327] | FFNN | ✓ | Genetic algorithm (GA) | Predicting the Output Power of a Photovoltaic Module | |||
| Eappen et al. [328] | ANN | ✓ | Advanced squirrel algorithm (ASA) | Cognitive radio-based air traffic control application | |||
| BACANIN et al. [329] | ANN | ✓ | ✓ | Artificial bee colony (ABC) | Five well-known medical benchmark datasets | ||
| Liu et al. [330] | BPNN | ✓ | Hybrid GA-PSO | Data fusion for multi-source sensors | |||
| Nguyen et al. [331] | BPNN | ✓ | Accelerated particle swarm optimization (APSO) | Robot precision positioning | |||
| Ge et al. [332] | Regression NN | ✓ | Grey wolf optimizer (GWO) | Short-term load forecasting of regional distribution network | |||
| Kaur and Chahal [333] | ANFIS | ✓ | Particle swarm optimization (PSO) | Prediction of Chikungunya disease | |||
| Zhang et al. [334] | BPNN | ✓ | Improved grey wolf optimizer (IGWO) | Energy Storage | |||
| Guo et al. [335] | ELMAN NN | ✓ | Whale optimization algorithm (WOA) | Monophenolase assay-analytical biochemistry | |||
| Xue et al. [336] | FFNN | ✓ | Differential evolution (DE) | Different classification problems | |||
| Ding et al. [337] | ANN | ✓ | Jaya algorithm (JA) | Simultaneous identification of structural damage | |||
| Zhu et al. [338] | ANN | ✓ | Adaptive genetic algorithm (AGA) | Wave energy converter arrays | |||
| Jnr et al. [339] | BPNN | ✓ | Aquila optimization algorithm (AOA) | Wind speed prediction | |||
| Zhao et al. [340] | ANN | ✓ | Multi-tracker optimization algorithm (MTOA) | Predicting compressive strength of concrete | |||
| Wua et al. [341] | ANN | ✓ | Bees algorithm (BA) | Welding sequence Engineering optimization | |||
| Si et al. [342] | MLPNN | ✓ | Equilibrium optimizer (EO) algorithm | Medical data classification | |||
| Khan et al. [343] | FLNN | ✓ | Accelerated particle swarm optimization (APSO) | Medical data classification | |||
| Li et al. [164] | MLPNN | ✓ | Biogeography-based optimization (BBO) | Medical data classification | |||
| Gülcü [344] | MLPNN | ✓ | Dragonfly algorithm (DA) | Real-world civil engineering and classification datasets | |||
| Netsanet et al. [345] | ANN | ✓ | Ant colony optimization (ACO) | Short-term PV power forecasting | |||
| Liang et al. [346] | MLPNN | ✓ | Hunger games search optimization (HGSO) | Building Engineering | |||
| Chondrodima et al. [347] | RBFNN | ✓ | Particle swarm optimization (PSO) | Public transport arrival time prediction | |||
| Ehteram et al. [348] | MLPNN | ✓ | Multi-objective salp swarm algorithm (MOSSA) | Predicting evaporation | |||
| Li et al. [349] | Elman NN | ✓ | Sparrow search algorithm (SSA) | Thermal error modeling of motorized spindle | |||
| Ibad et al. [350] | Spiking NN | ✓ | Salp swarm algorithm (SSA) | Time‑Series Classification Problem | |||
| Foong and Moayedi [351] | MLPNN | ✓ | Equilibrium optimization (EO) & VSA | Slope stability evaluation | |||
| Chatterjee et al. [352] | FFNN | ✓ | Chaotic whale optimization algorithm (COWOA) | Classification dataset | |||
| He et al. [353] | CFNN | ✓ | Grey wolf optimizer (GWO) | Predicting the compressibility of clay | |||
| Gülcü [354] | MLPNN | ✓ | Improved animal migration optimization (IAMO) | Classification dataset | |||
| Liu et al. [355] | BPNN | ✓ | Genetic algorithm (GA) | Electrical Engineering & Technology | |||
| Bataineh et al. [356] | MLPNN | ✓ | Clonal selection algorithms (CSA) | Five classification datasets | |||
| Han et al. [357] | FNN | ✓ | ✓ | Multi-objective PSO (MOPSO) | Nonlinear Systems Identification | ||
| Deepika and Balaji [358] | ANN | ✓ | ✓ | Differential evolution (DE) | Effective heart disease prediction problem | ||
| Kirankaya and Aykut [359] | ANN | ✓ | Artificial bee colony (ABC) algorithms | Classification dataset | |||
| Yan et al. [360] | MLPNN | ✓ | Chaotic grey wolf optimization (CGWO) | Energy | |||
| Li et al. [361] | BPNN | ✓ | Genetic algorithm (GA) | Coastal Bulk (Coal) Freight Index Forecasting | |||
| Kuo et al. [362] | BPNN | ✓ | Simulated annealing (SA) | Classification dataset (MNIST and FASHION) | |||
| Zhao et al. [363] | BPNN | ✓ | Sparrow search algorithm (SSA) | Predicting the Thickness of an Excavation Damaged Zone | |||
| Davar et al. [364] | BPNN | ✓ | Butterfly optimization algorithm (BOA) & PSO | Predicting Matric Suction in Expansive Clay Soil | |||
| Huang et al. [365] | BPNN | ✓ | Firefly algorithm (FA) | Micromachined Silicon Resonant Accelerometers | |||
| Wang et al. [366] | RBFNN | ✓ | Grey wolf optimizer (GWO) | Electrical Impedance Tomography | |||
Investigation of Optimized Components in ANNs
As an optimization problem, MH algorithms formulate the optimal estimation of ANN components (such as weights, number of layers, number of neurons, learning rate, etc.). This section examines the abundance of MH use for optimized components in neural networks (according to the papers in Table 2). Figure 12 shows the relative abundance of research on optimized components in ANNs using MH algorithms.
Fig. 12.
Relative abundance of research on optimized components in ANNs using MH algorithms
As shown in Fig. 12, in 221 studies (69%), weights and biases have been adjusted using MH algorithms, which shows a high percentage. In 47 studies (14%), the number of neurons in the layers has been adjusted using MH algorithms. Moreover, in 22 studies (7%), the number of layers in the neural network has been adjusted. Finally, in 31 studies (10%), learning parameters, learning algorithms or activation functions have been adjusted. Figure 13 also shows the relative abundance of research in the simultaneous optimization of two components of ANNs.
Fig. 13.
Relative abundance of research in the simultaneous optimization of two components of ANNs using MHs
As can be seen in Fig. 13, in 15 studies, weights and layers have been adjusted simultaneously. In 28 studies, weights and neurons; in 15 studies, weights and learning parameters; in 14 studies, the number of layers and neurons; in 6 studies, the number of layers and learning parameters; and in 14 studies, the number of neurons and learning parameters have been adjusted simultaneously. Figure 14 shows the relative abundance of research in the simultaneous optimization of three components of ANNs. As can be seen, in 6 studies, weights, the number of neurons and learning parameters have been adjusted simultaneously. In 7 studies, weights, number of layers and number of neurons; in 2 studies, weights, number of layers and learning parameters; in 5 studies, number of layers, number of neurons and learning parameters were adjusted simultaneously. According to Table 2, in only one study [143], all four neural network components were adjusted simultaneously. Therefore, little research has been done in this area.
Fig. 14.
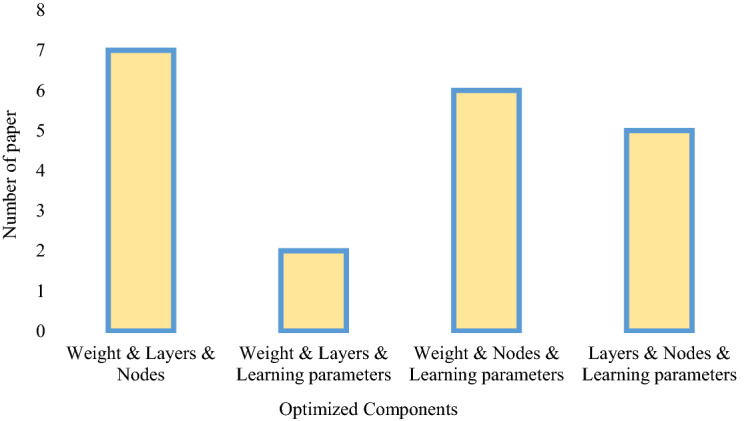
Relative abundance of research in the simultaneous optimization of three components of ANNs using MHs
Investigation of Meta-Heuristic Algorithms Used in Ann's Optimization
According to Table 2, many MH algorithms have been developed to optimize neural networks. Figure 15 shows the MH algorithms used to optimize ANNs. PSO, 76 implementations and GA, 47 implementations, was the most used MH algorithms. GWO, DE, SA, ABC, GSA, WOA, BBO, and FOA algorithms are also in the next ranks. Most researchers tend to extend novel hybrid algorithms by combining MHs to optimize the hyper-parameters of ANNs. The development of hybrid MHs helps improving algorithms performance and capable of solving complex optimization problems. According to the results of Table 2, many researches have used the modification and hybridization of meta-heuristic algorithms to optimize neural network parameters. Also, the performance of the proposed hybrid MH algorithms have been better than others.
Fig. 15.
Meta-heuristic algorithms used to optimize ANNs
Checking the Number of Papers Published in Journals and Years
In this section, the papers in Table 2 are categorized according to the type of journals and the year of their publication. Figure 16 shows the percentage of papers published in various journals (based on Table 2). As shown, 74 papers (44%) in Elsevier, 30 papers (21%) in Springer, 27 papers (13%) in IEEE, 16 papers (8%) in Taylor & Francis, 13 papers (6%) in John Wiley & Sons, and 14 papers (8%) in other journals have been published regarding the use of MH for ANNs.
Fig. 16.
Papers published in journals (based on Table 2)
Figure 17 also indicates the changes in the number of papers published in different years about the use of MH for Training ANNs. Between 1988 and 2002, few papers were developed for neural network optimization. From 2003 to 2010, neural network optimization received a little more attention from researchers, and the number of papers in this field increased. But from 2011 to 2022, many researchers have worked on neural network optimization. Especially since 2021, the number of these papers has been increasing. This implies that this problem is still a challenge and many problems need to be resolved.
Fig. 17.
Changes in the number of papers published in different years about the use of MH for Training ANNs
Applications of Hybrid MH-NNs
In this section, the application of the papers in Table 2 is evaluated. Figure 18 shows the application of the papers regarding the use of MH for ANNs. 77 papers in benchmark problem (Classification, prediction, time series, optimization, system identification), 53 papers in electrical engineering, signal processing and energy systems, 34 papers in civil engineering, 18 papers in mechanical engineering, 16 papers in biomedical and chemical engineering, 15 papers in medical image classification and medical diseases diagnosis, 8 papers in environmental management, 8 papers in economy and product quality, and 19 papers in other applications have been published regarding the use of MH for ANNs.
Fig. 18.
Application of papers regarding the use of MH for ANNs
As can be seen, most of the MH-ANNs were implemented on benchmark problems and datasets. The optimal solutions of the benchmark problems are known. Therefore, they are a very good criterion for evaluating algorithms. Also, many evolutionary ANNs have been implemented in electrical engineering, civil engineering, mechanical engineering, and medical image classification applications. The results of these papers show that the proposed hybrid ANNs architectures perform better than others. Therefore, it can be said that evolutionary artificial neural networks (MH-ANNs) are promising methods in these applications.
Contributions of Different Continents in Using the Hybrid MH-NN Models
Figure 19 shows the distribution of studied papers according to the affiliation of the authors for each continent. As can be seen, Asia has the largest portion of contributions in the world with the maximum number of papers from China, Korea, and India, while America has the lowest contributions.
Fig. 19.
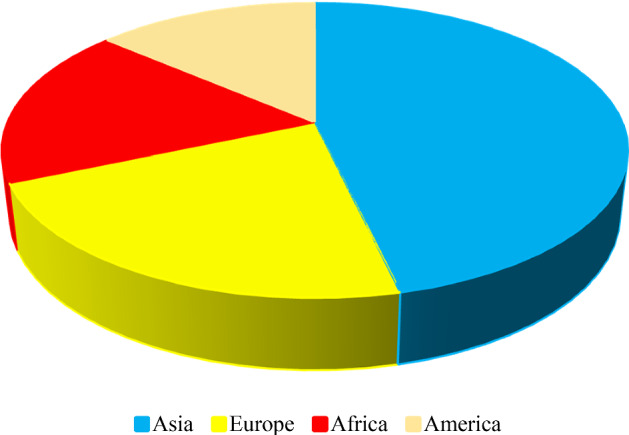
Contributions of different continents in using the hybrid MH-NN models
Review2: Training the DL Architectures by MH Algorithms
One of the weaknesses of DL architectures is finding the optimal value of algorithm parameters. This section provides a comprehensive overview of optimizing different DL architectures using MH algorithms. Optimization of DL architectures is often considered from several aspects: optimization of weights, hyper-parameters, network structure, activation nodes, learning parameters, learning algorithm, learning environment, etc. [9].
Ku et al. [367] used the genetic algorithm to optimize the weights of an RNN. The proposed approach (GA-RNN) was compared with Lamarckian and Baldwinian mechanisms, which indicated better results (convergence speed and accuracy). Blanco et al. [368] used the genetic algorithm (GA) to improve the performance of an RNN. The results indicated that the proposed algorithm solves the time complexity well. Delgado et al. [369] used multi-objective SPEA2 and NSGA_II algorithms to optimize the topology and structure of an RNN. The proposed architectures performed well for the time series problem. Bayer et al. [370] used the NSGA_II to train an LSTM architecture. The results showed that the proposed network performs well in learning sequences.
Lin and Lee [371] used the improved PSO algorithm to optimize the weights of an RFNN. The results indicated that the IPSO algorithm for controlling nonlinear systems performed better than other methods (traditional PSO and GA). Subrahmanya and Shin [372] used the combination of PSO and CMA-ES algorithms to optimize the structure and weights of an RNN. According to the results, the proposed architecture (HMH-RNN) indicated good performance. Hsieh et al. [373] used the artificial bee colony (ABC) algorithm to optimize the weights of an RNN. According to experiments, the proposed approach indicates good capital market performance and can be implemented in a trading system to predict stock prices and maximize profits.
David and Greental [41] used combined gradient-based learning and genetic algorithm strategy to train a deep neural network. The proposed architecture performed very well in the benchmark data set. Shinozaki and Watanabe [40] used GA and CMA-ES algorithms to optimize the structure and parameters of a DNN. The results demonstrated that the proposed algorithm is suitable for adjusting neural network parameters. Sheikhan et al. [374] used the GSA binary algorithm to optimize the structure and weights of an RNN network. The proposed algorithm (BGSA-RNN) was compared with gradient-based and PSO algorithms, which provided significant results. A combination of evolutionary algorithm and DBN network was used by Chen et al. [375] for image classification. The results indicated that the execution time decreases rapidly.
Real et al. [376] used an evolutionary algorithm for convolutional neural network (CNN) training to classify CIFAR-10 and CIFAR-100 datasets. The findings implied that the proposed approach could provide competitive results in two popular datasets. Tang et al. [377] used the PSO algorithm to optimize the weights of a DSNN. The proposed algorithm performed very well in feature extraction problems and EEG signal detection. Song et al. [378] used improved biogeography-based optimization (IBBO) to optimize the parameters and weights of DDEA. The results indicated that the proposed approach (IBBO-DDEA) for gastrointestinal complications prediction performed better than other methods (such as ANN and other common architectures).
Da Silva et al. [379] used the PSO algorithm to optimize the hyper-parameters of a convolutional neural network. Experiments on a CAD system indicated an improvement in the accuracy of the proposed algorithm. The WWO algorithm was used by Zhou et al. [380] to optimize the structure and weights of a DNN. Experiments on several benchmark datasets indicated that the proposed WWO-DNN approach performs better than the gradient-based methods. Shi et al. [381] used the PSO algorithm to optimize the number of neurons in the hidden layers of a deep neural network. Experimental results demonstrated that the detection rate in the proposed algorithm was improved by 9.4% and 8.8% compared to conventional DNN and support vector machine (SVM). In addition, another experiment compared to the genetic algorithm (GA) proved that the proposed particle swarm optimization (PSO) is more effective in deep neural network (DNN) optimization. Hong et al. [382] used the genetic algorithm (GA) to optimize the parameters and hyper-parameters of the CNN. Experimental results for the price forecasting problem showed that the proposed GA-CNN always offers higher forecasting accuracy and lower error rates than other forecasting methods.
Guo et al. [383] used a distributed particle swarm optimization (DPSO) algorithm to optimize the hyper-parameters of convolutional neural network (CNN). Experiments on the image classification dataset indicated that the proposed DPSO method improved the performance of the CNN model while reducing computational time compared to traditional algorithms. ZahediNasab and Mohseni [384] used the genetic algorithm (GA) to optimize the deep neural network (DNN) activation function. Experiments on the medical classification and MNIST datasets showed the proposed approach's superiority. It was also stated that selecting an appropriate adaptive activation function plays an important role in the quality of a deep neural network. Jallal et al. [385] used an improved PSO algorithm for DNN training to improve the prediction accuracy of a solar tracker. The DNN-RODDPSO algorithm performed better than the standard algorithms in the literature. Elmasry et al. [386] used the PSO algorithm to optimize the hyper-parameters of three DL algorithms called DNN, LSTM-RNN and DBN. Experiments on the network intrusion detection problem proposed that these three developed architectures performed better than conventional architectures.
Kan et al. [387] used the adaptive particle swarm optimization (APSO) algorithm to optimize the weights and biases of the convolutional neural network (CNN). According to the results, the proposed hybrid approach (APSO-CNN) performed well in IoT network intrusion detection. Also, the performance of the proposed hybrid architecture has been better than other algorithms. Kanna and Santhi, [388] used the black widow optimization (BWO) algorithm to optimize the weights of CNN-LSTM for intrusion detection systems. The results showed that the proposed hybrid architecture (BWO-CNN-LSTM) performs better than the other original architectures. Ragab et al. [389] used enhanced gravitational search optimization (EGSO) algorithm to optimize the weights and biases of the convolutional neural network (CNN). According to the results, the proposed hybrid approach (EGSO-CNN) performed well in COVID-19 diagnosis problem. Also, the performance of the proposed hybrid architecture has been better than other algorithms.
Table 3 summarizes the above research as well as many other studies. As can be seen, for each research, the author name, year of publication, type of DL, optimized components, type of MH algorithm used, application and data set used are listed. In the following, for a more comprehensive review, some statistical analysis of the research collected in Table 3 is presented.
Table 3.
A summary of meta-heuristic algorithm developments for training/optimization deep learning architectures
| Authors & dates | The deep learning categories | Optimized components: 1. Weights, 2. Layers & Nodes 3. Other Hyper parameters 4. Learning parameters & Activation function |
The meta-heuristic algorithm used for training deep learning | Application / dataset | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| Ku et al. [367] | RNN | ✓ | Genetic algorithm (GA) | Prediction and classification problems | |||
| Blanco et al. [368] | RNN | ✓ | Real-coded genetic algorithm (GA) | Benchmark datasets | |||
| Delgado et al. [369] | RNN | ✓ | ✓ | Strength pareto evolutionary algorithm2 & NSGA_II | Time-series benchmark problem | ||
| Bayer et al. [370] | LSTM | ✓ | Non-dominated sorting genetic algorithm (NSGA-II) | Sequence learning | |||
| Subrahmanya and Shin [372] | RNN | ✓ | ✓ | PSO and CMA-ES | Tow MIMO non-linear processes | ||
| Lin and Lee [371] | RFNN | ✓ | Improved particle swarm optimization (IPSO) | Non-linear system control | |||
| Hsieh et al. [373] | RNN | ✓ | Artificial bee colony algorithm (ABC) | Several international stock markets | |||
| Cheung and Sable [390] | CNN | ✓ | Evolutionary algorithm (EA) | MNIST Variations, rectangles-image and image classification | |||
| David and Greental [41] | DNN | ✓ | Genetic algorithm (GA) | MNIST hand-written digit recognition database | |||
| Shinozaki and Watanabe [40] | DNN | ✓ | ✓ | Genetic algorithm (GA) & CMA-ES | Phoneme recognition and spoken digit detection tasks | ||
| Lander and Shang [42] | DAE | ✓ | ✓ | ✓ | Evolutionary algorithm (EA) | MNIST handwritten digits 1 k dataset | |
| Sheikhan et al. [374] | RNN | ✓ | ✓ | Binary gravitational search algorithm (BGSA) | Emotion recognition and speech processing | ||
| Desell et al. [391] | RNN | ✓ | Ant colony optimization (ACO) | Predicting general aviation flight data | |||
| Rosa et al. [43] | CNN | ✓ | Harmony search algorithm (HS) | Fingerprint and handwritten digit recognition | |||
| Chen et al. [375] | DBN | ✓ | Evolutionary function array classification voter (EFACV) | MNIST dataset | |||
| Rosa et al. [44] | DBN | ✓ | ✓ | Firefly algorithm (FA) | MNIST and Semeion Handwritten Digit datasets | ||
| Papa et al. [392] | DBN | ✓ | ✓ | Harmony search algorithm (HSA) | Binary image reconstruction | ||
| Zhang et al. [393] | DBN | ✓ | ✓ | ✓ | Multi-objective evolutionary algorithm (MOEA) | Remaining Useful Life Estimation in Prognostics | |
| Tang et al. [377] | DSNN | ✓ | Particle swarm optimization (PSO) | Recognition of motor imagery EEG signals | |||
| Khalifa et al. [32] | CNN | ✓ | Particle swarm optimization (PSO) | Classification problem | |||
| Badem et al. [394] | DNN | ✓ | Hybrid artificial bee colony (HABC) | 15 benchmark data sets | |||
| Gelly and Gauvain [395] | RNN | ✓ | Particle swarm optimization (PSO) | Speech activity detection | |||
| Liu et al. [396] | CNN | ✓ | ✓ | Multi-objective evolutionary algorithm (MOEA) | The MNIST data set and the CIFAR-10 data set | ||
| Song et al. [378] | DDAE | ✓ | ✓ | Ecogeography-based optimization (EBO) | Predicting morbidity of gastrointestinal infections | ||
| ElSaid et al. [397] | LSTM-RNN | ✓ | Ant colony optimization (ACO) | Turbine engine vibration | |||
| Real et al. [376] | CNN | ✓ | ✓ | Evolutionary algorithm (EA) | The CIFAR-10 and CIFAR-100 datasets | ||
| Jiang et al. [22] | DNN | ✓ | ✓ | Modified genetic algorithm (MGA) | Demand Forecasting in Outpatient Department | ||
| Lopez-Rincon et al. [33] | CNN | ✓ | ✓ | Evolutionary algorithm (EA) | Cancer miRNA biomarkers classification | ||
| Ye [37] | DNN | ✓ | ✓ | ✓ | Particle swarm optimization (PSO) | Biological activity prediction datasets | |
| Kim et al. [398] | DBN | ✓ | Particle swarm optimization (PSO) | Highly class imbalance problem | |||
| Fujino et al. [399] | CNN | ✓ | Genetic algorithm (GA) | Recognition of human sketches problem | |||
| Lorenzo et al. [400] | DNN | ✓ | Particle swarm optimization (PSO) | MNIST and CIFAR-10 dataset | |||
| Dufourq and Bassett [34] | EDEN | ✓ | Genetic algorithm (GA) | Seven image and sentiment classification datasets | |||
| da Silva et al. [379] | CNN | ✓ | Particle swarm optimization (PSO) | Lung nodule false positive reduction on CT images | |||
| Chen et al. [401] | LSTM | ✓ | Extremal optimization algorithm (EO) | Wind speed forecasting | |||
| Passos et al. [402] | DBM | ✓ | Particle swarm optimization (PSO), AIWPSO, HS & IHS | Binary image reconstruction | |||
| Soon et al. [403] | CNN | ✓ | Particle swarm optimization (PSO) | Vehicle logo recognition | |||
| Peng et al. [38] | LSTM | ✓ | Evolutionary algorithm (EA) | Electricity price prediction problem | |||
| ElSaid et al. [404] | LSTM-RNN | ✓ | ✓ | Ant colony optimization (ACO) | Predict turbine engine vibration | ||
| Lorenzo and Nalepa [405] | DNN | ✓ | Memetic evolution algorithm (MEA) | segmenting medical images and CIFAR-10 benchmark | |||
| Pawełczyk et al. [406] | CNN | ✓ | ✓ | Genetic algorithm (GA) | MNIST set which contains grayscale images | ||
| Fielding and Zhang [407] | CNN | ✓ | ✓ | Particle swarm optimization (PSO) | CIFAR-10 image classification task | ||
| Martín et al. [45] | DNN | ✓ | ✓ | ✓ | Evolutionary algorithm (EA) | Dataset of handwritten digits images | |
| Sun et al. [408] | DNN | ✓ | ✓ | Evolutionary algorithm (EA) | Learning Meaningful Representations | ||
| Liang et al. [409] | DNN | ✓ | ✓ | Evolutionary algorithm (EA) | Omniglot Character Recognition problem | ||
| Wang et al. [35] | CNN | ✓ | ✓ | Hybrid differential evolution approach (HDE) | Image classification | ||
| Zhou et al. [380] | DNN | ✓ | ✓ | Water wave optimization (WWO) | Complex network optimization problems | ||
| Khodabandehlou and Fadali [410] | RNN | ✓ | Dynamical trajectory-based optimization (DTBO) | Three non- linear dynamical systems | |||
| Banharnsakun [46] | CNN | ✓ | Artificial bee colony (ABC) | MNIST handwritten image dataset (classification) | |||
| Gao and Li [411] | CNN | ✓ | ✓ | Segmented particle swarm optimization (SPSO) | Land cover and land use classification of RS images | ||
| Wang et al. [39] | CNN | ✓ | Particle swarm optimization (PSO) | Linear prediction model | |||
| Wang et al. [36] | GAN | ✓ | Evolutionary algorithm (EA) | Several image classification datasets | |||
| Fujino et al. [412] | CNN | ✓ | Genetic algorithm (GA) | Anime storyboard recognition problem | |||
| Li et al. [413] | CNN | ✓ | Particle swarm optimization (PSO) | Image classification | |||
| Li et al. [414] | DBNN | ✓ | ✓ | Multi-objective PSO (MOPSO) | Traffic flow forecasting | ||
| Nepomuceno [415] | RRNN | ✓ | Multi-objective optimization (MOO) | System identification and modelling | |||
| Wei et al. [416] | DBN | ✓ | Artificial fish swarm algorithm (AFSA)-GA-PSO | Intrusion detection classification model | |||
| Shi et al. [381] | DNN | ✓ | Particle swarm optimization (PSO) | Digital modulation recognition | |||
| Junior and Yen [417] | CNN | ✓ | ✓ | Particle swarm optimization (PSO) | Image classification | ||
| Navaneeth and Suchetha [418] | 1-D CNN | ✓ | Particle swarm optimization (PSO) | Real-time detection and classification applications | |||
| ZahediNasab and Mohseni [384] | CNN | ✓ | Genetic algorithm (GA) | CT brain and the MNIST hand written digits dataset | |||
| Goel et al. [419] | CNN | ✓ | Grey wolf optimizer (GWO) | An automatic diagnosis of COVID-19 | |||
| Gao et al. [420] | CNN | ✓ | Gradient-priority particle swarm optimization (GPSO) | EEG-based Emotion Recognition | |||
| Martín et al. [421] | CNN | ✓ | ✓ | Hybrid statistically coral reef optimization (HSCRO) | The CIFAR-10 and the CINIC-10 datasets | ||
| Lan et al. [51] | CNN | ✓ | Particle swarm optimization (PSO) | Enhancing heart disease and breast cancer detection | |||
| Tang et al. [422] | LSTM | ✓ | Genetic algorithm (GA) | Traffic Flow Prediction on Urban Road Network | |||
| Elmasry et al. [386] | LSTM-RNN | ✓ | Particle swarm optimization (PSO) | Network intrusion detection | |||
| Guo et al. [383] | CNN | ✓ | Distributed particle swarm optimization (DPSO) | Image classification benchmarks | |||
| Lima et al. [423] | CNN | ✓ | Simulating annealing (SA) | Toward classifying small lung nodules | |||
| Renukadevi and Karunakaran [424] | DBN | ✓ | ✓ | Grasshopper optimization algorithm (GOA) | Liver disease classification | ||
| Jallal et al. [385] | DNN | ✓ | Randomly occurring distributed delayed PSO | Monitoring the energy produced by solar trackers | |||
| Ali et al. [425] | DBN | ✓ | ✓ | Stacked genetic algorithm (SGA) | Heart Disease Prediction | ||
| Hong et al. [382] | CNN | ✓ | ✓ | Genetic algorithm (GA) | Locational Marginal Price Forecasting | ||
| Rajagopal et al. [426] | CNN | ✓ | ✓ | Multi-objective PSO (MOPSO) | Scene Classification in Unmanned Aerial Vehicles | ||
| Lu et al. [427] | CNN | ✓ | ✓ | Multi-objective genetic algorithm (MOGA) | Image Classification | ||
| Lin et al. [428] | DAE | ✓ | Ecogeography-based optimization (EBO) | In-Vehicle Networks-CAN Bus | |||
| Kavousi-Fard et al. [429] | GAN | ✓ | Modified firefly algorithm (MFA) | Securing Vehicles problem | |||
| Johnson et al. [430] | CNN | ✓ | Genetic algorithm (GA) | Image classification dataset: CIFAR10, MNIST and Caltech | |||
| Kan et al. [387] | CNN | ✓ | Adaptive particle swarm optimization (APSO) | IoT network intrusion detection | |||
| Zheng et al. [431] | CNN | ✓ | Genetic algorithm (GA) | Pattern Recognition (parametric eye modeling) | |||
| Pang et al. [432] | CNN & LSTM | ✓ | Particle swarm optimization (PSO) | Hyperspectral imaging classification | |||
| Gai et al. [433] | DBN | ✓ | Sparrow search algorithm (SSA) | Detection of gear fault severity | |||
| Sun et al. [434] | DBN | ✓ | Improved archimedes optimization algorithm (IAOA) | Energy | |||
| Samir et al. [435] | CNN | ✓ | Heuristic-based JSO optimization algorithm | Predicting heart diseases problem | |||
| Liu et al. [436] | DNN | ✓ | Improved particle swarm optimization (IPSO) | COVID-19 spread | |||
| Maoa et al. [437] | CNN | ✓ | ✓ | Genetic algorithm (GA) | Waste classification—Image recognition | ||
| Gao et al. [420] | CNN | ✓ | Particle swarm optimization (PSO) | EEG-based emotion recognition | |||
| Kim and Cho [438] | CNN-LSTM | ✓ | Particle swarm optimization (PSO) | Anomalous query access control | |||
| Zhang et al. [439] | CNN-LSTM | ✓ | Swarm-based optimization | Intelligent human action recognition | |||
| Li et al. [440] | CNN | ✓ | Sea lion insisted on dragon fly modification (SL-DU) | Hardening prediction in steel | |||
| Mohakud and Dash [441] | CNN | ✓ | Exponential grey wolf optimization (EN-GWO) | Skin cancer image segmentation | |||
| Martín et al. [421] | CNN | ✓ | ✓ | Hybrid coral reef optimization (HSCRO) | CIFAR-10 and the CINIC-10 Dataset | ||
| Altan et al. [442] | LSTM | ✓ | Grey wolf optimizer (GWO) Algorithm | Wind speed forecasting | |||
| Roder et al. [443] | DBN | ✓ | hill climb (HC) Metaheuristic optimization | Image classification Dataset | |||
| Mathe et al. [444] | CNN | ✓ | ✓ | Spider monkey-based electric fish optimization (SM-EFO) | Biomedical Signal Processing and Control | ||
| Mahesh et al. [445] | CNN | ✓ | ✓ | Jaya-based barnacle mating optimization (J-BMO) | Biomedical Signal Processing and Control | ||
| Singh et al. [446] | CNN | ✓ | Multi-level particle swarm optimization (MPSO) | Image classification Dataset | |||
| Kumar and Haider [447] | RNN–LSTM | ✓ | ✓ | ✓ | Flower pollination algorithm (FPA) | Prediction of Intra‑day Stock Market | |
| Kumar et al. [448] | DNN | ✓ | ✓ | ✓ | Genetic algorithm (GA) | Four Image classification Dataset | |
| Chitra and Kumar [449] | CNN | ✓ | ✓ | ✓ | Mutation-based atom search optimization (MASO) | Cervical cancer detection | |
| Deighan et al. [450] | CNN | ✓ | Genetic algorithm (GA) | Gravitational wave classification | |||
| Qu et al. [451] | DAE | ✓ | Non-dominated sorting genetic algorithm (NSGA_II) | Classification problem | |||
| Goel et al. [452] | CNN | ✓ | ✓ | Grey wolf optimizer (GWO) algorithm | Spread of coronavirus disease (COVID-19) | ||
| Liu and Nie [453] | SSAE | ✓ | Invasive weed optimization algorithm (IWO) | Image datasets | |||
| Kumar et al. [454] | LSTM | ✓ | Artificial bee colony (ABC) | Integrating big data driven sentiments polarity | |||
| Das et al. [455] | RNN | ✓ | ✓ | Flower pollination (FP) algorithm | Modeling of electron Beam welding process | ||
| Gong et al. [456] | LSTM | ✓ | ✓ | ✓ | Fireworks Algorithm (FWA) | Air-conditioning load data of a union office | |
| Chen et al. [457] | LSTM | ✓ | ✓ | Hybrid coding particle swarm optimization (HCPSO) | Series prediction and Nonlinear system identification | ||
| Bacanin et al. [458] | CNN | ✓ | Firefly algorithm (FA) | Medical image classification (IXI and cancer dataset) | |||
| Sherly and Jaya [459] | CNN | ✓ | Improved firefly algorithm (IFA) | Scene character recognition | |||
| Datta And Chakrabarti [460] | RNN | ✓ | Fire fly-oriented multi-verse optimizer (FF-MVO) | Classification problem | |||
| Alenazy and Alqahtani [461] | DBN | ✓ | Gravitational search algorithm (GSA) | Facial expression recognition (FER) | |||
| Sudha and alarmathi [462] | DBN | ✓ | Interactive autodidactic school (IAS) | Classification problem | |||
| Jammalamadaka and Parveen [463] | DBN | ✓ | Search and rescue (SAR) algorithm | Classification problem | |||
| Gadekallu et al. [464] | CNN | ✓ | Crow search algorithm (CSA) | Classification: Human–computer interaction (HCI) | |||
| Irmak [465] | CNN | ✓ | Grid search optimization (GSO) | Medical image classification | |||
| Arjunagi and Patil [466] | CNN | ✓ | Adaptive spider monkey optimization (AOSMO) | Identifying and diagnosing maize leaf diseases | |||
| Li et al. [467] | RNN | ✓ | ✓ | Adaptive dynamic particle swarm optimization (ADPSO) | Air Quality Index Prediction | ||
| Oyelade and Ezugwu [468] | CNN | ✓ | ✓ | Multiverse optimizer (MVO), SBO & LCBO | Medical image classification | ||
| Tripathi and Maktedar [469] | CNN | ✓ | Lion assisted firefly algorithm (LA-FF) | Classification problem | |||
| Karuppusamy et al. [470] | DBN | ✓ | Chronological salp swarm algorithm (CSSA) |
Intrusion detection system Intrusion detection in cloud |
|||
| Priya and Chacko [471] | CNN | ✓ | ✓ | Improved particle swarm optimized (IPSO) | Medical image classification | ||
| Danesh and Vasuhi [472] | CNN | ✓ | Glow worm swarm optimization (GWSO) | Spectrum sensing ranks | |||
| Zhang et al. [473] | LSTM | ✓ | ✓ | Genetic algorithm (GA) | Upper Limb Activities Recognition | ||
| Farrag et al. [474] | LSTM | ✓ | ✓ | Genetic algorithm (GA) | South Australia State (SA) power system | ||
| Arora et al. [475] | DAR | ✓ | Grasshopper optimisation algorithm (GOA) | Wind Power Forecasting | |||
| Goay et al. [476] | CNN-LSTM | ✓ | Adaptive successive halving Optimization (ASH-HPO) | Transient simulations of high-speed channels | |||
| Liu et al. [477] | LSTM | ✓ | ✓ | Adaptive particle swarm optimization (AHMPSO) | Monitoring of wastewater treatment plant (WWTP) | ||
| Davoudi and Thulasiraman [478] | CNN | ✓ | Genetic algorithm (GA) | Breast cancer classification problem | |||
| Li et al. [478] | DBN | ✓ | ✓ | Simulated annealing cuckoo search algorithm (SA-CSA) | Fault diagnosis of railway freight car wheelset | ||
| Liu et al. [479] | CNN | ✓ | Continuous particle swarm optimization (CPSO) | Hyperspectral Image Classification | |||
| Brodzicki et al. [480] | DNN | ✓ | Whale optimization algorithm (WOA) | Classification Dataset (MNIST) | |||
| Baniasadi et al. [481] | CNN | ✓ | Improved particle swarm optimization (NSBPSO) | Intrusion Detection in IoT Systems | |||
| Paul et al. [482] | LSTM-DBN | ✓ | Sparrow search optimization (SSO) | Water quality index prediction | |||
| Gonçalves et al. [483] | CNN | ✓ | ✓ | ✓ | Genetic algorithm (GA) & PSO | Cancer detection | |
| Glaret subin and Muthukannan [484] | CNN | ✓ | ✓ | ✓ | Flower pollination optimization algorithm (FPOA) | Multiple eye disease detection | |
| Xu et al. [485] | LSTM | ✓ | Particle swarm optimization (PSO) | Hydrology (Flood forecasting) | |||
| Antony Raj and Giftson Samuel [486] | DRBFNN | ✓ | Boosted salp swarm optimization (BSSO) | PhotoVoltaic (PV) systems | |||
| Hassanzadeh et al. [487] | CNN | ✓ | ✓ | ✓ | Genetic algorithm (GA) | Classification (CIFAR10, MNIST, and EMNIST) | |
| Palaniswamy [488] | CNN | ✓ | Swallow swarm optimization (SSO) | Automated bone age assessment and classification | |||
| Jalali et al. [489] | CNN | ✓ | Grey wolf optimization (GWO) algorithm | Wind power forecasting | |||
| Lokku et al. [490] | CNN | ✓ | ✓ | Fitness sorted rider optimization (FS-ROA) | Face recognition | ||
| Ewees et al. [491] | LSTM | ✓ | Heap-based optimizer (HBO) algorithm | wind power forecasting | |||
| Huo et al. [492] | TCN-LSTM | ✓ | Particle swarm optimization (PSO) | Prediction of reservoir key parameters | |||
| Li et al. [493] | CNN-LSTM | ✓ | ✓ | ✓ | Particle swarm optimization (PSO) | Reservoir production prediction | |
| Ge et al. [494] | DBN | ✓ | ✓ | ✓ | Whale optimization algorithm (WOA) | Safety prediction of shield tunnel construction | |
| Kanna and Santhi [388] | CNN-LSTM | ✓ | Black widow optimization (BWO) | Intrusion Detection Systems | |||
| Jalali et al. [495] | CNN | ✓ | ✓ | ✓ | Modified competitive swarm Optimizer (MCSO) | X-ray image based COVID-19 detection | |
| Li et al. [496] | LSTM | ✓ | ✓ | ✓ | Grey wolf optimization (GWO) | Wind speed forecasting | |
| Michael Mahesh et al. [497] | CNN | ✓ | Rider border collie optimization (RBCO) | Road intersection classification | |||
| Mohakud and Dash [498] | CNN | ✓ | Grey wolf optimization (GWO) | Medical image classification | |||
| Ahmad et al. [499] | DRaNN | ✓ | Particle swarm optimization (PSO) | Intrusion detection in the industrial internet of things | |||
| Chen et al. [500] | CNN | ✓ | Chimp optimization algorithm (ChOA) | Diagnose Parkinson’s disease | |||
| Karthiga et al. [501] | CNN | ✓ | ✓ | ✓ | Grey wolf optimization (GWO) & ABC | Biomedical Signal Processing and Control | |
| Kanipriya et al. [502] | CNN-LSTM | ✓ | ✓ | ✓ | Improved capuchin search algorithm (ICapSA) | Malignant lung nodule detection | |
| Hu et al. [503] | LSTM | ✓ | ✓ | Grasshopper optimization algorithm (GOA) | Building Engineering | ||
| Raziania and Azimbagirad [504] | CNN | ✓ | Moth flame optimization (MFO) | Sensor-based human activity recognition | |||
| Falahzadeh et al. [505] | CNN | ✓ | Grey wolf optimization (GWO) | Speech Emotion Recognition | |||
| Vigneshwaran et al. [506] | CNN | ✓ | ✓ | Particle swarm optimization (PSO) | Recognition of partial discharge (PD) | ||
| Jalali et al. [507] | LSTM | ✓ | ✓ | Grasshopper optimization algorithm (GOA) | wind speed forecasting | ||
| Surya and Senthilselvi [508] | LSTM | ✓ | Seagull optimization algorithm (SOA) | Identification of oil authenticity and adulteration | |||
| Balasubramanian et al. [509] | CNN | ✓ | ✓ | Particle swarm optimization (PSO) | Medical image classification | ||
| Pandey and Kamal Jain [510] | CNN | ✓ | ✓ | Opposition-based symbiotic organisms search (OSOS) | Medical image classification | ||
| Challapalli and Devarakonda [511] | CNN | ✓ | ✓ | Hybrid particle swarm grey wolf (HPSGW) | Classification of Indian classical dances | ||
| Rodrigues et al. [512] | CNN | ✓ | ✓ | Genetic algorithm (GA) | Medical image classification—MRI images | ||
| Sasank and Venkateswarlu [513] | CNN | ✓ | Adaptive rain optimizer algorithm (AROA) | Medical image classification | |||
| Kavitha and Prasad [514] | CNN | ✓ | Sand piper optimization (SPO) Algorithm | Medical image classification | |||
| Qader et al. [515] | CNN | ✓ | ✓ | ✓ | ✓ | Improved harris hawks optimization (HHO) | Medical image classification (brain tumor) |
| Karthik and Sethukarasi [516] | DBM | ✓ | Hybrid atom search arithmetic optimization (HASAO) | Natural language processing | |||
| Li et al. [517] | LSTM | ✓ | ✓ | ✓ | Grey wolf optimization (GWO) | Water resources management | |
| Gaurav et al. [518] | CNN | ✓ | Hosted cuckoo optimization (HCO) | Speaker identification framework | |||
| Kaushik et al. [519] | DBN | ✓ | Whale optimization algorithm (WOA) | Software development effort estimation | |||
| Liu et al. [520] | LSTM | ✓ | ✓ | Particle swarm optimization (PSO) | Short-term subway inbound passenger flow prediction | ||
| Souissi and Ghorbel [521] | LSTM | ✓ | Genetic algorithm (GA) | Click-through rate prediction- digital advertising industry | |||
| Balasubramanian et al. [522] | DBN | ✓ | Salp swarm optimization algorithm (SSA) | Medical image classification | |||
| Mukherjee et al. [523] | CNN | ✓ | ✓ | Grey wolf optimization (GWO) | Identification of the types of disease | ||
| Ponmalar and Dhanakoti [524] | CNN | ✓ | ✓ | Hybrid whale tabu optimization (HWTO) | Intrusion detection in big data | ||
| Suresh et al. [525] | RNN | ✓ | Flamingo search optimization (FSO) | Disease diagnosis | |||
| Xu et al. [526] | LSTM | ✓ | ✓ | ✓ | Whale optimization algorithm (WOA) | Short-term traffic flow prediction | |
| Tuerxun et al. [527] | LSTM | ✓ | ✓ | ✓ | Modified tuna swarm optimization (MTSO) | Wind speed prediction | |
| Chandraraju and Jeyaprakash [528] | DBN | ✓ | Chaotic Krill Herd optimization (CKHO) | Diagnosis of breast abnormalities | |||
| Jiang et al. [529] | CNN-LSTM | ✓ | Improved whale optimization algorithm (IWOA) | A Fault Feature Extraction | |||
| Fetanat et al. [530] | CNN-FENN | ✓ | ✓ | Improved Harris Hawks optimization (IHHO) | Medical image classification | ||
| Jiang et al. [531] | LSTM | ✓ | ✓ | Sine–Cosine algorithm (SCA-HHO) | Ship attitude prediction | ||
| Gampala et al. [532] | DBN | ✓ | Hosted cuckoo optimization algorithm (HO-COA) | Diagnosis of COVID-19 | |||
| Li et al. [533] | DBN | ✓ | Particle swarm optimization (PSO) | Product quality monitoring | |||
| Yu et al. [534] | CNN | ✓ | ✓ | Enhanced chicken swarm algorithm (ECSA) | Crack detection of concrete structures | ||
| Li et al. [535] | CNN | ✓ | ✓ | Multi-strategy particle swarm optimization (MSPSO) | Fault diagnosis method for aircraft EHA | ||
| Pellegrino et al. [536] | DNN | ✓ | ✓ | Particle swarm optimization (PSO) & GA | Predicting BRCA1/BRCA2 Pathogenicity | ||
| Mohapatra et al. [537] | CNN | ✓ | Cat swarm updated black widow (CSUBW) | Medical image classification | |||
| Ragab et al. [389] | CNN | ✓ | Enhanced gravitational search optimization (EGSO) | COVID-19 diagnosis | |||
| Shankar et al. [538] | RNN | ✓ | ✓ | ✓ | ✓ | Aquila optimization algorithm (AOA) | Fruit classification |
| Fan et al. [539] | CNN | ✓ | ✓ | ✓ | Hybrid Sparrow Search Algorithm (HSSA) | Image classification | |
Investigation of optimized components in DL architectures
As an optimization problem, MH algorithms formulate the optimal estimation of DL components (such as hyper-parameter, weights, number of layers, number of neurons, learning rate, etc.). This section examines the abundance of MH use for optimized components in DL architectures (according to the papers in Table 3). Figure 20 represents the relative abundance of research on optimized components in DLs using MH algorithms. As demonstrated in Fig. 20, in 61 studies (20%), weights and biases have been adjusted using MH algorithms. In 76 studies (26%), the number of layers and neurons in the layers have been adjusted using MH algorithms. Moreover, in 114 studies (38%), hyper-parameters in DL architectures have been adjusted. Finally, in 47 studies (16%), learning parameters, learning algorithms or activation functions have been adjusted.
Fig. 20.
Relative abundance of research on optimized components in DL architectures using MH algorithms
Figure 21 also indicates the relative abundance of research in the simultaneous optimization of two components of DLs. As can be seen in Fig. 21, in 14 studies, weights and layers, and neurons were adjusted simultaneously. In 12 studies, weights and hyper-parameter; in 4 studies, weights and learning parameters; in 40 studies, the number of layers and number of neurons and hyper-parameter; in 31 studies, the number of layers and number of neurons and learning parameters, and in 31 studies hyper-parameter and learning parameters have been adjusted simultaneously. Figure 22 also represents the relative abundance of research in the simultaneous optimization of three DL components (according to Table 3).
Fig. 21.
Relative abundance of research in the simultaneous optimization of two components of DL using MHs
Fig. 22.
Relative abundance of research in the simultaneous optimization of three components of DL using MHs
As can be seen, in 3 studies, weights, the number of layers and number of neurons and the hyper-parameter were adjusted simultaneously. In 3 studies, weights, number of layers and number of neurons and learning parameters; in 2 studies, weights, hyper-parameter and learning parameters; in 18 studies, hyper-parameter, number of layers and number of neurons and learning parameters were adjusted simultaneously. According to Table 3, in only 2 studies, all four DL components were adjusted simultaneously. Therefore, very little research has been done in this area (simultaneous optimization of three/four components).
Investigation of Meta-Heuristic Algorithms Used in DL's Optimization
According to Table 3, many MH algorithms have been developed to optimize DL architectures. Figure 23 represents the MH algorithms used to optimize DLs. PSO with 48 implementations and GA with 27 implementations were the most used algorithms. EA, GWO, FA, WOA, ABC, ACO, HS, NSGA_II, CMA-ES, and GOA algorithms are also in the next ranks.
Fig. 23.
Meta-heuristic algorithms used in DL's optimization
Investigating the Abundance of MHs Used for Different Types of DL Architectures
Some of the popular DL architectures are Long short-term memory (LSTM), Convolutional Neural Networks (CNNs), Deep Belief Networks (DBN), Recurrent Neural Networks (RNN), Deep Boltzmann Machines (DBM), Deep Auto Encoder (DAE), and Deep Neural Networks (DNN). In this section, the abundance of MHs used for different DL architectures is investigated (Fig. 24). CNN with 96 implementations, LSTM with 37 implementations, and DBN with 24 implementations were the most used DL architectures, which are set using MH algorithms. DNN, RNN, DAE, DBM, GAN, DSNN, DAR, and EDEN architectures are also in the next ranks.
Fig. 24.
The abundance of MHs used for different types of DL architectures
Checking the Number of Papers Published in Journals and Years
In this section, the papers in Table 3 are categorized according to the type of journals and the year of their publication. Figure 25 demonstrates the percentage of papers published in various journals (based on Table 3). As indicated, 71 papers (37%) in Elsevier, 39 papers (20%) in Springer, 25 papers (13%) in IEEE, 6 papers (3%) in Taylor & Francis, and 17 papers (9%) In John Wiley & Sons, and 35 papers (18%) in other journals have been published regarding the use of MH for DL architectures.
Fig. 25.
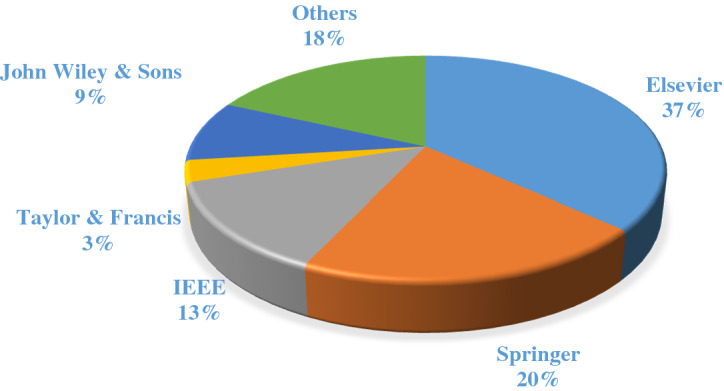
Papers published in journals (based on Table 3)
Figure 26 also represents the changes in the number of papers published in different years about the use of MH for Training DLs. Between 1988 and 2016, few papers were developed for DL optimization. From 2017 to 2020, DL optimization received a little more attention from researchers, and the number of papers in this field increased. But from 2021 to 2022, many researchers have worked on DL optimization. This problem is still a challenge, and many problems need to be resolved.
Fig. 26.
Changes in the number of papers published in different years about the use of MH for Training DLs
Applications of DLs
In this section, the application of the papers in Table 3 is evaluated. Figure 27 shows the application of the papers regarding the use of MH for DLs. 48 papers in medical image classification and medical diseases diagnosis, 46 papers in Benchmark problem (Classification, prediction, time series, optimization, recognition, system identification), 44 papers in electrical engineering, signal processing and energy systems, 23 papers in civil engineering and environmental management, 8 papers in mechanical engineering, 3 papers in biomedical and chemical engineering, 4 papers in economy and product quality, and 17 papers in other applications have been published regarding the use of MH for ANNs.
Fig. 27.
Application of papers regarding the use of MH for DLs
As can be seen, most of the DLs were implemented on medical image classification and benchmark problems (such as MNIST, CIFAR-10, Caltech, CINIC-10, and EMNIST datasets). According to Table 3, evolutionary CNN architectures have been used in many medical image classification applications. The results of these papers show that the proposed hybrid DL architectures perform better than others. Therefore, the combination of MH and CNNs methods can be useful for medical applications.
Contributions of Different Continents in Using the Hybrid MH-DL Models
Figure 28 shows the distribution of studied papers according to the affiliation of the authors for each continent. As can be seen, Asia has the largest portion of contributions in the world, while America has the lowest contributions.
Fig. 28.
Contributions of different continents in using the hybrid MH-DL models
Discussion, Statistical Results, Limitations, and Future Challenges
Discussion and Statistical Results of Tables 2 and 3
As can be seen from the results of Tables 2 and 3, neural network optimization has been considered by researchers from the past to the present. But the optimization of DL parameters has recently been considered, and more research is needed in this field. The main reason is that the DL concept has been seriously pursued since 2008. Therefore, many challenges and more research are needed in this field. The existence of many parameters in DL architectures has led to the use of MH algorithms to optimize them. According to Table 3, DL optimization has been considered by researchers since 2015.
According to the literature review, well-known MH algorithms such as GA and PSO have been used for training the NN and DL. But according to the No Free Lunch (NFL) theorem, each problem has its characteristics, and different algorithms must be tested to solve it [540]. According to the NFL theorem, it is very difficult to find a comprehensive MH algorithm to solve various problems [541]. Therefore, an MH algorithm may not be suitable for optimizing the NN and DL parameters. However, it works well in solving some problems. In addition, the only way to determine the convergence of the MH algorithm is through its experimental evaluations. Because MH algorithms search the problem space (based on their operators), it is difficult to choose the MH algorithm as the best method for a particular problem. Therefore, it is necessary to use different algorithms to optimize the NN and DL parameters.
In many research studies on optimization problems [18, 19, 542, 543], improving common versions of MH algorithms (and combination of algorithm) has increased exploitation and exploration power. In some recent research [66, 67, 120], new MH algorithms have been introduced, which have performed better than the old algorithms in many optimization problems. According to the literature review (Tables 2 and 3), in most research, common algorithms (such as PSO and GA) have been used to optimize NN and DL. Therefore, the development of old MH algorithms, as well as novel MH algorithms for optimizing NN and DL parameters, is a new challenge, which can be seen in recent papers in Tables 2 and 3.
It is complicated to find the best possible solution in the search space in large-scale optimization problems. Moreover, changing algorithm variables does not have much influence on the algorithm convergence. Therefore, for massive dataset with high complexity, even if the researchers have determined accurate initial parameters, the algorithm will not be able to perform adequate exploration and exploitation. Consequently, to achieve comprehensive global and local searches, we need to apply powerful operators to make better exploration and exploitation. MH algorithms can be combined with others and overcome this problem by using the advantages and operators of other algorithms. In recent decades, researchers have utilized a combination of algorithms to improve the performance of the optimization process. The weakness of an algorithm can be compensated by the operation of other algorithms.
Most researchers tend to extend novel hybrid algorithms by combining MHs to optimize the hyper-parameters of DLs and ANNs. The development of hybrid MHs helps improving algorithms performance and capable of solving complex optimization problems. According to the results, many researches have used the modification and hybridization of meta-heuristic algorithms to optimize ANN and DL parameters. Also, the performance of the proposed hybrid MH algorithms have been better than others.
In general, the optimal performance of the MHs should be able to achieve a suitable trade-off between exploration and exploitation features. The exploration operator can explore the search space more efficiently and perform a global search to avoid getting stuck in local minimum, but it may encounter slow convergence. On other hand, the exploitation operator leads to very high convergence rates, but may be trapped in a local minimum. Among the existing MH algorithms, some of them are better in convergence trend (exploitation) while others have more ability to avoid getting trapped in local optimum (exploration). Table 4 indicates the comparison of different MH algorithms in terms of their ability of finding global optimum, convergence trend, exploitation ability, exploration ability, parameter setting, and implementation. As can be seen, grey wolf optimizer, black widow optimization, chimp optimization algorithm, differential evolution, red fox optimization, capuchin search algorithm, and gannet optimization algorithm perform well in most properties and their operators can be used to improve other architectures. This framework is useful for researchers for their applications in improved hybrid algorithm.
Table 4.
Comparison of MH algorithms in different criteria
| MH algorithm | Exploitation ability | Exploration ability | Convergence trend | Ability of finding global optimum | Parameter setting | Implementation |
|---|---|---|---|---|---|---|
| Genetic algorithm | Medium | High | Very slow | Low | Medium | Simple |
| Particle swarm optimization | Very high | Low | Fast | Low | Medium | Simple |
| Simulated annealing | Medium | Medium | Very slow | Low | Easy | Simple |
| Differential evolution | High | Medium | Very fast | High | Easy | Medium |
| Artificial bee colony | High | Medium | Medium | Medium | Easy | Simple |
| Ant colony optimization | High | Medium | Fast | High | Hard | Medium |
| Tabu search (TS) | Low | High | Slow | Medium | Medium | Medium |
| Biogeography-based optimization | High | High | Very fast | High | Medium | Medium |
| Whale optimization algorithm | High | Medium | Medium | High | Easy | Medium |
| Gravitational search algorithm | High | Medium | Medium | Very high | Medium | Simple |
| Grasshopper optimization algorithm | Medium | High | Medium | High | Medium | Simple |
| Cuckoo search | High | Medium | Medium | Very high | Easy | Medium |
| Firefly algorithm | Medium | Low | Medium | Very low | Easy | Easy |
| Grey wolf optimizer | Very high | High | Very fast | Very high | Easy | Medium |
| Harmony search | High | High | Very fast | High | Easy | Simple |
| Interior search algorithm | Medium | High | Fast | Medium | Medium | Simple |
| Salp swarm algorithm | Medium | High | Medium | High | Easy | Medium |
| Weighted superposition attraction | Very high | Medium | Fast | High | Medium | Complex |
| Black widow optimization | Very high | High | Very fast | High | Easy | Medium |
| Chimp optimization algorithm | Very high | Very high | Very fast | High | Easy | Medium |
| Red fox optimization | Very high | Very high | Fast | Very high | Easy | Medium |
According to the statistical results of Table 2, in only one study, the simultaneous optimization of all components (weights, number of layers, number of neurons and learning functions/parameters) of neural networks has been investigated. Also, in two study, the simultaneous optimization of all components (weights, number of layers and neurons, hyper-parameter, and learning functions/parameters) of DLs has been investigated. However, there is no research on training DL (simultaneous optimization of all components). So researchers in the future can optimize all components simultaneously to improve network performance. This is a challenge for both neural networks and DL architectures. In addition, in neural networks, in most cases, the weight of the network is optimized. But in DL architectures, weight, hyper-parameter, and network structure are optimized equally. Since optimizing ANN and DL architectures is a complex and multi-objective problem (MOO), using multi-objective MH algorithms or developing new multi-objective MH algorithms is also challenging. While in very few papers, multi-objective MH algorithms have been used to optimize ANN and DL parameters (as represented in Tables 2 and 3).
In optimizing DL algorithms, CNN architecture is more trained. According to the NFL theorem for MH algorithms, implementing all DL algorithms for various problems is also challenging. In fact, different DL architectures need to be implemented for different problems and their experimental results evaluated. Therefore, optimizing other DL architectures can be considered to solve various problems in the future. Table 5 also indicates the advantages and disadvantages of compared techniques.
Table 5.
Advantages and disadvantages of compared DL techniques
| DL method | Advantages | Disadvantages |
|---|---|---|
| DNN |
1. Its implementation is simple. Deep neural networks with multiple hidden layers automatically discover the features of complex objects such as images 2. ANNs can be applied in parallel and work fast. Consequently, they are specially programmed to perform online processes 3. It is unnecessary to identify key criteria where DNN can define all criteria and then determine which criteria are relevant 4. DANN implementations allow developers to add learning capabilities to their applications 5. Self-organization and Usability in big data due to the training process |
1. Lack of sufficient theoretical foundation 2. Computationally cost. It requires a long training time. Learning a DNN when dealing with big data can take days or months 3. In DNNs, a large number of hyper-parameters need to be adjusted. Moreover, with an increasing number of hidden layers and nodes, the training algorithm is more likely get trapped in the local optimal 4. A large amount of training data is required to training process |
| DBN |
1. The training of DBNs is divided into two phases: the pre-training and the fine-tuning. In the pre-training process, an unsupervised algorithm based training is performed for the feature extraction; while in the fine-tuning process, a supervised algorithm is performed for further adjustment of the hyper-parameters 2. DBN networks have a level of flexibility 3. DBN is applied to applications with unlabeled data. Moreover, the overfitting and underfitting errors can be avoided |
1. Deep in time (two phases learning) 2. local information (Spatial data) is lost as the network gets deeper |
| CNN |
1. CNN is the first truly successful DL method due to the successful training of the hierarchical layers 2. CNN requires minimal pre-processing 3. It is suitable for feature extraction, image classification, image recognition, and prediction problems 4. CNN reduce the number of parameters by leverages spatial relationships 5. CNN Fine-tunes all the layers of the network |
1. A large amount of training data is required to training process 2. It requires a lot of time and computing resources |
| RNN |
1. RNNs Deal with sequential data 2. RNNs can capture longer context patterns 3. RNNs are used to earn metal |
1. It requires a long training time 2. Training process is difficult 3. The performance of RNN decreases rapidly |
| LSTM |
1. It allows information to flow in both forwards and backward processes within the network 2. It has a sensible processing for time series data 3. It can learn its tasks without ability to predict the local sequence |
1. Training process is difficult 2. Complex network structure 3. It is computationally expensive |
| DBM |
1. Able to learn internal representations 2. It is a fully connected NN 3. DBM Deals strongly with ambiguous inputs |
1. It requires a long training time 2. Difficult to train |
| DAE |
1. It has the ability to extract useful features during the propagation and filter the useless data 2. DAE is an unsupervised DL architecture used for dimensionality reduction |
1. Training process is difficult 2. DAE Requires pre-training |
Limitations of Deep Learning
Notwithstanding the positive outcomes of the reviewed papers, there are still some challenges and limitations related to deep learning and DL methods that should be addressed.
Over-fitting problem in a deep neural network Many parameters relate to unseen datasets in some complex applications. This can cause a difference in the error caused by the training dataset and the new unseen dataset.
Hyper-parameters optimization DL architectures have several hyper-parameters, for example, learning rate, number of hidden layers, number of neurons in each hidden layer, number of convolution and max-pooling layers, and so on. Most often these hyper-parameters are adjusted by trial and error method. MH algorithms formulate the optimal estimation of DL components (such as hyper-parameter, weights, number of layers, number of neurons, learning rate, etc.).
Computing Power Required High computing power is required to tackle a real-world problem using DL models. Therefore, experts are trying to develop high-performance multi-core GPUs and similar processing units such as TPUs in the future.
Gradient-based learning The learning process of DL architectures is considered one of the most challenging machine learning problems. Several past studies have used gradient-based methods to train DL architectures. However, gradient-based methods have major drawbacks such as stucking at local minimums in multi-objective cost functions, expensive execution time due to calculating gradient information with thousands of iterations and needing the cost functions to be continuous. Since training the ANNs and DLs is an NP-hard optimization problem, their structure and parameters optimization using the meta-heuristic algorithms has been considerably raised.
Dataset unavailability for various applications DL requires a large amount of training dataset. The classification accuracy of the DL architectures is highly dependent on the quality and size of the dataset. However, unavailability of the dataset is one the biggest barrier in the success of DL architectures.
Determining the type of DL architecture to solve a particular problem Many studies have used different DL architectures to solve engineering and medical problems. However, there is no explanation for how these architectures are chosen to solve specific problems.
Heterogeneity in image dataset The nature of data varies from hardware to hardware and thus, there are many variations in images due to sensors and other factors. In addition, the wide range of medical applications requires the combination of several different datasets for learning and accuracy of algorithms.
Architecture Implementation Cost Feature extraction can be done in advance and then the proper methods can be implemented. The purpose of this process is to reduce the computing runtime (training) and computing power required.
Lack of results of different DL architectures on benchmark database The lack of results of different DL architectures is still a challenge in solving many benchmark database or benchmark engineering problems. For example, in some studies [544, 545], the authors have used different DL architectures and compared the results with the decision tree.
Reasonable Computing Time Some applications with many variables in some deep learning methods, (such as DNN) have high dimensions, which poses a challenge for these models to obtain an accurate DNN in a reasonable execution time.
One-Shot Learning DL architectures require a lot of training data to provide high-quality results. For example, the Image-Net database contains more than a million images, and the DL architecture often requires thousands of instances to classify them correctly. Human does not need thousands of bicycle images to learn a picture of a bicycle. When a bicycle is shown to a child, they can often recognize another bicycle, even in different models, shapes, and colors.
Imbalanced data In this problem, one or more classes may have very few representatives in the training process. MH algorithms can be used to deal with such problems.
Theoretical backbone Unlike decision trees, SVMs, and other machine learning architectures, most of the DL methods are yet to possess a strong theoretical backbone.
Future Work
While deep learning models have been successfully applied in various application fields, there are future works and challenges that require to be addressed. Scientists and researchers should do more research and work to overcome the challenges facing the future of deep learning. In addition, more DL techniques and inspirations are needed to develop new DL architectures. New techniques will be necessary for complex applications. In addition, DL architectures can take advantage of various sub-domains of swarm intelligence and evolutionary computation that are still unexplored. In this section, according to the literature review, some relevant perspectives for future work are listed.
Design of DL methods Deep learning is used as an efficient method to deal with big data problem. Furthermore, DL method has get great success with a large number of unlabeled data. However, rather strong techniques are required when a limited training data is available. Therefore, it is important to consider designing DL techniques from multiple training datasets in the future.
DL and mobile devices The idea of DL chips has attracted the attention of many researchers. Deep learning techniques can be implemented in mobile devices with low-power energy.
Transfer Learning The learning architecture in the human brain has evolved over millions of years and has been transferred from generation to generation. Humans transfer part of their learning as an experience to future generations. In addition, humans constantly learn about different tasks that help them learn specific tasks faster. For this reason, learning different problems is achieved by making basic and easy settings. Developing the concept of transfer learning in DL is one of the challenges in this field and can be a new field of work for researchers in the future. Transfer learning reduces training time and the use of previous learning experiences in new tasks.
DL and Reinforcement Learning (RL) RL mainly involves goal-oriented algorithms that learn how to achieve a complex goal. Recently, the combination of DL and RL methods has attracted the attention of researchers. These methods have led to several applications such as self-driving cars and AlphaGo. Future works can focus on exploring MH algorithms in optimizing learning methods in deep RL.
Unsupervised Learning-Based DL Because having labeled data is usually costly, the next generation of DL techniques is more semi-supervised and unsupervised. Here, clustering concepts and algorithms can be used to improve the performance of DL algorithms.
Stability of DL Stability analysis of DL is considered an important problem in this field due to its numerous advantages for different applications. Therefore, we should focus on some problems such as stability analysis, state estimation, and synchronization for DLs.
Dimensionality reduction This problem is one of the most prevalent challenges needed to be addressed since the number of the features from deep learning method can be huge. This problem weakens the performance of the algorithm, since most of these features are redundant. To address this problem in the future, various MHs can be combined with DL models. MH algorithms first select the optimal features and then transfer them to a DL model.
Developing more challenging evolutionary DL models There are many papers in this field (EvoDL), but not much paper has been undertaken to evolve Generative Adversarial Network (GAN) by using MH algorithms. In addition, MH-based optimization algorithms may also be explored to evolve DL extensions of non-iterative learning paradigms.
Energy-efficient Learning Problem In most cases, DL architectures that work on big data are inefficient in energy consumption. On the other hand, the human brain requires very little energy to learning and often does not perform accurate calculations (estimates). This energy is enough to learn about many problems and can add to the power of generalization. Therefore, in the future, DL architectures must be designed to be energy efficient.
Improvement of MHs MH algorithms still need to be improved before applying them to the deep learning architecture. Since most of MHs have a high capability in exploration or exploitation, it is a challenging work to detect the MH that can balance between exploration and exploitation. Furthermore, many of the MH algorithms ranked in CEC competitions have not been used to optimize parameters of DLs.
Conclusions
Deep learning is a new approach to machine learning in recent years and has been successfully applied in various applications. DL techniques are superior to traditional ML algorithms due to data availability and systems processing power development. With the advent of the big data era, much faster data collection, storage, updating, and management advances have become possible. In addition, the development of GPU has made efficient processing in large data sets. These dramatic advances have led to recent advances in DL techniques. DL methods have been used in various applications, including image classification, prediction, Phoneme recognition, hand-written digit recognition, etc.
The learning process and hyper-parameter optimization of ANNs and DLs is considered one of the most difficult machines learning challenges and has recently attracted many researchers. Training the ANNs and DLs is an NP-hard optimization problem with several theoretical and computational limitations. MH algorithms formulate NN and DL components as an optimization problem. Therefore, this research presents a comprehensive review of NNs and DLs' optimization using meta-heuristic algorithms.
As can be seen from the results, neural network optimization has been considered by researchers from the past to the present. But the optimization of DL parameters has recently been considered. According to the literature review, well-known MH algorithms have been used for training the NN and DL. Therefore, the development of these algorithms, as well as novel MH algorithms for optimizing NN and DL parameters, is a new challenge. According to the statistical results, researchers can optimize all components of ANNs and DL architectures simultaneously to improve network performance in the future. In this way, they can use multi-objective algorithms to teach architectures better. According to the results, evolutionary CNN architectures have been used in many medical image classification applications. The results of these papers show that the proposed hybrid MH-CNN architectures perform better than others. Therefore, the combination of MH and CNNs can be useful for medical applications. In most papers, MHs have been used for image classification problems. Therefore, there is still room to apply these hybrid methods in different applications and evaluate their performance on different challenging real-world datasets.
In this paper, we have reviewed the latest developments in the use of MH algorithms in the DL methods, presented their disadvantages and advantages, and pointed out some research directions to fill the gaps between MHs and DL methods. Moreover, it has been explained that the evolutionary hybrid architecture still has limited applicability in the literature. Using MH algorithms to train DLs improves the learning process. This increases the accuracy of the algorithm and reduces its execution time. The combination of MH and DLs provides a good start to the DL process and improves the DL performance. It is difficult to assess whether the deep learning methods will be at the academic boundary (without the integration with MH). It is expected that in the coming years, combining DL with MH will accelerate the training process and maintain high performance. According to the review of papers, using MH algorithms to optimize DL architectures is still challenging, and more research is needed in this field. It is expected that MH algorithms will be used more in the coming years to improve the performance of DL architectures. However, relevant publications in this way are still rare.
Acknowledgements
Not applicable.
Funding
Not applicable.
Availability of data and material
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Declarations
Conflict of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Ethical approval
This paper does not contain any studies with human participants or animals.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Mehrdad Kaveh, m.kaveh11@email.kntu.ac.ir.
Mohammad Saadi Mesgari, Email: mesgari@kntu.ac.ir.
References
- 1.Skansi S. Introduction to deep Learning: from logical calculus to artificial intelligence. Cham: Springer; 2018. [Google Scholar]
- 2.Aggarwal CC. Neural networks and deep learning. Cham: Springer; 2018. [Google Scholar]
- 3.Bouwmans T, Javed S, Sultana M, Jung SK. Deep neural network concepts for background subtraction: a systematic review and comparative evaluation. Neural Netw. 2019;117:8–66. doi: 10.1016/j.neunet.2019.04.024. [DOI] [PubMed] [Google Scholar]
- 4.Schmidhuber J. Deep learning in neural networks: an overview. Neural Netw. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 5.Lanillos P, Oliva D, Philippsen A, Yamashita Y, Nagai Y, Cheng G. A review on neural network models of schizophrenia and autism spectrum disorder. Neural Netw. 2020;122:338–363. doi: 10.1016/j.neunet.2019.10.014. [DOI] [PubMed] [Google Scholar]
- 6.Boveiri HR, Khayami R, Javidan R, MehdiZadeh AR (2020) Medical image registration using deep neural networks: a comprehensive review. arXiv preprint arXiv:2002.03401
- 7.Lopez-Garcia TB, Coronado-Mendoza A, Domínguez-Navarro JA. Artificial neural networks in microgrids: a review. Eng Appl Artif Intell. 2020;95:103894. doi: 10.1016/j.engappai.2020.103894. [DOI] [Google Scholar]
- 8.Han F, Jiang J, Ling QH, Su BY. A survey on metaheuristic optimization for random single-hidden layer feedforward neural network. Neurocomputing. 2019;335:261–273. doi: 10.1016/j.neucom.2018.07.080. [DOI] [Google Scholar]
- 9.Ojha VK, Abraham A, Snášel V. Metaheuristic design of feedforward neural networks: a review of two decades of research. Eng Appl Artif Intell. 2017;60:97–116. doi: 10.1016/j.engappai.2017.01.013. [DOI] [Google Scholar]
- 10.Darwish A, Hassanien AE, Das S. A survey of swarm and evolutionary computing approaches for deep learning. Artif Intell Rev. 2020;53(3):1767–1812. doi: 10.1007/s10462-019-09719-2. [DOI] [Google Scholar]
- 11.Liu W, Wang Z, Liu X, Zeng N, Liu Y, Alsaadi FE. A survey of deep neural network architectures and their applications. Neurocomputing. 2017;234:11–26. doi: 10.1016/j.neucom.2016.12.038. [DOI] [Google Scholar]
- 12.Kubat M. An introduction to machine learning. Cham: Springer International Publishing AG; 2017. [Google Scholar]
- 13.Yingwei L, Sundararajan N, Saratchandran P. A sequential learning scheme for function approximation using minimal radial basis function neural networks. Neural Comput. 1997;9(2):461–478. doi: 10.1162/neco.1997.9.2.461. [DOI] [PubMed] [Google Scholar]
- 14.Ferrari S, Stengel RF. Smooth function approximation using neural networks. IEEE Trans Neural Netw. 2005;16(1):24–38. doi: 10.1109/TNN.2004.836233. [DOI] [PubMed] [Google Scholar]
- 15.Mosavi MR, Kaveh M, Khishe M (2016a) Sonar data set classification using MLP neural network trained by non-linear migration rates BBO. In: The fourth Iranian conference on engineering electromagnetic (ICEEM 2016), pp. 1–5
- 16.Mosavi MR, Kaveh M, Khishe M, Aghababaee M (2016b) Design and implementation a sonar data set classifier by using MLP NN trained by improved biogeography-based optimization. In: Proceedings of the second national conference on marine technology, pp. 1–6.
- 17.Mosavi MR, Kaveh M, Khishe M, Aghababaee M. Design and implementation a sonar data set classifier using multi-layer perceptron neural network trained by elephant herding optimization. Iran J Marine Technol. 2018;5(1):1–12. [Google Scholar]
- 18.Kaveh M, Khishe M, Mosavi MR. Design and implementation of a neighborhood search biogeography-based optimization trainer for classifying sonar dataset using multi-layer perceptron neural network. Analog Integr Circuits Signal Process. 2019;100(2):405–428. doi: 10.1007/s10470-018-1366-3. [DOI] [Google Scholar]
- 19.Khishe M, Mosavi MR, Kaveh M. Improved migration models of biogeography-based optimization for sonar dataset classification by using neural network. Appl Acoust. 2017;118:15–29. doi: 10.1016/j.apacoust.2016.11.012. [DOI] [Google Scholar]
- 20.Zhang GP. Neural networks for classification: a survey. IEEE Trans Syst Man Cybern Part C (Appl Rev) 2000;30(4):451–462. doi: 10.1109/5326.897072. [DOI] [Google Scholar]
- 21.Tong DL, Mintram R. Genetic algorithm-neural network (GANN): a study of neural network activation functions and depth of genetic algorithm search applied to feature selection. Int J Mach Learn Cybern. 2010;1(1–4):75–87. doi: 10.1007/s13042-010-0004-x. [DOI] [Google Scholar]
- 22.Jiang S, Chin KS, Wang L, Qu G, Tsui KL. Modified genetic algorithm-based feature selection combined with pre-trained deep neural network for demand forecasting in outpatient department. Expert Syst Appl. 2017;82:216–230. doi: 10.1016/j.eswa.2017.04.017. [DOI] [Google Scholar]
- 23.Shang L, Huang DS, Du JX, Zheng CH. Palmprint recognition using FastICA algorithm and radial basis probabilistic neural network. Neurocomputing. 2006;69(13–15):1782–1786. doi: 10.1016/j.neucom.2005.11.004. [DOI] [Google Scholar]
- 24.Zhao ZQ, Huang DS, Jia W. Palmprint recognition with 2DPCA+ PCA based on modular neural networks. Neurocomputing. 2007;71(1–3):448–454. doi: 10.1016/j.neucom.2007.07.010. [DOI] [Google Scholar]
- 25.Wang XF, Huang DS, Du JX, Xu H, Heutte L. Classification of plant leaf images with complicated background. Appl Math Comput. 2008;205(2):916–926. [Google Scholar]
- 26.Luo H, Yang Y, Tong B, Wu F, Fan B. Traffic sign recognition using a multi-task convolutional neural network. IEEE Trans Intell Transp Syst. 2017;19(4):1100–1111. doi: 10.1109/TITS.2017.2714691. [DOI] [Google Scholar]
- 27.Kaveh M, Mesgari MS, Khosravi A. Solving the local positioning problem using a four-layer artificial neural network. Eng J Geospat Inf Technol. 2020;7(4):21–40. [Google Scholar]
- 28.Hwang JN, Kung SY, Niranjan M, Principe JC. The past, present, and future of neural networks for signal processing. IEEE Signal Process Mag. 1997;14(6):28–48. doi: 10.1109/79.637299. [DOI] [Google Scholar]
- 29.Subudhi B, Jena D. Nonlinear system identification using memetic differential evolution trained neural networks. Neurocomputing. 2011;74(10):1696–1709. doi: 10.1016/j.neucom.2011.02.006. [DOI] [Google Scholar]
- 30.Razmjooy N, Ramezani M. Training wavelet neural networks using hybrid particle swarm optimization and gravitational search algorithm for system identification. Int J Mechatron Electr Comput Technol. 2016;6(21):2987–2997. [Google Scholar]
- 31.Gorin A, Mammone RJ. Introduction to the special issue on neural networks for speech processing. IEEE Trans Speech Audio Process. 1994;2(1):113–114. doi: 10.1109/89.260355. [DOI] [Google Scholar]
- 32.Khalifa MH, Ammar M, Ouarda W, Alimi AM (2017) Particle swarm optimization for deep learning of convolution neural network. In: 2017 Sudan conference on computer science and information technology (SCCSIT), pp. 1–5
- 33.Lopez-Rincon A, Tonda A, Elati M, Schwander O, Piwowarski B, Gallinari P. Evolutionary optimization of convolutional neural networks for cancer miRNA biomarkers classification. Appl Soft Comput. 2018;65:91–100. doi: 10.1016/j.asoc.2017.12.036. [DOI] [Google Scholar]
- 34.Dufourq E, Bassett BA (2017) Eden: evolutionary deep networks for efficient machine learning. In: 2017 pattern recognition association of South Africa and robotics and mechatronics (PRASA-RobMech), pp. 110–115
- 35.Wang B, Sun Y, Xue B, Zhang M (2018) A hybrid differential evolution approach to designing deep convolutional neural networks for image classification. In: Australasian joint conference on artificial intelligence. Springer, Cham, pp 237–250
- 36.Wang C, Xu C, Yao X, Tao D. Evolutionary generative adversarial networks. IEEE Trans Evol Comput. 2019;23(6):921–934. doi: 10.1109/TEVC.2019.2895748. [DOI] [Google Scholar]
- 37.Ye F. Particle swarm optimization-based automatic parameter selection for deep neural networks and its applications in large-scale and high-dimensional data. PLoS ONE. 2017;12(12):e0188746. doi: 10.1371/journal.pone.0188746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Peng L, Liu S, Liu R, Wang L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy. 2018;162:1301–1314. doi: 10.1016/j.energy.2018.05.052. [DOI] [Google Scholar]
- 39.Wang Y, Zhang H, Zhang G. cPSO-CNN: An efficient PSO-based algorithm for fine-tuning hyper-parameters of convolutional neural networks. Swarm Evol Comput. 2019;49:114–123. doi: 10.1016/j.swevo.2019.06.002. [DOI] [Google Scholar]
- 40.Shinozaki T, Watanabe S (2015) Structure discovery of deep neural network based on evolutionary algorithms. In: 2015 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE, pp. 4979–498
- 41.David OE, Greental I (2014). Genetic algorithms for evolving deep neural networks. In: Proceedings of the companion publication of the 2014 annual conference on genetic and evolutionary computation, pp. 1451–1452
- 42.Lander S, Shang Y (2015) EvoAE--a new evolutionary method for training autoencoders for deep learning networks. In: 2015 IEEE 39th annual computer software and applications conference, vol. 2, pp. 790–795
- 43.Rosa G, Papa J, Marana A, Scheirer W, Cox D (2015) Fine-tuning convolutional neural networks using harmony search. In: Iberoamerican congress on pattern recognition, pp. 683–690
- 44.Rosa G, Papa J, Costa K, Passos L, Pereira C, Yang XS (2016) Learning parameters in deep belief networks through firefly algorithm. In: IAPR workshop on artificial neural networks in pattern recognition, pp. 138–149
- 45.Martín A, Lara-Cabrera R, Fuentes-Hurtado F, Naranjo V, Camacho D. EvoDeep: a new evolutionary approach for automatic deep neural networks parametrisation. J Parallel Distrib Comput. 2018;117:180–191. doi: 10.1016/j.jpdc.2017.09.006. [DOI] [Google Scholar]
- 46.Banharnsakun A. Towards improving the convolutional neural networks for deep learning using the distributed artificial bee colony method. Int J Mach Learn Cybern. 2019;10(6):1301–1311. doi: 10.1007/s13042-018-0811-z. [DOI] [Google Scholar]
- 47.Van Der Smagt PP. Minimisation methods for training feedforward neural networks. Neural Netw. 1994;7(1):1–11. doi: 10.1016/0893-6080(94)90052-3. [DOI] [Google Scholar]
- 48.Battiti R. First-and second-order methods for learning: between steepest descent and Newton's method. Neural Comput. 1992;4(2):141–166. doi: 10.1162/neco.1992.4.2.141. [DOI] [Google Scholar]
- 49.Johnson R, Zhang T. Accelerating stochastic gradient descent using predictive variance reduction. Adv Neural Inf Process Syst. 2013;26:315–323. [Google Scholar]
- 50.Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980
- 51.Lan K, Liu L, Li T, Chen Y, Fong S, Marques JAL, Tang R. Multi-view convolutional neural network with leader and long-tail particle swarm optimizer for enhancing heart disease and breast cancer detection. Neural Comput Appl. 2020 doi: 10.1007/s00521-020-04769-y. [DOI] [Google Scholar]
- 52.Kilicarslan S, Celik M, Sahin Ş. Hybrid models based on genetic algorithm and deep learning algorithms for nutritional Anemia disease classification. Biomed Signal Process Control. 2021;63:102231. doi: 10.1016/j.bspc.2020.102231. [DOI] [Google Scholar]
- 53.Son NN, Chinh TM, Anh HPH. Uncertain nonlinear system identification using Jaya-based adaptive neural network. Soft Comput. 2020 doi: 10.1007/s00500-020-05006-3. [DOI] [Google Scholar]
- 54.Ertuğrul ÖF. A novel clustering method built on random weight artificial neural networks and differential evolution. Soft Comput. 2020 doi: 10.1007/s00500-019-04647-3. [DOI] [Google Scholar]
- 55.Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 56.LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86(11):2278–2324. doi: 10.1109/5.726791. [DOI] [Google Scholar]
- 57.Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Comput. 2006;18(7):1527–1554. doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- 58.Basak H, Kundu R, Singh PK, Ijaz MF, Woźniak M, Sarkar R. A union of deep learning and swarm-based optimization for 3D human action recognition. Sci Rep. 2022;12(1):1–17. doi: 10.1038/s41598-022-09293-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Glover F. Future paths for integer programming and links to artificial intelligence. Comput Oper Res. 1986;13(5):533–549. doi: 10.1016/0305-0548(86)90048-1. [DOI] [Google Scholar]
- 60.Holland John H. Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press; 1975. [Google Scholar]
- 61.Dorigo M, Maniezzo V, Colorni A. Ant system: optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybern Part B. 1996;26(1):29–41. doi: 10.1109/3477.484436. [DOI] [PubMed] [Google Scholar]
- 62.Eberhart R, Kennedy J (1995) A new optimizer using particle swarm theory. In: MHS'95. Proceedings of the sixth international symposium on micro machine and human science, pp. 39–43
- 63.Kirkpatrick S, Gelatt CD, Jr, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 64.Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Glob Optim. 1997;11(4):341–359. doi: 10.1023/A:1008202821328. [DOI] [Google Scholar]
- 65.Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Adv Eng Softw. 2014;69:46–61. doi: 10.1016/j.advengsoft.2013.12.007. [DOI] [Google Scholar]
- 66.Hayyolalam V, Kazem AAP. Black widow optimization algorithm: A novel meta-heuristic approach for solving engineering optimization problems. Eng Appl Artif Intell. 2020;87:103249. doi: 10.1016/j.engappai.2019.103249. [DOI] [Google Scholar]
- 67.Khishe M, Mosavi MR. Chimp optimization algorithm. Expert Syst Appl. 2020;149:113338. doi: 10.1016/j.eswa.2020.113338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Połap D, Woźniak M. Red fox optimization algorithm. Expert Syst Appl. 2021;166:114107. doi: 10.1016/j.eswa.2020.114107. [DOI] [Google Scholar]
- 69.Pan JS, Zhang LG, Wang RB, Snášel V, Chu SC. Gannet optimization algorithm: A new metaheuristic algorithm for solving engineering optimization problems. Math Comput Simul. 2022;202:343–373. doi: 10.1016/j.matcom.2022.06.007. [DOI] [Google Scholar]
- 70.Srinivas N, Deb K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol Comput. 1994;2(3):221–248. doi: 10.1162/evco.1994.2.3.221. [DOI] [Google Scholar]
- 71.Rubinstein RY. Optimization of computer simulation models with rare events. Eur J Oper Res. 1997;99(1):89–112. doi: 10.1016/S0377-2217(96)00385-2. [DOI] [Google Scholar]
- 72.Mladenović N, Hansen P. Variable neighborhood search. Comput Oper Res. 1997;24(11):1097–1100. doi: 10.1016/S0305-0548(97)00031-2. [DOI] [Google Scholar]
- 73.Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evol Comput. 2001;9(2):159–195. doi: 10.1162/106365601750190398. [DOI] [PubMed] [Google Scholar]
- 74.Geem ZW, Kim JH, Loganathan GV. A new heuristic optimization algorithm: harmony search. Simulation. 2001;76(2):60–68. doi: 10.1177/003754970107600201. [DOI] [Google Scholar]
- 75.Hanseth O, Aanestad M (2001) Bootstrapping networks, communities and infrastructures. On the evolution of ICT solutions in heath care. In: Proceedings of the 1st international conference on information technology in health care (ITHC’01)
- 76.Larrañaga P, Lozano JA, editors. Estimation of distribution algorithms: a new tool for evolutionary computation. Cham: Springer Science & Business Media; 2001. [Google Scholar]
- 77.Pham DT, Ghanbarzadeh A, Koç E, Otri S, Rahim S, Zaidi M (2006) The bees algorithm—a novel tool for complex optimisation problems. In: Intelligent production machines and systems, 2nd I*PROMS Virtual International Conference, pp. 454–459
- 78.Karaboga D (2005) An idea based on honey bee swarm for numerical optimization. Technical report-tr06, Erciyes university, engineering faculty, computer engineering department, vol. 200, pp. 1-10
- 79.Krishnanand KN, Ghose D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications. Multiagent Grid Syst. 2006;2(3):209–222. doi: 10.3233/MGS-2006-2301. [DOI] [Google Scholar]
- 80.Haddad OB, Afshar A, Mariño MA. Honey-bees mating optimization (HBMO) algorithm: a new heuristic approach for water resources optimization. Water Resour Manag. 2006;20(5):661–680. doi: 10.1007/s11269-005-9001-3. [DOI] [Google Scholar]
- 81.Mucherino A, Seref O (2007) Monkey search: a novel metaheuristic search for global optimization. In: AIP conference proceedings, American Institute of Physics, 953(1), 162-173
- 82.Atashpaz-Gargari E, Lucas C (2007) Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition. In: 2007 IEEE congress on evolutionary computation,pp. 4661–4667.
- 83.Simon D. Biogeography-based optimization. IEEE Trans Evol Comput. 2008;12(6):702–713. doi: 10.1109/TEVC.2008.919004. [DOI] [Google Scholar]
- 84.Teodorović D (2009) Bee colony optimization (BCO). Innovations in swarm intelligence. Stud Comput Intel 248:39–60
- 85.He S, Wu QH, Saunders JR. Group search optimizer: an optimization algorithm inspired by animal searching behavior. IEEE Trans Evol Comput. 2009;13(5):973–990. doi: 10.1109/TEVC.2009.2011992. [DOI] [Google Scholar]
- 86.Yang XS, Deb S (2009) Cuckoo search via Lévy flights. In: 2009 World congress on nature & biologically inspired computing (NaBIC), pp. 210–214
- 87.Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: a gravitational search algorithm. Inf Sci. 2009;179(13):2232–2248. doi: 10.1016/j.ins.2009.03.004. [DOI] [Google Scholar]
- 88.Kashan AH (2009) League championship algorithm: a new algorithm for numerical function optimization. In: 2009 international conference of soft computing and pattern recognition, pp. 43–48.
- 89.Kadioglu S, Sellmann M (2009) Dialectic search. In: International conference on principles and practice of constraint programming, pp. 486–500
- 90.Shah-Hosseini H. The intelligent water drops algorithm: a nature-inspired swarm-based optimization algorithm. Int J Bio-inspired Comput. 2009;1(1–2):71–79. doi: 10.1504/IJBIC.2009.022775. [DOI] [Google Scholar]
- 91.Yang XS (2009) Firefly algorithms for multimodal optimization. In: International symposium on stochastic algorithms, pp. 169–178
- 92.Battiti R, Brunato M, Mariello A (2019) Reactive search optimization: learning while optimizing. In: Handbook of metaheuristics, International Series in Operations Research & Management Science, vol. 272, pp. 479–511
- 93.Yang XS (2010) A new metaheuristic bat-inspired algorithm. In: Nature inspired cooperative strategies for optimization (NICSO 2010), studies in computational intelligence, vol. 284, pp. 65–74
- 94.Shah-Hosseini H. Principal components analysis by the galaxy-based search algorithm: a novel metaheuristic for continuous optimisation. Int J Comput Sci Eng. 2011;6(1–2):132–140. [Google Scholar]
- 95.Tamura K, Yasuda K. Spiral dynamics inspired optimization. J Adv Comput Intell Intell Inform. 2011;15(8):1116–1122. doi: 10.20965/jaciii.2011.p1116. [DOI] [Google Scholar]
- 96.Alsheddy A (2011) Empowerment scheduling: a multi-objective optimization approach using guided local search (Doctoral dissertation, University of Essex)
- 97.Rajabioun R. Cuckoo optimization algorithm. Appl Soft Comput. 2011;11(8):5508–5518. doi: 10.1016/j.asoc.2011.05.008. [DOI] [Google Scholar]
- 98.Gandomi AH, Alavi AH. Krill herd: a new bio-inspired optimization algorithm. Commun Nonlinear Sci Numer Simul. 2012;17(12):4831–4845. doi: 10.1016/j.cnsns.2012.05.010. [DOI] [Google Scholar]
- 99.Civicioglu P. Transforming geocentric cartesian coordinates to geodetic coordinates by using differential search algorithm. Comput Geosci. 2012;46:229–247. doi: 10.1016/j.cageo.2011.12.011. [DOI] [Google Scholar]
- 100.Sadollah A, Bahreininejad A, Eskandar H, Hamdi M. Mine blast algorithm: a new population based algorithm for solving constrained engineering optimization problems. Appl Soft Comput. 2013;13(5):2592–2612. doi: 10.1016/j.asoc.2012.11.026. [DOI] [Google Scholar]
- 101.Hatamlou A. Black hole: a new heuristic optimization approach for data clustering. Inf Sci. 2013;222:175–184. doi: 10.1016/j.ins.2012.08.023. [DOI] [Google Scholar]
- 102.Gandomi AH. Interior search algorithm (ISA): a novel approach for global optimization. ISA Trans. 2014;53(4):1168–1183. doi: 10.1016/j.isatra.2014.03.018. [DOI] [PubMed] [Google Scholar]
- 103.Cheng MY, Prayogo D. Symbiotic organisms search: a new metaheuristic optimization algorithm. Comput Struct. 2014;139:98–112. doi: 10.1016/j.compstruc.2014.03.007. [DOI] [Google Scholar]
- 104.Kashan AH. A new metaheuristic for optimization: optics inspired optimization (OIO) Comput Oper Res. 2015;55:99–125. doi: 10.1016/j.cor.2014.10.011. [DOI] [Google Scholar]
- 105.Kaveh A, Mahdavi VR (2015) Colliding bodies optimization: extensions and applications. Technology & Engineering, Springer International Publishing, pp. 284
- 106.Salimi H. Stochastic fractal search: a powerful metaheuristic algorithm. Knowl-Based Syst. 2015;75:1–18. doi: 10.1016/j.knosys.2014.07.025. [DOI] [Google Scholar]
- 107.Zheng YJ. Water wave optimization: a new nature-inspired metaheuristic. Comput Oper Res. 2015;55:1–11. doi: 10.1016/j.cor.2014.10.008. [DOI] [Google Scholar]
- 108.Doğan B, Ölmez T. A new metaheuristic for numerical function optimization: Vortex search algorithm. Inf Sci. 2015;293:125–145. doi: 10.1016/j.ins.2014.08.053. [DOI] [Google Scholar]
- 109.Wang GG, Deb S, Coelho LDS (2015) Elephant herding optimization. In: 2015 3rd international symposium on computational and business intelligence (ISCBI), pp. 1–5
- 110.Kashan AH, Akbari AA, Ostadi B. Grouping evolution strategies: an effective approach for grouping problems. Appl Math Model. 2015;39(9):2703–2720. doi: 10.1016/j.apm.2014.11.001. [DOI] [Google Scholar]
- 111.Mirjalili S. Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl. 2016;27(4):1053–1073. doi: 10.1007/s00521-015-1920-1. [DOI] [Google Scholar]
- 112.Liang YC, Cuevas Juarez JR. A novel metaheuristic for continuous optimization problems: virus optimization algorithm. Eng Optim. 2016;48(1):73–93. doi: 10.1080/0305215X.2014.994868. [DOI] [Google Scholar]
- 113.Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl-Based Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
- 114.Ebrahimi A, Khamehchi E. Sperm whale algorithm: an effective metaheuristic algorithm for production optimization problems. J Nat Gas Sci Eng. 2016;29:211–222. doi: 10.1016/j.jngse.2016.01.001. [DOI] [Google Scholar]
- 115.Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM. Salp swarm algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw. 2017;114:163–191. doi: 10.1016/j.advengsoft.2017.07.002. [DOI] [Google Scholar]
- 116.Baykasoğlu A, Akpinar Ş. Weighted superposition attraction (WSA): a swarm intelligence algorithm for optimization problems–Part 1: unconstrained optimization. Appl Soft Comput. 2017;56:520–540. doi: 10.1016/j.asoc.2015.10.036. [DOI] [Google Scholar]
- 117.Mortazavi A, Toğan V, Nuhoğlu A. Interactive search algorithm: a new hybrid metaheuristic optimization algorithm. Eng Appl Artif Intell. 2018;71:275–292. doi: 10.1016/j.engappai.2018.03.003. [DOI] [Google Scholar]
- 118.Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris hawks optimization: algorithm and applications. Futur Gener Comput Syst. 2019;97:849–872. doi: 10.1016/j.future.2019.02.028. [DOI] [Google Scholar]
- 119.Yapici H, Cetinkaya N. A new meta-heuristic optimizer: pathfinder algorithm. Appl Soft Comput. 2019;78:545–568. doi: 10.1016/j.asoc.2019.03.012. [DOI] [Google Scholar]
- 120.Kaur S, Awasthi LK, Sangal AL, Dhiman G. Tunicate swarm algorithm: a new bio-inspired based metaheuristic paradigm for global optimization. Eng Appl Artif Intell. 2020;90:103541. doi: 10.1016/j.engappai.2020.103541. [DOI] [Google Scholar]
- 121.Braik M, Sheta A, Al-Hiary H. A novel meta-heuristic search algorithm for solving optimization problems: capuchin search algorithm. Neural Comput Appl. 2021;33(7):2515–2547. doi: 10.1007/s00521-020-05145-6. [DOI] [Google Scholar]
- 122.Talatahari S, Azizi M, Tolouei M, Talatahari B, Sareh P. Crystal structure algorithm (CryStAl): a metaheuristic optimization method. IEEE Access. 2021;9:71244–71261. doi: 10.1109/ACCESS.2021.3079161. [DOI] [Google Scholar]
- 123.Eslami N, Yazdani S, Mirzaei M, Hadavandi E (2022) Aphid-ant mutualism: a novel nature-inspired metaheuristic algorithm for solving optimization problems. Math Comput Simul 201:362–395
- 124.Hashim FA, Houssein EH, Hussain K, Mabrouk MS, Al-Atabany W. Honey badger algorithm: new metaheuristic algorithm for solving optimization problems. Math Comput Simul. 2022;192:84–110. doi: 10.1016/j.matcom.2021.08.013. [DOI] [Google Scholar]
- 125.Oszust M, Sroka G, Cymerys K. A hybridization approach with predicted solution candidates for improving population-based optimization algorithms. Inf Sci. 2021;574:133–161. doi: 10.1016/j.ins.2021.04.082. [DOI] [Google Scholar]
- 126.Połap D, Kęsik K, Woźniak M, Damaševičius R. Parallel technique for the metaheuristic algorithms using devoted local search and manipulating the solutions space. Appl Sci. 2018;8(2):293. doi: 10.3390/app8020293. [DOI] [Google Scholar]
- 127.Chunkai Z, Yu L, Huihe S (2000) A new evolved artificial neural network and its application. In: Proceedings of the 3rd world congress on intelligent control and automation (Cat. No. 00EX393), vol. 2, pp. 1065–1068
- 128.Li K, Thompson S, Wieringa PA, Peng J, Duan GR. Neural networks and genetic algorithms can support human supervisory control to reduce fossil fuel power plant emissions. Cognit Technol Work. 2003;5(2):107–126. doi: 10.1007/s10111-002-0107-6. [DOI] [Google Scholar]
- 129.Leung FHF, Lam HK, Ling SH, Tam PKS. Tuning of the structure and parameters of a neural network using an improved genetic algorithm. IEEE Trans Neural Netw. 2003;14(1):79–88. doi: 10.1109/TNN.2002.804317. [DOI] [PubMed] [Google Scholar]
- 130.Meissner M, Schmuker M, Schneider G. Optimized particle swarm optimization (OPSO) and its application to artificial neural network training. BMC Bioinform. 2006;7(1):125. doi: 10.1186/1471-2105-7-125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Geethanjali M, Slochanal SMR, Bhavani R. PSO trained ANN-based differential protection scheme for power transformers. Neurocomputing. 2008;71(4–6):904–918. doi: 10.1016/j.neucom.2007.02.014. [DOI] [Google Scholar]
- 132.Yu J, Wang S, Xi L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing. 2008;71(4–6):1054–1060. doi: 10.1016/j.neucom.2007.10.013. [DOI] [Google Scholar]
- 133.Khayat O, Ebadzadeh MM, Shahdoosti HR, Rajaei R, Khajehnasiri I. A novel hybrid algorithm for creating self-organizing fuzzy neural networks. Neurocomputing. 2009;73(1–3):517–524. doi: 10.1016/j.neucom.2009.06.013. [DOI] [Google Scholar]
- 134.Lin CJ, Hsieh MH. Classification of mental task from EEG data using neural networks based on particle swarm optimization. Neurocomputing. 2009;72(4–6):1121–1130. doi: 10.1016/j.neucom.2008.02.017. [DOI] [Google Scholar]
- 135.Cruz-Ramírez M, Sánchez-Monedero J, Fernández-Navarro F, Fernández JC, Hervás-Martínez C. Memetic pareto differential evolutionary artificial neural networks to determine growth multi-classes in predictive microbiology. Evol Intell. 2010;3(3–4):187–199. doi: 10.1007/s12065-010-0045-9. [DOI] [Google Scholar]
- 136.Malviya R, Pratihar DK. Tuning of neural networks using particle swarm optimization to model MIG welding process. Swarm Evol Comput. 2011;1(4):223–235. doi: 10.1016/j.swevo.2011.07.001. [DOI] [Google Scholar]
- 137.Zhao L, Qian F. Tuning the structure and parameters of a neural network using cooperative binary-real particle swarm optimization. Expert Syst Appl. 2011;38(5):4972–4977. doi: 10.1016/j.eswa.2010.09.154. [DOI] [Google Scholar]
- 138.Green RC, II, Wang L, Alam M. Training neural networks using central force optimization and particle swarm optimization: insights and comparisons. Expert Syst Appl. 2012;39(1):555–563. doi: 10.1016/j.eswa.2011.07.046. [DOI] [Google Scholar]
- 139.Vasumathi B, Moorthi S. Implementation of hybrid ANN–PSO algorithm on FPGA for harmonic estimation. Eng Appl Artif Intell. 2012;25(3):476–483. doi: 10.1016/j.engappai.2011.12.005. [DOI] [Google Scholar]
- 140.Yaghini M, Khoshraftar MM, Fallahi M. A hybrid algorithm for artificial neural network training. Eng Appl Artif Intell. 2013;26(1):293–301. doi: 10.1016/j.engappai.2012.01.023. [DOI] [Google Scholar]
- 141.Dragoi EN, Curteanu S, Galaction AI, Cascaval D. Optimization methodology based on neural networks and self-adaptive differential evolution algorithm applied to an aerobic fermentation process. Appl Soft Comput. 2013;13(1):222–238. doi: 10.1016/j.asoc.2012.08.004. [DOI] [Google Scholar]
- 142.Ismail A, Jeng DS, Zhang LL. An optimised product-unit neural network with a novel PSO–BP hybrid training algorithm: applications to load–deformation analysis of axially loaded piles. Eng Appl Artif Intell. 2013;26(10):2305–2314. doi: 10.1016/j.engappai.2013.04.007. [DOI] [Google Scholar]
- 143.Das G, Pattnaik PK, Padhy SK. Artificial neural network trained by particle swarm optimization for non-linear channel equalization. Expert Syst Appl. 2014;41(7):3491–3496. doi: 10.1016/j.eswa.2013.10.053. [DOI] [Google Scholar]
- 144.Mirjalili S, Mirjalili SM, Lewis A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf Sci. 2014;269:188–209. doi: 10.1016/j.ins.2014.01.038. [DOI] [Google Scholar]
- 145.Jaddi NS, Abdullah S, Hamdan AR. Multi-population cooperative bat algorithm-based optimization of artificial neural network model. Inf Sci. 2015;294:628–644. doi: 10.1016/j.ins.2014.08.050. [DOI] [Google Scholar]
- 146.Jaddi NS, Abdullah S, Hamdan AR. Optimization of neural network model using modified bat-inspired algorithm. Appl Soft Comput. 2015;37:71–86. doi: 10.1016/j.asoc.2015.08.002. [DOI] [Google Scholar]
- 147.González B, Valdez F, Melin P, Prado-Arechiga G. Fuzzy logic in the gravitational search algorithm enhanced using fuzzy logic with dynamic alpha parameter value adaptation for the optimization of modular neural networks in echocardiogram recognition. Appl Soft Comput. 2015;37:245–254. doi: 10.1016/j.asoc.2015.08.034. [DOI] [Google Scholar]
- 148.Gaxiola F, Melin P, Valdez F, Castro JR, Castillo O. Optimization of type-2 fuzzy weights in backpropagation learning for neural networks using GAs and PSO. Appl Soft Comput. 2016;38:860–871. doi: 10.1016/j.asoc.2015.10.027. [DOI] [Google Scholar]
- 149.Karaboga D, Kaya E. An adaptive and hybrid artificial bee colony algorithm (aABC) for ANFIS training. Appl Soft Comput. 2016;49:423–436. doi: 10.1016/j.asoc.2016.07.039. [DOI] [Google Scholar]
- 150.Jafrasteh B, Fathianpour N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation. Neurocomputing. 2017;235:217–227. doi: 10.1016/j.neucom.2017.01.016. [DOI] [Google Scholar]
- 151.Ganjefar S, Tofighi M. Training qubit neural network with hybrid genetic algorithm and gradient descent for indirect adaptive controller design. Eng Appl Artif Intell. 2017;65:346–360. doi: 10.1016/j.engappai.2017.08.007. [DOI] [Google Scholar]
- 152.Aljarah I, Faris H, Mirjalili S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018;22(1):1–15. doi: 10.1007/s00500-016-2442-1. [DOI] [Google Scholar]
- 153.Heidari AA, Faris H, Aljarah I, Mirjalili S. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput. 2019;23(17):7941–7958. doi: 10.1007/s00500-018-3424-2. [DOI] [Google Scholar]
- 154.Hadavandi E, Mostafayi S, Soltani P. A grey wolf optimizer-based neural network coupled with response surface method for modeling the strength of siro-spun yarn in spinning mills. Appl Soft Comput. 2018;72:1–13. doi: 10.1016/j.asoc.2018.07.055. [DOI] [Google Scholar]
- 155.Haznedar B, Kalinli A. Training ANFIS structure using simulated annealing algorithm for dynamic systems identification. Neurocomputing. 2018;302:66–74. doi: 10.1016/j.neucom.2018.04.006. [DOI] [Google Scholar]
- 156.Pham BT, Nguyen MD, Bui KTT, Prakash I, Chapi K, Bui DT. A novel artificial intelligence approach based on multi-layer perceptron neural network and biogeography-based optimization for predicting coefficient of consolidation of soil. CATENA. 2019;173:302–311. doi: 10.1016/j.catena.2018.10.004. [DOI] [Google Scholar]
- 157.Han JW, Li QX, Wu HR, Zhu HJ, Song YL. Prediction of cooling efficiency of forced-air precooling systems based on optimized differential evolution and improved BP neural network. Appl Soft Comput. 2019;84:105733. doi: 10.1016/j.asoc.2019.105733. [DOI] [Google Scholar]
- 158.Rojas-Delgado J, Trujillo-Rasúa R, Bello R. A continuation approach for training Artificial Neural Networks with meta-heuristics. Pattern Recogn Lett. 2019;125:373–380. doi: 10.1016/j.patrec.2019.05.017. [DOI] [Google Scholar]
- 159.Khishe M, Mosavi MR. Classification of underwater acoustical dataset using neural network trained by chimp optimization algorithm. Appl Acoust. 2020;157:107005. doi: 10.1016/j.apacoust.2019.107005. [DOI] [Google Scholar]
- 160.Wang Y, Liu H, Yu Z, Tu L. An improved artificial neural network based on human-behaviour particle swarm optimization and cellular automata. Expert Syst Appl. 2020;140:112862. doi: 10.1016/j.eswa.2019.112862. [DOI] [Google Scholar]
- 161.Al-Majidi SD, Abbod MF, Al-Raweshidy HS. A particle swarm optimisation-trained feedforward neural network for predicting the maximum power point of a photovoltaic array. Eng Appl Artif Intell. 2020;92:103688. doi: 10.1016/j.engappai.2020.103688. [DOI] [Google Scholar]
- 162.Ansari A, Ahmad IS, Bakar AA, Yaakub MR. A hybrid metaheuristic method in training artificial neural network for bankruptcy prediction. IEEE Access. 2020;8:176640–176650. doi: 10.1109/ACCESS.2020.3026529. [DOI] [Google Scholar]
- 163.Zhang Y, Zhao J, Wang L, Wu H, Zhou R, Yu J. An improved OIF Elman neural network based on CSO algorithm and its applications. Comput Commun. 2021;171:148–156. doi: 10.1016/j.comcom.2021.01.035. [DOI] [Google Scholar]
- 164.Li XD, Wang JS, Hao WK, Wang M, Zhang M. Multi-layer perceptron classification method of medical data based on biogeography-based optimization algorithm with probability distributions. Appl Soft Comput. 2022;121:108766. doi: 10.1016/j.asoc.2022.108766. [DOI] [Google Scholar]
- 165.Engel J. Teaching feed-forward neural networks by simulated annealing. Complex Syst. 1988;2(6):641–648. [Google Scholar]
- 166.Montana DJ, Davis L (1989) Training feedforward neural networks using genetic algorithms. In: IJCAI, Vol. 89, pp. 762–767
- 167.Whitley D, Starkweather T, Bogart C. Genetic algorithms and neural networks: optimizing connections and connectivity. Parallel Comput. 1990;14(3):347–361. doi: 10.1016/0167-8191(90)90086-O. [DOI] [Google Scholar]
- 168.Belew RK, McInerney J, Schraudolph NN (1990) Evolving networks: using the genetic algorithm with connectionist learning. SFI studies in the sciences of complexity, pp. 511–547
- 169.Kitano H. Neurogenetic learning: an integrated method of designing and training neural networks using genetic algorithms. Phys D Nonlinear Phenom. 1994;75(1–3):225–238. doi: 10.1016/0167-2789(94)90285-2. [DOI] [Google Scholar]
- 170.Battiti R, Tecchiolli G. Training neural nets with the reactive tabu search. IEEE Trans Neural Netw. 1995;6(5):1185–1200. doi: 10.1109/72.410361. [DOI] [PubMed] [Google Scholar]
- 171.Yao X, Liu Y. A new evolutionary system for evolving artificial neural networks. IEEE Trans Neural Netw. 1997;8(3):694–713. doi: 10.1109/72.572107. [DOI] [PubMed] [Google Scholar]
- 172.Sexton RS, Alidaee B, Dorsey RE, Johnson JD. Global optimization for artificial neural networks: a tabu search application. Eur J Oper Res. 1998;106(2–3):570–584. doi: 10.1016/S0377-2217(97)00292-0. [DOI] [Google Scholar]
- 173.Sexton RS, Dorsey RE, Johnson JD. Beyond backpropagation: using simulated annealing for training neural networks. J Organ End User Comput. 1999;11(3):3–10. doi: 10.4018/joeuc.1999070101. [DOI] [Google Scholar]
- 174.Arifovic J, Gencay R. Using genetic algorithms to select architecture of a feedforward artificial neural network. Phys A Stat Mech Appl. 2001;289(3–4):574–594. doi: 10.1016/S0378-4371(00)00479-9. [DOI] [Google Scholar]
- 175.Alvarez A. A neural network with evolutionary neurons. Neural Process Lett. 2002;16(1):43–52. doi: 10.1023/A:1019747726343. [DOI] [Google Scholar]
- 176.Sarkar D, Modak JM. ANNSA: a hybrid artificial neural network/simulated annealing algorithm for optimal control problems. Chem Eng Sci. 2003;58(14):3131–3142. doi: 10.1016/S0009-2509(03)00168-4. [DOI] [Google Scholar]
- 177.García-Pedrajas N, Hervás-Martínez C, Muñoz-Pérez J. COVNET: a cooperative coevolutionary model for evolving artificial neural networks. IEEE Trans Neural Netw. 2003;14(3):575–596. doi: 10.1109/TNN.2003.810618. [DOI] [PubMed] [Google Scholar]
- 178.Ilonen J, Kamarainen JK, Lampinen J. Differential evolution training algorithm for feed-forward neural networks. Neural Process Lett. 2003;17(1):93–105. doi: 10.1023/A:1022995128597. [DOI] [Google Scholar]
- 179.Augusteijn MF, Harrington TP. Evolving transfer functions for artificial neural networks. Neural Comput Appl. 2004;13(1):38–46. doi: 10.1007/s00521-003-0393-9. [DOI] [Google Scholar]
- 180.Abraham A. Meta learning evolutionary artificial neural networks. Neurocomputing. 2004;56:1–38. doi: 10.1016/S0925-2312(03)00369-2. [DOI] [Google Scholar]
- 181.Lahiri A, Chakravorti S. Electrode-spacer contour optimization by ANN aided genetic algorithm. IEEE Trans Dielectr Electr Insul. 2004;11(6):964–975. doi: 10.1109/TDEI.2004.1387819. [DOI] [Google Scholar]
- 182.Shen Q, Jiang JH, Jiao CX, Lin WQ, Shen GL, Yu RQ. Hybridized particle swarm algorithm for adaptive structure training of multilayer feed-forward neural network: QSAR studies of bioactivity of organic compounds. J Comput Chem. 2004;25(14):1726–1735. doi: 10.1002/jcc.20094. [DOI] [PubMed] [Google Scholar]
- 183.Kim D, Kim H, Chung D (2005) A modified genetic algorithm for fast training neural networks. In: International symposium on neural networks, pp. 660–665
- 184.Chatterjee A, Pulasinghe K, Watanabe K, Izumi K. A particle-swarm-optimized fuzzy-neural network for voice-controlled robot systems. IEEE Trans Ind Electron. 2005;52(6):1478–1489. doi: 10.1109/TIE.2005.858737. [DOI] [Google Scholar]
- 185.Feng P, Jie C, Xuyan T, Jiwei F. Multilayered feed forward neural network based on particle swarm optimizer algorithm. J Syst Eng Electron. 2005;16(3):682–686. [Google Scholar]
- 186.Da Y, Xiurun G. An improved PSO-based ANN with simulated annealing technique. Neurocomputing. 2005;63:527–533. doi: 10.1016/j.neucom.2004.07.002. [DOI] [Google Scholar]
- 187.Salajegheh E, Gholizadeh S. Optimum design of structures by an improved genetic algorithm using neural networks. Adv Eng Softw. 2005;36(11–12):757–767. doi: 10.1016/j.advengsoft.2005.03.022. [DOI] [Google Scholar]
- 188.Tsai JT, Chou JH, Liu TK. Tuning the structure and parameters of a neural network by using hybrid Taguchi-genetic algorithm. IEEE Trans Neural Netw. 2006;17(1):69–80. doi: 10.1109/TNN.2005.860885. [DOI] [PubMed] [Google Scholar]
- 189.García-Pedrajas N, Ortiz-Boyer D, Hervás-Martínez C. An alternative approach for neural network evolution with a genetic algorithm: crossover by combinatorial optimization. Neural Netw. 2006;19(4):514–528. doi: 10.1016/j.neunet.2005.08.014. [DOI] [PubMed] [Google Scholar]
- 190.Ye J, Qiao J, Li MA, Ruan X. A tabu based neural network learning algorithm. Neurocomputing. 2007;70(4–6):875–882. doi: 10.1016/j.neucom.2006.10.018. [DOI] [Google Scholar]
- 191.Socha K, Blum C. An ant colony optimization algorithm for continuous optimization: application to feed-forward neural network training. Neural Comput Appl. 2007;16(3):235–247. doi: 10.1007/s00521-007-0084-z. [DOI] [Google Scholar]
- 192.Lin WQ, Jiang JH, Zhou YP, Wu HL, Shen GL, Yu RQ. Support vector machine based training of multilayer feedforward neural networks as optimized by particle swarm algorithm: application in QSAR studies of bioactivity of organic compounds. J Comput Chem. 2007;28(2):519–527. doi: 10.1002/jcc.20561. [DOI] [PubMed] [Google Scholar]
- 193.Ulagammai M, Venkatesh P, Kannan PS, Padhy NP. Application of bacterial foraging technique trained artificial and wavelet neural networks in load forecasting. Neurocomputing. 2007;70(16–18):2659–2667. doi: 10.1016/j.neucom.2006.05.020. [DOI] [Google Scholar]
- 194.Zhang JR, Zhang J, Lok TM, Lyu MR. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl Math Comput. 2007;185(2):1026–1037. [Google Scholar]
- 195.Lin CJ, Chen CH, Lin CT. A hybrid of cooperative particle swarm optimization and cultural algorithm for neural fuzzy networks and its prediction applications. IEEE Trans Syst Man Cybern Part C (Appl Rev) 2008;39(1):55–68. [Google Scholar]
- 196.Tsoulos I, Gavrilis D, Glavas E. Neural network construction and training using grammatical evolution. Neurocomputing. 2008;72(1–3):269–277. doi: 10.1016/j.neucom.2008.01.017. [DOI] [Google Scholar]
- 197.Goh CK, Teoh EJ, Tan KC. Hybrid multiobjective evolutionary design for artificial neural networks. IEEE Trans Neural Netw. 2008;19(9):1531–1548. doi: 10.1109/TNN.2008.2000444. [DOI] [PubMed] [Google Scholar]
- 198.Bashir ZA, El-Hawary ME. Applying wavelets to short-term load forecasting using PSO-based neural networks. IEEE Trans Power Syst. 2009;24(1):20–27. doi: 10.1109/TPWRS.2008.2008606. [DOI] [Google Scholar]
- 199.Kiranyaz S, Ince T, Yildirim A, Gabbouj M. Evolutionary artificial neural networks by multi-dimensional particle swarm optimization. Neural Netw. 2009;22(10):1448–1462. doi: 10.1016/j.neunet.2009.05.013. [DOI] [PubMed] [Google Scholar]
- 200.Slowik A. Application of an adaptive differential evolution algorithm with multiple trial vectors to artificial neural network training. IEEE Trans Industr Electron. 2010;58(8):3160–3167. doi: 10.1109/TIE.2010.2062474. [DOI] [Google Scholar]
- 201.Kordík P, Koutník J, Drchal J, Kovářík O, Čepek M, Šnorek M. Meta-learning approach to neural network optimization. Neural Netw. 2010;23(4):568–582. doi: 10.1016/j.neunet.2010.02.003. [DOI] [PubMed] [Google Scholar]
- 202.Lian GY, Huang KL, Chen JH, Gao FQ. Training algorithm for radial basis function neural network based on quantum-behaved particle swarm optimization. Int J Comput Math. 2010;87(3):629–641. doi: 10.1080/00207160802166465. [DOI] [Google Scholar]
- 203.Zhao C, Liu X, Ding F. Melt index prediction based on adaptive particle swarm optimization algorithm-optimized radial basis function neural networks. Chem Eng Technol. 2010;33(11):1909–1916. doi: 10.1002/ceat.201000218. [DOI] [Google Scholar]
- 204.Ma Y, Huang M, Wan J, Hu K, Wang Y, Zhang H. Hybrid artificial neural network genetic algorithm technique for modeling chemical oxygen demand removal in anoxic/oxic process. J Environ Sci Health Part A. 2011;46(6):574–580. doi: 10.1080/10934529.2011.562821. [DOI] [PubMed] [Google Scholar]
- 205.Ding S, Su C, Yu J. An optimizing BP neural network algorithm based on genetic algorithm. Artif Intell Rev. 2011;36(2):153–162. doi: 10.1007/s10462-011-9208-z. [DOI] [Google Scholar]
- 206.Subudhi B, Jena D. A differential evolution based neural network approach to nonlinear system identification. Appl Soft Comput. 2011;11(1):861–871. doi: 10.1016/j.asoc.2010.01.006. [DOI] [Google Scholar]
- 207.Ghalambaz M, Noghrehabadi AR, Behrang MA, Assareh E, Ghanbarzadeh A, Hedayat N. A hybrid neural network and gravitational search algorithm (HNNGSA) method to solve well known Wessinger's equation. Int J Mech Mechatron Eng. 2011;5(1):147–151. [Google Scholar]
- 208.Irani R, Nasimi R. Evolving neural network using real coded genetic algorithm for permeability estimation of the reservoir. Expert Syst Appl. 2011;38(8):9862–9866. doi: 10.1016/j.eswa.2011.02.046. [DOI] [Google Scholar]
- 209.Li J, Liu X. Melt index prediction by RBF neural network optimized with an MPSO-SA hybrid algorithm. Neurocomputing. 2011;74(5):735–740. doi: 10.1016/j.neucom.2010.09.019. [DOI] [Google Scholar]
- 210.Sun J, He KY, Li H. SFFS-PC-NN optimized by genetic algorithm for dynamic prediction of financial distress with longitudinal data streams. Knowl-Based Syst. 2011;24(7):1013–1023. doi: 10.1016/j.knosys.2011.04.013. [DOI] [Google Scholar]
- 211.Özbakır L, Delice Y. Exploring comprehensible classification rules from trained neural networks integrated with a time-varying binary particle swarm optimizer. Eng Appl Artif Intell. 2011;24(3):491–500. doi: 10.1016/j.engappai.2010.11.008. [DOI] [Google Scholar]
- 212.Carvalho AR, Ramos FM, Chaves AA. Metaheuristics for the feedforward artificial neural network (ANN) architecture optimization problem. Neural Comput Appl. 2011;20(8):1273–1284. doi: 10.1007/s00521-010-0504-3. [DOI] [Google Scholar]
- 213.Han M, Fan J, Wang J. A dynamic feedforward neural network based on Gaussian particle swarm optimization and its application for predictive control. IEEE Trans Neural Netw. 2011;22(9):1457–1468. doi: 10.1109/TNN.2011.2162341. [DOI] [PubMed] [Google Scholar]
- 214.Zanchettin C, Ludermir TB, Almeida LM. Hybrid training method for MLP: optimization of architecture and training. IEEE Trans Syst Man Cybern Part B. 2011;41(4):1097–1109. doi: 10.1109/TSMCB.2011.2107035. [DOI] [PubMed] [Google Scholar]
- 215.Vadood M, Semnani D, Morshed M. Optimization of acrylic dry spinning production line by using artificial neural network and genetic algorithm. J Appl Polym Sci. 2011;120(2):735–744. doi: 10.1002/app.33252. [DOI] [Google Scholar]
- 216.Mirjalili S, Hashim SZM, Sardroudi HM. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl Math Comput. 2012;218(22):11125–11137. [Google Scholar]
- 217.Khan K, Sahai A. A comparison of BA, GA, PSO, BP and LM for training feed forward neural networks in e-learning context. Int J Intell Syst Appl. 2012;4(7):23. [Google Scholar]
- 218.Huang M, Liu X, Li J. Melt index prediction by RBF neural network with an ICO-VSA hybrid optimization algorithm. J Appl Polym Sci. 2012;126(2):519–526. doi: 10.1002/app.36814. [DOI] [Google Scholar]
- 219.Irani R, Nasimi R. An evolving neural network using an ant colony algorithm for a permeability estimation of the reservoir. Pet Sci Technol. 2012;30(4):375–384. doi: 10.1080/10916466.2010.483442. [DOI] [Google Scholar]
- 220.Kulluk S, Ozbakir L, Baykasoglu A. Training neural networks with harmony search algorithms for classification problems. Eng Appl Artif Intell. 2012;25(1):11–19. doi: 10.1016/j.engappai.2011.07.006. [DOI] [Google Scholar]
- 221.Nandy S, Sarkar PP, Das A (2012) Analysis of a nature inspired firefly algorithm based back-propagation neural network training. arXiv preprint arXiv:1206.5360
- 222.Han F, Zhu JS. Improved particle swarm optimization combined with backpropagation for feedforward neural networks. Int J Intell Syst. 2013;28(3):271–288. doi: 10.1002/int.21569. [DOI] [Google Scholar]
- 223.Sharma N, Arun N, Ravi V. An ant colony optimisation and Nelder-Mead simplex hybrid algorithm for training neural networks: an application to bankruptcy prediction in banks. Int J Inf Decis Sci. 2013;5(2):188–203. [Google Scholar]
- 224.Li HZ, Guo S, Li CJ, Sun JQ. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl-Based Syst. 2013;37:378–387. doi: 10.1016/j.knosys.2012.08.015. [DOI] [Google Scholar]
- 225.Wang M, Yan X, Shi H. Spatiotemporal prediction for nonlinear parabolic distributed parameter system using an artificial neural network trained by group search optimization. Neurocomputing. 2013;113:234–240. doi: 10.1016/j.neucom.2013.01.037. [DOI] [Google Scholar]
- 226.Lu TC, Yu GR, Juang JC. Quantum-based algorithm for optimizing artificial neural networks. IEEE Trans Neural Netw Learn Syst. 2013;24(8):1266–1278. doi: 10.1109/TNNLS.2013.2249089. [DOI] [PubMed] [Google Scholar]
- 227.Askarzadeh A, Rezazadeh A. Artificial neural network training using a new efficient optimization algorithm. Appl Soft Comput. 2013;13(2):1206–1213. doi: 10.1016/j.asoc.2012.10.023. [DOI] [Google Scholar]
- 228.Li LK, Shao S, Yiu KFC. A new optimization algorithm for single hidden layer feedforward neural networks. Appl Soft Comput. 2013;13(5):2857–2862. doi: 10.1016/j.asoc.2012.04.034. [DOI] [Google Scholar]
- 229.Parra J, Trujillo L, Melin P. Hybrid back-propagation training with evolutionary strategies. Soft Comput. 2014;18(8):1603–1614. doi: 10.1007/s00500-013-1166-8. [DOI] [Google Scholar]
- 230.Piotrowski AP. Differential evolution algorithms applied to neural network training suffer from stagnation. Appl Soft Comput. 2014;21:382–406. doi: 10.1016/j.asoc.2014.03.039. [DOI] [Google Scholar]
- 231.Nasimi R, Irani R. Identification and modeling of a yeast fermentation bioreactor using hybrid particle swarm optimization-artificial neural networks. Energy Sources Part A Recovery Util Environ Eff. 2014;36(14):1604–1611. doi: 10.1080/15567036.2011.592903. [DOI] [Google Scholar]
- 232.Tapoglou E, Trichakis IC, Dokou Z, Nikolos IK, Karatzas GP. Groundwater-level forecasting under climate change scenarios using an artificial neural network trained with particle swarm optimization. Hydrol Sci J. 2014;59(6):1225–1239. doi: 10.1080/02626667.2013.838005. [DOI] [Google Scholar]
- 233.Raja MAZ. Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ANN optimised with PSO and SQP. Connect Sci. 2014;26(3):195–214. doi: 10.1080/09540091.2014.907555. [DOI] [Google Scholar]
- 234.Beheshti Z, Shamsuddin SMH, Beheshti E, Yuhaniz SS. Enhancement of artificial neural network learning using centripetal accelerated particle swarm optimization for medical diseases diagnosis. Soft Comput. 2014;18(11):2253–2270. doi: 10.1007/s00500-013-1198-0. [DOI] [Google Scholar]
- 235.Ren C, An N, Wang J, Li L, Hu B, Shang D. Optimal parameters selection for BP neural network based on particle swarm optimization: a case study of wind speed forecasting. Knowl-Based Syst. 2014;56:226–239. doi: 10.1016/j.knosys.2013.11.015. [DOI] [Google Scholar]
- 236.Svečko R, Kusić D. Feedforward neural network position control of a piezoelectric actuator based on a BAT search algorithm. Expert Syst Appl. 2015;42(13):5416–5423. doi: 10.1016/j.eswa.2015.02.061. [DOI] [Google Scholar]
- 237.Kumaran J, Ravi G. Long-term sector-wise electrical energy forecasting using artificial neural network and biogeography-based optimization. Electr Power Compon Syst. 2015;43(11):1225–1235. doi: 10.1080/15325008.2015.1028115. [DOI] [Google Scholar]
- 238.Cui H, Feng J, Guo J, Wang T. A novel single multiplicative neuron model trained by an improved glowworm swarm optimization algorithm for time series prediction. Knowl-Based Syst. 2015;88:195–209. doi: 10.1016/j.knosys.2015.07.032. [DOI] [Google Scholar]
- 239.Chen CH, Tsai YC, Jhang RZ. Approximation of the piecewise function using neural fuzzy networks with an improved artificial bee colony algorithm. J Autom Control Eng. 2015;3(6):18–21. doi: 10.12720/joace.4.1.18-21. [DOI] [Google Scholar]
- 240.Mirjalili S. How effective is the Grey Wolf optimizer in training multi-layer perceptrons. Appl Intell. 2015;43(1):150–161. doi: 10.1007/s10489-014-0645-7. [DOI] [Google Scholar]
- 241.Agrawal RK, Bawane NG. Multiobjective PSO based adaption of neural network topology for pixel classification in satellite imagery. Appl Soft Comput. 2015;28:217–225. doi: 10.1016/j.asoc.2014.11.052. [DOI] [Google Scholar]
- 242.Gharghan SK, Nordin R, Ismail M, Abd Ali J. Accurate wireless sensor localization technique based on hybrid PSO-ANN algorithm for indoor and outdoor track cycling. IEEE Sens J. 2015;16(2):529–541. doi: 10.1109/JSEN.2015.2483745. [DOI] [Google Scholar]
- 243.Vadood M, Johari MS, Rahai A. Developing a hybrid artificial neural network-genetic algorithm model to predict resilient modulus of polypropylene/polyester fiber-reinforced asphalt concrete. J Text Inst. 2015;106(11):1239–1250. doi: 10.1080/00405000.2014.985882. [DOI] [Google Scholar]
- 244.Yazdi MS, Rostami SL, Kolahdooz A. Optimization of geometrical parameters in a specific composite lattice structure using neural networks and ABC algorithm. J Mech Sci Technol. 2016;30(4):1763–1771. doi: 10.1007/s12206-016-0332-1. [DOI] [Google Scholar]
- 245.Jia W, Zhao D, Ding L. An optimized RBF neural network algorithm based on partial least squares and genetic algorithm for classification of small sample. Appl Soft Comput. 2016;48:373–384. doi: 10.1016/j.asoc.2016.07.037. [DOI] [Google Scholar]
- 246.Leema N, Nehemiah HK, Kannan A. Neural network classifier optimization using differential evolution with global information and back propagation algorithm for clinical datasets. Appl Soft Comput. 2016;49:834–844. doi: 10.1016/j.asoc.2016.08.001. [DOI] [Google Scholar]
- 247.Xia R, Huang X, Li M. Starch foam material performance prediction based on a radial basis function artificial neural network trained by bare-bones particle swarm optimization with an adaptive disturbance factor. J Appl Polym Sci. 2016 doi: 10.1002/app.44252. [DOI] [Google Scholar]
- 248.Melo H, Watada J. Gaussian-PSO with fuzzy reasoning based on structural learning for training a neural network. Neurocomputing. 2016;172:405–412. doi: 10.1016/j.neucom.2015.03.104. [DOI] [Google Scholar]
- 249.Chidambaram B, Ravichandran M, Seshadri A, Muniyandi V. Computational heat transfer analysis and genetic algorithm-artificial neural network-genetic algorithm-based multiobjective optimization of rectangular perforated plate fins. IEEE Trans Compon Packag Manuf Technol. 2017;7(2):208–216. [Google Scholar]
- 250.Pradeepkumar D, Ravi V. Forecasting financial time series volatility using particle swarm optimization trained quantile regression neural network. Appl Soft Comput. 2017;58:35–52. doi: 10.1016/j.asoc.2017.04.014. [DOI] [Google Scholar]
- 251.Islam B, Baharudin Z, Nallagownden P. Development of chaotically improved meta-heuristics and modified BP neural network-based model for electrical energy demand prediction in smart grid. Neural Comput Appl. 2017;28(1):877–891. doi: 10.1007/s00521-016-2408-3. [DOI] [Google Scholar]
- 252.Emary E, Zawbaa HM, Grosan C. Experienced gray wolf optimization through reinforcement learning and neural networks. IEEE Trans Neural Netw Learn Syst. 2017;29(3):681–694. doi: 10.1109/TNNLS.2016.2634548. [DOI] [PubMed] [Google Scholar]
- 253.Taheri K, Hasanipanah M, Golzar SB, Abd Majid MZ. A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Eng Comput. 2017;33(3):689–700. doi: 10.1007/s00366-016-0497-3. [DOI] [Google Scholar]
- 254.Chatterjee S, Sarkar S, Hore S, Dey N, Ashour AS, Balas VE. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput Appl. 2017;28(8):2005–2016. doi: 10.1007/s00521-016-2190-2. [DOI] [Google Scholar]
- 255.Song LK, Fei CW, Bai GC, Yu LC. Dynamic neural network method-based improved PSO and BR algorithms for transient probabilistic analysis of flexible mechanism. Adv Eng Inform. 2017;33:144–153. doi: 10.1016/j.aei.2017.05.005. [DOI] [Google Scholar]
- 256.Yan D, Zhou Q, Wang J, Zhang N. Bayesian regularisation neural network based on artificial intelligence optimisation. Int J Prod Res. 2017;55(8):2266–2287. doi: 10.1080/00207543.2016.1237785. [DOI] [Google Scholar]
- 257.Mansouri A, Majidi B, Shamisa A. Metaheuristic neural networks for anomaly recognition in industrial sensor networks with packet latency and jitter for smart infrastructures. Int J Comput Appl. 2018;43:257–266. [Google Scholar]
- 258.Rukhaiyar S, Alam MN, Samadhiya NK. A PSO-ANN hybrid model for predicting factor of safety of slope. Int J Geotech Eng. 2018;12(6):556–566. [Google Scholar]
- 259.Semero YK, Zhang J, Zheng D, Wei D. A GA-PSO hybrid algorithm based neural network modeling technique for short-term wind power forecasting. Distrib Gener Altern Energy J. 2018;33(4):26–43. [Google Scholar]
- 260.Bohat VK, Arya KV. An effective gbest-guided gravitational search algorithm for real-parameter optimization and its application in training of feedforward neural networks. Knowl-Based Syst. 2018;143:192–207. doi: 10.1016/j.knosys.2017.12.017. [DOI] [Google Scholar]
- 261.Mostafaeipour A, Goli A, Qolipour M. Prediction of air travel demand using a hybrid artificial neural network (ANN) with bat and firefly algorithms: a case study. J Supercomput. 2018;74(10):5461–5484. doi: 10.1007/s11227-018-2452-0. [DOI] [Google Scholar]
- 262.Camci E, Kripalani DR, Ma L, Kayacan E, Khanesar MA. An aerial robot for rice farm quality inspection with type-2 fuzzy neural networks tuned by particle swarm optimization-sliding mode control hybrid algorithm. Swarm Evol Comput. 2018;41:1–8. doi: 10.1016/j.swevo.2017.10.003. [DOI] [Google Scholar]
- 263.Huang Y, Liu H (2018) Research on price forecasting method of China’s carbon trading market based on PSO-RBF algorithm. In: International conference on bio-inspired computing: theories and applications, pp. 1–11
- 264.Nayak SC, Misra BB. Estimating stock closing indices using a GA-weighted condensed polynomial neural network. Financ Innov. 2018;4(1):21. doi: 10.1186/s40854-018-0104-2. [DOI] [Google Scholar]
- 265.Agrawal S, Agrawal J, Kaur S, Sharma S. A comparative study of fuzzy PSO and fuzzy SVD-based RBF neural network for multi-label classification. Neural Comput Appl. 2018;29(1):245–256. doi: 10.1007/s00521-016-2446-x. [DOI] [Google Scholar]
- 266.Mao WL, Hung CW. Type-2 fuzzy neural network using grey wolf optimizer learning algorithm for nonlinear system identification. Microsyst Technol. 2018;24(10):4075–4088. doi: 10.1007/s00542-017-3636-x. [DOI] [Google Scholar]
- 267.Tian D, Deng J, Vinod G, Santhosh TV, Tawfik H. A constraint-based genetic algorithm for optimizing neural network architectures for detection of loss of coolant accidents of nuclear power plants. Neurocomputing. 2018;322:102–119. doi: 10.1016/j.neucom.2018.09.014. [DOI] [Google Scholar]
- 268.Tang R, Fong S, Deb S, Vasilakos AV, Millham RC. Dynamic group optimisation algorithm for training feed-forward neural networks. Neurocomputing. 2018;314:1–19. doi: 10.1016/j.neucom.2018.03.043. [DOI] [Google Scholar]
- 269.Xu F, Pun CM, Li H, Zhang Y, Song Y, Gao H. Training feed-forward artificial neural networks with a modified artificial bee colony algorithm. Neurocomputing. 2019 doi: 10.1016/j.neucom.2019.04.086. [DOI] [Google Scholar]
- 270.Karkheiran S, Kabiri-Samani A, Zekri M, Azamathulla HM. Scour at bridge piers in uniform and armored beds under steady and unsteady flow conditions using ANN-APSO and ANN-GA algorithms. ISH J Hydraul Eng. 2019;27:220–228. doi: 10.1080/09715010.2019.1617796. [DOI] [Google Scholar]
- 271.Ong P, Zainuddin Z. Optimizing wavelet neural networks using modified cuckoo search for multi-step ahead chaotic time series prediction. Appl Soft Comput. 2019;80:374–386. doi: 10.1016/j.asoc.2019.04.016. [DOI] [Google Scholar]
- 272.Harandizadeh H, Armaghani DJ, Khari M. A new development of ANFIS–GMDH optimized by PSO to predict pile bearing capacity based on experimental datasets. Eng Comput. 2019;37:685–700. doi: 10.1007/s00366-019-00849-3. [DOI] [Google Scholar]
- 273.Jiang Q, Huang R, Huang Y, Chen S, He Y, Lan L, Liu C. Application of BP neural network based on genetic algorithm optimization in evaluation of power grid investment risk. IEEE Access. 2019;7:154827–154835. doi: 10.1109/ACCESS.2019.2944609. [DOI] [Google Scholar]
- 274.Xu L, Wang H, Lin W, Gulliver TA, Le KN. GWO-BP neural network based OP performance prediction for mobile multiuser communication networks. IEEE Access. 2019;7:152690–152700. doi: 10.1109/ACCESS.2019.2948475. [DOI] [Google Scholar]
- 275.Djema MA, Boudour M, Agbossou K, Cardenas A, Doumbia ML. Adaptive direct power control based on ANN-GWO for grid interactive renewable energy systems with an improved synchronization technique. Int Trans Electr Energy Syst. 2019;29(3):e2766. doi: 10.1002/etep.2766. [DOI] [Google Scholar]
- 276.Li A, Yang X, Xie Z, Yang C. An optimized GRNN-enabled approach for power transformer fault diagnosis. IEEJ Trans Electr Electron Eng. 2019;14(8):1181–1188. doi: 10.1002/tee.22916. [DOI] [Google Scholar]
- 277.Zhao R, Wang Y, Hu P, Jelodar H, Yuan C, Li Y, Rabbani M. Selfish herds optimization algorithm with orthogonal design and information update for training multi-layer perceptron neural network. Appl Intell. 2019;49(6):2339–2381. doi: 10.1007/s10489-018-1373-1. [DOI] [Google Scholar]
- 278.Faris H, Mirjalili S, Aljarah I. Automatic selection of hidden neurons and weights in neural networks using grey wolf optimizer based on a hybrid encoding scheme. Int J Mach Learn Cybern. 2019;10(10):2901–2920. doi: 10.1007/s13042-018-00913-2. [DOI] [Google Scholar]
- 279.Bui QT. Metaheuristic algorithms in optimizing neural network: a comparative study for forest fire susceptibility mapping in Dak Nong, Vietnam. Geomat Nat Hazards Risk. 2019;10(1):136–150. doi: 10.1080/19475705.2018.1509902. [DOI] [Google Scholar]
- 280.Yu W, Zhao F. Prediction of critical properties of biodiesel fuels from FAMEs compositions using intelligent genetic algorithm-based back propagation neural network. Energy Sources Part A Recovery Util Environ Eff. 2019;43:2063–2076. doi: 10.1080/15567036.2019.1641575. [DOI] [Google Scholar]
- 281.Ma T, Wang C, Wang J, Cheng J, Chen X. Particle-swarm optimization of ensemble neural networks with negative correlation learning for forecasting short-term wind speed of wind farms in western China. Inf Sci. 2019;505:157–182. doi: 10.1016/j.ins.2019.07.074. [DOI] [Google Scholar]
- 282.Raval PD, Pandya AS. A hybrid PSO-ANN-based fault classification system for EHV transmission lines. IETE J Res. 2020;68:3086–3099. doi: 10.1080/03772063.2020.1754299. [DOI] [Google Scholar]
- 283.Kuntoji G, Rao M, Rao S. Prediction of wave transmission over submerged reef of tandem breakwater using PSO-SVM and PSO-ANN techniques. ISH J Hydraul Eng. 2020;26(3):283–290. doi: 10.1080/09715010.2018.1482796. [DOI] [Google Scholar]
- 284.da Silva Veloso YM, de Almeida MM, de Alsina OLS, Passos ML, Mujumdar AS, Leite MS. Hybrid phenomenological/ANN-PSO modelling of a deformable material in spouted bed drying process. Powder Technol. 2020;366:185–196. doi: 10.1016/j.powtec.2019.12.047. [DOI] [Google Scholar]
- 285.Yadav A, Satyannarayana P. Multi-objective genetic algorithm optimization of artificial neural network for estimating suspended sediment yield in Mahanadi River basin, India. Int J River Basin Manag. 2020;18(2):207–215. doi: 10.1080/15715124.2019.1705317. [DOI] [Google Scholar]
- 286.Wu S, Yang J, Zhang R, Ono H. Prediction of endpoint sulfur content in KR desulfurization based on the hybrid algorithm combining artificial neural network with SAPSO. IEEE Access. 2020;8:33778–33791. doi: 10.1109/ACCESS.2020.2971517. [DOI] [Google Scholar]
- 287.Shen T, Chang J, Liang Z. Swarm optimization improved BP algorithm for microchannel resistance factor. IEEE Access. 2020;8:52749–52758. doi: 10.1109/ACCESS.2020.2969526. [DOI] [Google Scholar]
- 288.Huang Y, Xiang Y, Zhao R, Cheng Z. Air quality prediction using improved PSO-BP neural network. IEEE Access. 2020 doi: 10.1109/ACCESS.2020.2998145. [DOI] [Google Scholar]
- 289.Shen X, Zheng Y, Zhang R. A hybrid forecasting model for the velocity of hybrid robotic fish based on back-propagation neural network with genetic algorithm optimization. IEEE Access. 2020;8:111731–111741. doi: 10.1109/ACCESS.2020.3002928. [DOI] [Google Scholar]
- 290.Ghanem WAH, Jantan A, Ghaleb SAA, Nasser AB. An efficient intrusion detection model based on hybridization of artificial bee colony and dragonfly algorithms for training multilayer perceptrons. IEEE Access. 2020;8:130452–130475. doi: 10.1109/ACCESS.2020.3009533. [DOI] [Google Scholar]
- 291.Gong S, Gao W, Abza F. Brain tumor diagnosis based on artificial neural network and a chaos whale optimization algorithm. Comput Intell. 2020;36(1):259–275. doi: 10.1111/coin.12259. [DOI] [Google Scholar]
- 292.Zeng XP, Luo Q, Zheng JL, Chen GH. An efficient neural network optimized by fruit fly optimization algorithm for user equipment association in software-defined wireless sensor network. Int J Netw Manag. 2020;30(6):e2135. doi: 10.1002/nem.2135. [DOI] [Google Scholar]
- 293.Supraja P, Babu S, Gayathri VM, Divya G. Hybrid genetic and shuffled frog-leaping algorithm for neural network structure optimization and learning model to predict free spectrum in cognitive radio. Int J Commun Syst. 2020;34:e4532. [Google Scholar]
- 294.Fang H, Fan H, Lin S, Qing Z, Sheykhahmad FR. Automatic breast cancer detection based on optimized neural network using whale optimization algorithm. Int J Imaging Syst Technol. 2020;31:425–438. doi: 10.1002/ima.22468. [DOI] [Google Scholar]
- 295.Zafar S, Nazir M, Sabah A, Jurcut AD. Securing bio-cyber interface for the internet of bio-nano things using particle swarm optimization and artificial neural networks based parameter profiling. Comput Biol Med. 2021;136:104707. doi: 10.1016/j.compbiomed.2021.104707. [DOI] [PubMed] [Google Scholar]
- 296.Darabi H, Haghighi AT, Rahmati O, Shahrood AJ, Rouzbeh S, Pradhan B, Bui DT. A hybridized model based on neural network and swarm intelligence-grey wolf algorithm for spatial prediction of urban flood-inundation. J Hydrol. 2021;603:126854. doi: 10.1016/j.jhydrol.2021.126854. [DOI] [Google Scholar]
- 297.Qiao W, Khishe M, Ravakhah S. Underwater targets classification using local wavelet acoustic pattern and multi-layer perceptron neural network optimized by modified Whale optimization algorithm. Ocean Eng. 2021;219:108415. doi: 10.1016/j.oceaneng.2020.108415. [DOI] [Google Scholar]
- 298.Zheng X, Nguyen H, Bui XN. Exploring the relation between production factors, ore grades, and life of mine for forecasting mining capital cost through a novel cascade forward neural network-based salp swarm optimization model. Resour Policy. 2021;74:102300. doi: 10.1016/j.resourpol.2021.102300. [DOI] [Google Scholar]
- 299.Bahiraei M, Foong LK, Hosseini S, Mazaheri N. Predicting heat transfer rate of a ribbed triple-tube heat exchanger working with nanofluid using neural network enhanced by advanced optimization algorithms. Powder Technol. 2021;381:459–476. doi: 10.1016/j.powtec.2020.12.003. [DOI] [Google Scholar]
- 300.Njock PGA, Shen SL, Zhou A, Modoni G. Artificial neural network optimized by differential evolution for predicting diameters of jet grouted columns. J Rock Mech Geotech Eng. 2021;13(6):1500–1512. doi: 10.1016/j.jrmge.2021.05.009. [DOI] [Google Scholar]
- 301.Khatir S, Tiachacht S, Le Thanh C, Ghandourah E, Mirjalili S, Wahab MA. An improved Artificial Neural Network using Arithmetic Optimization Algorithm for damage assessment in FGM composite plates. Compos Struct. 2021;273:114287. doi: 10.1016/j.compstruct.2021.114287. [DOI] [Google Scholar]
- 302.Yeganeh A, Shadman A. Using evolutionary artificial neural networks in monitoring binary and polytomous logistic profiles. J Manuf Syst. 2021;61:546–561. doi: 10.1016/j.jmsy.2021.10.007. [DOI] [Google Scholar]
- 303.Guo Y, Yang Z, Liu K, Zhang Y, Feng W. A compact and optimized neural network approach for battery state-of-charge estimation of energy storage system. Energy. 2021;219:119529. doi: 10.1016/j.energy.2020.119529. [DOI] [Google Scholar]
- 304.Korouzhdeh T, Eskandari-Naddaf H, Kazemi R. Hybrid artificial neural network with biogeography-based optimization to assess the role of cement fineness on ecological footprint and mechanical properties of cement mortar expose to freezing/thawing. Constr Build Mater. 2021;304:124589. doi: 10.1016/j.conbuildmat.2021.124589. [DOI] [Google Scholar]
- 305.Li B, Ding J, Yin Z, Li K, Zhao X, Zhang L. Optimized neural network combined model based on the induced ordered weighted averaging operator for vegetable price forecasting. Expert Syst Appl. 2021;168:114232. doi: 10.1016/j.eswa.2020.114232. [DOI] [Google Scholar]
- 306.Cui L, Tao Y, Deng J, Liu X, Xu D, Tang G. BBO-BPNN and AMPSO-BPNN for multiple-criteria inventory classification. Expert Syst Appl. 2021;175:114842. doi: 10.1016/j.eswa.2021.114842. [DOI] [Google Scholar]
- 307.Bai B, Zhang J, Wu X, wei Zhu G, Li X. Reliability prediction-based improved dynamic weight particle swarm optimization and back propagation neural network in engineering systems. Expert Syst Appl. 2021;177:114952. doi: 10.1016/j.eswa.2021.114952. [DOI] [Google Scholar]
- 308.Ghersi DE, Loubar K, Amoura M, Tazerout M. Multi-objective optimization of micro co-generation spark-ignition engine fueled by biogas with various CH4/CO2 content based on GA-ANN and decision-making approaches. J Clean Prod. 2021;329:129739. doi: 10.1016/j.jclepro.2021.129739. [DOI] [Google Scholar]
- 309.Luo Q, Li J, Zhou Y, Liao L. Using spotted hyena optimizer for training feedforward neural networks. Cogn Syst Res. 2021;65:1–16. doi: 10.1016/j.cogsys.2020.09.001. [DOI] [Google Scholar]
- 310.Fetimi A, Dâas A, Benguerba Y, Merouani S, Hamachi M, Kebiche-Senhadji O, Hamdaoui O. Optimization and prediction of safranin-O cationic dye removal from aqueous solution by emulsion liquid membrane (ELM) using artificial neural network-particle swarm optimization (ANN-PSO) hybrid model and response surface methodology (RSM) J Environ Chem Eng. 2021;9(5):105837. doi: 10.1016/j.jece.2021.105837. [DOI] [Google Scholar]
- 311.Yibre AM, Koçer B. Semen quality predictive model using feed forwarded neural network trained by learning-based artificial algae algorithm. Eng Sci Technol Int J. 2021;24(2):310–318. [Google Scholar]
- 312.Sun K, Zhao T, Li Z, Wang L, Wang R, Chen X, Yang Q, Ramezani E. Methodology for optimal parametrization of the polymer membrane fuel cell based on Elman neural network method and quantum water strider algorithm. Energy Rep. 2021;7:2625–2634. doi: 10.1016/j.egyr.2021.04.058. [DOI] [Google Scholar]
- 313.Sheelwant A, Jadhav PM, Narala SKR. ANN-GA based parametric optimization of Al-TiB2 metal matrix composite material processing technique. Mater Today Commun. 2021;27:102444. doi: 10.1016/j.mtcomm.2021.102444. [DOI] [Google Scholar]
- 314.Medi B, Asadbeigi A. Application of a GA-Optimized NNARX controller to nonlinear chemical and biochemical processes. Heliyon. 2021;7(8):e07846. doi: 10.1016/j.heliyon.2021.e07846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 315.Zhang P, Cui Z, Wang Y, Ding S. Application of BPNN optimized by chaotic adaptive gravity search and particle swarm optimization algorithms for fault diagnosis of electrical machine drive system. Electr Eng. 2022;104(2):819–831. doi: 10.1007/s00202-021-01335-0. [DOI] [Google Scholar]
- 316.Zhao J, Nguyen H, Nguyen-Thoi T, Asteris PG, Zhou J. Improved Levenberg–Marquardt backpropagation neural network by particle swarm and whale optimization algorithms to predict the deflection of RC beams. Eng Comput. 2021 doi: 10.1007/s00366-020-01267-6. [DOI] [Google Scholar]
- 317.García-Ródenas R, Linares LJ, López-Gómez JA. Memetic algorithms for training feedforward neural networks: an approach based on gravitational search algorithm. Neural Comput Appl. 2021;33(7):2561–2588. doi: 10.1007/s00521-020-05131-y. [DOI] [Google Scholar]
- 318.Uzlu E. Estimates of greenhouse gas emission in Turkey with grey wolf optimizer algorithm-optimized artificial neural networks. Neural Comput Appl. 2021;33(20):13567–13585. doi: 10.1007/s00521-021-05980-1. [DOI] [Google Scholar]
- 319.Saffari A, Khishe M, Zahiri, SH (2022) Fuzzy-ChOA: an improved chimp optimization algorithm for marine mammal classification using artificial neural network. Anal Integr Circuits Signal Process 111(3):403–417 [DOI] [PMC free article] [PubMed]
- 320.Liu XH, Zhang D, Zhang J, Zhang T, Zhu H. A path planning method based on the particle swarm optimization trained fuzzy neural network algorithm. Clust Comput. 2021;24(3):1901–1915. doi: 10.1007/s10586-021-03235-1. [DOI] [Google Scholar]
- 321.Bui XN, Nguyen H, Tran QH, Nguyen DA, Bui HB. Predicting ground vibrations due to mine blasting using a novel artificial neural network-based cuckoo search optimization. Nat Resour Res. 2021;30(3):2663–2685. doi: 10.1007/s11053-021-09823-7. [DOI] [Google Scholar]
- 322.Raei B, Ahmadi A, Neyshaburi MR, Ghorbani MA, Asadzadeh F. Comparative evaluation of the whale optimization algorithm and backpropagation for training neural networks to model soil wind erodibility. Arab J Geosci. 2021;14(1):1–19. doi: 10.1007/s12517-020-06328-0. [DOI] [Google Scholar]
- 323.Cui CY, Cui W, Liu SW, Ma B. An optimized neural network with a hybrid GA-ResNN training algorithm: applications in foundation pit. Arab J Geosci. 2021;14(22):1–12. doi: 10.1007/s12517-021-08775-9. [DOI] [Google Scholar]
- 324.Sağ T, Jalil AJ, Z. Vortex search optimization algorithm for training of feed-forward neural network. Int J Mach Learn Cybern. 2021;12(5):1517–1544. doi: 10.1007/s13042-020-01252-x. [DOI] [Google Scholar]
- 325.Wang T, Wang JB, Zhang XJ, Liu C. A study on prediction of process parameters of shot peen forming using artificial neural network optimized by genetic algorithm. Arab J Sci Eng. 2021;46(8):7349–7361. doi: 10.1007/s13369-021-05385-1. [DOI] [Google Scholar]
- 326.Wang C, Li M, Wang R, Yu H, Wang S. An image denoising method based on BP neural network optimized by improved whale optimization algorithm. EURASIP J Wirel Commun Netw. 2021;2021(1):1–22. doi: 10.1186/s13638-021-02013-2. [DOI] [Google Scholar]
- 327.Al Turki FA, Al Shammari MM. Predicting the output power of a photovoltaic module using an optimized offline cascade-forward neural network-based on genetic algorithm model. Technol Econ Smart Grids Sustain Energy. 2021;6(1):1–12. doi: 10.1007/s40866-021-00113-y. [DOI] [Google Scholar]
- 328.Eappen G, Shankar T, Nilavalan R. Advanced squirrel algorithm-trained neural network for efficient spectrum sensing in cognitive radio-based air traffic control application. IET Commun. 2021;15(10):1326–1351. doi: 10.1049/cmu2.12111. [DOI] [Google Scholar]
- 329.Bacanin N, Bezdan T, Venkatachalam K, Zivkovic M, Strumberger I, Abouhawwash M, Ahmed AB. Artificial neural networks hidden unit and weight connection optimization by quasi-refection-based learning artificial bee colony algorithm. IEEE Access. 2021;9:169135–169155. doi: 10.1109/ACCESS.2021.3135201. [DOI] [Google Scholar]
- 330.Liu J, Huang J, Sun R, Yu H, Xiao R. Data fusion for multi-source sensors using GA-PSO-BP neural network. IEEE Trans Intell Transp Syst. 2020;22(10):6583–6598. doi: 10.1109/TITS.2020.3010296. [DOI] [Google Scholar]
- 331.Nguyen HX, Cao HQ, Nguyen TT, Tran TNC, Tran HN, Jeon JW. Improving robot precision positioning using a neural network based on Levenberg Marquardt–APSO algorithm. IEEE Access. 2021;9:75415–75425. doi: 10.1109/ACCESS.2021.3082534. [DOI] [Google Scholar]
- 332.Ge L, Xian Y, Wang Z, Gao B, Chi F, Sun K. Short-term load forecasting of regional distribution network based on generalized regression neural network optimized by grey wolf optimization algorithm. CSEE J Power Energy Syst. 2020;7(5):1093–1101. [Google Scholar]
- 333.Kaur S, Chahal KK. Prediction of Chikungunya disease using PSO-based adaptive neuro-fuzzy inference system model. Int J Comput Appl. 2021;44:641–649. [Google Scholar]
- 334.Zhang L, Gao T, Cai G, Hai KL. Research on electric vehicle charging safety warning model based on back propagation neural network optimized by improved gray wolf algorithm. J Energy Storage. 2022;49:104092. doi: 10.1016/j.est.2022.104092. [DOI] [Google Scholar]
- 335.Guo Z, Zhang L, Chen Q, Han M, Liu W. Monophenolase assay using excitation-emission matrix fluorescence and ELMAN neural network assisted by whale optimization algorithm. Anal Biochem. 2022;655:114838. doi: 10.1016/j.ab.2022.114838. [DOI] [PubMed] [Google Scholar]
- 336.Xue Y, Tong Y, Neri F. An ensemble of differential evolution and Adam for training feed-forward neural networks. Inf Sci. 2022;608:453–471. doi: 10.1016/j.ins.2022.06.036. [DOI] [Google Scholar]
- 337.Ding Z, Li J, Hao H. Simultaneous identification of structural damage and nonlinear hysteresis parameters by an evolutionary algorithm-based artificial neural network. Int J Non-Linear Mech. 2022;142:103970. doi: 10.1016/j.ijnonlinmec.2022.103970. [DOI] [Google Scholar]
- 338.Zhu K, Shi H, Han M, Cao F. Layout study of wave energy converter arrays by an artificial neural network and adaptive genetic algorithm. Ocean Eng. 2022;260:112072. doi: 10.1016/j.oceaneng.2022.112072. [DOI] [Google Scholar]
- 339.Jnr EON, Ziggah YY, Rodrigues MJ, Relvas S. A hybrid chaotic-based discrete wavelet transform and Aquila optimisation tuned-artificial neural network approach for wind speed prediction. Results Eng. 2022;14:100399. doi: 10.1016/j.rineng.2022.100399. [DOI] [Google Scholar]
- 340.Zhao Y, Hu H, Song C, Wang Z. Predicting compressive strength of manufactured-sand concrete using conventional and metaheuristic-tuned artificial neural network. Measurement. 2022;194:110993. doi: 10.1016/j.measurement.2022.110993. [DOI] [Google Scholar]
- 341.Wu C, Wang C, Kim JW. Welding sequence optimization to reduce welding distortion based on coupled artificial neural network and swarm intelligence algorithm. Eng Appl Artif Intell. 2022;114:105142. doi: 10.1016/j.engappai.2022.105142. [DOI] [Google Scholar]
- 342.Si T, Bagchi J, Miranda PB. Artificial neural network training using metaheuristics for medical data classification: an experimental study. Expert Syst Appl. 2022;193:116423. doi: 10.1016/j.eswa.2021.116423. [DOI] [Google Scholar]
- 343.Khan A, Bukhari J, Bangash JI, Khan A, Imran M, Asim M, Khan A (2020) Optimizing connection weights of functional link neural network using APSO algorithm for medical data classification. J King Saud Univ-Comput Inf Sci 34(6):2551–2561
- 344.Gülcü Ş. Training of the feed forward artificial neural networks using dragonfly algorithm. Appl Soft Comput. 2022;124:109023. doi: 10.1016/j.asoc.2022.109023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 345.Netsanet S, Zheng D, Zhang W, Teshager G (2022) Short-term PV power forecasting using variational mode decomposition integrated with Ant colony optimization and neural network. Energy Rep 8:2022–2035
- 346.Liang R, Le-Hung T, Nguyen-Thoi T. Energy consumption prediction of air-conditioning systems in eco-buildings using hunger games search optimization-based artificial neural network model. J Build Eng. 2022;59:105087. doi: 10.1016/j.jobe.2022.105087. [DOI] [Google Scholar]
- 347.Chondrodima E, Georgiou H, Pelekis N, Theodoridis Y. Particle swarm optimization and RBF neural networks for public transport arrival time prediction using GTFS data. Int J Inf Manag Data Insights. 2022;2(2):100086. [Google Scholar]
- 348.Ehteram M, Panahi F, Ahmed AN, Huang YF, Kumar P, Elshafie A. Predicting evaporation with optimized artificial neural network using multi-objective salp swarm algorithm. Environ Sci Pollut Res. 2022;29(7):10675–10701. doi: 10.1007/s11356-021-16301-3. [DOI] [PubMed] [Google Scholar]
- 349.Li Z, Zhu B, Dai Y, Zhu W, Wang Q, Wang B. Thermal error modeling of motorized spindle based on Elman neural network optimized by sparrow search algorithm. Int J Adv Manuf Technol. 2022;121:349–366. doi: 10.1007/s00170-022-09260-7. [DOI] [Google Scholar]
- 350.Ibad T, Abdulkadir SJ, Aziz N, Ragab MG, Al-Tashi Q. Hyperparameter optimization of evolving spiking neural network for time-series classification. N Gener Comput. 2022;40(1):377–397. doi: 10.1007/s00354-022-00165-3. [DOI] [Google Scholar]
- 351.Foong LK, Moayedi H. Slope stability evaluation using neural network optimized by equilibrium optimization and vortex search algorithm. Eng Comput. 2022;38(2):1269–1283. doi: 10.1007/s00366-021-01282-1. [DOI] [Google Scholar]
- 352.Chatterjee R, Mukherjee R, Roy PK, Pradhan DK. Chaotic oppositional-based whale optimization to train a feed forward neural network. Soft Comput. 2022 doi: 10.1007/s00500-022-07141-5. [DOI] [Google Scholar]
- 353.He Z, Nguyen H, Vu TH, Zhou J, Asteris PG, Mammou A. Novel integrated approaches for predicting the compressibility of clay using cascade forward neural networks optimized by swarm-and evolution-based algorithms. Acta Geotech. 2022;17(4):1257–1272. doi: 10.1007/s11440-021-01358-8. [DOI] [Google Scholar]
- 354.Gülcü Ş. An improved animal migration optimization algorithm to train the feed-forward artificial neural networks. Arab J Sci Eng. 2021;47:9557–9581. doi: 10.1007/s13369-021-06286-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 355.Liu G, Miao J, Zhao X, Wang Z, Li X. Life prediction of residual current circuit breaker with overcurrent protection based on BP neural network optimized by genetic algorithm. J Electr Eng Technol. 2022;17(3):2003–2014. doi: 10.1007/s42835-022-01011-8. [DOI] [Google Scholar]
- 356.Al Bataineh A, Kaur D, Jalali SMJ. Multi-layer perceptron training optimization using nature inspired computing. IEEE Access. 2022;10:36963–36977. doi: 10.1109/ACCESS.2022.3164669. [DOI] [Google Scholar]
- 357.Han HG, Sun C, Wu X, Yang H, Qiao J. Training fuzzy neural network via multi-objective optimization for nonlinear systems identification. IEEE Trans Fuzzy Syst. 2021;30:3574–3588. doi: 10.1109/TFUZZ.2021.3119108. [DOI] [Google Scholar]
- 358.Deepika D, Balaji N. Effective heart disease prediction with Grey-wolf with Firefly algorithm-differential evolution (GF-DE) for feature selection and weighted ANN classification. Comput Methods Biomech Biomed Eng. 2022 doi: 10.1080/10255842.2022.2078966. [DOI] [PubMed] [Google Scholar]
- 359.Kirankaya C, Aykut LG (2022) Training of artificial neural networks with the multi-population based artifical bee colony algorithm. Netw Comput Neural Syst 33(1):124–142 [DOI] [PubMed]
- 360.Yan Z, Zhu X, Wang X, Ye Z, Guo F, Xie L, Zhang G (2022) A multi-energy load prediction of a building using the multi-layer perceptron neural network method with different optimization algorithms. Energy Explor Exploit 40(4):1101–1312
- 361.Li Z, Piao W, Wang L, Wang X, Fu R, Fang Y. China coastal bulk (Coal) freight index forecasting based on an integrated model combining ARMA, GM and BP model optimized by GA. Electronics. 2022;11(17):2732. doi: 10.3390/electronics11172732. [DOI] [Google Scholar]
- 362.Kuo CL, Kuruoglu EE, Chan WKV. Neural network structure optimization by simulated annealing. Entropy. 2022;24(3):348. doi: 10.3390/e24030348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 363.Zhao G, Wang M, Liang W. A comparative study of SSA-BPNN, SSA-ENN, and SSA-SVR models for predicting the thickness of an excavation damaged zone around the roadway in rock. Mathematics. 2022;10(8):1351. doi: 10.3390/math10081351. [DOI] [Google Scholar]
- 364.Davar S, Nobahar M, Khan MS, Amini F. The development of PSO-ANN and BOA-ANN models for predicting matric suction in expansive clay soil. Mathematics. 2022;10(16):2825. doi: 10.3390/math10162825. [DOI] [Google Scholar]
- 365.Huang L, Jiang L, Zhao L, Ding X. Temperature compensation method based on an improved firefly algorithm optimized backpropagation neural network for micromachined silicon resonant accelerometers. Micromachines. 2022;13(7):1054. doi: 10.3390/mi13071054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 366.Wang G, Feng D, Tang W. Electrical impedance tomography based on grey wolf optimized radial basis function neural network. Micromachines. 2022;13(7):1120. doi: 10.3390/mi13071120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 367.Ku KWC, Mak MW, Siu WC. Adding learning to cellular genetic algorithms for training recurrent neural networks. IEEE Trans Neural Netw. 1999;10(2):239–252. doi: 10.1109/72.750546. [DOI] [PubMed] [Google Scholar]
- 368.Blanco A, Delgado M, Pegalajar MC. A real-coded genetic algorithm for training recurrent neural networks. Neural Netw. 2001;14(1):93–105. doi: 10.1016/S0893-6080(00)00081-2. [DOI] [PubMed] [Google Scholar]
- 369.Delgado M, Cuellar MP, Pegalajar MC. Multiobjective hybrid optimization and training of recurrent neural networks. IEEE Trans Syst Man Cybern Part B (Cybern) 2008;38(2):381–403. doi: 10.1109/TSMCB.2007.912937. [DOI] [PubMed] [Google Scholar]
- 370.Bayer J, Wierstra D, Togelius J, Schmidhuber J (2009) Evolving memory cell structures for sequence learning. In: International conference on artificial neural networks, pp. 755–764
- 371.Lin CJ, Lee CY. Non-linear system control using a recurrent fuzzy neural network based on improved particle swarm optimisation. Int J Syst Sci. 2010;41(4):381–395. doi: 10.1080/00207720903045783. [DOI] [Google Scholar]
- 372.Subrahmanya N, Shin YC. Constructive training of recurrent neural networks using hybrid optimization. Neurocomputing. 2010;73(13–15):2624–2631. doi: 10.1016/j.neucom.2010.05.012. [DOI] [Google Scholar]
- 373.Hsieh TJ, Hsiao HF, Yeh WC. Forecasting stock markets using wavelet transforms and recurrent neural networks: an integrated system based on artificial bee colony algorithm. Appl Soft Comput. 2011;11(2):2510–2525. doi: 10.1016/j.asoc.2010.09.007. [DOI] [Google Scholar]
- 374.Sheikhan M, Abbasnezhad Arabi M, Gharavian D. Structure and weights optimisation of a modified Elman network emotion classifier using hybrid computational intelligence algorithms: a comparative study. Connect Sci. 2015;27(4):340–357. doi: 10.1080/09540091.2015.1080224. [DOI] [Google Scholar]
- 375.Chen S, Liu G, Wu C, Jiang Z, Chen J (2016) Image classification with stacked restricted boltzmann machines and evolutionary function array classification voter. In: 2016 IEEE congress on evolutionary computation (CEC), pp. 4599–4606
- 376.Real E, Moore S, Selle A, Saxena S, Suematsu YL, Tan J, Kurakin A (2017) Large-scale evolution of image classifiers. arXiv preprint arXiv:1703.01041
- 377.Tang X, Zhang N, Zhou J, Liu Q. Hidden-layer visible deep stacking network optimized by PSO for motor imagery EEG recognition. Neurocomputing. 2017;234:1–10. doi: 10.1016/j.neucom.2016.12.039. [DOI] [Google Scholar]
- 378.Song Q, Zheng YJ, Xue Y, Sheng WG, Zhao MR. An evolutionary deep neural network for predicting morbidity of gastrointestinal infections by food contamination. Neurocomputing. 2017;226:16–22. doi: 10.1016/j.neucom.2016.11.018. [DOI] [Google Scholar]
- 379.da Silva GLF, Valente TLA, Silva AC, de Paiva AC, Gattass M. Convolutional neural network-based PSO for lung nodule false positive reduction on CT images. Comput Methods Programs Biomed. 2018;162:109–118. doi: 10.1016/j.cmpb.2018.05.006. [DOI] [PubMed] [Google Scholar]
- 380.Zhou XH, Zhang MX, Xu ZG, Cai CY, Huang YJ, Zheng YJ. Shallow and deep neural network training by water wave optimization. Swarm Evol Comput. 2019;50:100561. doi: 10.1016/j.swevo.2019.100561. [DOI] [Google Scholar]
- 381.Shi W, Liu D, Cheng X, Li Y, Zhao Y. Particle swarm optimization-based deep neural network for digital modulation recognition. IEEE Access. 2019;7:104591–104600. doi: 10.1109/ACCESS.2019.2932266. [DOI] [Google Scholar]
- 382.Hong YY, Taylar JV, Fajardo AC. Locational marginal price forecasting using deep learning network optimized by mapping-based genetic algorithm. IEEE Access. 2020;8:91975–91988. doi: 10.1109/ACCESS.2020.2994444. [DOI] [Google Scholar]
- 383.Guo Y, Li JY, Zhan ZH. Efficient hyperparameter optimization for convolution neural networks in deep learning: a distributed particle swarm optimization approach. Cybern Syst. 2020;52:36–57. doi: 10.1080/01969722.2020.1827797. [DOI] [Google Scholar]
- 384.ZahediNasab R, Mohseni H. Neuroevolutionary based convolutional neural network with adaptive activation functions. Neurocomputing. 2020;381:306–313. doi: 10.1016/j.neucom.2019.11.090. [DOI] [Google Scholar]
- 385.Jallal MA, Chabaa S, Zeroual A. A novel deep neural network based on randomly occurring distributed delayed PSO algorithm for monitoring the energy produced by four dual-axis solar trackers. Renew Energy. 2020;149:1182–1196. doi: 10.1016/j.renene.2019.10.117. [DOI] [Google Scholar]
- 386.Elmasry W, Akbulut A, Zaim AH. Evolving deep learning architectures for network intrusion detection using a double PSO metaheuristic. Comput Netw. 2020;168:107042. doi: 10.1016/j.comnet.2019.107042. [DOI] [Google Scholar]
- 387.Kan X, Fan Y, Fang Z, Cao L, Xiong NN, Yang D, Li X. A novel IoT network intrusion detection approach based on adaptive particle swarm optimization convolutional neural network. Inf Sci. 2021;568:147–162. doi: 10.1016/j.ins.2021.03.060. [DOI] [Google Scholar]
- 388.Kanna PR, Santhi P. Hybrid intrusion detection using mapreduce based black widow optimized convolutional long short-term memory neural networks. Expert Syst Appl. 2022;194:116545. doi: 10.1016/j.eswa.2022.116545. [DOI] [Google Scholar]
- 389.Ragab M, Choudhry H, HA Asseri, Binyamin SS, Al-Rabia MW (2022) Enhanced gravitational search optimization with hybrid deep learning model for COVID-19 diagnosis on epidemiology data. In: Healthcare (Vol. 10, No. 7, p. 1339). MDPI [DOI] [PMC free article] [PubMed]
- 390.Cheung B, Sable C (2011) Hybrid evolution of convolutional networks. In: 2011 10th international conference on machine learning and applications and workshops, vol. 1, pp. 293–297
- 391.Desell T, Clachar S, Higgins J, Wild B (2015) Evolving deep recurrent neural networks using ant colony optimization. In: European conference on evolutionary computation in combinatorial optimization, pp. 86–98. Springer, Cham
- 392.Papa JP, Scheirer W, Cox DD. Fine-tuning deep belief networks using harmony search. Appl Soft Comput. 2016;46:875–885. doi: 10.1016/j.asoc.2015.08.043. [DOI] [Google Scholar]
- 393.Zhang C, Lim P, Qin AK, Tan KC. Multiobjective deep belief networks ensemble for remaining useful life estimation in prognostics. IEEE Trans Neural Netw Learn Syst. 2016;28(10):2306–2318. doi: 10.1109/TNNLS.2016.2582798. [DOI] [PubMed] [Google Scholar]
- 394.Badem H, Basturk A, Caliskan A, Yuksel ME. A new efficient training strategy for deep neural networks by hybridization of artificial bee colony and limited–memory BFGS optimization algorithms. Neurocomputing. 2017;266:506–526. doi: 10.1016/j.neucom.2017.05.061. [DOI] [Google Scholar]
- 395.Gelly G, Gauvain JL. Optimization of RNN-based speech activity detection. IEEE/ACM Trans Audio Speech Lang Process. 2017;26(3):646–656. doi: 10.1109/TASLP.2017.2769220. [DOI] [Google Scholar]
- 396.Liu J, Gong M, Miao Q, Wang X, Li H. Structure learning for deep neural networks based on multiobjective optimization. IEEE Trans Neural Netw Learn Syst. 2017;29(6):2450–2463. doi: 10.1109/TNNLS.2017.2695223. [DOI] [PubMed] [Google Scholar]
- 397.ElSaid A, Wild B, Jamiy FE, Higgins J, Desell T (2017) Optimizing LSTM RNNs using ACO to predict turbine engine vibration. In: Proceedings of the genetic and evolutionary computation conference companion, pp. 21–22
- 398.Kim JK, Han YS, Lee JS. Particle swarm optimization–deep belief network–based rare class prediction model for highly class imbalance problem. Concurr Comput Pract Exp. 2017;29(11):e4128. doi: 10.1002/cpe.4128. [DOI] [Google Scholar]
- 399.Fujino S, Mori N, Matsumoto K (2017) Deep convolutional networks for human sketches by means of the evolutionary deep learning. In: 2017 joint 17th world congress of international fuzzy systems association and 9th international conference on soft computing and intelligent systems (IFSA-SCIS), pp. 1–5
- 400.Lorenzo PR, Nalepa J, Kawulok M, Ramos LS, Pastor JR (2017) Particle swarm optimization for hyper-parameter selection in deep neural networks. In: Proceedings of the genetic and evolutionary computation conference, pp. 481–488
- 401.Chen J, Zeng GQ, Zhou W, Du W, Lu KD. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers Manag. 2018;165:681–695. doi: 10.1016/j.enconman.2018.03.098. [DOI] [Google Scholar]
- 402.Passos LA, Rodrigues DR, Papa JP (2018) Fine tuning deep boltzmann machines through meta-heuristic approaches. In: 2018 IEEE 12th international symposium on applied computational intelligence and informatics (SACI). IEEE, pp. 000419–000424
- 403.Soon FC, Khaw HY, Chuah JH, Kanesan J. Hyper-parameters optimisation of deep CNN architecture for vehicle logo recognition. IET Intel Transp Syst. 2018;12(8):939–946. doi: 10.1049/iet-its.2018.5127. [DOI] [Google Scholar]
- 404.ElSaid A, El Jamiy F, Higgins J, Wild B, Desell T. Optimizing long short-term memory recurrent neural networks using ant colony optimization to predict turbine engine vibration. Appl Soft Comput. 2018;73:969–991. doi: 10.1016/j.asoc.2018.09.013. [DOI] [Google Scholar]
- 405.Lorenzo PR, Nalepa J (2018) Memetic evolution of deep neural networks. In: Proceedings of the genetic and evolutionary computation conference, pp. 505–512
- 406.Pawełczyk K, Kawulok M, Nalepa J (2018) Genetically-trained deep neural networks. In: Proceedings of the genetic and evolutionary computation conference companion, pp. 63–64.
- 407.Fielding B, Zhang L. Evolving image classification architectures with enhanced particle swarm optimisation. IEEE Access. 2018;6:68560–68575. doi: 10.1109/ACCESS.2018.2880416. [DOI] [Google Scholar]
- 408.Sun Y, Yen GG, Yi Z. Evolving unsupervised deep neural networks for learning meaningful representations. IEEE Trans Evol Comput. 2018;23(1):89–103. doi: 10.1109/TEVC.2018.2808689. [DOI] [Google Scholar]
- 409.Liang J, Meyerson E, Miikkulainen R (2018) Evolutionary architecture search for deep multitask networks. In: Proceedings of the genetic and evolutionary computation conference, pp. 466–473.
- 410.Khodabandehlou H, Fadali MS. Training recurrent neural networks via dynamical trajectory-based optimization. Neurocomputing. 2019;368:1–10. doi: 10.1016/j.neucom.2019.08.058. [DOI] [Google Scholar]
- 411.Gao Y, Li Q. A segmented particle swarm optimization convolutional neural network for land cover and land use classification of remote sensing images. Remote Sens Lett. 2019;10(12):1182–1191. doi: 10.1080/2150704X.2019.1671633. [DOI] [Google Scholar]
- 412.Fujino S, Hatanaka T, Mori N, Matsumoto K. Evolutionary deep learning based on deep convolutional neural network for anime storyboard recognition. Neurocomputing. 2019;338:393–398. doi: 10.1016/j.neucom.2018.05.124. [DOI] [Google Scholar]
- 413.Li Y, Xiao J, Chen Y, Jiao L. Evolving deep convolutional neural networks by quantum behaved particle swarm optimization with binary encoding for image classification. Neurocomputing. 2019;362:156–165. doi: 10.1016/j.neucom.2019.07.026. [DOI] [Google Scholar]
- 414.Li L, Qin L, Qu X, Zhang J, Wang Y, Ran B. Day-ahead traffic flow forecasting based on a deep belief network optimized by the multi-objective particle swarm algorithm. Knowl-Based Syst. 2019;172:1–14. doi: 10.1016/j.knosys.2019.01.015. [DOI] [Google Scholar]
- 415.Nepomuceno EG. A novel method for structure selection of the recurrent random neural network using multiobjective optimisation. Appl Soft Comput. 2019;76:607–614. doi: 10.1016/j.asoc.2018.10.055. [DOI] [Google Scholar]
- 416.Wei P, Li Y, Zhang Z, Hu T, Li Z, Liu D. An optimization method for intrusion detection classification model based on deep belief network. IEEE Access. 2019;7:87593–87605. doi: 10.1109/ACCESS.2019.2925828. [DOI] [Google Scholar]
- 417.Junior FEF, Yen GG. Particle swarm optimization of deep neural networks architectures for image classification. Swarm Evol Comput. 2019;49:62–74. doi: 10.1016/j.swevo.2019.05.010. [DOI] [Google Scholar]
- 418.Navaneeth B, Suchetha M. PSO optimized 1-D CNN-SVM architecture for real-time detection and classification applications. Comput Biol Med. 2019;108:85–92. doi: 10.1016/j.compbiomed.2019.03.017. [DOI] [PubMed] [Google Scholar]
- 419.Goel T, Murugan R, Mirjalili S, Chakrabartty DK. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl Intell. 2020;51:1351–1366. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 420.Gao Z, Li Y, Yang Y, Wang X, Dong N, Chiang HD. A GPSO-optimized convolutional neural networks for EEG-based emotion recognition. Neurocomputing. 2020;380:225–235. doi: 10.1016/j.neucom.2019.10.096. [DOI] [Google Scholar]
- 421.Martín A, Vargas VM, Gutiérrez PA, Camacho D, Hervás-Martínez C. Optimising convolutional neural networks using a hybrid statistically-driven coral reef optimisation algorithm. Appl Soft Comput. 2020;90:106–144. doi: 10.1016/j.asoc.2020.106144. [DOI] [Google Scholar]
- 422.Tang J, Zeng J, Wang Y, Yuan H, Liu F, Huang H. Traffic flow prediction on urban road network based on license plate recognition data: combining attention-LSTM with genetic algorithm. Transp Transp Sci. 2020;17:1217–1243. [Google Scholar]
- 423.Lima LL, Ferreira Junior JR, Oliveira MC. Toward classifying small lung nodules with hyperparameter optimization of convolutional neural networks. Comput Intell. 2020;37:1599–1618. doi: 10.1111/coin.12350. [DOI] [Google Scholar]
- 424.Renukadevi T, Karunakaran S. Optimizing deep belief network parameters using grasshopper algorithm for liver disease classification. Int J Imaging Syst Technol. 2020;30(1):168–184. doi: 10.1002/ima.22375. [DOI] [Google Scholar]
- 425.Ali SA, Raza B, Malik AK, Shahid AR, Faheem M, Alquhayz H, Kumar YJ. An optimally configured and improved deep belief network (OCI-DBN) approach for heart disease prediction based on ruzzo-tompa and stacked genetic algorithm. IEEE Access. 2020;8:65947–65958. doi: 10.1109/ACCESS.2020.2985646. [DOI] [Google Scholar]
- 426.Rajagopal A, Joshi GP, Ramachandran A, Subhalakshmi RT, Khari M, Jha S, Shankar K, You J. A deep learning model based on multi-objective particle swarm optimization for scene classification in unmanned aerial vehicles. IEEE Access. 2020;8:135383–135393. doi: 10.1109/ACCESS.2020.3011502. [DOI] [Google Scholar]
- 427.Lu Z, Whalen I, Dhebar Y, Deb K, Goodman E, Banzhaf W, Boddeti VN. Multi-objective evolutionary design of deep convolutional neural networks for image classification. IEEE Trans Evol Comput. 2020;25:277–291. doi: 10.1109/TEVC.2020.3024708. [DOI] [Google Scholar]
- 428.Lin Y, Chen C, Xiao F, Avatefipour O, Alsubhi K, Yunianta A. An evolutionary deep learning anomaly detection framework for in-vehicle networks-CAN bus. IEEE Trans Ind Appl. 2020 doi: 10.1109/TIA.2020.3009906. [DOI] [Google Scholar]
- 429.Kavousi-Fard A, Dabbaghjamanesh M, Jin T, Su W, Roustaei M. An evolutionary deep learning-based anomaly detection model for securing vehicles. IEEE Trans Intell Transp Syst. 2020;22:4478–4486. doi: 10.1109/TITS.2020.3015143. [DOI] [Google Scholar]
- 430.Johnson F, Valderrama A, Valle C, Crawford B, Soto R, Ñanculef R. Automating configuration of convolutional neural network hyperparameters using genetic algorithm. IEEE Access. 2020;8:156139–156152. doi: 10.1109/ACCESS.2020.3019245. [DOI] [Google Scholar]
- 431.Zheng Y, Fu H, Li R, Hsung TC, Song Z, Wen D. Deep neural network oriented evolutionary parametric eye modeling. Pattern Recogn. 2021;113:107755. doi: 10.1016/j.patcog.2020.107755. [DOI] [Google Scholar]
- 432.Pang L, Wang L, Yuan P, Yan L, Yang Q, Xiao J. Feasibility study on identifying seed viability of Sophora japonica with optimized deep neural network and hyperspectral imaging. Comput Electron Agric. 2021;190:106426. doi: 10.1016/j.compag.2021.106426. [DOI] [Google Scholar]
- 433.Gai J, Zhong K, Du X, Yan K, Shen J. Detection of gear fault severity based on parameter-optimized deep belief network using sparrow search algorithm. Measurement. 2021;185:110079. doi: 10.1016/j.measurement.2021.110079. [DOI] [Google Scholar]
- 434.Sun X, Wang G, Xu L, Yuan H, Yousefi N. Optimal estimation of the PEM fuel cells applying deep belief network optimized by improved archimedes optimization algorithm. Energy. 2021;237:121532. doi: 10.1016/j.energy.2021.121532. [DOI] [Google Scholar]
- 435.Samir AA, Rashwan AR, Sallam KM, Chakrabortty RK, Ryan MJ, Abohany AA. Evolutionary algorithm-based convolutional neural network for predicting heart diseases. Comput Ind Eng. 2021;161:107651. doi: 10.1016/j.cie.2021.107651. [DOI] [Google Scholar]
- 436.Liu D, Ding W, Dong ZS, Pedrycz W. Optimizing deep neural networks to predict the effect of social distancing on COVID-19 spread. Comput Ind Eng. 2022;166:107970. doi: 10.1016/j.cie.2022.107970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 437.Mao WL, Chen WC, Wang CT, Lin YH. Recycling waste classification using optimized convolutional neural network. Resour Conserv Recycl. 2021;164:105132. doi: 10.1016/j.resconrec.2020.105132. [DOI] [Google Scholar]
- 438.Kim TY, Cho SB. Optimizing CNN-LSTM neural networks with PSO for anomalous query access control. Neurocomputing. 2021;456:666–677. doi: 10.1016/j.neucom.2020.07.154. [DOI] [Google Scholar]
- 439.Zhang L, Lim CP, Yu Y. Intelligent human action recognition using an ensemble model of evolving deep networks with swarm-based optimization. Knowl-Based Syst. 2021;220:106918. doi: 10.1016/j.knosys.2021.106918. [DOI] [Google Scholar]
- 440.Li C, Yin C, Xu X. Hybrid optimization assisted deep convolutional neural network for hardening prediction in steel. J King Saud Univ-Sci. 2021;33(6):101453. doi: 10.1016/j.jksus.2021.101453. [DOI] [Google Scholar]
- 441.Mohakud R, Dash R (2022) Skin cancer image segmentation utilizing a novel EN-GWO based hyper-parameter optimized FCEDN. J King Saud Univ-Comput Inf Sci 34:6505–7840
- 442.Altan A, Karasu S, Zio E. A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl Soft Comput. 2021;100:106996. doi: 10.1016/j.asoc.2020.106996. [DOI] [Google Scholar]
- 443.Roder M, Passos LA, de Rosa GH, de Albuquerque VHC, Papa JP. Reinforcing learning in deep belief networks through nature-inspired optimization. Appl Soft Comput. 2021;108:107466. doi: 10.1016/j.asoc.2021.107466. [DOI] [Google Scholar]
- 444.Mathe M, Padmaja M, Krishna BT. Intelligent approach for artifacts removal from EEG signal using heuristic-based convolutional neural network. Biomed Signal Process Control. 2021;70:102935. doi: 10.1016/j.bspc.2021.102935. [DOI] [Google Scholar]
- 445.Mahesh DB, Murty GS, Lakshmi DR. Optimized local weber and gradient pattern-based medical image retrieval and optimized convolutional neural network-based classification. Biomed Signal Process Control. 2021;70:102971. doi: 10.1016/j.bspc.2021.102971. [DOI] [Google Scholar]
- 446.Singh P, Chaudhury S, Panigrahi BK. Hybrid MPSO-CNN: Multi-level particle swarm optimized hyperparameters of convolutional neural network. Swarm Evol Comput. 2021;63:100863. doi: 10.1016/j.swevo.2021.100863. [DOI] [Google Scholar]
- 447.Kumar K, Haider M, Uddin T. Enhanced prediction of intra-day stock market using metaheuristic optimization on RNN–LSTM network. N Gener Comput. 2021;39(1):231–272. doi: 10.1007/s00354-020-00104-0. [DOI] [Google Scholar]
- 448.Kumar P, Batra S, Raman B. Deep neural network hyper-parameter tuning through twofold genetic approach. Soft Comput. 2021;25(13):8747–8771. doi: 10.1007/s00500-021-05770-w. [DOI] [Google Scholar]
- 449.Chitra B, Kumar SS. An optimized deep learning model using mutation-based atom search optimization algorithm for cervical cancer detection. Soft Comput. 2021;25(24):15363–15376. doi: 10.1007/s00500-021-06138-w. [DOI] [Google Scholar]
- 450.Deighan DS, Field SE, Capano CD, Khanna G. Genetic-algorithm-optimized neural networks for gravitational wave classification. Neural Comput Appl. 2021;33(20):13859–13883. doi: 10.1007/s00521-021-06024-4. [DOI] [Google Scholar]
- 451.Qu J, Liu F, Ma Y. A dual encoder DAE neural network for imbalanced binary classification based on NSGA-III and GAN. Pattern Anal Appl. 2022;25(1):17–34. doi: 10.1007/s10044-021-01035-2. [DOI] [Google Scholar]
- 452.Goel T, Murugan R, Mirjalili S, Chakrabartty DK. OptCoNet: an optimized convolutional neural network for an automatic diagnosis of COVID-19. Appl Intell. 2021;51(3):1351–1366. doi: 10.1007/s10489-020-01904-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 453.Liu B, Nie L. Gradient based invasive weed optimization algorithm for the training of deep neural network. Multimed Tools Appl. 2021;80(15):22795–22819. doi: 10.1007/s11042-020-10495-3. [DOI] [Google Scholar]
- 454.Kumar R, Kumar P, Kumar Y. Integrating big data driven sentiments polarity and ABC-optimized LSTM for time series forecasting. Multimed Tools Appl. 2021 doi: 10.1007/s11042-020-08904-8. [DOI] [Google Scholar]
- 455.Das D, Das AK, Pal AR, Jaypuria S, Pratihar DK, Roy GG. Meta-heuristic algorithms-tuned Elman vs. Jordan recurrent neural networks for modeling of electron beam welding process. Neural Process Lett. 2021;53(2):1647–1663. doi: 10.1007/s11063-021-10471-4. [DOI] [Google Scholar]
- 456.Gong C, Wang X, Gani A, Qi H. Enhanced long short-term memory with fireworks algorithm and mutation operator. J Supercomput. 2021;77(11):12630–12646. doi: 10.1007/s11227-021-03679-7. [DOI] [Google Scholar]
- 457.Chen Z, Yang C, Qiao J. The optimal design and application of LSTM neural network based on the hybrid coding PSO algorithm. J Supercomput. 2022;78(5):7227–7259. doi: 10.1007/s11227-021-04142-3. [DOI] [Google Scholar]
- 458.Bacanin N, Bezdan T, Venkatachalam K, Al-Turjman F. Optimized convolutional neural network by firefly algorithm for magnetic resonance image classification of glioma brain tumor grade. J Real-Time Image Proc. 2021;18(4):1085–1098. doi: 10.1007/s11554-021-01106-x. [DOI] [Google Scholar]
- 459.Akin Sherly LT, Jaya T. Improved firefly algorithm-based optimized convolution neural network for scene character recognition. SIViP. 2021;15(5):885–893. doi: 10.1007/s11760-020-01810-4. [DOI] [Google Scholar]
- 460.Datta S, Chakrabarti S. Aspect based sentiment analysis for demonetization tweets by optimized recurrent neural network using fire fly-oriented multi-verse optimizer. Sādhanā. 2021;46(2):1–23. doi: 10.1007/s12046-021-01608-1. [DOI] [Google Scholar]
- 461.Alenazy WM, Alqahtani AS. Gravitational search algorithm based optimized deep learning model with diverse set of features for facial expression recognition. J Ambient Intell Humaniz Comput. 2021;12(2):1631–1646. doi: 10.1007/s12652-020-02235-0. [DOI] [Google Scholar]
- 462.Sudha MS, Valarmathi K. An optimized deep belief network to detect anomalous behavior in social media. J Ambient Intell Humaniz Comput. 2021 doi: 10.1007/s12652-020-02708-2. [DOI] [Google Scholar]
- 463.Jammalamadaka K, Parveen N. Testing coverage criteria for optimized deep belief network with search and rescue. J Big Data. 2021;8(1):1–20. doi: 10.1186/s40537-021-00453-7. [DOI] [Google Scholar]
- 464.Gadekallu TR, Alazab M, Kaluri R, Maddikunta PKR, Bhattacharya S, Lakshmanna K. Hand gesture classification using a novel CNN-crow search algorithm. Complex Intell Syst. 2021;7(4):1855–1868. doi: 10.1007/s40747-021-00324-x. [DOI] [Google Scholar]
- 465.Irmak E. Multi-classification of brain tumor MRI images using deep convolutional neural network with fully optimized framework. Iran J Sci Technol Trans Electr Eng. 2021;45(3):1015–1036. doi: 10.1007/s40998-021-00426-9. [DOI] [Google Scholar]
- 466.Arjunagi S, Patil NB. Optimized convolutional neural network for identification of maize leaf diseases with adaptive ageist spider monkey optimization model. Int J Inf Technol. 2021 doi: 10.1007/s41870-021-00657-3. [DOI] [Google Scholar]
- 467.Li P, Wang S, Ji H, Zhan Y, Li H. Air quality index prediction based on an adaptive dynamic particle swarm optimized bidirectional gated recurrent neural network-china region. Adv Theory Simul. 2021;4(12):2100220. doi: 10.1002/adts.202100220. [DOI] [Google Scholar]
- 468.Oyelade ON, Ezugwu AE. Characterization of abnormalities in breast cancer images using nature-inspired metaheuristic optimized convolutional neural networks model. Concurr Comput Pract Exp. 2022;34(4):e6629. doi: 10.1002/cpe.6629. [DOI] [Google Scholar]
- 469.Tripathi MK, Maktedar DD. Optimized deep learning model for mango grading: hybridizing lion plus firefly algorithm. IET Image Proc. 2021;15(9):1940–1956. doi: 10.1049/ipr2.12163. [DOI] [Google Scholar]
- 470.Karuppusamy L, Ravi J, Dabbu M, Lakshmanan S. Chronological salp swarm algorithm based deep belief network for intrusion detection in cloud using fuzzy entropy. Int J Numer Model Electron Netw Devices Fields. 2022;35(1):e2948. doi: 10.1002/jnm.2948. [DOI] [Google Scholar]
- 471.Krishna Priya R, Chacko S. Improved particle swarm optimized deep convolutional neural network with super-pixel clustering for multiple sclerosis lesion segmentation in brain MRI imaging. Int J Numer Methods Biomed Eng. 2021;37(9):e3506. doi: 10.1002/cnm.3506. [DOI] [PubMed] [Google Scholar]
- 472.Danesh K, Vasuhi S. An effective spectrum sensing in cognitive radio networks using improved convolution neural network by glow worm swarm algorithm. Trans Emerg Telecommun Technol. 2021;32(11):1–20. [Google Scholar]
- 473.Zhang J, Sun G, Sun Y, Dou H, Bilal A. Hyper-parameter optimization by using the genetic algorithm for upper limb activities recognition based on neural networks. IEEE Sens J. 2021;21(2):1877–1884. doi: 10.1109/JSEN.2020.3018629. [DOI] [Google Scholar]
- 474.Farrag TA, Elattar EE. Optimized Deep stacked long short-term memory network for long-term load forecasting. IEEE Access. 2021;9:68511–68522. doi: 10.1109/ACCESS.2021.3077275. [DOI] [Google Scholar]
- 475.Arora P, Jalali SMJ, Ahmadian S, Panigrahi BK, Suganthan P, Khosravi A. Probabilistic wind power forecasting using optimised deep auto-regressive recurrent neural networks. IEEE Trans Ind Inform. 2022 doi: 10.1109/TII.2022.3160696. [DOI] [Google Scholar]
- 476.Goay CH, Ahmad NS, Goh P. Transient simulations of high-speed channels using CNN-LSTM with an adaptive successive halving algorithm for automated hyperparameter optimizations. IEEE Access. 2021;9:127644–127663. doi: 10.1109/ACCESS.2021.3112134. [DOI] [Google Scholar]
- 477.Liu X, Shi Q, Liu Z, Yuan J. Using LSTM neural network based on improved PSO and attention mechanism for predicting the effluent COD in a wastewater treatment plant. IEEE Access. 2021;9:146082–146096. doi: 10.1109/ACCESS.2021.3123225. [DOI] [Google Scholar]
- 478.Davoudi K, Thulasiraman P. Evolving convolutional neural network parameters through the genetic algorithm for the breast cancer classification problem. Simulation. 2021;97(8):511–527. doi: 10.1177/0037549721996031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 479.Liu X, Zhang C, Cai Z, Yang J, Zhou Z, Gong X. Continuous particle swarm optimization-based deep learning architecture search for hyperspectral image classification. Remote Sens. 2021;13(6):1082. doi: 10.3390/rs13061082. [DOI] [Google Scholar]
- 480.Brodzicki A, Piekarski M, Jaworek-Korjakowska J. The whale optimization algorithm approach for deep neural networks. Sensors. 2021;21(23):8003. doi: 10.3390/s21238003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 481.Baniasadi S, Rostami O, Martín D, Kaveh M. A novel deep supervised learning-based approach for intrusion detection in IoT systems. Sensors. 2022;22(12):4459. doi: 10.3390/s22124459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 482.Paul V, Ramesh R, Sreeja P, Jarin T, Kumar PS, Ansar S, Ashraf GA, Pandey S, Said Z. Hybridization of long short-term memory with sparrow search optimization model for water quality index prediction. Chemosphere. 2022;307:135762. doi: 10.1016/j.chemosphere.2022.135762. [DOI] [PubMed] [Google Scholar]
- 483.Gonçalves CB, Souza JR, Fernandes H. CNN architecture optimization using bio-inspired algorithms for breast cancer detection in infrared images. Comput Biol Med. 2022;142:105205. doi: 10.1016/j.compbiomed.2021.105205. [DOI] [PubMed] [Google Scholar]
- 484.Muthukannan P (2022) Optimized convolution neural network based multiple eye disease detection. Comput Biol Med 146:105648 [DOI] [PubMed]
- 485.Xu Y, Hu C, Wu Q, Jian S, Li Z, Chen Y, Zhang G, Zhang Z, Wang S. Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J Hydrol. 2022;608:127553. doi: 10.1016/j.jhydrol.2022.127553. [DOI] [Google Scholar]
- 486.Antony Raj S, Giftson Samuel G. BOSS-D-RBFN: BOosted Salp Swarm optimization based Deep RBFN for MPPT under partial shading condition in photovoltaic systems. Optik. 2022;259:168876. doi: 10.1016/j.ijleo.2022.168876. [DOI] [Google Scholar]
- 487.Hassanzadeh T, Essam D, Sarker R. EvoDCNN: an evolutionary deep convolutional neural network for image classification. Neurocomputing. 2022;488:271–283. doi: 10.1016/j.neucom.2022.02.003. [DOI] [Google Scholar]
- 488.Palaniswamy T. Hyperparameter optimization based deep convolution neural network model for automated bone age assessment and classification. Displays. 2022;73:102206. doi: 10.1016/j.displa.2022.102206. [DOI] [Google Scholar]
- 489.Jalali SMJ, Ahmadian S, Khodayar M, Khosravi A, Shafie-khah M, Nahavandi S, Catalão JP. An advanced short-term wind power forecasting framework based on the optimized deep neural network models. Int J Electr Power Energy Syst. 2022;141:108143. doi: 10.1016/j.ijepes.2022.108143. [DOI] [Google Scholar]
- 490.Lokku G, Reddy GH, Prasad MG. OPFaceNet: OPtimized Face Recognition Network for noise and occlusion affected face images using hyperparameters tuned convolutional neural network. Appl Soft Comput. 2022;117:108365. doi: 10.1016/j.asoc.2021.108365. [DOI] [Google Scholar]
- 491.Ewees AA, Al-qaness MA, Abualigah L, Abd Elaziz M. HBO-LSTM: optimized long short term memory with heap-based optimizer for wind power forecasting. Energy Convers Manag. 2022;268:116022. doi: 10.1016/j.enconman.2022.116022. [DOI] [Google Scholar]
- 492.Huo F, Chen Y, Ren W, Dong H, Yu T, Zhang J. Prediction of reservoir key parameters in ‘sweet spot’on the basis of particle swarm optimization to TCN-LSTM network. J Petrol Sci Eng. 2022;214:110544. doi: 10.1016/j.petrol.2022.110544. [DOI] [Google Scholar]
- 493.Li W, Wang L, Dong Z, Wang R, Qu B. Reservoir production prediction with optimized artificial neural network and time series approaches. J Petrol Sci Eng. 2022;215:110586. doi: 10.1016/j.petrol.2022.110586. [DOI] [Google Scholar]
- 494.Ge S, Gao W, Cui S, Chen X, Wang S. Safety prediction of shield tunnel construction using deep belief network and whale optimization algorithm. Autom Constr. 2022;142:104488. doi: 10.1016/j.autcon.2022.104488. [DOI] [Google Scholar]
- 495.Jalali SMJ, Ahmadian M, Ahmadian S, Hedjam R, Khosravi A, Nahavandi S. X-ray image based COVID-19 detection using evolutionary deep learning approach. Expert Syst Appl. 2022;201:116942. doi: 10.1016/j.eswa.2022.116942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 496.Li Y, Peng T, Zhang C, Sun W, Hua L, Ji C, Shahzad NM. Multi-step ahead wind speed forecasting approach coupling maximal overlap discrete wavelet transform, improved grey wolf optimization algorithm and long short-term memory. Renew Energy. 2022;196:1115–1126. doi: 10.1016/j.renene.2022.07.016. [DOI] [Google Scholar]
- 497.Veluchamy S, Thirumalai J, Sureshkanna P. RBorderNet: Rider Border Collie Optimization-based Deep Convolutional Neural Network for road scene segmentation and road intersection classification. Digit Signal Process. 2022;129:103626. doi: 10.1016/j.dsp.2022.103626. [DOI] [Google Scholar]
- 498.Mohakud R, Dash R (2021) Designing a grey wolf optimization based hyper-parameter optimized convolutional neural network classifier for skin cancer detection. J King Saud Univ-Comput Inf Sci 34(8):6280–6291
- 499.Ahmad J, Shah SA, Latif S, Ahmed F, Zou Z, Pitropakis N. DRaNN_PSO: A deep random neural network with particle swarm optimization for intrusion detection in the industrial internet of things. J King Saud Univ-Comput Inf Sci. 2022 doi: 10.1016/j.jksuci.2022.07.023. [DOI] [Google Scholar]
- 500.Chen F, Yang C, Khishe M. Diagnose Parkinson’s disease and cleft lip and palate using deep convolutional neural networks evolved by IP-based chimp optimization algorithm. Biomed Signal Process Control. 2022;77:103688. doi: 10.1016/j.bspc.2022.103688. [DOI] [Google Scholar]
- 501.Karthiga M, Santhi V, Sountharrajan S. Hybrid optimized convolutional neural network for efficient classification of ECG signals in healthcare monitoring. Biomed Signal Process Control. 2022;76:103731. doi: 10.1016/j.bspc.2022.103731. [DOI] [Google Scholar]
- 502.Kanipriya M, Hemalatha C, Sridevi N, SriVidhya SR, Shabu SJ. An improved capuchin search algorithm optimized hybrid CNN-LSTM architecture for malignant lung nodule detection. Biomed Signal Process Control. 2022;78:103973. doi: 10.1016/j.bspc.2022.103973. [DOI] [Google Scholar]
- 503.Hu H, Xia X, Luo Y, Zhang C, Nazir MS, Peng T. Development and application of an evolutionary deep learning framework of LSTM based on improved grasshopper optimization algorithm for short-term load forecasting. J Build Eng. 2022;57:104975. doi: 10.1016/j.jobe.2022.104975. [DOI] [Google Scholar]
- 504.Raziani S, Azimbagirad M. Deep CNN hyperparameter optimization algorithms for sensor-based human activity recognition. Neurosci Inform. 2022;2:100078. doi: 10.1016/j.neuri.2022.100078. [DOI] [Google Scholar]
- 505.Falahzadeh MR, Farokhi F, Harimi A, Sabbaghi-Nadooshan R. Deep convolutional neural network and gray wolf optimization algorithm for speech emotion recognition. Circuits Syst Signal Process. 2022 doi: 10.1007/s00034-022-02130-3. [DOI] [Google Scholar]
- 506.Vigneshwaran B, Iruthayarajan MW, Maheswari RV. Enhanced particle swarm optimization-based convolution neural network hyperparameters tuning for transformer failure diagnosis under complex data sources. Electr Eng. 2022 doi: 10.1007/s00202-022-01501-y. [DOI] [Google Scholar]
- 507.Jalali SMJ, Ahmadian S, Khodayar M, Khosravi A, Ghasemi V, Shafie-khah M, Nahavandi S, Catalão JP. Towards novel deep neuroevolution models: chaotic levy grasshopper optimization for short-term wind speed forecasting. Eng Comput. 2021;38:1787–1811. doi: 10.1007/s00366-021-01356-0. [DOI] [Google Scholar]
- 508.Surya V, Senthilselvi A. Identification of oil authenticity and adulteration using deep long short-term memory-based neural network with seagull optimization algorithm. Neural Comput Appl. 2022;34(10):7611–7625. doi: 10.1007/s00521-021-06829-3. [DOI] [Google Scholar]
- 509.Balasubramanian K, Ananthamoorthy NP, Ramya K. An approach to classify white blood cells using convolutional neural network optimized by particle swarm optimization algorithm. Neural Comput Appl. 2022 doi: 10.1007/s00521-022-07279-1. [DOI] [Google Scholar]
- 510.Pandey A, Jain K. Plant leaf disease classification using deep attention residual network optimized by opposition-based symbiotic organisms search algorithm. Neural Comput Appl. 2022 doi: 10.1007/s00521-022-07587-6. [DOI] [Google Scholar]
- 511.Challapalli JR, Devarakonda N. A novel approach for optimization of convolution neural network with hybrid particle swarm and grey wolf algorithm for classification of Indian classical dances. Knowl Inf Syst. 2022 doi: 10.1007/s10115-022-01707-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 512.Rodrigues LF, Backes AR, Travençolo BAN, de Oliveira GMB. Optimizing a deep residual neural network with genetic algorithm for acute lymphoblastic leukemia classification. J Digit Imaging. 2022;35(3):623–637. doi: 10.1007/s10278-022-00600-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 513.Sasank VVS, Venkateswarlu S. Hybrid deep neural network with adaptive rain optimizer algorithm for multi-grade brain tumor classification of MRI images. Multimed Tools Appl. 2022;81(6):8021–8057. doi: 10.1007/s11042-022-12106-9. [DOI] [Google Scholar]
- 514.Kavitha TS, Prasad D, Satya K. A novel method of compressive sensing MRI reconstruction based on sandpiper optimization algorithm (SPO) and mask region based convolution neural network (mask RCNN) Multimed Tools Appl. 2022 doi: 10.1007/s11042-022-12940-x. [DOI] [Google Scholar]
- 515.Qader SM, Hassan BA, Rashid TA. An improved deep convolutional neural network by using hybrid optimization algorithms to detect and classify brain tumor using augmented MRI images. Multimed Tools Appl. 2022 doi: 10.1007/s11042-022-13260-w. [DOI] [Google Scholar]
- 516.Karthik E, Sethukarasi T (2022) A centered convolutional restricted boltzmann machine optimized by hybrid atom search arithmetic optimization algorithm for sentimental analysis. Neural Process Lett 54:4123–4151
- 517.Li BJ, Sun GL, Liu Y, Wang WC, Huang XD. monthly runoff forecasting using variational mode decomposition coupled with gray wolf optimizer-based long short-term memory neural networks. Water Resour Manag. 2022;36(6):2095–2115. doi: 10.1007/s11269-022-03133-0. [DOI] [Google Scholar]
- 518.Bhardwaj S, Agarwal R (2022) An efficient speaker identification framework based on Mask R-CNN classifier parameter optimized using hosted cuckoo optimization (HCO). J Ambient Intell Humaniz Comput 13:1–13
- 519.Kaushik A, Singal N, Prasad M (2022) Incorporating whale optimization algorithm with deep belief network for software development effort estimation. Int J Syst Assur Eng Manag 13:1637–1651
- 520.Liu J, Jiang R, Zhu D, Zhao J. Short-term subway inbound passenger flow prediction based on AFC Data and PSO-LSTM optimized model. Urban Rail Transit. 2022;8(1):56–66. doi: 10.1007/s40864-022-00166-x. [DOI] [Google Scholar]
- 521.Souissi B, Ghorbel A (2022) Upper confidence bound integrated genetic algorithm‐optimized long short‐term memory network for click‐through rate prediction. Appl Stoch Models Bus Ind 38(3):475–496
- 522.Balasubramanian K, Kishore R, Krishnamoorthy GD. Optimal knee osteoarthritis diagnosis using hybrid deep belief network based on Salp swarm optimization method. Concurr Comput Pract Exp. 2022;34(13):e6913. doi: 10.1002/cpe.6913. [DOI] [Google Scholar]
- 523.Mukherjee G, Chatterjee A, Tudu B (2022) Identification of the types of disease for tomato plants using a modified gray wolf optimization optimized MobileNetV2 convolutional neural network architecture driven computer vision framework. Concurr Comput Pract Exp 34(22):e7161
- 524.Ponmalar A, Dhanakoti V. Hybrid Whale Tabu algorithm optimized convolutional neural network architecture for intrusion detection in big data. Concurr Comput Pract Exp. 2022 doi: 10.1002/cpe.7038. [DOI] [Google Scholar]
- 525.Suresh T, Brijet Z, Subha TD. Modified local binary patterns based feature extraction and hyper parameters tuned attention segmental recurrent neural network classifier using flamingo search optimization algorithm for disease diagnosis model. Concurr Comput Pract Exp. 2022 doi: 10.1002/cpe.7182. [DOI] [Google Scholar]
- 526.Xu X, Liu C, Zhao Y, Lv X. Short-term traffic flow prediction based on whale optimization algorithm optimized BiLSTM_Attention. Concurr Comput Pract Exp. 2022;34(10):e6782. doi: 10.1002/cpe.6782. [DOI] [Google Scholar]
- 527.Tuerxun W, Xu C, Guo H, Guo L, Zeng N, Cheng Z. An ultra-short-term wind speed prediction model using LSTM based on modified tuna swarm optimization and successive variational mode decomposition. Energy Sci Eng. 2022 doi: 10.1002/ese3.1183. [DOI] [Google Scholar]
- 528.Chandraraju TS, Jeyaprakash A. Categorization of breast masses based on deep belief network parameters optimized using chaotic krill herd optimization algorithm for frequent diagnosis of breast abnormalities. Int J Imaging Syst Technol. 2022;32:1561–1576. doi: 10.1002/ima.22718. [DOI] [Google Scholar]
- 529.Jiang Y, Xia L, Zhang J (2021) A fault feature extraction method for DC-DC converters based on automatic hyperparameter-optimized one-dimensional convolution and long short-term memory neural networks. IEEE J Emerg Sel Top Power Elect 10(4):4703–4714
- 530.Fetanat M, Stevens M, Jain P, Hayward C, Meijering E, Lovell NH. Fully Elman neural network: a novel deep recurrent neural network optimized by an improved harris hawks algorithm for classification of pulmonary arterial wedge pressure. IEEE Trans Biomed Eng. 2021;69(5):1733–1744. doi: 10.1109/TBME.2021.3129459. [DOI] [PubMed] [Google Scholar]
- 531.Jiang Y, Jia M, Zhang B, Deng L. Ship attitude prediction model based on cross-parallel algorithm optimized neural network. IEEE Access. 2022;10:77857–77871. doi: 10.1109/ACCESS.2022.3193573. [DOI] [Google Scholar]
- 532.Gampala V, Rathan K, Shajin FH, Rajesh P. Diagnosis of COVID-19 patients by adapting hyper parametertuned deep belief network using hosted cuckoo optimization algorithm. Electromagn Biol Med. 2022 doi: 10.1080/15368378.2022.2065679. [DOI] [PubMed] [Google Scholar]
- 533.Li Q, Yang M, Lu Z, Zhang Y, Ba W. A soft-sensing method for product quality monitoring based on particle swarm optimization deep belief networks. Trans Inst Meas Control. 2022 doi: 10.1177/01423312221093166. [DOI] [Google Scholar]
- 534.Yu Y, Rashidi M, Samali B, Mohammadi M, Nguyen TN, Zhou X. Crack detection of concrete structures using deep convolutional neural networks optimized by enhanced chicken swarm algorithm. Struct Health Monit. 2022 doi: 10.1177/14759217211053546. [DOI] [Google Scholar]
- 535.Li X, Li Y, Cao Y, Duan S, Wang X, Zhao Z. Fault diagnosis method for aircraft EHA based on FCNN and MSPSO hyperparameter optimization. Appl Sci. 2022;12(17):8562. doi: 10.3390/app12178562. [DOI] [Google Scholar]
- 536.Pellegrino E, Brunet T, Pissier C, Camilla C, Abbou N, Beaufils N, Nanni-Metellus I, Métellus P, Ouafik LH. Deep learning architecture optimization with metaheuristic algorithms for predicting BRCA1/BRCA2 pathogenicity NGS analysis. BioMedInformatics. 2022;2(2):244–267. doi: 10.3390/biomedinformatics2020016. [DOI] [Google Scholar]
- 537.Mohapatra M, Parida AK, Mallick PK, Zymbler M, Kumar S. Botanical leaf disease detection and classification using convolutional neural network: a hybrid metaheuristic enabled approach. Computers. 2022;11(5):82. doi: 10.3390/computers11050082. [DOI] [Google Scholar]
- 538.Shankar K, Kumar S, Dutta AK, Alkhayyat A, Jawad AJAM, Abbas AH, Yousif YK. An automated hyperparameter tuning recurrent neural network model for fruit classification. Mathematics. 2022;10(13):2358. doi: 10.3390/math10132358. [DOI] [Google Scholar]
- 539.Fan Y, Zhang Y, Guo B, Luo X, Peng Q, Jin Z. A hybrid sparrow search algorithm of the hyperparameter optimization in deep learning. Mathematics. 2022;10(16):3019. doi: 10.3390/math10163019. [DOI] [Google Scholar]
- 540.Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi: 10.1109/4235.585893. [DOI] [Google Scholar]
- 541.Wolpert DH. The lack of a priori distinctions between learning algorithms. Neural Comput. 1996;8(7):1341–1390. doi: 10.1162/neco.1996.8.7.1341. [DOI] [Google Scholar]
- 542.Kaveh M, Mesgari MS. Hospital site selection using hybrid PSO algorithm-case study: district 2 of Tehran. Sci-Res J Geogr Data. 2019;28(111):7–22. [Google Scholar]
- 543.Kaveh M, Mesgari MS. Improved biogeography-based optimization using migration process adjustment: an approach for location-allocation of ambulances. Comput Ind Eng. 2019;135:800–813. doi: 10.1016/j.cie.2019.06.058. [DOI] [Google Scholar]
- 544.Reddy KK, Sarkar S, Venugopalan V, Giering M (2016) Anomaly detection and fault disambiguation in large flight data: A multi-modal deep auto-encoder approach. In: Annual conference of the prognostics and health management society, Vol. 2016
- 545.Liu X, Gao J, He X, Deng L, Duh K, Wang YY (2015) Representation learning using multi-task deep neural networks for semantic classification and information retrieval. In: Proceedings of NAACL, pp. 912–921
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.