Estimating muscle activation from EMG using deep learning-based dynamical systems models

Abstract

Objective:

To study the neural control of movement, it is often necessary to estimate how muscles are activated across a variety of behavioral conditions. One approach is to try extracting the underlying neural command signal to muscles by applying latent variable modeling methods to electromyographic (EMG) recordings. However, estimating the latent command signal that underlies muscle activation is challenging due to its complex relation with recorded EMG signals. Common approaches estimate each muscle activation independently or require manual tuning of model hyperparameters to preserve behaviorally-relevant features.

Approach:

Here, we adapted AutoLFADS, a large-scale, unsupervised deep learning approach originally designed to de-noise cortical spiking data, to estimate muscle activation from multi-muscle EMG signals. AutoLFADS uses recurrent neural networks (RNNs) to model the spatial and temporal regularities that underlie multi-muscle activation.

Main Results:

We first tested AutoLFADS on muscle activity from the rat hindlimb during locomotion and found that it dynamically adjusts its frequency response characteristics across different phases of behavior. The model produced single-trial estimates of muscle activation that improved prediction of joint kinematics as compared to low-pass or Bayesian filtering. We also applied AutoLFADS to monkey forearm muscle activity recorded during an isometric wrist force task. AutoLFADS uncovered previously uncharacterized high-frequency oscillations in the EMG that enhanced the correlation with measured force. The AutoLFADS-inferred estimates of muscle activation were also more closely correlated with simultaneously-recorded motor cortical activity than were other tested approaches.

Significance:

This method leverages dynamical systems modeling and artificial neural networks to provide estimates of muscle activation for multiple muscles. Ultimately, the approach can be used for further studies of multi-muscle coordination and its control by upstream brain areas.

Introduction

Executing movements often requires activating muscles distributed across the body in precisely coordinated time-varying patterns. Understanding how the nervous system selects and generates these patterns remains a central goal of motor neuroscience. Critical to this effort is obtaining estimates of the neural commands to muscles i.e., muscle activation signals, and evaluating how they are related both to task demands and to neural activity in motor related brain areas. However, a key barrier in this evaluation is the difficulty of estimating muscle activation from electromyographic (EMG) recordings.

EMG recordings are typically rectified, then smoothed to obtain an estimate of the activation envelope. A wide variety of filtering approaches have been proposed, ranging from a simple linear, low-pass filter (Clancy et al., 2001; D’Alessio and Conforto, 2001; Hogan and Mann, 1980) to nonlinear, adaptive Bayesian filtering that aims to model the time-varying statistics of the EMG (Hofmann et al., 2016; Sanger, 2007). Although these are reasonable approaches, determining the optimal parameters for these filters is challenging. Some parameter combinations may result in less smoothing that leads to more variable signals that are difficult to interpret, while others may lead to more smoothing that suppresses high-frequency features that may be relevant to behavior. Another common approach is to simplify signals further by averaging across repeats of the same behavior, which destroys any single-trial correspondence between EMG signals and simultaneously recorded behavioral variables.

In cases where EMG is simultaneously recorded from multiple muscles, most filtering approaches treat multi-muscle EMG recordings as independent signals, failing to leverage potential information in the coordinated muscle activation. Previous work in the field of muscle synergies has demonstrated underlying spatial and temporal regularities in multi-muscle activation across many model systems, suggesting that co-variation patterns across muscles may provide additional information for the estimation of individual muscle activations (Tresch and Jarc, 2009).

Here we adapted a large-scale deep learning approach, AutoLFADS (Keshtkaran et al., 2021), leveraging advances in deep generative modeling to estimate muscle activation from multi-muscle recordings. In particular, AutoLFADS models the dynamics (i.e., spatial and temporal regularities) underlying multi-muscle activity using recurrent neural networks (RNNs). The large-scale optimization approach allows AutoLFADS the flexibility to be trained out-of-the-box, i.e., without manual adjustment for different datasets.

A separate class of methods from those discussed here uses EMG and other signals, as well as musculoskeletal parameters, to estimate activation torques, joint torques and joint kinematics, with potential applications to musculoskeletal simulation and prosthetic device control (Nasr et al., 2021). However, such methods have a different focus – aside from their system inputs, there is no subsequent representation of muscle activation. In contrast, our approach uses simultaneously-recorded EMG from multiple muscles to make improved estimates of muscle activation itself. While our approach could be used as a preprocessing strategy to support classification and control, its primary goal is to produce a high-quality estimate of the underlying muscle activation signal(s), appropriate for understanding basic motor control properties of the brain. As such, we extend a large body of previous literature - particularly, linear filtering or Bayesian filtering - which has largely approached this problem by looking at the activity of a single muscle at a time (Clancy et al., 2001; Hofmann et al., 2016; Sanger, 2007). The key advantages of our approach are accounting for the known spatial and temporal regularities underlying EMG signals and the use of powerful deep learning methods to uncover these coordinated patterns on fast timescales and on individual trials.

In previous work, LFADS was used to model neuronal population dynamics in the cortical areas under study (Keshtkaran et al., 2021; Pandarinath et al., 2018; Sussillo et al., 2016). These cortical microelectrode recordings allow direct observation of activity in the dynamical system being modeled. In contrast, EMG recordings are observations of the output an unobserved dynamical system – i.e., spinal circuitry and inputs from the many different brain areas that play a role in activating muscles. Given this lack of access, the key question was whether dynamical systems modeling approaches could yield improvements in the quality of the estimates of muscle activation by modeling EMG as the output of a dynamical system.

We first applied AutoLFADS to multi-muscle recordings in rat hindlimb during locomotion. We found that AutoLFADS functions adaptively to adjust its frequency response characteristics dynamically according to the time course of different phases of behavior. As with other latent variable models (Hofmann et al., 2016; Sanger, 2007), we validated our approach by comparing how well the representations inferred by AutoLFADS correlated with behavioral output. We showed that AutoLFADS enables more accurate single-trial joint angular acceleration predictions from EMG than the predictions of standard filtering techniques (i.e., smoothing, Bayesian filtering). We next applied AutoLFADS to multi-muscle recordings in monkey forearm during an isometric force-control task. Unexpectedly, AutoLFADS identified previously uncharacterized 10–50 Hz oscillations shared across flexor muscles, and resulted in greater coherence at these frequencies with dF/dt. Finally, the AutoLFADS-inferred muscle activations corresponded closely to simultaneously recorded activity in the motor cortex, suggesting that the model preserves correlations with both descending motor commands and ensuing behavior. These results show that AutoLFADS reveals subtle features in muscle activity that may otherwise be overlooked or eliminated, and thus may allow new insights into motor control by elucidating relationships between muscle activation signals in the brain and spinal cord with high temporal precision on a single-trial level.

Methods

Section 1: Adapting AutoLFADS for EMG

We begin with a model schematic outlining the adapted AutoLFADS approach (Fig. 1). m[t] is the time-varying vector of rectified multi-muscle EMG. Our goal is to find $\widehat{m}[\text{t}]$, an estimate of muscle activation from m[t] that preserves the neural command signal embedded in the recorded EMG activity. Common approaches to estimating $\widehat{m}[\text{t}]$ typically involve applying a filter to each EMG channel independently, ranging from a simple linear smoothing filter to a nonlinear, adaptive Bayesian filter. While these approaches effectively reduce high-frequency noise, they have two major limitations. First, they require supervision to choose hyperparameters that affect the output of the filters. For example, using a smoothing (low-pass) filter requires a choice of a cutoff frequency and order, which sets an arbitrary fixed limit on the EMG frequency spectrum that is considered “signal”. Setting a lower cutoff yields smoother representations with less high-frequency content; however, this may also come at the expense of eliminating high-frequency activation patterns that may be behaviorally-relevant. Second, by filtering muscles independently, standard smoothing approaches fail to take advantage of potential information in the shared structure across muscles. Provided that muscles are not activated independently (Tresch and Jarc, 2009), the estimate of a given muscle’s activation can be improved by having access to recordings from other muscles.

Fig. 1 |. Modeling dynamics underlying EMG activity with AutoLFADS.

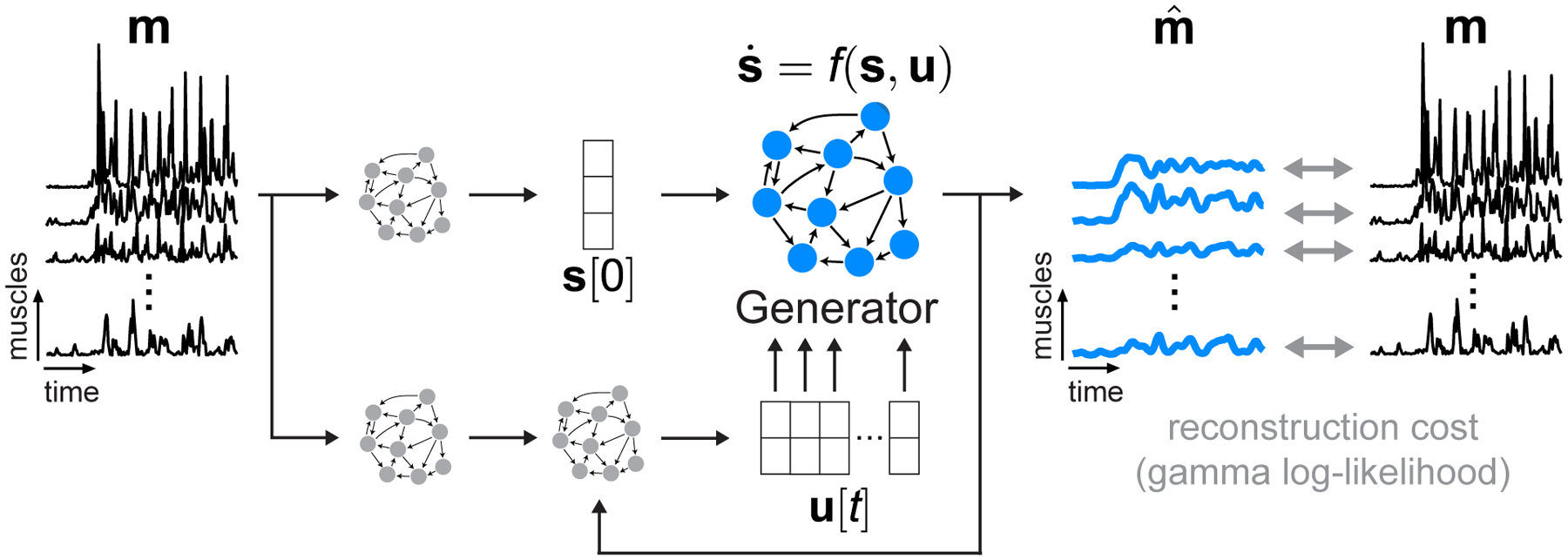
Model schematic. We modified AutoLFADS to accommodate the statistics of EMG activity using a gamma observation model rather than Poisson. m is a small window from a continuous recording of rectified EMGs from a group of muscles. m[t] is a vector representing the multi-muscle rectified EMG at each timepoint. $\widehat{m}[\text{t}]$ is an estimate of muscle activation from the EMG activation envelopes m[t]. Our approach models $\widehat{m}[\text{t}]$ as the output of a nonlinear dynamical system with shared inputs to the muscles. The Generator RNN is trained to model the state update function f, which captures the spatial and temporal regularities that underlie the coordinated activation of multiple muscles. The other RNNs provide the Generator with an estimate of initial state s[0] and a time-varying input u[t], allowing the dynamical system to evolve in time to generate s[t]. $\widehat{m}[\text{t}]$ is taken as a nonlinear transformation of s[t]. All of the model’s parameters are updated via backpropagation of the gamma log-likelihood of observing the input rectified EMG data.

Our approach overcomes the limitations of standard filtering by leveraging the shared structure and potential nonlinear dynamics describing the time-varying patterns underlying m[t]. We implemented this approach by adapting latent factor analysis via dynamical systems (LFADS), a deep learning tool previously developed to study neuronal population dynamics (Fig. 1) (Pandarinath et al., 2018). Briefly, LFADS comprises a series of RNNs that model observed data as the noisy output of an underlying nonlinear dynamical system. The internal state of one of these RNNs, termed the Generator, explicitly models the evolution of s[t] i.e., the state of the underlying dynamical system. The Generator is trained to model f i.e., the state update function, by tuning the parameters of its recurrent connections to model the spatial and temporal regularities governing the coordinated time-varying changes of the observed data. The Generator does not have access to the observed data so it has no knowledge of the identity of recorded muscles or the observed behavior. Instead, the Generator is only provided with an initial state s[0], and a low-dimensional, time-varying input u[t] to model the progression of s[t] as a discrete-time dynamical system. The model then generates $\widehat{m}[\text{t}]$, where m[t] is taken as a sample of $\widehat{m}[\text{t}]$ through a gamma observation model (details are provided in AutoLFADS architecture). The model has a variety of hyperparameters that control training and prevent overfitting. These hyperparameters are automatically tuned using the AutoLFADS large-scale optimization framework we previously developed (Keshtkaran et al., 2021; Keshtkaran and Pandarinath, 2019).

While the core LFADS model remains the same in its application for EMG activity as for cortical activity, we did not have a prior guarantee that adapting the observation model alone would provide us with good estimates of muscle activation from EMG. A key distinction to previous applications of LFADS is the application of data augmentation during model training. In our initial modeling attempts, we found that models could overfit to high-magnitude events that occurred simultaneously across multiple channels. To mitigate this issue, we implemented a data augmentation strategy (“temporal shift”) during model training to prevent the network from drawing a direct correspondence between specific values of the rectified EMG used both as the input to the model and at the output to compute the reconstruction cost (details provided in AutoLFADS training).

AutoLFADS network architecture

The AutoLFADS network architecture, as adapted for EMG, is detailed in Supplementary Fig. 1. The model operates on segments of multi-channel rectified EMG data (m[t]). The output of the model $\widehat{m}[\text{t}]$ is an estimate of muscle activation from m[t] in which the observed activity on each channel is modeled as a sample from an underlying time-varying gamma distribution. For channel j, ${\widehat{m}}_{\text{j}}[\text{t}]$ is the time-varying mean of the gamma distribution inferred by the model (i.e., AutoLFADS output). The two parameters for each gamma distribution, denoted α (concentration) and β (rate), are taken as separate linear transformations of the underlying dynamic state s[t] followed by an exponential nonlinearity. Because rectified EMG follows a skewed distribution (i.e., values are strictly positive), data were log transformed before being input to the model, resulting in data distributions that were more symmetric.

To generate s[t] for a given window of data m[t], a series of RNNs, implemented using Gated Recurrent Unit (GRU) cells, were connected together to explicitly model a dynamical system. At the input to the network, two RNNs (the Initial Condition & Controller Input Encoders) operate on the log-transformed m[t] to generate an estimate of the initial state s[0] and to encode information for a separate RNN, the Controller. The role of the controller is to infer a set of time-varying inputs into the final RNN, the Generator, u[t]. This Generator RNN represents the learned dynamical system, which models f to evolve s[t] at each timepoint. From s[0], the dynamical system is run forward in time with the addition of the u[t] at each timestep to evolve s[t].

In all experiments performed in this paper, the Generator, Controller, and Controller Input Encoder RNNs each had 64 units. The Initial Condition Encoder RNN had a larger dimensionality of 128 units to increase the capacity of the network to handle the complex mapping from the unfiltered rectified EMG onto the parameters of the initial condition distribution. The Generator RNN was provided with a 30-dimensional initial condition (i.e., s[0]) and a three-dimensional input (i.e., u[t]) from the Controller. A linear readout matrix restricted the output of the Generator RNN to describe the patterns of observed muscle activity using only 10 dimensions. Variance of the initial condition prior distribution was 0.1. The minimum variance of the initial condition posterior distribution was 1e-4.

AutoLFADS training

Training AutoLFADS models on rectified EMG data largely followed previous applications of LFADS (Keshtkaran et al., 2021; Keshtkaran and Pandarinath, 2019; Pandarinath et al., 2018; Sussillo et al., 2016), with key distinctions being the gamma emissions process chosen for EMG data, as described above, and a novel data augmentation strategy implemented during training (see below). Beyond this choice, model optimization followed previous descriptions; briefly, the model’s objective function is defined as the log likelihood of the observed EMG data (m[t]) given the time-varying gamma distributions output by the model for each channel $(\widehat{m}[\text{t}])$, marginalized over all latent variables. This is optimized in a variational autoencoder by maximizing a lower bound on the marginal data log-likelihood (Kingma and Welling, 2014). Network weights were randomly initialized. During training, network parameters are optimized using stochastic gradient descent and backpropagation through time. We scaled the loss prior to computing the gradients (scale: 1e4) to prevent numerical precision issues. We used the Adam optimizer (epsilon: 1e-8, beta1: 0.9, beta2: 0.99) to control weight updates, and implemented gradient clipping to prevent potential exploding gradient issues (max. norm=200). To prevent any potentially problematic large values in RNN state variables and achieve more stable training, we also limited the range of the values in GRU hidden state by clipping values greater than 5 and lower than −5.

Hyperparameter optimization.

Finding a high-performing model required finding a suitable set of model hyperparameters (HPs). To do so, we used an automated model training and hyperparameter framework we developed (Keshtkaran and Pandarinath, 2019), which is an implementation of the population based training (PBT) approach (Jaderberg et al., 2017). Briefly, PBT is a large-scale optimization method that trains many models with different HPs in parallel. PBT trains models for a generation - i.e., a user-settable number of training steps - then performs a selection process to choose higher performing models and eliminate poor performers. Selected high performing models are also “mutated” (i.e., their HPs are perturbed) to expand the HP search space. After many generations, the PBT process converges upon a high performing model with optimized HPs.

For both datasets, we used PBT to simultaneously train 20 LFADS models for 30 epochs per generation (where an “epoch” is a single training pass through the entire dataset). We distributed training across 5 GPUs (4 models were trained on each GPU simultaneously). The magnitude of the KL and L2 penalties was linearly ramped for the first 50 epochs of training during the first generation of PBT. Each training epoch consisted of ~10 training steps. Each training step was computed on 400-sample batches from the training data. PBT stopped when there was no improvement in performance after 10 generations. Runs typically took ~30–40 generations to complete. After completion, the model with the lowest validation cost (i.e., best performance) was returned and used as the AutoLFADS model for each dataset. AutoLFADS output was inferred 200 times for each model using different samples from initial condition and controller output posterior distributions. These estimates were then averaged, resulting in the final model output used for analysis.

PBT was allowed to optimize the model’s learning rate and five regularization HPs: L2 penalties on the Generator and Controller RNNs, scaling factors for the KL penalties applied to the initial conditions and time-varying inputs to the Generator RNN, and two dropout probabilities (see PBT Search Space in Supplementary Methods for specific ranges).

Data augmentation.

A key distinction of the AutoLFADS approach for EMG data with respect to previous applications of LFADS was the development and use of data augmentation strategies during training. In our initial modeling, we found that models could overfit to high-magnitude events that occurred simultaneously across multiple channels. To prevent this overfitting, we implemented a novel data augmentation strategy (“temporal shift”). During model training, we randomly shifted each channel’s data, i.e., we introduced small, random temporal offsets (selected separately for each channel) when inputting data to the model. The model input and the data used to compute reconstruction cost were shifted differently to prevent the network from overfitting by drawing a direct correspondence between specific values of the input and output (similar to the problem described in Keshtkaran and Pandarinath, 2019). During temporal shifting, each channel’s data was allowed to shift in time by a maximum of 6 bins. Shift values were drawn from a normal distribution (std. dev. = 3 bins) that was truncated such that any value greater than 6 was discarded and re-drawn.

Section 2: Data

Rat locomotion data

EMG recordings.

Chronic bipolar EMG electrodes were implanted into the belly of 12 hindlimb muscles during sterile surgery as described in (Alessandro et al., 2018). Recording started at least two weeks after surgery to allow the animal to recover. Differential EMG signals were amplified (1000X), band-pass filtered (30–1000 Hz) and notch filtered (60 Hz), and then digitized (5000 Hz).

Kinematics.

A 3d motion tracking system (Vicon) was used to record movement kinematics (Alessandro et al., 2020, 2018). Briefly, retroreflective markers were placed on bony landmarks (pelvis, knee, heel and toe) and tracked during locomotion at 200 Hz. The obtained position traces were low-pass filtered (Butterworth 4th order, cut-off 40 Hz). The 3-D knee position was estimated by triangulation using the lengths of the tibia and the femur in order to minimize errors due to differential movements of the skin relative to the bones (Bauman and Chang, 2010; Filipe et al., 2006). The 3d positions of the markers were projected into the sagittal plane of the treadmill, obtaining 2d kinematics data. Joint angles were computed from the positions of the top of the pelvis (rostral marker), the hip (center of the pelvis), the knee, the heel and the toe as follows. Hip: angle between the pelvis (line between pelvis-top and hip) and the femur (line between hip and knee). Knee: angle between the femur and the tibia (line between the knee and the heel). Ankle: angle between the tibia the foot (line between the heel and the toe). All joint angles are equal to zero for maximal flexion and increase with extension of the joints.

Joint angular velocities and accelerations were computed from joint angular position using a first-order and second-order Savitzky-Golay (SG) differentiation filter (MATLAB’s sgolay), respectively. SG FIR filter was designed with a 5^th order polynomial and frame length of 27.

Monkey isometric data

M1/EMG Recordings.

We recorded data from one 10 kg male macaca mulatta monkey (age 8 years when the experiments started) while he performed an isometric wrist task. All surgical and behavioral procedures were approved by the Animal Care and Use Committee at Northwestern University. The monkey was implanted with a 96-channel microelectrode silicon array (Utah electrode arrays, Blackrock Microsystems, Salt Lake City, UT) in the hand area of M1, which we identified intraoperatively through microstimulation of the cortical surface and identification of surface landmarks. The monkey was also implanted with intramuscular EMG electrodes in a variety of wrist and hand muscles. We report data from the following muscles: flexor carpi radialis, flexor carpi ulnaris, flexor digitorum profundus (2 channels), flexor digitorum superficialis (2 channels), extensor digitorum communis, extensor carpi ulnaris, extensor carpi radialis, palmaris longus, pronator teres, abductor pollicis brevis, flexor pollicis brevis, and brachioradialis. Surgeries were performed under isoflurane gas anesthesia (1–2%) except during cortical stimulation, for which the monkeys were transitioned to reduced isoflurane (0.25%) in combination with remifentanil (0.4 μg kg⁻¹ min⁻¹ continuous infusion). Monkeys were administered antibiotics, anti-inflammatories, and buprenorphine for several days after surgery.

Experimental Task.

The monkey was trained at a 2D isometric wrist task for which the relationship between muscle activity and force is relatively simple and well characterized. The left arm was positioned in a splint so as to immobilize the forearm in an orientation midway between supination and pronation (with the thumb upwards). A small box was placed around the monkey’s open left hand, incorporating a 6 DOF load cell (20E12, 100 N, JR3 Inc., CA) aligned with the wrist joint. The box was padded to comfortably constrain the monkey’s hand and minimize its movement within the box. The monkey controlled the position of a cursor displayed on a monitor by the force they exerted on the box. Flexion/extension force moved the cursor right and left, respectively, while forces along the radial/ulnar deviation axis moved the cursor up and down. Prior to placing the monkey’s hand in the box, the force was nulled in order to place the cursor in the center target. Being supported at the wrist, the weight of the monkey’s hand alone did not significantly move the cursor when the monkey was at rest. Targets were displayed either at the center of the screen (zero force), or equally spaced along a ring around the center target. All targets were squares with 4 cm sides.

Data preprocessing

Raw EMG data was first passed through a powerline interference removal filtering algorithm (Keshtkaran and Yang, 2014) that we specified to remove power at 60Hz and 2 higher frequency harmonics (120Hz, 180Hz). We added additional notch filters centered at 60Hz and 94Hz (isometric data) and 60Hz, 120Hz, 240Hz, 300Hz, and 420Hz (locomotion data) to remove noise peaks identified from observing the power spectral density estimates after the previous filtering step. We then filtered the EMG data with a 4th-order Butterworth high pass filter with cutoff frequency at 65 Hz. We finally full-wave rectified the EMG and down-sampled from the original sampling rate (rat: 5KHz, monkey: 2KHz) to 500Hz using MATLAB’s resample function which applies a poly-phase anti-aliasing filter prior to down-sampling the data.

We next removed infrequent electrical recording artifacts that caused large spikes in activity which had a particular effect on AutoLFADS modeling: during the modeling process (see Training), large anomalous events incurred a large reconstruction cost that disrupted the optimization process and prevented the model from capturing underlying signal. To remove artifacts, we clipped each channel’s activity such that any activation above a threshold value was set to the threshold. For the isometric data, we applied the same 99.99^th percentile threshold across all channels. For the locomotion data, we used a 99.9^th percentile threshold for all channels except for one muscle (semimembranosus) which required a 99^th percentile threshold to eliminate multiple high-magnitude artifacts only observed in the recordings for this channel. After clipping, we normalized each channel by the 95th percentile value to ensure that they had comparable variances.

For the monkey data, some artifacts remained even after clipping. To more thoroughly reject artifacts, we selected windows of data for successful trials (1.5s prior to 2.5s after force onset) and visually screened all muscles. Trials in which muscle activity contained high magnitude events (brief spikes 2–5x greater than typical range) that were not seen consistently across trials were excluded for subsequent analyses. After the rejection process, 271 of 296 successful trials remained.

We used AutoLFADS to model the EMG data without regard to behavioral structure (i.e., task or trial information). For the rodent locomotion data, the continuously recorded data (~2 min per session) from three speed conditions (10, 15, 20 m/min) was binned at 2ms and divided into windows of length 200ms, with 50ms of overlap between the segments. The start indices of each trial are stored so that after training, model output can be reassembled. After performing inference on each segment separately, the segments were merged at overlapping regions using a linear combination of the estimates from the end of the earlier segment with those from the beginning of the later segment. The merging technique weighted the ends of the segments as w = 1 − x and the beginning of segments as 1 − w, with x linearly increasing from 0 to 1 across the overlapping points. After weights were applied, the overlapping segments were summed to reconstruct the modeled data. Non-overlapping portions of the windows were concatenated to the array holding the reconstructed continuous output of the model, without any weighting. Due to the additional artifact rejection process for the monkey isometric data (mentioned above), we were unable to model the continuously recorded data (i.e., we could only model segments corresponding to trials that passed the artifact rejection process). These trial segments were processed using the same chopping process we administered to the rodent locomotion data.

Bayesian filtering

Model.

Bayesian filtering is an adaptive filtering method, that, depending on the model specifications, can be linear (Kalman filter) or nonlinear, and has previously been applied to surface EMG signals (Dyson et al., 2017; Hofmann et al., 2016; Sanger, 2007). A Bayesian filter consists of two components: (1) the temporal evolution model governing the time-varying statistics of the underlying latent variable and (2) the observation model that relates the latent variable to the observed rectified EMG. For this application, the temporal evolution model was implemented using a differential Chapman Kolmogorov equation reflecting diffusion and jump processes (Hofmann et al., 2016). For the observation model, we tested both a Gaussian distribution and Laplace distribution, which have previously been applied to surface EMG (Nazarpour et al., 2013). Empirically, we found that the Gaussian distribution produced slightly better decoding predictions (for both rat and monkey) than the Laplace distribution, so we used it for all comparisons. Our implementation of the Bayesian filter had four hyperparameters: (1) sigma_max, the upper interval bound for the latent variable, (2) N_bins, the number of bins used to define the histogram modeling the latent variable distribution, (3) alpha, which controls the diffusion process underlying the time-varying progression of the latent variable and (4) beta, which controls the probability for larger jumps of the latent variable. Sigma_max was empirically derived to be approximately an order of magnitude larger than the standard deviation measured from the aggregated continuous data. This value was set to 2 for both datasets after quantile normalizing the EMG data prior to modeling. N_bins was set to 100 to ensure the changes in the magnitude of the latent variable over time could be modeled with high enough resolution. The other two hyperparameters, alpha and beta, had a significant effect on the quality of modeling, therefore we performed a large-scale grid search to optimize the parameters for each dataset (described below). Each EMG channel is estimated independently using the same set of hyperparameters.

Hyperparameter optimization.

Two hyperparameters (alpha and beta) can be tuned to affect the output of the Bayesian filter. To ensure that the choice to use previously published hyperparameters (Sanger, 2007) was not resulting in sub-optimal estimates of muscle activation, we performed grid searches for each dataset to find an optimal set of hyperparameters to filter the EMG data. We tested 4 values of alpha (ranging from 1e-1 to 1e-4) and 11 values of beta (ranging from 1e0 to 1e-10), resulting in 44 hyperparameter combinations. To assess optimal hyperparameters for each dataset, we fit linear decoders from the Bayesian filtered EMG to predict joint angular acceleration (rat locomotion) or dF/dt (monkey isometric) following the same procedures used for decoding analyses (see Predicting joint angular acceleration or Predicting dF/dt for details). The hyperparameter combination that resulted in the highest average decoding performance across prediction variables was chosen for comparison to AutoLFADS. These were alpha=1e-2 and beta=1e-4 (rat locomotion) and alpha=1e-2 and beta=1e-2 (monkey isometric).

Section 3: Analyses

Metric.

To quantify decoding performance, we used Variance Accounted For (VAF). $VAF=1-\Sigma {(\widehat{y}-y)}^2/\Sigma \left(y-\overline{y}\right)$. $\widehat{y}$ is the prediction, y is the true signal, and $\overline{y}$ is the mean. This is often referred to as the coefficient of determination, or R².

Predicting joint angular acceleration (rat locomotion).

We used optimal linear estimation (OLE) to perform single timepoint decoding to map the muscle activation estimates of 12 muscles onto the 3 joint angular acceleration kinematic parameters (hip, knee, and ankle) at a single speed (20 cm/s). We performed a 10-fold cross validation (CV) to fit decoders (90% of the data) and evaluate performance (held-out 10% of data). Mean and standard error of the mean (SEM) for decoding performance was reported as the averaged cross-validated VAF across the 10 folds. During fitting of the decoders, we normalized the predictor (i.e., muscle activation estimate) and response (i.e., joint angular kin.) variables to have zero-mean and unit standard deviation. We also penalized the weights of the decoder using an L2 ridge regularization penalty of 1. We assessed significance using paired t-tests between the cross-validated VAF values from the AutoLFADS predictions and the predictions from the best performing low pass filter (10 CV folds). We performed a sweep ranging from 0 ms to 100 ms to find the optimal lag for each predictor with respect to each response variable. We separately optimized the lag of each decoder to account for potential differences in the delay between changes in the muscle activation estimates and changes in the joint angular kinematics, which could be different for each kinematic parameter. Optimal lag was determined based on the highest mean CV VAF value.

Estimating frequency responses.

We estimated frequency responses to understand how AutoLFADS differs from low pass (Butterworth) filtering, which applies the same temporally invariant frequency response to all channels. The goal was to see whether AutoLFADS optimizes its filtering properties differently for individual muscles around characteristic timepoints of behavior.

We chose two characteristic time points within the gait cycle of the rat locomotion dataset: (1) during the swing phase (at 25% of the time between foot off and foot strike) and (2) during the stance phase (50% between foot off and foot strike). We selected windows of 175 samples (350 ms) around both of these time points. The number of samples was optimized to be large enough to have a fine resolution in frequency space but small enough to include samples mainly from one of the locomotion phases (avg. stance: ~520 ms; avg. swing: ~155 ms). To reduce the effects of frequency resolution limits imposed by estimating PSDs on short sequences, we used a multi-taper method that matches the length of the windows used for the PSD estimates to the length of the isolated segment. This maximized the number of points of the isolated segments we could use without upsampling. We z-scored the signals within each phase and muscle to facilitate comparisons. Within each window, we computed the Thomson’s multitaper power spectral density (PSD) estimate using a MATLAB (Mathworks Inc, MA) built-in function pmtm. We set the time-bandwidth product to NW=3 to retain precision in frequency space and the number of samples for the DFT to equal the window length and otherwise retained default parameters. With a window of 175 samples, the DFT has a frequency resolution of 2.85 Hz.

We computed the PSD for the rectified EMG (PSD_raw), the output of AutoLFADS (PSD_AutoLFADS) and the output of a 20 Hz Butterworth low pass filter $\left(PS{D}_{l{f}_{20}}\right)$ within each window. We then computed the linear frequency responses as a ratio of the filtered and raw spectra. Finally, we computed the mean and SEM across each EMG and gait cycle.

Predicting dF/dt (monkey isometric).

Force onset was determined within a window 250ms prior and 750ms after the target appearance in successful trials by finding the threshold crossing point 15% of the max dF/dt within that window. We used OLE to perform single timepoint decoding to map the EMG activity of 14 muscle channels onto the X and Y components of dF/dt. We performed the same CV scheme used in the rat locomotion joint angular decoding analysis to evaluate decoding performance of the different EMG representations. During fitting of the decoders, we normalized the EMG predictors to have zero-mean and unit standard deviation. We penalized the weights of the decoder using an L2 ridge regularization penalty of 1.

Predicting M1 activity.

We used OLE as described above to perform single timepoint linear decoding to map the EMG activity of 14 muscle channels onto the 96 channels of Gaussian smoothed motor cortical threshold crossings (standard deviation of Gaussian kernel: 35ms). We performed a sweep for the optimal lag (ranging from 0 to 150ms) for each M1 channel. To assess significance, we performed a Wilcoxon signed-rank test using MATLAB command signrank to perform a one-sided nonparametric paired difference test comparing the mean CV VAF values for predictions of all 96 channels.

Oscillation analyses.

To visualize the consistency of the oscillations observed in AutoLFADS output from the monkey isometric task, we varied the lead or lag for single trials in order to minimize the residual between the single trial activity and the trial-average for a given condition (Williams et al., 2020). We provided the algorithm with a window of AutoLFADS output around the time of force onset (80ms prior, 240ms after), and constrained the algorithm to limit the maximum shift to be 35ms, approximately half the width of an oscillation, and for the trial-averaged templates for each condition to be non-negative. For all applications of the optimal shift algorithm, we applied a smoothness penalty of 1.0 on the L2 norm of second temporal derivatives of the warping templates.

For coherence analyses, we aligned the single-trial data around the alignment provided by the optimal shifting algorithm and isolated a window of EMG activity and dF/dt (300ms prior, 600ms after). For each condition, we used the MATLAB function mscohere to compute coherence between the single trial activity of a given muscle’s activity and dF/dt X or Y. We matched the Hanning window size and the number of FFT points (120 timepoints) and used 100 timepoints of overlap between windows.

Results

Applying AutoLFADS to EMG from locomotion

We first tested the adapted AutoLFADS approach using previously recorded data from the right hindlimb of a rat walking at constant speed on a treadmill (Alessandro et al., 2018). Seven markers were tracked via high-speed video, which allowed the 3 joint angular kinematic parameters (hip, knee, and ankle) to be inferred, along with the time of foot contact with the ground (i.e., foot strike) and the time when the foot left the ground (i.e., foot off) for each stride (Fig. 2a). We also recorded EMG signals from 12 hindlimb muscles using intramuscular electrodes. Continuous hindlimb EMG recordings were segmented using behavioral event annotations, considering foot strike as the beginning of each stride. Aligning estimates to behavioral events allowed us to decompose individual strides into the “stance” phase, where the foot is in contact with the ground, and the “swing” phase, where the foot is in the air in preparation for the next stride.

Fig. 2 |. Applying AutoLFADS to rat locomotion.

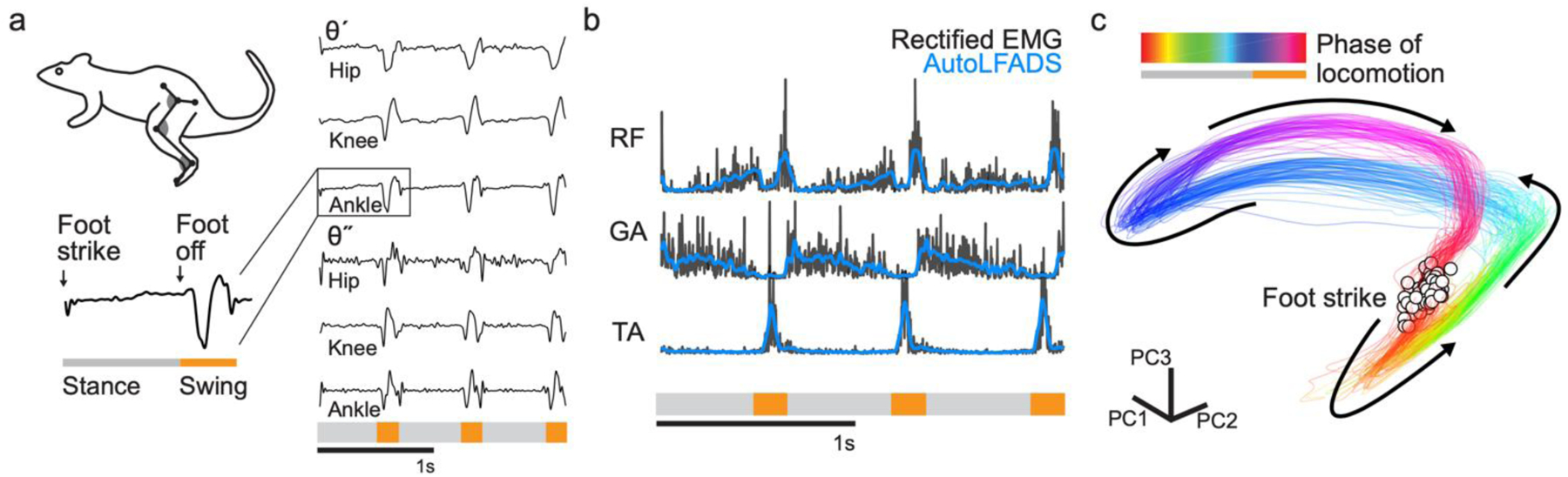
(a) Schematic of rat locomotion. Lower left trace indicates “stance” and “swing” phases during a single stride, swing labeled below in orange. On the right are joint angular velocities (θ’) and accelerations (θ”) for hip, knee and ankle over three consecutive strides. (b) Example AutoLFADS output (blue) overlaid on rectified, unfiltered EMG (black) for three muscles in the rat hindlimb (RF: rectus femoris, GA: gastrocnemius, TA: tibialis anterior). (c) Top 3 principal components of the AutoLFADS output for individual strides, colored by phase of locomotion (total variance explained: 92%). Arrows indicate the direction of the state evolution over time. Foot strike events are labeled with white dots.

AutoLFADS output substantially reduced high-frequency fluctuations while still tracking fast changes in the EMG (Fig. 2b), reflecting both slowly changing phases of the behavior (e.g., the stance phase) and rapid behavioral changes (e.g., the beginning of the swing phase. AutoLFADS models were trained in a completely unsupervised manner, which meant the models did not have information about the behavior, the identity of the recorded muscles, or any additional information outside of the rectified multi-muscle EMG activity. Visualizing muscle activity using state space representations helps to illustrate how AutoLFADS was capable of modeling dynamics. We performed dimensionality reduction via principal components analysis to reduce the 12 AutoLFADS output channels to the top three components (Fig. 2c). AutoLFADS estimates from individual strides followed a stereotyped trajectory through state space: state estimates were tightly clustered at the time of foot strike, and evolved in a manner where activity at each phase of the gait cycle occupied a distinct region of state space.

AutoLFADS adapts filtering to preserve behaviorally relevant, high-frequency features

A key feature that differentiates AutoLFADS from previous approaches is its ability to adapt its filtering properties dynamically to phases of behavior having signal content with different timescales. We demonstrated the adaptive nature of the AutoLFADS model by comparing its filtering properties during the swing and stance phases of locomotion. Swing phase contains higher-frequency transient features related to foot lift off and touch down, which contrast with the lower frequency changes in muscle activity during stance. We computed the power spectral density (PSD) for the AutoLFADS inferred muscle activations, rectified EMG smoothed with a 20 Hz low pass 4-pole Butterworth filter, and the unfiltered rectified EMG within 350 ms windows centered on the stance and swing phases of locomotion. We then used these PSD estimates to compute the frequency responses of the AutoLFADS model - i.e., approximating it as a linear filter - and of the 20 Hz low pass filter over many repeated strides within the two phases (see Methods).

As expected, the 20 Hz low pass filter had a consistent frequency response during the swing and stance phases (Fig. 3). In contrast, the AutoLFADS output resulted in substantially different frequency response estimates that enhanced high frequencies during the rapid changes of the swing phase and attenuated them during stance. Less obviously, the frequency responses estimated for AutoLFADS differed across muscles, despite its reliance on a shared dynamical system. Some AutoLFADS frequency responses (e.g., GS and RF) changed substantially between stance and swing in the 10–20 Hz frequency band; however, other muscles (e.g., IL and GA) shifted only slightly.

Fig. 3 |. AutoLFADS filtering adapts to preserve behaviorally relevant, high-frequency EMG features.

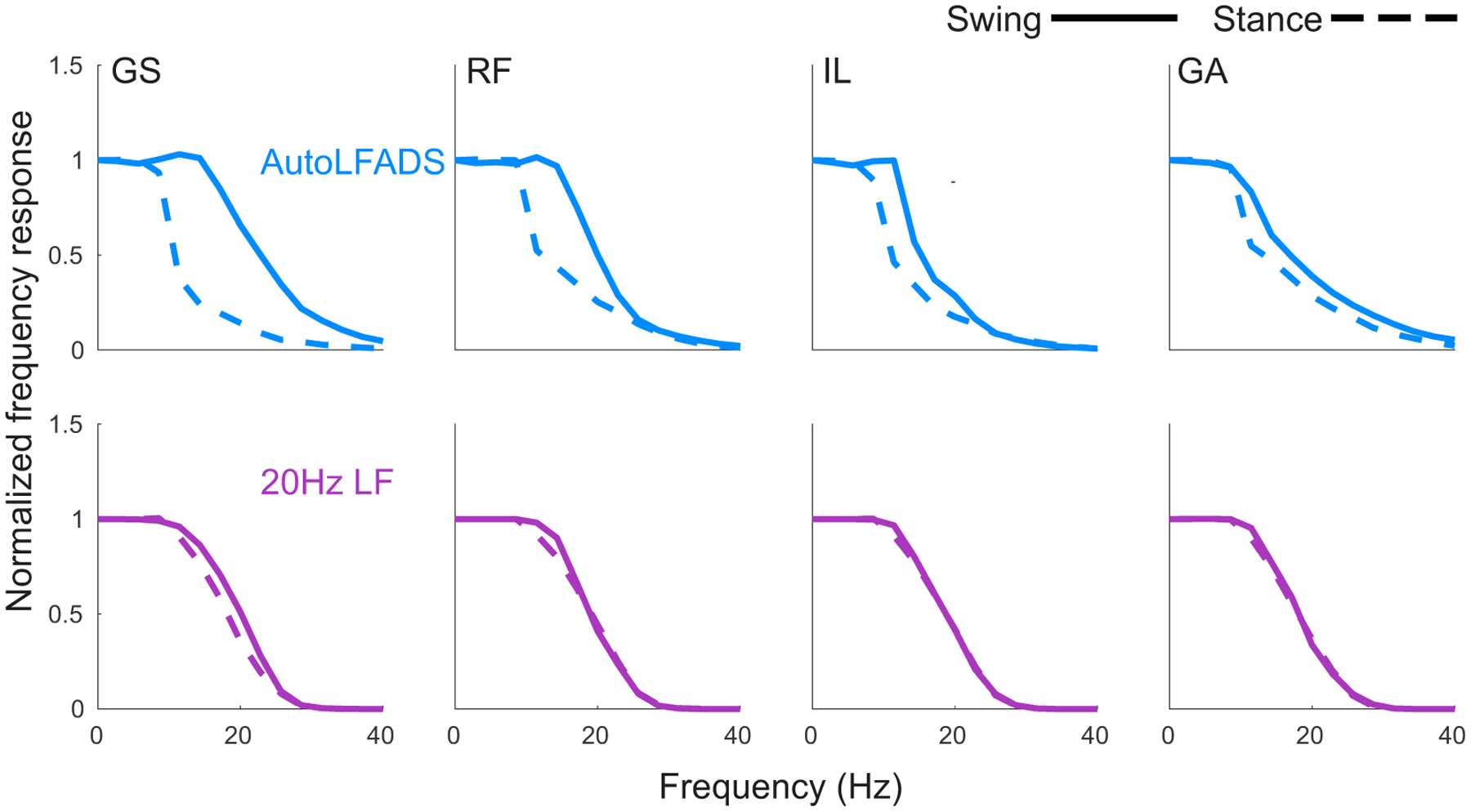
(a) Approximated frequency responses of lf₂₀ EMG (purple) and AutoLFADS (blue) for 4 muscles in the swing (solid) and stance (dashed) phases (GS: gluteus superficialis, RF: rectus femoris, IL: iliopsoas, GA: gastrocnemius). Shaded area represents SEM of estimated frequency responses from single stride estimates. Estimated frequency responses from single strides were highly consistent, resulting in small SEM. Gray vertical line at 20Hz signifies low pass filter cutoff.

AutoLFADS is more predictive of behavior than other filtering approaches

Training AutoLFADS models in an unsupervised manner (i.e., without any information about simultaneously recorded behavior, experiment cues, etc.) raises the question of whether the muscle activation estimates were informative about behavior. To assess this, we compared muscle activations estimated by AutoLFADS to those estimated using standard filtering approaches, by evaluating how well each estimate could decode simultaneously recorded behavioral variables (Fig. 4). We performed single-timestep optimal linear estimation (OLE) on joint angular accelerations (Fig. 4a) that captured high-frequency changes in the joint angular kinematics of rats during locomotion.

Fig. 4 |. AutoLFADS muscle activation estimates are more predictive of joint angular acceleration than are other filtering approaches.

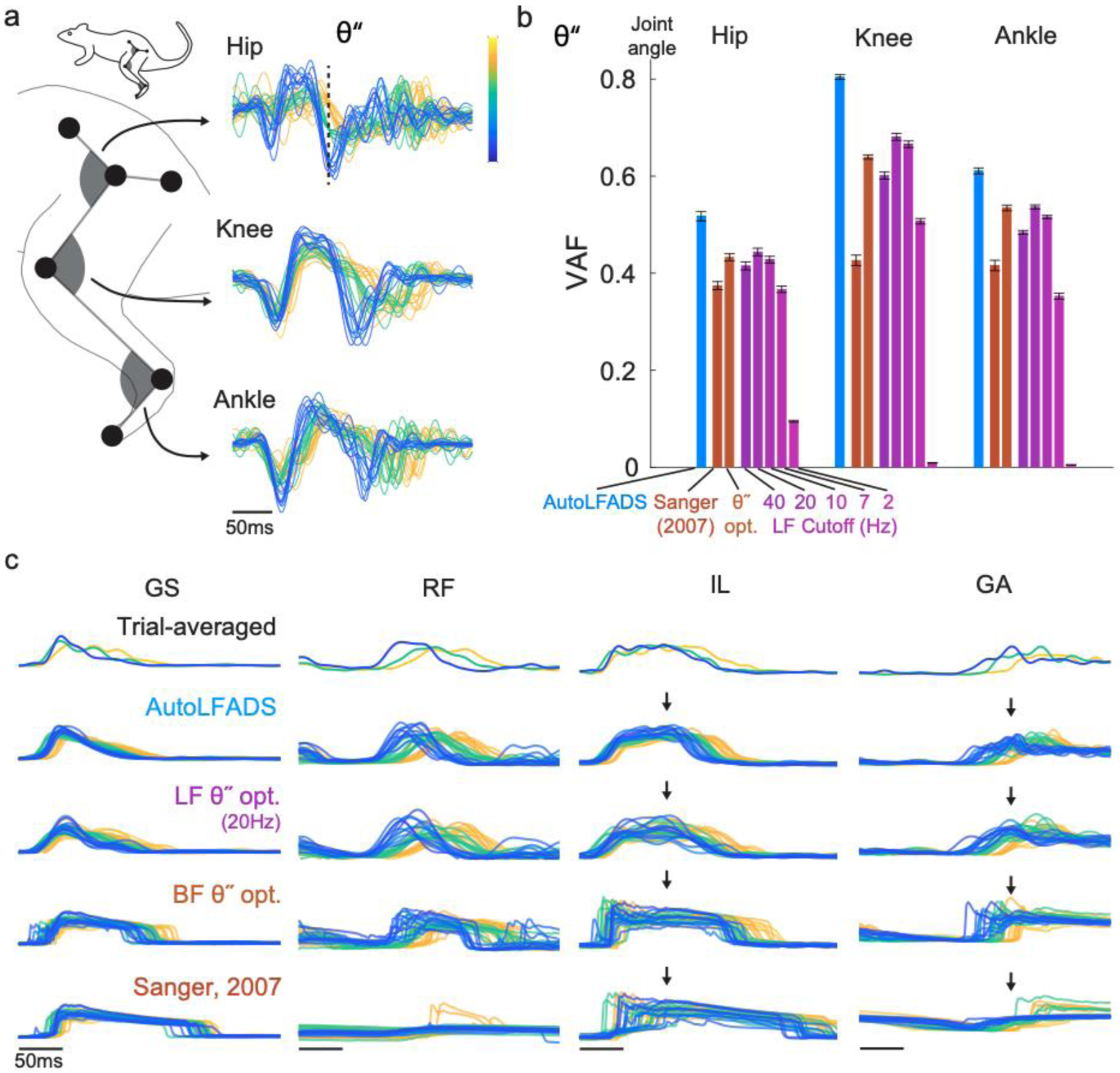
(a) Visualization of single trial joint angular accelerations (θ”) for hip, knee, and ankle joint angular kinematic parameters. Trials were aligned to the time of foot off using an optimal shift alignment method, then grouped and colored based on the magnitude of the hip angular acceleration at a specific time (indicated by dashed line). (b) Joint angular acceleration decoding performance for AutoLFADS, Bayesian filtering approaches, and multiple low-pass filter cutoff frequencies, quantified using variance accounted for (VAF). Each bar represents the mean +/− SEM across cross-validated prediction VAF values for a given joint. (c) Visualization of single trial muscle activation estimates for AutoLFADS, 20 Hz low-pass filter (LF θ” opt.), Bayesian filtering with hyperparameters optimized to maximize prediction of θ” (BF θ” opt.), and Bayesian filtering using the same hyperparameters as Sanger, 2007. Alignment and coloring of single trials are the same as (a). Arrows highlight visual features that differentiate muscle activation estimates from tested methods.

AutoLFADS significantly outperformed all low-pass filter cutoffs (ranging from 2 to 40Hz), as well as Bayesian filtering for prediction of angular acceleration at the hip, knee, and ankle joints, as quantified by the variance accounted for (VAF; Fig. 4b). AutoLFADS substantially outperformed the next-highest performing method for all joints (differences in VAF: hip: 0.10, knee: 0.13, ankle: 0.06, p<1e-05 for all comparisons, paired t-test). Visualizing the muscle activation estimates for individual strides underscored the differences between the approaches (Fig. 4c). Even Bayesian filters optimized to maximize prediction accuracy of joint angular accelerations did significantly worse than AutoLFADS. Qualitatively, we found that the Bayesian filter overestimated the amount of time each muscle was active during the gait cycle. Even though the AutoLFADS model was trained in an unsupervised manner with no knowledge of the joint angular accelerations, our approach outperformed other approaches that had manually tuned hyperparameters to yield the best possible decoding performance. Separately, we found that AutoLFADS generalized well across behavioral conditions – for example, by training on data from a single condition (locomotion speed, or treadmill incline) and testing on data from unseen conditions (detailed in Supplementary Fig. 2). Perhaps surprisingly, we also found that performance was robust to dataset size limitations (Supplementary Fig. 3).

Applying AutoLFADS to forearm EMG from isometric wrist tasks

To test the generalizability of our approach to other model systems, muscle groups, and behaviors, we also analyzed data from a monkey performing a 2-D isometric wrist task (Fig. 5a) (Gallego et al., 2020). EMG activity was recorded from 12 forearm muscles (with multiple recordings in two muscles) during a task requiring the monkey to generate isometric forces at the wrist. The monkey’s forearm was restrained and its hand placed securely in a box instrumented with a 6 DOF load cell. Brain activity was simultaneously recorded via a 96-channel microelectrode array in the hand area of contralateral M1. The monkey controlled the position of a cursor displayed on a monitor by modulating the force they exerted. Flexion and extension forces moved the cursor right and left, respectively, while forces along the radial and ulnar deviation axis moved the cursor up and down. The monkey controlled the on-screen cursor to acquire targets presented in one of eight locations in a center-out behavioral task paradigm. Each trial consisted of a step-like transition from a state of minimal muscle activity prior to target onset to one of eight phasic-tonic muscle activation patterns (i.e., one for each target) that enabled the monkey to hold the cursor at the target. The distinct, step-like muscle activation patterns across targets contrasted the cyclic behavior and highly repetitive activation patterns observed during rat locomotion, allowing us to evaluate AutoLFADS in two fundamentally different contexts.

Fig. 5|. Applying AutoLFADS to isometric wrist tasks.

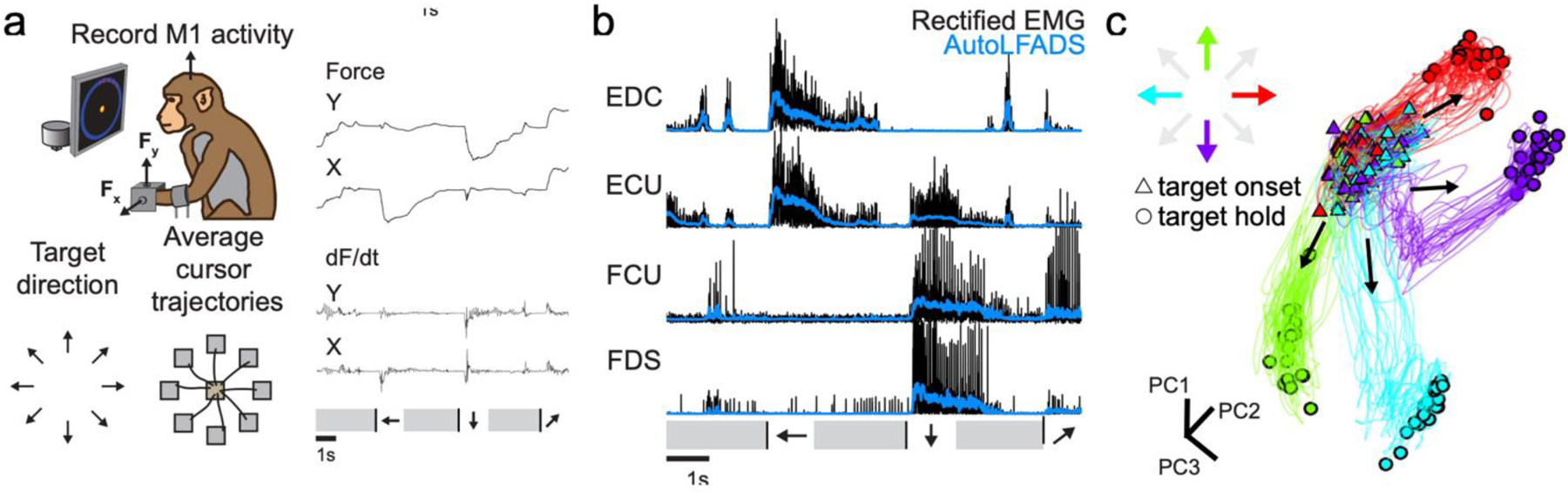
(a) Schematic of monkey isometric wrist task. Force and dF/dt are shown for three consecutive successful trials. The target acquisition phases are indicated by arrows corresponding to the target directions. Black lines denote target onset. Grey intervals denote return to and hold within the central target. (b) Example AutoLFADS output (blue) overlaid on rectified EMG (black) for four forearm muscles that have a moment about the wrist (EDC: extensor digitorum communis, ECU: extensor carpi ulnaris, FCU: flexor carpi ulnaris, FDS: flexor digitorum superficialis). (c) Top three principal components of AutoLFADS output for four conditions, colored by target hold location (total variance explained: 88%).

We trained an AutoLFADS model on EMG activity from the monkey forearm during the wrist isometric task to estimate the muscle activation for each muscle (Fig. 5b). As was the case for the locomotion data, AutoLFADS substantially reduced high-frequency fluctuations while still tracking changes in the rectified EMG, reflecting both smooth phases of the behavior (e.g., the period prior to target onset in the wrist task) and rapid behavioral changes (e.g., the target acquisition period in the wrist task). We again performed dimensionality reduction to reduce the 14 AutoLFADS outputs to the top three PCs. In the monkey data, the muscle activation estimates from AutoLFADS began consistently in a similar region of state space at the start of each trial, then separated to different regions at the target hold period. This demonstrates that the model was capable of inferring distinct patterns of muscle activity for different target directions, even without the cyclic, repeated task structure of the locomotion data (Fig. 5c).

AutoLFADS uncovers high-frequency oscillatory structure across muscles during isometric force production

An interesting attribute of the isometric wrist task is that for certain target conditions that require significant flexion of the wrist, the x component of force contains high-frequency oscillations – made evident by visualizing the dF/dt (Fig. 6a). Corresponding oscillatory structure can be seen in the EMG of flexor muscles (Fig. 6b). We found that muscle activation estimates of these high-frequency features differed across approaches (Fig. 6c) AutoLFADS output showed clear, consistent oscillations that lasted for 3–4 cycles, while other approaches such as Bayesian filtering (using the hyperparameters from Sanger, 2007) smoothed over these features. Oscillations in dF_x/dt were visible for three of the eight target conditions (Fig. 6d) and corresponding oscillations were observed across the flexor muscles in the AutoLFADS output (Fig. 6e) in those trials.

Fig. 6 |. AutoLFADS enhances high-frequency coherence with dF/dt.

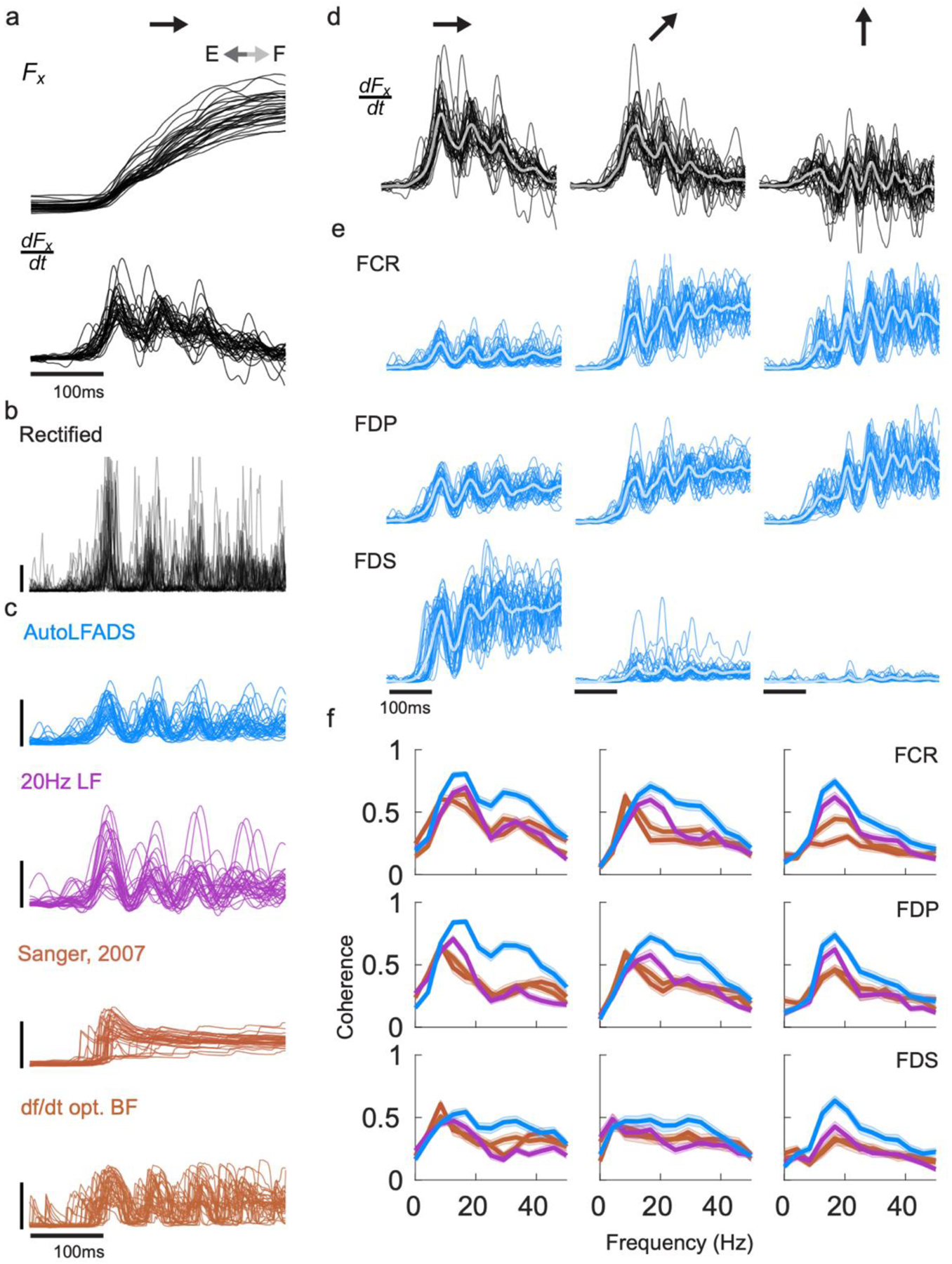
(a) Single trial oscillations were captured in the x component of recorded force (and more clearly in in dF_x/dt) for the flexion target direction. (b) Corresponding oscillations were faintly visible in the rectified EMG. (c) Single trial muscle activation estimates from different approaches (d) Single trial oscillations of dF_x/dt for three of the eight conditions, specifically to targets in the upper/right quadrant. Thick traces: trial average. (e) Single trial oscillations were also visible in AutoLFADS output across the wrist and digit flexor muscles (FCR: flexor carpi radialis, FDP: flexor digitorum profundus, FDS: flexor digitorum superficialis) (f) Magnitude-squared coherence computed between single trial EMG for a given muscle and dF_x/dt) and averaged across trials. Each line represents the mean +/− SEM coherence to dF_x/dt) for a given muscle activation estimate. Coherence was compared between AutoLFADS, lf₂₀ EMG, Bayesian filtering with hyperparameters optimized to maximize prediction of dF/dt, and Bayesian filtering using the same hyperparameters as Sanger, 2007.

To quantify this correspondence, we computed the coherence between the muscle activation estimates and dF_x/dt separately for each condition for single trials. If the high-frequency features conserved by AutoLFADS accurately reflect underlying muscle activation, then they should have a closer correspondence with behavior (i.e., dF_x/dt) than those features that remain after smoothing or Bayesian filtering. Coherence in the range of 10–50 Hz was significantly higher for AutoLFADS than for the other tested approaches, while all three muscle activation estimates had similar coherence with dF_x/dt below 10 Hz (Fig. 6f). These results further demonstrate the power of AutoLFADS to capture high-frequency features in the muscle activation estimates with higher fidelity than previous approaches.

AutoLFADS preserves information about descending cortical commands

Simultaneous recordings of motor cortical and muscle activity gave us the ability to test how accurately AutoLFADS could capture the influence of descending cortical signals on muscle activation. We trained linear decoders to map the different muscle activation estimates onto each of the 96 channels of smoothed motor cortical activity. Note that while the causal flow of activity is from M1 to muscles, we predicted in the opposite direction (muscles to M1) so that we had a consistent target (M1 activity) to assess the informativeness of the different muscle activation estimates. For each channel of M1 activity, we smoothed the observed threshold crossings using a Gaussian kernel with standard deviation of 35ms. We performed predictions in a window spanning 150 ms prior to 150 ms after force onset. For each neural channel, we found the optimal single decoding lag between neural and muscle activity by sweeping in a range from 0 to 100ms (i.e., we allowed predicted neural activity to precede the muscle activity predictors by up to 100 ms). AutoLFADS significantly improved the accuracy of M1 activity prediction when compared to 20Hz low pass filtering (Fig. 7; mean percentage improvement: 12.4%, p=2.32e-16, one-sided Wilcoxon paired signed rank test). Similarly, AutoLFADS significantly improved M1 prediction accuracy when compared to Bayesian filtering using previously published hyperparameters (mean percentage improvement: 22.2%, p=4.58e-16, one-sided Wilcoxon paired signed rank test) or using hyperparameters optimized to predict behavior (mean percentage improvement: 16.9%, p=7.37e-16, one-sided Wilcoxon paired signed rank test). This demonstrates that AutoLFADS not only captures behaviorally-relevant features, but also preserves signals that reflect activity in upstream brain areas that are involved in generating muscle activation commands.

Fig. 7 |. AutoLFADS improves correlation with motor cortical (M1) activity.

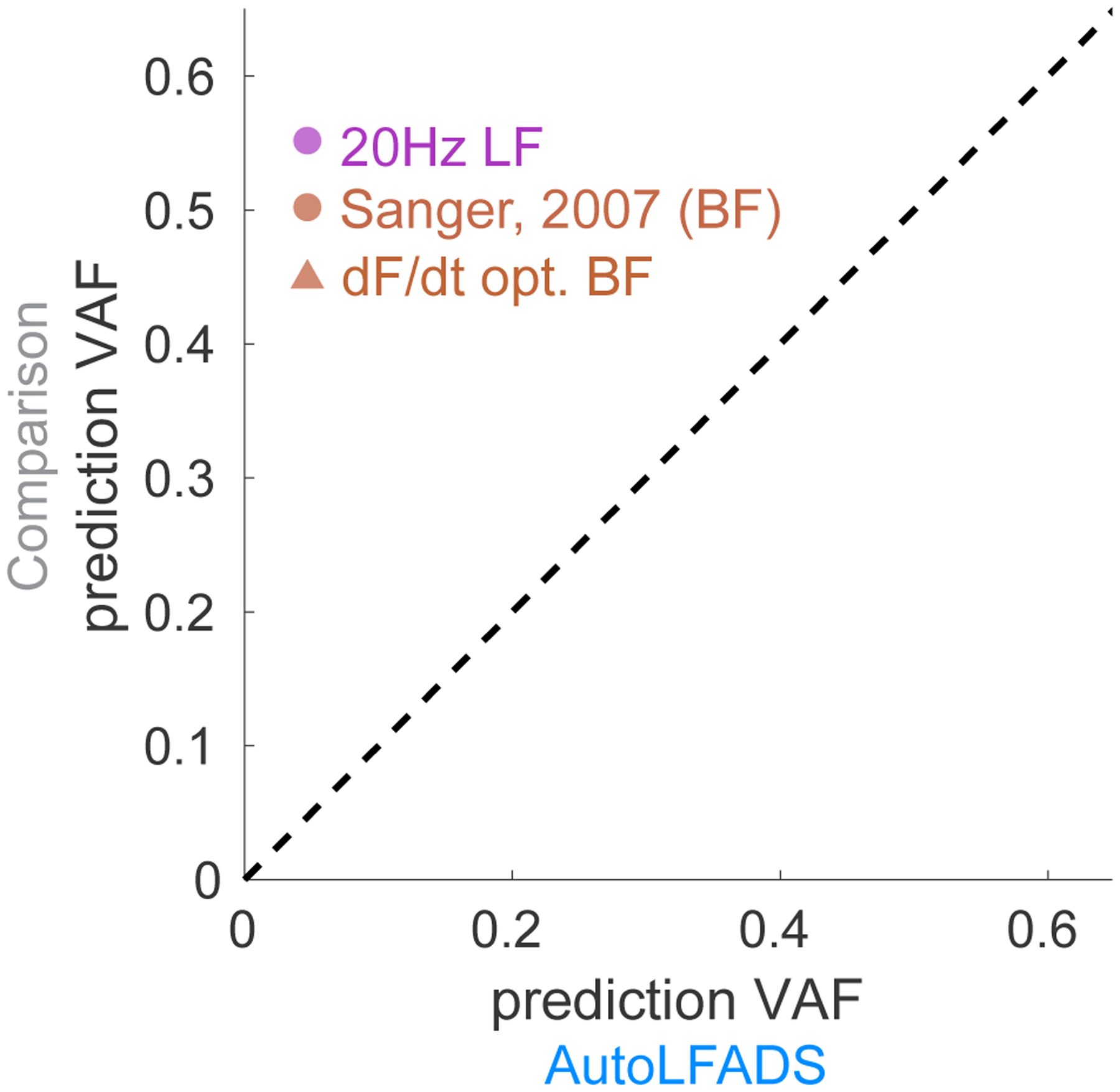
Scatter plot comparing accuracy of the prediction of motor cortical activity from EMG using different filtering approaches and AutoLFADS. Each dot represents prediction accuracy in terms of VAF for a single M1 channel.

Discussion

Relation to previous work

Substantial effort has been invested over the past 50 years to develop methods to estimate the latent command signal to muscles - termed the neural drive - through EMG recordings (Farina et al., 2014, 2004). This is a challenging problem as typical recordings reflect the summed activity of many different motor units, which can lead to interference among the biphasic potentials, and signal cancellation (Negro et al., 2015). As muscle contraction increases, the linear relationship between the number of active motor units and the amplitude of the recorded EMG becomes distorted, making it non-trivial to design methods that can extract neural drive (Dideriksen and Farina, 2019).

Higher spatial resolution recordings that isolate individual motor units may allow neural drive to be inferred with greater precision. For example, high-density EMG arrays have enabled access to as many as 30 to 50 individual motor units from the surface recordings of a single muscle (De Luca et al., 2006; Del Vecchio et al., 2020; Farina et al., 2016). By isolating, then recombining the activity of individual motor units, one can better extract the common input signal, yielding estimates that are more closely linked to force output than is the typical EMG (Boonstra et al., 2016; De Luca and Erim, 1994; Farina and Negro, 2015). Here, we showed that AutoLFADS similarly enhanced correspondence to force output and other behavioral parameters (e.g., joint angular acceleration) relative to standard EMG processing techniques; how well this improvement approaches that of inferring and recombining multiple motor unit recordings is not clear and should be the goal of future work.

AutoLFADS leverages recent advances at the intersection of deep learning and neuroscience to create a powerful model that describes both the spatial and temporal regularities that underlie multi-muscle coordination. Previous work has attempted to estimate neural drive to muscles by exploiting either temporal regularities in EMGs using Bayesian filtering techniques applied to single muscles (Hofmann et al., 2016; Sanger, 2007) or spatial regularities in the coordination of activity across muscles (Alessandro et al., 2012; d’Avella et al., 2003; Hart and Giszter, 2004; Kutch and Valero-Cuevas, 2012; Ting and Macpherson, 2005; Torres-Oviedo and Ting, 2007; Tresch et al., 2006, 1999). Conceptually, AutoLFADS approaches the problem in a different way by using an RNN to simultaneously exploit both spatial and temporal regularities. AutoLFADS builds on advances in training RNNs (e.g., using sequential autoencoders) that have enabled unsupervised characterization of complex dynamical systems, and large-scale optimization approaches that allow neural networks to be applied out-of-the-box to a wide variety of data. Capitalizing on these advances allows a great deal of flexibility in estimating the regularities underlying muscle coordination. For example, our approach does not require an explicit estimate of dimensionality, does not restrict the modelled muscle activity to the span of a fixed time-varying basis set (Alessandro et al., 2012; d’Avella et al., 2003), does not assume linear interactions in the generative model underlying the observed muscle activations, and has an appropriate (and easily adapted) noise model to relate inferred activations to observed data. This flexibility enabled us to robustly estimate neural drive to muscles across a variety of conditions: different phases of the same behavior (stance vs. swing), different animals (rat vs. monkey), behaviors with distinct dynamics (locomotion vs. isometric contractions), and different time scales (100’s of ms vs. several seconds). AutoLFADS can therefore be used by investigators studying motor control in a wide range of experimental conditions, behaviors, and organisms.

Limitations

EMG is susceptible to artifacts (e.g., powerline noise, movement artifact, cross-talk, etc.), therefore any method that aims to extract muscle activation from EMG necessitates intelligent choice of preprocessing to mitigate the potential deleterious effects of these noise sources (see Methods). As a powerful deep learning framework that is capable of modeling nonlinear signals, AutoLFADS has a specific sensitivity to even a small number of high-amplitude artifacts that can skew model training, since producing estimates that capture these artifacts can actually lower the reconstruction cost that the model is trying to minimize. Our implementation of data augmentation strategies during training helped mitigate the sensitivity of AutoLFADS to spurious high-magnitude artifacts. In particular, in the current datasets, muscle activation estimates from AutoLFADS were more informative about behavior and brain activity than standard approaches. This high performance suggests that noise sources in our multi-muscle EMG recordings did not critically limit the method’s ability to infer estimates of muscle activation. However, these factors may be more limiting in recordings with substantial noise. Future studies may be able to explore additional methods, such as regularization strategies or down-weighting reconstruction costs for high-magnitude signals, to further mitigate the effects of artifacts.

Potential Future Applications

The applications of AutoLFADS may extend beyond scientific discovery to improved clinical devices that require accurate measurement of muscle activation, such as bionic exoskeletons for stroke patients or myoelectric prostheses for control of assistive devices. Current state of the art myoelectric prostheses use supervised classification to translate EMGs into control signals (Ameri et al., 2018; Hargrove et al., 2017; Vu et al., 2020). AutoLFADS could complement current methods through unsupervised pre-training to estimate muscle activation from EMG signals before they are input to classification algorithms. The idea of unsupervised pre-training has gained popularity in the field of natural language processing (Qiu et al., 2020). In these applications, neural networks that are pre-trained on large repositories of unlabeled text data uncover more informative representations than do standard feature selection approaches, which improves accuracy and generalization in subsequent tasks. Similar advantages have been demonstrated for neural population activity by unsupervised pre-training using LFADS, where the model’s inferred firing rates enable decoding of behavioral correlates with substantially higher accuracy and better generalization to held-out data than standard methods of neural data pre-processing (Keshtkaran et al., 2021; Pandarinath et al., 2018).

Designing AutoLFADS models that require minimal or no network re-training to work across subjects could help drive translation to clinical applications. Another area of deep learning research - termed transfer learning - has produced methods that transfer knowledge from neural networks trained on one dataset (termed the source domain) to inform application to different data (termed the target domain) (Zhuang et al., 2020). Developing subject-independent AutoLFADS models using transfer learning approaches would reduce the need for subject-specific data collection that may be difficult to perform outside of controlled, clinical environments. Subject-independent models of muscle coordination may also benefit brain-controlled functional electrical stimulation (FES) systems that rely on mapping motor cortical activity onto stimulation commands to restore muscle function (Ajiboye et al., 2017; Ethier et al., 2012). Components of subject-independent AutoLFADS models trained on muscle activity from healthy patients, could be adapted for use in decoder models that aim to map simultaneous recordings of motor cortical activity onto predictions of muscle activation for patients with paralysis. These approaches may provide a neural network solution to decode muscle activation commands from brain activity more accurately, serving to improve the estimates of stimulation commands for FES implementations. Combining AutoLFADS with transfer learning methods could also enable the development of new myoelectric prostheses that infer the function of missing muscles by leveraging information about the coordinated activation of remaining muscles.

There are several aspects of the AutoLFADS approach that might provide additional insights into the neural control of movement. First, AutoLFADS also provides an estimate of the time-varying input to the underlying dynamical system (i.e., u[t]). The input represents an unpredictable change to the underlying muscle activation state, which likely reflects commands from upstream brain areas that converge with sensory feedback at the level of the spinal cord, as well as reflexive inputs. Analyzing u[t] in cases where we also have simultaneous recordings of relevant upstream brain areas may allow us to more precisely distinguish the contributions of different upstream sources to muscle coordination. Second, AutoLFADS may also be useful for studying complex, naturalistic behavior. In this study we applied AutoLFADS to activity from two relatively simple, yet substantially different motor tasks, each with stereotypic structure. However, because the method is applied to windows of activity without regard to behavior, it does not require repeated, similar trials or alignment to behavioral events. Even with this unsupervised approach, AutoLFADS preserved information about behavior (kinematics and forces) with higher fidelity than standard filtering to preserve behaviorally-relevant features. As supervision becomes increasingly challenging during behaviors that are less constrained or difficult to carefully monitor (e.g., free cage movements), unsupervised approaches like AutoLFADS may be necessary to extract precise estimates of muscle activity. AutoLFADS may therefore have the potential to overcome traditional barriers to studying neural control of movement by allowing investigators to study muscle coordination during unconstrained, ethologically-relevant behaviors rather than the constrained, artificial behaviors often used in traditional studies.

Conclusion

We demonstrate that AutoLFADS is a powerful tool to estimate muscle activation from EMG activity, complementing the analysis of cortical activity to which it has previously been applied. In our tests, AutoLFADS outperformed standard filtering approaches in estimating muscle activation. In particular, the AutoLFADS-inferred muscle activation commands were substantially more informative about both behavior and brain activity, all in an unsupervised manner that did not require manual tuning of hyperparameters. Further, we observed robust performance across data from two different species (rat and monkey) performing different behaviors that elicited muscle activations at varying timescales and with very different dynamics. The lack of prior assumptions about behaviorally-relevant timescales is critical, as there is growing evidence that precise timing plays an important role in motor control, and that high-frequency features may be important for understanding the structure of motor commands (Sober et al., 2018; Srivastava et al., 2017). We demonstrated that AutoLFADS is capable of extracting high-frequency features underlying muscle commands - such as the muscle activity related to foot off during locomotion, or the oscillations uncovered during isometric force contraction - that are difficult to analyze using conventional filtering. By improving our ability to estimate short-timescale features in muscle activation, AutoLFADS may serve to increase the precision with which we analyze EMG signals when studying motor control or translating them to control applications.

Data availability

Data will be made available upon reasonable request from the authors. An example rat locomotion dataset will be available with the AutoLFADS tutorial.