Simple Assessment of Red Blood Cell Deformability Using Blood Pressure in Capillary Channels for Effective Detection of Subpopulations in Red Blood Cells

Abstract

Assessment of red blood cell (RBC) deformability as a biomarker requires expensive equipment to induce and monitor deformation. In this study, we present a simple method for quantifying RBC deformability. We designed a microfluidic channel consisting of a micropillar channel and a coflowing channel connected in series. When blood (loading volume = 100 μL) was injected continuously into the device under constant pressure (1 bar), we monitored the boundary position of the blood and the reference flow in the coflowing channel. A decrease in the deformability of RBCs results in a growing pressure drop in the micropillar channel, which is mirrored by a decrease in blood pressure in the coflowing channel. Analysis of this temporal variation in blood pressure allowed us to define the clogging index (CI) as a new marker of RBC deformability. As a result of the analytical study and numerical simulation, we have demonstrated that the coflowing channel may serve as a pressure sensor that allows the measurement of blood pressure with accuracy. We have shown experimentally that a higher hematocrit level (i.e., more than 40%) does not have a substantial influence on CI. The CI tended to increase to a higher degree in glutaraldehyde-treated hardened RBCs. Furthermore, we were able to resolve the difference in deformability of RBCs between two different RBC density subfractions in human blood. In summary, our approach using CI provides reliable information on the deformability of RBCs, which is comparable to the readouts obtained by ektacytometry. We believe that our microfluidic device would be a useful tool for evaluating the deformability of RBCs, which does not require expensive instruments (e.g., high-speed camera) or time-consuming micro-PIV analysis.

1. Introduction

Red blood cells (RBCs) are highly deformable. When not in flow, the majority of human RBCs are shaped like biconcave disks with 6–8 μm diameter and 2.5 μm thickness.¹ While passing through the blood vessels, RBCs undergo shape transitions from discocyte to parachute, jellyfish, or torpedo shape depending on the vessel diameter and flow rate.² These shape changes enable the cells to pass through the micron-sized capillary vessels smaller in size than the RBC diameter without damage or membrane rupture, supporting the effective transport of gases (mainly oxygen and carbon dioxide) between the lungs and the peripheral tissues, capillary vessels, and peripheral tissues. The ability of RBCs to deform in response to shear stress is an essential feature that allows for effective microcirculation.³ It has been defined by several factors, such as biconcave-shaped discs with a high surface area–volume ratio, cytosolic viscosity, mechanical viscoelasticity of the membrane cytoskeleton, and integral membrane proteins. While effectively passing through a micron-sized capillary and splenic filter,⁴ each RBC deforms substantially under shear blood flow. RBCs that are unable to pass through the splenic filter (i.e., 0.65 × 1.9 × 2.5 μm³) are cleared. In healthy humans and patients, the splenic filter plays a major role in the removal of senescent or damaged cells.⁵ In patients presenting with major impairment of RBC deformability (i.e., sickle cell disease, thalassemia, hereditary spherocytosis, and malaria infection), intravascular hemolysis and entrapment of cells by the vascular endothelium also contribute to the development of anemic state.⁶ In sickle cell disease, low RBC deformability and intravascular hemolysis result in vascular damage, vaso-occlusion, multiple organ damage, and death.⁷

Currently, shear deformation between two surfaces (i.e., cone–plate or cocylinder) is applied as a conventional method to assess the bulk deformability of RBCs in whole blood or in RBC suspension.⁸ The RBC deformation capacity was assessed using a filtration assay or ektacytometry. These approaches, and the general clinical implications of RBC deformability, have been broadly established as disease markers. Ektacytometry (e.g., Lorrca Maxis) is the most frequently used method for detecting RBC disorders associated with alterations in deformability, hydration, and membrane stability in clinical settings. In the routine ektacytometry protocol, whole blood (100 μL) was suspended in a highly viscous isotonic polyvinylpyrrolidone (PVP) fluid. The resulting suspension of RBCs was loaded into the slit between the cap wall and rotational bob, which induced deformation of the RBCs. It allows measurement of the elongation index for RBCs at varying shear stress (τ = 0.5–30 Pa) and runs in a broad range of extracellular osmolarity (50–500 mOsm/kg) under unphysiologically high shear stress of τ = 30 Pa. During tank-treading behaviors of the RBC membrane,⁹ RBCs are elongated to an elliptical shape, which translates into a change in the laser diffraction pattern. This shape is uncommon when RBCs pass through the microvasculature, where multilobe structures, slippers, and jellyfish-like shapes are mostly observed.¹⁰ However, a robust and high-throughput Osmo-scan mode can provide information on the average bulk deformability of RBCs in a blood sample. The heterogeneity of RBCs cannot be resolved by this method, in which a diffraction pattern is generated for all cells, and minor RBC subfractions of poorly deformable cells remain unnoticed. For example, deformable young RBCs and poorly deformable damaged cells are present in moderate or severe hereditary spherocytosis, which could not be detected in the measurement.¹¹ Impaired RBC deformability and intravascular hemolysis in patients with hereditary spherocytosis are strongly associated with thrombotic complications.¹² Therefore, simple and high-throughput detection of RBCs with impaired deformability is crucial for diagnosing a patient’s severity.

The single RBC-cell approach¹³ resolves the properties of the individual RBCs. For example, individual RBCs can be sequentially injected into straight or funnel microfluidic channels. The deformability of RBCs is quantified by monitoring changes in morphology,¹⁴⁻¹⁸ transit time,¹⁹ occlusion,²⁰ RBC velocity,^21,22 lateral migration,^23,24 cortical tension,²⁵ Young’s modulus,²⁶ and electrical impedance.^27,28 This enabled us to study the heterogeneity of RBCs, which requires single RBC phenotyping with high sensitivity. However, owing to the necessity for precise manipulation of individual RBCs, low throughput has been considered a critical issue for clinical applications. On the other hand, to overcome the low throughput of the single RBC-based approach substantially, the population-based approach has been suggested. In this approach, blood suspensions with a high hematocrit are injected into microfluidic channels, such as capillary networks, comblike micropillars, and parallel micropillars. The deformability of RBCs is quantified by monitoring clogging,^29,30 cell-lysis rate,³¹ cell-to-liquid interface as pressure,³² and fraction of separated cells based on deformability.³³ Previously, our group reported that variations in blood flow (i.e., velocity or flow rate) are a potential index for quantifying the deformability of blood sample.³⁴ This approach detects minor differences in the RBC subpopulations.³⁵ However, this method has several technical bottlenecks owing to its broad use in clinical settings or laboratories. A redundant blood sample is required owing to the dead volume existing in fluidic connectors, including a syringe needle and a long tube. In addition, blood flow quantification requires a costly high-speed camera and a time-resolved microparticle image velocimetry (PIV) technique, which is only available to experts and requires time-consuming analysis. In addition, the accuracy of micro-PIV deteriorates when the hematocrit or flow rate changes over time,³⁶ which often occurs during the measurement. To address these issues, a new delivery method should be adopted to minimize dead volume in fluidic connectors. Furthermore, the previous method (i.e., the micro-PIV technique) must be replaced by a quantitative parameter that is equally meaningful (i.e., blood pressure).

This study presents a new, simple method for measuring the RBC deformability index using junction blood pressure quantified downstream of parallel micropillar channels. A blood sample was injected into one inlet at constant pressure to measure RBC deformability. Downstream of the micropillar channels, the blood flow is influenced by the degree of RBC deformability. RBCs with low deformability hinder their passage through micropillar channels. Thus, the blood velocity decreases significantly over time. Here, a single coflowing channel is located downstream of the micropillar channels to quantitatively monitor the blood flow. The flow rate of the reference fluid remained constant. Blood pressure was monitored by sequential microscopic imaging of the interface in the coflowing channel. The deformability index or clogging index of the RBCs was then obtained by analyzing the junction blood pressure.

Compared with previous methods, the present study has substantial merits. First, a blood sample was supplied to the microfluidic device with an air pressure controller. There was no dead volume through fluidic connectors other than the syringe pump. Therefore, the present method has the ability to measure RBC deformability with a smaller blood volume (100 μL approximately). Second, the blood pressure in a microfluidic channel was used to quantify the blood flow instead of the blood velocity fields. A new clogging index (CI) was proposed and quantified based on the temporal variations in blood pressure. The proposed method facilitates the measurement of RBC deformability without the use of costly instruments (e.g., high-speed cameras) and time-consuming micro-PIV analysis.

2. Experimental Section

2.1. Blood Sample Preparation

Venous heparinized blood (5–10 mL) was obtained after obtaining informed written consent from healthy volunteers in accordance with the Declaration of Helsinki at the Cantonal Hospital Winterthur, Switzerland. Blood samples (10 mL approximately) were obtained from the Clinical Laboratory of the Cantonal Hospital Winterthur. They were used to calibrate the blood analyzers, including ektacytometry and Lorrca MaxSis (RR Mechatronics). After centrifugation (Mikro 220, Hettich, Andreas Hettich Gmbh & Co.) (12 500 rpm = 14 674 rcf, 10 min), packed RBCs (bottom) and plasma (top) were collected, and the buffy coat was discharged. First, to evaluate the contribution of hematocrit to RBC deformability, the hematocrit (Hct) of blood samples was adjusted to Hct of 30%, 40%, and 50% by mixing RBCs with plasma in corresponding proportions. In other experiments, Hct was set to 50%, unless otherwise mentioned. Second, healthy RBCs were treated with a glutaraldehyde (GA) solution that partially cross-linked the surface proteins and reduced cellular deformability. Four solutions of GA (C_GA = 2.5, 5, 7.5, and 10 μL/mL) were prepared by adding a GA solution (Grade II, 25% in H₂O, Sigma-Aldrich) to 1× phosphate-buffered saline (PBS) for 10 min. Four samples of fixed blood were prepared by exposing normal RBCs to each concentration of the GA solution for 10 min. Fixed blood was immediately supplied to the microfluidic device without an additional washing procedure. Finally, to quantify the contribution of RBC density to RBC deformability, normal blood was fractioned with respect to the RBC density difference, as shown in Figure 1Ai. Fractionation of RBCs was performed in a continuous density gradient of an isotonic solution of Percoll (GE Healthcare, Sweden).³⁷ After setting the tube vertically in the gravitational direction, two fractions of RBCs (F₁, normal density; and F₂, high density) were collected in the middle and lower regions, respectively. Two blood samples were prepared by mixing RBCs with autologous plasma.

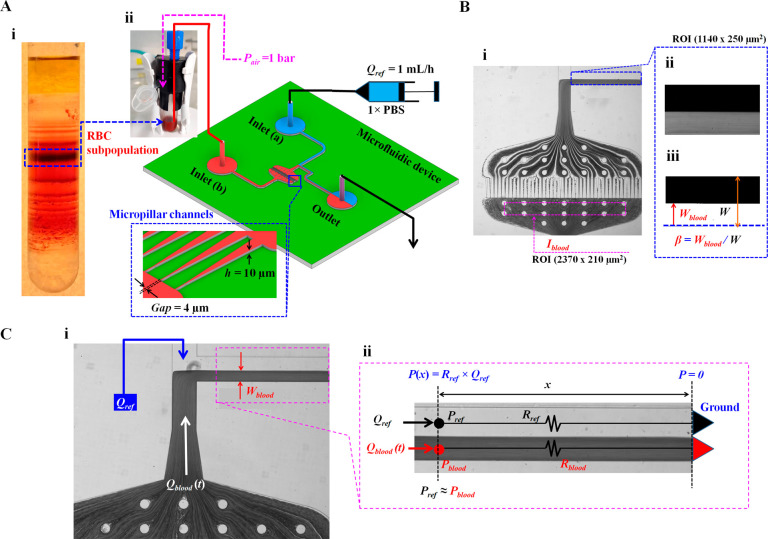
Figure 1.

Microfluidic-based deformability measurement for the effective monitoring of minor subpopulations in RBCs. (A) Schematic diagram of experimental setup including Percoll density gradient for collecting subpopulations in RBCs and a microfluidic system for measuring the RBCs’ deformability. (i) RBC subpopulation depending on the difference in density using the Percoll density gradient. (ii) Microfluidic system including a microfluidic device, a pressure controller for blood, and a syringe pump for reference fluid (1× PBS). The microfluidic device consists of two inlets (a, b), an outlet, and T-shaped channels (width [W] = 250 μm, and depth [h] = 10 μm). A micropillar channel (gap = 4 μm) is positioned between inlet a and the coflowing channel. Blood sample (0.1 mL approximately) was supplied into 1 mL tube. Using the pressure controller, blood was supplied into inlet a at a constant pressure of P_blood = 1 bar. The syringe pump is used to supply reference fluid into inlet b at the constant flow rate of Q_ref = 1 mL/h. (B) Two regions-of-interest (ROIs) selected for quantifying image intensity (I_blood) and interface in coflowing streams (β). (i) I_blood was calculated by averaging image intensity of blood flows based on ROI (2370 × 210 μm²) selected in the upstream of pillar channels. (ii) The grayscale image of the coflowing channel with ROI 1140 × 250 μm² was cropped after subtracting each grayscale image from the background image. (iii) Using a digital image procedure, the grayscale image was converted to a binary image. A blood-filled width (W_blood) was then calculated by averaging interfacial locations over the ROI. The β was defined as β = W_blood/W. (C) Simple mathematical model with a discrete fluidic circuit model for evaluating blood pressure in the coflowing channel (P_blood). (i) Coflowing channel filled with blood sample and reference fluid. Both fluids flow at the flow rates of Q_ref and Q_blood. Here, Q_blood is not specified and varied over time. (ii) Discrete fluidic circuit model of coflowing channel composed of fluidic resistances (R_ref, R_blood) and flow rates (Q_ref, Q_blood). Here, subscript ref and blood mean reference fluid and blood sample, respectively. As both fluid streams have the same pressure (i.e., P_ref = P_blood = P), blood pressure at a specific location [P(x)] is estimated analytically as P(x) = R_ref × Q_ref. ▶ represents P = 0 as the ground condition.

2.2. Microfluidic Device and Experimental Setup

Based on our previous study,³⁴ a microfluidic device was fabricated using a conventional microelectromechanical-system technique and soft lithography. As shown in Figure 1Aii, the microfluidic device is composed of two inlets (a, b), guide channels (upper and lower channels) connected to a single coflowing channel (width = 250 μm), and one outlet. The upper guide channel has a constant width of 250 μm. A lower guide channel with a constant width of 250 μm was connected to parallel micropillar channels (number of pillar channel = 43, minimum gap = 4 μm, and depth [h] = 10 μm). The coflowing channel was positioned downstream of the micropillar channels. The channel depth was set to 10 μm.

Each microfluidic device was mounted on an inverted microscope (IX81; Olympus, Tokyo, Japan) with a 4× objective lens (numerical aperture, NA = 0.13). To supply two fluids into an individual inlet, two polyethylene tubing pieces (length = 400 mm, PTFE no. 30, Cole-Parmer Instrument Co., Vernon Hills, United Kingdom) were connected to two inlets (a, b). A third piece of polyethylene tubing (length = 300 mm) was tightly fitted to the outlet. A disposable syringe (1 mL approximately) was filled with 1× PBS. The syringe needle was fitted at the end of the tubing connected to inlet a. Blood samples (0.1 mL approximately) were placed in Eppendorf tubes (1 mL). The end of the tubing connected to inlet b was dipped into blood. To avoid the formation of air bubbles and circumvent the nonspecific binding of plasma proteins into the microfluidic channels, the microfluidic device was purged and prefilled with PBS containing bovine serum albumin (2 mg/mL) manually through the outlet and allowed to equilibrate for 10 min. Subsequently, the fluid in the microfluidic device was replaced with albumin-free 1× PBS. The syringe was mounted on a syringe pump (NeMESYS; Cetoni GmbH). The syringe pump was set at a constant flow rate of 1 mL/h (Q_ref = 1 mL/h). A pressure controller (Flow EZ, 2 bar, Fluigent) was set to 1 bar to supply air pressure into the tube.

A digital sCMOS camera (Flash 4, Hamamatsu, Japan) was used to capture blood flow in the channels. The camera was set to an exposure time of 10 ms. Microscopic images were captured and saved at intervals of 1 s. All experiments were conducted at a constant room temperature.

2.3. Quantification of Microscopic Images of Blood Flow

RBC deformability was evaluated by evaluating the interface in the coflowing channel (Figure 1B). Additionally, the image intensity was used to monitor the blood flow upstream of the micropillar channels (Figure 1B). Digital image processing to obtain the image intensity and interface was conducted using MATLAB 2019 (MathWorks, Natick, MA). Two regions of interest (ROIs) were selected to quantify the image intensity (I_blood) and interfacial location in the coflowing streams (β).

First, the image intensity of blood flow was quantified upstream of the micropillar channel. As shown in Figure 1Bi, based on the ROI (2370 × 210 μm²) selected upstream of the micropillar channels, the averaged image intensity (I_blood) was obtained by averaging the grayscale image intensity distributed within the ROI.

Second, the interface was evaluated using three steps of digital image processing (background subtraction, image cropping, and binary image conversion) to quantify blood pressure in the coflowing channel. As shown in Figure 1Bii, the background image intensity was removed by subtracting the initial microscopic image without blood flow from the grayscale microscopic image captured at a specific time. The microscopic image was cropped by selecting an ROI (1140 × 250 μm²) in the coflowing channel. As shown in Figure 1Biii, an intensity level threshold (i.e., Otsu’s method)³⁸ is adopted to convert a grayscale image into a binary image. The blood-filled width in the coflowing channel (W_blood) was obtained by averaging the interface distributed within the ROI. The interface in the coflowing channel (β) was then obtained as β = W_blood/W by dividing the blood-filled width by the channel width (W).

2.4. Quantification of Junction Blood Pressure in the Blood Samples

A simple analytical model was developed using discrete circuit elements to derive the junction blood pressure (P_blood). As shown in Figure 1Ci, the coflowing channel was partially filled with two fluids. W_blood denotes the blood-filled width. Q_ref and Q_blood represent the reference fluid and blood sample flow rate, respectively. Downstream of the micropillar channels, the blood velocity was influenced by RBC deformability. If RBCs have low deformability, they hinder the flow of the micropillar channels. Partial clogging in the pillar channels resulted in a substantial increase in fluidic resistance. Otherwise, RBCs with normal deformability can easily pass through the channels. Therefore, Q_blood, which is influenced by RBC deformability, tends to vary continuously over time. As shown in Figure 1Cii, the coflowing channel was represented by discrete circuit elements, including fluidic resistances (R_ref, R_blood) and flow rates (Q_ref, Q_blood). The subscripts ref and blood represent the reference fluid and the blood sample, respectively. The symbol ▶ represents P = 0 as the ground condition. According to the fluidic circuit rule (i.e., Hagen–Poiseuille flow theorem), the increased pressure at a unique location (x) is estimated simply as P(x) = fluidic resistance (x) × flow rate.³⁹ For a rectangular microfluidic channel with a low aspect ratio, the corresponding pressure for each fluid (i.e., P_blood, pressure of blood sample; P_ref, pressure of reference fluid)^40,41 is derived analytically as

1

and

2

respectively. In eq 1, C_f(β) is the correction factor for compensating for the mathematical error caused by adopting an approximate model.⁴² Furthermore, P_blood cannot be estimated because the two terms (μ_blood and Q_blood) are not given. However, as the blood sample and reference fluid flow in a confined straight channel, the two fluid streams satisfy identical pressure conditions (i.e., P_ref = P_blood= P). Blood pressure can be estimated using eq 2, based on the same pressure condition.

2.5. Statistical Analysis

Commercial software (MINITAB version 19, Minitab Inc., State College, PA) was used for statistical analysis. Because the number of repeats for each experiment was much lower when assuming normal distributions, all data are graphically represented with box plots. The Kruskal–Wallis test and Mann–Whitney U-test were used as nonparametric tests to determine the statistical differences in the median value of CI for each group. First, the Kruskal–Wallis test was applied to evaluate the equality of the median value for CI with respect to groups (i.e., three hematocrit levels and five different levels in chemically fixed RBCs). Second, the Mann–Whitney U-test was used to determine the equality of the median value of CI with respect to two groups with density differences (i.e., normal density, F₁; high density, F₂). The group exhibited a statistically significant difference in all statistical tests if the p-value was less than 0.05.

3. Results

3.1. Clogging Index (CI) for Quantifying RBC Deformability as a Collective Cell Approach

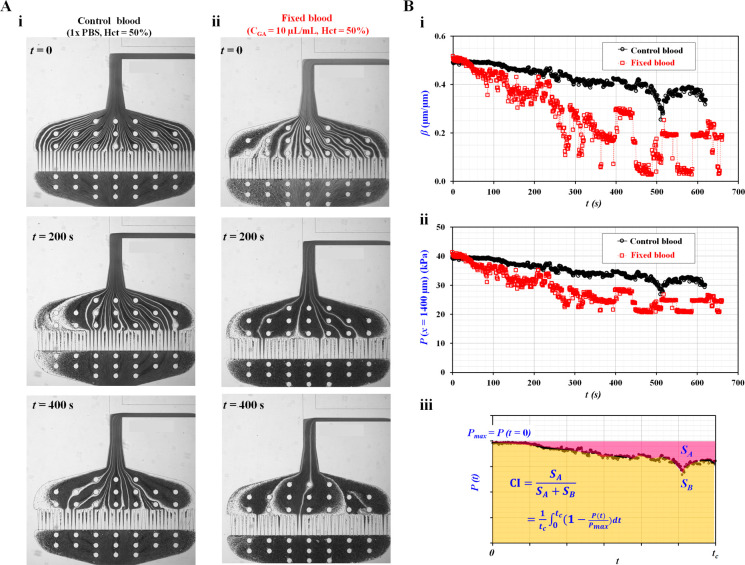
To explain the working principle suggested in the present study, control blood was adjusted to Hct = 50% by adding normal RBCs into 1× PBS. Fixed blood with Hct = 50% was prepared by exposing normal RBCs to a specific concentration of GA in 1× PBS (C_GA = 10 μL/mL). Microscopic images were captured sequentially for control and fixed blood. Figure 2Ai shows the variation in the microscopic image of the control blood over time (t) (t = 0, 200, and 400 s). On the other hand, Figure 2Aii illustrates the variation in the microscopic image of fixed blood for a specific time (t) (t = 0, 200, and 400 s).

Figure 2.

Definition of clogging index (CI) using temporal variations of blood pressure (P). Control blood (H_ct = 50%) was prepared by adding normal RBCs into 1× PBS. Additionally, fixed blood (Hct = 50%) was prepared by adding fixed RBCs with 10 μL of glutaraldehyde solution into 1× PBS. (A) Variations of microscopic images over time with respect to control blood and fixed blood. (i) Variation of the microscopic image of control blood over time (t) (t = 0, 200, and 400 s). (ii) Variation of the microscopic image of fixed blood with respect to specific time (t) (t = 0, 200, and 400 s). (B) Temporal variation of pressure (P) and definition of clogging index (CI). (i) Temporal variations of β with respect to control blood and fixed blood. (ii) Temporal variations of P(x = 1400 μm) with respect to control blood and fixed blood. (iii) Calculation of clogging index (CI) and deformability index (DI) using temporal variations of P(t) obtained for t = t_c. Here, maximum pressure (P_max) was defined as P(t = 0) = P_max. Using temporal variations of P, S_A and S_B were quantified as S_A = ∫₀^t=t_c(P_max – P[t]) dt and S_B = ∫₀P_max dt, respectively. Based on the definition of CI (CI = S_A/[S_A + S_B]), the CI was expressed analytically as CI = .

The image intensity of blood flow (I_blood) was acquired sequentially at a specific ROI selected within the micropillar channels to monitor changes in the hematocrit of the blood flow supplied from the reservoir tube. Additionally, to calculate the blood pressure in the coflowing channel, the interface (β) was obtained over time (Figure 2Bi). For control blood, β tended to decrease gradually over time but varied relatively stably. The fixation of RBCs was associated with a more pronounced time-dependent decrease in β, which was unstable and fluctuated after 400 s of perfusion. As shown in Figure S1 (Supporting Information), I_blood also showed variations over time, with an initial rapid drop followed by stabilization after 50 s of perfusion. The amplitude of the initial drop in blood was much more pronounced for fixed blood than for control blood. Based on eq 2, blood pressure at a specific location was quantified over time. As shown in Figure 2Bii, temporal variations in P(x = 1400 μm) were obtained for the control and fixed blood samples. Fixed RBCs were more prone to clogging micropillar channels and increasing fluidic resistance than fresh RBCs. Thus, the fraction of the coflowing channel filled with blood (i.e., the interface) tended to decrease over time. In other words, owing to consecutive clogging in the micropillar channels, the blood pressure in the coflowing channel decreased over time.

The clogging index (CI) and deformability index (DI) were determined from temporal variations in P(t), which served as markers of deformability. As shown in Figure 2Biii, the temporal variations in P(t) were obtained for t = t_c. Because P(t) tended to decrease over time, the maximum pressure (P_max) was determined at the initial time (i.e., P_max = P[t = 0]). Based on the temporal variations in P(t), S_A and S_B were calculated as S_A = ∫₀^t=t_c(P_max – P[t]) dt and S_B = ∫₀P_max dt, respectively. We defined the clogging index (CI = S_A/[S_A + S_B]) using eq 3:

3

In addition, based on the relationship between CI and DI (i.e., CI + DI = 1), the deformability index was expressed as DI = S_B/[S_A + S_B]). The equation for DI quantification was derived using eq 4.

4

According to eqs 3 and 4, fixed blood had a high CI value and a low DI value when compared with normal blood. From a physical point of view, both indices (CI and DI) appropriately represented variations in RBC deformability. Both the CI and DI showed a linear dependency (i.e., CI = 1 – DI). Here, the clogging index (CI) was used preferentially to quantify RBC deformability unless otherwise mentioned.

3.2. Validation of Analytical Formula for Pressure in the Coflowing Channel

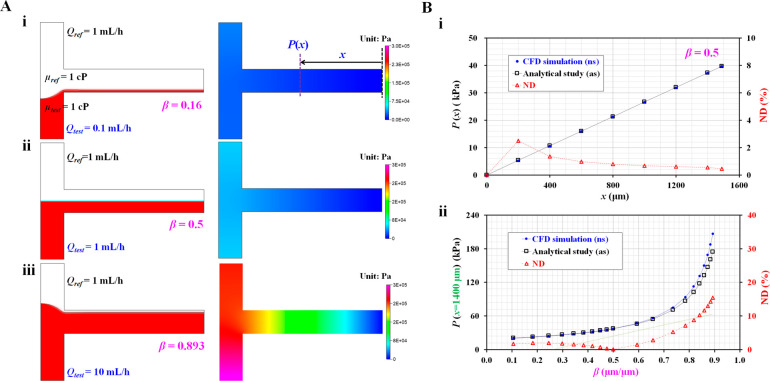
First, we validated the accuracy of eq 2 using commercial software (CFD-ACE+, Ver. 2019, ESI Group). The interfacial location in the coflowing channel was adopted to estimate the pressure drop downstream of the micropillar channels. With regard to eq 2, which is derived for estimating the junction pressure, it is necessary to validate the accuracy of the analytical formula. Based on the two-phase model, the interfacial location was varied by changing the flow-rate ratio of the two fluids. Here, it was assumed that both fluids (the test fluid and reference fluid) had identical viscosities (i.e., μ_ref = μ_test = 1 cP). The flow rate of the reference fluid was set as Q_ref = 1 mL/h. To vary β ranging from β = 0.1 to β = 0.9, flow rate of test fluid was adjusted from Q_test = 0.1 mL/h to Q_test = 10 mL/h. Figure 3A shows the blood pressure distributions in the coflowing channel with respect to interface (β) ([i] β = 0.16, [ii] β = 0.5, and [iii] β = 0.893). Based on the CFD simulation results, a higher interface (β) exhibited a substantial increase in the pressure distribution. As shown in Figure 3B, quantitative comparisons between the analytical expressions (eq 2) and CFD simulations were conducted by varying a special location along the coflowing channel and interface between fluids. First, to verify the difference in the pressure distributions along the location, the pressure distributions obtained by the two methods were plotted as a function of location (x) along the channel. As shown in Figure 3A, the CFD simulation indicated that the pressure remained constant across the channel width direction at a specific range of longitudinal locations (x). The pressure at a specific location was quantified by averaging the pressure distributions over the entire channel width. As shown in Figure 3Aii, where the interface between the two fluids was positioned at the middle of the channel width (β = 0.5), the pressures obtained using the two methods are represented with respect to location (x). Figure 3Bi shows the variations in pressure (P) and normalized difference (ND) with respect to location (x) and the two methods. The ND was calculated as ND = (P_ns – P_as)/P_ns × 100. The subscripts ns and as represent the numerical simulation and the analytical study, respectively. The pressure was found to increase linearly. Additionally, ND tended to gradually decrease over a large distance from the ground position. The ND was less than 3% from x = 200 μm to x = 1500 μm. From the results, it can be inferred that eq 2 can be reliably used to consistently estimate the pressure in the coflowing channel compared with the CFD simulation. Furthermore, the association between pressure (P) and β was explored at a specific point within a coflow channel, which was set to x = 1400 μm. Figure 3Bii shows the variations in P(x = 1400 μm) and ND with respect to the changes in β obtained using the two independent methods. Both methods showed consistent trends in changes in P as a function of β. ND was less than 10% at β = 0.8.

Figure 3.

Validation of the analytical formula of blood pressure by means of numerical simulation. (A) Numerical simulation with respect to interfacial location (β). We assume both fluids had the same viscosity (i.e., μ_ref = μ_test = 1 cP). Flow rate of reference fluid was fixed at Q_ref = 1 mL/h. Flow rate of test fluid was only changed to set a specific value of β. (i) Variations of blood pressure distributions along the coflowing channel at β = 0.16 (Q_test = 0.1 mL/h). (ii) Variations of blood pressure distributions along the coflowing channel at β = 0.5 (Q_test = 1 mL/h). (iii) Variations of blood pressure distributions along the coflowing channel at β = 0.893 (Q_test = 10 mL/h). (B) Quantitative comparison between analytical study and CFD simulation. (i) Variations of P and normalized difference (ND) with respect to location (x) and individual method. (ii) Variations of P(x = 1400 μm) and ND with respect to β and individual method.

3.3. Contribution of Hematocrit to Clogging Index for Quantifying RBC Deformability

Next, we verified whether our method is applicable to physiological conditions (e.g., hematocrit within 30–60%). The hematocrit measures the volume occupied by RBCs and is normalized to the total blood volume. The normal hematocrit is 40–54% and 36–48% for men and women, respectively. In addition, the hematocrit contributes to varying RBC sedimentation in the sample reservoir.⁴³ During blood delivery, changes in the hematocrit cause changes in the blood viscosity. The hematocrit then influences the blood flow in the microfluidic channel in the reservoir. Thus, it was necessary to evaluate the effect of the hematocrit on the clogging index.

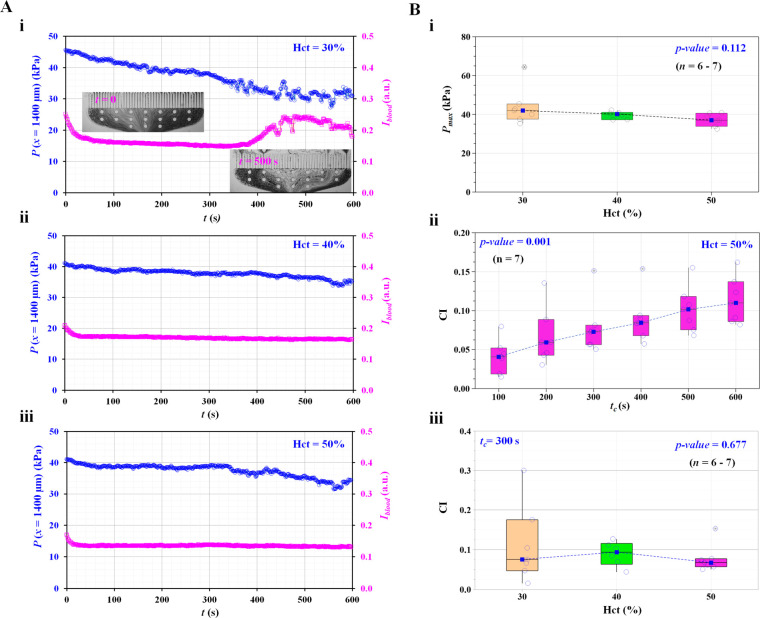
As shown in Figure 4A, temporal variations in pressure (P) and image intensity (I_blood) were obtained for hematocrits of 30%, 40%, and 50%. The hematocrit of the blood sample was adjusted by mixing RBCs and plasma in fixed proportions. Figure 4Ai shows the temporal variations in P and I_blood for Hct = 30%. The inset of Figure 4Ai shows a microscopic image upstream of the micropillar channel captured at a specific time (t) (t = 0 and 500 s). After 300 s, I_blood tended to increase significantly because the number of RBCs decreased significantly. The pressure (P) gradually decreased over time. Figure 4Aii,iii shows the temporal variations in P and I_blood with respect to Hct = 40% and 50%, respectively. Compared with blood samples with low hematocrit (Hct = 30%), blood samples with high hematocrit (Hct = 40% and 50%) showed consistent I_blood values over time. In other words, the measurement of a sample with a high hematocrit (e.g., Hct = 50%) should be carefully considered to circumvent hematocrit variation due to sedimentation during loading in the sample reservoir.

Figure 4.

Contribution of hematocrit (Hct) to clogging index (CI). (A) Quantitative evaluation of pressure (P) and image intensity (I_blood) with respect to hematocrit of blood sample and elapsed time. (i) Temporal variations of P and I_blood for normal blood (Hct = 30%). Inset shows microscopic images captured at a specific times (t) (t = 0 and 500 s). (ii) Temporal variations of P and I_blood for normal blood (Hct = 40%). (iii) Temporal variations of P and I_blood for normal blood (Hct = 50%). (B) Variations of CI and P_max with respect to Hct. (i) Variations of P_max with respect to Hct. (ii) Variations of CI with respect to t_c. Hematocrit of blood sample was fixed at Hct = 50%. (iii) Variations of CI with respect to Hct. Integration time (t_c) was fixed at t_c = 300 s.

Based on the temporal variations of P, as shown in Figure 4A, the maximum pressure (P_max) and clogging index (CI) were obtained with respect to Hct. Figure 4Bi shows the variations in P_max with respect to Hct. The P_max tended to decrease gradually. According to the statistical test, P_max was not significantly influenced by hematocrit (Kruskal–Wallis test, p-value = 0.112). Based on these results, the hematocrit of the blood sample was fixed at Hct = 50% for further experiments, unless otherwise mentioned. The time dependence of the changes in the CI was then explored to identify the optimal acquisition time (t_c) for the test. As shown in Figure 4Bii, the CI tended to increase significantly over time (Kruskal–Wallis test, p-value = 0.001), while the pressure (P) decreased with time (Figure 4Aiii). By referring to the definition of CI (i.e., CI = S_A/[S_A + S_B]), CI tended to increase because S_A tended to increase over time. The CI fluctuated largely at a low hematocrit rather than at a higher hematocrit. According to the statistical test, the hematocrit did not significantly influence the clogging index (CI) (Kruskal–Wallis test, p-value = 0.677); indeed, our method is applicable to the physiological condition of the blood.

3.4. Variations in the Clogging Index (CI) versus the Degree of RBC Deformability

Furthermore, we validated the trends in the clogging index (CI) by varying the degree of deformability of RBCs. The GA solution has been widely used to increase the rigidity of RBCs.⁴⁴ Normal RBCs were fixed with different concentrations of GA in 1× PBS (C_GA = 0, 2.5, 5, 7.5, and 10 μL/mL). After fixation, the RBCs were resuspended at Hct = 50%.

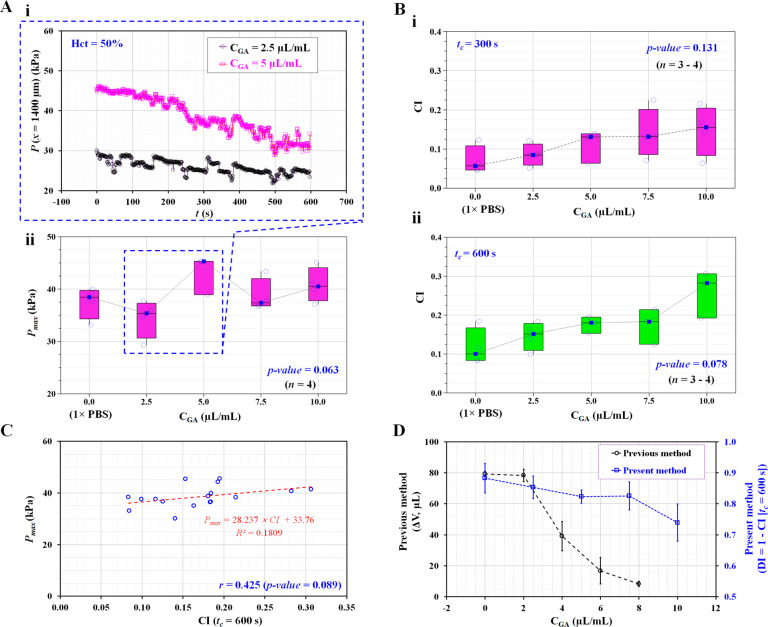
As shown in Figure 5Ai and Figure S2 (Supporting Information), temporal variations in blood pressure (P[x = 1400 μm]) were obtained as a function of time for two GA concentrations (i.e., C_GA = 2.5 and 5 μL/mL). The pressure (P) tended to decrease gradually for up to 600 s (the end of our measurement time) because RBC clogging occurred continuously over time. However, large variations were observed within the fixed blood samples prepared using the same concentration of GA for fixation. Using the temporal variations in blood pressure, the maximum pressure (P_max, pressure at the initial blood flow at t = 0) was measured with respect to the C_GA. To evaluate the variations in P_max with respect to various degrees of fixed RBCs, the variations in P_max were summarized with respect to C_GA. Repetitive tests (n = 4) were conducted to verify statistical significance. As shown in Figure 5Aii, there was no statistically significant relationship between P_max and C_GA (Kruskal–Wallis test, p-value = 0.063). P_max was determined from the initial blood flow, to which the deformability of RBCs partially contributed.

Figure 5.

Quantitative evaluation of clogging index versus degree in RBCs’ deformability. The degree in RBCs’ deformability was controlled by exposing normal RBCs to different concentrations of GA solution. Hardened blood (Hct = 50%) was then prepared by adding fixed RBCs into 1× PBS. (A) Contribution of concentration of GA solution to P_max. (i) Temporal variations of P(x = 1400 μm) with respect to C_GA = 2.5 and 5 μL/mL. (ii) Variations of P_max with respect to C_GA. (B) Variations of CI with respect to C_GA and acquisition time (t_c). (i) Variations of CI with respect to C_GA and t_c = 300 s. (ii) Variations of CI with respect to C_GA and t_c = 600 s. (C) Linear correlation between P_max and CI. (D) Quantitative comparison of RBCs’ deformability between the previous method (i.e., ΔV = A_c ∫₀^t=t_cU dt; A_c, cross-sectional area; and U, average velocity) and present method (i.e., DI = 1 – CI) with respect to C_GA.

According to Figure 4Bii, the clogging index (CI) varied depending on the acquisition time. The increase in CI over the prolonged acquisition time was largely due to continuous RBC clogging, accompanied by a gradual decrease in blood pressure. Thus, the contribution of the acquisition time (t_c) to the clogging index was evaluated for RBCs that were proven to exhibit differences in deformability. As shown in Figure 5B, the CI tended to increase gradually with an increase in C_GA, providing a higher rigidity of RBCs. The deviation of the CI in each fixed blood sample decreased at longer acquisition times from t_c = 300 s (Figure 5Bi) to t_c = 600 s (Figure 5Bii). According to the Kruskal–Wallis test, the corresponding p-value of the acquisition time decreased significantly from p-value = 0.131 (t_c = 300 s) to p-value = 0.078 (t_c = 600 s). The acquisition time was fixed at t_c = 600 s for consistent quantification of the clogging index (CI).

The clogging index (CI) and P_max were influenced by blood flow during longer acquisition times of t_c = 600 s. For this reason, it was necessary to evaluate the relationship between P_max and CI. P_max and CI are graphically represented using a scatter plot to validate the linear dependency between P_max and CI, as shown in Figure 5C. According to the linear regression analysis, there was no strong association between P_max and CI (i.e., correlation coefficient [r] = 0.425, p-value = 0.089). In other words, P_max, determined by the initial blood flow and CI, were two independent variables. Thus, P_max cannot be considered a potential factor interfering with the detection of RBC deformability using CI as a marker.

According to a previous method,³⁴ RBC deformability was quantified by analyzing temporal variations in the average velocity of blood passing through the micropillar channels. The velocity of the RBCs with high deformability remained constant for a sufficiently long time. However, RBCs with low deformability caused a significant decrease in the blood velocity over time. Based on the dependency between velocity and RBC deformability, the blood volume passing through pillar channels (i.e., ΔV= A_c ∫₀^t=t_cU dt; A_c, cross-sectional area; and U; averaged velocity) has been suggested to evaluate RBC deformability. All data obtained by the previous and present methods is presented as the mean ± standard deviation. The CI obtained for fixed blood samples was converted into DI using the relationship between DI and CI (i.e., DI = 1 – CI). As shown in Figure 5D, both indices obtained by the present method (DI) and the previous method (ΔV)⁴⁵ are represented graphically as a function of C_GA. Both DI and ΔV tended to decrease with increasing concentrations of GA in the solution, causing strong fixation and progressive impairment of deformability. As higher concentrations of the GA solution contributed to decreasing RBC deformability, the trends of both indices consistently showed variations in RBC deformability. As both methods (i.e., the previous method and the present method) have been demonstrated using micropillar channels with the same dimensions (i.e., width and depth), the difference in blood delivery (i.e., syringe pump and pressure controller) and quantification parameters (i.e., ΔV and CI) influenced the detection of stiffened RBC deformability.

3.5. RBC Deformability versus RBC Density

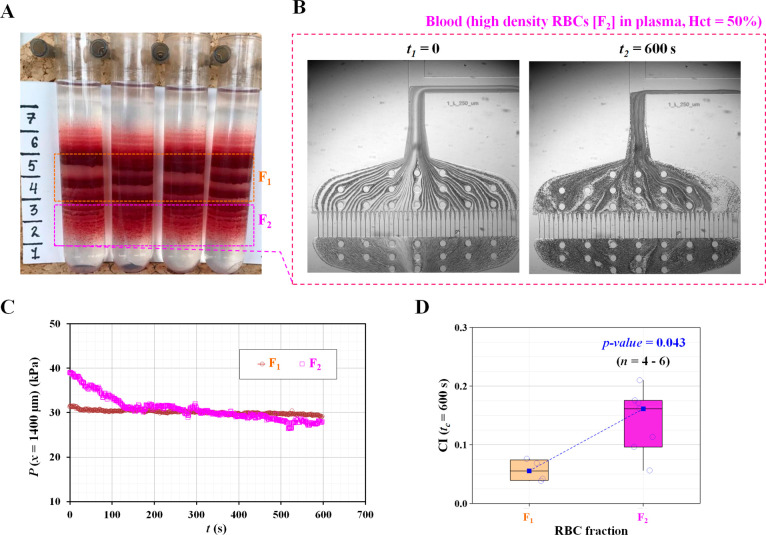
Finally, we used our device to associate RBC deformability with RBC density in a human blood sample. According to previous studies,⁴⁶ RBC heterogeneity resulting from age, environmental stress, and pathological factors contributes to the broad distribution of RBC deformability. For healthy human RBCs, younger RBCs had a lower density than mature RBCs. The aging of RBCs increases their density as a distinctive feature. As a demonstration, the present method was applied to measure the RBC deformability in fractions of RBCs of different densities obtained from the same sample. To separate RBCs based on their density, a simple method was developed that uses centrifugation-driven separation on the Percoll density gradient,⁴⁷ which is currently used for RBC fractionation and disease diagnostics.^11,37,46 Based on the protocol for fractionation on the Percoll density gradient,³⁷ RBCs donated from a healthy donor were separated into subpopulations of cells with low, high, and medium densities, as shown in Figure 6A.

Figure 6.

Quantitative evaluation of RBCs’ deformability with respect to density of RBCs. Percoll density gradient centrifugation was used to segregate RBCs depending on difference in density. (A) Snapshot showing the difference in density of RBCs. For convenience, two fractions of RBCs (F₁, normal density; F₂, high density) were selected to quantify RBCs’ deformability with respect to density difference. (B) Microscopic images captured at specific times (t) (t = 0 and 600 s) for blood sample prepared from the F₂ fraction. (C) Temporal variations of P(x = 1400 μm) with respect to F₁ and F₂. (D) Variations of clogging index (CI) with respect to the RBC fraction (F₁ and F₂).

During high-speed centrifugation, a density gradient of Percoll particles was created, and RBCs were accordingly distributed within the tube. The F₁ region represented the major fraction of RBCs located in the middle of the density distribution. The F₂ region containing senescent, poorly deformable, dehydrated RBC fractions remained below owing to the higher cell density. The experiment was designed to discriminate between RBCs with normal (F₁) and diminished deformability (F₂). Based on the proposed method, senescent dehydrated RBC populations (F₂) were progressively clogged during the 10 min of measurement, whereas major RBC populations (F₁) did not show significant changes in clogging over time. According to the sample preparation procedure, blood samples were prepared by adding RBCs collected from each fraction (F₁ or F₂) to autologous plasma. As shown in Figure 6B, two microscopic images of the blood samples with the RBC fraction (F₂) were captured at two different times (i.e., initial time, t = 0; and final time, t = 600 s). With an elapsed time of 600 s, the interface decreased substantially because of RBC clogging in the pillar channels. The RBC populations increased and caused a decrease in image intensity in front of the pillar channels. Figure 6C and Figure S3 (Supporting Information) show the temporal variations in P(x = 1400 μm) with respect to F₁ and F₂. The pressure of the F₂ fraction tended to decrease significantly compared with that of the F₁ fraction.

Based on eq 3, the variations in the CI were obtained with respect to each fraction. As shown in Figure 6D, the F₂ fraction had a higher CI value than the F₁ fraction (Mann–Whitney U-test, p-value = 0.043). In other words, RBCs with a high density (F₂) showed less deformability than RBCs with a normal density (F₁). From these results, it was inferred that RBC heterogeneity in density leads to a large distribution of CI. We compared the proposed method with a conventional method for the detection of RBC deformability. Laser diffractometry, the Lorrca Maxis (LORRCA, RR Mechatronics, Zwaag, Netherlands), measures the elongation index (EI) with respect to density in RBCs (i.e., F₁ and F₂). Figure S4A (Supporting Information) shows the variations in EI obtained for the F₁ and F₂ fractions in the isosmotic solution with respect to shear stress (τ). High-density RBCs (F₂) had mildly lower values of EI over a broad range of shear stress values compared to the major RBCs (F₁). Figure S4B (Supporting Information) shows the changes in EI within a wide osmolarity range from 100 to 500 mOsm/kg at τ = 30 Pa. High-density RBCs (F₂) showed dehydration (a leftward shift in the curve) and a lower value of EI within physiological ranges (285–310 mOsm/kg) as well as hyperosmotic ranges (310–450 mOsm/kg) when compared with lower-density RBCs (F₁). The elongation index at 300 mOsm/kg was compared to those of F₁ and F₂. As shown in Figure S4C (Supporting Information), RBCs with high density (F₂) showed a significant difference in the elongation index when compared with RBCs with lower density (F₁) (Mann–Whitney U-test, p-value = 0.052). Furthermore, the EI showed a consistent reciprocal relationship when compared with the CI obtained using the present method.

4. Discussion

In this study, two ROIs (one upstream and one downstream in the coflowing channel) were selected for monitoring the consistency in blood flows and pressure of blood flow, respectively. As shown in Figure 1Aii,Bi,Ci, blood was loaded under constant pressure conditions and traveled from the reservoir to the upstream region, to parallel micropillar channels, and flowed to the downstream region, sequentially. The reference fluid and blood were then brought together in the coflowing channel. RBCs were distributed heterogeneously in the upstream and downstream regions because RBC clogging occurred in the parallel micropillar channels. RBC clogging causes a decrease in the RBC population in the downstream region. In the upstream region, we chose the width of the ROI to be as large as possible, and the entire size of the camera sensor field of view. Based on the ROI function defined in MATLAB, the ROI of the upstream region was set to a simple rectangular shape (width × height). The image intensity of blood flow (I_b) was then calculated by analyzing the image intensity distributed within a specific ROI. Subsequently, it was used to detect the consistency of the blood flow supplied from the reservoir. As shown in Figure 4Ai, the image intensity varied significantly at a low hematocrit (30%). However, the average intensity remained constant over time with respect to the higher hematocrit levels (i.e., more than 40%). Based on the temporal variations in image intensity, it was confirmed that blood with 50% hematocrit was supplied consistently into the microfluidic channel from the reservoir. Similarly, as shown in Figure 1B, at a distance from the junction point, both fluids had a straight interface in the coflowing channel. From the specific location to the end of the channel, an ROI with a rectangular shape was selected in the coflowing channel. The interface between the fluids (β) was estimated by averaging the interfaces along the channel length. As shown in Figure 3Bi, the analytical results that needed an interface yielded consistent results when compared with the numerical results. From the results, it was confirmed that the ROI in the coflowing channel was suitable for estimating the blood flow pressure.

Blood behaves as a non-Newtonian fluid. Blood viscosity varied with the flow rate (or blood velocity) in the microfluidic channels (i.e., micropillar and coflowing channels). In the present device, the location of the interface (β) in the coflowing channel provides information on the non-Newtonian behavior of RBC suspensions. RBC clogging contributed to an increase in the pressure drop in the microchannel. To quantify the effect of RBC clogging on the pressure drop, blood pressure was quantified by monitoring the interface in the coflowing channel. As blood flowed under constant pressure conditions, RBCs clogging in the micropillar channel caused variations in blood pressure in the coflowing channel. Because our reference fluid (i.e., 1× PBS) behaved as a Newtonian fluid, the location of the interface (β) in the coflowing channel would have the information on non-Newtonian behavior (i.e., shear thinning in flow). The non-Newtonian behavior of RBC suspensions originates from the RBCs (i.e., hematocrit and deformability) and the suspending media (plasma). We demonstrate experimentally that our measurement of β corroborates the hematocrit and deformability. Recent experiments and predictions have revealed that blood plasma exhibits viscoelastic behavior.^48,49 Varchanis et al. predicted that the shear viscosity of human blood plasma remains constant for shear rates up to 10⁵ s^–1. For higher shear rates, shear thinning is predicted, leading to a slightly reduced shear viscosity.⁴⁹ Unfortunately, in our device, it is difficult to measure the shear rate of plasma locally, where it passes through the RBC-clogged micropillar.

As shown in Figure 2Biii, the pressure of the blood flow in the coflowing channel was obtained over time. RBC clogging in the micropillar channel caused an increase in pressure drop. As blood was supplied from the reservoir under constant pressure conditions, RBC clogging led to decreased pressure in the coflowing channel. Based on various experimental investigations, RBC clogging does not occur in regular or periodic patterns. Thus, the pressure does not exhibit typical polynomial expression trends. Two representative parameters (S_A and S_B) were obtained by integrating the pressure variations over a specific time period (i.e., t_c = 600 s). According to the results, the less deformable RBCs contributed to severe clogging in the micropillar channel, which resulted in a substantial increase in the pressure drop. As RBCs had less deformability, the S_A tended to increase substantially. Less deformable RBCs had a high CI value. However, for highly deformable RBCs, the S_A changed only slightly over time. More deformable RBCs had a small CI value. Therefore, CI could appropriately represent the degree of RBC clogging or deformability.

RBC clogging contributed to an increase in the pressure drop in the microchannel. As the pressure was measured in the coflowing channel, the blood flow pressure tended to decrease over time. According to eq 3, the clogging index (CI) was expressed as a function of maximum pressure (P_max). P_max was determined based on the initial blood flow. According to the Kruskal–Wallis test, the p-value was greater than 0.05 (Kruskal–Wallis test, p-value = 0.063). The results indicated that there was no statistically significant relationship between the maximum pressure and degree of RBC fixation. Thus, the initial blood flow (i.e., maximum blood pressure) did not consistently represent the degree of RBC deformability. However, the clogging index represents variations in the blood pressure resulting from RBC clogging in the micropillar channel. The less-deformable RBCs contributed substantially to the increasing variations in pressure. As shown in Figure 5Bi,ii, the CI increased significantly with increasing concentrations of GA. When native RBCs were exposed to an increasing concentration of GA, their deformability declined accordingly. The occurrence of RBC clogging has increased substantially over time.

We treated RBCs with four kinds of GA solutions (C_GA = 2.5, 5, 7.5, and 10 μL/mL) to quantify the effect on RBC deformability. The concentrations of the GA solution corresponded to 0.063%, 0.125%, 0.188%, and 0.25%, respectively. According to a previous study,⁴⁴ ektacytometry (i.e., Lorrca) did not distinguish deformability curves above a 0.01% GA solution. Here, we obtained variations of CI in the microfluidic device and concentrations of GA solution above 0.01%. As shown in Figure 5, the proposed method showed substantial differences with respect to the concentration of the GA solution (i.e., more than 0.063%). However, the clogging index (CI) did not exhibit a substantial difference between normal RBCs and fixed RBCs (<0.063%).

After fractioning RBCs using a Percoll density gradient, the high-density RBC fraction would have a nonhomogenous distribution, which may lead to a nonuniform distribution even at t = 0 s (initial loading). Here, t = 0 was set based on the specific time at which the pressure reached its maximum value. As shown in Figure S5 (Supporting Information), RBCs were heterogeneously distributed from t = −7 s to t = 0. The dynamic behavior of blood flow is influenced by fluidic system characteristics (i.e., flexible tubing, microfluidic device) as well as blood rheology (i.e., blood viscosity, hematocrit, and cell properties). We agree that the initial distribution provides information on the RBC properties of single cells.

Here, we demonstrate that our device can distinguish deformability differences between cell density subpopulations isolated by the Percoll density gradient. Interestingly, RBC senescence has been investigated by isolating the RBC population in cell density.⁵⁰ Human RBCs survive in circulation for 100–120 days. New RBCs are produced continuously, and senescent RBCs with partial loss of the cellular membrane are removed from circulation due to impaired deformability. Some proportions of senescent RBCs were present in every blood sample collected from healthy subjects. The aging of RBCs is associated with membrane loss, dehydration, and accumulation of damaged proteins. Taken together, these changes and membrane loss resulted in progressively diminishing deformability during the RBC lifespan. Senescent RBCs were easily detected and collected using a self-forming 90% Percoll density gradient. As shown in Figure 6, we successfully discriminated the fraction of poorly deformable RBCs in healthy subjects, confirming the ektacytometry findings (Figure S4). In a follow-up study, we defined a threshold for poorly deformable cells that can be detected using our new method. As we rely on the parameters that are related to the clogging of individual microchannels by individual cells, this method has the potential to detect small fractions of less deformable cells in whole blood. Preprocessing of the samples to reach optimal Hct and the use of microscopy for the detection of clogging leave us with some room for technological improvement before it may be used for screening patients with diseases compromising RBC deformability. Blood volume reduction for analysis, portable image acquisition, and tubingless fluid delivery are also planned.

5. Conclusions

In this study, we used a microfluidic platform-based method of RBC deformability to quantify RBC clogging by employing a coflowing channel as a pressure sensor. Consecutive RBC clogging in the micropillar channels leads to an increase in the pressure drop along them. The clogging index (CI) was newly adopted to quantify RBC deformability by analyzing temporal variations in blood pressure using a pressure sensor. First, the measurement accuracy of the coflowing channel as a pressure sensor was validated by a quantitative comparison between the analytical study and CFD simulation. Second, the hematocrit of blood in physiological conditions did not contribute to varying the clogging index (CI) or maximum pressure (P_max) when the hematocrit was set 40% higher. Third, we demonstrated the ability of our device to detect a decrease in the RBC deformability of cells fixed with GA solution. Finally, we resolved the differences in deformability between mature and senescent cells of high density isolated by fractionation on a Percoll density gradient. Differences in deformability obtained as a change in CI exhibited comparable results to those of ektacytometry. This new method has the potential to detect fractions of RBCs with low deformability in whole blood, which requires further investigation.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c04027.

• Temporal variations in I_blood with respect to normal blood and fixed blood with C_GA = 10 μL/mL, temporal variations in P(x = 1400 μm) with respect to the concentration of the GA solution, temporal variations in P(x = 1400 μm) with respect to the fraction of RBCs, elongation index (EI) obtained using the conventional method (i.e., Lorrca Maxis), and temporal variations of pressure and microscopic image for a high density of RBCs (F₂) (PDF)

Author Present Address

^∇ S.S.: University Hospital of Zurich, Research Unit Internal Medicine, Schlieren, 8952, Switzerland

Author Contributions

^# Y.J.K. and S.S. contributed to this work equally. A.B. and S.S.L. contributed to this work equally.

Y.J.K. received funding from Chosun University (2020) and the Basic Science Research Program through the NRF funded by the Ministry of Education (NRF-2021R1I1A3040338). A.B. received funding from the European Union’s Horizon 2020 research and innovation program under Grant Agreement 860436–EVIDENCE–H2020-MSCA-ITN-2019. S.S.L. acknowledges ETH Zurich for financial support. We also thank ScopeM of ETH Zurich for access to microscopy and microfluidics equipment.

The authors declare no competing financial interest.