Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Oct 18;7(43):38990–39001. doi: 10.1021/acsomega.2c04719

Relationship between Dielectric Relaxation Time and Permeability of High-Rank Coal in the Jiaozuo Mining Area

Yugui Zhang †,‡,§, Jian Li †,*, Dongji Lei †,‡,§
PMCID: PMC9631419  PMID: 36340149

Abstract

graphic file with name ao2c04719_0019.jpg

To evaluate the permeability of coal by the complex resistivity method, the real part of complex resistivity (R), the imaginary part of complex resistivity (X), capacitance (C), permeability (k), and strain (ε) of coal in different directions under variable pressure were measured. Based on the physicochemical structure characteristics of coal and its conductivity and dielectric mechanism, the experimental phenomenon was analyzed and correlated with the permeability of coal. The results demonstrated that (1) the R–X curve is U-shaped. With increasing frequency, the amplitude first decreases and then increases, forming an obvious trough. C decreases with increasing frequency. (2) The R–X curve is affected by pressure and directivity. The absolute value of the R–X curve amplitude gradually decreases and shifts to the left as the pressure increases; meanwhile, it decreases and shifts to the left in the order of the vertical bedding direction (z direction), the vertical main fracture direction in parallel bedding (y direction), and the main fracture direction in parallel bedding (x direction). There is also a related change law for C. (3) The dielectric relaxation time (τ) was optimized as the electrically sensitive parameter of coal. τ continues to decrease as pressure increases and decreases in the order of the z, y, and x directions. (4) The permeability of coal is strongly correlated with the dielectric relaxation time, and the relationship between them conforms to a logarithmic function. The relationship of strain and the dielectric relaxation time verifies the strong correlation between permeability and the dielectric relaxation time. This study provides an experimental basis and theoretical support for the subsequent accurate prediction and evaluation of coal permeability using the dielectric relaxation time.

1. Introduction

With the continuous consumption of energy and the gradual intensification of the greenhouse effect,1 coalbed methane (CBM), a high-quality clean unconventional energy, has been of wide concern.2−4 In China, exploration and development techniques are critical for improving the production of CBM,5 and U-, V-, and L-shaped horizontal wells and multilateral horizontal wells have been favored for CBM.6 Coal is a complex medium with a dual pore structure7 and is composed of a coal matrix and pores/fractures.8,9 The pore specific surface area and fracture volume of coal provide sufficient storage and migration space for CBM.10 The gas seepage characteristics and seepage evolution in coal are closely related to the pore/fracture system.11 Coal seam permeability is one of the most important bases for evaluating the degree of CBM development and the effect of mine gas drainage,12,13 but its measurement and evaluation are very difficult.14 Scholars have carried out many studies on the influencing factors and prediction of coal permeability.15−18 In situ stress,19,20 gas pressure and type,21,22 and the anisotropic characteristics of coal reservoirs23,24 determine the permeability of coal to varying degrees, and there are relevant coal permeability evaluation models25,26 to theoretically discuss the mechanism of its seepage law. However, most of the above coal permeability acquisition and evaluation methods are still in the laboratory measurement stage. Meanwhile, these methods have high costs, are time-consuming as well as laborious, and fail to consider pore structure information; thus, it is urgent to propose a convenient and effective coal permeability evaluation method.

In recent years, the complex resistivity method has become a highly discussed topic.27 This method realizes high-density measurements in the frequency domain and space domain over a relatively wide frequency range and has the characteristics of obtaining more electrical parameters and geoelectric information than other geophysical methods.28 In particular, compared with the direct current method, this method reflects the influence of frequency on the polarization of the dielectric and can optimize the electrical characteristics of the characteristic frequency points of the dielectric. The complex resistivity dispersion characteristics of rocks are closely related to their pore/fracture structure,29 water content,30 and mineral composition.31 Some scholars believed that the complex electrical dispersion phenomenon was caused by the dielectric polarization generated by the displacement current,32 while others proposed that the phenomenon was attributed to the induced polarization (IP) produced by the electrochemical effect.33 To describe the electrical and dielectric properties of rocks, the Debye model,34 Cole–Cole model,35 double Cole–Cole model36 and Warburg model34 were established.

Coal has dielectric properties, and the complex resistivity method is capable of studying pore/fracture structure characteristics. Before the volume expansion of coal, the change law of resistivity is related to the stress and the gradual closure of pores/fractures.37 Many scholars have found that the influencing factors of the complex electricity of coal are its physical parameters,38 metamorphic degree,39 measured area,40 and structural type.41 In addition, there is a resistance capacitance model to analyze the complex resistance dispersion characteristics of water-bearing coal.42 Most of the research work on the relationship between permeability and complex resistance is in the rock field. Through the correlation between the complex resistance and the specific surface area of rock particles,43 the effective particle size of the core,44 the formation factor,45 and the IP spectrum,46 the rock permeability is further obtained. The relationship model between resistivity and permeability failed to reflect the IP effect,47 neglected the electrical response of characteristic frequency points,48 and only explained the phenomena in the time domain.49

In summary, the frequency dispersion response characteristics of the complex resistance of the loaded coal need to be further studied, and there are only a few studies on the permeability and complex resistivity that characterize the IP effect of coal in the frequency domain. The complex resistivity method can provide information on coal pores/fractures, which is convenient and fast. It is an effective method to evaluate coal permeability. Therefore, this paper obtains the relationship between the coal dielectric relaxation time and permeability by measuring the coal electrical parameters, strain parameters, and permeability in different directions under variable pressure. This study lays a foundation for using the complex resistivity method to provide certain theoretical and experimental support for the prediction of coal and gas outbursts.

2. Samples and Experiments

2.1. Coal Sample Preparation

This paper selected anthracite coal from the Zhaogu no. 2 mine of the Jiaozuo Coal Industry Group, China, which is a single near-horizontal coal seam. According to the development of coal fissure cleat and bedding, the massive coal was drilled to Φ 50 mm × L 100 mm columnar coal in three directions: vertical bedding direction (z direction), vertical main fracture direction in parallel bedding (y direction), and main fracture direction in parallel bedding (x direction). As shown in Figures 1 and 2.

Figure 1.

Figure 1

Open in a new tab

Schematic diagram of coal sample drilling.

Figure 2.

Figure 2

Open in a new tab

Physical drawing of the coal sample.

Coal is composed of organic components and associated inorganic components, and the two components influence the electric properties of coal. The relevant basic information of the coal samples selected in this paper is as follows (Table 1).

Table 1. Maceral Composition and Vitrinite Reflectance of Coal.

  organic components (%)
 inorganic components (%)
  
mining area name vitrinite inertinite total clay sulfide carbonate total vitrinite reflectance R0max (%)
Zhaogu no. 2 mine of the Jiaozuo Coal Industry Group 85.00 5.00 90.00 8.60 0.30 1.20 10.00 2.99
Open in a new tab

2.2. Experimental Platform and Test Method

2.2.1. Experimental Platform

Based on the measurement of the complex electricity, permeability, and deformation of coal samples, this paper independently designed and built the corresponding experimental platform, and the system mainly comprised eight parts: an air pressure regulating unit (1 and 2), a triaxial stress element (6 and 7), a strain monitoring unit (14), a complex electricity measurement unit (12), a data collection and processing unit (13), a test tank (11), thermostatic equipment (10), and vacuum pumping equipment (8), as shown in Figure 4. Among them, the contact surface between the coal sample and the coal core plug in the test tank (11) is a copper plate, and the rest of the coal core plug is a PEEK material with strong insulation, which prevents the generation of the measurement error, as shown in Figure 3.

Figure 4.

Figure 4

Open in a new tab

R–X dispersion curve of coal under different pressures.

Figure 3.

Figure 3

Open in a new tab

Schematic diagram of the experiment platform. (1) Gas cylinder; (2) buffer tank; (3, 4, 5, 9) needle valves; (6) axial pressure pump; (7) circumferential pressure pump; (8) vacuum pump; (10) thermostatic chamber; (11) test tank; (12) LCR tester; (13) data collection and processing center; and (14) strain gauge.

2.2.2. Test Method

Six major processes constituted this test: (i) the airtightness of the system is checked. 1 MPa nitrogen is injected into the system, and it is left standing for 12 h. That the fluctuation range of the pressure indicator is ±0.01 MPa indicates that the system has good airtightness. (ii) Then, the system is cleared using a vacuum pump until the air pressure indicator is close to 5 Pa and remains unchanged for 2 h, then the vent valve and vacuum pump is closed in turn. (iii) The temperature of the system is maintained at 28 °C through the thermostatic chamber. After the axial pressure and confining pressure are stabilized, methane gas with a constant pressure of 1 MPa is injected into the system by adjusting the pressure reducing valve. When the inlet pressure and outlet pressure readings are consistent and stable, the coal sample reaches the gas adsorption equilibrium state. (iv) When the axial pressure, confining pressure, and air pressure are stable, the electrical parameters of loaded coal samples (the real part of complex resistance R, imaginary part of complex resistance X, and capacitance C, hereinafter referred to as R, X, and C, respectively) are measured through the constant current signal output using the LCR tester. (v) After, the permeability measurement software is opened, the parameters of the coal sample and gas (coal sample diameter, coal sample length, gas viscosity, and atmospheric pressure) are input, and the change in coal sample permeability is monitored until the change range of permeability value decreases until it tends to be stable. The strain monitoring unit is used to monitor the coal sample deformation in the adsorption equilibrium process and equilibrium state under different stresses in real time. When the strain curve is approximately horizontal, it is considered that the measured strain value in the pressure equilibrium state has been achieved. (vi) Change the different directions and the different stress sizes (a constant gas pressure 1MPa, a constant confining pressure 5MPa, and the maximum axial pressure loading to 7MPa), repeat steps (i) to (v), and monitor the electrical properties, permeability and strain parameters in their corresponding states.

3. Results and Discussion

3.1. Frequency Dispersion Characteristics of the R–X Diagram of Loaded Coal

3.1.1. Dispersion Characteristics of the R–X Diagram of Coal under Different Pressures

Under the condition of changing axial pressure, the R–X dispersion curves of coal samples in the x direction, y direction, and z direction were measured in the frequency band of 1–10 kHz, as shown in Figure 4.

In the above figure, the abscissa is R, and the ordinate is X. Different colors represent different pressures. The R–X curve has obvious dispersion characteristics and takes the shape of U. With increasing pressure, the absolute value of the curve amplitude gradually decreases and shifts to the left, and the degree of shift gradually decreases; with increasing frequency, the R–X curve shows two stages, first gradually decreasing and then increasing. When the frequency f = 49 Hz, the jumping point appears in the R–X curve, which is due to industrial electrical interference, and it can be ignored. R decreases gradually with increasing frequency, and the change laws of the X and R–X curves with frequency are the same. There are two stages: first a decrease and then an increase, which shows that X can better reflect the frequency dispersion characteristics of the complex resistance of loaded coal than R and has more geoelectric information. Therefore, the X spectrum curve is selected for model inversion in the following text.

The capacitance C measurement of coal under different pressures is shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Capacitance dispersion curve of coal under different pressures.

Under any pressure, the capacitance C dispersion characteristics of the coal samples in the three directions are similar. With increasing frequency, the capacitance decreases gradually; with increasing pressure, the capacitance decreases in turn, especially in the low frequency stage.

The reasons for the frequency dispersion of the complex resistance of loaded coal are as follows: under the action of an external excitation current, the dielectric coal is polarized, and its polarization form can be subdivided into displacement polarization, dipole orientation polarization, and interface polarization, as shown in Figure 6. With the continuous increase in frequency, the polarization time period is shortened, which causes the polarization completion degree to decrease, the polarization form gradually becomes single, only for orientation polarization and displacement polarization, and the resistance value continues to decrease. X shows the law of first decreasing and then increasing, and the upper limit of the curve is zero, which is capacitive. X is determined by the coal capacitance C and the measurement frequency f. It is considered that the coal capacitance C plays a leading role in the frequency band below the minimum point, and the frequency f plays a major role after the minimum point frequency.50 The dispersion characteristic of the capacitor C is determined by the polarization type and completion time. In addition, R and X of coal gradually decrease under the action of pressure. The main reason is that the condensation ring of anthracite is significantly increased, and the order of the macromolecule arrangement is enhanced, forming a large number of aromatic lamellae similar to the graphite structure. At the same time, due to the enhanced ordering, the aromatic lamellae are arranged more closely, the connectivity of the coal skeleton is enhanced, its ionic activity energy is increased, and the particle spacing is reduced, resulting in the closer contact of the electron clouds of adjacent molecules in various functional groups.51 Electrons in the captured state are more likely to be converted into free excited electrons by the electric field,52 and the electrons in the valence band are more likely to transition to the conduction band and become conductive interceptors. The orientation polarization and displacement polarization of the induced electric moment of the coal medium molecules are enhanced. The larger the vector sum of the electric dipole moment per unit volume, the stronger the conductivity, and the lower the resistance of the coal; in addition, as the pores/fractures space of the coal shrinks, the previously unconnected water may be penetrated, and the conductivity of the coal body is enhanced.

Figure 6.

Figure 6

Open in a new tab

Frequency diagram of the coal polarization form.

3.1.2. Dispersion Characteristics of R–X Diagram Loaded Coal in Different Directions

As shown in Figure 7, under the same pressure conditions, the R–X curve of the coal samples gradually shifts to the left in the order of the z direction, y direction, and x direction, and the R and the absolute value of X continue to decrease in the same direction. Among them, the R and the absolute value of X of coal samples in the z direction are much larger than those of coal samples in the y direction and x direction, and the R and X values of coal samples in the y direction are slightly larger than those of coal samples in the x direction.

Figure 7.

Figure 7

Open in a new tab

R–X dispersion curve of coal in different directions.

The comparison of capacitance C measurement of coal samples in different directions is shown in Figure 8.

Figure 8.

Figure 8

Open in a new tab

Capacitance C dispersion curve of coal in different directions under the same pressure.

Consistent with R and X, under the same pressure state, the capacitance C of the coal samples in the three directions decreases in the order of the z direction, y direction, and x direction, that is, Cz > Cy > Cx, especially in the low frequency stage. Among them, the capacitance value in the z direction is significantly greater than that in the two directions of parallel bedding, and the capacitance value in the y direction is slightly greater than that in the x direction.

The reason for this anisotropy is as follows: when charged particles of coal move and migrate in the z direction, it is necessary not only to overcome the attraction of the macromolecular structure to itself to produce a “standard barrier” but also to overcome the “penetration barrier” passing through the parallel stacking structure of coal macromolecules. However, the migration of charged particles in the bedding direction of coal only needs to overcome the “standard barrier”, so the conductivity of coal in the vertical bedding direction is worse than that in the parallel bedding direction. There are fewer pores and fractures in the x direction that hinder the migration of charged particles than in the y direction, which is conducive to the migration of charged particles. Therefore, the conductivity of coal in the x direction is stronger than that in the y direction.53 In addition, as a layered organic rock, the vertical bedding of the coal can be regarded as multiple resistors in series, and the parallel bedding can be considered multiple resistors in parallel. The resistance of the series circuit is greater than that of the parallel circuit, so the conductivity of the vertical stratification is significantly less than that of the parallel stratification. Moreover, the stratification phenomenon in the y direction is slightly more obvious than that in the x direction, resulting in the former being weaker than the latter.

3.2. Inversion of the Dielectric Relaxation Time of Loaded Coal

The relaxation phenomenon refers to the whole process in which a system changes from the original equilibrium state to another new equilibrium state after being affected by the outside for a period. In dielectric physics, the treatment of the polarization process involves carrier transport, and the relaxation time approximation method is considered to address the dielectric relaxation phenomenon.54

At present, to study the variation in the complex electrical dispersion characteristics of rocks, most scholars simplify the IP effect and replace it with a circuit composed of several electronic components, analyze its equivalent circuit, use the conductive model to invert the measured complex electrical data, and explain its complex electrical dispersion characteristics through the corresponding model parameters to further provide theoretical support for rock (ore) geophysical exploration. The commonly used models are shown in Table 2.

Table 2. Four Common Conductive Modelsa.

model expression
Cole–Cole model
graphic file with name ao2c04719_m010.jpg
double Cole–Cole model
graphic file with name ao2c04719_m011.jpg
Debye model
graphic file with name ao2c04719_m012.jpg
Warburg model
graphic file with name ao2c04719_m013.jpg
Open in a new tab
a

Here, Z(iω) is the measured impedance value; Z(0) is the zero-frequency impedance value; m, m1, and m2 are the polarizability values; τ, τ1, and τ2 are the relaxation times, given in seconds; c is the frequency correlation coefficient, ω is the angular frequency, and the relationship between ω and frequency f is ω = 2πf.

Based on the measured complex electricity data of coal samples in three directions under different pressure conditions, compared with R, X has a characteristic minimum point, which can better highlight the change law of the complex electricity of coal. For the X, in the low frequency band, the X values between the adjacent pressure points of the coal samples in the three directions have little difference, and there are industrial electrical interference frequency points; in the high frequency band, the X of coal samples in three directions is gradually strengthened by electromagnetic induction disturbance with increasing pressure, and the two frequency bands cause great interference to the model fitting processing; and the nearby frequency band, including the X minimum point, can better distinguish the differences in the characteristics of the IP response of coal bodies with different pressures and directions. Therefore, the frequency band of 423–5355 Hz in the characteristic area is uniformly selected for model inversion analysis and processing, and the results are shown in Figure 9.

Figure 9.

Figure 9

Open in a new tab

Inversion of measured X data of coal in different directions by four conductive models.

The above three figures are the measured data of coal samples in three directions, which are inversed and analyzed by the Cole–Cole model, double Cole–Cole model, Debye model, and Warburg model. Among them, the two models with the best inversion effect are the Cole–Cole model and the double Cole–Cole model. The Debye model has a large deviation between the inversion results of measured data and measured data. The Warburg model has the worst inversion effect on measured data; the coal sample in the x direction fails to invert the minimum points, and the coal samples in the other two directions have a large deviation from the measured data, although the minimum points are inverted. For the Cole–Cole model and the double Cole–Cole model, the inversion of the measured data is very good, but the model parameters in the double Cole–Cole model are Z(0), m1, c1, τ1, m2, c2, and τ2. Not only too many parameters have multiple solutions but also too many equivalent electronic components make the interpretation of experimental data more difficult. Therefore, the Cole–Cole model is selected in this paper to process the measured complex electrical dispersion data. The relationship curve between the inversion parameters of the corresponding model and different pressures is shown in Figure 10 below.

Figure 10.

Figure 10

Open in a new tab

Relationship between inversion parameters and pressure of the Cole–Cole model of coal samples in different directions.

It can be seen from the above figure that the Cole–Cole model inversion parameter c of coal samples in three directions changes irregularly and fluctuates disorderly with increasing pressure. The m of the coal sample in the x direction decreases with increasing pressure, while the coal sample m in the y direction decreases with increasing pressure, but there is no change in the middle pressure point. Meanwhile, the coal sample in the z direction shows the law that m increases first and then decreases with increasing pressure; in other words, the change law of the coal sample m in the three directions is inconsistent. Distinct from the above two, τ of the coal samples in the three directions shows the law of decreasing with increasing pressure. In addition, the directionality of the inversion parameter m and c values is poor, and τ indicates the completion speed of coal IP and further reflects the structural difference of coal pore/fracture directivity, which decreases in the order of the z direction, y direction, and x direction. Considering various factors comprehensively, the model parameter relaxation time τ is selected as the optimal model inversion parameter and represents its dielectric property (the following part denotes it as the dielectric relaxation time), that is, the complex electricity sensitive parameter of the loaded coal.

3.3. Relationship between the Dielectric Relaxation Time and Permeability of Loaded Coal

According to the development characteristics and directivity of coal pores/fractures, the permeability of coal is used to characterize its permeability performance under different pressure conditions and further reflects the changes in the coal pore/fracture structure. The complex electric characteristics of coal also play a positive role in evaluating the development characteristics and directivity of its pores/fractures, and the dielectric relaxation time τ is closely related to the pore diameter of coal. The larger the pore diameter is, the larger the dielectric relaxation time is, as shown in Formula 1. The permeability of coal can be seen from the Kozeny–Carman model (Formula 2),55 and there is a positive relationship between permeability and porosity. Therefore, the complex electricity and permeability of coal are inseparable.

3.3. 1

where r is the pore diameter, d is the diffusion coefficient of the solute, and τ is the dielectric relaxation time, given in seconds.

3.3. 2

where k is the coal permeability, given in millidarcy; φ is the coal porosity, given in percentage; c is the model coefficient, approximately 0.25; and av is the ratio of the exposed specific surface area to the solid volume, given in per meter.

Based on the measured permeability in different directions of the coal under different pressures, the graph is summarized and drawn, as shown in Figure 11.

Figure 11.

Figure 11

Open in a new tab

Permeability change of coal in three directions under different pressures.

With the continuous increase in pressure, the permeability of the coal samples in the three directions gradually decreases, the permeability curve gradually changes from a rapid decline to a slow decline, and the change range of permeability continues to decrease. The reason is that with the continuous action of pressure on the coal sample, the pores/fractures gradually shrink and close, resulting in the continuous reduction of the flow channel space of methane gas, the weakening of migration capacity, the poor permeability of coal, and the reduction of the permeability value. In the stage of applying small axial pressure, the pore/fracture space of coal is easily compressed, and the reduction in permeability is greater than that in the stage of applying large axial pressure.

The permeability of loaded coal is anisotropic; that is, under the same pressure, the permeability of coal samples decreases in the order of the x direction, y direction, and z direction (kx > ky > kz). To explain this phenomenon, the coal is first simplified into two directions: parallel bedding and vertical bedding, as shown in Figure 12.

Figure 12.

Figure 12

Open in a new tab

Equivalent analysis diagram of coal permeability.

The a direction is the vertical bedding direction of the coal, and the b direction is the parallel bedding direction. It is assumed that the thickness of each layer of the coal is di, and the permeability of each layer is ki (i = 1, 2, ..., n).

For the vertical bedding direction, that is, the gas is introduced from the a direction and the gas flow of each layer is equal (Q1 = Q2 = ... = Qn), while the pressure gradient is different. According to Darcy’s law, the gas flow per unit width area of the ith coal body can be obtained as follows

3.3. 3

where ΔDi is the inlet and outlet pressure difference of the ith coal; the negative sign indicates that with the decrease in the gas pressure difference, the flow Qi increases.

Assuming that the total equivalent permeability coefficient of n-layer coal is kz, then

3.3. 4

For the permeability of coal in the parallel bedding direction, the pressure gradient of each layer is equal (D1 = D2 = ... = Dn = D), and the gas flow is different. Similarly, the gas flow per unit width area of coal in the parallel bedding direction is.

3.3. 5

where dD/dl is the pressure gradient in the bedding direction.

Assuming that the total equivalent permeability coefficient of n-layer coal is ks, then

3.3. 6

From the above derivation, the permeability ks in the parallel bedding direction and the permeability kz in the vertical bedding direction of the coal can be obtained, and the two are compared

3.3. 7

The above formula is always greater than zero, that is, the permeability in the parallel bedding direction is greater than that in the vertical bedding direction. In addition, the parallel bedding direction of coal can be divided into the main fracture direction in parallel bedding and the vertical main fracture direction in parallel bedding. The former has a high degree of fracture penetration, so the permeability is better than that of the latter. The relationship between permeability in the three directions is kx > ky > kz.

According to the comparison between Figures 10c and 11, the τ value of loaded coal also changes according to the development characteristics and directional law of coal pores/fractures, and the τ value of coal samples in different directions gradually decreases with increasing pressure. The development degree and extension direction of pores/fractures of coal samples in the vertical bedding direction are more resistant to gas permeability and charge migration than those in the parallel bedding direction, resulting in smaller permeability and a longer completion time of IP, and the τ value is larger. In the parallel bedding direction of the coal, the permeability of the pores/fractures in the vertical main fracture direction in parallel bedding is weaker than that in the main fracture direction in parallel bedding, the permeability is lower, and the τ value is larger. Therefore, there is a strong correlation between the permeability and τ value.

The permeability of coal samples in three directions under different pressures is related to the dielectric relaxation time, and the relationship is shown in Figure 13.

Figure 13.

Figure 13

Open in a new tab

k value and τ value fitting diagram of coal in three directions under different pressures.

Under the same pressure, the τ value of coal in different directions is associated with the k value, and the relationship in Figure 14 is obtained.

3.3. 8

where k is the permeability under different pressures, τ is the dielectric relaxation time under different pressures, and α and β are fitting parameters, which are related to the pressure and directivity of the coal.

Figure 14.

Figure 14

Open in a new tab

k value and τ value fitting diagram of coal in different directions under same pressure.

The permeability k value and dielectric relaxation time τ value of coal samples in three directions show a good relationship (Figure 13): as the τ value decreases, the k value gradually decreases, that is, the greater the pressure of coal is, the shorter the completion time of the IP effect is, and the smaller the corresponding permeability is. This is related to the continuous compression and deformation of coal, as well as the reduction in the development degree of pores/fractures. The change law curve of the two conforms to the logarithmic function relationship (Formula 8).

Under the same pressure, the k value and τ values of coal samples in different directions also have a certain regular relationship (Figure 14): the smaller the τ value is, the larger the k value is, that is, the τ value decreases in the order of the z direction, y direction, and x direction, while the k value increases in the order of the same direction. The reason is that the pores/fractures of coal in the z direction are relatively complex, mostly in the direction of vertical gas flow and the electric field action, resulting in weak gas seepage ability and a long time to complete the IP effect. The development characteristics and directionality of pores/fissures of coal in the x direction are more conducive to the completion of gas seepage and the IP effect than those of coal in the y direction. The k value and τ value correspondence between values also conforms to the logarithmic function (Formula 8). It can be seen from the expression that whether it is fitting in different directions of coal or under different pressures, the parameters α and β all decrease regularly. Therefore, the parameters α and β are related to the pressure and direction of the coal.

From the above research, it can be seen that the change in permeability and complex electricity of coal is caused by the difference in its internal structure and the characteristic direction of pore/fracture development, and the corresponding differential deformation is produced at the same time.

The correlation between the permeability k value and strain ε value is shown in Figure 15 and Table 3. The k value and ε value in the three directions are all positively correlated; the smaller the ε value is, the smaller the k value is, that is, the greater the compression deformation of the coal is, the smaller the corresponding permeability is. Under the same pressure, the strain anisotropy characteristics of the coal samples are consistent with the permeability characteristics: it increases in the order of the z direction, y direction, and x direction (εx > εy > εz).

Figure 15.

Figure 15

Open in a new tab

Relationship of the k value and ε value of coal in three directions under different pressures.

Table 3. Statistical Table of the Coal Strain, Permeability Change Rate, and Proportional Coefficienta.

pressure/(MPa)
 strain change rate δε
 strain proportional coefficient
 permeability change rate λk
 permeability proportional coefficient
  βεx βεy βεz aε bε cε αkx αky αkz ak bk ck
1       1.188 1.152 1.031       7.130 1.899 3.756
3 0.108 0.176 0.199 1.285 1.175 1.094 0.258 0.282 0.377 7.488 2.186 3.883
5 0.188 0.336 0.371 1.371 1.186 1.155 0.486 0.496 0.609 9.370 2.444 3.833
7 0.25 0.426 0.492 1.417 1.205 1.176 0.599 0.626 0.812 15.154 3.769 4.024
Open in a new tab
a

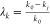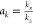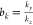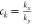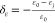Here, Inline graphic is the permeability change rate; k0 is the initial condition coal permeability, given in millidarcy; kj is the coal permeability under a certain pressure, given in millidarcy; Inline graphic ,Inline graphic, and Inline graphic are the permeability proportional coefficients in each direction; Inline graphic is the strain change rate; ε0 is the initial condition coal volumetric strain; εj is the coal strain under a certain pressure; and, 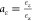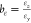Inline graphic, 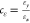Inline graphic, and Inline graphic are the strain proportional coefficients in each direction.

Under the same pressure, the strain change rate δε of coal decreases in the order of the z direction, y direction, and x direction (δεz > δεy > δεx), and the strain proportional coefficient in all three directions of coal increases with increasing pressure; that is, with increasing pressure, the anisotropy of coal deformation increases.

With increasing pressure, the strain ε value of coal is gradually reduced; that is, the coal volume is continuously compressed with increasing axial pressure, and the deformation shrinkage amplitude gradually decreases. In the stage of low pressure, the opening degree of coal pores/fractures is large, and it is easy to close and reduce. With increasing pressure, the gradually compressed coal is less prone to deformation. The strain change rate δε of coal increases with increasing pressure, indicating that the amount of coal compression deformation increases, which is consistent with the change law of the coal permeability change rate λk with pressure.

In summary, under the conditions of different pressures and different directions, the variation law between the coal strain ε value and permeability k value is consistent. Therefore, the strain of coal is correlated with the complex resistivity.

The relationships between the ε value and τ value of coal in three directions under different pressures are analyzed separately, as shown in Figure 16.

Figure 16.

Figure 16

Open in a new tab

ε value and τ value fitting diagram of coal in three directions under different pressures.

Under the same pressure, the ε value and τ value of coal in the three directions are associated, as shown in Figure 17.

3.3. 9

where ε is the strain value, given in microstrain; τ is the dielectric relaxation time, given in seconds; and a and b are the fitting parameters.

Figure 17.

Figure 17

Open in a new tab

ε value and τ value fitting diagram of coal in three directions under the same pressure.

The ε value and τ value of coal in the three directions show a good relationship. With the τ value of coal samples decreasing continuously, the ε value also gradually decreases; that is, the larger the pores and fissures gradually shrink and close, the shorter the completion time of its IP effect. The change curve between them conforms to the logarithmic function relationship. Under the same pressure, the ε value and τ value also have a certain regular relationship. The τ value decreases in the order of the z direction, y direction, and x direction, while the ε value increases in the same direction. The corresponding relationship between them can also be fitted by a logarithmic function.

4. Conclusions

  • (1)

    The R–X curve of coal shows U-shaped dispersion characteristics. With increasing frequency, the R–X curve shows two stages, first decreasing and then increasing, forming an obvious trough. The reason for this phenomenon lies in the polarization inside the dielectric coal. R is affected by the polarization degree of coal under different frequencies, and X is jointly determined by the capacitance and the frequency.

  • (2)

    The R–X curve and capacitance C dispersion curve all change regularly with the change in pressure and directivity. With increasing pressure, the absolute value of the R–X curve amplitude gradually decreases and shifts to the left, the offset amplitude gradually decreases, and the C value gradually reduces. The R–X curve gradually decreases and shifts to the left in the order of the z direction, y direction, and x direction, and the capacitance C decreases successively in the same direction.

  • (3)

    The dielectric relaxation time is optimized as the evaluation index of the complex electrical dispersion characteristics of coal. The conductive model is used to invert the complex electrical dispersion curve of coal, including the minimum point, and the dielectric relaxation time τ is optimized as the electrically sensitive parameter. With increasing pressure, τ continues to decrease; τ also decreases in the order of the z direction, y direction, and x direction. This change is related to the closure of coal pores and fissures caused by pressure and the development characteristics and directional differences of pores and fissures.

  • (4)

    There is a good logarithmic relationship between the permeability and the dielectric relaxation time of coal. With increasing pressure, the permeability decreases as the dielectric relaxation time decreases. The directional change in the permeability for the same pressure condition is opposite to the dielectric relaxation time. Both the strain and dielectric relaxation time conform to the logarithmic function relationship, which also verifies the correctness of the law between coal permeability and complex electricity.

Acknowledgments

We are grateful for the financial support of the research from the National Natural Science Foundation of China (51704101), China Postdoctoral Science Foundation (2019M652535), and Plan support for key scientific research projects of colleges and universities in Henan Province (20B620001).

The authors declare no competing financial interest.

References

  1. Uliasz-Misiak B.; Misiak J.; Lewandowska-Śmierzchalska J.; Matuła R. Environmental risk related to the exploration and exploitation of coalbed Methane. Energies 2020, 13, 6537. 10.3390/en13246537. [DOI] [Google Scholar]
  2. Niu Q. H.; Pan J. N.; Cao L. W.; Ji Z. M.; Wang H. C.; Wang K.; Wang Z. Z. The evolution and formation mechanisms of closed pores in coal. Fuel 2017, 200, 555–563. 10.1016/j.fuel.2017.03.084. [DOI] [Google Scholar]
  3. Li Y.; Pan S. Q.; Ning S. Z.; Shao L. Y.; Jing Z. H.; Wang Z. S. Coal measure metallogeny: Metallogenic system and implication for resource and environment. Sci. China Earth Sci. 2022, 65, 1211–1228. 10.1007/s11430-021-9920-4. [DOI] [Google Scholar]
  4. Li Y.; Yang J. H.; Pan Z. J.; Meng S. Z.; Wang K.; Niu X. L. Unconventional natural gas accumulations in stacked deposits: a discussion of upper paleozoic coal bearing strata in the east margin of the ordos basin, China. Acta Geol. Sin. 2019, 93, 111–129. 10.1111/1755-6724.13767. [DOI] [Google Scholar]
  5. Tao S.; Chen S. D.; Pan Z. J. Current status, challenges, and policy suggestions for coalbed methane industry development in China: A review. Energy Sci. Eng. 2019, 7, 1059–1074. 10.1002/ese3.358. [DOI] [Google Scholar]
  6. Tao S.; Pan Z. J.; Tang S. L.; Chen S. D. Current status and geological conditions for the applicability of CBM drilling technologies in China: A review. Int. J. Coal Geol. 2019, 202, 95–108. 10.1016/j.coal.2018.11.020. [DOI] [Google Scholar]
  7. Shi R.; Liu J. S.; Wang X. M.; Elsworth D.; Liu Z. H.; Wei M. Y.; Liu X. X.; Wang Z. Z. Experimental observations of heterogeneous strains inside a dual porosity sample under the influence of gas-sorption: A case study of fractured coal. Int. J. Coal Geol. 2020, 223, 103450. 10.1016/j.coal.2020.103450. [DOI] [Google Scholar]
  8. Li Y.; Zhang C.; Tang D. Z.; Gan Q.; Niu X. L.; Wang K.; Shen R. Y. Coal pore size distributions controlled by the coalification process: An experimental study of coals from the Junggar, Ordos and Qinshui basins in China. Fuel 2017, 206, 352–363. 10.1016/j.fuel.2017.06.028. [DOI] [Google Scholar]
  9. Li Y.; Wang Z. S.; Tang S. H.; Elsworth D. Re-evaluating adsorbed and free methane content in coal and its ad-and desorption processes analysis. Chem. Eng. J. 2021, 428, 131946. 10.1016/j.cej.2021.131946. [DOI] [Google Scholar]
  10. Guo H. J.; Wang K.; Cheng Y. P.; Yuan L.; Xu C. Model development and analysis of coal permeability based on the equivalent characteristics of dual-porosity structure. J. Geophys. Eng. 2020, 17, 313–327. 10.1093/jge/gxz108. [DOI] [Google Scholar]
  11. Zhang L.; Kan Z. H.; Xue J. H.; Li M. X.; Zhang C. Study on permeability law of intact and fractured coals under cyclic loading and unloading. Chin. J. Rock Mech. Eng. 2021, 40, 2487–2499. 10.13722/j.cnki.jrme.2021.0241. [DOI] [Google Scholar]
  12. Zou Q. L.; Lin B. Q. Fluid-solid coupling characteristics of gas-bearing coal subject to hydraulic slotting: an experimental investigation. Energy Fuels 2018, 32, 1047–1060. 10.1021/acs.energyfuels.7b02358. [DOI] [Google Scholar]
  13. Qin L.; Li S. G.; Zhai C.; Lin H. F.; Zhao P. X.; Shi Y.; Bai Y. Changes in the pore structure of lignite after repeated cycles of liquid nitrogen freezing as determined by nitrogen adsorption and mercury intrusion. Fuel 2020, 267, 117214. 10.1016/j.fuel.2020.117214. [DOI] [Google Scholar]
  14. Guo H. J.; Cheng Z. X.; Wang K.; Qu B. L.; Yuan L.; Xu C. Coal permeability evolution characteristics: Analysis under different loading conditions. Greenhouse Gases: Sci. Technol. 2020, 10, 347–363. 10.1002/ghg.1965. [DOI] [Google Scholar]
  15. Gao Z.; Li B. B.; Li J. H.; Wang B.; Ren C. H.; Xu J.; Chen S. Coal permeability related to matrix-fracture interaction at different temperatures and stresses. J. Petrol. Sci. Eng. 2021, 200, 108428. 10.1016/j.petrol.2021.108428. [DOI] [Google Scholar]
  16. Liu G.; Yu B. M.; Gao F.; Ye D. Y.; Yue F. T. Analysis of permeability evolution characteristics based on dual fractal coupling model for coal seam. Fractals 2021, 28, 2050133. 10.1142/s0218348x20501339. [DOI] [Google Scholar]
  17. Li Y.; Yang J. H.; Pan Z. J.; Tong W. S. Nanoscale pore structure and mechanical property analysis of coal: an insight combining AFM and SEM images. Fuel 2020, 260, 116352. 10.1016/j.fuel.2019.116352. [DOI] [Google Scholar]
  18. Li Y.; Tang D. Z.; Xu H.; Meng Y. J.; Li J. Q. Experimental research on coal permeability: the roles of effective stress and gas slippage. J. Nat. Gas Sci. Eng. 2015, 21, 481–488. 10.1016/j.jngse.2014.09.004. [DOI] [Google Scholar]
  19. Chen S. D.; Tang D. Z.; Tao S.; Liu P. C.; Mathews J. P. Implication of the in situ stress distribution for coalbed methane zonation and hydraulic fracturing in multiple seams, western Guizhou, China. J. Petrol. Sci. Eng. 2021, 204, 108755. 10.1016/j.petrol.2021.108755. [DOI] [Google Scholar]
  20. Fang X. J.; Wu C. F.; Jiang X. M.; Liu N. N.; Zhou D.; Ju Y. W. Characteristics of in situ stress and its influence on coal seam permeability in the Liupanshui Coalfield, Western Guizhou. Energy Sci. Eng. 2021, 9, 1773–1786. 10.1002/ese3.950. [DOI] [Google Scholar]
  21. Xue Y.; Ranjith P. G.; Dang F. N.; Liu J.; Wang S. H.; Xia T. Q.; Gao Y. N. Analysis of Deformation, Permeability and Energy Evolution Characteristics of Coal Mass Around Borehole After Excavation. Nat. Resour. Res. 2020, 29, 3159–3177. 10.1007/s11053-020-09644-0. [DOI] [Google Scholar]
  22. Liu T.; Lin B. Q.; Yang W. Impact of matrix-fracture interactions on coal permeability: Model development and analysis. Fuel 2017, 207, 522–532. 10.1016/j.fuel.2017.06.125. [DOI] [Google Scholar]
  23. Wang D. K.; Lv R. H.; Peng M.; Wei J. P.; Yao B. H.; Liu Y. Experimental study on anisotropic permeability rule of coal bearing methane. J. China Coal Soc. 2018, 43, 1008–1015. [Google Scholar]
  24. Zhao Y.; Zhang Y. G.; Yue G. W.; Zhou J. Y. Experimental study on anisotropic permeability of coal seam. China Coalbed Methane 2017, 14, 32–35. [Google Scholar]
  25. Guo H. J.; Tang H. L.; Wu Y. C.; Wang K.; Xu C. Gas seepage in underground coal seams: Application of the equivalent scale of coal matrix-fracture structures in coal permeability measurements. Fuel 2021, 305, 121550. 10.1016/j.fuel.2021.121550. [DOI] [Google Scholar]
  26. Ye D. Y.; Liu G. N.; Gao F.; Hu Y. H.; Yue F. T. A fractal model of thermal-hydrological-mechanical interaction on coal seam. Int. J. Therm. Sci. 2021, 168, 107048. 10.1016/j.ijthermalsci.2021.107048. [DOI] [Google Scholar]
  27. He S.; Guan J.; Wang Y.; Ji X.; Wang H. A hybrid correlation denoising method based on complex resistivity and application on spread-spectrum induced-polarization data. Geophysics 2021, 86, E297–E303. 10.1190/geo2018-0813.1. [DOI] [Google Scholar]
  28. Yang Z. W.; Xu J. T.; Zhao Q. F.; Li X. B. Current situation and review of complex resisitivity. Prog. Geophys. 2015, 30, 899–904. [Google Scholar]
  29. Tang T. Z.; Lu T.; Zhang H. N.; Jiang L. M.; Liu T. Y.; Meng H.; Wang F. F. Electrical characteristics of rocks in fractured and caved reservoirs. J. Geophys. Eng. 2017, 14, 1437–1444. 10.1088/1742-2140/aa8528. [DOI] [Google Scholar]
  30. Pan B. Z.; RuHan A.; Guo Y. H.; Zhang L. H.; Wei B. Y.; Zhou W. Y. Study on the relationship between complex resistivity and water saturation in fractured rock at low frequency. Chin. J. Geophys. 2021, 64, 3774–3787. 10.6038/cjg2021O0084. [DOI] [Google Scholar]
  31. Zhdanov M. S.; Burtman V.; Endo M.; Lin W. Complex resistivity of mineral rocks in the context of the generalised effective-medium theory of the induced polarisation effect. Geophys. Prospect. 2018, 66, 798–817. 10.1111/1365-2478.12581. [DOI] [Google Scholar]
  32. Chen H.; Di Q. Y.; Li D. Q. The discussion electrical properties of rocks base on frequency response characteristics. Prog. Geophys. 2010, 25, 918–925. 10.3969/j.issn.1004-2903.2010.03.027. [DOI] [Google Scholar]
  33. Ke S.-Z. Frequency-swept measurement of electrical parameters of rock. Prog. Geophys. 2010, 25, 512–515. 10.3969/j.issn.1004-2903.2010.02.018. [DOI] [Google Scholar]
  34. Dias C. A. Developments in a model to describe low-frequency electrical polarization of rocks. Geophysics 2000, 65, 437–451. 10.1190/1.1444738. [DOI] [Google Scholar]
  35. Sacks F. M.; Pfeffer M. A.; Moye L. A.; Rouleau J. L.; Rutherford J. D.; Cole T. G.; Brown L.; Warnica J. W.; Arnold J. M.; Wun C. C.; Davis B. R.; Braunwald E. The effect of pravastatin on coronary events after myocardial infarction in patients with average cholesterol levels. Cholesterol and Recurrent Events Trial investigators. New Engl. J. Med. 1996, 335, 1001–1009. 10.1056/nejm199610033351401. [DOI] [PubMed] [Google Scholar]
  36. Pelton W. H.; Ward S. H.; Hallof P. G.; Sill W. R.; Nelson P. H. Mineral discrimination and removal of inductive coupling with multifrequency IP. Geophysics 1978, 43, 588–609. 10.1190/1.1440839. [DOI] [Google Scholar]
  37. Wang E.-Y.; Chen P.; Li Z. H.; Shen R. X.; Xu J. K.; Zhu Y. F. Resistivity response in complete stress-strain process of loaded coal. J. China Coal Soc. 2014, 39, 2220–2225. 10.13225/j.cnki.jccs.2013.1070. [DOI] [Google Scholar]
  38. Guo X. J.; Xun X.; Gong W. D.; Zhang Y. G. Study on coal complex resistivity anisotropy and characteristics of frequency response. Coal Sci. Technol. 2017, 45, 167–170. [Google Scholar]
  39. Liu S.; Zhang Y. G.; Xu X. K.; Zhao C. G. Research on coal electrical experiment stimulated by frequency signal and its characteristics. Saf. Coal Mines 2017, 48, 65–67. [Google Scholar]
  40. Meng H.; Li J.; Lei D. J.; Wang Y. J. Experimental study on the frequency dispersion response of composite electrical properties of coal. Coal Geol. Explor. 2020, 48, 226–232. [Google Scholar]
  41. Zhang Y.; Li D. H.; Zhang Y. G. Cole-Cole model inversion of different types of tectonic coal and its induction mechanism. J. China Coal Soc. 2020, 45, 943–954. [Google Scholar]
  42. Zhao C. G.; Lei D. J.; Zhang Y. G. Orthogonal fracture resistance-capacitance model of complex re-sistance of containing water coal seam. J. China Coal Soc. 2020, 45, 3541–3547. [Google Scholar]
  43. Hördt A.; Blaschek R.; Kemna A.; Zisser N. Hydraulic conductivity estimation from induced polarisation data at the field Scale-the krauthausen case history. J. Appl. Geophys. 2007, 62, 33–46. 10.1016/j.jappgeo.2006.08.001. [DOI] [Google Scholar]
  44. Slater L.; Lesmes D. P. Electrical-hydraulic relation-ships observed for unconsolidated sediments. Water Resour. Res. 2002, 38, 31. 10.1029/2001wr001075. [DOI] [Google Scholar]
  45. Norbisrath J. H.; Weger R. J.; Eberli G. P. Complex resistivity spectra and pore geometry for predictions of reservoir properties in carbonate rocks. J. Petrol. Sci. Eng. 2017, 151, 455–467. 10.1016/j.petrol.2016.12.033. [DOI] [Google Scholar]
  46. Latt K. M. M.; Giao P. H. Prediction of permeability of cement-admixed soft clay using resistivity and time-domain IP measurements. J. Appl. Geophys. 2017, 137, 92–103. 10.1016/j.jappgeo.2016.12.015. [DOI] [Google Scholar]
  47. Ma J. B.; Tang X. G.; Xiang K. Study on the method of using resistivity to calculate rock permeability. J. Yangtze Univ., Nat. Sci. Ed. 2013, 10, 105–106. [Google Scholar]
  48. Huang L. S.; Zhang S. Y.; Chen C. J.; Liu Y. Research on calculating permeability with complex resistivity. Chin. J. Eng. Geophys. 2007, 5, 444–449. [Google Scholar]
  49. Tong M. S.; Li L.; Wang W. N.; Jiang Y. H. Determining capillary-pressure curve, pore-size distribution, and permeability from Induced polarization of shaley sand. Geophysics 2006, 71, N33–N40. 10.1190/1.2195989. [DOI] [Google Scholar]
  50. Liu S.The Experimental Study on Complex Electrical Frequency Dispersion Characteristics of Coal Containing Water; Henan Polytechnic University, 2017. [Google Scholar]
  51. Meng L.; Liu M. J.; Wang Y. G. Study on the rules of electrical resistivity variation of tectonic coal in uniaxial compression experiment. J. China Coal Soc. 2010, 35, 2028–2032. [Google Scholar]
  52. Chen J. J.; Jiang L. H.; Zhang Y. G.; Zhang T. Study on Coal Conductive Properties of Different Coal Structure. Coal Sci. Technol. 2011, 39, 90–92. [Google Scholar]
  53. Cao X.; Liao M. Z.; Gu X. Z.; Li L. F.; Wu G. S. Studies on intermolecular electron transfer using electrostatic potential approach II. application to photoelectric conversion simulating systems. Acta Chim. Sinica 1992, 05, 456–460. [Google Scholar]
  54. Yin Z. W.Dielectric Physics; Sci. Press, 2003. [Google Scholar]
  55. Liu Z.; Wang W. Y.; Cheng W.; Yang H.; Zhao D. W. Study on the seepage characteristics of coal based on the Kozeny-Carman equation and nuclear magnetic resonance experiment. Fuel 2020, 266, 117088. 10.1016/j.fuel.2020.117088. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES