Molecular Theory: A Tool for Predicting the Outcome of Self-Assembly of Polymers, Nanoparticles, Amphiphiles, and Other Soft Materials

Abstract

The supramolecular organization of soft materials, such as colloids, polymers, and amphiphiles, results from a subtle balance of weak intermolecular interactions and entropic forces. This competition can drive the self-organization of soft materials at the nano-/mesoscale. Modeling soft-matter self-assembly requires, therefore, considering a complex interplay of forces at the relevant length scales without sacrificing the molecular details that define the chemical identity of the system. This mini-review focuses on the application of a tool known as molecular theory to study self-assembly in different types of soft materials. This tool is based on extremizing an approximate free energy functional of the system, and, therefore, it provides a direct, computationally affordable estimation of the stability of different self-assembled morphologies. Moreover, the molecular theory explicitly incorporates structural details of the chemical species in the system, accounts for their conformational degrees of freedom, and explicitly includes their chemical equilibria. This mini-review introduces the general ideas behind the theoretical formalism and discusses its advantages and limitations compared with other theoretical tools commonly used to study self-assembled soft materials. Recent application examples are discussed: the self-patterning of polyelectrolyte brushes on planar and curved surfaces, the formation of nanoparticle (NP) superlattices, and the self-organization of amphiphiles into micelles of different shapes. Finally, prospective methodological improvements and extensions (also relevant for related theoretical tools) are analyzed.

1. Introduction

Materials that can be easily deformed by weak chemical and physical stimuli are commonly known as soft materials.¹ These systems are held together by weak interactions, whose energy scales are commensurable with the thermal energy, k_BT (where k_B is Boltzmann’s constant and T is the temperature). Because of the weak energies involved, soft materials have some degree of structural disorder and can dynamically explore a rich conformational landscape. Soft materials are also highly prone to form self-organized structures, i.e., to self-assembly, because of the competition among weak interactions on different length scales and the relevance of entropic effects. In this way, while self-organization is not exclusive to soft matter, many prototypical examples of self-assembly (block copolymers, surfactant micelles, colloidal and nanoparticle (NP) supercrystals, lipid membranes, etc.) are also prominent classes of soft materials.

There exist many and diverse methods to model, understand, and predict the outcome of self-assembly in soft-matter systems. Each approach has its own advantages and disadvantages. Since discussing them, even briefly, would largely exceed the scope and space of this mini-review, we refer the interested reader to some of the many excellent reviews in the literature.²⁻⁵ Let us roughly categorize these tools into two main families: (i) those methods that stochastically sample microstates of the system using a particle-based description, such as molecular dynamics (MD), Monte Carlo (MC), Brownian dynamics (BD), etc.² and (ii) theoretical approaches that resort to approximations to directly describe the (average) equilibrium structure of the system, such as self-consistent field (SCF) theories, classical density functional theories (cDFT), scaling arguments, etc.⁵ Still, there are tools that combine characteristics of both approaches and/or escape this simple classification, such as theoretical field simulations³ and single-chain in a mean-field (SCMF) simulations.⁴

In this mini-review, we describe the application of a molecular theory (hereafter, MOLT) pioneered by Szleifer’s group^5c to model self-assembly in soft materials. As we discuss next, this theory belongs to the second group of tools mentioned above (tools that directly describe the ensemble-averaged structure of the system). MOLT has some unique advantages over particle-based computer simulations: (i) It provides a direct estimation of the free energy of the system, which enables the construction of thermodynamic morphology diagrams. Moreover, MOLT can take advantage of the natural symmetries of the problem to further lower the computational cost. As we discuss below for specific systems, predicting free-energy differences with particle-based simulations is possible^6,7 but computationally very expensive. (ii) It can straightforwardly include chemical reaction equilibria, such as acid–base and redox reactions. Once again, constant pH or electrode potential simulations are possible but computationally expensive and complex to implement. MOLT shares some problems with coarse-grain (CG) MD simulations, such as the parametrization. On the other hand, computer simulations include more correlations than MOLT and provide information on the kinetics and nonequilibrium pathways, which are difficult to obtain with MOLT.

It is also insightful to compare MOLT with other theories that aim to directly describe the ensemble-average structure of the system, such as SCF and cDFT. These theories share the advantages mentioned in a previous paragraph (straightforward prediction of free energy, use of symmetries, and simple implementation of chemical equilibria) with MOLT. However, there is also a difference between these tools. We comment below on some salient points and refer the reader to ref (5f) for additional discussions. Self-consisting field (SCF or SCFT) theories typically describe chains as non-self-avoiding continuous curves, which follow Gaussian statistics in the absence of interactions.^5h,8 As we discuss below, MOLT uses explicit molecular conformations, which are self-avoiding and have a finite extensibility; therefore, SCF is best suited for long polymer chains, while MOLT is most useful for short polymers (<∼100 monomers/chain), such as amphiphiles and alkyl-chain ligands. cDFT methods are based on the functional minimization of the free energy of the system, which is formulated as a functional of the density of its different components. State-of-the-art functionals properly capture correlation effects related to different interactions, such as excluded-volume repulsions and chain connectivity.^5e MOLT uses explicit conformations and, therefore, excluded volume and chain connectivity (even for molecules of complex topologies) are treated exactly at the intrachain level; however, intermolecular excluded-volume repulsions are considered at a mean-field level.

The review is organized as follows. In the following section, we provide a concise description of the theoretical formulation and numerical implementation of MOLT. The mini-review then discusses selected application examples in different self-assembled systems: (i) self-patterned polymer-modified surfaces, nanoparticles, and nanochannels, (ii) the assembly of nanoparticle superlattices, and (iii) micellar aggregates of surfactants and amphiphiles in solution and their response to chemical stimuli. We finally provide some general conclusions and discuss opportunities to extend and improve the theory.

1.1. Molecular Theory: The Inner Workings

Before delving into the application examples, let us introduce the general ideas behind MOLT and explain what information this theory provides about self-assembly in soft-matter systems. For an in-deep description of the theoretical formalism, we refer the reader to previous works^5c,5f,9−13 and the corresponding Supporting Information sections. In Figure 1, we depict the different steps involved in formulating, deriving, and solving MOLT. In the first step, we write down an approximate functional for the (Helmholtz) free energy of the system, F, which depends on functions that describe its structure and that are a priori unknown. Some of these functions are the local number densities (particles per unit volume) of the different chemical species in the system, ρ_i(r); the probabilities of the different conformations of those molecules that have internal degrees of freedom, P(α); the local electrostatic potential, ψ(r); and the population of the different chemical states participating in chemical equilibria, f_j(r). The free energy functional formulated in terms of these unknown quantities contains different contributions (see Figure 1): the electrostatic (F_Elect) and short-range nonelectrostatic (F_SR) interaction free energies, the free energies associated with the translational (−T.S_Trans) and conformational (−T.S_Conf) entropies, and the free-energy contributions resulting from the presence of chemical equilibria, such as acid–base, redox, ligand–receptor binding, ion pairing, etc. (F_Chem and F_Int). The equilibrium state of the system is then obtained from the functional extrema of the free energy with respect to the unknown variables; i.e., we analytically compute δF/δg = 0 for g = ρ_i(r), P(α), f_j(r) and ψ(r). This step results in a set of integro-differential equations that should be numerically solved to obtain the structure and thermodynamics of the system. However, before solving these equations, we first exploit the symmetry of the system in order to lower the computational cost.

Figure 1.

Steps involved in formulating and solving the molecular theory, the required inputs, and provided outputs.

We leverage the natural symmetries of the system to reduce the dimensionality of the final numerical problem. For example, to model an homogeneous thin polymer layer on a planar surface, one can assume that the system is homogeneous in the planes parallel to that surface (plane x–y) and inhomogeneous in the normal direction (z); see “Cartesian 1D” example in Figure 1. If the system has a native cylindrical (e.g., a long polymer-coated nanorod or nanochannel) or spherical symmetry (e.g., a spherical nanoparticle), then the structural properties can be assumed to be heterogeneous only in the radial direction. In some cases, it is necessary to consider inhomogeneities in at least two coordinates, e.g., short nanorods or nanochannels (in which the system is heterogeneous in the r and z directions; see the cylindrical 2D case in Figure 1). Finally, sometimes it is necessary to allow heterogeneities in the three spatial dimensions, for example, to model self-assembly processes that spontaneously break the natural symmetries of the system (e.g., microphase separation) or complex systems such as arrays of ligand-coated NPs. In these cases, either Cartesian coordinates or other 3D coordinate systems can be used. Exploiting the symmetry of the system to reduce the computational burden of solving the molecular theory constitutes a key advantage compared to MC and MD simulations.

After obtaining the set of integro-differential equations from the extreme of the system’s free energy and applying symmetry considerations, we proceed to discretize the resulting equations using a finite-differences scheme. This step results in a set of coupled nonlinear equations, which are solved using numerical methods (a Jacobian-free Newton method). In this stage, MOLT is implemented into a computer code. As shown in Figure 1, the inputs required to solve the theory are the experimental conditions (such as the pH and salt concentration of the solution), the molecular structures of the chain-like molecules (which can have branches and segments with different properties), and the molecular properties of all chemical species and segments (molecular volume, charge, interaction parameters, equilibrium constants, etc.). In the case of polymers and other chain-like molecules, we also need to input a set of randomly generated conformations. The generation of a representative set of chain configurations deserves further discussion since it is one of the main differences between MOLT and related tools (such as SCF, which frequently uses Gaussian chains). MOLT uses explicit conformations, which (unlike Gaussian chains) have finite extensibility and are self-avoiding. In other words, intramolecular repulsions are exactly treated by including only self-avoiding configurations in the set. In principle, the set of chain conformations required as an input in the theory (see Figure 1) contains all possible conformations, each of them uniquely defined by the positions of all beads. In practice, however, it is enough to use a statistically representative set of conformations, which is randomly picked from the set of all possible conformations. When the set is statistically representative, any increase in the number of conformations in the set does not affect the structural predictions and shifts the conformation entropy by only a constant amount (which cancels when taking free-energy differences). Typically, a representative set for grafted chains of ∼50 segments requires 10⁵–10⁶ conformations. This number increases in the presence of strong interaction fields and rapidly grows with chain length; therefore, MOLT faces limitations to model long polymers. The representative set of randomly chosen conformations can be generated with the rotational isomeric state (RIS) model (where each segment has a fixed length and three possible dihedral angles). Alternatively, conformations can be extracted from long MD trajectories of single chains in the absence of interactions.¹⁴

The output of the molecular theory involves both structural and thermodynamic information. The structural information is encoded in the solution of the functions ρ_i(r), P(α), ψ(r), f_i(r). From these functions, we have access to the morphology and average properties of the system. The most important thermodynamic output is the system’s free energy. Note that determining free-energy differences from MD and MC simulations is computationally very costly because it requires the use of thermodynamic integration techniques or advanced sampling techniques. However, since MOLT is a free-energy functional method, it provides a direct estimation of this important variable. This characteristic enables the construction of thermodynamic phase diagrams to analyze and predict the outcome of self-assembly in soft materials.

Armed with a basic understanding of the inner workings of the molecular theory, we will now turn our attention to recent examples in the literature that illustrate the capabilities of MOLT to study self-assembly in different materials.

2. Examples of Self-Assembly in Soft Materials

2.1. Self-Assembly of Polymer and Polyelectrolyte Brushes

We will first review the application of MOLT to study the self-assembly of polymer brushes of different natures and on surfaces of different curvatures. Polymer- and polyelectrolyte-modified surfaces confer functionality and responsiveness to the material. Structural parameters, such as the curvature of the system, the type of polymers, their grafting density, as well as the properties of the solution (pH, the concentration of different species, etc.) play a complex role in the highly inhomogeneous conformational behavior of the polymers. In this section, we present examples of the use of MOLT that shed light on how the surface curvature, solvent quality, chemical equilibria (ion pairing and acid–base reactions), molecular structure of the polymers end-grafted to the surface, and physical–chemical environment dictate the self-organization of grafted polymer layers. In particular, we focus on different triggers for molecular self-assembly. In most of these examples, self-assembly results from microphase separation. Free polymer chains in a poor solvent (i.e., a solvent where effective polymer–polymer interactions are strong) macroscopically phase separate from the solvent, forming polymer-rich and a polymer-poor phases. Grafted polymers cannot phase separate because their end-groups are bound to the surface, so they locally phase segregate on a nano-/micrometer scale (i.e., they microphase separate), forming self-assembled aggregates.

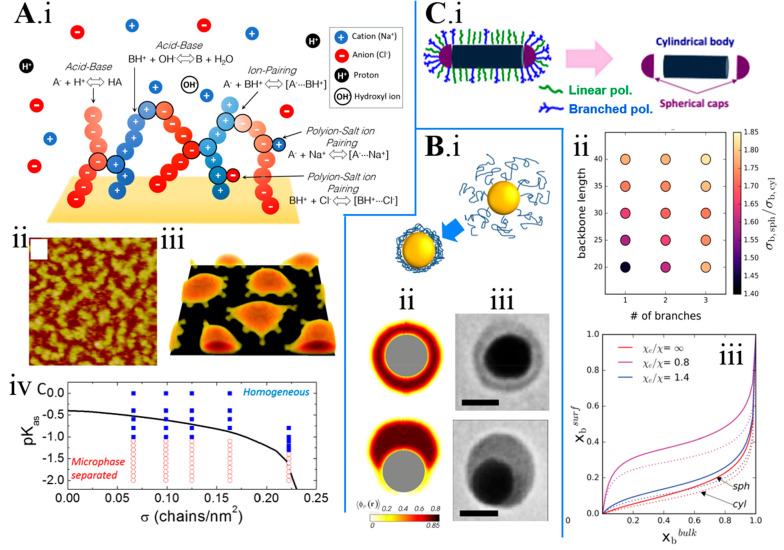
Figure 2A discusses the self-assembly of a mixed polyelectrolyte (PE) brush composed of polyanion and polycation chains; see scheme in Figure 2A.i.⁹ Polycation and polyanion mixtures in solution are known to separate into a polymer-dilute phase and a polymer-rich coacervate phase. As discussed above, the mixed brush cannot phase separate, but atomic force microscopy (AFM) studies revealed the formation of self-assembled microphase-separated aggregates (Figure 2A.ii).¹⁵ We theoretically studied this model with a 3D implementation of the molecular theory (allowing inhomogeneities in the three spatial directions). In this example, each individual PE is in good solvent conditions (there are no effective polymer–polymer van der Waals attractions); however, there are electrostatic attractions between the oppositely charged chains in the brush. To properly capture these interactions, we have explicitly included in the theory the formation of ion pairs (both between oppositely charged groups in the PEs and between the charged groups in the PEs and salt ions in solution) using a chemical reaction formalism.⁹ Note that this contribution to the free energy corrects the well-known inability of mean-field electrostatics to capture the formation of ion pairs. Our theory predicts microphase separated aggregates (Figure 2A.iii), in line with the experimental observations shown in Figure 2A.ii.¹⁵ MOLT also predicts the phase diagram of the system as a function of the surface coverage of the brush (σ) and the strength of the PE–PE ion-pairing association (pK_as); see Figure 2A.iv. We also included in the diagram predictions of a 1D implementation of the molecular theory, which determines the phase behavior of the system from thermodynamic considerations. Namely, the 1D implementation is used to determine under which conditions the laterally homogeneous system (which is the only system that can be studied within the 1D implementation) becomes unstable with respect to spinodal decomposition. This argument can be used to study self-organization in other systems; for example, Uline et al. applied it to study the effect of membrane tension on the phase diagram of lipid bilayers.¹⁸ In the case of the phase diagram of the mixed polyanion/polycation brush shown in Figure 2A.iv, the predictions of the 1D implementation (solid black line) are in good agreement with the 3D ones (symbols). The low computational requirements of the 1D implementation enabled a systematic analysis of the effect of several parameters (pH, salt concentration, grafting density, chains length, polyion–polyion, and ion-polyion association strengths) on the morphology of the system.⁹

Figure 2.

(A) i. Scheme of a mixed polyanion/polycation brush in a solution with salt ions (cations and anions), protons, and hydroxyl ions. The chemical equilibria considered by MOLT (acid–base, polyion–polyion association, and ion-polyion association) are explicitly shown. ii. Experimental AFM image of a mixed polyanion/polycation PAA/P2VP brush (Reproduced with permission from ref (15). Copyright 2018 American Chemical Society). iii. Microphase separated aggregates predicted by MOLT. iv. Predicted morphology diagram of a polyanion/polycation brush as a function of the total grafting density (σ) and the polyion–polyion association constant (pK_as, a more negative pK_as corresponds to a stronger polyion–polyion association). Red empty circles indicate self-assembled aggregates (like the ones shown in panel A.ii), and blue solid squares indicate an homogeneous brush. The black line is the threshold for microphase separation predicted by a 1D implementation of MOLT based on thermodynamic considerations (Reproduced with permission from ref (9). Copyright 2020 AIP Publishing). (B) i. Scheme of solvent-mediated polymer aggregation on Au spherical nanoparticles (NPs). ii. Color maps of the polymer volume fractions around a spherical Au NPs (R = 5 nm) modified with an end-grafted neutral polymer layer in poor-solvent conditions. The systems shown (eccentric, upper left panel, and janus, lower left panel) correspond to two minima of the free energy for the same conditions. (Reproduced and adapted with permission from ref (16). Copyright 2012 American Chemical Society). iii. TEM images of Au NPs (R = 20 nm) modified with polystyrene-50K showing morphologies similar to those in panel B.ii. (Reproduced and adapted with permission from ref (17). Copyright 2016 Springer Nature). (C) i. Schematic representation (not to scale) of the anisotropic surface functionalization of a nanorod (NR) upon adsorption from an aqueous solution containing a mixture of polymers of different molecular architectures (linear and branched). The NR is modeled as a combination of surfaces of different curvatures: cylinders and spheres, representing the NR’s body and caps, respectively. ii. Curvature-induced partition enhanced by polymer molecular architecture. The plot shows the partition of the branched polymer between a sphere and a cylinder of R = 5 nm for different molecular architectures (changing the length of the backbone or the number of branches). (The bulk solution in contact with the nanosurface is 90% branched polymer.) iii. Composition of the surface-adsorbed polymer mixture (molar fraction of the branched polymer) as a function of the polymer mixture in bulk solution (molar fraction of the branched polymer) for spherical (full lines) and cylindrical (dotted lines) surfaces of R = 5 nm. Red, magenta, and blue lines correspond to different solvent qualities, from good to poor solvent conditions (as indicated in the legend, Reproduced and adapted with permission from ref (11). Copyright 2016 the Royal Society of Chemistry).

Microphase separation of end-grafted polymer layers can be also triggered by changes in the quality of the solvent. Moreover, when polymers are grafted to NPs, the underlying curvature modulates the aggregation in poor-solvent conditions to form interesting surface patterns, breaking the original spherical symmetry of the system. In this line, the plasmonic properties of Au-NPs coated with neutral polymers in solvents of different qualities were studied with a combination of MOLT and electrodynamics calculations.¹⁶ Of particular interest to this mini-review is the result in Figure 2B.i that shows two different local minima of the free energy for polymer-coated NPs in a poor solvent. These two microphase-segregated structures are the eccentric (upper panel) and the janus (lower panel) morphologies. Interestingly, these theoretically predicted nanostructures for polymer-coated Au NPs in poor-quality solvent were later observed experimentally by Kumacheva’s group;¹⁷ see Figure 2B.iii (upper and lower panels).

Polymer self-assembly onto surfaces by adsorption of the terminal group is a routine strategy to functionalize NPs. In particular, resorting to nanostructures such as nanorods (NRs) that have different curvatures on the bodies and the caps offers a great opportunity to engineer anisotropic nanoconstructs. This strategy could be facilitated by combining molecular architecture, solvent quality, and surface-curvature effects. To explore such hypothesis, we applied MOLT to analyze the effect of surface curvature and molecular architecture on polymer adsorption from binary solutions onto NRs, which were modeled as a combination of spherical and cylindrical surfaces that represented the tips and body of the NR, respectively (Figure 2C.i).¹¹ Theoretical calculations suggested that a spatially resolved surface modification could be attained by tuning the molecular architecture of the polymer chains in the mixture (linear and branched), the composition of the bulk polymer solution, the quality of the solvent, and playing with the surface curvature. Combining linear and branched polymers leads to a competitive adsorption process that results from a nontrivial balance between repulsive steric forces and polymer–surface and polymer–polymer attractions. In this balance, surface curvature plays a major role: since the available volume at a given distance from the surface is larger for spherical surfaces than for cylindrical ones of the same size, bulkier (more branched) polymers in the mixture are found in a larger proportion on the spherical caps than on the NR body. This effect leads to a curvature-induced partition between spherical and cylindrical surfaces that strongly depends on the radius of the curved surface but can be adjusted by tailoring the molecular topology of the chains in the mixture, that is, changing the length of the backbone or the number of branches (Figure 2C.ii). Calculations also showed that the composition of the adsorbed mixture departs strongly from that of the bulk solution, and it depends on the curvature and morphology of the surface and the solvent quality (Figure 2C.iii). The overarching result of these calculations is that combining curvature at the nanoscale, tailored molecular architecture, and solvent conditions can confer anisotropic NPs with spatially enriched polymer domains. Also, applying MOLT to model polymer adsorption allowed us to outline useful design rules that would lead to a partition of the branched polymer toward regions of higher curvature, offering a path to engineer nanoconstructs with directional interactions.

In addition to the flat and convex surfaces discussed above, polymer brushes can also be used to modify concave surfaces, such as nanochannels and nanopores. Self-assembly of polymer-brush modified nanochannels is a promising strategy for gating the transport of particles as a response to external conditions. We used MOLT calculations to design a nanopore gate responsive to the externally induced electric field, E (Figure 3A.i).¹² In this example, a nanochannel modified by a weak polybase connects two reservoirs between which an electric potential is applied. The electric field inside the channel stretches the grafted chains, thereby triggering a sudden close-to-open conformation of the polymers (Figure 3A.i). This transition was studied as a function of the length of the polybase chains, the hydrophobicity of the backbone, the pH, and the salt concentration. Figure 3B.ii shows the polymer density in transversal cuts of the channel (i.e., cuts in the x–y plane) as a function of salt concentration and applied potential. In the absence of an electric field and poor solvent conditions, the end-grafted chains collapse to the center of the nanopore (upper panel in Figure 3A.i). For high applied electric fields and intermediate salt concentrations, the transmembrane potential forces the polymer chains to extend in the direction of the electric field, and change the collapsed structure from the center to near the wall of the nanopore (lower panel in Figure 3A.i), demonstrating the design of the voltage-gated nanochannel.

Figure 3.

(A) i. Schematic representation of a cylindrical nanochannel modified by an end-grafted layer of a weak polybase with a hydrophobic backbone. The channel connects two reservoirs containing identical aqueous salt solutions. Upon applying an electric potential between the electrodes in the reservoirs, the polybase layer switches from a closed, collapsed-to-the-center state (upper panel) to an open, collapsed-to-the-walls configuration (lower panel). ii. Color maps of the polymer volume fraction (density) along a cut perpendicular to the main axis of the nanochannel for different bulk salt concentrations and applied potentials (nanochannel radius = 5 nm and length of the polybase = 28 segments/chain, reproduced and adapted with permission from ref (12). Copyright 2020 American Chemical Society). (B) i. Scheme of a nanochannel modified with a polymer brush in good solvent conditions in the absence (upper panel, swollen state) and presence (lower panel, collapsed state) of soluble particles that reversibly cross-link the polymers. ii. Morphology diagram of the system in panel i as a function of the bulk density of cross-linkers (ρ_cl^bulk) and the length of the polymers (N_seg) for a nanochannel radius of 5 nm. The insets show color maps of the volume fraction of the polymer along a cut including the main axis of the channel for different values of N_seg. The red line delimits the regions of thermodynamic stability of the collapsed and swollen states. Green and black lines indicate the region of metastability. (Reproduced and adapted with permission from ref (19). Copyright 2021 the Royal Society of Chemistry).¹⁹

The nanochannel gate discussed in Figure 3A used a physical stimulus (electric field) to switch between two different organizations. Figure 3B discusses polymer collapse in response to a chemical cue: soluble cross-linker particles.¹⁹ In this work, the polymer brush (which is in good solvent conditions) collapses due to the presence of soluble cross-linkers (Figure 3B.i). We studied the effect of the length of chains, the cross-linker concentration, and the cross-linker-segment interaction strength on the morphology of the system. For long chains, the polymer brush self-assembles to the center of the channel (see panel for N_seg > 17 in the morphology diagram of Figure 3B.ii), which increases the free-energy barrier for the translocation of a cargo through the channel and shifts the route of translocation from the axis to the walls.¹⁹ On the other hand, short polymers assemble to the walls of the channel (panel for N_seg < 17 in Figure 3B.ii), which reduces the translocation barrier along the axis of the channel.

2.2. Nanoparticle Self-Assembly

In the previous section, we discussed theoretical predictions exemplifying the self-assembly of polymer brushes on surfaces of different curvatures, including nanoparticles (NPs). We now focus on the question of how the presence of polymer-like molecules (ligands) on the surface of the NPs mediates NP–NP interactions and can lead to their self-organization. NPs self-organize into nanoparticle superlattices (NPSLs),⁶ which are the nanoscale counterparts of atomic crystals. In other words, NPSLs are well-ordered arrays of (typically monodisperse) nanoparticles of diverse materials, such as metals and semiconductors. The shell of molecular ligands, e.g., alkyl-thiols, alkyl-carboxylic acids, or polymers, that are attached to the NP surface by covalent bonds stabilizes NPSLs via weak intermolecular and entropic interactions. Recent developments in the synthesis of NPs with complex shapes and tunable surface chemistry have enabled the fabrication of NPSLs for applications in fields like photonics and plasmonics.

We have recently developed an approach based on MOLT to study NPSLs that predicts the thermodynamic stability of different supercrystalline structures in the presence of a solvent (i.e., “wet” NPSLs).¹⁰ In this approach, NP cores are treated as impenetrable objects with explicit positions and shapes, whereas the ligands and solvent molecules are described using density fields and probability distribution functions (a fully 3D implementation of the MOLT was used for this problem). The prediction of the free-energy differences between supercrystalline structures using MD simulations is feasible,⁶ but it has a significant computational cost, which usually results in large associated statistical errors and precludes systematic analysis. On the other hand, MOLT calculations for NPSLs directly provide the free energy of different supercrystalline structures. Although these free energies are less exact than those obtained with MD (because MOLT neglects some correlations), they can be obtained at a small computational cost and, therefore, be used to construct systematic phase diagrams as a function of structural parameters such as the lattice parameters of the unit cell, the ligand surface coverage per NP, and the length of the ligands. For example, we used MOLT to study the thermodynamic stability of several crystal phases for NPSLs composed of spherical NPs coated by alkyl-chain ligands in a good solvent. These crystal phases included the face centered cubic (FCC), the hexagonal close packed (HCP), the body centered cubic (BCC), and the simple cubic (SC). We also considered the body centered tetragonal (BCT) structure, which is an intermediate structure between BCC and FCC; see unit cells in Figure 4A. It should be stressed that MOLT explicitly considers the molecular details of the ligands and predicts their distribution within the unit cell. For example, the lower panel of Figure 4B shows the distribution of the ligand volume fraction (proportional to its density) for the [100] plane (marked in the scheme of the upper panel) of an FCC structure.

Figure 4.

(A) Unit cells of FCC, BCT, and BCC supercrystals studied with MOLT. Each NP is composed of a hard-sphere core and a soft corona of short polymer-like ligands (ligands not shown). The FCC structure shows both the four-particle cubic and the two-particle tetragonal unit cells. (B) [100] plane of an FCC unit cell (upper panel) and color map of the ligand volume fraction in that plane predicted by MOLT calculations (lower plane). (C) Differences between the free energy per NP of BCC or BCT structures and that of the FCC structure (ΔF_FCC), as a function of the volume fraction of the solvent in the unit cell, Φ_SV. The upper bar indicates the stability zones for each structure. (D) Morphology diagram showing the stability regions of BCC in blue and of FCC in red for NPSLs of spherical NPs as a function of Φ_SV and the length of the ligands (beads per ligand, n_p). Reproduced with permission from ref (10). Copyright 2020 American Chemical Society¹⁰

Figure 4C exemplifies the use of MOLT to predict the relative stability of the different supercrystalline structures. This plot shows the (Helmholtz) free-energy difference per NP between either BCC or BCT structures and the FCC phase as a function of total solvent fraction in the unit cell (Φ_SV, note that the lattice constant of the NPSL monotonically increases with Φ_SV¹⁰). The SC and HPC phases were not included in this plot because SC always has a higher free energy than FCC and BCC, and HCP always had the same free energy as FCC within the precision of our calculations. We found an FCC–BCC phase transition at low Φ_SV, which is in excellent agreement with recent in situ X-ray scattering experiments for the crystallization of NPSLs.²⁰ Notably, in this case, the BCT structure is always less stable than the BCC and FCC phases; i.e., the theory predicts a direct FCC → BCC transition as the unit cell contracts without passing through the BCT intermediate. By repeating this analysis for other conditions, we constructed NPSLs phase diagrams as a function of the relevant parameters. For example, Figure 4E shows the effect of the ligand length (n_p) on the crystal structure of BCC. Keeping all other parameters fixed, increasing n_p stabilizes BCC over FCC, which is also in good agreement with previous experimental observations.²¹

As shown in Figure 4C, MOLT predicts that BCT is always an unstable phase for spherical nanoparticles. However, BCT structures are recurrently observed in experiments as an intermediate phase in FCC–BCC transitions,²⁰ so we tested possible explanations for this apparent contradiction.²² We considered two possible causes for the stabilization of the BCT low-symmetry phases: (i) the anisotropy generated by the interaction of NPSLs with a planar surface (on which the NPSL is deposited) and (ii) the anisotropy introduced by nonspherical NP shapes. The first effect (stabilization of BCT by the substrate) can explain only the formation of BCT structures in a very narrow range of conditions.²² To study the second effect (nonspherical NPs), we considered NPSLs of truncated octahedral (TO) NPs, which is the typical shape adopted by NPs of lead and cadmium chalcogenides. Figure 5A shows a BCC unit cell composed by TO NPs. Figure 5B shows some of the TO NPs that we modeled, where the shape parameter L_cube controls the area relation between square and triangular facets of the NPs and, therefore, defines the shape of the NP. The phase diagram in Figure 5C (obtained by comparing the free energies of the different supercrystals, see above) addresses the effect of L_cube and Φ_SV on the stability of the BCC, BCT, and FCC phases. The figure shows that nonspherical TO NPs can stabilize BCT structures in a wide region of the morphology diagram. In this way, for the TO NPs used in experiments, the predictions of MOLT qualitatively agree with the experimental observation of the BCT phase as a stable intermediate between BCC and FCC.²⁰ A detailed analysis of the interactions in the system reveals that BCT is stabilized for TO NPs because the interactions between a NP and its first and second neighbors involve different atomic crystal facets.²² Notably, this effect is purely geometric in nature, and it does not require different facets to have different chemical or physical properties, as was previous thought.

Figure 5.

(A) BCC unit cell of a NPSL of truncated octahedral NPs. The orientation of the NPs in the lattice corresponds to that experimental measured by Weidman et al.²⁰ (B) Different shapes of truncated octahedral NPs controlled by the shape parameter L_Cube. (C) Morphology diagram of NPSLs of truncated octahedral NPs as a function of the solvent fraction Φ_SV and the shape parameter L_Cube. The symbols show the thermodynamically most stable structure for each condition. Reproduced with permission from ref (22). Copyright 2021 the Royal Society of Chemistry.

2.3. Self-Assembly of Amphiphiles

So far, we applied MOLT to describe end-grafted molecules. We also used MOLT to study the self-assembly of molecules free in solution. In particular, we studied the self-organization of amphiphiles, which are molecules composed of a hydrophobic tail (typically, an alkyl chain) and a hydrophilic, usually charged, headgroup. The spatial separation of solvophilic and solvophobic residues in amphiphilic molecules triggers their assembly into aggregates of different shapes, including spherical micelles, cylindrical fibers, and lamellar structures (planar ribbons, vesicles, disks, etc.). The shape of the self-assembled amphiphilic nanostructures is of utter importance for the ubiquitous technological applications of amphiphiles and their biological roles. The morphology of the aggregates depends on the balance between two competitive interactions: the hydrophobic attraction of the tails and the steric and electrostatic repulsions of the head. This balance is determined by the molecular structure of the amphiphile and the conditions of the solution (e.g., the solution pH and ionic strength).

To use MOLT for finding the equilibrium morphology of an aggregate of amphiphiles, we first consider the possible shapes of the aggregate. Using a 1D implementation (which considers inhomogeneities in only one spatial direction, see Introduction), we can consider three ideal morphologies: spherical micelles, cylindrical fibers, and planar bilayers (lamellas). For each candidate, we compute the excess free energy per molecule as a function of the number of molecules per unit area (for lamellas), per unit length (fibers), or per aggregate (micelles); see bottom panel in Figure 6A. The structure (described by its aggregation number or density and the type of morphology) with the lowest free energy is the equilibrium structure of the system (see dotted lines in the bottom panel of Figure 6A). We used this approach to study the self-assembly of peptide amphiphiles^2e (PAs) formed by an alkyl tail and a headgroup of lysines,¹³ which are positively charged in acidic solutions. Namely, we considered PAs with the formula C_nK_m, where “n” is the number of carbon atoms in the tail and “m” is the number of lysines in the headgroup (see top panel in Figure 6A).¹³ Some PAs of this family are antimicrobial agents, whose bioactivity correlates well with the morphology of their aggregates.²³ For this reason, it is important to understand how the morphology of the nanostructures arises and to be able to predict and design the morphological outcome of PA self-assembly.

Figure 6.

(A) Coarse grain mapping of the peptide amphiphile C₁₆K₂ (upper panel) and excess free energy per molecule as a function of the number of molecules per unit area (lamellas, lower-left panel), per unit length (fibers, lower-center), or per aggregate (micelles, lower-right). (B) Morphology diagrams as a function of pH and added salt concentration predicted by MOLT for C₁₆K₂ (left) and C₁₆K₃ (right). (C) TEM images of the nanostructures formed by C₁₆K₂ at different pHs. The images show micelles at pH = 5, fibers at pH = 8, and a mixture of fibers and planar ribbons at pH = 9 (reproduced and adapted with permission from ref (24). Copyright 2017 American Chemical Society). (D) TEM (top) and AFM (bottom) images of the nanostructures formed by C₁₆K₃ at pH = 7.9 (micelles) and 10 (fibers). Reproduced and adapted with permission from ref (13). Copyright 2019 American Chemical Society.

Figure 6B (left) shows the theoretically predicted morphology diagram for C₁₆K₂ as a function of the salt concentration and pH. The diagram shows a transition from spherical micelles to cylindrical fibers to planar lamellas as the pH increases. This result is in agreement with cryotransmission electron microscopy (cryo-TEM) and small angle X-ray scattering (SAXS) experiments by Gao et al.;²⁴ see Figure 6C. The sphere-to-fiber transition can be explained in terms of the electrostatic interactions in the system. The solution pH controls the protonation state of the amino groups in the lysine side chains. At low (acidic) pH, the lysines are mostly protonated, so the repulsions between the headgroups are strong. This scenario favors highly curved nanostructures (spherical micelles), which maximize the distance between charged amino groups. As the pH increases and the lysines deprotonate, the electrostatic repulsions weaken, thereby leading to the formation of less curved aggregates: first cylindrical fibers and then lamellas.

The morphology diagram of C₁₆K₃ (Figure 6B, right) shows a micelle → fiber transition, while lamellas are not observed. This result agrees with the TEM and AFM experiments shown in Figure 6D. The micelle → fiber transition pH for C₁₆K₃ is higher than that for C₁₆K₂. This difference results from the fact that the polar headgroup of C₁₆K₃ is larger and has more chargeable amino groups than that of C₁₆K₂. Since the electrostatic and steric repulsions are stronger for C₁₆K₃ than for C₁₆K₂, the spherical micelles are more stable for C₁₆K₃ than for C₁₆K₂. A similar argument also explains why lamellas (which have no curvature) are absent in the morphology diagram of C₁₆K₃. In this case, however, the effect is mainly due to steric repulsions (i.e., arising from the size of the headgroup) because at high pH, where the fraction of charged amino groups is negligible, C₁₆K₃ forms fibers, while C₁₆K₂ self-assembles into planar bilayers.

The diagrams in Figure 6B show that aggregates progressively switch to higher-curvature structures when the amino groups in the lysine side chains become charged (decreasing pH). Therefore, structural changes are triggered by a need to minimize the increase in electrostatic repulsions caused by the protonation of the lysines. In other words, the morphological transitions that the aggregates suffer configure a mechanism by which the system regulates the electrostatic repulsions. The interesting combination of structural and thermodynamic information provided by MOLT reveals additional mechanisms of charge regulation in self-assembled amphiphilic nanostructures that occur in order to reduce electrostatic repulsions at the expense of other types of energetic or entropic penalties. Briefly, the aggregates minimize their charge by the combination of two mechanisms:¹³ (i) the well-known mechanism of charge regulation by shifting the acid–base equilibrium of chargeable groups, and (ii) a decrease in the size and aggregation number of the self-assembled aggregates.¹³ The former mechanism (regulation by shifting the acid–base equilibrium) demonstrates the capability of MOLT to properly describe chemical equilibria and their coupling to the local chemical environment at a much lower cost than simulation approaches. The second mechanism (“charge regulation by size regulation”) is particularly interesting because it is exclusive to self-assembled systems. This physical–chemical process can lead to some intriguing predictions; for example, under some conditions, the net charge of C₁₆K₂ micelles can be larger than that of C₁₆K₃ micelles, even while the latter molecule has one additional lysine unit.¹³ This prediction results from the fact that the aggregation numbers of C₁₆K₂ micelles can be significantly larger than those of C₁₆K₃ ones.

In addition to the pure-amphiphile aggregates discussed above, we also studied cylindrical fibers (wormlike micelles) of amphiphiles containing nonpolar host molecules.²⁵ These systems are relevant in several technological applications, such as drug delivery and viscosity enhancers for oil-extraction fluids and cosmetics. We modeled both the surfactant (cetyltrimethylammonium bromide, CTAB) and the nonpolar additive at a coarse grain level; see Figure 7A. MOLT predicts that CTAB wormlike micelles undergo a transition to spherical micelles with increasing additive content; see morphology diagram in Figure 7B. Experimental observations of this transition (known as “breaking” in the oil extraction community) are abundant in the literature (see ref (25) and references therein). We also found that the distribution of nonpolar molecules within the aggregates affects the mechanism by which the wormlike → spherical micelle transition occurs. The additive can be located either at the core or at the hydrophobic–hydrophilic interphase depending on its hydrophobicity (high vs mild); see Figure 7C and color map of Figure 7B. These two possible distributions define two regimes in the morphology diagram of Figure 7B. For mildly hydrophobic additives, the additive content needed to trigger the transition decreases with hydrophobicity. For highly hydrophobic additives, the opposite occurs.

Figure 7.

(A) Coarse grain mapping of the amphiphile CTAB and additive molecules (left) and a scheme of the cylindrical aggregates that they form (right). (B) Morphology diagram of aggregates formed by CTAB and additives as a function of the additive hydrophobicity (given by ϵ_NP-NP, a higher ϵ_NP-NP corresponds to a more hydrophobic additive) and the additive mole fraction (x_NP) in the aggregate. The color map shows the fraction of additive molecules located at the core (white) and at the hydrophilic–hydrophobic interphase (purple). Reproduced with permission from ref (25a). Copyright 2021 American Chemical Society. (C) Color maps of the volume fractions of CTAB and additive within short wormlike micelles for highly (top, correspond to ϵ_NP-NP = 7 k_BT in panel B) and mildly (bottom, ϵ_NP-NP = 2.5 k_BT) hydrophobic additives. (D) Scheme of the morphological behavior of CTAB wormlike micelles upon the addition of nonpolar molecules as a function of the additive content and hydrophobicity. The dashed line indicates the transition from wormlike to spherical micelles (same as in panel B). Reproduced with permission from ref (25b). Copyright 2021 Elsevier.

To understand how the wormlike micelles are affected by the additives before the breaking phenomenon, we developed a MOLT-based method to calculate the scission energy of wormlike micelles,^25b i.e., the free energy cost of cleaving a wormlike micelle into two shorter wormlike micelles and forming two hemispherical caps at the point of scission. The scission energy is directly related to the average contour length of the fibers (higher scission energies lead to longer micelles). The method requires the description of cylindrical aggregates through a 2D implementation of the molecular theory (which assumes heterogeneities in the radial and the axial coordinates; see discussion in the Introduction and Figure 7C) in order to consider fibers of finite length. We calculated the scission energy as a function of the additive hydrophobicity and content. We found that the scission energy of the wormlike micelles (and thus their length) decreases with the additive content, and it has a very interesting nonmonotonic dependence on the hydrophobicity of the additive, see scheme in Figure 7D. The latter result is in line with experimental data that shows the same trend for the viscosity of wormlike micelles loaded with additives of different polarities.^25b The scission energy of the wormlike micelles mainly depends on the location of the additive molecules: the enrichment of the hemispherical caps with the additive leads to a decrease in the scission energy. As we shown above (Figure 7C), the location of the additive within the micelle is strongly dependent on its hydrophobicity. Therefore, the dependence of the scission energy with the content and properties of the additive can be ultimately traced back to the distribution of the additive within the fibers, although the details of the underlying mechanisms can be rather complex.^25b

It is interesting to note that some methods to compute scission energies through coarse-grained MD simulations have been reported in the recent literature.⁷ These approaches involve a similar level of coarse-graining as MOLT. However, determining free-energies via MD simulations using umbrella sampling is computationally more expensive than with MOLT, which allows a less systematic exploration of the parameter space. Moreover, MOLT allows one to model larger systems than those achievable in MD simulations. This advantage is relevant for charged aggregates at low to intermediate ionic strengths because the umbrella sampling method used in simulations produces a scission of ∼3 nm (final separation between the end-caps), which is close to the characteristic length scale of the electrostatic interactions in solution (i.e., the Debye length, λ_D, which is 1 nm for a salt concentration of 100 mM). Therefore, the two caps produced by scission may interact electrostatically, resulting in a contribution to the scission energy that depends on the final distance between the end-caps.

2.4. Conclusions and Future Outlook

We have reviewed some recent applications of the molecular theory, originally developed by Szleifer and co-workers,^5c to study the self-assembly of soft materials. These application examples revealed one of the advantages of MOLT (and free-energy functional theories in general) over particle-based simulations at the time of predicting phase diagrams: the straightforward access to an estimation of the free energy of the system. While free-energy differences can be obtained from simulations,^6,7 this time-consuming task is further complicated by the fact that finding the proper reaction coordinate describing self-assembly is difficult for most soft matter systems. Another important advantage of the molecular theory over particle-based methods resides in its ability to exploit natural symmetries in order to decrease the computational burden of the calculations. This feature enables the systematic exploration of system’s parameters and allows us to construct phase diagrams such as those shown in Figures 2–7. MOLT can also easily incorporate the presence of chemical equilibria, which, once again, can only be treated by particle-based methods at an elevated computational cost. Notably, including acid–base equilibria allows us to address the effect of pH (an easily controlled and very relevant variable) on self-assembly, for example, in the results shown in Figure 6.

MOLT has, of course, limitations that result from the approximations involved. Some of these approximations (i.e., the choice of the coarse-grain molecular model) are shared with CG particle-based methods. One of the major challenges for soft-matter modeling is describing complex behaviors at the mesoscale and, at the same time, incorporating sufficient chemical details to enable predictions of specific chemical systems.^2d The MD community had addressed this challenge by developing multiscale simulation methods and back-mapping procedures, which aim to model systems at different length scales and with different levels of detail.^2d The incorporation of chemical details is, of course, also a challenge for theoretical approaches, including MOLT. Therefore, a prospective research direction for MOLT is to develop protocols to parametrize the theory in order to refine its level of molecular description. These protocols will lead to molecular models that capture specific chemical structures (see for example, our CG model for PAs in Figure 6) rather than relying on more generic models (i.e., neglecting the inner structure of the amphiphile headgroup). Developing multiscale parametrization schemes to describe the same system at different levels of coarse graining is another interesting research direction for MOLT and related approaches.

An important intrinsic limitation of MOLT (which is shared by other theoretical approaches, such as cDFT and SCF) is the mean-field approximation. The impact of this approximation may be difficult to evaluate a priori, and, therefore, comparison with experimental observations is an extremely valuable source of validation for MOLT. In this regard, it is noteworthy that MOLT can predict many experimentally accessible observables, such as the phase diagrams and structural details (size, morphology, charge) of the self-assembled nanoconstructs. In this mini-review, we compared the predictions of MOLT with several experimental observations: the morphology diagram of PAs,¹³ the FCC → BCC transition in NPSLs,^10,22 the formation of microphase-separated aggregates on planar⁹ and curved¹⁶ surfaces, and the effect of additive hydrophobicity and content on surfactant self-assembly.²⁵

It is important to recall that since the molecular theory is an equilibrium framework, the lack of information about molecular trajectories and nonequilibrium states possess an important limitation to the observables that can be predicted. There have been recent advances to extend MOLT to out-of-equilibrium systems; for example, generalized diffusion equations have been used to formulate a nonequilibrium molecular theory to describe ionic transport through polyelectrolyte-modified nanochannels.²⁶ In a another approach, the pathway and activation free energy for the transition between two self-assembled states of a polymer brush have been studied combining MOLT with a methodology known as the string method.²⁷ Despite these previous advances, the development of nonequilibrium approaches based on MOLT or similar frameworks remains as a very appealing (and challenging) research direction for the coming years.

As discussed in this mini-review, MOLT is a powerful approach to model self-assembly in soft-matter systems, and it can predict—at an affordable computational cost—many experimentally relevant observables, such as phase diagrams. Like all tools, MOLT has unique advantages as well as limitations. Exploiting the former and overcoming the latter will lead to new and exciting research directions in soft matter science.

Biographies

Dr. Gervasio Zaldivar received his Ph.D. from University of Buenos Aires (Argentina) in the field of self-assembled soft materials, supervised by Profs. Mario Tagliazucchi and Martin Conda-Sheridan. Currently, he holds a postdoctoral position at University of Cuyo (Argentina) studying the mechanochemistry of lipidic membranes, supervised by Profs. Mario del Popolo and Gabriel S. Longo. During his career, he was awarded fellowships from CONICET and the Fulbright Commission. His research interests focus on the theoretical modelling and experimental development of soft materials with technological applications in biomedicine and other fields.

Dr. Perez Sirkin is a staff researcher at the National Scientific and Technical Research Council of Argentina (CONICET). She received her Ph.D. in chemistry from the University of Buenos Aires in 2018, working on the thermodynamic properties of aqueous systems in the nanoscopic scale. From 2019 to 2022, she worked as a postdoc researcher at University of Buenos Aires on modeling the transport of ions and particles in polyelectrolyte-modified nanopores. In 2022, she became a researcher in the Soft Materials group at the University of Buenos Aires. Her research focuses on ionic and electronic transport in polymeric systems for energy applications.

Gabriel Debais received his B.Sc. degree in physics from University of Buenos Aires (UBA), Argentina in 2018. He is currently a Ph.D. student in chemical physics at UBA. His research interests primarily concern the role of ion pairing in polymeric systems (polyelectrolyte coacervates, polymeric brushes, layer-by-layer films) focusing on the structure, morphology, and self-assembly behavior from a theoretical/computational point of view.

María Fiora received her B.Sc. degree in physics from Buenos Aires University. Currently, she is a P.D. student in the Department of Inorganic, Analytical and Physical Chemistry of the University of Buenos Aires University, supervised by Dr. Mario Tagliazucchi and Dr. Gabriel Ybarra. She is also a researcher at the National Institute of Industrial Technology of Argentina (INTI). Her Ph.D. work involves studying the self-assembly of amphiphiles and their applications in molecular encapsulation using MOLT.

Leandro Missoni received his B.Sc. degree in chemistry from University of Buenos Aires (UBA) in 2018 and is now a Ph.D. student in physical chemistry at the same institution. His research interest lies in the study of thermodynamics of self-assembly of nanoparticles superlattices, photonics, and optical metamaterials. Currently, he is working in the inclusion of distinct nanostructure morphologies in the molecular theory (MOLT) and the optical properties of metallodielectric composites. Also, he works as a teaching assistant in the Department of Inorganic, Analytical and Physical Chemistry of UBA.

Dr. Gonzalez Solveyra is a staff researcher at the National Scientific and Technical Research Council of Argentina (CONICET) and an adjunct professor in the School of Science and Technology of the University of San Martín (UNSAM). She received her Ph.D. in chemistry from the University of Buenos Aires in 2014, working on water nanoconfinement in mesoporous oxides, combining molecular simulations and synthesis and characterization of materials. From 2014 to 2020, she worked as a postdoc researcher at Northwestern University in Prof. Igal Szleifer’s group. During that time, she focused on the development of theoretical methods to study multifunctional nanosystems, combining nanomaterials and soft matter. Upon her return to Argentina, she became a researcher in the nanoarchitectures group at the Institute of Nanosystems (UNSAM). Her research focuses on molecular modeling of bionanomaterials, with a focus on the physical–chemical properties of the interphase between nanomaterials and biological molecules.

Dr. Mario Tagliazucchi is a staff researcher of CONICET (the National Scientific and Technical Research Council of Argentina) and an Adjunct Professor at the University of Buenos Aires (UBA). He has received his Ph.D. in chemistry from UBA in 2009, working in the field of electroactive layer-by-layer self-assembly under the supervision of Prof. Ernesto Calvo. Between 2010 and 2014, he was a postdoctoral researcher at the Department of Chemistry of Northwestern University in the Szleifer and Weiss’s groups. In 2015, he established the Soft Materials group (softmaterials.qi.fcen.uba.ar) at the Department of Inorganic, Analytical and Physical Chemistry of FCEN-UBA/INQUIMAE-CONICET. His research involves theoretical and experimental studies in soft materials (polyelectrolytes, amphiphiles, and nanoparticles), with a special focus on their self-assembly behavior and electrochemical-related applications. He has received scholarships from the Fulbright Commission and the Alexander von Humboldt Foundation.

Author Contributions

^# G.Z. and Y.A.P.S. contributed equally to this work.

The authors declare no competing financial interest.