Recent advances in microresonators and supporting instrumentation for electron paramagnetic resonance spectroscopy

Abstract

Electron paramagnetic resonance (EPR) spectroscopy characterizes the magnetic properties of paramagnetic materials at the atomic and molecular levels. Resonators are an enabling technology of EPR spectroscopy. Microresonators, which are miniaturized versions of resonators, have advanced inductive-detection EPR spectroscopy of mass-limited samples. Here, we provide our perspective of the benefits and challenges associated with microresonator use for EPR spectroscopy. To begin, we classify the application space for microresonators and present the conceptual foundation for analysis of resonator sensitivity. We summarize previous work and provide insight into the design and fabrication of microresonators as well as detail the requirements and challenges that arise in incorporating microresonators into EPR spectrometer systems. Finally, we provide our perspective on current challenges and prospective fruitful directions.

I. INTRODUCTION

Electron paramagnetic resonance (EPR) spectroscopy is a non-invasive, sample-preservative method to observe microstructural environments in a wide range of paramagnetic materials.^1–3 This structural information is encoded in spectroscopic parameters, such as lineshapes, linewidths, spectral extent (for continuous wave or CW EPR), relaxation times, and modulations of echo decays (for pulse EPR). Therefore, EPR spectroscopy is a powerful method for studying structure–function relationships and dynamics in materials with exogenous or endogenous paramagnetic centers; for example, paramagnetic dopants in semiconductors^4–7 and ceramics,^1,8–10 transition metal ions in metalloenzymes,^11–15 and stable or transient free radicals.^16–22 When a paramagnetic material has been characterized comprehensively, EPR spectroscopy can then be used for sensing or quantification,^23,24 e.g., oximetry and EPR imaging through measurement of spectral and relaxation changes in stable free radicals interacting magnetically with oxygen.^25–27

Resonators are at the heart of every EPR spectrometer and are one of the main enabling technologies of EPR spectroscopy.²⁸ This Review focuses on microresonators and instrumentation for their use. Microresonators, which are miniaturized versions of resonators, are employed for inductive-detection EPR spectroscopy of mass-limited samples, including crystals with volumes smaller than 1 nl, epitaxial films, and limited-quantity biomacromolecules. In Sec. I, we will classify the application space for microresonators and present the conceptual foundation for analysis of resonator sensitivity. In Sec. II, we will delve into details of the process for microresonator design and fabrication. We will give an overview of microresonator designs implemented thus far, and we will also provide a perspective for future work in this field. Section III will describe instrumentation requirements/challenges that arise in deploying microresonators in EPR spectrometers and will delineate technological advances that may impact the future use of microresonators for EPR spectroscopy. Finally, Sec. IV will provide a summarized perspective on current challenges and prospective fruitful directions of research in microresonator development and application.

Inductive detection is the most broadly applicable scheme to detect EPR signals.²⁸ In this implementation, the sample consists of an ensemble of paramagnetic centers with magnetic energy levels separated by the Zeeman effect (i.e., by the application of an external static magnetic field, B₀). The statistical thermodynamic distribution of individual magnetic moments in the ensemble results in a collective magnetization that depends on the external magnetic field, temperature, and magnetic susceptibility of the material. When the resonance condition is met (i.e., when the energy difference between magnetic states matches the microwave frequency), transitions occur between these magnetic energy levels. The resonant absorption of microwave energy induces a current in the resonant or non-resonant sensing element, which is ultimately detected in the downstream circuitry as the EPR signal. The low polarization of electron spin ensembles (≈0.999 at 10 GHz, 300 mT, 298 K) necessitates the use of resonators or high-power microwave sources to increase the detection sensitivity. The resonator is the circuit component that interacts with the sample. It plays a dual role: first, it conveys and amplifies the intensity of the magnetic component (B₁) of incident microwaves that excite the magnetic transition, and second, it senses the precessing magnetization of the sample at resonance.

A. Defining a microresonator

We begin by defining the term “microresonator.” As stated earlier, one of the two main functions of a resonator in inductively detected EPR spectroscopy is to enhance the EPR excitation field B₁ over the region occupied by the sample. Conventional EPR resonators are cavities that support standing waves and produce resonant modes with B₁ maxima at the center of the cavity. The active volume (where most of the excitation field is concentrated) is proportional to the volume of the cavity, which in turn is directly proportional to λ³, where λ is the resonant wavelength. Sample concentration and resonator losses being constant, the signal intensity is maximized when the sample volume approaches or exceeds the active volume. At a frequency of 10 GHz, the sample volume required to fill the active volume of a conventional cavity resonator is several hundred microliters when using a Transverse Electric₁₀₂ (TE₁₀₂) mode rectangular cavity.²⁸ As frequency increases, the dimensions of the resonant cavity decrease proportionally to the wavelength so that active volumes are naturally scaled down to the sub-microliter level at frequencies >100 GHz. To avoid ambiguity introduced by comparison of absolute sizes, we define a microresonator as any device that reduces any sample dimension to the deep-subwavelength scale or, more specifically, reduces active (and thereby detectable) sample volume, v such that (v/λ³) < 10⁻⁶. For example, a volume of 1 mm³ (1 μl) at 10 GHz gives (v/λ³) = 3 × 10⁻⁵, while a volume of 0.1 mm³ (100 nl) at 10 GHz gives (v/λ³) = 3 × 10⁻⁶. Thus, by our definition, a resonator with an active volume of 100 nl at 10 GHz would qualify as a microresonator. Of course, this is an arbitrary cutoff. However, it is guided by the sensitivity limits posed by conventional cavity resonators for dilute samples that are of relevance to practical EPR spectroscopy. For example, a cavity resonator can detect even a nanoliter volume of a sample with high spin concentration, such as crystalline 2,2-diphenyl-1-picrylhydrazyl radical (DPPH) or α-γ-bisphenylene-β-phenylallyl radical (BDPA). However, most samples of relevance, such as solid-state materials with dopants and spin-labeled proteins, are studied at much lower spin concentrations.

B. Application space for EPR microresonators

The most common frequencies used in EPR spectroscopy are 10 GHz (wavelength, λ ≈ 3 cm) and 35 GHz (λ ≈ 1 cm). For example, a TE₁₀₂-mode metallic cavity resonant at 10 GHz produces a region of enhanced B₁ at the center of the cavity, i.e., an active volume of ≈50 μl. Thus, conventional cavity resonators are typically characterized by (v/λ³) ≈ 2 × 10⁻³, and it becomes difficult to detect EPR signals from dilute paramagnetic samples with (v/λ³) < 10⁻⁵ or volumes <1 μl and practically impossible to detect signals from dilute (<1 mmol l⁻¹) samples with volumes <1 nl (∼100 × 100 × 100 μm³). Besides extending the reach of EPR spectroscopy to microscale and nanoscale samples, miniaturization of resonators can also enable miniaturization of spectrometers. Important application spaces in which nanoliter or sub-nanoliter sized samples necessitate the use of microresonators are described below (see Fig. 1).

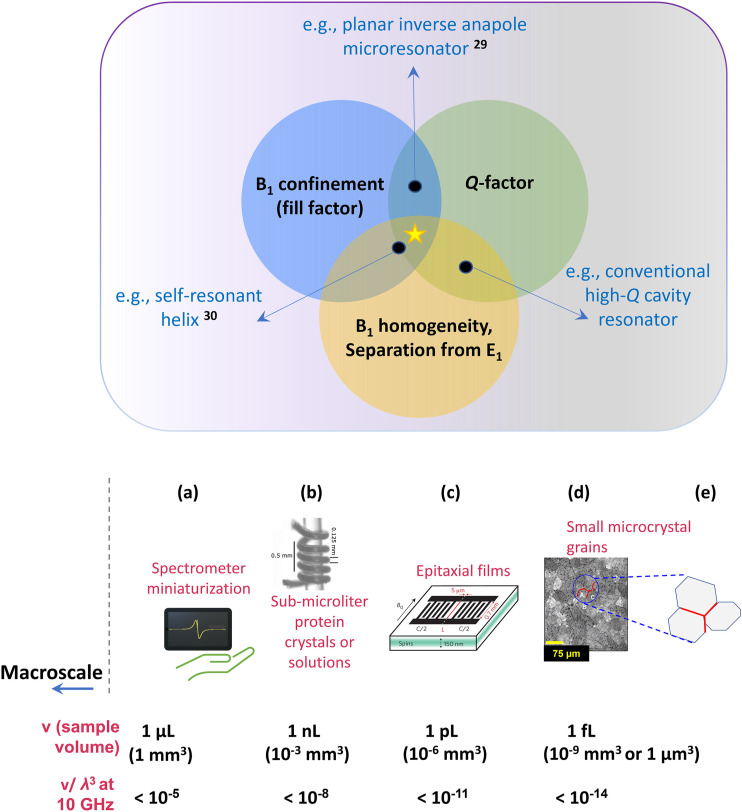
FIG. 1.

Overview of application space for microresonators over a range of sub-microliter to femtoliter sample volumes. The panel on the top shows the primary desirable characteristics of a microresonator: confinement of the excitation field B₁ to a small volume matching the sample shape and size, optimal quality factor Q, i.e., reduced losses through non-magnetic mechanisms of microwave absorption (high Q is particularly important for CW EPR experiments), and desired field distribution characteristics, i.e., homogeneous distribution of B₁ over the active volume (particularly important for quantitative CW EPR and pulse EPR experiments) and E₁ minimum in the region of B₁ maximum.^29,30 A more detailed description of desired microresonator characteristics is in Fig. 2. Examples of microresonator impact are in the areas of (a) miniaturization of EPR spectrometers; (b) solutions of limited-quantity biomacromolecules; (c) characterization of dopants and defects in epitaxial materials, including materials used to create spin qubits; (d) microcrystals with dimensions ≈1–100 μm (volumes ≈1 fl to 1 nl); and (e) grain boundaries and interfaces between thin films. Figures in the lower part of the panel have been reproduced with permission from Rahmati et al., Surf. Sci. 595, 115 (2005).³¹ Copyright 2005 Elsevier; Bienfait et al., Nat. Nanotechnol. 11(3), 253–257 (2016). Copyright 2016 Springer Nature; and Sidabras et al., Sci. Adv. 5(10), eaay1394 (2019). Copyright 2019 Author(s), licensed under a Creative Commons Attribution 4.0 License.

1. EPR spectroscopy of volume-limited samples

Example of two classes of volume-limited samples necessitating the use of microresonators are nanomaterials/microcrystals and limited-quantity proteins. High-performance inorganic ceramics and polycrystalline hybrid materials are widely utilized in applications ranging from piezoelectrics (sensors, capacitors), semiconductors, and now in photovoltaics. These polycrystalline materials have properties that critically depend on dopants and paramagnetic defects. Yet the electronic structure of these dopants and defects can be unambiguously characterized only through orientation-dependent EPR measurements on single crystals. Currently, EPR spectroscopy is often carried out on polycrystalline ceramics because single crystals of these materials are extremely difficult or impossible to grow to a size appropriate for use in conventional EPR resonators,²⁹ making microresonators key to obtaining such information. For biomacromolecules, analysis by EPR spectroscopy can corroborate structure–function and dynamics measurements obtained from optical and nuclear magnetic resonance (NMR) spectroscopies, crystallography, and even cryo-electron microscopy.^30,32–36 Producing sufficient quantities of a biomacromolecule for conventional EPR spectroscopy is often quite challenging, particularly for integral membrane proteins, such as G-protein coupled receptors (GPCRs). GPCRs constitute ∼35% of all drug targets, and there are over 1000 GPCRs in humans.^37,38 The structural and functional characterization of these proteins in solution remains difficult via EPR spectroscopy using currently available instrumentation. Increasing the reach of EPR spectroscopy to these types of volume-limited samples is the first broad application space of microresonators. EPR measurements of single crystals are also valuable for biomacromolecules that crystallize but form crystals that are not large enough for detection in conventional resonators.³⁰

2. Quantum sensing/quantum computing applications

EPR spectroscopy is a direct application of quantum mechanics and electron spins are candidates for spin qubits, the building blocks of quantum computers.^39,40 Electron spin ensembles have also been proposed for constructing quantum memory devices.^41,42 The aforementioned spin qubit devices use microwave resonators⁴³ or stripline structures for global excitation of spin qubits. On the other hand, magnetic control/readout of spin qubits and coupling of spin qubits requires strong coupling between the spin system (either a single artificial atom or an ensemble) and a resonant device. Such devices must also have high conversion factors to decrease power requirements for low-temperature operation. Microresonator development in the frequency range from 1 to 10 GHz has often been targeted for this application space.^44–51

3. Miniaturization of spectrometers

Due to their size, conventional resonators operating at 10 or 35 GHz are situated between a pair of large, bulky electromagnets to generate a sufficiently uniform static magnetic field across the sample. Homogeneity of the static magnetic field narrows the EPR lines and increases spectral resolution for a given frequency. The small active volumes of microresonators eases the field homogeneity requirement and allows usage of much smaller electromagnets. In some cases, even permanent magnet arrangements can provide a magnetic field of adequate homogeneity to produce resolved EPR lines suitable for most applications (see Sec. III C). The production of benchtop or even “pocket-size” spectrometers will decrease cost and may allow more widespread application of EPR spectroscopy for specific applications. Such miniature instrumentation is particularly suited to applications in which detection of a characteristic signal of a known analyte or measurand is important. In this case, EPR measurements are more of a sensor-type measurement, rather than spectroscopic in nature. Examples include detection of radiation dose (dosimetry)^52,53 or presence of undesirable or harmful free-radicals or metal-ions in food (food quality).^54,55

C. How to characterize resonator performance

As stated earlier, the resonator is an important enabling technology for EPR spectroscopy, playing a twofold role: first, it confines and amplifies B₁ over a small volume (called the active volume), and second, it increases the sensitivity with which the generated EPR signal can be detected. Confinement leads to field amplification and thus decreases the power output required of the microwave bridge. The first role is quantified by the fill-factor (η), whereas the second role is quantified by the quality-factor (Q). Because of their importance in dictating resonator performance, the fill-factor and quality-factor are standard metrics used to characterize resonators (see the top panel of Fig. 1).^28,56

1. Resonator characteristics and signal-to-noise ratio in inductive detection

Inductively detected EPR spectroscopy is the most common and broadly applicable form of signal detection for EPR spectroscopy. At resonance, the sample magnetization changes, affecting the electrical characteristics of the resonator. This change is ultimately recorded as a voltage, which is the signal in inductively detected EPR spectroscopy.^28,56,57 The sample signal is only detectable if the voltage produced is greater than the noise floor. The signal voltage in the linear detection regime of a reflecting, critically coupled resonator is given by

$$V_S\propto {\chi }^{″}\eta Q\sqrt{P{Z}_0},$$ (1)

where V_S is the signal voltage, χ″ is the magnetic susceptibility of the sample, η is the fill factor [Eq. (3)], Q is the quality factor [Eqs. (3) and (4)], P is the incident microwave power, and Z₀ is the impedance of the transmission line to which the resonator is attached.

The spatial confinement of B₁ can be visualized through the mode volume. Cavity perturbation theory defines mode volume of an electromagnetic cavity resonator in terms of the effect produced by a tiny dipole on the resonator characteristics when placed at the position (${\vec{r}}_{\max }$) of maximum B₁.⁵⁸ For the case of the magnetic interaction between a tiny magnetic dipole and the oscillating magnetic field in a resonator, the mode volume V_C is given by the following equation:

$$V_C({\vec{r}}_{\max })=\frac{{\int }_{\mathit{resonator}}{B}_1^{2}dV}{|B_1({\vec{r}}_{\max }){|}^2}.$$ (2)

Mode volume is inversely proportional to $|B_1({\vec{r}}_{\max }){|}^2$, which means B₁ intensity increases with its spatial confinement. For open resonant structures with inhomogeneous B₁ distributions, mode volume is difficult to estimate, but the above explanation attempts to illustrate the concept and encourage interested readers to peruse the indicated references.

The fill factor η [Eq. (3)] can be represented as the ratio of the sample volume to the resonator active volume, where the active volume refers to the volume over which B₁ is confined within the resonator. η is related to the mode volume because placement of a point-like sample in a device with a smaller mode volume produces a larger fill factor. Therefore, the mode volume may also be defined as the effective volume, which is the volume of a point-like sample divided by fill factor of this sample placed at the location of highest B₁ in the resonator.⁵⁹ When the active volume is comparable to the available sample volume, the fill factor approaches 1, which is one of the optimal conditions for maximum signal-to-noise ratio (SNR), assuming that the microwave electric field E₁ is spatially well-separated from the sample. Equation (2) shows that the fill factor is directly related to the volume integral of $B_{1x}^2+B_{1z}^2$ over the sample volume, which is proportional to the signal generated by the sample. Here, we assume that the static field is applied along y and EPR spectroscopy is conducted in the conventional perpendicular mode, i.e., only the x and z components of B₁ contribute to the EPR signal. For a cavity resonator, η is

$$\eta =\frac{{\int }_{\mathit{sample}}(B_{1x}^2+B_{1z}^2)dV}{{\int }_{\mathit{resonator}}(B_{1x}^2+B_{1z}^2)dV}.$$ (3)

The quality factor Q is a measure of how efficiently a resonator stores microwave energy. It is the ratio of the average energy stored per cycle in the resonator volume to the average energy dissipated through radiative, dielectric, and conductive losses [Eq. (4)] per cycle.²⁸ It also determines the sensitivity with which a generated signal can be detected because the detection sensitivity is related to the ability to distinguish the power reflected from the resonator in the presence vs absence of resonance,

$$Q=2\pi \frac{energystored}{energydissipatedpercycle}.$$ (4)

Because it is difficult to directly measure the energy stored and dissipated in a circuit, Q also is defined [Eq. (4)] in terms of measurable quantities, namely, resonator frequency (ν_res) and the resonator bandwidth (Δν),

$$Q=\frac{v_{\mathit{res}}}{\mathrm{\Delta }\nu }.$$ (5)

The resonator bandwidth is the full-width at half-maximum (FWHM, or 3 dB linewidth) of the frequency profile of the reflected microwave power (S₁₁). The S₁₁ return-loss measurement is carried out using a vector network analyzer (VNA), and the minimum in the trace (a dip) is the resonance frequency, ν_res. Optimal coupling of the resonator to the incident microwaves in most reflection-mode EPR spectrometers is signaled by generation of the narrowest, deepest minimum in the S₁₁ trace during the tuning (coupling) procedure. Because the signal intensity is proportional to Q [Eq. (1)], samples that degrade Q will result in lower sensitivity. Table I provides typical values of η and Q for the conventional resonators described in Sec. I D.

TABLE I.

Fill and quality factors of conventional EPR spectroscopy resonators used at 10 GHz.

Resonator type	Fill factor (1 μl sample)	Q-factor
Cavity28	0.0001	10 000
Dielectric ring42–48,60	0.1–1	1 000
Loop-gap50,51,56,57	≈1	1 000

Q and η (or mode volume) further determine the following additional properties that are important to consider:

• •
  Conversion factor (C_P): The conversion factor or conversion efficiency is the field produced per square root unit of power incident on the sample. For a cavity critically coupled to a waveguide,²⁸ C_P may be represented in terms of fill factor, as given by the following equation:

  $$C_P=\frac{⟨B_1⟩}{\sqrt{P}}\sim \sqrt{Q_L\eta A},$$ (6)

  where P is the incident power, Q_L is the loaded quality factor, and A is the ratio of the volume of one length of waveguide to sample volume.
  C_P can also be stated in terms of mode volume as in the following equation:

  $$C_P=\sqrt{\frac{{\mu }_{0}Q}{2\pi {\omega }_{mv}{V}_C}},$$ (7)

  where μ₀ is the magnetic permeability and ω_mv is the microwave frequency.

  Experimentally, conversion factor (or power-to-field conversion efficiency) c is defined as $c=B_1/\sqrt{QP}$, where P is the power output of the microwave source and B₁ is the field generated in the active volume of the resonator, and the factor $1\sqrt{Q}$ is introduced for normalization to the unloaded Q-factor. (Often, the conversion factor is not normalized to Q. Instead, it is reported as $c^{\prime }=B_1/\sqrt{P}$, which is an experimental quantity specific for the reported resonator design and measurement setup.) A high conversion factor means that even a small output power from the bridge can generate a large B₁ in the active volume. As shown by Eq. (6), the conversion factor is determined principally by the fill factor (mode volume) and quality factor (resonator losses). In general, smaller mode volumes and lower losses result in higher conversion factors with the dominant determinant of the conversion factor being mode volume. For example, smaller wavelengths in dielectric media result in correspondingly smaller mode volumes. This scaling is used to increase resonator conversion factors by dielectric loading.^61–63 Section II A 1 explains how the intrinsic loss of Q in microresonators places an asymptotic limit on the scaling of conversion efficiency with mode-volume confinement.

• •Bandwidth: For pulse EPR measurements, the resonator bandwidth determines the fraction of an EPR spectrum that can be simultaneously excited by a microwave pulse. Bandwidth is directly related to Q in that low-Q resonators provide higher bandwidths. For pulse EPR using resonators with Q > 1000, the resonator must be over-coupled to the microwave feed line to decrease Q and increase bandwidth. Microresonators display intrinsically low Q-factors combined with high conversion factors (see below), which permits pulse EPR experiments at critical coupling.
• •B₁ homogeneity: A homogeneous B₁ distribution over the sample volume is an important factor for quantitative EPR spectroscopy.
• •Spatial separation of B₁ and E₁: Aqueous solutions and other dielectric lossy samples or even sample holders may interact with the electric-field component E₁ of the incident microwaves. These lossy dielectric interactions deteriorate Q and shift the resonant frequency. The reduction in Q results in a loss of sensitivity. To avoid dielectric losses, resonators are typically designed to separate B₁ and E₁ maxima spatially, and the extent to which such spatial separation can be achieved directly affects resonator performance.

D. From macroresonators to microresonators

To understand design approaches for microresonators, it is useful to understand common design classes of conventional resonators (which handle sample volumes >1 μl at frequencies <35 GHz). The common classes of conventional macroresonators are described below.

1. Resonant cavities

These are rectangular or cylindrical metal devices that produce standing microwaves within a cavity. Resonant modes [e.g., TE₁₀₂, Transverse Magnetic (TM)₁₁₀, etc.] produce regions of highly enhanced excitation field B₁ maximum and E₁ minimum at the center of the cavity. The cavity size is limited by the wavelength of the exciting electromagnetic wave in air, which in turn limits the sample size by placing a lower limit on the B₁ spatial extent at the center of the cavity.²⁸

2. Dielectric resonators

Materials with relative dielectric permittivity (ɛ) higher than that of air shrink the microwave wavelength proportionally ($\lambda \propto 1\sqrt{{\epsilon }_r})$. Such resonators may be used in stand-alone form or inserted in a metallic cavity to further confine B₁. A range of dielectric materials may be used, most commonly, rutile, sapphire, and polytetrafluoroethylene (PTFE).^63–65 Ceramics with very high dielectric permittivities have also been demonstrated as materials for dielectric microwave resonators.^{61,62,66–68} However, the decrease in wavelength offered by dielectrics may still be insufficient to generate an active volume small enough for sub-nanoliter samples. A point of concern when choosing dielectric materials for resonator design is that many dielectrics, particularly at temperatures below 100 K, show large background signals originating from point defects. This may preclude the use of some ceramics and polycrystalline dielectrics in resonators for cryo-EPR spectroscopy.

3. Loop-gap resonators (LGRs)

A metallic loop interrupted by a slot or capacitive gap is the basic lumped-element resonator that allows confinement of low-frequency (≤10 GHz) microwaves to volumes ≈1 μl.^69–71 These types of resonators were the first in which the active volume was decreased to the microliter range. LGRs provide excellent spatial separation between the B₁ and E₁ fields, have large bandwidths, and because of their small size have correspondingly high fill and conversion factors. Dielectric materials miniaturize loop-gap resonators.⁷² Further miniaturization of loop-gap resonators and micro-coil structures using photolithographic processes achieves active volumes of the order of 1 nl.^42,73,74 This structure is the most commonly used for resonator miniaturization, as described in Sec. II.

Section II starts with a description of planar loop-gap microresonators and moves on to cover current and potential future microresonator design strategies. Section III describes the supporting instrumentation required for use of microresonators and our perspective on technical advances imminent in the field.

II. MICRORESONATOR DESIGN AND CHALLENGES

Section I provided an overview of the motivations for design and fabrication of microresonators. We also briefly surveyed the classes of resonators that are currently successfully used for measuring tens of microliters of typical EPR samples, i.e., solutions with paramagnet concentrations >10 μmol l⁻¹ or solid-state samples with paramagnet concentrations on the order of 10⁻⁴ dopants per site. In this section, we will elaborate on the strategies used to miniaturize resonators to the sub-nanoliter volume range. In Sec. II A, we will discuss the steps involved in designing and realizing microresonators. Section II B will provide an overview of current microresonator designs and the common challenges hindering broad applicability of microresonators. In Sec. II C, we will provide our perspective on possible future directions of research in microresonator design and deployment.

A. The microresonator design cycle

1. General considerations for resonator design

As stated in Sec. I and illustrated in Fig. 2, resonator performance can be quantified by two main metrics, η [fill-factor, Eq. (2)] and Q [quality-factor, Eq. (4)], which in turn determine the secondary characteristics including conversion factor and bandwidth. As the mode volume is decreased, η increases for correspondingly small samples (Table I). At frequencies ≥100 GHz, resonator sizes dictated by wavelength naturally produce sample volumes smaller than a microliter. Therefore, microresonators provide the greatest benefit in terms of allowing smaller sample sizes for spectroscopies in the lower frequency range (where resonator active volumes tend to be larger). The most common class of microresonators reported for operation ≤35 GHz includes metallic structures deposited on dielectric substrates using photolithographic techniques, typically with dimensions in the range of tens to hundreds of micrometers. However, structures in this size range suffer from deteriorated Q – a result of the increase in radiation losses with decreasing size of the metal-on-dielectric structure. Lowered Q-factors are a particular challenge for high-temperature (>50 K) applications that constitute a significant fraction of the full range of EPR spectroscopic functions.^29,75–78

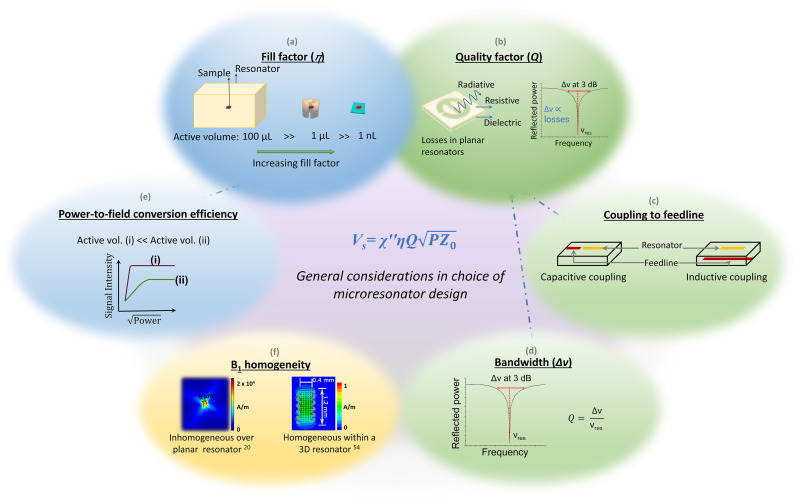
FIG. 2.

General considerations in choice of microresonator design. The resonator performance is characterized by two main metrics—fill factor η (a) and quality factor Q (b)—that directly determine signal intensity. Additional considerations when choosing a design are the ease and variability of coupling to the microwave feedline (c). Higher Q favors easier coupling and is desirable for CW EPR experiments. On the other hand, a lower Q provides a larger bandwidth (d), which is desirable for pulse EPR experiments. To realize short pulse lengths that maximize spectral excitation bandwidth, pulse EPR also requires a high power-to-field conversion efficiency (e). Finally, B₁ homogeneity (f) is most important for quantitative CW measurements and in pulse EPR. Surface or planar resonators provide high conversion efficiencies but suffer from poor B₁ homogeneity. 3D helical or ring resonators can provide homogeneous B₁ that is weak due to the relatively large sizes. In the case of pulse EPR, the effects of B₁ inhomogeneity can in principle be mitigated by applying shaped pulses. Images in panel (f) adapted from Abhyankar et al., Sci. Adv. 6(44), eabb0620 (2020). Copyright 2020 Author(s), licensed under a Creative Commons Attribution 4.0 License and Sidabras et al., Sci. Adv. 5(10), eaay1394 (2019). Copyright 2019 Author(s), licensed under a Creative Commons Attribution 4.0 License.

Microresonators provide the following advantages compared to conventional resonators:

• •Due to their small mode volumes, microresonators can provide gains of one to several orders of magnitude in the power-to-field conversion efficiency. The increase in conversion factor is one of the principal advantages of microresonators, resulting in access to short pulse lengths (for example, pulse lengths <100 ns can be obtained with powers <50 mW), which in turn decrease dead times and increase the fraction of the EPR spectral width that can be excited. As mentioned in Sec. I C 1, there is a limit to the strategy of increasing conversion efficiency by decreasing mode volume. For planar structures with feature sizes (loop diameter, capacitive gap) on the order of hundreds of micrometers, magnetic flux is no longer wholly contained within the loop and capacitive gaps show increased resistive/radiative losses. The lumped-circuit approximation, which is valid for larger loop-gap structures breaks down in the case of planar loop-gap microresonators, and increased losses lead to an intrinsic loss of Q-factor for microresonators. This intrinsic loss of Q with decreasing size places an asymptotic limit on the scaling of conversion efficiency with decreasing resonator size. Nonetheless, microresonators provide significantly higher conversion efficiencies through the shrinking of mode volume.
• •The intrinsic loss of Q at small sizes conversely provides gains in bandwidth. Bandwidths higher than 100 MHz are particularly desirable for pulse measurements since a higher bandwidth allows a higher spectral width, i.e., a larger spin ensemble to be excited. When conventional resonators are used, overcoupling is important for pulse EPR because it provides the requisite combination of increased bandwidth and high conversion efficiency for maximum sensitivity.⁷⁹ With intrinsically high conversion efficiencies and low Q, microresonators may be able to provide high bandwidth along with high conversion efficiency even at critical coupling.

Microresonators also have some associated disadvantages that must be considered and, if possible, avoided through design:

• •Coupling with the microwave feedline: The mechanism used to couple the microresonator to the feedline (e.g., microstrip or coplanar waveguide) must be chosen carefully. The intrinsically poor Q-factors of most microresonator designs may exacerbate coupling difficulties. Microresonators may be coupled to the feedline either capacitively or inductively [Fig. 2(c)]. Smaller structures are typically more difficult to couple to the microwave feedline (see Secs. II B 2 and III A). Simulations provide an estimate of the coupling strength in a proposed microresonator–feedline scheme. However, for pre-fabricated devices that rely on capacitive coupling, small variations in dimensions or position that result from fabrication-related uncertainties will cause deviations from expected device frequency and coupling. In the case of inductive coupling, smaller structures are less efficient at interacting with fringing fields from a feedline, such as a microstrip. However, with this coupling scheme, the resonator–feedline structure does not need to be fabricated in the coupled state, which means that resonator position can provide a route for variable coupling and tuning of the device.^29,75,76,78
• •B₁ homogeneity: Microresonators are typically fabricated as planar metallic structures with active dimensions on the order of 10–100 μm, deposited on dielectric substrates. The B₁ gradients around these open structures tend to be much steeper than in 3D cavities, resulting in highly inhomogeneous B₁ distributions in the immediate vicinity of the active volume. B₁ inhomogeneity is disadvantageous for pulse EPR measurements and quantitative CW EPR measurements. Fortunately, EPR spectrometers capable of pulse shaping can compensate for resonator B₁ inhomogeneity and deliver uniform excitation to the sample.^80–83
• •Spatial separation of B₁ and E₁: As the resonator size is decreased, spatially separating regions of B₁ and E₁ maxima becomes increasingly difficult, although this factor ultimately depends on sample size, i.e., whether the entire sample can be located within the B₁ maximum and outside the E₁ maxima. Some resonator designs provide excellent separation between regions of B₁ and E₁ intensity.²⁹

After choosing a viable resonator design taking into consideration the factors described above and in Fig. 2, the microresonator design and development cycle can proceed through the following stages (summarized in the flowchart presented in Fig. 3).

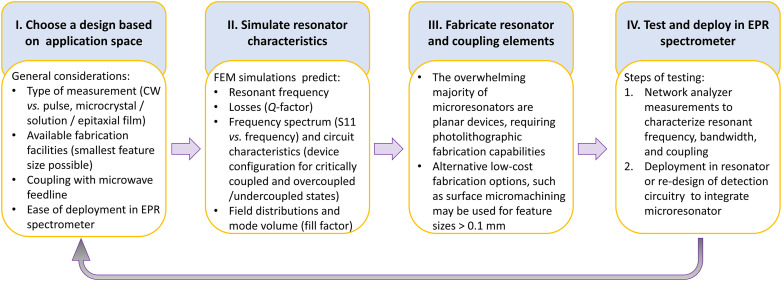
FIG. 3.

Flowchart describing the microresonator design cycle. Stage I: A suitable resonator design that can be adapted to EPR spectroscopy (see general considerations delineated in Sec. II A 1) is chosen based on the application space, desired resonator characteristics, coupling mechanism, and fabrication capabilities available (see Sec. II A 3). Stage II: Simulations are performed to optimize resonator dimensions for the desired resonant frequency and coupling to the feedline. Stage III: Devices are fabricated by electroplating/etching, photolithography, or other nanofabrication techniques as per availability. Stage IV: Fabricated devices are characterized using a vector network analyzer (VNA). If the expected characteristics are not obtained, the cycle is repeated to adjust the resonator design and/or fabrication. When the expected resonator characteristics have been obtained, the resonator is combined with additional detection circuity (Secs. II A 4 and III) to enable EPR spectroscopy.

2. Simulating field distributions and resonator characteristics

Predictive analytical models are available for rectangular and cylindrical resonant cavities.⁸⁴ Simple macroscale loop-gap structures, for which inductance and capacitance can be calculated from fundamental formulas, can also be designed through analytical models.^69,70 However, calculating the resonant frequencies and impedances for microresonators is made untenable by two factors. First, predictive analytical models are difficult to apply to more complex structures such as bow-tie resonators, diabolo antennas, and planar inverse anapole microresonators (see Sec. II B 1). Second, microstructures are highly sensitive to variations in the fabrication processes, e.g., actual resonant frequencies may differ by 10% or more from predicted frequencies. In comparison, numerical modeling or simulations derive device properties based on Maxwell’s equations. Simulations can provide a detailed picture of the device, including field distributions, loss characteristics, Q-factor, fill factor, coupling state, impedance, and resonant frequency. Simulations are commonly the first step in microresonator design and optimization. Simulation software may be based on either the finite element or the finite-difference time–domain methods.

The following points should be considered when constructing models:

• •Model the entire device: We define the entire device as the microresonator with the feedline. Including both elements in the model helps get an accurate representation of device characteristics. The physical properties of materials used in modeling should be as close as possible to those of the actual materials used. For example, dielectric constants should be those provided by the vendor or measured independently for the batch being used in fabrication.
• •Evaluate computational resources: If the computational cost is high (e.g., if the model is computationally large and requires several hours/days to yield a solution) and fabrication costs and times are low, it might be more cost-effective to conduct device optimization through fabrication rather than computation.
• •Devise physically realistic models: Over-reliance on modeling, however, should be avoided. It is important to couple simulations with the researcher’s judgment of what is physically realistic for the system of interest. Care must be taken to ensure that simulated device characteristics are not an artifact arising from improper mesh settings, physics in the model, etc.

3. Device fabrication

The vast majority of microresonators are hybrid structures in which a thin metal film deposited on a dielectric substrate is photolithographically patterned on a crystalline dielectric (e.g., rutile, sapphire, quartz, etc.) or etched out from metal films deposited on low-loss glass–epoxy composite laminates. Crystalline substrates can be polished to have surface roughness <5 nm, but photolithographic fabrication requires access to a cleanroom facility. Etching of a metal-coated epoxy laminate is accessible in terms of fabrication, at least up to 10 GHz where feature sizes are still large enough to allow such fabrication. The surface roughness of some epoxy laminates can adversely affect the properties of resulting devices. The approach utilized to fabricate microresonators and the surrounding coupling structures depends on several factors, including minimum feature size, patterning area, and overlay accuracy. Fabrication of resonator designs may not require access to a cleanroom facility if the smallest feature size is on the order of hundreds of micrometers. Such microresonators may be produced using direct laser cutting or surface micromachining.⁷⁶ In photolithography using masks or mask-less (direct laser write) approaches, a layer of photoresist is deposited on the substrate and patterned by exposure to ultraviolet light.^29,75,77 This patterning can be accomplished in common research labs with a resolution limit on the order of 1 μm. Some advanced nanofabrication facilities are now equipped with more exotic deep-ultraviolet stepper systems that enable patterning over a large area with a resolution down to ≈100 nm. The exposed photoresist pattern can then be transferred to a metal using a lift-off technique for larger features or dry-etched for smaller features. For resonator designs where the minimum desired feature size is sub-micrometer, a more common approach is to use electron-beam (e-beam) lithography because it offers a spatial resolution of ≈10 nm even though it is comparatively more time consuming. E-beam lithography may also be used for highly precise alignment of micrometer-sized features.^85,86 A property that cannot be accounted for during microresonator design is the background from impurities in the dielectric substrate, since this background signal can vary from batch to batch of dielectric material used for fabrication. Crystalline perovskite oxide dielectrics, for example, which offer low loss tangents and high dielectric constants that facilitate miniaturization, often exhibit significant background signals from dopants and defects. On the other hand, substrates such as sapphire, intrinsically pure Si, and fused silica do not offer high dielectric permittivities, but possess the desirable low loss tangents and display minimal background signals.

4. Device testing and deployment

After fabrication, device testing is conducted in two stages. To determine concurrence between experimental and simulated microresonator resonant frequencies, the microresonator is coupled to the same feedline on the benchtop as was set up in the simulation model. Typical coupling strategies include through a loop, inductive coupling with fringe fields radiating from a microstrip, or capacitive coupling with a microstrip patterned on the same substrate as the microresonator. Using a vector network analyzer, power reflected from the feedline-coupled resonator is measured as a function of frequency (S₁₁ trace). Critically coupled devices exhibit a dip in reflected power at the resonant frequency. The width of the dip at −3 dB from the baseline (bandwidth or fractional bandwidth) is inversely related to the Q-factor [Eq. (3); Fig. 2]. The Q-factor also affects the coupling of the resonator to the microwave feedline. As the resonator size decreases, it becomes increasingly difficult to inductively couple the resonator with fringing fields from a feedline. Therefore, capacitive coupling with prefabricated structures is often used for microresonators.^60,75,87 This approach, unfortunately, does not permit coupling adjustment, which is important when working with some sample types. As stated in Sec. II A 1, pre-fabricated microresonator/capacitive feedline coupling devices may not always exhibit the coupling behavior expected from simulations. Section III provides further details of microresonator–feedline coupling.

Once the resonator characteristics have been verified on the benchtop, the coupled devices are then deployed in the EPR spectrometer. The design tasks for this step may, of course, be conducted in parallel with microresonator design and fabrication. For example, successful microresonator deployment requires the design and fabrication of a holder that allows first, easy placement and replacement of the microresonator–feedline device in the spectrometer (including connections to the bridge and modulation coil drivers in the instrument) and, second, easy placement and replacement of the sample in the active region of the microresonator. If low-temperature EPR experiments are required, a variable-temperature setup incorporating the microresonator will need to be designed and tested. There are excellent examples of such variable temperature probes deploying microresonators, in which the probes are compatible with preexisting cryostats^30,32,88,89 or setups that incorporate Josephson parametric amplifiers for measurements at mK temperatures.^47,60

B. Existing microresonator designs

Here we present representative examples of microresonators (v/λ³ ≪ 10⁻⁶). We will then discuss the reasons that currently hinder broad application of these devices for routine EPR spectroscopy. As mentioned before, microresonators are impactful in the low-frequency (<35 GHz) regime, in which wavelength-dictated sample sizes tend to be greater than 10 μl.

1. Reported deep-subwavelength resonator designs for microwave frequencies

Table II lists representative examples of the microresonator design classes listed below. Because each of the microresonators listed employed a different coupling scheme, instrumentation, sample type, and experimental conditions, direct comparison of microresonator performance is not straightforward. Thus, Table II provides a list of parameters for a comprehensive comparison of various microresonator designs.

• •Planar microresonators (fields radiating from a flat surface): Lumped-circuit structures based on inductive loops and capacitive gaps offer the oldest yet still common strategy for miniaturizing microwave (EPR) or radio frequency (NMR) resonators to the microliter range.^{69,70,72,90,91} Photolithography and advances in nanofabrication have allowed extreme miniaturization of lumped-circuit microstrip-based resonators, with features in the range of 500 down to 1 μm. Established fabrication protocols allow wide variation of designs to produce a multitude of structures. Some of the prominent design classes of planar microresonators are listed below:
  • •Half-wavelength and quarter-wavelength stripline resonators and coplanar waveguide resonators.^92–94 These are planar equivalents of cavity resonators, in that their dimensions are multiples of λ/4, where λ is the wavelength of the propagating wave in the microstrip or coplanar waveguide.
  • •Planar microcoils/planar loop-gap structures, which are planar versions of slotted or loop-gap resonant structures. Photolithography can produce inner loop diameters down to 20 μm. In capacitively coupled planar loop-gap structures, the resonator and waveguide are patterned on the same side of the dielectric substrate. These designs may have low fabrication yield because they must be fabricated in the coupled state.^73,75,95 On the other hand, inductively coupled planar loop-gap structures are coupled to the feedline through the dielectric substrate.^77,78 Such designs can enable variable coupling through control of the microresonator position relative to the microstrip.
  • •Bow-tie like structures concentrate current over a small central bridge, leading to a small region of high B₁ Intensity. Such resonators are particularly suitable for microcrystals or sub-microliter volume liquid samples.^78,96
  • •Planar inverse anapole resonators use toroidal moment to cancel out dielectric radiative losses. This intrinsic reduction in radiative losses results in increased Q-factors at room temperature. As in the bow-tie like structures, B₁ is concentrated around a small bridge at the center of the design.²⁹
  • •Interdigitated structures and hairpin-like geometries are particularly suited to thin-film samples. These designs confine B₁ close to the resonator surface yet are spread over a large surface area, resulting in a B₁ distribution that can sense a thin layer of spins distributed in the layer adjacent to the resonator.^60,85,87
• •Volumetric microresonators (fields contained in a three-dimensional cavity structure): Cavities and helical microcoils²⁸ provide excellent B₁ homogeneity but are difficult to fabricate with small volumes. Self-resonant microcoils provide an attractive combination of a nanoliter-sized sample volume, B₁ homogeneity, and increased conversion factors.^30,32

TABLE II.

Representative examples of various reported microresonator designs and their performance parameters. Figures reproduced with permission from Narkowicz et al., J. Magn. Reson. 175(2), 275–284 (2005). Copyright 2005 Elsevier; from Dayan et al., Rev. Sci. Instrum. 89(12), 124707 (2018) with the permission of AIP Publishing; Bienfait et al., Nat. Nanotechnol. 11(3), 253–257 (2016). Copyright 2016 Springer Nature; Abhyankar et al., Sci. Adv. 6(44), eabb0620 (2020). Copyright 2020 Author(s), licensed under a Creative Commons Attribution 4.0 License; and Sidabras et al., Sci. Adv. 5(10), eaay1394 (2019). Copyright 2019 Author(s), licensed under a Creative Commons Attribution 4.0 License.

Omega-type loop-gap (2D)73		Experimental Q-factor (T, ν)	<50 (298 K, 14 GHz)
		Active volume	10–100 nl
		Coupling mechanism	Non-variable capacitive
			coupling to coplanar microstrip
		Conversion factor	5 mT/$\sqrt{\mathrm{W}}$
		π/2 pulse length (input power)	24 ns (17 mW)
		B1 homogeneity	>50% variation within
			active region
Bow-tie like structures (2D)78		Experimental Q-factor (T, ν)	<100 (298 K, 35 GHz)
		Active volume	0.5–5 nl
		Coupling mechanism	Variable inductive coupling
		Conversion factor	10 mT/$\sqrt{\mathrm{W}}$
		π/2 pulse length (input power)	⋯
		B1 homogeneity	>50% variation within
			active region
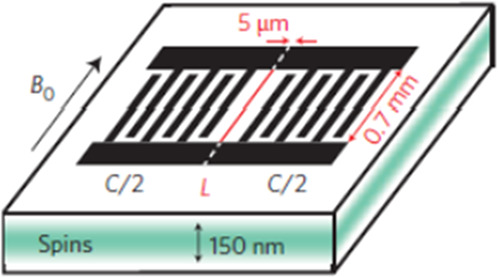
Interdigitated resonators (2D)60		Experimental Q-factor (T, ν)	3 × 105 (12 mK, 7 GHz)
		Active volume	0.02 nl
		Coupling mechanism	Non-variable capacitive
			coupling to input and
			output antennas
		Conversion factor	⋯
		π/2 pulse length (input power)	⋯
		B1 homogeneity	⋯
Planar inverse anapole (2D)29		Experimental Q-factor (T, ν)	200–300 (298 K, 10 or 35 GHz)
		Active volume	0.1 nl
		Coupling mechanism	Variable inductive
			coupling to microstrip
		Conversion factor	10 mT/$\sqrt{\mathrm{W}}$
		π/2 pulse length (input power)	⋯
		B1 homogeneity	>50% variation within
			active region
Self-resonant helix (3D)30		Experimental Q-factor (T, ν)	220 (298 K, 10 GHz)
		Active volume	1 nl
		Coupling mechanism	Variable inductive
			coupling to loop
		Conversion factor	10 mT/$\sqrt{\mathrm{W}}$
		π/2 pulse length (input power)	20 ns (20 mW)
		B1 homogeneity	<10% variation within
			active volume

2. Factors hindering broad applicability

There are often challenges in tuning the frequency and coupling of the microresonator to the feedline. This difficulty arises first because of the mismatch between the microresonator size and feedline dimensions and second due to the low Q-factors typically characteristic of a single microresonator. As described earlier briefly and in greater detail in Sec. III, inductive coupling schemes offer variable tuning and coupling,^29,77 but these must be conducted prior to placing the microresonator–feedline setup in the EPR spectrometer. If slight changes in coupling occur during the experiment, re-adjustment can only be carried out after removing the device from the spectrometer. Pre-fabricated capacitively coupled devices are robust to changes in coupling, but only a fraction of many fabricated devices may exhibit the predicted device characteristics. Aside from the intrinsically poor coupling due to low Q, the aforementioned engineering problems need to be solved in order to apply microresonators with the same versatility that is available for conventional resonators.

Another challenge is maintaining maximum operability (temperature range, scalability over frequency) for any microresonator design. To provide the same range of spectroscopic information as conventional resonators, microresonators should ideally be operable over a wide range of temperatures, typically between 10 and 300 K. This requires the development of variable-temperature probes incorporating the microresonator of choice, which is a non-trivial engineering problem. Finally, data collection at multiple frequencies is standard practice in EPR spectroscopy, making frequency scaling of microresonator designs highly desirable. While this capability has been demonstrated at 10 GHz by deploying a self-resonant microhelix in a commercial spectrometer,^30,32 most microresonator designs typically become impracticably small at higher frequencies. Therefore, microresonator design may need to be varied to adapt to the application space and experimental requirements (temperature, type of sample, frequency of operation).

Finally, reducing the cost of microresonators will foster wider adoption and integration of microresonators into commercial or custom-built systems. Ensuring that resonator cost is not prohibitive will promote microresonator integration in compact instrumentation and development of multiplexed assays and experiments requiring a parameter matrix. Currently, there are two main contributors to production costs:

• •Materials: To achieve high performance in terms of absolute and concentration sensitivities, microresonator designs often rely on expensive materials such as low-loss substrates⁷⁷ and/or superconducting materials.^86,97–99 This challenge needs to be overcome, particularly from a manufacturing perspective.
• •Fabrication: Depending on the choice of fabrication approach (Sec. II A 3), costs can vary considerably. Advanced nanofabrication provides the ability to reduce feature sizes, and thereby the resulting active volume, but may result in prohibitive costs. Even when fabrication requirements are not stringent, the low efficiency (both throughput and yield) of the fabrication process may increase the overall cost of production.

C. Future avenues in microresonator design

Section II B illustrated the wide range of design paradigms that have been applied for resonator miniaturization, enabled by photolithography and other advances in nano- and micro-fabrication techniques. Although microresonators offer high filling factors and power-to-field conversion efficiencies, the main challenges to overcome are losses resulting in low Q-factor and the poor efficiency of coupling with the feedline. An ideal microresonator would have a high filling factor in addition to strong and tunable coupling to the microwave feedline (which would further allow control of the Q-factor and resonator–sample coupling). The suitability of designs from other areas of research to EPR spectroscopy is dictated by the requirements of EPR spectroscopy, namely: (i) the presence of a well-defined sample volume where B₁ is spatially separated from E₁; (ii) strong coupling between the loaded resonator and feedline so that small changes in magnetization of the sample can be detected with high sensitivity; and (iii) perpendicular orientation of B₁ to B₀ for conventional EPR spectroscopy. Here, we present examples of potential avenues originating from research in optical metamaterials that could be leveraged to achieve these design goals.

1. Metamaterials

Photonic crystals have been used in the fabrication of EPR resonators for high-frequency applications,¹⁰⁰ and the photonic metamaterial literature is a rich resource for novel resonator designs. Photonic metamaterials are typically tailored with a view to customizing the dispersion characteristics, near and far-field radiation profiles, and interaction of incident light with the resonant modes supported by the metamaterial.¹⁰¹ To translate an optical metamaterial design to EPR spectroscopy, the key properties to look for are the existence of a magnetic dipole, its spatial separation from the electric field, and the associated Q-factor of the spectral resonance. Broadly, such metamaterials can be classified into two categories, plasmonic and dielectric metamaterials.

Plasmonic metamaterials are planar metallic or hybrid metallo-dielectric structures designed such that excitation of surface plasmon modes produces electromagnetic responses at length scales much smaller than the wavelength. A metallic split-ring resonator, with oscillating electric-field coupled to the ring, resulting in an out-of-plane magnetic-field at the center of the ring, first reported by Pendry et al.,¹⁰² is a seminal representative example of a plasmonic metamaterial. Other suitable plasmonic candidates include anapoles, oligomers of coupled metallic structures, and diabolo nano-antennas.

• •Anapoles: Radiative losses at dielectric discontinuities contribute to the low Q-factors of microresonators. In an anapole mode, the toroidal dipole moment interferes destructively with the electric dipole moment, resulting in a charge-current distribution that is characterized by diminished radiative losses from dielectric discontinuities [Fig. 4(a), top panel].¹⁰³ By decreasing radiative losses, anapoles create resonant structures with improved Q-factors in metallic¹⁰⁴ and hybrid metallo-dielectric^105,106 systems [Fig. 4(a), bottom left and right panels, respectively]. Recently, planar inverse anapole microresonators, made by applying Babinet’s principle to an anapole resonator, have been deployed for EPR spectroscopy on samples with sub-nanoliter active volumes.²⁹
• •Oligomers of coupled metallic structures: These designs can produce volumes in which B₁ is highly confined, thus circumventing the need to fabricate impracticably small rings for use at higher frequencies.^107,108 Surface plasmons,¹⁰⁹ localized spoof surface plasmons,¹¹⁰ and skyrmions¹¹¹ also confine the magnetic field close to the surface of a metallic structure on a dielectric substrate. Tighter confinement close to the metal surface can be achieved by structuring the metal surface.^112,113 Vertical 3D plasmonic structures can also produce volumetric confinement with enhanced B₁.¹¹⁴
• •Diabolo nano-antennas: Bow-tie shaped structures¹¹⁵ reported for confining optical magnetic fields have already been adapted for EPR spectroscopy,^78,116 providing B₁ enhancement that is 10 to 100-fold higher than conventional 3D loop-gap microresonator designs.

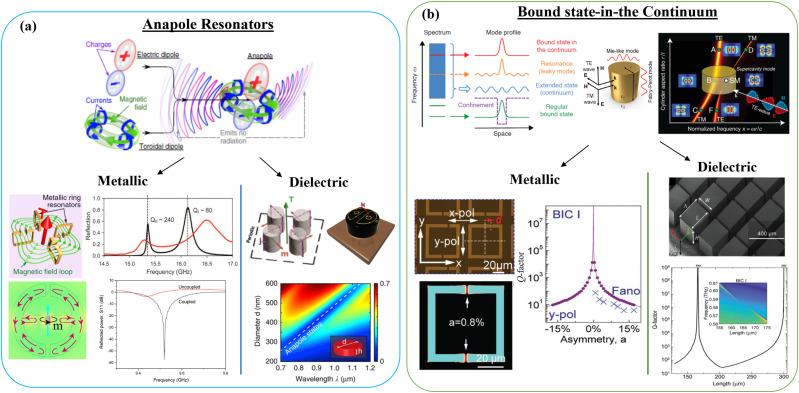
FIG. 4.

Summary of two classes of optical metamaterial resonators leveraging electromagnetic: (a) anapole modes, and (b) bound-state-in-the-continuum (BIC) modes. As illustrated in (a) top-panel, an anapole mode is excited through destructive interference in the far-field between an electric-dipole and the toroidal-dipole mode resulting in a device supporting extremely high Q-factors. Similarly, (b) top-panel illustrates the presence of a bound-state (red line) in the radiation continuum (blue region), that theoretically exhibits a Q-factor of infinity. Resonance frequency vs resonator size for an individual dielectric nanopillar resonator [(b), top-right] illustrates excitation of a various TE and TM modes with different field-distributions, including the excitation of a BIC mode that is characterized by a vanishing linewidth in the dispersion plot. Both anapole and BIC modes, through geometric engineering, can be excited in metallic [bottom-left panels in (a) and (b)] or dielectric [bottom-right panels in (a) and (b)] systems, and offer extremely high-Q factors in subwavelength modal volumes with mode-profile that could be geometrically engineered for application in EPR spectroscopy. Figures have been reproduced with permission from Savinov et al., Commun. Phys. 2, 69 (2019).¹¹⁷ Copyright 2019 Springer Nature; Abhyankar et al., Sci. Adv. 6(44), eabb0620 (2020). Copyright 2020 Author(s), licensed under a Creative Commons Attribution 4.0 License; Basharin et al., Phys. Rev. X 5, 011036 (2015).¹¹⁸ Copyright 2015 Author(s), licensed under a Creative Commons Attribution 3.0 Unported License; Kaelberer et al., Science 330(6010), 1510–1512 (2010). Copyright 2010 AAAS; Bogdanov et al., Adv. Photonics 1, 016001 (2019).¹¹⁹ Copyright 2019 Author(s), licensed under a Creative Commons Attribution 4.0 License; Totero Gongora et al., Nat. Commun. 8, 15535 (2017).¹²⁰ Copyright 2017 Springer Nature; Hsu et al., Nat. Rev. Mater. 1(9), 16048 (2016). Copyright 2016 Springer Nature; Rybin et al., Phys. Rev. Lett. 119, 243901 (2017).¹²¹ Copyright 2017 American Physical Society; Yang et al., Adv. Opt. Mater. 7, 1900546 (2019).¹²² Copyright 2019 Wiley; and Shi et al., Adv. Mater. 31, 1901673 (2019). Copyright 2019 Wiley.¹²³

Similar to metallic micro-resonators, resonators based on low-loss, easily patternable dielectric materials, such as Si, or other high-permittivity materials, such as KTaO₃ or SrTiO₃,¹²⁴ either suspended in air or placed on low-permittivity substrates (e.g., fused-silica) can generate a precisely tailored spectral response for EPR applications.^125,126 These resonators support simultaneous excitation of electric and magnetic dipolar and multipolar resonances, referred to as Mie resonances, where the resonance frequency depends on the geometric parameters (shape and size) of the resonator as well as the constituent material.^127–130 Precise engineering and spatial overlap of optical modes supported by the resonators have, for example, led to novel capabilities in the areas of biosensing,^131,132 nonlinear optics¹³³ and lasing.¹³⁴ The capability to precisely engineer the spectral response has been made possible by remarkable advances in nanofabrication over the last decade, particularly for dielectric systems wherein the fabrication process steps are compatible with those in a commercial foundry platform. Therefore, scaling the fabrication throughput or achieving higher milling resolution by leveraging advanced commercial foundry platforms becomes a possibility. Dielectric ring resonators made of high-permittivity dielectrics have also been implemented in EPR spectroscopy and MRI applications to decrease sample volume.^{62,63,68,72,135} In the context of fabrication, while Si offers the most flexibility, high-permittivity materials offer a promising route to further reduce resonator volume and increase fill factor, while maintaining high B₁ homogeneity. Structures fabricated from these materials offer the advantage of lower losses when compared to metallic structures such as split-ring resonators but may require further optimization to achieve similar confinement.

2. Bound state in the continuum

The spectral engineering of both plasmonic and dielectric metamaterials has, in recent years, been substantially improved by engineering the coupling between localized (single resonator) and lattice (periodic array of resonators) resonances.¹³⁶ These coupled systems can be engineered to support a variety of electromagnetic modes, such as Fano resonance,¹³⁷ electromagnetically induced transparency,¹³⁸ surface lattice resonance,¹³⁹ and bound state in the continuum^140,141—each offering high quality factors and some compromise between modal confinement and radiative losses, and an associated electromagnetic mode profile that may or may not be suited to EPR spectroscopy. For example, high-quality factors can simply be achieved by adapting the concept of bound states in the continuum (BIC) and extending them to the microwave frequencies. BICs represent a localized mode, supported by either an isolated dielectric resonator or a periodic array of resonators, with its energy contained within the continuum of radiative modes [Fig. 4(b), top panel]. Through geometric engineering, this localized mode can be fully decoupled from the radiating continuum, thereby creating a resonator that theoretically offers a quality factor (Q) of infinity at resonance. Experimentally, Q-factors in these systems have finite values because of sample size limitations, material losses, and imperfect fabrication leading to scattering losses [Fig. 4(b), bottom panels].^130,142,143 Such high Q-factor resonators leveraging BICs from single resonators to arrays of resonators have been used to realize small-footprint lasers and perform high-sensitivity chemical and biological sensing. Therefore, BICs offer a promising route for EPR applications requiring high-Q resonances.

III. EPR INSTRUMENTATION FOR MICRORESONATORS

This section presents EPR instrumentation considerations that must be addressed when using microresonators. Because of the size, coupling the incident microwave power to the microresonator structure can be nontrivial and the choice of coupling method impacts the excitation and detection (bridge) circuitry. Depending on the coupling method, the types and arrangements of magnets are also impacted. We present an overview of the spectrometer modifications and considerations that may be required for incorporating microresonators into existing EPR spectrometers. We conclude the section with a short discussion on the advantages that microresonators present for construction of compact spectrometers.

A. Coupling

Microresonators present a unique geometry with many positive attributes, but also there are some obstacles to their usage. The most striking difference between conventional cavity-based resonators and microresonators is the coupling methodology. Typically, cavity-based resonators used for continuous wave measurements are directly mated to the microwave excitation/detection subsystems via matched waveguides.²⁸ Most often, these rigid waveguides are geometrically matched to the resonator, which greatly minimizes transmission losses and phase uncertainties.²⁸ Efficient coupling (impedance matching the resonator/sample to the microwave transmission line) is accomplished via adjustment of a coupling mechanism between the transmission line and resonator aperture (e.g., iris screw, sliding short).²⁸ Use of frequency-matched waveguide is largely incompatible with microresonators due to the large mismatch between the spectrometer operating frequency (and corresponding wavelength) and microresonator dimensions.

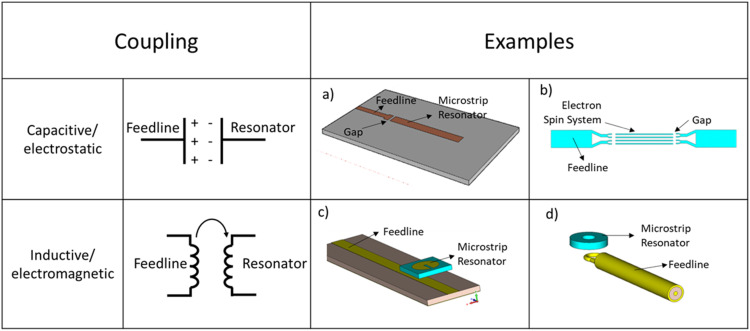
This size mismatch dictates use of less direct coupling schemes. Capacitive (electrostatic) and inductive coupling (electromagnetic) are the two major approaches used to establish the link between the incident microwaves supplied by the transmission line and a microresonator. Figure 5 schematically illustrates some examples of these coupling arrangements. Capacitive coupling introduces a discontinuity in the path of microwave propagation, which separates the microwave feedline from the resonant structure. Compared to inductive coupling, capacitive coupling is more sensitive to the dielectric medium of propagation, leading to steeper dielectric losses with increase in coupling distance. Inductive coupling is realized by placing the resonant structure parallel to the microwave propagation of the microwave feedline. The resonator acts like an antenna, allowing two-way communication (excitation and detection) with the microwave feedline. The antenna-like nature of inductive coupling introduces some additional considerations for microresonator incorporation.

FIG. 5.

Examples of (a) capacitively coupled microresonator with feedline and single gap microstrip microresonator,⁹⁴ (b) capacitively coupled microstrip line resonator with composite arrays,¹⁴⁴ and [(c) and (d)] inductively coupled microresonators.⁷⁴ Figures reproduced from Torrezan et al., Rev. Sci. Instrum. 80(7), 075111 (2009) with the permission of AIP Publishing; Mohebbi et al., J. Appl. Phys. 115(9), 094502 (2014) with the permission of AIP Publishing; and Twig et al., Rev. Sci. Instrum. 81(10), 104703 (2010) with the permission of AIP Publishing.

For planar microresonators, inductive coupling between the microresonator and a microstrip transmission line leads to a geometry in which the overlapping resonator–feedline region determines the coupling strength. Ideally, any resonator, including microresonators, store this coupled microwave energy (Q, see Sec. I) and spatially separates the electric and magnetic fields to ensure that the microwave magnetic field interacts with the sample. The dimensional mismatch between the microresonator geometry and wavelength leads to inescapable inefficiencies due to spreading of the electromagnetic fields beyond the active volume of the microresonator. Recent efforts⁷⁷ detail a more efficient multistage excitation scheme in which an intermediate-sized loop gap resonator is placed between the feedline and the microresonator. The somewhat larger intermediate resonator efficiently couples to the input microwaves and concentrates the electromagnetic fields to a smaller region, which in turn efficiently couples to the much smaller microresonator. For example, a planar resonator⁷³ with diameter >200 μm can be used as an intermediate antenna¹⁴⁵ to excite a smaller microresonator structure²⁹ with overall external dimensions <20 μm, which was observed to improve coupling strength while maintaining the high fill factors synonymous with microresonators.

The chosen microresonator–feedline coupling mechanism impacts the design geometry of the microresonator and the subsequent coupling efficiency. However, the microwave feedline design also has a significant impact, being the sole vector of interaction with the microresonator. The microwave feedline is constructed from the lowest loss components that are compatible with the overall system geometry. This transmission line shuttles electromagnetic fields between the microresonator and the microwave excitation/detection circuitry. The interaction of the propagating microwaves and the microresonator generates an impedance change that results in a reflected and transmitted microwave that carries the EPR spectroscopic information. Depending on the feedline termination, EPR signal detection proceeds in transmission or reflection mode.^73,77 If the feedline is terminated with an open or a short impedance, the feedline/microresonator operates in reflection mode with all the spectroscopic information contained in the reflected microwaves. In this scenario, the open/short termination separates the electric and magnetic field distributions into frequency-dependent positions on the feedline.⁷⁶ An understanding of the resultant microwave field distributions is required to ensure proper placement of the microresonator on the feedline to maximize coupling. In contrast, 50 Ω termination of the feedline does not separate the electric and magnetic fields along the feedline, thereby removing the requirement for frequency-dependent placement of the microresonator on the feedline. The measurement can proceed in either reflection mode or transmission mode and the proper choice is largely dependent on the dielectric losses of the microresonator/sample structure.¹⁴⁶ However, this regained freedom means that a portion of the spectroscopic information (either the transmitted or reflected waves) is lost due to resistive dissipation. One can employ dual detection schemes to recapture this lost information,¹⁴⁶ but these are somewhat uncommon, especially when interfacing microresonators with commercial EPR spectrometers.

B. Excitation and detection circuitry

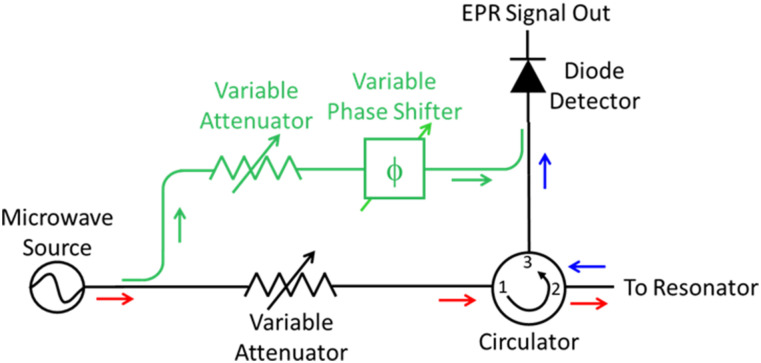
Successful replacement of a conventional microwave resonator with a microresonator/feedline requires consideration of the microwave excitation and detection circuitry. Figure 6 shows a simplified schematic of the microwave excitation and detection circuitry (bridge) for a continuous wave EPR spectrometer. The microwave source [e.g., voltage-controlled oscillator (VCO), klystron, Gunn diode, digital synthesizer] provides microwave power into the transmit path (red arrows) of the circuit. Minimally, the transmit path also includes an attenuator and circulator. The variable attenuator controls the incident microwave amplitude (power) at the resonator/sample. The circulator is a directional device that acts like a traffic roundabout with the reflected microwave power transferred to the next sequential port. Almost all commercial ESR spectrometers operate in reflection mode with the spectroscopic information encoded in the reflected microwave signal coming from the resonator/sample. The receive path (blue arrows) of the microwave bridge includes all hardware after the microwave signal has been reflected from the sample/resonator and exits the circulator. In most CW systems, the reflected microwave signal is directed to a Schottky diode detector, which is a phase-independent detector. If a reference arm (green) is present in the bridge, it ensures that the diode is biased in the most sensitive linear regime.¹⁴⁷ The reference arm diverts a portion of the input microwaves, the phase and amplitude of which are adjusted by a variable attenuator and phase shifter for two main purposes. The first is to adjust the reference arm phase to ensure that the microwaves that exit the reference arm and recombine with the reflected microwaves from the resonator are in phase with each other (coherent). The second purpose is to adjust the microwave amplitude (via the attenuator) of the reference arm to ensure that, after recombination, the Schottky diode has sufficient bias to operate in the linear regime.¹⁴⁷ In this way, the reference arm provides a phase-dependent “bias” to the Schottky diode to maximize the measurement sensitivity. The oversimplified microwave circuitry schematic (Fig. 6) omits the automatic frequency control (AFC) circuit. The purpose of the AFC is to introduce a small adjustment to the source frequency (which is equivalent to a phase shift) to match the resonance-induced phase change in the resonator and ensure proper absorption lineshapes. Integration of a microresonator into a spectrometer system that uses AFC needs to account for the AFC circuit–microresonator interaction.

FIG. 6.

Simplified schematic of the microwave excitation and detection circuitry in a continuous wave EPR spectrometer. Excitation occurs along the transmit pathway (red arrows). Detection occurs along the receive pathway (blue arrows). The reference arm (green) combines with the receive pathway to ensure optimal detector biasing.

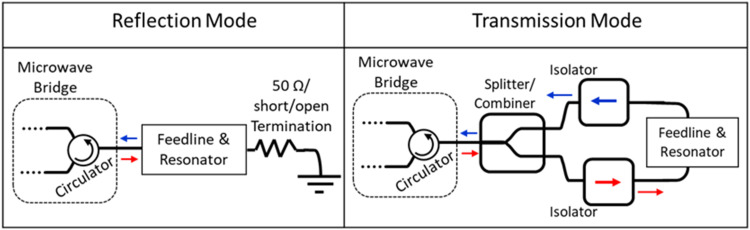
Conventional EPR microwave bridges operating in reflection mode can usually accommodate replacement of a typical cavity resonator with a custom microresonator/feedline/termination structure as shown in Fig. 7(a). There are, however, some consequences of this replacement. To interface the incident microwaves with the microresonator requires replacement of the waveguide by a coaxial transmission-line. Replacing the fixed length/low loss waveguide transmission line with the coaxial transmission-line invariably introduces a variation in the length of the transmission-line and the associated variation of the microwave signal phase. This phase variation destroys the phase coherence of the reflected microwaves emanating from the circulator and the reference arm. Position adjustment of the microresonator along the feedline can introduce a second experimental phase consideration that needs to be calibrated out. Most modern commercial spectrometers allow for an adjustment of the input phase.¹⁴⁷ Another issue is that power losses in the microresonator/feedline coupling can possibly result in only a small fraction of microwave power being reflected from the resonator. This power difference between the reflected microwave signal and the reference arm can force the Schottky diode out of the linear operating mode. Again, most modern commercial spectrometers allow for adjustment of the attenuator in the reference arm to ensure that the diode is properly biased.

FIG. 7.

Simplified schematic diagram of the interface between the microwave excitation/detection circuitry and the feedline/resonator operated in the (left) reflection mode and (right) transmission mode.

In some situations, utilizing the microresonator in a transmission mode measurement makes experimental sense. Rather than reflecting the microwave signal from the microresonator back into the circulator, the signal is transmitted through the feedline and then back into the circulator and subsequent microwave detection circuitry. When using transmission mode, a small modification must be made to the detection circuitry to introduce directionality. A simple approach is shown in Fig. 7(b) where a microwave splitter/combiner and two isolators direct the microwaves to the input of the feedline and then direct the transmitted microwaves back into the circulator in the microwave bridge. An (optional) external phase shifter can also be added to this simple circuit to provide external phase adjustment that can ensure observation of absorption line shapes. It is important to note that transitioning from the waveguide transmission line to the coaxial transmission line right at the output of the spectrometer allows this small helper circuit to be composed of commercially available, connectorized coaxial components.

Our discussion has largely ignored the impact of microresonator incorporation on the AFC circuitry.²⁸ AFC systems typically utilize feedback on a low frequency modulation of the source microwaves. As the magnetic field is swept through resonance, the frequency modulation emanating from the resonator becomes out of phase with the source frequency modulation. The AFC utilizes a phase detector (mixer) to translate the source/resonator phase difference into an error signal that imparts a very small correction to the source carrier frequency to minimize the phase difference. This correction produces a deconvolved (absorption or dispersion) line shape. Unsurprisingly, the AFC circuit functions with some baseline expectations of resonator Q. In part because microresonators have lower Q factors, replacement of the cavity resonator with a microresonator/feedline structure can create problems for the AFC circuit. The transition from the waveguide to coaxial transmission line, the coaxial transmission line to the feedline, and transition from the feedline to the microresonator generate additional reflections that can be comparable in magnitude to the absorption at the microresonator resonance frequency. These secondary reflections can have Q factors similar to that of the microresonator, which means the AFC feedback circuitry cannot distinguish the microresonator resonance from the secondary reflections. In addition, these unavoidable transitions add frequency dispersion that can broaden the microwave resonance, which impacts the AFC circuit’s ability to adjust as the sample passes through magnetic resonance. These issues result in an AFC circuit that either locks to the wrong frequency or cannot maintain the lock for the duration of the measurement. Solutions to these issues depend on the microresonator design, the chosen feedline coupling mechanism, and the interface with the excitation and detection circuitry. Simple spectrum analyzer measurements of the microresonator/feedline structure in both reflection and transmission modes can provide a means to better tune the placement of the microresonator on the feedline and identify the resultant parasitic resonances that impact the effectiveness of AFC. Troubleshooting solutions include switching from reflection to transmission mode to eliminate certain resonances or adding microwave filters to eliminate unwanted resonances.

The discussion of the excitation and detection circuitry has been framed through the lens of continuous wave EPR instrumentation. Except for the frequency and phase shifts, the issues described above also apply to pulsed EPR instrumentation. The addition of a microresonator to a pulsed EPR spectrometer generates new obstacles too. It is important to evaluate microresonator ring-down times to protect detection circuitry electronics, particularly low noise amplifiers. The low Q factors of most microresonators typically result in sufficiently short ring-down times that receiver protection timings need minimal adjustment and the spectrometer deadtime is not affected. If the power-to-field conversion is low, pulsed excitation of the spin ensemble requires longer pulse lengths to generate the correct tip angle. These longer pulses excite a narrower EPR signal bandwidth, which can lead to decreased SNR especially for broad spectra. Detection sensitivity can be improved with the application of specific pulse sequences (e.g., Carr–Purcell–Meiboom–Gill).¹⁴⁸ Longer pulses can also result in resonator heating, which introduces baseline artifacts requiring corrections to account for these shifts. Additional concerns center around the power handling capability of the components used for microresonator incorporation. Most coaxial cabling has sufficient breakdown strength to handle the increased microwave powers used for pulsed measurements; however, dielectric losses can cause the cabling to heat and add additional phase variables. This dielectric loss-induced heating is also a concern for the chosen feedline (typically microstrip). If additional helper circuitry is utilized (Fig. 7), care should be taken to ensure that the components will not be damaged by the peak pulse microwave power and duty cycle.

The goal of this discussion was to emphasize that incorporation of a microresonator into a conventional continuous-wave microwave bridge circuit is readily achievable. Some basic understanding of the microresonator input power, reflected power, and phase can help ameliorate most problems. For the more adventurous EPR experimentalists, recent work has detailed methods to construct interferometric bridge designs that can simultaneously capture reflected and transmitted EPR signals.¹⁴⁶ This excitation and detection approach may prove beneficial for measurements using microresonators.

C. Magnets

Traditionally, EPR spectroscopy at frequencies up to 34 GHz (1.2 T) is performed using an electromagnet. This situation is in stark contrast to modern, high-field NMR spectroscopy [e.g., 300 MHz (7 T)¹H NMR], which almost exclusively uses superconducting magnets. In recent years, benchtop NMR spectrometers relying on permanent magnets have been gaining ground. However, in the case of EPR spectroscopy, very few permanent magnet systems have been reported in the literature, and these systems are often in combination with a sweep coil (hybrid magnets).^149–153

In this section, we will discuss the two most common magnets used in EPR spectroscopy: electromagnets and permanent magnets. Although superconducting magnets are used in high-field EPR spectroscopy, they are not suitable for compact EPR spectrometers, which we envision as the most impactful secondary benefit of the implementation of microresonators.

The overall design of electromagnets for EPR spectroscopy has not changed in more than 80 years, which makes the sturdy floor-based model the ubiquitous standard in many EPR laboratories. In a CW EPR experiment, and to some extent in pulsed EPR spectroscopy, the magnetic field is swept through the resonance condition. This approach was necessary when stabilizing the output frequency of the microwave source (e.g., klystron) was more difficult than generating a stable magnetic field with an electromagnet.¹⁵⁴ Electromagnets are versatile and produce a stable, homogeneous static magnetic field, large enough to encompass the entire EPR resonator. Although smaller electromagnets weighing 300–400 kg are sometimes used in EPR spectroscopy, the more common magnets weigh about 1800 kg and require water-cooling and high-power electrical service to operate. When treated properly, these magnets are almost indestructible. The large power supplies of the past can now be replaced by much more compact and efficient power supplies. A major advantage of the floor-model magnets is the magnetic field homogeneity of typically <0.1 µT (<0.3⋅10⁻⁶ at 0.35 T) across a 10 mm diameter of spheric volume (DSV). This high magnetic field homogeneity is often required to determine the complex hyperfine structure of organic radicals in solution.¹⁵⁵ In the context of microresonators, the large airgap in electromagnets makes prototyping new resonators easy and enables the use of commercially available cryostats for low-temperature experiments. However, with EPR spectroscopy moving toward compact and portable spectrometers for on-site/in-field applications, the weight, power, and cooling requirements of the traditional electromagnets is undesirable.

In recent years, commercial vendors are offering benchtop EPR spectrometer systems. Although still relying on electromagnets, the magnets for these spectrometers are typically air-cooled and the entire system weighs no more than 45 kg. Although significantly lighter, the homogeneity of these magnets is reduced to >4.5 µT (>13 · 10⁻⁶ at 0.35 T) across a 10 mm DSV. Although more than an order of magnitude lower compared to floor-based electromagnets, this magnetic field homogeneity is sufficient for many solution-state EPR experiments, whether it be confirming that a spin-label is (still) attached to a protein or quantifying radicals captured by a spin-trap.

Permanent magnets made their debut for magnetic resonance spectroscopy in the early 2000s. Specifically, Raich and Blümler,¹⁵⁵ relying on Halbach type magnets from the 1970s,¹⁵⁶ developed a new permanent magnet layout suitable for magnetic resonance spectroscopy. This design, known as the Mandhalas (Magnet Arrangements for Novel Discrete Halbach Layout), relies on a permanent magnet array constructed from individual, identical permanent (bar-)magnets.¹⁵⁵ The arrangement of the magnets in the array is compact and provides a field with sufficient homogeneity for NMR spectroscopy. This example illustrates that it is possible to design compact magnets; due to the high density of the magnetic materials in permanent magnets and because such arrays are used with probeheads (NMR) or resonators (EPR) for conventional magnetic resonance spectroscopy, this layout tends to be quite heavy. Larger arrays are necessary for highly homogeneous magnetic fields across larger (10 mm) DSVs. However, because microresonators are small, a spectrometer with a microresonator would require a smaller DSV (field homogeneity). This DSV decrease means that the permanent magnet—single or an array—can be lighter, enabling more compact instrument designs overall.

EPR spectroscopy, in contrast to NMR spectroscopy, has only a few examples of the use of permanent magnets. Most of these applications are related to oximetry or dosimetry measurements.^149–152 For example, there is a system for alanine dosimetry that operates at 0.2 GHz with a permanent magnet field of 41 mT and pole gap of 50 cm.¹⁴⁹ Another example is a compact 3 GHz (S-band) spectrometer that uses a hybrid magnet.¹⁵³

Permanent magnets used in magnetic resonance applications are commonly either sintered blocks of neodymium–iron–boron (NeFeB) or samarium–cobalt (SmCo).^157,158 One major drawback of permanent magnets is that the magnetic flux is highly temperature dependent. Although NeFeB magnets provide the highest magnetic field strength, SmCo permanent magnets show smaller temperature induced drifts. Typically, NeFeB magnets have a temperature coefficient of ≈1000 · 10⁻⁶ °C⁻¹, and SmCo magnets typically have a coefficient of ≈400 · 10⁻⁶ °C⁻¹.^159,160 This difference makes SmCo magnets the better choice for applications that require high resolution and small field drifts. As a result of the magnetic materials’ properties in permanent magnets, high-resolution magnetic resonance spectroscopy must be performed in temperature-stabilized environments with temperature variations <0.1 K. The magnetic field drift associated with permanent magnets is acceptable for EPR spectroscopy and does not require an additional lock circuit.^161,162

1. Magnet designs

In general, there are two permanent magnet designs suitable for magnetic resonance spectroscopy: stray-field magnets and center-field magnets.¹⁶³

Stray-field magnets are optimized for easy sample access. The sensed volume is outside the magnet assembly.¹⁶⁴ Stray-field magnets typically exhibit lower field homogeneity than center-field magnets, but can produce a magnetic field with a direction that is either parallel to the magnet surface or perpendicular to it. The first configuration can be used to create an active volume that is a thin slice; the latter can be used for bulk analysis of materials. A good example of the usage of a stray-field magnet in NMR spectroscopy is the single-sided magnetic resonance spectrometer, the NMR-Mouse.^165,166 Here, the intrinsic inhomogeneities (gradients) of the magnetic field profile are used to spatially encode the NMR signal.¹⁶⁶ Another example of a stray-field magnet for EPR measurements is an annular permanent magnet for X-Band EPR measurements using a near-field, non-resonant probe (Fig. 8).¹⁶⁷ Although stray-field magnets are often light and easy to construct, they present much larger safety concerns (exposed high field surface) compared to center-field magnets.

FIG. 8.

Overview of different types of permanent magnet shapes: (a) Annular stray-field permanent magnet used in EPR spectroscopy using a non-resonant, near-field probe. Figure reproduced with permission from Campbell et al., Anal. Chem. 87(9), 4910–4916 (2015). Copyright 2015 American Chemical Society. (b) C-shaped center field permanent magnet. Center field 342.1 mT, pole gap distance 3.5 cm, weight ≈15 kg. Figure reproduced with permission from Überrück et al., J. Magn. Reson. 314, 106724 (2020). Copyright 2020 Elsevier. (c) Dipole center-field permanent magnet used for ODNP measurements. Top: CAD model courtesy of Maly. Bottom: Magnet with resonator placed inside laboratory incubator for temperature control. Photo credit Maly.

Center-field magnets are typically optimized for magnetic field homogeneity. They are designed to create a sweet spot for the magnetization inside the magnet assembly. Compared to stray-field magnets, center-field magnets are typically slightly larger and bulkier. Two common center-field magnet designs are the open magnet and the Halbach magnet.

An example of an open magnet is shown in Fig. 8(b). The magnetic field is produced by an array of hexagonally shaped permanent magnets mounted to pole pieces that are in turn mounted to the C-shaped magnet yoke.¹⁶⁸ The yoke guides the return flux and contains the stray field; the maximum magnetic field strength is about 0.34 mT. In Fig. 8(c) (top), the computer-aided design (CAD) model of a dipole magnet is shown. The magnet uses a small array of SmCo permanent magnets to produce a center field of about 350 mT. The distance between the pole faces is 35 mm, and the three support columns double as the return flux guides. The 0.5 mT line is located at about 5 cm away from the magnet. The pole pieces of the dipole magnet have small indents, commonly referred to as a Rose Ring, to increase the magnetic field homogeneity.¹⁶⁹ To reduce the temperature-dependent field drift, the complete magnet assembly is housed in a small incubator to stabilize the temperature to <0.1 K [Fig. 8(c), bottom]. Both pole pieces have integrated sweep coils to vary the static magnetic field for EPR spectroscopy. The coils produce magnetic fields up to ±10 mT with a current of only a few amps.¹⁷⁰ The intrinsic magnetic field homogeneity is <3.5 µT (<10⁻⁵) for a 10 mm DSV. The homogeneity can be further improved by an order of magnitude through use of active shims. Although the magnet is located inside an incubator to minimize field drifts, high-resolution spectroscopy measurements with long acquisition times require more stringent field drift corrections, an example of which is the use of interleaved referencing to avoid additional hardware for a field/frequency-lock circuit.¹⁷⁰

The Halbach magnet is another commonly used center-field magnet for magnetic resonance spectroscopy.^155,156 Halbach magnets do not have yokes, which avoids inhomogeneities due to saturation effects, and allow these magnets to be assembled in linear, circular, or spherical arrangements (Fig. 9).^171,172 Although a Halbach magnet is typically slightly bulkier and heavier compared to a C-shaped magnet, it is advantageous because it can be designed with the B₀ field direction perpendicular to the magnet bore. Depending on the particular arrangement, a small Halbach array can have a native homogeneity of >800 · 10⁻⁶ (e.g., ΔB > 0.25 mT at 310 mT) without shimming (see Table 1 in Raich and Blümler¹⁵⁵). Figure 9 shows different circular arrangements for Halbach magnets. Some of these designs require either custom shapes or magnets with custom magnetization profiles; however, the NMR-Mandhala [Fig. 9(c)] can be fabricated from off-the-shelf, horizontally polarized bar/cube-shaped magnets. Halbach magnets and their derivatives offer the opportunity to shape the magnetic field. For spectroscopy applications, the magnetic field must be highly homogeneous. In contrast, imaging applications require a (well characterized) gradient for spatial encoding. The imaging magnet developed by Cooley et al. has an off-center static field gradient that is moved across the imaging space by rotating the array, thereby providing the required spatial resolution.^172,173

FIG. 9.

Different realizations of an annular Halbach magnet. (a) ideal magnet, (b) discretized version of (a) and (c) NMR-Mandhala with 16 elements, (d) octagonal magnet form trapezoidal pieces, and (e) wedge design. Figure reproduced with permission from H. Soltner and P. Blümler, Concepts Magn. Reson., Part A 36A, 211–222 (2010). Copyright 2010 John Wiley & Sons.

For CW EPR spectroscopy using a high-Q cavity (narrow bandwidth), the magnetic field must be swept through the resonance condition. This is more difficult to implement when using permanent magnets rather than electromagnets. To provide field sweep capability, an additional coil can be added to the permanent magnet.^174,175 Alternatively, the magnetic field of a Halbach magnet array can be mechanically swept by rotating the three nested rings of the magnet array with respect to each other. This approach has been demonstrated for a Halbach magnet with a center field of about 350 mT and a sweep range of 15 mT. The homogeneity of this system is sufficient to perform CW, electron-nuclear double resonance (ENDOR), electron spin echo envelope modulation (ESEEM), and Overhauser dynamic nuclear polarization (ODNP) experiments.^176–178

2. Shimming

The resolution of a magnetic resonance experiment is typically dominated by the homogeneity of the magnetic field: lower field homogeneity leads to lower spectral resolution. Depending on the type of magnet and the fabrication process, field gradients can be present, which spoil the homogeneity. One approach to increase spectral resolution is to compensate for the reduced homogeneity via shimming.

Shimming the magnetic field to increase the homogeneity is less common in EPR spectroscopy compared to NMR spectroscopy. However, depending on the quality of the individual permanent magnets, the homogeneity of a permanent magnet array may not be sufficient for high-resolution spectroscopy. For example, some organic radicals such as lithium phthalocyanine (LiPc) or lithium naphthalocyanine (LiNc) can have very narrow line widths of 1 µT (LiPc) or 5.1 µT (LiNc). At a static field of 350 mT, this corresponds to a linewidth of 3 and 145 ppm, respectively, and the quality of the magnetic field has to be sufficient.¹⁷⁹

In general, the field homogeneity can be increased by using active or passive shims. Passive shimming is achieved using small pieces of magnetic or high permeable materials to increase/decrease the magnetic field in certain areas. A common example of the use of passive shims is in MRI magnets.¹⁸⁰ In multi-shell Halbach magnets, passive shimming can be performed by removing magnet material from certain positions or rotating the individual permanent magnets of the array.^181,182 More recently, it has been demonstrated that 3D printing techniques can be used to produce optimized pole pieces printed from materials loaded with iron particles.¹⁸³ These pole pieces are then affixed to the permanent magnet yolks to achieve the desired field homogeneity.

Active shims, while very common in high-resolution NMR spectroscopy, are not common in EPR spectroscopy. Active shims consist of small coils placed around the sample to cancel out static magnetic field gradients. Typically, these coils produce specific components of a spherical harmonic^184,185 that destructively interfere with the existing field gradients. Matrix shims are another alternative. In this case, an array of individual identical coils surrounds the sample, each coil being driven by a separate power supply. The effect of each individual coil with respect to the overall magnetic field is mapped out and a computer algorithm optimizes the contribution of each coil.¹⁸⁶ An advantage of matrix shims is that all coils can be identical; a drawback is that the set of coils required to achieve sufficient homogeneity is often large, making this approach less desirable for compact spectrometer development.

Shimming to improve field homogeneity and thereby increase spectral resolution is an established method regardless of resonator type. Another approach is to reduce the sample size, which decreases the dimensions of the homogeneous applied field needed to excite the sample. This second approach is where microresonators are particularly beneficial.

IV. IMPLICATIONS OF MICRORESONATORS IN EPR SYSTEMS

In this Review, we present use cases, design and fabrication, and instrumentation considerations to highlight the impact and possible future of microresonators for EPR spectroscopy. By including suggestions from balancing design, modeling, and fabrication with costs and material availability to metamaterials that might be mined for future designs, we anticipate increased efforts in these areas. To speed broader implementation of microresonator technology for EPR spectroscopy, instrumentation considerations must be addressed to encourage investigators who are not in the position of building an entire spectrometer system to adopt these devices.

The field of metamaterials converges with microresonator design through the shared aim of producing electromagnetic responses at deep-subwavelength scales. Microwave metamaterials are actively researched and some of the first reported metamaterials were for microwave frequencies. However, adapting metamaterial design paradigms for magnetic resonance spectroscopies requires attention to the considerations delineated in Secs. I and II. We have pointed out design strategies from metamaterials research that may be applied to EPR microresonator design, e.g., the use of toroidal moment and bound states in the continuum to increase Q factors at room temperature. Interested researchers should consider the requirements of their application while choosing a design as a starting point for microresonator development. It is exactly this design flexibility and ability to tailor the “sensor” to the application that makes microresonators for EPR spectroscopy an attractive field of research.

Focusing on instrumentation, low-risk modifications to commercial spectrometers reap the benefits of a highly concentrated B₁ region through the simple replacement of a commercial resonator with a custom feedline/microresonator structure. A more adventurous minority of researchers⁷³ have realized additional improvements in measurement fidelity by extending the modifications to more purposeful microresonator integrations (i.e., modifications to the excitation/detection circuitry). These modifications, while more involved, allow for the acquisition of EPR information in reflection mode, transmission mode, or both modes. The inherent broadband nature of microresonators (Q < 100) also largely removes the requirement of an AFC system, leading to further simplification of EPR instruments. In recent years, sophisticated microwave devices, such as in-phase and quadrature (IQ) mixers, have become widely commercially available to replace the more common detection diode. In general, advances in the telecommunication sector (e.g., 5G, 6G mobile networks) will lead to greater availability of sophisticated microwave components and (dielectric) materials. Just as RADAR technology led to development of the first EPR instruments after World War II, we envision mobile communication technology leading to new compact microwave technology that will be mined for use in EPR instrumentation development.

Concurrently, instrumentation modifications will extend to the magnetic field sub-system. The drastic reduction in sample volume made possible by microresonators reduces the size of the homogeneous DSV region. This consequence requires smaller magnets and a commensurate reduction in the size of the sweep/modulation/shim coils. Using smaller coils reduces the inductive load and allows for higher modulation frequency that increases the overall spectrometer sensitivity. For rapid scan experiments, this means faster sweep rates/ranges, which also translates to increased sensitivity. All these gains come with the added benefit of more compact systems that can conceivably be used in diverse measurement environments, including in the field.

The logical extension of spectrometer miniaturization is the recent development of on-chip EPR spectrometers. These spectrometers utilize custom application-specific integrated circuits that shrink the entire microwave excitation and detection circuitry as well as the resonator to the size of a microchip.^187–192 Although the micro-coil resonators employed in these spectrometers do not necessarily qualify as microresonators, they are closely related and would likely benefit from the additional B₁ amplitude achievable using microresonators. As illustrated in the more recent on-chip EPR literature,^{188,193–195} there are also major benefits to creating EPR systems that sacrifice laboratory sensitivity levels for compact and deployable designs. Such EPR-based sensor systems will reproducibly and accurately detect concentrations of well-characterized paramagnetic species, allowing expansion to process monitoring (real-time) and portability (on-site).

As expected, most efforts to include microresonators or reoptimize EPR spectrometers for the inclusion of microresonators has occurred in academic research settings focused on providing advanced spectroscopy measurement capability. However, microresonators offer the possibility of creating new EPR instrumentation schemes, which can change the EPR measurement to better suit the sample of interest. This luxury is almost never afforded to EPR spectroscopists but will become more plausible through the adoption of microresonator-based EPR systems.

AUTHOR DECLARATIONS

Conflict of Interest

T. Maly is co-founder and currently Vice President of Magnetic Resonance at Bridge12 Technologies, Inc. A Cooperative Research and Development Agreement (CN-21-0122) is in place between NIST and Bridge12 Technologies for work unrelated to the topic of this Review.

Author Contributions

All authors contributed to writing, preparing figures, and editing the manuscript.

Amit Agrawal: Writing – original draft (equal); Writing – review & editing (supporting). Jason Campbell: Writing – original draft (equal); Writing – review & editing (supporting). Thorsten Maly: Writing – original draft (equal); Writing – review & editing (supporting). Veronika Szalai: Writing – original draft (lead); Writing – review & editing (equal).

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.