ABSTRACT
BACKGROUND:
Leg length discrepancy (LLD) may play a key role in exercise biomechanics. Although the Podoprint platform has been used in dynamic pressure studies, there are no data regarding the reliability and repeatability of dynamic measurements under simulated LLD conditions.
OBJECTIVES:
To determine the intra and intersession repeatability and reliability of dynamic parameters of the Podoprint pressure platform under simulated LLD conditions.
DESIGN AND SETTING:
Observational cross-sectional study at a public university.
METHODS:
Thirty-seven healthy volunteers participated in this study. LLD was simulated using ethyl vinyl acetate plantar lifts with heights of 5 mm, 10 mm, 15 mm and 20 mm located under the right shoe of each volunteer. The procedure was performed to capture the dynamic parameters of each participant under five different simulated LLD conditions. Stance time, mean pressure and peak pressure measurements were registered in three trials for each foot and each LLD level. Data were collected during two separate testing sessions, in order to establish intrasession and intersession reliability.
RESULTS:
The intraclass correlation coefficients (ICCs) for intrasession reliability ranged from 0.775 to 0.983 in the first session and from 0.860 to 0.985 in the second session. The ICCs for intersession reliability ranged from 0.909 to 0.990. Bland-Altman plots showed absence of systematic measurement errors.
CONCLUSIONS:
The results from this study indicate that the Podoprint platform is a reliable system for assessing dynamic parameters under simulated LLD conditions. Future studies should evaluate plantar pressures under LLD conditions, in association with exercise, biomechanics and musculoskeletal disorders.
KEYWORDS (MeSH terms): Leg length inequality, Gait, Equipment failure analysis
AUTHORS’ KEYWORDS: Pressure platform, Lower limbs, Reliability analysis
INTRODUCTION
Leg length discrepancy (LLD) is a situation in which the lower limbs have different lengths.1 LLD has been discussed in the clinical and research communities for decades. However, there is no consensus regarding many aspects of LLD, including its prevalence, the scope of its clinical significance, assessment of measurement methods and its impact on several neuromusculoskeletal alterations.2 LLD is estimated to affect 40-70% of the population and approximately 0.1% present inequality greater than 2 cm.1 Knutson conducted a meta-analysis on 573 subjects and concluded that only 10% of the population had equal lower-limb lengths.3
LLD can be classified as anatomical when the difference in length between the limbs can be measured directly in the tibias, femurs, or both; or it can be classified as functional when the discrepancy is caused by postural inaccuracies.4 LLD has been correlated with several pathological conditions, such as hip or knee osteoarthritis, due to inappropriate distribution of mechanical loads.5,6 Asymmetry in the kinetics of LLD-induced gait has also been linked to the etiology of plantar fasciitis,7 lower back pain8 and knee pain.9 Concretely, LLD may play a key role in skeletal malalignment disorders such as patellofemoral conditions.10 Asymmetries in the kinematics of human gait have been correlated with different degrees of anatomical LLD,5 such as pelvic drop and hip adduction in the stance phase.11,12 Additional studies have found flexion abnormalities in the sagittal plane of the hip, knee, ankle and first metatarsophalangeal joint.11,13,14,15 LLD also appears to be related to decreased load times in the shorter limb, reduced gait velocity, decreased stride length on the shorter leg and increased cadence.16 In addition, several studies have found that LLD produces asymmetrical pressure patterns.17,18
As described in the literature, there are two methods for studying LLD: evaluation of real LLD cases or simulation of LLD in healthy subjects, to assess the role of LLD regarding gait alterations. The first method has limitations because subjects with LLD commonly develop physical anomalies as a result of compensations and therefore cannot be considered to be pure LLD subjects. Moreover, LLD may frequently be associated with several disease processes that can also alter gait.2 To address these limitations, Betsch et al. designed a noninvasive method for simulating and studying LLD and its consequences on the musculoskeletal apparatus, using plantar lifts.19,20
Pedobarography is the study of foot-ground pressures. It has been used to study foot interactions with the ground and with posture,21 and to screen for plantar footprint alterations in healthy subjects that could lead to pathological conditions.22 Foot pressure measurement devices, essentially consisting of platforms and instrumented insoles, are used to quantify the static and dynamic parameters between the foot and floor; foot and shoe; and shoe and floor.23,24 These devices are generally intended for both clinical and research use.
Consequently, assessments on the reliability, validity and effectiveness of pressure systems are extremely relevant.22,25 A variety of plantar pressure devices are available, but one of the most commonly used devices in clinical podiatry is the Podoprint platform (Namrol Group, Barcelona, Spain). While this platform has been used in dynamic pressure and postural analysis studies,24,26,27 there are no data regarding the reliability and repeatability of dynamic measurements made using the platform. As previously mentioned, although a few studies have reported that LLD causes alterations to gait time and pressure patterns, the reliability and validity of the platform measurements have not, to the best of our knowledge, been addressed.28,29
OBJECTIVE
Our aim was to assess the reliability and repeatability of the Podoprint platform for measuring dynamic plantar parameters obtained from healthy subjects under simulated LLD conditions. We hypothesized that the pressure platform could be accurately used to assess gait dynamic parameters, in order to study simulated LLD effects.
METHODS
Design and sample
Thirty-seven healthy volunteers (24 women and 13 men) aged 19 to 76 years participated in this study (Table 1). We used an observational cross-sectional research design in accordance with the criteria of Strengthening the Reporting of Observational Studies in Epidemiology (STROBE)30 and a nonrandom consecutive sampling technique. The inclusion criteria were that the subjects needed to be over 18 years of age; have a normal gait pattern;31 and have normal leg and foot joint ranges. Subjects were excluded if they reported having pain, anatomical or functional LLD,32 previous lower limb surgery, congenital or acquired deformities of the lower extremities upon clinical examination, or any other condition that might affect their gait.
Table 1. Descriptive data on the study participants showing demographics and anthropometric characteristics for the total sample and according to sex.
| Variable | Male n = 13 | Female n = 24 | Total (n = 37) |
|---|---|---|---|
| mean ± SD (95% CI) | mean ± SD (95% CI) | mean ± SD (95% CI) | |
| Age (years) | 48.08 ± 17.38 (37.57-58.58) | 42.17 ± 14.76 (35.93-48.40) | 44.24 ± 15.75 (38.99-49.50) |
| Weight (kg) | 73.38 ± 8.31 (68.36-78.40) | 64.50 ± 12.95 (59.02-69.97) | 67.62 ± 12.19 (63.55-71.68) |
| Height (cm) | 174.46 ± 9.27 (168.85-180.06) | 163.62 ± 8.54 (160.01-167.23) | 167.43 ± 10.14 (164.05-170.81) |
| BMI (kg/m2) | 24.18 ± 2.82 (22.47-25.89) | 24.74 ± 5.32 (22.49-26.99) | 24.54 ± 4.56 (23.02-26.07) |
| Foot size (EC) | 42.23 ± 2.37 (40.79-43.66) | 38 ± 1.37 (37.41-38.58) | 39.48 ± 2.69 (38.58-40.38) |
BMI = body mass index; SD = standard deviation; 95% CI = 95 percent confidence interval; EC = Europe countries.
The sample size was calculated using the GRANMO software, version 7.12, which was previously developed through a research program on inflammatory and cardiovascular disorders, at IMIM-Hospital del Mar, Barcelona, Spain.33 A study on the correlation between the dynamic parameters of gait and different degrees of simulated LLD was used as a reference.28 With a standard deviation (SD) of 4.34-3.48, 80% statistical power (β = 20%), a 95% confidence interval (α = 0.05) and two-tailed tests, it was calculated that 37 participants were required to detect a difference greater than or equal to 0.4 units. A SD of 0.86 and a loss to follow-up rate of 0% was assumed.
Dynamic data collection
LLD was simulated using ethyl vinyl acetate plantar lifts of 70A Shore hardness and heights of 5 mm, 10 mm, 15 mm or 20 mm, which were attached with adhesive double-sided tape to the bottom of the volunteer´s own right shoe. This method mimics LLD by producing pelvic obliquity. In order to record the dynamic parameters, a Podoprint platform was integrated into the center of a flat 4.8 m walkway at ground level. The platform measured 610 mm x 580 mm with a thickness of 10 mm and a weight of 6.6 kg. It was composed of a self-calibrating system with 1600 10 mm x 10 mm resistive sensors.
Each subject was instructed to walk naturally while looking forward. The starting position was determined so that the footstep would coincide on the platform. Participants walked at a self-selected speed for all trials; however, speeds were within the limits considered to be normal cadence under laboratory conditions, which range from 81-138 steps per minute.34
The procedure was performed with the aim of capturing the dynamic parameters of each participant under five simulated LLD conditions with increasing amounts of plantar lift (0 mm, 5 mm, 10 mm, 15 mm and 20 mm). Stance time (ms), mean pressure (g/cm2), and peak pressure (g/cm2) measurements were recorded. These parameters were regarded as the ones most frequently used in functional foot appraisals under pathological conditions.25
Two testing sessions were conducted on seven separated days. Three trials for each foot and LLD level were collected per session. Before recording the dynamic data, all subjects completed three minutes of walking on the walkway to familiarize themselves with the platform and the plantar lifts. Four steps of each foot were registered per trial using the “multiple dynamic” mode of the platform, which automatically provides averaged parameters. The sampling rate was 100 Hz. The same researcher measured all subjects.
The data obtained from the platform were processed and stored using the manufacturer-specific software Podoprint for Windows, version 8.6.5 (Namrol Group, Barcelona, Spain), on a computer.
Statistical analysis
All data were checked for normal distribution by means of the one-sample Kolmogorov-Smirnov test. Normally distributed data were presented as the mean and standard deviation.
Intrasession reliability was measured from three repeated trials for each simulated LLD condition and for each foot during the first and second testing sessions. The intraclass correlation coefficient (ICC) obtained using the (2,1) model (two-way random, single-measurement, absolute agreement ICC model) was calculated first, in order to analyze the reliability between trials.35 The coefficient of variation (CoV)36 was used to refer to the relationship between the size of the mean and the variability of each of the variables studied. The standard error of measurement (SEM) was expressed as a percentage of the mean (SEM%).37
In addition, the minimum detectable change (MDC) was calculated. This was defined as the magnitude of the value variation of each scale, below which change can be interpreted as inherent to the variability of the measurement method, without any real change to the clinical situation of the subject. MDC was calculated as a standardized mean (95% MDC).38,39
Intersession reliability was ascertained by retesting all subjects seven days after the first session. The average of the measurements for each session, for each subject and LLD condition, was used to calculate the ICC (2,1). For absolute comparison of the results obtained in the two sessions, CoV, SEM and MDC were expressed as percentages of the mean. The repeatability coefficient (RC) was also calculated as a percentage of the average values from the two measurement sessions, while the limits of agreement (LoA)37 were calculated to define the amount of variation that might be influencing the measurements. In addition, we used Bland-Altman plots to evaluate systematic measurement errors.
Paired Student’s t tests were used to determine systematic differences between the first and second sessions. From this, P-values were obtained, such that if P < 0.05, then there was a difference between the two variables. The IBM SPSS for Windows statistical package, version 22.0, was used for data analysis (SPSS, Inc., Chicago, Illinois, United States).
Ethical considerations
The Research Ethics Committee of Universidad Rey Juan Carlos, Spain, issued the authorization certificate number 0904201907519, approved on May 22, 2019, for this study, which followed the ethical principles of the Helsinki declaration.40 All subjects signed an informed consent statement before participating in this study.
RESULTS
Intrasession reliability
Normative data (represented by mean ± SD) and reliability data (represented by ICC, CoV, SEM% and MDC%) for the first session are presented in Table 2. The ICC for intrasession reliability ranged from 0.775 to 0.983 and the SEM ranged from 0.059% to 1.095%. The CoV ranged from 0.322% to 2.474% and the MDC ranged from 0.051% to 3.037%.
Table 2. Repeatability of dynamic variables for each foot under simulated LLD conditions. First session.
| Variable | Mean ± SD | CoV (%) | ICC (2.1) (95% CI) | SEM% | 95% MDC% |
|---|---|---|---|---|---|
| 0 mm of LLD | |||||
| Stance time left (ms) | 780.360 ± 7.131 | 0.913 | 0.898 (0.825-0.944) | 0.291 | 0.808 |
| Stance time right (ms) | 772.613 ± 6.698 | 0.866 | 0.917 (0.857-0.954) | 0.249 | 0.692 |
| Mean pressure left (g/cm2) | 763.027 ±11.271 | 1.447 | 0.915 (0.854-0.953) | 0.43 | 0.156 |
| Mean pressure right (g/cm2) | 769.324 ± 7.263 | 0.944 | 0.892 (0.813-0.941) | 0.31 | 0.111 |
| Peak pressure left (g/cm2) | 1449.297 ± 13.402 | 0.924 | 0.914 (0.852-0.953) | 0.271 | 0.051 |
| Peak pressure right (g/cm2) | 1445.532 ± 17.208 | 1.19 | 0.931 (0.881-0.962) | 0.312 | 0.866 |
| 5 mm of LLD | |||||
| Stance time left (ms) | 778.396 ±13.756 | 1.767 | 0.873 (0.783-0.930) | 0.628 | 1.743 |
| Stance time right (ms) | 770.351 ± 14.163 | 1.839 | 0.775 (0.613-0.876) | 0.872 | 2.417 |
| Mean pressure left (g/cm2) | 776.240 ± 7.500 | 0.966 | 0.940 (0.896-0.967) | 0.237 | 0.656 |
| Mean pressure right (g/cm2) | 761.991 ± 10.201 | 1.339 | 0.912 (0.849-0.952) | 0.397 | 1.101 |
| Peak pressure left (g/cm2) | 1495.225 ± 12.651 | 0.846 | 0.906 (0.837-0.948) | 0.259 | 0.719 |
| Peak pressure right (g/cm2) | 1365.090 ± 16.766 | 1.228 | 0.928 (0.877-0.961) | 0.33 | 0.913 |
| 10 mm of LLD | |||||
| Stance time left (ms) | 787.207 ± 6.588 | 0.837 | 0.973 (0.954-0.985) | 0.138 | 0.381 |
| Stance time right (ms) | 793.063 ± 5.697 | 0.718 | 0.976 (0.959-0.987) | 0.111 | 0.308 |
| Mean pressure left (g/cm2) | 780.432 ± 5.791 | 0.742 | 0.965 (0.940-0.981) | 0.139 | 0.385 |
| Mean pressure right (g/cm2) | 741.081 ± 12.886 | 1.739 | 0.919 (0.861-0.956) | 0.495 | 1.372 |
| Peak pressure left (g/cm2) | 1456.297 ± 9.645 | 0.662 | 0.909 (0.843-0.950) | 0.2 | 0.554 |
| Peak pressure right (g/cm2) | 1274.694 ± 26.494 | 2.078 | 0.869 (0.774-0.928) | 0.752 | 2.085 |
| 15 mm of LLD | |||||
| Stance time left (ms) | 786.486 ± 7.819 | 0.994 | 0.983 (0.970-0.991) | 0.13 | 0.359 |
| Stance time right (ms) | 798.378 ±7.206 | 0.903 | 0.980 (0.965-0.989) | 0.128 | 0.354 |
| Mean pressure left (g/cm2) | 779.225 ± 2.512 | 0.322 | 0.966 (0.942-0.982) | 0.059 | 0.165 |
| Mean pressure right (g/cm2) | 721.721 ± 5.353 | 0.742 | 0.922 (0.866-0.957) | 0.207 | 0.574 |
| Peak pressure left (g/cm2) | 1451.928 ± 7.477 | 0.515 | 0.889 (0.807-0.939) | 0.172 | 0.476 |
| Peak pressure right (g/cm2) | 1247.279 ± 22.891 | 1.835 | 0.778 (0.617-0.878) | 0.865 | 2.397 |
| 20 mm of LLD | |||||
| Stance time left (ms) | 788.288 ± 3.357 | 0.426 | 0.975 (0.956-0.986) | 0.067 | 0.187 |
| Stance time right (ms) | 807.928 ± 4.092 | 0.506 | 0.976 (0.959-0.987) | 0.078 | 0.217 |
| Mean pressure left (g/cm2) | 782.468 ± 3.751 | 0.479 | 0.964 (0.938-0.980) | 0.091 | 0.252 |
| Mean pressure right (g/cm2) | 723.595 ± 2.566 | 0.355 | 0.894 (0.817-0.942) | 0.115 | 0.32 |
| Peak pressure left (g/cm2) | 1446.685 ± 23.562 | 1.629 | 0.917 (0.857-0.954) | 0.469 | 1.301 |
| Peak pressure right (g/cm2) | 1232.351 ± 30.494 | 2.474 | 0.804 (0.663-0.892) | 1.095 | 3.037 |
SD = standard deviation; CoV = coefficient of variation; ICC = intraclass correlation coefficient; 95% CI = 95 percent confidence interval; SEM% = standard error of measurement percentage; MDC% = minimum detectable change percentage; LLD = leg length discrepancy.
Normative data and reliability data for the second session are shown in Table 3. The ICC for intrasession reliability ranged from 0.860 to 0.985 and the SEM ranged from 0.014% to 0.635%. The CoV ranged from 0.077% to 1.848% and the MDC ranged from 0.038% to 1.759%.
Table 3. Repeatability of dynamic variables for each foot under simulated LLD conditions. Second session.
| Variables | Mean ± SD | CoV (%) | ICC (2.1) (95% CI) | SEM% | MDC% |
|---|---|---|---|---|---|
| 0 mm of LLD | |||||
| Stance time left (ms) | 775.099 ± 0.595 | 0.077 | 0.968 (0.945-0.983) | 0.014 | 0.038 |
| Stance time right (ms) | 771.712 ± 5.022 | 0.651 | 0.974 (0.955-0.986) | 0.105 | 0.291 |
| Mean pressure left (g/cm2) | 776.775 ± 6.734 | 0.867 | 0.958 (0.929-0.977) | 0.178 | 0.492 |
| Mean pressure right (g/cm2) | 786.541 ± 7.346 | 0.934 | 0.923 (0.867-0.958) | 0.259 | 0.718 |
| Peak pressure left (g/cm2) | 1473.108 ± 9.370 | 0.636 | 0.923 (0.868-0.958) | 0.177 | 0.489 |
| Peak pressure right (g/cm2) | 1476.541 ± 14.250 | 0.965 | 0.958 (0.927-0.977) | 0.198 | 0.548 |
| 5 mm of LLD | |||||
| Stance time left (ms) | 781.739 ± 11.497 | 1.471 | 0.860 (0.758-0.923) | 0.55 | 1.525 |
| Stance time right (ms) | 781.532 ± 5.250 | 0.672 | 0.982 (0.968-0.990) | 0.09 | 0.25 |
| Mean pressure left (g/cm2) | 772.883 ± 3.435 | 0.444 | 0.957 (0.925-0.976) | 0.092 | 0.255 |
| Mean pressure right (g/cm2) | 774.243 ± 11.728 | 1.515 | 0.922 (0.865-0.957) | 0.423 | 1.173 |
| Peak pressure left (g/cm2) | 1467.964 ± 14.614 | 0.996 | 0.927 (0.874-0.960) | 0.269 | 0.746 |
| Peak pressure right (g/cm2) | 1361.396 ± 10.761 | 0.79 | 0.948 (0.910-0.971) | 0.18 | 0.5 |
| 10 mm of LLD | |||||
| Stance time left (ms) | 789.550 ± 3.527 | 0.447 | 0.982 (0.969-0.990) | 0.06 | 0.166 |
| Stance time right (ms) | 785.045 ± 6.698 | 0.853 | 0.976 (0.958-0.987) | 0.132 | 0.366 |
| Mean pressure left (g/cm2) | 777.108 ± 2.357 | 0.303 | 0.966 (0.942-0.981) | 0.056 | 0.155 |
| Mean pressure right (g/cm2) | 733.541 ± 5.050 | 0.688 | 0.913 (0.851-0.952) | 0.203 | 0.563 |
| Peak pressure left (g/cm2) | 1468.613 ± 24.001 | 1.634 | 0.930 (0.880-0.962) | 0.432 | 1.199 |
| Peak pressure right (g/cm2) | 1277.036 ± 13.052 | 1.022 | 0.930 (0.879-0.961) | 0.27 | 0.75 |
| 15 mm of LLD | |||||
| Stance time left (ms) | 792.162 ± 2.742 | 0.346 | 0.985 (0.975-0.992) | 0.042 | 0.118 |
| Stance time right (ms) | 806.757 ± 3.375 | 0.418 | 0.981 (0.967-0.990) | 0.058 | 0.16 |
| Mean pressure left (g/cm2) | 785.369 ± 6.983 | 0.889 | 0.968 (0.944-0.982) | 0.159 | 0.441 |
| Mean pressure right (g/cm2) | 728.414 ± 8.107 | 1.113 | 0.944 (0.903-0.969) | 0.263 | 0.73 |
| Peak pressure left (g/cm2) | 1470.207 ± 10.147 | 0.69 | 0.945 (0.906-0.970) | 0.162 | 0.449 |
| Peak pressure right (g/cm2) | 1262.550 ± 12.141 | 0.962 | 0.899 (0.826-0.945) | 0.306 | 0.847 |
| 20 mm of LLD | |||||
| Stance time left (ms) | 793.784 ± 3.783 | 0.477 | 0.976 (0.959-0.987) | 0.074 | 0.205 |
| Stance time right (ms) | 807.658 ± 4.904 | 0.607 | 0.986 (0.975-0.992) | 0.072 | 0.199 |
| Mean pressure left (g/cm2) | 785.207 ± 4.703 | 0.599 | 0.964 (0.937-0.980) | 0.114 | 0.315 |
| Mean pressure right (g/cm2) | 724.856 ± 8.859 | 1.222 | 0.889 (0.810-0.939) | 0.407 | 1.129 |
| Peak pressure left (g/cm2) | 1457.306 ± 26.924 | 1.848 | 0.882 (0.798-0.935) | 0.635 | 1.759 |
| Peak pressure right (g/cm2) | 1247.450 ± 3.442 | 0.276 | 0.878 (0.790-0.933) | 0.096 | 0.265 |
SD = standard deviation; CoV = coefficient of variation; ICC = intraclass correlation coefficient; 95% CI = 95 percent confidence interval; SEM% = standard error of measurement percentage; MDC% = minimum detectable change percentage; LLD = leg length discrepancy.
Intersession reliability
The average for measurements from each test session and the ICC, CoV, SEM%, MDC%, RC% and Student’s t test for intersession reliability are presented in Table 4. The ICC for intersession reliability ranged from 0.909 to 0.990 and the SEM ranged from 0.05% to 0.49%. The CoV ranged from 0.5% to 1.70%, the MDC ranged from 0.14% to 1.36% and the RC ranged from 0.84% to 19.22%. All variables were compared using Student’s t test and had P-values > 0.05.
Table 4. Intersession reliability of dynamic variables for each foot under simulated LLD conditions.
| Variables | Mean ± SD | CoV (%) | ICC (2.1) (95% CI) | SEM% | MDC% | RC% | STS |
|---|---|---|---|---|---|---|---|
| 0 mm of LLD | |||||||
| Stance time left (ms) | 777.730 ± 5.365 | 0.69 | 0.960 (0.936-0.977) | 0.14 | 0.38 | 11.37 | 0.483 |
| Stance time right (ms) | 772.162 ± 5.318 | 0.69 | 0.969 (0.951-0.982) | 0.12 | 0.34 | 9.18 | 0.88 |
| Mean pressure left (g/cm2) | 769.901 ± 11.210 | 1.46 | 0.962 (0.940-0.978) | 0.28 | 0.79 | 13.17 | 0.115 |
| Mean pressure right (g/cm2) | 777.932 ± 11.472 | 1.47 | 0.946 (0.914-0.969) | 0.34 | 0.95 | 15.67 | 0.101 |
| Peak pressure left (g/cm2) | 1461.203 ± 16.645 | 1.14 | 0.954 (0.926-0.973) | 0.24 | 0.68 | 14.12 | 0.177 |
| Peak pressure right (g/cm2) | 1461.036 ± 22.094 | 1.51 | 0.956 (0.930-0.975) | 0.32 | 0.88 | 19.22 | 0.196 |
| 5 mm of LLD | |||||||
| Stance time left (ms) | 780.068 ± 11.486 | 1.47 | 0.923 (0.878-0.956) | 0.41 | 1.13 | 16.46 | 0.758 |
| Stance time right (ms) | 775.941 ± 11.347 | 1.46 | 0.936 (0.898-0.963) | 0.37 | 1.03 | 13.36 | 0.207 |
| Mean pressure left (g/cm2) | 774.577 ± 5.537 | 0.71 | 0.974 (0.959-0.985) | 0.12 | 0.32 | 9.00 | 0.566 |
| Mean pressure right (g/cm2) | 768.117 ± 11.903 | 1.55 | 0.953 (0.925-0.973) | 0.34 | 0.93 | 13.66 | 0.172 |
| Peak pressure left (g/cm2) | 1481.595 ± 19.287 | 1.30 | 0.955 (0.928-0.974) | 0.28 | 0.77 | 12.88 | 0.097 |
| Peak pressure right (g/cm2) | 1363.243 ± 12.762 | 0.94 | 0.967 (0.947-0.981) | 0.17 | 0.47 | 10.11 | 0.751 |
| 10 mm of LLD | |||||||
| Stance time left (ms) | 788.378 ± 4.897 | 0.62 | 0.990 (0.984-0.994) | 0.06 | 0.17 | 3.80 | 0.357 |
| Stance time right (ms) | 789.054 ± 7.086 | 0.90 | 0.986 (0.978-0.992) | 0.11 | 0.29 | 6.90 | 0.088 |
| Mean pressure left (g/cm2) | 778.770 ± 4.353 | 0.56 | 0.984 (0.974-0.991) | 0.07 | 0.20 | 0.84 | 0.427 |
| Mean pressure right (g/cm2) | 737.311 ± 9.678 | 1.31 | 0.961 (0.938-0.978) | 0.26 | 0.72 | 8.78 | 0.173 |
| Peak pressure left (g/cm2) | 1462.455 ± 17.696 | 1.21 | 0.957 (0.932-0.975) | 0.25 | 0.70 | 12.48 | 0.426 |
| Peak pressure right (g/cm2) | 1275.865 ± 18.723 | 1.47 | 0.943 (0.909-0.967) | 0.35 | 0.97 | 13.69 | 0.874 |
| 15 mm of LLD | |||||||
| Stance time left (ms) | 789.324 ± 6.093 | 0.77 | 0.990 (0.985-0.994) | 0.08 | 0.21 | 6.63 | 0.204 |
| Stance time right (ms) | 802.568 ± 6.811 | 0.85 | 0.987 (0.979-0.992) | 0.10 | 0.27 | 8.66 | 0.159 |
| Mean pressure left (g/cm2) | 782.297 ± 5.775 | 0.74 | 0.984 (0.974-0.991) | 0.09 | 0.26 | 6.91 | 0.184 |
| Mean pressure right (g/cm2) | 725.068 ± 7.155 | 0.99 | 0.964 (0.943-0.980) | 0.19 | 0.52 | 11.48 | 0.344 |
| Peak pressure left (g/cm2) | 1461.068 ± 12.798 | 0.88 | 0.957 (0.932-0.976) | 0.18 | 0.50 | 12.42 | 0.238 |
| Peak pressure right (g/cm2) | 1225.914 ± 18.399 | 1.50 | 0.909 (0.855-0.948) | 0.45 | 1.25 | 16.40 | 0.382 |
| 20 mm of LLD | |||||||
| Stance time left (ms) | 791.036 ± 4.392 | 0.56 | 0.986 (0.978-0.992) | 0.07 | 0.18 | 6.84 | 0.234 |
| Stance time right (ms) | 807.793 ± 4.042 | 0.50 | 0.990 (0.984-0.994) | 0.05 | 0.14 | 5.86 | 0.946 |
| Mean pressure left (g/cm2) | 783.838 ± 4.090 | 0.52 | 0.980 (0.969-0.989) | 0.07 | 0.20 | 8.96 | 0.645 |
| Mean pressure right (g/cm2) | 724.225 ± 5.874 | 0.81 | 0.948 (0.917-0.970) | 0.18 | 0.51 | 10.24 | 0.84 |
| Peak pressure left (g/cm2) | 1451.995 ± 23.364 | 1.61 | 0.951 (0.922-0.972) | 0.36 | 0.99 | 12.00 | 0.472 |
| Peak pressure right (g/cm2) | 1239.901 ± 21.097 | 1.70 | 0.917 (0.868-0.952) | 0.49 | 1.36 | 12.67 | 0.259 |
SD = standard deviation; CoV = coefficient of variation; ICC = intraclass correlation coefficient; 95% CI = 95 percent confidence interval; SEM% = standard error of measurement percentage; MDC% = minimum detectable change percentage; RC% = repeatability coefficient percentage; STS = Student’s t test significance; LLD = leg length discrepancy.
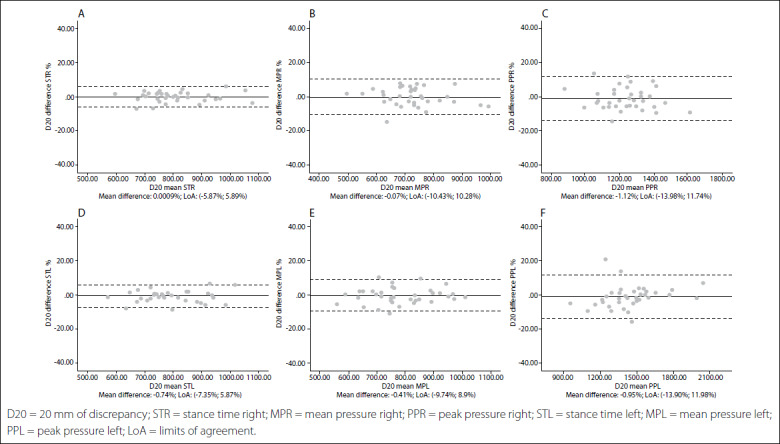
Intersession limits of agreement and Bland-Altman plots are shown in Figures 1,2,3,4,5. The mean differences between sessions for the variables studied ranged from -2.15% to 1.69%.
Figure 1. Bland-Altman plots for dynamic variables for each foot without leg length discrepancy (LLD). Differences between sessions plotted against the mean. Stance time right (A); Mean pressure right (B); Peak pressure right (C); Stance time left (D); Mean pressure left (E); Peak pressure left (F). Abbreviations: D00, 0 mm of discrepancy; STR, stance time right; MPR, mean pressure right; PPR, peak pressure right; STL, stance time left; MTL, mean pressure left; PPL, peak pressure left; LoA, limits of agreement.
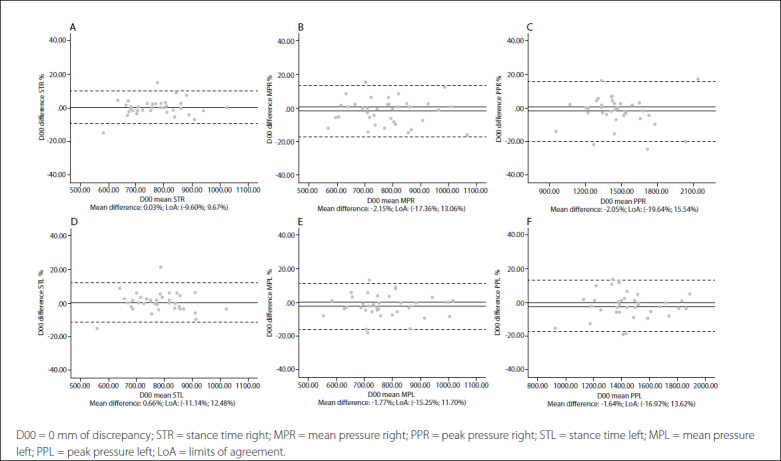
Figure 2. Bland-Altman plots for dynamic variables for each foot with 5 mm of leg length discrepancy (LLD). Differences between sessions plotted against the mean. Stance time right (A); Mean pressure right (B); Peak pressure right (C); Stance time left (D); Mean pressure left (E); Peak pressure left (F).
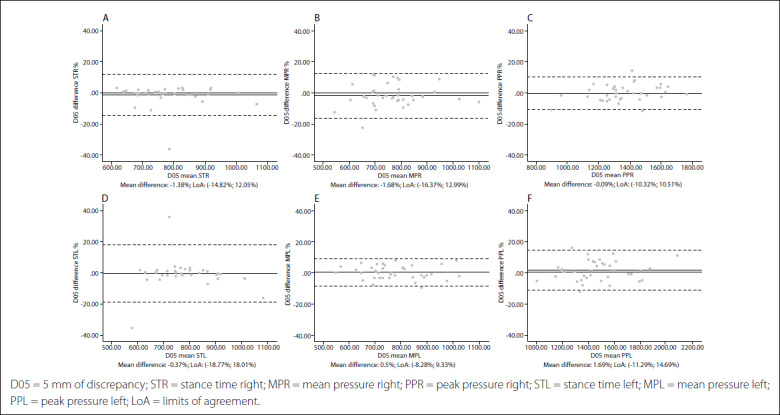
Figure 3. Bland-Altman plots for dynamic variables for each foot with 10 mm of leg length discrepancy (LLD). Differences between sessions plotted against the mean. Stance time right (A); Mean pressure right (B); Peak pressure right (C); Stance time left (D); Mean pressure left (E); Peak pressure left (F).
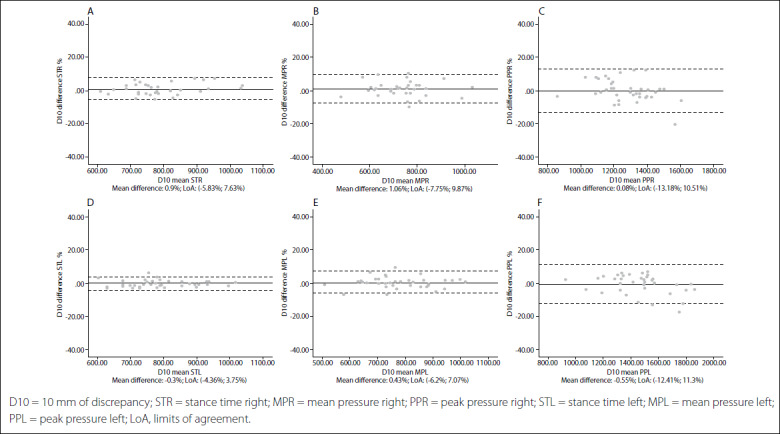
Figure 4. Bland-Altman plots for dynamic variables for each foot with 15 mm of leg length discrepancy (LLD). Differences between sessions plotted against the mean. Stance time right (A); Mean pressure right (B); Peak pressure right (C); Stance time left (D); Mean pressure left (E); Peak pressure left (F).
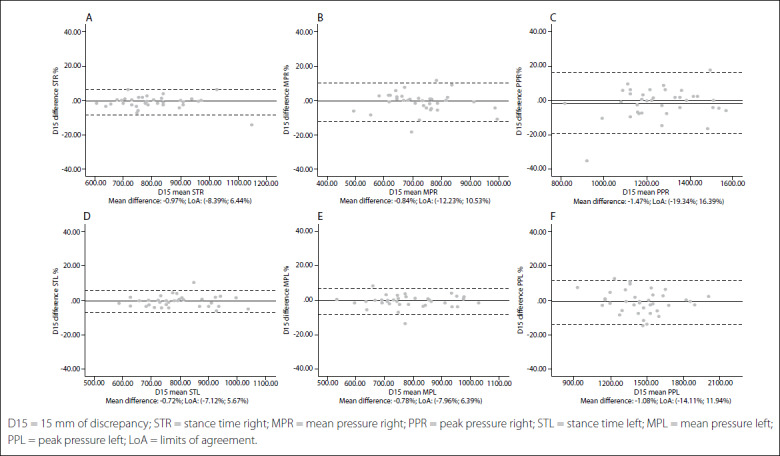
Figure 5. Bland-Altman plots for dynamic variables for each foot with 20 mm of leg length discrepancy (LLD). Differences between sessions plotted against the mean. Stance time right (A); Mean pressure right (B); Peak pressure right (C); Stance time left (D); Mean pressure left (E); Peak pressure left (F).
DISCUSSION
Plantar pressure platforms are clinical devices that are used to assess foot interactions with the ground,21 and to screen gait patterns that could lead to pathological conditions.22 The Podoprint platform system is commonly used by clinicians and researchers as a tool to develop their work. One of the applications of this technology could be to study LLD and its consequences on the patient’s health.28 Hence, the aim of this study was to determine the intra and intersession repeatability and reliability of dynamic parameters of this pressure platform among subjects with simulated leg length discrepancy.
The ICC is an extensively used descriptive statistic for quantifying the repeatability of a measurement. Using the classification proposed by Landis and Koch, ICC values between 0.40 and 0.60 have moderate reliability, whereas scores in the highest category, ranging from 0.80 to 1.00, are considered nearly perfect.35 Other authors have indicated that an ICC value of at least 0.7536 needs to be available to obtain reliability. According to Portney and Watkins’ recommendations, clinical measurements with an ICC greater than 0.90 improve the probability of valid measurements.37 In our study, the results showed consistent intra and intersession reliability and repeatability of the Podoprint platform under all LLD conditions. Intrasession variability was very low. All ICCs were higher than 0.775 and most were higher than 0.9.
SEM is considered to represent the amount of measurement error of a test and MDC shows the value for the smallest change needed in order to recognize that the observed change is real and not a result from instrument measurement error.41,42 In this study, the SEMs were in most of the cases lower than 1% and the MDC ranged from 0.038% and 3.037%. Low MDC values strengthened the ICCs. These results indicated that the reliability measurements were higher than those in other similar studies.22,43 One explanation for this may be that the measurements were obtained using the multiple dynamic mode of the platform. In this mode, the platform software automatically provides the average results from four measurements for each foot.
According to Becerro de Bengoa et al., the expected physiological changes in muscle activity, posture and gait velocity can affect variables during the measurements. Therefore, using a single trial to obtain foot dynamic parameters from a sample is not sufficient. By averaging multiple trials, the variability of gait patterns is decreased.22 Other authors have suggested that three trials are sufficient to obtain a consistent outcome.44 In our three-trial protocol, each trial needed four measurements from each foot. In fact, this is equivalent to 12 trials per session.
Gurney et al. conducted a study on the between-day reliability of repeated plantar pressure distribution measurements in a healthy population by analyzing 10-foot areas. Their intersession ICCs for total area averages were higher than 0.8 and the highest CoV was 13%.44 Izquierdo-Renau et al. also found ICC values greater than 0.89.44 In the present study, intersession repeatability was extremely high. All ICCs were greater than 0.9 for all measured dynamic variables and the highest CoV was 1.7%, which was concordant with the outcomes from previous studies.22,25,43 We did not find any significant differences between the first and second sessions when comparing means, with P-values > 0.05. All of the variables evaluated were highly homogeneous across all LLD conditions and for both feet.
In addition, the limits of agreement and Bland-Altman plots were also calculated and showed differences between sessions plotted against the mean.38 This complementary analysis revealed that the distribution of such graphs did not show any systematic measurement errors or heteroscedasticity. All of the values for the variables were similar, independent of the LLD condition, and also presented very high repeatability and reliability in all cases.
One limitation of the present study was that pressures were evaluated for total foot plantar surface. Previous investigations have found greater intrasession variability when using a regional analysis.25,45 Furthermore, the lifts were used in non-randomized order and, thus, the potential learning effects may have influenced the outcomes. Future studies should consider the relationship between several dynamic parameters measured on pressure platforms, such as total stance time, mean pressure, peak pressure and degree of simulated LLD. In addition, patients who have skeletal malalignment disorders such as patellofemoral or hip disorders should be dynamically evaluated using this plantar pressures device under conditions of leg length discrepancy.10
CONCLUSIONS
The results from this study indicate that the Podoprint platform is a reliable system for assessing dynamic parameters for both normal and simulated LLD subjects, due to its high reliability, independent of the LLD condition. This testing device can be confidently used by researchers and clinicians to assess dynamic parameters during research or clinical screenings. Given the reliability results from this study, future studies should evaluate plantar pressures under conditions of length leg discrepancy that are associated with skeletal malalignment disorders such as patellofemoral disorders.
Footnotes
School of Nursing, Physiotherapy and Podiatry, Universidad Complutense de Madrid, Madrid, Spain
Sources of funding: None
REFERENCES
- 1.Gurney B. Leg length discrepancy. Gait Posture. 2002;15(2):195–206. doi: 10.1016/s0966-6362(01)00148-5. [DOI] [PubMed] [Google Scholar]
- 2.Khamis S, Carmeli E. Relationship and significance of gait deviations associated with limb length discrepancy: A systematic review. Gait Posture. 2017;57:115–23. doi: 10.1016/j.gaitpost.2017.05.028. [DOI] [PubMed] [Google Scholar]
- 3.Knutson GA. Anatomic and functional leg-length inequality: a review and recommendation for clinical decision-making. Part II. The functional or unloaded leg-length asymmetry. Chiropr Osteopat. 2005;13:12. doi: 10.1186/1746-1340-13-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Langer S. Structural leg shortage. A case report. J Am Podiatry Assoc. 1976;66(1):38–40. doi: 10.7547/87507315-66-1-38. [DOI] [PubMed] [Google Scholar]
- 5.McCaw ST, Bates BT. Biomechanical implications of mild leg length inequality. Br J Sports Med. 1991;25(1):10–3. doi: 10.1136/bjsm.25.1.10. Erratum in: Br J Sports Med 1991;25(4):190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McWilliams AB, Grainger AJ, O’Connor PJ, et al. A review of symptomatic leg length inequality following total hip arthroplasty. Hip Int. 2013;23(1):6–14. doi: 10.5301/HIP.2013.10631. [DOI] [PubMed] [Google Scholar]
- 7.Mahmood S, Huffman LK, Harris JG. Limb-length discrepancy as a cause of plantar fasciitis. J Am Podiatr Med Assoc. 2010;100(6):452–5. doi: 10.7547/1000452. [DOI] [PubMed] [Google Scholar]
- 8.Kendall JC, Bird AR, Azari MF. Foot posture, leg length discrepancy and low back pain--their relationship and clinical management using foot orthoses--an overview. Foot (Edinb) 2014;24(2):75–80. doi: 10.1016/j.foot.2014.03.004. [DOI] [PubMed] [Google Scholar]
- 9.Carlson M, Wilkerson J. Are differences in leg length predictive of lateral patello-femoral pain? Physiother Res Int. 2007;12(1):29–38. doi: 10.1002/pri.351. [DOI] [PubMed] [Google Scholar]
- 10.Akşahin E, Güzel A, Erdoğan AO, et al. The patellofemoral kinematics in patients with untreated developmental dislocation of the hip suffering from patellofemoral pain. Knee Surg Sports Traumatol Arthrosc. 2012;20(11):2337–47. doi: 10.1007/s00167-011-1807-3. [DOI] [PubMed] [Google Scholar]
- 11.Aiona M, Do KP, Emara K, Dorociak R, Pierce R. Gait patterns in children with limb length discrepancy. J Pediatr Orthop. 2015;35(3):280–4. doi: 10.1097/BPO.0000000000000262. [DOI] [PubMed] [Google Scholar]
- 12.Li J, McWilliams AB, Jin Z, et al. Unilateral total hip replacement patients with symptomatic leg length inequality have abnormal hip biomechanics during walking. Clin Biomech (Bristol, Avon) 2015;30(5):513–9. doi: 10.1016/j.clinbiomech.2015.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Resende RA, Kirkwood RN, Deluzio KJ, Morton AM, Fonseca ST. Mild leg length discrepancy affects lower limbs, pelvis and trunk biomechanics of individuals with knee osteoarthritis during gait. Clin Biomech (Bristol, Avon) 2016;38:1–7. doi: 10.1016/j.clinbiomech.2016.08.001. [DOI] [PubMed] [Google Scholar]
- 14.Simón-Pérez E, Simón-Pérez C, Alonso-Peña D, et al. Stiffness degree of ankle range of motion in diabetic patients with atypical amputation. Rev Assoc Med Bras (1992) 2020;66(2):216–21. doi: 10.1590/1806-9282.66.2.216. [DOI] [PubMed] [Google Scholar]
- 15.Sánchez-Gómez R, Becerro-de-Bengoa-Vallejo R, Losa-Iglesias ME, Calvo-Lobo C, Navarro-Flores E, Palomo-López P, Romero-Morales C, López-López D. Reliability Study of Diagnostic Tests for Functional Hallux Limitus. Foot Ankle Int. 2020;41(4):457–62. doi: 10.1177/1071100719901116. [DOI] [PubMed] [Google Scholar]
- 16.Bhave A, Paley D, Herzenberg JE. Improvement in gait parameters after lengthening for the treatment of limb-length discrepancy. J Bone Joint Surg Am. 1999;81(4):529–34. doi: 10.2106/00004623-199904000-00010. [DOI] [PubMed] [Google Scholar]
- 17.Perttunen JR, Anttila E, Södergård J, Merikanto J, Komi PV. Gait asymmetry in patients with limb length discrepancy. Scand J Med Sci Sports. 2004;14(1):49–56. doi: 10.1111/j.1600-0838.2003.00307.x. [DOI] [PubMed] [Google Scholar]
- 18.Kaufman KR, Miller LS, Sutherland DH. Gait asymmetry in patients with limb-length inequality. J Pediatr Orthop. 1996;16(2):144–50. doi: 10.1097/00004694-199603000-00002. [DOI] [PubMed] [Google Scholar]
- 19.Betsch M, Wild M, Große B, Rapp W, Horstmann T. The effect of simulating leg length inequality on spinal posture and pelvic position: a dynamic rasterstereographic analysis. Eur Spine J. 2012;21(4):691–7. doi: 10.1007/s00586-011-1912-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Betsch M, Rapp W, Przibylla A, et al. Determination of the amount of leg length inequality that alters spinal posture in healthy subjects using rasterstereography. Eur Spine J. 2013;22(6):1354–61. doi: 10.1007/s00586-013-2720-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gross KD, Felson DT, Niu J, et al. Association of flat feet with knee pain and cartilage damage in older adults. Arthritis Care Res (Hoboken) 2011;63(7):937–44. doi: 10.1002/acr.20431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Becerro de Bengoa Vallejo R, Losa Iglesias ME, Zeni J, Thomas S. Reliability and repeatability of the portable EPS-platform digital pressure-plate system. J Am Podiatr Med Assoc. 2013;103(3):197–203. doi: 10.7547/1030197. [DOI] [PubMed] [Google Scholar]
- 23.Pérez-Soriano P, Llana-Belloch S, Martínez-Nova A, Morey-Klapsing G, Encarnación-Martínez A. Nordic walking practice might improve plantar pressure distribution. Res Q Exerc Sport. 2011;82(4):593–9. doi: 10.1080/02701367.2011.10599795. [DOI] [PubMed] [Google Scholar]
- 24.Sánchez-Sáez JM, Palomo-López P, Becerro-de-Bengoa-Vallejo R, et al. Stability of Three Different Sanitary Shoes on Healthcare Workers: A Cross-Sectional Study. Int J Environ Res Public Health. 2019;16(12):2126. doi: 10.3390/ijerph16122126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gurney JK, Kersting UG, Rosenbaum D. Between-day reliability of repeated plantar pressure distribution measurements in a normal population. Gait Posture. 2008;27(4):706–9. doi: 10.1016/j.gaitpost.2007.07.002. [DOI] [PubMed] [Google Scholar]
- 26.Oviedo GR, Guerra-Balic M, Baynard T, Javierre C. Effects of aerobic, resistance and balance training in adults with intellectual disabilities. Res Dev Disabil. 2014;35(11):2624–34. doi: 10.1016/j.ridd.2014.06.025. [DOI] [PubMed] [Google Scholar]
- 27.Azevedo R, Teixeira N, Abade E, Carvalho A. Effects of noise on postural stability when in the standing position. Work. 2016;54(1):87–91. doi: 10.3233/WOR-162280. [DOI] [PubMed] [Google Scholar]
- 28.O’Toole GC, Makwana NK, Lunn J, Harty J, Stephens MM. The effect of leg length discrepancy on foot loading patterns and contact times. Foot Ankle Int. 2003;24(3):256–9. doi: 10.1177/107110070302400310. [DOI] [PubMed] [Google Scholar]
- 29.White SC, Gilchrist LA, Wilk BE. Asymmetric limb loading with true or simulated leg-length differences. Clin Orthop Relat Res. 2004;(421):287–92. doi: 10.1097/01.blo.0000119460.33630.6d. [DOI] [PubMed] [Google Scholar]
- 30.von Elm E, Altman DG, Egger M, et al. The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement: guidelines for reporting observational studies. Int J Surg. 2014;12(12):1495–9. doi: 10.1016/j.ijsu.2014.07.013. [DOI] [PubMed] [Google Scholar]
- 31.Kuo AD, Donelan JM. Dynamic principles of gait and their clinical implications. Phys Ther. 2010;90(2):157–74. doi: 10.2522/ptj.20090125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Neelly K, Wallmann HW, Backus CJ. Validity of measuring leg length with a tape measure compared to a computed tomography scan. Physiother Theory Pract. 2013;29(6):487–92. doi: 10.3109/09593985.2012.755589. [DOI] [PubMed] [Google Scholar]
- 33.Marrugat J. Versión 7.12 Abril 2012. Calculadora de tamaño muestral GRANMO. Available from: https://www.imim.cat/ofertadeserveis/software-public/granmo/. Accessed in 2021 (Mar 3) [Google Scholar]
- 34.Tudor-Locke C, Rowe DA. Using cadence to study free-living ambulatory behaviour. Sports Med. 2012;42(5):381–98. doi: 10.2165/11599170-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 35.Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159–74. [PubMed] [Google Scholar]
- 36.Burdock EI, Fleiss JL, Hardesty AS. A new view of inter-observer agreement. Personnel Psychology. 1963;16:373–84. doi: 10.1111/j.1744-6570.1963.tb01283.x. [DOI] [Google Scholar]
- 37.Watkins MP, Portney L. Foundations of clinical research: applications to practice. 3rd ed. Pearson Prentice Hall; Nueva Jersey: 2009. [Google Scholar]
- 38.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1(8476):307–10. [PubMed] [Google Scholar]
- 39.Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86(2):420–8. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
- 40.General Assembly of the World Medical Association World Medical Association Declaration of Helsinki: ethical principles for medical research involving human subjects. J Am Coll Dent. 2014;81(3):14–8. [PubMed] [Google Scholar]
- 41.Harvill LM. Standard Error of Measurement. An NCME Instructional Module on. Educational Measurement: Issues and Practice. 1991;10(2):33–41. doi: 10.1111/j.1745-3992.1991.tb00195.x. [DOI] [Google Scholar]
- 42.de Vet HCW, Terwee CB, Mokkink LB, Knol DL. Reliability. In: de Vet HCW, Terwee CB, Mokkink LB, Knol DL, editors. Measurement in Medicine. Cambridge University Press; Cambridge: 2011. pp. 96–149. [Google Scholar]
- 43.Izquierdo-Renau M, Pérez-Soriano P, Ribas-García V, Queralt A. Intra and intersession repeatability and reliability of the S-Plate® pressure platform. Gait Posture. 2017;52:224–6. doi: 10.1016/j.gaitpost.2016.12.001. [DOI] [PubMed] [Google Scholar]
- 44.van der Leeden M, Dekker JH, Siemonsma PC, Lek-Westerhof SS, Steultjens MP. Reproducibility of plantar pressure measurements in patients with chronic arthritis: a comparison of one-step, two-step, and three-step protocols and an estimate of the number of measurements required. Foot Ankle Int. 2004;25(10):739–44. doi: 10.1177/107110070402501008. [DOI] [PubMed] [Google Scholar]
- 45.Ramanathan AK, Kiran P, Arnold GP, Wang W, Abboud RJ. Repeatability of the Pedar-X in-shoe pressure measuring system. Foot Ankle Surg. 2010;16(2):70–3. doi: 10.1016/j.fas.2009.05.006. [DOI] [PubMed] [Google Scholar]


