Model Personalization in Behavioral Interventions using Model-on-Demand Estimation and Discrete Simultaneous Perturbation Stochastic Approximation

Abstract

This paper presents the use of discrete Simultaneous Perturbation Stochastic Approximation (DSPSA) to optimize dynamical models meaningful for personalized interventions in behavioral medicine, with emphasis on physical activity. DSPSA is used to determine an optimal set of model features and parameter values which would otherwise be chosen either through exhaustive search or be specified a priori. The modeling technique examined in this study is Model-on-Demand (MoD) estimation, which synergistically manages local and global modeling, and represents an appealing alternative to traditional approaches such as ARX estimation. The combination of DSPSA and MoD in behavioral medicine can provide individualized models for participant-specific interventions. MoD estimation, enhanced with a DSPSA search, can be formulated to provide not only better explanatory information about a participant’s physical behavior but also predictive power, providing greater insight into environmental and mental states that may be most conducive for participants to benefit from the actions of the intervention. A case study from data collected from a representative participant of the Just Walk intervention is presented in support of these conclusions.

I. INTRODUCTION

The unprecedented availability of data made possible today by advances in technology and increased use of mobile devices has allowed dynamic modeling to become a primary source of data-driven solutions to problems in many fields, including behavioral medicine. However, moving from data to dynamical models presents many challenges, as the informative utility of data is limited by its ability to be operationalized in both an explanatory and predictive sense. This means that special attention must be given to 1) experimental design for obtaining quality data and 2) estimating useful models. This paper focuses on the latter.

Despite the availability of data (or the relative ease by which we are able to collect data), distilling a comprehensive and useful model often requires exhaustive search and high computational power. These difficulties arise from the large number of measured features that are potential model inputs and the presence of noise. To more efficiently find optimal models, we demonstrate the use of discrete simultaneous perturbation stochastic approximation (DSPSA), a simulation-based technique that optimizes models through stochastic search [1], [2]. In this paper, we illustrate the results of DSPSA as a tool for feature selection, model order selection, and parameter estimation, which will allow users to more easily obtain models from large volumes of data and utilize more computationally-demanding models. This will be shown thorough the use and optimization of Model-on-Demand (MoD) estimation, which is an appealing approach for modeling noisy, nonlinear systems [3], [4].

Behavioral medicine presents a rich field of opportunities to apply MoD, as there has been a push for idiographic (i.e., “single subject”) approaches to understand each individual’s specific barriers to health-promoting behavior and personalized behavior-change interventions. The Just Walk study [5], [6], [7], explores increasing physical activity (PA) to mitigate the risk of chronic disease in people who are primarily sedentary and may be at higher risk for a variety of illnesses. While the benefits of increased PA are well-documented, there remains an issue in how to promote sustained increases in physical activity. Providing individuals with information about improving their health through increased PA, alone, is not enough to benefit at-risk populations. Significant improvement requires that participants sustain engagement at higher levels of PA over extended periods of time.

Just Walk addresses a lack of physical activity by presenting individualized PA interventions via idiographically-developed dynamical models of walking behavior, delivered to participants through mobile health (mHealth) technologies. Combining control systems theory, behavioral science, and informatics, the study utilized system identification principles to design goal setting and positive reinforcement models. Through this trans-disciplinary approach, Just Walk not only demonstrated the benefit of system identification principles in the development of personalized interventions, but also highlighted the significance of individualized interventions, noting the complexity of physical activity (its dependence on environmental and mental factors) and the limitations of nomothetic approaches (i.e. finding general governing laws or principles), which are the current dominant paradigm, to successfully model individual participant behavior.

An individual’s walking behavior is complex and idiosyncratic, influenced by a variety of factors that themselves may be context dependent. To develop a useful model of behavior, it is necessary to capture complexity and nonlinearity. While dynamic models for behavior have been developed with linear AutoRegressive with eXogenous input (ARX) modeling, these may be too simple to provide sufficient explanation for an individual’s behavior that can be translated into an intervention which requires predictive information about the factors that promote walking for specific participants. The simplicity of ARX models restrict the model’s ability to capture nonlinearity in individual behavior and may not allow for sufficient prediction or explanation of behavior as an individual’s environment or mental state changes. Consequently, MoD presents an appealing approach, as it fits a local model at each operating point, allowing it more flexibility and adaptability to build models “on demand.” While MoD may provide a better method to model PA, it is more computationally-demanding than ARX and requires greater prior knowledge, as there are additional parameters that need to be specified. However, this increase in complexity can be mitigated by DSPSA, making MoD more accessible and applicable in a broader set of application settings.

The paper is organized as follows: Section II provides an overview of the MoD estimation framework, while Section III describes DSPSA. Section IV demonstrates the application of MoD and DSPSA with a representative participant from the Just Walk intervention study. Section V provides conclusions and directions for future work.

II. MODEL-ON-DEMAND OVERVIEW

The primary advantage of Model-on-Demand, compared to traditional global estimation methods, is that the model is optimized locally. MoD applies a weighted regression to generate local estimates, adjusting the neighborhood size from a stored database of observations to build models ‘on demand.’ This optimizes the bias/variance trade-off locally, allowing MoD to achieve lower errors for a fixed model structure. This is particularly useful as the number of observations increases, as it becomes more difficult to obtain a global model that is optimal over an entire data set [3].

The MoD modeling formulation can be described with a single input single output (SISO) process as demonstrated by the approach of [4]. Consider a SISO process with nonlinear ARX structure,

$$y(t)=m(\phi (t))+e(t)$$ (1)

in which m(·) is an unknown nonlinear mapping and e(k) is an error term. The error is modeled as a random signal with zero mean and variance ${\sigma }_k^2$. The MoD predictor attempts to estimate output predictions, ŷ(i), based on a local neighborhood of the regressor space φ(t). The regressor vector takes on the form of a linear ARX as shown in Equation 2.

$$\phi (t)={\left[y(t-1)\dots y\left(t-n_a\right)u\left(t-n_k\right)\dots u\left(t-n_b-n_k\right)\right]}^T$$ (2)

where n_a denotes the number of previous outputs, n_b denotes the number of previous inputs, and n_k denotes the delay in the model. Note that for multi-output systems, n_a is specified for each output, and for a multi-input system, n_b and n_k are specified for each input.

A local estimate ŷ(i) is then obtained at each operating point from the solution of the weighted regression problem, shown in Equation 3:

$$\begin{gathered} \widehat{\beta }=\text{arg\hspace{0.17em}}\underset{\widehat{\beta }}{\text{min}}\sum _{i=1}^N\ell (y(i)-\widehat{m}(\phi (i),\widehat{\beta })) \\ \times W\left(\frac{\parallel \phi ()-\phi (t){\parallel }_M}{h}\right) \end{gathered}$$ (3)

in which ℓ(·) is a quadratic norm function, ${\Vert u\Vert }_M\triangleq \sqrt{u^{T}Mu}$ is a scaled distance function on the regressor space, h is a bandwidth parameter controlling the size of the local neighborhood, and W (·) is a window function (also referred to as the kernel) assigning weights to each remote data point based on its distance from φ(t) [4]. The window is typically a bell-shaped function with bounded support. MoD users specify k_min, k_max, and a goodness-of-fit criterion, which then affect the bandwidth parameter and the window function. Two common goodness-of-fit criteria include the Akaike information criterion (AIC) and generalized cross validation (GCV), but many others may also be considered. Assuming a local model structure,

$$m(\phi (t),\beta )={\beta }_0+{\beta }_1^T(\phi (i)-\phi (t))$$ (4)

which is linear in the unknown parameters, a MoD estimate can be computed using least squares methods. Denoting β₀ and β₁ as the minimizers of Equation 3 using the model from Equation 4, a one-step ahead prediction is given by

$$\widehat{y}(i)=\alpha +{\beta }_1^T\phi (i)$$ (5)

where $\alpha ={\beta }_0-{\beta }_1^T\phi (t)$. Each local regression problem produces a single prediction ŷ(i) corresponding to the current regression vector φ(t). To obtain a prediction at other operating points in the regressor space, MoD adapts both the relative weights and the selection of data to optimize a new local model at the next operating point. This diverges from global modeling techniques in which the model is estimated from the data once, and then the data is discarded. The bandwidth h, which is computed adaptively at each prediction, controls the neighborhood size governing the trade-off between the bias and variance errors of the estimated model.

In application, users can specify the ARX structure used in φ(t), the local polynomial order in m(·), k_min, k_max, and the goodness-of-fit criterion; these variables impact the size of the neighborhood chosen to fit the local model.

III. Simulation-Based Optimization using Discrete SPSA

While Model-on-Demand provides a method to estimate models for noisy, nonlinear dynamics, choosing the parameters that produce an optimal model presents a separate challenge. The MoD parameters include choices of local polynomial order, ARX structure, and goodness-of-fit criterion, in addition to the features or inputs used to estimate the model, giving rise to a large number of combinations, across which an exhaustive “brute force” search would be impractical. For example, a model with 10 features available would require a search over 2¹⁰ − 1 = 1023 combinations. To estimate optimal model parameters and bypass the need for exhaustive search, we propose the use of a discrete form of Simultaneous Perturbation Stochastic Approximation (DSPSA), a simulation-based optimization technique.

SPSA [1] is a popular technique that is useful in contexts where a closed-form objective function is not available and where noise may be present. It provides a non-deterministic approach to typical gradient descent methods. For feature selection, Binary SPSA (BSPSA) was found to outperform other methods, including Binary Genetic Algorithms, and conventional feature selection methods such as Sequential Forward Selection, Sequential Backward Selection, and Sequential Forward Floating Selection. These methods were evaluated on multiple datasets, in which BSPSA was found to perform at least comparably in small datasets (less than 100 features) and highly favorably in large datasets (over 100 features), as measured by cross-validation error [8].

To use SPSA, we start with a guess of the model parameter values $\widehat{\theta }$, which are updated with each iteration. To obtain an estimated gradient, all model parameters are subjected to a random, two-sided simultaneous perturbation, which are then used to evaluate the objective function, $J(\widehat{\theta })$. These two evaluations are then used to approximate the gradient, which is subsequently used to update the parameter values. This is repeated for a user-specified number of iterations k.

The objective function chosen for the optimization problem often takes on the form of a loss function, L, which is not readily available or explicit and can instead be approximated by noisy measurements, J(θ) = L(θ) + ϵ(θ). SPSA then minimizes the loss function through a process that resembles gradient descent, iterating and updating θ.

SPSA has been used in many problems spanning a diverse set of fields, including supply chain management and public health ([2], [9]). As will be demonstrated in this paper, SPSA is also useful in behavioral medicine, providing model parameter estimations and feature selection for individualized health interventions. SPSA can be used to search simultaneously across both continuous and discrete parameter values. Discrete SPSA (DSPSA) will be shown here, used for both model parameters and for feature selection.

The following summarizes the DSPSA process for k iterations, as described in [2] and [8]:

1. Initialize the Input Vector and Gain Sequences. Specify an initial p-dimensional input vector, $\widehat{\theta }$, in which p corresponds to the number of features or parameters subject to stochastic search. The gain sequences a_k and c_k define the step size of each iteration and perturbation, respectively.

2. Generate the Perturbation Vector. Generate a perturbation vector (Δ_k) of dimension p using a Bernoulli ±1 distribution with probability 1/2.

3. Create Two Input Vectors for Gradient Approximation. From the input vector, create a new vector, $\pi \left({\widehat{\theta }}_k\right)={\widehat{\theta }}_k+1_p/2$, in which ⌊·⌋ is the floor operator and 1_p is a p-dimensional vector of ones. From $\pi \left({\widehat{\theta }}_k\right)$, create two input vectors for gradient approximation, ${\widehat{\theta }}_k^{+}=\pi \left({\widehat{\theta }}_k\right)+c_k{\Delta }_k$ and ${{\widehat{\theta }}^{-}}_k=\pi \left({\widehat{\theta }}_k\right)-c_k{\Delta }_k$. Apply bounds to limit between discrete values and round ${\widehat{\theta }}_k^{+}$ and ${\widehat{\theta }}_k^{-}$.

4. Approximate the Gradient. Evaluate the objective function J(·) at the bounded and rounded input vectors, ${\theta }_k^{+}$ and ${\theta }_k^{-}$. Use these two evaluations to approximate the gradient using a finite difference approximation:

   $${\widehat{g}}_k=\frac{J\left({\widehat{\theta }}_k^{+}\right)-J\left({\widehat{\theta }}_k^{-}\right)}{2c_k{\Delta }_k}$$ (6)
5. Update the Input Vector. Using the gradient approximation, update the input vector:

   $${\widehat{\theta }}_{k+1}={\widehat{\theta }}_k-a_k{\widehat{g}}_k$$ (7)

   Apply bounds to limit between discrete values and round the new input vector.

6. Report the Best Solution Vector. Once the SPSA search has reached its final iteration, report the best solution.

In a binary application of DSPSA (where the parameter choices are limited to only 0 and 1), it is necessary to correspondingly limit the input vector between 0 and 1 at each iteration (i.e. at steps 3 and 5).

IV. CASE STUDY: JUST WALK

Just Walk is a 12 week study that explored the development of dynamical models to explain individual walking behavior via system identification principles [5], [7]. The study recorded changes in physical activity (measured in steps) due to goals and rewards sent through a mobile app. Participants in Just Walk were sent step goals and obtained points (expected points) upon completing these goals.

Using data provided by the Just Walk study, DSPSA and MoD were used as methods to obtain dynamical models that describe walking behavior to both explain the factors that influence an individual’s physical behavior and predict their responsiveness to goals and rewards, given their mental state and environment. In earlier studies, ARX models were used to model an individual’s walking behavior, and so MoD results will be compared to ARX models here [6].

From the Just Walk data, we can explore 8+ inputs that influence an individual’s walking. The recorded inputs (8) include goals, expected points, granted points, predicted busyness, predicted stress, predicted typical, weekend, and weather (temperature). Goals refers to the daily step goals sent to participants. These goals are attached to expected points, which are the daily points available for the participant to earn. If participants meet their goals, they receive some amount of points, which are considered granted points. Predicted busyness, predicted stress and predicted typical are psychosocial measures determined each morning by ecological momentary assessment. Weekend is a binary input, in which weekend = 1 if the current day is either Saturday or Sunday, and weekend = 0 otherwise. We can also explore beyond the eight inputs in the original study by creating new inputs in the form of interaction terms, such as an interaction between expected points and predicted busyness.

For the following case study, the goal is to find a model to 1) understand the factors that contribute to an individual’s walking behavior and 2) have predictive power for use in behavioral interventions. DSPSA was used to optimize the MoD model. Given data on factors that may have influence, the DSPSA algorithm is used to choose factors (i.e. environmental factors, subjective mental states) and MoD design variables (i.e. ARX orders, local polynomial order, etc.) to achieve the ‘best’ model. In this case, the term ‘best’ is a function of the model’s capacity to fit an individual’s data on three fronts: 1) prediction (on validation data), 2) estimation (on the estimation data used to create the model), and 3) overall fit (on the participant’s entire data set – both validation and estimation data). This is reflected in the objective function defined in the DSPSA algorithm, which as described in the ensuing section is a weighted average of the NRMSE MoD fit percentages.

Since we are searching over features, but not the values of those features, this requires a binary search (a discrete search bounded between 0 and 1), as we are evaluating whether or not the feature should be included in the model. The SPSA search over the model parameters is also discrete, as the values that get used in the model must be integers (i.e. polynomial orders that define the local ARX regressor).

A. DSPSA Initialization

Applying SPSA to a representative participant in the Just Walk study, the following parameters were subjected to stochastic search: features (i.e. inputs), ARX orders (i.e. n_a, n_b, n_k) for each input/output, and local polynomial order (per Equation 4). The features vector consisted of 9 inputs: all 8 inputs from the Just Walk study and an interaction term between expected points and predicted busyness.

All features were initialized in a single vector, ${\widehat{\theta }}^w\in {ℝ}^9$. The input vector is binary (0: the input is not used in the model, 1: the input is used in the model), and so the vector was bound between 0 and 1 and rounded such that it can only take on values of 0 or 1 when used to evaluate a model. Between iterations, the vector was allowed to take on values between 0 and 1. The vector was simply rounded before being used to define the inputs being used for a specific model. The convergence of these values was not demonstrated as clearly as in cases with continuous-valued input vectors, as demonstrated in [9].

The ARX orders (n_a, n_b, n_k) were each initialized as individual vectors, ${\widehat{\theta }}^{n_a}\in {ℝ}^1$, ${\widehat{\theta }}^{n_b}\in {ℝ}^9$, and ${\widehat{\theta }}^{n_k}\in {ℝ}^9$. The values of ${\widehat{\theta }}^{n_a}$ and ${\widehat{\theta }}^{n_b}$ were both bound between 0 and 3, while ${\widehat{\theta }}^{n_k}$ was bound between 0 and 1. These orders could take on higher values, but we chose to limit them to keep the regressor structure simple. The local polynomial order was also initialized as its own vector $\left({\widehat{\theta }}^P\in {ℝ}^1\right)$, and was restricted between 0 and 2.

Similar to the input vector, the ARX orders and local polynomial order values were allowed take on any value between their respective bounds. However, they were rounded before evaluating the model.

Gain sequences were specified for each input vector. These were determined by the relative size of approximated gradient compared to the values of the input vectors as well as the relative size of the perturbation. While these have to be determined by the user, they are typically not difficult to narrow down. The same c_k and a_k values were used for the input vectors corresponding to n_a, n_b, and n_k, but this does not have to be the case. For the ARX orders c_k = 0.1 and a_k = 0.005 were used; for feature selection c_k = 0.1 and a_k = 0.0002 were used, while for the local polynomial order, c_k = 0.2 and a_k = 0.003 were used. These gains were sufficient to allow the search to span the full range of values for each of the parameters across the iterations.

The following fixed parameters were chosen for MoD: k_min = 40, k_max = 400, and the goodness of fit criterion was generalized cross validation (GCV).

As noted previously, the DSPSA algorithm is set up to maximize the weighted average of the MoD model’s ability to fit (1) validation data, $J_v(\widehat{\theta })$, (2) estimation data, $J_e(\widehat{\theta })$, and (3) overall data, $J_o(\widehat{\theta })$, where J_{v,e,o} corresponds to the Normalized Root-Mean-Square Error (NRMSE), which is calculated at each iteration by Eqn. 8

$$J_{\left\{v,e,o\right\}}(\theta )=100\text{\%}\times \left(1-\frac{\parallel y-\widehat{y}{\parallel }_2}{\parallel y-\overline{y}{\parallel }_2}\right)$$ (8)

ŷ is the model output, while $\overline{y}$ is the average of the data. The fit percentages were then weighted as 4/6, 1/6, and 1/6, respectively. The predictive fit was weighted heavier than both the estimation and overall fits, since the predictive fit is typically much lower than the other two (and sometimes negative) and since the predictive ability of the model serves a significant purpose in future behavioral health interventions, namely to predict whether a participant is in a state or environment conducive towards their behavioral goals (i.e. walking more). These weights and fits then give us our objective function, which in this case takes on the form of a maximization problem (or minimization of the negative of the weighted fit).

$$\underset{\theta \in {\mathbb{Z}}_{+}}{\text{max}}J(\theta )$$ (9)

$$J(\theta )=\frac{4}{6}{J}_v(\theta )+\frac{1}{6}{J}_e(\theta )+\frac{1}{6}{J}_o(\theta )$$ (10)

in which θ^w, ${\theta }^{n_a}$, ${\theta }^{n_b}$, ${\theta }^{n_k}$, θ^P ∈ θ, and the optimized solution found by SPSA is θ*. As shown by Eqn. 9 and 10, all input vectors are used to simultaneously update the same objective function. They are not evaluated independently.

B. DSPSA Results

The NRMSE fit for both MoD and ARX model’s evaluated at the k^th iteration of inputs (features, ARX orders, local polynomial order) are shown in Figure 1. The largest weighted average of the MoD fits occurs at k = 22. The exact fits of the model evaluated at the optimal iteration are listed in Table I. In each evaluation, the NRMSE and RMS fits provided by the MoD model is superior, corresponding to just under double that of the ARX model. The model evaluations on each data set outlined in Table I are shown in further detail in Figures 2, and 3.

Fig. 1.

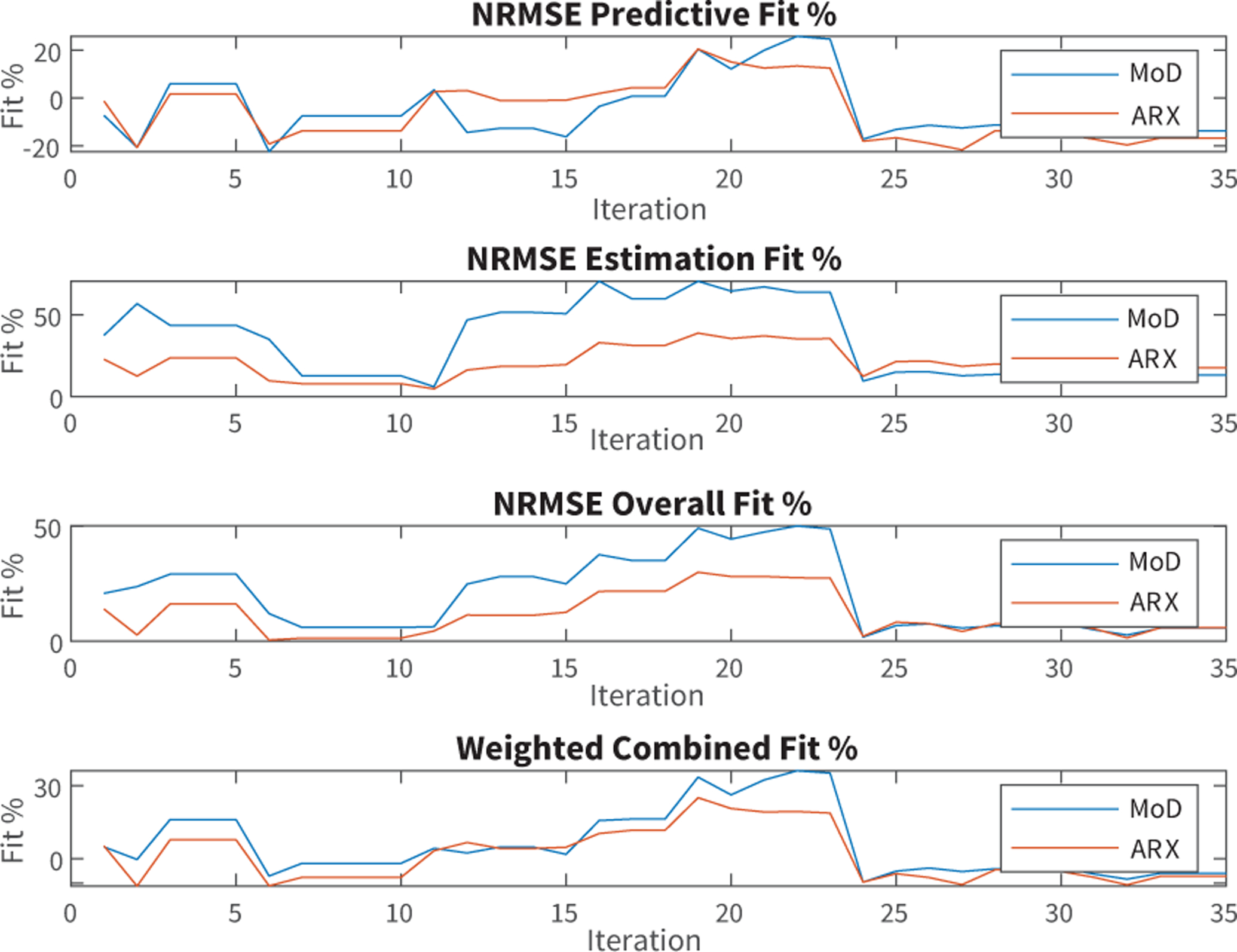
NRMSE Fit Percentages Per DSPSA Iteration. The weighted fit is a weighted average of the prediction, estimation, and overall fits, with their respective weights being 4/6, 1/6, and 1/6. The best model was chosen as the one that maximizes the weighted combined fit.

TABLE I.

MoD and ARX Comparisons for θ*

	NRMSE Fit (%)		RMS Error (steps)		Max Error (steps)
	MoD	ARX	MoD	ARX	MoD	ARX
Prediction	25.73	13.35	1877.42	2192.41	5585.31	4289.08
Estimation	63.89	35.52	837.01	1499.33	3876.73	4208.57
Overall	50.03	27.55	1189.39	1724.26	5536.66	4807.34

Fig. 2.

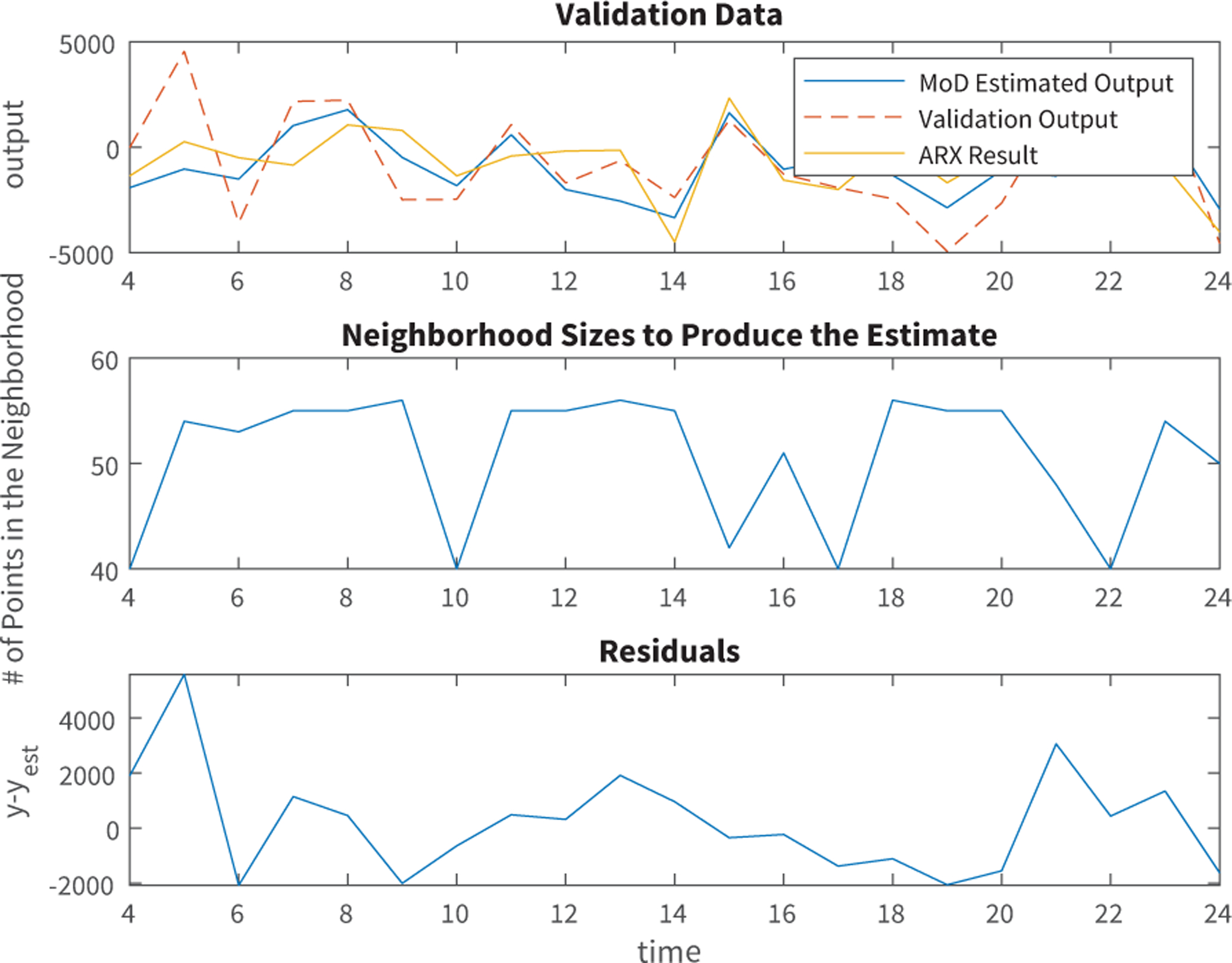
MoD and ARX Models on Validation Data (25% of Participant Data). The output is measured in steps.

Fig. 3.

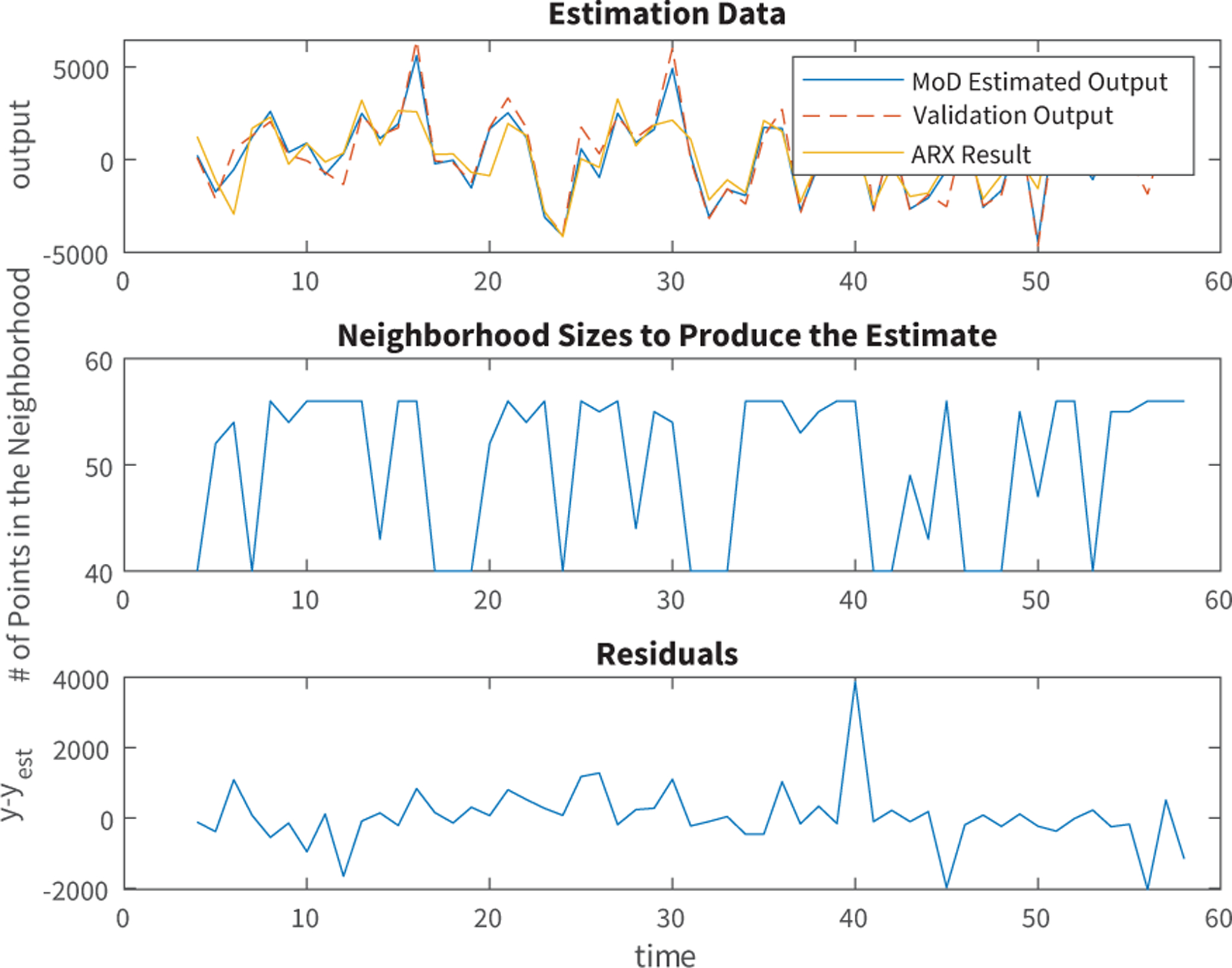
MoD and ARX Models on Estimation Data (75% of Participant Data). The output is measured in steps.

The features used in the optimal iteration as well as their respective n_b and n_k orders are outlined in Table II. These are also the features used in the model evaluated in Figures 2 and 3. The n_a value is common to all inputs, so there is only one value being optimized. In this case, the optimal n_a value found by DSPSA is n_a = 2, so two prior lags of the output (steps) are used in the model.

TABLE II.

Feature Selection and n_b, n_k orders for θ* (n_a = 2, P = 1)

Initialized Features	Selected Features	n b	n k
Goals	Goals	1	1
Expected Points	Expected Points	2	0
Granted Points	Granted Points	2	0
Predicted Busyness	Predicted Busyness	1	0
Predicted Stress	Predicted Stress	0	1
Predicted Typical	Predicted Typical	2	1
Weekend	Weekend	1	1
Temperature	-	-	-
Expected Points/Predicted Busyness	-	-	-

In Figures 2 and 3, the validation data is taken from the last 25% of the participant’s data, while the initial 75% is used to estimate the model. The change in neighborhood size, used by MoD to estimate a local model, is also shown in the middle plot of both figures.

Figure 4 illustrates the features used in both the MoD and ARX models at each iteration. The features used in the optimal iteration and demonstrated in Figures 2 and 3 are: goals, expected points, granted points, predicted busyness, predicted stress and weekend, which is a reduced set of features from the original nine.

Fig. 4.

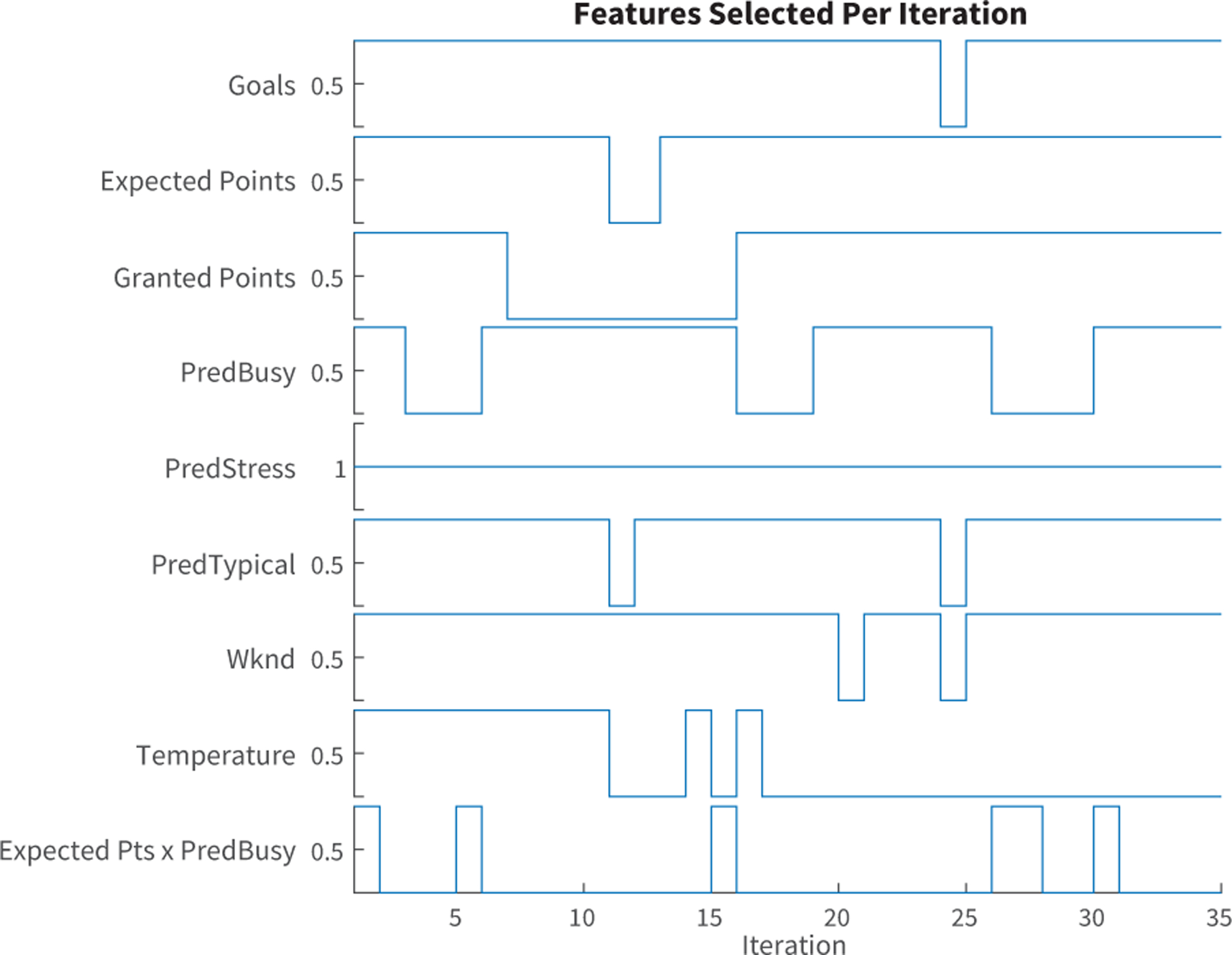
Features used at each iteration $\left({\widehat{\theta }}_k^w\right)$

The n_a, n_b, and n_k values evaluated at each iteration, are updated for all initialized inputs, regardless of which inputs are used in the model at that same iteration. However, the ARX orders are only used in the model if its corresponding feature is also used in the model (which can be identified in Figure 4). An additional constraint was placed on the DSPSA search regarding n_b and n_k values, since they cannot simultaneously be zero in the regressor structure. Correspondingly, n_k values were set to 1 whenever n_b = 0.

V. CONCLUSIONS AND FUTURE WORK

The results obtained from the Just Walk case study show that Model-on-Demand estimation can provide better individualized models than ARX, with both more explanative and predictive power. Though the challenge of choosing the right parameters to inform the MoD model can be tedious and require a search over many combinations, DSPSA provides an efficient means to determine the inputs of the highest-performing models. DSPSA can be used not only for feature selection but can also provide insights into additional model parameters such as the MoD local polynomial order and ARX orders. DSPSA also bridges the gap between using MoD and using ARX in terms of modeling expertise or additional information to search over MoD’s adjustable parameters. The case shown here only searched over ARX orders and the local polynomial order, but SPSA can readily be used to search over other MoD parameters.

While the parameters during DSPSA do not appear to converge as it performs ‘gradient descent,’ DSPSA still allows users to obtain an optimized set of model parameters efficiently and with modest effort, while avoiding a brute force search. However, this highlights one limitation in SPSA, in that there is no ‘natural stopping point’ as the algorithm runs until it hits a stall limit or finishes the iterations defined by the user (common to both continuous and discrete applications). With DSPSA, the inability to observe a clear convergence also prevents users from readily inferring whether the model identified is the best model (or the near best model). Due to the discrete inputs (and lack of an explicit function), there is also already a limit to our ability to infer how combinations of features contribute to model proficiency (i.e. whether taking one feature away or adding one will help or hurt the model, given the other features already being implemented); this problem is not unique to the SPSA framework. Visualization of the exact iterations or parameter values in continuous space may still be useful for analyses. These may allow DSPSA users to observe the step size taken at each iteration, to better understand the approximated gradient resulting from the particular simultaneous perturbation.

Despite these limitations, using DSPSA in conjunction with MoD has demonstrated that MoD can provide better models than ARX for behavioral health interventions. This also highlights the need for more robust modeling for individualized solutions, which is better achieved by MoD than ARX. Given the ease by which DSPSA can be set up and the efficiency by which it finds optimal models, using DSPSA also provides a method to find idiographic dynamic models for personalized interventions for a large number of participants, making the concept of personalized interventions scalable.

The combined use of MoD and DSPSA may further be used for model predictive control (MPC) in behavioral intervention settings, as shown by [10]. With the MoD models, optimized by DSPSA, Model-on-Demand predictive controllers can be developed to provide adaptive interventions for participants, further improving their effectiveness. Other objective functions may also be useful to consider, such as including a term to favor parsimony or lower ARX orders. DSPSA may also be useful to search over different sets of estimation and validation data (i.e., splitting an individual’s data into segments).