Inference on moderation effect with third-variable effect analysis – application to explore the trend of racial disparity in oncotype dx test for breast cancer treatment

Abstract

Third variable effect refers to the effect from a third variable that explains an observed relationship between an exposure and an outcome. Depending on whether there is causal relationship, typically, a third variable takes the format of a mediator or a confounder. A moderation effect is a special case of the third-variable effect, where the moderator and other variables have an interactive effect on the outcome. In this paper, we extend the R package ‘mma’ for moderation analysis so that third-variable effects can be reported at different levels of the moderator. The proposed moderation analysis use tree-structured models to automatically detect moderation effects and can handle both categorical and numerical moderators. We propose algorithms and graphical methods for making inference on moderation effects and illustrate the method under different scenarios of moderation effects. Finally, we apply the proposed method to explore the trend of racial disparities in the use of Oncotype DX recurrence tests among breast cancer patients. We found that the unexplained racial differences in using the tests have decreased from 2010 to 2015.

1. Introduction

Breast cancer is the most commonly diagnosed cancer for American women of all races. It is also the second leading cause of cancer death. Breast cancer has been categorized into subgroups for prognosis and treatment purposes. One common way of classifying breast cancer and recommending treatment is based on the expression of estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER 2) [12]. The subtype ER positive and/or PR positive (ER+/PR+) and HER2 negative (HER2-) breast cancer is the most common subtype, has the best prognosis and responds well to adjuvant endocrine therapy and/or chemotherapy. However, even within this subtype, patients have different recurrence risk and may respond to chemotherapy differently [13,14].

Precision medicine has been developed significantly in today's cancer treatment. Oncotype DX® (ODX) is a genomic test which can differentiate ER+/PR+ and HER2- patients by the risk of recurrence to project prognosis and chemotherapy benefit. ODX test is based on 21-gene expression levels and it produces a recurrence score, a number between 0 and 100. A raised ODX score indicates a higher probability of cancer recurrence and more benefit from chemotherapy. The National Comprehensive Cancer Network (NCCN) cancer treatment guidelines published in 2008 recommended ODX test to patients with ER+/PR+, HER2-, and negative lymph node breast cancer to identify those that are more likely to benefit from chemotherapy. However, research shows that there are racial and ethnic disparities among breast cancer patients in terms of the survival rate, recurrence rate, and health-related quality of life [22,23]. The disparity was also discovered in the use of ODX test [9,16,17]. Our previous work has shown that among all female breast cancer patients who were considered to be able to benefit from the ODX exam, non-Hispanic whites had a significantly higher rate of using the test, compared with non-Hispanic blacks [24]. In addition, the proportion of using ODX tests has been increasing over the last decade within both black and white patients. It is interesting to know whether the racial gap in ODX test has been reduced over time during the last decade. Furthermore, if there is a reduction in the gap, what factors contribute to this improvement?

One of the techniques for inferences on the trend of racial disparity in ODX exam is on the moderation effect inferences with a third-variable effect analysis (TVEA) approach. Third-variable effect refers to the intervening effect of a third-variable on the observed relationship between an exposure and an outcome. The TVEA differentiates the effect from multiple third variables (TV) that explains the established exposure-outcome relationship, i.e. the effect on the path $exposure-TV\to outcome$. Both exposure and third-variables influence the outcome. Depending on whether there is a causal relationship from the exposure to the third variable, the third-variable effect can be categorized into two major groups: mediation effect where a causal relationship is assumed and confounding effect where there is no causal relationship assumed from the exposure to the third-variable. Accordingly, the third variable is called a mediator or confounder respectively. A causal relationship can be established through randomized experiments, while statistical inference cannot prove a causal association. In terms of the statistical inference on the third-variable effect, the mediation effect and confounding effect are equivalent [11]. The authors proposed a third-variable effect analysis method using a resampling method. Using the method, third-variable effect can be differentiated from different paths, nonlinear relationships among variables can be modeled, and different formats (categorical, continuous, time-to-event) of the outcomes are allowed [10,19]. Moderation effect refers to the interactive effect of two or more variables on the outcome. Within the TVEA, the interaction effect can be between the moderator and the exposure, where the relationship between the exposure and outcome (direct moderation effect) and/or the relationship between the exposure and a third variable are different at different levels of the moderator. In addition, the interaction effect can be between the moderator and any third-variables such that the third-variable and outcome relationship is different at various level of the moderator(see Figure 1). One of the main purposes of moderation analysis within TVEA is to make inferences on and compare the change of third-variable effects at different levels of the moderator. We propose to explore the trend of racial disparities in ODX exam from 2010 to 2015 using a moderation effect inference with TVEA. In this case, the exposure variable is the race (non-Hispanic blacks vs. non-Hispanic whites), the outcome is the use of ODX test (yes/no), and third-variables are all variables that can explain the racial difference in ODX usage. The moderator is the diagnosis year.

Figure 1.

Moderation Diagram. X is the exposure variable, $M_1$ is a third variable, Y is the outcome, MO is the moderator, and Z is the vector of other covariates.

Moderation has been widely used in the psychological research, behavior science, and public health studies. Recently many research has combined the moderation analysis with the third-variable effect analysis method [2,3,7]. However, there are still many challenges exist in the field such as automatically identify interaction terms and to deal with potentially nonlinear relationship. The main contributions of this work are as follows.

• The Multiple Additive Regression Trees (MART) [5,21] are used in the TVEA. Because of the tree structure of MART, interaction effects among variables are allowed and selected automatically through the model building process. Therefore, the third-variable moderated TVE and direct moderation effect (see Figure 1) can be estimated without manually creating interaction terms and put into the predictive model.

• Nonlinear relationship among variables is allowed with the predictive models. We use MART to predict the outcome based on all other variables, and smoothing splines to model relationships from the exposure variable to each third-variable.

• Development and validation of the moderation inference with TVEA. The method is used to explore the trend in racial disparities in ODX exam, which can inform health-care policy makers about the change in racial disparities and contributing factors that explain the change.

• The R package mma is further developed to include the moderation effect analysis. The package can now be used to make inferences on third-variable effects with or without moderation. For the moderation analysis, the inferences on the third-effects are made on each level of the moderator(s). The mma package also provides visual aids to help understand the trend and direction of associations among variables.

Following the review of a general TVEA method in Section 2, we develop a method to make inferences on moderation effect. The algorithm and R package are also discussed in the section. We then illustrate the proposed method through simulations at different moderation scenarios in Section 3. In Section 4, the method is used to explore the trend of racial disparities in the ODX usage. Finally, the conclusion and future research are discussed in Section 5.

2. Inference on moderation effect with third-variable effect analysis

The third-variable effects mainly include direct and indirect effect. The direct effect refers to the causal or non-causal relationship between the exposure and the outcome after adjusting for other variables. The indirect effect of a third variable is the effect from exposure to the third variable to the outcome. A general TVEA inference method has been proposed by Yu et al. [18], where the total effect is defined as the changing rate in the outcome, y, with the change in the exposure variable, x, i.e. $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$. By the definition, the effect is defined in terms of the changing rate, but not the absolute magnitude of change in y. Therefore, the effect is invariant to the scale of x. Assume that there are P third-variables. The direct effect from x to y not through the $p_{th}$ third-variable, $m_p,p=1,\dots ,P$, is similarly defined as the changing rate of y with x when the relationship between x and $m_j$ is broken. In turn, the indirect effect of $m_j$ is defined as the difference between the total effect and the direct effect not through $m_j$. Through the definition, the TVEA method is generalized to be applicable to different types of response variable: binary, categorical, continuous or time-to-event. Any predictive models can be used to model the relationship among variables. Furthermore, the outcome and the exposure variables can be multivariate. Yu et al. [22,23] have applied the method to explore racial disparities in breast cancer survival rate, and in the health related quality-of-life measurements among cancer survivors.

When there is no interaction effect, TVEA are used to differentiate indirect effect from multiple third-variables. It is not uncommon that the relationship between an exposure variable and an outcome changes at different levels of an interactive variable. We usually call the interactive variable a moderator. A moderation effect is basically the interaction effect of the moderator with other predictors on the response variable(s). The moderation analysis is to differentiate indirect effect through multiple third-variables at each level of the moderator. In TVEA, the moderator takes into effect in three basic forms: exposure-moderated third-variable effect (TVE), third-variable moderated TVE, and direct moderation effect as is shown in Figure 1. The exposure-moderated TVE is that at different level of the moderator (MO), the effect of the exposure (X) on the third variable (M), is different. The third-variable moderated TVE indicates that the interactive effect is between the third variable and the moderator on the outcome (Y). The direct moderation is that the exposure and the moderator are interactively related to the outcome. The moderation relationship can be easily extended to multiple third variables.

Usually, to make inferences on moderation effects with regression models, we create interaction terms that potentially have the moderation effect and put the terms in predictive models. The test of significant moderation effect depends on the format of the moderation effect. For the exposure-moderated TVE, a significant moderation effect is established when there is a significant interaction effect of the exposure and the potential moderator on the third-variable when all other variables are adjusted. A third-variable moderated TVE is established when there is a significant interaction effect of the third-variable and the potential moderator on the outcome when all other variables are adjusted. To establish a direct moderation, there should be an interaction effect of the exposure and the potential moderator on the outcome [8]. Since moderation effect involves interactions, it is important that TVEs be explained at different levels of the moderator. That is, hierarchical models need to be interpreted in terms of the highest-order effect.

In this study, we propose a moderation effect analysis method that can automatically select important interactive terms and make inferences on moderation effects. The method is an extension to the general TVEA method proposed by Yu et al. [18]. It adopts properties of multiple additive regression trees (MART). We have also revised the R package mma to incorporate the proposed moderation analysis. The method is used to check the trend in using of ODX among early stage breast cancer patients.

2.1. Moderation effect analysis with MART

MART is a special case of the generic gradient boosting approach on trees [4]. It employs two algorithms: classification and regression trees (CART) [1] and boosting which builds and combines a collection of models. CART is a binary recursive partitioning algorithm that provides a nonparametric alternative to traditional parametric models for regression and classification problems. Specifically, with the algorithm, a multidimensional covariate (sub)space is cut into two regions at each iteration. An optimal variable and a split point are selected by a comprehensive test on all variables and their realized values in the covariate space. The split continues on one or both of these sub-regions until some pre-specified stop rules are met. Then responses are modeled as a constant in each terminal region. Although CART represents information in a way that is intuitive and easy to be visualized, it is usually not as accurate as its competitors. Boosting is one of the enhancements to tree-based methods that have met with considerable success in predictive accuracy. In boosting, models such as regression trees are fitted iteratively to the training data and appropriate methods are employed to put extra weights on observations modeled poorly by the current collection of trees. Inheriting the benefits from both algorithms, MART has been proved to have excellent predictive accuracy (e.g. [5,21]). Due to the hierarchical structure of the tree method, MART can pick up important interaction effect among variables without the necessity to include specific interactive terms. In addition, MART can model potential nonlinear relationship among variables without transforming covariates. We use these special properties of MART in the general TVEA for inferences on moderation effects.

In our study, the exposure variable is race, a binary variable for non-Hispanic white or non-Hispanic black. The following Algorithm outlines steps for making inferences on moderation effect with a general exposure (binary or continuous). Assume we have the observations $(y_i,x_i,M_{1i},\dots ,M_{Pi})$, for $i=1,\dots ,n.$ Let $D_x=\{x_i|x_i\in domai{n}_{x^{\ast }}\}$ and N be a large number.

Algorithm For Moderation Analysis

1. Fit a MART on the response variable, $y_i$, where the predictors are the exposure variable ( $x_i$), all potential third variables ( $M_{1i},\dots ,M_{pi}$), and the moderator (denote as $M{O}_i$) such that

   $$E\left(Y_i\right)=f(x_i,M_{1i},\dots ,M_{Pi},M{O}_i),\text{for }i=1,\dots ,n,$$ (1)
2. Fit joint models where the exposure variable, moderators, and other covariates are used to predict the third-variables $M_p$, $p=1,\dots ,P$. Ignoring the covariates for now, the fitted models have the following format:

   $$\left(\left.\begin{array}{c}{l}_1\left(M_{1i}\right)\\ l_2\left(M_{2i}\right)\\ \dots \\ l_P\left(M_{Pi}\right)\end{array}\right|x_i\right)\sim \mathbf{\Pi }\left(\left(\begin{array}{c}{\mathbf{g}}_{\mathbf{1}}\mathbf{(}{\mathbf{x}}_{\mathbf{i}}\mathbf{,}\mathbf{M}{\mathbf{O}}_{\mathbf{i}}\mathbf{)}\\ g_2(x_i,M{O}_i)\\ \dots \\ g_P(x_i,M{O}_i)\end{array}\right)\mathbf{,}\mathbf{\Sigma }\right)\mathbf{,}$$ (2)

   where $l_p$s are link functions that link each third-variable with the fitted models $g_p$, so that we can deal with different format of the third-variables. For the fitted models $g_p$, we proposed to use smoothing splines, so that nonlinear relationships and low-level interactions can be considered in the model fitting. $\mathbf{\Pi }$ is the joint distribution of $\mathbf{M}$ given X, which has a mean vector $\mathbf{g}(x_i,M{O}_i)$ and variance-covariance matrix Σ.
3. At each level, k, of the moderator, estimate the third variable effect, $k=1,\dots ,K$:

   1. To estimate the total effect at level k within the subpopulation where $M{O}_i$=k:

      1. Randomly draw N xs from $D_x$ with replacement, denote that as $\{x_j,j=1,\dots ,N\}$.
      2. Randomly draw $(M_{1j1},\dots ,M_{Pj1}{)}^T$ given $X=x_j$ from Equation (2) for $j=1,\dots ,N$.
      3. Randomly draw $(M_{1j2},\dots ,M_{pj2}{)}^T$ given $X=x_j+a$ from Equation (2) for $j=1,\dots ,N$.
      4. The total effect at level k of MO is estimated as $T{E}_k=\frac{1}{Na}\left[\sum _{j=1}^{N}f\right(x_j+a,M_{1j2},\dots ,M_{Pj2},M{O}_i=k)-\sum _{j=1}^{N}f(x_j,M_{1j1},\dots ,M_{Pj1},M{O}_i=k\left)\right].$
   2. To estimate the direct effect not through $M_p$, for $p=1,\dots ,P$:

      1. Randomly draw $2N$ $M_{p}s$ from the observed $\{M_{pi},i=1,\dots ,n\},$ with replacement, denote that as ${\tilde{M}}_{pj},j=1,\dots ,N$.
      2. Randomly draw $(M_{1j1},\dots ,M_{p-1,j1},M_{p+1,j1},\dots ,M_{p_{j}1}{)}^T$ given $X=x_j$ from distribution derived from Equation (2), where $x_{j}s$ were obtained at step (1)(a), $j=1,\dots ,N$.
      3. Randomly draw $(M_{1j2},\dots ,M_{p-1,j2},M_{p+1,j2},\dots ,M_{p_{j}2}{)}^T$ given $X=x_j+a$ from distribution derived from Equation (2).
      4. The direct effect not form $M_p$ at level k of MO, $D{E}_{k,\mathrm{\setminus }{M}_p}$ is estimated by $D{E}_{k,\mathrm{\setminus }{M}_p}=\frac{1}{Na}\left[\sum _{j=1}^{N}f\right(x_j+a,M_{1j2},\dots ,M_{p-1,j2},{\tilde{M}}_{pj},M_{p+1,j2},\dots ,M_{Pj2},M{O}_i=k)-\sum _{j=1}^{N}f(x_j,M_{1j1},\dots ,M_{p-1,j1},{\tilde{M}}_{p,(N+j)},M_{p+1,j1},\dots ,M_{Pj1},M{O}_i=k\left)\right].$
   3. The average indirect effect of $M_p$ at level k is $I{E}_{k,p}=T{E}_k-D{E}_{k,\mathrm{\setminus }{M}_p}$.

The following are some comments for the algorithm:

• If there is an interaction effect of the moderator with the exposure variable or with any of the third-variable on the outcome, the MART modeling should be able to pick up the interaction(s) automatically. By setting a limit to the depth of trees in MART, we can restrict the level of interactions that can be considered. For example, a tree with depth=3 allows for two-way interactions but not three-way or any higher rank interactions.

• The interaction effect of exposure and the moderator on any third-variable is taken care by the resampling of third-variables at each combined level of x and MO.

• The levels of a continuous moderator can be decided according to the analysis purposes. Usually the levels can be chosen by the quartiles/quintiles of the moderator within the original data. Step 3(1)(b) in the above algorithm will be conducted within the kth interval of the moderator, where the intervals are exclusive and the combination of the K intervals covers the range of the moderator.

• When there are multiple moderators, the moderators are combined to from one moderator where the levels of the combined moderator are any combinations of the levels of the original multiple moderators.

• Bootstrap method can be used to measure the variances of estimated third-variable effects at each level of the moderator.

• The above algorithm is for a single exposure variable. It can be extended to a multi-categorical exposure and multiple exposures. Yu et al. [18,20] have proposed the general TVEA method to deal with multiple exposures of any forms. In the moderation analysis, the general TVEA is performed to estimate third-variable effects at different levels of the moderator.

2.2. The R package mma

The mma package, available on the Comprehensive R Archive Network (CRAN), has been generated for the implementation of general TVEA. Readers are refereed to Yu et al. [22,23] for more details on the package. Both linear and nonlinear predictive models can be used for TVEA. A more recent version of the mma (version 8.0−0, published after March 28, 2019) package includes the algorithms for moderation analysis within TVEA. The mma package provides generic functions to summarize the inference results of third-effects estimates at each level of the moderator. The inference includes the estimates of each third-variable effect (direct/indirect effect), standard deviations and confidence intervals. In addition, plot tools are provided to help explain the direction of third-variable effect that explains the exposure-response relationship, and the change of the TVE at different levels of the moderator. Yu et al. [19] discussed in detail on how to use the package. We illustrate the use of the package for moderation analysis and explain the results from the package in Section 4.

3. Illustration of moderation effects

In this section, we use simple simulations to show moderation effects at different formats. All codes for simulations are provided in the supplementary material. As shown in Figure 1, the moderation effect can be of three formats. We illustrate the effect of the three types of moderation effects from the outcome of the mma package.

3.1. Direct moderation

When the moderator is at different levels, the direct effects of the exposure variable on outcome could be different. This type of moderation is called the direct moderation effect. The effect can be inferred in predictive models by including an interaction term of the exposure variable and the moderator. In the following simulation, we have one third-variable ( $m_i$), one moderator ( $m{o}_i$), a predictor ( $pre{d}_i$) and a covariate ( $c_i$). The data are generated in the following way:

$$\begin{array}{rl}{c}_i,pre{d}_i,m{o}_i& \stackrel{ind}{\sim }N(0,1);i=1,\dots ,n\\ m_i& =pre{d}_i+{ϵ}_{1i};\\ y_i& =pre{d}_i+m_i+c_i+m{o}_i+m{o}_i\cdot pre{d}_i+{ϵ}_{2i};\end{array}$$

where ${ϵ}_{1i}$ and ${ϵ}_{2i}$ are independent random errors with a standard normal distribution. All n are set as 200 in the simulations. In moderation analysis, we generally report the TVE at different levels of the moderator since a moderation effect is basically an interaction effect. In this simulation, the moderator is numerical. By default, the mma package evenly divide the moderator to five quantiles and report the moderation effect at each of the quantiles. Let $q_k$ denote the kth quantile of the moderator. Theoretically, the direct effect at the kth quantile of the moderator should be $1+E(m{o}_i|m{o}_i\in q_k)$ for this simulation. The R package mma used two methods to predict the outcome: the linear method uses the generalized linear models, while the nonlinear method use the MART. If the linear method is used for the moderation analysis, the interaction term predictor×moderator needs to be added in the general TVEA as a covariate. If the nonlinear method is used, adding the interaction is not necessary. But if it is believed that there is a direct moderation effect, it would be more effective to add the interactive term as a covariate. Figure 2 shows the direct effect (DE) of pred at different level of mo from MART and from linear regression separately. The y-axis is the expected mo at each quantile. The x-axis gives the estimated direct effect with the confidence interval. Both graphs show an increasing trend of direct effect with the moderator as expected. Linear model is more efficient since the simulation was based on linear models.

Figure 2.

Direct Moderation Effect from Simulation 1. The y-axis is denoted by the mean of the moderator at each quantile. The x-axis gives the estimated direct effect and its confidence interval at different levels. The true value is denoted by a red bar.

3.2. Exposure-moderated TVE

Next we illustrate the exposure-moderated TVE, where there is an exposure-moderator interactive effect on the third-variable. The data set is generated by:

$$\begin{array}{rl}{c}_i,pre{d}_i,m{o}_i& \stackrel{ind}{\sim }N(0,1);i=1,\dots ,n\\ m_i& =pre{d}_i+m{o}_i+m{o}_i\cdot pre{d}_i+{ϵ}_{1i};\\ y_i& =pre{d}_i+m_i+c_i+{ϵ}_{2i};\end{array}$$ (3)

Using the ‘mma’ package, if the exposure variable is continuous, the relationship between the exposure variable and potential third-variables adjusting for other covariates is individually fitted by smoothing splines (Equation (2)). Therefore for both linear and nonlinear method, the interaction terms of the exposure and the moderator should be included as a covariate to fit the third-variable. Readers are referred to the supplementary material for how to set this up. The ‘mma’ package provides a function form.interaction that can help to form interaction terms between any two variables. For a categorical variable of k levels, the function first transforms the variable into k−1 binary variables and then form the interactive terms by multiplying each binary variable with the other variable. Thus moderation effect can be inferred for combinations of any types of variables. The upper panel of Figure 3 show the indirect effect of m from MART and the linear model separately.

Figure 3.

Indirect Moderation Effect from Simulations 2 (upper panel) and 3 (lower panel). The y axis is denoted by the mean of the moderator at each quantile. The true value is denoted by a red bar. The x-axis is the estimated indirect effect and its confidence interval at each level of the moderator.

The plot function delineates how the indirect effect forms from the aspects of the exposure-third variable relationship and the third variable-outcome relationship separately at different levels of the moderator variable. Figure 4 shows how the relationship between m and pred changes at different quantile of mo. We see that the slope increases as mo increases, which correctly catch the exposure-moderator interaction effect on the third variable.

Figure 4.

Exposure-third variable relationship at different levels of the moderator for simulation 2. The lines are fitted between the predictor and m at different levels of the moderator.

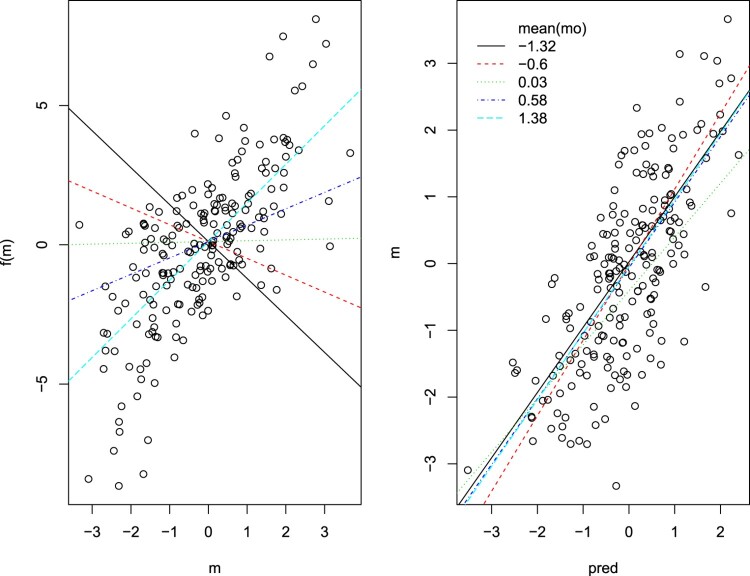
3.3. Third-variable-moderated TVE

Finally, the third-variable-moderated TVE means that there is an third variable-moderator interaction effect on the outcome. Therefore, the indirect effect of the third variable would be different at different level of the moderator. The data set is generated by:

$$\begin{array}{rl}{c}_i,pre{d}_i,m{o}_i& \stackrel{ind}{\sim }N(0,1);i=1,\dots ,n\\ m_i& =pre{d}_i+{ϵ}_{1i};\\ y_i& =pre{d}_i+m_i+c_i+m{o}_i+m{o}_i\cdot m_i+{ϵ}_{2i}.\end{array}$$

Compared with the data generation scheme in Section 3.2, for given mo, the indirect effect of m is also $E(m{o}_i|m{o}_i\in q_k)+1$. However the moderation effect comes from the interaction effect of m and mo to the outcome. The lower panel of Figure 3 shows the indirect effect of m at different levels of mo by MART and by linear regression respectively. Of the same method and equivalent third-variable indirect effect, the confidence intervals are comparable for the exposure-moderated and the third-variable-moderated TVE.

Figure 5 is drawn by the plot function of the ‘mma’ package. It shows the pred-m and m-y relationship at each level of the moderator from the linear model. We see that the pred-m relationship is the same but the m-y relationship is different at different level of the moderator.

Figure 5.

Exposure(x-axis)-third variable(y-axis) (right panel) and third variable(x-axis)-outcome(y-axis) (left panel) relationships at different level of the moderator for simulation 3. A line is fitted at each level of the moderator.

4. Explore the trend of racial disparity in ODX utilization among breast cancer patients

We are interested to know if the use of ODX is different between blacks and whites. If there is a racial disparity, we would like to know what factors contribute to the difference. In addition, whether the disparity changes over time and whether the contribution from third variables in explaining the racial disparity changes over time.

4.1. Data description

The Surveillance, Epidemiology, and End Results (SEER) Program is a population-based cancer surveillance program, sponsored by the national cancer institute, which routinely collects standardized demographics information, primary tumor characteristics, first course of treatment, and survival information for all cancer patients through funded SEER cancer registries. It covers approximately 34% of cancer cases of the US population. SEER is an authoritative source for cancer statistics in US (https://seer.cancer.gov). Genomic Health Inc. (Redwood City, CA) is a unique company that provides the ODX test in the United States (US). SEER program made an effort to link the ODX dataset from the Genomic Health Inc. with SEER data on breast cancer patients diagnosed between 2004 and 2015. More information about the data linkage and available variables can be found at Petkov et al. [15].

In this study, we are interested in finding out whether there is a racial disparity in ODX utilization and whether the racial difference changes with time. For this purpose, we select cases from the linked dataset that includes non-Hispanic white or black women diagnosed with American Joint Committee on Cancer (AJCC) stage I, II or III, ER+/PR+ and HER2-, and negative lymph node breast cancer. Since SEER began collecting HER2 information from the year 2010, we include cases that were diagnosed between 2010 and 2015 only. In addition, we exclude cases that were identified from death certificate or autopsy only.

Out of 101, 104 eligible cases, 14.61% were diagnosed in 2010, 15.89% in 2011, 16.54% in 2012, 17.23% in 2013, 17.51% in 2014 and 18.21% in 2015. A patient is categorized to have an ODX testing if the ODX test was performed within one year after the breast cancer diagnosis. Table 1 shows the proportion of the ODX use separated by race and diagnosis year. We found that in general, the proportion of breast cancer patients who had the ODX test increased over time regardless of race and ethnicity. The proportion of ODX testing was higher for NHWs than NHBs in all the years, but the racial differences were diminished and became not significant in 2013 and after.

Table 1.

Racial differences of using the ODX test by year.

year	non-hispanic black	non-hispanic white	p-value
2010	$34.27\mathrm{\%}$	$38.56\mathrm{\%}$	0.0012
2011	$37.94\mathrm{\%}$	$42.03\mathrm{\%}$	0.0009
2012	$38.75\mathrm{\%}$	$43.32\mathrm{\%}$	0.0001
2013	$43.03\mathrm{\%}$	$43.59\mathrm{\%}$	0.6397
2014	$44.27\mathrm{\%}$	$45.08\mathrm{\%}$	0.4985
2015	$43.98\mathrm{\%}$	$45.07\mathrm{\%}$	0.3428

Other variables used in this study include demographic information for patients (e.g. age and insurance), cancer characteristics (e.g. tumor size and grade), and population characteristics at the county level (e.g. rural/urban and proportion of household below the federal poverty level). Besides race, year of diagnosis and the outcome variable (ODX test), we include 31 variables that can potentially explain the use and the racial disparity in the use of ODX test. In the analysis, we did not include factors on the first-course treatment because ODX test can guide the choice of treatment but not the reverse. Since we are interested in the trend of the racial disparity in ODX and how the effect of contributing factors in explaining the racial disparity varied with year, year-of-diagnosis was used as the moderator. A third-variable is defined as a variable that is significantly related to the exposure variable (race), and significantly related to the outcome (having an ODX test within one year of diagnosis). A covariate is a variable significantly associated with the outcome, but not with the exposure variable. We first tested each variable to identify potential third-variables and covariates. The significance level of tests is set at 0.05. Table 2 shows the potential third-variables and covariates as a result of tests.

Table 2.

Racial differences of using the ODX test by year.

Potential Third Variables
Demographic Variables	age at diagnosis, marital status, insurance
Tumor Characteristics	cancer grade, AJCC stage, tumorsize
County-Level (ACS)	% persons age $<18$, % families below poverty, % unemployed, median
Environmental factors	household income, % $<9th$ grade, % < high school, % at least bachelors
	degree, % household $>1$ one person/room, % foreign born, % language
	isolation, % no migration in the year, % move within county, % move within
	state, % move out-of-state, % move from out-of-US, Rural-Urban code
Potential Covariates	histology type

4.2. Third-variable effects and the trend

We use the R package mma to explore the racial disparities in ODX test over the years 2010 to 2015. Since there are potential interaction effects between year and other factors, the third-variable effects need to be explained at each year. In model fitting, there is no need to include the year x third-variable interaction, MART will find interaction automatically. Figure 6 shows the third variable effects of all variables at 2010, ordered from the biggest to the smallest effect. A 95% confidence interval for each estimated third-effect is also shown in the bar plot. The estimated total effect is negative, meaning that compared with non-Hispanic whites, the blacks have a lower probability of using the ODX test. If the third effect is negative as the total effect, it means that if blacks and whites could have the same distribution of the third-variable, the racial disparity in ODX usage can be partially explained by the variable. On the contrary, if a third-effect is positive, it means that if the variable can be manipulated to be equally distributed between blacks and whites, the disparity in ODX would increase, rather than reduce. These variables are called depressors. For example, age is a depressor. For the year 2010, variables % persons age $<18$, insurance, % move out-of-state, % no migration in the year, % foreign born, % move within county, and % household >1 one person/room have significant third-variable effects to explain the racial disparity in ODX exam. We explain the direction of some third-variable effects later in this section. After controlling for all other variables, the direct effect of race was still significantly negative. That is, there was remained racial disparity in ODX test that could not be explained by the variables included in this study. The figures for other years are shown in the supplementary material.

Figure 6.

Third-variable effect of the racial disparity in ODX test in the year 2010. The x-axis denotes the estimated third-variable effect with the confidence intervals.

To compare the change in racial disparity in ODX usage over years, the mma R package provides a summary and plot tool to describe the trend. The left panel of Figure 7 describes the direct effect of race with a confidence interval after adjusting for other variables in each year. We find that there was a significant unexplained racial disparity in ODX test, but the effect decreased from the year 2010 to 2015. The mma package provides a ‘test.moderation’ function, that checks if there is significant direct moderation effect between the predictor (race) and the moderator (year) in explaining the use of ODX. The test with the interaction term in the generalized linear model shows a p-value $<0.001$ and the H-statistics is 0.0427. H-statistics is the measure of the significance of the interaction effect in MART. To interpret the H-statistics, readers are referred to Friedman and Popescu [6].

Figure 7.

The unexplained racial disparity (left) and the indirect effect of insurance status on the racial disparity in ODX test over the years 2010 to 2015. The x-axis denotes the estimated effects (direct or indirect effect) and confidence intervals.

The third-variable effects can be similarly described using the plot tool provided by mma. An interesting plot is the indirect effect of insurance. We see in the right panel of Figure 7 that insurance can significantly explain part of the racial disparity. In addition, the indirect effect increased from 2010 to 2013 and then reduced in 2014 and 2015. This might be explained by that from 2012, medicare started to cover a wider range of ODX test. Also the Obama care act came into force in 2014. If readers are interested, please contact authors for plots for all other third-variables.

Lastly, we use the plot tool to explore how third variables explain the racial disparity in ODX over the years. We use age-at-diagnosis as an example. Figure 8 shows the interactive effect of year and age on the odds of using ODX. Looking horizontally over the diagnosis years, the log-odds of using ODX increased with age until around 40, when the use of ODX reached the highest odds. The odds kept high until around the age of 60, when the odds began to decrease with age. MART caught the nonlinear relationship between age and the log-odds of using ODX. Look vertically over the age, the color seems to get lighter over the years, indicating that in general, the odds of using ODX increased over year at the same age. Next we check if the age at diagnosis is different between blacks and whites. Figure 9 displays the age distributions separated by white or black population in the year 2010. It shows that there were a larger proportion of black patients diagnosed between the age 40 and 60, during which patients were more likely to use the ODX diagnosis to guide treatment. Therefore, if the age at diagnosis could be manipulated to distribute similarly between blacks and whites, the racial disparity in ODX would become large rather than be reduced. The age at diagnosis for blacks and whites had the same pattern of distribution for other years and the density plots for each year are provided in the supplementary material. The plots depicting the direction of other third-variable-effect are also included in the supplementary material. The plots can help better understand the third-variable effect and provide explanations on mechanism underlying the racial disparity in ODX test.

Figure 8.

The interactive effect of year and age on the odds of using ODX.

Figure 9.

The age distribution by race in 2010.

5. Conclusions and future works

We developed an inference method with TVEA to make inference on interaction/moderation effect. We illustrate the moderation effect at different scenarios using the ‘mma’ package that extends the analysis of third-variable effect to moderation effect. The proposed method can automatically identify significant moderation effect and allows for potential nonlinear relationship among variables. The method is used to explore the change of racial disparities in the use of ODX test among breast cancer patients from 2010 to 2015. We found that the unexplained racial disparity decreased over the years and some interesting trends of third variables effect on the racial disparity. A limitation of this research of racial disparity in the use of ODX among breast cancer patients is that only early stage breast cancer patients can benefit from the ODX diagnosis. However, there is a racial disparity in the breast cancer stage at diagnosis. Black people are more likely to be diagnosed at a later stage. Therefore, the stage of cancer has a confounding effect on the racial disparity of using ODX. As a future plan, we would use the diagnosis at late stage as a competitive risk when exploring the racial disparity in ODX usage. Another field of future research is to extend the third-variable-effect analysis and the moderation analysis to multilevel models so that hierarchical data structure (e.g. environmental factor and individual characteristics) can be considered in data analysis.

Funding Statement

This work was supported by National Institute on Minority Health and Health Disparities [R15MD012387].

Disclosure statement

No potential conflict of interest was reported by the authors.