Matching 3D Facial Shape to Demographic Properties by Geometric Metric Learning: A Part-Based Approach

Abstract

Face recognition is a widely accepted biometric identifier, as the face contains a lot of information about the identity of a person. The goal of this study is to match the 3D face of an individual to a set of demographic properties (sex, age, BMI, and genomic background) that are extracted from unidentified genetic material. We introduce a triplet loss metric learner that compresses facial shape into a lower dimensional embedding while preserving information about the property of interest. The metric learner is trained for multiple facial segments to allow a global-to-local part-based analysis of the face. To learn directly from 3D mesh data, spiral convolutions are used along with a novel mesh-sampling scheme, which retains uniformly sampled points at different resolutions. The capacity of the model for establishing identity from facial shape against a list of probe demographics is evaluated by enrolling the embeddings for all properties into a support vector machine classifier or regressor and then combining them using a naive Bayes score fuser. Results obtained by a 10-fold cross-validation for biometric verification and identification show that part-based learning significantly improves the systems performance for both encoding with our geometric metric learner or with principal component analysis.

I. INTRODUCTION

Recent advances in DNA phenotyping of the human face have increased interest in the field and attracted the attention of forensic biologists and anthropologists [1]. E.g., in forensics the prediction of the facial appearance of an unknown person from biological material found at a crime scene could be matched with known faces of subjects of interest, e.g., suspects. This process is referred to as facial recognition from DNA. However, directly predicting the unknown face from DNA remains a challenging and unsolved problem. Nevertheless, the human face contains substantial information about both genetic and environmental factors related to the identity of a person. This makes the face a widely used and accepted subject for biometric analysis. In a recently proposed paradigm shift to facial recognition from DNA, a biometric system that aims to predict DNA-related properties from facial images with known identity was proposed [2]. These properties can then be matched to the properties extracted from the DNA of an unidentified individual. The difference to predicting an unknown face from DNA, as in DNA phenotyping, is that given existing faces (e.g., from a facial gallery of known identities) are now classified into DNA-based properties and classes.

Following the paradigm shift, this paper is an extension of work originally presented at ICPR 2020 [3] in which a 2-step neural based pipeline for matching 3D facial shape to multiple demographic properties was proposed. The properties that were considered can either be decoded directly - sex, genomic background (GB) - or inferred indirectly (e.g., using epigenetics) – age, Body Mass Index (BMI) - from DNA. The first step of the pipeline consisted of a triplet loss metric learner to compress facial shape into a lower dimensional embedding while preserving information about the property of interest. The second step was a multi-biometric fusion by a fully connected neural network. The fusion network predicted whether a 3D face, represented by its lower dimensional encoding, and a given set of demographic properties belonged to the same individual or not. Although results proved this pipeline to be an effective approach for face to DNA mapping, the impact of different localized facial regions was understudied. The proposed method took the face as a whole into account and neglected the fact that the human face comprises multiple integrated parts that are distinct from each other based on their anatomy, embryological origin, and function. Inspired by this biological background information, the main contribution of this extension is the implementation of a global-to-local part-based approach that improves the metric learning step of the previously proposed pipeline. In other words, the lower dimensional metric embeddings are learned by a geometric metric learner (GML) for multiple facial segments. The embeddings of all segments are then concatenated to form a final representation for each property. Other technical contributions of this extension include: 1) an improved implementation of the GML using an updated convolution technique which facilitates more efficient training of the GMLs; 2) an added a singular value decomposition layer to the GML for imposing orthogonality on the metric space as to avoid redundant information across dimensions and 3) an identification analysis which is carried out in addition to the previously used verification analysis for the evaluation of the models.

II. RELATED WORK

A. Metric Learning

In many computer vision problems, projecting raw data into a compact yet meaningful space is crucial. Metric learning refers to the task of learning a semantic representation of data, based on the similarity measures defined by optimal distance metrics [4]. With the recent success of deep learning techniques, researchers of the field have introduced multiple deep metric learning tools [5], [6], [7], [8], [9]. Among those commonly used for face recognition, verification or person re-identification [7], [10], [11], are Siamese [12] and Triplet networks [13], which are twin or triple architectures with identical subnetworks. Some studies [14], [15], [16] suggest that the combination of a classification and verification loss can have a superior performance specifically for person re-identification. However, [17] claims that triplet loss and its variants outperform most other published methods by a large margin. The importance of a proper triplet mining strategy is a topic of discussion in the literature. [13] uses an online mining strategy of the negative samples that ensures a consistently increasing difficulty throughout the training within a face recognition system. In [7], however, a moderate mining for person re-identification is incorporated. Inspired by the literature, in this work, triplet architectures are adopted to learn compact embeddings of 3D facial meshes.

B. Geometric Deep Learning

This work studies 3D mesh data, which means regular deep learning techniques are not directly applicable. One option suggested in literature is to transform the data to the Euclidean domain and use UV- or voxel-representations [18], [19], [20]. However, these transformations often involve a loss of data quality. Another option is to learn from the point cloud as in [21], but since this approach ignores the local connectivity of the mesh, it also comes with significant information loss. Instead of transforming the data to suit existing techniques, it is also possible to adapt those techniques to accept the data in its original form. To this end, Geometric Deep Learning was introduced.

Geometric Deep Learning is a term that refers to methods that are designed for applying deep learning techniques onto non-Euclidean domains such as graphs and manifolds [22]. The application of deep learning methods to non-Euclidean data poses several problems. The first challenge is in defining a convolutional operator for graphs or meshes. Within geometric deep learning, there are two tracks to address this problem. On the one hand, spectral methods [23] involve those that are based on the frequency domain. The main drawbacks of these methods for shape analysis are that 1) the filters are basis dependent and can vary significantly for small perturbations on the shape, and 2) that there is no guaranteed spatial localization of the filters. However, these drawbacks can be tackled by spectrum-free approaches [24], [25] that represent the filters via a polynomial expansion instead of operating explicitly in the frequency domain [22]. On the other hand, spatial methods [26], [27] define a local system of coordinates along with a set of weighting functions. This results in a patch-operator that can be applied to each vertex of the graph or manifold. The second challenge is defining a pooling operator. Several graph coarsening or mesh decimation methods that are suitable for this task were proposed by [28], [29], [30].

In [31] an elegant and simple spatial convolution operator in the shape of a spiral defined on a mesh is introduced. This spiral acts as an anisotropic filter that slides over the mesh similar to convolutional filters on Euclidean domains. In [32] this technique was successfully applied to develop a generative model that is able to learn 3D deformable shapes with fixed topology such as facial and body scans. In a follow-up paper [33] a more efficient training and definition of the spiral convolutions was introduced. In this work, we extend the use of the last approach to discriminative models that are trained to differentiate between facial shapes based on DNA-related soft traits or properties.

C. Part-Based Learning

In the literature, part-based approaches have been employed, mostly for 2D images, in which separate models are trained for local regions such as the eyes, nose, mouth and chin, along with the entire face [34], [35], [36], [37]. Defining local regions on high resolution 3D facial meshes is challenging. A data-driven, hierarchical 3D facial surface segmentation using spectral clustering was presented in [38]. The segmentation was based on ~ 8,000 3D facial images of individuals from an unselected/non-clinical European population. The segmentation sequentially splits the vertices of the facial surface into smaller subsets called segments, such that covariation within segments is maximized and covariation between segments is minimized. We use this segmentation to extract metric embeddings for each segment separately.

D. Face-to-DNA Matching

In recent work [2], Sero et al. introduced a novel approach for matching between different identifiers (facial shape and DNA). Multiple face-to-DNA classifiers were trained, followed by a classification-based score-level fusion. In the first step, binary support vector machine (SVM) classifiers of 3D facial images were trained for the following DNA-related properties: sex, age, BMI, genomic background represented by 987 principal components, and individual genetic loci that are discovered to be associated with facial variation in a genome-wide association scan (GWAS). The face was analyzed in a global-to-local way by performing a hierarchical segmentation of the facial shape. For each segment, a PCA model was built to construct unsupervised multi-dimensional shape features. Association studies based on canonical correlation analysis were performed to investigate the correlation between each of the segments and each of the demographic properties. Significant segments were then used to train the SVM classifiers which generate matching scores for each of the properties. Subsequently, the scores of different properties were fused into an overall matching score using a classification-based naive Bayes biometric fuser. The output of the biometric fuser indicates how likely it is that a given face and set of properties belong to the same individual. This work has proven that matching different identifiers can lead to a successful biometric system. In our previous paper [3], we proposed an alternative approach as a 2-step neural-based pipeline for 3D data that is efficiently trainable with fewer data partitions, and at the same time improves the performance of the existing biometric system. In essence, this work is an integration of the part-based approach in [2] with the more advanced GML from [3].

III. MATERIALS AND METHODS

A. Dataset

The dataset used in this paper originated from studies at Pennsylvania State University (PSU) and Indiana University-Purdue University Indianapolis (IUPUI). A total sample size of n = 2,145 is used. The dataset includes texture-free 3D facial images, self-reported properties such as sex, age and BMI at the time of the collection, and genotypic data from individuals. The majority are female (68%), the age range is from 5 years old to 80 years old with an average of 27.39 years, and the BMI ranges from 11.87 kg/m² to 62.11 kg/m² with an average of 25.03 kg/m². Recruited individuals are genetically heterogeneous, which implies that they originate from different background populations and admixtures thereof (e.g., European, Afro-American).

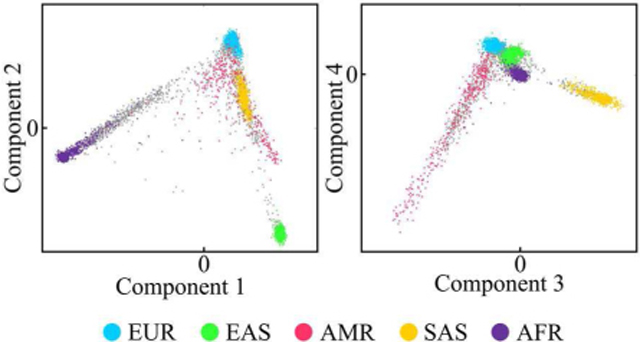
Study participants were sampled under Institutional Review Board (IRB) approved protocols (PSU IRB #44929, #45727, #2503, #4320, #32341 and IUPUI #1409306349) and were genotyped by 23andMe (23andMe, Mountain View, CA) on the v4 genome-wide SNP (single nucleotide polymorphism) array and on the Illumina Multi-539 Ethnic Global Array (MEGA), respectively. Genotypes were imputed to the 1000 Genomes (1KGP) Project Phase 3 reference panel. SHAPEIT2 was used for prephasing of haplotypes and the Sanger Imputation Server PBWT pipeline was used for imputation. SNPs are elements along your DNA that vary from one person to another. In [39], Li et al. proposed a method that projects SNP data onto a low dimensional SUGIBS space which captures the largest covariances in the data. Even though the construction of such a space is unsupervised, it results in a layout that co-aligns with population background. For this work, a 25-dimensional SUGIBS space based on the genetic data from the 1KGP was constructed using approximately 3.7M SNPs. Subsequently, the participants from our dataset were projected onto that space (Fig. 1). This resulted in an array of 25 components representing genomic background for each participant.

Fig. 1.

Scatterplot showing the first four GB components for our dataset (gray) and labeled 1KGP reference dataset. Populations: EUR = European, EAS = East Asian, AMR = Ad Mixed American, SAS = South Asian, AFR = African.

The 3D images were captured using 3DMD or Vectra H1 3D imaging systems. Participants were asked to close their mouths and keep a neutral expression. A spatially dense registration is performed on the images using MeshMonk [40]. Images are purified by removing hair and ears. Afterwards, five landmarks are roughly positioned on the corners of the eyes, nose tip and mouth corners to guide a rigid surface registration of an anthropometric mask using the Iterative Closest Point (ICP) algorithm. Then, the mask, that consists of 7,160 quasi-landmarks, is registered to the faces, using non-rigid ICP, which leads to obtaining meshes with the same topology across the dataset. Meshes are then symmetrized by averaging them with their reflected image. Finally, Generalized Procrustes Analysis is performed to eliminate differences in scale, position and orientation [41].

B. Methodology

Our proposed triplet loss network takes a 3D facial shape and a property as input. The network encodes the face into a lower dimensional embedding which is structured according to the property of interest, meaning that the embeddings of faces with a similar label are closer to each other than those with different labels. The encodings of the faces are then used as input to train an SVM classification or regression model. Finally, the SVM scores for the different properties are combined and matched with properties extracted from DNA using a naive Bayes score fuser (Fig. 2). The output of the score fuser is a matching score which represents the probability that the properties extracted from face and DNA match, or belong to the same individual, or not.

Fig. 2.

Pipeline for matching facial shape with DNA-related properties. The GMLs extract low-dimensional embeddings from facial shape, which are then passed onto SVMs. The scores obtained by the SVMs are matched with DNA-related properties using a naive Bayes score fuser.

1). Triplet Selection:

A separate triplet network is trained for sex, age, BMI, and GB. The networks are trained with triplets of (anchor, positive, negative), where anchor and positive are samples from the same class, while the negative sample is from a different class. However, this definition is not easily applicable to properties represented by continuous values (age, BMI and GB). Inspired by Jeong et al. [42], samples for age and BMI are considered positive when their label is within a certain distance from the label of the anchor, and negative otherwise. The distance thresholds for age (T = 10) and BMI (T = 2) were selected after experimenting with multiple values between [1:20] for age and [1:5] for BMI. The continuous GB components were transformed to binary vectors by a threshold of zero. GB is the only multi-component property. To take the correlation between different components (Fig. 3a) into account, a single triplet network is trained for all 25 components jointly. In each training batch, triplets are generated with respect to one specific component. This component is selected according to a weighted random number generator, where weights are the inverse of their prediction accuracy at the previous epoch. Selecting a proper triplet mining strategy can have a significant impact on efficiency and accuracy of the training. After experimenting with different triplet mining strategies, random mining showed superior performances for all properties.

Fig. 3.

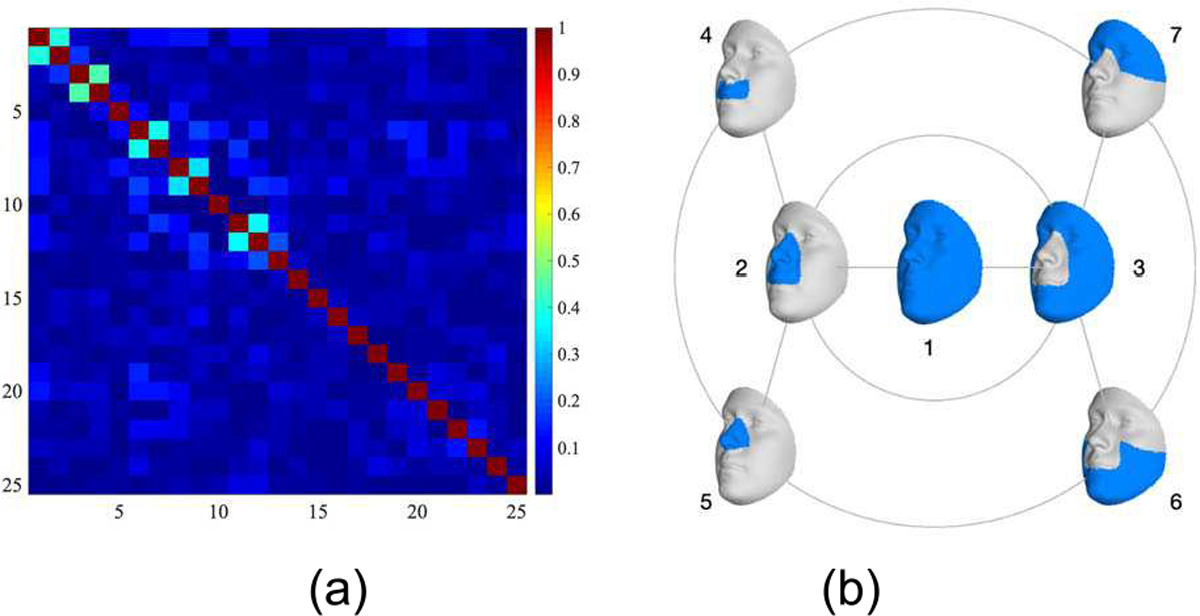
Correlation matrix for genomic background components. (b) The first three levels of the hierarchical segmentation of the face

2). Network Design:

We use geometric deep learning to learn directly from the 3D facial meshes and optimally utilize the data structure. The spiral convolution is used as a convolution operator, since, in contrast to most traditional graph neural networks, it produces anisotropic filters, and is especially powerful for shapes represented on a fixed topology. We use spiral convolutions as defined in [33]. For each vertex of the mesh, a spiral is defined by stepping to a random neighbor and then proceeding to form an outward spiral in counterclockwise direction until a fixed length of nine vertices is reached. This spiral will operate similar to a standard convolution filter. Regular 1D convolutions can be expressed as

$${(f\ast g)}_i=\sum _{j=0}^{J-1}{f}_{i-j}{g}_j+b$$ (1)

where f is the signal to which filter g with size J is applied and b is an added bias. For the spiral convolution, a weight is assigned to each point of the spiral. Using these weights, the spiral can act as a filter applied to each point of the mesh:

$${(f\ast g)}_i=\sum _{j\in spira{l}_i}{f}_j{g}_j+b$$ (2)

The weights of the spiral filters are learned by the network in the backpropagation step.

Aside from the convolution operator, a pooling operator for meshes must be introduced. Until now, most implementations for geometric deep learning rely on established mesh decimation techniques that reduce the number of vertices such that a good approximation of the original shape remains, but they result in irregularly sampled meshes at different steps of resolution. We in [3], however, developed a 3D Mesh down- and up-sampling scheme that retains the property of equidistant mesh sampling. This is done so under the assumption that convolutional shape filters might benefit from the constant vertex density along the surface, such that they become more equally applicable on different regions of the shapes under investigation. This may improve the learning process, alongside the generalizability of the shape filters. The sampling scheme is based on the remeshing technique proposed in [43] and is computed by the following steps (Fig. 4)

1. The 3D mesh is mapped to a 2D unit square by means of a conformal mapping [44][45]. The boundary constraints forces all vertices at the boundary of the mesh to be mapped to one of the sides of the unit square.

2. The vertices of the original 3D meshes are distributed equidistantly over the surface of the shapes. However, as a consequence of the conformal mapping, some regions more than others, such as the nose (indicated by a red circle in Fig. 4), are sampled more densely in the 2D representation. In an attempt to correct for this, and therefore to avoid losing information in these regions, the points are redistributed over the Image plane. A vector field is created to move the points towards a better distribution. Points lying close to each other, will push their neighbors away, while points far away from each other will pull their neighbors closer. Further details on the redistribution process are provided in [3].

3. The irregular 2D mesh is transformed to the Euclidean domain by interpolation with barycentric coordinates, resulting in three arrays containing x-, y- and z-values for each point.

4. New meshes at different levels of resolution are constructed by defining a low-resolution base mesh which is then further refined. The base mesh consists of five vertices: four vertices at the corners of a unit square and one central vertex that is placed at the tip of the nose in the output of step (ii). Each side of the square serves as an edge and all corners are connected to the central vertex. The refinement is done with loop subdivision [46] by splitting each triangular face of the mesh into four smaller triangles by connecting the midpoints of the edges. Figure 5 shows meshes at different levels of resolution.

5. Finally, the meshes generated in step (iv) are reformed to represent the original facial shape by linear interpolation over the x-, y- and z-values in the output arrays of step (iii).

Fig. 4.

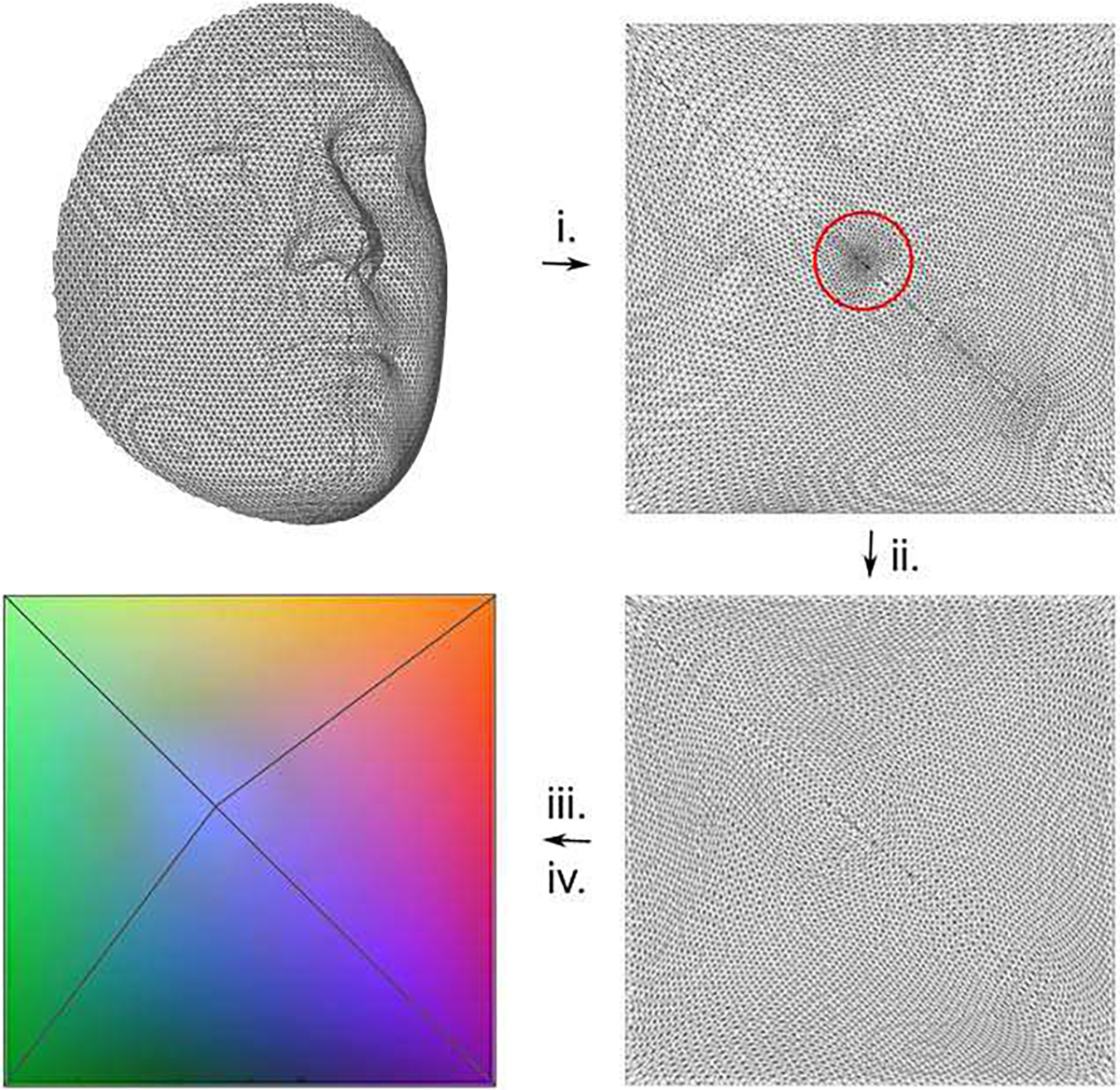
Steps for generating the mesh sampling scheme. The red circle indicates a densely sampled region as a result of the conformal mapping in step (i). To avoid losing information in these regions, the points are redistributed over the image plane in step (ii). The result of step (iii) is displayed as an RGB image where different colors represent different dimensions (R = x-values, G = y-values, B = z-values).

Fig. 5.

GML network architecture consisting of four spiral convolutional layers, each followed by a down-sampling step, one fully connected layer and a low-rank singular value decomposition.

Since all faces in the database are represented on the same topology, the first two steps are executed only once on a canonical template mesh. Then, the Euclidean representation (step (iii)) is computed for every individual in the dataset and used to reconstruct the original shapes in step (v). These steps are executed once, as a preprocessing step before training.

The GML network (Fig. 5) consists of four spiral convolutional layers, comprising 64, 64, 64, and 128 filters, respectively. Each spiral convolutional layer is followed by a mesh sampling step. To further reduce the dimensionality, a fully connected layer is added after the last convolutional layer. Finally, a low-rank singular value decomposition (SVD) [47] is applied to the output of the fully connected layer. The output of the SVD projection is a compact latent space with uncorrelated dimensions, inspired by the orthogonality of the spaces constructed by PCA.

3). Part-Based Learning:

To implement the GML for facial segments, we adopted the first three levels of the modular segmentation from [38], leaving us with seven facial segments as shown in Fig. 3b. A 3D face is described as a manifold triangle mesh $M=(V,\mathcal{E},\text{Φ})$, where $V={\left\{v_i\right\}}_{i=1}^{8,321}$ is a set of 8,321 vertices defining the mesh geometry, and $\mathcal{E}$ and Φ are sets of edges and faces which define the mesh topology. Since all meshes in the dataset are represented on the same topology, $\mathcal{E}$ and Φ are fixed. Each segment c is a subset of the full face and is defined as $c=\{\left(V_c,{\mathcal{E}}_c,{\text{Φ}}_c\right)\mid V_c\subseteq V,{\mathcal{E}}_c\subseteq \mathcal{E},{\text{Φ}}_c\subseteq \text{Φ}\}$ where ${\mathcal{E}}_c$ and Φ_c are fixed and predefined. In the part-based approach, each 3D segment is processed separately by the GML. This means that for every facial mesh M, a set of embeddings is learned for each segment. Localized GMLs were implemented using 3D mesh-padding. More specifically, for the i^th individual, the facial data for training a GML on segment c, which is noted as $M_c^i$, consists of the corresponding vertices of the segment c padded with the vertices of the average face of all groups $M^{\widehat{\mu }}$. This is defined as

$$M_c^i=\{\begin{array}{l}\left(v_c^i,{\epsilon }_c,{\varphi }_c\right)\hfill \\ \left(v_{\widehat{\mu }},\mathcal{E}\backslash {\epsilon }_c,\text{Φ}\backslash {\varphi }_c\right)\hfill \end{array}$$

Using a part-based approach requires fusion of information across multiple facial segments. We use feature-level fusion by concatenating embeddings from all segments into one long vector. To maintain consistency, we keep the same number of dimensions for each part-based GML. This means, for sex, age, and BMI, a 4-dimensional embedding and for GB an 8-dimensional embedding is learned for each segment. There are seven segments in the first three levels of the hierarchical segmentation, therefore our final embeddings are 28-dimensional for sex, age, and BMI, and 56-dimensional for GB. Once embeddings are learned and fused for all properties, their concatenation serves as input to the next step of the pipeline which is consists of SVM classification followed by a naive Bayes score fuser.

4). Biometric Score Fusion:

In this paper, we improve the GML introduced in [3] by proposing a part-based GML to increase the capacity and richness of the low dimensional embeddings for each property. However, this means that the dimensionality of the concatenated part-based embeddings is seven times higher than for the full face only. To replicate the second step of our previously proposed neural pipeline [3] and train a fusion-net, the concatenated embeddings must be stacked together to form an even larger embedding vector as the input to the multilayer perceptron. This causes the number of model parameters of the fusion-net to increase significantly for the part-based approach. Unfortunately, we found that those larger models were prone to overfitting and practically hard to train with a limited dataset. Moreover, this extension does not only consider biometric verification, as in [3], but also evaluates the model in a biometric identification scenario. A replication of the pipeline presented in [3] (Suppl. 2), indicates that, as opposed to the biometric verification results, the identification results using the fusion-net are slightly lower than those for the linear fuser. This is not unexpected since the fusion-net was designed and trained specifically to validate or reject a match between two inputs, which resonates with the definition of a verification test. Therefore, due to the impractical training and low contribution of the fusion-net in previous experiments, we evaluate and compare the capacity of the part-based model in this paper with linear SVMs and a naive Bayes score fuser instead.

To implement the linear fuser, an SVM classification or regression model is trained that takes the stacked output embeddings of the part-based-GMLs of a property as input and provides a score value for that property. SVMs are used for both classification and regression, as they were the best performing models among multiple tested techniques which included linear discriminant analysis, SVM and K-nearest-neighbor for classification, and linear regression, SVM and regression trees for regression (data not shown). After training an SVM model for each property, the SVM scores are concatenated into one property vector which is then compared to a property vector extracted from DNA using a naive Bayes score fuser. To train the score fuser, a two-class classification is defined that predicts whether a combination of property vectors is a true (genuine) or false (imposter) match. In other words, the score fuser predicts whether the properties extracted from face and DNA belong to the same individual or not.

5). Training and Evaluation Strategy:

In order to evaluate our model, the dataset is divided into 10 folds (i) for cross-validation. For each fold, 10% of the data is devoted to the test set (test_i), and the remaining is used for training the GML, the SVM classifier/regressor and the naive Bayes score fuser. Hence, the training data is further split into three non-overlapping partitions ${\text{train}}_{\text{i}}^1(60\%)$, ${\text{train}}_{\text{i}}^2(20\%)$, and ${\text{train}}_{\text{i}}^3(20\%)$. We perform four experiments to evaluate both independent and combined effects of using our proposed GML and the part-based approach.

1. Full face PCA: The first experiment consists of three steps: 1) obtaining a lower dimensional representation of the 3D faces, 2) training classification and regression models for prediction of the properties, and 3) training a score fuser that combines prediction scores for different properties into a final matching score. 1) In the first step, the facial meshes are compressed into a compact representation by applying PCA to training set ${\text{train}}_{\text{i}}^1$. The result is a 20-dimensional embedding space, which corresponds to a captured variance of 95.3%. 2) Next, ${\text{train}}_{\text{i}}^2$ is used to train four independent SVMs for the four properties, respectively. Classification of sex and GB is done by binary, linear SVMs, and linear SVM regressors are used to predict age and BMI. Classification scores are calculated from the signed distance between each sample to the SVM decision boundary. Regression scores are signed values calculated from T- (|predicted-ground truth|), in which T refers to the distance threshold of 10 for age and 2 for BMI. 3) Finally, ${\text{train}}_{\text{i}}^3$ is used for training a naive Bayes score fuser which fuses scores from all properties into a single matching score. Step 2) and 3) remain unchanged for all four experiments, while the approach to compress data into a lower dimensional representation (step 1)) will differ across experiments.

2. Part-based PCA: The second experiment represents the related approach proposed in [2] and is designed to measure the influence of the part-based approach. In this experiment, as extension to experiment 1, a PCA space is constructed for each of the seven facial segments. The embeddings for the different segments are then concatenated to form a 140-dimensional representation. This combined embedding then serves as the input to the SVM classifiers and regressors.

3. Full face GML: The next experiment focuses on compressing 3D facial data using the GML and is therefore representative for the related method proposed in [3]. For each of the four properties, a GML is trained to construct a latent space that is structured according to the property of interest. The constructed latent spaces are 4-dimensional for sex, age, and BMI, and 8-dimensional for GB. Concatenating the latent spaces together results in a single 20-dimensional representation.

4. Part-based GML: The final experiment combines (ii) and (iii) to obtain a compression of the facial shape using both the GML and the part-based learning and is therefore representative of the proposed extensions in this work compared to [2] and [3]. To this end, 28 independent GMLs are trained, representing each of the four properties and each of the seven facial segments. The resulting embeddings of all models are concatenated into a 140-dimensional embedding.

All experiments are evaluated for seven independent tests, each with a different set of properties included. First, the performance is investigated for each property separately (4 out 7 tests). Then, age, BMI and GB are gradually added to sex in order build stronger multibiometric systems (remaining 3 out of 7 tests).

It is worth mentioning that the impact of (1) the updated spiral definition and (2) the orthogonality of the embeddings is not quantitatively evaluated because (1) the improved spiral definition primarily aids the efficiency of the training, thus causing shorter training times, but does not significantly change the functionality or performance of the network; and (2) we found that the imposed orthogonality of the embeddings had no significant influence on the outcome of the network. However, we still believe that this added orthogonality is an improvement of the network structure, since it guarantees that the embedding space is optimally used by minimizing redundant information.

IV. RESULTS AND DISCUSSION

Matching a known person to an unidentified DNA sample can be done in different ways. The most accurate approach is DNA profiling, in which DNA samples from different sources (e.g., crime scene and suspect) are compared to each other. However, in some cases, the DNA sample of a person of interest is not available. An alternative approach in such cases is to predict the phenotype based on the DNA which is called DNA phenotyping. Due to many unknowns in the facial effects of both genetic and non-genetic factors on facial morphology, predicting faces from DNA has not been successful so far. To tackle this problem, we create an intermediate latent space to which primary identifiers, which are characteristics that can reliably define a person’s identity, are projected [2], [3]. The projected identifiers are then matched against each other in the intermediate space. The primary identifiers of this study are facial shape and DNA. The intermediate embedding space is the space of properties inferred from both DNA and facial shape, which are sex, age, BMI, and GB. Since we match different identifiers (faces and DNA), the accuracies are expected to be inferior compared to DNA profiling where DNA is matched to DNA. Moreover, it is important to note that the properties that make up the intermediate embedding space are known as soft biometrics, meaning that they do not carry sufficient information for identification purposes. However, these soft traits can improve biometric performance if combined or accompanied by primary identifiers.

The results in this extension are evaluated in both biometric verification and identification scenarios. Biometric verification is a one-to-one comparison, which evaluates whether a given combination of an embedding and a property is either a match or a no-match, by testing the matching score against a threshold. The results are shown on a receiver operator characteristic (ROC) curve, which plots the true positive (TP) rate against the false positive (FP) rate for decreasing threshold. A large area under the curve (AUC) and low equal error rate (EER) indicate better performance. Sensitivity is the probability that a positive example is correctly classified as positive, and the specificity indicates the chances of correctly denying a negative example. Biometric identification is a one-to-many comparison, which retrieves an ordered list of individuals based on the matching scores. The results are shown on a cumulative match characteristic (CMC) curve, which plots the probability of observing the correct identity in the top k-ranks.

Table I provides the EER and the AUC for verification, and Rank 1%, 10%, and 20% performance for identification. The individual curves for all experiments can be found in Suppl. 1. In a first instance, we observe a significant impact of analyzing the localized facial segments for both PCA and the GML. The comparison between experiments iii and iv confirms that the part-based extension improves the metric learner proposed in [3]. Moreover, comparing experiment iv to the best performing approach of [3] (Suppl. 2b) shows that a part-based GML combined with a linear fuser generates a stronger biometric system than a full face GML followed by neural fusion. Additionally, the results for experiment iv are generally better than those for experiment ii, which reflects the methodology of [2]. This finding is consistent with that of [3] where it was shown that a supervised metric learner outperforms linear PCA for the encoding of facial shapes in a biometric setting. Fig. 6 (right) illustrates that both the use of a GML and the addition of localized facial segments contribute to stronger biometric systems and that the combination of the two yields the best results. This can be seen from the ROC curves which are pushed up- and leftwards, indicating increased sensitivity and specificity, and the CMC curves which show a similar trend. As expected, the overall performance increases by combining multiple properties together (Fig. 6, left). Further research should be undertaken to investigate the addition of other properties, as they could lead to even stronger biometric systems. Possible examples of such properties are iris texture [48], independent genetic loci affecting facial shape [2], or texture driven attributes such as hair, skin and eye color. Furthermore, the current GML requires topologically normalized 3D mesh data. This is a limitation for future studies which can be addressed by exploring alternatives for learning from random 3D point clouds instead. However, we do anticipate that larger datasets will be necessary to deal with the added data variability and complexity.

TABLE I.

Results of Identification and Verification Tests After 10-Fold Cross Validation.

			Sex	Age	BMI	GB	Sex + Age	Sex + Age + BMI	Sex + Age + BMI + GB
(i)	Ver.	EER	.37 ±.01	.43 ± .02	.40 ± .02	.33 ± .01	.33 ± .02	.30 ± .02	.21 ± .01
		AUC	.70 ± .02	.61 ± .01	.63 ± .01	.74 ± .02	.74 ± .02	.77 ± .01	.86 ± .01
	Iden.	Rl(%)	2 ± 00	3 ± 01	2 ± 01	4 ± 01	4 ± 01	7 ± 01	13 ± 02
		R10(%)	19 ± 00	21 ± 01	22 ± 02	30 ± 03	31 ± 02	42 ± 02	62 ± 03
		R20(%)	39 ± 00	37 ± 02	38 ± 02	51 ± 04	54 ± 03	64 ± 03	83 ± 03
(ii)	Ver.	EER	.37 ± .01	.39 ± .01	.40 ± .01	.31 ± .01	.29 ± .01	.26 ± .01	.17 ± .01
		AUC	.71 ± .01	.66 ± .01	.64 ± .02	.77 ± .02	.78 ± .01	.81 ± .01	.90 ± .01
	Iden.	Rl(%)	2 ± 00	3 ± 01	3 ± 01	4 ± 01	5 ± 01	8 ± 02	17 ± 02
		R10(%)	20 ± 00	25 ± 04	21 ± 03	35 ± 02	36 ± 03	49 ± 03	73 ± 03
		R20(%)	39 ± 01	43 ± 03	38 ± 02	55 ± 04	60 ± 03	72 ± 02	91 ± 02
(iii)	Ver.	EER	.37 ±.01	.37 ± .01	.39 ± .01	.36 ± .01	.27 ± .01	.24 ± .01	.17 ± .01
		AUC	.71 ± .01	.69 ± .01	.65 ± .01	.72 ± .01	.81 ± .01	.83 ± .01	.89 ± .01
	Iden.	Rl(%)	2 ± 00	3 ± 01	2 ± 01	3 ± 01	5 ± 01	10 ± 02	17 ± 02
		R10(%)	20 ± 00	29 ± 01	23 ± 03	30 ± 03	40 ± 02	54 ± 02	75 ± 02
		R20(%)	40 ± 00	48 ± 04	42 ± 04	50 ± 03	64 ± 02	77 ± 02	92 ± 02
(iv)	Ver.	EER	.36 ± .01	.36 ± .01	.37 ± .01	.32 ± .01	.26 ± .01	.22 ± .01	.14 ± .01
		AUC	.71 ± .01	.71 ± .02	.67 ± .01	.76 ± .01	.82 ± .01	.85 ± .01	.92 ± .01
	Iden.	Rl(%)	2 ± 00	4 ± 01	3 ± 01	4 ± 01	6 ± 01	11 ± 01	21 ± 02
		R10(%)	20 ± 00	29 ± 05	25 ± 03	35 ± 03	42 ± 03	57 ± 02	79 ± 03
		R20(%)	39 ± 00	48 ± 04	43 ± 04	54 ± 03	66 ± 02	79 ± 02	94 ± 02

Mean ± standard deviation of area under the curve (AUC) and equal error rate (EER) for verification (ver.) and k-rank (Rk) identification (iden.) for each of the experiments: (i) full face PCA, (ii) part-based PCA [2], (iii) full face GML [3], and (iv) part-based GML.

Fig. 6.

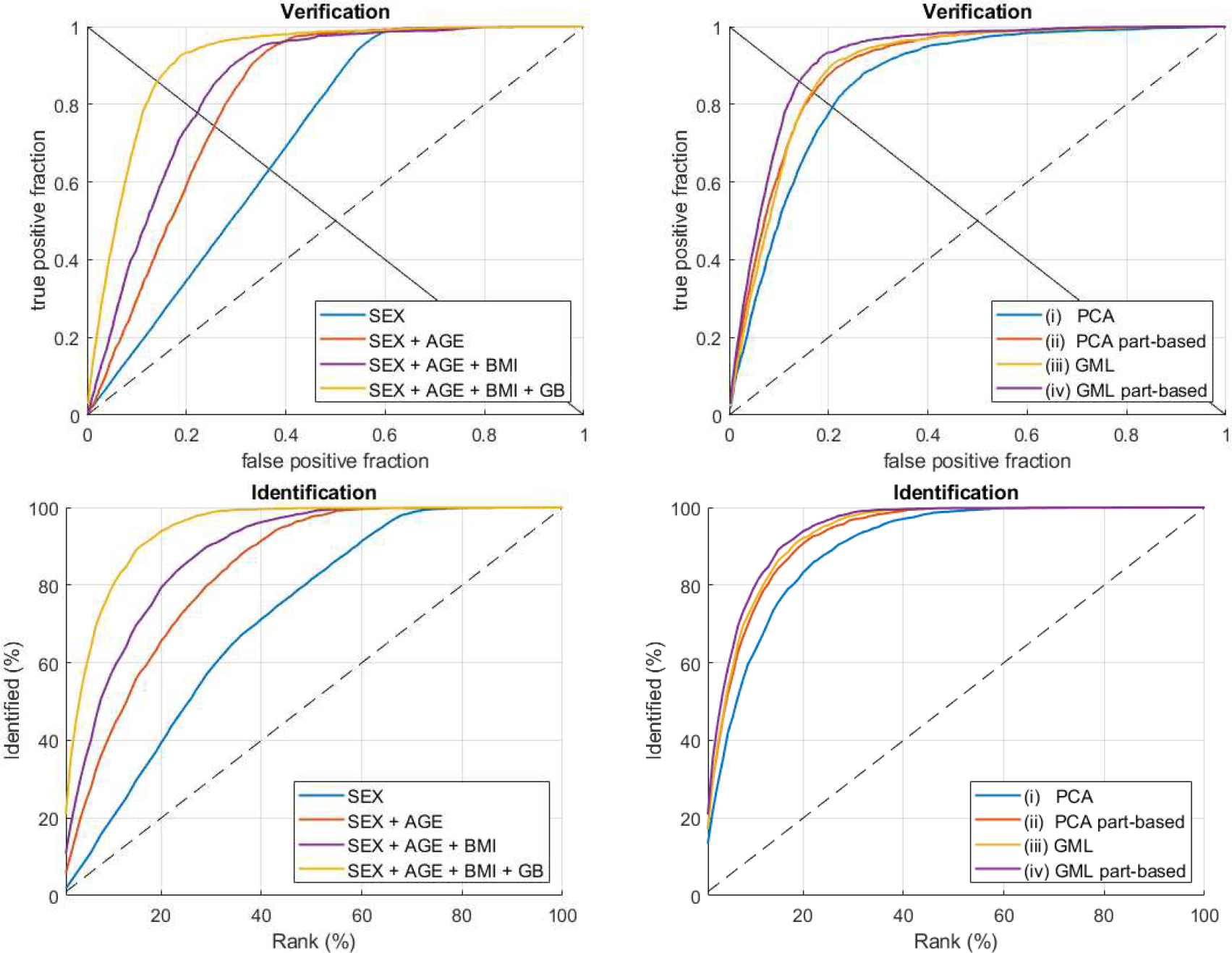
Verification and identification curves for (left) the part-based geometric metric learner (iv) for an increasing number of properties injected into the system, and (right) the cumulative biometric system for the four different experiments.

V. CONCLUSION

This paper proposed a neural network that can be used for matching 3D facial shapes to demographic properties. The network is a metric learner which extracts important facial information with regard to the properties of interest. The metric learner is implemented using geometric deep learning techniques, deploying spiral convolutions in combination with an equidistant mesh sampling. The main contribution of this paper is the use of a hierarchical segmentation of the face to train part-based metric learners and combine global and local analysis of the face. Using a part-based scheme, localized information of the face is forcefully injected into the model by multiple modular encoders. This means that localized shape variation, that might be lost in the context of the full face, remains available. The proposed part-based model is followed by an SVM classifier and a naive Bayes score fuser. The resulting model was evaluated in biometric verification and identification scenarios. The results show that both the metric learner and the part-based approach contribute to create a stronger biometric system.

Biographies

Nele Nauwelaers obtained a master’s degree in Mathematical engineering at KU Leuven in 2018. After her studies she started a PhD at the Medical Imaging Research Center located at the university hospital. In her research she applies state-of-the-art geometric deep learning techniques to shapes represented on 3D meshes, with a highlighted interest in applications that exploit the relationship between facial shape and human genetics.

Soha Mahdi received a M.S. in Artificial Intelligence from KU Leuven, Belgium, where she is currently a PhD student. Her research includes computer-aided diagnosis of genetic syndromes, and more specifically applications of geometric deep learning in analysing craniofacial malformations associated with genetic syndromes.

Philip Joris received his bachelor’s degree in Electronics and ICT Engineering Technology in 2011 from Artesis Antwerp, Belgium. He then completed an internship at the Fraunhofer Institute for Integrated Circuits in Nuremberg, Germany, and received his master’s degree in Electronics and ICT Engineering Technology in 2012 from Artesis Antwerp. In 2013, he received the master’s degree in Artificial Intelligence from KU Leuven, Belgium. In 2018, he received the degree of Doctor of Engineering Science in Electrical Engineering from KU Leuven, focusing on Forensic Image Computing methods. Most recently, he received a research grant at KU Leuven, allowing him to further advance his research on Forensic Image Computing methods.

Shunwang Gong is currently a PhD student and Research Assistant at the Department of Computing, Imperial College London. Previously, he received the M.Sc. degree in advanced computing from Imperial College London, U.K., in 2018 and was awarded the distinguished project. His research interests lie in graph neural networks, 3D computer vision, generative models and machine learning.

Giorgos Bouritsas received his MEng Diploma in Electrical and Computer Engineering from the National Technical University of Athens (NTUA) in 2017. Since 2018, he is a PhD student in Machine Learning at the Department of Computing, Imperial College London. His current research interests lie in the intersection of machine learning with graph theory and network science. He is primarily focused on the theoretical underpinnings of graph neural networks, on deep probabilistic models for graph generation and compression, as well as on relevant applications to network analysis, bioinformatics and computer vision.

Susan Walsh received a MSc. in DNA profiling from University of Central Lancashire in the UK in 2006 and a Ph.D. in Forensic Genetics from Erasmus University in the Netherlands in 2013. She is now an Associate Professor of Biology at Indiana-University-Purdue-University-Indianapolis (IUPUI), IN, USA, where her laboratory focuses on understanding the genetics of human physical appearance and its prediction from DNA. She is a member of the International Society for Forensic Genetics (ISFG) and the American Academy of Forensic Sciences (AAFS).

Mark D. Shriver graduated from the School of Biomedical Sciences, University of Texas Health Science Center at Houston in 1993. He is now a professor of Anthropology and Genetics at the department of Anthropology, Penn State University, Pennsylvania. His major research interests include human population genomics and the perception of genetic ancestry and sex in faces.

Michael Bronstein received his PhD from the Technion in 2007. In 2018, he joined the Department of Computing of Imperial College, London as Professor. He has also served as a professor at USI Lugano, Switzerland since 2010 and held visiting positions at Stanford, Harvard, MIT, TUM, and Tel Aviv University. His main expertise is in theoretical and computational geometric methods for machine learning and data science.

Peter Claes graduated in 2002 at the KU Leuven, department of Electrical engineering (ESAT), with a major in multimedia and signal processing. In 2007, he obtained a PhD in engineering, at the KU Leuven. He continued into a postdoc at the Melbourne Dental School, University of Melbourne from 2007 until 2011. In 2018, he was a visiting scholar at the University of Oxford at the Biomedical Engineering Department, UK. Since 2014, He is an honorary research fellow at the Murdoch Children’s Research Institute, Melbourne, Australia. Since October 2019, he is a research associate professor in a joint appointment at the department of ESAT-PSI and the department of Human Genetics.