Value-free reinforcement learning: policy optimization as a minimal model of operant behavior

Abstract

Reinforcement learning is a powerful framework for modelling the cognitive and neural substrates of learning and decision making. Contemporary research in cognitive neuroscience and neuroeconomics typically uses value-based reinforcement-learning models, which assume that decision-makers choose by comparing learned values for different actions. However, another possibility is suggested by a simpler family of models, called policy-gradient reinforcement learning. Policy-gradient models learn by optimizing a behavioral policy directly, without the intermediate step of value-learning. Here we review recent behavioral and neural findings that are more parsimoniously explained by policy-gradient models than by value-based models. We conclude that, despite the ubiquity of ‘value’ in reinforcement-learning models of decision making, policy-gradient models provide a lightweight and compelling alternative model of operant behavior.

1. Introduction

What is value? In spite of the ubiquity of this term in the field of value-based decision making, there are a number of different ways of defining value, and one’s chosen definition has important implications for the kinds of inferences that one is likely to draw about the cognitive and neural processes that subserve operant behavior [1, 2, 3, 4, 5].

In typical usage, ‘value’ is an explanatory variable that quantifies the degree to which an individual prefers (or is willing to work for) one good or outcome over others [6, 7]. So, for instance, a child who consistently chooses a chocolate bar over fresh fruit would be said to value chocolate more highly. Value—as typically defined—is therefore a latent construct that scaffolds choice behavior by providing a common currency for comparison of different actions (often loosely identified with the similar economic concept of utility [8, 9]). In support of the hypothesis that choice behavior is supported by the computation of value, proponents frequently note (e.g., [10]) that reward-related dopaminergic neural activity is consistent with a class of value-learning algorithms from the field of reinforcement learning (RL) [11, 12]. This argument implicitly assumes that different theoretical frameworks each use the term ‘value’ in the same way. However, there are important differences between typical usage of ‘value’ and value as defined in RL.

In RL, value is defined as expected cumulative future reward [13] (see Box 1). As such, an action’s value in RL is not merely a relative quantification of preference, as in the typical usage of ‘value’; instead, it exactly quantifies the total amount of future reward¹ that an agent expects to receive if it takes that action. At first glance, this definition of value appears consonant with typical usage, since it seems reasonable that one should prefer actions with greater expected cumulative future reward. Crucially, however, although in RL differences in learned value between two actions do indeed entail differences in choice behavior, the converse is not true. That is, we may observe differences in an individual’s preference for different actions despite the agent not having learned different values (in the RL sense) for those actions. This is because there is an entire separate branch of RL algorithms—policy-gradient RL—in which agents learn to choose actions by optimizing a behavioral policy directly, without ever taking the intermediate step of learning their values [14].

Box 1: Glossary of Reinforcement-Learning Terms.

Policy: a function, often denoted π, that specifies a probability distribution over actions given the agent’s current state. Actions are sampled from the policy at the time of choice. A policy is an essential component of all RL algorithms—including value-based RL algorithms, which must specify a policy-mapping function (see below) that computes a policy given a set of action-values.

Value: expected discounted cumulative future reward. In value-based RL, values can be defined both for states (V^π(s): the expected future reward associated with being in state s and choosing actions according to the policy π) and actions (Q^π(s, a): the expected future reward associated with taking action a in state s, and choosing actions according to the policy π thereafter).

Policy-mapping function: a function that specifies choice probabilities for a set of actions given their estimated values, in value-based RL algorithms. Also known as a ‘choice rule’. Examples include arg max, ϵ-greedy, and softmax.

• arg max: a policy-mapping function that deterministically selects the action with the highest estimated value

• ϵ-greedy: a policy mapping function that selects either the action with the highest estimated value (with probability 1 − ϵ) or a random action (with probability ϵ)

• softmax: a policy-mapping function that stochastically selects actions with a probability that increases based on their estimated value relative to the values of alternative options:

  $$\pi (a)=\frac{e^{\beta \cdot Q^{\pi }(s,a)}}{{\sum }_{\widehat{a}\in A}{e}^{\beta \cdot Q^{\pi }(s,\widehat{a})}}$$ (1)

  The degree of stochasticity in this mapping is controlled by the inverse temperature parameter β, such that all actions are equally likely when β = 0 and the softmax function becomes the arg max function as β → ∞

Policy gradient: For RL algorithms that use a parameterized policy, the policy gradient is a vector that indicates how much extra reward the agent expects to receive if it made an incremental change to each of the parameters of its policy (technically, the gradient is the vector of partial derivatives of the expected reward function with respect to policy parameters). The gradient of a policy is the key variable estimated (or approximated) by policy-gradient RL algorithms, and is used to adjust the parameters of the policy in the direction in which expected reward is expected to increase most steeply. For this reason, policy-gradient algorithms must use a policy that is everywhere differentiable with respect to its parameters.

Here we give an introduction to the distinction between value-based and policy-gradient RL (also termed ‘indirect’ and ‘direct’ actors, respectively [15]), and review recent work suggesting that policy-gradient RL provides a good account of neural and behavioral data. We suggest that value (in the RL sense) is not strictly entailed by data from typical laboratory tasks, and propose that value need only be invoked as an explanatory latent construct for phenomena that cannot be accounted for under simpler algorithms like policy-gradient RL. This does not exclude the possibility that the brain does compute value in some circumstances; however, we would argue that policy-gradient RL models are generally favoured by the principle of parsimony, and that ‘value’ should only be added to these models to explain data that cannot be explained by policy-gradient models alone.

2. Value-based RL versus policy-gradient RL

Value-based RL is a prominent computational model of the cognitive processes subserving simple operant behavior and of the neural substrates of these processes (e.g., [16, 17, 18, 19]). Briefly, in a prototypical value-based RL model (Figure 1A), the agent learns the value of each of a set of discrete actions by trial-and-error, and chooses between actions by mapping these estimated values into a behavioral policy using a policy mapping function (see Box 1). As such, using a value-based RL model as a model of a subject’s behavior implicitly assumes that, at an algorithmic level of description, the subject learns action-values and makes choices by comparing them.

Figure 1:

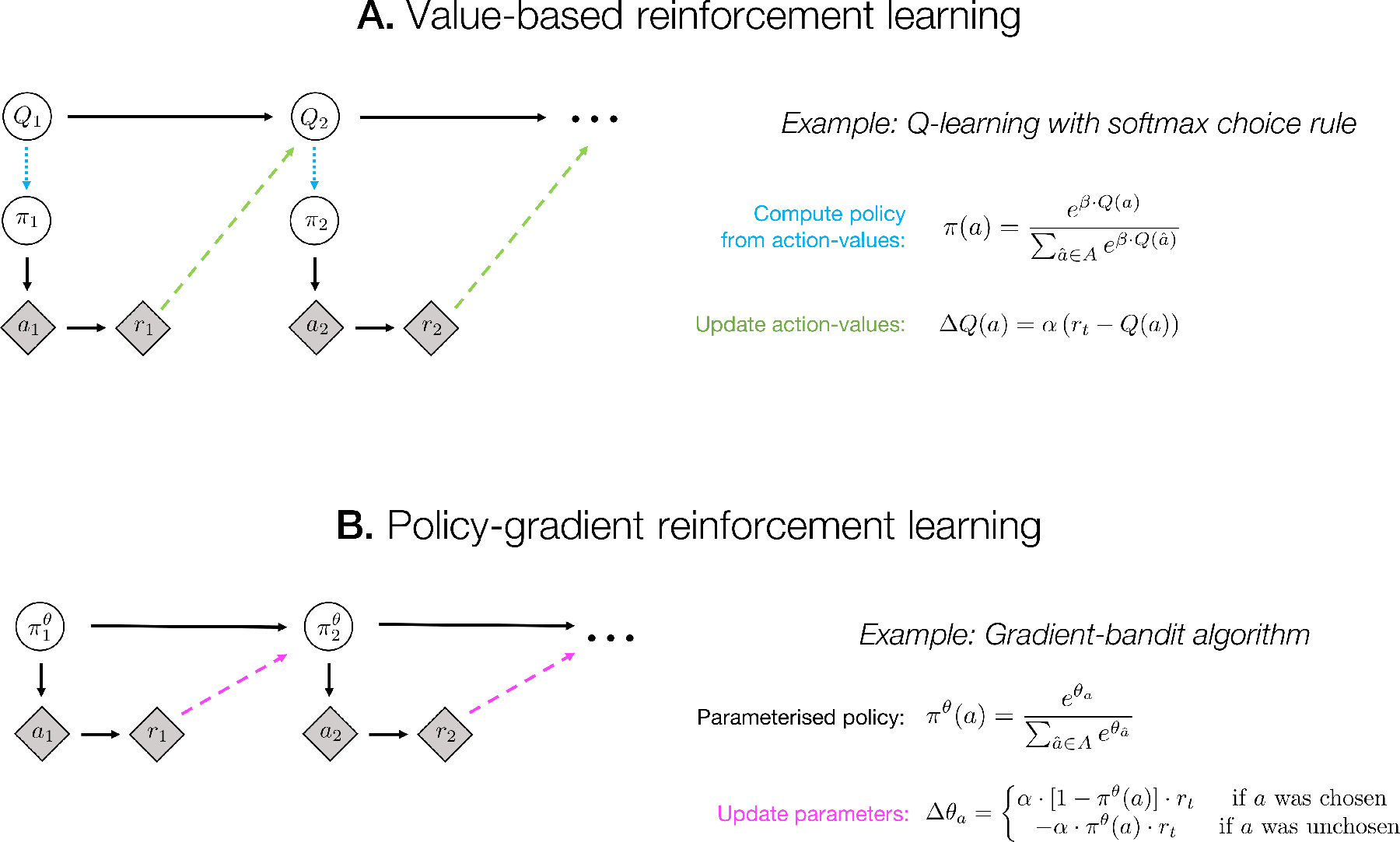
Update schematics for example value-based and policy-gradient RL algorithms. Shaded diamond nodes denote observable variables, unshaded circular nodes denote latent variables that are internal to the RL agent, and arrows denote dependencies. For simplicity, in these algorithms we do not show the environmental state, which would be an additional (potentially partially) observable variable. A: in a value-based RL algorithm (such as the Q-learning model presented here), actions (a, chosen from a discrete set A) are a product of the agent’s policy π, which in turn is determined (dotted cyan arrow) by the learned action-values (Q). The update rule for action-values (dashed green arrow) depends on the action-values and received reward (r) at the previous timestep, and only indirectly on the policy. This algorithm has two adjustable parameters: the learning rate α and the softmax inverse temperature β. B: a policy-gradient algorithm (such as the gradient-bandit algorithm presented here; see [13]) selects actions according to a parameterised policy π^θ, and updates the parameters θ of this policy directly (dashed magenta arrow; in the gradient-bandit algorithm, θ is a vector of action preferences), without the intermediate step of learning action-values. In the policy-gradient algorithm, by contrast with the value-based algorithm, the size of the update to θ depends more directly on the current policy, since the size of the update to each action preference is scaled by the probability of that action under the policy.

According to the principle of parsimony, however, in modelling subjects’ behavior we should attempt to find the model that best explains the data while minimizing model complexity (i.e., invoking as few latent explanatory constructs as possible) [20]. This raises the question: do value-based models provide the simplest RL account of behavior, or can simpler models (such as policy-gradient RL; Figure 1B) account for behavior equally well?

In a policy-gradient algorithm, the agent chooses actions according to a parameterized policy, observes the outcomes of these actions, and then adjusts the parameters of its policy so as to increase the probability of actions associated with more reward and decrease the probability of actions associated with less reward (i.e., it adjusts the parameters of its policy according to the gradient² of reward with respect to the parameters of its policy). Rather than the indirect algorithm of value-based RL (learning the values of different actions, and acting by mapping these values into a policy), policy-gradient RL is a conceptually simpler algorithm that directly adjusts the policy without troubling with the intermediate latent construct of value. Consequently, policy-gradient RL is also simpler than value-based RL in implementation as a cognitive model: in its simplest form, policy-gradient RL requires one adjustable parameter per participant (a learning rate for updates to the policy parameters), compared to two adjustable parameters for the simplest form of value-based RL (a learning rate for value updates, plus a policy mapping parameter such as the softmax inverse temperature β)³.

In the simplest choice setting, where a subject repeatedly chooses between a fixed set of actions in a single environmental state, policy-gradient RL algorithms can, in principle, explain behavior as well as value-based RL algorithms. For instance, the gradient-bandit algorithm described by Sutton and Barto [13] (based on the REINFORCE algorithm of Williams [23]) uses a softmax policy parameterized by a vector of preferences for different actions. These preferences are reminiscent of values, but unlike values they are not interpretable as expected discounted future reward; instead, as policy parameters, they directly determine choice probabilities. For instance, consider a state with three actions associated with reward magnitudes of 1 unit, 9 units, and 10 units, respectively. A gradient-bandit agent that learns an optimal policy will show a low preference for the second-best (9-unit) option relative to the best (10-unit) option, in spite of the fact that the values of these two actions are relatively similar. As such, value-based and policy-gradient RL have different representations of actions in the environment: whereas value-based algorithms maintain a representation the expected future reward of different actions, policy-gradient algorithms can be thought of as representing actions in terms of which should be taken and which should be avoided. This means that policy-gradient algorithms do not represent the reward amounts associated with different actions. In general, however, this sparser representation does not prevent a policy-gradient RL agent from learning to behave in a manner that maximises its expected future reward.

In more complex choice settings, the policy optimized by the RL agent need not be parameterized by preferences. In environments with a continuous one-dimensional action space, for instance, actions might be selected according to a Gaussian policy (e.g., [24]); in such a case, the parameters of the agent’s policy would control the mean and variance of the probability distribution over actions that is produced by the policy.

3. Behavioral and neural evidence for policy-gradient RL

The greater parsimony of policy-gradient RL is one reason to prefer it over value-based RL as a model of simple operant behavior. A second reason is that, in some decision-making tasks, policy-gradient methods provide a good account of behavioral and neural data that are more difficult to explain with value-based RL models.

3.1. Behavioral evidence for policy-gradient RL

Two behavioral phenomena better explained by policy-gradient RL than value-based RL are context-dependent preference learning and continuous-action learning.

Context-dependent preference learning.

When given a choice between two options with equivalent reinforcement histories, but where one option was learned in a rich environmental context (high reward availability) and the other was learned in a lean context (low reward availability), humans and other animals display a marked preference for the lean-context option [25, 26, 27, 28]. That is, animals’ learned preferences between different options are a function not only of each option’s reinforcement history, but also of the environmental context within which each option was experienced. Since action-values in value-based RL are defined cardinally as expected cumulative future reward conditional on taking an action (i.e., action-values are not contextually modulated by the value of their associated environmental state), this phenomenon is difficult to account for using value-based RL models absent additional post-hoc assumptions regarding the reward function (e.g., [28]).

By contrast, context-dependent preference learning emerges straightforwardly from the principles of policy-gradient RL. In a gradient-bandit algorithm, for instance, because the goal of the agent is to update action-preferences to optimize its policy (rather than to learn action-values), learned preferences for each action are solely a function of whether taking an action within its environmental state will lead to maximization of future reward. As such, a gradient-bandit agent will learn positive preferences for actions that are the best available in a state (i.e., actions that should be taken when possible), and learn negative preferences for actions that are the worst available in a state (i.e., actions that should be avoided). If, after learning, the agent is given a choice between the worst action from a rich state versus the best option from a lean state, it will tend to prefer the lean-state action (because of its positive learned preference as the best action in its state) over the rich-state action (because of its negative learned preference as the worst action in its state), even if the reinforcement histories of the two actions are identical.

Continuous-action learning.

In natural environments, behavior frequently involves selecting actions from a continuous action space (e.g., controlling a mouse cursor, or driving a car; see [29]). Standard value-based RL models like Q-learning typically perform poorly in such environments, because they operate over a tabular representation of actions in which all actions are equally (dis)similar to one another. This tabular representation leads to inefficient learning in continuous action spaces, since the algorithm cannot generalize between similar actions (e.g., steering a car 10 degrees left is similar to steering 11 degrees left, but dissimilar from steering 40 degrees right). Although there exist continuous extensions of value-based RL involving value-function approximation (e.g., [30]), these approaches have historically focused on continuous state spaces rather than continuous action spaces. Applying value-function approximation to continuous action spaces is not straightforward, because actions need not only be evaluated, but also sampled according to their estimated value. This implies estimation of the whole function (we need evaluate only the current state, but to select an action we need to evaluate all possible actions), which, even for simple choice rules such as those considered here, is computationally intractable for most value-function approximators [31].

By contrast, since policy-gradient methods optimise an overall policy, rather than learning the values of a number of distinct actions, policy-gradient RL algorithms are straightforwardly applicable to continuous action spaces, providing that the functional form of the policy can be sampled from (e.g., a two-parameter gamma distribution for reaction time choices; [32]). In learning a continuous action space, a policy-gradient RL agent will respond to the reinforcement of an action by adjusting the policy such as to increase the choice probability not only of the chosen action, but also of similar actions. This leads to efficient generalization of learning across continuous action spaces.

In line with this proposal, recent research in the field of motor control has suggested that online recalibration processes for motor execution are well-explained by direct updating of an implicit behavioral policy [33, 34]. For instance, a recent study by Hadjiosif et al. [35] used mirror-reversed visual feedback in a sensorimotor adaptation task, and found that subjects’ patterns of post-reversal errors were well explained by a model in which an implicit behavioral policy was updated according to a sensory prediction error. As such, policy-gradient RL also represents a point of contact between models of simple operant behavior and models of higher-order motor control. Indeed, even apparently simple operant behaviours such as discrete choice can also be conceptualized as involving continuous actions if we consider that the latency and vigour of these choices constitute a continuously-distributed action space [32].

3.2. Neural evidence for policy-gradient RL

Sensory and action components of midbrain dopamine responses.

Phasic bursts from midbrian dopamine (DA) neurons have been proposed as a neural correlate of the reward prediction error (RPE) signal central to RL theories [36, 11, 37, 38]. This hypothesis regarding the role of dopamine stands for policy-based RL as well. Indeed, the difference between value- and policy-based RL frameworks lies not in the dependence on an RPE, but in what kind of representation is updated by this teaching signal. Decades of evidence in classical conditioning tasks have demonstrated phasic DA responses to sensory stimuli that predict the delivery of a reward, consistent with the learning of a‘subjective value’ for the predictive stimulus. However, in instrumental settings, DA activity (both phasic and tonic) has also been associated with movement signaling and control: phasic responses in dorsal-striatum-projecting DA neurons can trigger locomotion [39], and movement initiation and response vigor are bidirectionally modulated by transient activity in DA neurons in the substantia nigra pars compacta [40].

Action dependence of DA activity is not restricted to the substantia nigra; ventral tegmental area DA responses are attenuated unless the correct movement is initiated in an operant go/no-go task [41]. More recently, close inspection of DA responses during very early learning in a classical conditioning task show that the timing of the initiation of licking accounts for phasic DA response to rewards at this stage, before more stereotypical sensory components of the RPE signal have emerged [42]. These results suggest that representations of action are, at least in these settings, central to the formation and update of reward predictions. That is, neural reward predictions in dopaminergic circuits appear to be deeply intertwined with neural representations of actions themselves. This stands in contrast with simple value-based RL models, where the learned values of actions are represented separately and only transformed into a policy as needed at the time of choice (top panel, Figure 1).

Neural signatures of policy learning.

The basal ganglia are a central locus in the brain for the initiation and control of movement [43]. Accordingly, much of the evidence for policy learning in the brain hinges on the interpretation of neural activity in the striatum during various instrumental tasks. Representations associated with action-values have been reported in striatal regions [19, 44, 45]; however, unambiguous identification of these activity patterns as value signals rather than action preferences or other related constructs is complicated by the presence of temporal correlations in neural activity recorded from different brain regions [46].

Distinguishing value representations from other arbiters of preference, such as policy, suffers also from the confound that these quantities are correlated in almost all learning models. In fact, specific considerations in task design are necessary to establish the condition in which predictions from value- and policy-based accounts of learning can be disambiguated: policy-based methods predict updates to all (within-context) action probabilities subsequent to the outcome of a single action, leading to a fundamentally relative representation of action preference. Indeed, in a task in which information about the outcome of forgone as well as chosen options is provided, the BOLD signal in the striatum was consistent with a policy-update signal, rather than an action-value update [47]. Neural correlates of context-dependent effects in choice implicate the medial prefrontal cortex and ventral striatum in the relative update of preferences [28], while dopaminergic error-signals related to counterfactual outcomes have been identified in human striatum [48]. These findings speak to interactions between chosen and non-chosen options that are the hallmark of policy-based RL, and suggest such learning recruits the same neural regions and mechanisms that have previously been closely identified with value-based learning in the brain.

4. The intersection of value and policy

In the preceding sections, we have drawn a sharp contrast between value-based and policy-gradient RL. However, this is a false dichotomy, since an entire class of algorithms—actor-critic RL—marries value-based and policy-gradient RL. Although we have not discussed these algorithms here, they form the basis of much state-of-the-art work in computer science applications of reinforcement learning [49, 50, 51], alongside other methods that incorporate components of both value-based and policy-gradient RL (e.g., [52, 53]). In the domain of behavioral science, actor-critic RL has shown great promise as a model of diverse phenomena—including conditioned avoidance, matching behavior in response to variable-interval reinforcement, and mood [54, 55, 56]—that are not readily accounted for by either value-based or policy-gradient models alone. In neuroscience, similarly, it has been suggested that dopaminergic neural activity in the basal ganglia is accounted for well by actor-critic models [57, 58]. As such, actor-critic RL represents a potentially fruitful avenue for developing a general model of operant behavior that may resolve the tensions between value-based and policy-gradient RL that we have reviewed here.

More broadly, our advocating for policy-gradient RL as a minimal model of learning in operant settings does not preclude the possibility that more nuanced representations of outcomes—and even value as defined in RL—are recruited in various behavioral tasks. To be clear, there exist a number of phenomena that appear better explained by value-based and model-based RL models than by policy-gradient RL alone. For instance, reward expectations are clearly formed and exploited in classical conditioning [59, 60, 61], outcome devaluation procedures, suggest that a specific expectation of future outcomes is formed and used to guide choice in an adaptive manner [62], and sensory preconditioning studies show that conditioning can result in the formation of associations between different stimuli, and not only between stimuli and responses or stimuli and rewards [63]. Indeed, theories of model-based learning and decision making rely on specifying the precise interaction between states, values and policies to account for flexible behavior in uncertain and dynamic environments [64, 65]. Once again, our argument is not that the brain only ever uses policy-gradient RL; rather, we suggest that, in modelling data, policy-gradient models should typically be favoured in the interests of parsimony, and that the latent construct of value should only be invoked to explain phenomena that are not explicable under this simpler model.

Finally, part of the disjunction between value-based and policy-based RL theories of behavior derives from the historical delineation between operant and classical conditioning paradigms, with the former assumed to pertain to policies for action, and the latter construed as a selective window on value learning. In general, however, the construct of policy is not restricted to discrete choice paradigms; indeed, any engagement in a situation that involves motivationally relevant outcomes will require some targeted regulation of movement, which implies the existence of a policy. More expansive consideration of policies that include continuous action spaces [29, 66], the withholding as well as execution of movements [67], and the inclusion of ‘internal’ actions such as the control of attentional focus [68, 69], naturally complicate the boundary between operant and classical conditioning, merging perspectives from policy- and value-learning into a more integrated whole.

Highlights.

• Reinforcement learning models can be divided into value-based and policy-gradient

• Policy-gradient RL gives a more parsimonious account of many operant behaviors

• These behaviors can therefore be explained without invoking the notion of ‘value’